Integrating PolSAR and Optical Data for Forest Aboveground Biomass Estimation with an Interpretable Bayesian-Optimized XGBoost Model
Abstract
1. Introduction
2. Materials and Methods
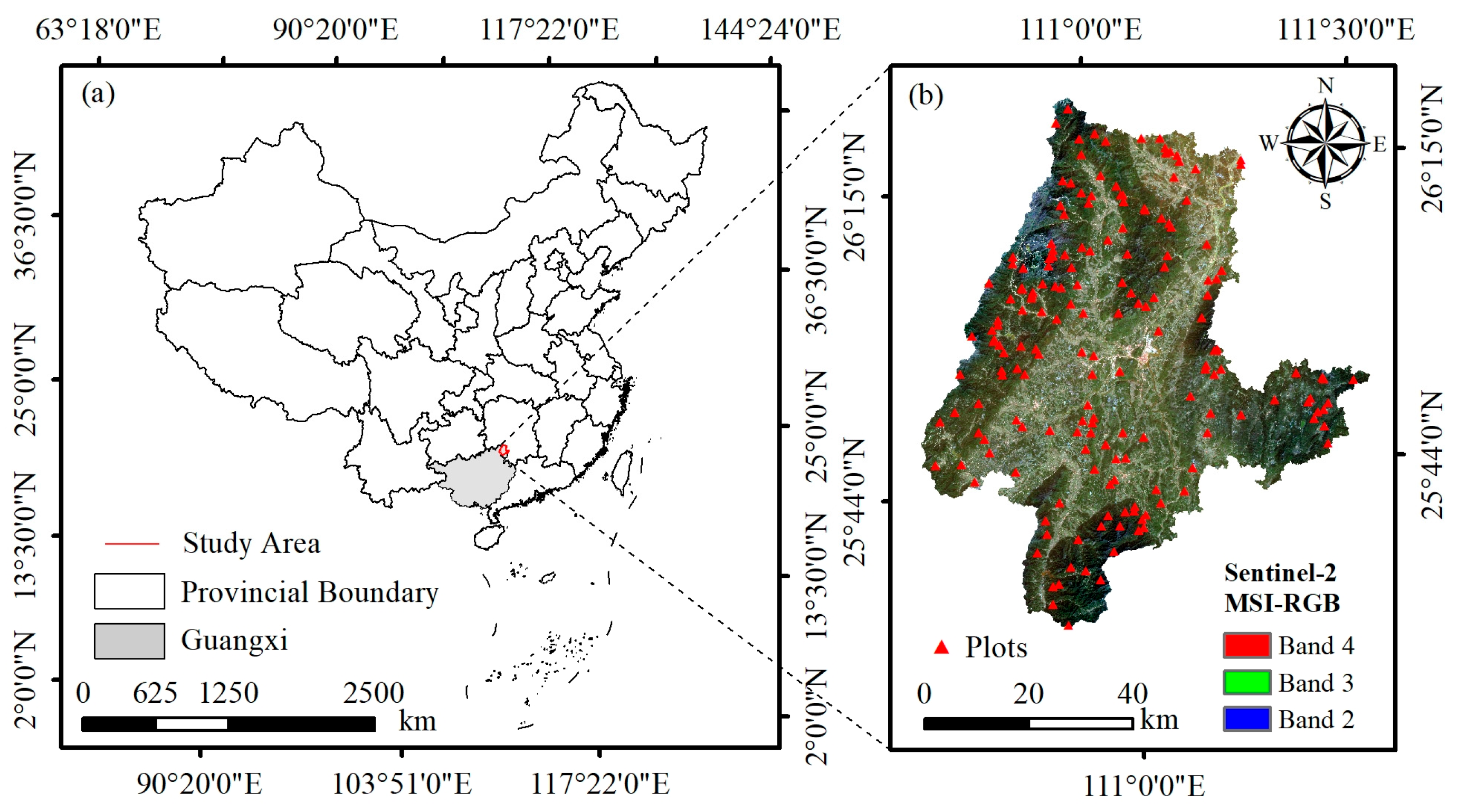
2.1. Study Area
2.2. Measured Forest AGB Data Processing
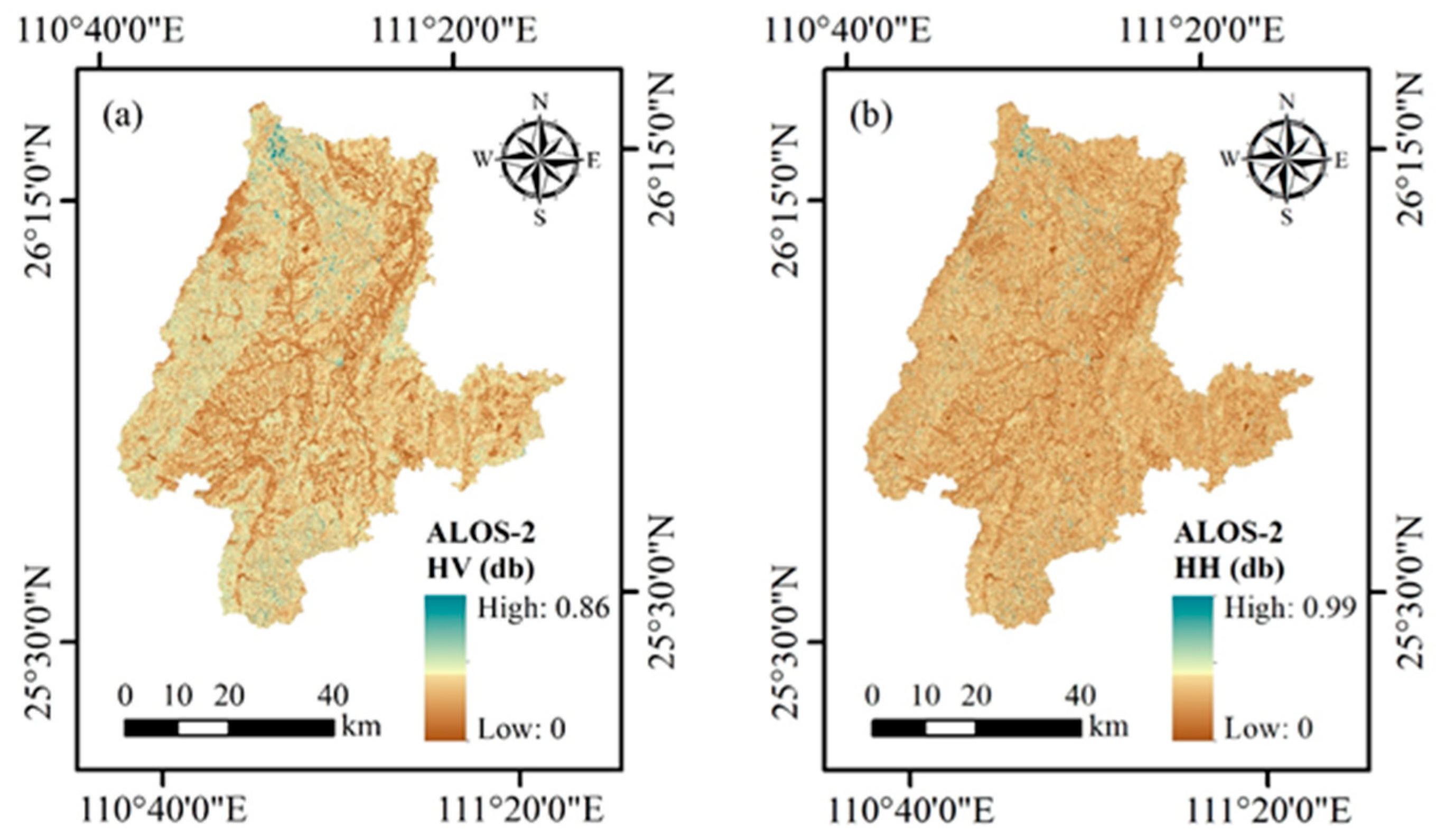
2.3. Remote-Sensing Data and Preprocessing
2.4. Feature Extraction and Selection
2.5. Model Construction and Evaluation
2.5.1. Nonparametric Models
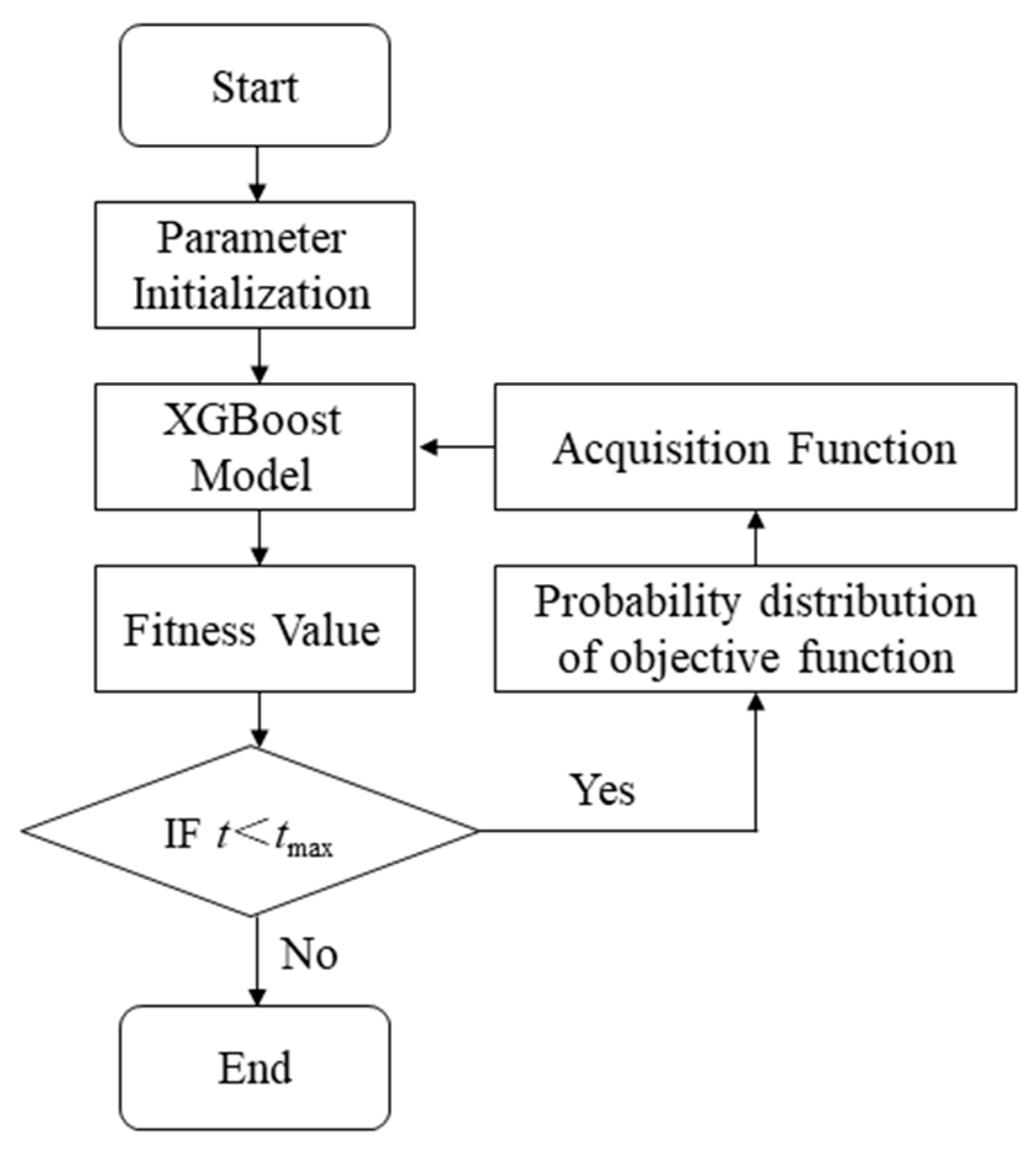
2.5.2. The Bayesian-Optimized XGBoost Model (BO-XGBoost)
2.5.3. Model Accuracy Assessment
3. Results
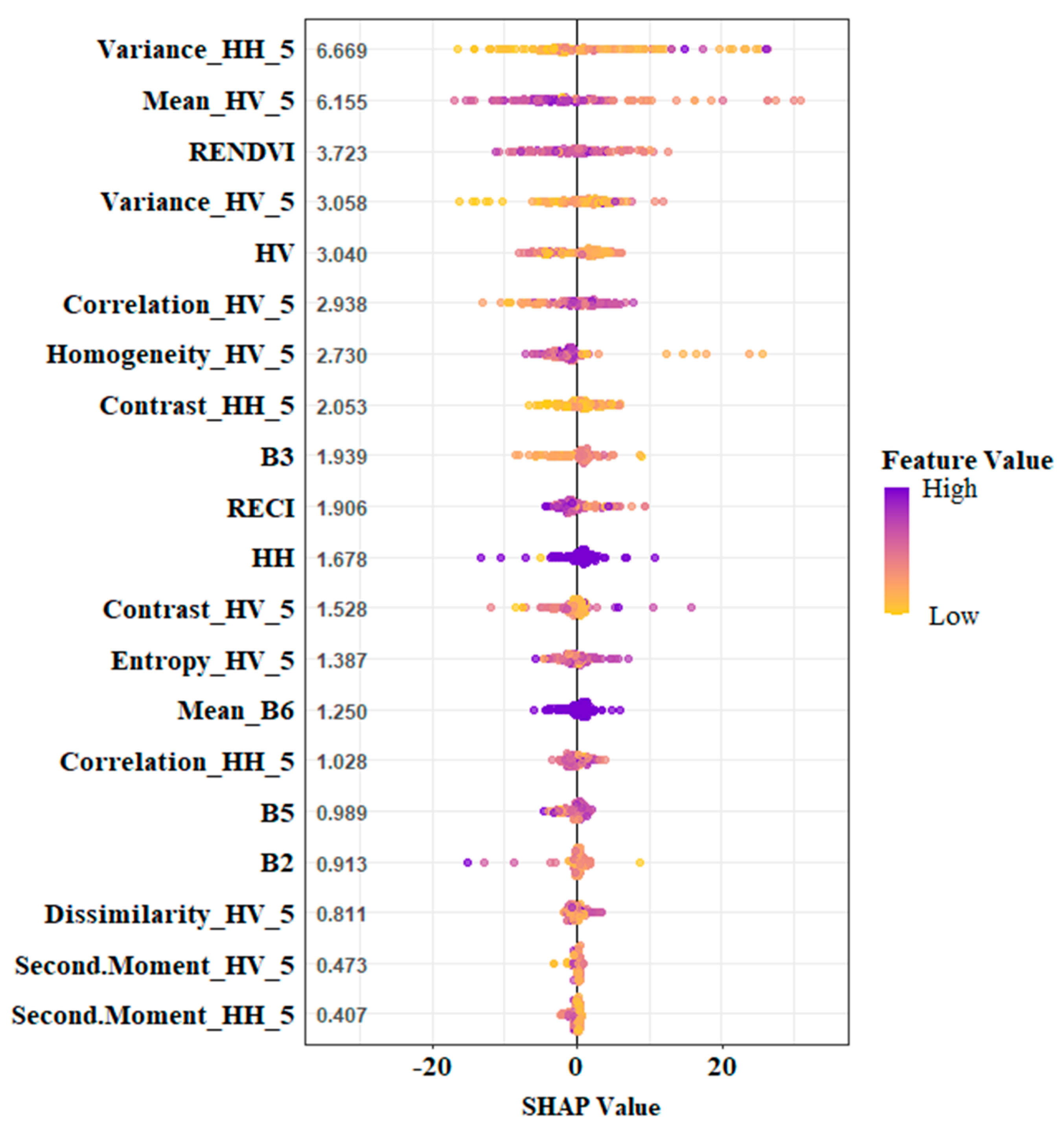
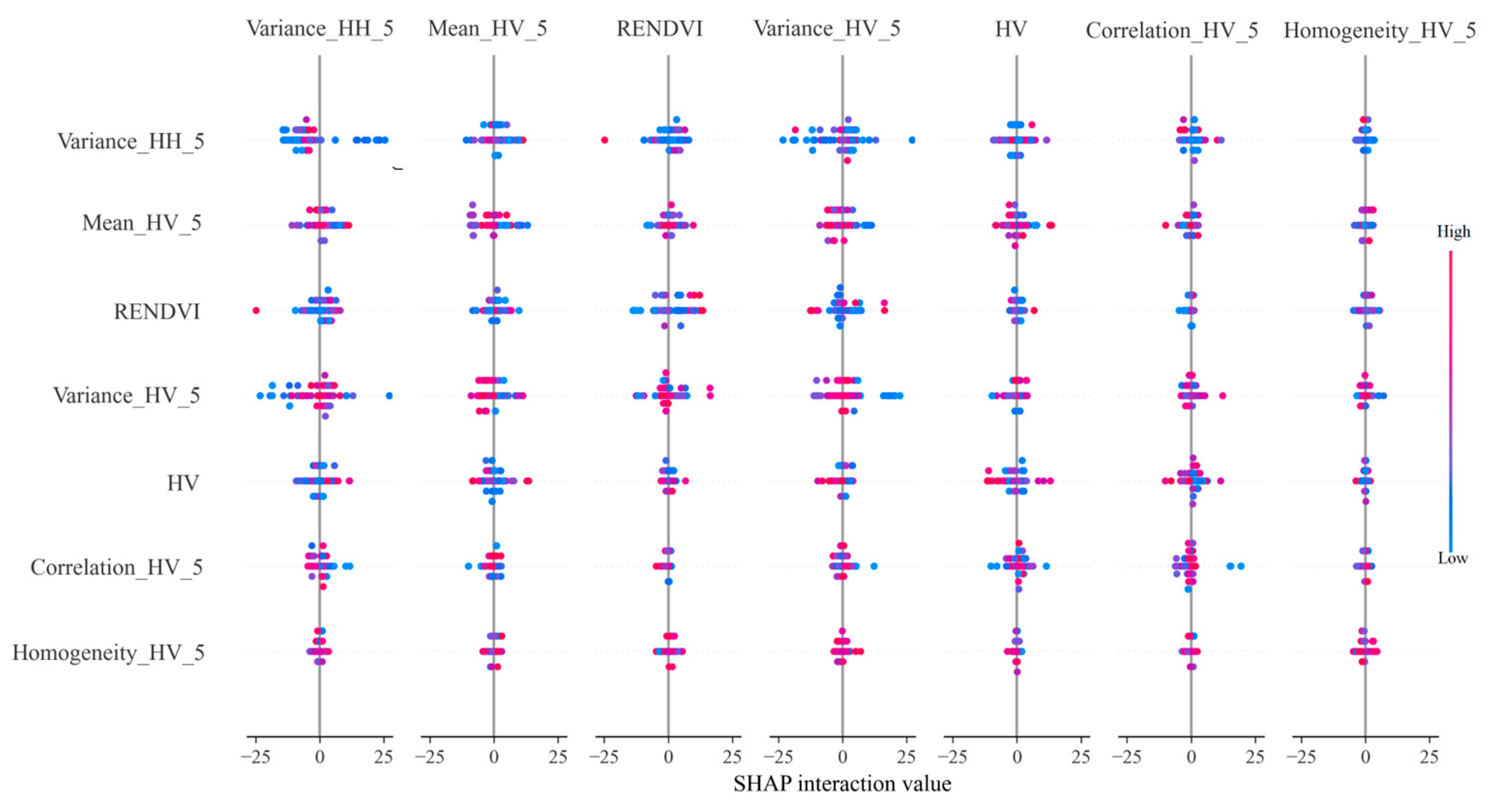
3.1. Feature Evaluation and Selection
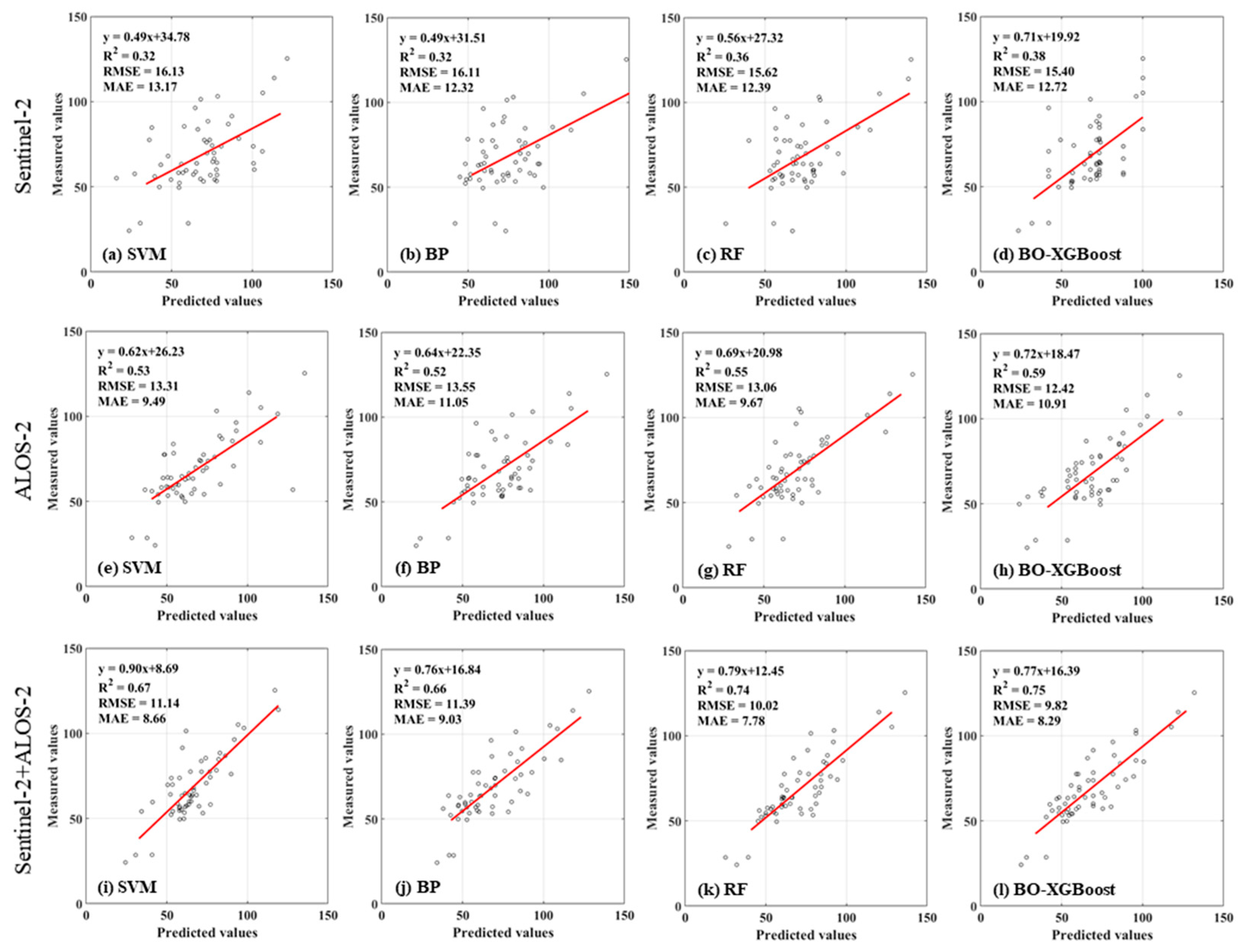
3.2. Results of Forest AGB Estimation
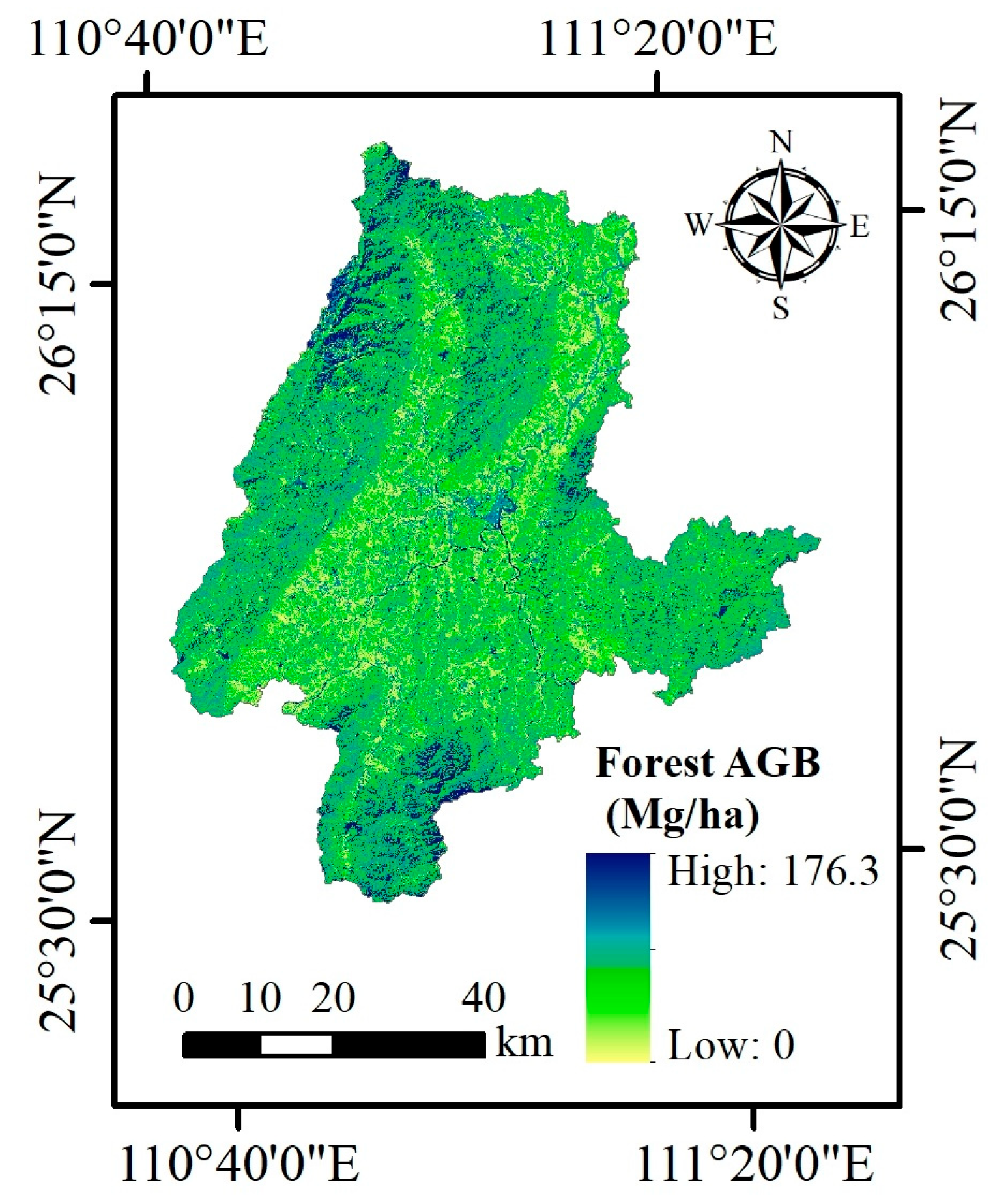
3.3. Continuous Mapping of Forest AGB
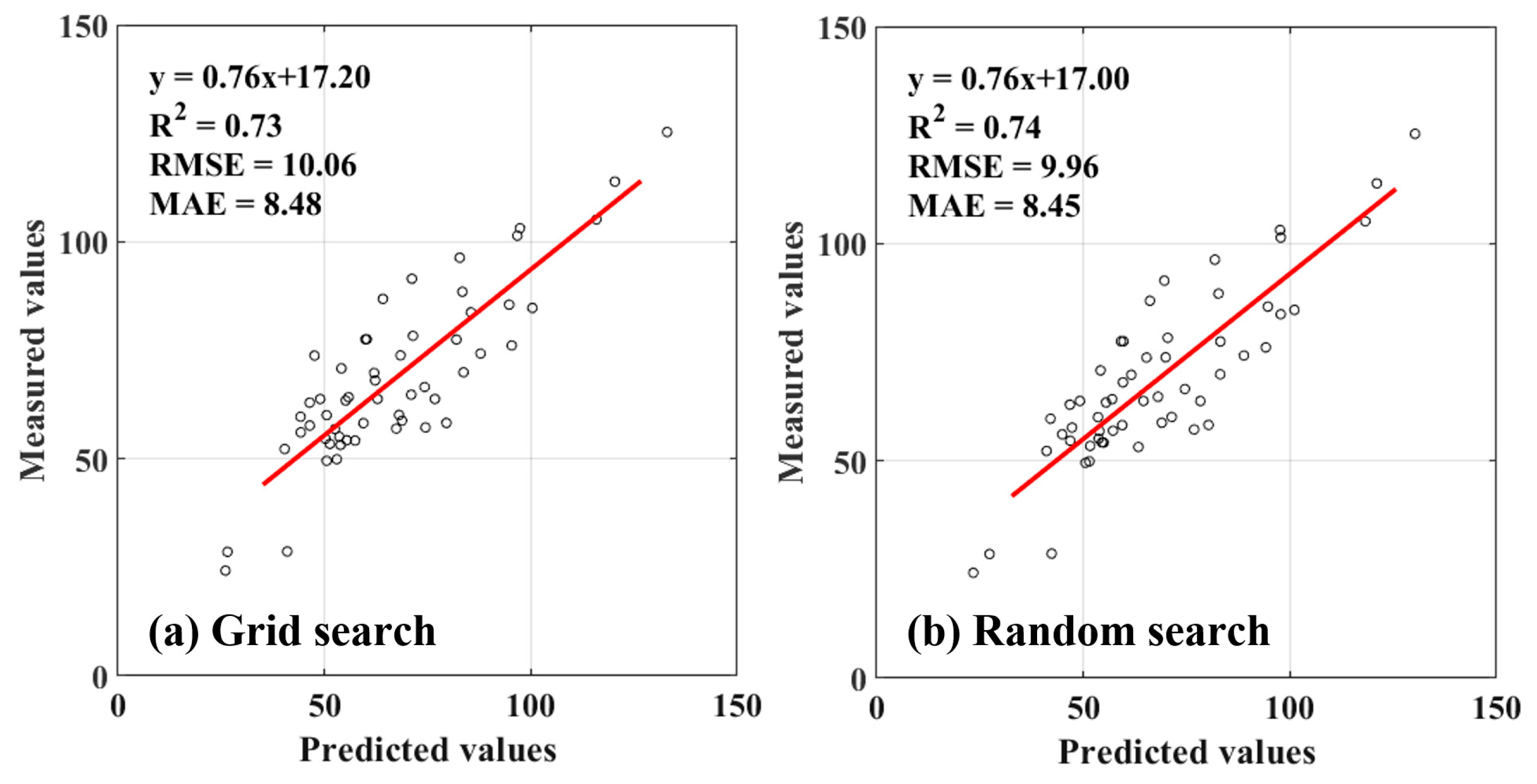
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mokany, K.; Raison, R.J.; Prokushkin, A.S. Critical analysis of root: Shoot ratios in terrestrial biomes. Glob. Change Biol. 2006, 1, 84–96. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Ji, P.; Li, H.; Wei, S.; Peng, D. Evaluating Forest Aboveground Biomass Products by Incorporating Spatial Representativeness Analysis. Remote Sens. 2025, 17, 2898. [Google Scholar] [CrossRef]
- Zhang, R.; Zhou, X.; Ouyang, Z.; Avitabile, V.; Qi, J.; Chen, J.; Giannico, V. Estimating aboveground biomass in subtropical forests of China by integrating multisource remote sensing and ground data. Remote Sens. Environ. 2019, 232, 111341. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, X.; Pan, X.; Wu, T.; Lei, J.; Chen, X.; Li, Y.; Chen, Y. Estimating Forest Aboveground Biomass in Tropical Zones by Integrating LiDAR and Sentinel-2B Data. Sustainability. 2025, 17, 3631. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, Y.; Xu, J.; Fang, Q.; Xuan, J.; Huang, L.; Li, X.; Mao, F.; Sun, Y.; Du, H. UAV-LiDAR-Based Study on AGB Response to Stand Structure and Its Estimation in Cunninghamia Lanceolata Plantations. Remote Sens. 2025, 17, 2842. [Google Scholar] [CrossRef]
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Pham, T.D.; Yokoya, N.; Bui, D.T.; Yoshino, K.; Friess, D.A. Remote sensing approaches for monitoring mangrove species, structure, and biomass: Opportunities and challenges. Remote Sens. 2019, 11, 230. [Google Scholar] [CrossRef]
- Wu, J.; Yao, W.; Choi, S.; Park, T.; Myneni, R.B. A Comparative Study of Predicting DBH and Stem Volume of Individual Trees in a Temperate Forest Using Airborne Waveform LiDAR. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2267–2271. [Google Scholar] [CrossRef]
- Pham, L.T.H.; Brabyn, L. Monitoring mangrove biomass change in Vietnam using SPOT images and an object-based approach combined with machine learning algorithms. ISPRS J. Photogramm. 2017, 128, 86–97. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, K.; Liu, L.; Myint, S.W.; Wang, S.; Liu, H.; He, Z. Exploring the Potential of WorldView-2 Red-Edge Band-Based Vegetation Indices for Estimation of Mangrove Leaf Area Index with Machine Learning Algorithms. Remote Sens. 2017, 9, 1060. [Google Scholar] [CrossRef]
- Song, J.; Liu, X.; Adingo, S.; Guo, Y.; Li, Q. A Comparative Analysis of Remote Sensing Estimation of Aboveground Biomass in Boreal Forests Using Machine Learning Modeling and Environmental Data. Sustainability 2024, 16, 7232. [Google Scholar] [CrossRef]
- Wai, P.; Su, H.; Li, M. Estimating Aboveground Biomass of Two Different Forest Types in Myanmar from Sentinel-2 Data with Machine Learning and Geostatistical Algorithms. Remote Sens. 2022, 14, 2146. [Google Scholar] [CrossRef]
- Zolkos, S.G.; Goetz, S.J.; Dubayah, R. A meta-analysis of terrestrial aboveground biomass estimation using lidar remote sensing. Remote Sens. Environ. 2013, 128, 289–298. [Google Scholar] [CrossRef]
- Lee, M.-K.; Lee, Y.-J.; Lee, D.-Y.; Park, J.-S.; Lee, C.-B. Biomass Estimation of Apple and Citrus Trees Using Terrestrial Laser Scanning and Drone-Mounted RGB Sensor. Remote Sens. 2025, 17, 2554. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A new method for segmenting individual trees from the LiDAR point cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The Ice, Cloud, and Land Elevation Satellite-2 (ICESat-2): Science Requirements, Concept, and Implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Chen, X.; Sun, Q.; Hu, J. Generation of Complete SAR Geometric Distortion Maps Based on DEM and Neighbor Gradient Algorithm. Appl. Sci. 2018, 8, 2206. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Liu, L.; Li, D.; Zhu, J.; Yu, S. Forest aboveground biomass estimation in Zhejiang Province using the integration of Landsat TM and ALOS PALSAR data. Int. J. Appl. Earth. Obs. 2016, 53, 1–15. [Google Scholar] [CrossRef]
- Hu, Y.; Tian, B.; Yuan, L.; Li, X.; Huang, Y.; Shi, R.; Jiang, X.; Wang, L.; Sun, C. Mapping Coastal Salt Marshes in China Using Time Series of Sentinel-1 SAR. ISPRS J. Photogramm. Remote Sens. 2021, 173, 122–134. [Google Scholar] [CrossRef]
- Tang, X.; Fehrmann, L.; Guan, F.; Forrester, D.I.; Guisasola, R.; Kleinn, C. Inventory-based estimation of forest biomass in Shitai County, China: A comparison of five methods. Ann. For. Res. 2016, 59, 269–280. [Google Scholar] [CrossRef]
- Li, G.; Xie, Z.; Jiang, X.; Lu, D.; Chen, E. Integration of ZiYuan-3 Multispectral and Stereo Data for Modeling Aboveground Biomass of Larch Plantations in North China. Remote Sens. 2019, 11, 2328. [Google Scholar] [CrossRef]
- Whelan, A.W.; Cannon, J.B.; Bigelow, S.W.; Rutledge, B.T.; Meador, A.J.S. Improving generalized models of forest structure in complex forest types using area-and voxel-based approaches from LiDAR. Remote Sens. Environ. 2023, 284, 113362. [Google Scholar] [CrossRef]
- Tokola, T.; Pitkänen, J.; Partinen, S.; Muinonen, E. Point accuracy of a non-parametric method in estimation of forest characteristics with different satellite materials. Int. J. Remote Sens. 1996, 17, 2333–2351. [Google Scholar] [CrossRef]
- Tang, L.; Yu, L.; Wang, S.; Li, J.; Wang, S. A novel hybrid ensemble learning paradigm for nuclear energy consumption forecasting. Appl. Energy 2012, 93, 432–443. [Google Scholar] [CrossRef]
- Na, Q.; Lai, Q.; Bao, G.; Xue, J.; Liu, X.; Gao, R. Estimation of Gross Primary Productivity Using Performance-Optimized Machine Learning Methods for the Forest Ecosystems in China. Forests 2025, 16, 518. [Google Scholar] [CrossRef]
- Bui, Q.-T.; Pham, Q.-T.; Pham, V.-M.; Tran, V.-T.; Nguyen, D.-H.; Nguyen, Q.-H.; Nguyen, H.-D.; Do, N.T.; Vu, V.-M. Hybrid Machine Learning Models for Aboveground Biomass Estimations. Ecol. Inf. 2024, 79, 102421. [Google Scholar] [CrossRef]
- Fu, W.; Guo, H.; Li, X.; Tian, B.; Sun, Z. Extended Three-Stage Polarimetric SAR Interferometry Algorithm by Dual-Polarization Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2792–2802. [Google Scholar]
- Jian, K.; Lu, D.; Lu, Y.; Li, G. Improving Forest Canopy Height Mapping in Wuyishan National Park Through Calibration of ZiYuan-3 Stereo Imagery Using Limited Unmanned Aerial Vehicle LiDAR Data. Forests 2025, 16, 125. [Google Scholar] [CrossRef]
- Zhao, M.; Yang, J.; Zhao, N.; Liu, Y.; Wang, Y.; Wilson, J.P.; Yue, T. Estimation of China’s forest stand biomass carbon sequestration based on the continuous biomass expansion factor model and seven forest inventories from 1977 to 2013. For. Ecol. Manag. 2019, 448, 528–534. [Google Scholar] [CrossRef]
- Fang, J.Y.; Chen, A.P.; Peng, C.H.; Zhao, S.Q.; Ci, L.J. Changes in forest biomass carbon storage in China between 1949 and 1998. Science 2001, 292, 2320–2322. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Zizala, D.; Saberioon, M.; Boruvka, L. Soil Organic Carbon and Texture Retrieving and Mapping using Proximal, Airborne and Sentinel-2 Spectral Imaging. Remote Sens. Environ. 2018, 218, 89–103. [Google Scholar] [CrossRef]
- Jiang, F.; Zhao, F.; Ma, K.; Li, D.; Sun, H. Mapping the Forest Canopy Height in Northern China by Synergizing ICESat-2 with Sentinel-2 Using a Stacking Algorithm. Remote Sens. 2021, 13, 1535. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F.; Motagh, M. Random forest wetland classification using ALOS-2 L-band, RADARSAT-2 C-band, and TerraSAR-X imagery. ISPRS J. Photogramm. Remote Sens. 2017, 130, 13–31. [Google Scholar] [CrossRef]
- Shimada, M. New global forest/non-forest maps from ALOS PALSAR data (2007-2010). Remote Sens. Environ. 2014, 155, 13–31. [Google Scholar] [CrossRef]
- Motohka, T.; Nasahara, K.N.; Oguma, H.; Tsuchida, S. Applicability of Green-Red Vegetation Index for Remote Sensing of Vegetation Phenology. Remote Sens. 2010, 2, 2369–2387. [Google Scholar] [CrossRef]
- Zhou, J.-J.; Zhou, Z.; Zhao, Q.; Han, Z.; Wang, P.; Xu, J.; Dian, Y. Evaluation of Different Algorithms for Estimating the Growing Stock Volume of Pinus massoniana Plantations Using Spectral and Spatial Information from a SPOT6 Image. Forests 2020, 11, 540. [Google Scholar] [CrossRef]
- Puliti, S.; Saarela, S.; Gobakken, T.; Ståhl, G.; Næsset, E. Combining UAV and Sentinel-2 auxiliary data for forest growing stock volume estimation through hierarchical model-based inference. Remote Sens. Environ. 2018, 204, 485–497. [Google Scholar] [CrossRef]
- Qi, J.G.; Chehbouni, A.R.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Sun, H.; Wang, Q.; Wang, G.; Lin, H.; Luo, P.; Li, J.; Zeng, S.; Xu, X.; Ren, L. Optimizing kNN for Mapping Vegetation Cover of Arid and Semi-Arid Areas Using Landsat images. Remote Sens. 2018, 10, 1248. [Google Scholar] [CrossRef]
- Dong, T.; Liu, J.; Shang, J.; Qian, B.; Ma, B.; Kovacs, J.M.; Walters, D.; Jiao, X.; Geng, X.; Shi, Y. Assessment of red-edge vegetation indices for crop leaf area index estimation. Remote Sens. Environ. 2019, 222, 133–143. [Google Scholar] [CrossRef]
- Chi, H.; Sun, G.; Huang, J.; Guo, Z.; Ni, W.; Fu, A. National Forest Aboveground Biomass Mapping from ICESat/GLAS Data and MODIS Imagery in China. Remote Sens. 2015, 7, 5534–5564. [Google Scholar] [CrossRef]
- Jiang, F.-G.; Li, M.-D.; Chen, S.-W. Adaptive Gaussian-PSO XGBoost Model for Alpine Forests Aboveground Biomass Estimation Using Spaceborne PolSAR and LiDAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 10157–10171. [Google Scholar] [CrossRef]
- Baraldi, A.; Parmiggiani, F. Investigation of the textural characteristics associated with gray level cooccurrence matrix statistical parameters. IEEE Trans. Geosci. Remote Sens. 1995, 33, 293–304. [Google Scholar] [CrossRef]
- Lu, D. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Jain, A.; Zongker, D. Feature selection: Evaluation, application, and small sample performance. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 153–158. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Liao, B.; Zhou, T.; Liu, Y.; Li, M.; Zhang, T. Tackling the Wildfire Prediction Challenge: An Explainable Artificial Intelligence (XAI) Model Combining Extreme Gradient Boosting (XGBoost) with SHapley Additive exPlanations (SHAP) for Enhanced Interpretability and Accuracy. Forests 2025, 16, 689. [Google Scholar] [CrossRef]
- Liu, G.; Zheng, L.; Long, P.; Yang, L.; Zhang, L. Ensemble Learning and SHAP Interpretation for Predicting Tensile Strength and Elastic Modulus of Basalt Fibers Based on Chemical Composition. Sustainability 2025, 17, 7387. [Google Scholar] [CrossRef]
- Yuan, H.; Yang, G.; Li, C.; Wang, Y.; Liu, J.; Yu, H.; Feng, H.; Xu, B.; Zhao, X.; Yang, X. Retrieving Soybean Leaf Area Index from Unmanned Aerial Vehicle Hyperspectral Remote Sensing: Analysis of RF, ANN, and SVM Regression Models. Remote Sens. 2017, 9, 309. [Google Scholar] [CrossRef]
- Tomppo, E.O.; Gagliano, C.; De Natale, F.; Katila, M.; McRoberts, R.E. Predicting categorical forest variables using an improved k-Nearest Neighbour estimator and Landsat imagery. Remote Sens. Environ. 2009, 113, 500–517. [Google Scholar] [CrossRef]
- Lv, D.; Liu, G.; Ou, J.; Wang, S.; Gao, M. Prediction of GPS Satellite Clock Offset Based on an Improved Particle Swarm Algorithm Optimized BP Neural Network. Remote Sens. 2022, 14, 2407. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wong, T.T. Performance evaluation of classification algorithms by k-fold and leave-one-out cross validation. Pattern Recognit. 2015, 48, 2839–2846. [Google Scholar] [CrossRef]
- Wang, Y.; Hancock, S.; Dong, W.; Ji, Y.; Zhao, H.; Wang, M. Analysis of the Application of Machine Learning Algorithms Based on Sentinel-1/2 and Landsat 8 OLI Data in Estimating Above-Ground Biomass of Subtropical Forests. Forests 2025, 16, 559. [Google Scholar] [CrossRef]
- Fu, Y.; Tan, H.; Kou, W.; Xu, W.; Wang, H.; Lu, N. Estimation of Rubber Plantation Biomass Based on Variable Optimization from Sentinel-2 Remote Sensing Imagery. Forests 2024, 15, 900. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, C.; Zhu, J.; Fu, H.; Han, W.; Xie, H. Forest Aboveground Biomass Estimation in Subtropical Mountain Areas Based on Improved Water Cloud Model and PolSAR Decomposition Using L-Band PolSAR Data. Forests 2023, 14, 2303. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, Y.; Tian, C.; Yun, T.; Li, M. Estimation of Subtropical Forest Aboveground Biomass Using Active and Passive Sentinel Data with Canopy Height. Remote Sens. 2025, 17, 2509. [Google Scholar] [CrossRef]
- Ma, Y.; Wu, H.; Xiong, S.; Li, Z.; Li, X. Remote sensing estimation of forest biomass based on IRS-P6 data: A case study of Yaoshan in Guilin. J. Hunan Univ. Sci. Technol. 2012, 27, 2. (In Chinese) [Google Scholar]
- Jiang, F.; Li, M.; Chen, S. PolSAR Forest Height Estimation Enhancement With Polarimetric Rotation Domain Features and Multivariate Sensitivity Analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 19470–19480. [Google Scholar] [CrossRef]

| Plot Number | Range of Values | Mean | Standard Deviation | Coefficient of Variation (%) |
|---|---|---|---|---|
| 180 | 1.05–183.9 | 67.5 | 50.1 | 74.1 |
| Data Source | Feature Type | Feature Name | Abbreviation |
|---|---|---|---|
| Sentinel-2 | Spectral variable | Band reflectance (band i; i = 5, 6, 7, 8A) | Band i |
| Normalized difference vegetation index | NDVI | ||
| Red–green vegetation index | RGVI | ||
| Atmospherically resistant vegetation index | ARVI | ||
| Enhanced vegetation index | EVI | ||
| Visible atmospherically resistant index | VARI | ||
| Soil-adjusted vegetation index | SAVI | ||
| Modified soil-adjusted vegetation index | MSAVI | ||
| Red-edge normalized difference vegetation index | RENDVI | ||
| Red-edge chlorophyll index | RECI | ||
| Red-edge spectral ratio index | RESR | ||
| ALOS-2 | Backscattering coefficient | HH | - |
| HV | - |
| Data Source | Model | R2 | RMSE (Mg/ha) | MAE (Mg/ha) |
|---|---|---|---|---|
| Sentinel-2 | SVM | 0.32 | 16.13 | 13.17 |
| BP | 0.32 | 16.11 | 12.32 | |
| RF | 0.36 | 15.62 | 12.39 | |
| BO-XGBoost | 0.38 | 15.40 | 12.72 | |
| ALOS-2 | SVM | 0.53 | 13.31 | 13.55 |
| BP | 0.52 | 13.55 | 11.05 | |
| RF | 0.55 | 13.06 | 9.67 | |
| BO-XGBoost | 0.59 | 12.42 | 10.91 | |
| Sentinel-2 + ALOS-2 | SVM | 0.67 | 11.14 | 8.66 |
| BP | 0.66 | 11.39 | 9.03 | |
| RF | 0.74 | 10.02 | 7.78 | |
| BO-XGBoost | 0.75 | 9.82 | 8.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Wang, Z.; Wang, Z.; Wang, Y.; Li, C.; Huang, T. Integrating PolSAR and Optical Data for Forest Aboveground Biomass Estimation with an Interpretable Bayesian-Optimized XGBoost Model. Sustainability 2025, 17, 9749. https://doi.org/10.3390/su17219749
Zhou X, Wang Z, Wang Z, Wang Y, Li C, Huang T. Integrating PolSAR and Optical Data for Forest Aboveground Biomass Estimation with an Interpretable Bayesian-Optimized XGBoost Model. Sustainability. 2025; 17(21):9749. https://doi.org/10.3390/su17219749
Chicago/Turabian StyleZhou, Xinshao, Zhiqiang Wang, Zhaosheng Wang, Yonghong Wang, Chaokui Li, and Tian Huang. 2025. "Integrating PolSAR and Optical Data for Forest Aboveground Biomass Estimation with an Interpretable Bayesian-Optimized XGBoost Model" Sustainability 17, no. 21: 9749. https://doi.org/10.3390/su17219749
APA StyleZhou, X., Wang, Z., Wang, Z., Wang, Y., Li, C., & Huang, T. (2025). Integrating PolSAR and Optical Data for Forest Aboveground Biomass Estimation with an Interpretable Bayesian-Optimized XGBoost Model. Sustainability, 17(21), 9749. https://doi.org/10.3390/su17219749








