Exploring Optimal Regional Energy-Related Green Low-Carbon Socioeconomic Development Policies by an Extended System Planning Model
Abstract
1. Introduction
2. Methods
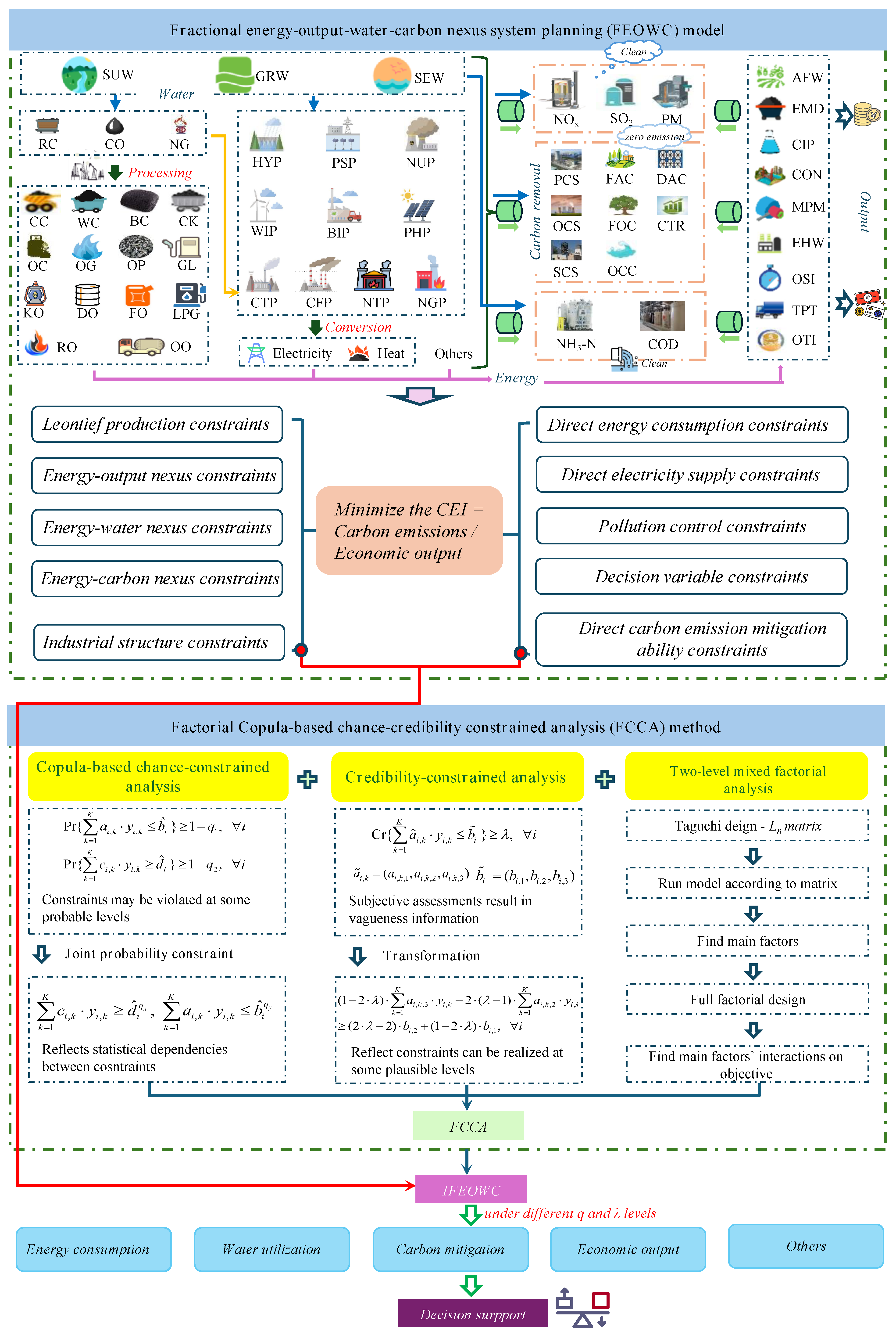
2.1. Fractional Energy–Output–Water–Carbon Nexus System Planning (FEOWC) Model
2.1.1. Objective Function
2.1.2. Constraints
2.2. Factorial Copula-Based Chance-Credibility Constrained Analysis (FCCA) Method
2.2.1. Copula-Based Chance-Constrained Analysis
2.2.2. Credibility-Constrained Analysis
2.2.3. Mixed Factorial Analysis
3. Case Study
3.1. Study Area
3.2. Data Collection and Processing
3.3. Scenario Design
4. Results and Discussion
4.1. Carbon Emissions Intensity
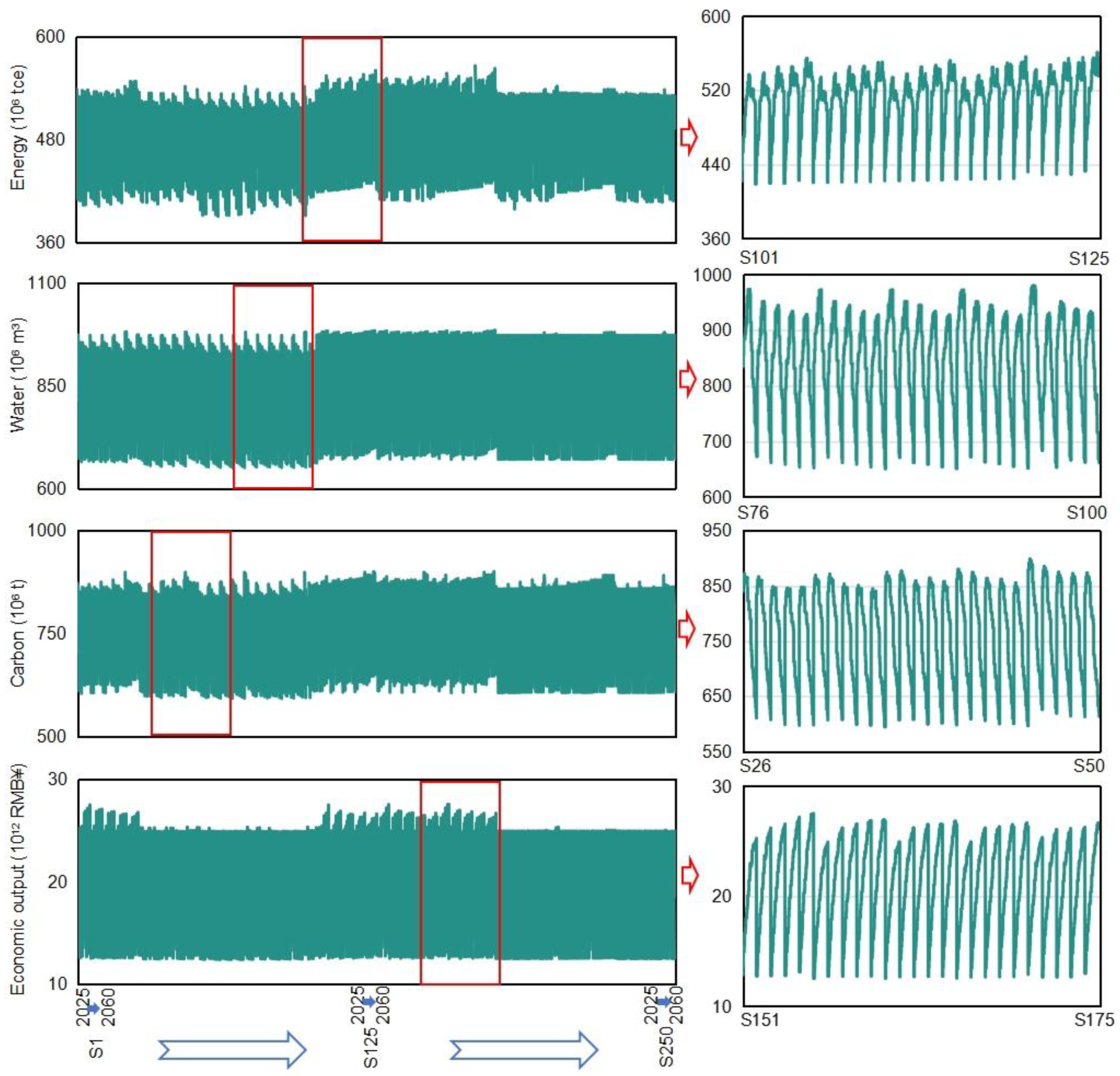
4.2. Energy Consumption


4.3. Water Utilization

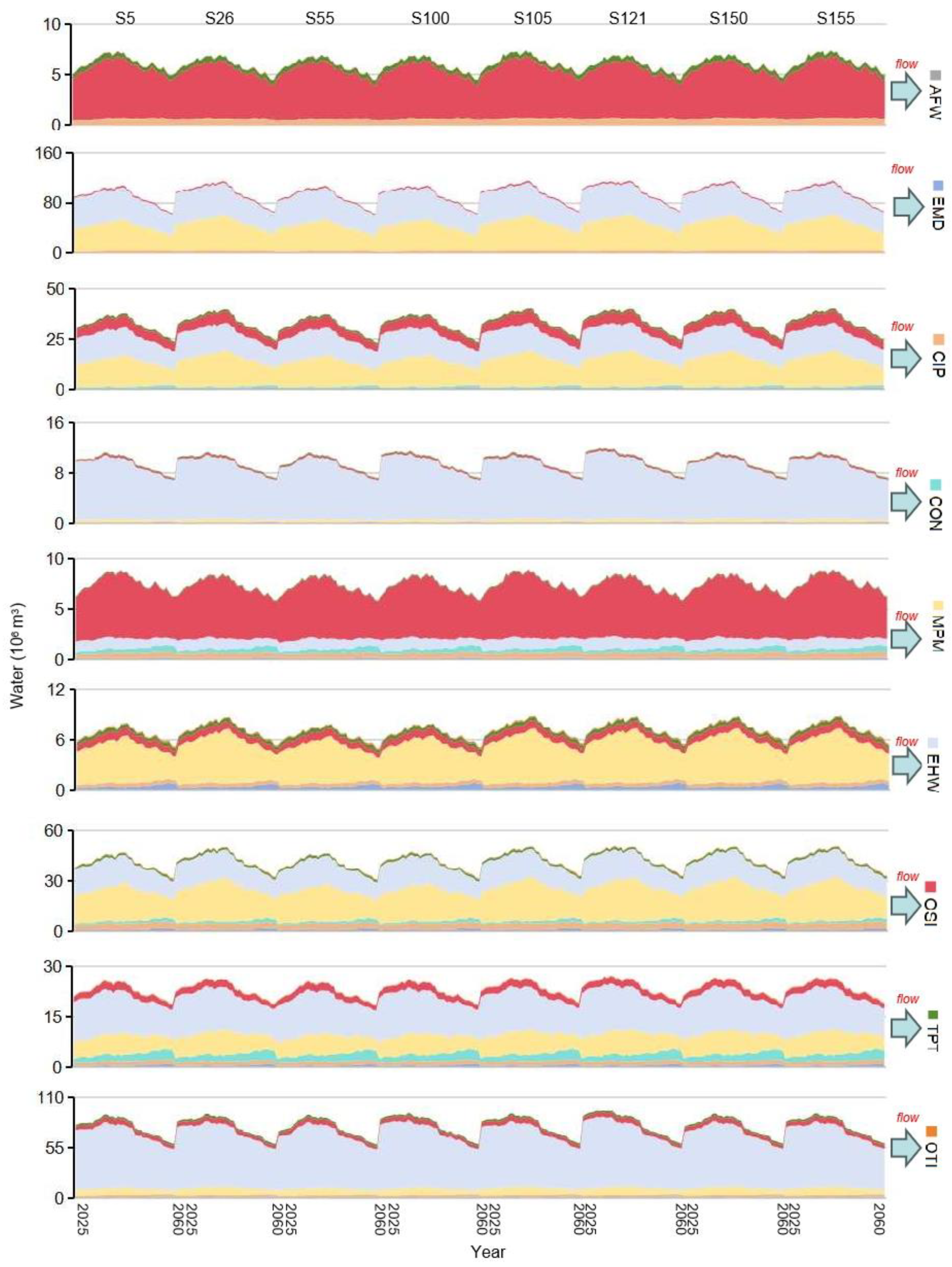
4.4. Carbon Emissions


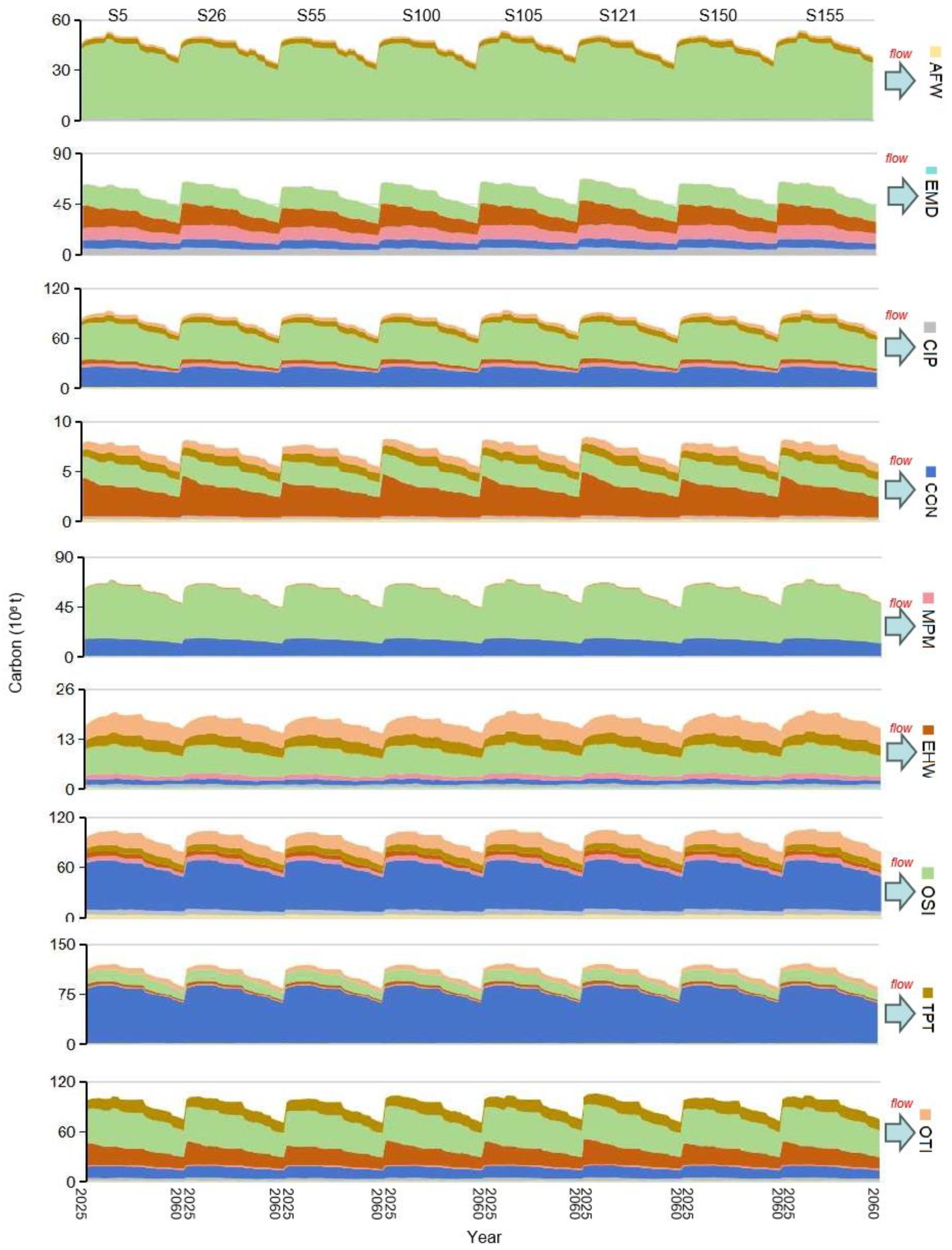
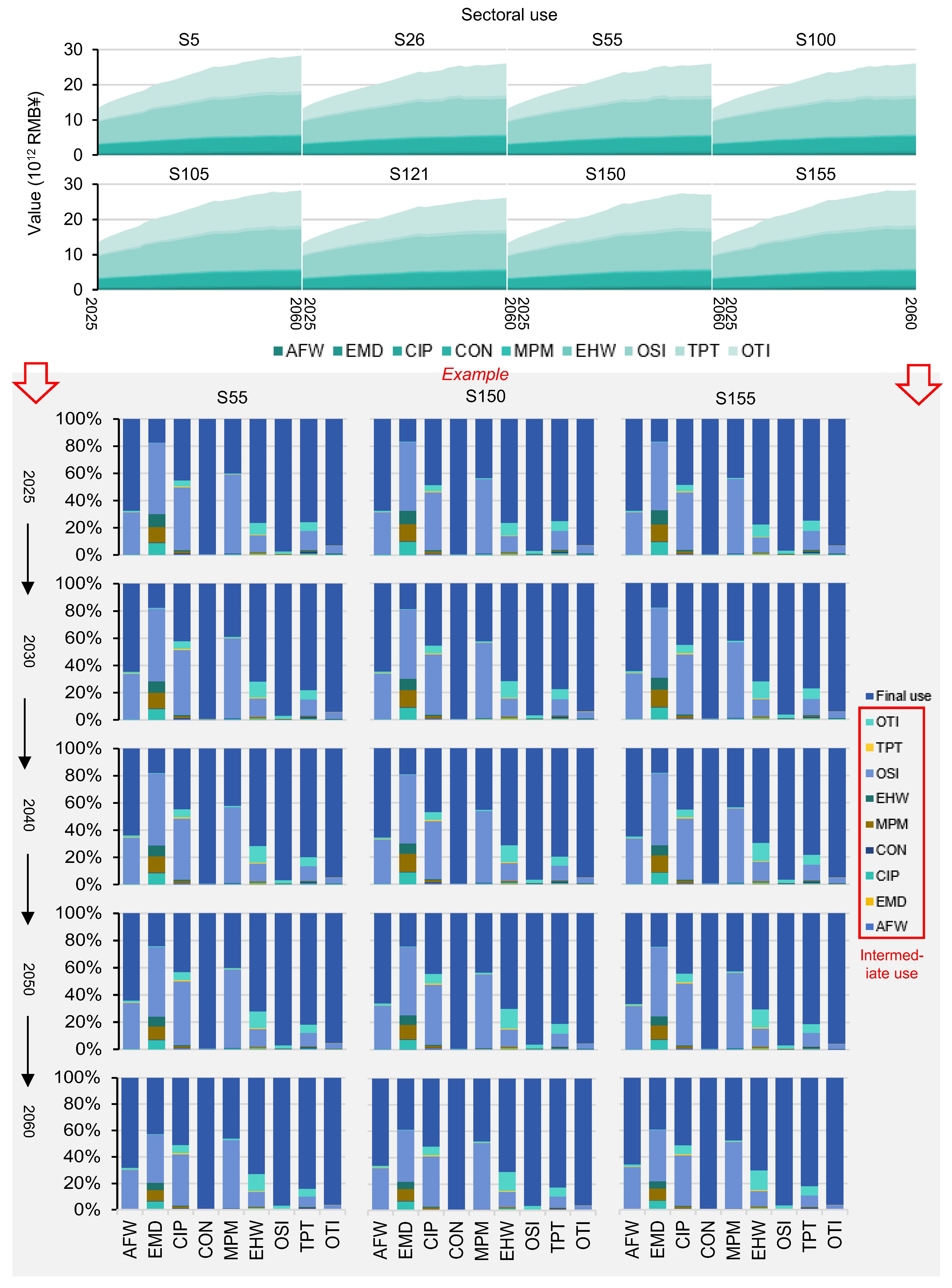
4.5. Economic Growth
4.6. Policy Implications
- (1)
- The adoption of advanced technologies for green low-carbon fossil fuel production is critical, given planned consumption would surge to 185.72 × 106 tce by 2060.
- (2)
- The investment of low-carbon energy conversion capacities for green low-carbon electricity generation, e.g., WIP, PHP, and NUP would expand to 40.12 GW, 36.35 GW, and 31.78 GW by 2060;
- (3)
- The conduction of end-removal actions for reducing carbon in the air is essential, the contributions would plan to be CTR 18.73%, CCS 6.64%, CSI 3.14%, and DAC 0.27% in 2035, and CSI 40.40%, CCS 35.82%, and DAC 23.78% in 2060;
- (4)
- The strategic advancement of key sectors (e.g., CON, OSI and OTI) is significant to obtain great total economic outputs;
- (5)
- The reduction in freshwater allocation to the system is helpful for relieving water shortage, e.g., decreasing to 362.96 × 106 m3 in 2030, and to 254.26 × 106 m3 in 2060;
- (6)
- The seawater extraction volume should maintain at a stable level, e.g., 258.34 × 106 m3 2030 and 248.44 × 106 m3 in 2060.
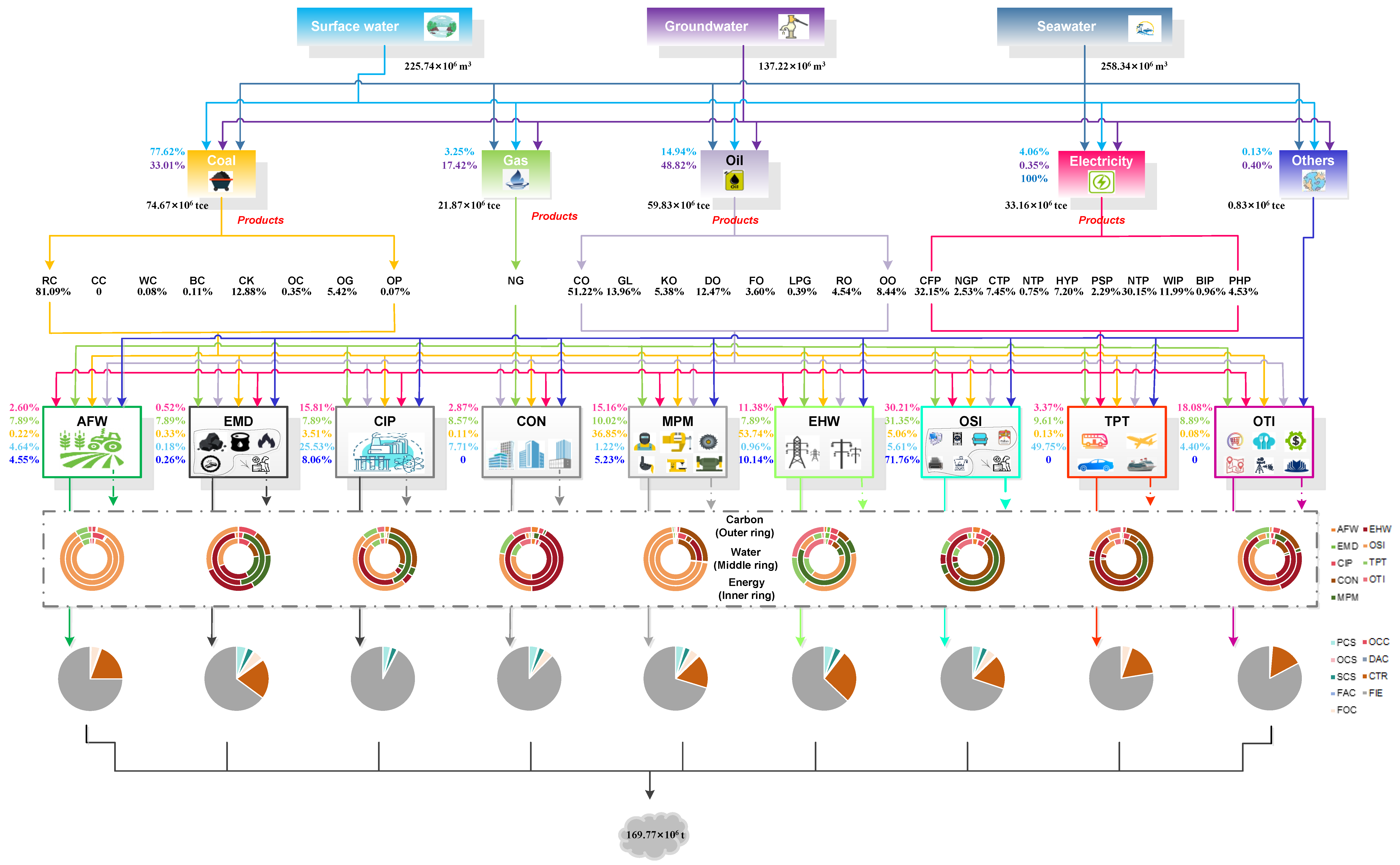

4.7. Identifying Key Factors
4.8. Comparison with Previous Studies
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Method and Model: | Carbon Emission Mitigation: | ||
| CHA | Copula-based chance-constrained analysis | CEI | Carbon emissions intensity |
| CRA | Credibility-constrained analysis | CCS | Carbon capture and storage |
| EOC | Energy-output-carbon nexus system planning | CSI | Carbon sink |
| EWC | Energy-water-carbon nexus system planning | CTR | Carbon trade mechanism |
| EOWC | Energy-output-water-carbon nexus system planning | DAC | Direct air capture |
| FRP | Fractional programming | FAC | Forest CSI |
| FCCA | Factorial Copula-based chance-credibility constrained analysis | FOC | Farmland CSI |
| FEOWC | Fractional energy-output-water-carbon nexus system planning | FIE | Final carbon emission |
| IFEOWC | Inexact fractional energy-output-water-carbon nexus system planning | OCS | Oxy-combustion CCS |
| Energy and water: | OCC | Ocean CSI | |
| BC | Briquettes | PCS | Pre-combustion CCS |
| CC | Cleaned coal | SCS | Post-combustion CCS |
| CK | Coke | Pollutant: | |
| CO | Crude oil | NH3-N | Ammonia nitrogen |
| DO | Diesel oil | COD | Chemical oxygen demand |
| FO | Fuel oil | SO2 | Sulfur dioxide |
| GL | Gasoline | NOx | Oxynitride |
| KO | Kerosene | PM | Particulate matter |
| LPG | Liquefied petroleum gas | ||
| NG | Natural gas | ||
| OC | Coke oven gas | ||
| OG | Other gas | ||
| OP | Other coking products | ||
| OO | Other petroleum products | ||
| RC | Raw coal | ||
| RO | Refinery gas | ||
| WC | Other washed coal | ||
| GRW | Groundwater | ||
| SUW | Surface water | ||
| SEW | Seawater | ||
| Electricity: | |||
| BIP | Biomass power | ||
| CFP | Coal-fired power | ||
| CTP | Coal-fired thermal power | ||
| HYP | Hydropower | ||
| NGP | Natural gas-fired power | ||
| NTP | Natural gas-fired thermal power | ||
| NUP | Nuclear power | ||
| PSP | Pumped storage power | ||
| PHP | Photovoltaic power | ||
| WIP | Wind power | ||
Nomenclature
| Subscripts | |
| k | a sector that provides products (and services) to other sectors and end-users |
| n | a sector that obtains raw materials from other sectors or obtain added investments from government, enterprises etc. |
| t | planning period |
| i | energy source, i = 1 to 20 for RC, CC, WC, BC, CK, OC, OG, OP, NG, CO, GL, KO, DO, FO, LPG, RO, OO, heat, electricity, and other energy |
| w | water source, w = 1 to 3 for SUW, GRW, and SEW |
| v | carbon capture and storage type, v = 1 to 3 for PCS, OCS, and SCS |
| u | carbon sink type, u = 1 to 3 for FAC, FOC, and OCC |
| j | electricity source, j = 1 to 10 for CFP, NGP, CTP, NTP, HYP, PSP, NTP, WIP, BIP, and PHP |
| Decision variables | |
| economic output (CNY) | |
| direct energy consumption (ton, m3, kJ, kWh or tce) | |
| electricity generation (kWh) | |
| expansion capacity (kW) | |
| electricity generation capacity (kW) | |
| carbon emissions mitigated by CCS (ton) | |
| carbon emissions reduced by CSI (ton) | |
| carbon emissions reduced by DAC (ton) | |
| sectoral initial carbon quota under CTR (ton C) | |
| sectoral sold carbon quota under CTR (ton C) | |
| sectoral purchased carbon quota under CTR (ton C) | |
| Parameters | |
| embodied energy per unit of output (tce/CNY) | |
| embodied carbon emissions per unit of energy (ton C/tce) | |
| direct monetary consumption coefficient among sectors | |
| direct carbon emissions coefficient (ton C/ton, ton C/m3, ton C/kJ, ton C/kWh or ton C/tce) | |
| final use, including end-users’ consumption, gross fixed capital, and export (CNY) | |
| import (CNY) | |
| standard coal coefficient (tce/ton, tce/m3, tce/kJ or tce/kWh) | |
| indirect energy consumption allowance (tce) | |
| water utilization per unit of energy consumption (m3/tce) | |
| direct water consumption (m3) | |
| indirect water utilization allowance (m3) | |
| direct carbon emissions allowance (ton C) | |
| indirect carbon emissions allowance (ton C) | |
| energy loss rate | |
| available energy (ton, m3, kJ, kWh or tce) | |
| energy conversion efficiencies of coal products | |
| energy conversion efficiency of coal-fired power electricity generation (ton/kWh) | |
| energy conversion efficiency of coal-fired thermal power electricity generation (ton/kWh) | |
| raw coal demand (ton) | |
| energy conversion efficiencies of oil products (ton) | |
| crude oil demand (ton) | |
| energy conversion efficiency of natural gas-fired power electricity generation (m3/kWh) | |
| energy conversion efficiency of natural gas -fired thermal power electricity generation (m3/kWh) | |
| coal product demand (ton) | |
| oil product demand (ton) | |
| natural gas demand (m3) | |
| heat demand (kJ) | |
| other energy demand (tce) | |
| initial capacity at beginning of the planning period (kW) | |
| retired capacity (kW) | |
| working time (hour) | |
| heat generation coefficient (kJ/kWh) | |
| household electricity consumption (kWh) | |
| electricity demand (kWh) | |
| heat demand (kJ) | |
| household electricity demand (kWh) | |
| minimum capacity (kW) | |
| maximum capacity (kW) | |
| minimum carbon removal abilities of carbon capture and storage technologies (ton C) | |
| maximum carbon removal abilities of carbon capture and storage technologies (ton C) | |
| minimum carbon quota (ton C) | |
| carbon quota allocated by government (ton C) | |
| investment for purchasing carbon quota (CNY) | |
| carbon price in trading market (CNY/ton C) | |
| minimum carbon removal abilities of DAC (ton) | |
| maximum carbon removal abilities of DAC (ton) | |
| minimum carbon removal abilities of CSI (ton) | |
| maximum carbon removal abilities of CSI (ton) | |
| crop carbon absorption ratio (ton C/ton); | |
| crop economic yield (ton); | |
| crop moisture coefficient | |
| crop root-to-shoot ratio coefficient | |
| economic coefficient | |
| forest area (m2) | |
| unit forest land area of carbon stock (ton C/m2); | |
| biomass conversion and expansion coefficient | |
| volume coefficient | |
| carbon absorption coefficient of plants under trees | |
| forest carbon conversion coefficient | |
| dry matter carbon content | |
| a seawater sample’s chlorophyll a concentration (mg/m2) | |
| assimilation index (ton C/(mg·day)) | |
| sea area (m2) | |
| T | number of days (day) |
| algae production (ton) | |
| algae carbon content (ton C/ton) | |
| proportion of carbon absorbed by the photosynthesis of algae | |
| shellfish yield (ton) | |
| dry shell weight coefficient | |
| shell carbon content (ton C/ton) | |
| direct water utilization coefficients of raw coal productions (m3/ton) | |
| direct water utilization coefficients of other coal productions (m3/ton) | |
| direct water utilization coefficients of crude oil productions (m3/ton) | |
| direct water utilization coefficients of other oil productions (m3/ton) | |
| direct water availabilities for coal and oil (m3) | |
| direct water availabilities for coal and oil (m3) | |
| direct water utilization coefficients of natural gas productions (m3/m3 gas) | |
| direct water utilization coefficients of other energy productions (m3/tce) | |
| available direct water for natural gas (m3) | |
| available direct water for other energy (m3) | |
| direct water utilization coefficients of electricity generation (m3/kWh) | |
| available direct water for electricity generation (m3) | |
| available direct water for carbon emissions mitigation (m3) | |
| direct water utilization coefficients of CCS (m3/ton C) | |
| direct water utilization coefficients of CSI (m3/ton C) | |
| total available water (m3) | |
| proportion of secondary industry | |
| proportion of tertiary industry | |
| minimum final use (CNY) | |
| maximum final use (CNY) | |
| NH3-N discharge coefficient (ton/ton, ton/m3, ton/kJ, ton/kWh or ton/tce) | |
| COD discharge coefficient (ton/ton, ton/m3, ton/kJ, ton/kWh or ton/tce) | |
| NH3-N removal efficient | |
| COD removal efficient | |
| NH3-N discharge allowance (ton) | |
| COD discharge allowance (ton) | |
| SO2 emission coefficient (ton/ton, ton/m3, ton/kJ, ton/kWh or ton/tce) | |
| NOx emission coefficient (ton/ton, ton/m3, ton/kJ, ton/kWh or ton/tce) | |
| PM emission coefficient (ton/ton, ton/m3, ton/kJ, ton/kWh or ton/tce) | |
| direct SO2 removal efficiency | |
| direct NOx removal efficiency | |
| direct PM removal efficiency | |
| direct SO2 emission allowance (ton) | |
| direct NOx emission allowance (ton) | |
| direct PM emission allowances (ton) | |
Appendix A. Framework of an Input-Output Table
| Sector (n) | Intermediate Use | Final Use | Total Output | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sector (k) | AFW | EMD | CIP | CON | MPM | EHW | OSI | TPT | OTI | |||
| Intermediate input | AFW | |||||||||||
| EMD | ||||||||||||
| CIP | ||||||||||||
| CON | ||||||||||||
| MPM | ||||||||||||
| EHW | ||||||||||||
| OSI | ||||||||||||
| TPT | ||||||||||||
| OTI | ||||||||||||
| Added value | ||||||||||||
| Total input | ||||||||||||
Appendix B. Scenario Design Framework
| Random Parameter Correlation (10) | Joint Probability (5) | Fuzzy Parameter | Credibility Level (5) | Scenario Design |
|---|---|---|---|---|
| Energy demand-available water | 0.01, 0.05, 0.10, 0.15, 0.20 | Parameters related to abilities and allowances | 0.5, 0.6, 0.7, 0.8, 0.9, 1.0 | 10 × 5 × 5 = 250 |
| Energy demand-carbon emission allowance | 0.01, 0.05, 0.10, 0.15, 0.20 | |||
| Energy demand-electricity demand | 0.01, 0.05, 0.10, 0.15, 0.20 | |||
| Energy demand-maximum final use | 0.01, 0.05, 0.10, 0.15, 0.20 | |||
| Available water-carbon emission allowance | 0.01, 0.05, 0.10, 0.15, 0.20 | |||
| Available water-electricity demand | 0.01, 0.05, 0.10, 0.15, 0.20 | |||
| Available water-maximum final use | 0.01, 0.05, 0.10, 0.15, 0.20 | |||
| Carbon emission allowance-electricity demand | 0.01, 0.05, 0.10, 0.15, 0.20 | |||
| Carbon emission allowance-maximum final use | 0.01, 0.05, 0.10, 0.15, 0.20 | |||
| Electricity demand-maximum final use | 0.01, 0.05, 0.10, 0.15, 0.20 |
Appendix C. Solution of the IFEOWC Model
- Step 1: Select 5 types of random variables, determine 10 groups of potential copula-based chance constraints and fuzzy parameter information.
- Step 2: Set 5 joint probabilities (qjoint = 0.01, 0.05, 0.10, 0.15, and 0.20) and 5 credibility degrees (λ = 0.5, 0.6, 0.7, 0.8, 0.9, and 1.0).
- Step 3: Convert copula-based chance constraints and fuzzy credibility constraints into deterministic constraints:
- Step 4: Transform the model into a linear model: assume that the model solution set is non-empty and bounded, and that the objective function is continuously differentiable. For all the feasible regions Y = (y1, … yn) can be ordered if the denominator is always positive or negative, and the numerator and denominator of the objective function are simultaneously multiplied by a constant τ such that the denominator is 1 and the decision variable is converted to , , and multiply both sides by the constant τ.
- Step 5: Input deterministic parameter data, input random variable and fuzzy parameters data under specific group of copula-based chance constraints, qjoint and λ to solve the model.
- Step 6: Gain the value of the objective function, the solution of the decision variable , and the optimal solution of the model are obtained.
- Step 7: Repeat Setp 6 and Setp 7 to solve different group of copula-based chance constraints, solutions under qjoint and λ, and obtain solutions under all scenarios of the model.
- Step 8: According to Section 2.2.3, select parameters for mixed factor analysis.
- Step 9: Determine the impact of the main effects of each factor and the interaction between key factors on the system objective function value.
References
- Duan, H.Y.; Sun, X.H.; Song, J.N.; Xing, J.H.; Yang, W. Peaking carbon emissions under a coupled socioeconomic-energy system: Evidence from typical developed countries. Resour. Conserv. Recycl. 2022, 187, 106641. [Google Scholar] [CrossRef]
- Energy Institute (EI). Statistical Review of World Energy 2024; Energy Institute: London, UK, 2024. [Google Scholar]
- Liu, J.; Zhao, S.H.; Li, Y.P.; Sun, Z.M. Development of an interval double-stochastic carbon-neutral electric power system planning model: A case study of Fujian province, China. J. Clean. Prod. 2023, 425, 138877. [Google Scholar] [CrossRef]
- Yu, Z.; Khan, S.A.R.; Ponce, P.; Jabbour, A.B.L.D.S.; Jabbour, C.J.C. Factors affecting carbon emissions in emerging economies in the context of a green recovery: Implications for sustainable development goals. Technol. Forecast. Soc. Change 2022, 176, 121417. [Google Scholar] [CrossRef]
- Cao, R.; Huang, G.H.; Chen, J.P.; Li, Y.P. A fractional multi-stage simulation-optimization energy model for carbon emissions management of urban agglomeration. Sci. Total Environ. 2021, 774, 144963. [Google Scholar] [CrossRef]
- Liang, M.S.; Huang, G.H.; Chen, J.P.; Li, Y.P. Energy-water-carbon nexus system planning: A case study of Yangtze River Delta urban agglomeration, China. Appl. Energy 2022, 308, 118144. [Google Scholar] [CrossRef]
- Lin, X.J.; Huang, G.H.; Zhou, X.; Zhai, Y.Y. An inexact fractional multi-stage programming (IFMSP) method for planning renewable electric power system. Renew. Sustain. Energy Rev. 2023, 187, 113611. [Google Scholar] [CrossRef]
- Zheng, Y.L.; Huang, G.H.; Li, Y.P.; Chen, J.P.; Zhou, X.; Luo, B.; Fu, Y.P.; Lin, L.J.; Xu, Z.P.; Tang, W.C. An in deterministic fractional two-stage inter-regional energy system optimization model: A case study for the Province of Shanxi, China. J. Clean. Prod. 2024, 435, 140330. [Google Scholar] [CrossRef]
- Li, H.; Wang, J.; Lu, Z.; Zhang, Y.; Hou, G.; Xue, L. Process analysis-based industrial production modelling with uncertainty: A linear fractional programming for joint optimization of total carbon emissions and emission intensity. Appl. Energy 2025, 382, 125204. [Google Scholar] [CrossRef]
- Tabatabaie, S.M.H.; Murthy, G.S. Development of an input-output model for food-energy-water nexus in the pacific northwest, USA. Resour. Conserv. Recycl. 2021, 168, 105267. [Google Scholar] [CrossRef]
- He, P.; Ng, T.S.; Su, B. Energy-economic resilience with multi-region input-output linear programming models. Energy Econ. 2019, 84, 104569. [Google Scholar] [CrossRef]
- Zhou, X.; Gu, A. Impacts of household living consumption on energy use and carbon emissions in China based on the input-output model. Adv. Clim. Change Res. 2020, 11, 118–130. [Google Scholar] [CrossRef]
- Kang, J.D.; Ng, T.S.; Su, B.; Milovanoff, A. Electrifying light-duty passenger transport for CO2 emissions reduction: A stochastic-robust input-output linear programming model. Energy Econ. 2021, 104, 105623. [Google Scholar] [CrossRef]
- Kang, J.D.; Wu, Z.; Ng, T.; Su, B. A stochastic-robust optimization model for inter-regional power system planning. Eur. J. Oper. Res. 2023, 310, 1234–1248. [Google Scholar] [CrossRef]
- Zhang, Q.Q.; Jie, D.; Li, J.; Zhou, J. Carbon compensation cost in Jing-Jin-Ji region under the carbon neutrality goal: Considering emission responsibility and carbon abatement cost. J. Clean. Prod. 2024, 467, 142950. [Google Scholar] [CrossRef]
- Alyousif, M.; Belaid, F.; Almubarak, A.; Almulhim, T. Mapping Saudi Arabia’s low emissions transition path by 2060: An input-output analysis. Technol. Forecast. Soc. Change 2025, 211, 123920. [Google Scholar] [CrossRef]
- Tan, Q.; Liu, Y.; Ye, Q. The impact of clean development mechanism on energy-water-carbon nexus optimization in Hebei, China: A hierarchical model based discussion. J. Environ. Manag. 2020, 264, 110441. [Google Scholar] [CrossRef] [PubMed]
- Mehrjerdi, H.; Aljabery, A.A.M. Modeling and optimal planning of an energy-water-carbon nexus system for sustainable development of local communities. Adv. Sustain. Syst. 2021, 5, 2100024. [Google Scholar] [CrossRef]
- Liang, M.S.; Huang, G.H.; Chen, J.P.; Li, Y.P. Development of non-deterministic energy-water-carbon nexus planning model: A case study of Shanghai, China. Energy 2022, 246, 123300. [Google Scholar] [CrossRef]
- Yu, D.M.; Li, Z.M.; Fan, S.Y.; Sun, T.Y. Optimal management of an energy-water-carbon nexus employing carbon capturing and storing technology via downside risk constraint approach. J. Clean. Prod. 2023, 418, 138168. [Google Scholar] [CrossRef]
- Valencia-Díaz, A.; Toro, E.M.; Hincapié, R.A. Optimal planning and management of the energy-water-carbon nexus in hybrid AC/DC microgrids for sustainable development of remote communities. Appl. Energy 2025, 377, 124517. [Google Scholar] [CrossRef]
- Zhu, Y.; Chen, M.; Yang, Q.; Alshwaikh, M.J.M.; Zhou, H.; Li, J.; Liu, Z.; Zhao, H.; Zheng, C.; Bartocci, P.; et al. Life cycle water consumption for oxyfuel combustion power generation with carbon capture and storage. J. Clean. Prod. 2021, 281, 124419. [Google Scholar] [CrossRef]
- Rosa, L.; Sanchez, D.L.; Realmonte, G.; Baldocchi, D.; D’Odorico, P. The water footprint of carbon capture and storage technologies. Renew. Sustain. Energy Rev. 2021, 138, 110511. [Google Scholar] [CrossRef]
- Zhang, D.; Zuo, X.; Zang, C. Assessment of future potential carbon sequestration and water consumption in the construction area of the Three-North Shelterbelt Programme in China. Agric. For. Meteorol. 2021, 303, 108377. [Google Scholar] [CrossRef]
- Wu, H.; Guo, S.; Guo, P.; Shan, B.; Zhang, Y. Agricultural water and land resources allocation considering carbon sink/source and water scarcity/degradation footprint. Sci. Total Environ. 2022, 819, 152058. [Google Scholar] [CrossRef]
- Daneshvar, M.; Mohammadi-Ivatloo, B.; Asadi, S.; Anvari-Moghaddam, A.; Rasouli, M.; Gharehpetian, G.B. Chance-constrained models for transactive energy management of interconnected microgrid clusters. J. Clean. Prod. 2020, 271, 122177. [Google Scholar] [CrossRef]
- Li, H.W.; Li, Y.P.; Huang, G.H.; Gao, P.P. Identifying optimal land-use patterns using a copula-based interval stochastic programming model for urban agglomeration under uncertainty. Ecol. Eng. 2020, 142, 105616. [Google Scholar] [CrossRef]
- Wang, Y.M.; Zhu, G.C. A mixed integer fuzzy-interval credibility-constrained programming for booster optimization in water distribution system under uncertainty. J. Water Process Eng. 2022, 50, 103300. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, P. An inexact multi-objective mixed-integer nonlinear programming approach for water-soil-fertilizer management under uncertainty considering “footprint family-planetary boundary” assessment. J. Hydrol. 2023, 626, 129471. [Google Scholar] [CrossRef]
- Jankovic, A.; Chaudhary, G.; Goia, F. Designing the design of experiments (DOE)-An investigation on the influence of different factorial designs on the characterization of complex systems. Energy Build. 2021, 250, 111298. [Google Scholar] [CrossRef]
- Colette, D.A.; Martial, D.A.C.; Joseph, A.Y.; Benjamin, Y.K.; Patrick, D.A. Optimization of the compressive strength of used tire/cement phase composite concretes using a full factorial design. Constr. Build. Mater. 2023, 404, 133252. [Google Scholar] [CrossRef]
- Wang, G.Y.; Li, Y.P.; Liu, J.; Huang, G.H.; Chen, L.R.; Yang, Y.H.; Gao, P. A two-phase factorial input-output model for analyzing CO2-emission reduction pathway and strategy from multiple perspectives—A case study of Fujian province. Energy 2022, 248, 123615. [Google Scholar] [CrossRef]
- Leontief, W.W. Input-Output Economics, 2nd ed.; Oxford University Press: Oxford, UK, 1986. [Google Scholar]
- Kang, J.D.; Ng, T.S.; Su, B.; Yuan, R. Optimizing the Chinese electricity mix for CO2 emission reduction: An input-output linear programming model with endogenous capital. Environ. Sci. Technol. 2020, 54, 697–706. [Google Scholar] [CrossRef]
- Jirdehi, M.A.; Tabar, V.S. Multi-objective long-term expansion planning of electric vehicle infrastructures integrated with wind and solar units under the uncertain environment considering demand side management: A real test case. Sustain. Cities Soc. 2023, 96, 104632. [Google Scholar] [CrossRef]
- Nazloo, H.T.; Babazadeh, R.; Varmazyar, M. Optimal Configuration and Planning of Distributed Energy Systems Considering Renewable Energy Resources. J. Environ. Inform. 2024, 43, 50–64. [Google Scholar]
- Yu, L.; Zheng, S.; Gao, Q. Independent or collaborative management? Regional management strategy for ocean carbon sink trading based on game theory. Ocean Coast. Manag. 2023, 235, 106484. [Google Scholar] [CrossRef]
- Ke, S.; Zhang, Z.; Wang, Y. China’s forest carbon sinks and mitigation potential from carbon sequestration trading perspective. Ecol. Indic. 2023, 148, 110054. [Google Scholar] [CrossRef]
- Song, S.; Kong, M.; Su, M.; Ma, Y. Study on carbon sink of cropland and influencing factors: A multiscale analysis based on geographical weighted regression model. J. Clean. Prod. 2024, 447, 141455. [Google Scholar] [CrossRef]
- Sun, B.; Fan, B.; Wu, C.; Xie, J. Exploring incentive mechanisms for the CCUS project in China’s coal-fired power plants: An option-game approach. Energy 2024, 288, 129694. [Google Scholar] [CrossRef]
- Hu, Y.; Gani, R.; Sundmacher, K.; Zhou, T. Assessing the future impact of 12 direct air capture technologies. Chem. Eng. Sci. 2024, 298, 120423. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Deng, Y.; Xu, D.; Tian, Y.; Xie, K. Water consumption and conservation assessment of the coal power industry in China. Sustain. Energy Technol. Assess. 2021, 47, 101464. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, Y.; Xu, Y.; Zheng, L.; Fan, Y. A factorial inexact copula stochastic programming (FICSP) approach for water-energy- food nexus system management. Agric. Water Manag. 2023, 277, 108069. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, J.; Wei, Z.; Zhu, Y.; Chang, S.; Li, Y.; Li, S.; Guo, Y. Analysis of Extreme Random Uncertainty in Energy and Environment Systems for Coal-Dependent City by a Copula-Based Interval Cost–Benefit Stochastic Approach. Sustainability 2024, 16, 745. [Google Scholar] [CrossRef]
- Kaytez, F. Evaluation of priority strategies for the expansion of installed wind power capacity in Turkey using a fuzzy analytic network process analysis. Renew. Energy 2022, 196, 1281–1293. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, G.; Wang, C.; Huo, Z. Linking agricultural water-food-environment nexus with crop area planning: A fuzzy credibility-based multi-objective linear fractional programming approach. Agric. Water Manag. 2023, 277, 108135. [Google Scholar] [CrossRef]
- Huang, K.; Fang, Y.R. Parameter Uncertainty and Sensitivity Evaluation of Copula-Based Multivariate Hydroclimatic Risk Assessment. J. Environ. Inform. 2021, 38, 131–144. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Li, Y.P.; Huang, G.H.; Ding, Y.K.; Yang, X. Developing a copula-based input-output method for analyzing energy-water nexus of Tajikistan. Energy 2023, 266, 126511. [Google Scholar] [CrossRef]
- Zhang, T.; Tan, Q.; Cai, Y.; Hu, K. A copula-based inexact model for managing agricultural water-energy-food nexus under differentiated composite risks and dual uncertainties. J. Clean. Prod. 2024, 434, 139707. [Google Scholar] [CrossRef]
- Liu, J.; Nie, S.; Shan, B.G.; Li, Y.P.; Huang, G.H.; Liu, Z.P. Development of an interval-credibility-chance constrained energy-water nexus system planning model-case study of Xiamen, China. Energy 2019, 181, 677–693. [Google Scholar] [CrossRef]
- Hwang, H.; Kim, S. Investigation on the effective factor calculation of electropolishing using full factorial design and mechanism model by microscopic analysis for super austenitic stainless steel. Surf. Interfaces 2023, 37, 102730. [Google Scholar] [CrossRef]
- National Bureau of Statistics (NBS). China Statistic Yearbook; China Statistics Press: Beijing, China, 2022.
- Fujian Statistics Bureau (FSB). Fujian Statistical Yearbook; China Statistics Press: Beijing, China, 2022.
- GB 20426-2006; Emission Standard for Pollutants from Coal Industry. Ministry of Ecology and Environment of the People’s Republic of China: Shanghai, Chian, 2006.
- GB 13223-2011; Emission Standard of Air Pollutants for Thermal Power Plants. Ministry of Ecology and Environment of the People’s Republic of China: Shanghai, Chian, 2011.
- GB 39728-2020; Emission Standard of Air Pollutants for Onshore Oil and Gas Exploitation and Production Industry. Ministry of Ecology and Environment of the People’s Republic of China: Shanghai, Chian, 2020.
- China Emission Accounts & Datasets (CAEDs). Latest Energy Inventories for China and its 30 Provinces and Cities. Compiled by Tsinghua University, China Emission Accounts & Datasets. 2021. Available online: https://www.ceads.net/data/province/energy_inventory/ (accessed on 15 October 2024).
- Jia, C.H.; Yan, P.; Liu, P.; Li, Z. Energy industrial water withdrawal under different energy development scenarios: A multi-regional approach and a case study of China. Renew. Sustain. Energy Rev. 2021, 135, 110224. [Google Scholar] [CrossRef]
- Fujian Provincial Department of Water Resources (FWR). Fujian Water Resources Bulletin; FWR: Fuzhou, China, 2022.
- Fujian Provincial Department of Ecology and Environment (FDE). Fujian Province Industrial Carbon Peak Implementation Plan. Guided by Ministry of Ecology and Environment of the People’s Republic of China; FDE: Fuzhou, China, 2023.
- DB35/T 772-2023; Norm of Water Intake of Industries. Fujian Province Market Supervision Administration: Fuzhou, China, 2023.
- Cao, X.; Liu, C.; Wu, M.X.; Li, Z.; Wang, Y.H.; Wen, Z.G. Heterogeneity and connection in the spatial-temporal evolution trend of China’s energy consumption at provincial level. Appl. Energy 2023, 336, 120842. [Google Scholar] [CrossRef]
- Dong, H.H.; Yang, J. Study on regional carbon quota allocation at provincial level in China from the perspective of carbon peak. J. Environ. Manag. 2024, 351, 119720. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Huang, G.; Chen, J.; Luo, B. Development of a multi-regional factorial optimization model for supporting electric power system’s low-carbon transition—A case study of Canada. Resour. Conserv. Recycl. 2023, 194, 106995. [Google Scholar] [CrossRef]
- Zhen, J.; Liu, X.; Wu, C.; Ji, L.; Huang, G. Operation optimization and performance evaluation of photovoltaic-wind-hydrogen-based integrated energy system under carbon trading mechanism and uncertainty for urban communities. J. Clean. Prod. 2024, 476, 143688. [Google Scholar] [CrossRef]
- Wang, S.; Huang, G.; Zhou, X.; Tian, C. A dual-interval fractional energy systems optimization for Nova Scotia, Canada. Renew. Sustain. Energy Rev. 2025, 212, 115455. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, G.; Liu, Y.; Luo, B.; Wang, S.; Li, Y.; LI, X. Energy-water-carbon system management in response to climate change in China under uncertainties (2026–2050). Resour. Conserv. Recycl. 2025, 212, 107957. [Google Scholar] [CrossRef]



| Sector | qjoint | Raw Coal Demand–Available Surface Water qjoint, qx − qy: 0.010, 0.010 − 0.010 0.100, 0.073 − 0.100 0.200, 0.198 − 0.163 | Raw Coal Demand–Carbon Emissions Allowance qjoint, qx − qy: 0.010, 0.010 − 0.010 0.100, 0.064 − 0.057 0.200, 0.141 − 0.141 | Available Surface Water–Carbon Emissions Allowance qjoint qx − qy: 0.010, 0.010 − 0.010 0.100, 0.063 − 0.058 0.200, 0.133 − 0.149 | Available Surface Water–Electricity Demand qjoint, qx − qy: 0.010, 0.010 − 0.010 0.100, 0.073 − 0.100 0.200, 0.198 − 0.163 | Electricity Demand–Maximum Final Use qjoint, qx − qy: 0.010, 0.010 − 0.010 0.100, 0.078 − 0.099 0.200, 0.200 − 0.091 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Year: 2030 | Year: 2060 | Year: 2030 | Year: 2060 | Year: 2030 | Year: 2060 | Year: 2030 | Year: 2060 | Year: 2030 | Year: 2060 | ||
| AFW | 0.010 | 0.15 − 1.23 | 0.10 − 3.45 | 0.15 − 3.48 | 0.10 − 0 | 1.23 − 3.48 | 3.45 − 0 | 1.23 − 7.93 | 3.45 − 17.38 | 7.93 − 0.39 | 17.38 − 0.55 |
| 0.100 | 0.14 − 1.35 | 0.09 − 3.80 | 0.14 − 3.74 | 0.095 − 0 | 1.33 − 3.72 | 3.72 − 0 | 1.33 − 7.22 | 3.74 − 15.83 | 7.31 − 0.43 | 16.03 − 0.59 | |
| 0.200 | 0.13 − 1.29 | 0.09 − 3.90 | 0.13 − 3.88 | 0.090 − 0 | 1.38 − 3.89 | 3.86 − 0 | 1.41 − 7.02 | 3.95 − 15.38 | 6.92 − 0.42 | 15.17 − 0.59 | |
| EMD | 0.010 | 0.22 − 0.77 | 0.21 − 3.25 | 0.22 − 1.99 | 0.21 − 0 | 0.77 − 1.99 | 3.25 − 0 | 0.77 − 1.58 | 3.25 − 1.61 | 1.58 − 0.036 | 1.61 − 0.13 |
| 0.100 | 0.20 − 0.85 | 0.19 − 3.58 | 0.20 − 2.14 | 0.19 − 0 | 0.83 − 2.13 | 3.50 − 0 | 0.84 − 1.44 | 3.52 − 1.46 | 1.45 − 0.039 | 1.48 − 0.15 | |
| 0.200 | 0.19 − 0.87 | 0.18 − 3.67 | 0.19 − 2.22 | 0.18 − 0 | 0.86 − 2.23 | 3.63 − 0 | 0.88 − 1.40 | 3.72 − 1.42 | 1.38 − 0.039 | 1.40 − 0.14 | |
| CIP | 0.010 | 2.40 − 9.11 | 1.64 − 7.24 | 2.40 − 12.63 | 1.64 − 0 | 9.11 − 12.63 | 7.24 − 0 | 9.11 − 48.21 | 7.24 − 70.31 | 48.21 − 0.21 | 70.31 − 0.33 |
| 0.100 | 2.19 − 10.03 | 1.49 − 7.98 | 2.21 − 13.58 | 1.50 − 0 | 9.82 − 13.51 | 7.81 − 0 | 9.88 − 43.89 | 7.86 − 64.02 | 44.44 − 0.23 | 64.82 − 0.36 | |
| 0.200 | 2.05 − 10.30 | 1.40 − 8.19 | 2.10 − 14.11 | 1.43 − 0 | 10.18 − 14.15 | 8.10 − 0 | 10.42 − 42.65 | 8.29 − 62.20 | 42.07 − 0.23 | 61.35 − 0.36 | |
| CON | 0.010 | 0.015 − 1.80 | 0.01 − 3.88 | 0.015 − 4.09 | 0.01 − 0 | 1.80 − 4.09 | 3.88 − 0 | 1.80 − 8.77 | 3.88 − 18.39 | 8.77 − 2.80 | 18.39 − 4.14 |
| 0.100 | 0.014 − 1.99 | 0.009 − 4.27 | 0.014 − 4.40 | 0.009 − 0 | 1.94 − 4.38 | 4.18 − 0 | 1.96 − 7.98 | 4.21 − 16.74 | 8.08 − 3.02 | 16.95 − 4.47 | |
| 0.200 | 0.013 − 2.04 | 0.008 − 4.39 | 0.013 − 4.57 | 0.009 − 0 | 2.02 − 4.59 | 4.34 − 0 | 2.06 − 7.76 | 4.44 − 16.27 | 7.65 − 3.01 | 16.04 − 4.45 | |
| MPM | 0.010 | 1.40 − 144.46 | 1.11 − 94.23 | 1.40 − 22.82 | 1.11 − 0 | 144.46 − 22.82 | 94.23 − 0 | 144.46 − 46.24 | 94.23 − 59.71 | 46.24 − 0.17 | 59.71 − 0.27 |
| 0.100 | 1.28 − 159.14 | 1.02 − 103.81 | 1.29 − 24.55 | 1.02 − 0 | 155.73 − 24.43 | 101.58 − 0 | 156.74 − 42.10 | 102.24 − 54.37 | 42.63 − 0.19 | 55.05 − 0.29 | |
| 0.200 | 1.19 − 163.38 | 0.95 − 106.57 | 1.22 − 25.50 | 0.97 − 0 | 161.53 − 25.57 | 105.36 − 0 | 165.27 − 40.91 | 107.80 − 52.83 | 40.35 − 0.19 | 52.11 − 0.29 | |
| EHW | 0.010 | 12.98 − 11.65 | 7.99 − 5.57 | 12.98 − 60.44 | 7.99 − 0 | 11.65 − 60.44 | 5.57 − 0 | 11.65 − 34.71 | 5.57 − 39.30 | 34.71 − 0.22 | 39.30 − 0.27 |
| 0.100 | 11.86 − 12.84 | 7.30 − 6.13 | 11.94 − 65.01 | 7.35 − 0 | 12.56 − 64.69 | 6.00 − 0 | 12.64 − 31.60 | 6.04 − 35.78 | 32.00 − 0.24 | 36.23 − 0.29 | |
| 0.200 | 11.08 − 13.18 | 6.82 − 6.29 | 11.37 − 67.53 | 7.00 − 0 | 13.03 − 67.73 | 6.22 − 0 | 13.33 − 30.71 | 6.37 − 34.77 | 30.29 − 0.24 | 34.29 − 0.29 | |
| OSI | 0.010 | 2.29 − 31.82 | 1.19 − 23.53 | 2.29 − 12.18 | 1.19 − 0 | 31.82 − 12.18 | 23.53 − 0 | 31.82 − 92.12 | 23.53 − 119.23 | 92.12 − 4.34 | 119.23 − 6.42 |
| 0.100 | 2.09 − 35.05 | 1.08 − 25.92 | 2.11 − 13.10 | 1.09 − 0 | 34.30 − 13.04 | 25.37 − 0 | 34.52 − 83.88 | 25.53 − 108.56 | 84.93 − 4.69 | 109.92 − 6.93 | |
| 0.200 | 1.95 − 35.99 | 1.01 − 26.62 | 2.00 − 13.61 | 1.04 − 0 | 35.58 − 13.65 | 26.31 − 0 | 36.40 − 81.50 | 26.92 − 105.48 | 80.39 − 4.67 | 104.04 − 6.91 | |
| TPT | 0.010 | 0.013 − 6.04 | 0.005 − 6.08 | 0.013 − 18.06 | 0.005 − 0 | 6.04 − 18.06 | 6.08 − 0 | 6.04 − 10.27 | 6.08 − 19.66 | 10.27 − 0.51 | 19.66 − 0.99 |
| 0.100 | 0.012 − 6.65 | 0.005 − 6.70 | 0.012 − 19.43 | 0.005 − 0 | 6.51 − 19.33 | 6.56 − 0 | 6.55 − 9.35 | 6.60 − 17.90 | 9.47 − 0.55 | 18.12 − 1.07 | |
| 0.200 | 0.011 − 6.83 | 0.005 − 6.88 | 0.011 − 20.18 | 0.005 − 0 | 6.75 − 20.24 | 6.80 − 0 | 6.91 − 9.09 | 6.96 − 17.39 | 8.96 − 0.55 | 17.15 − 1.06 | |
| OTI | 0.010 | 0.06 − 1.05 | 0.035 − 3.38 | 0.06 − 2.77 | 0.035 − 0 | 1.05 − 2.77 | 3.38 − 0 | 1.05 − 55.15 | 3.38 − 76.14 | 55.15 − 3.74 | 76.14 − 7.24 |
| 0.100 | 0.055 − 1.16 | 0.032 − 3.72 | 0.055 − 2.98 | 0.032 − 0 | 1.13 − 2.97 | 3.64 − 0 | 1.14 − 50.22 | 3.66 − 69.32 | 50.85 − 4.04 | 70.19 − 7.82 | |
| 0.200 | 0.051 − 1.19 | 0.030 − 3.82 | 0.052 − 3.10 | 0.031 − 0 | 1.17 − 3.11 | 3.77 − 0 | 1.20 − 48.79 | 3.86 − 67.36 | 48.13 − 4.02 | 66.44 − 7.79 | |
| Parameter | Credibility | Year | AFW | EMD | CIP | CON | MPM | EHW | OSI | TPT | OTI |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Indirect water utilization allowance (unit: 106 m3) | λ = 0.6 | 2030 | 6.78 | 2.45 | 38.76 | 11.09 | 184.88 | 461.14 | 54.15 | 53.04 | 4.79 |
| 2060 | 6.20 | 2.50 | 32.46 | 8.58 | 153.66 | 306.35 | 47.27 | 38.48 | 4.89 | ||
| λ = 0.8 | 2030 | 6.58 | 2.37 | 37.59 | 10.76 | 179.32 | 447.27 | 52.52 | 51.44 | 4.65 | |
| 2060 | 6.02 | 2.43 | 31.48 | 8.33 | 149.03 | 297.13 | 45.85 | 37.32 | 4.74 | ||
| λ = 1.0 | 2030 | 6.37 | 2.30 | 36.43 | 10.42 | 173.76 | 433.40 | 50.89 | 49.85 | 4.51 | |
| 2060 | 5.83 | 2.35 | 30.50 | 8.07 | 144.41 | 287.92 | 44.42 | 36.17 | 4.60 | ||
| Indirect carbon emissions allowance (unit: 106 t) | λ = 0.6 | 2030 | 20.68 | 2.08 | 5.97 | 298.83 | 2.98 | 2.43 | 409.45 | 36.05 | 162.78 |
| 2060 | 8.52 | 2.62 | 0.02 | 224.20 | 7.54 | 40.17 | 312.94 | 39.58 | 159.71 | ||
| λ = 0.8 | 2030 | 20.05 | 2.01 | 5.79 | 289.84 | 2.89 | 2.36 | 397.13 | 34.96 | 157.89 | |
| 2060 | 8.27 | 2.54 | 0.02 | 217.45 | 7.31 | 38.96 | 303.52 | 38.39 | 154.91 | ||
| λ = 1.0 | 2030 | 19.43 | 1.95 | 5.61 | 280.86 | 2.80 | 2.29 | 384.82 | 33.88 | 152.99 | |
| 2060 | 8.01 | 2.46 | 0.02 | 210.71 | 7.08 | 37.75 | 294.11 | 37.20 | 150.10 | ||
| Maximum carbon capture and storage ability (unit: 106 t) | λ = 0.6 | 2030 | 0 | 0.29 | 1.87 | 0.61 | 3.39 | 8.97 | 1.81 | 0 | 0 |
| 2060 | 0 | 5.02 | 11.83 | 6.93 | 21.51 | 20.44 | 11.07 | 0 | 0 | ||
| λ = 0.8 | 2030 | 0 | 0.29 | 1.82 | 0.59 | 3.29 | 8.70 | 1.75 | 0 | 0 | |
| 2060 | 0 | 4.87 | 11.48 | 6.72 | 20.86 | 19.82 | 10.73 | 0 | 0 | ||
| λ = 1.0 | 2030 | 0 | 0.28 | 1.76 | 0.57 | 3.18 | 8.43 | 1.70 | 0 | 0 | |
| 2060 | 0 | 4.72 | 11.12 | 6.51 | 20.21 | 19.21 | 10.40 | 0 | 0 | ||
| Maximum forest carbon sink ability (unit: 106 t) | λ = 0.6 | 2030 | 0.27 | 0.17 | 1.08 | 0.35 | 1.95 | 5.16 | 1.04 | 1.42 | 0.22 |
| 2060 | 3.37 | 2.24 | 5.28 | 3.09 | 9.60 | 9.13 | 4.94 | 9.64 | 2.42 | ||
| λ = 0.8 | 2030 | 0.26 | 0.16 | 1.04 | 0.34 | 1.88 | 4.99 | 1.01 | 1.38 | 0.21 | |
| 2060 | 3.26 | 2.17 | 5.11 | 2.99 | 9.28 | 8.82 | 4.78 | 9.32 | 2.34 | ||
| λ = 1.0 | 2030 | 0.26 | 0.16 | 1.01 | 0.33 | 1.82 | 4.81 | 0.97 | 1.33 | 0.20 | |
| 2060 | 3.15 | 2.09 | 4.93 | 2.89 | 8.96 | 8.51 | 4.61 | 8.99 | 2.26 | ||
| Carbon quota investment (unit: 109 CNY) | λ = 0.6 | 2030 | 0.049 | 0.028 | 0.179 | 0.058 | 0.323 | 0.855 | 0.172 | 0.256 | 0.039 |
| 2060 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| λ = 0.8 | 2030 | 0.048 | 0.027 | 0.173 | 0.056 | 0.313 | 0.830 | 0.167 | 0.248 | 0.038 | |
| 2060 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| λ = 1.0 | 2030 | 0.046 | 0.026 | 0.168 | 0.054 | 0.304 | 0.804 | 0.162 | 0.240 | 0.037 | |
| 2060 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Li, J.; Zhao, S.; Liu, J.; Gao, P. Exploring Optimal Regional Energy-Related Green Low-Carbon Socioeconomic Development Policies by an Extended System Planning Model. Sustainability 2025, 17, 9739. https://doi.org/10.3390/su17219739
Li X, Li J, Zhao S, Liu J, Gao P. Exploring Optimal Regional Energy-Related Green Low-Carbon Socioeconomic Development Policies by an Extended System Planning Model. Sustainability. 2025; 17(21):9739. https://doi.org/10.3390/su17219739
Chicago/Turabian StyleLi, Xiao, Jiawei Li, Shuoheng Zhao, Jing Liu, and Pangpang Gao. 2025. "Exploring Optimal Regional Energy-Related Green Low-Carbon Socioeconomic Development Policies by an Extended System Planning Model" Sustainability 17, no. 21: 9739. https://doi.org/10.3390/su17219739
APA StyleLi, X., Li, J., Zhao, S., Liu, J., & Gao, P. (2025). Exploring Optimal Regional Energy-Related Green Low-Carbon Socioeconomic Development Policies by an Extended System Planning Model. Sustainability, 17(21), 9739. https://doi.org/10.3390/su17219739






