Multi-Scale Analysis of Influencing Factors for Temporal and Spatial Variations in PM2.5 in the Yangtze River Economic Belt
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Research Scale
2.3. Data Sources and Preprocessing
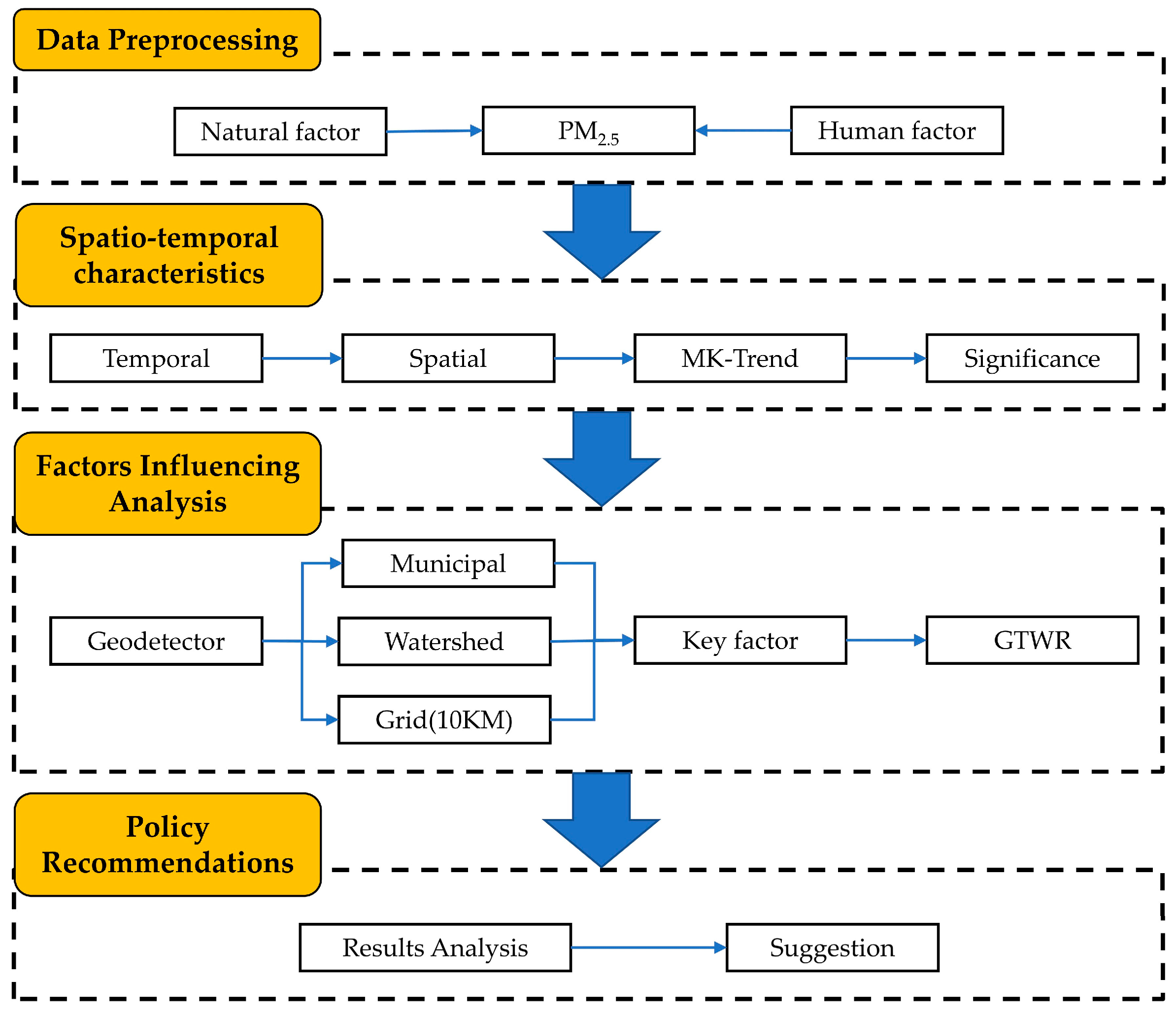
2.4. Method and Technique Process
3. Results
3.1. Spatial–Temporal Variability of PM2.5
3.2. Analysis of Factors Influencing PM2.5
3.2.1. Geodetector Results
3.2.2. GTWR Results
4. Discussion
4.1. Multi-Scale Factor Analysis
4.2. Policy Recommendations
4.3. Shortcomings and Outlook
5. Conclusions
- From 2005 to 2020, the annual average PM2.5 concentration in the Yangtze River Economic Belt exhibited an inverted U-shaped trend over time, with 2013 serving as the inflection point. Spatially, the annual average PM2.5 concentration in the Yangtze River Economic Belt showed a distribution pattern of lower levels in the west and higher levels in the central and eastern regions, revealing distinct agglomeration characteristics.
- From 2005 to 2020, the annual average PM2.5 concentration in the Yangtze River Economic Belt showed a significant overall downward trend in both spatiotemporal variations, with no regions exhibiting a notable increase. PM2.5 concentrations decreased slowly in the western region, while they declined more rapidly in the central and eastern regions.
- At the municipal, watershed, and grid scales, the spatial variation in annual average PM2.5 concentrations along the Yangtze River Economic Belt is primarily influenced by three factors: PFA, PISA, and PD. The impacts of NTL and AR are relatively minor. NDVI and PWA exert a stronger influence at larger scale, while MAT and SDE exert greater influence at smaller scale. Human activity-related factors exert a greater influence on the spatial variation in PM2.5 concentrations within the region.
- NDVI, CVO, and PM2.5 concentration primarily exhibit a negative correlation; MAT, PFA, PD, and SDE primarily exhibit a positive correlation with PM2.5 concentration; and PWA and PISA exert dual effects on PM2.5 concentrations within the region, each covering approximately half the area. At different scales, the spatial distribution of the same factor’s impact on PM2.5 concentrations is largely consistent, though some variations exist. A smaller scale would yield more refined results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
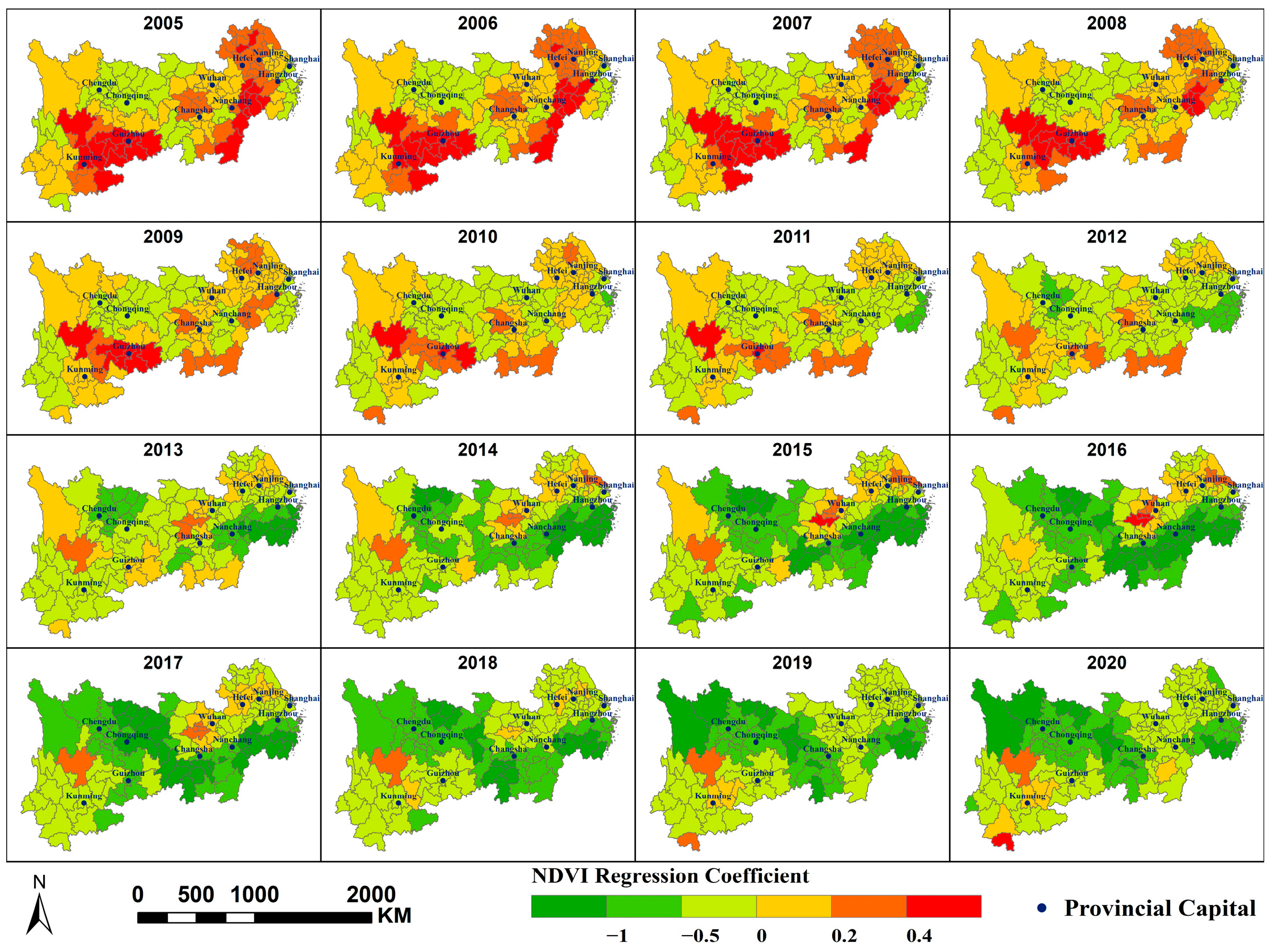
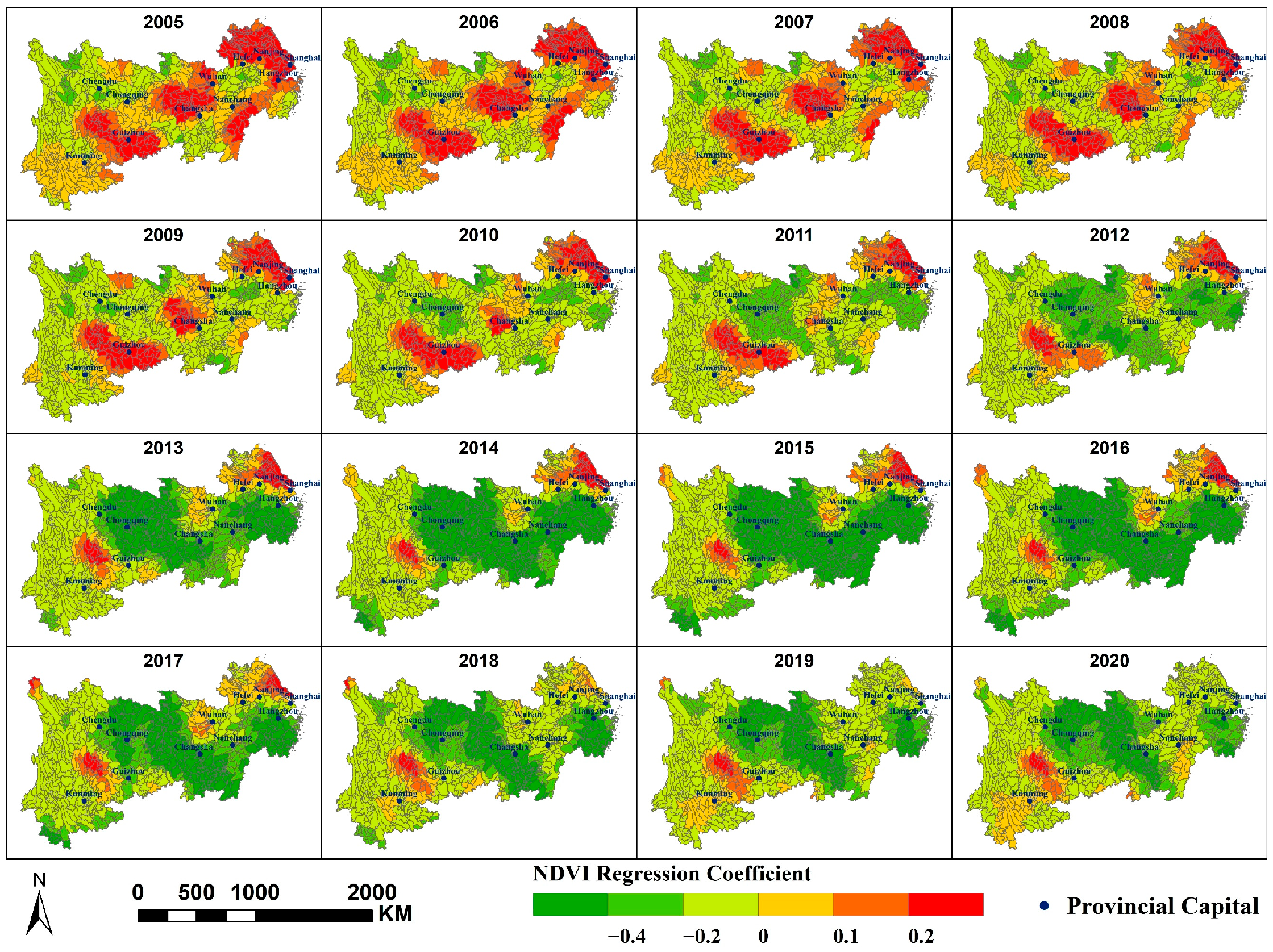

Appendix A.2


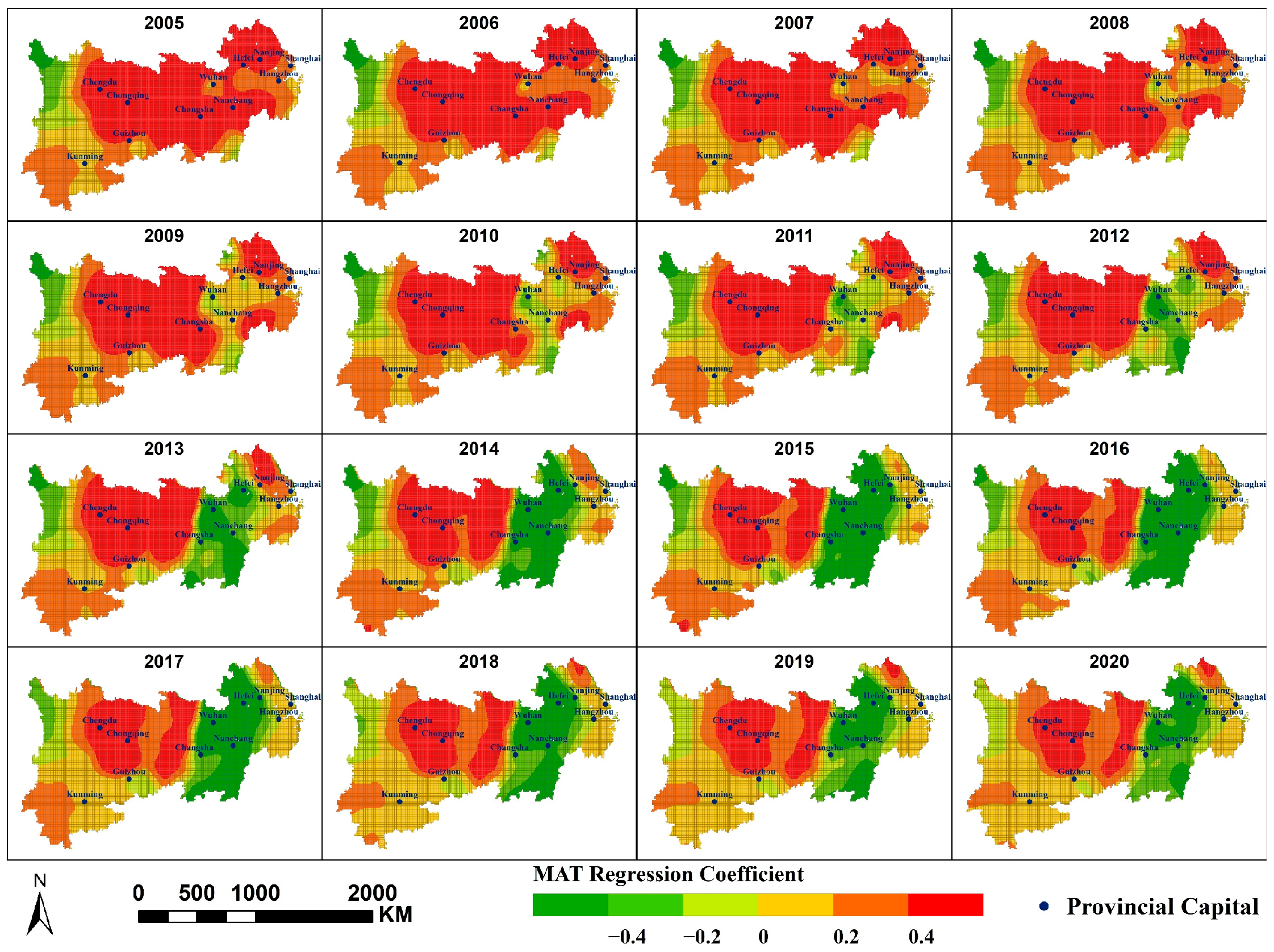
Appendix A.3
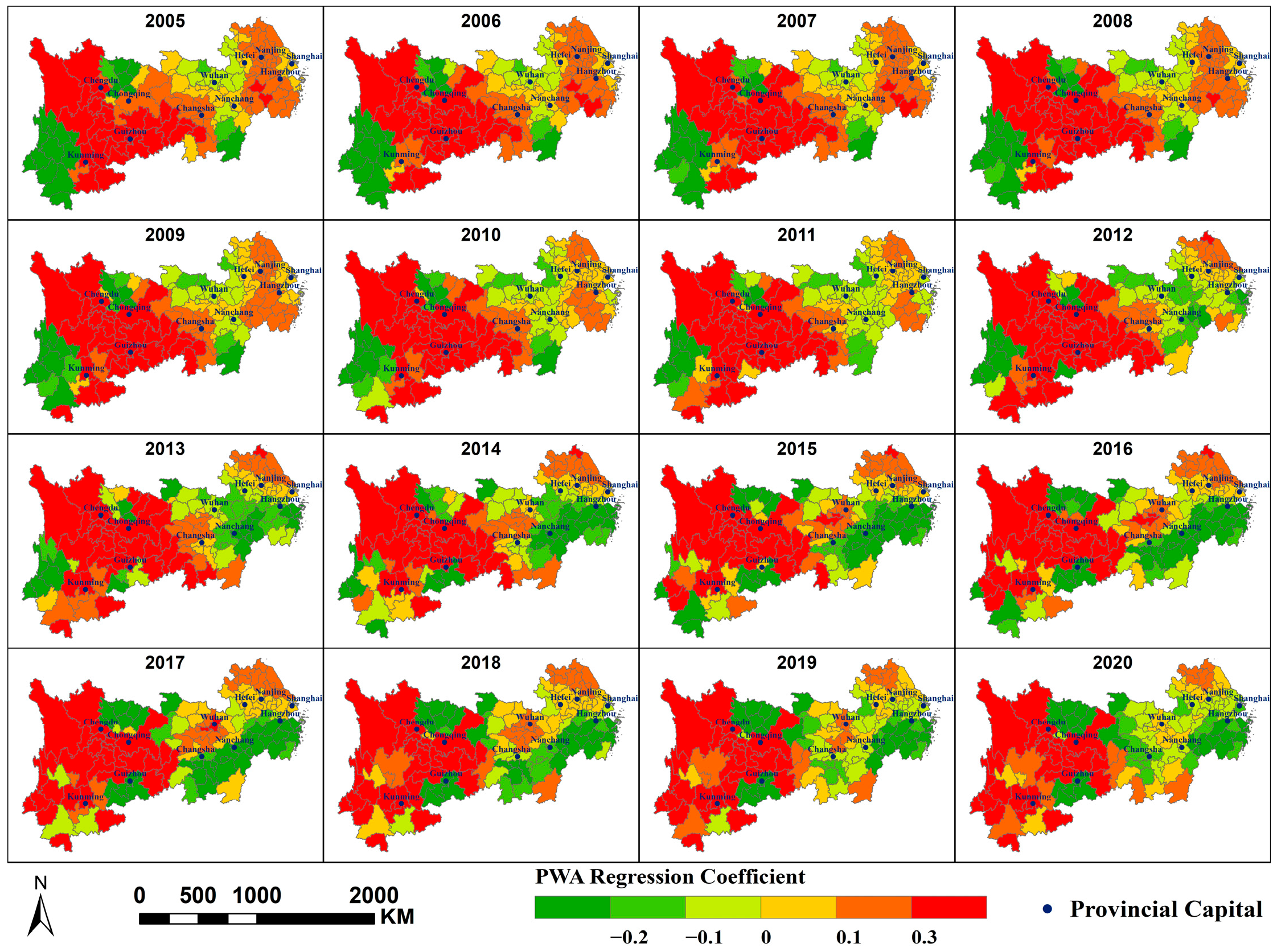


Appendix A.4
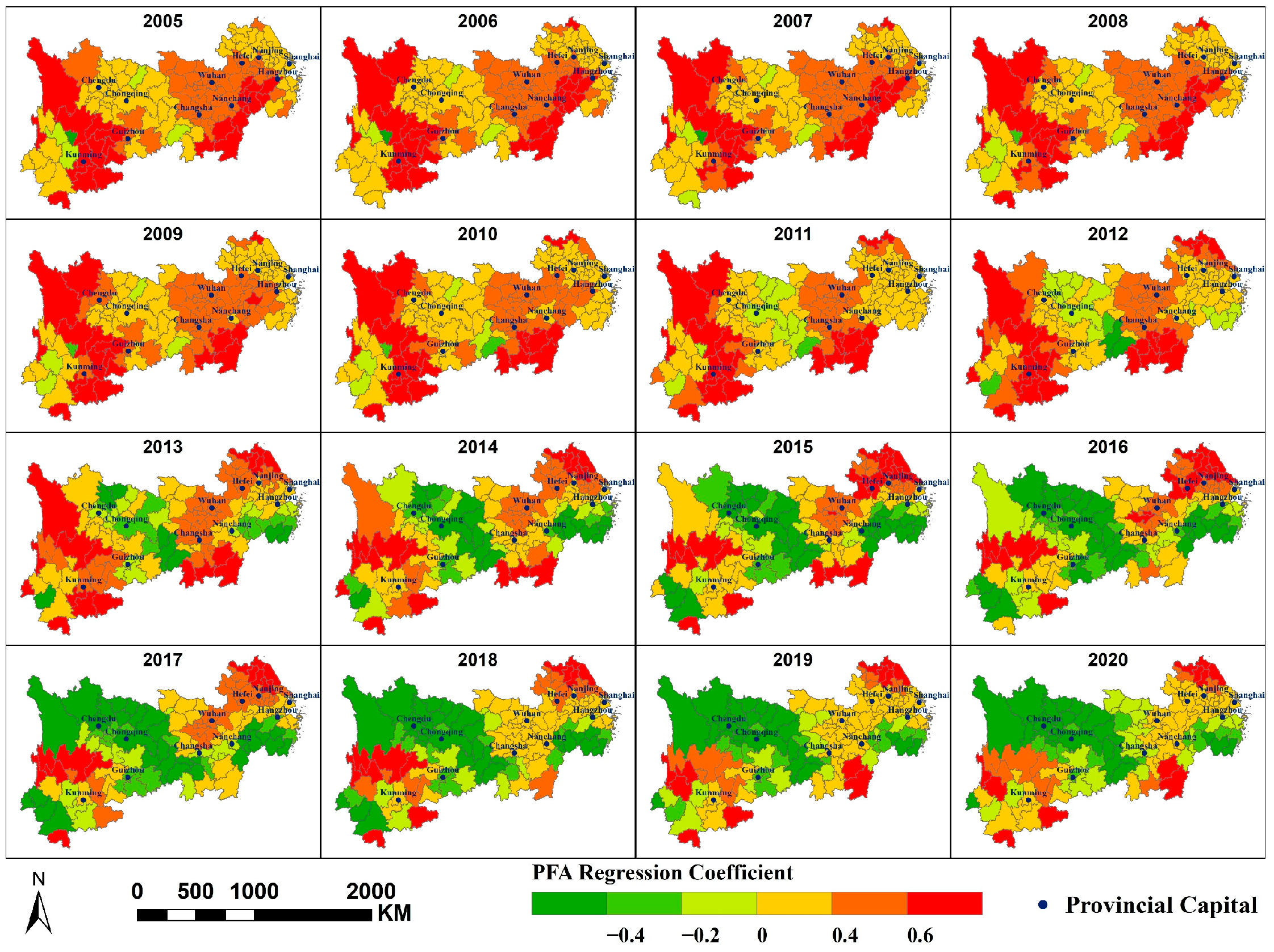
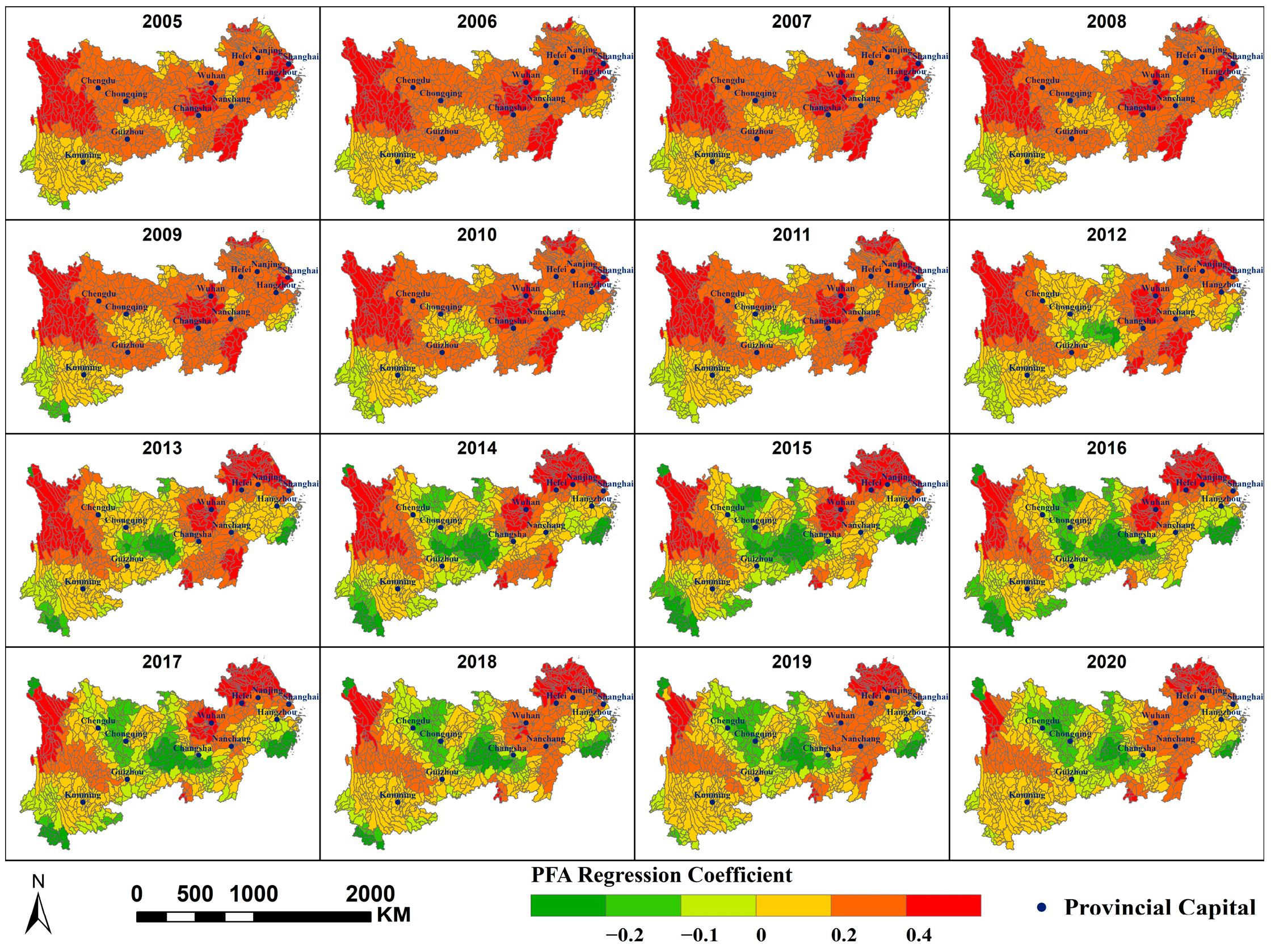
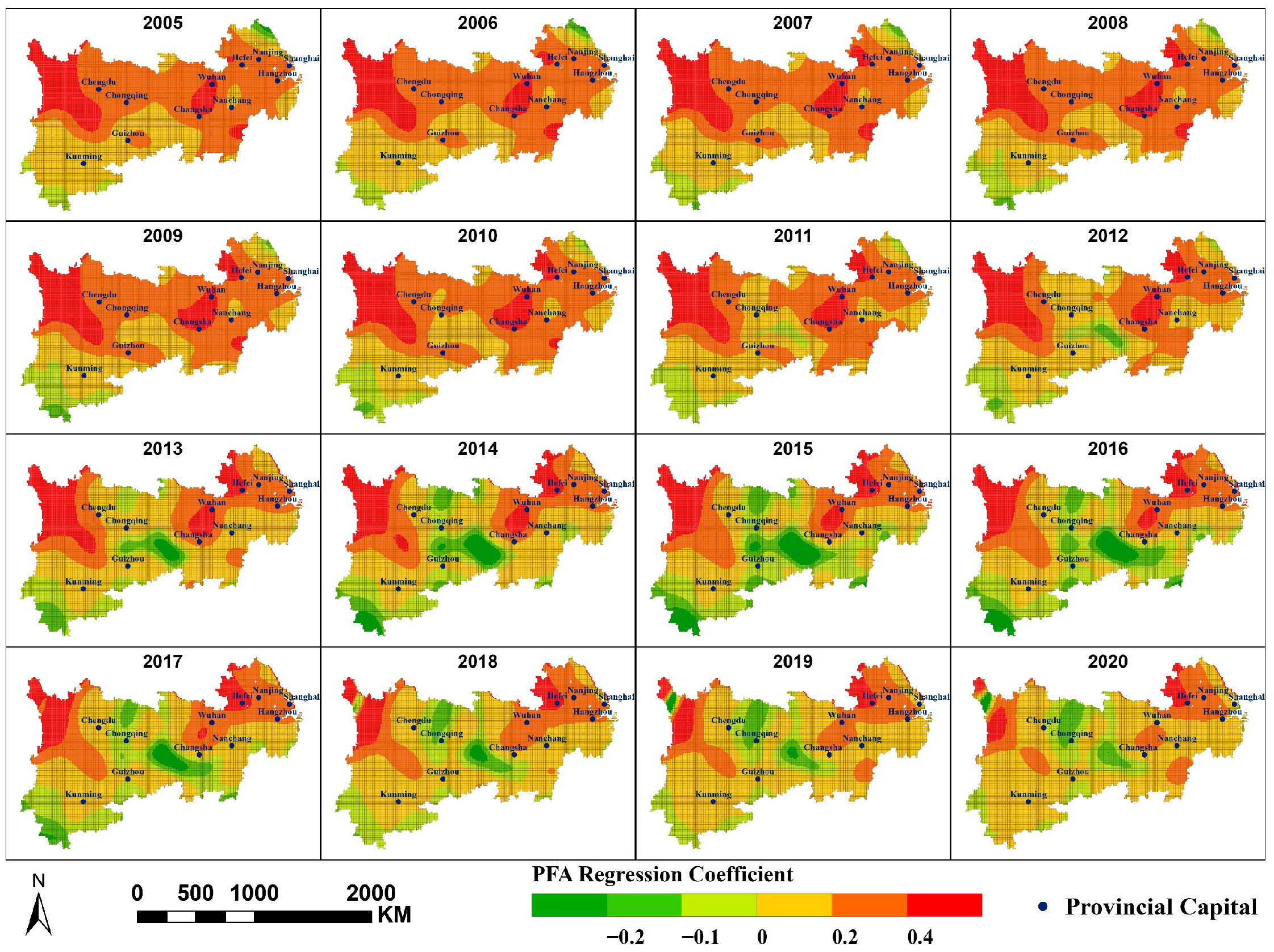
Appendix A.5
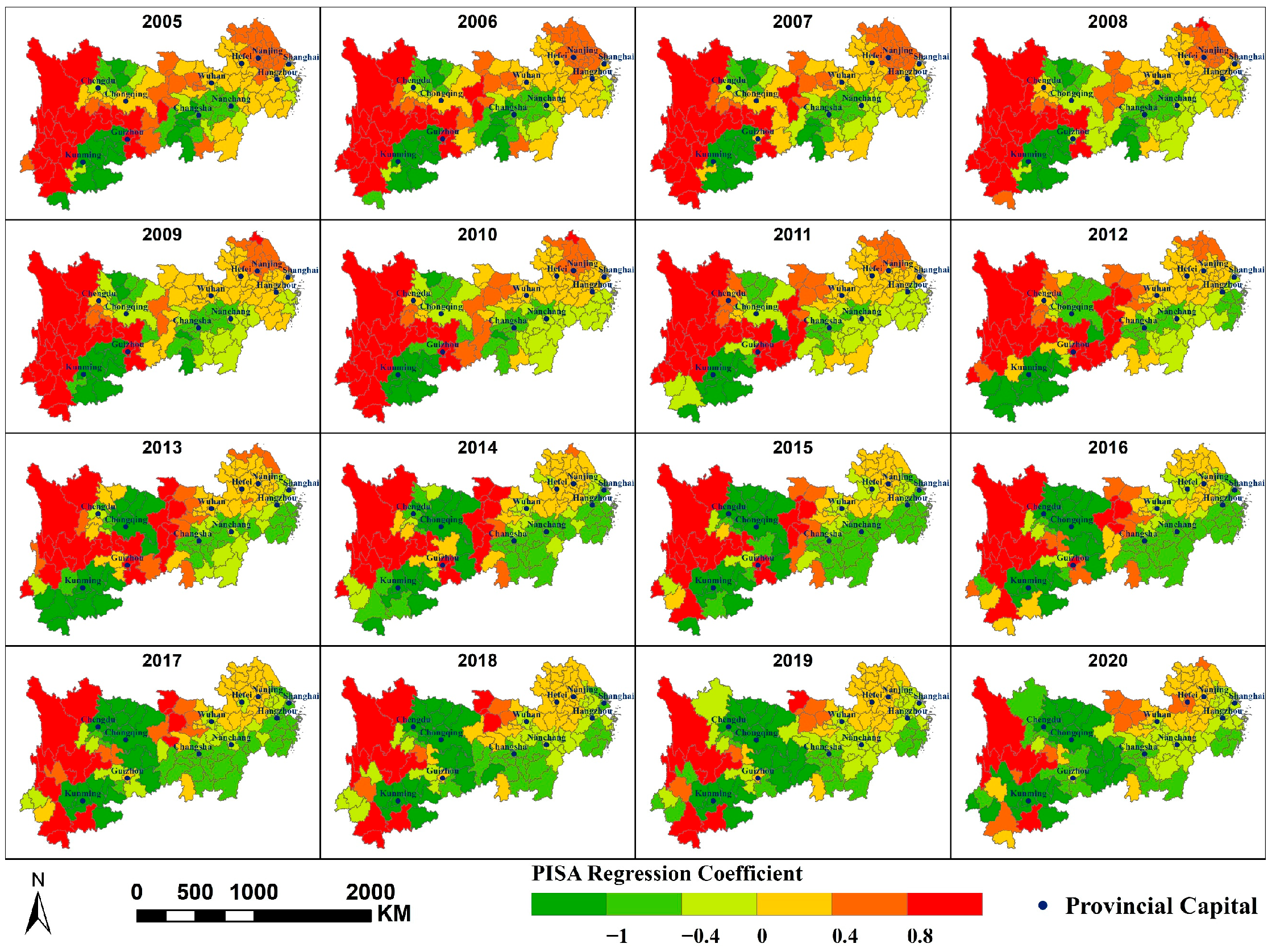
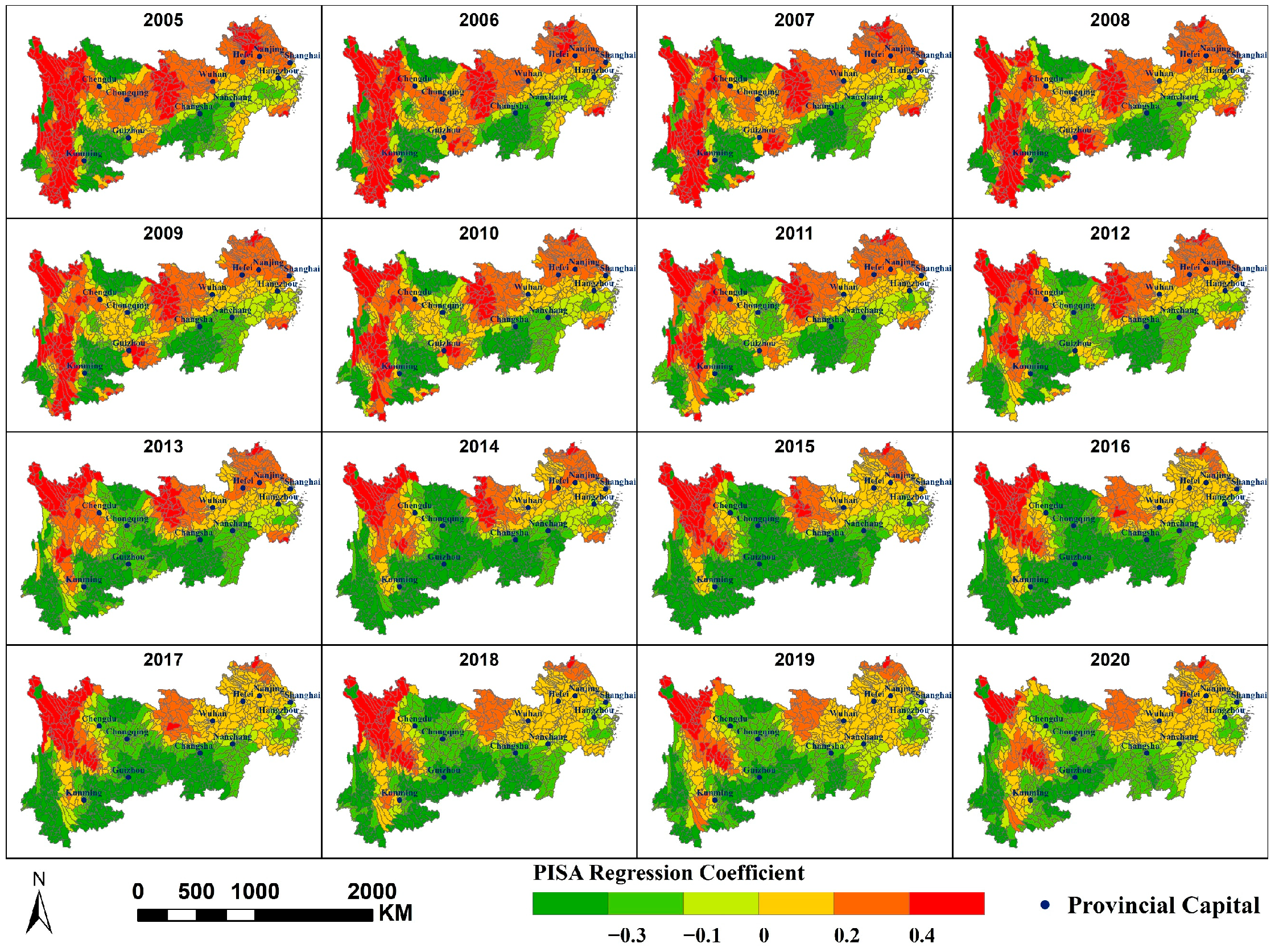

Appendix A.6
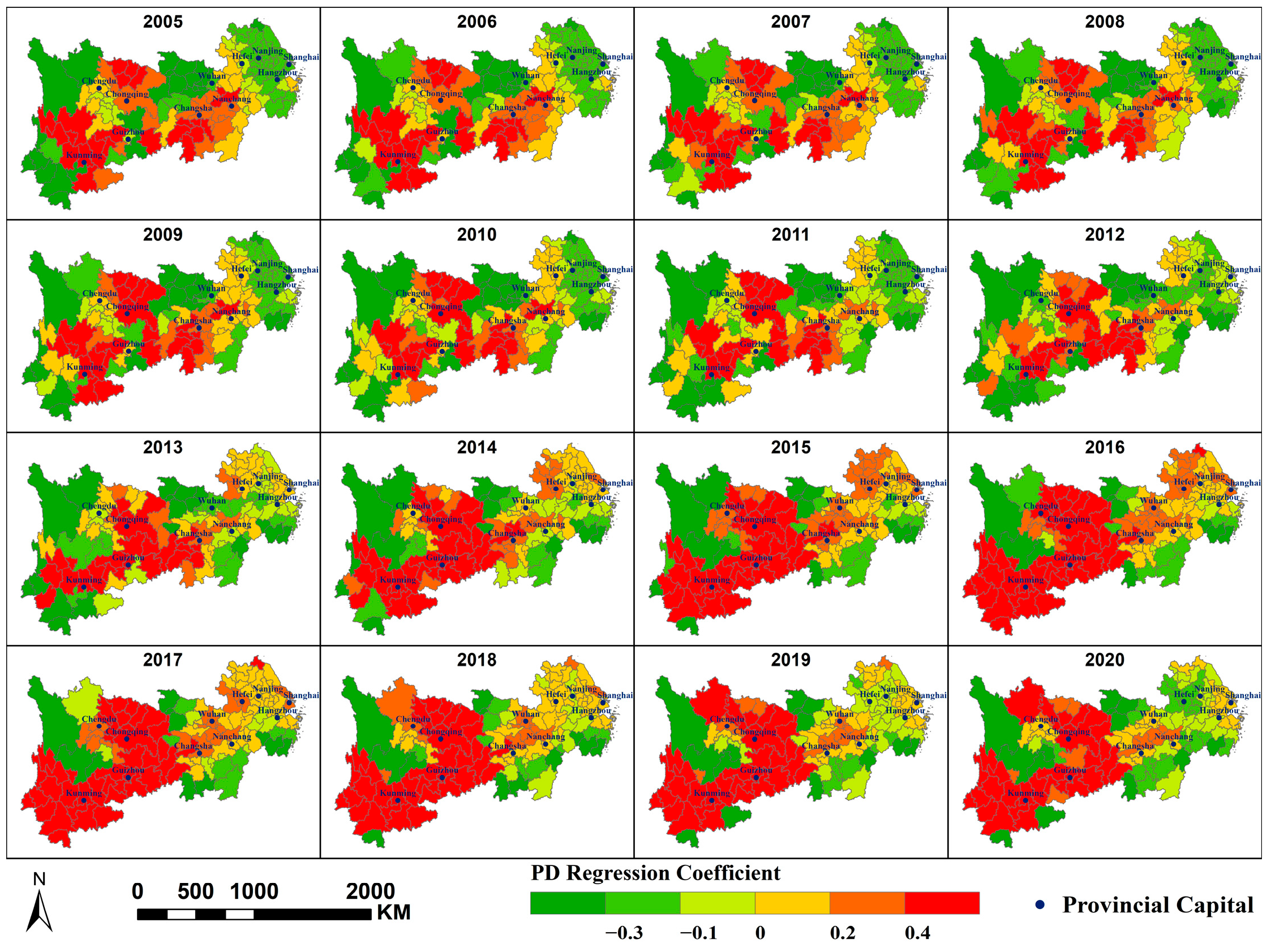
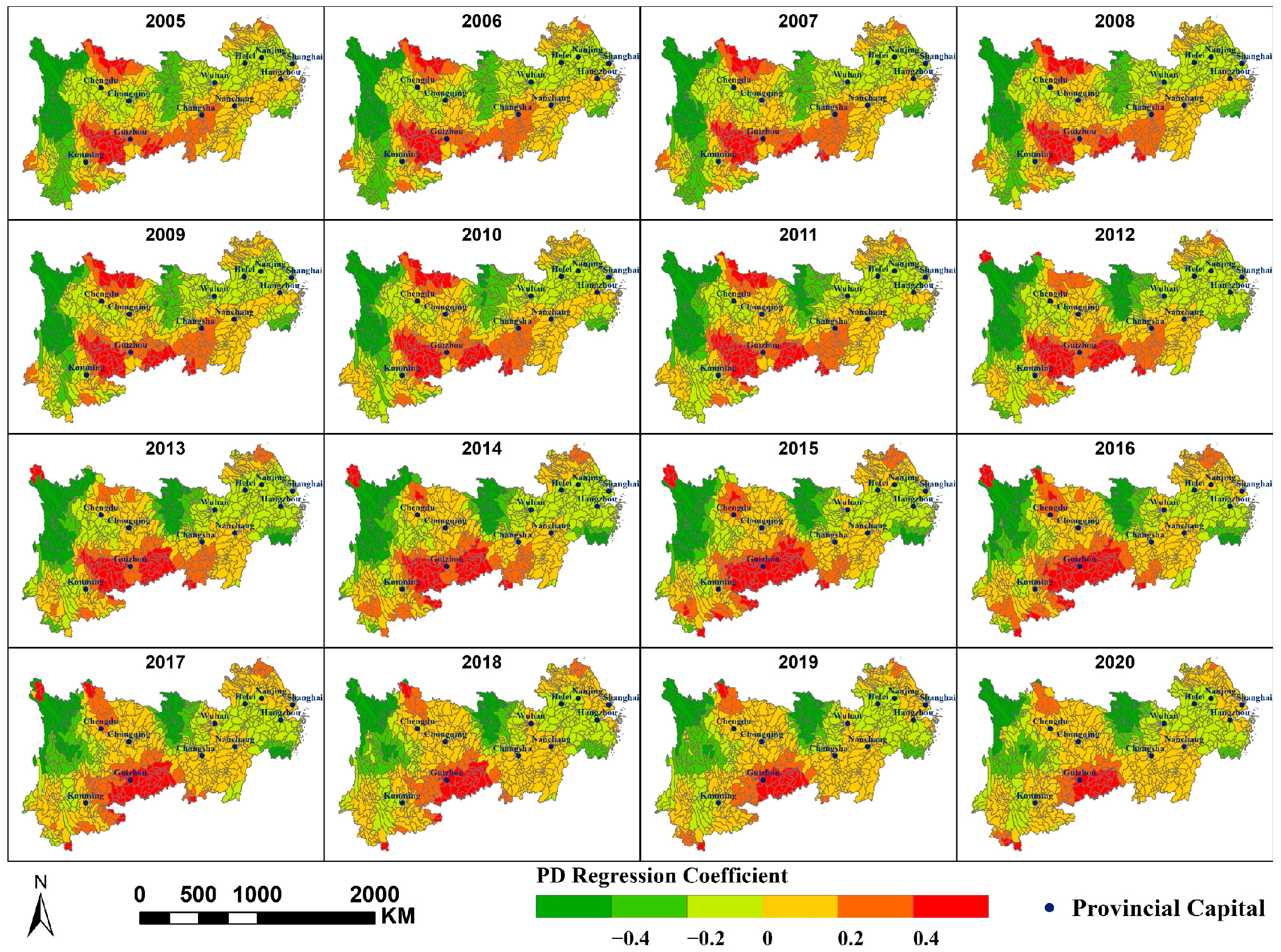
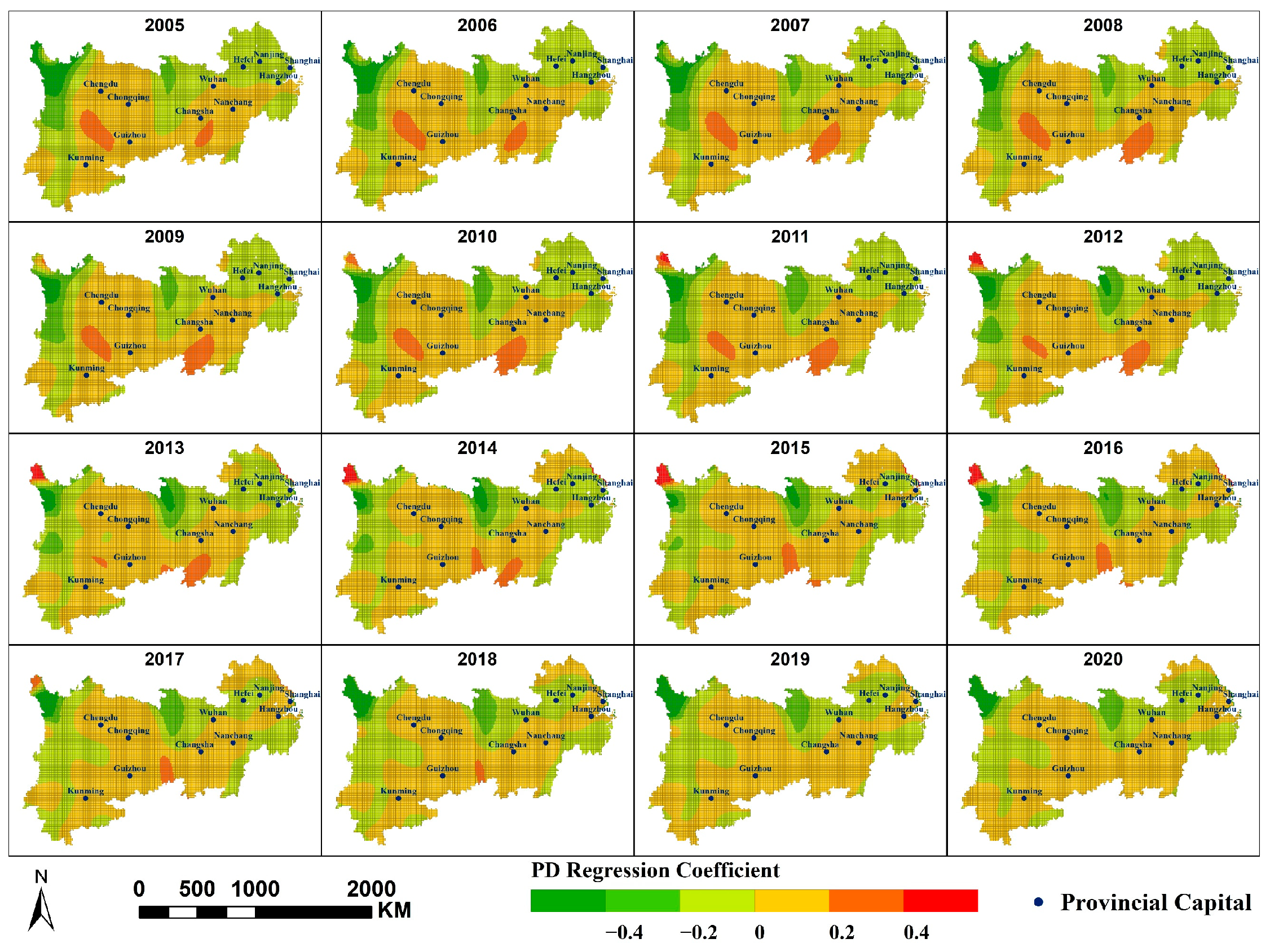
Appendix A.7
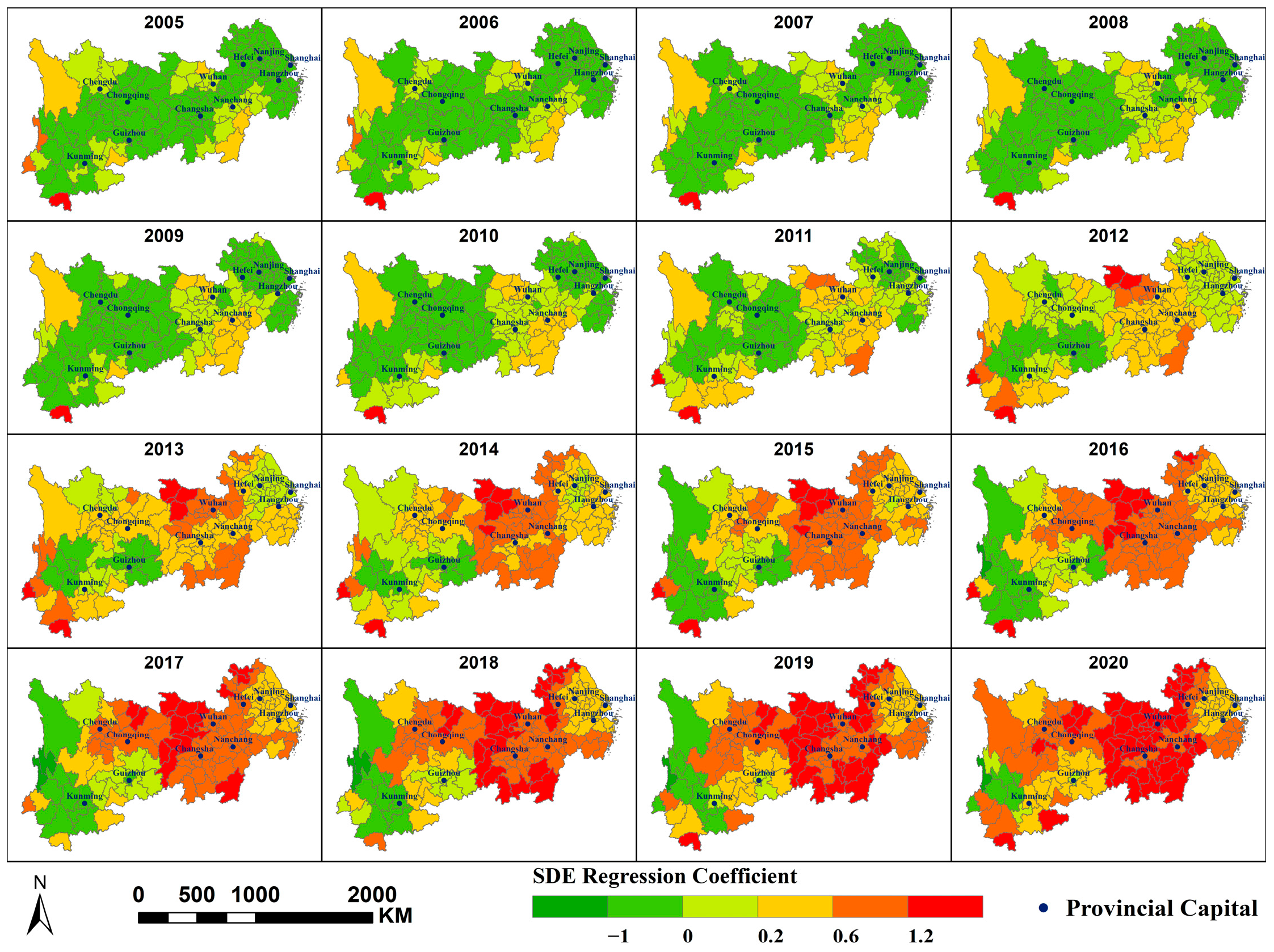


Appendix A.8
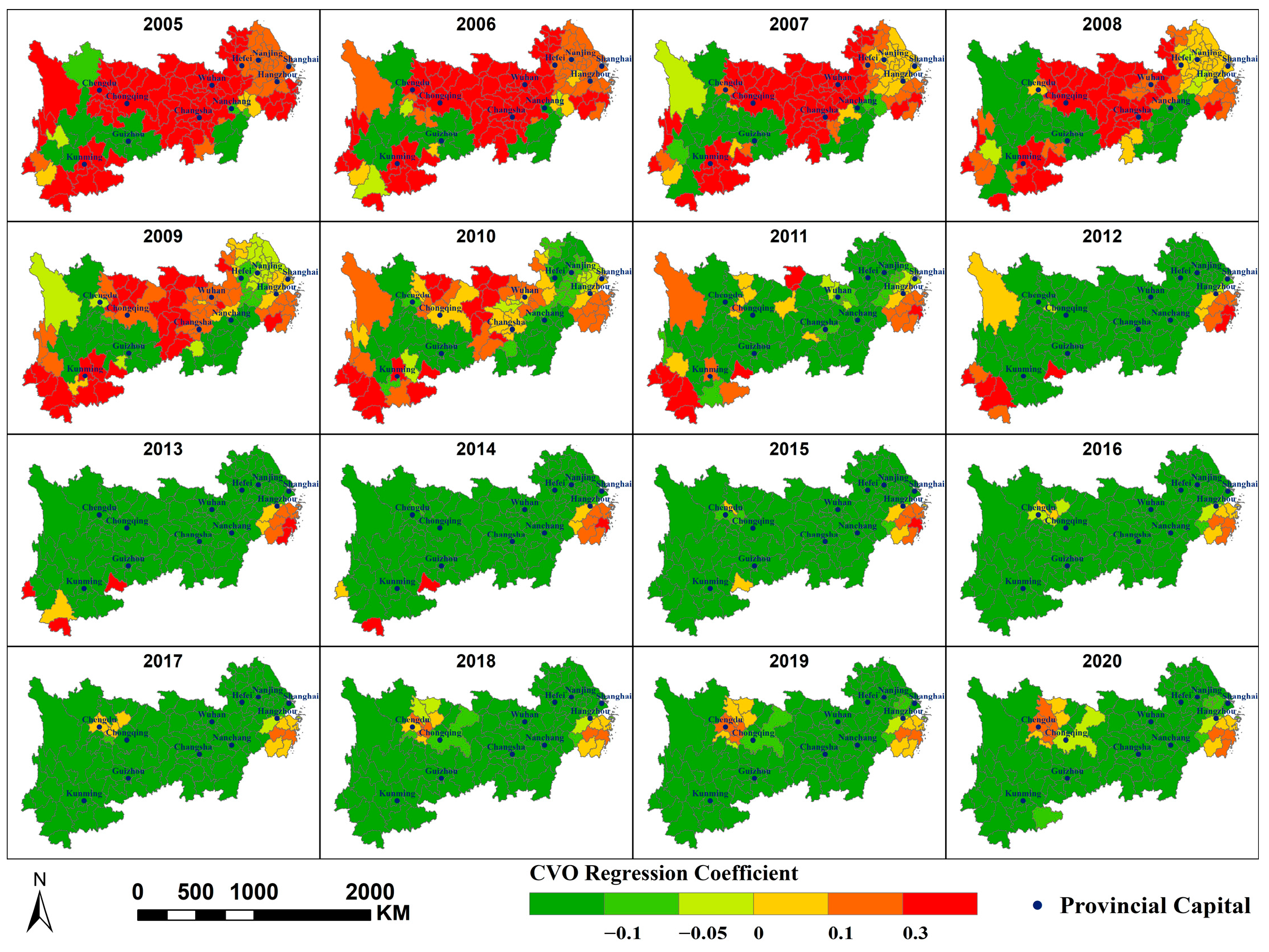
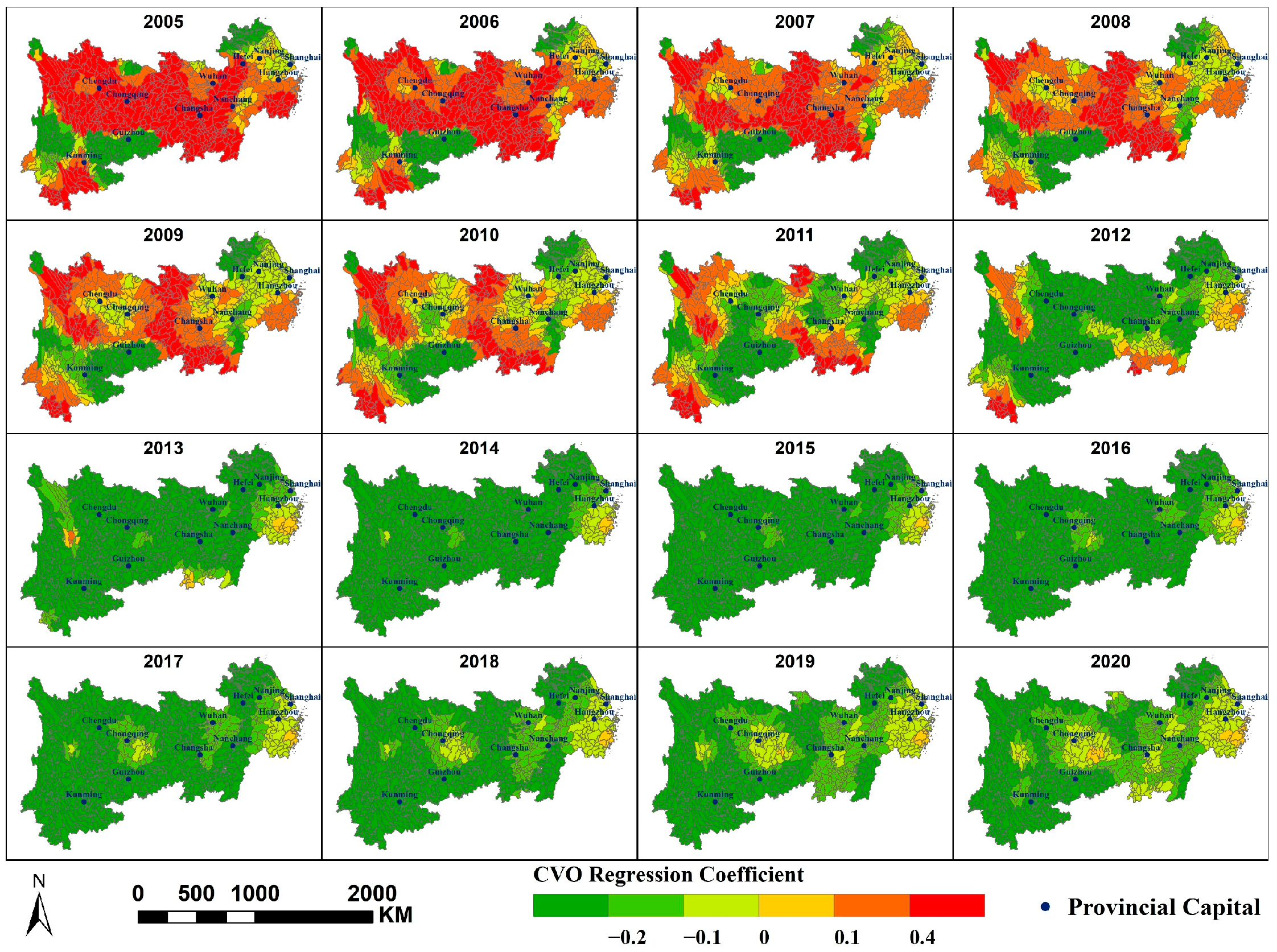
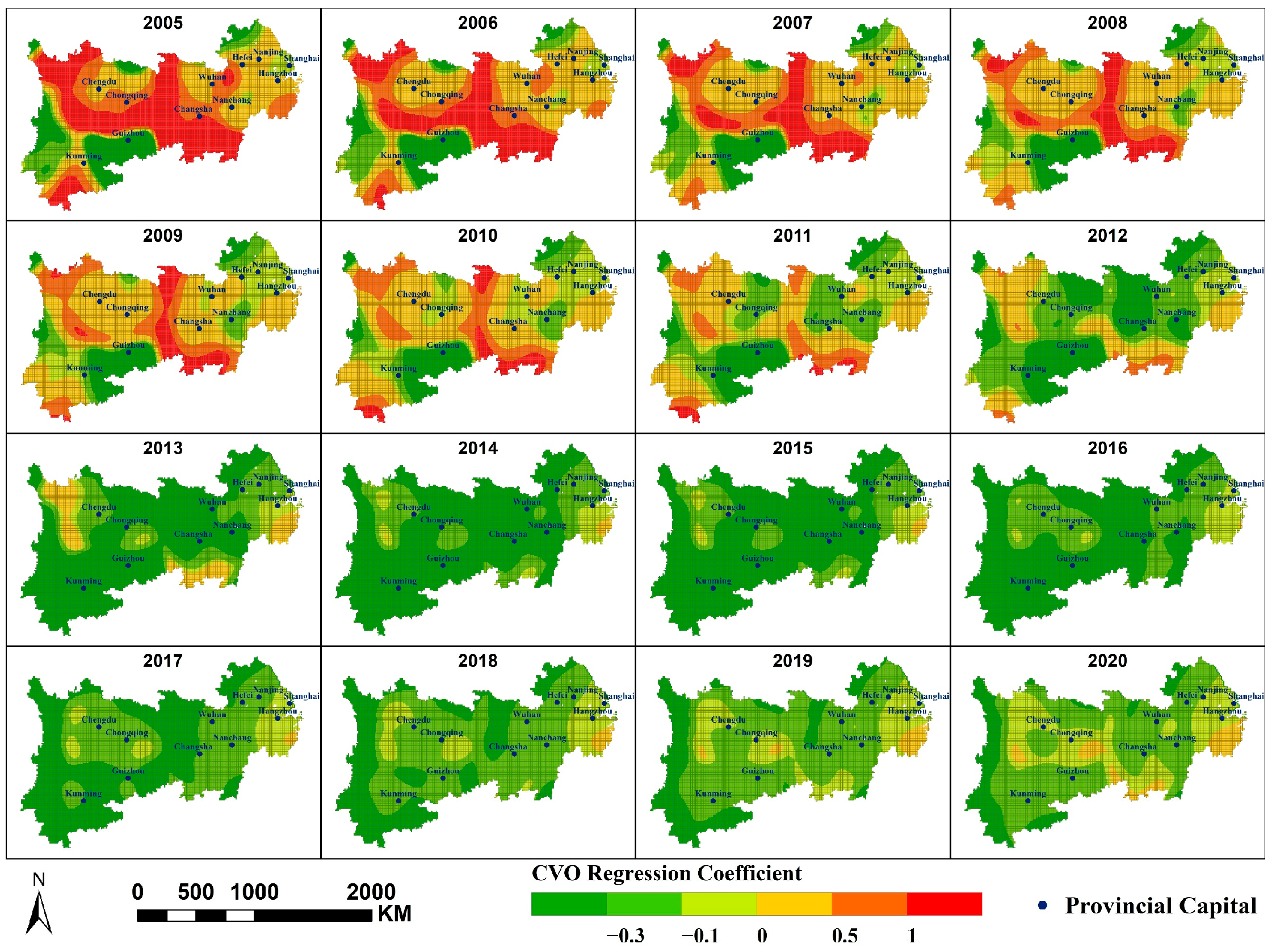
Appendix B
Appendix B.1
Appendix B.2
Appendix B.3
Appendix B.4
References
- Lin, G.; Fu, J.; Jiang, D.; Hu, W.; Dong, D.; Huang, Y.; Zhao, M. Spatio-Temporal Variation of PM2.5 Concentrations and Their Relationship with Geographic and Socioeconomic Factors in China. Int. J. Environ. Res. Public. Health 2014, 11, 173–186. [Google Scholar] [CrossRef] [PubMed]
- Yousefi, S.; Shahsavani, A.; Hadei, M. Applying EPA’s instruction to calculate air quality index (AQI) in Tehran. J. Air Pollut. Health 2019, 4, 81–96. [Google Scholar] [CrossRef]
- Zhu, S.; Lian, X.; Wei, L.; Che, J.; Shen, X.; Yang, L.; Qiu, X.; Liu, X.; Gao, W.; Ren, X.; et al. PM2.5 forecasting using SVR with PSOGSA algorithm based on CEEMD, GRNN and GCA considering meteorological factors. Atmos. Environ. 2018, 183, 20–32. [Google Scholar] [CrossRef]
- Zhou, C.; Chen, J.; Wang, S. Examining the effects of socioeconomic development on fine particulate matter (PM2.5) in China’s cities using spatial regression and the geographical detector technique. Sci. Total Environ. 2018, 619–620, 436–445. [Google Scholar] [CrossRef]
- Juarez, P.D.; Tabatabai, M.; Burciaga Valdez, R.; Hood, D.B.; Im, W.; Mouton, C.; Colen, C.; Al-Hamdan, M.Z.; Matthews-Juarez, P.; Lichtveld, M.Y.; et al. The Effects of Social, Personal, and Behavioral Risk Factors and PM2.5 on Cardio-Metabolic Disparities in a Cohort of Community Health Center Patients. Int. J. Environ. Res. Public Health 2020, 17, 3561. [Google Scholar] [CrossRef] [PubMed]
- Cao, Q.; Liang, Y.; Niu, X. China’s Air Quality and Respiratory Disease Mortality Based on the Spatial Panel Model. Int. J. Environ. Res. Public Health 2017, 14, 1081. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Liu, Y.; Gao, H.; Ma, J.; Mao, X.; Wang, Y.; Ma, X. Forecasting PM2.5 induced male lung cancer morbidity in China using satellite retrieved PM2.5 and spatial analysis. Sci. Total Environ. 2017, 607–608, 1009–1017. [Google Scholar] [CrossRef]
- Yun, G.; He, Y.; Jiang, Y.; Dou, P.; Dai, S. PM2.5 Spatiotemporal Evolution and Drivers in the Yangtze River Delta between 2005 and 2015. Atmosphere 2019, 10, 55. [Google Scholar] [CrossRef]
- Yan, J.-W.; Tao, F.; Zhang, S.-Q.; Lin, S.; Zhou, T. Spatiotemporal Distribution Characteristics and Driving Forces of PM2.5 in Three Urban Agglomerations of the Yangtze River Economic Belt. Int. J. Environ. Res. Public Health 2021, 18, 2222. [Google Scholar] [CrossRef]
- He, J.; Gong, S.; Yu, Y.; Yu, L.; Wu, L.; Mao, H.; Song, C.; Zhao, S.; Liu, H.; Li, X.; et al. Air pollution characteristics and their relation to meteorological conditions during 2014–2015 in major Chinese cities. Environ. Pollut. 2017, 223, 484–496. [Google Scholar] [CrossRef]
- Guo, X.; Mu, X.; Ding, Z.; Qin, D. Nonlinear effects and driving mechanism of multidimensional urbanization on PM2.5 concentrations in the Yangtze River Delta. Acta Geogr. Sin. 2021, 76, 1274–1293. [Google Scholar] [CrossRef]
- Huang, H.; Jiang, P.; Chen, Y. Analysis of the Social and Economic Factors Influencing PM2.5 Emissions at the City Level in China. Sustainability 2023, 15, 16335. [Google Scholar] [CrossRef]
- Xu, Y.; Guo, Z.; Zheng, Z.; Dai, Q.; Zhao, C.; Huang, W. Study of the PM2.5 Concentration Variation and its Influencing Factors in the Beijing-Tianjin-Hebei Urban Agglomeration Using Geo-Detector. Res. Environ. Sci. 2023, 36, 649–659. [Google Scholar] [CrossRef]
- Li, S.; Wei, G.; Liu, Y.; Bai, L. Multi-Scale Analysis of PM2.5 Concentrations in the Yangtze River Economic Belt: Investigating the Combined Impact of Natural and Human Factors. Remote Sens. 2023, 15, 3356. [Google Scholar] [CrossRef]
- Fang, K.; Wang, T.; He, J.; Wang, T.; Xie, X.; Tang, Y.; Shen, Y.; Xu, A. The distribution and drivers of PM2.5 in a rapidly urbanizing region: The Belt and Road Initiative in focus. Sci. Total Environ. 2020, 716, 137010. [Google Scholar] [CrossRef]
- Liang, M.; Li, H.; Li, W.; Jia, X.; Wang, M.; Feng, C. Spatial-Temporal Distribution Characteristics of PM2.5 and PM10 in the Northeast Tibetan Plateau and the Influence of Meteorological Factors. Northwest. Geol. 2024, 57, 285–296. [Google Scholar] [CrossRef]
- Fu, Z.; Li, R. The contributions of socioeconomic indicators to global PM2.5 based on the hybrid method of spatial econometric model and geographical and temporal weighted regression. Sci. Total Environ. 2020, 703, 135481. [Google Scholar] [CrossRef] [PubMed]
- Zhao, R.; Zhan, L.; Yao, M.; Yang, L. A geographically weighted regression model augmented by Geodetector analysis and principal component analysis for the spatial distribution of PM2.5. Sustain. Cities Soc. 2020, 56, 102106. [Google Scholar] [CrossRef]
- Lan, T.; Han, L.; Tian, J.; Qi, C.; Xiao, Q. Important factors affecting the multi-scale variation of PM2.5 and O3 in Xingtai City and their contributions. China Environ. Sci. 2024, 44, 4786–4795. [Google Scholar] [CrossRef]
- Huang, C.; Lo, K.; Wu, Y.; Wang, F.; Shiu, Y.; Chen, C.; Lin, Y.; Kuo, C.; Liao, H.; Lin, T.; et al. Estimating and characterizing spatiotemporal distributions of elemental PM2.5 using an ensemble machine learning approach in Taiwan. Atmos. Pollut. Res. 2025, 16, 102463. [Google Scholar] [CrossRef]
- Wang, S.; Ren, Y.; Xia, B. PM2.5 and O3 concentration estimation based on interpretable machine learning. Atmos. Pollut. Res. 2023, 14, 101866. [Google Scholar] [CrossRef]
- Liao, D.; Hong, Y.; Huang, H.; Choi, S.; Zhuang, Z. Machine learning exploring the chemical compositions characteristics and sources of PM2.5 from reduced on-road activity. Atmos. Pollut. Res. 2024, 15, 102265. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.; Kim, S.; Lee, K.; Kim, P.; Kim, H.; Song, H. Development and interpretation of PM2.5 estimation model for the Seoul Metropolitan Area using machine learning and explainable AI. Atmos. Pollut. Res. 2025, 16, 102672. [Google Scholar] [CrossRef]
- He, J.; Jing, Y.; Ran, D. Is There a Relationship between Increased Land-Use Intensity and the Rise in PM2.5 Pollution Levels in the Yangtze River Economic Belt, China (2000–2021)? Atmosphere 2023, 14, 1097. [Google Scholar] [CrossRef]
- He, Q.; Kong, F.; Wen, C. Evolution of Harmonious Coexistence Between Humans and Nature in the Yangtze River Economic Belt: A Production-Living-Ecological Balance Perspective. J. Hubei Univ. Econ. 2020, 18, 109–119. [Google Scholar] [CrossRef]
- Lehner, B.; Grill, G. Global river hydrography and network routing: Baseline data and new approaches to study the world’s large river systems. Hydrol. Process. 2013, 27, 2171–2186. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Lyapustin, A.; Sun, L.; Peng, Y.; Xue, W.; Su, T.; Cribb, M. Reconstructing 1-km-resolution high-quality PM2.5 data records from 2000 to 2018 in China: Spatiotemporal variations and policy implications. Remote Sens. Environ. 2021, 252, 112136. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Cribb, M.; Huang, W.; Xue, W.; Sun, L.; Guo, J.; Peng, Y.; Li, J.; Lyapustin, A.; et al. Improved 1 km resolution PM2.5 estimates across China using enhanced space-time extremely randomized trees. Atmos. Chem. Phys. 2020, 20, 3273–3289. [Google Scholar] [CrossRef]
- Peng, S.; Ding, Y.; Wen, Z.; Chen, Y.; Cao, Y.; Ren, J. Spatiotemporal change and trend analysis of potential evapotranspiration over the Loess Plateau of China during 2011–2100. Agric. For. Meteorol. 2017, 233, 183–194. [Google Scholar] [CrossRef]
- Ding, Y.; Peng, S. Spatiotemporal Trends and Attribution of Drought across China from 1901–2100. Sustainability 2020, 12, 477. [Google Scholar] [CrossRef]
- Peng, S.; Ding, Y.; Liu, W.; Li, Z. 1 km monthly temperature and precipitation dataset for China from 1901 to 2017. Earth Syst. Sci. Data 2019, 11, 1931–1946. [Google Scholar] [CrossRef]
- Peng, S.; Gang, C.; Cao, Y.; Chen, Y. Assessment of climate change trends over the loess plateau in China from 1901 to 2100. Int. J. Climatol. 2017, 38, 2250–2264. [Google Scholar] [CrossRef]
- Peng, S. 1-km Monthly Precipitation Dataset for China (1901–2024). National Tibetan Plateau/Third Pole Environment Data Center. 2020. Available online: https://data.tpdc.ac.cn/en/data/faae7605-a0f2-4d18-b28f-5cee413766a2 (accessed on 28 October 2025).
- Peng, S. 1-km Monthly Mean Temperature Dataset for China (1901–2024). National Tibetan Plateau/Third Pole Environment Data Center. 2019. Available online: https://cstr.cn/18406.11.Meteoro.tpdc.270961 (accessed on 28 October 2025).
- Chen, J.; Gao, M.; Cheng, S.; Hou, W.; Song, M.; Liu, X.; Liu, Y. Global 1 km × 1 km gridded revised real gross domestic product and electricity consumption during 1992–2019 based on calibrated nighttime light data. Sci. Data 2022, 9, 202. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Gao, M. Global 1 km × 1 km Gridded Revised Real Gross Domestic Product and Electricity Consumption During 1992–2019 Based on Calibrated Nighttime Light Data. 2021. Available online: https://figshare.com/articles/dataset/Global_1_km_1_km_gridded_revised_real_gross_domestic_product_and_electricity_consumption_during_1992-2019_based_on_calibrated_nighttime_light_data/17004523/1?file=31456837 (accessed on 28 October 2025).
- Gao, M.; Chen, J. PSO-BP. Codes for Modelling the Relationships Between the National GDP and Nighttime Light Data. 2022. Available online: https://figshare.com/articles/dataset/PSO-BP_codes_for_modelling_the_relationships_between_the_national_GDP_and_nighttime_light_data/19517272/1?file=34691536 (accessed on 28 October 2025).
- WorldPop. Global High Resolution Population Denominators Project. Available online: https://hub.worldpop.org/doi/10.5258/SOTON/WP00674 (accessed on 28 October 2025).
- Chen, Z.; Yu, B.; Yang, C.; Zhou, Y.; Yao, S.; Qian, X.; Wang, C.; Wu, B.; Wu, J. An Extended Time-Series (2000–2018) of Global NPP-VIIRS-like Nighttime Light Data. Earth Syst. Sci. Data 2021, 13, 889–906. [Google Scholar] [CrossRef]
- Yang, J.; Huang, X. The 30 m annual land cover dataset and its dynamics in China from 1990 to 2019. Earth Syst. Sci. Data 2021, 13, 3907–3925. [Google Scholar] [CrossRef]
- Wu, J.; Wang, X.; Wang, C.; He, X.; Ye, M. The status and development trend of disaggregation of socio-economic data. J. Geo-Inf. Sci. 2018, 20, 1252–1262. [Google Scholar] [CrossRef]
- Guo, H.; Zhu, W. A review on the spatial disaggregation of socioeconomic statistical data. Acta Geogr. Sin. 2022, 77, 2650–2667. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Christakos, G.; Liao, Y.; Zhang, T.; Gu, X.; Zheng, X. Geographical detectors-based health risk assessment and its application in the neural tube defects study of the Heshun region, China. Int. J. Geogr. Inf. Syst. 2010, 24, 107–127. [Google Scholar] [CrossRef]
- Wang, J.; Xu, C. Geodetector: Principle and prospective. Acta Geogr. Sin. 2017, 72, 116–134. [Google Scholar] [CrossRef]
- Huang, B.; Wu, B.; Barry, M. Geographically and temporally weighted regression for modeling spatio-temporal variation in house prices. Int. J. Geog. Inf. Sci. 2010, 24, 383–401. [Google Scholar] [CrossRef]
- Fotheringham, A.; Charlton, M.; Brunsdon, C. The geography of parameter space: An investigation of spatial non-stationarity. Int. J. Geogr. Inf. Syst. 1996, 10, 605–627. [Google Scholar] [CrossRef]
- Lv, W.; Lei, Y.; Liu, F.; Yan, J.; Song, Y.; Zhao, W. gdverse: An R Package for Spatial Stratified Heterogeneity Family. Trans. GIS. 2025, 29, e70032. [Google Scholar] [CrossRef]






| Category | Abbreviation | Description | Unit | Source |
|---|---|---|---|---|
| PM2.5 | PM2.5 | 2.5-micrometer Particulate Matter | μg/m3 | https://zenodo.org/records/6398971 (accessed on 28 October 2025) |
| natural factor | NDVI | Normalized Difference Vegetation Index | - | https://search.earthdata.nasa.gov/search/granules?p=C2327962326-LPCLOUD&pg[0][v]=f&pg[0][gsk]=-start_date&q=MOD13A3 (accessed on 28 October 2025) |
| AR | Annual Rainfall | mm | https://data.tpdc.ac.cn/en/data/faae7605-a0f2-4d18-b28f-5cee413766a2 (accessed on 28 October 2025) | |
| MAT | Mean Annual Temperature | °C | https://cstr.cn/18406.11.Meteoro.tpdc.270961 (accessed on 28 October 2025) | |
| PWA | Proportion of Water Area | - | https://zenodo.org/records/15853565 (accessed on 28 October 2025) | |
| Human factor | PFA | Proportion of Farmland Area | - | https://zenodo.org/records/15853565 (accessed on 28 October 2025) |
| PISA | Proportion of Impervious Surface Area | - | https://zenodo.org/records/15853565 (accessed on 28 October 2025) | |
| PD | Population Density | people/km2 | https://hub.worldpop.org/geodata/listing?id=76 (accessed on 28 October 2025) | |
| NTL | Nighttime Lights | - | https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/YGIVCD (accessed on 28 October 2025) | |
| GDP | Gross Domestic Product | dollars | https://figshare.com/articles/dataset/Global_1_km_1_km_gridded_revised_real_gross_domestic_product_and_electricity_consumption_during_1992-2019_based_on_calibrated_nighttime_light_data/17004523/1?file=31456837 (accessed on 28 October 2025) | |
| SDE | Sulfur Dioxide Emissions | ton | https://www.stats.gov.cn/ (accessed on 28 October 2025) | |
| CVO | Civil Vehicle Ownership | ton | https://www.stats.gov.cn/ (accessed on 28 October 2025) |
| Factor | VIF | ||
|---|---|---|---|
| Municipal | Watershed | Grid | |
| NDVI | 6.78 | 4.90 | 3.88 |
| MAT | 2.09 | 3.58 | 3.30 |
| PWA | 3.54 | 2.35 | 1.74 |
| PD | 5.79 | 3.12 | 2.50 |
| SDE | 1.92 | 1.38 | 1.24 |
| CVO | 3.14 | 1.61 | 1.48 |
| PFA | 2.83 | 2.68 | 2.43 |
| PISA | 3.74 | 3.56 | 3.20 |
| Spatial Bandwidth | Temporal Bandwidth | R-Squared | Adjusted R-Squared | AICc | |
|---|---|---|---|---|---|
| Municipal | 100,000 | 2 | 0.968 | 0.960 | −201.894 |
| Watershed | 0.963 | 0.961 | −5434.839 | ||
| Grid | 0.949 | 0.949 | −42,395.559 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Chen, Y.; Wei, Y. Multi-Scale Analysis of Influencing Factors for Temporal and Spatial Variations in PM2.5 in the Yangtze River Economic Belt. Sustainability 2025, 17, 9721. https://doi.org/10.3390/su17219721
Zhang Y, Chen Y, Wei Y. Multi-Scale Analysis of Influencing Factors for Temporal and Spatial Variations in PM2.5 in the Yangtze River Economic Belt. Sustainability. 2025; 17(21):9721. https://doi.org/10.3390/su17219721
Chicago/Turabian StyleZhang, Yufei, Yu Chen, and Yongming Wei. 2025. "Multi-Scale Analysis of Influencing Factors for Temporal and Spatial Variations in PM2.5 in the Yangtze River Economic Belt" Sustainability 17, no. 21: 9721. https://doi.org/10.3390/su17219721
APA StyleZhang, Y., Chen, Y., & Wei, Y. (2025). Multi-Scale Analysis of Influencing Factors for Temporal and Spatial Variations in PM2.5 in the Yangtze River Economic Belt. Sustainability, 17(21), 9721. https://doi.org/10.3390/su17219721







