Abstract
In recent years, China has faced the dual challenge of achieving high-quality economic development (HQED) alongside carbon emission reduction (CER), with new-quality productivity (NQP) emerging as a key driver integrating both agendas. Research on the coordinated development of these three dimensions remains limited but is critical for effective policy-making. Based on panel data from 30 Chinese provinces (2014–2023), this study constructs the NQP-CER-HQED evaluation indicator system; calculates the composite index using the entropy weight method and composite index calculation model; computes the coupling coordination degree (CCD) of the three components via the CCD model; analyzes the temporal evolution and future trends of CCD using kernel density and GM(1,1) models; examines the spatial evolution of CCD through Moran’s I index; employs traditional Markov chains and spatial Markov chains to investigate the spatial-temporal evolution patterns of CCD; and applies the geographic detector method to analyze the influencing factors of CCD among NQP, CER and HQED. The findings reveal that (1) the CCD of China’s NQP-CER-HQED has undergone six levels, showing an overall upward trend; (2) temporally, CCD levels improve annually, with all provinces expected to achieve coordinated development by 2026; (3) spatially, the CCD exhibits a “high-east, low-west” tiered distribution; (4) spatially/temporally, the transition of the CCD levels is primarily gradual rather than leapfrogging; and (5) the level of opening up and new-quality labor resources are identified as dominant influencing factors, with the interaction between new-quality labor resources and government support showing the strongest explanatory power. This study provides an analytical framework for understanding the NQP-CER-HQED synergy and offers a scientific basis for sustainable policy formulation.
1. Introduction
In recent years, amid an intensifying global warming trend, the environmental crisis driven by greenhouse gas emissions has emerged as a pressing and universal challenge, confronting all nations worldwide. Against this backdrop, China, as the world’s largest energy consumer and carbon emitter [1], has solemnly pledged at the 2020 United Nations General Assembly to “strive to reach peak carbon dioxide emissions by 2030 and strive to achieve carbon neutrality by 2060”, which not only demonstrates China’s leadership in addressing climate change [2] but also represents a strategic choice to promote green economic transformation and high-quality development. However, China faces dual constraints in achieving its “dual-carbon” goals: on the one hand, it needs to accelerate its low-carbon transition to alleviate ecological and environmental pressures; on the other hand, it needs to maintain “effective improvement in quality” and “reasonable growth in quantity” of its economy. China is forced to face the dual challenge of promoting HQED while completing its CER tasks. Therefore, how to strike a balance between CER and HQED has become a core issue for China’s development in the new era, and it urgently needs new driving forces to boost it.
As a new engine of development, NQP have garnered significant attention from policymakers, who view them as a key driver for promoting CER and HQED. On 31 January 2024, during the 11th collective study session of the Central Political Bureau of the Communist Party of China, General Secretary Xi Jinping emphasized that “developing NQP is an intrinsic requirement and a key focus for promoting high-quality development” and that “NQP are inherently green productive forces.” Scholarly research has revealed that NQP demonstrate significant potential in promoting CER and HQED. In terms of achieving CER, NQP accelerate the transformation of the energy structure from coal-based to renewable energy-based, enhance the precision of energy, management and utilization, and boost the potential for CER. They reduce carbon emissions intensity through pathways such as improving total factor productivity and optimizing the energy consumption structure [3]. Additionally, by enhancing the quality of production factors and establishing digital networks, they optimize resource allocation on a larger scale, thereby improving economic efficiency and CER capabilities [4]. In terms of promoting HQED, NQP creates more efficient production methods, releases idle resources, and promotes economic development that benefits more social strata by improving production efficiency and optimizing resource allocation [5]. It drives HQED through innovation-driven growth, industrial upgrading, and demand-driven growth [6]. Therefore, to address the dual challenges of CER and HQED faced by China, it is necessary to explore the relationship between NQP, CER and HQED. By studying the intrinsic connections and mutual influence mechanisms among these three elements, we can promote their deep integration and coordinated development, thereby addressing the practical issue of how to utilize NQP methods to achieve CER targets while promoting HQED.
However, previous studies have primarily focused on CER and HQED [7]. Scholars have explored the relationship between CER and HQED [8], primarily from three dimensions: regional coordination, policy tools and factor market mechanisms. From the perspective of regional coordination, Chen et al. (2023) used an improved gravity model and social network analysis to find that urban agglomerations like the Yangtze River Delta and Pearl River Delta exhibit a “core–periphery” emissions reduction structure [9,10], with core cities leveraging resource allocation to lead regional collaborative emissions reduction; Wu et al. (2024) further confirmed that compact urban development can reduce carbon emissions intensity, though regions like the Beijing–Tianjin–Hebei area still exhibit development polarization by CCD mode [11]. In terms of policy tools, Fan et al. (2023) used an interleaved DID model to demonstrate that green fiscal policies achieve synergies in pollution reduction and carbon emission reduction by weakening GDP performance evaluations and promoting green innovation [12]; Wang et al. (2024) used the SCM method to quantify the carbon efficiency enhancement effects of the Beijing–Tianjin–Hebei regional coordination strategy, averaging 10.43% annually [13]. In terms of factor market mechanisms emphasizing technology-economic synergy, Peng et al. (2024) through DID model found that the “Broadband China” policy reduces carbon emissions through green industrial structure transformation [14]; Sha et al. (2024) pointed out that correcting energy price distortions, especially coal, can release 1.81% of economic-emission reduction synergy potential by Tobit mode [15]. These studies provide a dual perspective and a dynamic coordination foundation for discussing the relationship between CER and HQED. CER and HQED share a synergistic and symbiotic interaction mechanism: On one hand, HQED drives the low-carbon transformation of economic structures through its green development principles, directing capital toward green technological innovation and fostering institutional frameworks such as carbon markets, thereby providing fundamental momentum and institutional safeguards for CER. On the other hand, effective CER fosters new growth points in green industries, enhances energy security and economic resilience, and generates synergistic environmental and health benefits. It not only constitutes a core manifestation of HQED but also provides critical support for its advancement. The dialectical unity of “goal-driven direction” and “path-enabling support” behind HQED sets the strategic direction for CER, while CER provides the implementation pathways for HQED. However, they do not incorporate the systemic driving force of NQP and are relatively insufficient in terms of spatial heterogeneity and coupled coordination driving factors.
NQP have brought about theoretical breakthroughs, forming a new paradigm of three-dimensional synergy [16,17,18]. In terms of structural optimization driving CER, Zhao et al. (2025) constructed a four-dimensional evaluation system (talent-technology-industry-production methods) and confirmed that for every 1-unit increase in its development index, carbon emissions intensity decreased by 0.63%, with new production methods contributing 42.1% [19]; Hu et al. (2025) used dynamic QCA to discover a significant substitution effect between industrial digital productivity and resource-saving productivity, with their combination reducing carbon emission intensity by 23–31% [20]; Yang et al. (2025) revealed that NQP unlock emission reduction potential by enhancing total factor productivity and decarbonizing energy structures, with stronger marginal effects in high-carbon regions [21]. In reshaping high-quality development pathways, NQP has become the core driving force of economic transformation. Sun Xiaoting et al. (2024) validated that green technological innovation promotes high-quality development of a low-carbon economy by fostering NQP, and that a dual threshold effect exists [22]; Yang et al. (2025) found, based on data from 244 cities, that NQP enhances economic quality by activating entrepreneurial vitality and talent aggregation, but its role is limited in resource-based cities [23]; Hou et al. (2024) emphasize that the revitalization of Northeast China requires leveraging NQP to address the “bottlenecks” of rigid industrial structure and talent outflow, and to promote the integration of traditional industries with emerging technologies [24]. Scholars have also developed new insights into dynamic synergistic mechanisms. Regarding factor substitution effects, Hu et al. (2025) identified three low-carbon development configurations, where digital industrial productivity and environmentally friendly productivity can substitute for each other to form equivalent pathways, overturning the traditional single-factor dependency model [20]. In terms of spatial heterogeneity patterns, emission reduction effects exhibit an “eastern > central > western” gradient, while in the agricultural sector, they follow a “major grain-producing regions > non-major grain-producing regions” pattern [25]. In terms of nonlinear regulatory mechanisms, Zhao et al. (2025) found that industrial agglomeration exhibits an inverted U-shaped regulatory effect, with an inflection point density of 0.85; moderate agglomeration helps strengthen emission reduction effects [19]. Rural aging positively regulates CER in agricultural NQP, also reflecting the synergistic value of labor force structural transformation [26]. Recent environmental studies reveal that the penetration of ICT and the deployment of artificial intelligence introduce both opportunities and asymmetric challenges for energy sustainability and carbon mitigation in industrialized economies [27,28,29]. These intricate interconnections underscore the importance of examining how technology-driven new-quality productivity couples with carbon constraints within a high-quality development framework.
In summary, in previous studies, most scholars have focused their research on the relationship between CER and HQED. A small number of scholars have noted the positive impact of NQP on CER and HQED, and have studied the pairwise relationships among NQP, CER and HQED. However, current research largely remains at the level of examining the impact of NQP on a single aspect [30,31], lacking a systematic analysis of their comprehensive effects. Few scholars have considered the role of NQP in promoting both HQED and the achievement of CER targets, nor have they studied the coupled and coordinated relationship among the three systems of NQP, CER and HQED.
The theoretical framework of this study is primarily grounded in endogenous growth theory, the environmental Kuznets curve, and sustainable development theory. Endogenous growth theory guided the construction of the NQP indicator system, the environmental Kuznets curve theory underpinned the analysis of the relationship between CER and HQED, while sustainable development theory provided the basis for the comprehensive evaluation of HQED. Together, these theories collectively support the research on the synergistic mechanism of the ternary system.
While prior literature has extensively examined the bilateral relationships between CER and HQED, studies that integrate NQP into a unified framework remain scarce. Against this backdrop, the marginal contributions of this study are threefold. First, it moves beyond the traditional two-system perspective to construct a novel provincial-level evaluation system and empirically measure the CCD within the NQP-CER-HQED ternary system, offering a more holistic assessment framework. Second, it leverages a comprehensive suite of spatial analysis techniques—including Moran’s I, kernel density estimation, spatial Markov chains, and the GM(1,1) model—to provide a multi-dimensional diagnosis of the CCD’s spatial–temporal evolution, dynamic distribution, transitional probabilities, and future trends, thereby uncovering patterns that previous fragmented methodological approaches might overlook. Third, by applying the Geographical Detector model, it quantitatively identifies the dominant drivers and their interactive effects on the spatial heterogeneity of CCD, which offers empirically grounded evidence for crafting spatially differentiated and tailored policy combinations, a significant advancement over generic policy recommendations.
2. Materials and Methods
2.1. Data Sources and Pre-Processing
Considering the representativeness, availability and completeness of the data, 30 provinces in China (excluding Hong Kong, Macao, Taiwan and Tibet) were selected for this study, with a time span of 2014–2023. In order to better analyze regional differences, this study divides China’s economic regions into four major regions: eastern, central, western and northeastern (e.g., Figure 1), based on the “Opinions of the Central Committee of the Communist Party of China and the State Council on the Promotion of the Rise of the Central Region,” the “Opinions of the State Council on the Implementation of Certain Policies and Measures on the Development of Western China,” and the spirit of the report of the 16th CPC National Congress. This study utilizes data from authoritative public sources. Socioeconomic data were derived from the National Bureau of Statistics of China, accessible via its online National Data platform or the published China Statistical Yearbook series. Data on CER were sourced from the China Carbon Accounting Database (CEADs). The primary missing data occurred in carbon emission statistics for 2022–2023 and partial energy consumption data. The overall dataset exhibited a low missing rate of less than 3%. For these missing values, we employed linear interpolation for consecutive missing years and used province-specific means for cross-sectional data gaps.
Figure 1.
China’s four major regions.
2.2. Establishment of an Indicator System
Guided by the principles of scientific rigor, systematicity, operational feasibility, and comparability, this research integrates theoretical frameworks with contextual realities to construct a comprehensive evaluation index system. The developed framework consists of 35 indicators distributed across 11 distinct dimensions, as systematically presented in Table 1. By establishing this structured assessment tool, the study offers a novel analytical perspective and a scientifically grounded basis for promoting the integrated development of subsystems associated with advancing NQP, CER and HQED. This study references the Decision of the Central Committee of the Communist Party of China on Further Deepening Reforms and Promoting Chinese-Style Modernization, adopted at the Third Plenary Session of the 20th Central Committee of the Communist Party of China, and follows the views of most scholars [32,33,34,35,36] to measure NQP from the perspectives of new-quality laborers, new-quality labor objects and new-quality labor resources, encompassing a total of 14 indicators. Among these, “public library collections” serves as a proxy for knowledge infrastructure and information accessibility. In the knowledge economy, the availability of knowledge resources represents fundamental “new-quality means of labor” that enable innovation and technological progress. Mobile phone exchange capacity, a indicator measures digital infrastructure capacity, which constitutes essential “new-quality means of labor” in the digital economy. It reflects the hardware foundation for information transmission and digital technology application. “Per capita urban road area” measures the physical infrastructure for factor mobility. Efficient road networks are essential for supporting modern logistics, intelligent transportation systems, and the deployment of digital economy hardware, thereby enabling the smooth circulation and integration of advanced production means. While these indicators may not directly represent high-tech tools, they capture the fundamental enabling environment required for new-quality productivity development. All of these indicators have been adopted and validated in Wang et al. (2024)’s study on the impact of NQP on CER, and both were confirmed to have positive effects [30]. Regarding CER, this study is based on the “Opinions on Fully, Accurately, and Comprehensively Implementing the New Development Philosophy to Advance Carbon Peaking and Carbon Neutrality Work,” the “Action Plan for Carbon Peaking Before 2030,” and the views of numerous scholars [37,38]. It constructs a CER indicator system from three aspects: emission control, reducing carbon emissions, and increasing carbon absorption. Among these, the “emission control” dimension is target-oriented, focusing on structural management and outcome constraints. It incorporates indicators such as total carbon emissions and carbon emissions per unit of GDP, which reflect absolute or intensity-based emission caps and serve as binding policy targets. The “reducing carbon emissions” dimension is process-oriented, emphasizing efficiency gains and transitional efforts during implementation. It includes indicators such as total energy consumption and energy consumption per unit of GDP, which capture the operational measures and progressive actions taken to achieve the control targets. This system includes eight indicators, aiming to comprehensively assess the status of carbon emissions reduction. Among these, the “total public bus (electric) passenger transport volume” serves as a core indicator for monitoring low-carbon transformation in the transportation sector. Its weighting reflects the varying degrees of progress cities have made in promoting bus electrification, highlighting the critical role of transportation electrification in the current emissions reduction phase. For the construction of the HQED system, this study is based on the core guiding principles of HQED, namely the new development philosophy, and combines relevant research to establish an indicator system covering the five development concepts of coordination, innovation, greenness, openness and sharing [37,38,39].

Table 1.
Indicators of NQP, CER and HQED system.
This study involves multi-region, multi-year calculations of NQP, CER and HQED, and there are differences in the dimensions of the various indicators. The entropy weight method is grounded in information entropy theory. It objectively assigns weights by measuring the dispersion degree of indicator data, thereby effectively mitigating biases inherent in subjective evaluation. Based on this advantage, the present study employs the method to determine the weights for the indicators listed in Table 1, which enhances the scientific rigor and objectivity of the weighting process. Comprehensive details regarding the data sources for each indicator, including their specific query paths and direct access links on the National Data platform (data.stats.gov.cn) (accessed on 25 February 2025), are provided in Appendix A.
2.3. Research Methods
This study implements a comprehensive analytical procedure, as outlined in Figure 2. The process begins with the construction of an evaluation index system for NQP-CER-HQED. Firstly, the comprehensive indices for NQP, CER, and HQED across 30 Chinese provinces (2014–2023) are calculated using the entropy weight method and a comprehensive index model, followed by the calculation of their CCD. Secondly, the spatial–temporal dynamics of the CCD are examined through multiple approaches: its temporal distribution and trends are analyzed using kernel density and GM(1,1) models; its spatial agglomeration is assessed with the Moran index; and its evolution patterns are explored via traditional and spatial Markov chains. Finally, the geographic detector method is applied to identify the influencing factors. This multi-faceted approach systematically reveals the CCD’s evolution characteristics and drivers, offering a scientific basis for policy-making.
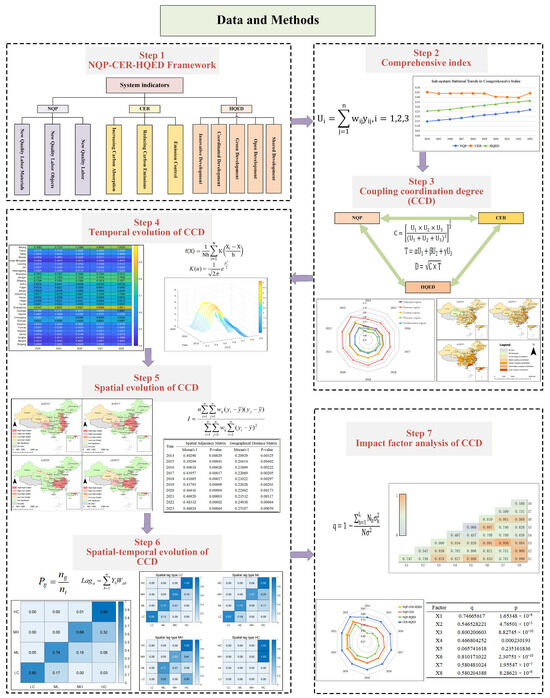
Figure 2.
Methodology flowchart.
2.3.1. Analysis Model of CCD
Firstly, the data of each indicator are standardized by the method of extreme difference to eliminate the influence of the data on the calculation results due to the inconsistency of the indicator’s outline, positive and negative orientation, and unit order of magnitude; secondly, the entropy weighting method is used to determine the weights of each indicator; and lastly, the comprehensive evaluation model is used to measure the comprehensive evaluation index of each province in each year [40,41]. The formula is as follows:
U1, U2, U3 are the comprehensive evaluation indexes of NQP, CER, and HQED, respectively. Within each of these three systems, n denotes the total count of indicators, wij refers to the weight assigned to an individual indicator, and Yij signifies the standardized value of that indicator.
The coupling coordination degree (CCD) can measure the overall “efficacy” and “synergy” effect of the system [42,43,44], and determine whether the coupling between the three systems is benign. We construct the CCD model of NQP, CER, and HQED, with the following formula:
U1, U2, U3 are the comprehensive evaluation indexes of NQP, CER, and HQED, respectively. C is the degree of coupling, T is the comprehensive evaluation index of the three systems, α, β, γ are the weight coefficients of each system, and D is the CCD. NQP, CER, and HQED have equal importance in this study, so α = β = γ = 1/3. Drawing on the research results of existing scholars [45], this paper classifies the CCD into the types as shown in Table 2.

Table 2.
Coupling coordination levels and classification criteria.
2.3.2. Spatial–Temporal Evolution Analysis Model of CCD
This study uses kernel density curve analysis to examine the distribution, morphology, and extensibility of CCD [46,47,48,49], further revealing the temporal evolution characteristics of the CCD between NQP, CER, and HQED. The formula for calculating the kernel density function is:
where N is the number of observations; h is the bandwidth; K(·) is the kernel function; Xi is the independent and identically distributed CCD observation value; X is the mean value of the CCD. The Gaussian kernel function selected in this paper is:
In addition, kernel density curve can only analyze the temporal evolution trend of the current CCD, but cannot predict its future development direction. Since this study needs to predict the CCD, so the GM(1,1) gray prediction method is introduced [50,51]. The prediction model formula is as follows:
X(0) refers to the original data sequence, which in this paper is the CCD data from 2014 to 2023; X(1) is the new sequence obtained after one accumulation; X(1)(k + 1) is the accumulated forecast value of the CCD; a is the development coefficient, μ is the endogenous control gray number, and n is 10.
This study referred to the GM(1,1) accuracy test standard (Table 3) and judged the fitting effect of the results by calculating the p value and C value.

Table 3.
GM(1,1) accuracy verification standard.
Considering that the CCD of NQP, CER, and HQED system may exhibit a clustered state at the provincial spatial level, this study uses the global Moran index to test the spatial correlation of the system’s CCD [52,53]. The calculation formula is as follows:
I represents the spatial correlation of the CCD of the three systems; n is 30; wij denotes the spatial weight matrix between regions wi and wj. Drawing on existing literature, this study employs both adjacency matrices and geographic distance matrices. The Moran index I ranges from [−1, 1]. When 0 < I ≤ 1, it indicates that the CCD exhibits spatial positive correlation; when −1 ≤ I < 0, it indicates that the CCD exhibits spatial negative correlation; when I = 0, it indicates that the CCD exhibits a random spatial distribution.
In addition, in order to conduct a more detailed analysis of each spatial unit and calculate the correlation between each spatial unit and its neighborhood, this study introduced the local Moran index to identify different types of spatial correlation patterns [52,54], such as “high-high” “high-low” “low-high” and “low-low”. The calculation formula is as follows:
To further study the spatial–temporal dynamic evolution characteristics of the CCD and reveal its intrinsic evolution laws, this study introduces Markov chains and spatial Markov chains. Markov chains can describe the transition probabilities of the CCD between different states and analyze its dynamic changes over time [47,55]. The calculation formula is as follows:
Pij is the probability of transferring the coupling coordination level from grade i in year t − 1 to grade j in year t. Among them, nij is the total number of regions transferring from grade i in year t − 1 to grade j in year t, and ni is the total number of regions in grade i in year t − 1.
Spatial Markov chains account for the spatial spillover effects resulting from geographical proximity [56]. By incorporating spatial factors into the analytical framework, they more accurately reflect the temporal and spatial evolution of coupling coordination levels, thereby providing robust support for a deeper understanding of the spatial–temporal coupling relationships among the three. This research uses the quartile method to divide the CCD of 30 provinces into four groups in ascending order: low coupling (LC), medium-low coupling (ML), medium-high coupling (MH), and high coupling (HC). The probabilities of transition and change for each type are then calculated to obtain an N × N traditional Markov transition probability matrix. The concept of spatial lag is then introduced to transform the N × N transition probability matrix into an N × (N × N) spatial Markov transition probability matrix, with the specific formula being:
Among them, Laga represents the spatial lag term of province a, n is the number of provinces, Yb is the observed value of province b, and Wab represents the spatial weight matrix of province a and province b. This paper uses an adjacency weight matrix, where two provinces are adjacent is 1, otherwise is 0.
2.3.3. Influence Factor Analysis Model of CCD
Variable Selection To further confirm the constraining effect of NQP on the level of coupling coordination, drawing on literature, three variables were selected from the perspectives of new-quality laborers, new-quality labor objects, and new-quality labor resources: full-time equivalent R&D personnel in large-scale industrial enterprises, average wage of employed persons, and the proportion of software business and information technology services revenue in GDP. Additionally, considering that the coupling of the three systems involves a complex system encompassing resources, the economy, and society, this research introduced five variables—level of economic development, level of industrial structure, level of opening up, level of government support, and level of scientific and technological innovation—based on the methods outlined in the literature. The indicators representing each variable are shown in Table 4. It is acknowledged that the openness measure in the factor analysis (“total foreign investment”) and the open development indicator in the HQED system (“total imports and exports as a percentage of GDP”) are conceptually linked. However, they are retained as distinct variables to capture different facets of regional openness—the former reflecting the absolute scale of external economic interaction, and the latter indicating its relative intensity within the local economy.

Table 4.
Variable description.
The Geodetector can effectively identify the linear and nonlinear effects of independent variables on dependent variablesl [56,57]. The single-factor detection method is used to evaluate the explanatory power of each influencing factor on the CCD. The calculation method is shown in Equation (14).
In the formula, q is the explanatory power of the influencing factor on the CCD, and the value range of q is [0, 1]. The larger the value, the greater the influence of the factor on the CCD. h is the number of indicator levels, and are the sample size and variance of a specific layer, respectively, and N and σ2 are the total sample size and variance, respectively.
Use an interaction detector to assess the interaction between each explanatory variable, and determine the type of two-factor interaction by comparing the explanatory power of the three (Table 5).

Table 5.
Types of interactions of geographic detectors and criteria for discrimination.
3. Results
3.1. CCD of NQP-CER-HQED in China from 2014 to 2023
As shown in Figure 3, from a national perspective, the average CCD of NQP-CER-HQED increased from 0.4936 in 2014 to 0.5790 in 2023, showing an overall upward trend. From a regional perspective, the eastern region increased from 0.5756 to 0.6641, the central region from 0.4795 to 0.5872, the western region from 0.4329 to 0.5138, and the northeastern region from 0.4708 to 0.5180. All four regions show an upward trend, but there are significant differences in the coupling coordination levels across regions: the eastern region has the highest coupling coordination level, initially at the barely coordinated level, and reached the basic coordinated level starting in 2018; The other three regions initially all started at the near-disharmonious level, with CCD showing a pattern of central region > northeastern region > western region. The central region reached the barely coordinated level in 2016, while the northeastern and western regions both caught up to reach the barely coordinated level in 2023. It can be seen that from 2014 to 2023, the overall level of CCD between China’s NQP, CER and HQED showed an improving trend, with all regions in a transitional development stage.
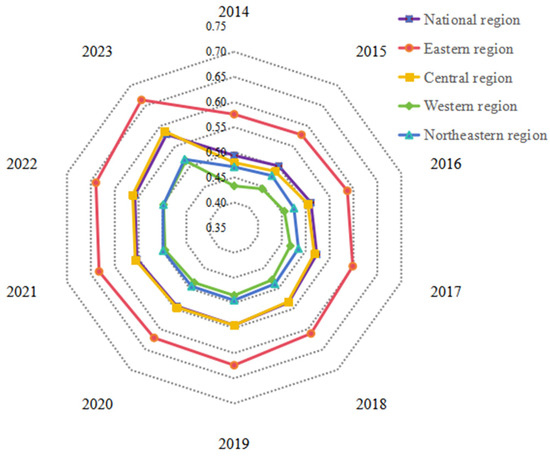
Figure 3.
Trends in the development of CCD in NQP-CER-HQED systems.
Additionally, to better observe the spatial distribution of CCD, Figure 4 was plotted. As shown in Figure 4, China’s NQP-CER-HQED coupling coordination has undergone six levels. In 2014, the CCD of most provinces was in the transitional development stage, with three provinces in the imbalanced decline stage. Among them, Beijing, Shanghai, Guangdong, Jiangsu and Zhejiang provinces had the highest CCD, being in the initial coordinated development stage. By 2019, the CCD levels of all had entered the coordination stage, with 9 provinces in the near-imbalance stage, 16 provinces in the barely coordinated development stage, 3 provinces in the initial coordinated development stage, and Guangdong and Jiangsu provinces entering the intermediate coordinated development stage. Compared to the baseline year of 2014, the majority of provinces have demonstrated a marked improvement in their CCD. This positive trend has been accompanied by a notably narrowed development gap between the central and eastern regions, indicating a movement toward more balanced regional development. By 2023, the coupling coordination levels of all provinces have further improved, with 6 provinces in the near-imbalance stage, 12 in the barely coordinated stage, 8 in the initial coordination stage, 3 in the intermediate coordination stage, and 1 in the good coordination stage. Among these, Guangdong Province is in the good coordination development stage, with its development consistently leading by a wide margin. Additionally, most provinces are in the barely coordinated and initial coordination development stages, while Gansu, Qinghai, Ningxia, Xinjiang, Inner Mongolia and Shanxi provinces are developing more slowly and are in the near-imbalance development stage.
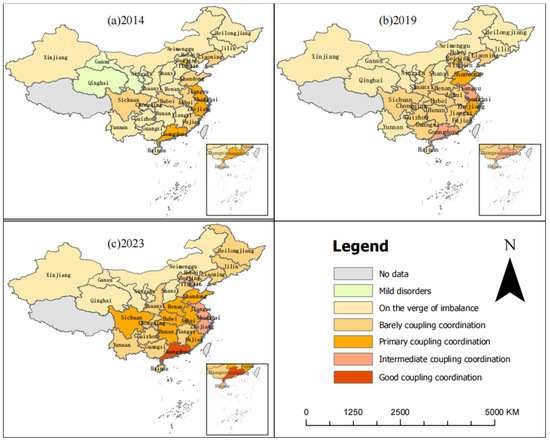
Figure 4.
Spatial distribution of CCD in China in 2014, 2019, and 2023.
3.2. Spatial–Temporal Evolution Analysis of CCD
3.2.1. Temporal Analysis of CCD
To more vividly and intuitively illustrate the temporal evolution of the CCD between NQP, CER and HQED, this study introduces a three-dimensional dynamic kernel density, as shown in Figure 5. The following conclusions can be drawn: First, there is an overall upward trend: The distribution epicenter of the CCD exhibits a continuing rightward shift, indicating that the CCD levels of the three systems across provinces are continuously improving. This phenomenon precisely reflects the synergistic effects of China’s regional coordinated development policies and green transformation strategies. Second, the distribution structure exhibits a “main-side” double-peak pattern: provinces with medium to low coupling coordination levels form the main peak, which saw a slight increase in height in 2019 but has generally declined in other years, with the bandwidth gradually widening. This suggests that the coordination levels of most provinces are further dispersing within the medium to low range, potentially leading to widening internal disparities; The side peak is formed by high coordination levels, with the peak height showing minor fluctuations without a clear upward or downward trend, but the bandwidth has been increasing annually, indicating that differences between high-level coordination regions are also widening, potentially leading to a “the strong get stronger” differentiation phenomenon. The coexistence of the main peak and side peaks over the long term reflects a pronounced polarization within the system, where groups with medium-to-low coordination and high coordination have formed relatively independent clusters, and the system has not converged toward a balanced state.
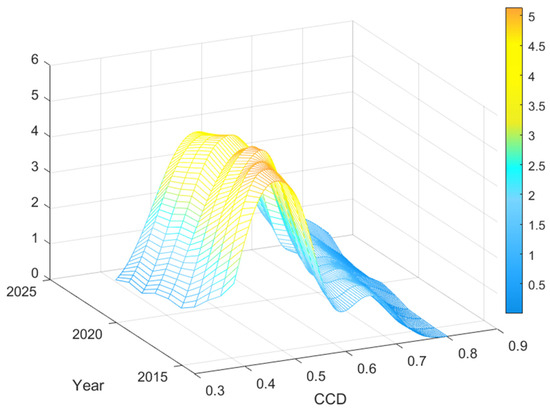
Figure 5.
Nuclear density map of CCD between NQP-CER-HQED. (Note: The Z-axis is the dimensionless probability density).
To predict the future trend of the CCD between NQP, CER and HQED, this study introduces the gray model GM(1,1). It was selected for prediction based on its particular suitability for analyzing systems with limited data and gray characteristics, which aligns well with the evolutionary nature of coupling coordination degree data in our study. To rigorously validate the model’s performance, we conducted comprehensive accuracy tests according to the standard GM(1,1) assessment framework. The results show that both the posteriori error ratio and small error probability achieve the “Very high” accuracy grade, confirming the model’s excellent fit and reliability for our forecasting purposes. This systematic validation approach ensures the credibility of our predictions while maintaining methodological coherence with gray system theory principles commonly applied in similar sustainability studies. Using the CCD of 30 provinces in China from 2014 to 2023 as simulation values, the study predicts the CCD of NQP, CER and HQED from 2024 to 2028. The corresponding results are presented in Figure 6.
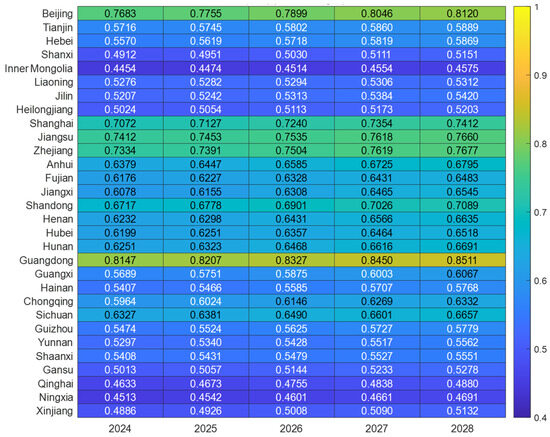
Figure 6.
Trend prediction of CCD.
From a temporal perspective, the CCD across Chinese provinces is projected to demonstrate a consistent upward trajectory from 2024 to 2028. Specifically, the national average is forecast to rise from 0.5882 to 0.6175, which corresponds to a significant growth rate of 4.99%. This indicates that the synergistic relationship among NQP, CER and HQED is gradually improving, and policy measures and adjustments to development models are beginning to yield results in promoting such synergy. From a regional perspective, the CCD levels of different regions vary significantly in terms of starting points and growth rates, primarily manifesting in three typical evolutionary patterns. The high-level steady-state evolutionary zone, represented by developed regions such as Beijing, Zhejiang and Shanghai, has a high initial value exceeding 0.7 and maintains a steady annual growth rate of over 1.15% during the forecast period. Some central and western regions, such as Jiangxi, Anhui, Henan and Hunan, have relatively low initial values, concentrated between 0.6 and 0.7, but they possess significant growth potential, with annual growth rates ranging from 1.58% to 1.87%, which is more than 28% higher than the national average, categorizing them as high-potential catch-up growth zones. Guangdong Province is the core leading region, exhibiting leapfrog development characteristics. Since advancing to the intermediate coordinated development stage in 2023 with a value of 0.8147, it has maintained its leading advantage. It is projected that by 2026, all provinces except Inner Mongolia, Ningxia, and Qinghai will achieve coordinated development levels.
3.2.2. Spatial Variation Analysis of CCD
According to the formula for calculating the global Moran’s I index (Table 6), the spatial auto-correlation of the CCD of the three systems in each province of China is determined. As shown in the table, the values of the global Moran’s I index from 2014 to 2023 are all positive and have passed the significance test, indicating that the CCD of the NQP, CER and HQED systems exhibits a positive spatial correlation. It is worth noting that the I values increased from 0.40290 and 0.20929 in 2014 to 0.46824 and 0.25187 in 2023, which may indicate that the spatial correlation between regions gradually strengthened during the period from 2014 to 2023, meaning that the degree of mutual influence between regions increased.

Table 6.
Global spatial autocorrelation of CCD.
The global spatial auto-correlation statistics indicate that the CCD exhibits spatial clustering, but they do not reveal the degree of similarity or difference between observed values and those of neighboring regions. Therefore, to better observe the spatial spillover extent of the CCD, this study introduced a local spatial auto-correlation model and plotted the local Moran’s I distribution maps for 30 provinces in 2014, 2017, 2020, and 2023 (Figure 7).

Figure 7.
Local Moran’s Index Distribution Maps for 2014, 2017, 2020, and 2023.
From the perspective of spatial pattern evolution, from 2014 to 2023, the spatial spillover pattern of the CCD exhibited dynamic evolutionary characteristics. In 2014 and 2017, spatial association patterns such as high-high clustering and low-low clustering were relatively dispersed. By 2020 and 2023, the trend of high-high clustering in advantageous regions such as the eastern coastal areas had significantly strengthened, reflecting the synergistic effects of NQP, CER and HQED are accelerating in advantageous regions over time, with the “polarization effect” of spatial spillover gradually becoming apparent. From the perspective of cluster types, high-high clusters have long been concentrated in eastern coastal provinces such as Jiangsu, Zhejiang, Shanghai and Fujian. From 2014 to 2023, their scope continued to consolidate and expand slightly, confirming the “self-reinforcing” and “radiation-driven” characteristics of such regions—they have a high level of coordinated development and through factor mobility and technology spillover, drive surrounding regions to integrate into the coordinated development network, strengthening positive spatial associations. The low-low cluster primarily consists of certain inland provinces in central and western China. Although its scope narrowed in 2023 compared to 2014, it still maintains a certain scale, reflecting that such regions are influenced by the “lock-in effect,” with their CCD levels remaining at low levels over the long term. They are also prone to forming low-level cycles through spatial spillover, becoming weak links in collaborative development. Additionally, high-low and low-high outliers are scattered and primarily concentrated in the transitional zones between eastern, central, and western regions, with Sichuan Province being particularly notable.
3.2.3. Spatial–Temporal Evolution Analysis of CCD
To further analyze the spatial–temporal evolution trends of the CCD levels across regions, this study employs a combined framework of traditional and spatial Markov chains. These models are utilized to estimate the transition probabilities of regional CCD levels shifting from one state to another. For the analysis, the CCD values of all 30 provinces are categorized into four distinct types using the quartile method, ranked sequentially from the lowest to the highest: low coupling coordination (LC), medium-low coupling coordination (ML), medium-high coupling coordination (MH), and high coupling coordination (HC). The corresponding results are presented in Figure 8.
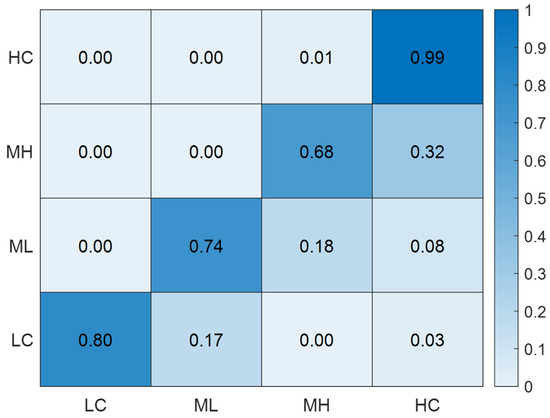
Figure 8.
Markov transition probability matrix.
As shown in Figure 8: First, the maximum probability on the diagonal is 0.99, and the minimum probability is 0.68, both of which are greater than the probability values off the diagonal. This indicates that the transfer of the CCD among provinces exhibits stability, with a higher probability of maintaining the original state and a certain degree of solidification. Second, under both low-level and high-level conditions, the CCD is highly likely to maintain its original state in the next phase, indicating the presence of a “club phenomenon.” Third, the non-diagonal probability values greater than zero are closely distributed on both sides of the diagonal, indicating that the evolution of the CCD primarily occurs between adjacent levels. This suggests that the transition of the CCD levels is a gradual and long-term process, and it is almost impossible to achieve leapfrog development.
Further considering the spatial environment of each province, if two provinces are adjacent, they are assigned a value of 1; otherwise, they are assigned a value of 0, resulting in a spatial Markov transition probability matrix (Figure 9). It can be observed that the CCD of NQP, CER and HQED is easily influenced by the spatial spillover effects of neighboring regions within a certain geographical scope. The self-transition probability of the LC unit ranges from 0.82 to 0.88, with an upward transition probability of less than 0.2, indicating a significant “low-level lock-in” effect; ML units have self-transition probabilities of 0.75–0.79, maintaining relative stability but with a risk of degradation, with the highest probability reaching 0.13, and limited upward transition capacity, with probabilities ranging from 0.08 to 0.21; MH units exhibit transitional characteristics; HC units demonstrate absolute stability, with self-transition probabilities as high as 0.96–1.00. This indicates that the LC neighborhood exacerbates the locking effect of local LC units through negative spillover and increases the degradation risk of ML units; while the HC neighborhood can promote the upgrading of MH units, its driving effect on ML units is limited.
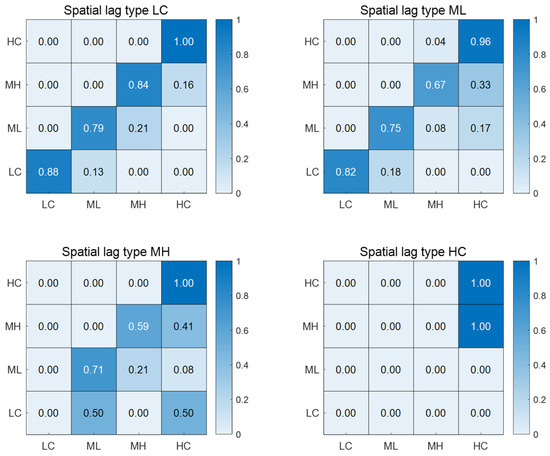
Figure 9.
Spatial Markov transition probability matrix.
3.3. Influencing Factors of the CCD Analysis
The coupled relationship among NQP, CER and HQED involves three two-system couplings, and the coordination status of the two-system couplings has a significant impact on the coordination level of the three-system coupling. To explore the key factors influencing the fluctuations in the CCD of the three-system, this study analyzes the relationship between the two-system coupling and the three-system coupling at the national level, as shown in Figure 10.
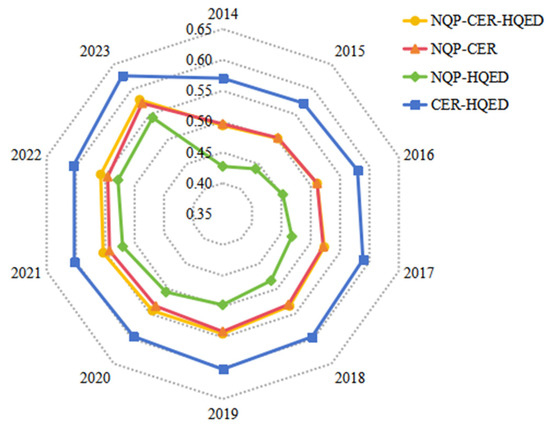
Figure 10.
Trends in CCD between two-system and three-system.
Comparing the average changes in CCD between the two-system and three-system at the national level reveals that the overall trends in these averages are converging. Among these, the average CCD between CER and HQED has been steadily increasing since 2014, indicating that CER and HQED can be advanced in tandem, and suggesting the feasibility of achieving both the strategic goals of carbon peaking and carbon neutrality alongside HQED. The average CCD between these two systems is significantly higher than that of the three-system, exerting the greatest promotional effect on the coordinated development of the three-system coupling. The average CCD between NQP and CER is roughly on par with the average of the three systems, but it is gradually being surpassed by the coupling coordination level of the three systems, with its promotional role declining. This indicates that the technological support provided by NQP for CER and their promotional role in enhancing the CCD level of the three systems both require further strengthening. The average CCD level between NQP and HQED is at the lowest level, with the smallest promotional effect on the coordinated development of the three systems. This also indicates that there is significant room for improvement in the promotional role of NQP in driving HQED and the coordinated development of the three systems. Overall, the positive interaction among NQP, CER and HQED is insufficient, failing to effectively leverage its supportive role in enhancing the CCD level of the three systems.
3.3.1. Single-Factor Analysis
Using the geographic probe method to analyze the impact of the eight selected factors on the CCD of the three systems, the single-factor probe results (Table 7) show that the explanatory power of each factor on the CCD of NQP-CER-HQED is ranked as follows: level of opening up (X6, q = 0.8102) > new-quality labor resources (X3, q = 0.8002) > new-quality laborers (X1, q = 0.7467) > level of government support (X7, q = 0.5804) > level of scientific and technological innovation (X8, q = 0.5802) > new-quality labor objects (X2, q = 0.5465) > level of economic development (X4, q = 0.4668) >level of industrial structure (X5, q = 0.0657). Except for X5, the remaining seven factors all passed the 1% significance level test, indicating that these factors have a significant driving effect on the CCD. Specifically, the level of opening up has the strongest explanatory power, accounting for 81.02%, indicating that it has a decisive influence on the coordination of the three systems and is the core driving force. Among these, the core elements of NQP play a prominent role, while new-quality labor resources and new-quality laborers second and third, respectively, serving as key internal factors for improving resource efficiency and driving low-carbon transformation. The explanatory power of the level of scientific and technological innovation and the level of government support is comparable and significant. The former provides fundamental solutions for green technology, while the latter creates a favorable environment through policies, regulations and incentive mechanisms. The level of economic development has a moderate foundational role, providing material support for the transition. It is worth noting that the influence of the level of industrial structure is weak and statistically insignificant.

Table 7.
Single-factor detection results for CCD.
3.3.2. Interaction Analysis
This study further investigates whether the interaction effects between different factors enhance or weaken their capacity to explain the CCD. The results of this analysis, which quantify the combined influence of these factors, are visually presented in Figure 11. The explanatory power of all factor combinations on CCD is significantly higher than that of single-factor effects, and the interaction types are all nonlinear enhancement or two-factor enhancement, indicating that the development of CCD is the result of the combined effects of multiple factors. Specifically, first, the synergistic effects of the core elements of NQP are prominent. The interaction between new-quality labor resources and the level of government support has the strongest explanatory power (q = 0.936), indicating that smart green production tools require policy incentives such as equipment subsidies and green standards to unlock their emission reduction potential; the interaction between new-quality labor resources and the level of opening up (q = 0.891) highlights the critical role of international technological cooperation in accelerating the adoption of advanced equipment. The high interaction between new-quality laborers and the level of scientific and technological innovation (q = 0.899) reveals that high quality talent must rely on R&D platforms to drive technological breakthroughs, such as new energy teams tackling decarbonization technologies. Second, open innovation and policy regulation are deeply coupled. The most obvious example is the interaction between the level of opening up and the level of scientific and technological innovation (q = 0.868), reflecting that the introduction of international technologies such as carbon capture technology can compensate for local innovation shortcomings; the synergy between the level of opening up and the level of government support (q = 0.861) highlights the regulatory role of green foreign investment access rules in controlling the benefits of openness. The catalytic effect of the level of government support on new-quality labor resources further validates the pivotal role of institutional safeguards. Third, the economic foundation indirectly drives coordination by empowering new-quality factors. Although the single-factor explanatory power of the level of economic development is moderate (q = 0.467), its q value surges to 0.834 when interacting with new-quality labor resources, reflecting that economically developed regions are more capable of bearing the costs of smart equipment upgrades; when combined with the level of opening up (q = 0.788), it indicates that regions with higher economic levels have stronger capabilities to attract green foreign investment. Fourth, the level of industrial structure exhibits “passive coordination” characteristics. Its single-factor effect is insignificant (q = 0.066), but its explanatory power significantly increases when interacting with core factors. When interacting with the level of opening up, the q value jumps to q = 0.887, reflecting how international green trade rules are forcing the transformation of high-carbon industries; when interacting with new-quality labor, the q value reaches 0.888, revealing how talent structure upgrades drive the upgrading of industrial value chains. Overall, coupled coordinated development is the result of the combined influence of multiple social-economic factors.
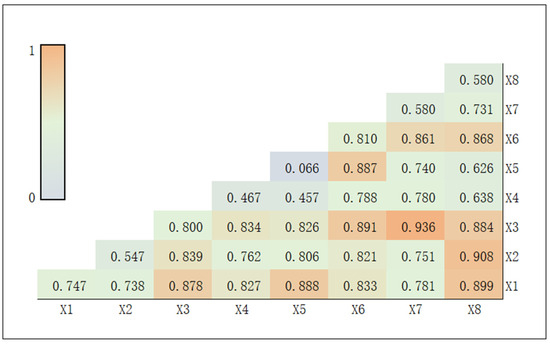
Figure 11.
Interactive detection results of CCD.
4. Discussion
4.1. CCD of NQP-CER-HQED in China from 2014 to 2023
From 2014 to 2023, the CCD level of NQP-CER-HQED in 30 provinces of China showed an upward trend, with the smallest increase occurring between 2019 and 2020, possibly due to the impact of the COVID-19 pandemic on the macro-economy in 2020. Regional differences were evident, with the eastern region ranking higher than the central region, which in turn ranked higher than the northeastern region, which ranked higher than the western region. The reasons for this are as follows: the eastern region has a higher level of economic development, with enterprises possessing significant advantages in terms of funding and technology for low-carbon transformation, resulting in a higher level of CCD; the western region lags behind in economic development, with a higher proportion of traditional energy and metallurgy industries, and insufficient support for NQP in low-carbon transformation, leading to a lower level of CCD. This overall upward trajectory aligns with the findings of Zhu et al. (2024) [37] and Tang et al. (2024) [39], who documented similar positive trends in subsystem coordination within China’s regional development. Furthermore, the distinct “high-east, low-west” spatial pattern we identified is consistent with the well-documented regional disparities in economic development [37] and environmental quality [39], reinforcing the robustness of our findings at the ternary system level. The central region has an economic development level intermediate between the eastern and western regions, with CCD also at an intermediate level. The northeastern region has a high proportion of traditional heavy industries and faces significant pressure for transformation toward HQED, resulting in a lower level of CCD. Given the significant differences in coordination levels and development speeds across the four regions, the state should tailor its support based on each region’s actual conditions: increasing support for the western region, stabilizing development in the eastern region, leveraging the potential of the central region, and revitalizing the northeastern region’s economy to promote balanced and coordinated development of the NQP-CER-HQED system nationwide.
Guangdong Province is in a stage of well-coordinated development, with its development consistently maintaining a significant lead. In contrast, most other provinces are in a stage of barely coordinated or preliminary coordinated development, while six provinces—Gansu, Qinghai, Ningxia, Xinjiang, Inner Mongolia and Shanxi—are developing more slowly and are in a stage of nearly uncoordinated development. Because Guangdong Province’s economic development and the advancement of NQP have consistently far exceeded the national average. In recent years, Guangdong Province has actively promoted carbon reduction efforts through the implementation of the “Energy Conservation and Carbon Reduction Action Plan,” the “Guangdong Province 14th Five-Year Plan for Energy Conservation and Emission Reduction,” and the construction of low-carbon pilot cities. In addition, through the deployment of the “10 + 5” NQP industrial system, namely 10 strategic emerging industrial clusters such as the semiconductor and integrated circuit industry and the high-end equipment manufacturing industry, and 5 future industrial clusters such as future electronics and information technology and future life sciences and health, Guangdong Province has preliminarily established a comprehensive innovation ecosystem chain encompassing “basic research + technological breakthroughs + technology transfer + science and technology finance + talent support,” providing important support and impetus for the vigorous development of NQP. However, the six provinces of Gansu, Qinghai, Ningxia, Xinjiang, Inner Mongolia, and Shanxi have lagged behind in development due to multiple constraints, including a single-industry structure heavily reliant on resource-based economies, weak innovation and talent reserves, and infrastructure and institutional bottlenecks.
4.2. Spatial–Temporal Evolution of CCD
As shown in the kernel density plot, the distribution center of the CCD has been shifting to the right from 2014 to 2023, indicating that the CCD levels of the three systems across provinces have been continuously improving. This phenomenon precisely reflects the synergistic effects of China’s regional coordinated development policies and green transformation strategies. From 2014 to 2023, the spatial auto-correlation of the CCD has generally strengthened, with the clustering structure evolving from “initial formation” to “clear characteristics.” In the early stage (2014–2017), spatial spillover effects were in a “tentative transmission” phase, with weak interaction between regions; In the later period (2020–2023), with the deepening of industrial coordination policies and the accelerated flow of NQP, the agglomeration effects of advantageous regions and the lock-in effects of disadvantaged regions strengthened simultaneously, and the spatial association network gradually matured, confirming that under the driving force of NQP, the spatial mechanism for multi-objective coordinated development continues to improve over time. LC neighbors exacerbate the lock-in effect of local LC units through negative spillover effects and increase the risk of degradation for ML units; while HC neighbors can promote the upgrading of MH units, their driving effect on ML units is limited. This may be due to issues such as unreasonable industrial structures, shortages of resource elements, and incomplete development mechanisms in medium-to-low-level regions, which hinder the effective inflow and conversion of advantageous elements from medium-to-high-level regions. This spatial heterogeneity leads to a “core–periphery” differentiation pattern in the system, where the polarization effect of HC units coexists with the marginalization of LC units. While the existence of spatial agglomeration is supported by prior research on individual dimensions like economy or emissions, our study, by employing spatial Markov chains, provides a novel contribution by quantifying the stability of this spatial structure and the low transition probability for low-level provinces. This nuanced finding, less captured in previous bilateral studies, highlights the persistence of regional disparities within the complex ternary system and underscores the necessity of targeted policy interventions. Therefore, the state should formulate corresponding policies to fully leverage the driving role of high-level coupled neighboring provinces and prevent the aggregation of low-level coupled provinces.
5. Conclusions
5.1. Conclusions
This study construct the NQP-CER-HQED evaluation indicator system and calculates the CCD, analyzes the spatial–temporal evolution characteristics and influencing factors of the CCD, and quantitatively reveals the development characteristics and trends of the NQP, CER and HQED system at the provincial level. Several key conclusions emerge.
First, the results show that from 2014 to 2023, the overall coordination of NQP, CER and HQED has been on the rise. It is expected that from 2024 to 2028, the coordination between provinces will continue to improve, and the synergy between NQP, CER and HQED will gradually improve.
Second, the level of the CCD exhibits a stepped spatial distribution pattern of “higher in the east and lower in the west” and an evolutionary pattern of “the east leading and the west catching up.” High-high clusters have long been concentrated in eastern coastal provinces such as Jiangsu, Zhejiang, Shanghai and Fujian, driving surrounding provinces like Jiangxi, Anhui, Hunan and Hubei to integrate into the coordinated development network. Low-low clusters, on the other hand, are primarily composed of certain inland provinces in central and western China, with their scope continuing to narrow.
Third, the transfer of the CCD levels among provinces exhibits stability, with a high probability of maintaining the status quo and a certain degree of solidification. Evolution primarily occurs between adjacent levels, and the transformation is a gradual, long-term process, with leapfrog development being virtually unattainable.
Fourth, the level of opening up and new-quality labor resources are the dominant factors influencing the CCD levels, while the impact of the leve of industrial structure is minimal. The interactive explanatory power between new-quality labor resources and government support is the strongest.
5.2. Implications for Management
Based on the empirical findings of this study, we propose the following targeted policy recommendations to enhance the coordinated development of NQP, CER, and HQED:
Leverage Dominant Factors to Strengthen Systemic Synergy: Given that the level of opening up and new-quality labor resources are identified as the dominant factors influencing CCD, policymakers should: 1. Intensify efforts to attract high-quality foreign direct investment in green technologies and facilitate international collaboration in R&D for low-carbon innovations. 2. Prioritize the development of new-quality labor resources by expanding higher education and vocational training programs in fields critical to NQP, such as artificial intelligence, new energy, and advanced semiconductors.
Implement Differentiated Regional Strategies Based on Spatial Patterns: In response to the persistent “east-high, west-low” spatial disparity and the stability of CCD transitions, region-specific policies are crucial: 1. Eastern regions should focus on sustaining their lead by strengthening innovation ecosystems, accelerating the commercialization of green patents, and serving as demonstration zones for policy innovation. 2. Central and Western regions require targeted support to break the “lock-in” effect. Investments should be directed towards green infrastructure (e.g., smart grids, EV charging networks) and creating incentives to attract and retain skilled talent. Carbon reduction targets for these regions should be context-specific, avoiding a one-size-fits-all approach that could hinder economic catch-up. 3. Northeastern regions should pursue industrial revitalization through low-carbon transformation, leveraging pilot projects for carbon capture, utilization, and storage (CCUS) in traditional heavy industries.
Foster Collaborative Networks to Facilitate Positive Spillovers: The findings on spatial agglomeration (e.g., the high-high cluster in the east) and the limited driving effect of high-level neighbors on low-level areas highlight the need for structured inter-regional cooperation: 1. Establish cross-provincial “Low-Carbon Coordinated Development Zones” to encourage joint ventures, technology transfer, and shared infrastructure projects. 2. Implement a robust regional carbon sink compensation mechanism, where economically advanced, high-CCD provinces provide financial and technical support to less-developed provinces in exchange for recognized carbon offset credits.
Optimize Policy Coordination to Maximize Interactive Effects: Since the interaction between new-quality labor resources and government support exhibits the strongest explanatory power, policies must be well-aligned: 1. Government R&D funding and subsidies should be strategically channeled to support industries and enterprises that intensively utilize new-quality labor, thereby amplifying the synergistic effect. 2. Develop a cohesive policy framework that integrates S&T policy, industrial policy, and environmental policy, ensuring that signals sent to the market are consistent and mutually reinforcing.
5.3. Limitations and Future Prospects
This study has certain limitations. Firstly, the setting of the contribution coefficients α, β, and γ assumes that NQP, CER, and HQED are equally important. This approach offers a balanced perspective but overlooks potential regional and developmental differences. Future research could incorporate sensitivity analyses to examine the effects of varying weight configurations, thereby enhancing the model’s accuracy and scientific robustness. Secondly, this study employs a geographic distance matrix in its spatial analysis, which may inadequately capture asymmetric interactions driven by regional economic disparities. For instance, developed areas often exert stronger spillover effects on surrounding regions—a phenomenon not fully explained by geographical distance alone. Future research could adopt an economic-geographic nested matrix that integrates economic indicators (e.g., GDP, per capita income) with geographical distance to better characterize multidimensional spatial dependence. Thirdly, the geographical detector method, while effective in identifying spatial stratified heterogeneity and factor explanatory power (q-statistics), cannot establish causal relationships. Future research could employ rigorous econometric models (e.g., panel regression with instrumental variables) to validate the causal mechanisms behind the spatial associations identified in this study.
Author Contributions
Conceptualization, methodology, and writing—review and editing, X.W.; software, validation, formal analysis, data curation, writing—original draft preparation, J.X.; investigation, resources, G.L.; supervision, project administration, H.L.; visualization, S.N. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the 2025 Graduate Student Innovation Special Fund Project of Jiangxi University of Science and Technology (Grant number: XY2025-S030) and Open Fund of the Key Laboratory of Ionic Rare Earth Resources and Environment, Ministry of Natural Resources (ID: 2024IRERE302).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets analyzed during the current study are available in the manuscript and its appendix materials. Specifically, all original data sources and direct links to the publicly available datasets are provided in Appendix A. Processed data and analysis code are available from the corresponding author on reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| NQP | new-quality productivity |
| CER | carbon emission reduction |
| HQED | high-quality economic development |
| CCD | coupling coordination degree |
Appendix A
| Variables | Reference | Data Source | Specific Location | Direct Access Link (URL) |
| Number of students enrolled in ordinary higher education institutions | [30] | National Data (data.stats.gov.cn) | Annual Data by Province-Education—Higher Education Institutions: Undergraduate and Vocational Colleges and Student Enrollment | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Full-time equivalent R&D personnel in industrial enterprises above designated size | [31] | National Data (data.stats.gov.cn) | Annual Data by Province-Science and Technology—Research and Development (R&D) Activities in Industrial Enterprises Above Designated Size | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Average wage of employed persons in urban units | [31] | National Data (data.stats.gov.cn) | Annual Data by Province-Employment and Wages—Urban Unit Employees by Industry | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Software business and information technology services revenue/GDP | [31] | National Data (data.stats.gov.cn) | Annual Data by Province-Transportation and Postal Services—Key Economic Indicators for Software and Information Technology Services | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Number of enterprises engaged in e-commerce transactions | [31] | National Data (data.stats.gov.cn) | Annual Data by Province-Transportation and Postal Services—Enterprise Informatization and E-commerce Status | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Number of websites owned by every 100 companies | [31] | National Data (data.stats.gov.cn) | Annual Data by Province-Transportation and Postal Services—Enterprise Informatization and E-commerce Status | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Environmental protection expenditure/government public finance expenditure | [31] | National Data (data.stats.gov.cn) | Annual Data by Province-Finance—Local Government Expenditures | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Mobile phone penetration rate | [31] | National Data (data.stats.gov.cn) | Annual Data by Province-Transportation and Postal Services—Telecommunications Service Levels | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Internet broadband access ports | [31] | National Data (data.stats.gov.cn) | Annual Data by Province-Transportation and Postal Services—Development of Key Internet Indicators | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Public library collections | [31] | National Data (data.stats.gov.cn) | Annual Data by Province-Culture—Public Libraries | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Mobile phone exchange capacity | [31] | National Data (data.stats.gov.cn) | Annual Data by Province-Transportation and Postal Services—Key Telecommunications Capacity | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Per capita urban road area | [31] | National Data (data.stats.gov.cn) | Annual Data by Province-Urban Overview—Urban Facility Levels | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Information technology service industry revenue | [31] | National Data (data.stats.gov.cn) | Annual Data by Province-Transportation and Postal Services—Key Economic Indicators for Software and Information Technology Services | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Research and development expenditure on new products by large-scale industrial enterprises | [30] | National Data (data.stats.gov.cn) | Annual Data by Province-Science and Technology—New Product Development and Production Status of Industrial Enterprises Above Designated Size | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Total urban carbon emissions | [37] | China Carbon Accounting Database (CEADs) | Provincial Energy Inventory | https://www.ceads.net.cn/data/province/ (accessed on 25 February 2025) |
| Carbon emissions per unit of GDP | [37] | China Carbon Accounting Database (CEADs) | Provincial Energy Inventory | https://www.ceads.net.cn/data/province/ (accessed on 25 February 2025) |
| Total energy consumption | [37] | National Data (data.stats.gov.cn) | Annual Data by Province-Energy—Consumption of Major Energy Products | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Energy consumption per unit of GDP | [37] | National Data (data.stats.gov.cn) | Annual Data by Province-Energy—Consumption of Major Energy Products, National Economic Accounts—Regional Gross Domestic Product | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Carbon emissions per unit of secondary industry added value | [37] | National Data (data.stats.gov.cn) | Annual Data by Province-Energy—Consumption of Major Energy Products, National Economic Accounts—Regional Gross Domestic Product | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Total public bus (electric) passenger transport volume | [37] | National Data (data.stats.gov.cn) | Annual Data by Province-Urban Overview—Urban Public Transportation | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Urban green space area | [37] | National Data (data.stats.gov.cn) | Annual Data by Province-City Overview—Urban Green Spaces and Landscaping | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Green coverage rate in built-up areas | [37] | National Data (data.stats.gov.cn) | Annual Data by Province-City Overview—Urban Green Spaces and Landscaping | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Proportion of science and technology expenditure in fiscal expenditure | [38] | National Data (data.stats.gov.cn) | Annual Data by Province-Finance—Local Government Expenditures | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Proportion of education expenditure in fiscal expenditure | [38] | National Data (data.stats.gov.cn) | Annual Data by Province-Finance—Local Government Expenditures | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Proportion of secondary industry added value in GDP | [38] | National Data (data.stats.gov.cn) | Annual Data by Province-National Economic Accounts—Regional Gross Domestic Product | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Proportion of tertiary industry added value in GDP | [38] | National Data (data.stats.gov.cn) | Annual Data by Province-National Economic Accounts—Regional Gross Domestic Product | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Income gap between urban and rural residents | [38] | National Data (data.stats.gov.cn) | Annual Data by Province-People’s Livelihood—Per Capita Disposable Income of Residents | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Urbanization rate (urban population/total population) | [38] | National Data (data.stats.gov.cn) | Annual Data by Province-Population—Total Population | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Urban built-up area green coverage rate | [38] | National Data (data.stats.gov.cn) | Annual Data by Province-City Overview—Urban Green Spaces and Landscaping | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Urban domestic waste harmless treatment rate | [38] | National Data (data.stats.gov.cn) | Annual Data by Province-Resources and Environment—Municipal Solid Waste Collection and Disposal | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Total imports and exports as a percentage of GDP | [38] | National Data (data.stats.gov.cn) | Annual Data by Province-Foreign Trade and National Economic Accounts—Regional Gross Domestic Product | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Total foreign direct investment as a percentage of GDP | [38] | National Data (data.stats.gov.cn) | Annual Data by Province-Foreign Trade and National Economic Accounts—Regional Gross Domestic Product | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Number of medical institution beds per thousand people | [38] | National Data (data.stats.gov.cn) | Annual Data by Province-Health—Number of Hospital Beds per 10,000 Population | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Average number of books per capita in public libraries | [37] | National Data (data.stats.gov.cn) | Annual Data by Province-Culture—Public Libraries | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
| Average education expenditure per capita | [38] | National Data (data.stats.gov.cn) | Annual Data by Province-Finance—Local Government Expenditures Population—Total Population | https://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 25 February 2025) |
References
- Su, Y.; Dai, H.; Kuang, L.; Liu, J.; Gu, D.; Zou, C.; Huang, H. Corrigendum to “Contemplation on China’s Energy-Development Strategies and Initiatives in the Context of Its Carbon Neutrality Goal”. Engineering 2022, 11, 154. [Google Scholar] [CrossRef]
- Rao, Y.; Wang, X.; Li, H.; Ruan, Y. How Can the Pearl River Delta Urban Agglomeration Achieve the Carbon Peak Target: Based on the Perspective of an Optimal Stable Economic Growth Path. J. Clean. Prod. 2024, 439, 140879. [Google Scholar] [CrossRef]
- Tao, A. Study on the Path of Coordinated Development between Carbon Emission Reduction and Economy in Guangdong Province. Energy Rep. 2022, 8, 477–481. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, L.; Zhou, P.; Zhu, X.; Cudjoe, D. Coordination between Economic Growth and Carbon Emissions: Evidence from 178 Cities in China. Econ. Anal. Policy 2024, 81, 164–180. [Google Scholar] [CrossRef]
- Yan, D.; Liu, C.; Li, P. Effect of Carbon Emissions and the Driving Mechanism of Economic Growth Target Setting: An Empirical Study of Provincial Data in China. J. Clean. Prod. 2023, 415, 137721. [Google Scholar] [CrossRef]
- Chen, L.; Li, X.; Zhao, J.; Kang, X.; Liu, L.; Wang, M.; Chen, W. Coupling and Coordinated Evolution Characteristics of Regional Economy-Energy-Carbon Emission Multiple Systems: A Case Study of Main China’s Basin. J. Environ. Sci. 2024, 140, 204–218. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, J.; Li, Y.; Huang, H. Coupling Analysis and Driving Factors between Carbon Emission Intensity and High-Quality Economic Development: Evidence from the Yellow River Basin, China. J. Clean. Prod. 2023, 423, 138831. [Google Scholar] [CrossRef]
- Lu, S.; Li, Y.; Gu, W.; Xu, Y.; Ding, S. Economy-Carbon Coordination in Integrated Energy Systems: Optimal Dispatch and Sensitivity Analysis. Appl. Energy 2023, 351, 121871. [Google Scholar] [CrossRef]
- Chen, X.; Di, Q.; Jia, W.; Hou, Z. Spatial Correlation Network of Pollution and Carbon Emission Reductions Coupled with High-Quality Economic Development in Three Chinese Urban Agglomerations. Sustain. Cities Soc. 2023, 94, 104552. [Google Scholar] [CrossRef]
- Chen, X.; Di, Q.; Liang, C. The Mechanism and Path of Pollution Reduction and Carbon Reduction Affecting High Quality Economic Development-Taking the Yangtze River Delta Urban Agglomeration as an Example. Appl. Energy 2024, 376, 124340. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, Q. The Confrontation and Symbiosis of Green and Development: Coupling Coordination Analysis between Carbon Emissions and Spatial Development in Urban Agglomerations of China. Sustain. Cities Soc. 2024, 106, 105391. [Google Scholar] [CrossRef]
- Fan, H.; Liang, C. The Pollutant and Carbon Emissions Reduction Synergistic Effect of Green Fiscal Policy: Evidence from China. Financ. Res. Lett. 2023, 58, 104446. [Google Scholar] [CrossRef]
- Wang, Y.; Li, W.; Li, G.; Tan, S. Assessing the Impact of Regional Coordinated Development on a Low-Carbon Future: Evidence from the Beijing-Tianjin-Hebei Coordinated Development Strategy. J. Clean. Prod. 2024, 481, 144140. [Google Scholar] [CrossRef]
- Peng, H.-R.; Ling, K.; Zhang, Y.-J. The Carbon Emission Reduction Effect of Digital Infrastructure Development: Evidence from the Broadband China Policy. J. Clean. Prod. 2024, 434, 140060. [Google Scholar] [CrossRef]
- Sha, R.; Qian, J.; Li, C.; Ge, T. A Win-Win Opportunity for Economic Growth and Carbon Emissions Reduction in China: The Perspective from Correcting Energy Price Distortions. Energy Strategy Rev. 2024, 53, 101406. [Google Scholar] [CrossRef]
- Lan, C.; Li, X.; Peng, B.; Li, X. Unlocking Urban Ecological Resilience: The Dual Role of Environmental Regulation and Green Technology Innovation. Sustain. Cities Soc. 2025, 128, 106466. [Google Scholar] [CrossRef]
- Wang, Y.-R.; Xie, X.-Q.; Yang, Y. How Does New Quality Productivity Empower High-Quality Economic Development: From the Perspective of Innovation Factor Allocation. Xinjiang Soc. Sci. 2024, 6, 42–53. (In Chinese) [Google Scholar] [CrossRef]
- Cheng, H.-F.; Zhu, Z. The Mechanism and Path of High-Quality Development of First-Economy Under the Background of New Quality Productivity. China Bus. Mark. 2025, 39, 9–20. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, H.; Li, C.; Yang, Z.; Zhang, Z.; Jin, C.; Guo, S. How Can New Quality Productivity Decrease Carbon Emission Intensity? Evidence from 30 Provincial Regions in China. Energy 2025, 327, 136487. [Google Scholar] [CrossRef]
- Hu, X.-F.; Gu, D.-M.; Chen, M.-L.; Zhang, J.-N. How Does New Quality Productivity Empower Regional Carbon Emission Reduction: A Dynamic QCA Analysis Based on Provincial Panel Data. J. Tech. Econ. Manag. 2025, 5, 1–7. (In Chinese) [Google Scholar]
- Yang, W.-P.; Huang, R.-Y. New Quality Productivity Boosts the Potential of Carbon Emission Reduction: Effect Measurement and Realization Mechanism. East. China Econ. Manag. 2025, 39, 56–68. (In Chinese) [Google Scholar] [CrossRef]
- Sun, X.-T.; Li, M. Green Technology Innovation, New Quality Productivity and High-Quality Development of Low-Carbon Economy. Stat. Decis. 2024, 40, 29–34. (In Chinese) [Google Scholar] [CrossRef]
- Yang, Y.; Guo, J.-Q.; Gao, Y. Research on the Mechanism and Effect of New Quality Productivity Enabling High-Quality Economic Development. Stat. Decis. 2025, 41, 109–113. (In Chinese) [Google Scholar] [CrossRef]
- Hou, G.-Y.; Zhang, Z.-Y. The Triple Logic of New Quality Productivity Enabling High-Quality Economic Development in Northeast China. Urban Dev. Stud. 2024, 31, 61–66. (In Chinese) [Google Scholar]
- Wang, X.-Z.; Jiang, X.-F.; Yin, T. Impact of Agricultural New Quality Productivity on China’s Agricultural Carbon Emission Reduction Under the “Dual Carbon” Goals. Bull. Soil Water Conserv. 2025, 45, 295–306. (In Chinese) [Google Scholar] [CrossRef]
- Qiao, J.; Tai, D.-J.; Qiu, Y.-Z. The Mechanism and Effect of Agricultural New Quality Productivity Enabling Agricultural Carbon Emission Reduction. Contemp. Econ. Manag. 2024, 46, 42–55. (In Chinese) [Google Scholar] [CrossRef]
- Rasheed, M.Q.; Yuhuan, Z.; Haseeb, A.; Ahmed, Z.; Saud, S. Asymmetric Relationship between Competitive Industrial Performance, Renewable Energy, Industrialization, and Carbon Footprint: Does Artificial Intelligence Matter for Environmental Sustainability? Appl. Energy 2024, 367, 123346. [Google Scholar] [CrossRef]
- Rasheed, M.Q.; Yuhuan, Z.; Nazir, M.; Ahmed, Z.; Yu, X. How Do Semiconductors, Artificial Intelligence, Geopolitical Risk, and Their Moderating Effects Shape Renewable Energy Production in Leading Semiconductor Manufacturing Countries? Technol. Soc. 2025, 80, 102761. [Google Scholar] [CrossRef]
- Rasheed, M.Q.; Yuhuan, Z.; Ahmed, Z.; Haseeb, A.; Saud, S. Information Communication Technology, Economic Growth, Natural Resources, and Renewable Energy Production: Evaluating the Asymmetric and Symmetric Impacts of Artificial Intelligence in Robotics and Innovative Economies. J. Clean. Prod. 2024, 447, 141466. [Google Scholar] [CrossRef]
- Wang, S.; Xu, Z.; Deng, Y. Research on the Impact of New Quality Productivity on Carbon Emission Reduction. Enterp. Econ. 2024, 43, 36–47. (In Chinese) [Google Scholar] [CrossRef]
- Wang, H.-Y. The Impact of New Quality Productivity on Carbon Emission Efficiency: From the Dual Perspectives of Industrial Structure Advancement and Rationalization. Stat. Decis. 2024, 40, 24–29. (In Chinese) [Google Scholar] [CrossRef]
- An, B.-W.; Xu, P.-Y.; Lu, Y.-F.; Li, C.-Y. New Quality Productivity Promotes High-Quality Economic Development: Power Source and Regional Coordination. J. Ind. Technol. Econ. 2025, 44, 14–23. (In Chinese) [Google Scholar]
- Li, Y.; Chen, H.-L.; Tian, M.-Z. Statistical Measurement and Spatio-Temporal Evolution Characteristics of New Quality Productivity Level. Stat. Decis. 2024, 40, 11–17. (In Chinese) [Google Scholar] [CrossRef]
- Wang, K.; Guo, X.-X. China’s New Quality Productivity Level, Regional Differences and Spatio-Temporal Evolution Characteristics. Stat. Decis. 2024, 40, 30–36. (In Chinese) [Google Scholar] [CrossRef]
- Wang, J.; Wang, R.-J. New Quality Productivity: Indicator Construction and Spatio-Temporal Evolution. J. Xi’an Univ. Financ. Econ. 2024, 37, 31–47. (In Chinese) [Google Scholar] [CrossRef]
- Chen, S.-G.; Liu, Y.-X.; Wang, B. New Quality Productivity Empowers High-Quality Economic Development: Mechanism of Action and Spatial Spillover Effects. Stat. Decis. 2025, 41, 107–112. (In Chinese) [Google Scholar] [CrossRef]
- Zhu, Z.-M.; Xu, J.; Lin, W.-X. Spatio-Temporal Coupling and Driving Factors of Carbon Emission Reduction and High-Quality Economic Development in the Yangtze River Delta Urban Agglomeration. Resour. Environ. Yangtze Basin 2024, 33, 2285–2298. (In Chinese) [Google Scholar]
- Li, Y.; Wu, M.-S. Analysis of Spatio-Temporal Coupling and Influencing Factors of Green Technology Innovation, Carbon Emission Reduction and High-Quality Economic Development. Stat. Decis. 2023, 39, 77–81. (In Chinese) [Google Scholar] [CrossRef]
- Tang, X.-B.; Yan, X.-T.; Yang, M.-Y.; Geng, Y.-J. Research on the Coupling and Coordination of New Smart Cities, High-Quality Economic Development and Environmental Quality: A Case Study of Chinese Megacities. World Surv. Res. 2024, 12, 17–30. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, D.; Li, C.; Wang, Q.; Yuan, J. Comprehensive Evaluation of National Electric Power Development Based on Cloud Model and Entropy Method and TOPSIS: A Case Study in 11 Countries. J. Clean. Prod. 2020, 277, 123190. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, J.; Bi, J.; Zhou, Q. Comprehensive Evaluation of Air Pollution Emission Permit Allocation: Effectiveness, Efficiency, and Equity in China’s Environmental Management Framework. J. Clean. Prod. 2024, 434, 139855. [Google Scholar] [CrossRef]
- Bian, D.; Yang, X.; Xiang, W.; Sun, B.; Chen, Y.; Babuna, P.; Li, M.; Yuan, Z. A New Model to Evaluate Water Resource Spatial Equilibrium Based on the Game Theory Coupling Weight Method and the Coupling Coordination Degree. J. Clean. Prod. 2022, 366, 132907. [Google Scholar] [CrossRef]
- Xue, R.; Gu, R.; Ong, T. How Does Coupling Coordination between Industrial Structure Optimization and Ecosystem Services Dynamically Affect Carbon Emissions in the Yellow River Basin? J. Clean. Prod. 2025, 517, 145872. [Google Scholar] [CrossRef]
- Yang, Z.; Hu, J.; Wang, Z.; Chen, S. A New Model Based on Coupling Coordination Analysis Incorporates the Development Rate for Urbanization and Ecosystem Services Assessment: A Case of the Yangtze River Delta. Ecol. Indic. 2024, 159, 111596. [Google Scholar] [CrossRef]
- Dong, W.; Sun, H.; Tan, J.; Li, Z.; Zhang, J.; Yang, H. Regional Wind Power Probabilistic Forecasting Based on an Improved Kernel Density Estimation, Regular Vine Copulas, and Ensemble Learning. Energy 2022, 238, 122045. [Google Scholar] [CrossRef]
- Jiang, Q.-H.; Zhang, J.-Z.; Zhang, D.-M.; Huang, H.-W. Simulation of Geological Uncertainty Based on Improved Three-Dimensional Coupled Markov Chain Model. Eng. Geol. 2024, 340, 107647. [Google Scholar] [CrossRef]
- Qian, W.; Wang, J. An Improved Seasonal GM (1,1) Model Based on the HP Filter for Forecasting Wind Power Generation in China. Energy 2020, 209, 118499. [Google Scholar] [CrossRef]
- Torres, M.; Srubar, W.V. Characterizing Statistical Uncertainty and Variability of Building Material Emissions in Probabilistic Whole-Building Life Cycle Assessment Using Kernel Density Estimation. Build. Environ. 2025, 284, 113442. [Google Scholar] [CrossRef]
- Wang, Z.-X.; Wang, Z.-W.; Li, Q. Forecasting the Industrial Solar Energy Consumption Using a Novel Seasonal GM (1,1) Model with Dynamic Seasonal Adjustment Factors. Energy 2020, 200, 117460. [Google Scholar] [CrossRef]
- Abban, O.J.; Rajaguru, G.; Acheampong, A.O. The Spillover Effect of Economic Institutions on the Environment: A Global Evidence from Spatial Econometric Analysis. J. Environ. Manag. 2025, 373, 123645. [Google Scholar] [CrossRef]
- Yang, W.; Chen, J.; Ding, T.; Yan, X.; Gong, W. Supply-Demand Security Assessment of Water-Energy-Food Systems: A Perspective on Intra-City Coupling and Inter-City Linkages of Ecosystem Services. Sustain. Cities Soc. 2024, 117, 105964. [Google Scholar] [CrossRef]
- De Abreu Dos Santos, D.; Lopes, T.R.; Damaceno, F.M.; Duarte, S.N. Evaluation of Deforestation, Climate Change and CO2 Emissions in the Amazon Biome Using the Moran Index. J. S. Am. Earth Sci. 2024, 143, 105010. [Google Scholar] [CrossRef]
- Wang, X.; Liu, E.; Yan, M.; Zheng, S.; Fan, Y.; Sun, Y.; Li, Z.; Xu, J. Contamination and Source Apportionment of Metals in Urban Road Dust (Jinan, China) Integrating the Enrichment Factor, Receptor Models (FA-NNC and PMF), Local Moran’s Index, Pb Isotopes and Source-Oriented Health Risk. Sci. Total Environ. 2023, 878, 163211. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Gao, J.; Yin, X.; Chen, J.; Wu, X. Risk Assessment and Simulation of Gas Pipeline Leakage Based on Markov Chain Theory. J. Loss Prev. Process Ind. 2024, 91, 105370. [Google Scholar] [CrossRef]
- Wang, W.; Yang, Y. Spatial-Temporal Differentiation Characteristics and Driving Factors of China’s Energy Eco-Efficiency Based on Geographical Detector Model. J. Clean. Prod. 2024, 434, 140153. [Google Scholar] [CrossRef]
- Guo, L.; Li, P.; Zhang, J.; Xiao, X.; Peng, H. Do Socio-Economic Factors Matter? A Comprehensive Evaluation of Tourism Eco-Efficiency Determinants in China Based on the Geographical Detector Model. J. Environ. Manag. 2022, 320, 115812. [Google Scholar] [CrossRef]
- Xu, W.; Jin, J.; Zhang, J.; Yuan, S.; Liu, Y.; Guan, T.; He, R.; Zhu, L. Coupling Coordination Degree, Interaction Relationship and Driving Mechanism of Water Resources Carrying Capacity of Beijing-Tianjin-Hebei Urban Agglomeration in China. J. Clean. Prod. 2025, 504, 145433. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).