The Considering Sales Manipulation of Fresh Product Enterprises Game
Abstract
1. Introduction
2. Literature Review
2.1. Sales Manipulation Research
2.2. Fresh Products Research
3. Model
3.1. Basic Assumptions
3.2. The Game Model
3.2.1. Model with Neither Fresh Product Firm Engages in Sales Manipulation: NN Model
3.2.2. Model with the Fresh Firm G Engages in Sales Manipulation: YN Model
3.2.3. Model with the Fresh Firm D Engages in Sales Manipulation: NY Model
3.2.4. Model with Both Fresh Product Firms Engage in Sales Manipulation: YY Model
4. Model Comparative
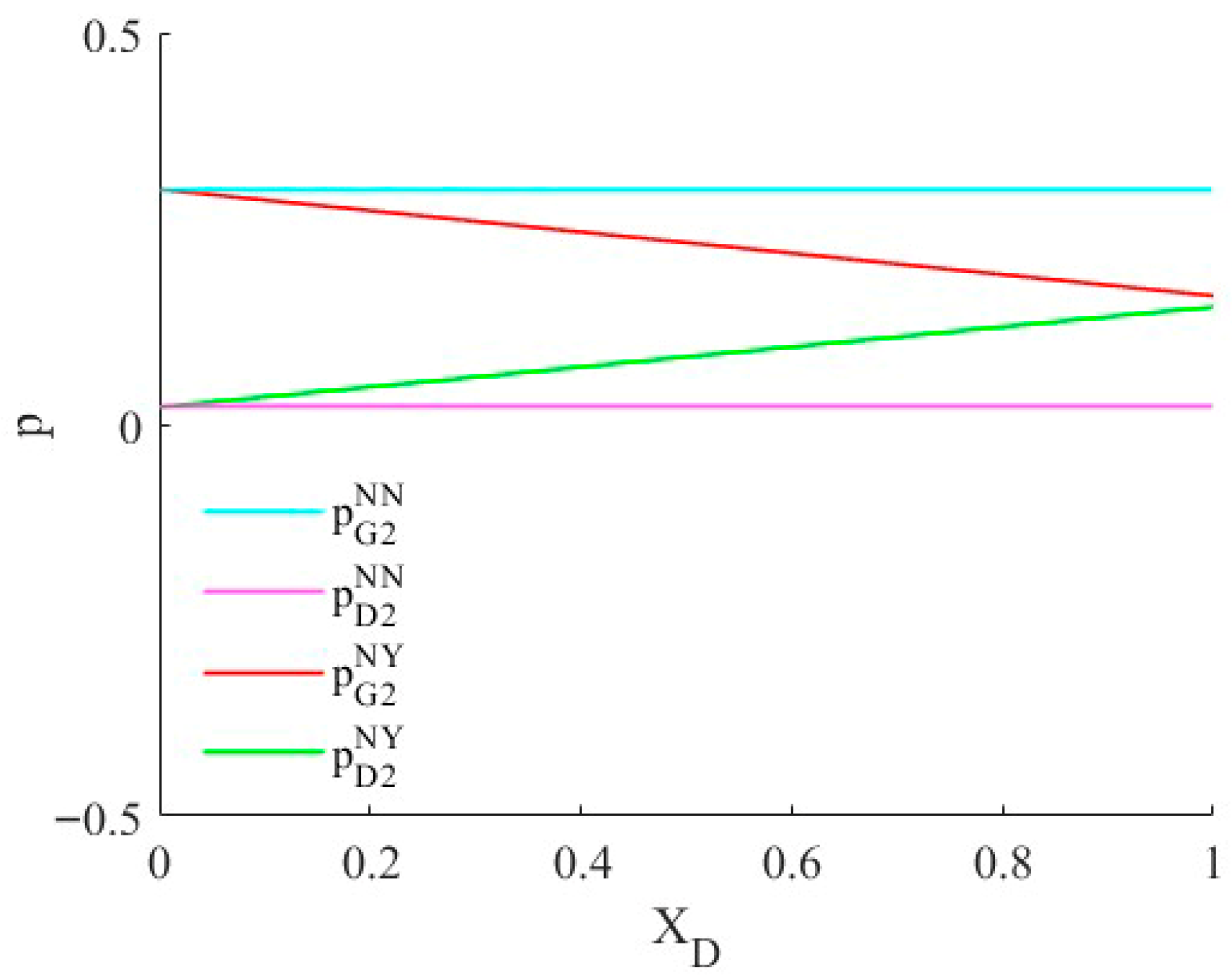
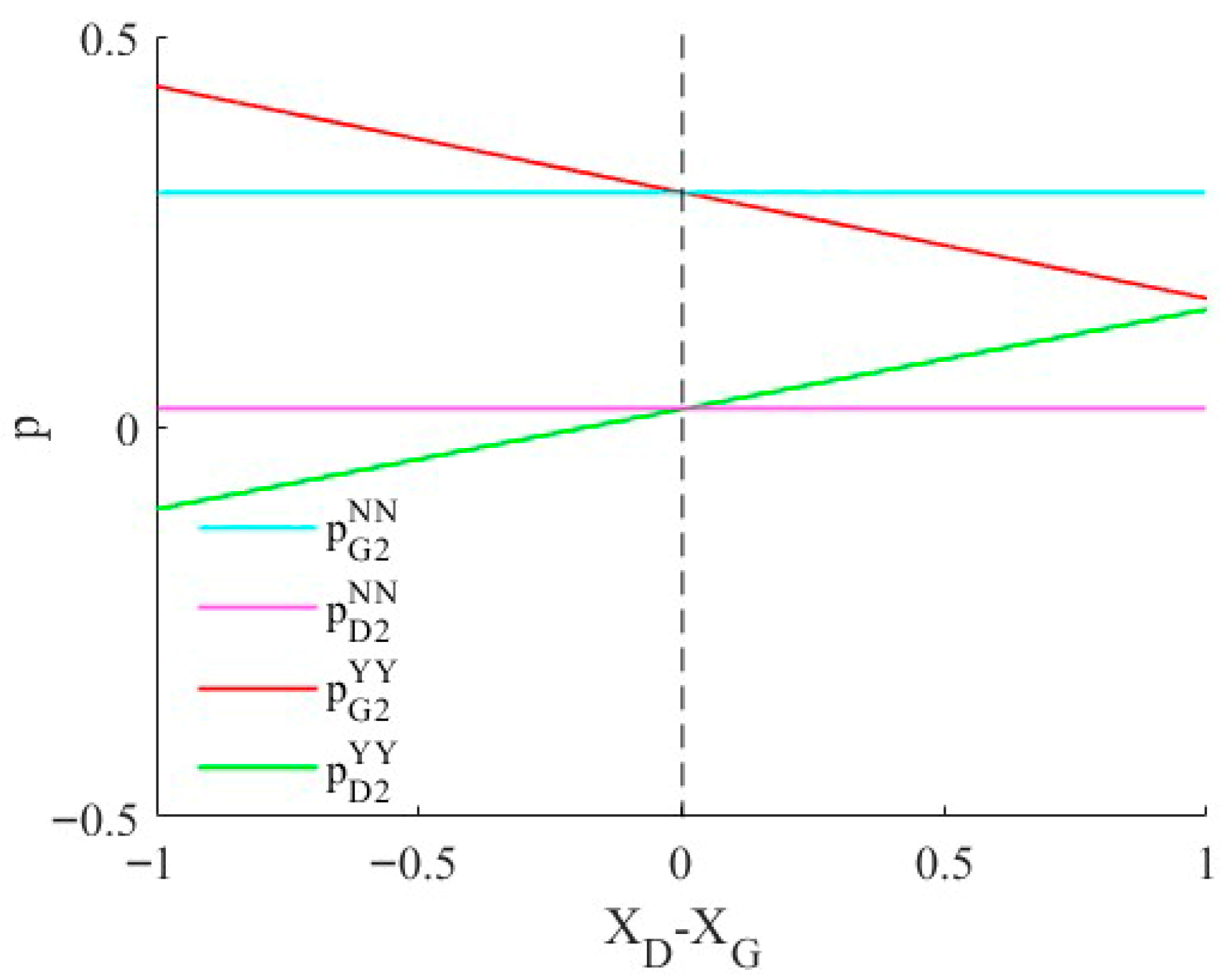
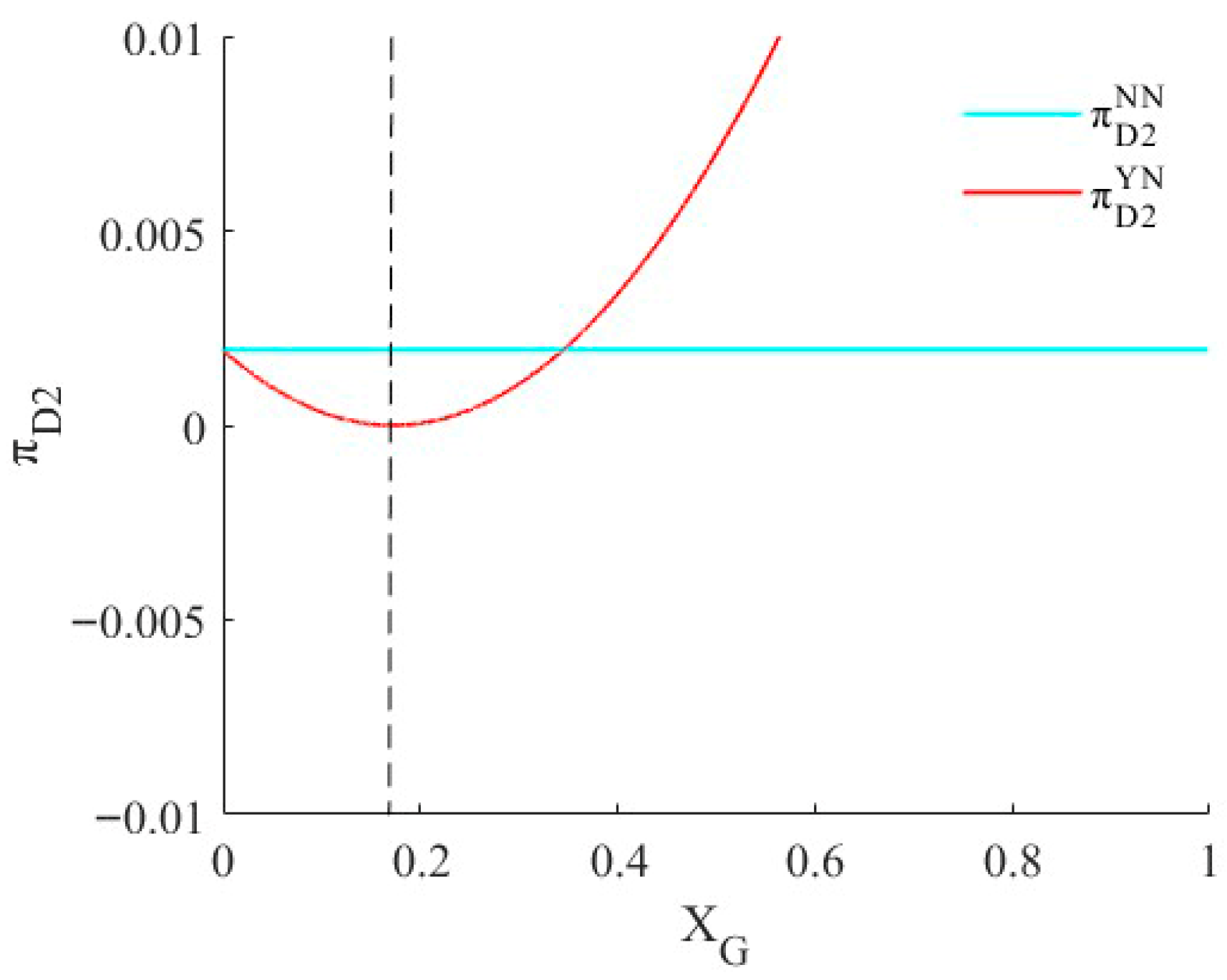
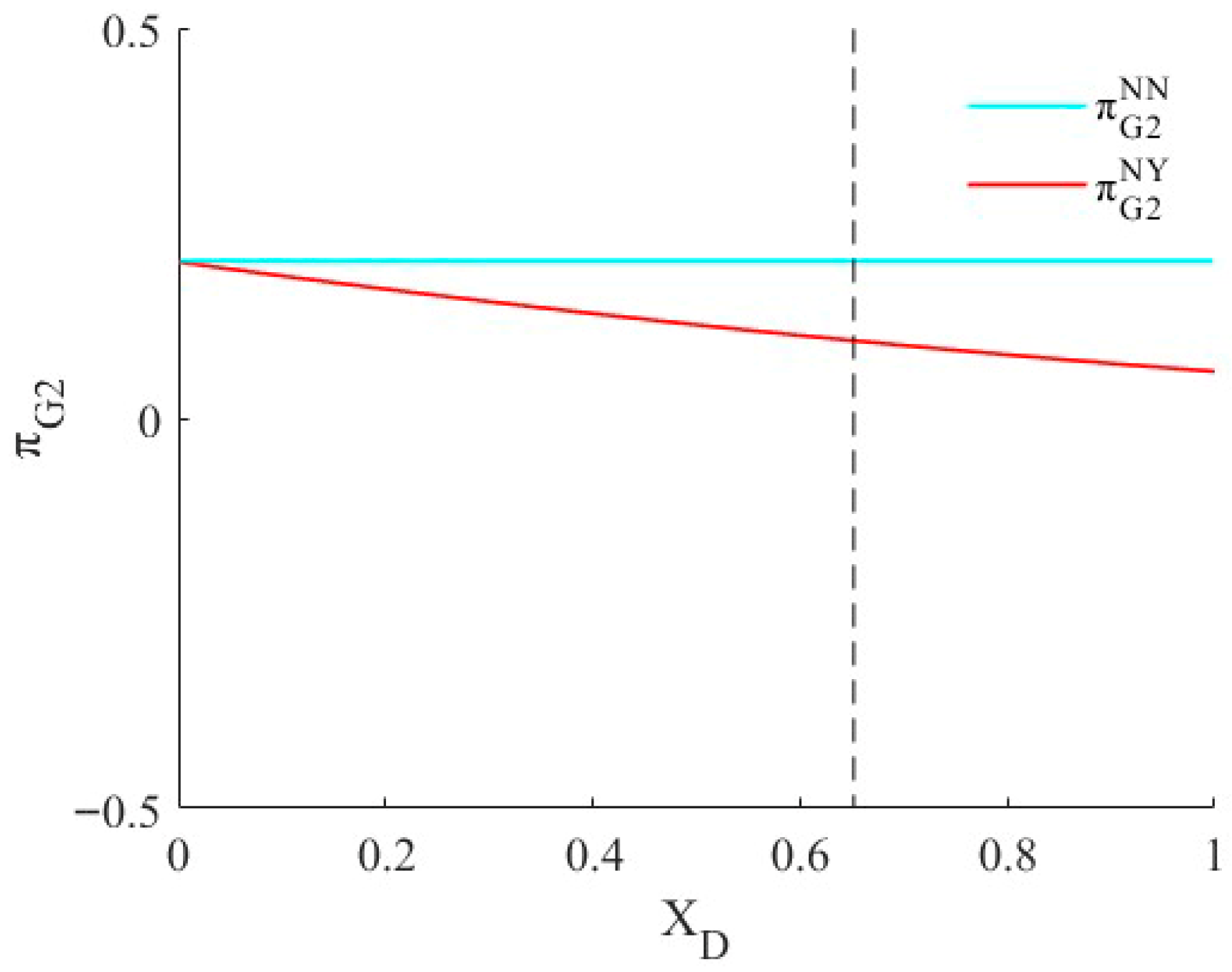
4.1. The Effect of Sales Manipulation on Product Prices
- (1)
- Only firm G is manipulating sales; we have ,
- (2)
- Only firm D is manipulating sales; we have ,
- (3)
- Both firms are manipulating sales:
- (i)
- When , we have and
- (ii)
- When , we have and
4.2. The Effect of Sales Manipulation on Market Share
- (1)
- Only firm G is manipulating sales; we have ,,
- (2)
- Only firm D is manipulating sales; we have ,
- (3)
- Both firms are manipulating sales:
- (i)
- When ,,,
- (ii).
- When, we have ,,
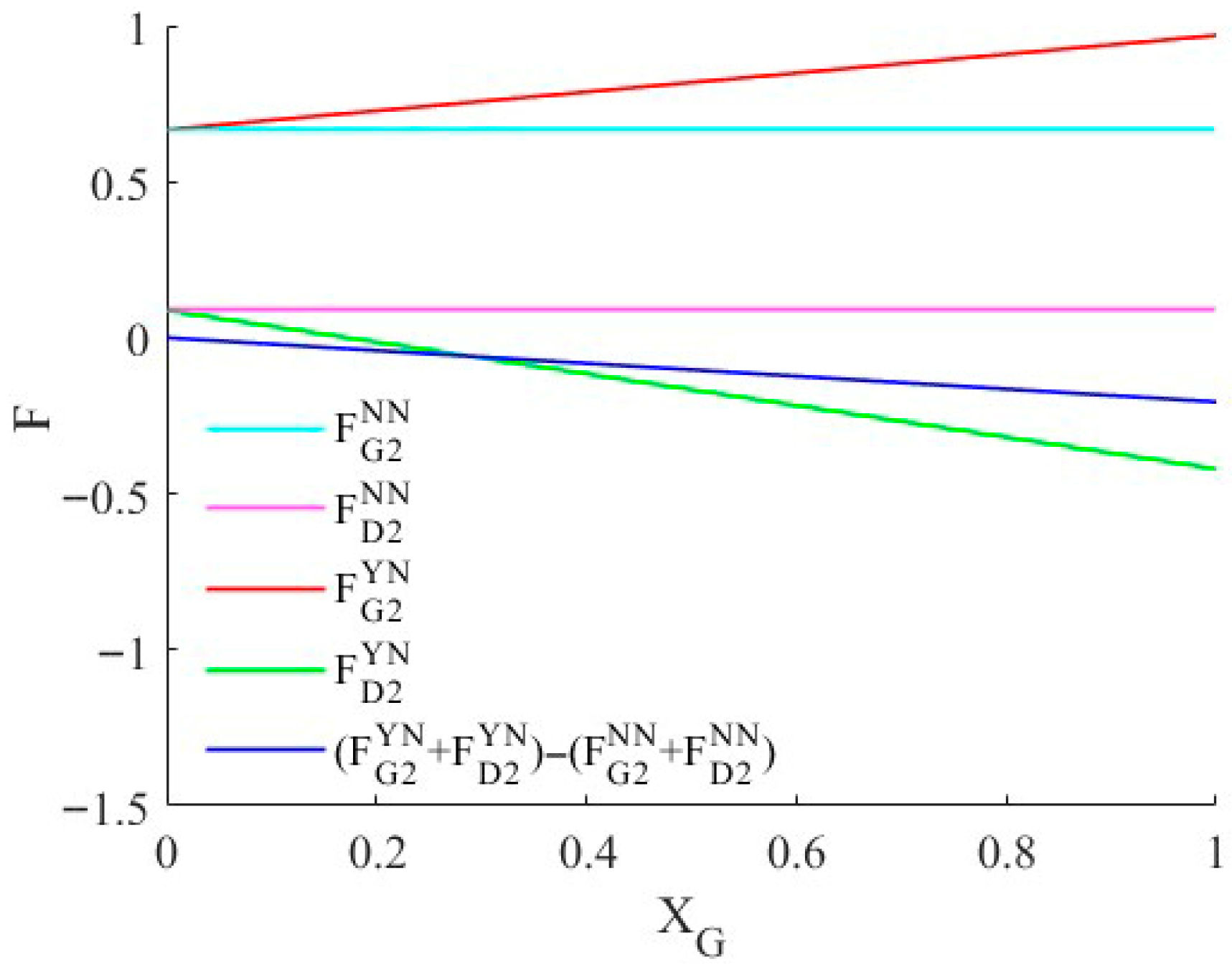
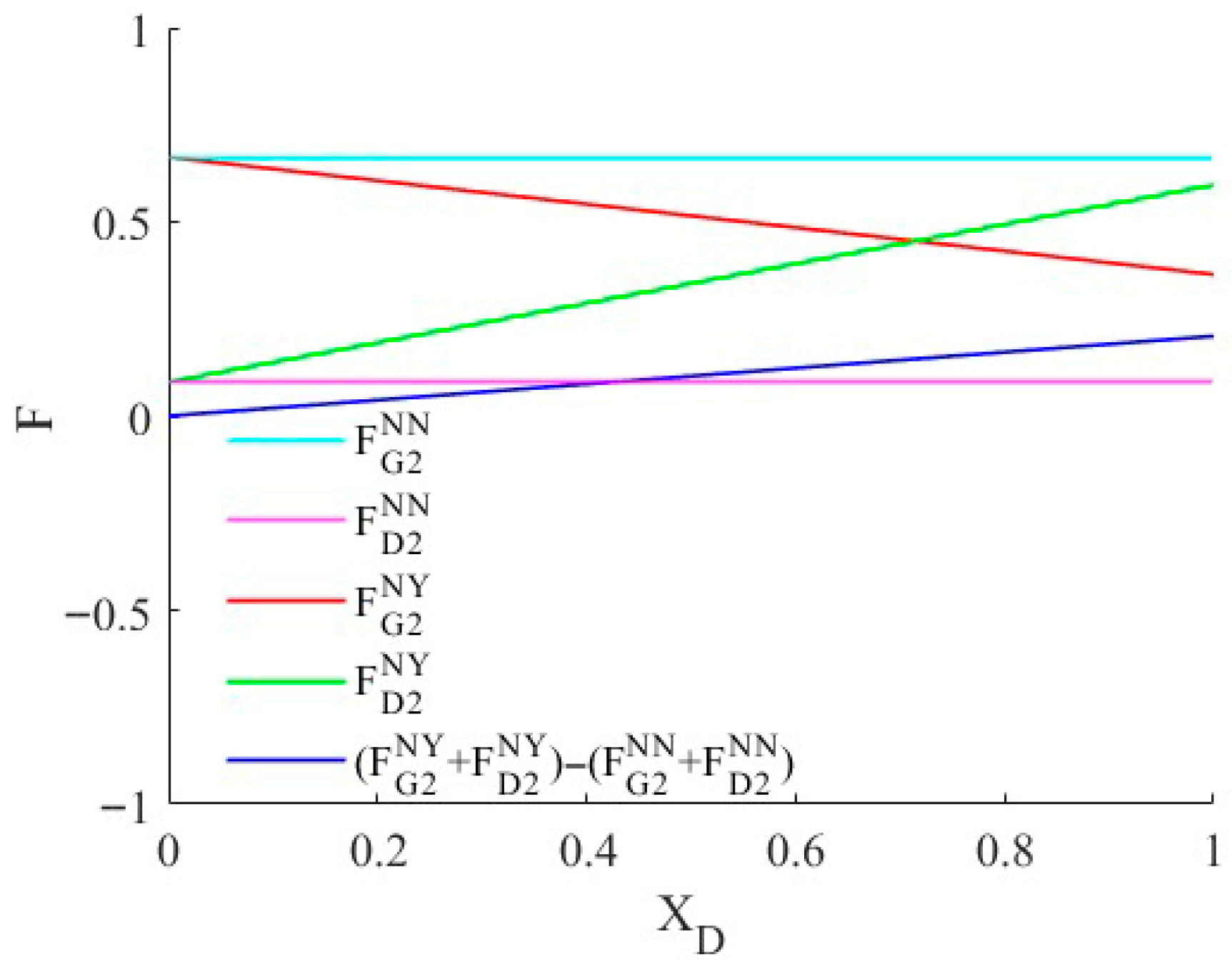
4.3. The Effect of Sales Manipulation on Firm Profit
- (1)
- Only firm G is manipulating sales:
- (i)
- For firm G: ,; When and ,; When and , , where:
- (ii)
- For firm D:
- (2)
- Only firm D is manipulating sales:
- (i)
- For firm G,
- (ii)
- For firm D, when , ; when and , ; when and , , where:
- (3)
- When both firms engage in sales manipulation:
- (i)
- For firm G, when ,; when, , where:
5. Numerical Analysis
5.1. The Effect of Sales Manipulation for Product Prices
5.2. The Effect of Sales Manipulation for Market Share
5.3. The Effect of Sales Manipulation for Firm Profit
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jin, C.; Yang, L.; Hosanagar, K. To Brush or Not to Brush: Product Rankings, Consumer Search, and Fake Orders. Inf. Syst. Res. 2023, 34, 532–552. [Google Scholar] [CrossRef]
- Kim, D.Y.; Kim, S.Y. The Impact of Customer-Generated Evaluation Information on Sales in Online Platform-Based Markets. J. Retail. Consum. Serv. 2022, 68, 103016. [Google Scholar] [CrossRef]
- Xia, X.; Li, C.; Zhu, Q. Game Analysis for the Impact of Carbon Trading on Low-Carbon Supply Chain. J. Clean. Prod. 2020, 276, 123220. [Google Scholar] [CrossRef]
- Schwarz, J.A.; Tan, B. Optimal Sales and Production Rollover Strategies under Capacity Constraints. Eur. J. Oper. Res. 2021, 294, 507–524. [Google Scholar] [CrossRef]
- Nie, S.; Cai, G.; Huang, Y.; He, J. Deciphering Stakeholder Strategies in Electric Vehicle Battery Recycling: Insights from a Tripartite Evolutionary Game and System Dynamics. J. Clean. Prod. 2024, 452, 142174. [Google Scholar] [CrossRef]
- Fernandes, E.; Moro, S.; Cortez, P.; Batista, F.; Ribeiro, R. A Data-Driven Approach to Measure Restaurant Performance by Combining Online Reviews with Historical Sales Data. Int. J. Hosp. Manag. 2021, 94, 102830. [Google Scholar] [CrossRef]
- Yannopoulou, N.; Chandrasapth, K.; Bian, X.; Jin, B.; Gupta, S.; Liu, M.J. How Disinformation Affects Sales: Examining the Advertising Campaign of a Socially Responsible Brand. J. Bus. Res. 2024, 182, 114789. [Google Scholar] [CrossRef]
- Cai, H.; Chen, Y.; Fang, H. Observational Learning: Evidence from a Randomized Natural Field Experiment. Am. Econ. Rev. 2009, 99, 864–882. [Google Scholar] [CrossRef]
- Chen, Y.-F. Herd Behavior in Purchasing Books Online. Comput. Hum. Behav. 2008, 24, 1977–1992. [Google Scholar] [CrossRef]
- Wang, L.; Mo, J.; Li, B. Fake It Till You Make It: An Empirical Investigation of Sales Fraud in E-Commerce. In Proceedings of the PACIS, Xi’an, China, 8–12 July 2019. [Google Scholar]
- Zhou, J.; Xu, R.; Jiang, C. Sales Volume and Online Reviews in a Sequential Game. J. Oper. Res. Soc. 2023, 74, 2277–2288. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, M.; Wu, H. The Brushing Game in Online Marketplaces. Int. J. Electron. Commer. 2023, 27, 163–184. [Google Scholar] [CrossRef]
- Long, F.; Liu, Y. Platform Manipulation in Online Retail Marketplace with Sponsored Advertising. Mark. Sci. 2024, 43, 317–345. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, J.; Xiao, T. Sales Manipulation Strategies of Competitive Firms on an E-commerce Platform: Beneficial or Harmful? Decis. Sci. 2024, 55, 491–509. [Google Scholar] [CrossRef]
- Liu, X.; He, Y.; Hooshmand Pakdel, G.; Li, S. Dynamic Optimization of E-Commerce Supply Chains for Fresh Products with Blockchain and Reference Effect. Technol. Forecast. Soc. Change 2025, 214, 124040. [Google Scholar] [CrossRef]
- Liu, C.; Lv, J.; Hou, P.; Lu, D. Disclosing Products’ Freshness Level as a Non-Contractible Quality: Optimal Logistics Service Contracts in the Fresh Products Supply Chain. Eur. J. Oper. Res. 2023, 307, 1085–1102. [Google Scholar] [CrossRef]
- Ma, Z.; Li, R. Consideration of Quantity Loss in Packaging Strategies for the Fresh Agricultural Products Supply Chain. Sustain. Oper. Comput. 2025, 6, 104–115. [Google Scholar] [CrossRef]
- Yuan, H.; Zhang, L.; Cao, B.-B.; Chen, W. Optimizing Traceability Scheme in a Fresh Product Supply Chain Considering Product Competition in Blockchain Era. Expert. Syst. Appl. 2024, 258, 125127. [Google Scholar] [CrossRef]
- Yu, Q.; Zhang, M.; Mujumdar, A.S. Blockchain-Based Fresh Food Quality Traceability and Dynamic Monitoring: Research Progress and Application Perspectives. Comput. Electron. Agric. 2024, 224, 109191. [Google Scholar] [CrossRef]
- Chen, Z.; Dan, B.; Lei, T.; Ma, S. Demand Information Disclosure in Fresh Produce Supply Chain Considering Competition between Geographical Indication and Local Suppliers. Socio-Econ. Plan. Sci. 2025, 98, 102177. [Google Scholar] [CrossRef]
- Feng, L.; Wang, W.-C.; Teng, J.-T.; Cárdenas-Barrón, L.E. Pricing and Lot-Sizing Decision for Fresh Goods When Demand Depends on Unit Price, Displaying Stocks and Product Age under Generalized Payments. Eur. J. Oper. Res. 2022, 296, 940–952. [Google Scholar] [CrossRef]
- Waqas Iqbal, M.; Iqbal Malik, A.; Babar Ramzan, M.; Saad Memon, M.; Irshad Mari, S.; Salman Habib, M. Consumer Response to Adjustable Price and Shelf-Life of Fresh Food Products under Effective Preservation Policy. Comput. Ind. Eng. 2024, 188, 109897. [Google Scholar] [CrossRef]
- Yu, Y.; Xiao, T. Pricing and Cold-Chain Service Level Decisions in a Fresh Agri-Products Supply Chain with Logistics Outsourcing. Comput. Ind. Eng. 2017, 111, 56–66. [Google Scholar] [CrossRef]
- Mohan Modak, N.; Senapati, T.; Simic, V.; Pamucar, D.; Saha, A.; Cárdenas-Barrón, L.E. Managing a Sustainable Dual-Channel Supply Chain for Fresh Agricultural Products Using Blockchain Technology. Expert. Syst. Appl. 2024, 244, 122929. [Google Scholar] [CrossRef]
- Dan, B.; Lei, T.; Zhang, X.; Liu, M.; Ma, S. Modeling of the Subsidy Policy in Fresh Produce Wholesale Markets under Yield Uncertainty. Econ. Model. 2023, 126, 106413. [Google Scholar] [CrossRef]
- Liu, M.; Jia, W.; Yan, W.; He, J. Factors Influencing Consumers’ Repurchase Behavior on Fresh Food e-Commerce Platforms: An Empirical Study. Adv. Eng. Inform. 2023, 56, 101936. [Google Scholar] [CrossRef]
- Fan, T.; Xu, C.; Tao, F. Dynamic Pricing and Replenishment Policy for Fresh Produce. Comput. Ind. Eng. 2020, 139, 106127. [Google Scholar] [CrossRef]
- Liu, L.; Zhao, L.; Ren, X. Optimal Preservation Technology Investment and Pricing Policy for Fresh Food. Comput. Ind. Eng. 2019, 135, 746–756. [Google Scholar] [CrossRef]
- Wang, X.; He, T. The Community Group Buying Models and Strategic Management for Fresh Food under Supply Uncertainty. Comput. Ind. Eng. 2025, 204, 111083. [Google Scholar] [CrossRef]
- Özbilge, A.; Hassini, E.; Parlar, M. Optimal Pricing and Donation Policy for Fresh Goods. Eur. J. Oper. Res. 2024, 312, 198–210. [Google Scholar] [CrossRef]
- Tan, C.; Zeng, Y. Two-Stage Pricing Strategy of the O2O Supply Chain for Fresh Produce Based on Blockchain Technology. Chin. J. Manag. 2023, 20, 904–915. [Google Scholar]
- Li, S.; Qu, S.; Wahab, M.I.M.; Ji, Y. Low-Carbon Supply Chain Optimisation with Carbon Emission Reduction Level and Warranty Period: Nash Bargaining Fairness Concern. Int. J. Prod. Res. 2024, 62, 6665–6687. [Google Scholar] [CrossRef]
- Zhao, S.; Cao, X. Sustainable Suppliers-to-Consumers’ Sales Mode Selection for Perishable Goods Considering the Blockchain-Based Tracking System. Sustainability 2024, 16, 3433. [Google Scholar] [CrossRef]
- Pan, H.; Song, X.; Hou, J.; Tan, S. Evolutionary Game Analysis Between Large Power Consumers and Power Sellers in the Context of Big-Data-Driven Value-Added Services. Sustainability 2024, 16, 8974. [Google Scholar] [CrossRef]
- Berger, J.; Sorensen, A.T.; Rasmussen, S.J. Positive Effects of Negative Publicity: When Negative Reviews Increase Sales. Mark. Sci. 2010, 29, 815–827. [Google Scholar] [CrossRef]







| Notations | Definitions |
|---|---|
| t | period, t = 1, 2 |
| i | The subscript i represents the fresh product firm, where G denotes the high-quality fresh product firm, and D denotes the low-quality fresh product firm. Firm G sells product G, while firm D sells product D |
| j | The superscript j represents the sales manipulation strategy adopted by the firms, where NN indicates that neither fresh product firm engages in sales manipulation, YN indicates that fresh product firm G engages in sales manipulation, NY indicates that fresh product firm D engages in sales manipulation, and YY indicates that both fresh product firms engage in sales manipulation |
| m | the consumer’s internal valuation of the product, and m follows a uniform distribution over the interval [0, 1] |
| Consumers’ expected quality of the product, and | |
| Consumers’ preference to the relative sales of a company’s product | |
| Fresh product retail price | |
| Consumer economic utility | |
| Firm profit | |
| Firm market share | |
| Sales manipulation volume, where , and constant in each stage | |
| c | The constant that represents the linear relationship between sales manipulation cost and sales manipulation volume |
| Consumers who have no preference between purchasing product G and product D in stage t | |
| Consumers in stage t who are indifferent between purchasing product D and not making a purchase |
| Parameter | β | γG | γD |
|---|---|---|---|
| Value | 0.2 | 0.8 | 0.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, N.; Qu, S.; Ji, Y. The Considering Sales Manipulation of Fresh Product Enterprises Game. Sustainability 2025, 17, 9688. https://doi.org/10.3390/su17219688
Sun N, Qu S, Ji Y. The Considering Sales Manipulation of Fresh Product Enterprises Game. Sustainability. 2025; 17(21):9688. https://doi.org/10.3390/su17219688
Chicago/Turabian StyleSun, Ning, Shaojian Qu, and Ying Ji. 2025. "The Considering Sales Manipulation of Fresh Product Enterprises Game" Sustainability 17, no. 21: 9688. https://doi.org/10.3390/su17219688
APA StyleSun, N., Qu, S., & Ji, Y. (2025). The Considering Sales Manipulation of Fresh Product Enterprises Game. Sustainability, 17(21), 9688. https://doi.org/10.3390/su17219688








