An Evaluation of a New Building Energy Simulation Tool to Assess the Impact of Water Flow Glazing Facades on Maintaining Comfortable Temperatures and Generating Renewable Energy
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of Proposed Simulation Tool
2.1.1. Spectral Problem of Water Flow Glazing
2.1.2. Thermal Problem of Water Flow Glazing
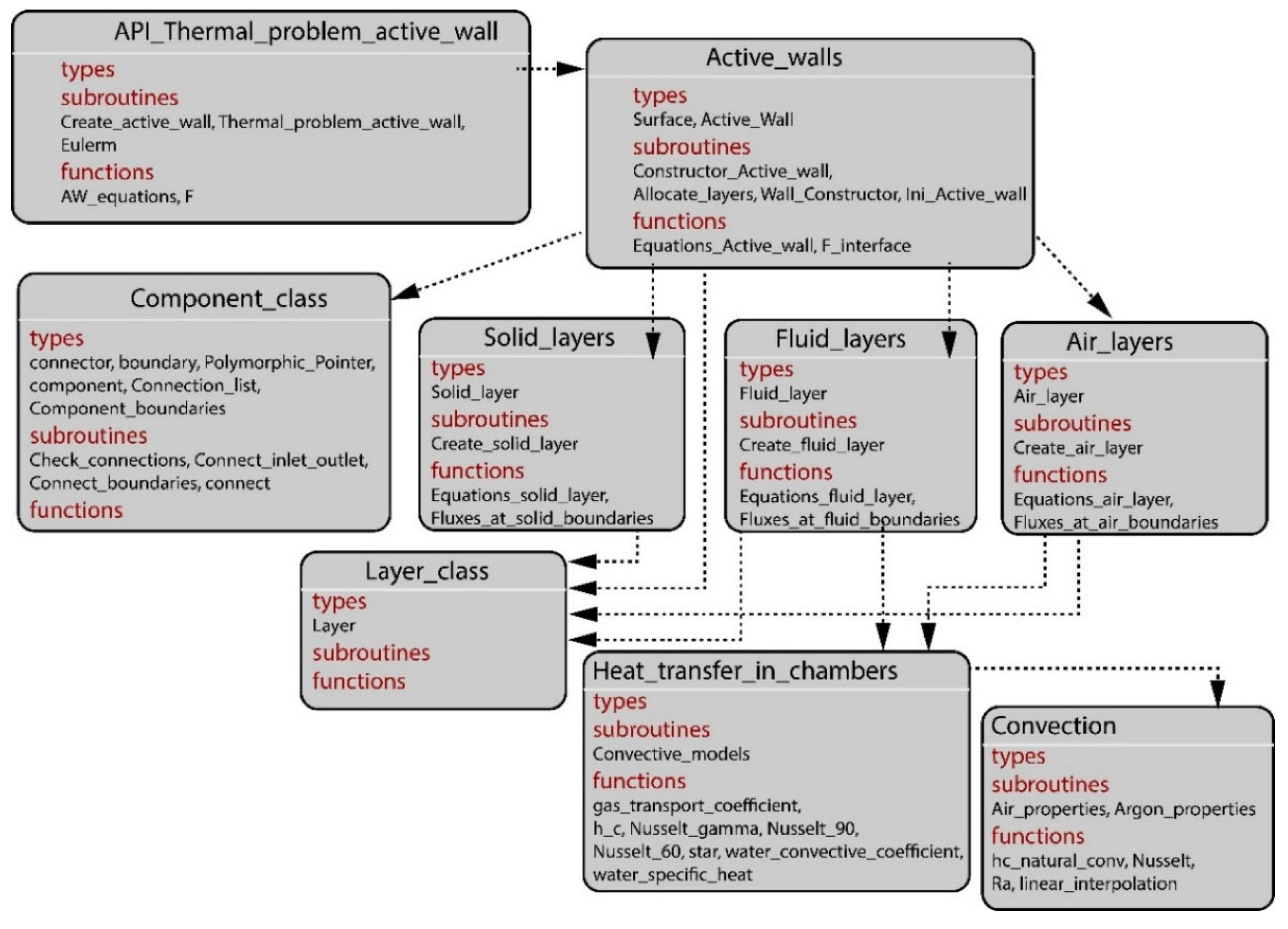
2.1.3. Numerical Implementation of the Proposed Tool
2.2. Setting the Parameters of Water Flow Glazing in IDA-ICE
2.3. Description of Water Flow Glazing Types
2.4. Description of Experimental Prototype
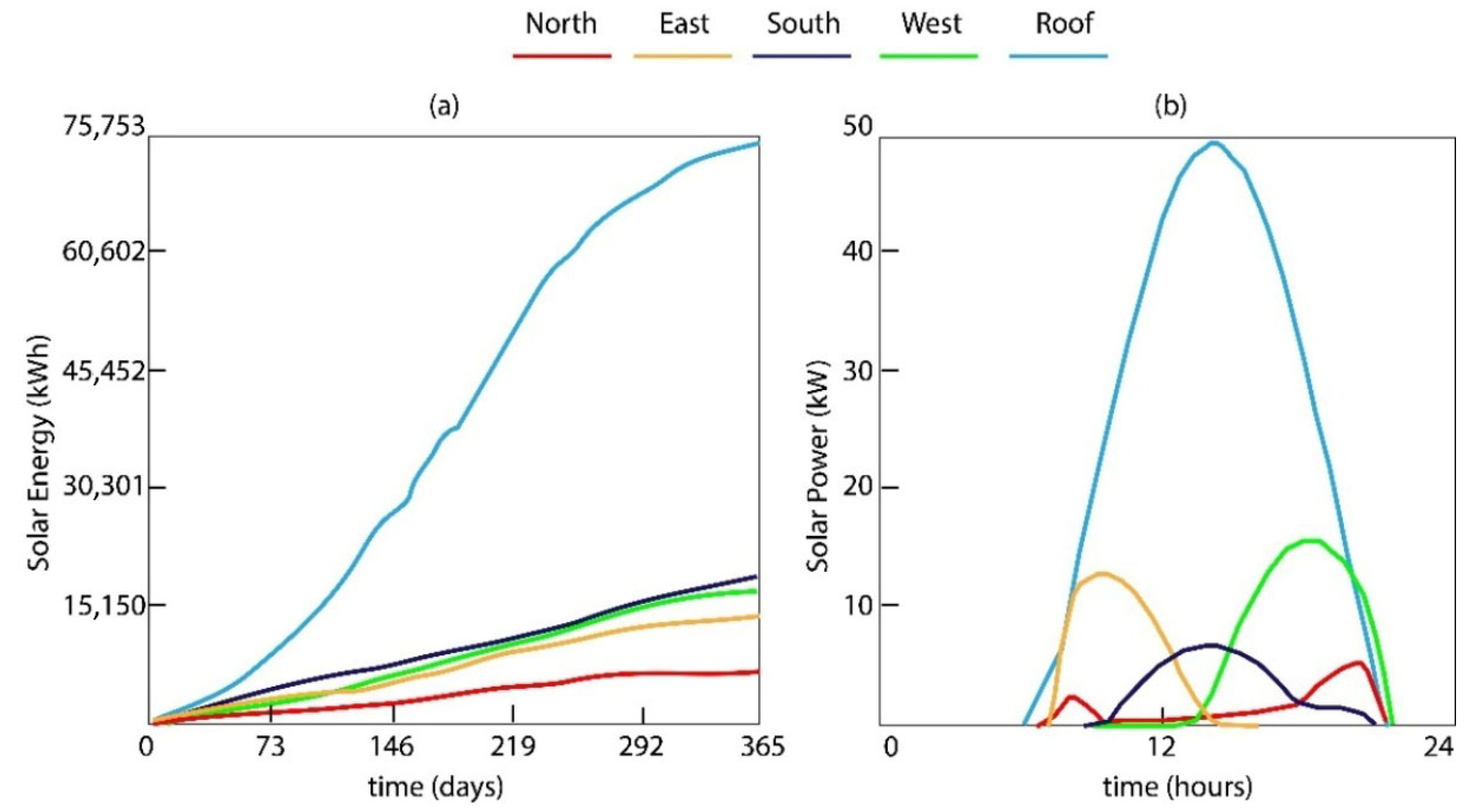
3. Results
3.1. Results from Studied Tool
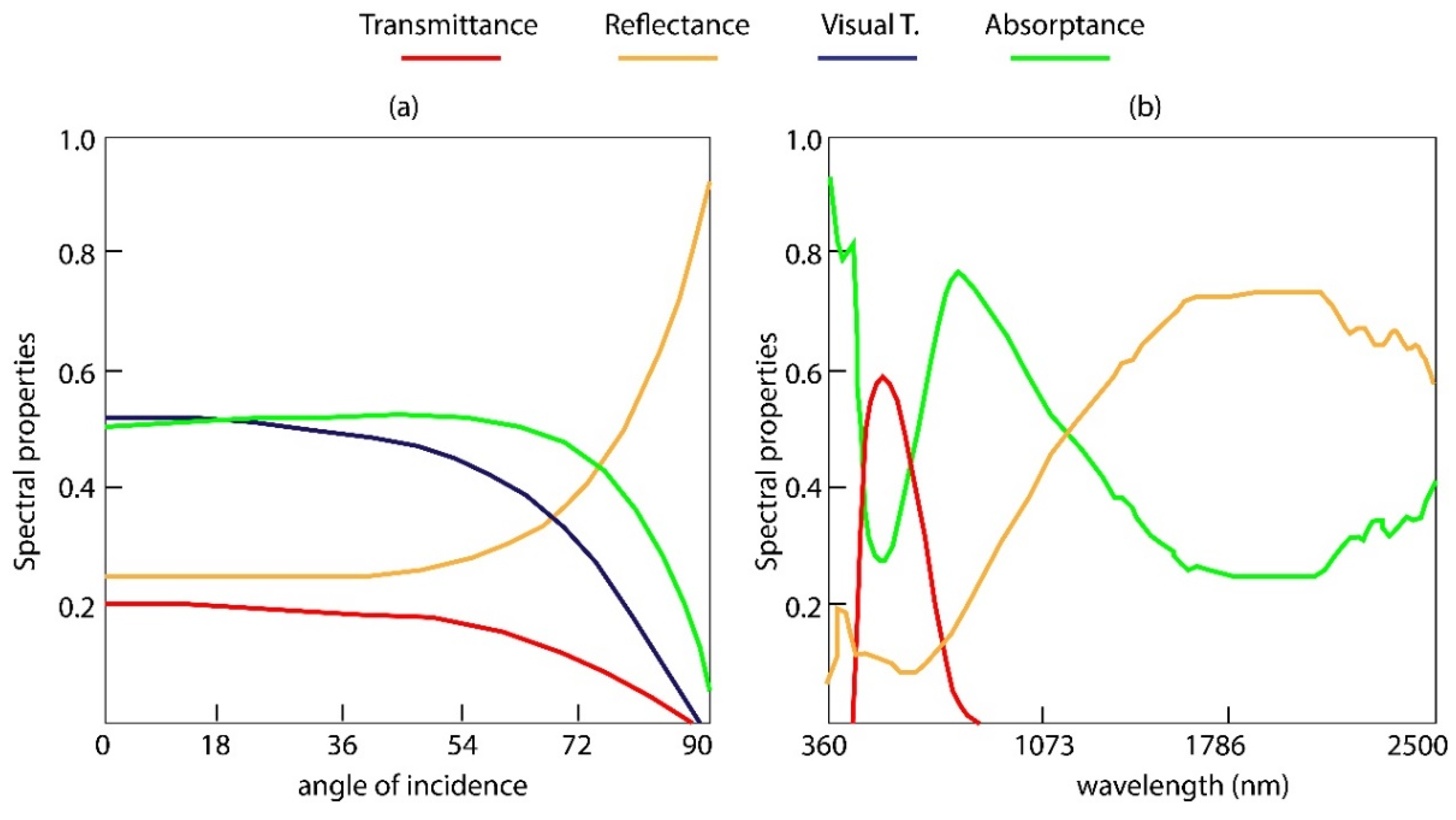
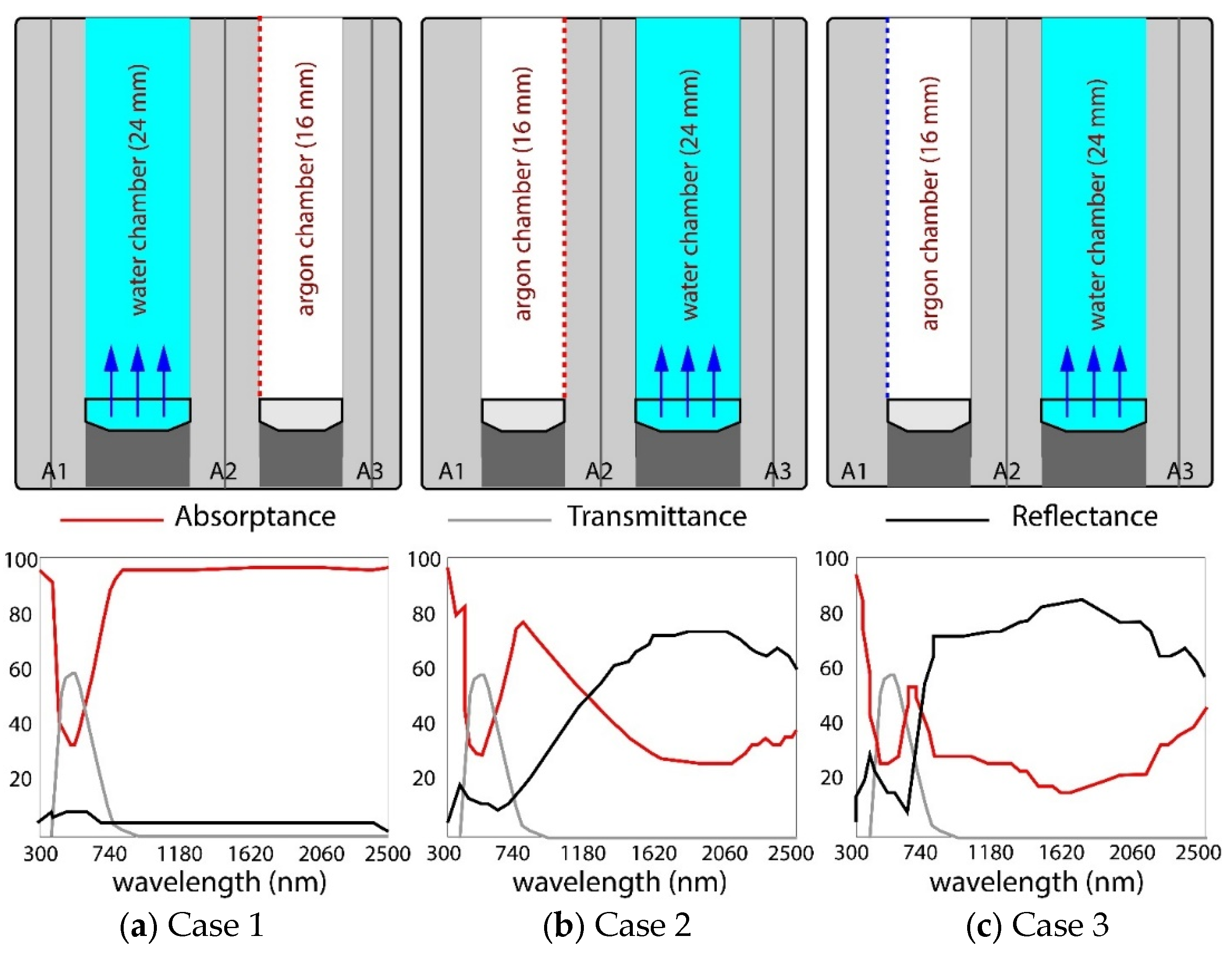
3.1.1. Spectral Results of the WFG Case Studies
3.1.2. Thermal Results
3.2. Water Flow Glazing Panel
3.2.1. WFG Panel: Steady State
3.2.2. WFG Panel: Transient State
3.3. Water Flow Glazing Facade in an Insulated Room: Transient State
4. Discussion
4.1. Water Flow Glazing Facade in an Insulated Room: Steady State
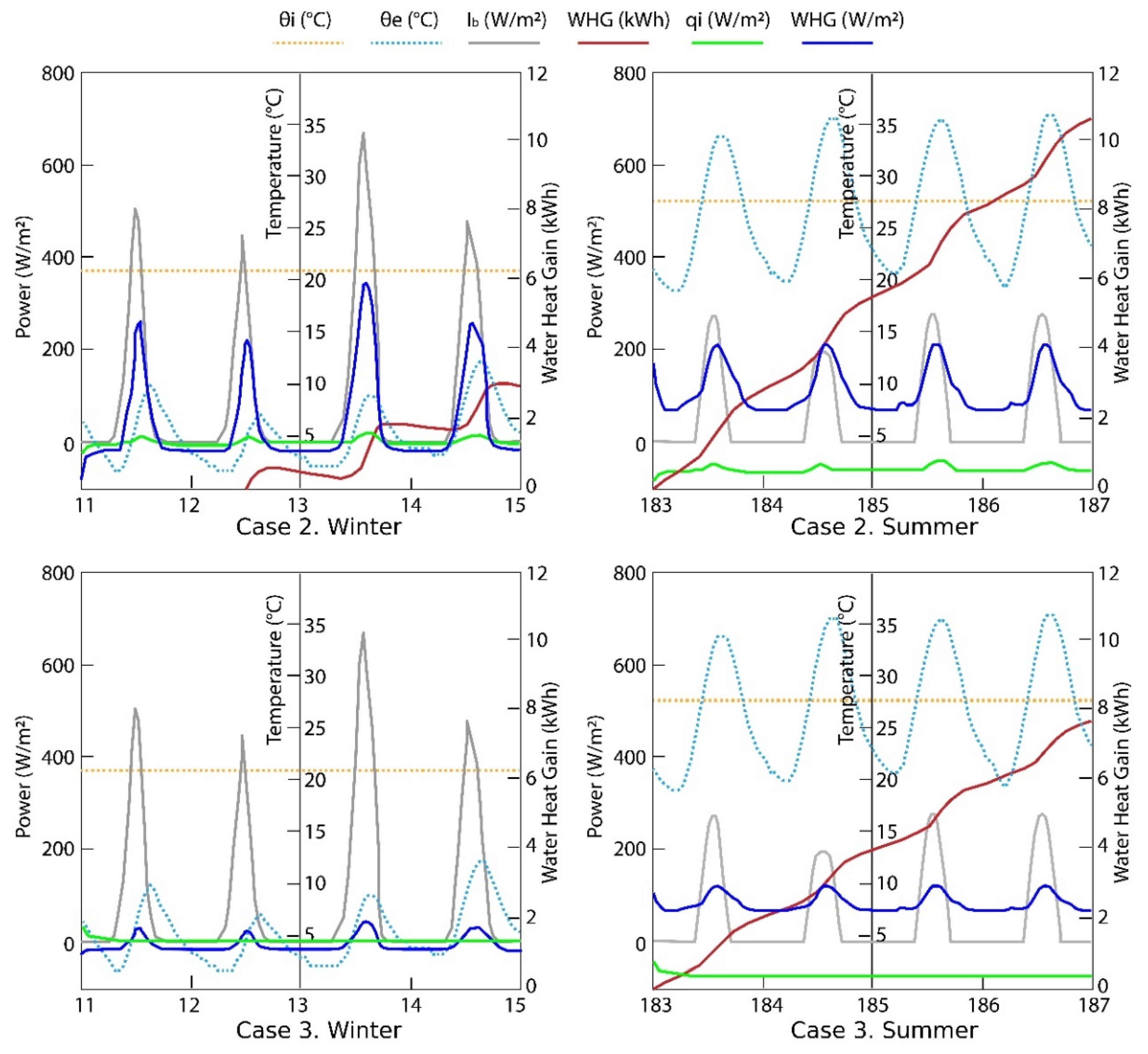
4.2. Water Flow Glazing Facade in an Insulated Room: Transient-State Cases 2 and 3
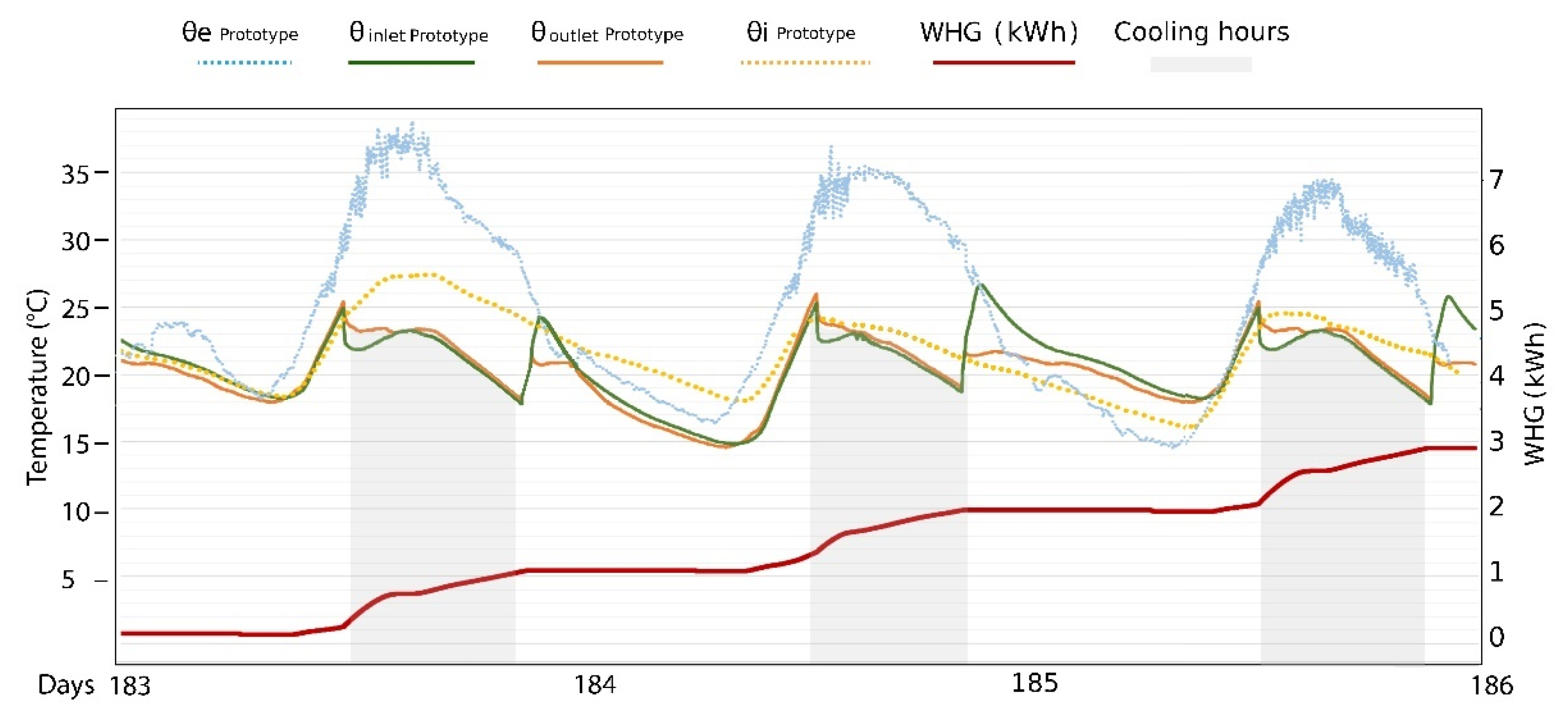
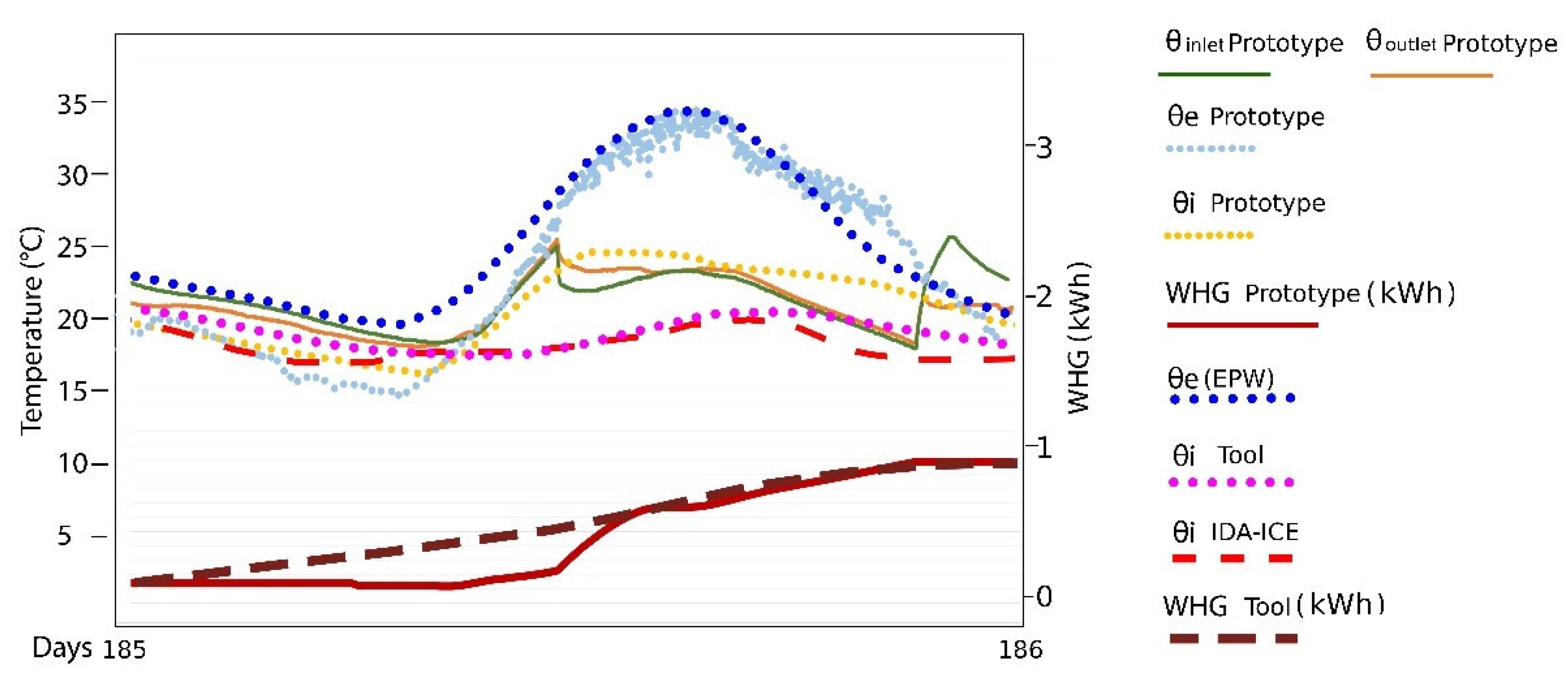
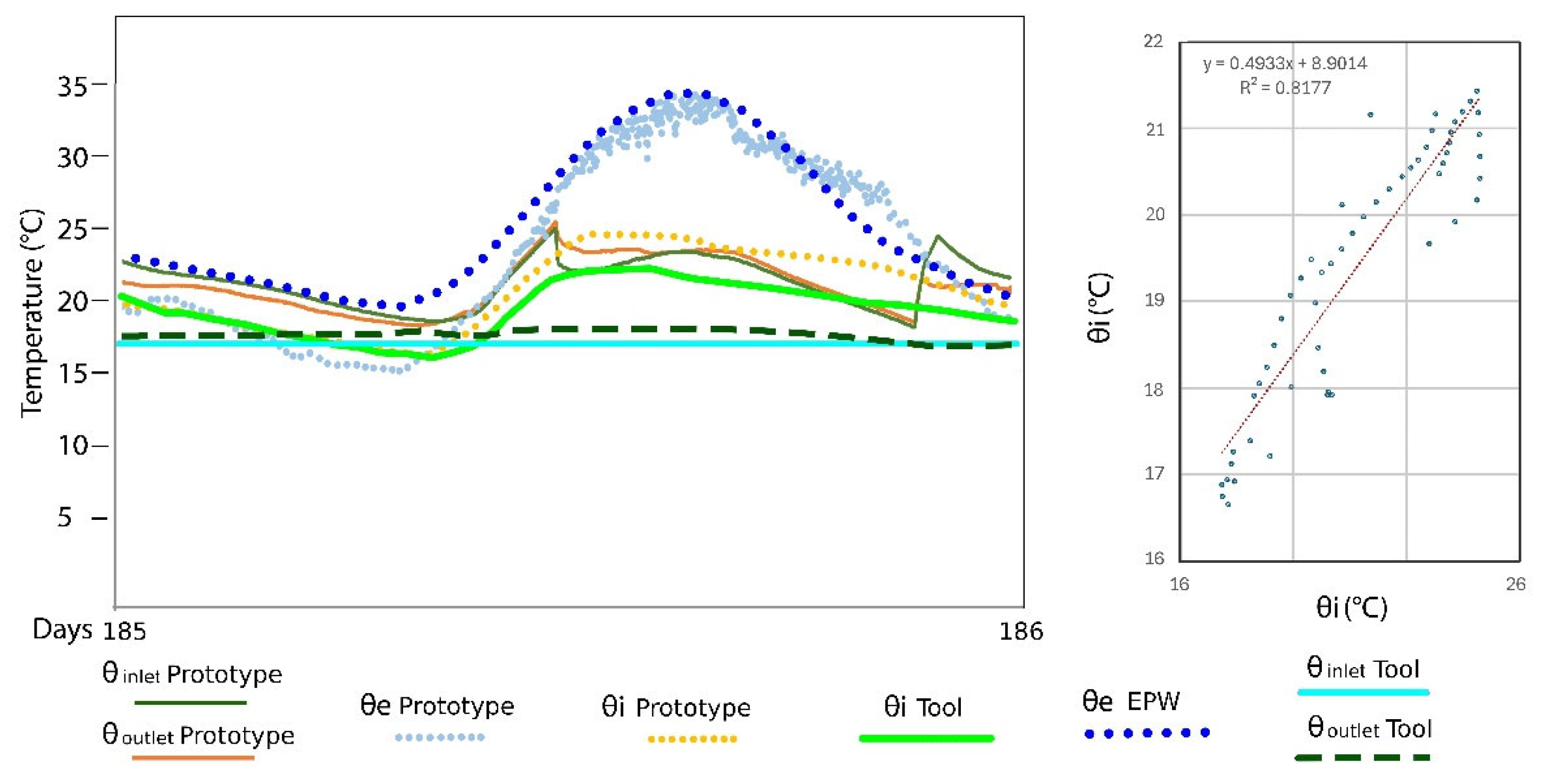
4.3. Experimental Validation in a Prototype with a Water Flow Glazing Facade: Transient-State Case 3
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- European Union. Directive (EU) 2018/844 of the European Parliament and of the Council of 30 May 2018. Amending Directive 2010/31/EU on the Energy Performance of Buildings and Directive 2012/27/EU on Energy Efficiency. 2018. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32018L0844&from=EN (accessed on 10 June 2025).
- Sudhakar, K.; Winderl, M.; Shanmuga Priya, S. Net-zero building designs in hot and humid climates: A state-of-art. Case Stud. Therm. Eng. 2019, 13, 100400. [Google Scholar] [CrossRef]
- Katili, A.R.; Boukhanouf, R.; Wilson, R. Space cooling in buildings in hot and humid climate—A review of the effect of humidity on the applicability of existing cooling techniques. In Proceedings of the International Conference on Sustainable Energy Technologies—SET, Nottingham, UK, 25–27 August 2015. [Google Scholar]
- Dhariwal, J.; Banerjee, R. An approach for building design optimization using design of experiments. Build. Simul. 2017, 10, 323–336. [Google Scholar] [CrossRef]
- Lai, C.M.; Wang, Y.H. Energy-saving potential of building envelope design in residential house in Taiwan. Energies 2011, 4, 2061–2076. [Google Scholar] [CrossRef]
- Jia, Z.; Xiang, C. Smart solar windows for an adaptive future: A comprehensive review of performance, methods and applications. Energy Build. 2025, 346, 116227. [Google Scholar] [CrossRef]
- Wu, S.; Sun, H.; Duan, M.; Mao, H.; Wu, Y.; Zhao, H.; Lin, B. Applications of thermochromic and electrochromic smart windows: 574 Materials to buildings. Cell Rep. Phys. Sci. 2023, 4, 101370. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, J.; He, E.; Li, D.; Si, W.; Wei, B.; Wang, G. Photothermal performance investigation of a reversible window combining paraffin and silica aerogel. Energy 2025, 329, 136646. [Google Scholar] [CrossRef]
- Gutai, M.; Kheybari, A.G. Energy consumption of water-filled glass (WFG) hybrid building envelope. Energy Build. 2020, 218, 110050. [Google Scholar] [CrossRef]
- Nur-E-Alam, M.; Vasiliev, M.; Yap, B.K.; Islam, M.A.; Fouad, Y.; Kiong, T.S. Design, fabrication, and physical properties analysis of 567 laminated Low-E coated glass for retrofit window solutions. Energy Build. 2024, 318, 114427. [Google Scholar] [CrossRef]
- Chow, T.T.; Li, C.; Lin, Z. Thermal characteristics of water-flow double-pane window. Int. J. Therm. Sci. 2010, 50, 140–148. [Google Scholar] [CrossRef]
- Rashevski, M.; Slavtchev, S.; Stoyanova, M. Natural and mixed convection in a vertical water-flow chamber in the presence of solar radiation. Eng. Sci. Technol. Int. J. 2022, 33, 101073. [Google Scholar] [CrossRef]
- Torregrosa-Jaime, B.; Martínez, P.J.; González, B.; Payá-Ballester, G. Modelling of a variable refrigerant flow system in EnergyPlus for building energy simulation in an Open Building Information modelling environment. Energies 2019, 12, 22. [Google Scholar] [CrossRef]
- Priarone, A.; Silenzi, F.; Fossa, M. Modelling Heat Pumps with Variable EER and COP in EnergyPlus: A Case Study Applied to Ground Source and Heat Recovery Heat Pump Systems. Energies 2020, 13, 794. [Google Scholar] [CrossRef]
- Lee, S.H.; Jeon, Y.; Chung, H.J.; Cho, W.; Kim, Y. Simulation-based optimization of heating and cooling seasonal performances of an air-to-air heat pump considering operating and design parameters using genetic algorithm. Appl. Therm. Eng. 2018, 144, 362–370. [Google Scholar] [CrossRef]
- Xamán, J.; Olazo-Gómez, Y.; Chávez, Y.; Hinojosa, J.; Hernández-Pérez, I.; Hernández-López, I.; Zavala-Guillén, I. Computational fluid dynamics for thermal evaluation of a room with a double glazing window with a solar control film. Renew. Energy 2016, 94, 237–250. [Google Scholar] [CrossRef]
- Sorooshnia, E.; Rashidi, M.; Rahnamayiezekavat, P.; Mahmoudkelayeh, S.; Pourvaziri, M.; Kamranfar, S.; Gheibi, M.; Samali, B.; Moezzi, R. A novel approach for optimized design of low-E windows and visual comfort for residential spaces. Energy Built Environ. 2025, 6, 27–42. [Google Scholar] [CrossRef]
- Sowunmi, A.R.; Anafi, F.O.; Folayan, C.O.; Ajayi, O.A.; Omisanya, N.O. TRNSYS 16: A veritable solar modelling and programming simulation tool used in the design of a continuous solar powered adsorption refrigeration system. J. Mech. Eng. Res. 2021, 12, 49–60. [Google Scholar]
- Mazzeo, D.; Matera, N.; Cornaro, C.; Oliveti, G.; Romagnoni, P.; Santoli, L. EnergyPlus, IDA ICE and TRNSYS predictive simulation accuracy for building thermal behaviour evaluation by using an experimental campaign in solar test boxes with and without a PCM module. Energy Build. 2020, 212, 109812. [Google Scholar] [CrossRef]
- Bring, A.; Sahlin, P.; Vuolle, M. Models for Building Indoor Climate and Energy Simulation, a Report of IEA SHC Task 22: Building Energy Analysis Tools, Subtask B: Model Documentation. 1999. Available online: https://www.equa.se/dncenter/T22Brep.pdf (accessed on 5 June 2025).
- Del Ama Gonzalo, F.; Moreno Santamaría, B.; Montero Burgos, M.J. Assessment of Building Energy Simulation Tools to Predict Heating and Cooling Energy Consumption at Early Design Stages. Sustainability 2023, 15, 1920. [Google Scholar] [CrossRef]
- U.S. Department of Energy. Building Energy Software Tools Directory. Available online: https://www.energy.gov/eere/buildings/listings/software-tools (accessed on 15 July 2025).
- Magni, M.; Ochs, F.; de Vries, S.B.; Maccarini, A.; Sigg, F. Detailed cross-comparison of building energy simulation tools results using a reference office building as a case study. Energy Build. 2021, 250, 111260. [Google Scholar] [CrossRef]
- Kim, M.; Jung, S.; Kang, J. Artificial Neural Network-Based Residential Energy Consumption Prediction Models Considering Residential Building Information and User Features in South Korea. Sustainability 2020, 12, 109. [Google Scholar] [CrossRef]
- Zevenhoven, R.; Fält, M.; Gomes, L.P. Thermal radiation heat transfer: Including wavelength dependence into modelling. Int. J. Therm. Sci. 2014, 86, 189–197. [Google Scholar] [CrossRef]
- Baetens, R.; Jelle, B.P.; Gustavsen, A. Properties, requirements and possibilities of smart windows for dynamic daylight and solar energy control in buildings: A state-of-the-art review. Sol. Energy Mater. Sol. Cells 2010, 94, 87–105. [Google Scholar] [CrossRef]
- Echarri, V.; Espinosa, A.; Rizo, C. Thermal Transmission through Existing Building Enclosures: Destructive Monitoring in Intermediate Layers versus Non-Destructive Monitoring with Sensors on Surfaces. Sensors 2017, 17, 2848. [Google Scholar] [CrossRef] [PubMed]
- Moreno, B.; Hernández, J.A. Analytical solutions to evaluate solar radiation overheating in simplified glazed rooms. Build. Environ. 2018, 140, 162–172. [Google Scholar] [CrossRef]
- Energy Plus. Available online: https://energyplus.net/documentation (accessed on 15 July 2025).
- Energy Plus. Available online: https://energyplus.net/weather-location/europe_wmo_region_6/ESP/ESP_Madrid.082210_IWEC (accessed on 15 July 2025).
- REF Berkeley Lab. Available online: https://windows.lbl.gov/igdb-knowledge-base (accessed on 24 July 2025).
- Zhang, R.; Hong, T. Modeling and Simulation of Operational Faults of HVAC Systems using EnergyPlus. In Proceedings of the ASHRAE/IBPSA-USA Building Simulation Conference SimBuild, Salt Lake City, UT, USA, 10–12 August 2016. [Google Scholar]
- ISO 15099:2003; Thermal Performance of Windows, Doors and Shading Devices—Detailed Calculations. International Organization for Standardization: Geneva, Switzerland, 2003.
- Schaffer, M.; Bugenings, L.A.; Andersen, K.H.; Melgaard, S.P. Experience-Based User Guide for IDA-ICE; Department of the Built Environment, Aalborg University: Aalborg, Sweden, 2023. [Google Scholar]
- Sierra, P.; Hernandez, J.A. Solar heat gain coefficient of water flow glazing. Energy Build. 2017, 139, 133–145. [Google Scholar] [CrossRef]
- Moreno Santamaria, B.; Gonzalo, F.d.A.; Pinette, D.; Lauret Aguirregabiria, B.; Hernandez Ramos, J.A. Industrialization and Thermal Performance of a New Unitized Water Flow Glazing Facade. Sustainability 2020, 12, 7564. [Google Scholar] [CrossRef]
- Arroyo, J.; Spiessens, F.; Helsen, L. Comparison of optimal control techniques for building energy management. Front. Built Environ. 2022, 8, 849754. [Google Scholar] [CrossRef]
- D’Agostino, D.; Landolfi, R.; Nicolella, M.; Minichiello, F. Experimental Study on the Performance Decay of Thermal Insulation and Related Influence on Heating Energy Consumption in Buildings. Sustainability 2022, 14, 2947. [Google Scholar] [CrossRef]
- Royapoor, M.; Roskilly, T. Building model calibration using energy and environmental data. Energy Build. 2015, 94, 109–120. [Google Scholar] [CrossRef]
- Magrini, A.; Lentini, G. NZEB Analyses by Means of Dynamic Simulation and Experimental Monitoring in Mediterranean Climate. Energies 2020, 13, 4784. [Google Scholar] [CrossRef]
- Jones, P.; Li, X.; Coma Bassas, E.; Perisoglou, E.; Patterson, J. Energy-Positive House: Performance Assessment through Simulation and Measurement. Energies 2020, 13, 4705. [Google Scholar] [CrossRef]
- Shaw, T.A.; Stevens, B. The other climate crisis. Nature 2025, 639, 877–887. [Google Scholar] [CrossRef]
- Neymark, J.; Judkoff, R.; Knabe, G.; Le, H.T.; Dürig, M.; Glass, A.; Zweifel, G. Applying the building energy simulation test (BESTEST) diagnostic method to verification of space conditioning equipment models used in whole-building energy simulation programs. Energy Build. 2002, 34, 917–931. [Google Scholar] [CrossRef]
- ASHRAE Guideline 14-2014; Measurement of Energy and Demand Savings. American Society of Heating Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 2014.
- Raftery, P.; Keane, M.; Costa, A. Calibrating whole building energy models: Detailed case study using hourly measured data. Energy Build. 2011, 43, 3666–3679. [Google Scholar] [CrossRef]
- Hensen, J.L.M.; Lamberts, R. Building Performance Simulation for Design and Operation; Routledge: London, UK, 2019. [Google Scholar]
- Alghoul, K.S. A Comparative Study of Energy Consumption for Residential HVAC Systems Using EnergyPlus. Am. J. Mech. Ind. Eng. 2017, 2, 98. [Google Scholar] [CrossRef]
- Lam, K.P.; Zhao, J.; Ydstie, B.E.; Wirick, J.; Qi, M.; Park, J. An Energyplus Whole Building Energy Model Calibration Method for Office Buildings Using Occupant Behavior Data Mining and Emprirical Data. In Proceedings of the ASHRAE/IBPSA-USA Building Simulation Conference, Atlanta, GA, USA, 10–12 September 2014; pp. 160–167. [Google Scholar]
- Judkoff, R.; Polly, B.; Marcus, B.; Neymark, J.; Kennedy, M. Building Energy Simulation Test for Existing Homes (BESTEST-EX): Instructions for Implementing the Test Procedure, Calibration Test Reference Results, and Example Acceptance-Range Criteria; National Renewable Energy Laboratory Report NREL/TP-5500-52414; US Department of Energy: Washington, DC, USA, 2011. [Google Scholar] [CrossRef]






| Argument | Type | Role | Description |
|---|---|---|---|
| RADirIn | Rad | in | Exterior beam solar radiation perpendicular to the glazing [W/(m2)] |
| RADiffIn | Rad | in | Exterior diffuse solar radiation [W/(m2)] |
| RBDirIn | Rad | in | Interior beam radiation perpendicular to the glazing [W/(m2)] |
| RBDiffIn | Rad | in | Interior diffuse irradiance [W/(m2)] |
| RADirOut | Rad | out | Exterior beam solar radiation perpendicular to the Glazing [W/(m2)] |
| RADiffOut | Rad | out | Exterior diffuse solar radiation [W/(m2)] |
| RBDirOut | Rad | out | Interior beam radiation perpendicular to the glazing [W/(m2)] |
| RBDiffOut | Rad | out | Interior diffuse irradiance [W/(m2)] |
| Tsout | Temp | in | Exterior Surface window temperature [°C] |
| Qe | HeatFlux | out | Exterior heat flux [W/(m2)] |
| Tsin | Temp | in | Interior Surface window temperature [°C] |
| Qi | HeatFlux | out | Interior heat flux [W/(m2)] |
| Te | Temp | in | Exterior temperature [°C] |
| QABackCv | HeatFlux | out | Back convection from the window curtains, in this model is set to zero [W/(m2)] |
| Ti | Temp | in | Interior temperature [°C] |
| QBBackCv | HeatFlux | out | Back convection from the window curtains, in this model is set to zero [W/(m2)] |
| Tin | Temp | in | Inlet water temperature [°C] |
| Tw | Temp | out | Outlet water temperature [°C] |
| P | HeatFlux | out | Power obtained [W/(m2)] |
| flow rate | MassFlow | in | Flow rate in the water chamber [kg/(s m2)] |
| ElevSun | Angle | in | Angle of sun elevation in radians |
| AzimutSun | Angle | in | Angle of sun azimuth in radians |
| WindVel | Vel | in | Local wind speed [m/s] |
| ID WFG | Factor | S_P | WFG identifier (Case 1 = 1; Case 2 = 2; Case 3 = 3; Case 4 = 4). |
| AWindow | Area | S_P | Window area |
| c | Heatcp | S_P | Heat capacity of the fluid |
| azimutWind | Angle | S_P | Azimuth of window surface |
| slopeWind | Angle | S_P | Slope of window surface |
| deg2rad | Factor | C_P | Conversion factor from Deg to Rad |
| rad2deg | Factor | C_P | Conversion factor from Rad to Deg |
| Glazing | A1 | A2 | A3 | Aw | Av | T | Ui W/(m2K) | Ue (W/(m2K) | U (W/(m2K) | Uw (W/(m2K) | g |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | 0.685 | 0.033 | 0.012 | 0.004 | 0.51 | 0.20 | 0.99 | 15.75 | 0.128 | 0.977 | 0.22 |
| Case 2 | 0.069 | 0.432 | 0.019 | 0.002 | 0.44 | 0.21 | 6.89 | 1.08 | 0.066 | 6.459 | 0.24 |
| Case 3 | 0.291 | 0.028 | 0.019 | 0.001 | 0.06 | 0.21 | 6.89 | 1.08 | 0.063 | 6.462 | 0.22 |
| Season | θe (°C) | θi (°C) | θINLET (°C) | he W/(m2 °C) | hi W/(m2 °C) | hg W/(m2 °C) | hw W/(m2 °C) | Ib W/(m2) | Id W/(m2) |
|---|---|---|---|---|---|---|---|---|---|
| Winter | 0 | 21 | 21 | 23 | 8 | 1.16 | 50 | 600 | 0.0 |
| Summer | 35 | 28 | 17 | 23 | 8 | 1.16 | 50 | 800 | 0.0 |
| Season | Glazing | WHG W/(m2) | TIb W/(m2) | qi W/(m2) | θINLET (°C) | θOUTLET (°C) |
|---|---|---|---|---|---|---|
| Winter | Case 1 | 19.9 | 123.7 | 7.4 | 21 | 21.2 |
| Case 2 | 227.4 | 128.4 | 13.7 | 21 | 22.9 | |
| Case 3 | 12.9 | 129.2 | 2.6 | 21 | 21.1 | |
| Summer | Case 1 | 556.1 | 164.9 | 3.5 | 17 | 21.6 |
| Case 2 | 413.3 | 171.2 | −44.4 | 17 | 20.4 | |
| Case 3 | 127.2 | 172.3 | −59.2 | 17 | 18.1 |
| Software | Glazing | WHG W/(m2) | TIb W/(m2) | qi W/(m2) | θINLET (°C) | θOUTLET (°C) |
|---|---|---|---|---|---|---|
| Tool 1 | Case 1 | 130.4 | 123.7 | 105.1 | 21 | 22.1 |
| Case 2 | 355.6 | 128.3 | 109.0 | 21 | 24.1 | |
| Case 3 | 133.4 | 129.2 | 109.8 | 21 | 22.1 | |
| IDA-ICE | Case 1 | 125.0 | 123.7 | 108.9 | 21 | 21.8 |
| Case 2 | 354.2 | 128.4 | 111.1 | 21 | 23.9 | |
| Case 3 | 128.6 | 129.4 | 113.1 | 21 | 22.1 |
| Software | Glazing | WHG W/(m2) | TIb W/(m2) | qi W/(m2) | θINLET (°C) | θOUTLET (°C) |
|---|---|---|---|---|---|---|
| Tool 1 | Case 1 | 697.1 | 164.9 | 140.1 | 17 | 22.8 |
| Case 2 | 532.2 | 171.1 | 145.4 | 17 | 21.5 | |
| Case 3 | 232.0 | 172.3 | 146.4 | 17 | 18.9 | |
| IDA-ICE | Case 1 | 642.7 | 164.9 | 145.1 | 17 | 22.4 |
| Case 2 | 520.9 | 171.2 | 148.2 | 17 | 21.3 | |
| Case 3 | 220.5 | 172.3 | 150.8 | 17 | 18.8 |
| RMSE(θi) | nARi > 0 (θi) | NRMSE(θi) | RMSE(WHG) | nARi > 0 (WHG) | NRMSE(WHG) | |
|---|---|---|---|---|---|---|
| Case 2 | 1.28 | 87 | 6.60 | 17.21 | 95 | 26.97 |
| Case 3 | 1.20 | 87 | 6.14 | 10.44 | 85 | 32.69 |
| Volume (Tool) | θINLET Tool | RMSE(θi) | nARi > 0 (θi) | NRMSE(θi) | R2(θi) | |
|---|---|---|---|---|---|---|
| Iteration 1 | 7 m × 7 m × 3 m | 17 °C | 3.20 | 50 | 25.06 | 0.43 |
| Iteration 2 | 1 m × 1 m × 0.75 m | 17 °C | 2.34 | 50 | 10.99 | 0.81 |
| Iteration 3 | 1 m × 1 m × 0.75 m | θINLET Prototype | 0.51 | 50 | 2.41 | 0.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Del Ama Gonzalo, F.; Moreno Santamaría, B.; Hernandez Ramos, J.A. An Evaluation of a New Building Energy Simulation Tool to Assess the Impact of Water Flow Glazing Facades on Maintaining Comfortable Temperatures and Generating Renewable Energy. Sustainability 2025, 17, 9669. https://doi.org/10.3390/su17219669
Del Ama Gonzalo F, Moreno Santamaría B, Hernandez Ramos JA. An Evaluation of a New Building Energy Simulation Tool to Assess the Impact of Water Flow Glazing Facades on Maintaining Comfortable Temperatures and Generating Renewable Energy. Sustainability. 2025; 17(21):9669. https://doi.org/10.3390/su17219669
Chicago/Turabian StyleDel Ama Gonzalo, Fernando, Belén Moreno Santamaría, and Juan Antonio Hernandez Ramos. 2025. "An Evaluation of a New Building Energy Simulation Tool to Assess the Impact of Water Flow Glazing Facades on Maintaining Comfortable Temperatures and Generating Renewable Energy" Sustainability 17, no. 21: 9669. https://doi.org/10.3390/su17219669
APA StyleDel Ama Gonzalo, F., Moreno Santamaría, B., & Hernandez Ramos, J. A. (2025). An Evaluation of a New Building Energy Simulation Tool to Assess the Impact of Water Flow Glazing Facades on Maintaining Comfortable Temperatures and Generating Renewable Energy. Sustainability, 17(21), 9669. https://doi.org/10.3390/su17219669








