Predicting Patent Life Using Robust Ensemble Algorithm
Abstract
1. Introduction
- I.
- Direct Prediction of Patent Life: This study proposes a novel approach by directly predicting patent life, distinguishing itself from prior research. By framing the problem as a regression task instead of classification, the proposed method provides a more precise assessment of patent quality. Furthermore, the directly predicted patent life serves as a critical variable for quantifying the intrinsic value of patents.
- II.
- Robust Ensemble Modeling: To identify the optimal model for patent life prediction, this study compares the performance of various machine learning and deep learning models. By ensemble the best-performing models, the robustness and accuracy of predictions are enhanced. Unlike existing studies that focus on single-model approaches, the proposed ensemble method complements the limitations of individual models, leading to improved overall performance.
- III.
- Support for Rapid and Precise Decision-Making in Patent Portfolio Management: As discussed in Section 3.1, the proportion of maintained patents gradually slows down over time, largely influenced by the assignee’s strategic intentions. In this context, the model’s ability to directly predict patent life—closely linked to patent quality—offers valuable insights to support long-term decisions such as whether to maintain or abandon a patent. By enabling rapid and precise evaluation of the economic value of individual patents, the proposed model facilitates fast-track decision-making in critical contexts, including determining patent maintenance, assessing the feasibility of technology transfer, and prioritizing technology investments. This capability is particularly meaningful in practical environments involving the management of large-scale patent portfolios or the pursuit of technology commercialization. Ultimately, this approach enhances the strategic management of patent portfolios while aligning these decisions with the pursuit of sustainable technological innovation.
2. Literature Review
2.1. Proxy as a Patent Quality
2.2. Prediction of Patent Life
2.3. Stacking Ensemble
3. Data & Methodology
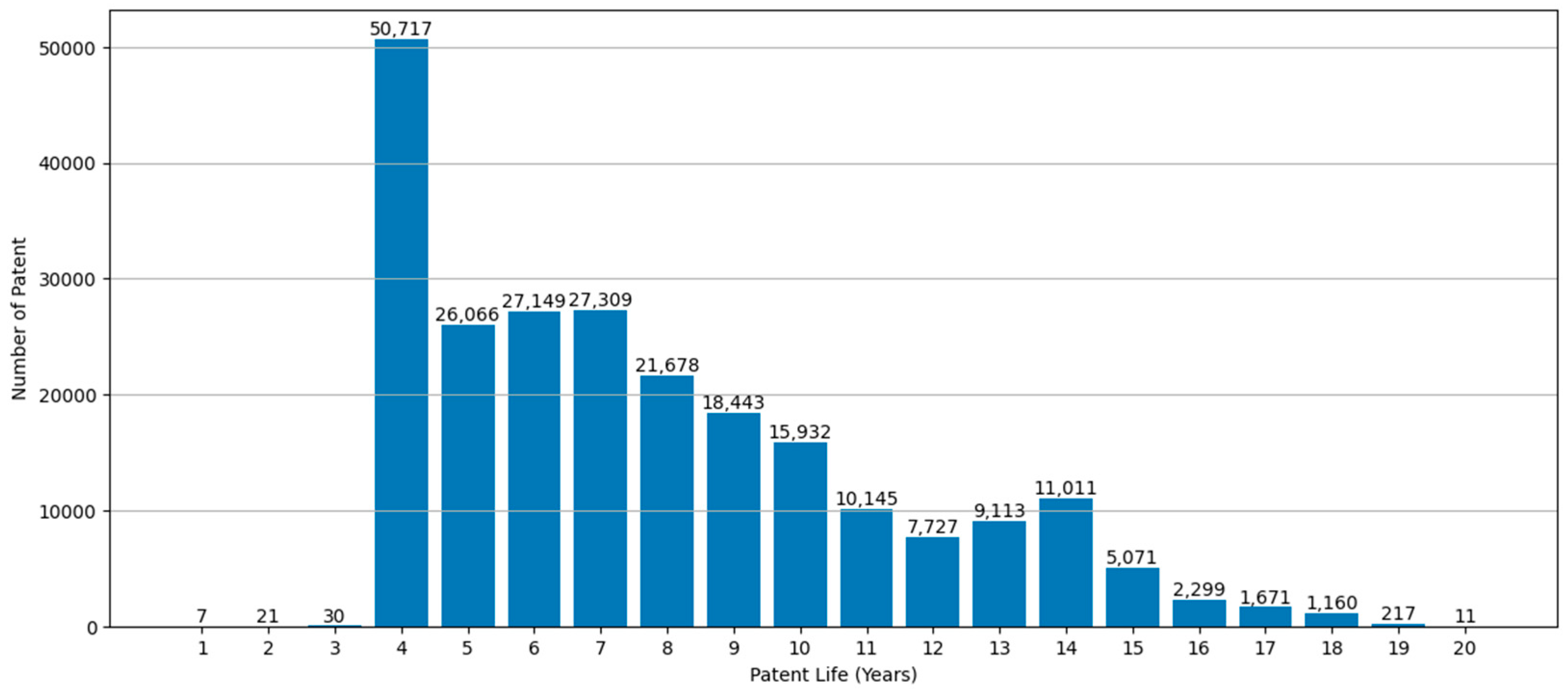
3.1. Data
3.1.1. Data Collection & Preprocessing
- (i)
- Patent data after 2000.
- (ii)
- Expired patents as of the data collection date.
- (iii)
- Patents without missing data.
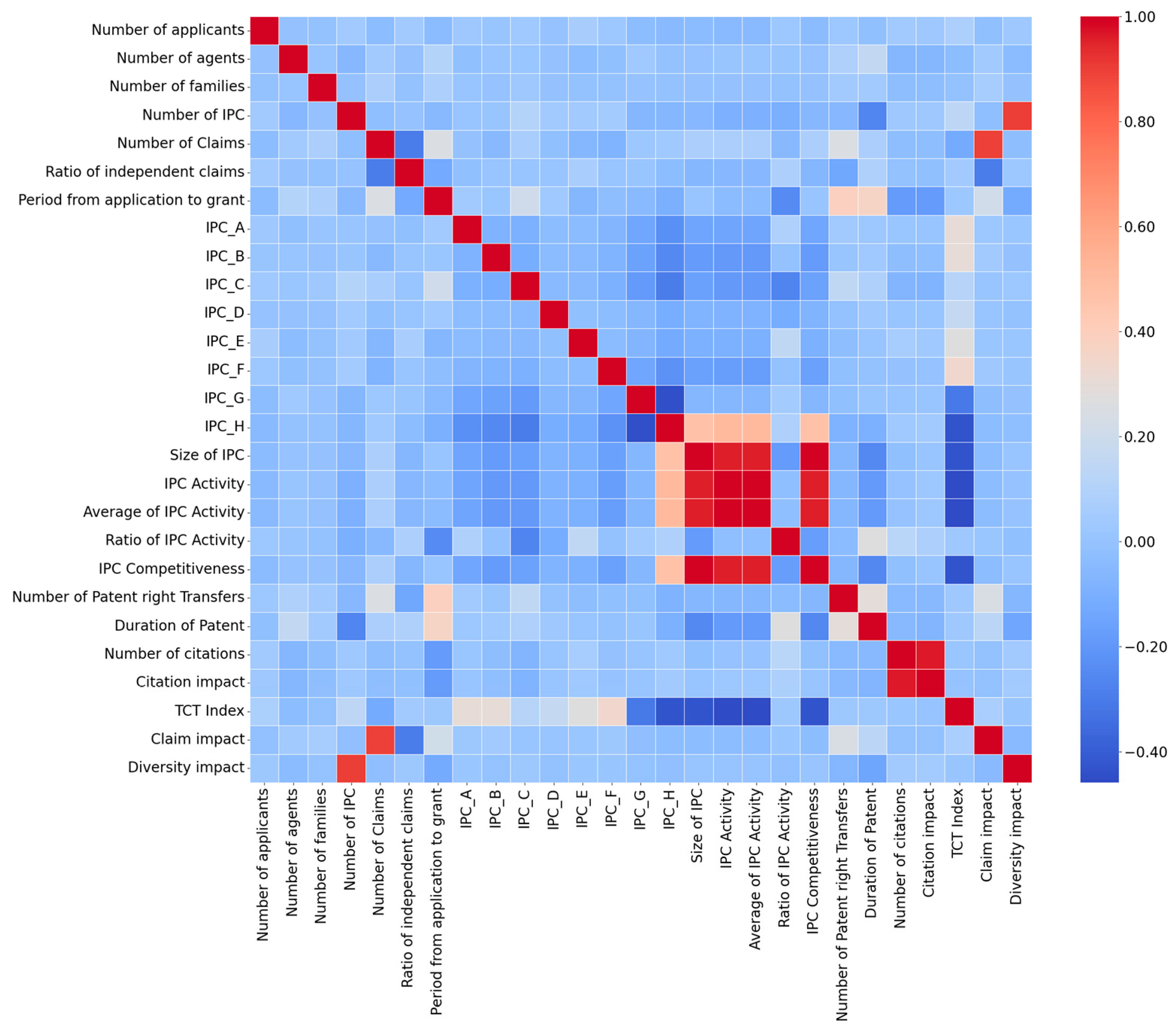
3.1.2. Features
3.2. Experiment Setting & Methodology
3.2.1. Experiment Setting
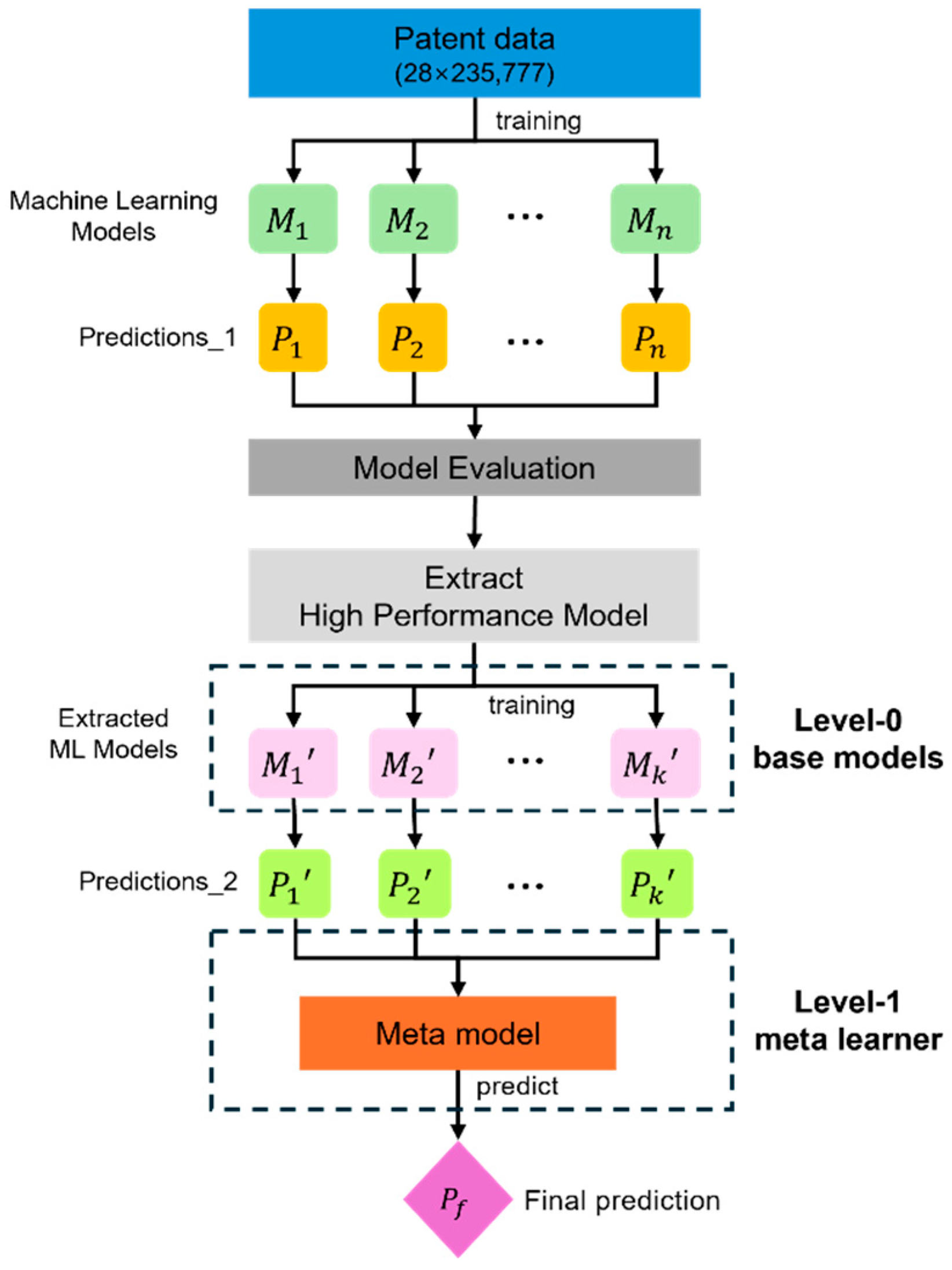
3.2.2. Methodology
4. Experimental Results
5. Discussion
6. Conclusions and Further Studies
6.1. Conclusions
6.2. Further Studies
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Seven Machine Learning Techniques Used in This Study
Appendix A.1. Random Forest (RF)
Appendix A.2. XGBoost (XGB)
Appendix A.3. Light Gradient Boosting Machine (LGBM)
Appendix A.4. Deep Neural Network (DNN)
Appendix A.5. Support Vector Regression (SVR)
Appendix A.6. Linear Regression (LR)
Appendix A.7. Auto Encoder (AE)
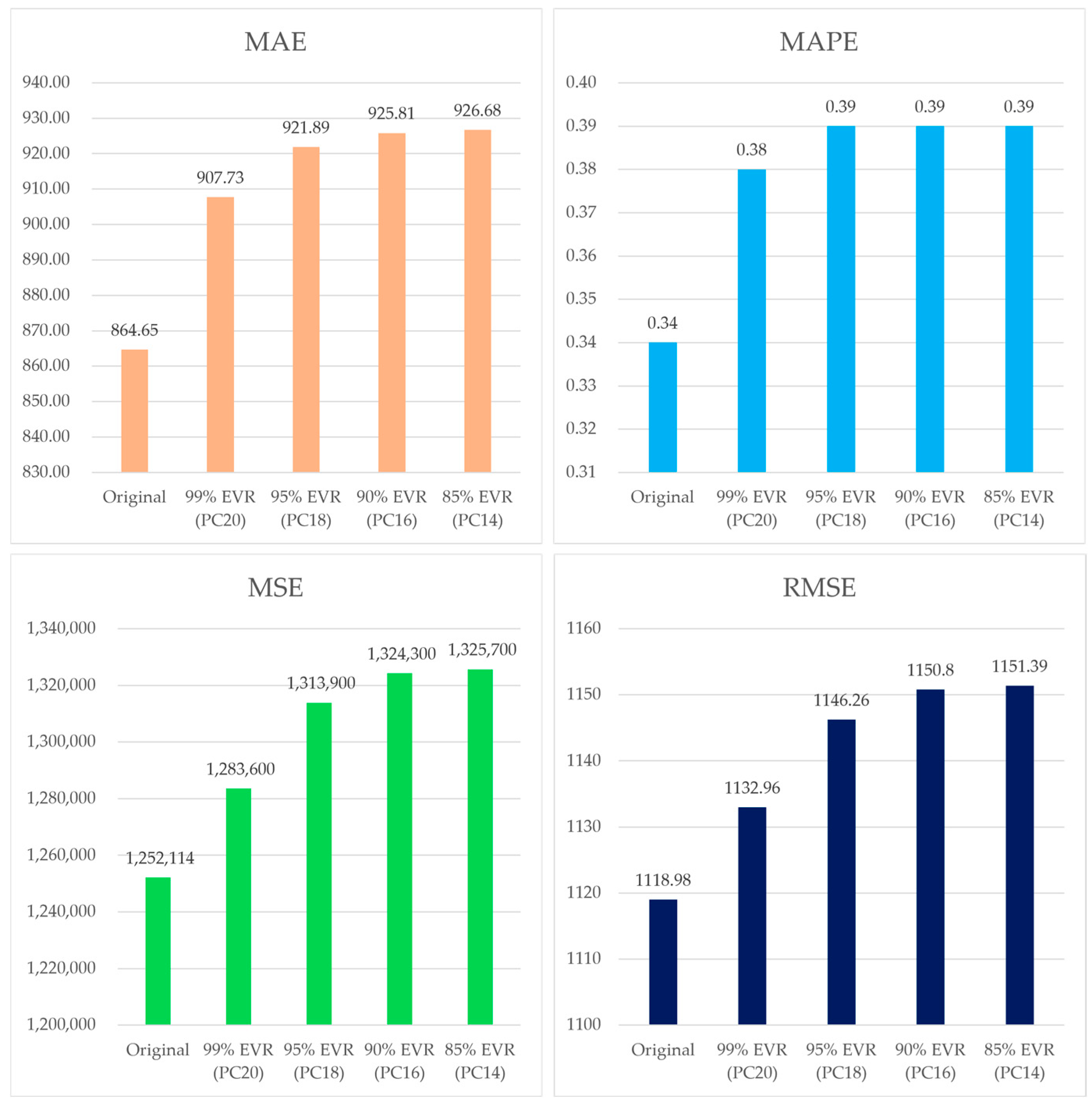
Appendix B. Detailed Principal Component Analysis (PCA) Results
| Component | EVR | Cumulative EVR |
|---|---|---|
| PC1 | 0.179047 | 0.179047 |
| PC2 | 0.097834 | 0.276881 |
| PC3 | 0.075285 | 0.352166 |
| PC4 | 0.074607 | 0.426773 |
| PC5 | 0.056315 | 0.483088 |
| PC6 | 0.052387 | 0.535474 |
| PC7 | 0.048419 | 0.583893 |
| PC8 | 0.041608 | 0.625501 |
| PC9 | 0.040267 | 0.665768 |
| PC10 | 0.039635 | 0.705402 |
| PC11 | 0.03933 | 0.744732 |
| PC12 | 0.038132 | 0.782864 |
| PC13 | 0.036764 | 0.819628 |
| PC14 | 0.035369 | 0.854997 |
| PC15 | 0.0337 | 0.888697 |
| PC16 | 0.030493 | 0.919191 |
| PC17 | 0.025603 | 0.944794 |
| PC18 | 0.022843 | 0.967637 |
| PC19 | 0.014057 | 0.981694 |
| PC20 | 0.009846 | 0.991541 |
References
- Hall, B.H.; Jaffe, A.B.; Trajtenberg, M. Market value and patent citations: A first look. Rand J. Econ. 2005, 36, 16–38. [Google Scholar]
- Squicciarini, M.; Dernis, H.; Criscuolo, C. Measuring patent quality: Indicators of technological and economic value. OECD Sci. Technol. Ind. Work. Pap. 2013. [CrossRef]
- Schankerman, M.; Pakes, A. Estimates of the value of patent rights in European countries during the post-1950 period. Econ. J. 1986, 96, 1052–1076. [Google Scholar] [CrossRef]
- Kyung, S.T. The quality of patents: A multilateral evaluation for Korea. J. Intellect. Prop. 2013, 8, 99–120. [Google Scholar] [CrossRef]
- Higham, K.; de Rassenfosse, G.; Jaffe, A.B. Patent quality: Towards a systematic framework for analysis and measurement. Res. Policy 2021, 50, 104215. [Google Scholar] [CrossRef]
- Griliches, Z. Patent statistics as economic indicators: A survey. In R&D and Productivity: The Econometric Evidence; University of Chicago Press: Chicago, IL, USA, 1998; pp. 287–343. [Google Scholar]
- Park, S.T.; Kim, Y.K. A study on patent valuation for the activation of IP finance. J. Digit. Converg. 2012, 10, 315–321. [Google Scholar]
- Girgin Kalıp, N.G.; Öcalan, Ö.; Aytekin, Ç. Qualitative and quantitative patent valuation methods: A systematic literature review. World Pat. Inf. 2022, 69, 102111. [Google Scholar] [CrossRef]
- Choi, Y.M.; Cho, D. A study on the effect of the renewal-fee payment cycle in the decision of patent right retention: Focusing on the sunk cost and endowment perspective. J. Digit. Converg. 2021, 19, 65–79. [Google Scholar]
- Hikkerova, L.; Doat, M.; Carayol, N. Patent life cycle: New evidence. Technol. Forecast. Soc. Change 2014, 88, 313–324. [Google Scholar] [CrossRef]
- Guellec, D.; van Pottelsberghe de la Potterie, B. Applications, grants, and the value of patent. Econ. Lett. 2000, 69, 109–114. [Google Scholar] [CrossRef]
- van Zeebroeck, N.; van Pottelsberghe de la Potterie, B. The vulnerability of patent value determinants. Econ. Innov. New Technol. 2011, 20, 283–308. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, M.G.; Kim, Y.M. Prediction of patent lifespan and analysis of influencing factors using machine learning. J. Intell. Inf. Syst. 2022, 28, 147–170. [Google Scholar] [CrossRef]
- Chiu, Y.J.; Chen, Y.W. Using AHP in patent valuation. Math. Comput. Model. 2007, 46, 1054–1062. [Google Scholar] [CrossRef]
- Kim, M.S.; Lee, J.H.; Oh, E.-S.; Lee, C.-H.; Choi, J.-H.; Jang, Y.-J.; Lee, J.-H.; Sung, T.-E. A study on deep learning-based intelligent technology valuation: Focusing on the models of qualitative evaluation factors estimation using deep neural networks. J. Korea Technol. Innov. Soc. 2021, 24, 1141–1162. [Google Scholar] [CrossRef]
- Harhoff, D.; Narin, F.; Scherer, F.M.; Vopel, K. Citations, family size, opposition and the value of patent rights. Res. Policy 2003, 32, 1343–1363. [Google Scholar] [CrossRef]
- Trappey, A.J.; Wu, C.Y.; Lin, C.-W.; Trappey, C.V. A patent quality analysis for innovative technology and product development. Adv. Eng. Inform. 2012, 26, 26–34. [Google Scholar] [CrossRef]
- Lanjouw, J.O.; Pakes, A.; Putnam, J. How to count patents and value intellectual property: The uses of patent renewal and application data. J. Ind. Econ. 1998, 46, 405–432. [Google Scholar] [CrossRef]
- Liu, X.; Yan, J.; Xiao, S.; Wang, X.; Zha, H.; Chu, S.M. On predictive patent valuation: Forecasting patent citations and their types. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 1438–1444. [Google Scholar] [CrossRef]
- Carpenter, M.P.; Narin, F.; Woolf, P. Citation rates to technologically important patents. World Pat. Inf. 1981, 3, 160–163. [Google Scholar] [CrossRef]
- Albert, M.B.; Avery, D.; Narin, F.; McAllister, P. Direct validation of citation counts as indicators of industrially important patents. Res. Policy 1991, 20, 251–259. [Google Scholar] [CrossRef]
- Yang, G.C.; Li, G.; Li, C.Y.; Zhao, Y.H.; Zhang, J.; Liu, T.; Chen, D.-Z.; Huang, M.H. Using the comprehensive patent citation network (CPC) to evaluate patent value. Scientometrics 2015, 105, 1319–1346. [Google Scholar] [CrossRef]
- Thomas, P. The effect of technological impact upon patent renewal decisions. Technol. Anal. Strateg. Manag. 1999, 11, 181–197. [Google Scholar] [CrossRef]
- Baudry, M.; Dumont, B. Patent renewals as options: Improving the mechanism for weeding out lousy patents. Rev. Ind. Organ. 2006, 28, 41–62. [Google Scholar]
- Grönqvist, C. The private value of patents by patent characteristics: Evidence from Finland. J. Technol. Transf. 2009, 34, 159–168. [Google Scholar] [CrossRef]
- Han, E.J.; Sohn, S.Y. Patent valuation based on text mining and survival analysis. J. Technol. Transf. 2015, 40, 821–839. [Google Scholar] [CrossRef]
- Choi, Y.M.; Cho, D. A study on the time-dependent changes of the intensities of factors determining patent lifespan from a biological perspective. World Pat. Inf. 2018, 54, 1–17. [Google Scholar] [CrossRef]
- Choi, Y.M.; Kim, J.H.; Lee, H.S. A three-dimensional patent evaluation model that considers the factors for calculating the internal and external value of a patent: Arrhenius chemical reaction kinetics-based patent lifespan prediction. J. Digit. Converg. 2021, 19, 113–132. [Google Scholar]
- Choo, K.N.; Park, K.H. A study on the determinants of the economic value of patents using renewal data. Knowl. Manag. Res. 2010, 11, 65–81. [Google Scholar]
- Danish, M.S.; Yousaf, Z.; Ali, R.; Ahmad, T. Determinants of patent survival in emerging economies: Evidence from residential patents in India. J. Public Aff. 2021, 21, e2211. [Google Scholar] [CrossRef]
- Jang, K.Y.; Yang, D.W. The empirical study on determinants affecting patent life cycle: Using Korean patents renewal data. J. Intellect. Prop. 2014, 9, 79–108. [Google Scholar] [CrossRef]
- Kim, M.S.; Lee, J.-H.; Lee, S.-H.; Lee, S.-H.; Rhee, J.; Park, S.-H.; Sung, T.-E. A study on the effect of intrinsic and extrinsic factors on patent life: Focusing on medical device industry and macroeconomic conditions. J. Korea Technol. Innov. Soc. 2023, 26, 479–497. [Google Scholar] [CrossRef]
- Choi, J.; Jeong, B.; Yoon, J.; Coh, B.-Y.; Lee, J.-M. A novel approach to evaluating the business potential of intellectual properties: A machine learning-based predictive analysis of patent lifetime. Comput. Ind. Eng. 2020, 145, 106544. [Google Scholar] [CrossRef]
- Liu, J.; Li, P.; Liu, X. Patent lifetime prediction using LightGBM with a customized loss. PeerJ Comput. Sci. 2024, 10, e2044. [Google Scholar] [CrossRef]
- Okuno, S.; Aihara, K.; Hirata, Y. Forecasting high-dimensional dynamics exploiting suboptimal embeddings. Sci. Rep. 2020, 10, 664. [Google Scholar] [CrossRef]
- Kwon, H.; Park, J.; Lee, Y. Stacking ensemble technique for classifying breast cancer. Healthc. Inform. Res. 2019, 25, 283–288. [Google Scholar] [CrossRef]
- Rahman, M.S.; Rahman, H.R.; Prithula, J.; Chowdhury, M.E.H.; Ahmed, M.U.; Kumar, J.; Murugappan, M.; Khan, M.S. Heart failure emergency readmission prediction using stacking machine learning model. Diagnostics 2023, 13, 1948. [Google Scholar] [CrossRef] [PubMed]
- Kamateri, E.; Salampasis, M.; Diamantaras, K. An ensemble framework for patent classification. World Pat. Inf. 2023, 75, 102233. [Google Scholar] [CrossRef]
- Kamateri, E.; Salampasis, M. Ensemble method for classification in imbalanced patent data. In Proceedings of the PatentSemTech@SIGIR 2023, Taipeh, Taiwan, 23–27 July 2023; pp. 27–32. [Google Scholar]
- Korean Intellectual Property Rights Information Service. KIPRIS Main Page. Available online: https://www.kipris.or.kr/khome/main.do (accessed on 11 February 2025).
- Cokluk, O.; Kayri, M. The effects of methods of imputation for missing values on the validity and reliability of scales. Educ. Sci. Theory Pract. 2011, 11, 303–309. [Google Scholar]
- Lim, J.; Kim, C.; Gu, J. Analysis of causal relationship between patent indicators and firm performance. Korean Manag. Sci. Rev. 2011, 28, 63–74. [Google Scholar]
- Ko, N.; Kim, Y.; Park, J. An intellectual property evaluation model using patent transactions: A deep neural network approach. In Proceedings of the Korean Institute of Industrial Engineers Conference, Daejeon, Republic of Korea, 2–3 November 2017. [Google Scholar]
- Korean Intellectual Property Office (Patent System Division). Notice on the Application for Batch Examination of Patents, Utility Models, Trademarks, and Designs. Patent Office Notice No. 2023-22, 29 December 2023. Available online: https://www.law.go.kr/admRulLsInfoP.do?admRulId=44250&efYd=0 (accessed on 29 December 2023).
- Fischer, T.; Henkel, J. Patent trolls on markets for technology–An empirical analysis of NPEs’ patent acquisitions. Res. Policy 2012, 41, 1519–1533. [Google Scholar] [CrossRef]
- Harhoff, D.; Wagner, S. The duration of patent examination at the European patent office. Manag. Sci. 2009, 55, 1969–1984. [Google Scholar] [CrossRef]
- Chen, C. Using machine learning to forecast patent quality—Take ‘vehicle networking’ industry for example. In Transdisciplinary Engineering: A Paradigm Shift; IOS Press: Amsterdam, The Netherlands, 2015; pp. 993–1002. [Google Scholar]
- Cockburn, I.M.; MacGarvie, M. Entry and patenting in the software industry. Manag. Sci. 2006, 57, No. 12563. [Google Scholar] [CrossRef]
- Jeongmin, O.; Jung, T. Research on the relationship between technology cycle time and technology lifespan—Focusing on the patents from National R&D projects in Korea. Technol. Manag. 2021, 6, 57–75. [Google Scholar]
- Ebrahimighahnavieh, M.A.; Luo, S.; Chiong, R. Deep learning to detect Alzheimer’s disease from neuroimaging: A systematic literature review. Comput. Methods Programs Biomed. 2020, 187, 105242. [Google Scholar] [CrossRef] [PubMed]
- Singh, T.; Kalra, R.; Mishra, S.; Satakshi; Kumar, M. An efficient real-time stock prediction exploiting incremental learning and deep learning. Evol. Syst. 2023, 14, 919–937. [Google Scholar]
- Jain, S. A Comparative Study of Stock Market Prediction Models. In Deep Learning Tools for Predicting Stock Market Movements; Wiley: Hoboken, NJ, USA, 2024; pp. 249–269. [Google Scholar] [CrossRef]
- Palma, G.; Geraci, G.; Rizzo, A. Federated Learning and Neural Circuit Policies: A Novel Framework for Anomaly Detection in Energy-Intensive Machinery. Energies 2025, 18, 936. [Google Scholar] [CrossRef]
- Chan, J.Y.L.; Leow, S.M.H.; Bea, K.T.; Cheng, W.K.; Phoong, S.W.; Hong, Z.W.; Chen, Y.L. Mitigating the multicollinearity problem and its machine learning approach: A review. Mathematics 2022, 10, 1283. [Google Scholar] [CrossRef]
- Sundus, K.I.; Hammo, B.H.; Al-Zoubi, M.B.; Al-Omari, A. Solving the multicollinearity problem to improve the stability of machine learning algorithms applied to a fully annotated breast cancer dataset. Inform. Med. Unlocked 2022, 33, 101088. [Google Scholar] [CrossRef]
- Alabduljabbar, H.; Khan, M.; Awan, H.H.; Eldin, S.M.; Alyousef, R.; Mohamed, A.M. Predicting ultra-high-performance concrete compressive strength using gene expression programming method. Case Stud. Constr. Mater. 2023, 18, e02074. [Google Scholar] [CrossRef]
- Khan, M.; Javed, M.F. Towards sustainable construction: Machine learning based predictive models for strength and durability characteristics of blended cement concrete. Mater. Today Commun. 2023, 37, 107428. [Google Scholar] [CrossRef]
- Javed, M.F.; Siddiq, B.; Onyelowe, K.; Khan, W.A.; Khan, M. Metaheuristic optimization algorithms-based prediction modeling for titanium dioxide-assisted photocatalytic degradation of air contaminants. Results Eng. 2024, 23, 102637. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, 2nd ed.; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Duda, R.; Hart, P.; Stork, D. Pattern Classification, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- De Rassenfosse, G.; Jaffe, A.B. Are patent fees effective at weeding out low-quality patents? J. Econ. Manag. Strategy 2018, 27, 134–148. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NeurIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Curran Associates: Red Hook, NY, USA, 2017; pp. 5998–6008. [Google Scholar]
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. BERT: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (NAACL-HLT 2019), Volume 1 (Long and Short Papers), Minneapolis, MN, USA, 2–7 June 2019; Association for Computational Linguistics: Minneapolis, MN, USA, 2019; pp. 4171–4186. [Google Scholar] [CrossRef]
- Kim, Y. Convolutional neural networks for sentence classification. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; Association for Computational Linguistics: Doha, Qatar; pp. 1746–1751. [Google Scholar] [CrossRef]
- Liu, B.; Song, W.; Zheng, M.; Fu, C.; Chen, J.; Wang, X. Semantically enhanced selective image encryption scheme with parallel computing. Expert Syst. Appl. 2025, 279, 127404. [Google Scholar] [CrossRef]
- Soni, S.; Chouhan, S.S.; Rathore, S.S. TextConvoNet: A convolutional neural network based architecture for text classification. Appl. Intell. 2023, 53, 14249–14268. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Shehadeh, A.; Alshboul, O.; Al Mamlook, R.E.; Hamedat, O. Machine learning models for predicting the residual value of heavy construction equipment: An evaluation of modified decision tree, LightGBM, and XGBoost regression. Autom. Constr. 2021, 129, 103827. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A highly efficient gradient boosting decision tree. In Advances in Neural Information Processing Systems, Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.E.; Mohamed, A.-R.; Jaitly, N.; Senior, A.; Vanhoucke, V.; Nguyen, P.; Sainath, T.N.; et al. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Zhan, Y.; Zhang, H.; Liu, Y. Forecast of meteorological and hydrological features based on SVR model. In Proceedings of the 4th International Conference on Advanced Electronic Materials, Computers and Software Engineering (AEMCSE), Changsha, China, 26–28 March 2021; pp. 579–583. [Google Scholar] [CrossRef]
- Weisberg, S. Applied Linear Regression; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Wang, Y.; Yao, H.; Zhao, S. Auto-encoder based dimensionality reduction. Neurocomputing 2016, 184, 232–242. [Google Scholar] [CrossRef]

| Study (Ref.) | Core Principle & Method | Similarities | Differences |
|---|---|---|---|
| [26] | Survival analysis with Weibull distribution | Based on survival analysis; uses intrinsic factors | Early survival model; assumes Weibull distribution |
| [27] | Cox proportional hazards model | Based on survival analysis; uses intrinsic factors | Applies the Cox proportional hazards model; categorizes factors into three groups |
| [28] | Model grounded in Arrhenius chemical reaction rate theory | Uses intrinsic factors | Applies reaction rate theory; discrete classification |
| [29] | Cox proportional hazards model | Based on survival analysis; uses intrinsic factors | Combines assignee (external) characteristics with intrinsic factors |
| [32] | Time-dependent Cox regression model | Based on survival analysis; uses various factors | Time-dependent Cox model; considers three factor groups (intrinsic/extrinsic/industry) in an integrated manner |
| [13] | Gradient Boosting Model | Uses intrinsic and extrinsic factors; discrete classification | Employs a machine learning model; four-class classification |
| [33] | Feed-Forward Neural Network (FFNN) | Uses intrinsic and extrinsic factors; discrete classification | Uses a tuning (FFNN) model; reports the highest performance (0.85); proposes a nine-stage evaluation system |
| [34] | LightGBM with focal loss | Uses intrinsic and extrinsic factors; discrete classification | Uses a machine learning model (LightGBM); demonstrates the usefulness of the neural-network model through comparison with FFNN |
| Feature | Explanation |
|---|---|
| Number of applicants | The number of applicants having applied for the patent |
| Number of agents | An agent is a patent attorney appointed when filing a patent application |
| Number of families | The number of international patent applications that are connected through their subject matter and that follow claims of priority |
| Number of IPC | The number of different IPC assigned to the patent application |
| Number of Claims | Counts the number of claims the patent makes |
| Ratio of independent claims | The percentage of independent claims in entire claims |
| Period from application to grant | The number of days between filing a patent application and receiving the patent grant. |
| IPC(A~H) | One-hot encoded binary variables for the eight IPC sections (A to H), resulting in 8 distinct features. |
| Size of IPC | The number of patents that were registered in the main IPC at the time of the patent was registered. |
| IPC Activity | The number of patents registered in the main IPC in the five years since the patent was registered. |
| Average of IPC Activity | IPC activity at time of registration/5. |
| Ratio of IPC Activity | IPC activity at time of registration/IPC size. |
| IPC Competitiveness | Number of applicants with patents registered in the main IPC at the time of filing |
| Number of Patent right Transfers | The frequency of legal events related to patent ownership transference |
| Duration of Patent | Maximum remaining legal life of a patent |
| Number of citations | The number of times the patent has been cited in the literature or patents |
| Citation impact | The extent to which the patent has influenced technological innovation activities since its filing |
| TCT Index | The Cycle of Technology |
| Claim impact | Number of Claims/Average number of Claims that same IPC and registered year |
| Diversity impact | Number of IPCs in the patent/average number of IPCs in the patent family with the same registration year and IPC |
| Software | |
| Library | Version |
| Data Handling Library | |
| pandas | 2.2.1 |
| numpy | 1.26.4 |
| ML Model Library | |
| scikit-learn | 1.4.1.post1 |
| xgboost | 2.0.3 |
| tensorflow | 2.10.1 |
| keras | 2.10.0 |
| lightgbm | 4.3.0 |
| Hardware | |
| Feature | Specification |
| CPU Architecture & Model | Intel Core i7-13700K |
| CPU Cores | 16 |
| CPU Threads | 24 |
| CPU Base/Max Frequency (GHz) | 3.4/5.3 |
| GPU Architecture & Model | NVIDIA GeForce RTX 3060 |
| CUDA Cores | 3584 |
| GPU Memory (GB) | 12, GDDR6 |
| RAM (GB) | 64, DDR5-5600 |
| Operating System | Windows 11, version 23H2 |
| No | Model | Hyperparameters | Search SPACE |
|---|---|---|---|
| 1 | RF | n_estimators: 280 max_depth: 30 min_samples_leaf: 1 min_samples_split: 2 | 50 to 300 5 to 30 1 to 5 2 to 10 |
| 2 | XGB | n_estimators: 290 max_depth: 14 learning_rate: 0.03259162240984821 colsample_bytree: 0.8780425750115004 subsample: 0.9229737811346409 | 50 to 300 3 to 15 0.01 to 0.3 0.5 to 1.0 0.5 to 1.0 |
| 3 | LGBM | n_estimators: 280 max_depth: 15 learning_rate: 0.23326321741873107 colsample_bytree: 0.8787077808247973 | 50 to 300 3 to 15 0.01 to 0.3 0.5 to 1.0 |
| 4 | DNN | epoch: 200 learning rate: 0.0012536297097257307 optimizer: Adam activation: relu loss function: Mean Absolute Error batch size: 128 | Dense unit1 to unit4: 8 to 256 Learning rate: 0.0001 to 0.01 Dropout 1 to 4 rate: 0.1 to 0.5 - - [64, 128, 256] |
| 5 | SVR | C: 19.62581040283463 epsilon: 0.6967828360688615 kernel: ‘rbf’ | to 0.01 to 1.0 [‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’] |
| 6 | LR | - | - |
| 7 | AE | Epochs: 300 learning_rate: 0.001 optimizer: Adam decoder_activation: relu loss function: Mean Absolute Error encoding_dim: 32 | - [0.0001, 0.001, 0.01] - [‘sigmoid’, ‘relu’] - [16, 32, 64, 128] |
| No | Model | MAE | MAPE | MSE | RMSE |
|---|---|---|---|---|---|
| 1 | RF | 863.87 | 0.36 | 1,206,533.66 | 1098.42 |
| 2 | XGB | 866.19 | 0.36 | 1,210,977.01 | 1100.44 |
| 3 | LGBM | 892.67 | 0.38 | 1,243,363.19 | 1115.06 |
| 4 | DNN | 881.48 | 0.34 | 1,337,037.92 | 1156.3 |
| 5 | SVR | 932.11 | 0.38 | 1,372,223.57 | 1171.42 |
| 6 | LR | 956.04 | 0.41 | 1,352,985.65 | 1163.18 |
| 7 | AE | 928.25 | 0.38 | 1,394,592.92 | 1180.93 |
| No | Configurations | MAE | MAPE | MSE | RMSE |
|---|---|---|---|---|---|
| 1 | RF, XGB | 860.80 | 0.35 | 1,194,991.14 | 1093.16 |
| 2 | RF, DNN | 852.81 | 0.35 | 1,193,663.10 | 1092.55 |
| 3 | XGB, DNN | 861.83 | 0.34 | 1,224,178.35 | 1106.43 |
| 4 | RF, XGB, DNN | 857.94 | 0.36 | 1,209,822.37 | 1099.92 |
| K | MAE | MAPE | MSE | RMSE |
|---|---|---|---|---|
| 3 | 863.12 | 0.34 | 1,239,151.14 | 1113.16 |
| 5 | 852.52 | 0.34 | 1,222,869.6 | 1105.76 |
| 7 | 856.66 | 0.34 | 1,228,866.32 | 1108.51 |
| Application Number | Filing Date | Current Duration (Days) | Predicted Life (Days) | Difference Between Duration and Prediction (Days) |
|---|---|---|---|---|
| 1020140029920 | 13 March 2014 | 3992 | 4979.67 | 987.67 |
| 1020180004470 | 12 January 2018 | 2591 | 3241.81 | 650.81 |
| 1020170091204 | 18 July 2017 | 2769 | 5470.13 | 2701.13 |
| 1020140130055 | 29 September 2014 | 3792 | 4444.85 | 652.85 |
| 1020140034255 | 24 March 2014 | 3981 | 5192.61 | 1211.61 |
| Right | Fee Type | 1~3 Years (SRF) | 4~6 Years (ARF) | 7~9 Years (ARF) | 10~12 Years (ARF) | 13~25 Years (ARF) |
|---|---|---|---|---|---|---|
| Patent | Base fee | ₩ 13,000 | ₩ 36,000 | ₩ 90,000 | ₩ 216,000 | ₩ 324,000 |
| Additional fee (Per Claim) | ₩ 12,000 | ₩ 20,000 | ₩ 34,000 | ₩ 49,000 | ₩ 49,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.-H.; Kim, M.-S.; Rhee, J.; Lee, S.-H.; Kim, J.K.; Oh, S.-H.; Sung, T.-E. Predicting Patent Life Using Robust Ensemble Algorithm. Sustainability 2025, 17, 9658. https://doi.org/10.3390/su17219658
Park S-H, Kim M-S, Rhee J, Lee S-H, Kim JK, Oh S-H, Sung T-E. Predicting Patent Life Using Robust Ensemble Algorithm. Sustainability. 2025; 17(21):9658. https://doi.org/10.3390/su17219658
Chicago/Turabian StylePark, Sang-Hyeon, Min-Seung Kim, Jaewon Rhee, Sang-Hwa Lee, Jeong Kyu Kim, Si-Hyun Oh, and Tae-Eung Sung. 2025. "Predicting Patent Life Using Robust Ensemble Algorithm" Sustainability 17, no. 21: 9658. https://doi.org/10.3390/su17219658
APA StylePark, S.-H., Kim, M.-S., Rhee, J., Lee, S.-H., Kim, J. K., Oh, S.-H., & Sung, T.-E. (2025). Predicting Patent Life Using Robust Ensemble Algorithm. Sustainability, 17(21), 9658. https://doi.org/10.3390/su17219658









