Blend Prediction Model for Vapor Pressure of Jet Fuel Range Hydrocarbons

Abstract

The ability to predict the vapor pressure and vapor-phase composition of hydrocarbon mixtures (such as jet fuel, sustainable aviation fuel or its un-refined precursors) and partially vaporized hydrocarbon mixtures is important to simulations of processes that involve vaporization such as distillations, flash points, combustion properties of partially vaporized fuels, etc. Raoult’s Law provides a simple algebraic formula relating liquid composition and temperature to vapor composition and pressure. However, Raoult’s Law is not accurate at low mole fractions, which is typical for complex mixtures such as fuels. A common approach to correcting Raoult’s Law is to apply a scale factor, a so-called activity coefficient. Numerous models exist for predicting activity coefficients. Here we benchmark against the UNIFAC model, which predicts activity coefficients based on mole fractions, group fractions, Van der Waals volume and surface area and temperature-dependent interaction terms between groups. While this approach is truly predictive, its accuracy at very low mole fractions has not been validated, and it is computationally intensive, particularly for simulations (especially optimizations) that require vapor composition or pressure within the inner-most loop. Here we present an alternative correction to Raoult’s law, where the vapor pressure of the i^th component is represented by a modified form of the Clausius–Clapeyron equation. The reference temperature ($T_{ref}$) is replaced by a simple algebraic function that converges to $T_{ref}$ as $x_i$ approaches 1 while smoothly increasing from this value as $x_i$ decreases. Simultaneously, the heat of vaporization ($\mathsf{\Delta }{H}_{vap,i}\left(T\right)$) term is replaced by another simple algebraic expression that converges to $\mathsf{\Delta }{H}_{vap,i}\left(T\right)$ as $x_i$ approaches 1 while smoothly decreasing as $x_i$ decreases. In this model, the temperature-dependent heat of vaporization is tuned at each temperature such that the Clausius–Clapeyron equation reproduces the correct vapor pressure of the neat material, while the parameterized algebraic corrections are tuned to vapor pressure data of mixtures involving n-pentane, toluene, and dodecane, where the mole fractions of n-pentane and toluene are maintained below 10%_mol. Validation of the resulting model is accomplished by comparing modeled vapor–liquid equilibrium systems with experimental measurements. This approach improves the accuracy and computational efficiency of volatility predictions, thereby supporting the development, certification, and adoption of sustainable aviation fuel.

1. Introduction

Volatility properties of jet fuels are known to have some impact on the safe operation of aircraft. As such, certain representative properties are specified in governing specifications such as ASTM D1655 [1], DEF STAN 91-091 [2], GOST 10227 [3] or GB 6537 [4]. The flash point relates to aircraft-level fire safety. The initial boiling point relates to fuel pump cavitation and fuel control instabilities that could be caused by two-phase flow. The temperature at which 10% of petroleum-derived jet fuel (T₁₀) has vaporized is correlated with engine ignition characteristics. During thermal soak-back after a jet engine is shut off, the vapor pressure inside the closed circuit from the fuel metering unit to the fuel nozzle valves could exceed the valve cracking pressure and lead to fuel burping into the fuel nozzles where it can bake until it turns to coke. A similar phenomenon can happen during part-power operation, when some fuel circuits are turned off (called staging). The dry-out rate of passively purged, staged fuel circuits, similar to droplet evaporation rates, depends on the mass transfer rate, vapor pressure and liquid-phase surface area. Finally, the end point of the distillation is correlated with combustor coking and unburned hydrocarbon emissions. None of these relationships are one-to-one. Moreover, the above listing of operating concerns that could potentially be impacted by fuel properties is not exhaustive. Indeed, an exhaustive list of potential concerns is not generally known [5]. Motivated by such known and unknown factors, two volatility properties, (T₅₀–T₁₀) and (T₉₀–T₁₀), where the subscript refers to the volume fraction distilled, were added as “extended requirements” in the quality specification, ASTM D7566 [6], governing aviation turbine fuels containing synthesized hydrocarbons.

Specifically, the rate of evaporation across a plurality of temperature, convective, and dwell time conditions is directly related to potential operating concerns. Unlike T_n, the vapor pressure (P_vap) of fuel droplets or sheets is directly proportional to their evaporation rate under all operating conditions. The importance of this is recognized by the community, and as such, the vapor pressure as a function of temperature is listed as a Tier 2 property in ASTM D4054 [7], “Standard Practice for Evaluation of New Aviation Turbine Fuels and Fuel Additives”. While maintaining an approximate match to a family of P_vap vs. temperature curves derived from a representative survey of petroleum-derived jet fuels is a prudent goal for developers of sustainable aviation fuel (SAF) or other fuels with synthetic components, it is neither sufficient nor necessary in all circumstances.

SAF and synthetic blending components (SBCs) are considered mid-term solutions to help decarbonize the aviation sector by 2050 [8]. The term SAF is primarily used in policy and regulatory contexts, whereas SBC is the corresponding technical term used in fuel qualification standards. Currently, SBCs are limited up to 50% by volume when blended with conventional jet fuel, because some pathways (e.g., HEFA-SPK) lack certain hydrocarbon classes such as aromatics, which are necessary for elastomer swelling and ensuring proper fuel system performance. To overcome this limitation and enable 100% synthetic ‘drop-in’ jet fuels, the aviation community is exploring blending multiple ASTM D7566 annexes. However, original equipment manufacturers (OEMs), prioritizing safety and reliability, have emphasized the need to evaluate ASTM D4054 Tier 2 or fit-for-purpose (FFP) properties to ensure that fully synthetic fuels meet operational requirements. Measuring all FFP properties experimentally is costly and often beyond the capabilities of many refineries. As a result, the ability to accurately predict FFP properties, particularly volatility and vapor pressure, has become a high priority within the fuel community, as it would accelerate certification, enable higher SAF blend limits, and ultimately support aviation decarbonization efforts.

The chemical (and, to a lesser extent, transport) properties of fuel vapor vary throughout the evaporation time scale, and so do the volatility properties of the liquid that has yet to evaporate. Chemical properties, represented by the derived cetane number, radical index, threshold sooting index, etc., play an important role in lean blowout, particulate matter (nvPM) emissions and the rate of heat release during combustion—indicating a potential impact on combustion dynamics, combustor temperature distribution and combustion efficiency, for example. The composition of the remaining liquid, in tandem with the temperature at its interface with air, determines its vapor pressure and hence its evaporation rate for the relevant transport conditions. All these variances are hereafter referred to as preferential evaporation in this article.

Property models that neglect to track changes in liquid-phase composition throughout the evaporation time scale sacrifice the capability to directly capture the impact of preferential evaporation. However, through correlation with specific points on the ASTM D86 distillation curve, some indirect capturing of preferential evaporation may occur, provided that the relative population distribution of each type of hydrocarbon in the boiling sample is similar to the database of fuel samples from which the model was built. Mendes et al. [9] published a regression model to predict the Reid vapor pressure (P_vap @37.8 °C) of conventional gasoline based on its ASTM D86 [10] distillation curve. Two groups [11,12] published separate regression models built from Raman spectrographic data to predict Reid vapor pressure and octane numbers of petroleum fuels. Flumignan et al. [13] built a regression model built from chromatographic data to predict the density, distillation curve and octane numbers of Brazilian gasoline, while Cocco et al. [14] used chromatographic data of 25 samples to build an artificial neural network model to predict the density, distillation curve and Reid vapor pressure of Brazilian gasoline. It is unknown whether any of these models capture the impact of preferential evaporation, even for petroleum-derived gasoline, or whether any are valid for jet fuel range hydrocarbons.

Other notable examples of simulate, D86 distillation curves include ASTM D2887 [15] (which employs chromatographic data) and the work of Mondragon et al. [16] (which employs thermogravimetric data). The intense interest around this task is a testimonial to its value, which appears to be rooted in the reduction in sample volume required to determine properties that are controlled by some quality specification. Not only do such models neglect to directly capture the impact of preferential vaporization, but they offer little value to efforts, such as those described by Miller et al. [17], to maximize biomass in SAF by optimal selection of distillation fractions or other refinement processes of the synthetic blend component. Furthermore, such models, barring a simulation of the base data, do still necessitate some mass of representative sample to obtain the input data.

Within the so-called tier-$\alpha$ suite of property models published by Yang et al. [18], vapor pressure is calculated by Dalton’s Law, with partial pressured calculated by Raoult’s Law, and simulated D86 distillation is carried out by incremental mass extraction per the composition of the simulated vapor phase. Miller et al. [17] now execute simulated distillation using this same approach and have observed significant error in the prediction of T90. Such error could stem from distillation assumptions (e.g., the number of theoretical plates), inaccurate composition input or propagated errors in components’ vapor pressures.

In a provocative article published in 1995, Hawkes [19] proclaimed that Raoult’s Law is deceptive, which is somewhat interesting in that Wilson’s model of activity coefficients was introduced in 1964 [20], and it was already common by then, in some circles, to use activity coefficients to scale the partial pressures that are predicted by Raoult’s Law to arrive at a more accurate description of the vapor–liquid-phase equilibrium. By 1975, the unsettling fact that vapor–liquid equilibrium data was needed to determine one or more of the parameters used in the Wilson model (and several of its off-shoots) was addressed by Fredenslund et al. [21] by relating these terms to groups (e.g., >C<, -CH₃, aromatic CH, etc.) that are contained in all molecules where the contributions from each group were determined by fitting to vapor–liquid equilibrium data for a variety of binary mixtures, which in theory would permanently establish these contributions so they could be used without modification for other molecules and mixtures that were not part of the original database. This model is called the UNIFAC model and is included in publicly available software such as Aspen Plus V15, DWSIM v9.0.5, and ChemCAD 8.2.0.18575. It is simple enough to be implemented within a spreadsheet such as Excel™, which is what we did to enable comparisons with the new model presented in this work. This spreadsheet is included in the Supplementary Materials, entitled, “UNIFAC Vapor Pressures”. Yet more fundamental models based on intermolecular potentials (RGEMC) [22] or simulated osmotic pressure (OMD) [23] are available in molecular dynamics software such as LAMMPS 22 July 2025, while REFPROP 10.0 [24] employs mixing rules to develop an equation of state for the mixture [25] from which many properties can be calculated, including vapor pressure.

Here, our goal is to evaluate simpler corrections to Raoult’s Law as fuels comprise thousands of different molecules, and simulated fuel distillations may require several thousand determinations of the vapor–liquid equilibrium. Among these thousands of molecules, only seven carbon types are significantly represented; four aliphatic carbon types (-CH₃, -CH₂-, >CH- and >C<) and three aromatic carbon types (protonated aromatic carbon, substituted aromatic carbon and bridgehead aromatic carbon). Within UNIFAC, four terms are used to represent the four aliphatic carbon types, and two terms are used to represent aromatic carbon, protonated or not protonated. In contrast, we are not distinguishing between carbon types or molecular structure. Rather, we acknowledge that every molecule is forced into an environment determined by the liquid mixture’s Gibbs energy minima, which differs significantly from that of pure liquids and is the root cause of a non-zero heat of mixing. While the magnitude of the heat of mixing is ~500 times less than the magnitude of the heat of vaporization, we postulate that enthalpy difference can have a significant impact on the vapor pressure of each liquid mixture component. The main effect on the heat of mixing of jet fuel-range hydrocarbons is the mole fraction, not molecular structure, so here we develop a model framework that is based exclusively on mole fractions as input and a tuning database of binary mixture vapor pressures where the (much) more volatile component is present at mole fractions ranging from 0.01 to 0.09. Over this range of mole fractions, the traditional activity coefficient approach to correcting Raoult’s Law is not validated to the best of the authors’ knowledge.

The approach we consider is described in Section 2 of this article, which directly follows this paragraph. Then, we describe the materials, test conditions and testing methodology used to support determination of the adjustable parameters of this modeling approach, and this is followed by Section 4 where the empirically based correction is derived. Validation of the resulting model is accomplished by comparing modeled vapor–liquid equilibrium systems with experimental measurements. Finally, a summary of the major findings of this study is presented in Section 5.

2. Theory

2.1. Background

The earliest model of vapor pressure can be traced back to Clapeyron [26], nearly 190 years ago. Since then, many model refinements have been published, starting with Clausius [27], who published the form that is found in many current physical or general chemistry textbooks. These models relate the vapor pressure of a liquid to its latent heat of vaporization ($\mathsf{\Delta }{H}_{vap}$) and imply that $(\mathsf{\Delta }{H}_{vap}/R)$ equals the slope of $\ln \left(P_{vap}\right)$ versus inverse temperature $\left(1/T\right)$. Interestingly, the general form of this model can also be derived from kinetic theory, although it was originally conceived entirely from fundamental principles of thermodynamics. In 1884, Trouton [28] shared a recognition that the entropy of vaporization at the ambient pressure of most liquids is approximately the same, 87.3 J·K⁻¹·mol⁻¹, which implies that $\mathsf{\Delta }{H}_{vap}$ is directly proportional to the normal boiling point.

By definition, the vapor pressure of a substance is the pressure at which the rate of adsorption of gaseous molecules that strike the surface of a liquid equals the rate of desorption of molecules from the surface of that liquid. The evaporation rate is the difference between the rate of desorption and the rate of adsorption and goes to zero at equilibrium. Theoretically, the rate of desorption of any component in a liquid mixture could be limited by the diffusion of volatile molecules to the surface or by the fundamental process of desorption.

As accommodated by Antoine’s [29] semiempirical correction to the vapor pressure model, published in 1888, the activation energies of whatever steps control the rate of desorption in pure materials are not generally equal to $\mathsf{\Delta }{H}_{vap}$ as, by definition, $\mathsf{\Delta }{H}_{vap}$ is the enthalpy difference between the liquid and gaseous phases of the material. The activation energy is coincidentally nearly equal to $\mathsf{\Delta }{H}_{vap}$ in many systems. However, the desorption process could occur in multiple steps, and the activation energy governing the rate of each step is, more likely than not, greater than the energy difference between the two geometrical configurations that define the step. In other words, even for pure materials, the slope of $\ln \left(P_{vap}\right)$ versus inverse temperature $\left(1/T\right)$ could be higher or lower than $\mathsf{\Delta }{H}_{vap}$.

As recognized by Antoine [29] and many authors since then [30], $\ln \left(P_{vap}\right)$ is not exactly linear with $\left(1/T\right)$, which suggests that the rate limiting steps in the desorption process are influenced by the bulk change in molar volume as temperature varies. In other words, it matters how many first or second nearest neighbors to a desorbing molecule are vacant. By extension, it should also matter how many first or second nearest neighbors are heterogeneous molecules. To estimate the order of magnitude of this effect, we compare the heat of mixing, which is approximately 25 J/mol [31] for jet fuel-range hydrocarbons, to the heat of vaporization of a representative fuel molecule, n-dodecane, which is 44,000 J/mol. While the heat of mixing has a small (<0.1%) impact on the heat of vaporization, its impact on the desorption rate is approximately 0.6% at the normal boiling temperature of n-dodecane. Intuitively, this impact increases as the mole fraction decreases because molecules of this mixture component are progressively less likely to have homogeneous neighbors as the mole fraction decreases.

For a more fundamental description of the relationship between the molecular arrangements in the condensed phase and the mobility of molecules or vacancies within the condensed phase, the reader is referred to Gaudin and Ma [32]. Briefly, in the condensed phase (the liquid), the desorbing molecule from a mixture sometimes originates (departs) from a shallower (potential energy surface) well than it would if it were not mixed with heterogeneous molecules, but essentially never originates from a deeper well. This is because optimal molecular packing in the condensed phase occurs when all the molecules are the same size and solutes are essentially forced into a packing arrangement that is determined by the solvent. The corresponding transition state, however, is less impacted by the mixture-induced geometric distortions of the condensed-phase lattice. This results in a lower effective activation energy. Quantifying this energy difference from first principles would be very difficult. Instead, we simply acknowledge that it should be lower and dependent on the mole fraction and use measured vapor pressures to gage its magnitude.

Raoult’s Law, in combination with a somewhat modified version of the Clausius–Clapeyron equation, is reproduced here as Equation (1), where $x_i$ is the mole fraction, $P_{ref}$ is 1 atmosphere, $T_{ref,i}$ is the normal boiling point of pure component i and the remaining term is expanded below. The activation energy ($E_{a,i})$ varies with temperature and the actual vapor pressure of pure component i according to Equation (2), such that Equation (1) returns a correct vapor pressure at all temperatures, within the range of the data, when the mole fraction is unity. Pragmatically, an Antoine equation or a Wagner equation [33] is used to represent discrete ($T,P_{vap,i}$) data points continuously, for each pure component. A spline is used to represent $E_{a,i}$ over the range of temperature ±5 °C from the normal boiling point, otherwise Equation (2) is used.

$$P_{vap,i}=x_i\times P_{ref}\times \mathrm{e}\mathrm{x}\mathrm{p}[\left(E_{a,i}/T_{ref,i}\right)\times (1-\left(T_{ref,i}/T\right)]$$

(1)

$$E_{a,i}=\ln \left({\displaystyle \frac{P_{vap,i}}{P_{ref}}}\right)/[\left(1/T_{ref,i}\right)-\left(1/T\right)]$$

(2)

The reason why Equation (1) fails to accurately represent the actual partial pressure of component i in the vapor phase ($P_{vap,i}$) is not just because $E_{a,i}$ varies as the identity of nearest neighbors changes but also because the reference temperature ($T_{ref,i}$, the temperature at which $P_{vap,i}=x_i\times 1$ atm) varies as the effective surface area of the i^th component, its concentration, varies. The desorption rate scales with the mole fraction (surface coverage) while the adsorption rate does not. In other words, both ($E_{a,i}$) and ($T_{ref,i}$) are concentration-dependent but the conventional approach to remediate the failure of Raoult’s Law is to maintain each of these terms as constant and instead scale the resulting partial pressure by an activity coefficient, which depends not only on the identity of the i^th component but also on its concentration, the temperature of the system and the identity and concentration of every other component in the mixture. Here, we evaluate simpler ways to make this correction.

2.2. Data Reduction Strategy

We consider replacing ($E_{a,i}$) and/or either or both occurrences of ($T_{ref,i}$) in Equation (1) with a simple, parameterized function of the mole fraction, the exact form of which is to be determined, for the purpose of minimizing the root mean square error (RMSE) of the predicted vapor pressure relative to the measured vapor pressure. These variants of Equation (1) are expressed here as Equations (3)–(6). Ultimately, one (or none) of these equations will be recommended for the vapor pressure, evaporation rate and distillation simulation of complex fuels. For comparison, the activity coefficient approach is represented by the UNIFAC model, which is described in Section 2.3.

$$P_{vap,i}=x_i\times P_{ref}\times \mathrm{e}\mathrm{x}\mathrm{p}[\left(E_{a,i}/T_{ref,i}\right)\times (1-\left(A\left(x_i\right)/T\right)]$$

(3)

$$P_{vap,i}=x_i\times P_{ref}\times \mathrm{e}\mathrm{x}\mathrm{p}[\left(B\left(x_i\right)/T_{ref,i}\right)\times (1-\left(T_{ref,i}/T\right)]$$

(4)

$$P_{vap,i}=x_i\times P_{ref}\times \mathrm{e}\mathrm{x}\mathrm{p}[\left(E_{a,i}/C\left(x_i\right)\right)\times (1-\left(C\left(x_i\right)/T\right)]$$

(5)

$$P_{vap,i}=x_i\times P_{ref}\times \mathrm{e}\mathrm{x}\mathrm{p}[\left(B\left(x_i\right)/C\left(x_i\right)\right)\times (1-\left(C\left(x_i\right)/T\right)]$$

(6)

In these equations, $A\left(x_i\right)$ and $C\left(x_i\right)$ are scaled reference temperatures, while $B\left(x_i\right)$ is a scaled activation energy. Two functional forms of the scale factor were tried for each term, where $s$ is adjusted to minimize the RMSE. The trial 1 scale factor provided a lower RMSE in every case.

$$\begin{array}{l}Trial 1 scaling: A\left(x\right),C\left(x\right)=T_{ref}^0\times (1+s-s\times x_i) \mathrm{or} B\left(x\right)=E_a^0\ast (1+s-s\times x_i)\\ Trial 2 scaling:A\left(x\right),C\left(x\right)=T_{ref}^0\times (1-s/1.001+s/(x_i+0.001)) \mathrm{or}\\ B\left(x\right)=E_a^0\times (1-s/1.001+s/(x_i+0.001))\end{array}$$

The same value of $s$ applies to all three components, n-pentane, toluene and n-dodecane, as well as (conceptually) every component in jet fuel. A different value of $s$ was determined for each model; (3)–(6). For model (6), two separate tuning parameters were derived, one for $B\left(x_i\right)$ and one for $C\left(x_i\right)$, and not surprisingly, this model provided the lowest RMSE of the set. Relative to the UNIFAC modeling scheme, this modeling approach sacrifices dependencies on component identity (differences in interaction energies, molecular shape and size) in favor of simplicity and generality. It also potentially gains an ability to elegantly capture some of the composition-specific temperature dependencies through its linkage to the Clausius–Clapeyron equation and the best available, temperature-dependent component data.

2.3. Reference Model (UNIFAC) Description

The UNIFAC model is described in detail by Fredenslund et al. [21] and is one of several derivatives of earlier models of activity coefficients. In this model, the activity coefficient of component i is assumed to be a product of two terms: the combinatorial term and the residual term.

The log of the combinatorial term is then estimated by the sum of four more terms, involving six different terms, one of which is the mole fraction of component i, and another of which is a modeling constant set equal to 10. The four remaining terms are different arithmetic combinations of mole fractions, van der Waals volumes, and van der Waals surface areas of every component in the mixture.

The log of the residual term is the sum, over all groups (-CH₃, etc.) in the mixture, of the difference between two new terms, where one of these relates to the group’s contribution in the mixture and the other relates to the group’s contribution in pure component i. The same expression is used to define each of the ‘new’ terms. The independent paraments in this expression include the van der Waals surface area of each group, as well as the group fraction (analogous to the mole fraction), and it involves a group interaction parameter. A large set of group interaction parameters was determined by Fredenslund et al. [21] through a non-linear, least squares data reduction scheme, where vapor–liquid (and liquid–liquid) equilibrium data of binary systems from 200 different sources was used as the foundational database.

The molecules used in this work comprise four groups: -CH₃, -CH₂-, arCH and arC-CH₃. The methyl group of toluene is combined with the aromatic carbon that it is bound to, and this pair is treated as one group. All four of these groups contribute uniquely to the van der Waals volume and surface area calculations, but for the purpose of interaction parameters, the methyl and ethyl groups are considered identical. However, the interaction terms ($a$) are not symmetric so $a_{mn}\ne a_{nm}$, meaning that we have to consider six interaction terms rather than three. A compilation of the values used in this work is provided in

Table 1. Fundamental UNIFAC parameters used in this work.

Molecular Group	vdW Volume	vdW Surface Area	${\mathit{a}}_{12}$	${\mathit{a}}_{21}$
-CH3	0.9011	0.848	-	-
-CH2-	0.6744	0.540	-	-
arCH	0.5313	0.400	-	-
arC-CH3	1.2663	0.968	-	-
CH2 :: arCH	-	-	32.08	15.26
CH2 :: arC-CH3	-	-	26.78	−15.84
arCH :: arC-CH3	-	-	167.0	−146.8

. The spreadsheet used to compile all of the arithmetic combinations of these parameters is provided in the Supplementary Material, entitled “UNIFAC Vapor Pressures”.

2.4. Comparative Summary of Pressure Models

A number of different models applicable to pressure have already been mentioned in this manuscript (summarized in

Table 2. Summary of pressure models mentioned in this work.

Model	Mathematical Form	Comment	System	Complexity
Clausius–Clapeyron	$d\left(lnP\right)/d\left({\displaystyle \frac{1}{T}}\right)=\mathsf{\Delta }{H}_{vap}/R$	Explains temperature dependence	Pure liquids	Very low
Antoine	$lnP=f\left(T\right)$	Three empirically tuned parameters	Pure liquids	Low
Wagner	$\mathrm{l}\mathrm{n}\left({\displaystyle \frac{P}{P_{cr}}}\right)=f\left(T/T_{cr}\right)$	Four empirically tuned parameters	Pure liquids	Low
Equation of State	Many versions from Van der Waals to Span–Wagner		Gases, but extendable	High
Raoult’s Law	$P_i\left(T\right)=x_{i,liq}\times P_i^0\left(T\right)$	Fundamental	Liquid mixtures	Very low
Wilson	$P_i\left(T\right)=a_i\times x_{i,liq}\times P_i^0\left(T\right)$	Tunable activity coefficient $\left(a_i\right)$	Specific liquid mixtures	Data required
UNIFAC	$P_i\left(T\right)=a_i\times x_{i,liq}\times P_i^0\left(T\right)$	Activity coefficient found from standard inputs	Liquid mixtures	Moderate
This Work	$P_i\left(T\right)=x_{i,liq}\times P_i^0(T,x_{i,liq})$	Integrated Clausius–Clapeyron to introduce dependence on mole fraction	Liquid mixtures	Low

), and these are merely representative of a much larger population of models that we segregate into three intersecting purposes. Vapor pressure models of pure compounds (Clausius–Clapeyron, Antoine, Wagner) describe the relationship between the temperature of the system and its vapor pressure, where the gas and liquid phases are in equilibrium. The algebraically simplest of these, the Clausius–Clapeyron equation, is derived from fundamental theory and contains no empirically tuned parameters to correct for assumptions made in its derivation. The Antoine and Wagner equations leverage the fundamental relationship that vapor pressure is exponentially related to the inverse of temperature, but use empirically tuned parameters to extend the applicable temperature and pressure range of the model, where the Wagner model extends applicability well into the supercritical region, beyond the critical temperature $\left(T_{cr}\right)$ and critical pressure $\left(P_{cr}\right)$. The Antoine and Wagner equations, via their reliance on measured pressures and temperatures, necessarily account for real gas deviation from ideal gas behavior. The simplest of all equations of state is the ideal gas law, but it applies only to gases with weak intermolecular force fields with a mean free path much larger than the molecular diameter. Several other equations of state similarly apply only to gases but with allowance, through empirically tuned parameters, for intermolecular attractions/repulsions and molecular volume. Some of the more sophisticated equations of state can also be used for characterizing the boundary (in pressure, temperature coordinates) between the gas and liquid phases, which is an alternative way of saying, ‘the vapor pressure curve’. Most of these models were developed for pure materials but can be extended to mixtures. For example, Opacich et al. [34] used measured data to fit an Antoine equation for each jet fuel within scope in order to characterize its vapor pressure across a broad temperature range. Rauch [35] made a systematic accuracy assessment for alternative aviation fuel evaporation models, which included an examination of fuel surrogates and simple vapor pressure models. In another approach, blending rules can be applied to the tuning parameters used in equations of state, with the complication that heterogeneous intermolecular interaction terms require measured data to determine their values. In both of these examples, the necessity for some measured data to build (or refine) the model severely restricts their scope of applicability.

Enter Raoult’s Law. This model captures the two main effects that contribute to the vapor pressure of a liquid mixture; namely the set of liquid-phase mole fractions and the set of the vapor pressures of each corresponding liquid component, but it is not as accurate as required for many applications. Among the early attempts to improve Raoult’s Law, Wilson [20] introduced a scaling term (activity coefficient) that ultimately required some measured data pertaining to the mixture of scope to empirically derive parameters used in their model and predict activity coefficients. This approach, whether or not it yielded a more robust model than a mixture-specific Antoine (or Wagner) equation, suffers from a similar restriction on its scope of applicability for the same reason; measured data pertaining to the liquid of scope is required to finish constructing the model. The UNIFAC model eliminated the need for mixture-specific measurements to finish the model. However, its accuracy is not great, and it is more complex than desired for some applications. This work combines Raoult’s Law with a generalized form of the Clausius–Clapeyron equation, yielding a simple algebraic equation that depends on two tuned parameters that are applicable to all aliphatic and aromatic hydrocarbons, the set of liquid-phase mole fractions, the vapor pressures of each component of the mixture and their normal boiling points.

3. Methods and Materials

3.1. Vapor Pressure Measurement

The Eravap device, manufactured by Eralytics (Vienna, Austria), was used to measure vapor pressure of liquid samples. The device employs factory-installed software to control sample volume, fill temperature and sample temperature as per user-selected test methodology. We considered the ASTM D6378 [36] triple-point expansion method, as well as the Eralytics lowVP module. For both methods, the sample is pulled into the measuring cell (see Figure 1) via an actuated piston. A pre-set number of rinse cycles are used to saturate the gas in the measuring cell with sample vapor. Upon conclusion of this conditioning operation, the piston is positioned to a depth corresponding to a chamber volume equal to 4 mL. The suction created by moving the piston up to a depth corresponding to 5 mL is responsible for pulling 1 mL of liquid sample into the measuring cell. During the filling process, sensed pressure is monitored to flag potential filling errors. Once the sensed pressure is found to be within 5 kPa of the (air-only) ambient pressure, which was recorded prior to rinsing, a second timer (t₂) is activated, and the first timer (t₁) is stopped. The first timer starts upon opening the inlet valve (see Figure 1) to the sample. In the controller module, called ASTM D6378, the inlet valve is closed when t₂ = t₁/3.

The ASTM D6378 module employs four pre-set volumes (the smallest being 4 mL), which are created by moving the piston within the sealed measuring cell (see Figure 1). The slope of PV vs. V at constant T is the vapor pressure of the sample at that temperature. The total number of moles, as well as the number of sample moles, is determined from the ideal gas law, using total pressure and vapor pressure, respectively, as inputs. The number of moles of air is the difference between these two determined quantities. The Eralytics low VP module differs from the ASTM D6378 module in several ways. Notable differences include longer fill times achieved by decreasing the pressure variation from ±5 kPa to a lower value (~±0.15 kPa), implementing a degassing procedure to rid the liquid phase of any trapped bubbles and executing a triple expansion at a temperature higher than the test temperature to determine the number of moles of air in the sealed measuring cell. For further description of this method, readers are referred to the Eralytics User Manual for the Eravap device.

For three pure solvents, n-pentane, toluene and n-decane, the indicated vapor pressure as a function of temperature was compared to reference data published by NIST [37]. When using the ASTM D6378 module, we found discrepancies of ±1.5 kPa, which is much higher than desired for this work. For this reason, we selected the Eralytics lowVP module for all vapor pressure determinations reported here. According to Eralytics, this method has a repeatability of ±0.15 kPa for all samples at temperatures between −20 °C and 120 °C, with a vapor pressure between 1.0 kPa and 1000 kPa. Our observations are consistent with the quoted repeatability value.

3.2. Materials and Temperatures

The solvents listed in

Table 3. Materials used in hydrocarbon mixtures.

Name	Normal Boiling Point, °C [38]	Supplier	Purity (%)
n-pentane	36.0	Thermo Scientific (Dublin, Ireland)	99
cyclohexane	80.8	Fisher Scientific (Sumner, WA, USA)	99.8
n-heptane 1	98.4	Alpha Aesar (Federal Way, WA, USA)	99
isooctane	99.2	Sigma Aldrich (St. Louis, MO, USA)	99.5
toluene	110.6	Thermo Scientific (Dublin, Ireland)	99.7
ethylbenzene 1	136.2	Thermo Scientific (Richland, WA, USA)	99
o-xylene	143.8	TCI (Portland, OR, USA)	98
n-nonane 1	150.6	Thermo Scientific (Richland, WA, USA)	99
n-propylbenzene 1	158.8	Alpha Aesar (Federal Way, WA, USA)	98
n-decane 1	174.1	Thermo Scientific (Richland, WA, USA)	99
n-dodecane (TCD)	216.3	Thermo Scientific (Dublin, Ireland)	99
n-dodecane (WSU) 1		Thermo Scientific (Richland, WA, USA)	99
n-tridecane 1	233.8	TCI (Portland, OR, USA)	99
n-tetradecane	249.8	Thermo Scientific (Richland, WA, USA)	99

¹ These seven materials were part of a 10-component mixture that was distilled as part of this project. The data pertaining to that distillation is available by request to the correspondence author.

were used to make a variety of mixtures containing 0–10%_mol of light components. The heaviest component (n-dodecane or n-tetradecane) used in 2- or 3-component mixtures was present at higher concentration.

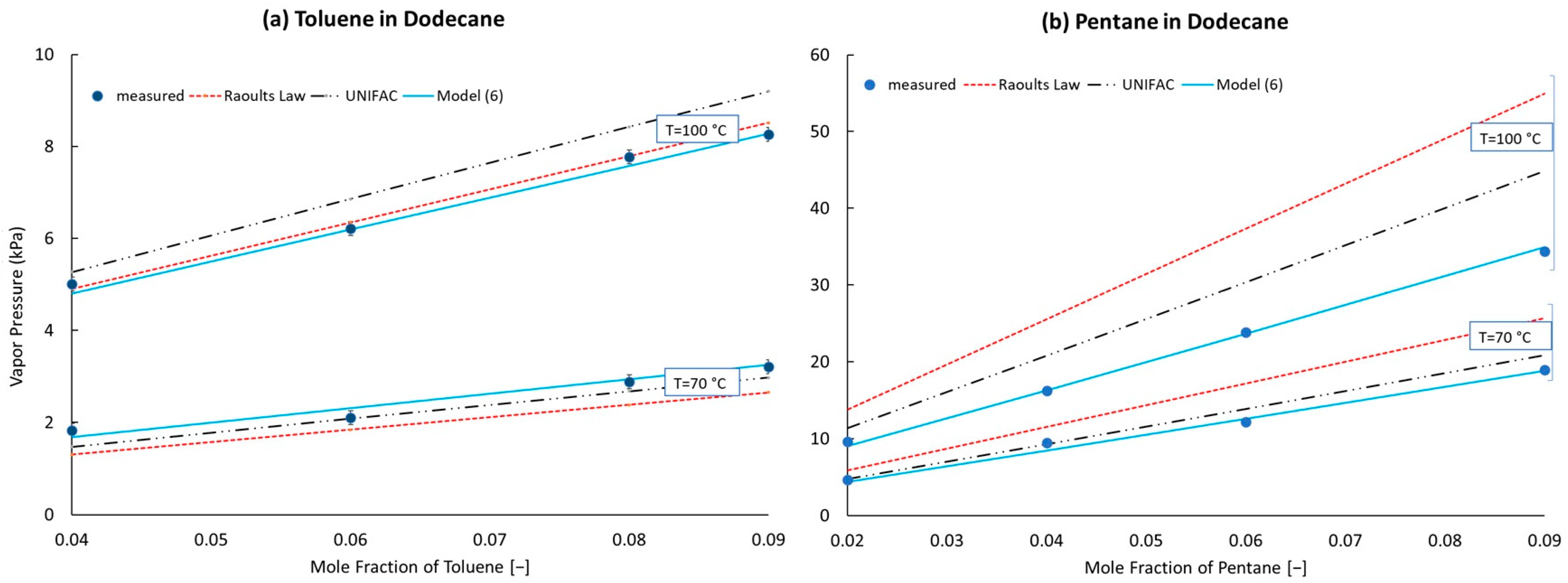
Binary mixtures of n-pentane or toluene in n-dodecane, each at 4 different blending ratios and heated to 70 or 100 °C, were used to determine the tuning parameter(s), $c$. Both sets of binary mixtures included 0.04, 0.06 and 0.09 mole fractions of the lighter component, while the n-pentane/n-dodecane set also included one mixture with a 0.02 mole fraction of n-pentane, and the toluene/n-dodecane set also included one mixture with a 0.06 mole fraction of toluene. A large difference in volatility was deliberately chosen to minimize the impact of errors stemming from the vapor–liquid equilibrium of the solvent, focusing instead on a single volatile component at low mole fractions. For example, the liquid mixture containing 0.04 mole fraction toluene produces a vapor at 100 °C that consists of at least 60% toluene, with wide variation depending on which model is used to predict the component vapor pressures.

Ternary mixtures of n-pentane, toluene and n-dodecane were used as a first level of model validation. In these mixtures, the mole fractions of toluene and n-pentane were made equal to each other: 0.01, 0.04, 0.07 and 0.09. At minimum, the model developed in this work should predict the vapor pressure of these mixtures at 70 and 100 °C more accurately than any of the general models, regardless of its relative simplicity, because its parameters were trained specifically on n-pentane and toluene data. Extension of this model to higher temperatures, corresponding to the ambient-pressure bubble points, is somewhat more stressful, but each of the models considered in detail here employ the same vapor pressure curves of the pure components, so even here, the model developed in this work should be more accurate than Raoult’s Law and the correction to it based on UNIFAC-determined activity coefficients.

Ternary mixtures, (cyclohexane, o-xylene, n-tetradecane) and (isooctane, o-xylene, n-tetradecane), were used to evaluate the generality of the model. In one experiment, the pot temperature of a mixture made from 2.55 g of cyclohexane, 2.56 g of o-xylene and 44.99 g of n-tetradecane was compared with the modeled liquid temperature of a system for which 0 or 1.0%_vol of the liquid is assumed to have vaporized, but to be present in the reflux apparatus (Figure 2) above the surface of the boiling liquid and below the condenser. In another experiment, 100 mL of a mixture made from A (10.36 g of cyclohexane, 10.04 g of o-xylene and 90.93 g of n-tetradecane) or B (10.02 g of isooctane, 10.01 g of o-xylene and 79.96 g of n-tetradecane) was distilled according to the method described as ASTM D86. A brief description of this experiment is provided in this Section 3.4 under the “Distillations” heading.

Finally, data was extracted from the work of Hung et al. [39]. Although none of the ninety (T, P) vapor–liquid equilibrium points they measured satisfy our predetermined filter criteria, the dataset serves as a valuable benchmark for assessing how our model performs when applied to systems clearly outside the training set’s range. For the record, our predetermined filter criteria were non-associated components, a <0.10 mole fraction of the volatile component(s), which we call solute, a >100 K difference between the solute and solvent’s normal boiling points, and a mixture vapor pressure between 1.5 and 101.3 kPa. Their study involved five sets of binary mixtures involving n-nonane, n-octane, methylcyclohexane and methylcyclopentane and three fixed temperatures (120, 160, 200 °C). We selected the points at 120 °C to minimize the confounding effects of real gas behavior, as model (6) does not address heterogeneous intermolecular attractions/repulsions in the gas phase. Three older datasets by different authors were also evaluated, but the data contained in those reports, relative to Raoult’s Law predictions, showed deviations much different from our observations, leading us to question whether we properly understand the experiment they conducted.

3.3. Reflux Experiment

The glassware shown in Figure 2 was used to measure the liquid temperature of a boiling mixture. Type K thermocouples (±2.2 °C) were used to measure temperature. Fifty milliliters of a cyclohexane/o-xylene/tetradecane mixture were inserted into the 100 mL round-bottom flask and heated until a steady-state reflux was established. Ordinary tap water was used as the coolant, fed through the condenser sleeve from the bottom port upward, through the top port. Negligible pot temperature (lower thermocouple) variation was observed as the heat flux (vigorousness of the boil) varied. However, the condensate temperature (upper thermocouple) varied significantly with heat flux, with subtle changes in its vertical position. For this reason, the upper thermocouple temperature is not reported here, although it was used to verify internal coherence. For the purpose of comparing the measured liquid (pot) temperature with the theoretical bubble point of the liquid mixture, the dynamic holdup was approximated to contain the equivalent of 1%_vol of the sample, or 0.5 mL at reference (lab) temperature. The theoretical temperature corresponding to 1%_v distilled was compared with the measured pot temperature. Additionally, the measured temperature corresponding to the first visual observation of bubbles was recorded, as well as the bubble point, as predicted by the vapor pressure model. In this way, there is a band represented for both the measured and modeled temperatures.

3.4. Distillations

Distillations were carried out with the apparatus shown in Figure 3, achieving a collection rate of 1.5–3.0 mL/min from 5% distilled to 50% distilled, which is lower than the requirement stated in ASTM D86 (4–5 mL/min). As a consequence, the degree of separation attained in this set-up is likely somewhat higher than is typical of apparatuses used in conjunction with ASTM D86. The vertical placement of the thermocouple junction is controlled by its sub-assembly, which fits into the ground-glass fitting at the top of the column. Its depth was determined from prior work, manually tuned to reproduce the distillation curve determined with a commercial apparatus conforming fully to the specifications of ASTM D86. The condenser arm is water-cooled, and the collection cylinder is bathed in quiescent air at ambient temperature and pressure. The only vent in the distillation apparatus is at the exit of the condenser arm. Heat is applied via an electrically controlled hot-plate to the bottom of a 125 mL round-bottom flask, which is filled initially with 100 mL of sample. The dimensions of the distillation column, condenser and collection cylinder (100 mL, graduated) are similar to those of the corresponding pieces as specified in ASTM D86. No fractionating media is present in the column.

The volume of dynamic holdup (which includes all mass, liquid or vapor that is not present as liquid in the pot or collection cylinder) varies with the temperature gradient [40] between the bubble point of the liquid phase (in the pot) and the dew point of the vapor phase at the inflection point in the condenser arm, as well at the heat flux applied to the bottom of the round-bottom flask. By adjusting the heating rate periodically to maintain a distillate collection rate of 1.5–3.0 mL/min, the variation in dynamic holdup throughout the course of the distillation is reduced. The dynamic holdup volume is the largest source of mismatch between the recorded distillation curve temperatures (Tn) and the actual distillate temperature throughout a distillation. It can be anywhere from 0.5 to 10 mL, depending on sample composition [40], but is more commonly ~2.6 mL.

Larger dynamic holdup volumes suggest a higher degree of fractionation, because liquid that forms upstream of the inflection point on the condenser arm will drain toward the heat and re-vaporize (whether fully or partially) prior to blending back into the pot. Bounding assumptions of one or two theoretical plates of separation are assumed here for the purpose of comparing modeled distillations with measured distillation curves and distillate compositions. The theoretically estimated temperatures should be consistently higher than the measured temperatures (Tn) if they accurately reflect the actual temperature of a system with n%_v ‘not-in-pot’, which includes dynamic holdup volume and collection volume, instead of n%_v collected.

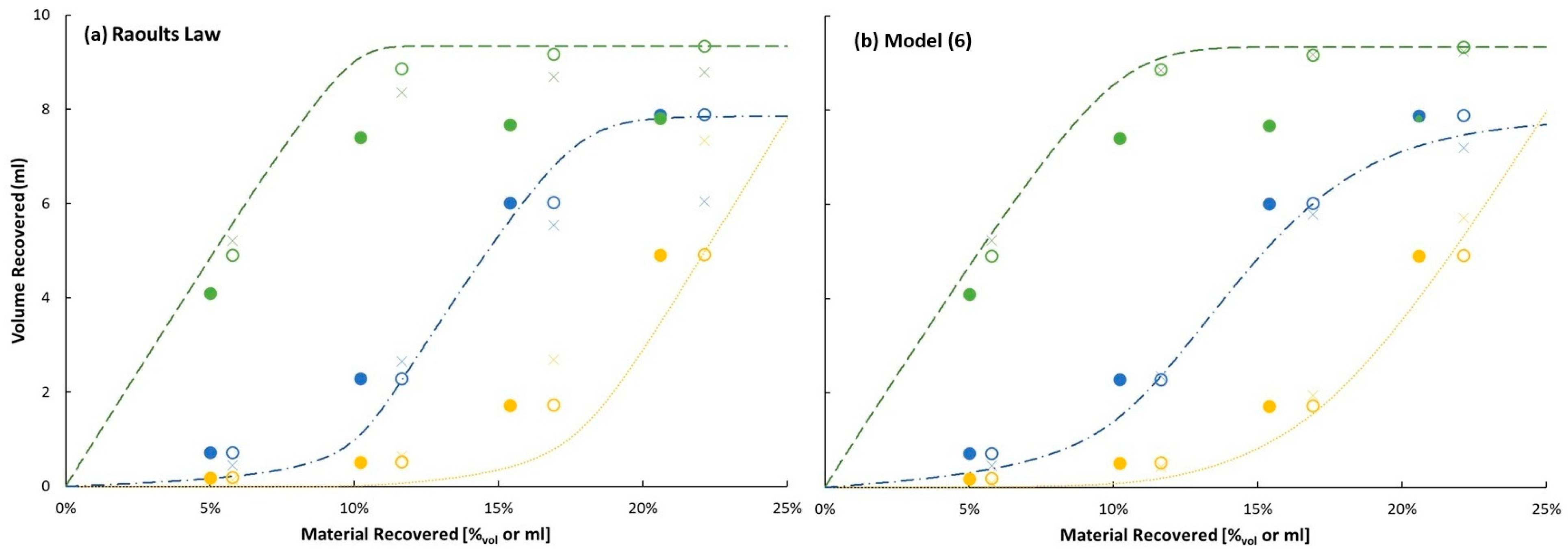
The fraction distilled is defined as the volume of distillate collected, divided by the volume of sample charge, which is 100 mL. The temperature can be monitored throughout the distillation, although usually the operator will only record the temperature at pre-determined distillate volumes. For example, at 10%_V distilled, the operator may record T10 if 10%_V is a pre-determined test point. In this work, the operator has recorded four points for distillation of the ternary mixture (T5, T10, T15 and T20). Specific to this work, a 0.2 mL sample of distillate was pipetted from the collection cylinder at each of the scheduled test points for the purpose of characterizing its composition via GCxGC/FID. The composition of distillate is not subject to errors introduced by the dynamic holdup. To minimize distillate sample inhomogeneity, the material in the graduated cylinder was swirled and agitated by pulsing with five pipette volumes prior to each collection, and to minimize the risk of evaporative loss from the sample, it was immediately transferred to the gas chromatograph. The sampled volumes were not compensated for later collections, meaning the actual collected distillate volume at the second test point, for example, was 0.2 mL greater than indicated by the test point schedule, which consistently referenced the volume of material in the graduated cylinder.

3.5. Distillate Composition Analyses

The composition of each distillate was determined by two-dimensional gas chromatography with an in-series flame ionization detector (FID), according the method described originally by Striebich and Shafer [41] and later by Trinklein et al. [42] In these experiments, the composition determination was particularly simple because the samples were made of just three highly pure components that eluted over easily distinguished time/time domains.

One micro-liter of undiluted sample was injected into the head of the gas chromatograph. The integrated FID response corresponds to the mass of each component that elutes over the user-defined time domain of the integration. Since all masses are determined, and the identity of all species are known in advance, the corresponding mass, mole or volume fractions of each component can be readily determined.

3.6. Modeled Distillation

Idealized 1-plate and 2-plate distillations were completed for each experimentally distilled mixture and each vapor pressure model (this work and Raoult’s Law). The initial condition is 100 mL of a test mixture of a known composition at ambient temperature and pressure (P_amb), from which total moles are determined. This mixture is heated (or cooled) in increments of 0.001 K until its vapor pressure reaches (P_amb ± 0.001) kPa. At that point, for 1-plate distillations, 0.1%_mol of material, with its composition determined by the modeled vapor phase, is removed from the system. The dew point of this drop is determined by cooling (or heating) the vapor in increments of 0.001 K until a liquid of that composition produces a vapor pressure of (P_amb ± 0.001) kPa. For 2-plate distillations, two vapor-phase compositions are tracked. The first one (the higher-temperature one) is determined by the temperature and composition of material in the pot; and the second one (the lower-temperature one) is determined by the temperature and composition of the first drop. The second bubble point temperature is equal to the first dew point temperature. This temperature, along with the composition of the first drop (as well as the first vapor phase), determines the composition of the second phase. At this point, for 2-plate distillations, 0.1%_mol of material, with its composition determined by the second modeled vapor phase, is removed from the system. The dew point of this (second) drop is determined by cooling (or heating) the vapor in increments of 0.001 K until a liquid of that composition produces a vapor pressure of (P_amb ± 0.001) kPa. In each case the modeled (final) dew point is compared with experimentally measured condensate temperatures.

To model a significant span of the distillation curve, this process is repeated up to 1000 steps, with an incremental reduction in liquid in the pot at each step. To avoid numerical issues that are likely to arise somewhere (between 950 and 1000 steps) as the quantity of material being extracted becomes significant relative to the total material left in the system, we stop the numerical distillations at 950 steps. The (first) bubble point temperature, (final) dew point temperature and composition of the extracted drop are recorded at each step. The fully mixed distillate composition is also updated at each step.

4. Results

4.1. Tuning Vapor Pressure Models

The mixtures of n-pentane in n-dodecane and toluene in n-dodecane were used to represent the vapor pressure of an aliphatic or aromatic solute dissolved in a hydrocarbon solvent. A large volatility difference between the solute and solvent was chosen so that the composition of the vapor phase would be predominantly one component, the solute, even as the solute mole fraction in the liquid phase was taken down to 0.02 (n-pentane) or 0.04 (toluene). Thus, the confounding impact of solvent vapor pressure was minimized.

Table 4. Antoine coefficients of selected materials: ${\log }_{10}\left(P\right)=A-B /(T+C).$

Material	nBP (°C)	A	B (K)	C (K)
n-pentane	36.0	3.9892	1070.617	−40.454
toluene	110.6	4.0783	1343.9	−53.77
n-dodecane	216.3	4.10549	1625.928	−92.839
cyclohexane	80.8	3.96988	1203.526	−50.287
o-xylene	143.8	4.12928	1478.244	−59.076
n-tetradecane	249.8	4.13735	1739.623	−105.616
isooctane	99.2	3.9368	1257.8	−52.42

documents the normal boiling points and the Antoine coefficients for each of these three materials, where the Antoine equation was used to obtain the values of $P_{vap,i}$ that were used in Equation (2). The singularity (in Equation (2)) that occurs when the temperature equals the normal boiling point does not arise at the tuning stage of this work because only test temperatures (70 and 100 °C) not equal to the normal boiling point of any component were selected. Two values of temperature were chosen, effectively decoupling variation in $E_{a,i}$ from normal boiling point variation. A mix of aliphatic and aromatic hydrocarbons (one each) was deliberately selected because the entropy of vaporization, which effectively relates the normal boiling point temperature and the heat of vaporization, is somewhat different for each; approximately 86.5 and 72.5 J/mol/K for alkanes and aromatics, respectively. Our intent here is to model each in the same way and to assess the error introduced by neglecting this difference. For reference, the approximate entropies of vaporization of cycloalkanes and alkenes are 85.0 and 82.5 J/mol/K, respectively, within the bounds of the representatives chosen for this work.

For the n-pentane/n-dodecane mixtures, vapor pressure data was recorded for mixtures with 2, 4, 6 and 9%_mol n-pentane at 70 and 100 °C. For the toluene/n-dodecane mixtures, vapor pressure data was recorded for mixtures with 4, 6, 8 and 9%_mol toluene at 70 and 100 °C. These 16 data points were used to train the models. Figure 4 displays the best fit for each of the models defined in Equations (3)–(6). The toluene/n-dodecane data is confined to panel (a) and the n-pentane/n-dodecane data is confined to panel (b). The motivation for showing all of these fits is to underscore the improvement offered by the second tuning parameter. For model (6), the root mean square and mean absolute errors are 0.35 and 0.25 kPa, respectively, substantially better than any of the single-parameter models. More importantly, for model (6), the error is split evenly between each of the four groupings of data, resulting in a mean error of just 0.09 kPa and a mean absolute relative error (MARE) of 3.5%. In contrast, the errors of the single-parameter models are heavily skewed toward the toluene/n-dodecane mixtures, while a temperature-dependent pattern is also apparent. The tuned values of s, applicable to model (6), are reported in Equations (7) and (8).

C(x_i) = T_ref,i⁰ (1.0154 − 0.0154 ∗ x_i)

(7)

B(x_i) = E_a,i⁰ (0.77275 + 0.22725 ∗ x_i)

(8)

A comparison of model (6) with other global models, UNIFAC and Raoult, is displayed in Figure 5. Surprisingly to these authors, the zero-parameter Raoult’s Law misrepresents the n-pentane/n-dodecane vapor pressures at 100 °C by a whopping 22–60%, while it essentially matches the toluene/n-dodecane vapor pressures at 100 °C. Across the 16 points, its MARE is 26.6%. Compared with the 100 °C data, at 70 °C, Raoult’s Law predictions decrease relative to the data for both sets of mixtures, which is a characteristic shared by the UNIFAC model predictions. The “corrections” to Raoult’s Law offered by the UNIFAC activity coefficients scale the vapor pressures of the toluene/n-dodecane mixtures (activity coefficients > 1) to higher values, which drives it in the wrong direction at 100 °C and the right direction at 70 °C. For the n-pentane/n-dodecane mixtures, the UNIFAC model (activity coefficients < 1) scales Raoult’s Law vapor pressures to lower values, which is closer to the data at both 70 and 100 °C, but still wrong by up to 31% at 100 °C for the mixture containing 9.0%_mol n-heptane. Across the 16 points, its MARE is 12.6%. Clearly, the two-parameter model developed here shows greater promise than the activity coefficient approach represented here by the UNIFAC model, which has a total of seven tuned parameters that are applicable to these mixtures.

4.2. Modeled Vapor Pressure Validation

The first level of validation to be discussed is to compare predictions to measurements of systems under slightly different conditions compared with the tuning dataset. Here we use ternary mixtures of n-pentane, toluene and n-dodecane. For convenience of reporting, the mole factions of toluene and n-pentane were prepared equal to each other. According to Raoult’s Law and model (6), the vapor pressure of this mixture should be essentially the sum of the vapor pressures of the respective binary mixtures, because these models do not consider potential differences between components of differing identities, and the slight reduction in n-dodecane’s contribution to the total vapor pressure is small, because its vapor pressure is much lower than those of n-pentane and toluene. In contrast, the activity coefficients of the UNIFAC model are impacted by the identities of the other components. For example, at 9%_mol, the activity coefficient of n-pentane is 0.811 at 70 °C for the binary mixture and 0.837 for the ternary mixture. Very astute readers may be able to see the effect of this difference by comparing Figure 5 and Figure 6, as the UNIFAC model is slightly more wrong for the ternary mixture than the binary mixture at this temperature, even though it gets the vapor pressure of toluene right at this temperature. Comparison to the equation-of-state model [25] (EOS) used in REFPROP [24], which lacks key features relevant to complex mixtures such a fuels, reveals several notable observations. Although exaggerated relative to the measured vapor pressure curves, the EOS model predicts some curvature to the vapor pressure as a function of the mole fraction, whereas this characteristic of model (6) (clearly present based on Equations (7) and (8)) is not visibly apparent on the viewing scales of Figure 4, Figure 5 and Figure 6. The temperature dependence of the EOS model brings it closer to the measured values at 100 °C than at 70 °C, which may not be surprising, because the critical temperature is a focal point within that model’s framework. Most surprising to the authors, however, was the magnitude of the errors afforded by this model in spite of its complexity and specificity to these three materials. In numerical summary, the MAREs of model (6), Raoult’s Law, UNIFAC and REFPROP are 44.6%, 24.3%, 33.6% and 5.5%, respectively. Only model (6) has a lower MRE magnitude (5.1%) than MARE.

The next level of validation is to introduce a greater variety of materials and temperatures, resulting in vapor pressure up to ambient pressure. One simple way to obtain this data is to measure the temperature of a refluxing mixture. The temperature of the liquid phase is easy to get right, and the pressure is the barometric pressure of the lab, but the composition of the liquid phase is somewhat confounded because some mass of sample exists as dynamic holdup: vapor or condensed vapor that has not yet fallen back into the pot. In Figure 7, we show the measured reflux temperature of a mixture of o-xylene (8.6%_mol), cyclohexane (10.8%_mol) and tetradecane (80.6%_mol) in comparison with the predicted bubble point resulting from model (6), Raoult’s Law and the UNIFAC model. To account for the uncertainty of the liquid-phase composition, predictions corresponding to 0 and 1%_vol are reported. The measured temperatures correspond to the moment when the first bubble was observed (bottom) and the moment it reached a steady-state temperature (top). For each of the models, the $P_{vap,i}$ term in Equation (2) was represented by an Antoine equation, with coefficients as documented in Table 4. As is quite evident from Figure 7, model (6) predicts a normal boiling point and refluxing temperature, in far better agreement with the measured values than Raoult’s Law or the UNIFAC model. While none of the models predict the measured result to within the ±2.2 °C reproducibility of the thermocouple, the vapor pressure predicted by model (6) at the lower edge of the measured temperature uncertainty band is just 11% higher than lab pressure, much closer than the other models. The liquid phase composition of 1%_vol distilled for both model (6) and UNIFAC reflux temperatures (upper) was based on model (6), and one theoretical plate was assumed since no removal of material was occurring in this system.

4.3. Literature Data

Recently, Hung et al. [39] measured and predicted the vapor pressure of 20 different binary mixtures involving n-nonane, n-octane, methylcyclohexane or methylcyclopentane at 120, 160 or 200 °C. Their predictions were made via Aspen Plus V11 using COSMO-SAC, UNIFAC-DMD and two additional models with coefficients of binary interactions re-tuned to their measurements and Hayden-O’Connell fugacity coefficients. A description of the UNIFAC-DMD model (highlighting modifications to UNIFAC) was provided by Gmehling et al. [43], while a description of the COSMO-SAC model was provided by Hsieh et al. [44] The MAREs of UNIFAC-DMD and COSM0-SAC were 1.5% and 5.1%, respectively. Comparatively, the simple two-parameter model presented here results in a MARE of 5.1% and mean relative error (MRE), or over-prediction, of −0.7%, considering only the data at 120 °C to avoid having to account for real gas differences relative to an ideal gas. As seen in Figure 8, model (6) overpredicts the vapor pressure of eleven mixtures while underpredicting the vapor pressure of nine mixtures. In contrast, Raoult’s Law over-predicts the vapor pressure of all 20 mixtures, two of them by more than 40%, and has a MARE of 13.7%.

It is worth noting here that the performance of model (6) on this dataset is consistent with the authors original intent, which was to develop an algebraically simple model (suitable for hand calcs, spreadsheets or codes/applications that require vapor pressure or composition many thousands of times per run) that provides much-improved accuracy relative to Raoult’s Law while remaining comparatively accurate to the more complicated and mature models used in commercially available applications that serve process engineering and industrial simulations. Model (6) is not intended to replace models such as UNIFAC but rather to reach applications (through its simplicity) that are not currently pragmatic for UNIFAC. Specifically, this model does not address heterogeneous, real gas effects and should not be applied to conditions where such terms are expected to be important. It can be applied to our research goals, which are to support conceptual-level distillation cut-point optimization, as exemplified by Yang et al. [45], bubble point prediction in the fuel system at chop from cruise to flight idle, preferential evaporation effects on lean blow at this same (jet engine) operating condition and evaporation rate predictions in (future) simulations of ignition in jet engines. Of these, the only one that is pragmatic for applications like ASPEN is the check on bubble point in the fuel system at the min-thrust/max-altitude (combustor) design point, but jet engine combustor designers do not generally have access to any such commercial application.

4.4. Modeled Distillation Validation

The final validation of the vapor pressure model compares predicted distillation curves with measured distillation curves. However, the model of the distillation process may be more important to these curves than the vapor pressure model. Figure 9 is used to compare the measured distillation curve of the ternary blend initially containing 18.2%_mol (9.3%_vol) cyclohexane and 14.0%_mol (7.8%_vol) o-xylene, with the balance being tetradecane. Clearly the difference resulting from the variable number of theoretical plates assumed for the distillation, one or two, has a much larger impact on the modeled distillation curve than the choice of vapor pressure model, Raoult or model (6). Regardless of vapor pressure model, the assumption of two theoretical plates results in a predicted distillation curve that more closely matches the measured data. Two sets of points are used to represent the measured distillation curve. One set corresponds to the measured temperature at the moment the collected distillate volume equals the first drop, 5 mL, 10 mL, 15 mL and 20 mL. The latter three points are shifted to the right to account for the distillate sample volume removed for later composition analysis. The second set of points accounts for the dynamic holdup volume, which we estimate to be 2.6 ± 1.2 mL. By comparing the curves displayed in panel (a) with those displayed in panel (b), it is apparent that Raoult’s Law predicts more separation between the components for both distillation models; more featured and greater difference between the initial boiling point (IBP) and the temperature at 20%_vol distilled (T₂₅). Relative to the measured data, Raoult’s Law with two theoretical plates over-separates the mixture while model (6) under-separates the mixture. An optimized linear combination of the 1- and 2-plate curves for Raoult’s Law and model (6), respectively, results in a rms error of 12.3 and 9.2 °C. The 2-plate curve weighting coefficient is 70% for Raoult’s Law and 91% for model (6).

To gain further insight into which vapor pressure model more accurately represents this distillation process, the measured and predicted distillate composition is compared in Figure 10. The dynamic holdup volume is not applicable to this data. The measured compositions were determined from GCxGC/FID analysis of samples drawn from the collection vessel. To account for the disconnect (1.53 mL) between the total volume of cyclohexane collected and its volume in the initial ternary mixture, we assume it was lost as vapor throughout the distillation. The open symbols in Figure 10 represent the measured data, corrected under this assumption. The vapor loss at each point is scaled by the ratio of liquid cyclohexane collected at each point divided by the final volume of cyclohexane collected. Relative to these points, it is clear that both vapor pressure models, within the two-theoretical-plate distillation model, predict greater separation at the first data point, overrepresenting cyclohexane and underrepresenting both o-xylene and n-tetradecane. By the second data point, when most of the cyclohexane is distilled, both vapor pressure models result in a predicted o-xylene concentration that matches the corrected data. Neither model captures the full extent of n-tetradecane bleed-through into the distillate. The missed n-tetradecane content may seem small in the context of vapor pressure, but the freeze point of this distillate is determined by n-tetradecane, where a mole fraction of 1% is expected result in a freeze point of −40 °C [46]. The difference between a measured mole fraction of 1.9% and a predicted mole fraction of 0.7% (or less) is the difference between having a product that will pass inspection or fail inspection. While model (6) with two theoretical plates of separation is closer to reality than Raoult’s Law with two theoretical plates, this distillation experiment falls somewhat short of two theoretical plates. The symbol x in Figure 10 corresponds to the prediction that weights a two-plate distillation by 70% and 91% for Raoult’s Law and model (6), respectively. The agreement between the measured distillate composition and its prediction based on model (6) with two plates of separation weighted by 91% and one plate of separation weighted by 9% is remarkable at 5, 10 and 15% distilled, but at 20% distilled, it under-predicts o-xylene concentration while over-predicting n-tetradecane concentration. In contrast, the modeled distillation based on Raoult’s Law vapor pressures with 70% two-plate separation and 30% one-plate separation is wildly inconsistent with measured distillate composition at 15 and 20% recovered.

In order to reduce the confounding effect of evaporative losses, a second ternary mixture was distilled. This mixture initially contained 15.0%_mol (11.1%_vol) isooctane and 16.1%_mol (8.6%_vol) o-xylene, with the balance being tetradecane. A comparison between the measured distillation curve and its prediction based on model (6) vapor pressures and a two-plate distillation or a 96% two-plate plus 4% two-plate distillation is provided in Figure 11. The rms error of the weighted distillation curves is 10.5 °C, stemming almost entirely from the big miss at 15–20% distilled, where the recorded temperature (130.9 °C) is substantially less than the normal boiling point of o-xylene (143.8 °C). The measured and modeled distillate compositions are displayed in Figure 12. Consistent with the previous result, the predicted recovery of o-xylene is noticeably under-represented by the model, while isooctane is over-represented at all four points of comparison, and n-tetradecane content is over-represented by the model at 20% recovery.

5. Conclusions

A global two-parameter vapor pressure model that is rooted in our physical understanding of evaporation of hydrocarbon mixtures has been developed. Sixteen vapor pressure measurements involving two different temperatures, two binary systems and four concentrations were used to tune the parameters, which were used to scale both the activation energy (or heat of vaporization) term and reference temperature term in the Clausius–Clapeyron equation as a function of the mole fraction.

Comparisons to twenty-nine points (T, P, {x_i}) and four temperature curves have been presented, showing dramatically better accuracy relative to Raoult’s Law and comparable accuracy relative to the UNIFAC model. Additionally, two comparisons between measured and predicted distillation curves and distillate compositions of two different ternary mixtures further demonstrate that the simple vapor pressure model presented here outperforms Raoult’s Law, but these comparisons also highlight the fact that modelling the distillation process is challenging.

The confounding of distillation process modeling errors with vapor pressure (and vapor composition) modeling errors makes it difficult to validate either from data collected during a distillation experiment. To get around this issue and the uncertainty it causes, crude oil (whether synthetic or petroleum in origin) refiners may employ somewhat more fractionation than necessary, which also desensitizes the process to vapor pressure model accuracy. Alternatively, mature yet computationally extensive options available through Aspen Plus, DWSIM or ChemCAD may offer more accurate process simulations, but it would be impractical to put such tools within the inner-most loop of decision logic to select the cut points of crude oil refinement, and essentially impossible to nest them into computational fluid dynamics simulation of evaporation under combustor operating conditions near ignition, lean blow out or any other important combustor operating point. The model presented here provides dramatic improvement relative to Raoult’s Law, with a very modest increase in computational complexity.