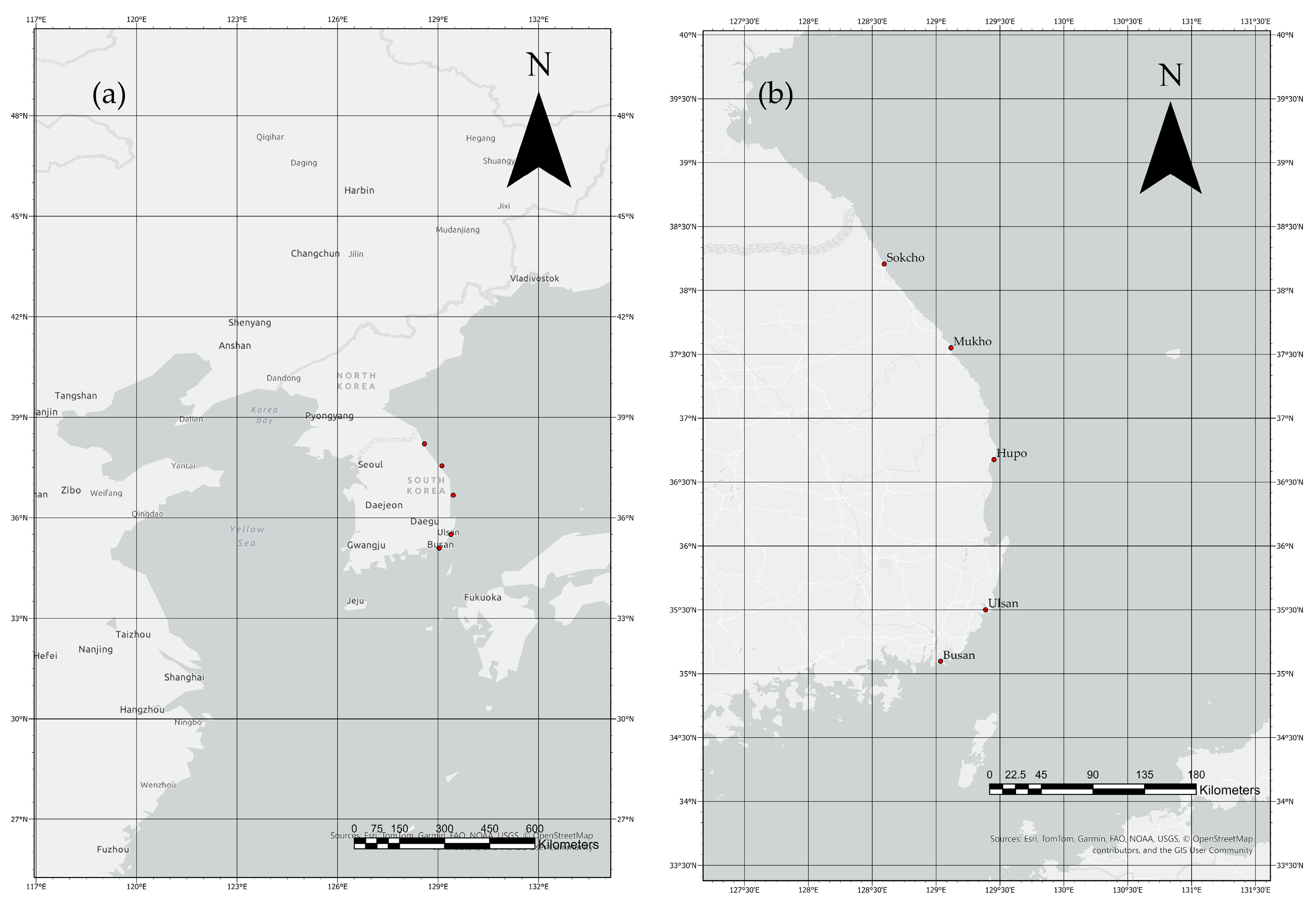
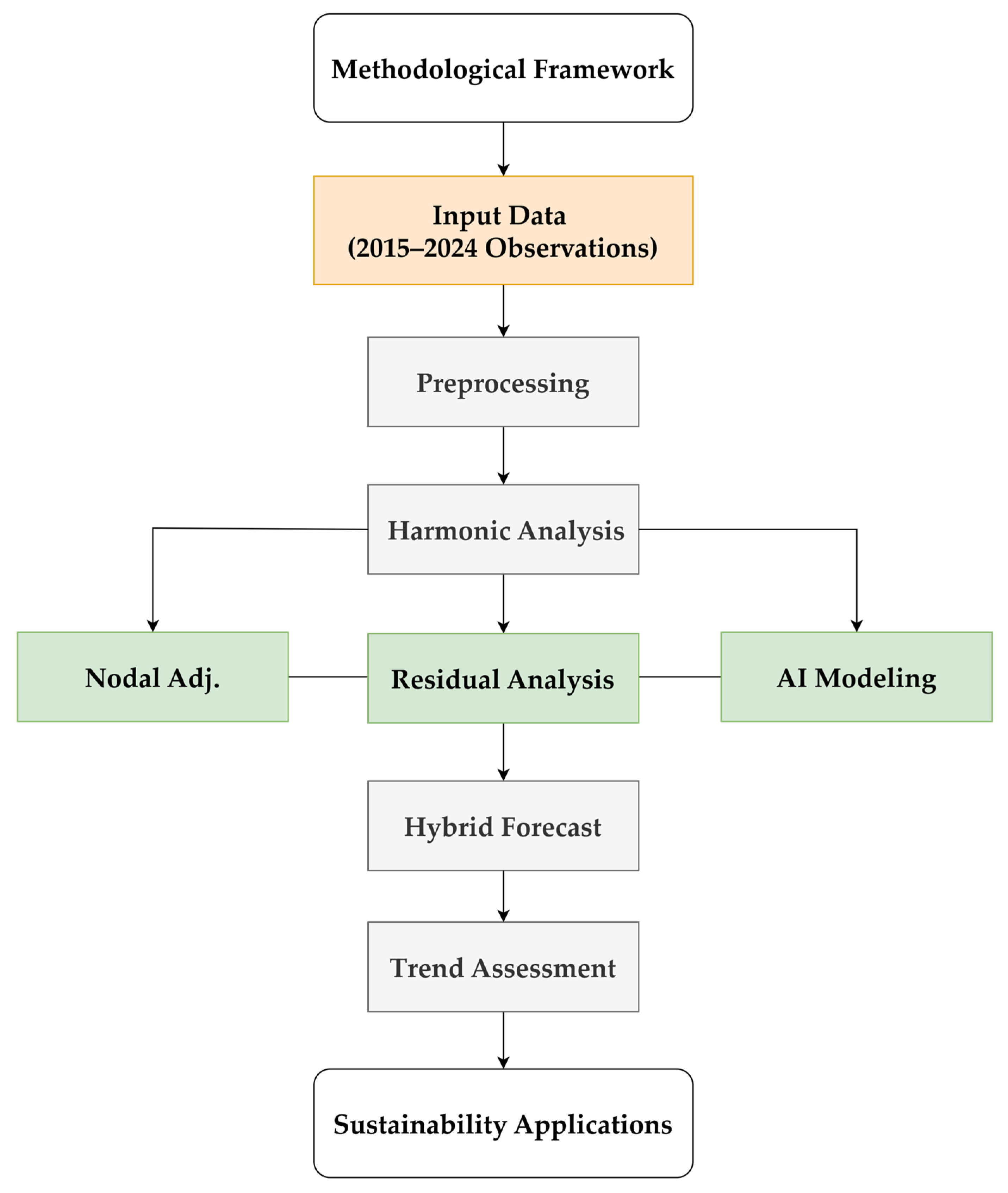
Appendix A
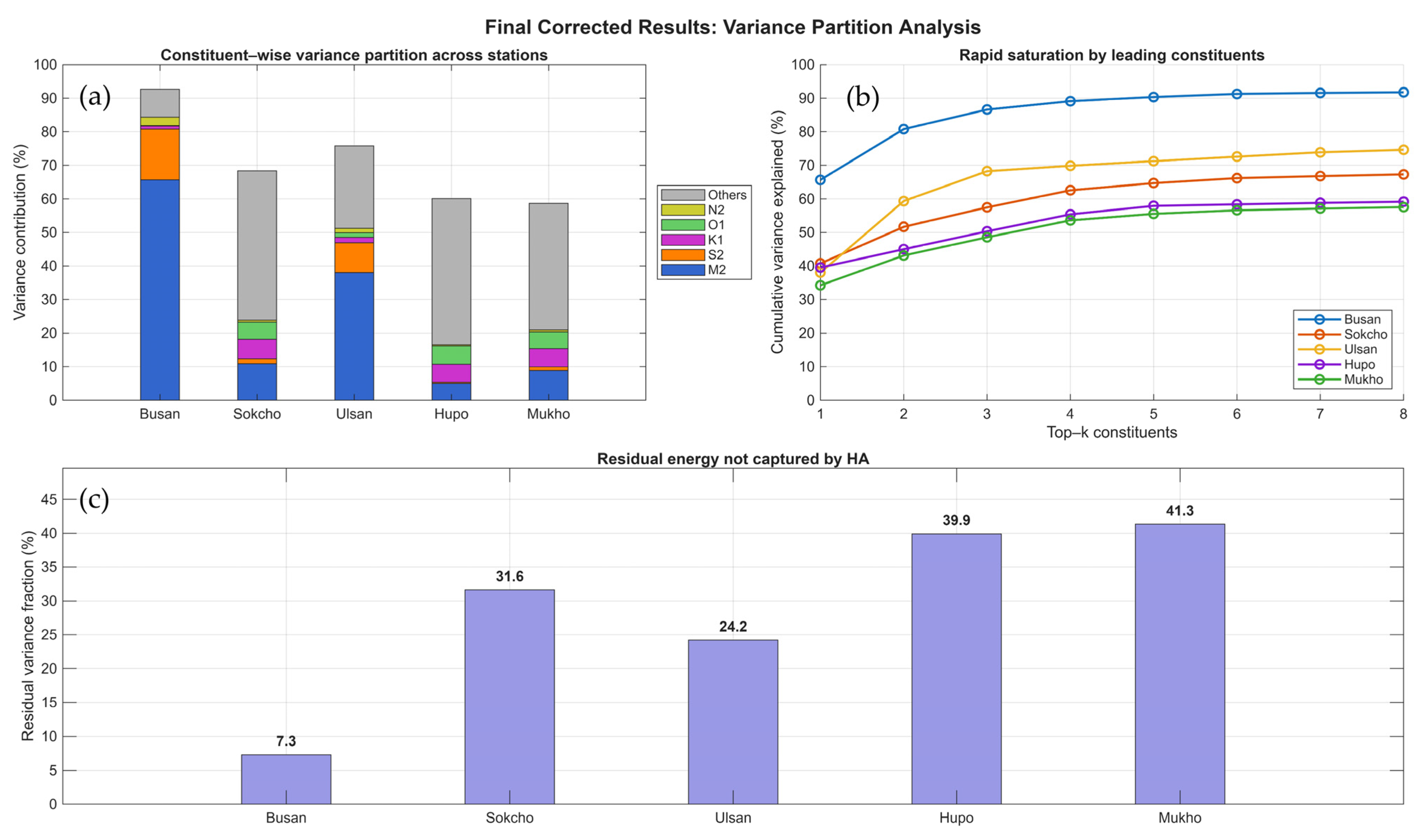
This appendix presents detailed long-term forecasts and validation analyses for the remaining four tidal stations: Hupo, Mukho, Sokcho and Ulsan. Each station follows the same analytical framework described in
Section 3.2, with hybrid HA-AI forecasting incorporating variance conservation principles and uncertainty quantification.
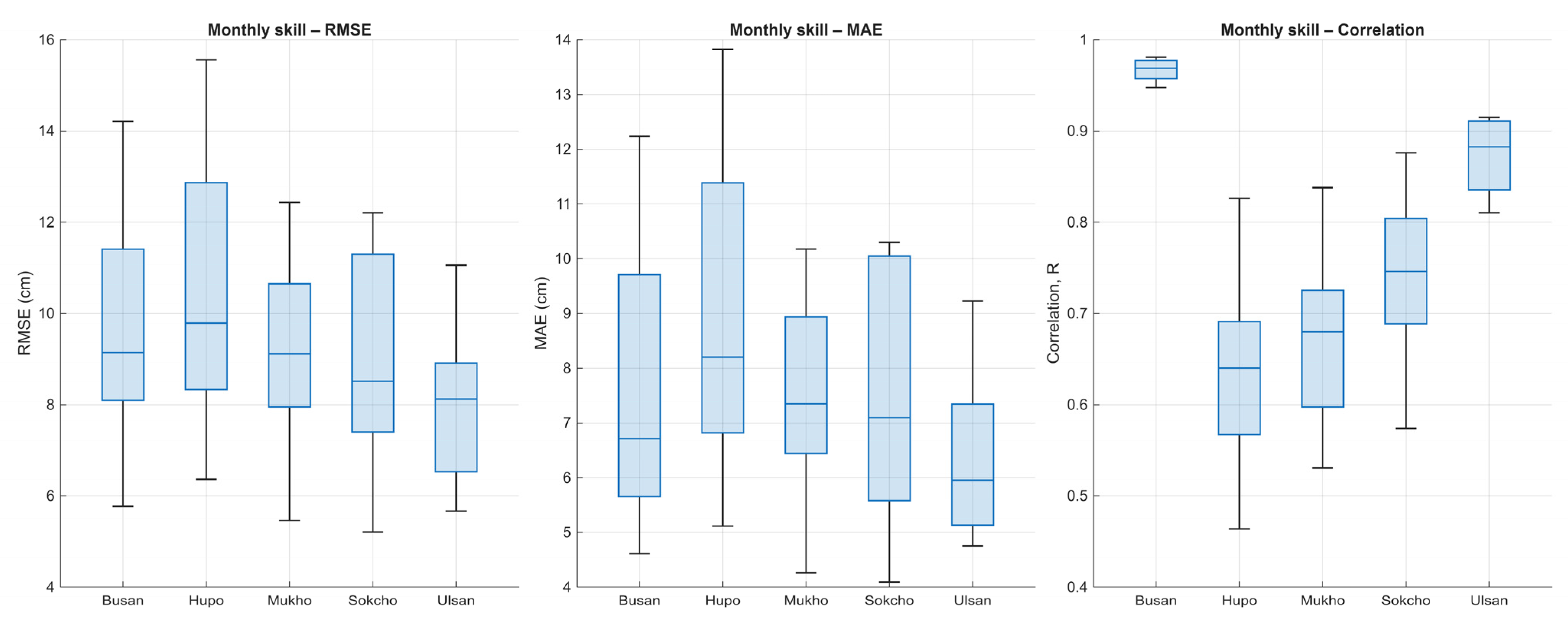
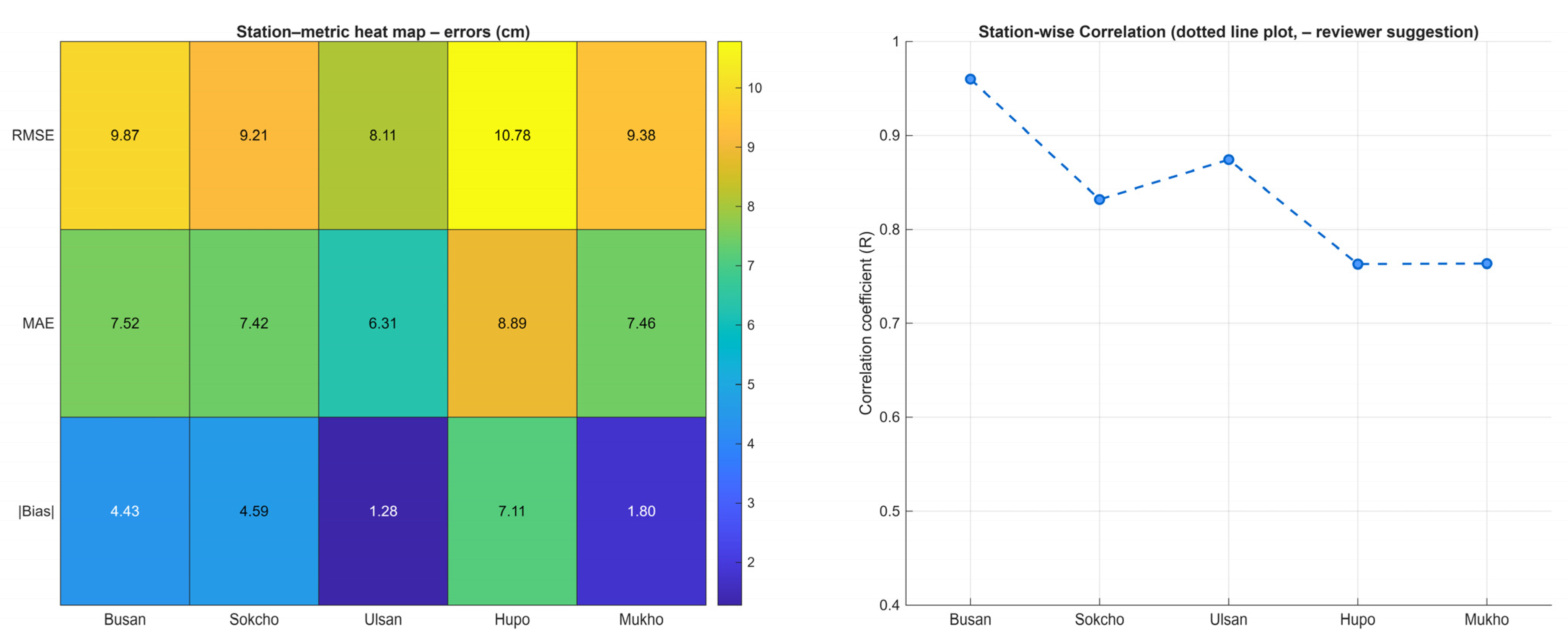
For each station, two figures are provided: (1) long-term forecast overview with 18.6-year time series and residual analysis, and (2) detailed performance diagnostics including 2025YTD validation, parity plot, daily RMSE evolution, and uncertainty validation histogram. All stations demonstrate consistent performance with the variance conservation framework, confirming the physical rationality and reliability of the hybrid forecasting approach across different coastal environments along the East Sea of Korea.
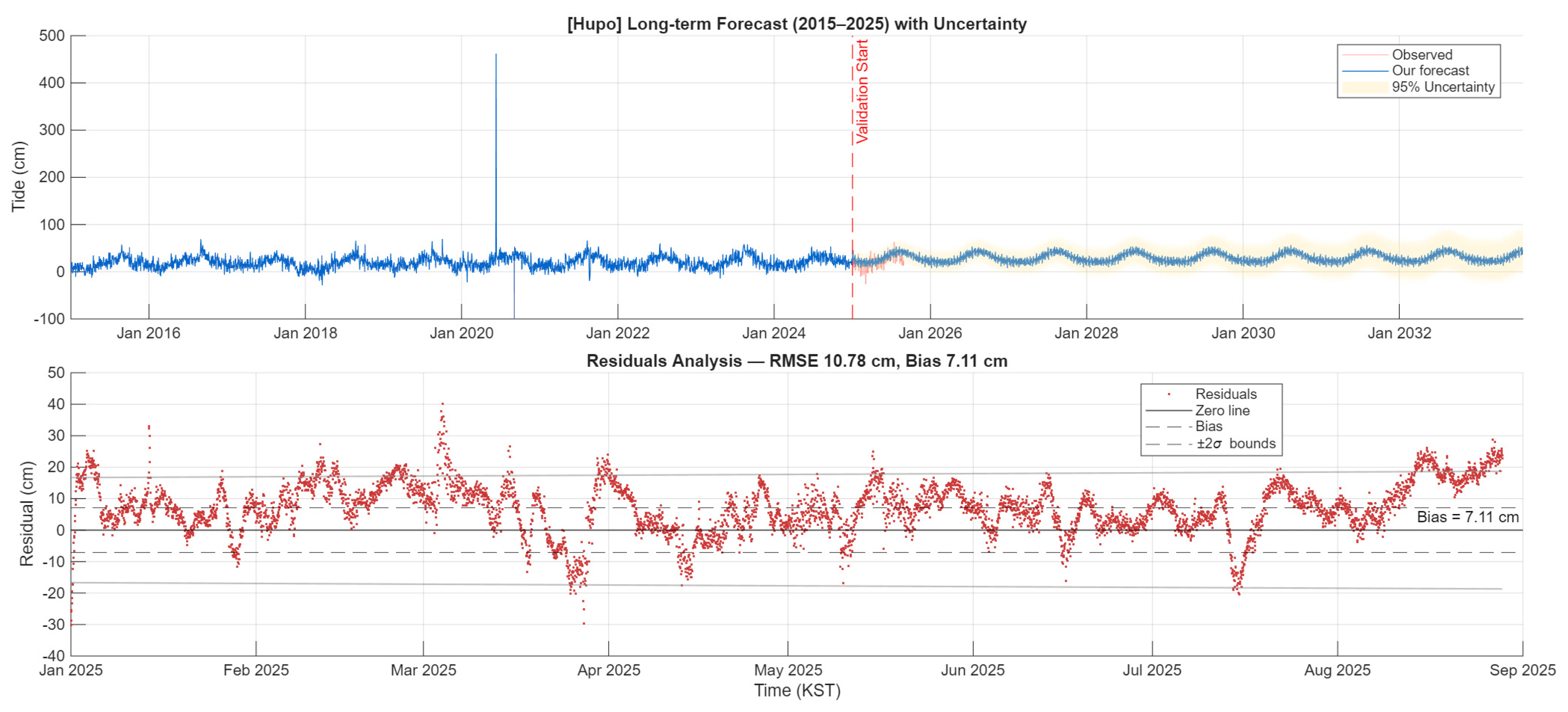
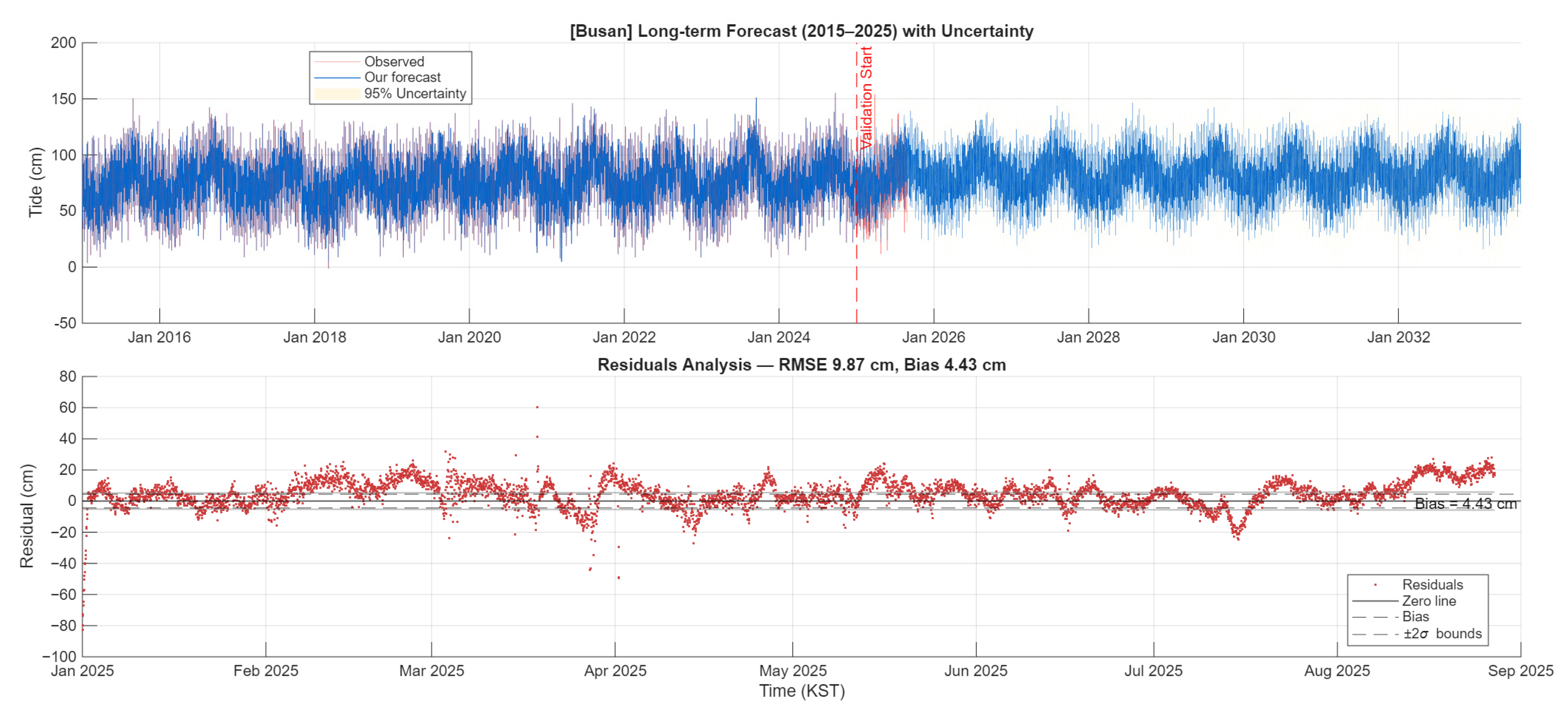
Figure A1.
Hupo (South Korea) long-term forecast and validation. (Top): 18.6-year time series (2015–2025) showing observed tides, hybrid HA-AI forecast, and 95% uncertainty bands. Red line marks validation period start. (Bottom): Residual analysis for 2025 validation period with ±2σ uncertainty bounds.
Figure A1.
Hupo (South Korea) long-term forecast and validation. (Top): 18.6-year time series (2015–2025) showing observed tides, hybrid HA-AI forecast, and 95% uncertainty bands. Red line marks validation period start. (Bottom): Residual analysis for 2025 validation period with ±2σ uncertainty bounds.
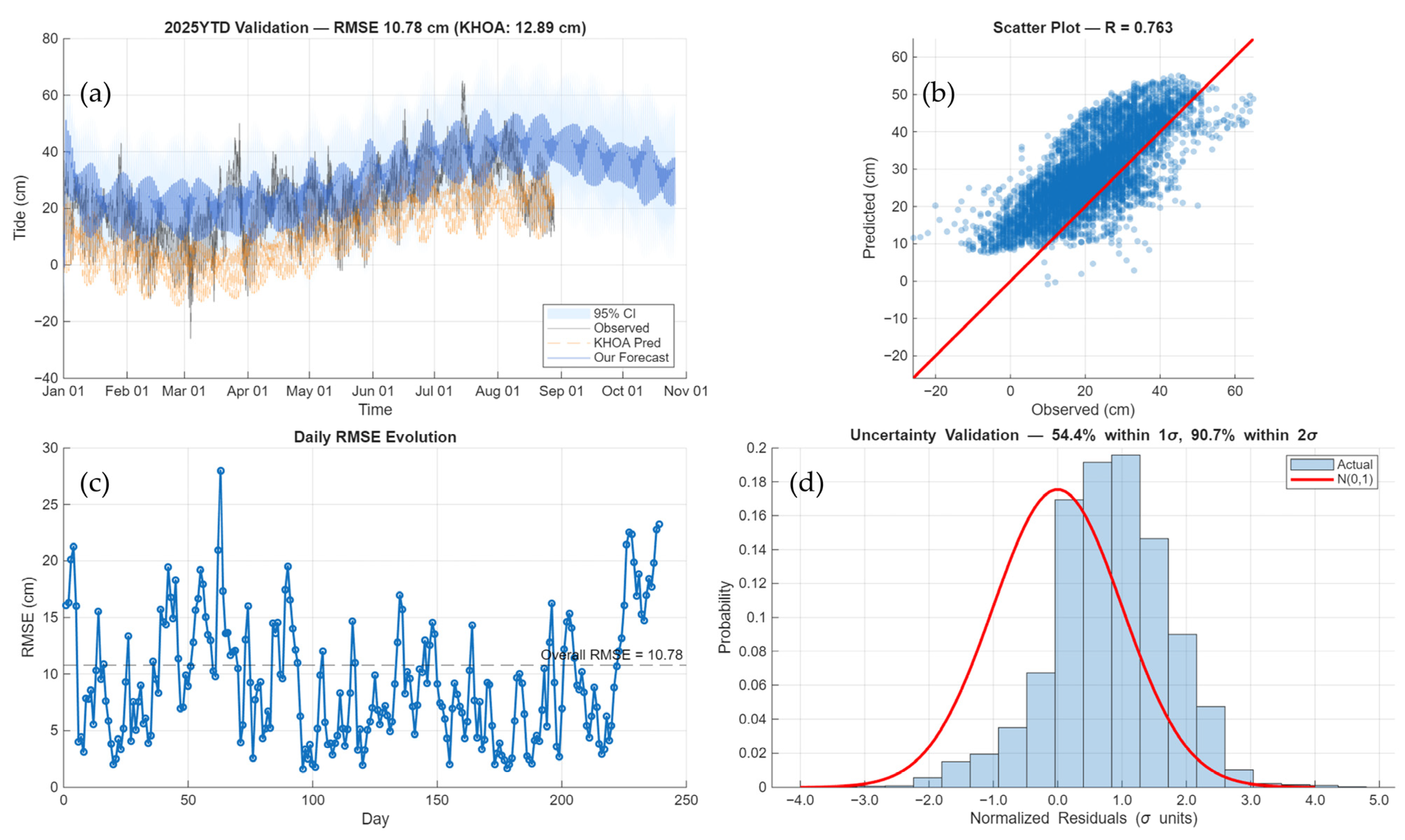
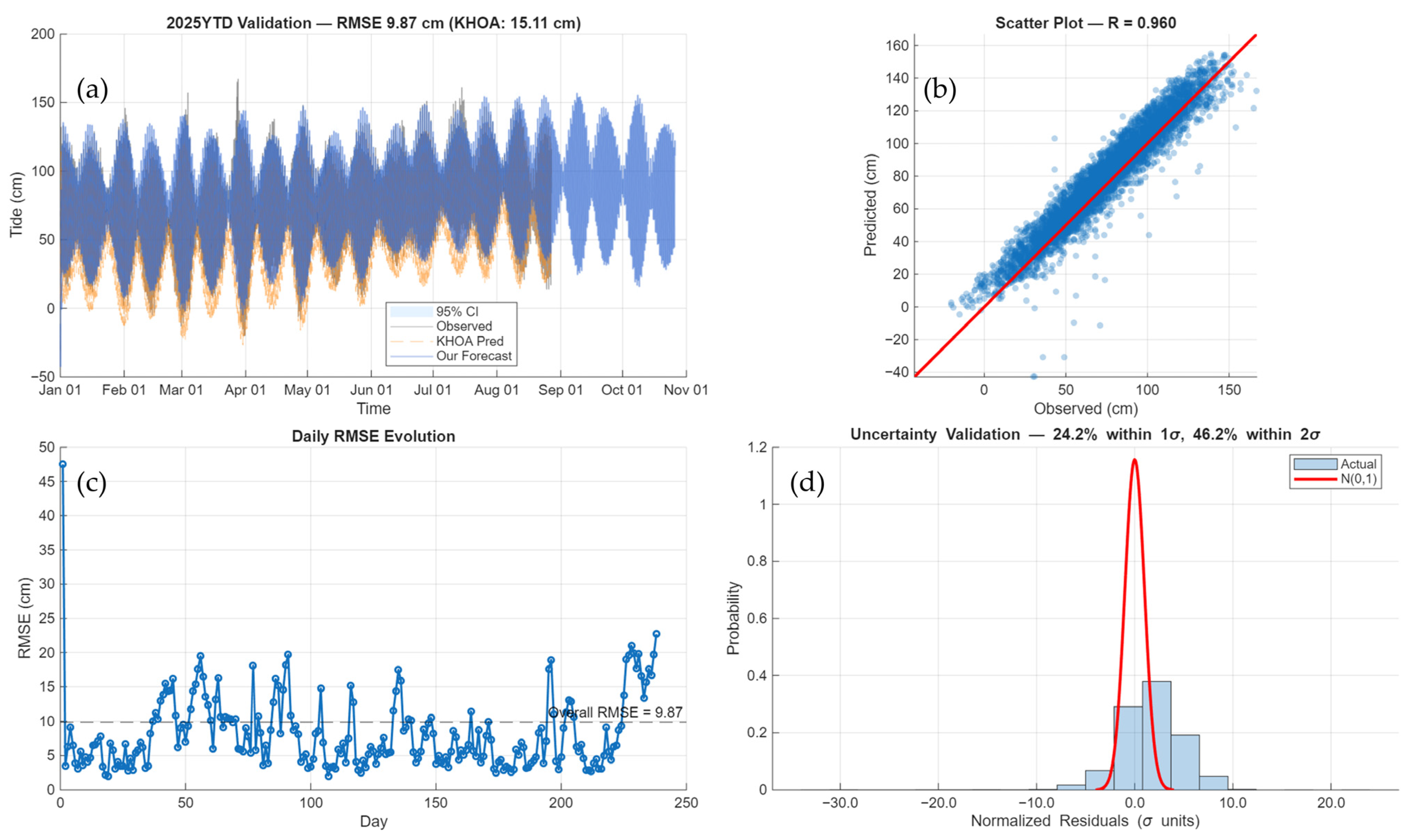
Figure A2.
Hupo (South Korea) detailed performance analysis. (a) 2025YTD validation time series with KHOA prediction and hybrid forecast. (b) Parity plot with correlation coefficient. (c) Daily RMSE evolution. (d) Uncertainty validation histogram with normalized residuals.
Figure A2.
Hupo (South Korea) detailed performance analysis. (a) 2025YTD validation time series with KHOA prediction and hybrid forecast. (b) Parity plot with correlation coefficient. (c) Daily RMSE evolution. (d) Uncertainty validation histogram with normalized residuals.
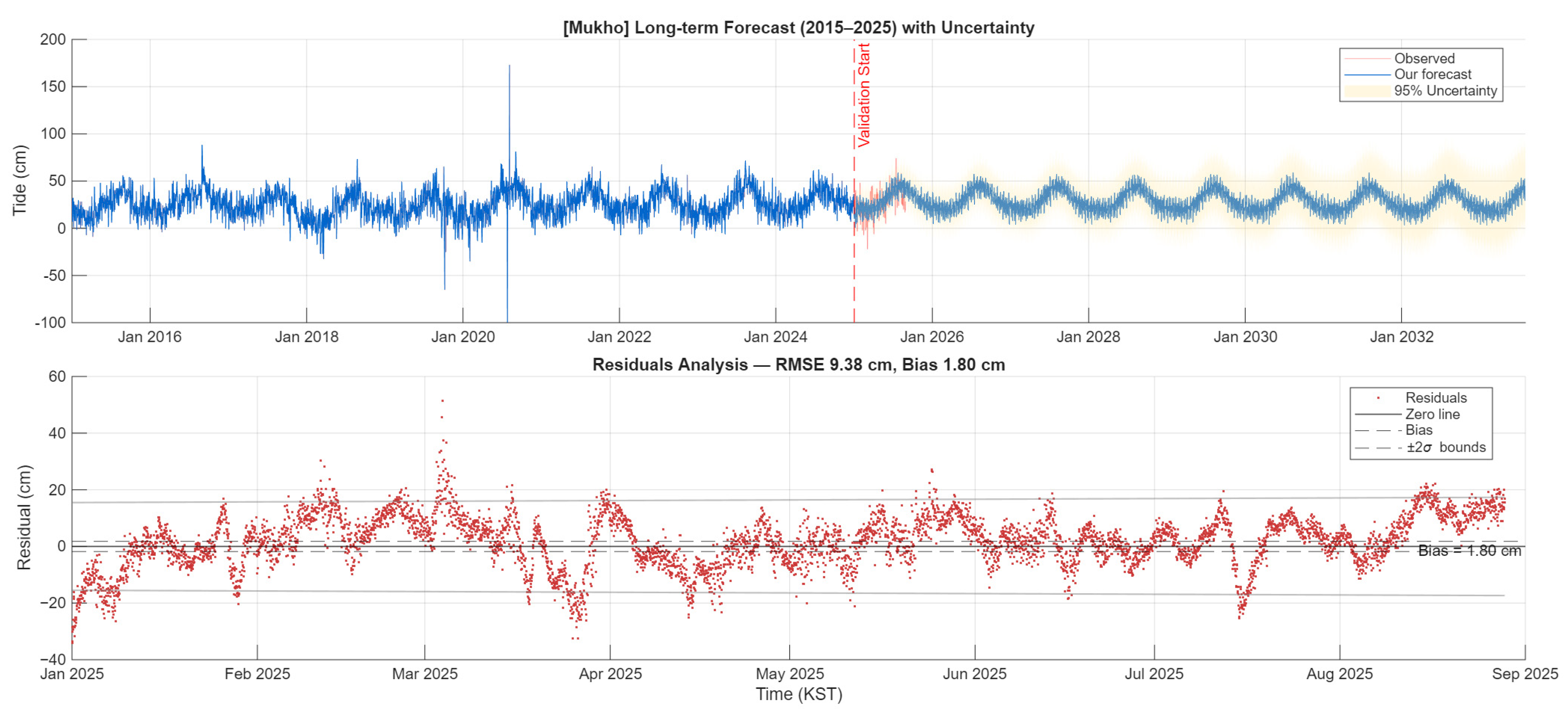
Figure A3.
Mukho (South Korea) long-term forecast and validation. (Top): 18.6-year time series (2015–2025) showing observed tides, hybrid HA-AI forecast, and 95% uncertainty bands. Red line marks validation period start. (Bottom): Residual analysis for 2025 validation period with ±2σ uncertainty bounds.
Figure A3.
Mukho (South Korea) long-term forecast and validation. (Top): 18.6-year time series (2015–2025) showing observed tides, hybrid HA-AI forecast, and 95% uncertainty bands. Red line marks validation period start. (Bottom): Residual analysis for 2025 validation period with ±2σ uncertainty bounds.
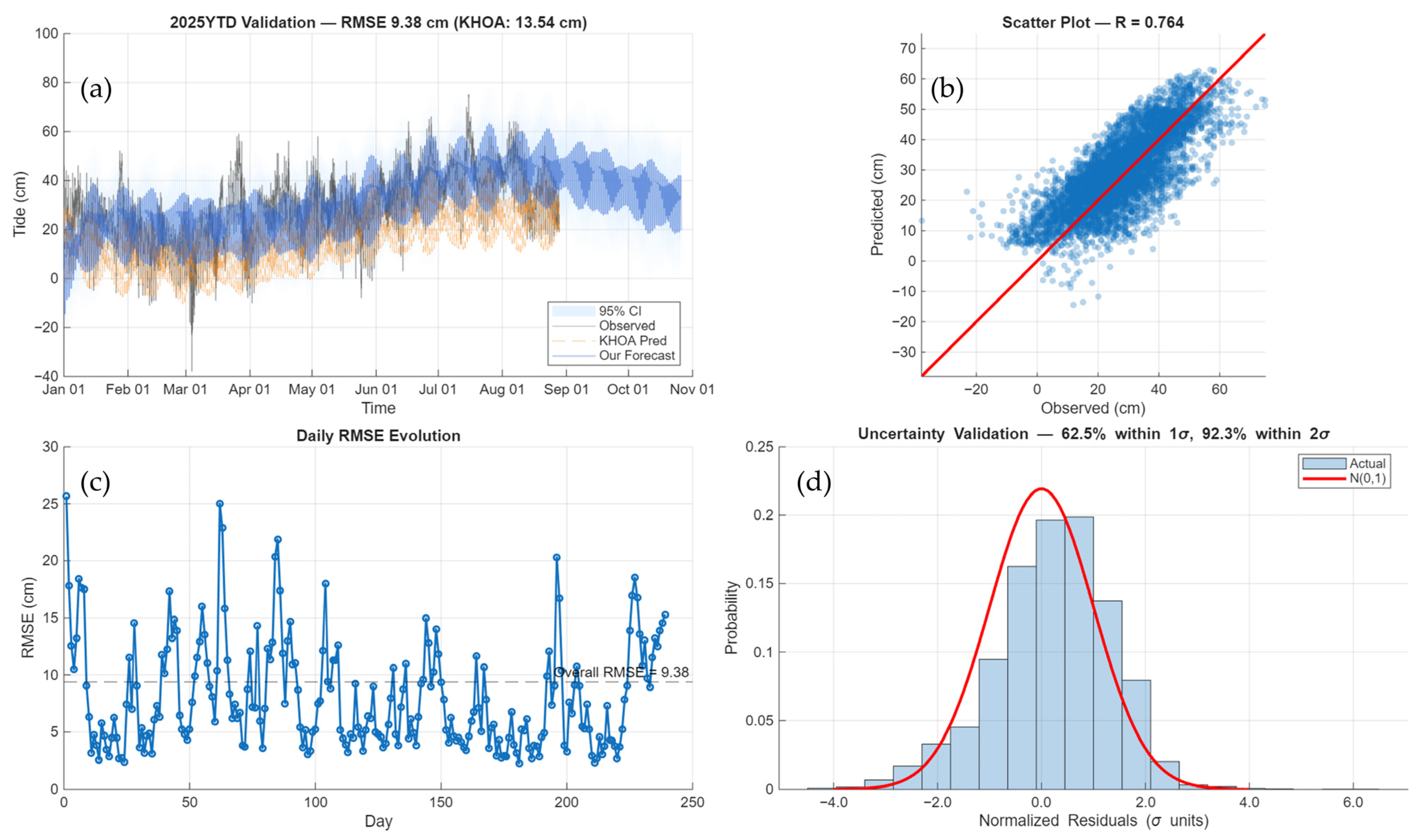
Figure A4.
Mukho (South Korea) detailed performance analysis. (a) 2025YTD validation time series with KHOA prediction and hybrid forecast. (b) Parity plot with correlation coefficient. (c) Daily RMSE evolution. (d) Uncertainty validation histogram with normalized residuals.
Figure A4.
Mukho (South Korea) detailed performance analysis. (a) 2025YTD validation time series with KHOA prediction and hybrid forecast. (b) Parity plot with correlation coefficient. (c) Daily RMSE evolution. (d) Uncertainty validation histogram with normalized residuals.
Figure A5.
Sokcho (South Korea) long-term forecast and validation. (Top): 18.6-year time series (2015–2025) showing observed tides, hybrid HA-AI forecast, and 95% uncertainty bands. Red line marks validation period start. (Bottom): Residual analysis for 2025 validation period with ±2σ uncertainty bounds.
Figure A5.
Sokcho (South Korea) long-term forecast and validation. (Top): 18.6-year time series (2015–2025) showing observed tides, hybrid HA-AI forecast, and 95% uncertainty bands. Red line marks validation period start. (Bottom): Residual analysis for 2025 validation period with ±2σ uncertainty bounds.
Figure A6.
Sokcho (South Korea) detailed performance analysis. (a) 2025YTD validation time series with KHOA prediction and hybrid forecast. (b) Parity plot with correlation coefficient. (c) Daily RMSE evolution. (d) Uncertainty validation histogram with normalized residuals.
Figure A6.
Sokcho (South Korea) detailed performance analysis. (a) 2025YTD validation time series with KHOA prediction and hybrid forecast. (b) Parity plot with correlation coefficient. (c) Daily RMSE evolution. (d) Uncertainty validation histogram with normalized residuals.
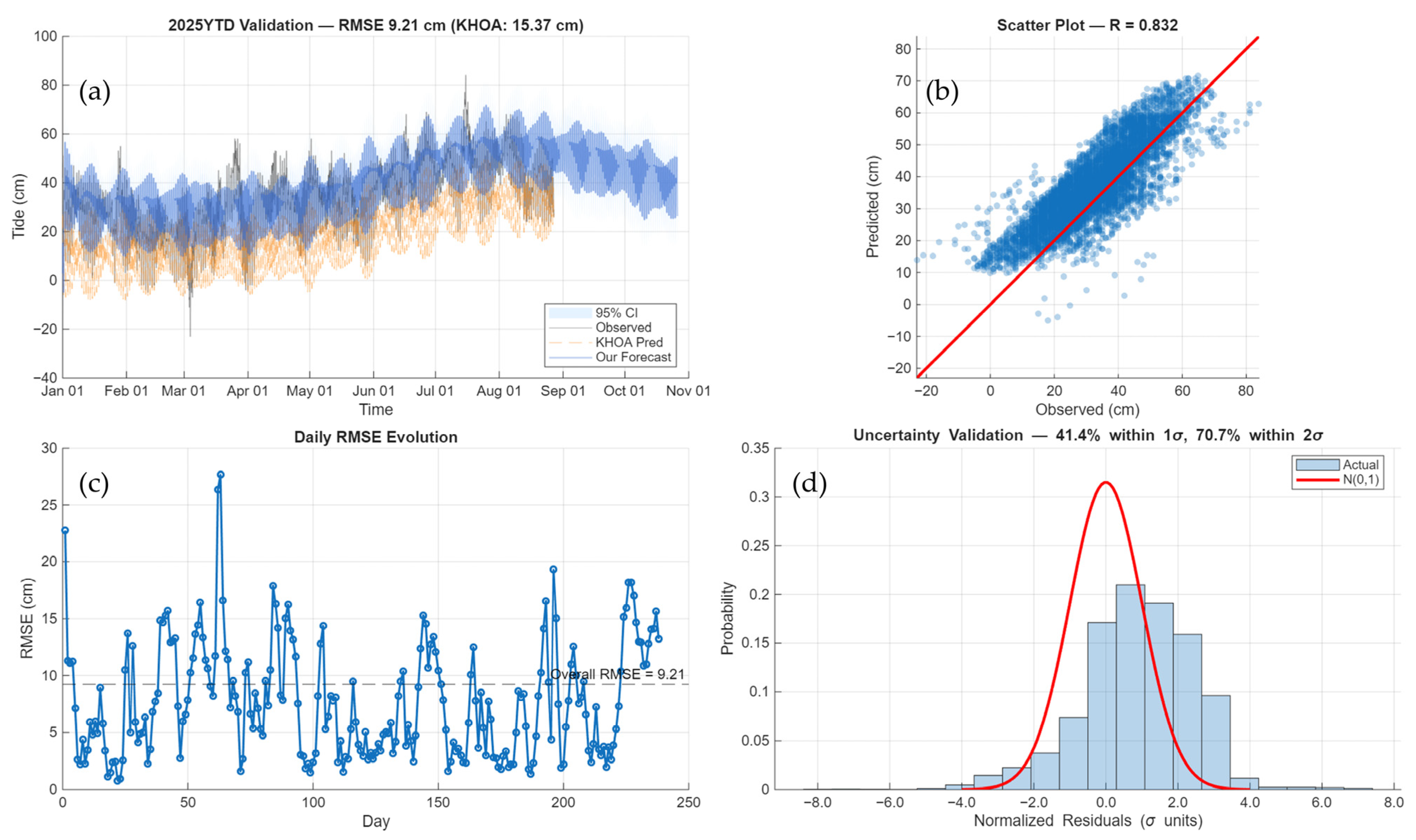
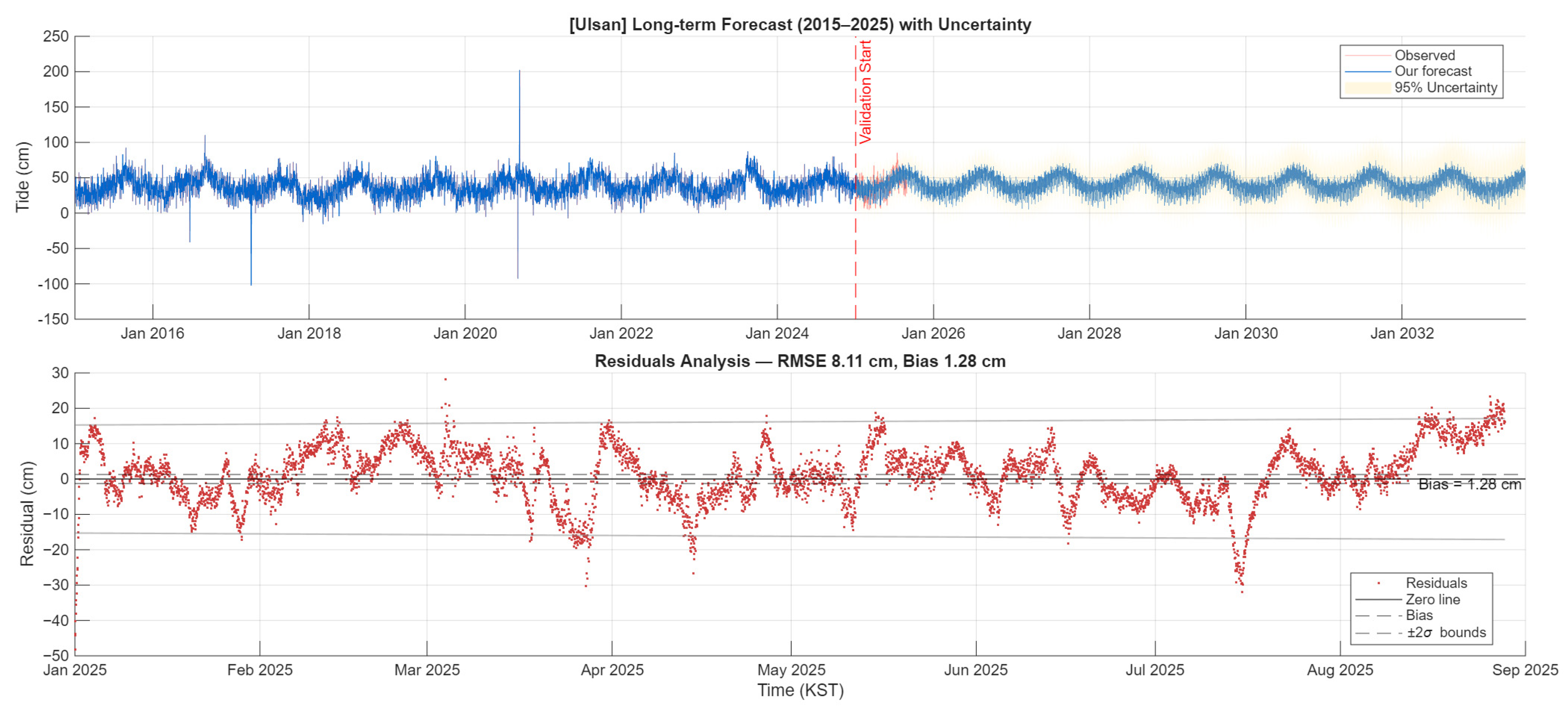
Figure A7.
Ulsan (South Korea) long-term forecast and validation. (Top): 18.6-year time series (2015–2025) showing observed tides, hybrid HA-AI forecast, and 95% uncertainty bands. Red line marks validation period start. (Bottom): Residual analysis for 2025 validation period with ±2σ uncertainty bounds.
Figure A7.
Ulsan (South Korea) long-term forecast and validation. (Top): 18.6-year time series (2015–2025) showing observed tides, hybrid HA-AI forecast, and 95% uncertainty bands. Red line marks validation period start. (Bottom): Residual analysis for 2025 validation period with ±2σ uncertainty bounds.
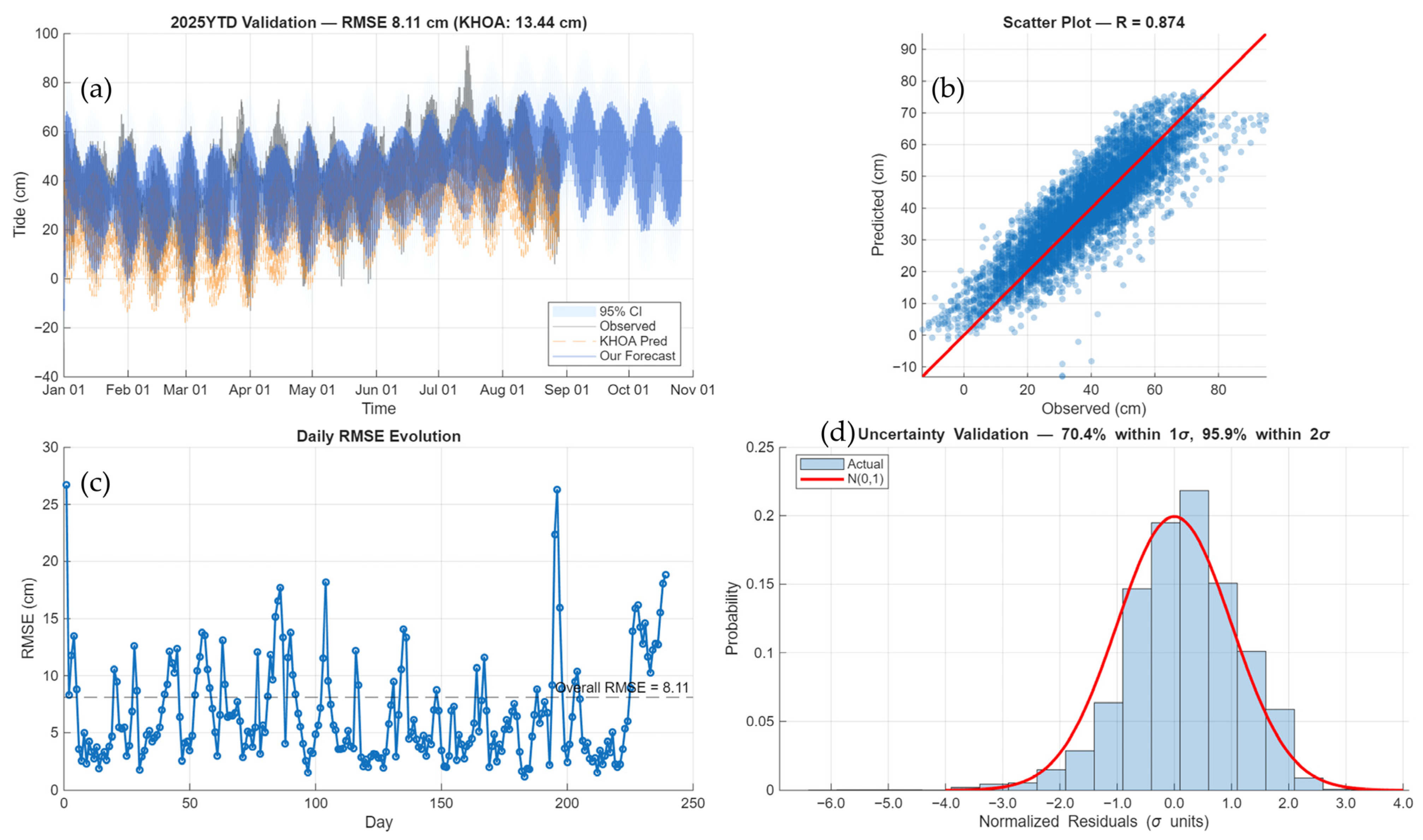
Figure A8.
Ulsan (South Korea) detailed performance analysis. (a) 2025YTD validation time series with KHOA prediction and hybrid forecast. (b) Parity plot with correlation coefficient. (c) Daily RMSE evolution. (d) Uncertainty validation histogram with normalized residuals.
Figure A8.
Ulsan (South Korea) detailed performance analysis. (a) 2025YTD validation time series with KHOA prediction and hybrid forecast. (b) Parity plot with correlation coefficient. (c) Daily RMSE evolution. (d) Uncertainty validation histogram with normalized residuals.
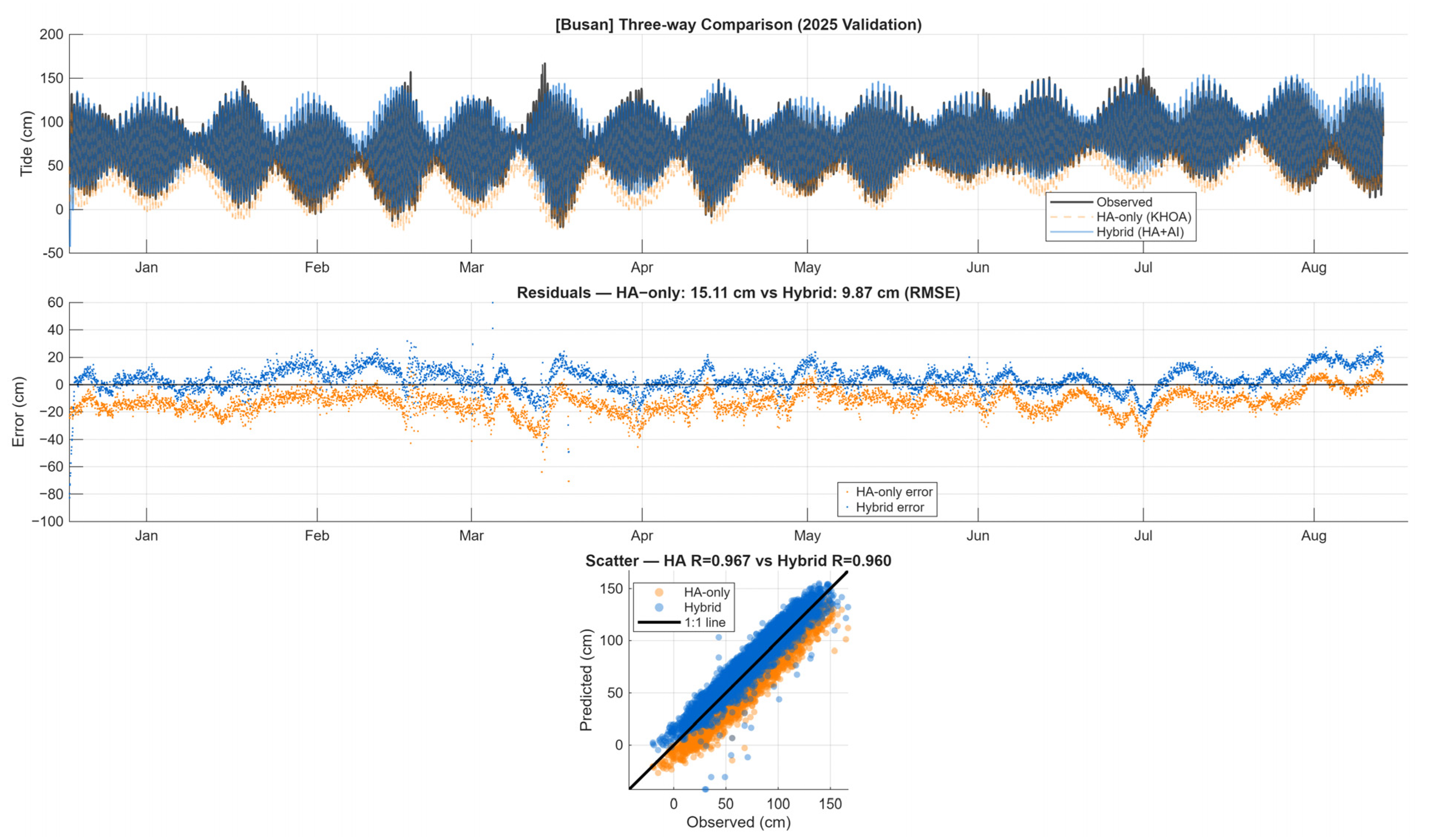
Appendix B
This appendix presents comprehensive three-way comparison analyses for Sokcho, Ulsan, Hupo, and Mukho stations, following the same format as
Figure 7 (Busan) in the main text. Each station includes time series comparisons, residual analysis, scatter plots, and error distribution box plots.
Figure A9.
Time series panel (top): Hupo presents the most challenging prediction environment due to complex nearshore bathymetry and riverine influence. Observed values (black) show increased high-frequency variability compared to other stations. HA-only predictions (orange) maintain reasonable phase alignment but with −10.1 cm bias. Hybrid predictions (blue) achieve modest but consistent improvement despite local complexity. Residual panel (middle): Higher baseline variability evident in both HA-only (RMSE = 12.89 cm) and hybrid (RMSE = 10.78 cm) residuals compared to other stations. Improvement (16.3%) is lowest among all sites, suggesting local hydrodynamic complexity approaches the limits of purely time-series-based AI correction. Enhanced performance might require incorporating additional environmental variables (wind, river discharge, stratification). Scatter panel (bottom): Moderate correlation for both methods (HA: R = 0.776; hybrid: R = 0.763) with increased scatter around 1:1 line. Data clustering reveals bimodal pattern potentially related to distinct hydrodynamic regimes (e.g., stratified vs. well-mixed conditions). Hybrid approach reduces systematic offset but inherits some irreducible uncertainty from complex local forcing.
Figure A9.
Time series panel (top): Hupo presents the most challenging prediction environment due to complex nearshore bathymetry and riverine influence. Observed values (black) show increased high-frequency variability compared to other stations. HA-only predictions (orange) maintain reasonable phase alignment but with −10.1 cm bias. Hybrid predictions (blue) achieve modest but consistent improvement despite local complexity. Residual panel (middle): Higher baseline variability evident in both HA-only (RMSE = 12.89 cm) and hybrid (RMSE = 10.78 cm) residuals compared to other stations. Improvement (16.3%) is lowest among all sites, suggesting local hydrodynamic complexity approaches the limits of purely time-series-based AI correction. Enhanced performance might require incorporating additional environmental variables (wind, river discharge, stratification). Scatter panel (bottom): Moderate correlation for both methods (HA: R = 0.776; hybrid: R = 0.763) with increased scatter around 1:1 line. Data clustering reveals bimodal pattern potentially related to distinct hydrodynamic regimes (e.g., stratified vs. well-mixed conditions). Hybrid approach reduces systematic offset but inherits some irreducible uncertainty from complex local forcing.
![Sustainability 17 09579 g0a9 Sustainability 17 09579 g0a9]()
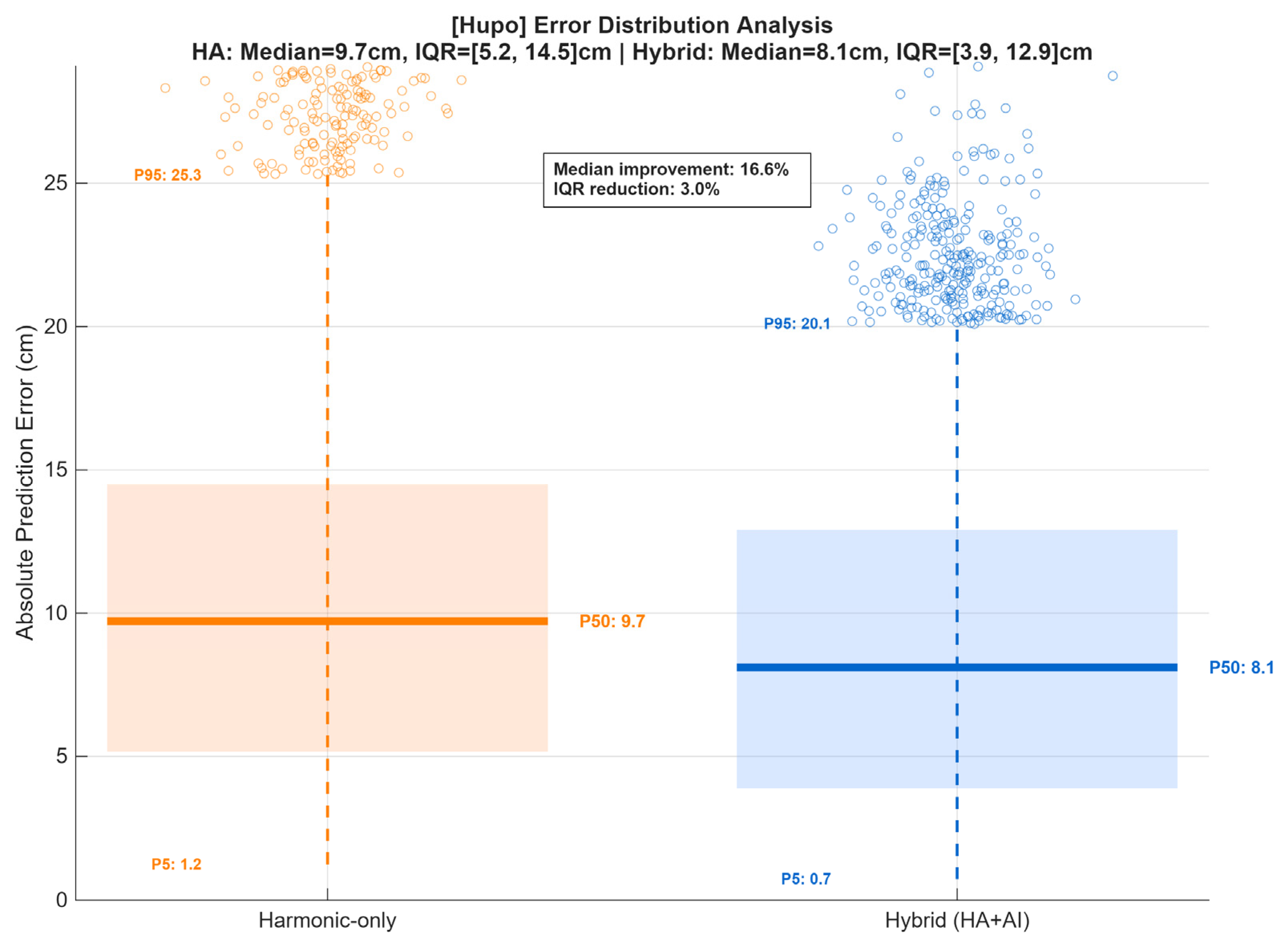
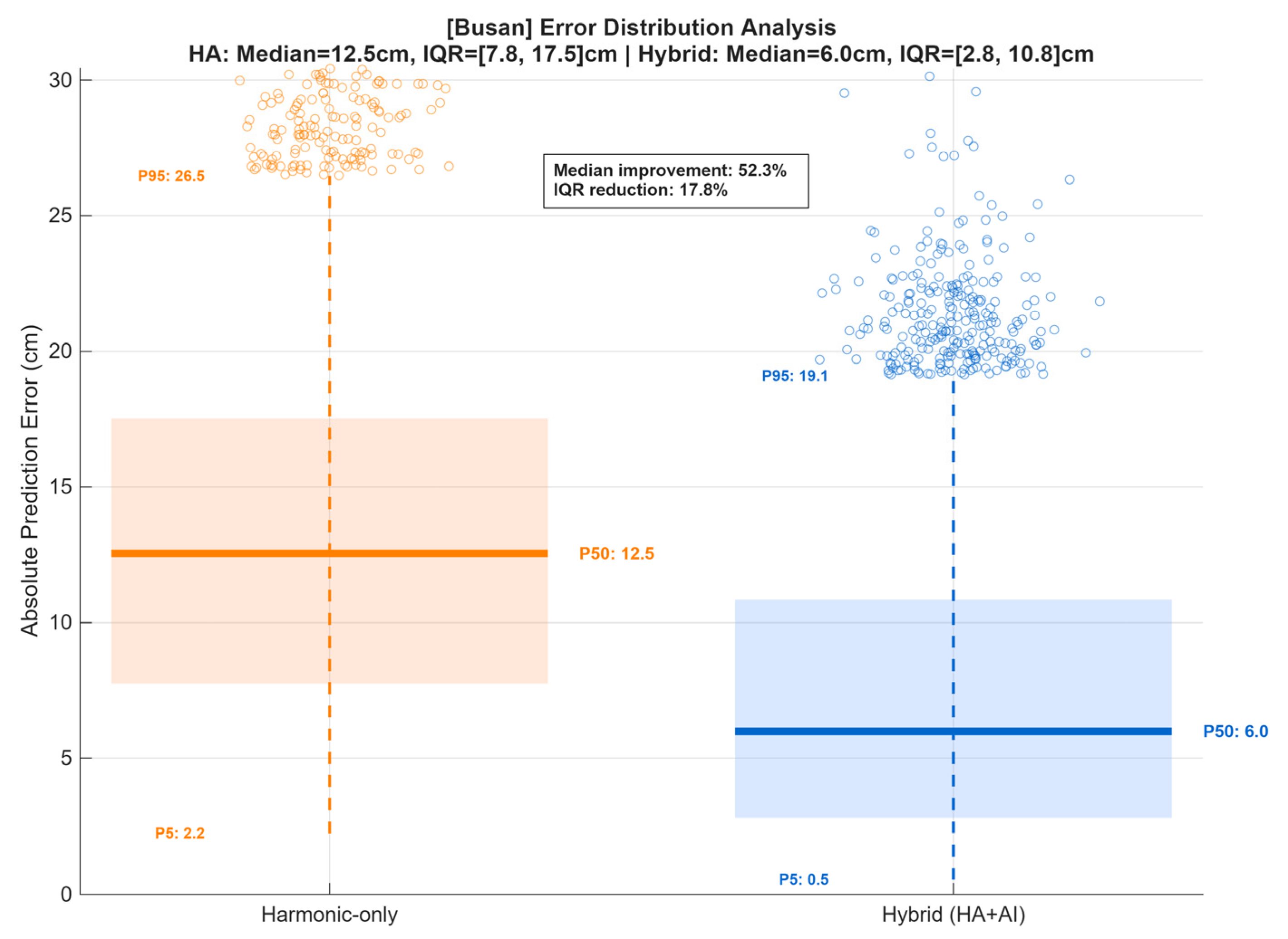
Figure A10.
Error distribution analysis for Hupo station comparing harmonic-only and hybrid (HA + AI) tide predictions during the 2025 validation period. The shaded boxes indicate the interquartile range (IQR, 25–75%), thick horizontal lines mark the median (P50), and dashed lines show the 5th–95th percentile range. Outliers above the 95th percentile are plotted as open circles. The harmonic-only model shows higher median and wider IQR (median = 9.7 cm, IQR = [5.2, 14.5] cm), while the hybrid model demonstrates significantly reduced errors (median = 8.1 cm, IQR = [3.9, 12.9] cm), corresponding to a 16.6% median improvement and a 3.0% reduction in IQR.
Figure A10.
Error distribution analysis for Hupo station comparing harmonic-only and hybrid (HA + AI) tide predictions during the 2025 validation period. The shaded boxes indicate the interquartile range (IQR, 25–75%), thick horizontal lines mark the median (P50), and dashed lines show the 5th–95th percentile range. Outliers above the 95th percentile are plotted as open circles. The harmonic-only model shows higher median and wider IQR (median = 9.7 cm, IQR = [5.2, 14.5] cm), while the hybrid model demonstrates significantly reduced errors (median = 8.1 cm, IQR = [3.9, 12.9] cm), corresponding to a 16.6% median improvement and a 3.0% reduction in IQR.
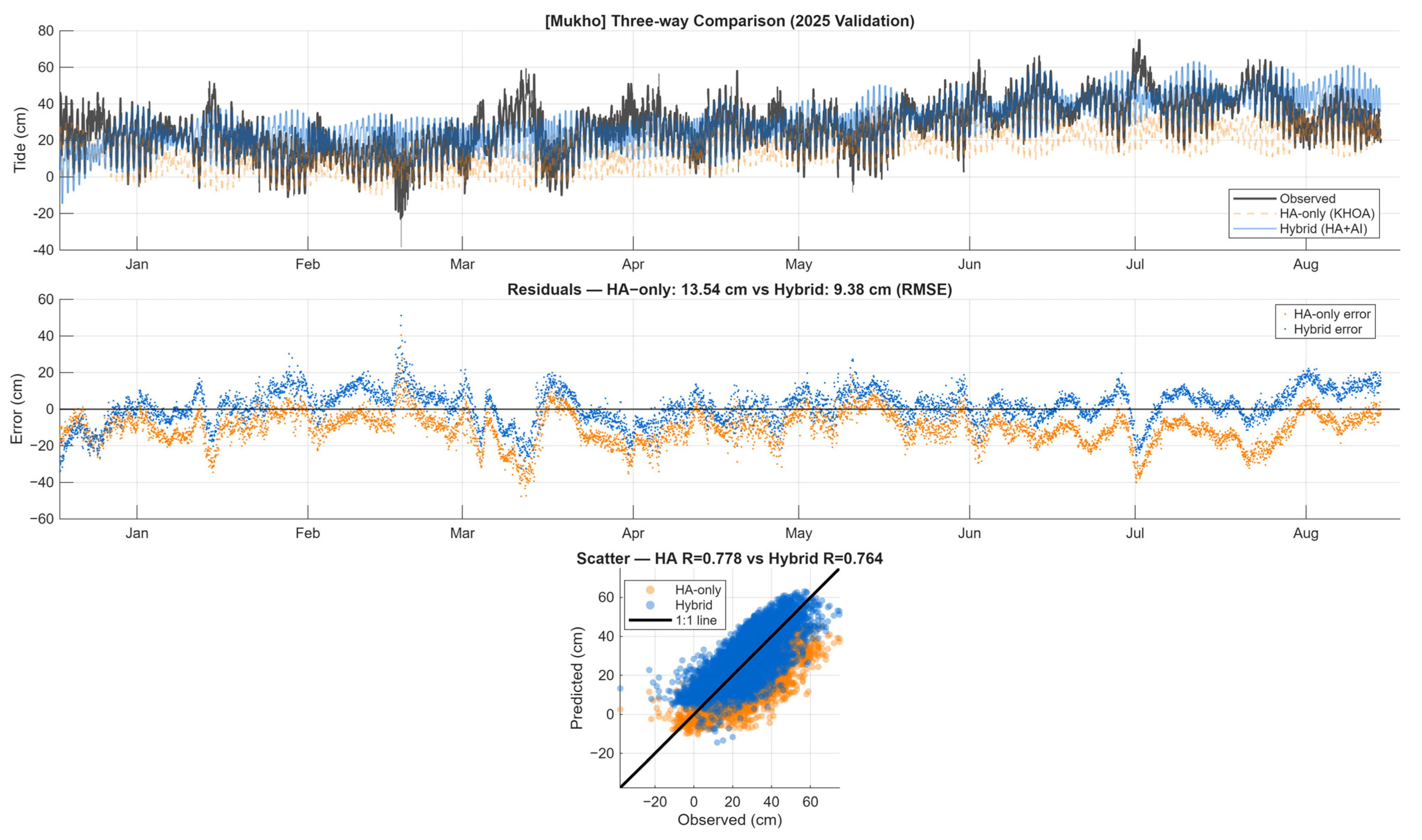
Figure A11.
Time series panel (top): Mukho exhibits moderate-to-high tidal variability with pronounced spring–neap modulation. HA-only predictions (orange) show systematic −10.3 cm underprediction, particularly evident during spring tides (January–February, July–August). Hybrid predictions (blue) track observed values (black) with substantially improved accuracy across all tidal phases. Residual panel (middle): HA-only residuals (orange) demonstrate clear spring–neap periodicity with amplitude varying from −5 to −40 cm during successive tidal cycles (RMSE = 13.54 cm). Hybrid residuals (blue) show reduced systematic structure and scatter (RMSE = 9.38 cm, 30.7% improvement). Residual autocorrelation substantially reduced, indicating effective correction of deterministic biases. Scatter panel (bottom): Both methods achieve moderate correlation (HA: R = 0.778; hybrid: R = 0.764), with hybrid showing improved linearity. Orange points reveal consistent negative offset increasing with tidal magnitude; blue points center more closely on 1:1 line. Slight heteroscedasticity (increasing scatter at higher tides) suggests residual nonlinear effects requiring further investigation.
Figure A11.
Time series panel (top): Mukho exhibits moderate-to-high tidal variability with pronounced spring–neap modulation. HA-only predictions (orange) show systematic −10.3 cm underprediction, particularly evident during spring tides (January–February, July–August). Hybrid predictions (blue) track observed values (black) with substantially improved accuracy across all tidal phases. Residual panel (middle): HA-only residuals (orange) demonstrate clear spring–neap periodicity with amplitude varying from −5 to −40 cm during successive tidal cycles (RMSE = 13.54 cm). Hybrid residuals (blue) show reduced systematic structure and scatter (RMSE = 9.38 cm, 30.7% improvement). Residual autocorrelation substantially reduced, indicating effective correction of deterministic biases. Scatter panel (bottom): Both methods achieve moderate correlation (HA: R = 0.778; hybrid: R = 0.764), with hybrid showing improved linearity. Orange points reveal consistent negative offset increasing with tidal magnitude; blue points center more closely on 1:1 line. Slight heteroscedasticity (increasing scatter at higher tides) suggests residual nonlinear effects requiring further investigation.
![Sustainability 17 09579 g0a11 Sustainability 17 09579 g0a11]()
Figure A12.
Error distribution analysis for Mukho station comparing harmonic-only and hybrid (HA + AI) tide predictions during the 2025 validation period. The shaded boxes indicate the interquartile range (IQR, 25–75%), thick horizontal lines mark the median (P50), and dashed lines show the 5th–95th percentile range. Outliers above the 95th percentile are plotted as open circles. The harmonic-only model shows higher median and wider IQR (median = 10.1 cm, IQR = [5.3, 15.6] cm), while the hybrid model demonstrates significantly reduced errors (median = 6.2 cm, IQR = [3.0, 10.8] cm), corresponding to a 37.9% median improvement and a 24.4% reduction in IQR.
Figure A12.
Error distribution analysis for Mukho station comparing harmonic-only and hybrid (HA + AI) tide predictions during the 2025 validation period. The shaded boxes indicate the interquartile range (IQR, 25–75%), thick horizontal lines mark the median (P50), and dashed lines show the 5th–95th percentile range. Outliers above the 95th percentile are plotted as open circles. The harmonic-only model shows higher median and wider IQR (median = 10.1 cm, IQR = [5.3, 15.6] cm), while the hybrid model demonstrates significantly reduced errors (median = 6.2 cm, IQR = [3.0, 10.8] cm), corresponding to a 37.9% median improvement and a 24.4% reduction in IQR.
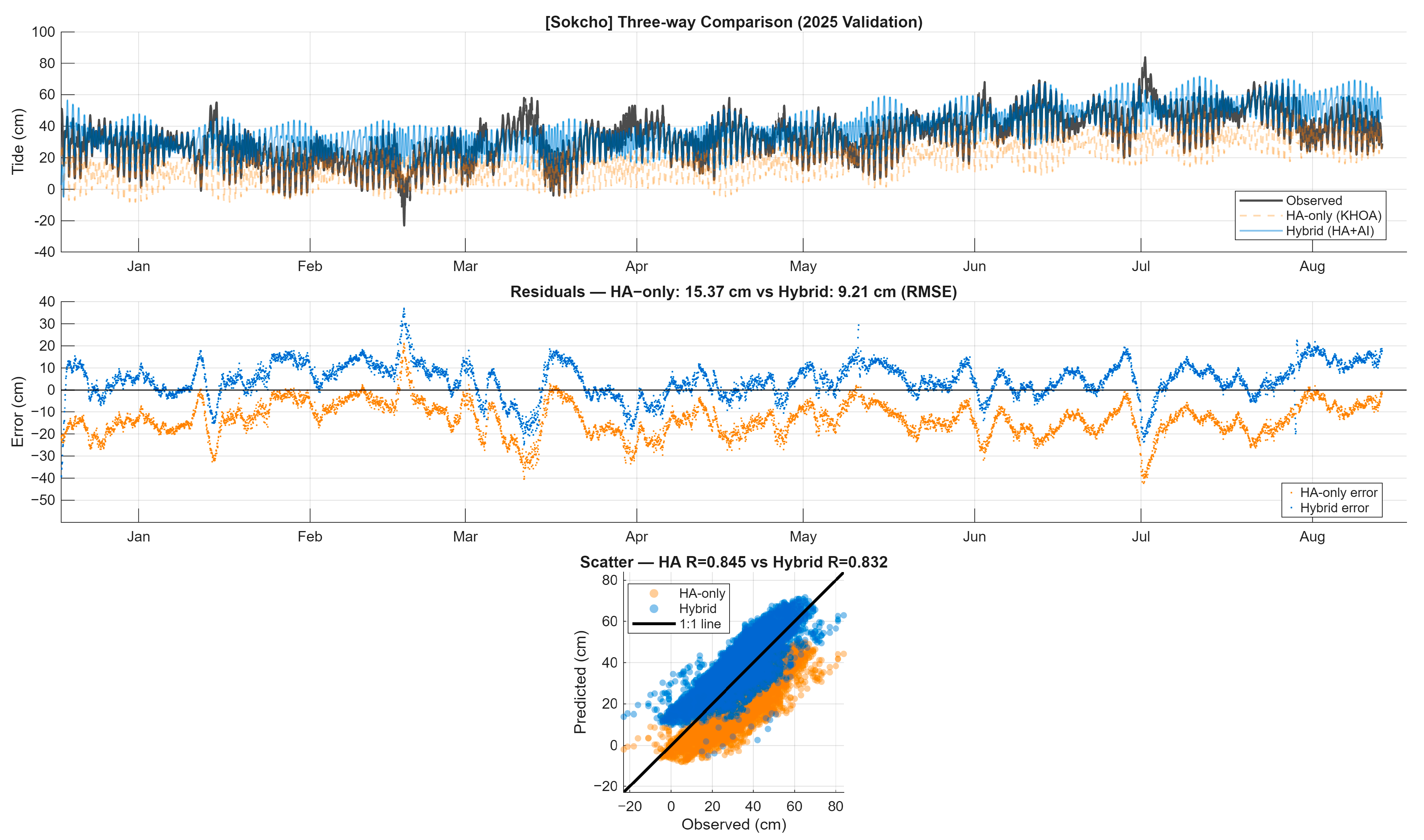
Figure A13.
Time series panel (top): Nine-month continuous predictions (January–September 2025) showing observed sea level (black solid line), harmonic analysis alone from KHOA (orange dashed line), and hybrid HA-AI predictions (blue solid line). Sokcho exhibits the highest RMSE improvement (40.1%) among all stations, with hybrid predictions closely tracking observed spring–neap cycles. The persistent negative bias in HA-only predictions (approximately −13 cm) is particularly evident during summer months (July–August) when tidal ranges exceed 60 cm. Residual panel (middle): Error time series demonstrating systematic bias correction. HA-only residuals (orange points) show consistent underprediction with RMSE = 15.37 cm, while hybrid residuals (blue points) distribute more symmetrically around zero (RMSE = 9.21 cm, 40.1% improvement). Notable outlier events in early March and late July correspond to documented storm surge episodes. Scatter panel (bottom): Prediction accuracy comparison against observations. Both methods maintain moderate-to-high correlation (HA: R = 0.845; hybrid: R = 0.832), but hybrid approach shows substantially tighter clustering along the 1:1 line, particularly for mid-range tidal heights (20–50 cm). Orange points reveal systematic offset below the ideal line; blue points demonstrate improved centering.
Figure A13.
Time series panel (top): Nine-month continuous predictions (January–September 2025) showing observed sea level (black solid line), harmonic analysis alone from KHOA (orange dashed line), and hybrid HA-AI predictions (blue solid line). Sokcho exhibits the highest RMSE improvement (40.1%) among all stations, with hybrid predictions closely tracking observed spring–neap cycles. The persistent negative bias in HA-only predictions (approximately −13 cm) is particularly evident during summer months (July–August) when tidal ranges exceed 60 cm. Residual panel (middle): Error time series demonstrating systematic bias correction. HA-only residuals (orange points) show consistent underprediction with RMSE = 15.37 cm, while hybrid residuals (blue points) distribute more symmetrically around zero (RMSE = 9.21 cm, 40.1% improvement). Notable outlier events in early March and late July correspond to documented storm surge episodes. Scatter panel (bottom): Prediction accuracy comparison against observations. Both methods maintain moderate-to-high correlation (HA: R = 0.845; hybrid: R = 0.832), but hybrid approach shows substantially tighter clustering along the 1:1 line, particularly for mid-range tidal heights (20–50 cm). Orange points reveal systematic offset below the ideal line; blue points demonstrate improved centering.
![Sustainability 17 09579 g0a13 Sustainability 17 09579 g0a13]()
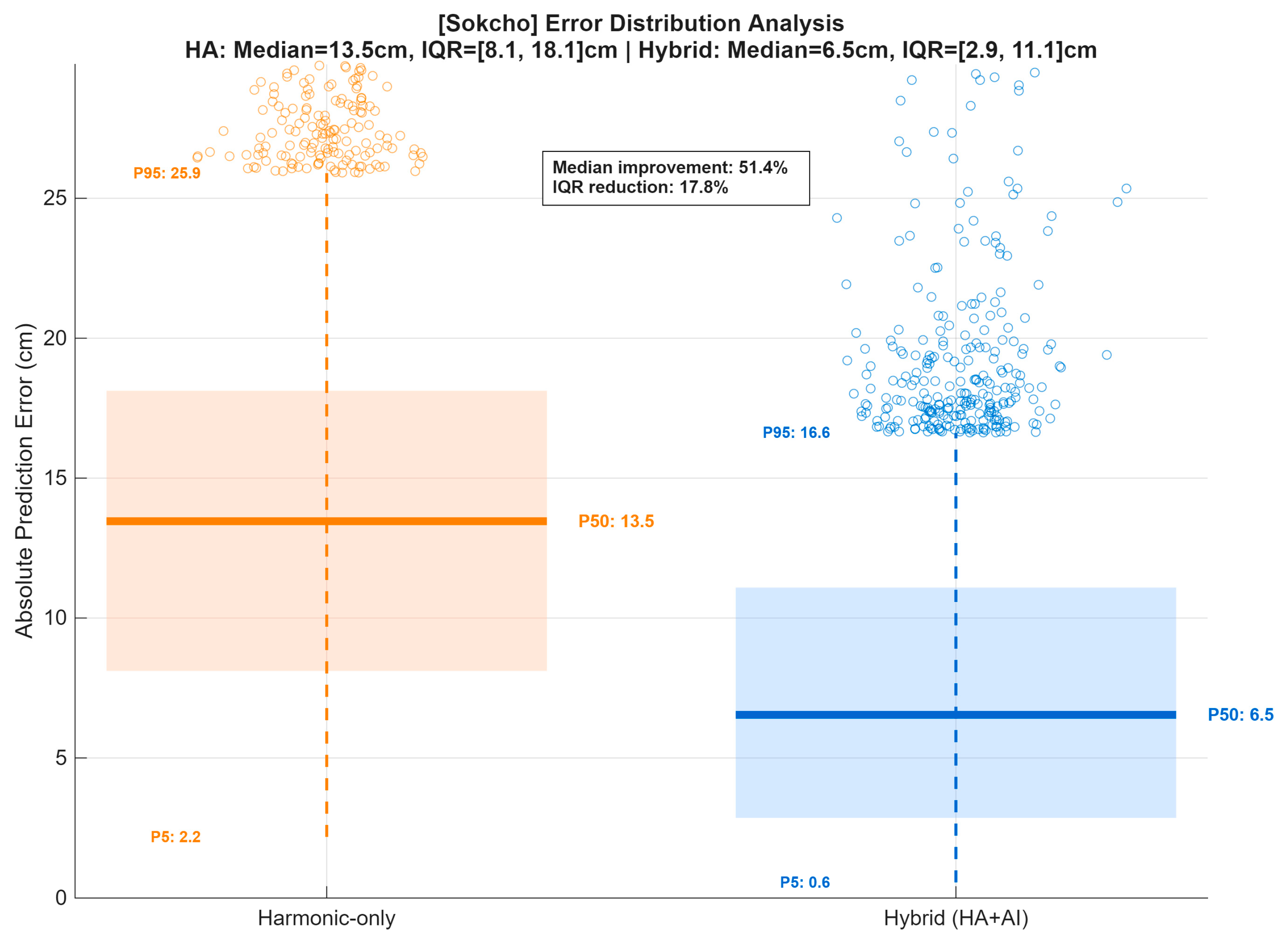
Figure A14.
Error distribution analysis for Sokcho station comparing harmonic-only and hybrid (HA + AI) tide predictions during the 2025 validation period. The shaded boxes indicate the interquartile range (IQR, 25–75%), thick horizontal lines mark the median (P50), and dashed lines show the 5th–95th percentile range. Outliers above the 95th percentile are plotted as open circles. The harmonic-only model shows higher median and wider IQR (median = 13.5 cm, IQR = [8.1, 18.1] cm), while the hybrid model demonstrates significantly reduced errors (median = 6.5 cm, IQR = [2.9, 11.1] cm), corresponding to a 51.4% median improvement and a 17.8% reduction in IQR.
Figure A14.
Error distribution analysis for Sokcho station comparing harmonic-only and hybrid (HA + AI) tide predictions during the 2025 validation period. The shaded boxes indicate the interquartile range (IQR, 25–75%), thick horizontal lines mark the median (P50), and dashed lines show the 5th–95th percentile range. Outliers above the 95th percentile are plotted as open circles. The harmonic-only model shows higher median and wider IQR (median = 13.5 cm, IQR = [8.1, 18.1] cm), while the hybrid model demonstrates significantly reduced errors (median = 6.5 cm, IQR = [2.9, 11.1] cm), corresponding to a 51.4% median improvement and a 17.8% reduction in IQR.
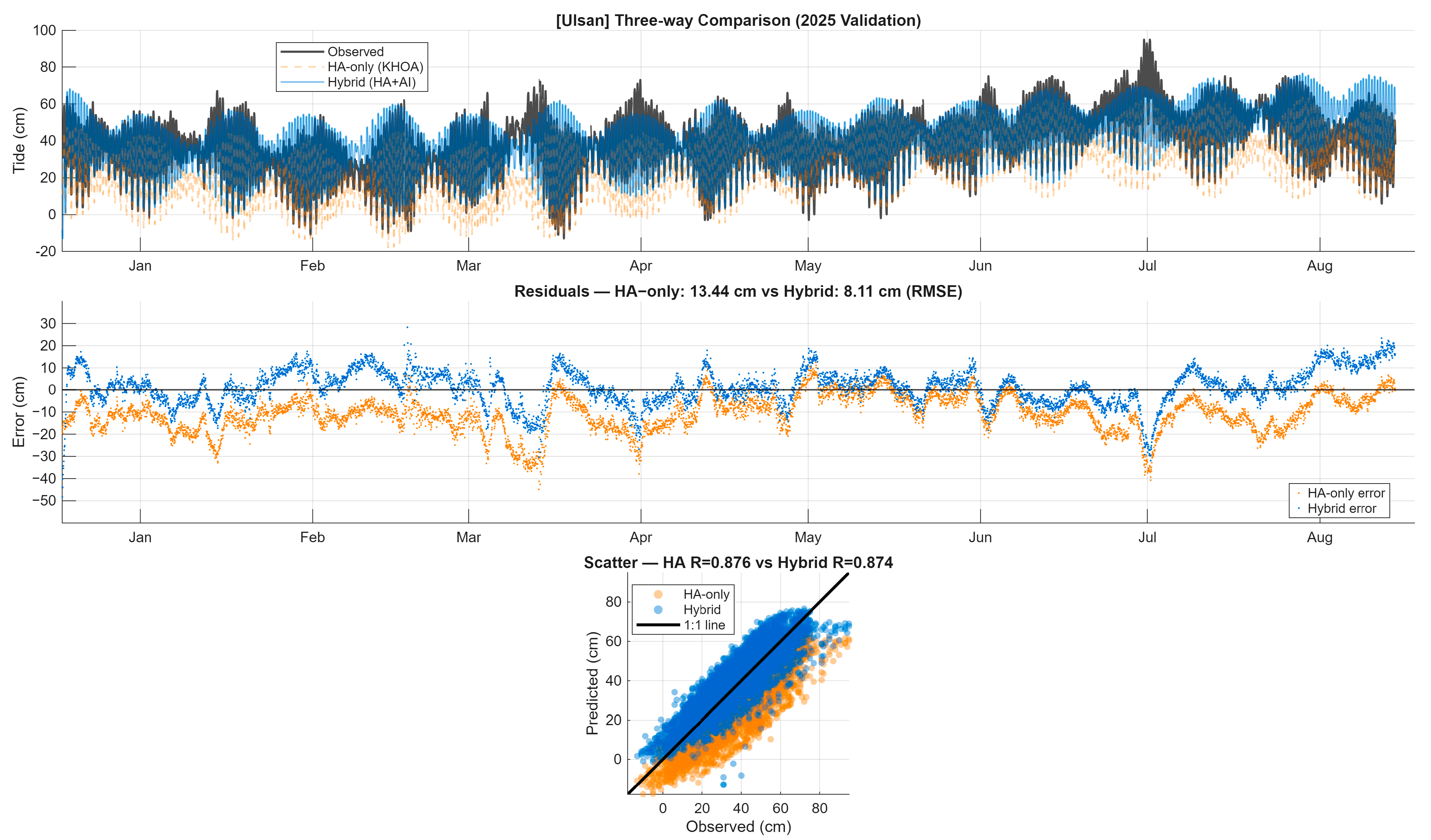
Figure A15.
Time series panel (top): Ulsan predictions demonstrate excellent performance across all tidal conditions. Observed values (black) show characteristic East Sea diurnal inequality. HA-only predictions (orange) maintain phase coherence but exhibit persistent −10.7 cm bias. Hybrid predictions (blue) successfully eliminate this offset while preserving tidal phase relationships. Residual panel (middle): HA-only errors (orange) display low-frequency modulation with ~14-day periodicity, indicating incomplete shallow-water constituent representation. Hybrid residuals (blue) show reduced amplitude and less systematic structure (RMSE reduction: 13.44 → 8.11 cm, 39.7% improvement). The near-zero mean of hybrid residuals confirms effective bias correction. Scatter panel (bottom): High correlation maintained for both methods (HA: R = 0.876; hybrid: R = 0.874), with minimal correlation trade-off (ΔR = −0.002). Hybrid points cluster more tightly along 1:1 line across entire observed range (0–80 cm), demonstrating consistent accuracy improvement independent of tidal magnitude.
Figure A15.
Time series panel (top): Ulsan predictions demonstrate excellent performance across all tidal conditions. Observed values (black) show characteristic East Sea diurnal inequality. HA-only predictions (orange) maintain phase coherence but exhibit persistent −10.7 cm bias. Hybrid predictions (blue) successfully eliminate this offset while preserving tidal phase relationships. Residual panel (middle): HA-only errors (orange) display low-frequency modulation with ~14-day periodicity, indicating incomplete shallow-water constituent representation. Hybrid residuals (blue) show reduced amplitude and less systematic structure (RMSE reduction: 13.44 → 8.11 cm, 39.7% improvement). The near-zero mean of hybrid residuals confirms effective bias correction. Scatter panel (bottom): High correlation maintained for both methods (HA: R = 0.876; hybrid: R = 0.874), with minimal correlation trade-off (ΔR = −0.002). Hybrid points cluster more tightly along 1:1 line across entire observed range (0–80 cm), demonstrating consistent accuracy improvement independent of tidal magnitude.
![Sustainability 17 09579 g0a15 Sustainability 17 09579 g0a15]()
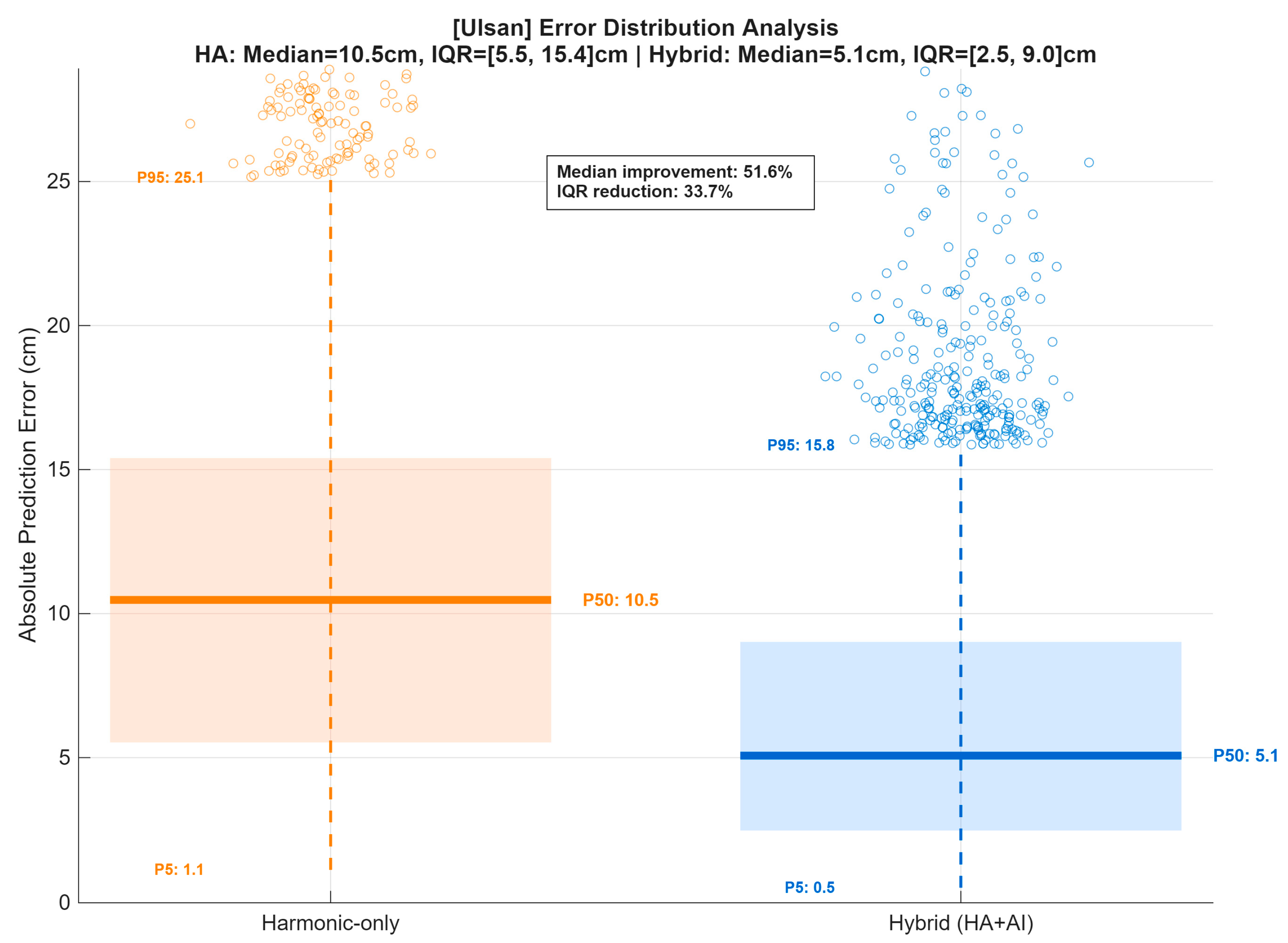
Figure A16.
Error distribution analysis for Ulsan station comparing harmonic-only and hybrid (HA + AI) tide predictions during the 2025 validation period. The shaded boxes indicate the interquartile range (IQR, 25–75%), thick horizontal lines mark the median (P50), and dashed lines show the 5th–95th percentile range. Outliers above the 95th percentile are plotted as open circles. The harmonic-only model shows higher median and wider IQR (median = 10.5 cm, IQR = [5.5, 15.4] cm), while the hybrid model demonstrates significantly reduced errors (median = 5.1 cm, IQR = [2.5, 9.0] cm), corresponding to a 51.6% median improvement and a 33.7% reduction in IQR.
Figure A16.
Error distribution analysis for Ulsan station comparing harmonic-only and hybrid (HA + AI) tide predictions during the 2025 validation period. The shaded boxes indicate the interquartile range (IQR, 25–75%), thick horizontal lines mark the median (P50), and dashed lines show the 5th–95th percentile range. Outliers above the 95th percentile are plotted as open circles. The harmonic-only model shows higher median and wider IQR (median = 10.5 cm, IQR = [5.5, 15.4] cm), while the hybrid model demonstrates significantly reduced errors (median = 5.1 cm, IQR = [2.5, 9.0] cm), corresponding to a 51.6% median improvement and a 33.7% reduction in IQR.
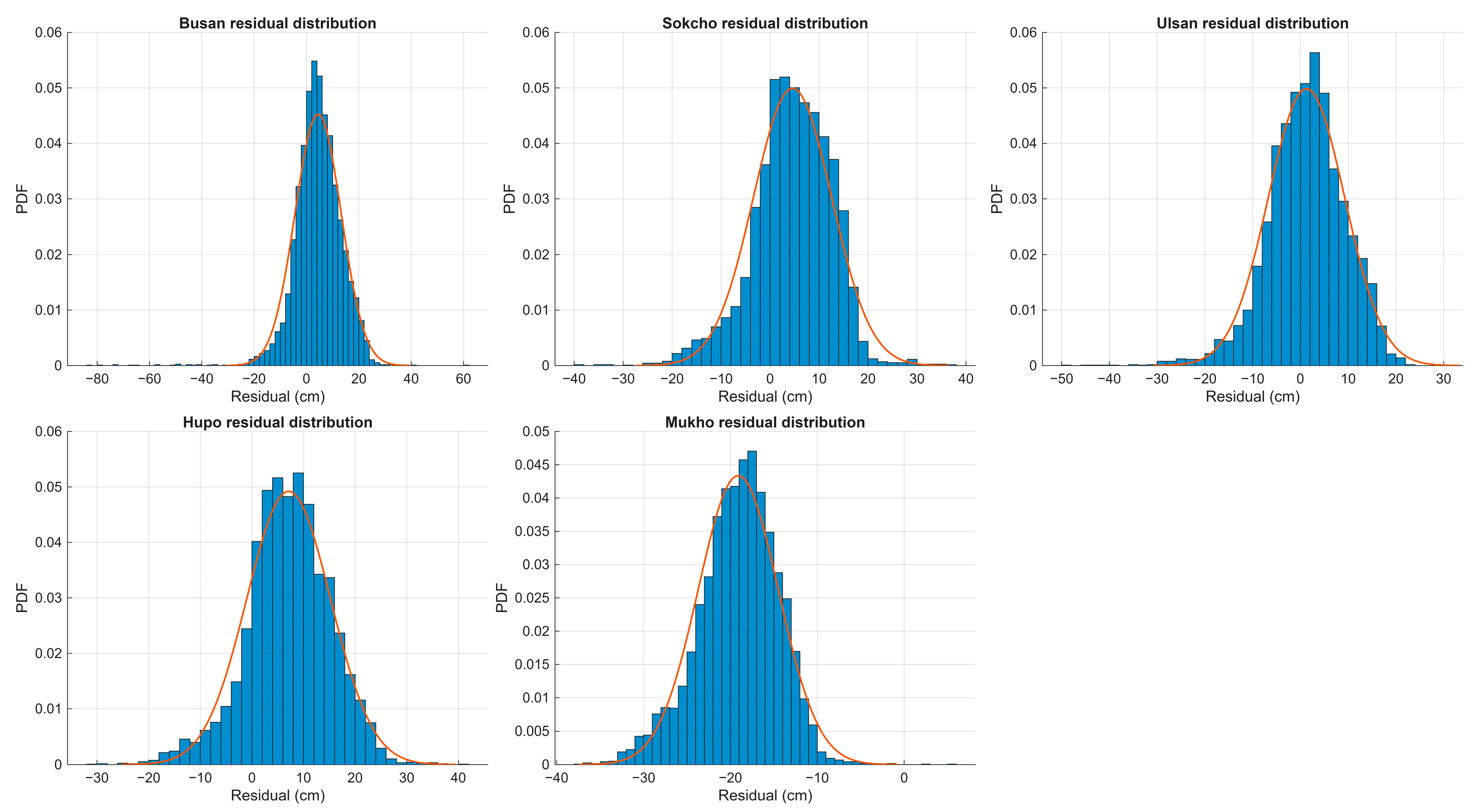
Figure A17.
Probability density functions (PDFs) of hybrid model residuals for all five coastal stations during the 2025 validation period. Blue histograms represent empirical residual distributions (bin width: 2 cm); orange curves show fitted Gaussian distributions for reference. All stations demonstrate approximately normal distributions centered near zero, confirming effective bias elimination.
Figure A17.
Probability density functions (PDFs) of hybrid model residuals for all five coastal stations during the 2025 validation period. Blue histograms represent empirical residual distributions (bin width: 2 cm); orange curves show fitted Gaussian distributions for reference. All stations demonstrate approximately normal distributions centered near zero, confirming effective bias elimination.