Figure 1.
Top-15 protected tree species (count). Extremely right-skewed; Japanese Zelkova (S01) dominates the inventory, followed by Chinese hackberry (S02). Species mix implies heterogeneous risk response even under similar climate exposure.
Figure 1.
Top-15 protected tree species (count). Extremely right-skewed; Japanese Zelkova (S01) dominates the inventory, followed by Chinese hackberry (S02). Species mix implies heterogeneous risk response even under similar climate exposure.
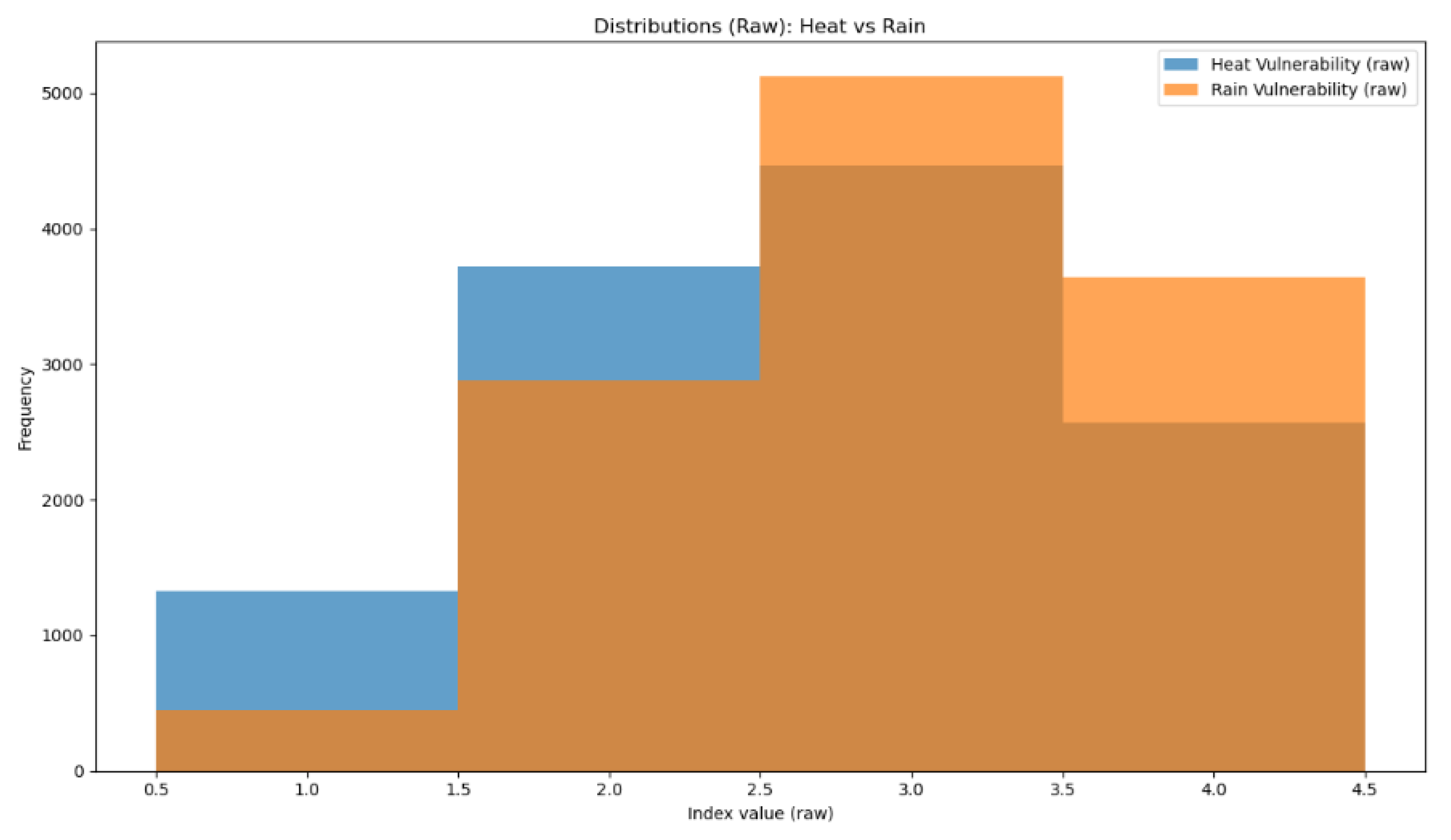
Figure 2.
Distributions before min-max normalization (raw indices). The darker brown areas are simply the overlap of the two histograms (alpha = 0.7), not a separate series requiring its own legend. This overlap visually indicates bins where Heat (blue) and Rain (orange) have simultaneously high frequencies.
Figure 2.
Distributions before min-max normalization (raw indices). The darker brown areas are simply the overlap of the two histograms (alpha = 0.7), not a separate series requiring its own legend. This overlap visually indicates bins where Heat (blue) and Rain (orange) have simultaneously high frequencies.
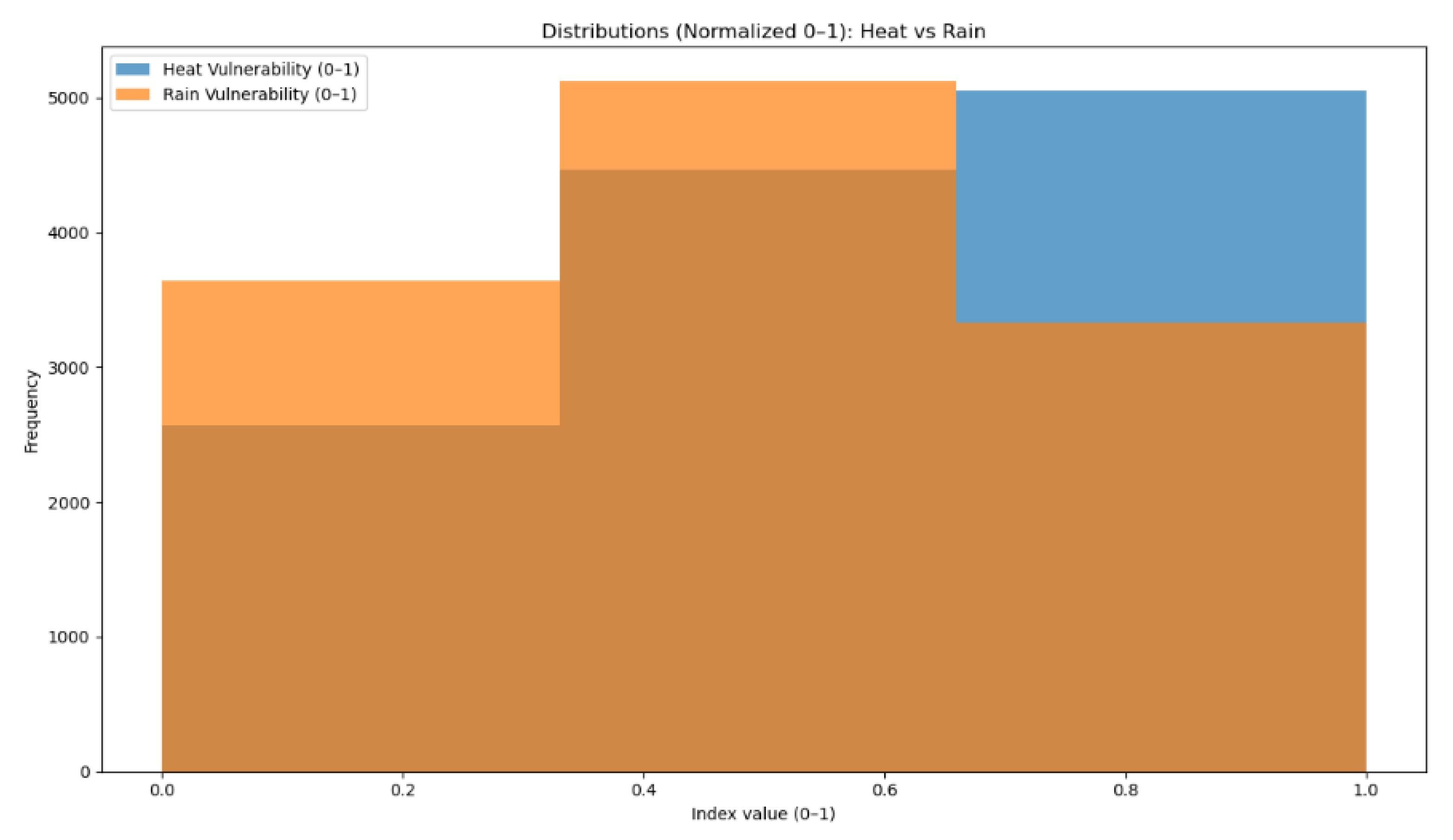
Figure 3.
Distributions after min–max normalization to [0, 1]. Min–max normalization preserves ranks while aligning scales.
Figure 3.
Distributions after min–max normalization to [0, 1]. Min–max normalization preserves ranks while aligning scales.
Figure 4.
ECDF (Empirical Cumulative Distribution Function) overlays. These plots allow a visual check of how the positions of tail segments (e.g., the top 10%) in the original data correspond to those in the normalized [0, 1] scale.
Figure 4.
ECDF (Empirical Cumulative Distribution Function) overlays. These plots allow a visual check of how the positions of tail segments (e.g., the top 10%) in the original data correspond to those in the normalized [0, 1] scale.
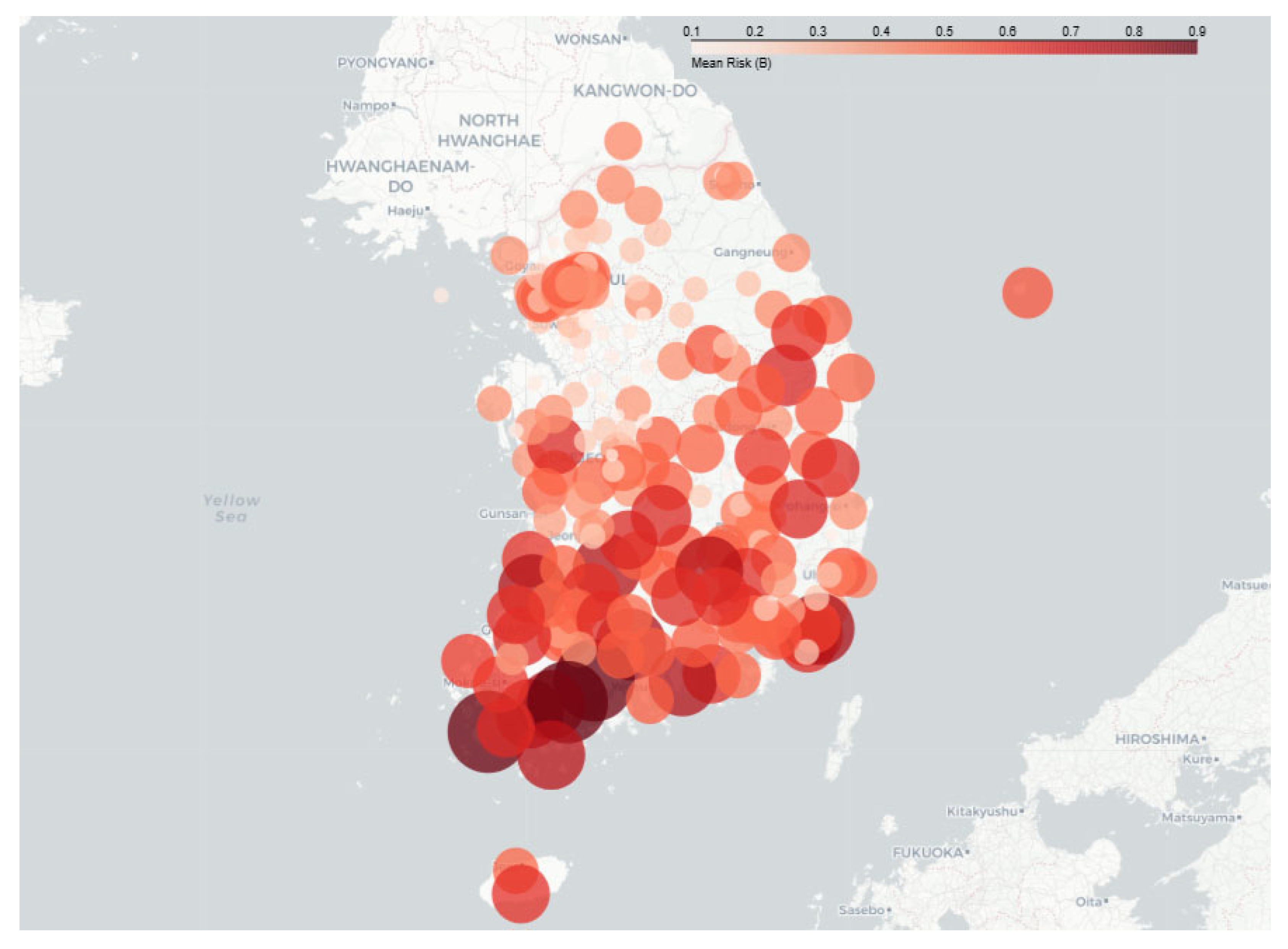
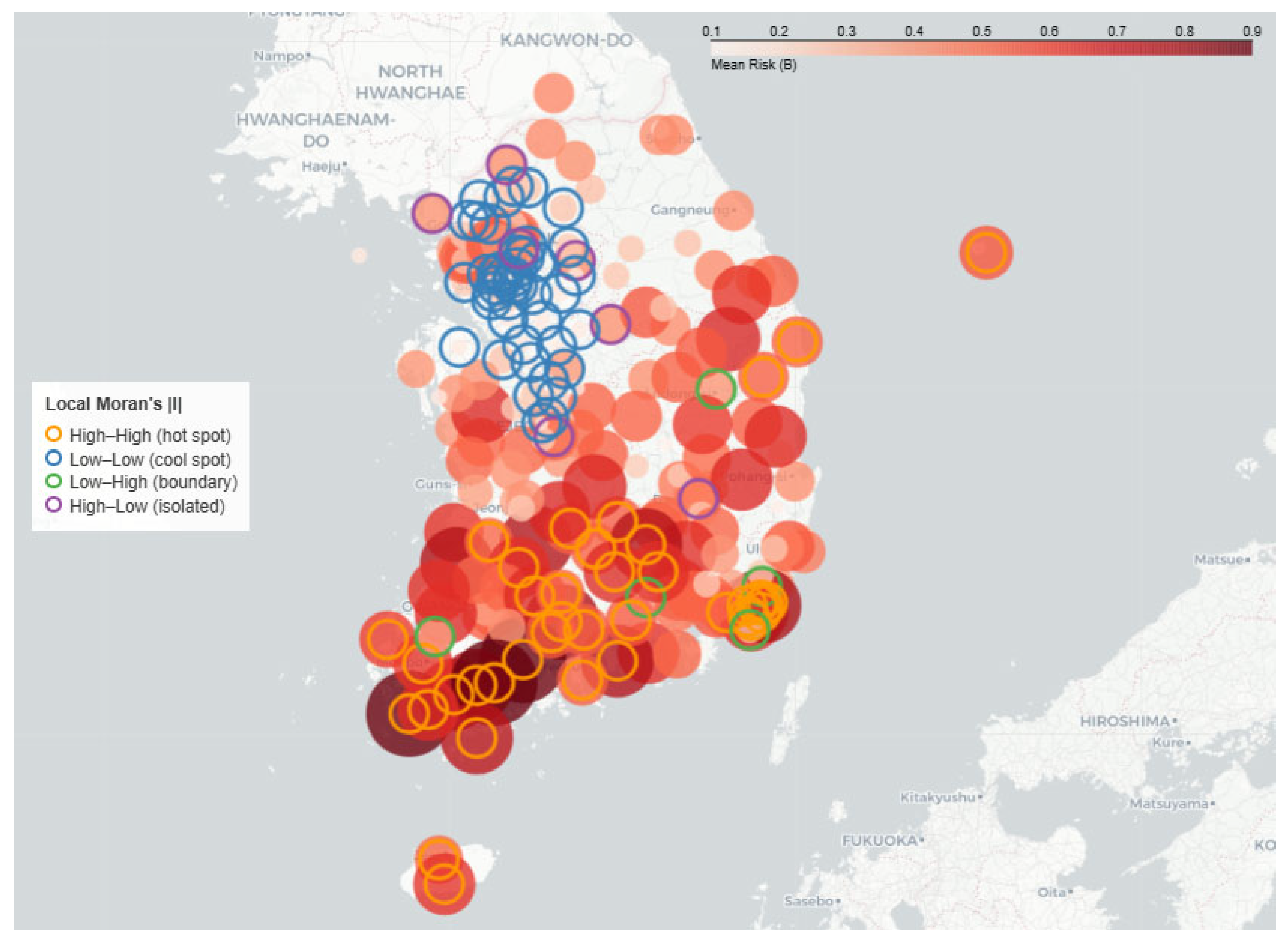
Figure 5.
National mean risk map under Scenario B (kNN = 8, permutations = 199, p < 0.05). Statistically significant clusters are observed in the southwestern region and in certain inland mountainous areas.
Figure 5.
National mean risk map under Scenario B (kNN = 8, permutations = 199, p < 0.05). Statistically significant clusters are observed in the southwestern region and in certain inland mountainous areas.
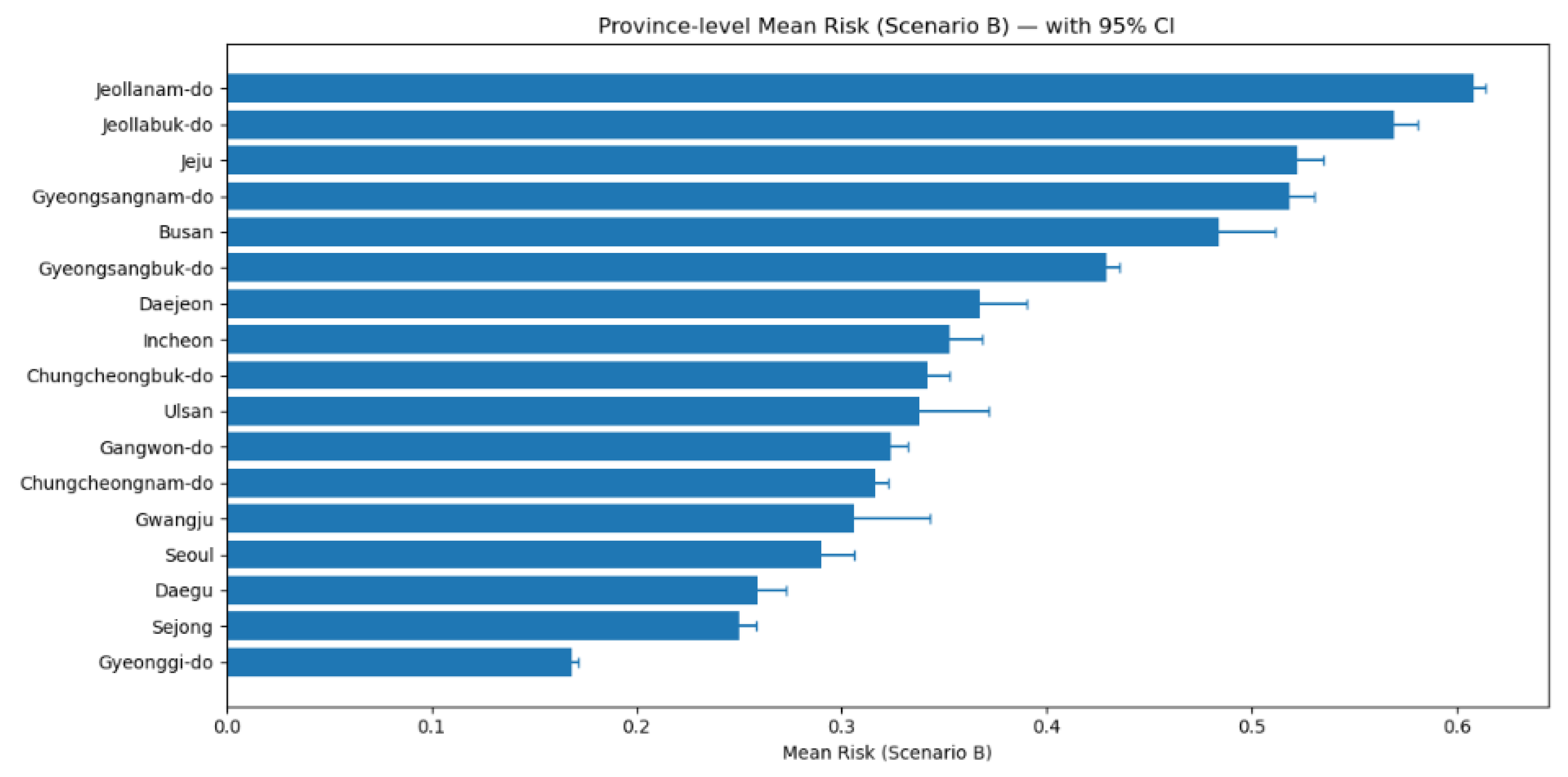
Figure 6.
Provincial-level mean risk (Scenario B, 95% CI). Horizontal axis shows provincial means with 95% confidence intervals. Jeollanam-do, Jeollabuk-do, and Gyeongsangnam-do occupy the highest ranks, while metropolitan areas exhibit comparatively low values.
Figure 6.
Provincial-level mean risk (Scenario B, 95% CI). Horizontal axis shows provincial means with 95% confidence intervals. Jeollanam-do, Jeollabuk-do, and Gyeongsangnam-do occupy the highest ranks, while metropolitan areas exhibit comparatively low values.
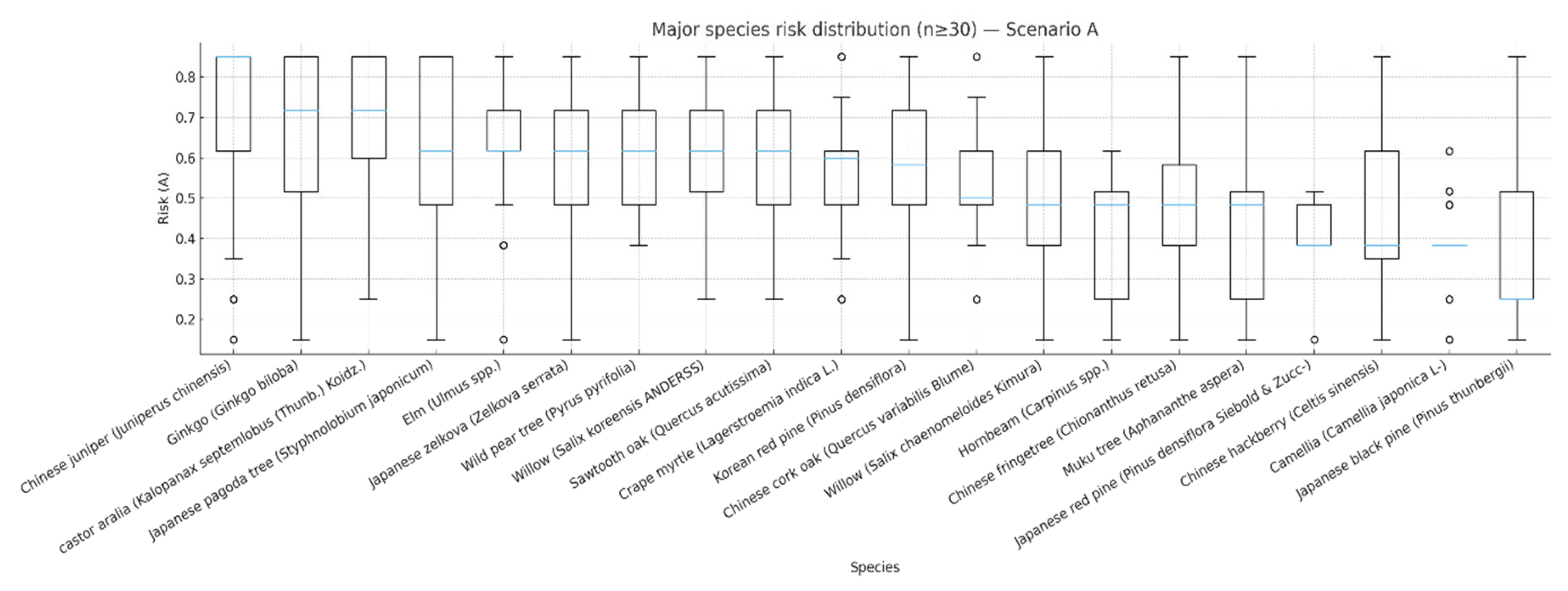
Figure 7.
Distribution of risk scores for major species under Scenario A (n ≥ 30). The absence of a box indicates that the data for this species have little variation or too few observations to form an interquartile range. The blue line marks the median, and the circles denote outliers.
Figure 7.
Distribution of risk scores for major species under Scenario A (n ≥ 30). The absence of a box indicates that the data for this species have little variation or too few observations to form an interquartile range. The blue line marks the median, and the circles denote outliers.
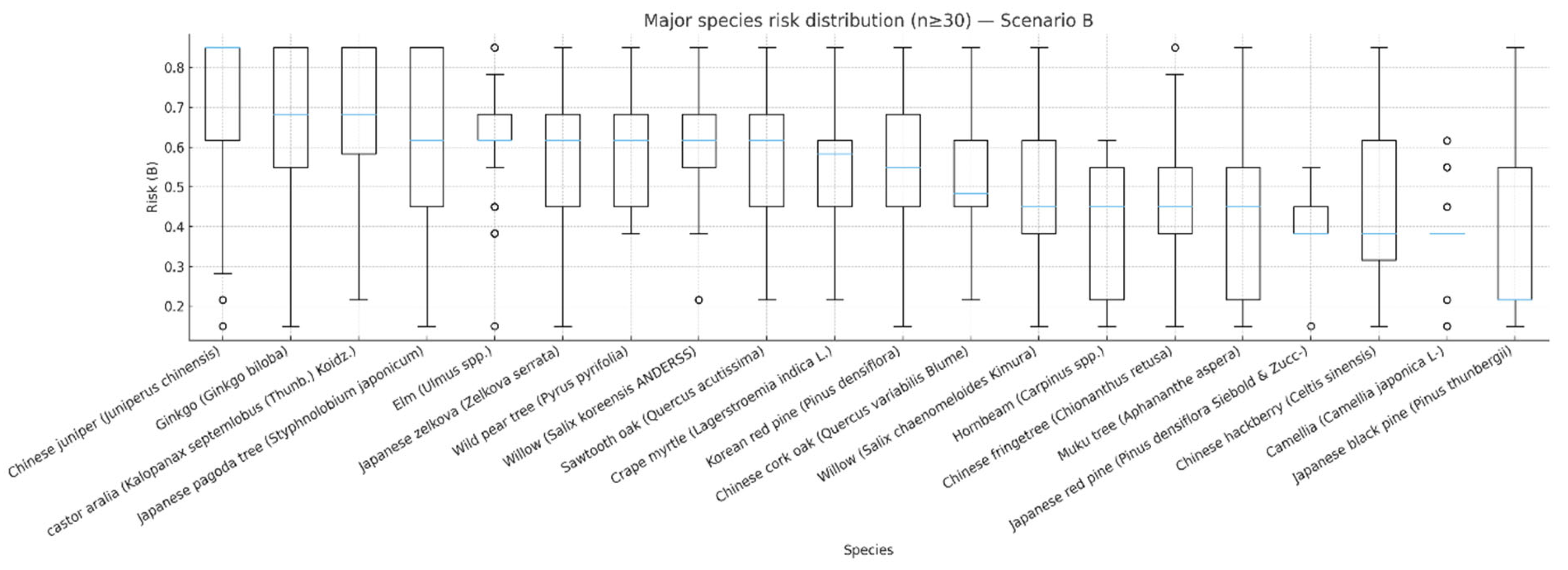
Figure 8.
Distribution of risk scores for major species under Scenario B (
n ≥ 30). While relative rankings are largely preserved across scenarios, species sensitive to rainfall exhibit slightly higher medians and thicker upper tails under Scenario B compared to Scenario A. Please refer to the explanation in
Figure 7 for the meaning of the absence of a box.
Figure 8.
Distribution of risk scores for major species under Scenario B (
n ≥ 30). While relative rankings are largely preserved across scenarios, species sensitive to rainfall exhibit slightly higher medians and thicker upper tails under Scenario B compared to Scenario A. Please refer to the explanation in
Figure 7 for the meaning of the absence of a box.
Figure 9.
Distribution of risk scores for major species under Scenario C (
n ≥ 30). For some heat-sensitive species, medians are relatively higher than under Scenario A, and variance is enlarged in certain cases. Please refer to the explanation in
Figure 7 for the meaning of the absence of a box.
Figure 9.
Distribution of risk scores for major species under Scenario C (
n ≥ 30). For some heat-sensitive species, medians are relatively higher than under Scenario A, and variance is enlarged in certain cases. Please refer to the explanation in
Figure 7 for the meaning of the absence of a box.
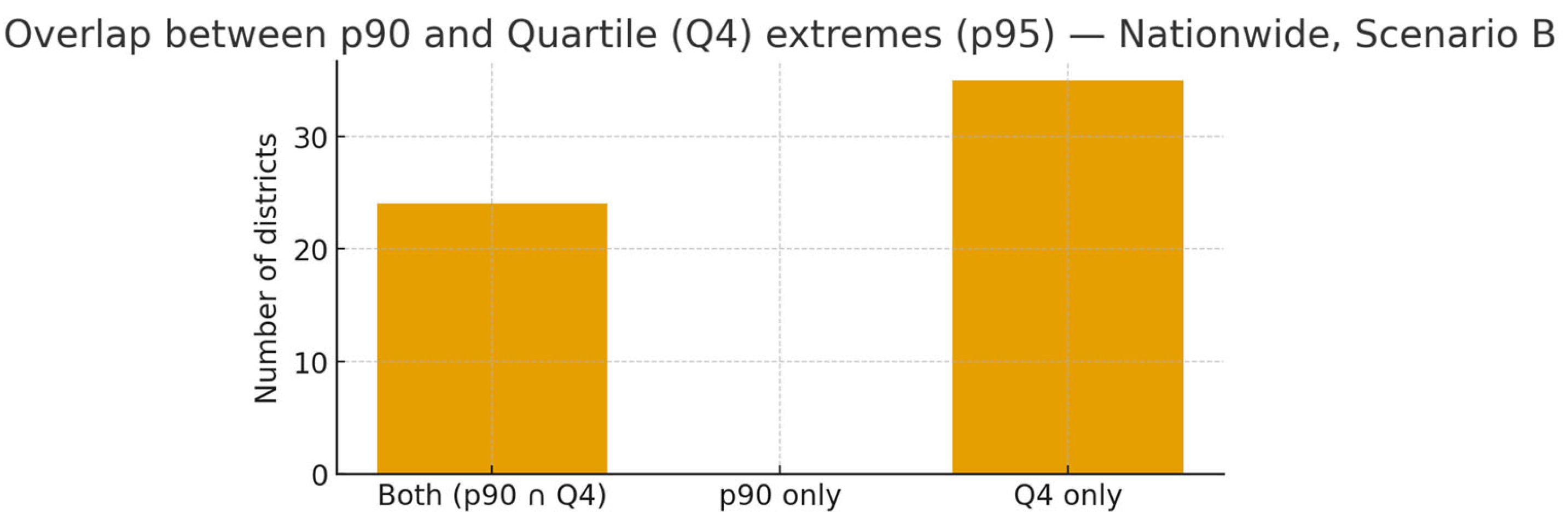
Figure 10.
Overlap between p90 (top decile) and quartile (Q4, top quartile) extremes on district-level p95 (Scenario B). A simple overlap view shows that the p90 extreme set is fully nested within the Q4 set: p90 provides a conservative tail while Q4 broadens coverage to the mid-tail. Thresholds are computed on the national distribution (ties included).
Figure 10.
Overlap between p90 (top decile) and quartile (Q4, top quartile) extremes on district-level p95 (Scenario B). A simple overlap view shows that the p90 extreme set is fully nested within the Q4 set: p90 provides a conservative tail while Q4 broadens coverage to the mid-tail. Thresholds are computed on the national distribution (ties included).
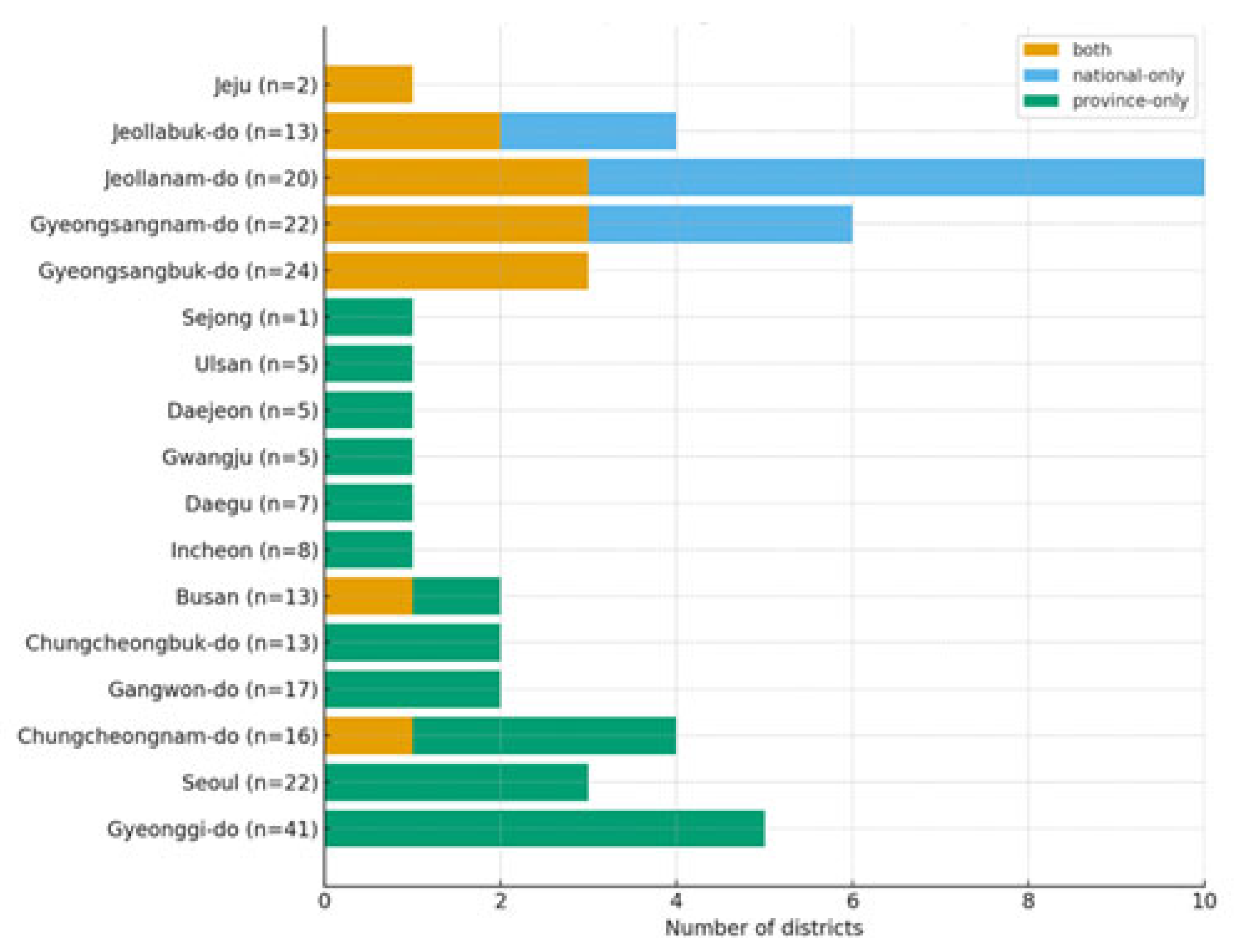
Figure 11.
National vs. province-specific 90th percentile on district-level 95th percentile (Scenario B)—counts. Each row is a province (labeled with n), and the bar length shows the number of districts (not shares). Orange (“both”) are districts classified as priority by both rules and therefore indicate the size of the priority core; blue (“national-only”) are districts priority by the national rule but not by the province rule, indicating cases that look extreme nationally but are not top-decile within their own province; green (“province-only”) are districts priority only under the province rule, i.e., additional screening workload that emerges when within-province thresholds are used. Practically, a long orange segment means strong agreement and a sizable core; a long green segment means province-specific thresholds add many margin cases and are therefore most informative in that province (often where within-province dispersion is higher). A long blue segment suggests districts that rank high nationally but not within their province, informing potential re-prioritization at the provincial level.
Figure 11.
National vs. province-specific 90th percentile on district-level 95th percentile (Scenario B)—counts. Each row is a province (labeled with n), and the bar length shows the number of districts (not shares). Orange (“both”) are districts classified as priority by both rules and therefore indicate the size of the priority core; blue (“national-only”) are districts priority by the national rule but not by the province rule, indicating cases that look extreme nationally but are not top-decile within their own province; green (“province-only”) are districts priority only under the province rule, i.e., additional screening workload that emerges when within-province thresholds are used. Practically, a long orange segment means strong agreement and a sizable core; a long green segment means province-specific thresholds add many margin cases and are therefore most informative in that province (often where within-province dispersion is higher). A long blue segment suggests districts that rank high nationally but not within their province, informing potential re-prioritization at the provincial level.
![Sustainability 17 09589 g011 Sustainability 17 09589 g011]()
Figure 12.
Spatial patterns indicated by LISA under Scenario B. Multiple regional clusters are shown in distinct colors. Concentrated HH clusters are observed in much of Jeollanam-do and parts of Gyeongsangnam-do (including Hadong, Namhae, and Hapcheon).
Figure 12.
Spatial patterns indicated by LISA under Scenario B. Multiple regional clusters are shown in distinct colors. Concentrated HH clusters are observed in much of Jeollanam-do and parts of Gyeongsangnam-do (including Hadong, Namhae, and Hapcheon).
Figure 13.
National composite risk map under Scenario B. District-level mean risks (bubbles) are partially overlain with outlines of LISA High–High clusters (k = 8, permutations = 199, p < 0.05). Significant clustering is observed in the southwestern region and certain inland mountainous areas.
Figure 13.
National composite risk map under Scenario B. District-level mean risks (bubbles) are partially overlain with outlines of LISA High–High clusters (k = 8, permutations = 199, p < 0.05). Significant clustering is observed in the southwestern region and certain inland mountainous areas.
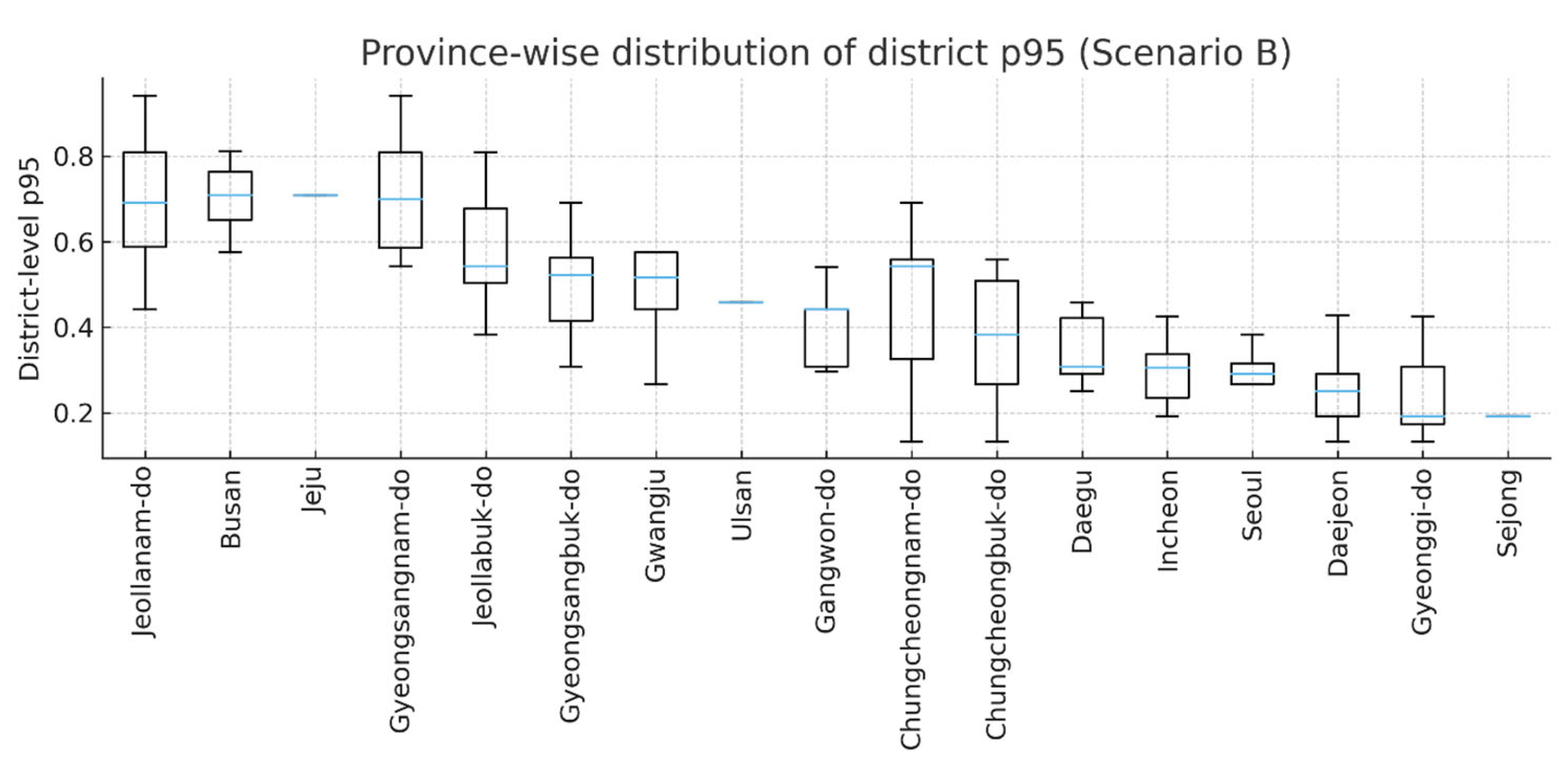
Figure 14.
Province-wise distribution of district-level p95 (Scenario B). Boxplots summarize p95 across districts within each province (ordered by provincial mean). The central line denotes the median; boxes span the interquartile range (Q1–Q3); whiskers extend to 1.5 × IQR; outliers are suppressed for readability. Computed from districts with ≥1 protected tree under Scenario B weighting (wH = 0.35, wR = 0.40, wS = 0.25). These province-wise boxplots (Scenario B) also indicate pronounced between-province inequality and within-province heterogeneity of district-level p95. The blue line for Jeju indicates the p95 value of a single district (no box is shown).
Figure 14.
Province-wise distribution of district-level p95 (Scenario B). Boxplots summarize p95 across districts within each province (ordered by provincial mean). The central line denotes the median; boxes span the interquartile range (Q1–Q3); whiskers extend to 1.5 × IQR; outliers are suppressed for readability. Computed from districts with ≥1 protected tree under Scenario B weighting (wH = 0.35, wR = 0.40, wS = 0.25). These province-wise boxplots (Scenario B) also indicate pronounced between-province inequality and within-province heterogeneity of district-level p95. The blue line for Jeju indicates the p95 value of a single district (no box is shown).
Figure 15.
Fuzzy boundary for national 90th percentile on district-level p95 (Scenario B; B = 1000). Scatter of districts (x: p95; y: probability of priority status μ, i.e., the fraction of bootstrap replicates in which the district is classified as priority). The vertical dashed line marks the empirical national 90th-percentile cutoff (p95 = 0.6917); the horizontal dotted line marks μ = 0.5. Points near the intersection denote threshold-sensitive districts likely to flip under small perturbations; upper-right points indicate robust priority (μ ≈ 1). Values are computed from per-tree risk (Scenario B); ties at the threshold are included.
Figure 15.
Fuzzy boundary for national 90th percentile on district-level p95 (Scenario B; B = 1000). Scatter of districts (x: p95; y: probability of priority status μ, i.e., the fraction of bootstrap replicates in which the district is classified as priority). The vertical dashed line marks the empirical national 90th-percentile cutoff (p95 = 0.6917); the horizontal dotted line marks μ = 0.5. Points near the intersection denote threshold-sensitive districts likely to flip under small perturbations; upper-right points indicate robust priority (μ ≈ 1). Values are computed from per-tree risk (Scenario B); ties at the threshold are included.
Table 1.
Examples of heat-related indicators for selected counties. Out of 251 counties in total, ten were randomly selected. Indicators range from 1 to 4, with lower values representing higher vulnerability.
Table 1.
Examples of heat-related indicators for selected counties. Out of 251 counties in total, ten were randomly selected. Indicators range from 1 to 4, with lower values representing higher vulnerability.
| | Province | District | Heat_Exposure | Heat_Sensitivity | Heat_Vulnerability |
|---|
| 1 | Seoul | Jongno-gu | 4 | 3 | 4 |
| 2 | Busan | Saha-gu | 2 | 2 | 2 |
| 3 | Gyeonggi-do | Guri-si | 4 | 3 | 4 |
| 4 | Incheon | Yeonsu-gu | 4 | 1 | 3 |
| 5 | Gwangju | Seo-gu | 3 | 3 | 3 |
| 6 | Gyeongsangbuk-do | Uiseong-gun | 1 | 1 | 1 |
| 7 | Gangwon-do | Sokcho-si | 2 | 2 | 2 |
| 8 | Chungcheongbuk-do | Boeun-gun | 1 | 2 | 2 |
| 9 | Jeollanam-do | Hampyeong-gun | 1 | 2 | 2 |
| 10 | Jeju | Seogwipo-si | 3 | 1 | 2 |
Table 2.
Examples of rainfall-related indicators for selected counties. As with the heat indicators, there are 251 counties in total, and the same ten counties selected in
Table 1 are listed here for consistency. Indicators again range from 1 to 4, with lower values indicating greater vulnerability.
Table 2.
Examples of rainfall-related indicators for selected counties. As with the heat indicators, there are 251 counties in total, and the same ten counties selected in
Table 1 are listed here for consistency. Indicators again range from 1 to 4, with lower values indicating greater vulnerability.
| | Province | District | Rain_Exposure | Rain_Sensitivity | Rain_Vulnerability |
|---|
| 1 | Seoul | Jongno-gu | 4 | 3 | 4 |
| 2 | Busan | Saha-gu | 1 | 3 | 2 |
| 3 | Gyeonggi-do | Guri-si | 3 | 3 | 3 |
| 4 | Incheon | Yeonsu-gu | 4 | 3 | 4 |
| 5 | Gwangju | Seo-gu | 2 | 3 | 3 |
| 6 | Gyeongsangbuk-do | Uiseong-gun | 4 | 1 | 3 |
| 7 | Gangwon-do | Sokcho-si | 2 | 3 | 3 |
| 8 | Chungcheongbuk-do | Boeun-gun | 4 | 2 | 3 |
| 9 | Jeollanam-do | Hampyeong-gun | 2 | 1 | 2 |
| 10 | Jeju | Seogwipo-si | 1 | 3 | 2 |
Table 3.
Examples of species-specific sensitivities to heat and rainfall (waterlogging). Species sensitivities are expressed on a three-point scale.
Table 3.
Examples of species-specific sensitivities to heat and rainfall (waterlogging). Species sensitivities are expressed on a three-point scale.
| | Scientific Name | Common Name | Heat Vulnerability | Rainfall Vulnerability |
|---|
| 1 | Zelkova serrata | Japanese Zelkova | 0.3 | 0.9 |
| 2 | Celtis sinensis | Chinese-hackberry | 0.3 | 0.6 |
| 3 | Ginkgo biloba | Ginkgo | 0.6 | 0.9 |
| 4 | Pinus densiflora | Korean red pine | 0.6 | 0.9 |
| 5 | Sophora japonica L. | Pagoda tree | 0.3 | 0.6 |
| 6 | Juniperus chinensis L. | Chinese juniper | 0.6 | 0.9 |
| 7 | Salix koreensis Andersson | Willow | 0.6 | 0.3 |
| 8 | Pinus thunbergii | Black pine | 0.6 | 0.9 |
| 9 | Aphananthe aspera | Muku tree | 0.3 | 0.6 |
| 10 | Camellia japonica L. | Camellia | 0.6 | 0.9 |
Table 4.
Tail mass and percentile summary. The table reports 50th percentile, 90th percentile, and 99th percentile, the proportion of individuals in the top 10% (raw scale vs. 0–1 scale), and skewness. Because normalization is intended to adjust scales rather than alter distributional shape, skewness is generally preserved before and after normalization. Indeed, the table confirms that the distribution of individual-level risk values retains a similar skewness pattern after normalization.
Table 4.
Tail mass and percentile summary. The table reports 50th percentile, 90th percentile, and 99th percentile, the proportion of individuals in the top 10% (raw scale vs. 0–1 scale), and skewness. Because normalization is intended to adjust scales rather than alter distributional shape, skewness is generally preserved before and after normalization. Indeed, the table confirms that the distribution of individual-level risk values retains a similar skewness pattern after normalization.
| | Heat | Rainfall |
|---|
| p50_raw | 3.0000 | 3.0000 |
| p90_raw | 4.0000 | 4.0000 |
| p99_raw | 4.0000 | 4.0000 |
| p50_norm | 0.3333 | 0.3333 |
| p90_norm | 1.0000 | 0.6667 |
| p99_norm | 1.0000 | 1.0000 |
| tail_>90%_raw | 0.0000 | 0.0000 |
| tail_>0.9_norm | 0.1101 | 0.0373 |
| skew_raw | −0.1629 | −0.3699 |
| skew_norm | 0.1629 | 0.3699 |
Table 5.
Provincial summary (Scenarios A/B/C: mean, standard error, Δrank). Provincial means, standard errors, and rank-order tables.
Table 5.
Provincial summary (Scenarios A/B/C: mean, standard error, Δrank). Provincial means, standard errors, and rank-order tables.
| Province | B_Mean | B_Se | B_Rank | A_Mean | A_Se | A_Rank | Δrank_A_vs_B | C_Mean | C_Se | C_Rank | Δrank_C_vs_B |
|---|
| Jeollanam-do | 0.608 | 0.003 | 1 | 0.590 | 0.003 | 1 | 0 | 0.581 | 0.003 | 1 | 0 |
| Jeollabuk-do | 0.570 | 0.006 | 2 | 0.571 | 0.006 | 2 | 0 | 0.572 | 0.007 | 2 | 0 |
| Jeju | 0.522 | 0.006 | 3 | 0.481 | 0.007 | 4 | 1 | 0.461 | 0.008 | 4 | 1 |
| Gyeongsangnam-do | 0.519 | 0.006 | 4 | 0.496 | 0.007 | 3 | −1 | 0.485 | 0.007 | 3 | −1 |
| Busan | 0.484 | 0.014 | 5 | 0.454 | 0.014 | 5 | 0 | 0.440 | 0.014 | 5 | 0 |
| Gyeongsangbuk-do | 0.429 | 0.003 | 6 | 0.418 | 0.003 | 6 | 0 | 0.413 | 0.004 | 6 | 0 |
| Daejeon | 0.367 | 0.012 | 7 | 0.365 | 0.013 | 7 | 0 | 0.364 | 0.013 | 7 | 0 |
| Incheon | 0.353 | 0.008 | 8 | 0.334 | 0.008 | 8 | 0 | 0.324 | 0.008 | 9 | 1 |
| Chungcheongbuk-do | 0.342 | 0.006 | 9 | 0.326 | 0.006 | 10 | 1 | 0.318 | 0.006 | 10 | 1 |
| Ulsan | 0.338 | 0.017 | 10 | 0.292 | 0.017 | 12 | 2 | 0.270 | 0.018 | 12 | 2 |
| Gangwon-do | 0.324 | 0.004 | 11 | 0.330 | 0.004 | 9 | −2 | 0.334 | 0.004 | 8 | −3 |
| Chungcheongnam-do | 0.317 | 0.003 | 12 | 0.303 | 0.003 | 11 | −1 | 0.297 | 0.003 | 11 | −1 |
| Gwangju | 0.306 | 0.019 | 13 | 0.268 | 0.018 | 14 | 1 | 0.250 | 0.017 | 15 | 2 |
| Seoul | 0.290 | 0.008 | 14 | 0.273 | 0.008 | 13 | −1 | 0.265 | 0.009 | 13 | −1 |
| Daegu | 0.259 | 0.007 | 15 | 0.230 | 0.009 | 16 | 1 | 0.215 | 0.010 | 16 | 1 |
| Sejong | 0.250 | 0.004 | 16 | 0.257 | 0.004 | 15 | −1 | 0.260 | 0.004 | 14 | −2 |
| Gyeonggi-do | 0.168 | 0.002 | 17 | 0.146 | 0.002 | 17 | 0 | 0.135 | 0.002 | 17 | 0 |
Table 6.
Provincial summary (Top 15 provinces by mean risk under Scenario B;
wH = 0.35,
wR = 0.4,
wS = 0.25). Same format as
Table 5.
Table 6.
Provincial summary (Top 15 provinces by mean risk under Scenario B;
wH = 0.35,
wR = 0.4,
wS = 0.25). Same format as
Table 5.
| Province | Mean | Std | Count | p95 | Max | Global_Top10_Share | Within_Province_Top10_Share |
|---|
| Jeollanam-do | 0.608 | 0.159 | 2822 | 0.883 | 0.942 | 0.341 | 0.105 |
| Jeollabuk-do | 0.570. | 0.144 | 648 | 0.750 | 0.808 | 0.205 | 0.157 |
| Jeju | 0.522 | 0.081 | 157 | 0.692 | 0.750 | 0.096 | 0.102 |
| Gyeongsangnam-do | 0.519 | 0.178 | 899 | 0.756 | 0.867 | 0.197 | 0.131 |
| Busan | 0.484 | 0.135 | 96 | 0.731 | 0.825 | 0.115 | 0.115 |
| Gyeongsangbuk-do | 0.429 | 0.142 | 1920 | 0.633 | 0.750 | 0.021 | 0.106 |
| Daejeon | 0.367 | 0.151 | 163 | 0.500 | 0.500 | 0.000 | 0.515 |
| Incheon | 0.353 | 0.085 | 111 | 0.471 | 0.558 | 0.000 | 0.117 |
| Chungcheongbuk-do | 0.342 | 0.158 | 771 | 0.558 | 0.617 | 0.000 | 0.289 |
| Ulsan | 0.338 | 0.124 | 53 | 0.575 | 0.575 | 0.000 | 0.132 |
| Gangwon-do | 0.324 | 0.097 | 532 | 0.500 | 0.633 | 0.000 | 0.164 |
| Chungcheongnam-do | 0.317 | 0.138 | 1963 | 0.558 | 0.692 | 0.004 | 0.181 |
| Gwangju | 0.306 | 0.163 | 76 | 0.517 | 0.575 | 0.000 | 0.237 |
| Seoul | 0.290 | 0.125 | 237 | 0.500 | 0.558 | 0.000 | 0.106 |
| Daegu | 0.259 | 0.087 | 146 | 0.367 | 0.558 | 0.000 | 0.164 |
Table 7.
Top 20 counties by mean risk under Scenario B (wH = 0.35, wR = 0.4, wS = 0.25).
Table 7.
Top 20 counties by mean risk under Scenario B (wH = 0.35, wR = 0.4, wS = 0.25).
| Province | District | Mean | p95 | Global_Top10_Share | Within_Province_Top10_Share | Count |
|---|
| Jeollanam-do | Jangheung-gun | 0.877 | 0.942 | 1.000 | 0.688 | 141 |
| Jeollanam-do | Boseong-gun | 0.872 | 0.942 | 1.000 | 0.739 | 234 |
| Jeollanam-do | Jindo-gun | 0.870 | 0.942 | 1.000 | 0.490 | 51 |
| Busan | Suyeong-gu | 0.769 | 0.825 | 1.000 | 1.000 | 9 |
| Gyeongsangnam-do | Hadong-gun | 0.761 | 0.808 | 0.988 | 0.716 | 81 |
| Gyeongsangnam-do | Namhae-gun | 0.748 | 0.808 | 1.000 | 0.750 | 28 |
| Jeollabuk-do | Imsil-gun | 0.744 | 0.750 | 0.960 | 0.920 | 25 |
| Jeollabuk-do | Gochang-gun | 0.744 | 0.808 | 0.924 | 0.752 | 105 |
| Jeollabuk-do | Haenam-gun | 0.742 | 0.808 | 0.946 | 0.000 | 314 |
| Gyeongsangnam-do | Hapcheon-gun | 0.742 | 0.750 | 0.915 | 0.830 | 47 |
| Jeollanam-do | Gangjin-gun | 0.733 | 0.781 | 1.000 | 0.000 | 16 |
| Jeollanam-do | Wando-gun | 0.731 | 0.808 | 1.000 | 0.000 | 61 |
| Gyeongsangbuk-do | Bonghwa-gun | 0.647 | 0.692 | 0.383 | 0.867 | 60 |
| Jeollabuk-do | Muju-gun | 0.639 | 0.692 | 0.125 | 0.000 | 56 |
| Jeollabuk-do | Jinan-gun | 0.637 | 0.692 | 0.085 | 0.000 | 59 |
| Chungcheongnam-do | Cheongyang-gun | 0.635 | 0.692 | 0.096 | 1.000 | 83 |
| Jeollanam-do | Hampyeong-gun | 0.634 | 0.692 | 0.304 | 0.000 | 296 |
| Gyeongsangbuk-do | Yeongcheon-si | 0.634 | 0.692 | 0.239 | 0.804 | 46 |
| Gyeongsangnam-do | Sancheong-gun | 0.631 | 0.689 | 0.071 | 0.000 | 42 |
| Jeollanam-do | Gokseong-gun | 0.630 | 0.692 | 0.119 | 0.000 | 176 |
Table 8.
Top 20 counties by p95 risk under Scenario B (wH = 0.35, wR = 0.4, wS = 0.25). These figures highlight the upper-tail distribution of risk. Unlike simple averages, the p95 criterion identifies which regions should be prioritized for management when the focus is on extreme events such as sustained heat waves or localized heavy rainfall.
Table 8.
Top 20 counties by p95 risk under Scenario B (wH = 0.35, wR = 0.4, wS = 0.25). These figures highlight the upper-tail distribution of risk. Unlike simple averages, the p95 criterion identifies which regions should be prioritized for management when the focus is on extreme events such as sustained heat waves or localized heavy rainfall.
| Province | District | p95 | Mean | Global_Top10_Share | Within_Province_Top10_Share | Count |
|---|
| Jeollanam-do | Jangheung-gun | 0.942 | 0.877 | 1.000 | 0.688 | 141 |
| Jeollanam-do | Boseong-gun | 0.942 | 0.872 | 1.000 | 0.739 | 234 |
| Jeollanam-do | Jindo-gun | 0.942 | 0.870 | 1.000 | 0.490 | 51 |
| Busan | Suyeong-gu | 0.825 | 0.769 | 1.0000 | 1.0000 | 9 |
| Gyeongsangnam-do | Hadong-gun | 0.808 | 0.761 | 0.988 | 0.716 | 81 |
| Gyeongsangnam-do | Namhae-gun | 0.808 | 0.748 | 1.000 | 0.750 | 28 |
| Jeollabuk-do | Gochang-gun | 0.808 | 0.744 | 0.924 | 0.752 | 105 |
| Jeollabuk-do | Haenam-gun | 0.808 | 0.742 | 0.946 | 0.000 | 314 |
| Jeollanam-do | Wando-gun | 0.808 | 0.731 | 1.000 | 0.000 | 61 |
| Jeollanam-do | Gangjin-gun | 0.781 | 0.733 | 1.000 | 0.000 | 16 |
| Jeollabuk-do | Imsil-gun | 0.750 | 0.744 | 0.960 | 0.920 | 25 |
| Gyeongsangnam-do | Hapcheon-gun | 0.750 | 0.742 | 0.915 | 0.830 | 47 |
| Gyeongsangbuk-do | Bonghwa-gun | 0.692 | 0.647 | 0.383 | 0.867 | 60 |
| Jeollabuk-do | Muju-gun | 0.692 | 0.639 | 0.125 | 0.000 | 56 |
| Jeollabuk-do | Jinan-gun | 0.692 | 0.637 | 0.085 | 0.000 | 59 |
| Chungcheongnam-do | Cheongyang-gun | 0.692 | 0.635 | 0.096 | 1.000 | 83 |
| Jeollanam-do | Hampyeong-gun | 0.692 | 0.634 | 0.304 | 0.000 | 296 |
| Gyeongsangbuk-do | Yeongcheon-si | 0.692 | 0.634 | 0.239 | 0.804 | 46 |
| Jeollanam-do | Gokseong-gun | 0.692 | 0.630 | 0.119 | 0.000 | 176 |
| Gyeongsangbuk-do | Yeongdeok-gun | 0.692 | 0.628 | 0.130 | 0.815 | 54 |
Table 9.
Intersection of Top 20 counties across Scenarios A, B, and C (based on both mean and p95 rankings).
Table 9.
Intersection of Top 20 counties across Scenarios A, B, and C (based on both mean and p95 rankings).
| Province | District | Mean_A | p95_A | Rank_Mean_A | Rank_p95_A | Mean_B | p95_B | Rank_Mean_B | Rank_p95_B | Mean_C | p95_C | Rank_Mean_C | Rank_p95_C |
|---|
| Jeollanam-do | Jangheung-gun | 0.854 | 0.925 | 1 | 1 | 0.877 | 0.942 | 1 | 1 | 0.843 | 0.917 | 1 | 1 |
| Jeollanam-do | Jindo-gun | 0.851 | 0.925 | 2 | 1 | 0.870 | 0.942 | 3 | 1 | 0.842 | 0.917 | 2 | 1 |
| Jeollanam-do | Boseong-gun | 0.845 | 0.925 | 3 | 1 | 0.871 | 0.942 | 2 | 1 | 0.831 | 0.917 | 3 | 1 |
| Gyeongsangnam-do | Hadong-gun | 0.774 | 0.825 | 4 | 4 | 0.761 | 0.808 | 5 | 5 | 0.781 | 0.833 | 4 | 4 |
| Gyeongsangnam-do | Namhae-gun | 0.756 | 0.825 | 6 | 4 | 0.748 | 0.808 | 6 | 5 | 0.760 | 0.833 | 6 | 4 |
| Jeollanam-do | Haenam-gun | 0.758 | 0.825 | 5 | 4 | 0.742 | 0.808 | 9 | 5 | 0.766 | 0.833 | 5 | 4 |
| Jeollabuk-do | Gochang-gun | 0.754 | 0.825 | 7 | 4 | 0.744 | 0.808 | 8 | 5 | 0.759 | 0.833 | 7 | 4 |
| Gyeongsangnam-do | Hapcheon-gun | 0.748 | 0.768 | 8 | 10 | 0.742 | 0.750 | 10 | 11 | 0.752 | 0.779 | 8 | 9 |
| Jeollabuk-do | Imsil-gun | 0.747 | 0.750 | 9 | 11 | 0.744 | 0.750 | 7 | 11 | 0.748 | 0.750 | 10 | 10 |
| Busan | Suyeong-gu | 0.719 | 0.775 | 11 | 9 | 0.769 | 0.825 | 4 | 4 | 0.694 | 0.750 | 11 | 11 |
| Jeollanam-do | Wando-gun | 0.745 | 0.825 | 10 | 4 | 0.731 | 0.808 | 12 | 5 | 0.751 | 0.833 | 9 | 4 |
| Jeollanam-do | Gangjin-gun | 0.677 | 0.719 | 12 | 14 | 0.733 | 0.781 | 11 | 10 | 0.648 | 0.688 | 15 | 15 |
| Gyeongsangbuk-do | Bonghwa-gun | 0.626 | 0.675 | 16 | 16 | 0.647 | 0.692 | 13 | 13 | 0.615 | 0.667 | 16 | 17 |
| Jeollanam-do | Hampyeong-gun | 0.612 | 0.675 | 18 | 16 | 0.634 | 0.692 | 17 | 13 | 0.601 | 0.667 | 18 | 17 |
| Gyeongsangbuk-do | Yeongcheon-si | 0.609 | 0.675 | 20 | 16 | 0.634 | 0.692 | 18 | 13 | 0.597 | 0.667 | 20 | 17 |
Table 10.
Scenario-specific Top 20 counties. driver_this_scenario indicates the dominant factor in a given district under the specified scenario (A, B, or C). driver_mode_across_selected denotes the modal dominant factor across all scenarios in which the district appears. ‘Scenarios included’ specifies the number of scenarios (0–3) in which the district is included in the Top 20. For example, a value of 3 indicates that the district appears under all three scenarios, suggesting a robust high-risk status independent of weighting assumptions.
Table 10.
Scenario-specific Top 20 counties. driver_this_scenario indicates the dominant factor in a given district under the specified scenario (A, B, or C). driver_mode_across_selected denotes the modal dominant factor across all scenarios in which the district appears. ‘Scenarios included’ specifies the number of scenarios (0–3) in which the district is included in the Top 20. For example, a value of 3 indicates that the district appears under all three scenarios, suggesting a robust high-risk status independent of weighting assumptions.
| Province | District | Mean_Risk | Driver_This_Scenario | N_Trees_in_District | Rank | Scenario | A | B | C | Scenarios Included | Driver |
|---|
| Jeollanam-do | Jangheung-gun | 0.854 | Mixed | 141 | 1 | A | 1 | 1 | 1 | 3 | Mixed |
| Jeollanam-do | Jindo-gun | 0.851 | Mixed | 51 | 2 | A | 1 | 1 | 1 | 3 | Mixed |
| Jeollanam-do | Boseong-gun | 0.845 | Mixed | 234 | 3 | A | 1 | 1 | 1 | 3 | Mixed |
| Gyeongsangnam-do | Hadong-gun | 0.774 | Heat | 81 | 4 | A | 1 | 1 | 1 | 3 | Heat |
| Jeollanam-do | Haenam-gun | 0.758 | Heat | 314 | 5 | A | 1 | 1 | 1 | 3 | Heat |
| Gyeongsangnam-do | Namhae-gun | 0.756 | Heat | 28 | 6 | A | 1 | 1 | 1 | 3 | Heat |
| Jeollabuk-do | Gochang-gun | 0.754 | Heat | 105 | 7 | A | 1 | 1 | 1 | 3 | Heat |
| Gyeongsangnam-do | Hapcheon-gun | 0.748 | Heat | 47 | 8 | A | 1 | 1 | 1 | 3 | Heat |
| Jeollabuk-do | Imsil-gun | 0.747 | Heat | 25 | 9 | A | 1 | 1 | 1 | 3 | Heat |
| Jeollanam-do | Wando-gun | 0.745 | Heat | 61 | 10 | A | 1 | 1 | 1 | 3 | Heat |
| Busan | Suyeong-gu | 0.719 | Rain | 9 | 11 | A | 1 | 1 | 1 | 3 | Rain |
| Jeollanam-do | Gangjin-gun | 0.677 | Rain | 16 | 12 | A | 1 | 1 | 1 | 3 | Rain |
| Jeollabuk-do | Sunchang-gun | 0.655 | Heat | 146 | 13 | A | 1 | 0 | 1 | 2 | Heat |
| Jeollabuk-do | Buan-gun | 0.645 | Heat | 14 | 14 | A | 1 | 0 | 1 | 2 | Heat |
| Gyeongsangbuk-do | Uiseong-gun | 0.640 | Heat | 84 | 15 | A | 1 | 0 | 1 | 2 | Heat |
| Gyeongsangbuk-do | Bonghwa-gun | 0.626 | Mixed | 60 | 16 | A | 1 | 1 | 1 | 3 | Mixed |
| Busan | Seo-gu | 0.613 | Mixed | 2 | 17 | A | 1 | 0 | 1 | 2 | Mixed |
| Jeollanam-do | Hampyeong-gun | 0.612 | Mixed | 296 | 18 | A | 1 | 1 | 1 | 3 | Mixed |
| Jeollabuk-do | Muju-gun | 0.609 | Mixed | 56 | 19 | A | 1 | 1 | 0 | 2 | Mixed |
| Gyeongsangbuk-do | Yeongcheon-si | 0.609 | Mixed | 46 | 20 | A | 1 | 1 | 1 | 3 | Mixed |
| Jeollanam-do | Jangheung-gun | 0.877 | Mixed | 141 | 1 | B | 1 | 1 | 1 | 3 | Mixed |
| Jeollanam-do | Boseong-gun | 0.872 | Mixed | 234 | 2 | B | 1 | 1 | 1 | 3 | Mixed |
| Jeollanam-do | Jindo-gun | 0.870 | Mixed | 51 | 3 | B | 1 | 1 | 1 | 3 | Mixed |
| Busan | Suyeong-gu | 0.769 | Rain | 9 | 4 | B | 1 | 1 | 1 | 3 | Rain |
| Gyeongsangnam-do | Hadong-gun | 0.761 | Heat | 81 | 5 | B | 1 | 1 | 1 | 3 | Heat |
| Gyeongsangnam-do | Namhae-gun | 0.748 | Heat | 28 | 6 | B | 1 | 1 | 1 | 3 | Heat |
| Jeollabuk-do | Imsil-gun | 0.744 | Heat | 25 | 7 | B | 1 | 1 | 1 | 3 | Heat |
| Jeollabuk-do | Gochang-gun | 0.744 | Heat | 105 | 8 | B | 1 | 1 | 1 | 3 | Heat |
| Jeollanam-do | Haenam-gun | 0.742 | Heat | 314 | 9 | B | 1 | 1 | 1 | 3 | Heat |
| Gyeongsangnam-do | Hapcheon-gun | 0.742 | Heat | 47 | 10 | B | 1 | 1 | 1 | 3 | Heat |
| Jeollanam-do | Gangjin-gun | 0.733 | Rain | 16 | 11 | B | 1 | 1 | 1 | 3 | Rain |
| Jeollanam-do | Wando-gun | 0.731 | Heat | 61 | 12 | B | 1 | 1 | 1 | 3 | Heat |
| Gyeongsangbuk-do | Bonghwa-gun | 0.647 | Mixed | 60 | 13 | B | 1 | 1 | 1 | 3 | Mixed |
| Jeollabuk-do | Muju-gun | 0.639 | Mixed | 56 | 14 | B | 1 | 1 | 0 | 2 | Mixed |
| Jeollabuk-do | Jinan-gun | 0.637 | Mixed | 59 | 15 | B | 0 | 1 | 0 | 1 | Mixed |
| Chungcheongnam-do | Cheongyang-gun | 0.635 | Mixed | 83 | 16 | B | 0 | 1 | 0 | 1 | Mixed |
| Jeollanam-do | Hampyeong-gun | 0.634 | Mixed | 296 | 17 | B | 1 | 1 | 1 | 3 | Mixed |
| Gyeongsangbuk-do | Yeongcheon-si | 0.634 | Mixed | 46 | 18 | B | 1 | 1 | 1 | 3 | Mixed |
| Gyeongsangnam-do | Sancheong-gun | 0.631 | Mixed | 42 | 19 | B | 0 | 1 | 0 | 1 | Mixed |
| Jeollanam-do | Gokseong-gun | 0.630 | Mixed | 176 | 20 | B | 0 | 1 | 0 | 1 | Mixed |
| Jeollanam-do | Jangheung-gun | 0.843 | Mixed | 141 | 1 | C | 1 | 1 | 1 | 3 | Mixed |
| Jeollanam-do | Jindo-gun | 0.842 | Mixed | 51 | 2 | C | 1 | 1 | 1 | 3 | Mixed |
| Jeollanam-do | Boseong-gun | 0.831 | Mixed | 234 | 3 | C | 1 | 1 | 1 | 3 | Mixed |
| Gyeongsangnam-do | Hadong-gun | 0.781 | Heat | 81 | 4 | C | 1 | 1 | 1 | 3 | Heat |
| Jeollanam-do | Haenam-gun | 0.766 | Heat | 314 | 5 | C | 1 | 1 | 1 | 3 | Heat |
| Gyeongsangnam-do | Namhae-gun | 0.760 | Heat | 28 | 6 | C | 1 | 1 | 1 | 3 | Heat |
| Jeollabuk-do | Gochang-gun | 0.759 | Heat | 105 | 7 | C | 1 | 1 | 1 | 3 | Heat |
| Gyeongsangnam-do | Hapcheon-gun | 0.752 | Heat | 47 | 8 | C | 1 | 1 | 1 | 3 | Heat |
| Jeollanam-do | Wando-gun | 0.751 | Heat | 61 | 9 | C | 1 | 1 | 1 | 3 | Heat |
| Jeollabuk-do | Imsil-gun | 0.748 | Heat | 25 | 10 | C | 1 | 1 | 1 | 3 | Heat |
| Busan | Suyeong-gu | 0.694 | Rain | 9 | 11 | C | 1 | 1 | 1 | 3 | Rain |
| Jeollabuk-do | Sunchang-gun | 0.673 | Heat | 146 | 12 | C | 1 | 0 | 1 | 2 | Heat |
| Jeollabuk-do | Buan-gun | 0.664 | Heat | 14 | 13 | C | 1 | 0 | 1 | 2 | Heat |
| Gyeongsangbuk-do | Uiseong-gun | 0.663 | Heat | 84 | 14 | C | 1 | 0 | 1 | 2 | Heat |
| Jeollanam-do | Gangjin-gun | 0.648 | Rain | 16 | 15 | C | 1 | 1 | 1 | 3 | Rain |
| Gyeongsangbuk-do | Bonghwa-gun | 0.615 | Mixed | 60 | 16 | C | 1 | 1 | 1 | 3 | Mixed |
| Busan | Seo-gu | 0.604 | Mixed | 2 | 17 | C | 1 | 0 | 1 | 2 | Mixed |
| Jeollanam-do | Hampyeong-gun | 0.601 | Mixed | 296 | 18 | C | 1 | 1 | 1 | 3 | Mixed |
| Jeollanam-do | Yeongam-gun | 0.598 | Mixed | 108 | 19 | C | 0 | 0 | 1 | 1 | Mixed |
| Gyeongsangbuk-do | Yeongcheon-si | 0.597 | Mixed | 46 | 20 | C | 1 | 1 | 1 | 3 | Mixed |
Table 11.
Species-level summary of major species (n ≥ 30) across Scenarios A, B, and C. Includes sample size, mean, standard deviation, and proportion in the top 10% for each scenario. Relative rankings are generally stable across scenarios, though certain species exhibit more pronounced high-risk tails.
Table 11.
Species-level summary of major species (n ≥ 30) across Scenarios A, B, and C. Includes sample size, mean, standard deviation, and proportion in the top 10% for each scenario. Relative rankings are generally stable across scenarios, though certain species exhibit more pronounced high-risk tails.
| Species | n | Mean_A | Sd_A | Top10_A | Mean_B | Sd_B | Top10_B | Mean_C | Sd_C | Top10_C |
|---|
| Zelkova serrata | 6694 | 0.589 | 0.182 | 0.178 | 0.578 | 0.188 | 0.178 | 0.601 | 0.179 | 0.178 |
| Celtis sinensis | 1147 | 0.454 | 0.186 | 0.051 | 0.450 | 0.195 | 0.051 | 0.458 | 0.181 | 0.051 |
| Ginkgo biloba | 840 | 0.663 | 0.181 | 0.326 | 0.654 | 0.187 | 0.326 | 0.671 | 0.177 | 0.326 |
| Pinus densiflora | 804 | 0.562 | 0.182 | 0.141 | 0.549 | 0.190 | 0.141 | 0.574 | 0.177 | 0.141 |
| Sophora japonica L. | 328 | 0.630 | 0.178 | 0.268 | 0.624 | 0.189 | 0.268 | 0.637 | 0.168 | 0.268 |
| Juniperus chinensis L. | 286 | 0.734 | 0.165 | 0.580 | 0.727 | 0.174 | 0.580 | 0.740 | 0.158 | 0.580 |
| Salix chaenomeloides Kimura | 277 | 0.509 | 0.168 | 0.054 | 0.496 | 0.179 | 0.054 | 0.523 | 0.159 | 0.054 |
| Pinus thunbergii Parl. | 230 | 0.363 | 0.169 | 0.017 | 0.356 | 0.189 | 0.017 | 0.370 | 0.153 | 0.017 |
| Salix koreensis Andersson | 168 | 0.639 | 0.156 | 0.173 | 0.624 | 0.161 | 0.173 | 0.653 | 0.152 | 0.173 |
| Aphananthe aspera | 146 | 0.420 | 0.169 | 0.014 | 0.426 | 0.185 | 0.014 | 0.414 | 0.156 | 0.014 |
| Camellia japonica L. | 83 | 0.383 | 0.080 | 0 | 0.382 | 0.083 | 0 | 0.384 | 0.079 | 0 |
| Ulmus davidiana var. japonica | 79 | 0.625 | 0.129 | 0.038 | 0.610 | 0.125 | 0.038 | 0.641 | 0.135 | 0.038 |
| Quercus acutissima | 74 | 0.598 | 0.174 | 0.203 | 0.587 | 0.183 | 0.203 | 0.610 | 0.167 | 0.203 |
| Chionanthus retusa | 61 | 0.463 | 0.176 | 0.033 | 0.462 | 0.188 | 0.033 | 0.464 | 0.168 | 0.033 |
| Lagerstroemia indica L. | 54 | 0.551 | 0.141 | 0.074 | 0.537 | 0.153 | 0.074 | 0.565 | 0.131 | 0.074 |
| Quercus variabilis Blume | 52 | 0.558 | 0.124 | 0.019 | 0.545 | 0.139 | 0.019 | 0.572 | 0.114 | 0.019 |
| Kalopanax septemlobus (Thunb.) Koidz. | 51 | 0.689 | 0.160 | 0.412 | 0.677 | 0.170 | 0.412 | 0.700 | 0.152 | 0.412 |
| Carpinus laxiflora | 43 | 0.432 | 0.153 | 0 | 0.427 | 0.169 | 0 | 0.438 | 0.142 | 0 |
| Pinus densiflora Siebold & Zucc- | 36 | 0.430 | 0.074 | 0 | 0.425 | 0.077 | 0 | 0.434 | 0.079 | 0 |
| Pyrus pyrifolia | 34 | 0.578 | 0.136 | 0.059 | 0.564 | 0.138 | 0.059 | 0.593 | 0.137 | 0.059 |
Table 12.
Distribution of sensitivity labels (heat vs. flood) for high-risk individuals (≥90th percentile) in species located within the Top 20 counties common to all three scenarios.
Table 12.
Distribution of sensitivity labels (heat vs. flood) for high-risk individuals (≥90th percentile) in species located within the Top 20 counties common to all three scenarios.
| | Species_Heat_Label | Species_Rainfall_Label | Count | Scenario |
|---|
| 1 | Strong | Weak | 446 | A |
| 2 | Moderate | Weak | 402 | A |
| 3 | Strong | Moderate | 322 | A |
| 4 | Moderate | Strong | 40 | A |
| 5 | Moderate | Moderate | 10 | A |
| 6 | Weak | Weak | 3 | A |
| 1 | Strong | Weak | 446 | B |
| 2 | Moderate | Weak | 402 | B |
| 3 | Strong | Moderate | 335 | B |
| 4 | Moderate | Moderate | 10 | B |
| 5 | Moderate | Strong | 9 | B |
| 6 | Weak | Weak | 3 | B |
| 1 | Strong | Weak | 446 | C |
| 2 | Strong | Moderate | 332 | C |
| 3 | Moderate | Weak | 279 | C |
| 4 | Moderate | Strong | 40 | C |
| 5 | Moderate | Moderate | 10 | C |
| 6 | Weak | Weak | 3 | C |
Table 13.
Differences in species-level median risk values within counties that are hot spots (HH) across all three scenarios (A, B, C). Here, n_nat denotes the number of individuals of the species nationwide, while n_hot is the number of individuals of that species located within counties that are consistently HH across scenarios. The table reports the median risk within the hot-spot set (med_hot) and compares it with the nationwide median (med_nat), with the difference expressed as Δmed. This allows identification of species that are disproportionately elevated in high-risk areas.
Table 13.
Differences in species-level median risk values within counties that are hot spots (HH) across all three scenarios (A, B, C). Here, n_nat denotes the number of individuals of the species nationwide, while n_hot is the number of individuals of that species located within counties that are consistently HH across scenarios. The table reports the median risk within the hot-spot set (med_hot) and compares it with the nationwide median (med_nat), with the difference expressed as Δmed. This allows identification of species that are disproportionately elevated in high-risk areas.
| | Species | n_nat | med_nat | n_hot | med_hot | Delta(Δ)_Med |
|---|
| 1 | Ginkgo tree (Ginkgo biloba) | 840 | 0.250 | 70 | 0.633 | 0.383 |
| 2 | Juniper (Juniperus spp.) | 286 | 0.192 | 14 | 0.558 | 0.367 |
| 3 | Korean red pine (Pinus densiflora) | 804 | 0.442 | 154 | 0.692 | 0.250 |
| 4 | Crape myrtle (Lagerstroemia indica) | 54 | 0.383 | 6 | 0.633 | 0.250 |
| 5 | Sawtooth oak (Quercus acutissima) | 74 | 0.375 | 14 | 0.625 | 0.250 |
| 6 | Japanese pagoda tree (Styphnolobium japonicum) | 328 | 0.317 | 27 | 0.550 | 0.233 |
| 7 | Zelkova tree (Zelkova serrata) | 6694 | 0.383 | 1169 | 0.617 | 0.233 |
| 8 | Hornbeam (Carpinus laxiflora) | 43 | 0.575 | 26 | 0.808 | 0.233 |
| 9 | Elm (Ulmus spp.) | 79 | 0.375 | 6 | 0.567 | 0.192 |
| 10 | Willow (Salix chaenomeloides) | 277 | 0.425 | 69 | 0.558 | 0.133 |
| 11 | Willow (Salix koreensis) | 168 | 0.308 | 9 | 0.425 | 0.117 |
| 12 | Chinese fringetree (Chionanthus retusus) | 61 | 0.575 | 32 | 0.692 | 0.117 |
| 13 | Muku tree (Aphananthe aspera) | 146 | 0.450 | 98 | 0.567 | 0.117 |
| 14 | Camellia (Camellia japonica L.) | 83 | 0.692 | 17 | 0.692 | 0.000 |
| 15 | Oriental white oak (Quercus variabilis) | 52 | 0.492 | 18 | 0.492 | 0.000 |
| 16 | Hackberry (Celtis sinensis) | 1147 | 0.567 | 609 | 0.567 | 0.000 |
| 17 | Black pine (Pinus thunbergii) | 230 | 0.808 | 198 | 0.808 | 0.000 |
Table 14.
Component decomposition summary of counties included in the Top 20 across all scenarios (based on mean risk). Includes normalized values for heat, rainfall, and species sensitivity components.
Table 14.
Component decomposition summary of counties included in the Top 20 across all scenarios (based on mean risk). Includes normalized values for heat, rainfall, and species sensitivity components.
| Province | District | Heat_
Vulner | Rain
_Vulner | Spcies
_Heat | Species
_Rainfall | Species
_S_A | Species
_S_B | Species
_S_C |
|---|
| Busan | Suyeong-gu | 0.667 | 1.000 | 0.278 | 0.778 | 0.478 | 0.544 | 0.444 |
| Gyeongsangbuk-do | Bonghwa-gun | 0.667 | 0.667 | 0.250 | 0.883 | 0.503 | 0.588 | 0.461 |
| Gyeongsangbuk-do | Yeongcheon-si | 0.667 | 0.667 | 0.141 | 0.880 | 0.437 | 0.536 | 0.388 |
| Gyeongsangnam-do | Hadong-gun | 1.000 | 0.667 | 0.259 | 0.852 | 0.496 | 0.575 | 0.457 |
| Gyeongsangnam-do | Hapcheon-gun | 1.000 | 0.667 | 0.075 | 0.872 | 0.394 | 0.500 | 0.340 |
| Gyeongsangnam-do | Namhae-gun | 1.000 | 0.667 | 0.125 | 0.875 | 0.425 | 0.525 | 0.375 |
| Jeollabuk-do | Gochang-gun | 1.000 | 0.667 | 0.133 | 0.838 | 0.415 | 0.509 | 0.368 |
| Jeollabuk-do | Imsil-gun | 1.000 | 0.667 | 0.020 | 0.940 | 0.388 | 0.511 | 0.327 |
| Jeollanam-do | Boseong-gun | 1.000 | 1.000 | 0.058 | 0.861 | 0.379 | 0.486 | 0.326 |
| Jeollanam-do | Gangjin-gun | 0.667 | 1.000 | 0.031 | 0.719 | 0.306 | 0.398 | 0.260 |
| Jeollanam-do | Haenam-gun | 1.000 | 0.667 | 0.223 | 0.745 | 0.432 | 0.502 | 0.397 |
| Jeollanam-do | Hampyeong-gun | 0.667 | 0.667 | 0.182 | 0.846 | 0.448 | 0.537 | 0.404 |
| Jeollanam-do | Jangheung-gun | 1.000 | 1.000 | 0.142 | 0.826 | 0.416 | 0.507 | 0.370 |
| Jeollanam-do | Jindo-gun | 1.000 | 1.000 | 0.177 | 0.745 | 0.404 | 0.480 | 0.366 |
| Jeollanam-do | Wando-gun | 1.000 | 0.667 | 0.139 | 0.738 | 0.379 | 0.459 | 0.339 |
Table 15.
Policy and priority list based on Scenario B (90th-percentile threshold applied nationwide). In the recommendation field, X refers to “drainage channel maintenance/permeable paving and rain gardens/securing soil depth/improving root respiration of flood-sensitive species (through soil aeration and mounding)”, while Y refers to “providing shade/installing shade nets and managing evapotranspiration (e.g., mulching)/optimizing irrigation schedules/protecting trunks with reflective coatings/monitoring soil moisture.”
Table 15.
Policy and priority list based on Scenario B (90th-percentile threshold applied nationwide). In the recommendation field, X refers to “drainage channel maintenance/permeable paving and rain gardens/securing soil depth/improving root respiration of flood-sensitive species (through soil aeration and mounding)”, while Y refers to “providing shade/installing shade nets and managing evapotranspiration (e.g., mulching)/optimizing irrigation schedules/protecting trunks with reflective coatings/monitoring soil moisture.”
| Province/District | Exceed_n | Exceed_rate | Dom_Heat | Dom_Rainfall | Top3_Species | Recommendation |
|---|
| Jeollanam-do/Haenam-gun | 297 | 0.946 | Strong | Moderate | Hackberry, Black pine, Zelkova | X |
| Jeollanam-do/Boseong-gun | 234 | 1.000 | Strong | Weak | Zelkova, Hackberry, Muku tree | X |
| Jeollanam-do/Jangheung-gun | 141 | 1.000 | Strong | Weak | Zelkova, Hackberry, Red pine | X |
| Jeollabuk-do/Gochang-gun | 97 | 0.924 | Strong | Weak | Zelkova, Red pine, Hackberry | X |
| Jeollanam-do/Hampyeong-gun | 90 | 0.304 | Moderate | Weak | Camellia, Red Pine, Chinese quince | Y |
| Gyeongsangnam-do/Hadong-gun | 80 | 0.988 | Moderate | Weak | Zelkova, Red pine, Hackberry | Y |
| Jeollanam-do/Wando-gun | 61 | 1.000 | Strong | Moderate | Hackberry, Zelkova, Black pine | X |
| Jeollanam-do/Jindo-gun | 51 | 1.000 | Strong | Moderate | Hackberry, Black pine, Zelkova | X |
| Gyeongsangnam-do/Hapcheon-gun | 43 | 0.915 | Strong | Weak | Zelkova, Ginkgo, Hackberry | X |
| Jeollanam-do/Yeongam-gun | 36 | 0.333 | Moderate | Weak | Black pine, Red pine, Chinese quince | Y |
| Gyeongsangnam-do/Namhae-gun | 28 | 1.000 | Strong | Weak | Zelkova, Hackberry, Red pine | X |
| Jeollabuk-do/Imsil-gun | 24 | 0.960 | Strong | Weak | Zelkova, Ginkgo, Hackberry | X |
| Gyeongsangbuk-do/Bonghwa-gun | 23 | 0.383 | Moderate | Weak | Red pine, Wild pear, Korean fir | Y |
| Jeollanam-do/Gokseong-gun | 21 | 0.119 | Moderate | Weak | Red pine, Chinese fringetree, Maple | Y |
| Jeollanam-do/Gangjin-gun | 16 | 1.000 | Strong | Moderate | Hackberry, Zelkova, Black pine | X |
| Jeju/Seogwipo-si | 15 | 0.357 | Moderate | Weak | Camellia, Japanese big-leaf magnolia, Red pine | Y |
| Gyeongsangbuk-do/Yeongcheon-si | 11 | 0.239 | Moderate | Weak | Juniper, Red pine, Dwarf pine | Y |
| Jeollanam-do/Sinan-gun | 10 | 0.086 | Moderate | Weak | Red pine, Black pine, Camellia | Y |
| Busan/Suyeong-gu | 9 | 1.000 | Moderate | Weak | Red pine, Hackberry | Y |
| Gyeongsangnam-do/Goseong-gun | 9 | 0.192 | Moderate | Weak | Red pine, Black pine, Wild pear | Y |
| Gyeongsangnam-do/Haman-gun | 8 | 0.116 | Moderate | Weak | Chinese fringetree, Redvein dogwood, Wild pear | Y |
| Chungcheongnam-do/Cheongyang-gun | 8 | 0.096 | Moderate | Weak | Red pine, Cudrania, Wild pear | Y |
| Gyeongsangbuk-do/Yeongdeok-gun | 7 | 0.130 | Moderate | Weak | Red pine, Redvein dogwood, Chinese pistache | Y |
| Jeollabuk-do/Muju-gun | 7 | 0.125 | Moderate | Weak | Red pine | Y |
| Jeollabuk-do/Jinan-gun | 5 | 0.085 | Moderate | Weak | Red pine | Y |
| Jeollanam-do Yeonggwang-gun | 5 | 0.057 | Moderate | Weak | Red pine, Japanese torreya | Y |
| Gyeongsangnam-do Changnyeong-gun | 4 | 0.083 | Moderate | Weak | Chinese fringetree, Red pine | Y |
| Gyeongsangnam-do Sancheong-gun | 3 | 0.071 | Moderate | Weak | Persimmon, Japanese apricot, Red pine | Y |
| Gyeongsangnam-do Uiryeong-gun | 2 | 0.039 | Moderate | Weak | Chinese soapberry, Red pine | Y |
| Busan Seo-gu | 1 | 0.500 | Moderate | Weak | Black pine | Y |
| Busan Sasang-gu | 1 | 0.167 | Moderate | Weak | Red pine | Y |
Table 16.
Extreme-risk membership by definition (p90 vs. Q4) on district-level p95 (Scenario B). Under the national p90 rule (top decile), districts with p95 ≥ 0.9234 are classified as extreme (n = 24). Under the quartile rule (Q4, top quartile), districts with p95 ≥ 0.8290 are classified as extreme (n = 59). Q4 fully contains p90 (intersection = 24; p90-only = 0; Q4-only = 35; Jaccard = 0.407). The table lists members only (both/Q4-only), ordered by p95. All thresholds are based on the national distribution (ties included). The analysis covers 234 districts with ≥1 protected tree.
Table 16.
Extreme-risk membership by definition (p90 vs. Q4) on district-level p95 (Scenario B). Under the national p90 rule (top decile), districts with p95 ≥ 0.9234 are classified as extreme (n = 24). Under the quartile rule (Q4, top quartile), districts with p95 ≥ 0.8290 are classified as extreme (n = 59). Q4 fully contains p90 (intersection = 24; p90-only = 0; Q4-only = 35; Jaccard = 0.407). The table lists members only (both/Q4-only), ordered by p95. All thresholds are based on the national distribution (ties included). The analysis covers 234 districts with ≥1 protected tree.
| Province | District | p95 | Mean | Size (n) | Category |
|---|
| Gyeongsangnam-do | Goseong-gun | 0.942 | 0.870 | 47 | both |
| Gyeongsangnam-do | Namhae-gun | 0.942 | 0.881 | 28 | both |
| Jeollanam-do | Boseong-gun | 0.942 | 0.872 | 234 | both |
| Jeollanam-do | Jangheung-gun | 0.942 | 0.877 | 141 | both |
| Jeollanam-do | Jindo-gun | 0.942 | 0.870 | 51 | both |
| Gyeongsangnam-do | Sancheong-gun | 0.939 | 0.881 | 42 | both |
| Busan | Seo-gu | 0.935 | 0.879 | 2 | both |
| Jeollanam-do | Gangjin-gun | 0.898 | 0.850 | 16 | both |
| Gyeongsangnam-do | Haman-gun | 0.825 | 0.759 | 69 | both |
| Gyeongsangnam-do | Sacheon-si | 0.825 | 0.769 | 32 | both |
| Busan | Sasang-gu | 0.810 | 0.732 | 6 | both |
| Gyeongsangbuk-do | Bonghwa-gun | 0.808 | 0.764 | 60 | both |
| Gyeongsangbuk-do | Yeongcheon-si | 0.808 | 0.751 | 46 | both |
| Gyeongsangnam-do | Changnyeong-gun | 0.808 | 0.738 | 48 | both |
| Gyeongsangnam-do | Hadong-gun | 0.808 | 0.761 | 81 | both |
| Gyeongsangnam-do | Miryang-si | 0.808 | 0.743 | 48 | both |
| Jeollabuk-do | Gochang-gun | 0.808 | 0.744 | 105 | both |
| Jeollabuk-do | Jinan-gun | 0.808 | 0.754 | 59 | both |
| Jeollabuk-do | Muju-gun | 0.808 | 0.756 | 56 | both |
| Jeollanam-do | Gokseong-gun | 0.808 | 0.747 | 176 | both |
| Jeollanam-do | Haenam-gun | 0.808 | 0.742 | 314 | both |
| Jeollanam-do | Hampyeong-gun | 0.808 | 0.751 | 296 | both |
| Jeollanam-do | Wando-gun | 0.808 | 0.731 | 61 | both |
| Busan | Buk-gu | 0.767 | 0.719 | 7 | both |
| Busan | Saha-gu | 0.763 | 0.714 | 9 | q4_only |
| Gyeongsangnam-do | Uiryeong-gun | 0.750 | 0.735 | 52 | q4_only |
| Gangwon-do | Taebaek-si | 0.747 | 0.721 | 2 | q4_only |
| Busan | Haeundae-gu | 0.708 | 0.672 | 10 | q4_only |
| Busan | Nam-gu | 0.708 | 0.708 | 5 | q4_only |
| Busan | Suyeong-gu | 0.708 | 0.653 | 9 | q4_only |
| Busan | Yeonje-gu | 0.708 | 0.708 | 1 | q4_only |
| Gyeongsangnam-do | Jinhae-gu (Changwon-si) | 0.708 | 0.663 | 9 | q4_only |
| Gyeongsangnam-do | Seongsan-gu (Changwon-si) | 0.708 | 0.630 | 8 | q4_only |
| Jeju | Jeju-si | 0.708 | 0.622 | 115 | q4_only |
| Jeju | Seogwipo-si | 0.708 | 0.631 | 42 | q4_only |
| Jeollanam-do | Suncheon-si | 0.708 | 0.641 | 108 | q4_only |
| Jeollanam-do | Yeongam-gun | 0.708 | 0.643 | 108 | q4_only |
| Busan | Busanjin-gu | 0.702 | 0.646 | 2 | q4_only |
| Chungcheongnam-do | Cheongyang-gun | 0.692 | 0.635 | 83 | q4_only |
| Gangwon-do | Goseong-gun | 0.692 | 0.644 | 12 | q4_only |
| Gangwon-do | Samcheok-si | 0.692 | 0.643 | 52 | q4_only |
| Gyeonggi-do | Yeoncheon-gun | 0.692 | 0.647 | 12 | q4_only |
| Gyeongsangbuk-do | Yeongju-si | 0.692 | 0.636 | 128 | q4_only |
| Gyeongsangnam-do | Tongyeong-si | 0.692 | 0.626 | 21 | q4_only |
| Jeollabuk-do | Wanju-gun | 0.677 | 0.631 | 46 | q4_only |
| Gyeongsangbuk-do | Cheongdo-gun | 0.675 | 0.613 | 29 | q4_only |
| Gyeongsangbuk-do | Yeongdeok-gun | 0.675 | 0.611 | 54 | q4_only |
| Jeollanam-do | Gurye-gun | 0.675 | 0.604 | 108 | q4_only |
| Jeollanam-do | Sinan-gun | 0.675 | 0.562 | 117 | q4_only |
| Gyeongsangnam-do | Gimhae-si | 0.665 | 0.612 | 36 | q4_only |
| Jeollanam-do | Yeonggwang-gun | 0.655 | 0.600 | 88 | q4_only |
| Busan | Geumjeong-gu | 0.650 | 0.606 | 6 | q4_only |
| Gyeongsangnam-do | Masanhappo-gu (Changwon-si) | 0.650 | 0.597 | 33 | q4_only |
| Gyeongsangnam-do | Masanhoewon-gu (Changwon-si) | 0.650 | 0.637 | 10 | q4_only |
| Busan | Dongnae-gu | 0.640 | 0.600 | 4 | q4_only |
| Jeollanam-do | Mokpo-si | 0.630 | 0.600 | 2 | q4_only |
| Gyeongsangnam-do | Hapcheon-gun | 0.617 | 0.608 | 47 | q4_only |
| Jeollabuk-do | Imsil-gun | 0.617 | 0.611 | 25 | q4_only |
| Jeollanam-do | Gwangyang-si | 0.592 | 0.524 | 154 | q4_only |
Table 17.
Province-level comparison of national vs. province-specific 90th-percentile thresholds (district p95, Scenario B)—counts. For each province (labeled with n), we report the number of districts classified as priority by both rules, national-only, and province-only, together with the agreement rate (share of districts where the two rules agree: both priority or both non-priority) and dispersion indicators (CV/IQR). Using counts avoids small-n exaggeration (e.g., Sejong n = 1; Jeju n = 2).
Table 17.
Province-level comparison of national vs. province-specific 90th-percentile thresholds (district p95, Scenario B)—counts. For each province (labeled with n), we report the number of districts classified as priority by both rules, national-only, and province-only, together with the agreement rate (share of districts where the two rules agree: both priority or both non-priority) and dispersion indicators (CV/IQR). Using counts avoids small-n exaggeration (e.g., Sejong n = 1; Jeju n = 2).
| Province | n_
Districts | Both_
Count | National_
Only_Count | Province_
Only_Count | Agreement
_Rate | CV_
p95 | IQR_
p95 |
|---|
| Sejong | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| Gwangju | 5 | 0 | 0 | 1 | 0.800 | 0.393 | 0.192 |
| Daejeon | 5 | 0 | 0 | 1 | 0.800 | 0.332 | 0.061 |
| Ulsan | 5 | 0 | 0 | 1 | 0.800 | 0.220 | 0.117 |
| Chungcheongnam-do | 16 | 1 | 0 | 3 | 0.813 | 0.436 | 0.279 |
| Chungcheongbuk-do | 13 | 0 | 0 | 2 | 0.846 | 0.408 | 0.317 |
| Daegu | 7 | 0 | 0 | 1 | 0.857 | 0.410 | 0.191 |
| Seoul | 22 | 0 | 0 | 3 | 0.864 | 0.308 | 0.125 |
| Incheon | 8 | 0 | 0 | 1 | 0.875 | 0.301 | 0.149 |
| Gyeonggi-do | 41 | 0 | 0 | 5 | 0.878 | 0.379 | 0.131 |
| Gangwon-do | 17 | 0 | 0 | 2 | 0.882 | 0.250 | 0.133 |
| Busan | 13 | 1 | 0 | 1 | 0.923 | 0.198 | 0.130 |
| Gyeongsangbuk-do | 24 | 3 | 0 | 0 | 1 | 0.339 | 0.150 |
| Gyeongsangnam-do | 22 | 3 | 3 | 0 | 0.864 | 0.305 | 0.231 |
| Jeollabuk-do | 13 | 2 | 2 | 0 | 0.846 | 0.278 | 0.265 |
| Jeollanam-do | 20 | 3 | 7 | 0 | 0.650 | 0.219 | 0.217 |
| Jeju | 2 | 1 | 0 | 0 | 1 | 0.092 | 0.058 |
Table 18.
Summary of Local Moran’s I (a form of LISA) under Scenario B. mean_r indicates the mean risk in Scenario B for each district. local_I is the Local Moran’s I statistic, representing the degree to which a district’s value moves in tandem with its neighbors (higher values indicate stronger similarity, such as “I am high and my neighbors are also high”). p_local reports the p-values of Local Moran’s I obtained through permutation tests (two-sided). Significance is set at p < 0.05, based on 999 permutations.
Table 18.
Summary of Local Moran’s I (a form of LISA) under Scenario B. mean_r indicates the mean risk in Scenario B for each district. local_I is the Local Moran’s I statistic, representing the degree to which a district’s value moves in tandem with its neighbors (higher values indicate stronger similarity, such as “I am high and my neighbors are also high”). p_local reports the p-values of Local Moran’s I obtained through permutation tests (two-sided). Significance is set at p < 0.05, based on 999 permutations.
| | Province | District | Mean_r | Local_I | p_Local | Cluster |
|---|
| 1 | Jeollanam-do | Jindo-gun | 0.870 | 3.995 | 0.001 | HH |
| 2 | Jeollanam-do | Jangheung-gun | 0.877 | 3.798 | 0.001 | HH |
| 3 | Jeollanam-do | Haenam-gun | 0.742 | 3.515 | 0.001 | HH |
| 4 | Jeollanam-do | Wando-gun | 0.731 | 3.424 | 0.001 | HH |
| 5 | Jeollanam-do | Boseong-gun | 0.872 | 3.170 | 0.001 | HH |
| 6 | Jeollanam-do | Gangjin-gun | 0.733 | 2.793 | 0.001 | HH |
| 7 | Jeju | Seogwipo-si | 0.614 | 2.268 | 0.001 | HH |
| 8 | Jeollanam-do | Yeongam-gun | 0.626 | 2.221 | 0.001 | HH |
| 9 | Jeollanam-do | Mokpo-si | 0.600 | 1.924 | 0.001 | HH |
| 10 | Gyeongsangnam-do | Hadong-gun | 0.761 | 1.902 | 0.005 | HH |
| 11 | Gyeonggi-do | Cheoin-gu (Yongin-si) | 0.134 | 1.731 | 0.001 | LL |
| 12 | Gyeonggi-do | Anseong-si | 0.140 | 1.704 | 0.001 | LL |
| 13 | Gyeonggi-do | Jangan-gu (Suwon-si) | 0.133 | 1.615 | 0.001 | LL |
| 14 | Gyeonggi-do | Bundang-gu (Seongnam-si) | 0.140 | 1.598 | 0.001 | LL |
| 15 | Gyeonggi-do | Pyeongtaek-si | 0.137 | 1.586 | 0.001 | LL |
| 16 | Gyeonggi-do | Giheung-gu (Yongin-si) | 0.141 | 1.583 | 0.001 | LL |
| 17 | Chungcheongbuk-do | Jincheon-gun | 0.133 | 1.545 | 0.001 | LL |
| 18 | Gyeongsangnam-do | Namhae-gun | 0.748 | 1.535 | 0.016 | HH |
| 19 | Gyeonggi-do | Yeongtong-gu (Suwon-si) | 0.133 | 1.520 | 0.001 | LL |
| 20 | Gyeonggi-do | Hwaseong-si | 0.132 | 1.515 | 0.001 | LL |
| 21 | Busan | Suyeong-gu | 0.769 | 1.466 | 0.027 | HH |
| 22 | Gyeongsangnam-do | Hapcheon-gun | 0.742 | 1.446 | 0.019 | HH |
| 23 | Gyeonggi-do | Ilsandong-gu (Goyang-si) | 0.107 | 1.437 | 0.003 | LL |
| 24 | Gyeonggi-do | Icheon-si | 0.141 | 1.435 | 0.001 | LL |
| 25 | Gyeonggi-do | Gwonseon-gu (Suwon-si) | 0.155 | 1.408 | 0.001 | LL |
| 26 | Chungcheongnam-do | Seobuk-gu (Cheonan-si) | 0.139 | 1.389 | 0.001 | LL |
| 27 | Chungcheongnam-do | Eumseong-gun | 0.135 | 1.361 | 0.003 | LL |
| 28 | Gyeonggi-do | Gwangju-si | 0.135 | 1.358 | 0.002 | LL |
| 29 | Gyeonggi-do | Suji-gu (Yongin-si) | 0.140 | 1.350 | 0.002 | LL |
| 30 | Gyeonggi-do | Yeoju-si | 0.147 | 1.316 | 0.001 | LL |
Table 19.
LISA neighbor sensitivity summary (α = 0.05, permutations = 999, Scenario B). n_sig indicates the number of significant LISA locations; HH, LH, LL, and HL refer to the counts of significant clusters by type. global_I and global_p denote the global Moran’s I and its significance level, respectively. jaccard_vs_k8 reports the Jaccard similarity of HH/LL locations compared with the baseline k = 8.
Table 19.
LISA neighbor sensitivity summary (α = 0.05, permutations = 999, Scenario B). n_sig indicates the number of significant LISA locations; HH, LH, LL, and HL refer to the counts of significant clusters by type. global_I and global_p denote the global Moran’s I and its significance level, respectively. jaccard_vs_k8 reports the Jaccard similarity of HH/LL locations compared with the baseline k = 8.
| | Neighbor | n_sig | HH | LH | LL | HL | Global_I | Global_p | Jaccard_vs_k8_HH | Jaccard_vs_k8_LL |
|---|
| 1 | knn6 | 90 | 39 | 4 | 41 | 6 | 0.494 | 0.001 | 0.902 | 0.826 |
| 2 | knn7 | 88 | 38 | 4 | 40 | 6 | 0.482 | 0.001 | 0.974 | 0.886 |
| 3 | knn8 | 93 | 39 | 4 | 43 | 7 | 0.476 | 0.001 | 1.000 | 1.000 |
| 4 | knn9 | 98 | 43 | 8 | 41 | 6 | 0.460 | 0.001 | 0.907 | 0.867 |
| 5 | knn10 | 106 | 43 | 10 | 44 | 9 | 0.447 | 0.001 | 0.864 | 0.851 |
| 6 | knn11 | 116 | 46 | 12 | 50 | 8 | 0.432 | 0.001 | 0.771 | 0.789 |
| 7 | knn12 | 120 | 46 | 15 | 51 | 8 | 0.414 | 0.001 | 0.700 | 0.774 |
Table 20.
Province-level dispersion highlights (district p95, Scenario B). Top and bottom provinces by district-level p95 dispersion (CV). Values are computed under Scenario B; ordered within each group by CV. Interpret Jeju (n = 2) with caution due to small sample size.
Table 20.
Province-level dispersion highlights (district p95, Scenario B). Top and bottom provinces by district-level p95 dispersion (CV). Values are computed under Scenario B; ordered within each group by CV. Interpret Jeju (n = 2) with caution due to small sample size.
| Province | CV (p95) | IQR (p95) | n_Districts | Dispersion Group (by CV) |
|---|
| Gyeonggi-do | 0.484 | 0.134 | 41 | High-dispersion (Top 5 CV) |
| Daejeon | 0.432 | 0.099 | 5 | High-dispersion (Top 5 CV) |
| Chungcheongbuk-do | 0.418 | 0.242 | 13 | High-dispersion (Top 5 CV) |
| Chungcheongnam-do | 0.376 | 0.233 | 16 | High-dispersion (Top 5 CV) |
| Incheon | 0.357 | 0.102 | 8 | High-dispersion (Top 5 CV) |
| Jeju | 0 | 0 | 2 | Low-dispersion (Bottom 5 CV) |
| Busan | 0.135 | 0.113 | 13 | Low-dispersion (Bottom 5 CV) |
| Ulsan | 0.195 | 0 | 5 | Low-dispersion (Bottom 5 CV) |
| Jeollanam-do | 0.210 | 0.221 | 20 | Low-dispersion (Bottom 5 CV) |
| Daegu | 0.236 | 0.130 | 7 | Low-dispersion (Bottom 5 CV) |
Table 21.
Scenario-based sensitivity (Spearman ρ). Scenario-based sensitivity checks indicate that district rankings are highly stable across weighting schemes (Spearman’s ρ: A–B = 0.983, A–C = 0.999, B–C = 0.976; all p < 0.001). These results suggest that our substantive conclusions are robust to reasonable changes in the relative weights of heat, precipitation, and species sensitivity.
Table 21.
Scenario-based sensitivity (Spearman ρ). Scenario-based sensitivity checks indicate that district rankings are highly stable across weighting schemes (Spearman’s ρ: A–B = 0.983, A–C = 0.999, B–C = 0.976; all p < 0.001). These results suggest that our substantive conclusions are robust to reasonable changes in the relative weights of heat, precipitation, and species sensitivity.
| Comparison | Spearman p | p-Value |
|---|
| A–B | 0.983 | p < 0.001 |
| A–C | 0.999 | p < 0.001 |
| B–C | 0.976 | p < 0.001 |
Table 22.
Top 20 counties with the largest rank fluctuations across scenarios.
Table 22.
Top 20 counties with the largest rank fluctuations across scenarios.
| | Province | District | Rank_A | Rank_B | Rank_C | Rank_var | Rank_Total_Shift |
|---|
| 1 | Jeollabuk-do | Gunsan-si | 97 | 139 | 85 | 28.355 | 108 |
| 2 | Daegu | Dong-gu | 95 | 135 | 82 | 27.623 | 106 |
| 3 | Seoul | Gangbuk-gu | 96 | 134 | 88 | 24.576 | 92 |
| 4 | Seoul | Yeongdeungpo-gu | 82 | 46 | 88 | 22.716 | 84 |
| 5 | Gyeongsangnam-do | Jinhae-gu (Changwon-si) | 74 | 41 | 79 | 20.648 | 76 |
| 6 | Busan | Geumjeong-gu | 152 | 137 | 173 | 18.083 | 72 |
| 7 | Gyeongsangbuk-do | Yeongju-si | 79 | 45 | 81 | 20.232 | 72 |
| 8 | Gyeongsangnam-do | Sacheon-si | 78 | 44 | 80 | 20.232 | 72 |
| 9 | Gwangju | Dong-gu | 86 | 53 | 88 | 19.655 | 70 |
| 10 | Ulsan | Jung-gu | 73 | 43 | 76 | 18.248 | 66 |
| 11 | Gyeongsangnam-do | Masanhoewon-gu (Changwon-si) | 88 | 62 | 94 | 17.010 | 64 |
| 12 | Gwangju | Nam-gu | 77 | 47 | 78 | 17.616 | 62 |
| 13 | Seoul | Gwangjin-gu | 175 | 145. | 176 | 17.616 | 62 |
| 14 | Gyeonggi-do | Paldal-gu (Suwon-si) | 177 | 147 | 178 | 17.616 | 62 |
| 15 | Gyeonggi-do | Guri-si | 173 | 144 | 174 | 17.039 | 60 |
| 16 | Daejeon | Daedeok-gu | 179 | 149 | 179 | 17.321 | 60 |
| 17 | Busan | Yeonje-gu | 42 | 38 | 68 | 16.289 | 60 |
| 18 | Busan | Nam-gu | 42 | 38 | 68 | 16.289 | 60 |
| 19 | Jeollanam-do | Suncheon-si | 85 | 57 | 87 | 16.773 | 60 |
| 20 | Busan | Busanjin-gu | 76 | 48 | 77 | 16.462 | 58 |
Table 23.
Threshold-sensitive (near-threshold) districts under the national 90th-percentile rule (Scenario B; B = 1000). Districts identified by either criterion—within ±2 percentiles of the national 90th-percentile cutoff or with μ ∈ [0.4,0.6]. Columns: n (trees), p95, 95% CI, Priority status (national 90th-percentile rule) [0/1], Probability of priority status (μ, bootstrap B = 1000), and Percentile rank of p95 in the national distribution. This shortlist is intended for targeted review of threshold-sensitive cases.
Table 23.
Threshold-sensitive (near-threshold) districts under the national 90th-percentile rule (Scenario B; B = 1000). Districts identified by either criterion—within ±2 percentiles of the national 90th-percentile cutoff or with μ ∈ [0.4,0.6]. Columns: n (trees), p95, 95% CI, Priority status (national 90th-percentile rule) [0/1], Probability of priority status (μ, bootstrap B = 1000), and Percentile rank of p95 in the national distribution. This shortlist is intended for targeted review of threshold-sensitive cases.
| Province | District | n_Trees | p95 | p95_
CI_Low | p95_
CI_High | Priority (National p90 Rule) | Priority Membership Probability | Percentile Rank of p95 |
|---|
| Gyeongsangnam-do | Sancheong-gun | 42 | 0.689 | 0.633 | 0.692 | 0 | 0.377 | 0.889 |
| Busan | Seo-gu | 2 | 0.685 | 0.567 | 0.692 | 0 | 0.272 | 0.885 |
| Busan | Sasang-gu | 6 | 0.677 | 0.567 | 0.692 | 0 | 0.295 | 0.880 |
| Gyeongsangnam-do | Changnyeong-gun | 48 | 0.692 | 0.633 | 0.692 | 1 | 0.549 | 0.921 |







_Li.png)



