Sustainable Optimal Capacity Allocation for Grid-Connected Microgrids Incorporating Carbon Capture and Storage Retrofitting in Multi-Market Contexts: A Case Study in Southern China
Abstract
1. Introduction
- CCS modeling
- Microgrid capacity allocation
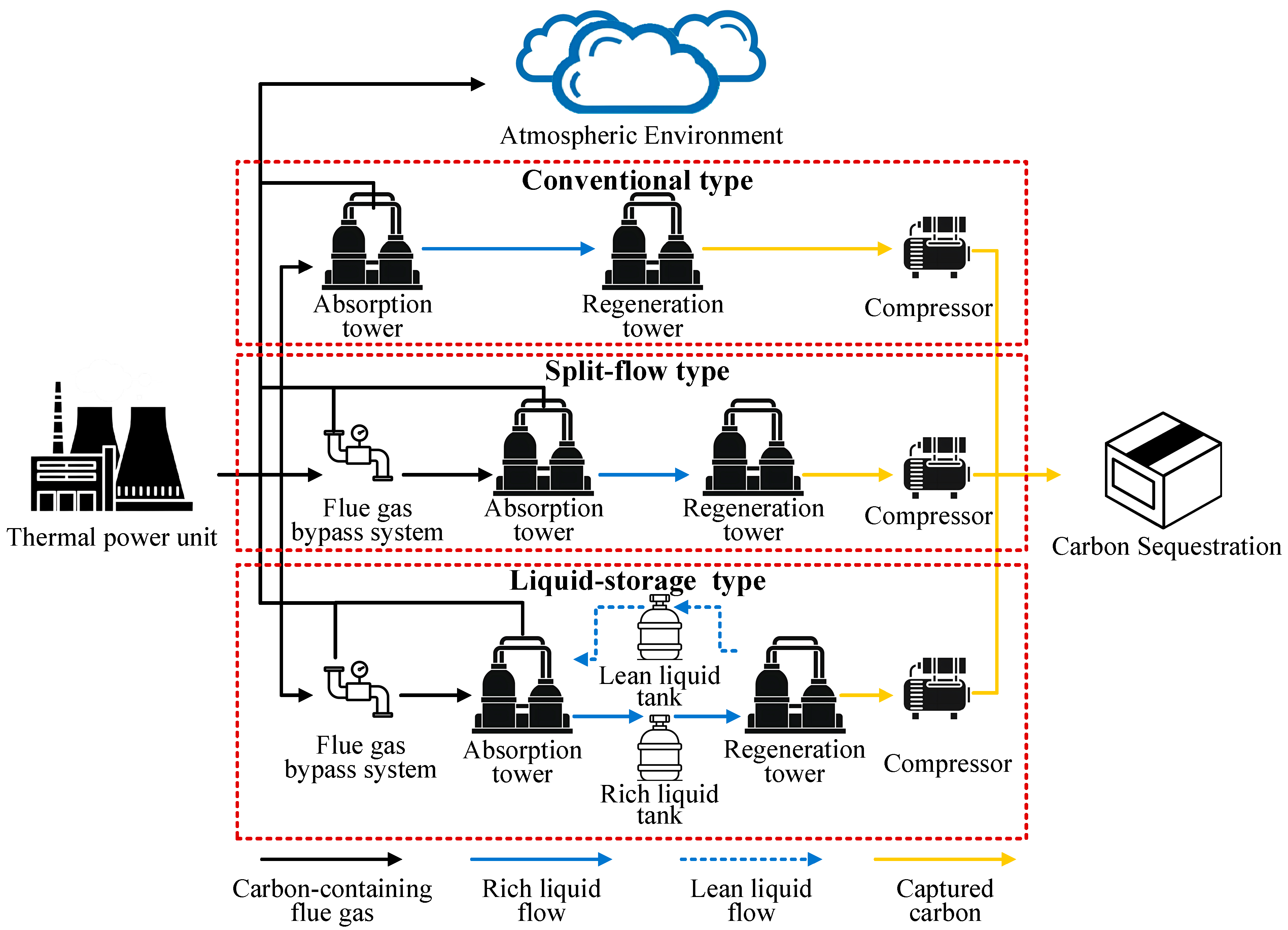
- From the perspective of CCS modeling, this study incorporates monoethanolamine (MEA) absorption characteristics, along with constraints on absorption/desorption rates, compression efficiency, and initial/final liquid tank levels, to construct a liquid-storage CCS/CCPP model. The proposed framework explicitly describes the decoupling processes between carbon capture/release/compression dynamics and between carbon capture intensity and unit output. This approach addresses the limitations of prior research that neglected relationships between CCS electro–carbon coupling characteristics and unit flexibility, thereby failing to fully exploit the temporal optimization potential of CCPPs in coordinating renewable energy, power generation capacity, and carbon capture capability.
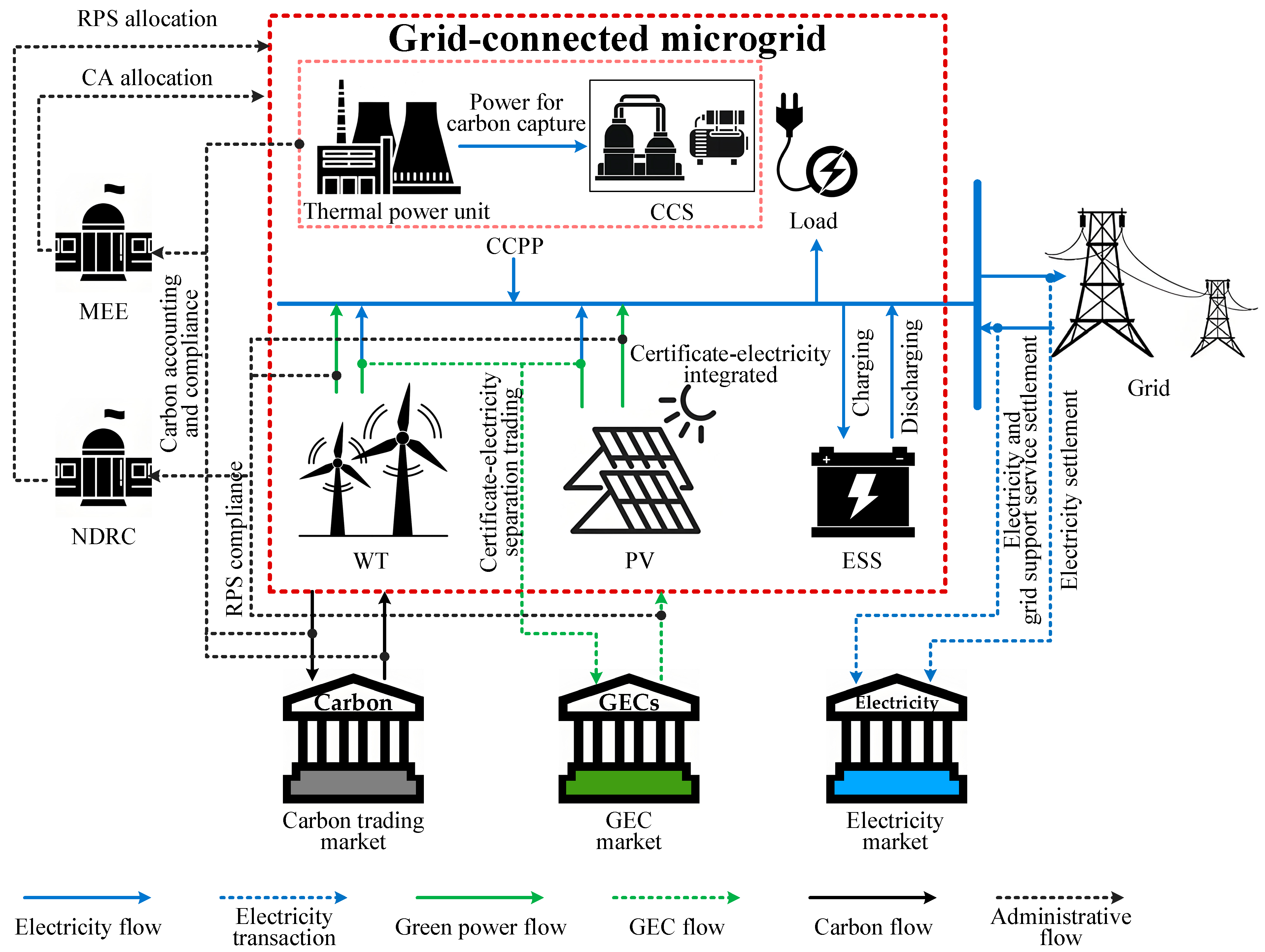
- From the perspective of microgrid capacity allocation, this manuscript incorporates the impact of institutional arrangements (including RPS, CA, and direct green power connections) on the investment and operational decisions of profit-driven microgrid operators. A bi-level optimization framework is developed to characterize how multi-market interactions influence microgrid capacity allocation and operation, addressing the limitations of prior research that suffered from unrealistic policy assumptions and poor temporal adaptability. This manuscript provides practical guidance for microgrid cost structure optimization, investment decision making, energy sustainable development, and energy policy effectiveness assessment.
2. A Grid-Connected Microgrid Capacity Allocation Framework in Multi-Markets
2.1. CCS Retrofitting and Flexibility Analysis of CCPPs
2.2. Capacity Allocation Framework
2.2.1. Market Context and Institutional Arrangements
2.2.2. Microgrid Capacity Allocation Assumptions
3. Capacity Allocation Modeling and Solution
3.1. Upper Planning Model
3.1.1. Objective Function
- Investment cost and maintenance cost
- Replacement cost
- Grid support services cost
- Residual value income
3.1.2. Constraints
- Equipment investment capacity constraint
3.2. Lower Operational Model
3.2.1. Objective Function
- Variable operating cost of equipment
- WT/PV curtailment cost
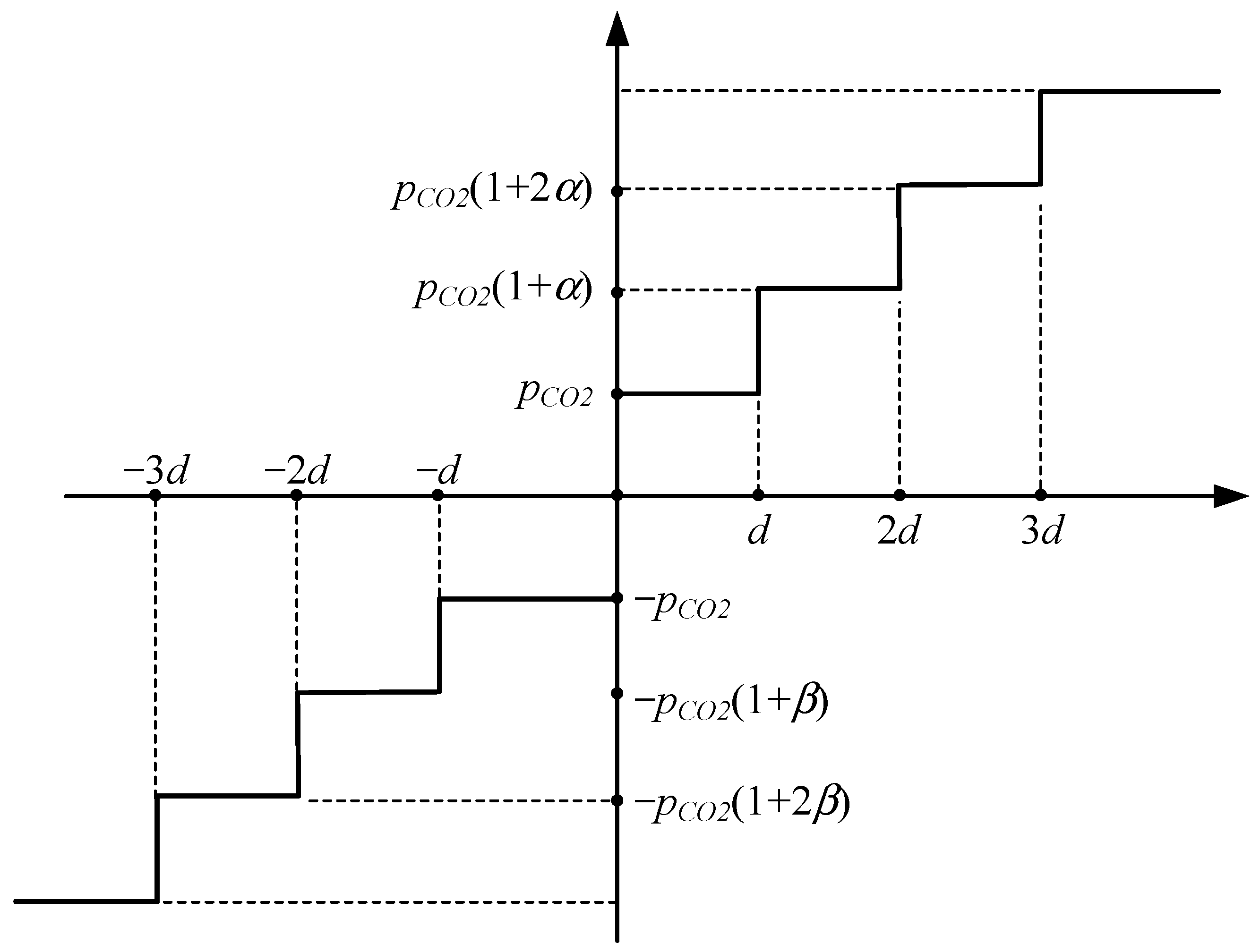
- Carbon trading cost
- GEC trading cost
- Grid power exchange cost
3.2.2. Constraints
- Supply–demand balance constraint of the microgrid
- Constraints on CCPP
- Renewable energy unit output constraints
- ESS constraints
- Grid power exchange constraints
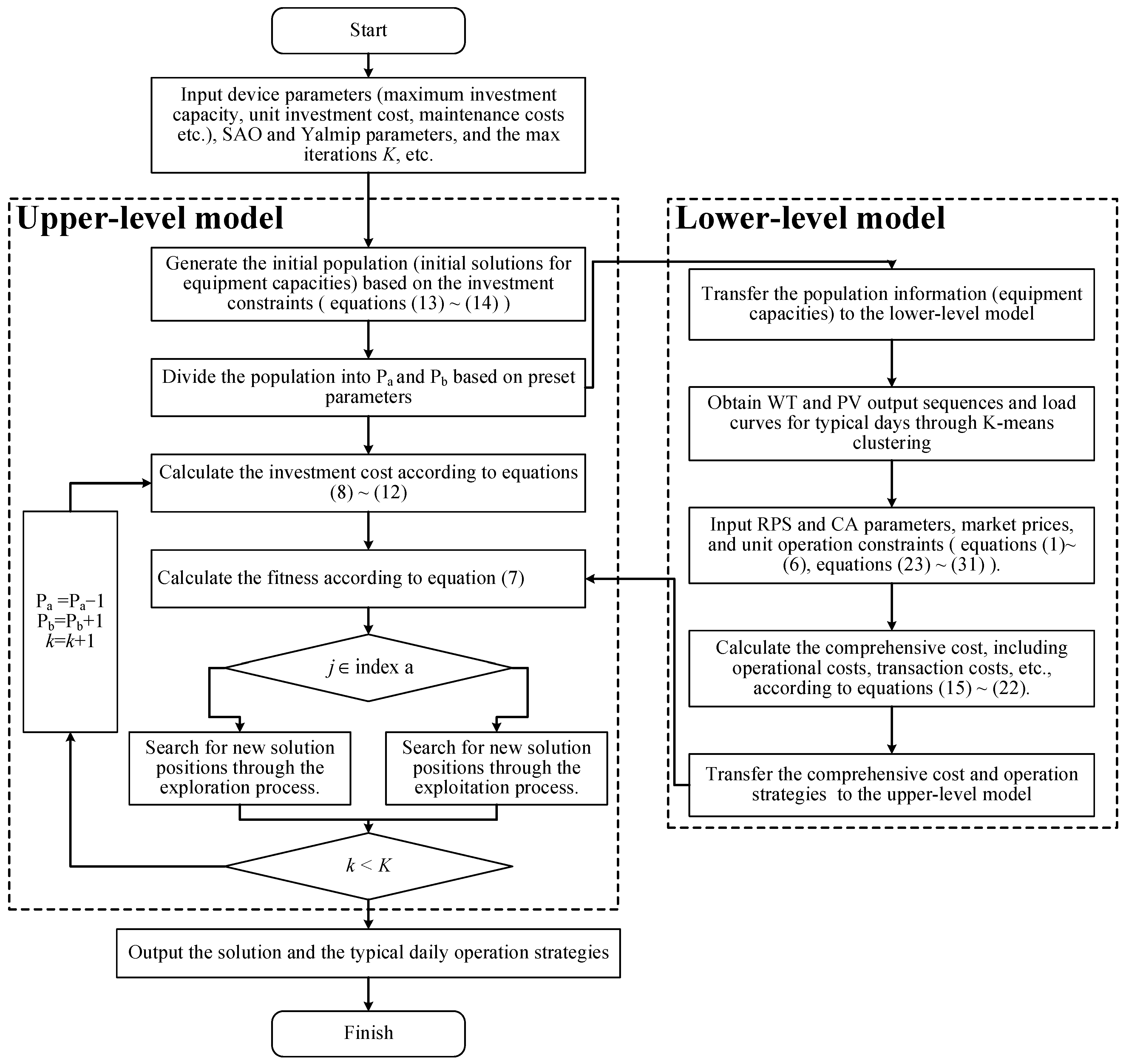
3.3. Solution
- Initial solution generation
- Exploitation
- Exploration
4. Results and Discussion
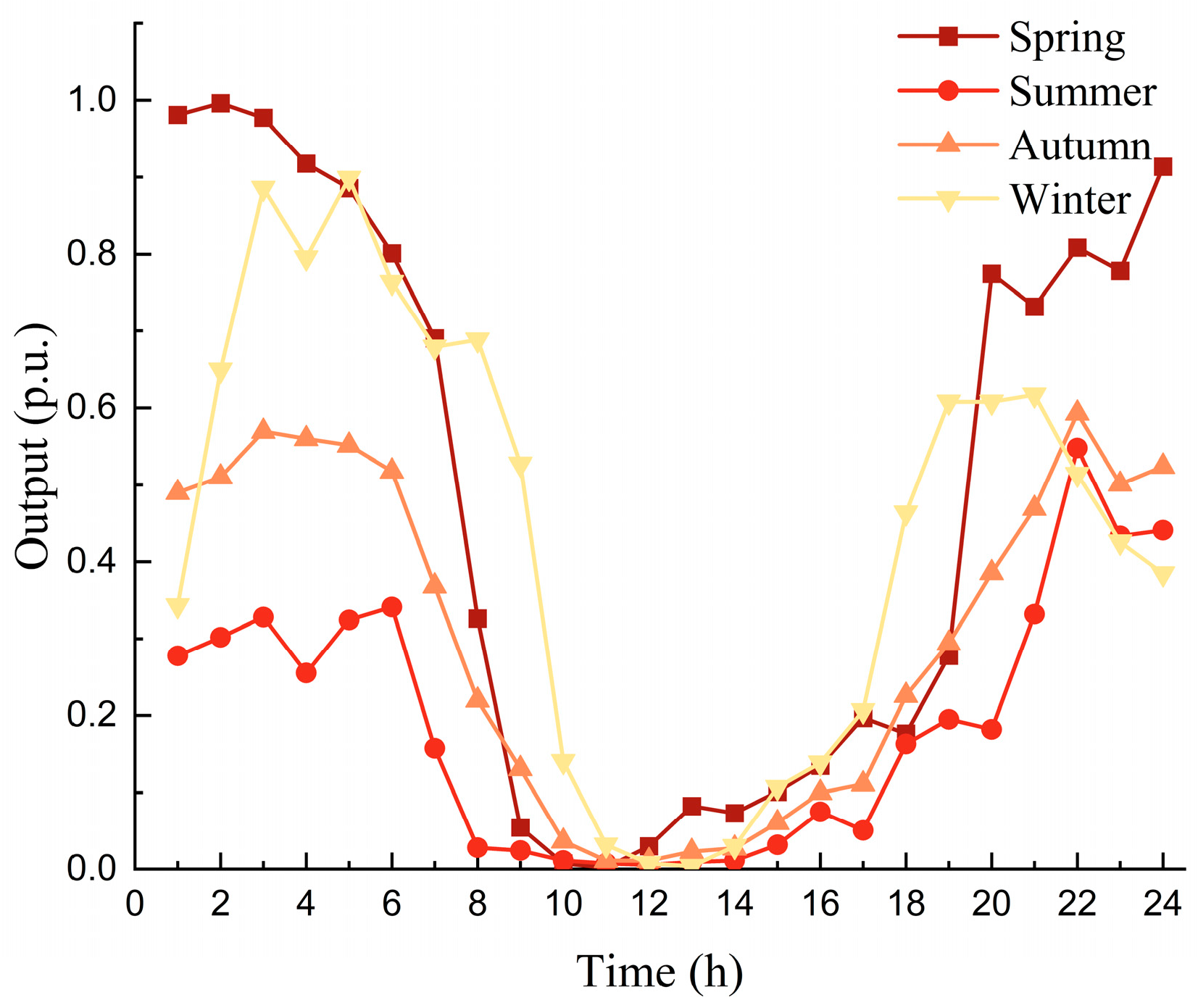
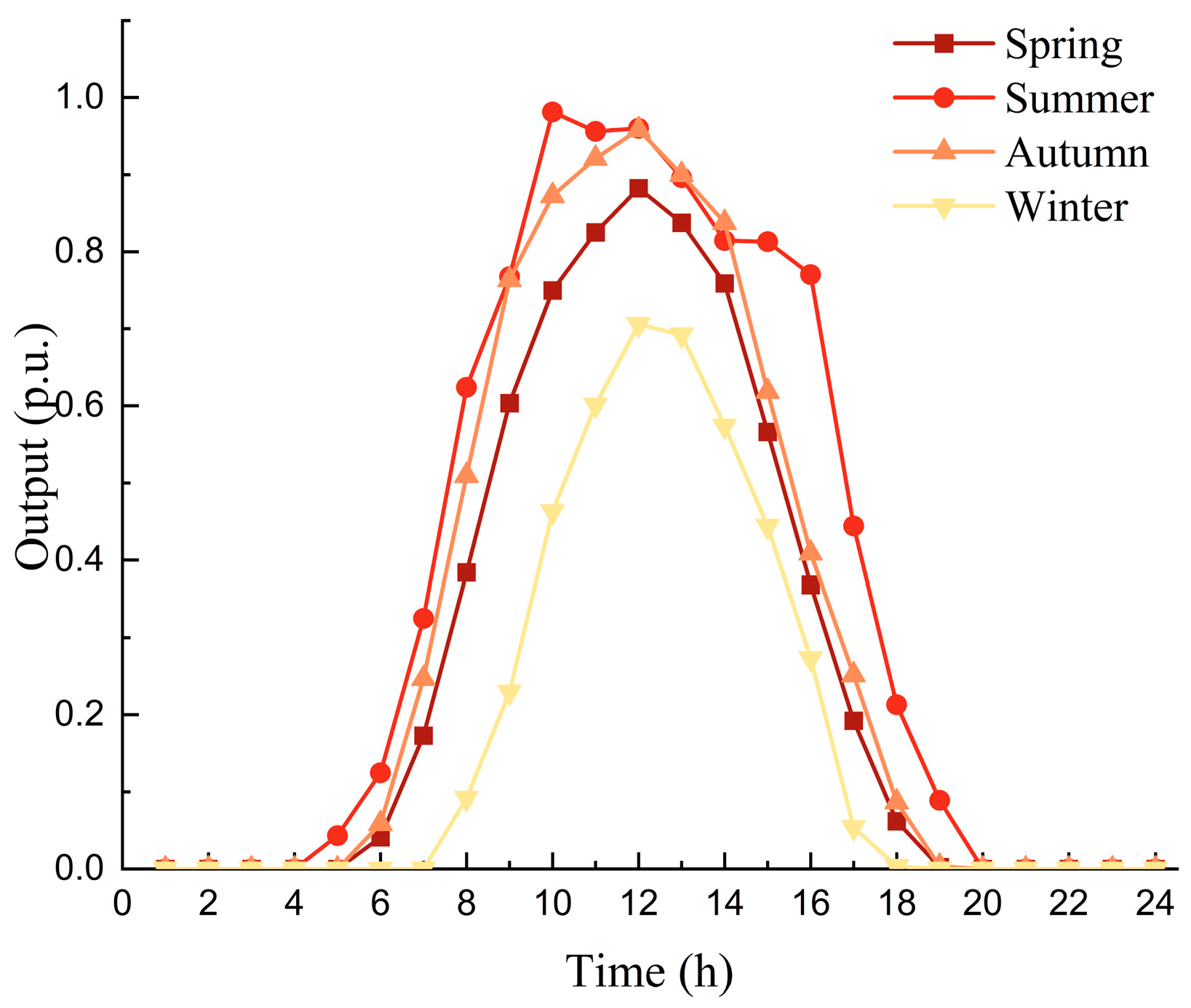
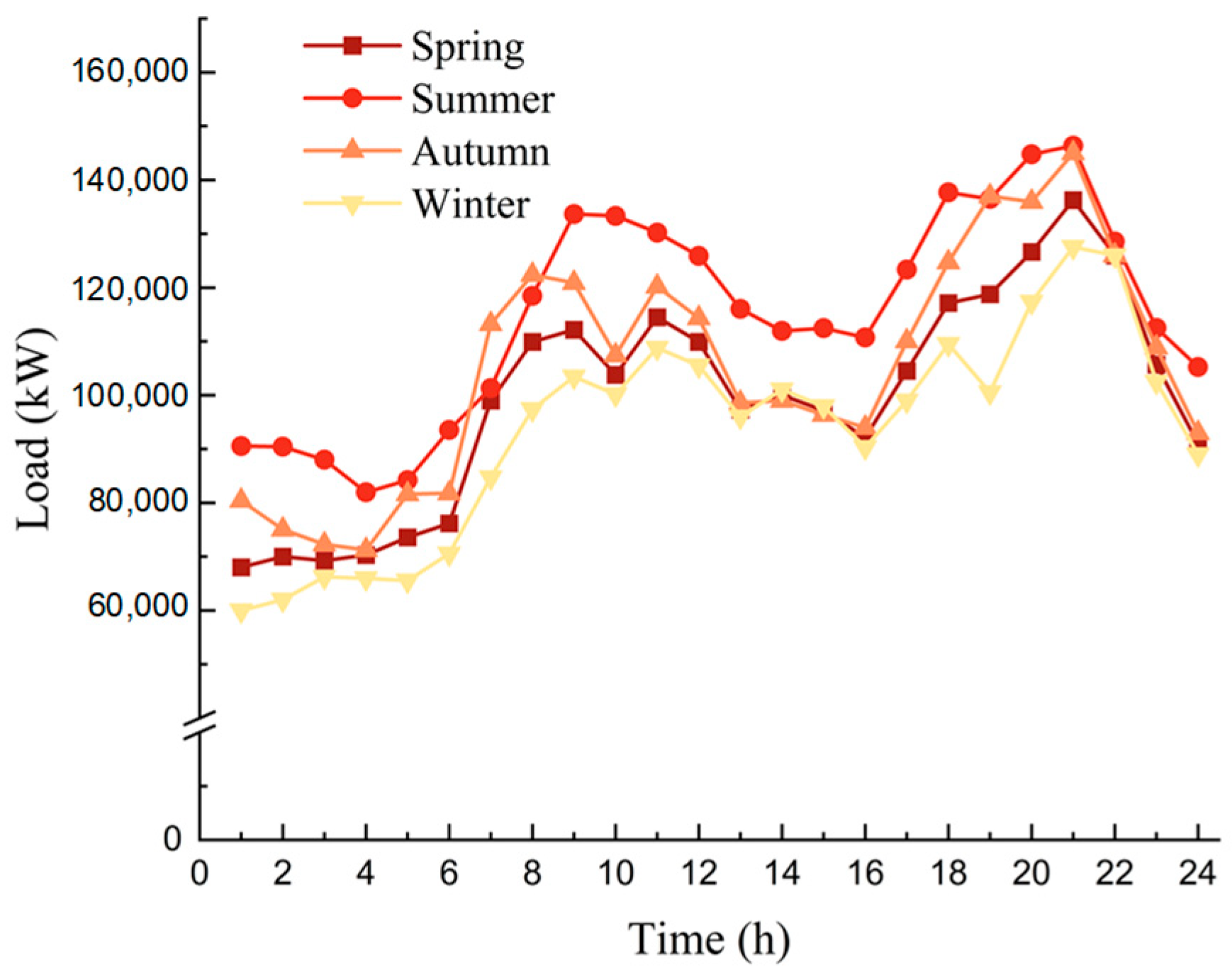
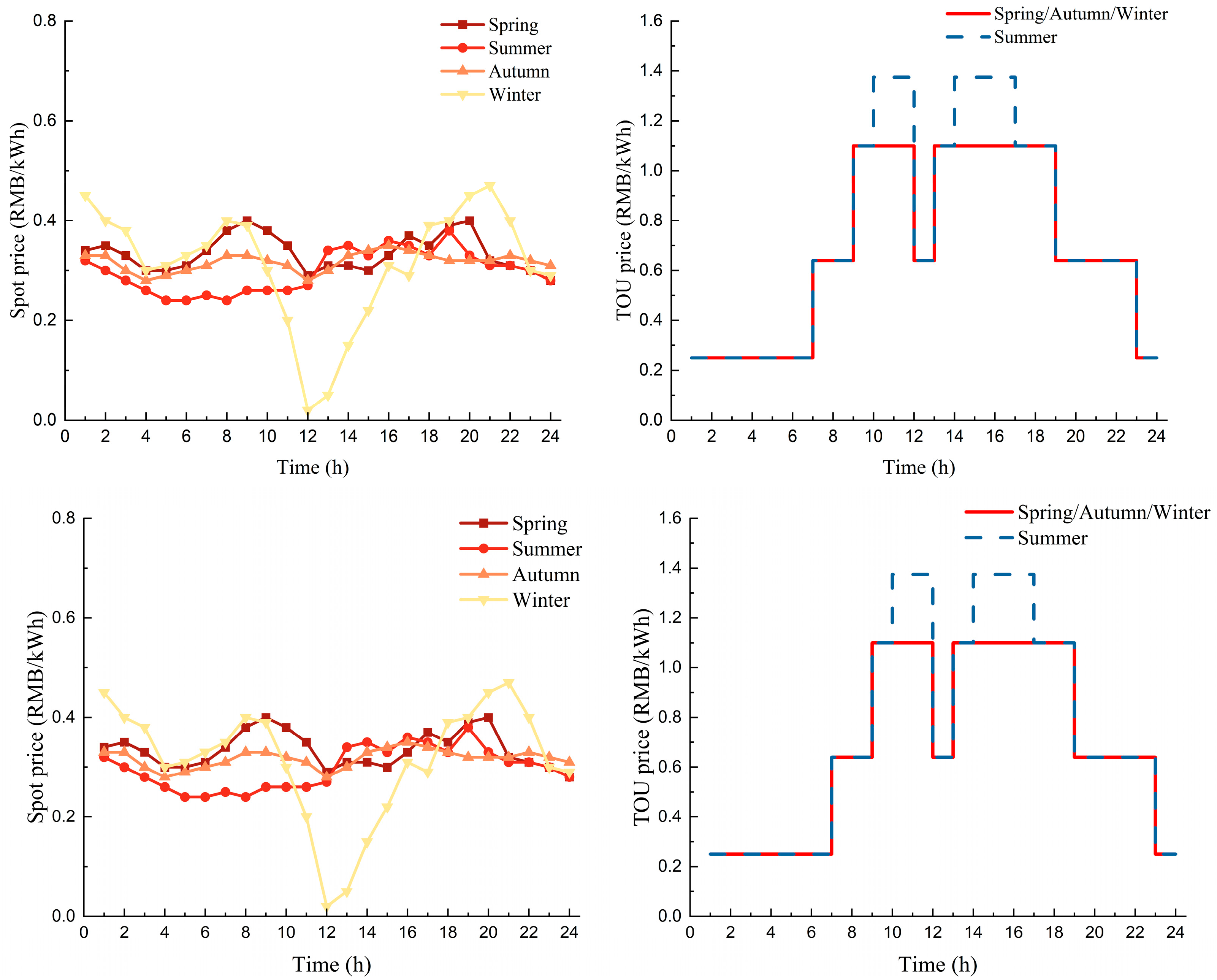
4.1. Case Introduction and Basic Data
4.2. Scenarios and Results
4.3. Discussions
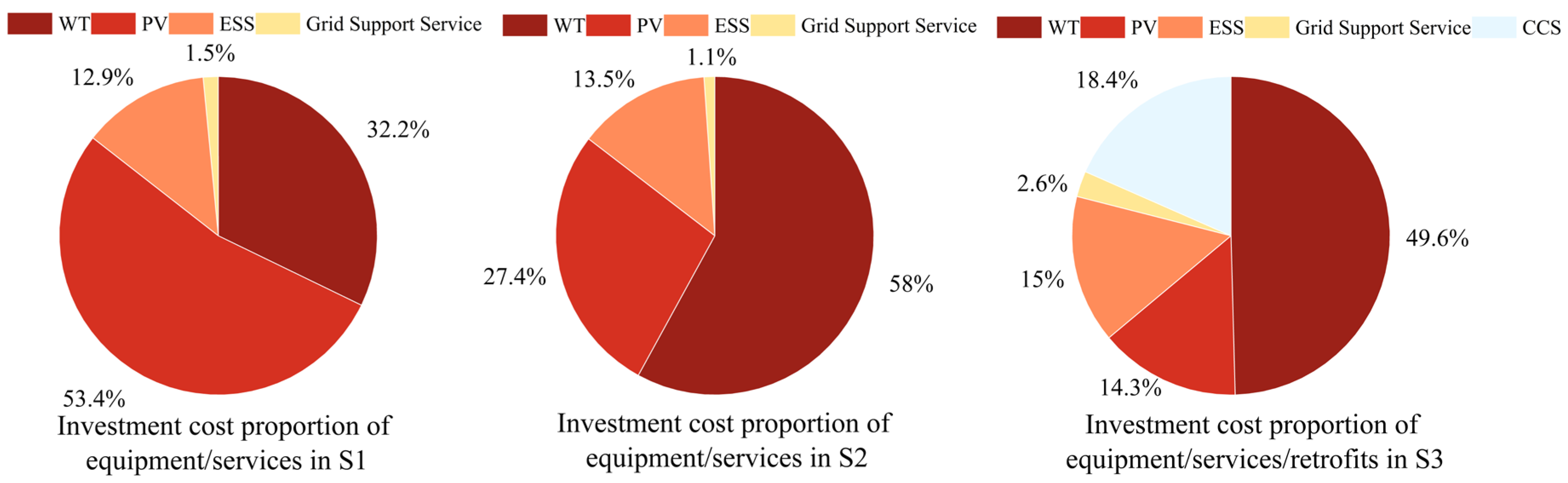
4.3.1. Economic Characteristics of Allocation Schemes
4.3.2. Environmental Characteristics of Allocation Schemes
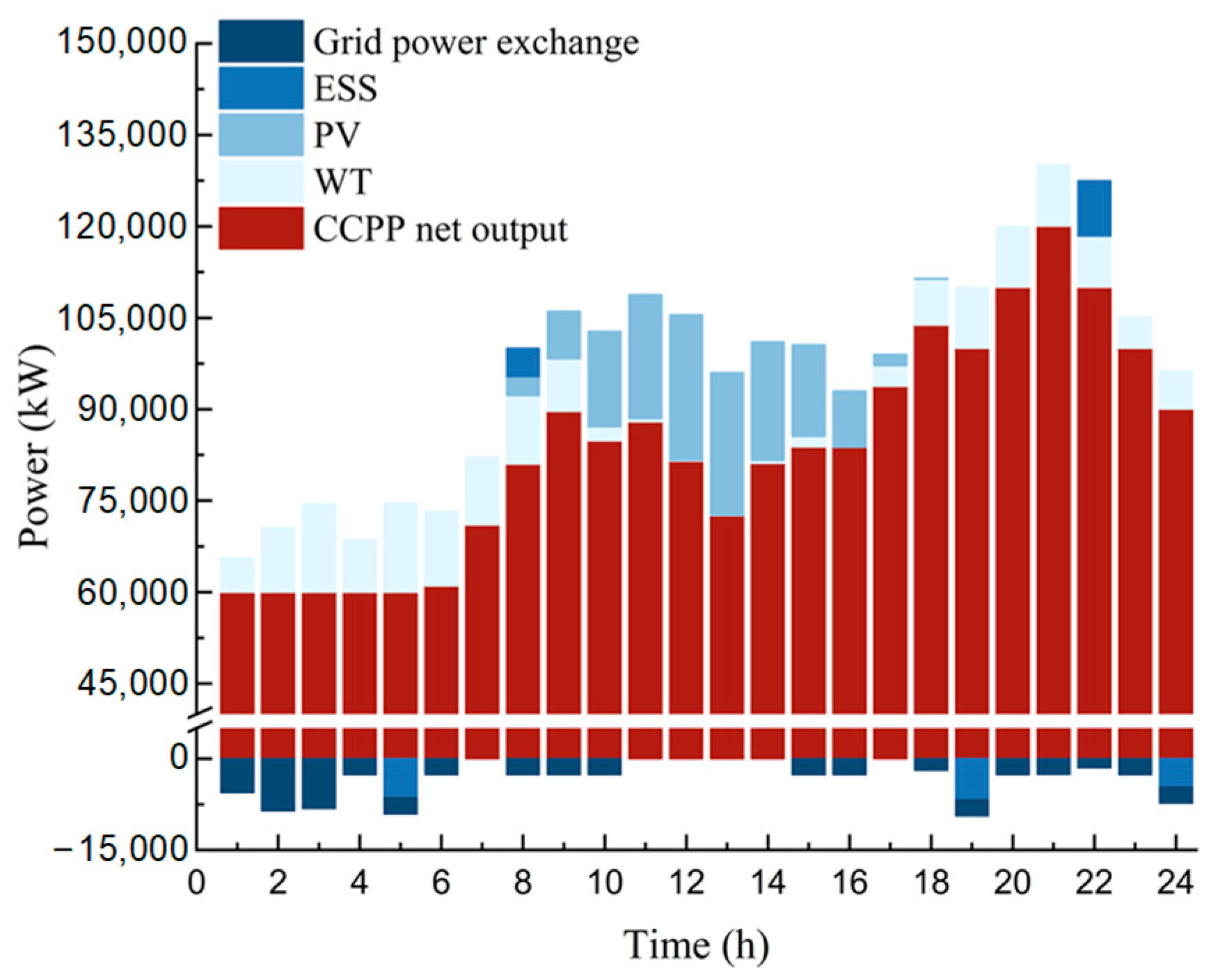
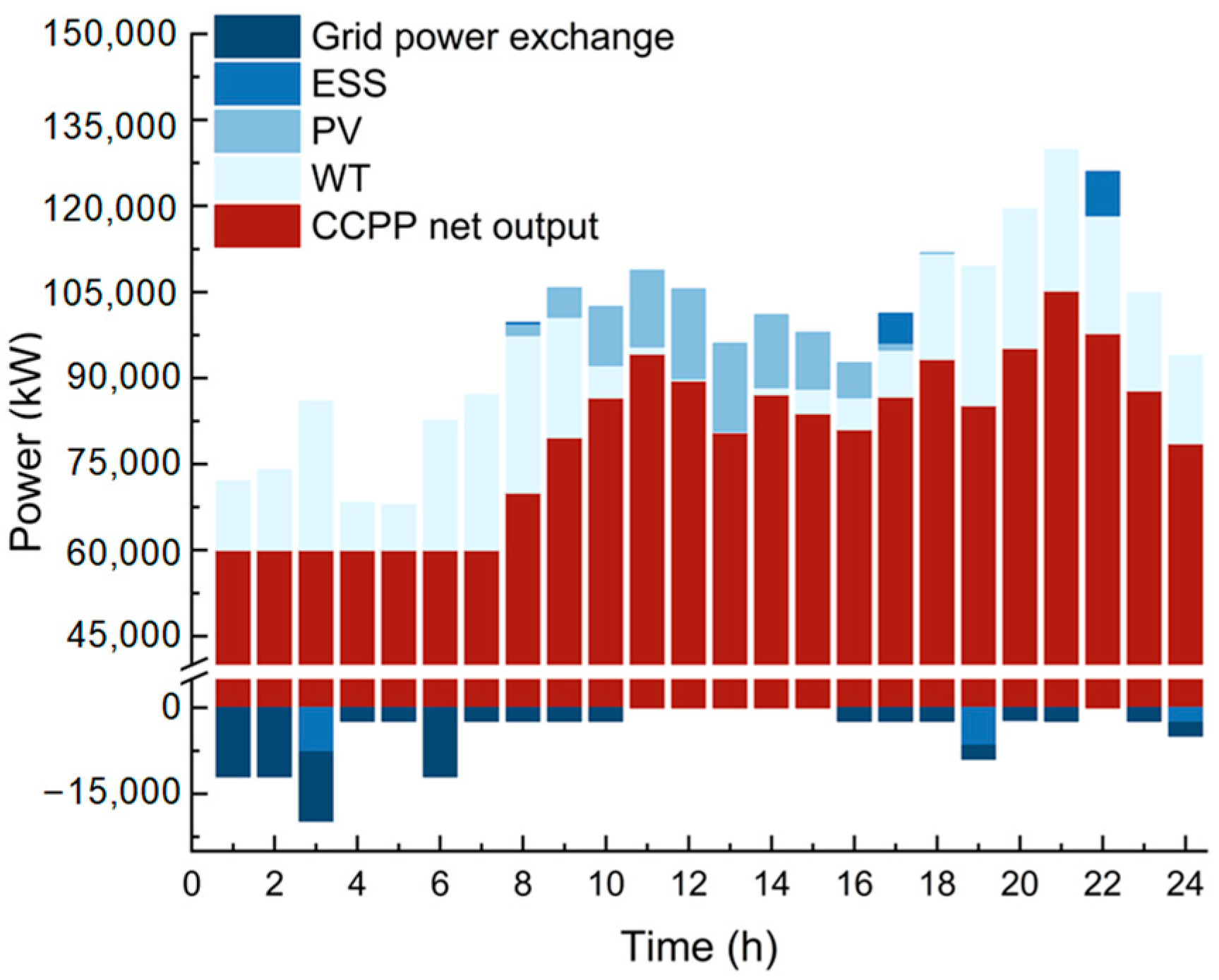
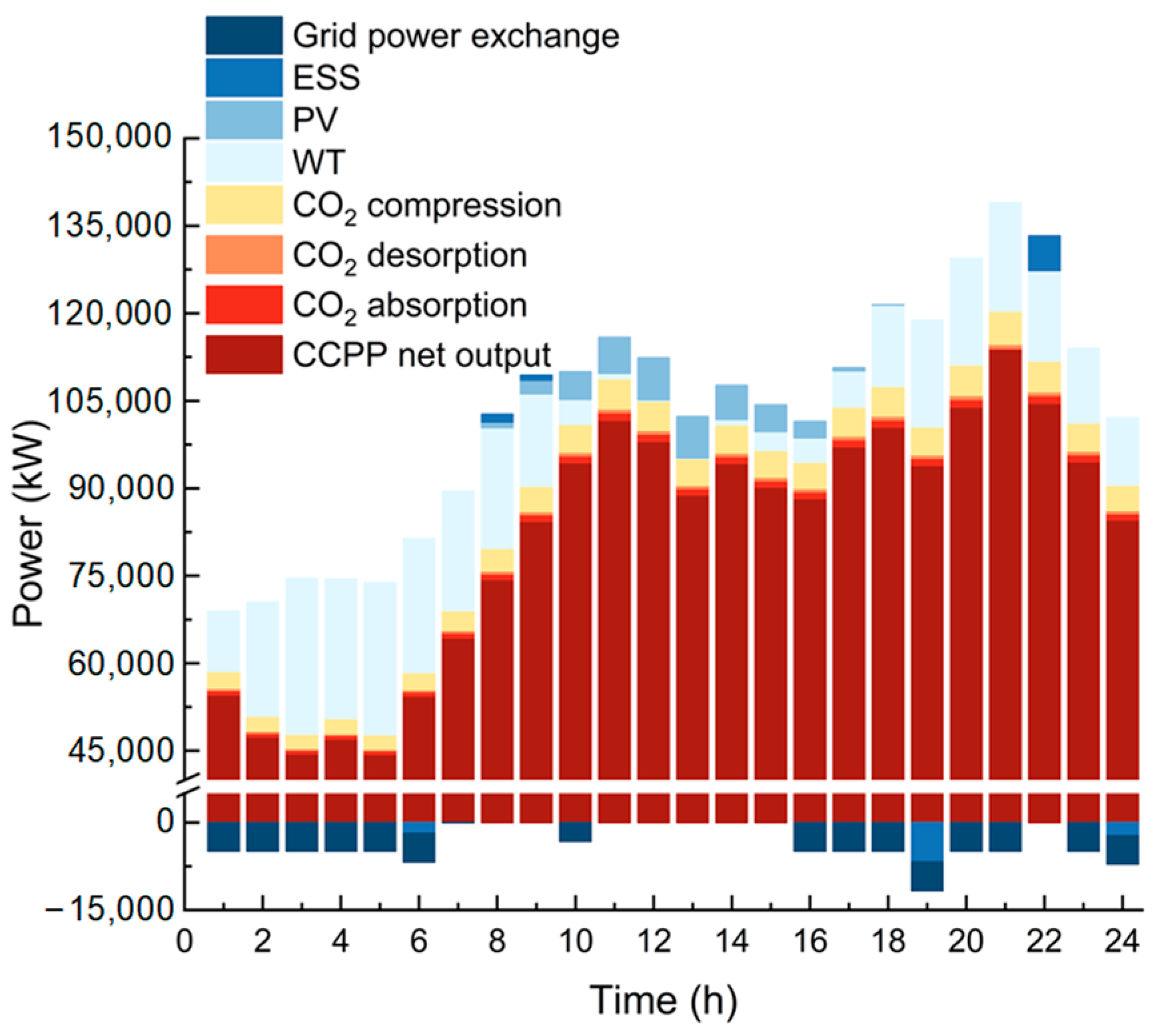
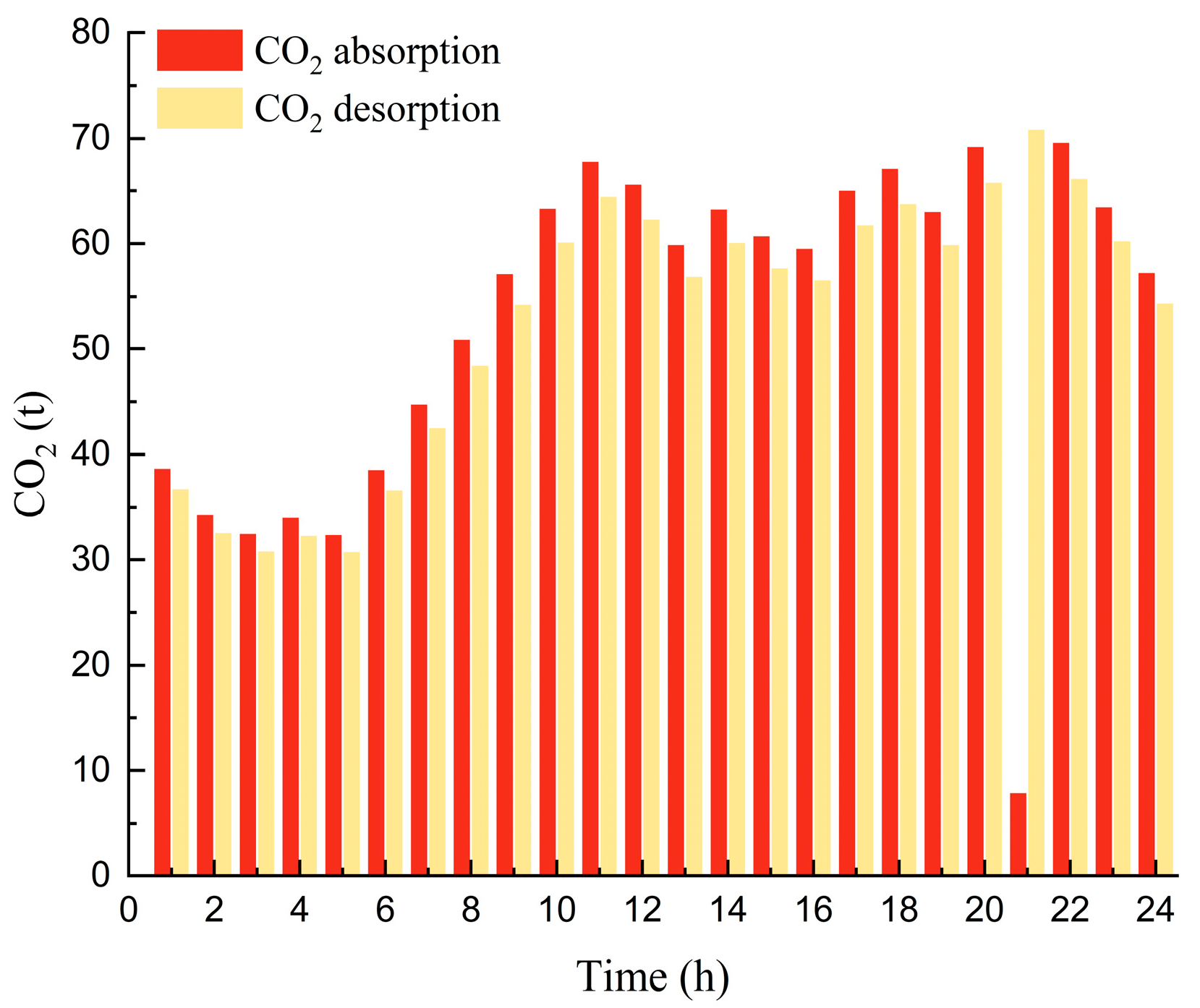
4.3.3. Operational Characteristics
5. Conclusions and Implications
5.1. Conclusions
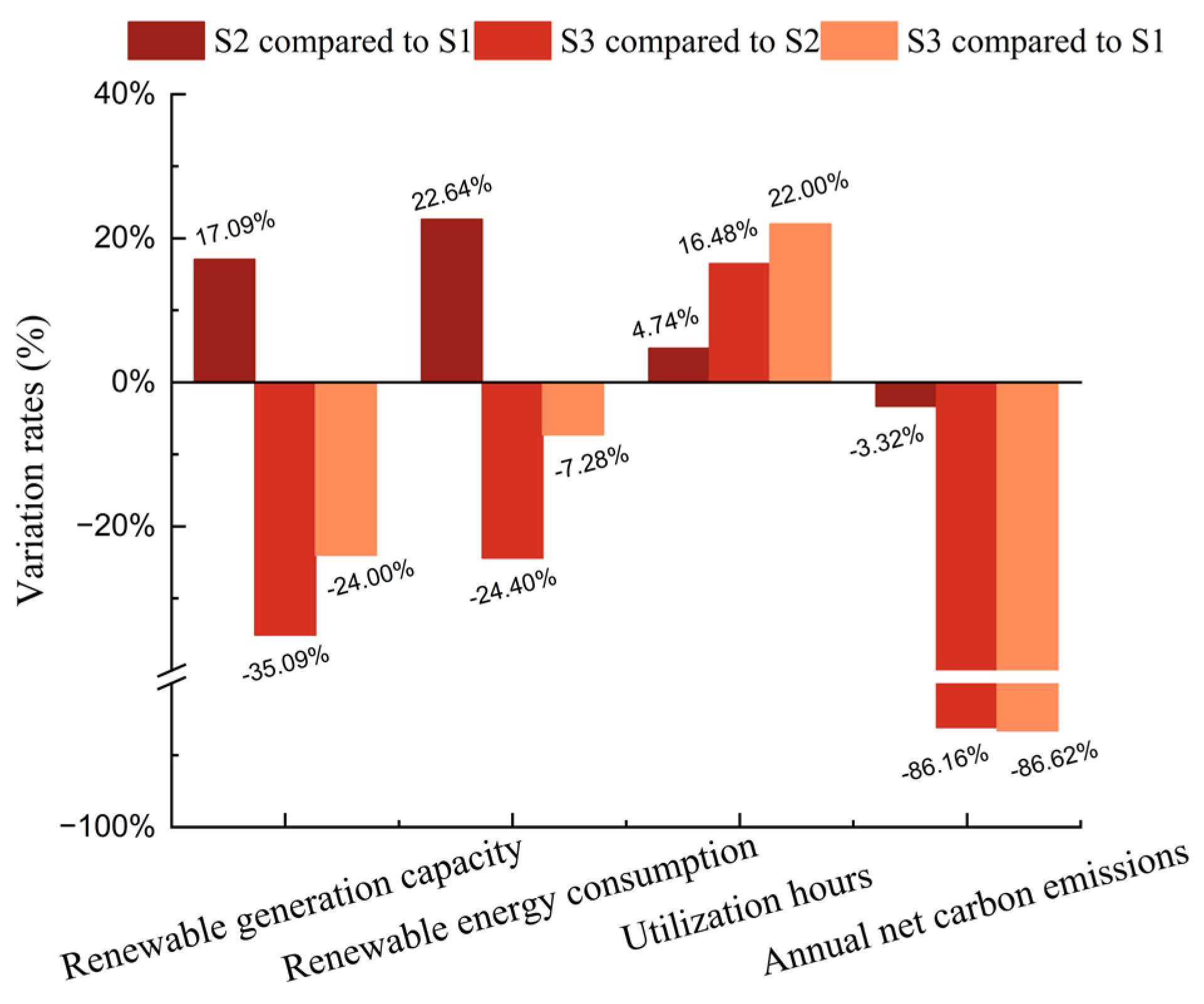
- Under the guidance of China’s carbon neutrality goals and the application of multi-markets, grid-connected microgrids will increase the investment in renewable energy generator units and ESSs. Although this leads to a significant improvement in renewable energy consumption, the reduction achieved in carbon emissions is limited. Additionally, owing to the combined effects of low curtailment penalties and constrained adjustment ranges/ramping capabilities of thermal power units, the amount of curtailed electricity may rise noticeably. Consequently, this results in a decline in investment and development efficiency. In the case study, compared to the traditional microgrid capacity allocation scenario, the installed capacity of renewable energy increased by 17.09%, renewable energy consumption rose by 22.64%, and net carbon emissions decreased by only 3.32%. However, the amount of curtailed electricity nearly doubled. This situation, to a certain extent, deviates from the original intentions of policies such as carbon neutrality and renewable energy incentives and is not conducive to sustainable energy development. It also represents a potential risk that has been largely overlooked in most existing studies.
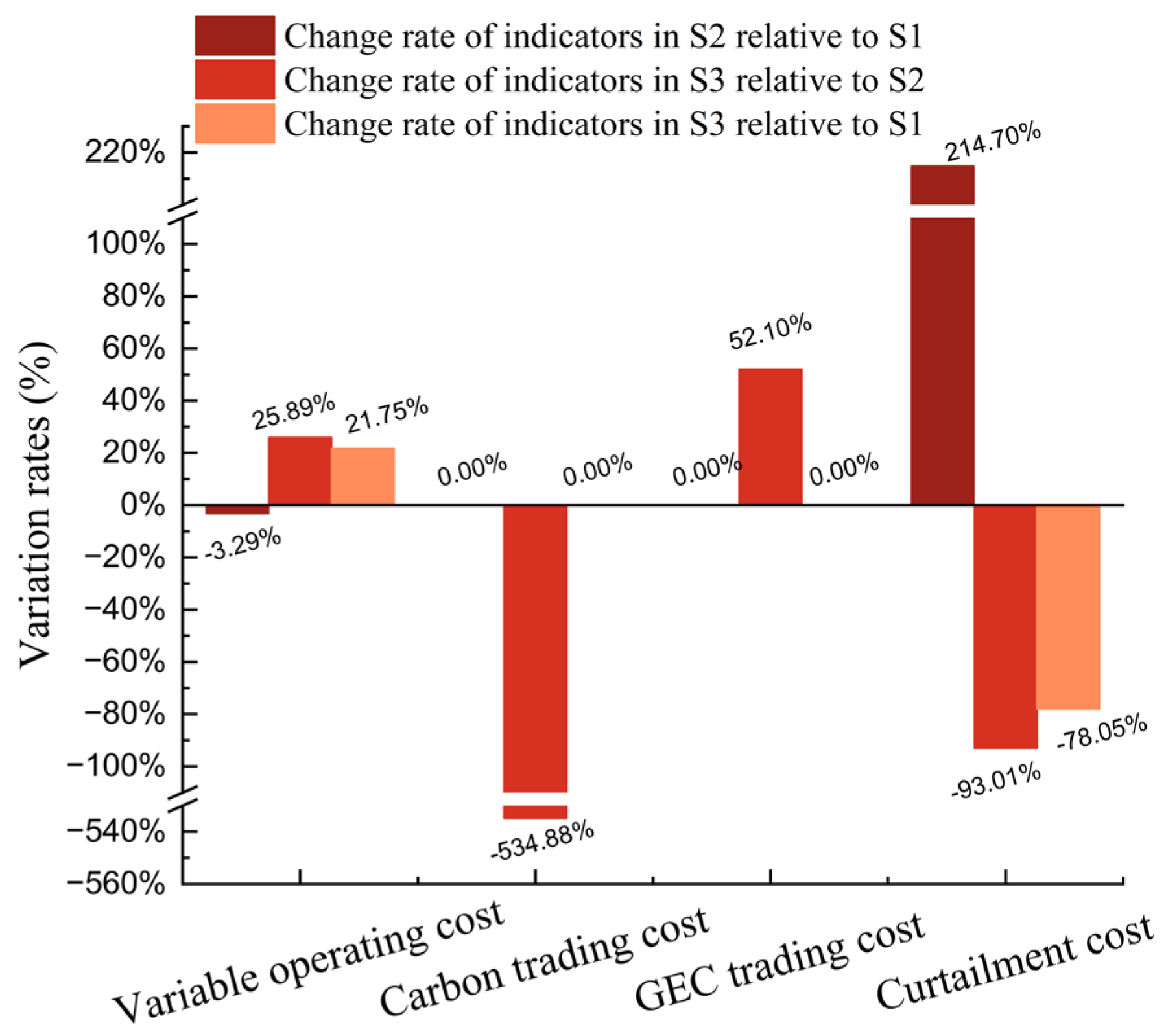
- Incorporating CCS retrofitting does not necessarily result in an increased investment scale in renewable energy generation units but can significantly enhance the utilization hours of renewable energy units and reduce curtailment and correspondingly costs. In the case study, compared to the traditional scenario, the installed capacity of renewable energy units in the scheme incorporating CCS retrofitting decreased by 24.00%. However, renewable energy consumption only declined by 7.28%. Moreover, the utilization hours increased by 22.00%, and the amount of curtailed power dropped by 78.05%. The application of liquid-storage CCS markedly improved the asset utilization efficiency of renewable energy unit and reduced the risk of redundant capacity configuration. This provides a technical pathway reference for the transformation and sustainable development of the energy sector and also offers crucial support for the realization of China’s carbon neutrality goals.
- CCS retrofitting can significantly reduce the net carbon emissions and carbon trading costs but may lead to a certain degree of increase in the overall cost of the scheme. In the case study, compared to the traditional scenario and the multi-market scenario without considering CCS retrofitting, the application of CCS could reduce net carbon emissions by over 86%. Nevertheless, the equivalent annual worth of the comprehensive cost increased by 8.93% and 3.68%, respectively. Constrained by factors such as the currently limited scale of carbon trading revenues and the suboptimal techno-economic performance of CCS, there arises a conflict between balancing environmental protection and economic efficiency. This poses significant challenges for the large-scale promotion of CCS in practical engineering projects.
5.2. Implications
- In terms of research directions, this manuscript exhibits certain limitations in risk factors and scenario design. In the future, as multi-market operations normalize and CCS technology advances, research on capacity allocation can be conducted with respect to the following scenarios: uncertain risk factors related to cross-market pricing systems and demand-side management; competitive–cooperative game trading among microgrids; phased CCS retrofitting integrated with multi-objective optimization; and scenarios considering grid infrastructure constraints.
- In terms of policy formulation, working towards the carbon neutrality goal, despite the varying focuses of different renewable energy policies (RPS emphasizes incentivizing the demand side to consume renewable energy, while penalties for curtailment focus on guiding the supply side to enhance utilization efficiency), the emergence of multi-market entities with dual producer–consumer roles, represented by grid-connected microgrids, may lead to redundant assessments among different renewable energy policy tools. Moreover, the current average price in China’s carbon market is approximately 95 RMB/t, which still lags behind that of the EU carbon market (around 80 USD/t, equivalent to approximately 570 RMB/t) and the California carbon market in the United States (about 45 USD/t, equivalent to approximately 320 RMB/t). Despite China’s proactive efforts to integrate into the global carbon trading market system, mechanisms regarding carbon pricing remain unclear, posing arbitrage risks. In summary, future attention should be focused on environmental value allocation, information sharing and value conversion/calculation/offset/cancellation among different markets/mechanisms, setting limits on transaction price fluctuations, as well as aligning mechanisms for quota allocation. Research and formulation of policies that meet the demands of a cross-market, cross-policy system, and even a cross-international market mechanism, will be key.
- In terms of practical work, the government can target entities such as public utility companies and other entities and expedite the iterative process between the research, development, and application of CCS by formulating reasonable subsidy and financing mechanisms, flexibly adopting diverse business models represented by Public–Private Partnerships (PPPs), and establishing CCS–microgrid pilot demonstration projects. These measures will drive advancements in the technical and economic characteristics of related industries, providing vital technological support for the realization of carbon neutrality. For market entities represented by microgrids, given that China’s carbon market is in its nascent stage with relatively low price levels, the corresponding transaction costs account for less than 10% of a microgrid’s annual total costs. However, as China gradually integrates into the international trading system, market supply, trading mechanisms, and price levels may encounter significant uncertainties and disruptions. Market entities need to actively monitor relevant policy trends, take into account the maturity and technical–economic characteristics of zero-carbon and negative-carbon technologies, and formulate reasonable equipment/system construction plans and business expansion strategies to enhance their resilience against operational risks.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- National Energy Administration. National Electric Power Industry Statistical Data from January to June 2025. Available online: https://www.nea.gov.cn/20250723/d7a5d6cc916e40bcb04c7d7e74d03213/c.html (accessed on 21 August 2025).
- Li, G.; Liu, X.; Xin, Y.; Jiang, T.; Yan, K.; Wang, T. Research on frequency stability of power system with high penetration renewable energy: A review. High Volt. Eng. 2024, 50, 1165–1181. [Google Scholar]
- Wu, Q.; Bose, A.; Singh, C.; Chow, J.H.; Mu, G.; Sun, Y.; Liu, Z.; Li, Z.; Liu, Y. Control and stability of large-scale power system with highly distributed renewable energy generation: Viewpoints from six aspects. CSEE J. Power Energy Syst. 2023, 9, 8–14. [Google Scholar] [CrossRef]
- National Energy Administration. Notification on Matters Concerning the Orderly Promotion of Direct Green Power Connection Development. Available online: https://www.ndrc.gov.cn/xxgk/zcfb/tz/202505/t20250530_1398138.html (accessed on 21 August 2025).
- Liu, T.; Shu, Y.; Shu, T.; Liu, N.; Zhao, L.; Huang, H.; Zhao, Y. Optimization configuration method of hybrid energy storage for desert-gobi-wasteland new energy base considering retrofit of molten salt heat storage coupled with thermal power unit. Proc. CSEE 2025, 1–15. [Google Scholar] [CrossRef]
- Yuan, T.; Wang, K.; Teng, Y.; Deng, Z. Review and prospect of hydrogen energy to enhance the flexibility of thermal power generating units. High Volt. Eng. 2025, 51, 2061–2077. [Google Scholar] [CrossRef]
- Chu, Z.; Yuan, J. Optimization and scheduling of comprehensive energy systems considering ammonia refrigeration and ammonia blending in thermal power plants. Electr. Power Constr. 2025, 46, 92–104. [Google Scholar]
- Cui, Y.; Jiang, S.; Fu, X.; Tong, X.; Xu, Y. Optimal scheduling strategy of integrated energy system considering low carbon energy transfer under carbon market incentive. Power Syst. Technol. 2025, 49, 3324–3333. [Google Scholar]
- Wang, R.; Zhao, X.; Ma, X.; Huang, Y.; Yang, Y.; Zhao, X. Progress of research on heat integration of coal-fired power plants with carbon dioxide capture. Therm. Power Gener. 2025, 54, 168–177. [Google Scholar]
- Cheng, W.; Jiang, H.; Xiong, Z.; Zhao, Y.; Chen, G.; Hu, Y.; Zhang, H.; Zhang, J. Analysis of the development path for efficiency and carbon reduction in coal-fired power plants. Coal Convers. 2025, 1–25. Available online: https://link.cnki.net/urlid/14.1163.TQ.20250821.1355.002 (accessed on 4 October 2025).
- Yang, L.; Lv, H.; Li, Y.; Zhang, X. Dynamic optimization of carbon capture technology deployment targeting carbon neutrality, cost efficiency and water stress: Evidence from China’s electric power sector. Energy Econ. 2023, 125, 106871. [Google Scholar] [CrossRef]
- Li, X.; Wang, R.; Liu, J.; Huang, X.; Jing, R.; Li, Q.; Zhang, P. Progress on Carbon Capture, Utilization and Storage Technology Application in China’s Power Industries. Low-Carbon Chem. Chem. Eng. 2025, 1–13. Available online: https://link.cnki.net/urlid/51.1807.TQ.20250813.1826.007 (accessed on 29 August 2025).
- Gu, B. Current Status and Prospects of Carbon Capture, Utilization and Storage Technology in the Context of International Carbon Neutrality Strategic Goals; EDP Sciences: Les Ulis, France, 2023. [Google Scholar]
- Wu, K.; Shan, L.; Bo, L.; Ceng, X.; Liu, X. Optimization methodology for carbon capture reformation schemes in thermal power plants considering the power flexible ramping demand. Electr. Power Constr. 2025, 46, 27–41. [Google Scholar]
- Ma, Y.; Wang, M.; Xin, T.; Xu, C. Wide-load operation regulation and economic assessment of a carbon capture coal-fired power plant integrated with a heat pump and solvent storage process. Proc. CSEE 2025, 1–13. [Google Scholar] [CrossRef]
- Zou, S.; Cao, Y.; Zhang, H.; Xiao, J.; Hou, J.; Zhao, X. Joint grid-storage planning considering operational flexibility of carbon capture power plant. High Volt. Eng. 2024, 50, 5164–5173. [Google Scholar]
- Zhu, M.; Liu, Y.; Wu, X.; Shen, J. Dynamic modeling and comprehensive analysis of direct air-cooling coal-fired power plant integrated with carbon capture for reliable, economic and flexible operation. Energy 2023, 263, 125490. [Google Scholar] [CrossRef]
- Wang, Q.; Yi, C.H.; Zhang, X.; Xue, D. Optimization of energy storage capacity sizing considering carbon capture intensity and renewable energy consumption. Proc. CSEE 2023, 45, 8295–8309. [Google Scholar]
- Li, J.; Zhang, S.; Shao, X. Low carbon economic dispatch of virtual power plants considering dual response and carbon capture. J. Univ. Shanghai Sci. Technol. 2025, 47, 79–88. [Google Scholar]
- Xuan, A.; Liu, J.; Peng, W.; Shen, X.; Shen, H. Planning method and carbon footprint assessment for retrofitting coal-based hydrogen power plant with carbon capture, utilization and storage. Proc. CSEE 2025, 45, 5431–5443. [Google Scholar]
- Chen, J.; Ye, P.; Liu, Y.; Chen, S.; Guan, F. Optimization dispatch of virtual power plant with carbon capture and high-energy-consumption loads based on stepped carbon trading. Power Syst. Technol. 2025, 1–17. [Google Scholar] [CrossRef]
- Liu, D.; Lin, H. Optimal operation of thermoelectric system considering generalized energy storage and carbon capture thermal power plant. Electr. Meas. Instrum. 2025, 62, 11–20. [Google Scholar]
- Hu, J.; Shan, Y.; Yang, Y.; Parisio, A.; Li, Y.; Amjady, N.; Rodríguez, J. Economic model predictive control for microgrid optimization: A review. IEEE Trans. Smart Grid 2023, 15, 472–484. [Google Scholar] [CrossRef]
- Zhou, S.; Han, Y.; Mahmoud, K.; Darwish, M.M.; Lehtonen, M.; Yang, P.; Zalhaf, A.S. A novel unified planning model for distributed generation and electric vehicle charging station considering multi-uncertainties and battery degradation. Appl. Energy 2023, 348, 121566. [Google Scholar] [CrossRef]
- Song, X.; Zhang, H.; Fan, L.; Zhang, Z.; Peña-Mora, F. Planning shared energy storage systems for the spatiotemporal coordination of multi-site renewable energy sources on the power generation side. Energy 2023, 282, 128976. [Google Scholar] [CrossRef]
- Long, Y.; Li, Y.; Wang, Y.; Cao, Y.; Jiang, L.; Zhou, Y.; Deng, Y.; Nakanishi, Y. Low-carbon economic dispatch considering integrated demand response and multistep carbon trading for multi-energy microgrid. Sci. Rep. 2022, 12, 6218. [Google Scholar] [CrossRef]
- Torabi, R.; Gomes, Á.; Morgado-Dias, F. Electricity, transportation, and water provision of 100%renewable energy for remote areas. Energies 2023, 16, 4146. [Google Scholar] [CrossRef]
- Liao, G.; Yang, X.; Lou, S.; Qin, W.; Liu, J.; Hong, X. Multi-objective capacity planning for expressway microgrid considering photovoltaic panel dust removal maintenance. J. Phys. Conf. Ser. 2023, 2588, 12003. [Google Scholar] [CrossRef]
- Chen, H.; Li, X.; Wang, Y. Optimal capacity configuration of island photovoltaic storage microgrid system with electric ship charging station. Smart Power 2024, 52, 48–54. [Google Scholar]
- Situ, Y.; Zhou, L.; Chen, F.; Li, M.; Zhao, A.; Zeng, M. Research on configuration of multi-energy microgrid in smart park based on typical scenarios. Acta Energiae Solaris Sin. 2022, 43, 515–526. [Google Scholar]
- Bakhtiari, H.; Zhong, J.; Alvarez, M. Uncertainty modeling methods for risk-averse planning and operation of standalone renewable energy-based microgrids. Renew. Energy 2022, 199, 866–880. [Google Scholar] [CrossRef]
- Wang, Z.; Hou, H.; Wei, R.; Li, Z. A distributed market-aided restoration approach of multi-energy distribution systems considering comprehensive uncertainties from typhoon disaster. IEEE Trans. Smart Grid 2025, 16, 3743–3757. [Google Scholar] [CrossRef]
- Wang, Z.; Hui, H.; Bo, Z.; Zhang, L.; Shi, Y.; Xie, C. Risk-averse stochastic capacity planning and P2P trading collaborative optimization for multi-energy microgrids considering carbon emission limitations: An asymmetric Nash bargaining approach. Appl. Energy 2024, 357, 122505. [Google Scholar] [CrossRef]
- Li, L.; Liu, S.; Ning, C. Data-driven distributionally robust planning of electricity-heat-hydrogen-ammonia microgrid considering the electrothermal-aging effect of SOEC. Power Syst. Technol. 2025, 49, 22–31. [Google Scholar]
- Zou, S.; Jiang, Y.; Lin, Q.; Wen, B.; Liao, J.; Xu, C. Double-layer coordinated planning for electricity and water in zero-carbon microgrids on an independent island considering the dynamic aging characteristics of energy storage. South Power Syst. Technol. 2025, 1–12. Available online: https://link.cnki.net/urlid/44.1643.tk.20250708.1024.004 (accessed on 29 August 2025).
- Lu, S.; Gu, W.; Xu, Y.; Dong, Z.; Sun, L.; Zhang, H.; Ding, S. Unlock the thermal flexibility in integrated energy systems: A robust nodal pricing approach for thermal loads. IEEE Trans. Smart Grid 2023, 14, 2734–2746. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, H.; Cao, Y. Photovoltaic-hydrogen energy storage multi-agent decentralized cooperative scheduling based on stochastic-nash-harsanyi bargaining game. Trans. China Electro Tech. Soc. 2024, 39, 2652–2666. [Google Scholar]
- Dong, J.; Guo, H.; Jiang, T.; Du, E.; Zhang, N.; Kang, C. Research on electricity-carbon coupling trading in the new power system. Proc. CSEE 2025, 45, 5752–5771. [Google Scholar]
- Ren, Y.; Sun, F.; Yang, X.; Zhang, J. Analysis of the dynamic transmission efficiency of carbon prices from the perspective of the electricity-carbon market linkage. Stat. Decis. 2024, 40, 183–188. [Google Scholar]
- Wu, C.; Yang, X.; Wan, Z.; Yang, F.; Wu, Z.; Zhou, Q.; Xu, J. Two-stage robust optimal scheduling for virtual power plants considering carbon-green certificate interlinked trading. Smart Power 2025, 53, 16–23. [Google Scholar]
- Xiao, B.; Zhang, Q.; Qin, W.; Qu, G.; Kong, Y.; Zhang, X. Source-grid-load-storage synergistic planning considering electricity-carbon coupling and flexible supply-demand balance. Electr. Power Constr. 2025, 46, 116–127. [Google Scholar]
- Shen, M.; Hu, Z.; Kong, F.; Tong, L.; Yin, S.; Liu, C.; Zhang, P.; Wang, L.; Ding, Y. Comprehensive technology and economic evaluation based on the promotion of large-scale carbon capture and storage demonstration projects. Rev. Environ. Sci. Bio/Technol. 2023, 22, 823–885. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, D.; Cheng, H.; Song, Y.; Yuan, K.; Du, W. Key Technologies and challenges of low-carbon integrated energy system planning for carbon emission peak and carbon neutrality. Autom. Electr. Power Syst. 2022, 46, 189–207. [Google Scholar]
- Zhang, W.; Zhai, X.; Zhou, J.; Wang, S.; Yin, S. Review of carbon dioxide capture technology. South Energy Constr. 2025, 1–11. [Google Scholar] [CrossRef]
- Abdilahi, A.M.; Mustafa, M.W.; Abujarad, S.Y.; Mustapha, M. Hamessing flexibility potential of flexible carbon capture power plants for future low carbon power systems. Renew. Sustain. Energy Rev. 2018, 81, 3101–3110. [Google Scholar] [CrossRef]
- Cui, Y.; Deng, G.; Zeng, P.; Zhong, W.; Zhao, Y.; Liu, X. Multi-time scale source-load dispatch method of power system with wind power considering low-carbon characteristics of carbon capture power plant. Proc. CSEE 2022, 42, 5869–5886+6163. [Google Scholar]
- He, Y.; Wang, Y. Low-carbon economic scheduling of virtual power plants with hydrogen-blended gas and liquid-storage CCS coupled P2G. Power Gener. Technol. 2025, 1–14. Available online: http://kns.cnki.net/kcms/detail/33.1405.tk.20250307.1119.002.html (accessed on 12 July 2025).
- Mu, Y.; Wu, Z.; Wang, C.; Yu, X.; Jia, H.; Zhang, Y. Optimal configuration method for park-level integrated energy system based on information gap decision theory-utility entropy. Autom. Electr. Power Syst. 2024, 48, 41–53. [Google Scholar]
- Liu, S.; Wu, S.; Liu, W.; Liu, C.; Wang, X.; Kang, J. Capacity optimization of wind-solar pumped storage power generation system considering uncertainties. J. Hydroelectr. Eng. 2024, 43, 43–56. [Google Scholar]
- Wang, Y.; Wang, Y. Dynamic programming of park-level integrated energy system considering electricity hydrogen production and carbon capture. J. China Univ. Pet. (Ed. Nat. Sci.) 2024, 48, 142–150. [Google Scholar]
- Qiu, Z.; Wang, B.; Ben, S.; Hu, N. Bi-level optimal configuration planning model of regional integrated energy system considering uncertainties. Electr. Power Autom. Equip. 2019, 39, 176–185. [Google Scholar]
- Deng, L.; Liu, S. Snow ablation optimizer: A novel metaheuristic technique for numerical optimization and engineering design. Expert Syst. Appl. 2023, 225, 120069. [Google Scholar] [CrossRef]
- Ma, L.; Cheng, S.; Shi, Y. Enhancing learning efficiency of brain storm optimization via orthogonal learning design. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 6723–6742. [Google Scholar] [CrossRef]
- Xiao, B.; Han, K.; Zhang, X. Robust IGDT planning for stand-alone microgrid with hydrogen energy storage. Electr. Power Constr. 2024, 45, 77–88. [Google Scholar]
- Cui, S.; Gao, Y.; Chang, W.; Xie, H.; Zhu, R. Integrated optimization of distribution network considering ladder-type carbon trading. China Meas. Test 2025, 51, 139–147. [Google Scholar]
- Zhang, J.; Yao, Y. A multi-user integrated energy service sharing method considering stepped carbon emission cost. Mod. Electr. Power 2025, 42, 987–999. [Google Scholar] [CrossRef]


| Symbol | Description | Symbol | Description |
|---|---|---|---|
| Upper limits of carbon absorption efficiency. | Upper limits of carbon desorption efficiency. | ||
| , | Coefficients of carbon price variation. | , , | Operational cost coefficients for the CCPP. |
| Flow diversion coefficient of the flue gas bypass system. | Investment cost. | ||
| Replacement cost. | Maintenance cost. | ||
| Cost of grid support services. | CCS retrofitting cost. | ||
| One-time capital cost of CCS retrofitting. | Initial investment cost of the i-th type of equipment. | ||
| Variable operating costs of all equipment types. | Penalty costs for wind/solar curtailment. | ||
| Carbon trading costs. | GEC trading costs. | ||
| Cost of power exchange with the grid. | Variable operating cost of the CCPP. | ||
| Variable operating costs of WT. | Variable operating costs of PV. | ||
| Operating operational cost of the CCS. | Specific investment cost per unit capacity of the ESS. | ||
| Unit capacity annual maintenance cost for equipment type i. | Unit capacity investment cost for equipment type i. | ||
| Unit investment cost of storage tanks. | Operational cost coefficients for WT, can be considered negligible (approximated as zero). | ||
| Operational cost coefficients for PV, which can be considered negligible (approximated as zero). | Cost coefficient for ESS charging/discharging operations. | ||
| MEA cost coefficient. | Carbon sequestration cost coefficient. | ||
| Penalty cost for WT and PV curtailment. | Concentration of MEA. | ||
| Step length of the carbon emission interval in the tiered carbon pricing mechanism, representing the proportion of the exceeded/reduced carbon amount to the total allowance. | , , | The quantities of CO2 absorbed, desorbed, and compressed at time t. | |
| Carbon emissions diverted to the carbon capture system from the CCPP at time t. | Ei | Installed capacity of equipment type i. | |
| Maximum investment capacity for the i-th type of equipment. | Amount of CO2 captured. | ||
| Carbon emission intensity of the unit. | Positions of each particle in the initial solutions of SAO. | ||
| Centroid position of the particles in the population during the k-th iteration of SAO. | Centroid position of the particles whose fitness ranks in the top 50% of the population. | ||
| Designed capacity of storage tanks. | , | Investment capacities of the rich solution tank and lean solution tank. | |
| Comprehensive operational cost transmitted from the lower-level model. | Elite population in the k-th iteration of SAO. | ||
| Residual value recovery income from equipment disposal. | I | Number of distinct equipment types. | |
| K | Maximum number of iterations of SAO. | , | Constraint coefficients for the maximum charge and discharge power of the ESS, with their values ranging from (0, 1). |
| Load of the microgrid at time t. | Molar mass of MEA. | ||
| Snow-melting process simulated based on the degree-day method. | N, D | Population size and the number of decision variables in the upper-level model of SAO, respectively. | |
| Number of days for typical scenario d. | Exchange power between the microgrid and the grid at time t, where a positive value indicates electricity purchase from the grid and a negative value indicates electricity sale to the grid. | ||
| Net output of the CCPP. | The fixed power consumptions of the CCPP’s carbon capture system. | ||
| Operational power consumptions of the CCPP’s carbon capture system. | , | Minimum and maximum power outputs of the CCPP. | |
| Annual maximum net load declared by the microgrid. | Unit capacity charge for grid support services. | ||
| Maximum capacity of the tie-line. | Output of CCPP. | ||
| Output of WT. | Output of PV. | ||
| Discharging power of the ESS at time t. | Charging power of the ESS at time t. | ||
| , | Maximum charging power and discharging power of the ESS. | , , | Maximum available output of the renewable energy unit, WT, and PV, respectively. |
| , , | Actual output of the renewable energy unit, WT, and PV, respectively. | Benchmark carbon price. | |
| Unit price of GECs. | Penalty for failing to meet the RPS. | ||
| Penalty imposed when the exchange power exceeds the declared net load (grid support services) of the microgrid. | Excess consumption amount of renewable energy power in the microgrid. | ||
| Excess emission amount. | Actual carbon emissions of the microgrid. | ||
| Carbon allowance of the microgrid. | Replacement coefficient. | ||
| , | Upward and downward ramping capabilities of the CCPP. | r | Discount rate. |
| , | Maximum and minimum values of of SAO. | Search step size of particle j in the k-th iteration, which follows a standard normal distribution. | |
| T | Number of dispatch intervals. | , | Upper and lower bound constraints of each decision variable of SAO. |
| , | MEA volumes in the lean solution tank at the beginning and end of the scheduling period. | , | MEA volumes in the rich solution tank at the beginning and end of the scheduling period. |
| MEA volume required per unit of CO2 absorbed and desorbed. | MEA volume required per unit of CO2 absorbed. | ||
| Yi | Service life of equipment i. | YCCS | Lifespan of CCS equipment. |
| Lifespans of ESS and the microgrid. | Lifespans of the microgrid. | ||
| Optimal solution in the k-th iteration of SAO. | , | Positions of the second-best and third-best particles of SAO, respectively. | |
| , , | Self-discharge coefficient, charging efficiency, and discharging efficiency of the ESS. | Charge-discharge state coefficient. | |
| A random number within the range of [0, 1]. | A random number within the range of [0, 1]. | ||
| A random number within the range of (0, 1) of SAO. | Recovery coefficient of the i-th type of equipment. | ||
| , , | Energy consumption per unit of CO2 for absorption, desorption, and compression during the capture process. | Correction factor for the absorption/desorption capacity of MEA. | |
| The MEA density. | MEA loss coefficient during CO2 capture. | ||
| The set of typical days for the microgrid. | Carbon emission factor of the grid. | ||
| Weighting coefficient for carbon allowance. | Weighting coefficient for the RPS. |
| Item | Description | Equations |
|---|---|---|
| Objective function | Upper-level model objective function and the calculation of its sub-components. | (7)~(12) |
| Lower-level model objective function and the calculation of its sub-components. | (15)~(22) | |
| Constraints | Equipment investment capacity constraint. | (13)~(14) |
| Supply–demand balance constraint of the microgrid. | (23) | |
| Constraints on CCPP. | (2), (5), (24)~(27) | |
| Renewable energy unit output constraints. | (28) | |
| ESS constraints. | (29)~(30) | |
| Grid power exchange constraint. | (31) |
| Item | Value | Item | Value |
|---|---|---|---|
| (MW) | 60 | (MW) | 200 |
| , (MW/h) | 10 | (MW) | 8 |
| (t/MWh) | 0.8 | , | 90 |
| (MWh/tCO2) | 0.0229 | (MWh/tCO2) | 0.029 |
| (MWh/tCO2) | 0.108 | (%) | 0.8 |
| 0.01 | (m3/tCO2) | 18.5 | |
| (kg/m3) | 1.01 | (g/mol) | 61.08 |
| (g/mol) | 44 | 248 | |
| 0.3 | 0.9 | ||
| , | 0.9 | , | 0.8 |
| (MW) | 12 | (t/MWh) | 0.7 |
| Item | Value | Item | Value |
|---|---|---|---|
| 0.08 | (RMB/MW2) | 0.00005 | |
| (RMB/MW) | 210 | (RMB) | 5000 |
| (RMB/kW) | 4500 | (RMB/kW) | 2500 |
| (RMB/kW) | 1500 | (RMB/m3) | 700 |
| (RMB) | 1,500,000 | (RMB/kW) | 110 |
| (RMB/kW) | 50 | (RMB/kW) | 70 |
| (RMB/m3) | 100 | , (RMB/kWh) | 0 |
| (RMB/kWh) | 0.1 | (RMB/m3) | 200 |
| (RMB/t) | 21 | (RMB/kWh) | 0.1 |
| (RMB/kW·year) | 165 | 0.1 |
| Item | Value | Item | Value |
|---|---|---|---|
| (%) | 10 | (%) | 10 |
| (%) | 10 | (RMB/kWh) | 0.47 |
| (kg/kWh) | 0.5 | (%) | 25 |
| , (RMB/piece) | 50 | (RMB/tCO2) | 96 (spring) 90 (summer) 94 (autumn) 106 (winter) |
| Item | S1 | S2 | S3 |
|---|---|---|---|
| Multi-markets | Unimplemented | Implemented | Implemented |
| CCS retrofitting | No | No | Yes |
| WT (kW) | 17,980 | 39,870 | 30,050 |
| PV (kW) | 34,980 | 22,140 | 10,200 |
| ESS (kW) | 12,030 | 15,460 | 15,180 |
| Grid support services (kW) | 2636 | 2310 | 4890 |
| CCS Liquid Storage Tank (m3) | / | / | 37,000 |
| Annualized total cost (Million RMB) | 240.42 | 252.57 | 261.88 |
| Annual GEC trading cost (Million RMB) | / | 3.61 | 5.49 |
| Annual curtailment cost (Million RMB) | 0.76 | 2.37 | 0.16 |
| Annual carbon trading cost (Million RMB) | / | 7.31 | −31.79 |
| Annual carbon emissions (kt) | 543.68 | 525.62 | 72.77 |
| Item | Performance Characteristics | SAO | PSO |
|---|---|---|---|
| S1 | Average convergence value (Million RMB) | 240.42 | 244.87 |
| Average computation time (s) | 592.44 | 621.12 | |
| Average iteration count at convergence | 15 | 20 | |
| Coefficient of variation (%) | 2.61 | 3.43 | |
| S2 | Average convergence value (Million RMB) | 252.57 | 271.72 |
| Average computation time (s) | 632.74 | 701.25 | |
| Average iteration count at convergence | 16 | 26 | |
| Coefficient of variation (%) | 2.56 | 8.22 | |
| S3 | Average convergence value (Million RMB) | 261.89 | 289.43 |
| Average computation time (s) | 723.81 | 801.22 | |
| Average iteration count at convergence | 20 | 29 | |
| Coefficient of variation (%) | 2.92 | 9.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Ma, J.; Liao, Y.; Kuang, S.; Luo, S.; Zeng, M. Sustainable Optimal Capacity Allocation for Grid-Connected Microgrids Incorporating Carbon Capture and Storage Retrofitting in Multi-Market Contexts: A Case Study in Southern China. Sustainability 2025, 17, 9588. https://doi.org/10.3390/su17219588
Xu Y, Ma J, Liao Y, Kuang S, Luo S, Zeng M. Sustainable Optimal Capacity Allocation for Grid-Connected Microgrids Incorporating Carbon Capture and Storage Retrofitting in Multi-Market Contexts: A Case Study in Southern China. Sustainability. 2025; 17(21):9588. https://doi.org/10.3390/su17219588
Chicago/Turabian StyleXu, Yanbin, Jiaxin Ma, Yi Liao, Shifang Kuang, Shasha Luo, and Ming Zeng. 2025. "Sustainable Optimal Capacity Allocation for Grid-Connected Microgrids Incorporating Carbon Capture and Storage Retrofitting in Multi-Market Contexts: A Case Study in Southern China" Sustainability 17, no. 21: 9588. https://doi.org/10.3390/su17219588
APA StyleXu, Y., Ma, J., Liao, Y., Kuang, S., Luo, S., & Zeng, M. (2025). Sustainable Optimal Capacity Allocation for Grid-Connected Microgrids Incorporating Carbon Capture and Storage Retrofitting in Multi-Market Contexts: A Case Study in Southern China. Sustainability, 17(21), 9588. https://doi.org/10.3390/su17219588





