Research on Regional Disparities and Determinants of Carbon Emission Efficiency: A Case Study of Hubei Province, China
Abstract
1. Introduction
2. Literature Review
3. Study Area and Methods
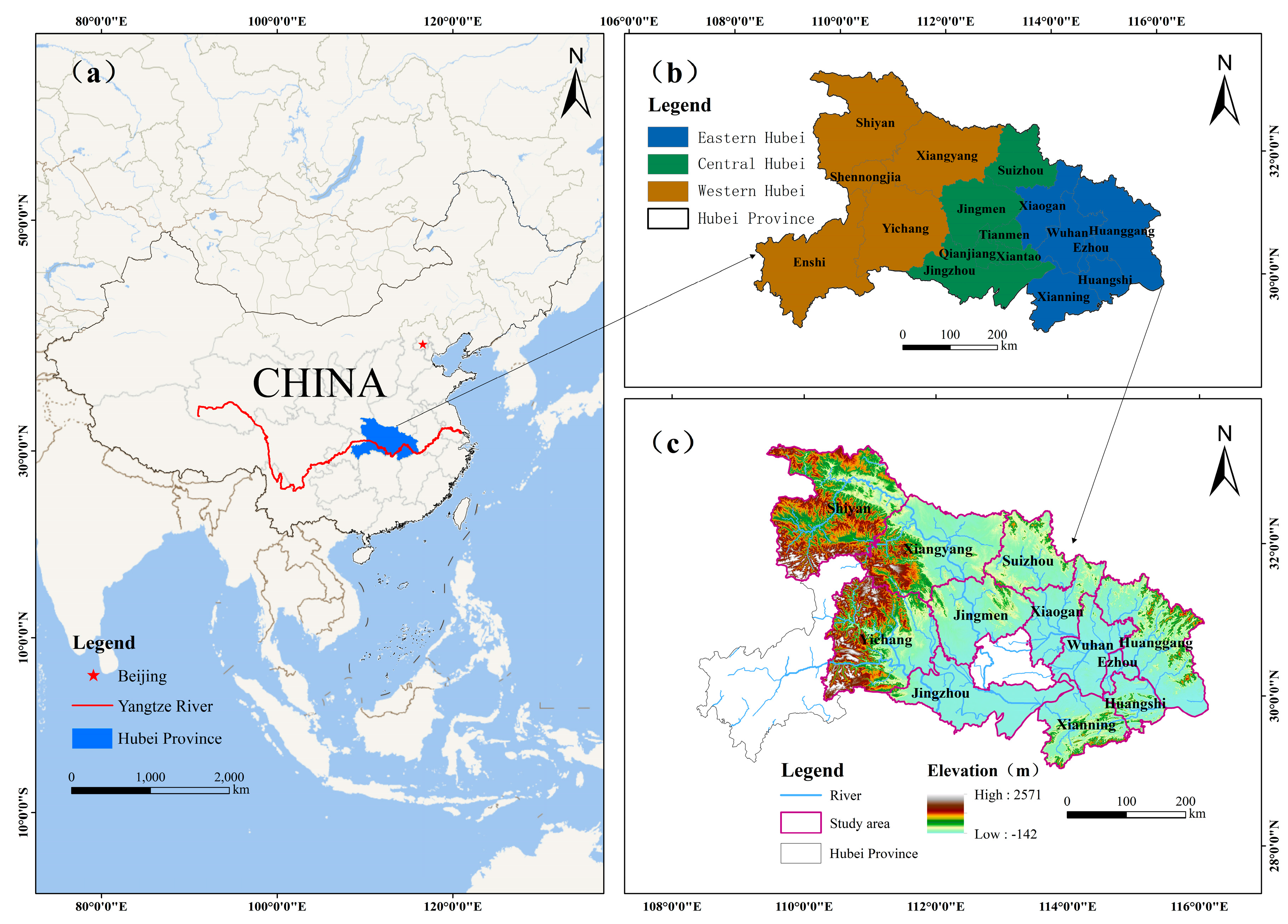
3.1. Study Area
3.2. Research Methods
3.2.1. Super-SBM Model
3.2.2. Standard Deviation Ellipse
3.2.3. Kernel Density Estimation
3.2.4. Spatial Markov Chain
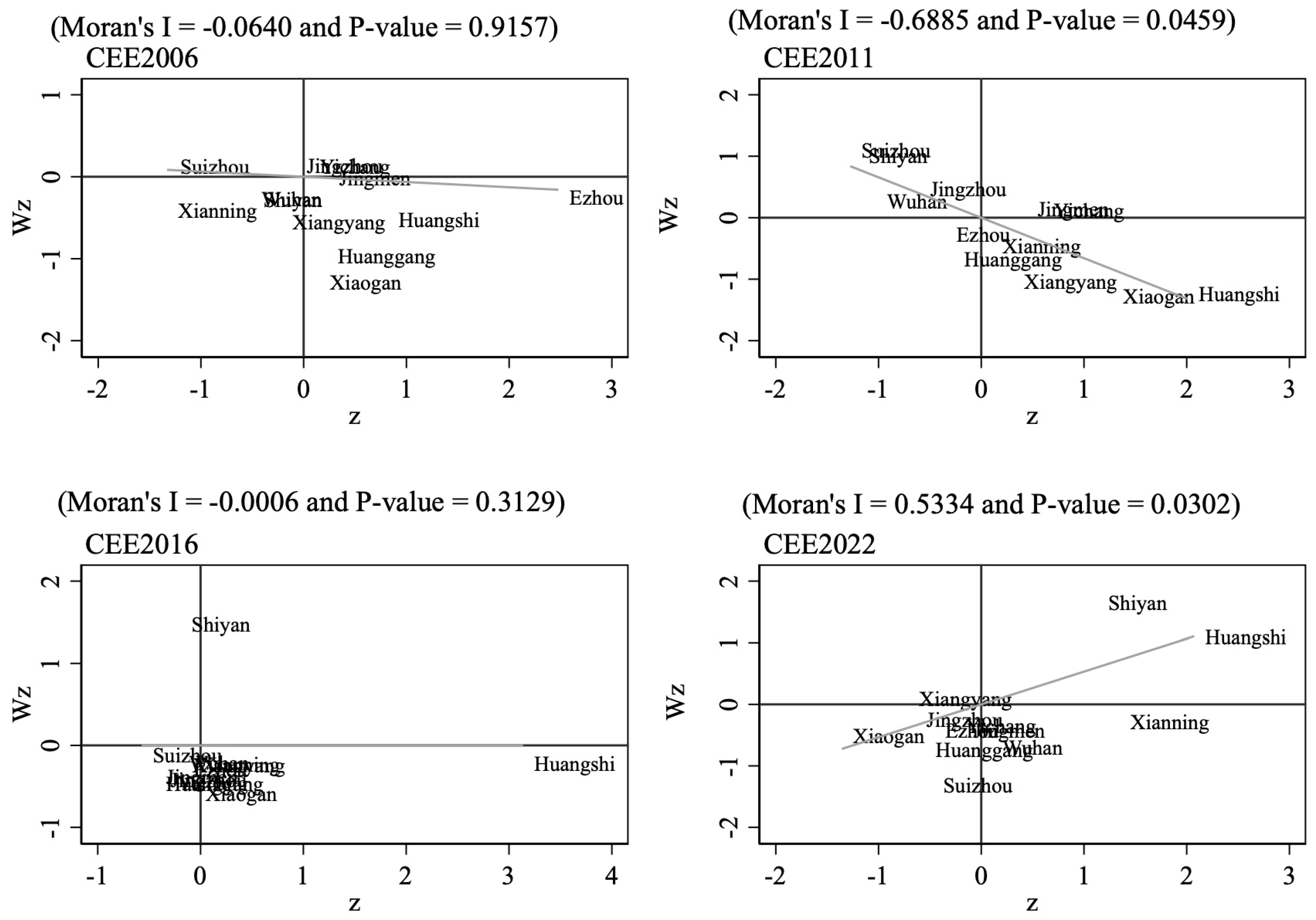
3.2.5. Exploratory Spatial Data Analysis
3.2.6. Spatial Durbin Model
3.2.7. Geographically and Temporally Weighted Regression
4. Results
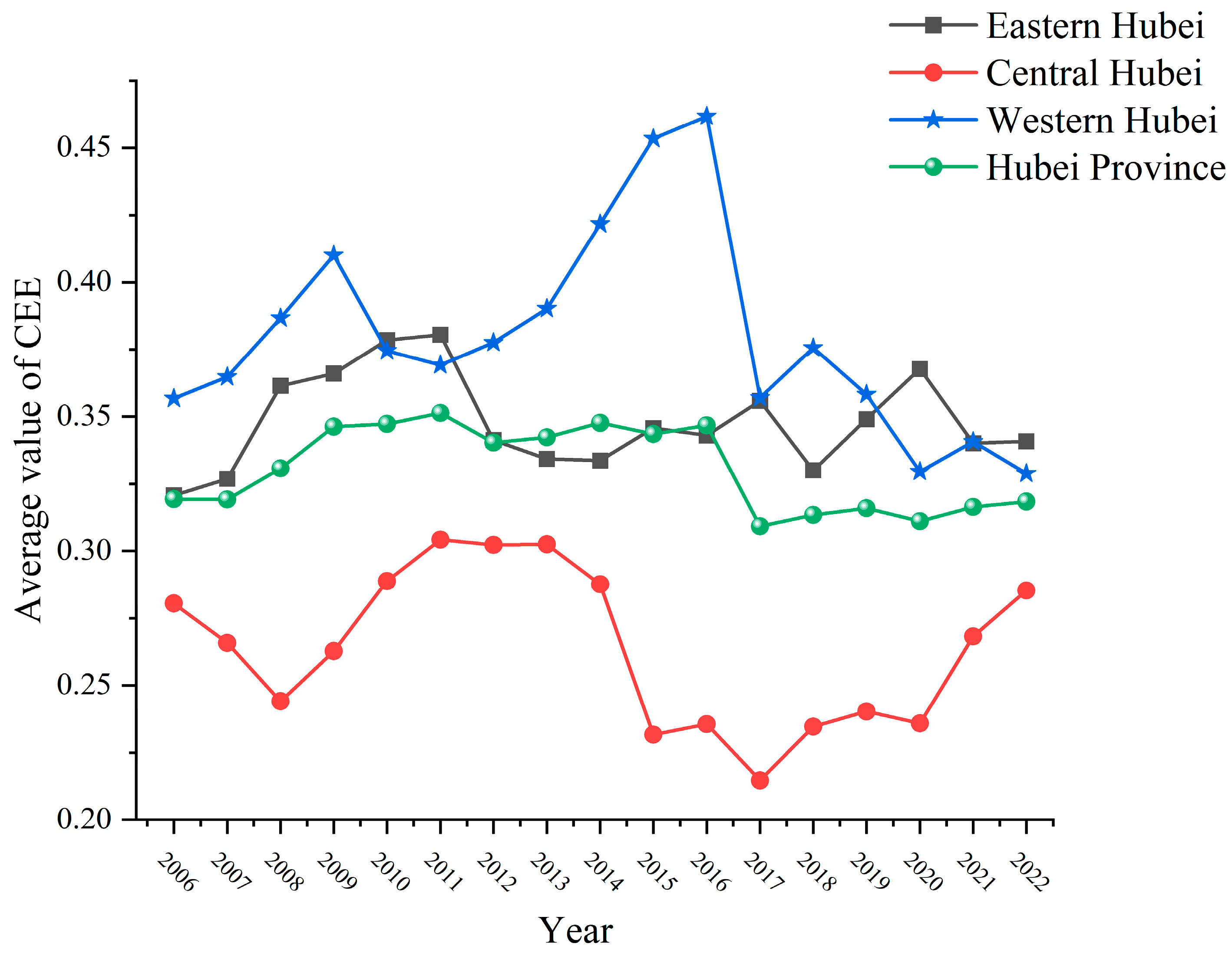
4.1. Spatiotemporal Characteristics of CEE in Hubei
4.2. Evolution Trend of Hubei’s City-Level CEE
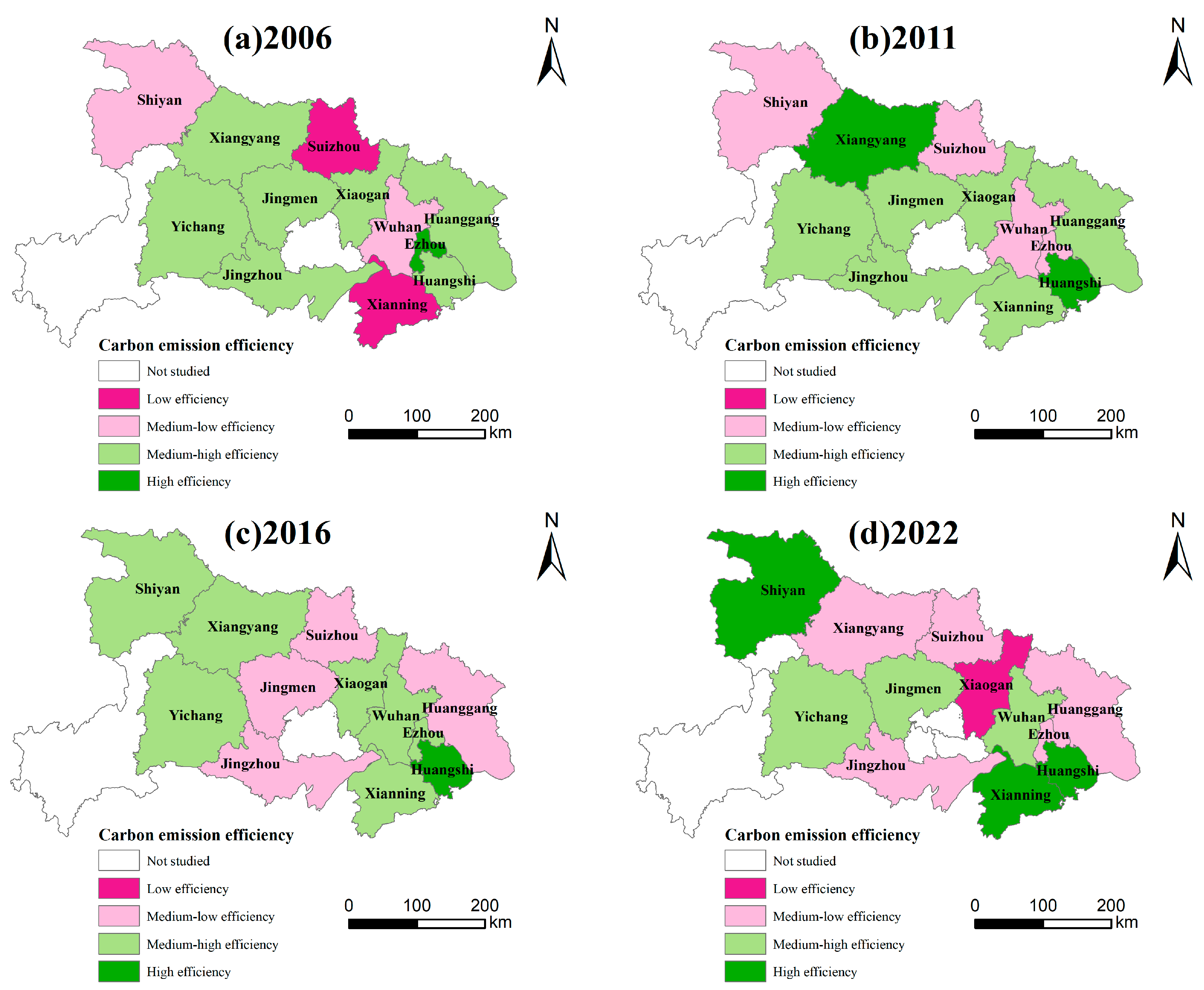
4.2.1. The Dynamic Evolution of CEE in Prefecture-Level Cities of Hubei
4.2.2. The Long-Term Transfer Trend of CEE in Prefecture-Level Cities of Hubei
4.3. Temporal Features of CEE in Prefecture-Level Cities of Hubei
4.4. CEE Determinants Analysis
4.4.1. Overall Average Impact of Determinants
4.4.2. Spatiotemporal Heterogeneity in the Effects of Determinants
5. Discussion
5.1. Trends in Regional Differentiation
5.2. Characterization of Influencing Factors
5.3. Limitations and Future Research Directions
6. Conclusions and Policy Implications
6.1. Conclusions
6.2. Policy Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
Appendix A.2
Appendix A.3
| Variable | Unit | Source |
|---|---|---|
| Per capita regional GDP | 10,000 CNY/person | Hubei Statistical Yearbook |
| Energy intensity | tonne of SCE/10,000 CNY | China City Statistical Yearbook |
| Population Density | person/km2 | China City Statistical Yearbook |
| Share of the secondary sector | % | Hubei Statistical Yearbook |
| Urbanization Rate | % | China City Statistical Yearbook |
| Resident population | 10,000 persons | Hubei Statistical Yearbook |
| Variable | Direct Effect | Indirect Effect | Total Effect |
|---|---|---|---|
| Energy intensity | 0.1276 *** | −0.0037 | 0.1238 *** |
| (0.0020) | (0.0031) | (0.0032) | |
| Proportion of hydropower | 0.6165 | −1.0279 | −0.4114 |
| (0.5986) | (0.8828) | (0.8297) | |
| Per capita regional GDP | 0.1029 *** | 0.0006 | 0.1034 *** |
| (0.0029) | (0.0039) | (0.0035) | |
| Share of the secondary sector | 0.1002 *** | −0.0789 *** | 0.0213 |
| (0.0079) | (0.0119) | (0.0148) | |
| Resident population | 0.1003 *** | 0.0006 | 0.1010 *** |
| (0.0013) | (0.0024) | (0.0027) | |
| Population density | 0.1013 *** | −0.0119 *** | 0.0894 *** |
| (0.0018) | (0.0026) | (0.0029) | |
| Urbanization rate | 0.0978 *** | −0.0108 | 0.0870 *** |
| (0.0039) | (0.0093) | (0.0089) | |
| Regional fixed effect | Yes | Time fixed effect | Yes |
| R2 | 0.939 |
| Variable | Standardized Beta |
|---|---|
| Energy intensity | −0.178 |
| Proportion of hydropower | 0.298 |
| Per capita regional GDP | −0.575 |
| Share of the secondary sector | 0.859 |
| Resident population | 0.102 |
| Population density | −1.103 |
| Urbanization rate | 0.083 |
References
- Huang, L.; Kelly, S.; Lv, K.; Giurco, D. A systematic review of empirical methods for modeling sectoral carbon emissions in China. J. Clean. Prod. 2019, 215, 1382–1401. [Google Scholar] [CrossRef]
- Zhao, Q.; Gao, W.; Su, Y.; Wang, T. Carbon emissions trajectory and driving force from the construction industry with a city-scale: A case study of Hangzhou, China. Sustain. Cities Soc. 2023, 88, 104283. [Google Scholar] [CrossRef]
- Chen, L.; Yang, H.N.; Xiao, Y.; Tang, P.Y.; Liu, S.Y.; Chang, M.; Huang, H. Exploring spatial pattern optimization path of urban building carbon emission based on low-carbon cities analytical framework: A case study of Xi’an, China. Sustain. Cities Soc. 2024, 111, 105551. [Google Scholar] [CrossRef]
- IEA. CO2 Total Emissions by Region, 2000–2023; IEA: Paris, France, 2024; Available online: https://www.iea.org/data-and-statistics/charts/co2-total-emissions-by-region-2000-2023 (accessed on 27 February 2024).
- Yang, B.; Jahanger, A.; Usman, M.; Khan, M.A. The dynamic linkage between globalization, financial development, energy utilization, and environmental sustainability in GCC countries. Environ. Sci. Pollut. Res. 2021, 28, 16568–16588. [Google Scholar] [CrossRef]
- National Development and Reform Commission. Introduction to the “1+N” Planning Policy System for the Development of the Yangtze River Economic Belt During the 14th Five-Year Plan Period (I). 2021. Available online: https://www.ndrc.gov.cn/fggz/fgzy/shgqhy/202111/t20211122_1304650.html (accessed on 6 November 2021).
- Wen, W.; Wang, Q. Re-examining the realization of provincial carbon dioxide emission intensity reduction targets in China from a consumption-based accounting. J. Clean. Prod. 2020, 244, 118488. [Google Scholar] [CrossRef]
- Pan, X.; Guo, S.; Xu, H.; Tian, M.; Pan, X.; Chu, J. China’s carbon intensity factor decomposition and carbon emission decoupling analysis. Energy 2022, 239, 122175. [Google Scholar] [CrossRef]
- National Development and Reform Commission. Notice on Launching Pilot Programs for Low-Carbon Provinces and Low-Carbon Cities. 2010. Available online: https://www.ndrc.gov.cn/xxgk/zcfb/tz/201008/t20100810_964674.html (accessed on 8 August 2010).
- Wuhan Water Authority. Floods and Droughts Are Not Constant, and Rivers Are Safe—CKRC Actively Responds to the Rare Drought in the Yangtze River Basin in 2022. Available online: https://swj.wuhan.gov.cn/tzdt/jcss/202211/t20221125_2102612.html (accessed on 25 November 2022).
- Wang, W.; Wang, H.; Sun, D.; Liu, G.; Fang, Z.; He, W. Carbon emission reduction or biodiversity conservation? Insights gained from interregional hydropower transmission. Resour. Conserv. Recycl. 2025, 212, 108014. [Google Scholar] [CrossRef]
- General Office of Wuhan Municipal People’s Government. Notice of the General Office of Wuhan Municipal People’s Government on Issuing the Work Plan for Promoting Carbon Reduction and Developing a Low-Carbon Industry in Wuhan (Document No. WZB [2021] 95). Available online: http://hbj.wuhan.gov.cn/hjsj/ztzl/hbcyzcqd/cygzlfz/202109/t20210914_1777522.html (accessed on 2 September 2021).
- Chen, H.; Chen, W. Carbon mitigation of China’s building sector at the city level: Pathways and policy implications based on a case study of a low-carbon province. J. Clean. Prod. 2019, 224, 207–217. [Google Scholar] [CrossRef]
- Ke, N.; Lu, X.; Kuang, B.; Zhang, X. Regional disparities and evolution trend of city-level carbon emission intensity in China. Sustain. Cities Soc. 2023, 88, 104288. [Google Scholar] [CrossRef]
- Fisher-Vanden, K.; Jefferson, G.H.; Ma, J.; Xu, J. Technology development and energy productivity in China. Energy Econ. 2006, 28, 690–705. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, F.; Ma, X.; He, L. Carbon emissions efficiency in China: Key facts from regional and industrial sector. J. Clean. Prod. 2019, 206, 850–869. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Y.; Gao, Y.; Wang, J. Carbon emission trading policy and carbon emission efficiency: An empirical analysis of China’s prefecture-level cities. Front. Energy Res. 2021, 9, 793601. [Google Scholar] [CrossRef]
- Maziotis, A.; Sala-Garrido, R.; Mocholi-Arce, M.; Molinos-Senante, M. Evaluating carbon performance in the water industry: A longitudinal analysis of England and Wales. Results Eng. 2024, 24, 103580. [Google Scholar] [CrossRef]
- Dong, F.; Li, Y.; Gao, Y.; Zhu, J.; Qin, C.; Zhang, X. Energy transition and carbon neutrality: Exploring the non-linear impact of renewable energy development on carbon emission efficiency in developed countries. Resour. Conserv. Recycl. 2022, 177, 106002. [Google Scholar] [CrossRef]
- Zheng, H.; Wu, Y.; He, H.; Delang, C.O.; Lu, J.; Yao, Z.; Dong, S. Urbanization and urban energy eco-efficiency: A meta-frontier super EBM analysis based on 271 cities of China. Sustain. Cities Soc. 2024, 101, 105089. [Google Scholar] [CrossRef]
- Cui, L.; Chen, L.; Yang, X. Evaluation and analysis of green efficiency of China’s coastal ports under the “double carbon” goal: Two improved DEA models with CO2 emissions. Environ. Dev. Sustain. 2024, 26, 29099–29128. [Google Scholar] [CrossRef]
- Song, M.; Wu, J.; Song, M.; Zhang, L.; Zhu, Y. Spatiotemporal regularity and spillover effects of carbon emission intensity in China’s Bohai Economic Rim. Sci. Total Environ. 2020, 740, 140184. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Khan, S.U.; Deng, Y.; Zhao, M. Spatiotemporal heterogeneity, convergence and its impact factors: Perspective of carbon emission intensity and carbon emission per capita considering carbon sink effect. Environ. Impact Assess. Rev. 2022, 92, 106699. [Google Scholar] [CrossRef]
- Song, H.; Gu, L.; Li, Y.; Zhang, X.; Song, Y. Research on carbon emission efficiency space relations and network structure of the Yellow River Basin City cluster. Int. J. Environ. Res. Public Health 2022, 19, 12235. [Google Scholar] [CrossRef]
- Li, R.; Li, L.; Wang, Q. The impact of energy efficiency on carbon emissions: Evidence from the transportation sector in 30 Chinese provinces. Sustain. Cities Soc. 2022, 82, 103880. [Google Scholar] [CrossRef]
- Wei, Q.; Xue, L.; Zhang, H.; Chen, P.; Yang, J.; Niu, B. Spatiotemporal analysis of carbon emission efficiency across economic development stages and synergistic emission reduction in the Beijing-Tianjin-Hebei region. J. Environ. Manag. 2025, 377, 124609. [Google Scholar] [CrossRef] [PubMed]
- Kuang, B.; Lu, X.; Zhou, M.; Chen, D. Provincial cultivated land use efficiency in China: Empirical analysis based on the SBM-DEA model with carbon emissions considered. Technol. Forecast. Soc. Change 2020, 151, 119874. [Google Scholar] [CrossRef]
- Kim, D. Exploratory study on the spatial relationship between emerging infectious diseases and urban characteristics: Cases from Korea. Sustain. Cities Soc. 2021, 66, 102672. [Google Scholar] [CrossRef]
- Agovino, M.; Crociata, A.; Sacco, P.L. Proximity effects in obesity rates in the US: A spatial Markov chains approach. Soc. Sci. Med. 2019, 220, 301–311. [Google Scholar] [CrossRef]
- Chen, X.; Chen, W.; Hu, T.; Yang, B.; Zeng, J. Regional carbon efficiency and corporate cash holdings: Evidence from China. Humanit. Soc. Sci. Commun. 2023, 10, 511. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X.; Liu, X.; Li, X.; Liao, F.; Tang, H.; He, Q. Spatiotemporal evolution and influencing factors of carbon emission efficiency in China’s resource-based cities based on super-efficiency SBM–GML measurement and spatial econometric tests. Sustainability 2025, 17, 7540. [Google Scholar] [CrossRef]
- Wang, L.; Sun, Y.; Xu, D. Study on the spatial characteristics of the digital economy on urban carbon emissions. Environ. Sci. Pollut. Res. 2023, 30, 80261–80278. [Google Scholar] [CrossRef]
- Zeng, G.; Sang, Y.; Gui, Q.; Li, J.; Yuan, J.; Zhu, K. Research on carbon emission efficiency and spatial-temporal factors in the transportation industry: Evidence from the Yangtze River Economic Belt. Glob. Nest J. 2024, 26, 4. [Google Scholar]
- Zhang, X.; Zhang, N.; Wang, S.; Dong, J.; Pan, X. Spatiotemporal evolution and influencing factors of carbon emission efficiency in western valley cities in China. Sustainability 2025, 17, 5025. [Google Scholar] [CrossRef]
- Yang, D.; Guo, R.; O’Connor, P.; Zhou, T.; Zhang, S.; Meng, H.; Ma, W. Embodied carbon transfers and employment-economic spillover effects in China’s inter-provincial trade. Front. Environ. Sci. 2023, 11, 1088997. [Google Scholar] [CrossRef]
- Song, C.; Zhang, Z.; Xu, W.; Elshkaki, A. The spatial effect of industrial transfer on carbon emissions under firm location decision: A carbon neutrality perspective. J. Environ. Manag. 2023, 330, 117139. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, T.; Wang, J.; Guo, F.; Kan, X.; Yuan, R. Spatial analysis on carbon emission abatement capacity at provincial level in China from 1997 to 2014: An empirical study based on SDM model. Atmos. Pollut. Res. 2019, 10, 97–104. [Google Scholar] [CrossRef]
- Wei, L.; Zeng, B. Urban technology transfer, spatial spillover effects, and carbon emissions in China. Sustainability 2024, 16, 9662. [Google Scholar] [CrossRef]
- Tian, Y.; Pang, J. Promoting the achievement of carbon neutrality targets: Systematic review of research dimensions and measure methods on carbon equity in China. Environ. Sci. Technol. 2024, 58, 9912–9924. [Google Scholar] [CrossRef]
- Tone, K. Dealing with undesirable outputs in DEA: A slacks-based measure (SBM) approach. GRIPS Discuss. Pap. 2015, 1, 1–15. [Google Scholar]
- Song, C.; Liu, Q.; Song, J.; Jiang, Z.; Lu, Z.; Chen, Y. Land Use Efficiency in the Yellow River Basin in the Background of China’s Economic Transformation: Spatial-Temporal Characteristics and Influencing Factors. Land 2022, 11, 2306. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, G.; Zhang, J. The estimation of China’s provincial capital stock: 1952–2000. Econ. Res. J. 2004, 10, 35–44. (In Chinese) [Google Scholar]
- GB/T 2589-2020; General Rules for Calculation of Comprehensive Energy Consumption. National Public Service Platform for Standards Information: Beijing, China, 2020. Available online: https://std.samr.gov.cn/gb/search/gbDetailed?id=B13990C15C2D5DDAE05397BE0A0A0D35 (accessed on 29 September 2020).
- Wu, J.; Guo, Z. Convergence analysis of China’s carbon emissions based on the continuous dynamic distribution approach. Stat. Res. 2016, 33, 54–60. (In Chinese) [Google Scholar]
- Zhao, Y.; Wu, Q.; Wei, P.; Zhao, H.; Zhang, X.; Pang, C. Explore the mitigation mechanism of urban thermal environment by integrating geographic detector and standard deviation ellipse (SDE). Remote Sens. 2022, 14, 3411. [Google Scholar] [CrossRef]
- Katkovnik, V.; Shmulevich, I. Kernel density estimation with adaptive varying window size. Pattern Recognit. Lett. 2002, 23, 1641–1648. [Google Scholar] [CrossRef]
- Phadkantha, R.; Tansuchat, R. Dynamic impacts of energy efficiency, economic growth, and renewable energy consumption on carbon emissions: Evidence from Markov Switching model. Energy Rep. 2023, 9, 332–336. [Google Scholar] [CrossRef]
- Le Gallo, J. Space-time analysis of GDP disparities among European regions: A Markov chains approach. Int. Reg. Sci. Rev. 2004, 27, 138–163. [Google Scholar] [CrossRef]
- Yan, D.; Lei, Y.; Li, L.; Song, W. Carbon emission efficiency and spatial clustering analyses in China’s thermal power industry: Evidence from the provincial level. J. Clean. Prod. 2017, 156, 518–527. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, H.; Lv, Y.; Zhang, N. The effect of new-type urbanization on energy consumption in China: A spatial econometric analysis. J. Clean. Prod. 2017, 163, S299–S305. [Google Scholar] [CrossRef]
- Huang, B.; Wu, B.; Barry, M. Geographically and temporally weighted regression for modeling spatio-temporal variation in house prices. Int. J. Geogr. Inf. Sci. 2010, 24, 383–401. [Google Scholar] [CrossRef]
- Zhao, R.; Wu, J.; Sun, J. Analysis of disequilibrium and driving factors of carbon emission efficiency: Evidence from five major urban agglomerations in China. J. Clean. Prod. 2024, 478, 143908. [Google Scholar] [CrossRef]
- Li, W.; Dong, F.; Ji, Z. Evaluation of carbon emission efficiency and reduction potential of 336 cities in China. J. Clean. Prod. 2023, 428, 139372. [Google Scholar] [CrossRef]
- Liu, C.; Sun, W.; Li, P.; Zhang, L.; Li, M. Differential characteristics of carbon emission efficiency and coordinated emission reduction pathways under different stages of economic development: Evidence from the Yangtze River Delta, China. J. Environ. Manag. 2023, 330, 117018. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, H.; Guo, B.; Liu, X.; Deng, C.; Zhao, Z.; Jang, X.; Li, Y. Characteristics and formation mechanism of carbon emission efficiency spatial correlation network: Perspective from Shandong Province. Ecol. Indic. 2025, 170, 112996. [Google Scholar] [CrossRef]
- Lin, W.; Yin, J.; Huang, Z. Study on the Carbon Emission Efficiency of Pearl River Delta Ports Based on the Super-SBM-GML Index Model. In Proceedings of the International Conference on Neural Computing for Advanced Applications, Guilin, China, 5–7 July 2024; Springer Nature: Singapore; pp. 263–277. [Google Scholar]
- Wang, Q.; Zhao, M.; Li, R.; Su, M. Decomposition and decoupling analysis of carbon emissions from economic growth: A comparative study of China and the United States. J. Clean. Prod. 2018, 197, 178–184. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, B.; Deng, H.; Du, H.; Yang, R.; Ju, L.; Liu, S. Analysis on the evolution law and influencing factors of Beijing’s power generation carbon emissions. Energy Rep. 2022, 8, 1689–1697. [Google Scholar] [CrossRef]
- Zhu, E.; Qi, Q.; Chen, L.; Wu, X. The spatial-temporal patterns and multiple driving mechanisms of carbon emissions in the process of urbanization: A case study in Zhejiang, China. J. Clean. Prod. 2022, 358, 131954. [Google Scholar] [CrossRef]
- Xin, L.; Jia, J.; Hu, W.; Zeng, H.; Chen, C.; Wu, B. Decomposition and decoupling analysis of CO2 emissions based on LMDI and two-dimensional decoupling model in Gansu Province, China. Int. J. Environ. Res. Public Health 2021, 18, 6013. [Google Scholar] [CrossRef]
- Pan, X.; Pan, X.; Li, C.; Song, J.; Zhang, J. Effects of China’s environmental policy on carbon emission efficiency. Int. J. Clim. Change Strateg. Manag. 2019, 11, 326–340. [Google Scholar] [CrossRef]
- Wang, T.; Li, H. Have regional coordinated development policies promoted urban carbon emission efficiency? —Evidence from the urban agglomerations in the middle reaches of the Yangtze River. Environ. Sci. Pollut. Res. 2023, 30, 39618–39636. [Google Scholar] [CrossRef]
- Yang, Y.; Dong, S.; Li, F.; Cheng, H.; Chi, Y.; Li, Z.; Li, Y. Interregional polarized and trickling-down effect of carbon emission space and the optimization policies: Case studies of the Jing-Jin-Ji region. J. Clean. Prod. 2022, 370, 133426. [Google Scholar] [CrossRef]
- Shiyan Municipal People’s Government. Notice on Issuing the Implementation Plan for the National Carbon Peaking Pilot (Shiyan). Available online: http://www.yrdcpcn.org.cn/c55951/20240807/i116369.phtml (accessed on 2 August 2024).
- Xianning Municipal Development and Reform Commission. The First Announcement of Environmental Impact Assessment for the Clean Energy Development Plan of Xianning City (2023–2035). Available online: http://fgw.xianning.gov.cn/zwdt/tzgg/202404/t20240425_3560508.shtml (accessed on 25 April 2024).



| First-Level Indicators | Second-Level Indicators | Third-Level Indicators and Calculation Method Explanations |
|---|---|---|
| Input indicators | Labor | End-of-year employment Directly adopt data from the Statistical Yearbook |
| Capital | Capital stock Calculated by the perpetual inventory method, the formula is: Where : Capital stock of the city in the year : Capital depreciation rate, with the depreciation rate being 9.6%, this study employs the estimation method proposed by Zhang et al. [42] : Capital flow | |
| Energy | Total energy consumption Converted to standard coal, for specific standards, refer to the General Rules for Comprehensive Energy Consumption Calculation [43]. The formula is: Where : Total energy consumption of the city in the year : The standard-coal conversion factor : The final consumption of fuel Natural gas: 1.33 kgce/m3 Liquefied petroleum gas:1.7143 kg tec/kg Electricity: 0.1229 kgce/(kW·h) | |
| Output indicators | Desirable output | Gross Regional Product (constant price in 2006) GDP deflator adjustment |
| Undesirable output | Carbon dioxide emissions Calculated with reference to the IPCC method: Including emissions from direct energy (natural gas or liquefied petroleum gas) and indirect energy (electricity or heat). The specific carbon emission calculation method refers to Wu et al. [44]. |
| Studies | Research Area | Period | CEE Range/Average Efficiency |
|---|---|---|---|
| Zhao et al., [52] | China’s five national urban agglomerations | 2006–2020 | 0.51 |
| Li et al., [53] | China | 2020 | 0.31 |
| Liu et al., [54] | the Yangtze River Delta | 2000–2019 | 0.608–0.648 |
| Zhang et al., [55] | Shandong | 2006–2021 | 0.167–0.834 |
| Lin et al., [56] | ports in the Pearl River Delta region | 2010–2022 | ≥1 |
| Year | Center X(°E) | Center Y(°N) | Semi-Major Axis (km) | Semi-Minor Axis(km) | Rotation (°) |
|---|---|---|---|---|---|
| 2006 | 113.4050 | 30.8114 | 222.2218 | 87.5147 | 109.1531 |
| 2011 | 113.3173 | 30.8171 | 217.5849 | 93.6150 | 111.5365 |
| 2016 | 113.5564 | 30.7056 | 230.1388 | 84.4041 | 114.7495 |
| 2022 | 113.2957 | 30.7876 | 244.5751 | 91.6982 | 115.6474 |
| Type of Space | t/(t + 1) | I | II | III | IV | |
|---|---|---|---|---|---|---|
| Traditional | No lag | I | 0.7917 | 0.2083 | 0.0000 | 0.0000 |
| II | 0.1522 | 0.6739 | 0.1522 | 0.2170 | ||
| III | 0.8000 | 0.1000 | 0.6000 | 0.2200 | ||
| IV | 0.0000 | 0.2080 | 0.2083 | 0.7708 | ||
| Spatial | I | I | 0.5000 | 0.5000 | 0.0000 | 0.0000 |
| II | 0.2727 | 0.7273 | 0.0000 | 0.0000 | ||
| III | 0.1333 | 0.6670 | 0.8000 | 0.0000 | ||
| IV | 0.000 | 0.0000 | 0.0000 | 0.1000 | ||
| II | I | 0.6923 | 0.3077 | 0.0000 | 0.0000 | |
| II | 0.6670 | 0.7333 | 0.2000 | 0.0000 | ||
| III | 0.0000 | 0.2000 | 0.5333 | 0.2667 | ||
| IV | 0.0000 | 0.0000 | 0.1176 | 0.8824 | ||
| III | I | 0.9333 | 0.6670 | 0.0000 | 0.0000 | |
| II | 0.8330 | 0.5833 | 0.2500 | 0.8330 | ||
| III | 0.1429 | 0.7140 | 0.4286 | 0.3571 | ||
| IV | 0.0000 | 0.4760 | 0.2381 | 0.7143 | ||
| IV | I | 0.8571 | 0.1429 | 0.0000 | 0.0000 | |
| II | 0.2500 | 0.6250 | 0.1250 | 0.0000 | ||
| III | 0.0000 | 0.0000 | 0.6667 | 0.3333 | ||
| IV | 0.0000 | 0.0000 | 0.3750 | 0.6250 | ||
| Year | I | E(I) | Sd(I) | Z | p-Value |
|---|---|---|---|---|---|
| 2006 | −0.0640 | −0.0909 | 0.2542 | 0.1058 | 0.9157 |
| 2007 | −0.1152 | −0.0909 | 0.2646 | −0.0917 | 0.9269 |
| 2008 | −0.2738 | −0.0909 | 0.2829 | −0.6465 | 0.5180 |
| 2009 | −0.3206 | −0.0909 | 0.2895 | −0.7935 | 0.4275 |
| 2010 | −0.6743 | −0.0909 | 0.2928 | −1.9925 | 0.0463 |
| 2011 | −0.6885 | −0.0909 | 0.2993 | −1.9964 | 0.0459 |
| 2012 | −0.6577 | −0.0909 | 0.2923 | −1.9391 | 0.0525 |
| 2013 | −0.6248 | −0.0909 | 0.2533 | −2.1075 | 0.0351 |
| 2014 | −0.2483 | −0.0909 | 0.1375 | −1.1448 | 0.2523 |
| 2015 | −0.0307 | −0.0909 | 0.0855 | 0.7041 | 0.4814 |
| 2016 | −0.0006 | −0.0909 | 0.0895 | 1.0092 | 0.3129 |
| 2017 | 0.5134 | −0.0909 | 0.305 | 1.9816 | 0.0475 |
| 2018 | 0.5477 | −0.0909 | 0.3073 | 2.0784 | 0.0377 |
| 2019 | 0.5251 | −0.0909 | 0.2814 | 2.1893 | 0.0286 |
| 2020 | 0.8757 | −0.0909 | 0.2959 | 3.267 | 0.0011 |
| 2021 | 0.6643 | −0.0909 | 0.2879 | 2.6236 | 0.0087 |
| 2022 | 0.5334 | −0.0909 | 0.288 | 2.1675 | 0.0302 |
| Variable | VIF | 1/VIF |
|---|---|---|
| Per capita GDP | 6.62 | 0.15 |
| Energy intensity | 3.00 | 0.33 |
| Proportion of hydropower | 2.44 | 0.41 |
| Share of the secondary sector | 2.51 | 0.40 |
| Resident population | 2.10 | 0.48 |
| Population density | 1.36 | 0.74 |
| Urbanization rate | 2.11 | 0.47 |
| Mean VIF | 2.88 | |
| Variable | Direct Effect | Indirect Effect | Total Effect |
|---|---|---|---|
| Energy intensity | 0.1286 *** | −0.0038 | 0.1248 *** |
| (0.0020) | (0.0033) | (0.0038) | |
| Proportion of hydropower | 0.5811 | −1.0212 | −0.4401 |
| (0.6316) | (1.0003) | (0.9263) | |
| Per capita regional GDP | 0.1048 *** | 0.0018 | 0.1066 *** |
| (0.0028) | (0.0043) | (0.0039) | |
| Share of the secondary sector | 0.0950 *** | −0.0902 *** | 0.0047 |
| (0.0077) | (0.0133) | (0.0154) | |
| E | 0.1008 *** | −0.0003 | 0.1005 *** |
| (0.0014) | (0.0024) | (0.0028) | |
| Population density | 0.1033 *** | −0.0117 *** | 0.0916 *** |
| (0.0016) | (0.0027) | (0.0031) | |
| Urbanization rate | 0.0999 *** | −0.0112 | 0.0887 *** |
| (0.0039) | (0.0099) | (0.0101) | |
| −0.2230 ** | |||
| −0.0953 | |||
| −0.0000 *** | |||
| (0.0000) | |||
| Regional fixed effect | Yes | Time fixed effect | Yes |
| R2 | 0.958 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, M.; Han, X.; Yi, M.; Zhang, J.; Zhang, W.; Huang, M. Research on Regional Disparities and Determinants of Carbon Emission Efficiency: A Case Study of Hubei Province, China. Sustainability 2025, 17, 9465. https://doi.org/10.3390/su17219465
Lei M, Han X, Yi M, Zhang J, Zhang W, Huang M. Research on Regional Disparities and Determinants of Carbon Emission Efficiency: A Case Study of Hubei Province, China. Sustainability. 2025; 17(21):9465. https://doi.org/10.3390/su17219465
Chicago/Turabian StyleLei, Ming, Xu Han, Ming Yi, Juan Zhang, Wei Zhang, and Mengke Huang. 2025. "Research on Regional Disparities and Determinants of Carbon Emission Efficiency: A Case Study of Hubei Province, China" Sustainability 17, no. 21: 9465. https://doi.org/10.3390/su17219465
APA StyleLei, M., Han, X., Yi, M., Zhang, J., Zhang, W., & Huang, M. (2025). Research on Regional Disparities and Determinants of Carbon Emission Efficiency: A Case Study of Hubei Province, China. Sustainability, 17(21), 9465. https://doi.org/10.3390/su17219465






