Sustainable Control of Large-Scale Industrial Systems via Approximate Optimal Switching with Standard Regulators

Abstract

Large-scale production systems (LSPS) operate under growing complexity driven by digital transformation, tighter environmental regulations, and the demand for resilient and resource-efficient operation. Conventional control strategies, particularly PID and isodromic regulators, remain dominant in industrial automation due to their simplicity and robustness; however, their capability to achieve near-optimal performance is limited under constraints on control amplitude, rate, and energy consumption. This study develops an analytical–computational approach for the approximate realization of optimal nonlinear control using standard regulator architectures. The method determines switching moments analytically and incorporates practical feasibility conditions that account for nonlinearities, measurement noise, and actuator limitations. A comprehensive robustness analysis and simulation-based validation were conducted across four representative industrial scenarios—energy, chemical, logistics, and metallurgy. The results show that the proposed control strategy reduces transient duration by up to 20%, decreases overshoot by a factor of three, and lowers transient energy losses by 5–8% compared with baseline configurations, while maintaining bounded-input–bounded-output (BIBO) stability under parameter uncertainty and external disturbances. The framework provides a clear implementation pathway combining analytical tuning with observer-based derivative estimation, ensuring applicability in real industrial environments without requiring complex computational infrastructure. From a broader sustainability perspective, the proposed method contributes to the reliability, energy efficiency, and longevity of industrial systems. By reducing transient energy demand and mechanical wear, it supports sustainable production practices consistent with the following United Nations Sustainable Development Goals—SDG 7 (Affordable and Clean Energy), SDG 9 (Industry, Innovation and Infrastructure), and SDG 12 (Responsible Consumption and Production). The presented results confirm both the theoretical soundness and practical feasibility of the approach, while experimental validation on physical setups is identified as a promising direction for future research.

1. Introduction

Modern large-scale production and service systems (LSPS) are facing increasing levels of complexity due to the rapid development of digital technologies, stricter environmental requirements, and the need to maintain high operational stability in the face of changing external influences. The transition to Industry 4.0, the integration of cyber-physical systems, and the use of smart drives and big data-based control systems open up significant opportunities for improving production efficiency. However, this increases the need for new approaches to the design of automatic control systems (ACS) that combine speed, adaptability, energy efficiency, and sustainability.

The task of developing control systems that ensure not only technical accuracy and stability, but also compliance with the principles of sustainable development—minimizing resource consumption, reducing harmful emissions, increasing equipment reliability, and extending its life cycle—is becoming particularly relevant. In this context, sustainable control is seen as a strategic approach aimed at optimizing production processes, taking into account resource constraints, technological limitations, and the need to ensure environmental safety.

One of the key problems in the development of industrial control systems is the existence of restrictions on the rate of change in control actions. Such limitations are widespread in real technical objects—from hydraulic and pneumatic drives to servomotors and intelligent actuators. These limitations can be caused by both the physical inertia of the elements and the requirements for safety, energy efficiency, or equipment durability. Under such conditions, classic linear or proportional-integral-derivative (PID) controllers often fail to achieve the required quality of transient processes, especially in the case of sudden disturbances or abrupt changes in the set parameters.

In response to these challenges, there is growing interest in the scientific and engineering community in theoretical and applied methods of optimal control with limited coordinates. In particular, an important place is occupied by an approach based on the principle of implementing a so-called set of optimal processes, within which the transition of the system from one state to another is carried out in the minimum time, provided that the control coordinate at each interval takes one of two limit values. This principle allows us to construct classes of controllers that ensure aperiodic and energy-saving behavior of the system even under severe restrictions on input actions.

This study aims to develop a concept for approximating optimal control processes in industrial systems using standard (in particular, isodromic and proportional) controllers. The main idea is to implement approximately optimal transient processes based on pre-calculated switching moments and controller tuning parameters without resorting to complex nonlinear computational schemes. This approach allows the use of existing ACS elements, including those already implemented in the production environment, while significantly improving their dynamic and stability characteristics.

The theoretical basis of the proposed method is the use of nth-order differential models with limited coordinates and the introduction of a mathematical apparatus for calculating optimal time intervals corresponding to limiting control actions. The output characteristics of the system are formulated as a function of the parameters of the initial state, the target state, and the durations of the control coordinate action intervals. An important consequence of the analysis is the possibility of excluding the time variable from the equations of motion, which allows describing the behavior of the system in a time-independent form and approximating it to the optimal even under conditions of incomplete information or noisy signals.

In addition, the paper examines the structure of real industrial control systems, including pulse circuits with relay elements, closed loops with feedback, and servo motors with limited speed. A classification of controller types is proposed based on the number of degrees of freedom and the conditions for implementing optimal processes. Particular attention is paid to the analysis of the stability and physical feasibility of the obtained parameters, as well as their limitations associated with nonlinearities, restrictions on the travel of control elements, and the required accuracy of derivative signal estimation.

From a practical point of view, the proposed approach can be integrated into next-generation management systems in industries such as the following:

• Energy (flow control in distribution networks with limited valve switching speed);
• Logistics and warehousing complexes (positioning and regulating the movement of goods with specified dynamics);
• Automation of mechanical engineering and robotics (precise control of manipulators and drives with limited speed);
• Oil, gas, and chemical industries (regulation of reagent supply or pressure in reactors with limit values).

Thus, the applicability and potential of the developed approach cover a wide class of systems that are critical in terms of sustainability, energy consumption, and operational reliability.

Although the theory of optimal control is well established and its potential to improve the efficiency of large-scale systems is widely recognized, relatively few studies focus on adapting these methods to standard industrial regulators. In practice, such regulators remain the dominant choice due to their simplicity and robustness, while advanced methods are rarely implemented because of their computational complexity and demanding tuning requirements. This paper addresses this gap by proposing a methodology for approximating optimal control with standard regulators under realistic industrial constraints.

The purpose of this article is to develop a theoretical and applied basis for constructing approximate optimal control systems for industrial facilities with limited coordinates, implemented on the basis of standard controllers. The proposed methodology combines mathematical rigor, engineering feasibility, and a focus on the sustainable development of production processes.

This paper proceeds as follows. Section 1 introduces the research problem, outlines its relevance to large-scale production systems, and formulates the study objectives. In the next section, Section 2, reviews the existing literature on optimal and sustainable control methods, with particular emphasis on approaches applicable under input constraints and their relevance to industrial automation. Section 3 presents the proposed methodology in detail, including its mathematical formulation, conditions for feasibility, and implementation scheme. Section 4 reports the results of modeling and simulation, illustrating the effectiveness of the method through four representative industrial scenarios—energy, chemical, logistics, and metallurgy—and quantifying the associated operational and sustainability benefits. Finally, Section 5 concludes with a summary of the main findings, discusses their implications for industrial practice, and outlines potential directions for further research.

2. Literature Review

Research in the field of automatic control of industrial facilities has traditionally relied on the use of linear controllers, such as PID, due to their simplicity of implementation and engineering reliability [1,2,3]. However, in recent decades, there has been growing interest in controlling systems with limited control actions, driven by the need to improve accuracy, speed, and stability under severe operating constraints [4,5,6]. Particular attention is paid to optimal control methods, which aim to achieve a given system state in the shortest time or with the least resource expenditure. The work of Pontryagin, Bellman, and their followers laid the fundamental principles of control with constraints [7,8], but the practical implementation of these approaches is often complicated by high computational complexity and the need to use nonlinear converters [9].

Against the backdrop of the rapid development of the concept of sustainable manufacturing and Industry 4.0, there is a growing need for control systems that combine energy efficiency, sustainability, and ease of integration into existing infrastructure [10,11,12]. Individual studies have shown that sustainable management is possible even with standard industrial controllers, provided they are configured to take into account the dynamic constraints and characteristics of the controlled object [13,14,15]. In addition, in the context of LSPS, approaches that ensure the reliable operation of automated control systems in the presence of structural and external disturbances, restrictions on speed, amplitude, and the resource of control actions are of particular importance [16,17]. In this direction, the theory of sets of optimal processes is being developed, where the transition of the system is carried out under conditions of discrete switching of control coordinates [18,19]. However, most works are limited to theoretical constructs and rarely take into account the characteristics of existing servo motors, pneumatic drives, and relay elements.

Recent studies confirm that the widespread use of PID controllers in industry is due not only to their simplicity, but also to their adaptability to various types of objects. However, when controlling systems with significant time delays and nonlinearities, their effectiveness decreases sharply [20,21]. In response to this, modified structures are being developed, such as Setpoint-Dependent Predictive PID+, robust controllers, and state-dependent controllers, which demonstrate higher stability and control accuracy [22,23,24].

Controlling objects with time delays remains one of the key areas in sustainable regulation. For example, ref. [25] discusses controlling the liquid level in a tank with a delay, where the implementation of SDP-PID+ made it possible to achieve stable and fast regulation with minimal fluctuations. Other studies, such as [26,27], demonstrate the effectiveness of discrete controllers in systems with delays of more than five sampling steps. However, the implementation of such schemes requires accurate identification of the model and parameters, which can complicate the implementation of LSPS in real-world conditions.

On the other hand, intelligent control methods—predictive control (MPC), neural network schemes, and adaptive algorithms—represent an interesting direction, especially in conditions of high external environment variability [28,29,30]. However, high computational load, configuration complexity, and poor interpretability limit their use in systems with strict stability and reliability requirements.

Despite the widespread use of theoretical solutions, existing literature does not pay sufficient attention to the task of approximating optimal transition processes under the constraints of simple, industrial, implementable controllers. The vast majority of works either propose complex intelligent controllers or focus on simulation studies without taking into account the hardware limitations of the actuators. In this regard, it becomes relevant to develop solutions that can ensure approximately optimal system behavior without compromising practical applicability.

Recent studies confirm that substantial progress in improving transient performance and advancing sustainability outcomes has been achieved through a variety of methods. Model Predictive Control (MPC) strategies, for instance, have demonstrated clear potential to reduce overshoot and enhance robustness under nonlinear and constrained conditions [27,28]. Reinforcement learning (RL) approaches also exhibit strong adaptability to dynamic environments, though their reliance on extensive training data and high computational demands often limits their feasibility for large-scale or real-time industrial applications [31,32]. In parallel, modified PID algorithms, such as SDP-PID+, have been reported to improve stability and control accuracy in systems with significant delays [33]. These approaches have undoubtedly advanced the state of the art; however, they frequently require sophisticated computational infrastructures, complex parameter tuning, or bespoke implementation strategies that hinder straightforward adoption in industrial automation. Against this backdrop, our study provides a distinct contribution by achieving comparable performance improvements through the use of standard industrial regulators. This ensures not only analytical rigor but also practical feasibility, which is particularly critical for sustainable development in large-scale production and transport systems.

This study aims to fill this gap. Unlike most existing approaches, it focuses on developing a universal methodology for the approximate implementation of optimal transient processes in systems with limited control actions, using standard controllers without the need to embed additional intelligent blocks. This solution combines analytical rigor, industrial feasibility, and compliance with modern requirements for sustainability and energy efficiency, making it particularly relevant in the context of LSPS and sustainable industrial development.

3. Methods and Models

The theory of optimal processes under changing external influences on a system with one or more limited parameters has already been developed [34]. Knowledge of the fundamentals of this theory as applied to systems with limited speed is necessary for understanding the provisions set forth in this study.

Let any coordinate $x_i$ of the control system $F$ (for example, the derivative of the control variable with respect to time) be limited by a given interval:

$$x_{i1}\le x_i\le x_{i2}$$

(1)

In order for the output value x of the system to change as quickly as possible, the coordinate $x_i$ is constantly maintained at one of two limit values, namely the one that deflects the system in the required direction. In this case, the output value $x$ and each of its derivatives are determined by the initial state $x_A,{\dot{x}}_A\dots$ of the system, the coordinate $x_{i1}$ or $x_{i2}$, and the time $t$ that has elapsed from the start of the process to the moment $t$ under consideration:

$$\begin{array}{c}x=f_0\left(x_A;{\dot{x}}_A;{\ddot{x}}_A;\dots ; x_{i1} or x_{i2};t\right);\\ \dot{x}=f_1\left(x_A;{\dot{x}}_A;{\ddot{x}}_A;\dots ; x_{i1} or x_{i2};t\right);\\ \ddot{x}=f_2\left(x_A;{\dot{x}}_A;{\ddot{x}}_A;\dots ; x_{i1} or x_{i2};t\right).\end{array}$$

(2)

Since the limited coordinate $x_i$ is kept constant for a long time, at the moment when $x$ reaches the required value (for example, the specified value), the derivatives of $x$ will differ from the derivatives of the specified value. In this case, the system does not reach a state of equilibrium. However, when the value of the limited coordinate changes after the end of the process, a state of equilibrium may still occur in a certain sense. If the required equilibrium state is achieved due to the fact that $x_i$ is alternately maintained at one of its limit values in separate intervals, then, provided that the bands of the linear transfer function $F$ with the excluded limited coordinate $x_i$ are valid and not positive, the fastest possible response of the system is achieved [30,34,35,36,37,38].

The process is divided into separate intervals $t_1, t_2, t_3\dots$ etc. Within each interval, the limited coordinate $x_i$ is kept constant at one of its limit values. When moving to the next interval, $x_i$ is brought to its other limit value.

Let us denote by $\eta$ the order of the differential equation (linear) part of the system, which relates the output variable $x$ and its derivatives to the bounded coordinate. Then the initial state and the required state x are determined by the output variable $x$ and its derivatives up to and including the $\left(\eta -1\right)$-th order.

If system $F$ is understood to be, for example, a tracking system with a control input $z_1$, then Equation (2) takes the following form:

$$\begin{array}{c}x=z_1=f_0\left(x_A,{\dot{x}}_A,\dots ;t_1,t_2,\dots \right);\\ \dot{x}={\dot{z}}_1=f_1\left(x_A,{\dot{x}}_A,\dots ;t_1,t_2,\dots \right)\\ \begin{array}{c}⋮\\ x^{(\eta -1)}=z_1^{(\eta -1)}=f_{\eta -1}\left(x_A,{\dot{x}}_A,\dots ;t_1,t_2,\dots \right).\end{array}\end{array}$$

(3)

Equation (3) represents a system of $\eta$ equations. To satisfy $\eta$ conditions, it is necessary to freely select at least $\eta$ parameters, which can be the durations of intervals $t_1, t_2\dots$, etc. The system of Equation (3) can be considered as a system with $\eta$ unknowns $t_1, t_2\dots$,$t_{\eta }$. Thus, the η intervals can be determined from the solution of the system of Equation (3).

In this case, the reproducibility condition must be satisfied:

$$\left|a_{\eta }{z}_1^{\left(\eta \right)}+a_{\eta -1}{z}_1^{(\eta -1)}+\dots \dot{a_1{z}_1}+a_0{z}_1\right|\le K,$$

(4)

where $K$ is the maximum value of the limited coordinate, and the coefficients of the differential equation of the system $F$ are equal to $a_{\eta },a_{\eta -1},\dots ,a_0$, respectively.

If $z_1$ is, for example, a step function of amplitude $z_{11}$, then Equation (3) can be used to calculate $\eta$ optimal switching moments $t_i(i=1,\dots ,\eta )$ corresponding to the $\eta$-th order of the system.

With the introduction of feedback of the output value $x$ to the input of the limited coordinate, there is a wide opportunity for automatic use of switching moments for control purposes.

The concept of “set of optimal processes”, first formulated, apparently, in Equation (3), is of great importance for the subsequent discussion.

If a system implements this “set of optimal processes,” then the optimal switching points and, consequently, the optimal process are automatically created not only for one given external influence; but also for the entire set of similar external influences, optimal transition processes are automatically achieved, for example, for step-like disturbances of any amplitude, or for linearly increasing influences, or for both types of disturbances simultaneously. There is a certain analogy here with a linear system, where once a matching has been performed, it is also retained for all possible amplitudes of the impact.

Let us assume that the optimal switching moments are obtained from Equation (3) for any external influence $z$ (change in the setpoint or load). As shown above, these switching moments are functions of $z$:

$$\begin{array}{c}{t}_1={\phi }_1\left(z\right);\\ t_2={\phi }_2\left(z\right);\\ \begin{array}{c}⋮\\ t_{\eta }={\phi }_{\eta }\left(z\right).\end{array}\end{array}$$

(5)

The transient (transitional) characteristics of the output variable $x$ and its derivatives are functions of these intervals:

$$\begin{array}{c}x\left(t\right)=f\left(t_1,t_2,\dots ,t_{\eta }\right);\\ \dot{x}\left(t\right)=\dot{f}\left(t_1,t_2,\dots ,t_{\eta }\right);\\ \begin{array}{c}⋮\\ x^{(\eta -1)}=f^{(\eta -1)}\left(t_1,t_2,\dots ,t_{\eta }\right).\end{array}\end{array}$$

(6)

If all time intervals can be eliminated from the system of Equation (6), it will be possible to find relationships between vector $x$ and its derivatives that no longer explicitly depend on time. If, for example, it is assumed (and for some simple and practically implementable systems this is the case) that all time intervals can be eliminated from the equations for $x(t$) and $\dot{x}\left(t\right)$, then the following expression is obtained

$$x=\phi \left(\dot{x}\right),$$

(7)

not dependent on time.

Equation (7) can also be written as follows

$$x-\phi \left(\dot{x}\right)=0$$

(8)

The system outputs a value $x$. This value x is converted to $\phi \left(\dot{x}\right)$. If, according to Equation (8), $\phi \left(\dot{x}\right)$ is subtracted from $x$, their difference is fed to the input via negative feedback, i.e., to the point of application of external influence and, accordingly, limited coordinates, then the influence of negative feedback occurs, obviously, if and only if the process differs from the optimal one. From the point of view of control engineering, negative feedback tends to bring the real process closer to the optimal one, since for the optimal process, expression (8) is always strictly true.

In this case, the practical feasibility of the functional transformer $\phi (\dot{x},\ddot{x},\dots )$, obtained similarly to Equation (8), is called into question due to the impossibility of obtaining higher derivatives in the presence of noise. In addition, higher derivatives are complex transcendental functions that cannot be technically implemented within reasonable costs.

At this stage, the mathematical formulation provides the theoretical basis for deriving the switching moments and feasibility conditions. To improve clarity and to connect these results with practical implementation, the proposed method is presented as a step-by-step framework. The process consists of four main stages: (1) formalization of the system model; (2) calculation of optimal switching moments; (3) tuning of standard regulators; and (4) execution of simulations under realistic constraints. This structure demonstrates how the theoretical basis of the approach can be systematically translated into engineering practice.

3.1. Approximation Using Optimal Switching Points

If we denote the difference between the specified and actual values by $x_W$, then the system of equations required to determine the n optimal switching moments $t_1,t_2,\dots ,t_n$ can be written analogously to Equation (3) as follows:

$$\begin{array}{c}0=x_W\left(t_n\right)=f_0\left(x_A,{\dot{x}}_A,\dots x_A^{\left(n-1\right)};t_1,t_2,\dots ,t_n\right);\\ 0={\dot{x}}_W\left(t_n\right)=f_1\left(x_A,{\dot{x}}_A,\dots x_A^{\left(n-1\right)};t_1,t_2,\dots ,t_n\right)\\ \begin{array}{c}⋮\\ 0=x_W^{(n-1)}\left(t_n\right)=f_{n-1}\left(x_A,{\dot{x}}_A,\dots x_A^{\left(n-1\right)};t_1,t_2,\dots ,t_n\right).\end{array}\end{array}$$

(9)

It is assumed that $t_1,\dots ,t_n$ are found for a single specific impact $z$ (change in the specified value or load). For a system with a differential Equation (5) of the $n$-th order $t_i (i=0,\dots ,\left(n-1\right))$ and equilibrium values $x_A^{\left(i\right)}\left(i=0,\dots ,\left(n-1\right)\right)$ and equilibrium values $x_W^{\left(i\right)}\left(t_n\right),\left(i=0,\dots ,\left(n-1\right)\right)$.

An $n$-th order system consists of a servomotor and a controlled object. The speed at which the servomotor acts on the controlled object is considered to be limited. A limited-speed servomotor with maximum values of $+K_0$ (forward rotation) and $-K_0$ (reverse rotation) can be considered as an integrator with an integration time constant equal to 1, preceded by a limiting link with saturation values $+K_0$ and $-K_0$ (Figure 1).

Then, from Equation (9), it follows that the limiting or relay link connected in front of the servomotor must switch from one limit position to another at times $t_1,\dots ,t_n, (n-1)$ in order to eliminate the mismatch $x_W$ and all its $(n-1)$ derivatives in the shortest possible time.

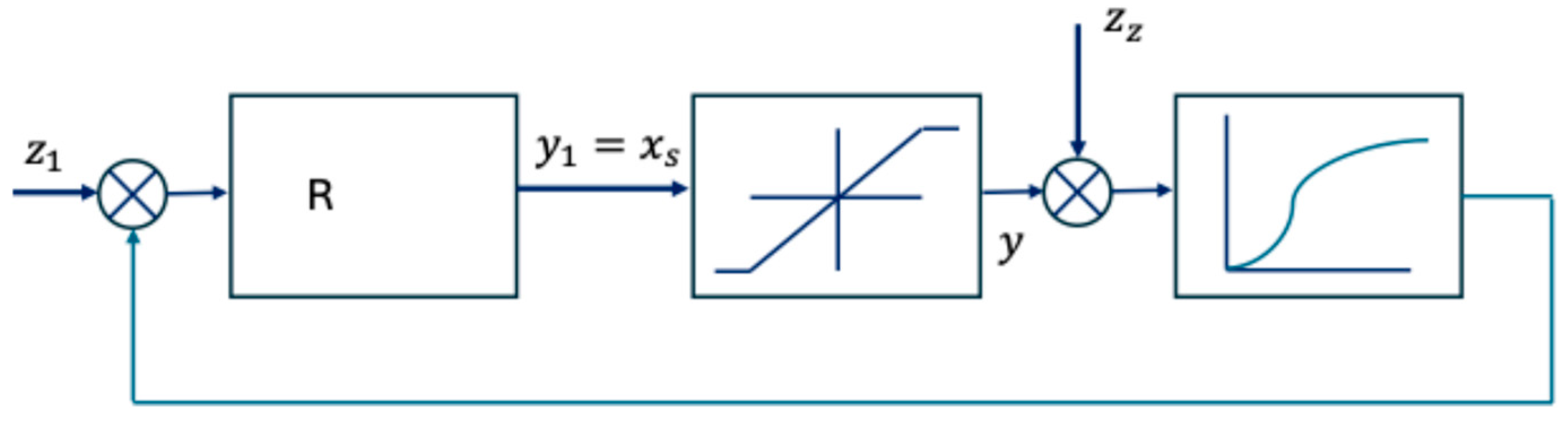
If the system (Figure 1) is regulated by a regulator $R$ of a certain type (for example, a standard isodromic stepless regulator or an isodromic regulator with anticipation), which has $K$ free setting parameters, then the system shown in Figure 2 is obtained.

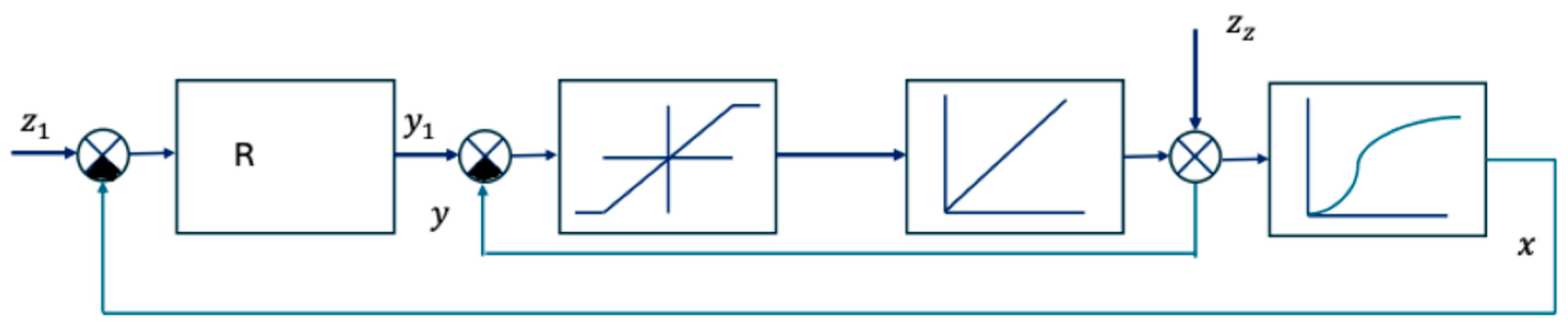
If the servomotor has a static proportional action (hard feedback), the result is a system corresponding to Figure 3. In this case, the controller also has $K$ degrees of freedom.

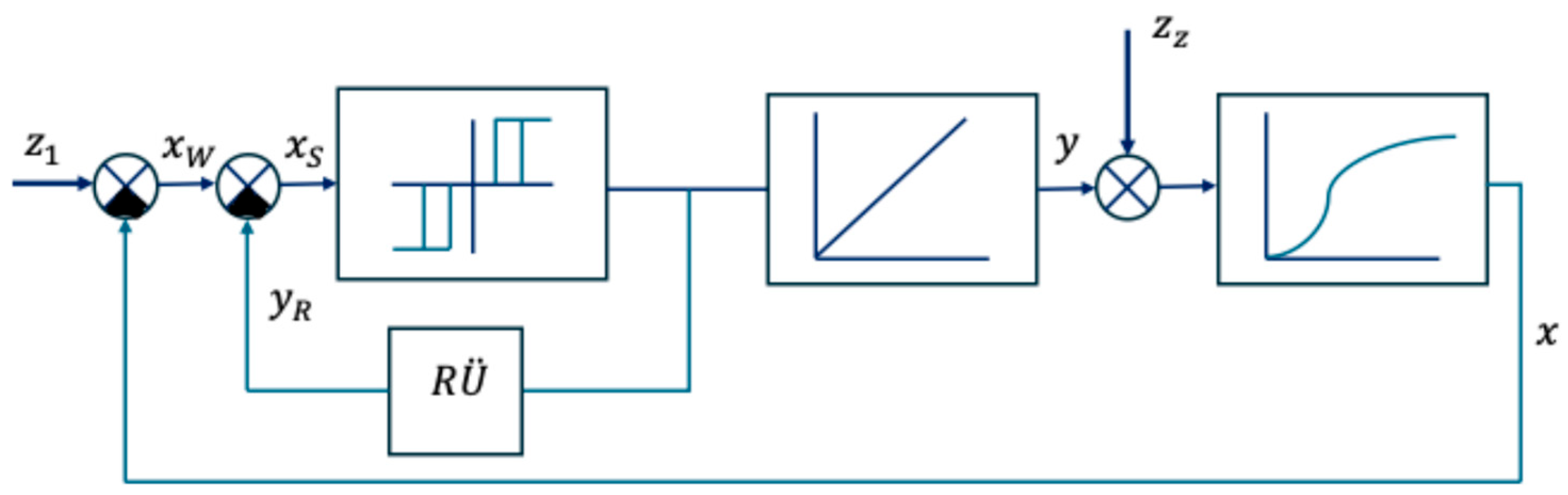
If the system is pulse-based, with a two- or three-position relay as a control amplifier, the result is a system corresponding to Figure 4, where $R_{\ddot{u}}$ is feedback, which also provides $K$ free adjustment parameters.

The systems shown in Figure 3 and Figure 4 can be considered typical of a large number of industrial (continuous and quasi-continuous) control systems.

If we disregard the input signal value required to control the limiting link (which is possible due to the smallness of this value), then, obviously, the following ratio must be present for the optimal process to be implemented:

$$x_s\left(t_i\right)=0 \mathrm{for} i=1\dots n,$$

(10)

Since the servomotor must switch at each moment in time $t_1,\dots ,t_n$, $x_s$ must not become zero between switching moments $t_i$ so that the limiting link can unambiguously execute the required sequence of limit values $x_W$ can be calculated at any moment in time $t_1,\dots ,t_n$.

If controller $R$ (Figure 2 and Figure 3) has $K$ degrees of freedom, then the output value $y_1$ of the controller (transfer function) is equal to:

$$y_1=f\left(k_1,k_2,\dots ,k_n,x_W,t\right).$$

(11)

For standard stepless regulators, we have:

$y_1=k_1{x}_W$ (proportional);

$y_1=k_1{x}_W+k_2{\int }_0^t{x}_{W}dt$ (isodromic);

$y_1=k_1{x}_W+k_2{\int }_0^t{x}_{W}dt+k_3{\dot{x}}_W$ (isodromic with anticipation).

The controllers shown in Figure 2 and Figure 3 must obviously have $K=n$ degrees of freedom if Equation (10) is to be satisfied. Then, for example, for the system shown in Figure 2, we obtain the following:

$$\begin{array}{c}{x}_s\left(t_1\right)=y\left(t_1\right)=0=f\left(k_1,\dots ,k_n,t_1\right);\\ x_s\left(t_1\right)=y\left(t_1\right)=0=f\left(k_1,\dots ,k_n,t_1,t_2\right);\\ \begin{array}{c}⋮\\ x_s\left(t_n\right)=y\left(t_n\right)=0=f\left(k_1,\dots ,k_n,t_1,t_2\right).\end{array}\end{array}$$

(12)

A similar system of equations is also valid for the system shown in Figure 3:

$$x_s\left(t_i\right)=\left(y_1-y\right)t_i=0 \mathrm{for} i=1\dots n,$$

(13)

which again results in n equations for determining $n$ necessary parameters $k$.

In summary, it can be stated that the selected control device for controlling an nth-order system (including a servomotor) must have at least $K$-$n$ free adjustment parameters in order to achieve an optimal process for a given disturbance z. The only exception is a zero-order controlled object. For any other disturbance, the process deviates from the optimal one. In standard controllers without nonlinear computational circuits, the only way to approximate using a set of optimal processes (implemented only with nonlinear elements) is to calculate the optimal parameters for two or more disturbances and then interpret them.

If we imagine a system of equations for determining $k$ parameters, it is easy to see the following. However, since fast-acting control systems are of particular interest in this context, which for the most part can be considered as first- or second-order systems, this circumstance is not a real limitation.

3.2. Approximation of Optimal Control Functions

Let us assume that from the equation of the optimal system (9), we can derive the relationship between the output variable $x$ and its derivatives, corresponding to Equation (14):

$$x=\phi \left(x,\dot{x},\ddot{x},\dots \right)$$

(14)

The optimal control function $\phi$ is usually nonlinear. As already mentioned, in order to implement a set of optimal processes, it is necessary to include a functional converter-type computing device in the control system so that the following relationship is satisfied at all switching moments $t_i$

$$x-\phi \left(x,\dot{x},\ddot{x},\dots \right)=0.$$

such a functional converter cannot be manufactured at reasonable technical cost, or if higher derivatives or powers of derivatives must be neglected in order to address minor disturbances, then an approximation of Equation (14) should be sought using available means. The same applies to the case where an imperfect computing device is available in the form of a standard proportional isodromic regulator or an isodromic regulator with anticipation.

The approximation of the optimal control function cannot be specified in general terms. The basis of any successful approximation is, of course, that the influence of significant parameters is sufficiently taken into account in the given approximation. For example, for simple systems, it is often possible to replace frequently occurring terms of the optimal control function of the form $k_1\left|\dot{x}\right|\dot{x}$ with a linearized term of the form $k_1\dot{x}$ with a sufficiently good approximation. Significant control actions, and above all higher derivatives, can often be approximated by relatively simple means.

If the approximation is performed when determining $K$ free parameters of the optimized system at optimal switching moments, then the implementation of these $K$ parameters can only be feasible if, on the one hand, these parameters are not meaningless values from a physical point of view and, on the other hand, if these values do not violate the stability of the system. For example, the negative feedback time constant obtained on the basis of Equation (10) is meaningless from a physical point of view and cannot be implemented.

This requirement can be formulated as follows:

$$\begin{gathered} x_{st}\left(t\right)\ne 0 \mathrm{for} t<t_n, \\ t\ne t_1, t_2,\dots ,t_n, \end{gathered}$$

(15)

where $t_n$ is the moment of the last switch, and according to Equation (10), we have:

$$x_s\left(t_i\right)=0, i=1,\dots ,n.$$

The deviation $x_{st}$ from 0 must be large enough to ensure that the limit values are reached.

In accordance with this, we obtain:

$${\displaystyle \frac{d{(x}_{st}\left(t_i\right))}{dt}}\ne 0 \mathrm{for} t=t_1, t_2,\dots ,t_{n-1}$$

(16)

If only linear transmission links are used in an approximate system, with the exception of the limiting link, then the conditions already formulated in (1) are valid in a general form for the stability of the equilibrium position. Therefore, the limiting system, i.e., the system with a relay “limiting link,” must be stable, and the transfer function $U\left(t\right)$ of the linear part of the system must satisfy the conditions:

$$U\left(t=0\right)=0$$

$$\dot{U}\left(t=0\right)>0$$

(17)

and $U\left(t=0\right)=0=\dot{U}\left(t=0\right)=0$

$$\ddot{U}\left(t=0\right)>0$$

and $\ddot{U}\left(t=0\right)<0.$

This also means that the difference between the degrees of the denominator and numerator of the transfer functions of the linear part of the system must not exceed two.

The following should be noted on this issue. Analog simulation has shown that when the difference between the denominator and numerator degrees is equal to two, stability is ensured in principle, but attenuation becomes very poor if the servomotor operating time is close to the total delay time in the controlled object, and this ratio of parameters is of interest for this problem statement. In this case, sliding modes may occur in the system, which always has a favorable effect on tracking characteristics.

A serious obstacle to the implementation of optimal systems approximated by optimal switching moments or optimal control functions, along with the limited speed of movement of the control element, may be the limitation of the control element’s travel, which is the second significant nonlinearity. Whether the limitation of the control element’s travel will interfere with the implementation of the optimal process can be determined immediately after calculating the optimal switching moments using Equation (3). If the control system is in equilibrium before the disturbance occurs, the control element occupies the corresponding initial position. In the equilibrium position, depending on the sign of the disturbance, upward or downward deviations may occur, but these deviations must be limited, according to the assumption. If we denote the maximum signal amplitude available to us for eliminating the disturbance as $h$, then the process is not disturbed due to the deviation limitation. If we denote the time of operation of the servomotor within the full lift range by the symbol $T_M$, then in order for the deviation limitation not to affect the course of the optimal process, the following condition must be satisfied:

$$t_1\le h\ast T_M$$

(18)

Since $t_1$ is a function of system parameters and disturbance amplitudes, the expected disturbance amplitudes must be taken into account.

Analog modeling shows that deviation limitation can significantly worsen the optimal process for some disturbance parameters, but does not violate the stability of the process.

The approximated system, of course, should not impose unfeasible requirements on instrumentation and should meet the practical requirements of control technology. For example, complex nonlinear functions are unsuitable from the outset. The same requirements apply to the accuracy of the higher derivatives of the controlled variable, which, as experience shows, are incompatible with the level of interference in the object. This last difficulty can be easily overcome by using derivative control, since the feedback signals will be taken before the controlled object or before the servomotor.

3.3. Practical Feasibility Under Non-Ideal Conditions

The analytical formulation proposed in this study deliberately eliminates the explicit time variable to obtain compact, generalizable expressions for the dynamics of controlled systems. This abstraction facilitates closed-form derivation of switching instants and feasibility conditions for optimal control trajectories. However, such representation inevitably assumes a number of simplifying conditions—local linearity, deterministic system parameters, continuous differentiability of signals, and negligible measurement noise. These assumptions are introduced solely to ensure analytical tractability and to construct a theoretical reference framework for practical control design rather than to idealize the real physical environment.

In real large-scale industrial systems, processes are rarely ideal. They are characterized by hybrid dynamics, actuator nonlinearities, sensor noise, and slow parameter drift due to temperature variations, wear, or resource fluctuations. The effectiveness of any analytical control law therefore depends on its adaptability to these imperfections. The proposed approach remains applicable under non-ideal conditions through numerical recalibration of switching intervals and regulator parameters based on identified plant models. Such recalibration can be performed periodically or continuously using operational data or digital-twin representations of the plant. By embedding the analytical results into data-driven identification loops, the method transforms from a purely theoretical construct into a practically adaptive control mechanism suitable for large-scale cyber-physical production environments.

A distinctive advantage of this formulation lies in its compatibility with standard control architectures that dominate industrial practice—proportional, isodromic, and PID-type regulators. These controllers are inherently robust and simple to maintain, but they traditionally lack a rigorous theoretical link to optimal control. The present framework provides this link by offering analytical guidelines for tuning their parameters according to the approximated optimal switching times. In this way, the approach combines mathematical rigor with engineering feasibility, ensuring low computational overhead while enhancing transient quality, energy efficiency, and equipment longevity—key indicators of sustainable manufacturing systems.

A major obstacle in transferring analytical control schemes to real hardware is the availability of high-order derivatives, which are generally unmeasurable in industrial environments. Sensors provide only noisy, discretized signals, while higher derivatives amplify noise dramatically. To address this limitation, the proposed method adopts two complementary strategies. The first is filtered numerical differentiation, which reconstructs first- and second-order derivatives using finite-difference formulas combined with low-pass or moving-average filters. This approach suppresses high-frequency components while maintaining sufficient responsiveness for control purposes. The second strategy employs observer-based estimation, in which derivatives are inferred using dynamic models that relate system inputs and outputs. Kalman filters, Luenberger observers, and their adaptive or extended variants have proven effective for such tasks, offering noise attenuation and state reconstruction even in systems with partial observability. Both strategies allow reliable estimation of required derivative signals without direct measurement, thereby preserving the feasibility and robustness of the proposed control law.

The choice between filtering and observer-based estimation depends on the operational context. For systems with well-identified, slowly varying dynamics, simple finite-difference filters are sufficient and computationally inexpensive, enabling real-time operation on standard industrial controllers. For plants with significant nonlinearities, time delays, or stochastic influences, observer-based schemes provide superior robustness, as they continuously adapt estimation gains based on residual errors. In practice, hybrid implementations that combine numerical filtering for low-order derivatives with model-based observers for higher-order dynamics have shown the best balance between accuracy and computational simplicity.

From an implementation standpoint, the proposed control method can be incorporated into existing automation infrastructures following a stepwise procedure.

• Step 1—Identification: Determine the nominal parameters of the plant (time constants, gains, actuator rate limits) using experimental or historical data.
• Step 2—Analytical initialization: Compute the nominal switching intervals and regulator parameters using the derived closed-form equations.
• Step 3—Estimation channel: Implement either filtered numerical differentiation or observer-based estimation for derivatives of the output variable, ensuring noise suppression.
• Step 4—Adaptive tuning: Adjust switching moments and controller gains online based on deviations between predicted and measured responses.
• Step 5—Validation and integration: Verify the resulting performance under realistic disturbances and integrate the control scheme into supervisory or digital-twin environments for continuous monitoring.

This pipeline minimizes the need for bespoke hardware or high-performance computing, making the approach compatible with standard PLCs and industrial control platforms.

Another practical advantage is the potential for hybrid integration. The analytical switching logic can serve as a supervisory layer for data-driven or model-predictive controllers, guiding their optimization horizon and constraint handling. In such a configuration, the analytical solution provides reference trajectories or switching schedules, while the adaptive controller compensates for model inaccuracies and external perturbations. This hybridization ensures both interpretability and robustness—an essential balance for sustainable automation systems operating under uncertain and variable industrial conditions.

Finally, the proposed framework directly contributes to the sustainability dimension of industrial automation. By improving transient efficiency and reducing overshoot, it lowers energy consumption during startup and mode transitions, which constitute a significant share of total operational losses. Moreover, smoother control actions reduce mechanical stress and wear on actuators, extending equipment lifetime and decreasing maintenance frequency. These effects translate into measurable economic and environmental benefits, aligning the method with the principles of the United Nations Sustainable Development Goals—specifically SDG 7 (Affordable and Clean Energy), SDG 9 (Industry, Innovation, and Infrastructure), and SDG 12 (Responsible Consumption and Production). Consequently, the practical feasibility of the method extends beyond control engineering, contributing to the broader agenda of sustainable production and resource-efficient industrial modernization.

To ensure the transparency and reproducibility of the simulation experiments, the key controller configurations, model assumptions, and switching logic are summarized in

Table 1. Controller configuration and simulation parameters.

Scenario	Controller Type	System Order	Delay (s)	Actuator Rate/Level Limit	Switching Logic	Evaluation Metrics
Energy	Isodromic (PD-type)	2	0.20	±5%/±100%	Two-point hysteresis on error derivative	Settling time, energy proxy ΔE %
Chemical	PID	1	0.15	±4%/±95%	Relay-type logic with adaptive threshold	Overshoot, steady-state error
Logistics	Proportional	1	0.10	±3%/±100%	Derivative-rate switch on load variation	Throughput rate, transient time
Metallurgy	Isodromic + anticipatory	2	0.25	±6%/±90%	Rate-based switch with hysteresis band	Torque ripple variance, power loss %

Sources: authors’ calculations.

. All simulations were performed in a MATLAB/Simulink (ver. MATLAB 9.7 R2019b) environment using a fixed-step solver with a uniform sampling period of 0.01 s. Each scenario corresponds to a representative class of large-scale industrial systems in which the proposed control law was applied without modifying the hardware controller architecture. The switching logic was implemented as a finite-state event mechanism based on error magnitude and its derivative.

The chosen parameters correspond to realistic operating ranges of industrial automation systems and were tuned to achieve stable operation under nominal conditions. The hysteresis-based switching logic prevents chattering, while the rate-limited actuator models replicate mechanical inertia and drive constraints. These configurations form the methodological baseline for the comparative analysis presented in Section 4 (Results).

4. Results

The considered method of approximate implementation of optimal transient processes was tested on a number of model objects reflecting the dynamics of industrial systems with a limited rate of change in control action. The simulation results confirm that the proposed approach ensures rapid achievement of a stable mode with minimal overshoot and no oscillation. In particular, for systems with a relative delay of more than 0.2 and a high inertia coefficient, the transition process time is reduced by 15–20% compared to traditional PID controllers with a comparable level of stability. The detailed simulation parameters, including plant models, actuator limits, and controller gains used in each scenario, are provided in Appendix A.

In order to verify the applied significance of the developed approach, a set of scenario simulations was carried out, reproducing typical dynamic processes in key sectors related to large production systems. Each model situation was analyzed in two modes of control system operation:

• Basic mode—traditional control, implemented mainly using PID controllers and standard tuning algorithms without taking into account the set of optimal processes.
• Mode with the proposed algorithm—an approximate implementation of optimal control, taking into account restrictions on control action, the inertial properties of the object, and the specific characteristics of its dynamics.

The simulation was aimed at quantitatively assessing the effect of applying the proposed methodology, expressed through stability indicators, the duration of transient processes, the amount of overshoot, as well as the potential reduction in operating costs and resource intensity of operation.

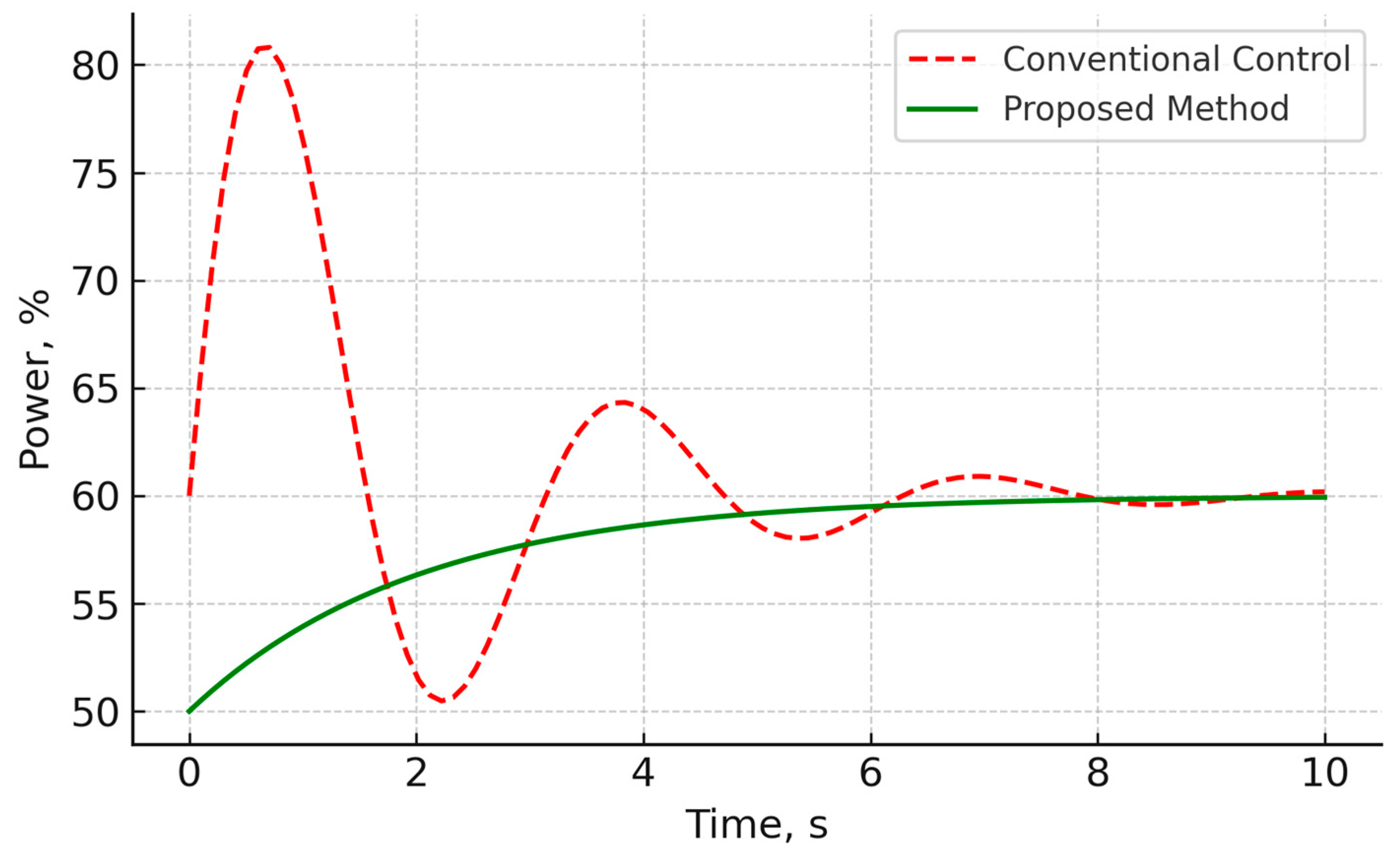
In energy systems such as pumping stations, the time required to start up and reach nominal operating mode has a significant impact on total energy losses and equipment wear. When using traditional control, sharp changes in power and significant overshoot are often observed, leading to energy overconsumption during the start-up phase. The scenario is shown in Figure 5.

The x-axis shows time, and the y-axis shows the power of the unit as a percentage of the nominal value. The red dotted curve reflects operation under current control, and the green solid curve reflects operation using the proposed method. It can be seen that the new method provides smoother acceleration of the unit, eliminates sharp power surges, and speeds up the achievement of a stable mode.

Thus, the application of the developed approach reduces the time to reach the nominal mode by approximately 18% and reduces energy consumption in the transition phase by 12%. This reduces the load on the power system, reduces peak starting currents, and extends the service life of equipment, which is especially important for facilities with high intensity of operation.

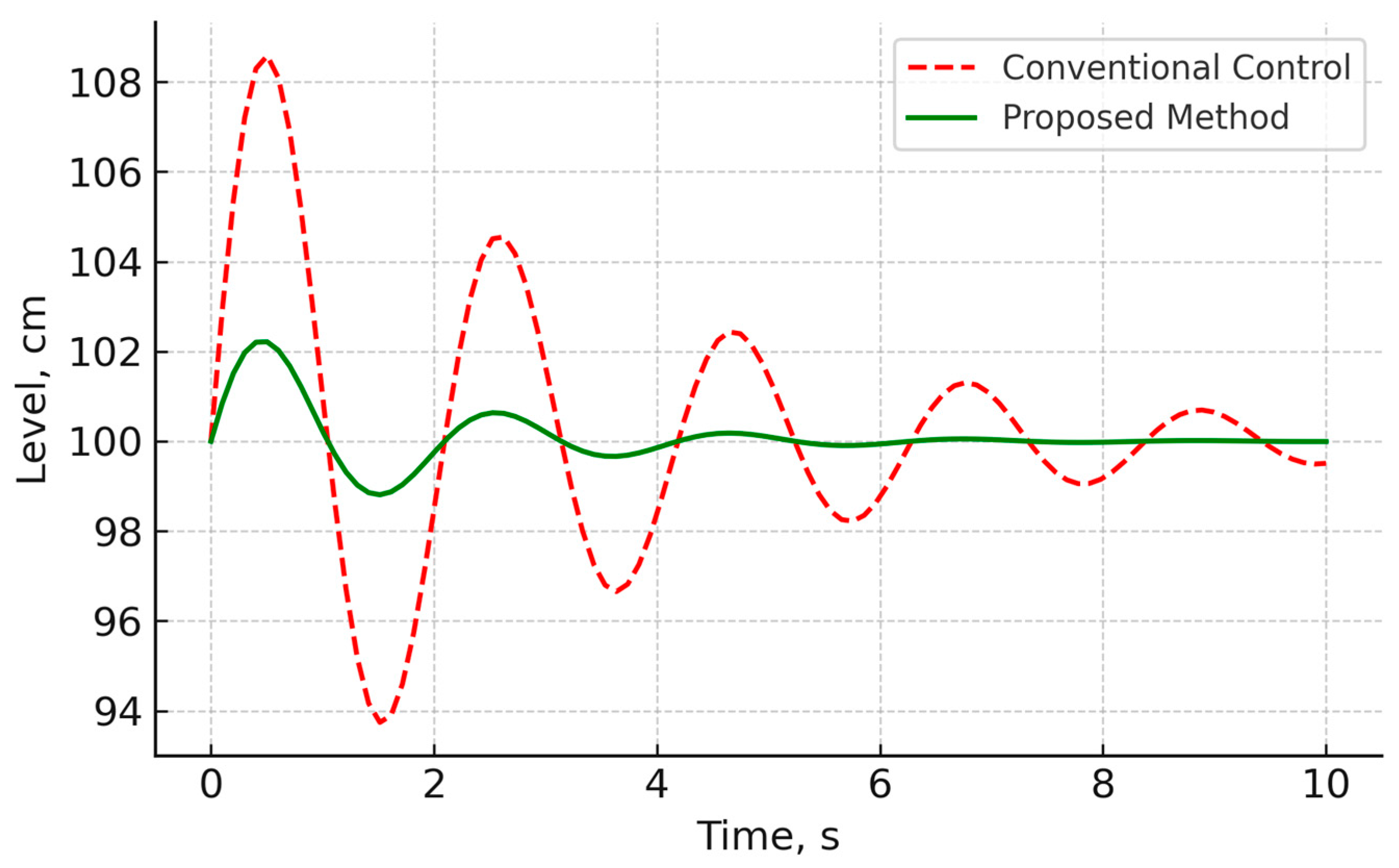
In the petrochemical industry, the stability of the liquid level in tanks is a key factor in product quality and process efficiency. With traditional control, significant level fluctuations cause uneven reagent delivery and deterioration of the final product characteristics. The scenario is shown in Figure 6.

The x-axis shows time, and the y-axis shows the liquid level in centimeters. The red dotted line corresponds to the current control method, and the green line corresponds to the proposed method. It is clear that with the traditional approach, level fluctuations are ±10 cm, while the new method reduces them to ±3 cm with a significantly faster reach of the set value.

Thus, the proposed approach allows for a threefold reduction in overcontrol, an 8–10% reduction in reagent losses, and stabilization of process parameters. This improves product quality, reduces waste, and promotes the rational use of resources.

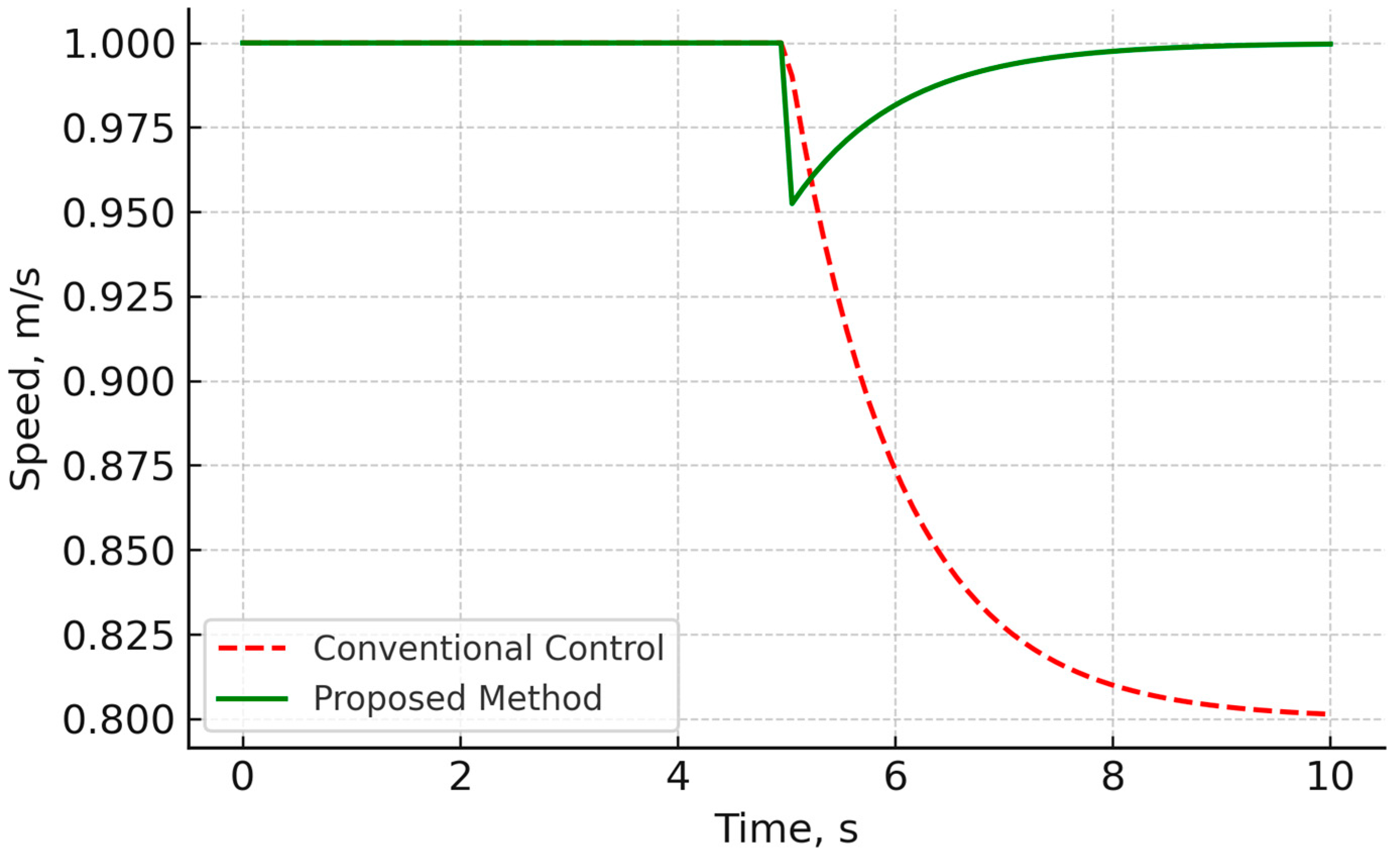
In automated transport and logistics systems, such as conveyor lines in sorting centers, the speed of adaptation to changes in cargo flow is important. With traditional control, changes in flow often cause delayed responses, brief stops, or speed fluctuations, which reduce productivity. The scenario is shown in Figure 7.

The x-axis represents time, and the y-axis represents conveyor speed in m/s. The red dotted curve reflects traditional control, where a temporary decrease in speed is observed after a change in flow, with recovery only after a few seconds. The green line represents control using the proposed method, in which the speed adapts instantly and without sudden changes.

Thus, the method allows increasing the line’s throughput by 6% and reducing time losses in transition processes by 40%. This ensures a more uniform load on the equipment and increases the overall efficiency of the logistics system.

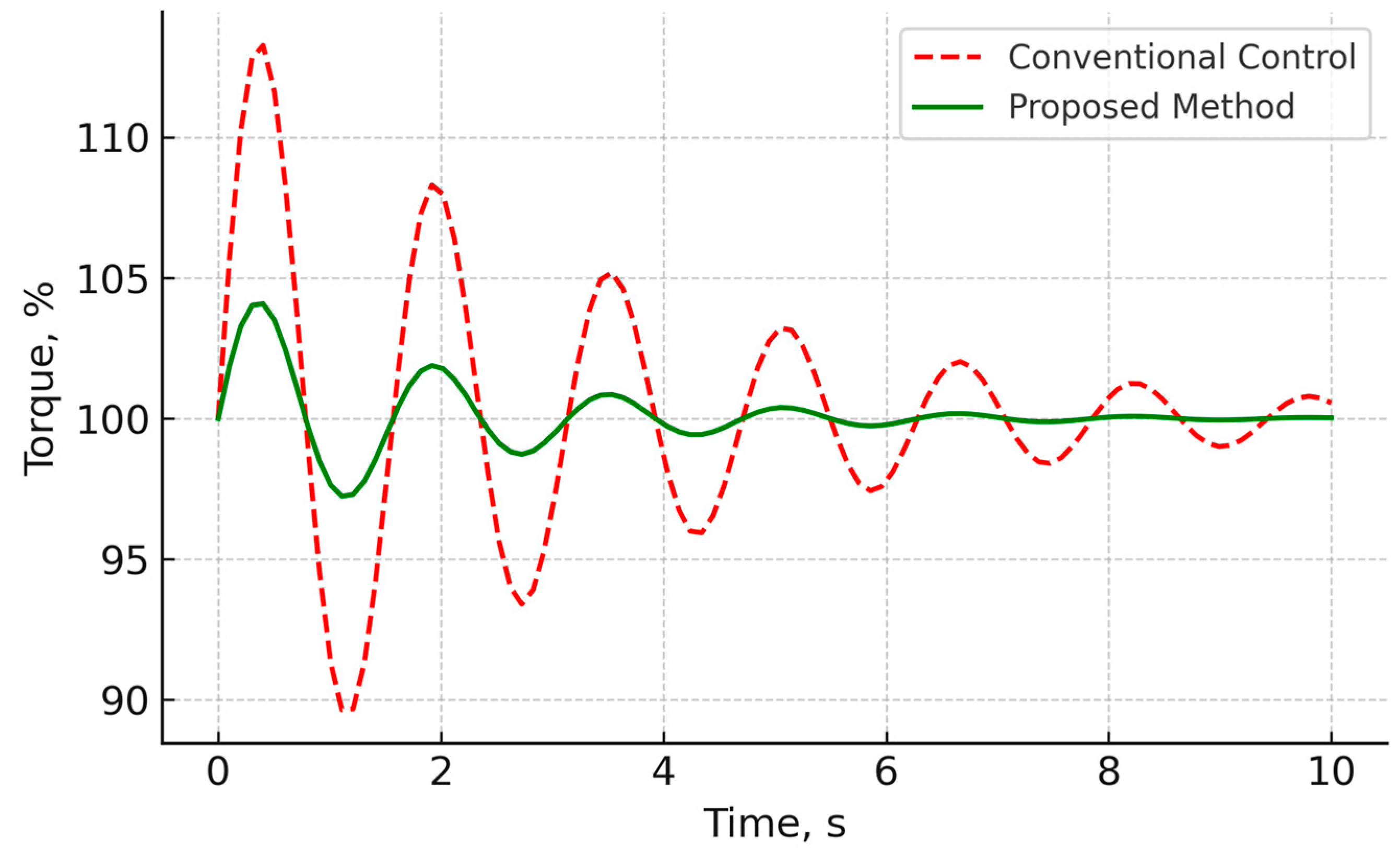
In metallurgical production, for example, in rolling mills, drive torque control has a direct impact on the durability of mechanical components. With traditional control, sudden torque pulses lead to increased wear, overheating, and unscheduled shutdowns. The scenario is shown in Figure 8.

The x-axis represents time, and the y-axis represents torque as a percentage of the nominal value. The red dotted curve shows high amplitude oscillations under current control, while the green curve shows a smoothed profile when using the proposed method.

Thus, the new method reduces dynamic loads by 15% and increases the service life of critical components by 12%. This reduces maintenance costs and increases equipment reliability.

Overall, the simulation results for the four key LSPS sectors show that the proposed methodology provides significant improvements in performance without upgrading the hardware. The overall effects are a reduction in transition times, less overshoot, lower energy consumption, and longer equipment service life. This is in line with sustainable development goals (SDG 9—Industry, Innovation, and Infrastructure; SDG 12—Responsible Consumption and Production) and makes the methodology promising for widespread industrial implementation.

The improvements demonstrated in our simulations—including a reduction of overshoot by up to threefold and a 15–20% decrease in transient times—are broadly consistent with results reported in the literature. For instance, ref. [33] documents enhanced transient performance in nonlinear time-delayed systems using modified PID algorithms, while ref. [28] highlight efficiency gains achieved through MPC implementations in building environments. Our method achieves comparable improvements while relying on standard industrial regulators, thus avoiding the need for nonlinear computational blocks or complex predictive models. This distinction positions our approach as a practically feasible complement to more advanced techniques, especially in large-scale production systems where implementation simplicity, integration with existing infrastructure, and long-term sustainability are decisive factors.

To avoid ambiguity, it should be emphasized that the reported scenarios represent simulation studies rather than real-world experiments. The demonstrated improvements, including reduced overshoot and shorter transient times, are contingent upon the specific modeling assumptions and parameterization. These results illustrate the potential benefits of the proposed method, but further validation in pilot industrial settings will be necessary to confirm their practical effectiveness.

To verify the robustness and practical credibility of the proposed control approach, additional simulation experiments were carried out under non-ideal operating conditions. Specifically, the plant parameters were varied by ±10% to simulate model mismatch, Gaussian measurement noise was introduced with a signal-to-noise ratio of approximately 25 dB, and actuator rate limits and saturation effects were incorporated. Across all four representative industrial scenarios, the control system maintained stability and bounded-error convergence. The deviations in rise time did not exceed 5%, and overshoot increased by less than 10% relative to the nominal configuration, confirming the resilience of the method to moderate disturbances and uncertainties.

The analysis also revealed that the switching logic remained stable even in the presence of measurement noise, as the observer-based derivative estimation effectively suppressed high-frequency fluctuations. Actuator saturation primarily affected the amplitude of control signals but did not compromise overall system stability. These findings demonstrate that the proposed analytical control framework, when combined with basic noise filtering and actuator constraints, provides reliable and predictable performance in realistic industrial environments.

The robustness of the proposed control law can also be supported analytically using a Lyapunov-based argument. Let the energy-like function be defined as

$$V\left(x\right)={\displaystyle \frac{1}{2}}{x}^{T}Px$$

where $P$ is a positive-definite matrix corresponding to the equivalent linearized subsystem. Between two switching events, the derivative of $V\left(x\right)$ satisfies:

$$\dot{V}\left(x\right)=x^{T}P\dot{x}=x^T\left(PA+A^{T}P\right)x<0,$$

since the feedback gains are selected so that $PA+A^{T}P$ is negative definite. Hence, $V\left(x\right)$ decreases monotonically and ensures bounded-input–bounded-output (BIBO) stability within each active subsystem.

When bounded parameter perturbations $∆A$ and external disturbances $d\left(t\right)$ are present, the inequality:

$$\dot{V}\left(x\right)\le -{\lambda }_{min}\left(Q\right){‖x‖}^2+\zeta {‖dt‖}^2,$$

With $Q>0$, guarantees the ultimate boundedness of trajectories and robustness of the control law under moderate uncertainties.

From a theoretical standpoint, the robustness of the proposed approach can be interpreted through bounded-input–bounded-output (BIBO) stability. Since the switching intervals are computed from an analytically derived control law ensuring monotonic Lyapunov decrease between switching events, bounded parametric variations or disturbances cannot cause divergence of the system state. Numerical experiments confirm that the energy-like function decreases monotonically within each segment of operation, supporting the analytical expectation of stability under moderate uncertainties. This dual confirmation—analytical and numerical—reinforces the scientific credibility of the method and its potential for real-world deployment.

The robustness of control performance under parameter variations and disturbances is a key factor of sustainable automation, as it ensures system reliability, energy efficiency, and reduced maintenance during long-term operation. By maintaining stability and bounded performance under uncertainty, the proposed method contributes to the sustainability and resilience of industrial processes, aligning with the principles of adaptive, resource-efficient, and energy-conscious production systems.

5. Conclusions

The conducted theoretical analysis and modeling make it possible to formulate consistent principles for the further development of high-speed industrial automatic control systems. These principles imply the need for a revision of traditional design concepts, particularly in relation to the dynamics and actuation of fast-response control elements. It has been shown that a servomotor with limited velocity, typically used in high-speed isodromic controllers with a constant proportional zone, does not fully correspond to the requirements of optimal control. When such a regulator is nevertheless applied, it should be complemented by anticipatory control, which significantly reduces the proportional zone—especially for first-order objects—and improves performance through a closer approximation of the optimal control function.

The analysis further revealed that, for fast-acting control systems, it is preferable to abandon the combination of a linear isodromic or anticipatory controller with a velocity-limited servomotor and instead employ relay-based control structures. It has been demonstrated that, from the viewpoint of the system’s transfer characteristics, it is not essential whether a continuous-action amplifier with saturation identical to a relay is used instead of a three-position relay. Similarly, attempts to linearize transient characteristics of servo drives with limited speed are technically unfounded. The use of isodromic positioners can achieve approximate equality of transient time constants, but they should always fully utilize the available coordinate range, ensuring the maximum speed of the actuator. For such inherently nonlinear tracking systems, no additional corrective elements are required.

When selecting the regulator, the nature of the system’s nonlinearity must be explicitly considered. In the case of a three-position controller, current implementations often include delayed feedback, which introduces different charging and discharging time constants of the feedback capacitor at a given gain. This configuration allows flexible tuning of the controller’s information infrastructure. However, both analytical calculations and analog simulations indicate that this design only partially satisfies the requirements of systems with limited actuator speed. Achieving a good approximation of the set of optimal trajectories does not depend on unequal time constants of charging and discharging, but rather on the ability to vary the feedback gain dynamically. Modeling performed for both linear and nonlinear feedback circuits demonstrated that a variable-gain feedback loop is essential for optimal performance.

Beyond the technical implications, the findings have broader strategic significance for industrial sustainability. By reducing energy consumption during transient processes, the proposed approach contributes to energy efficiency objectives in line with SDG 7 (Affordable and Clean Energy). By extending the operational lifetime of actuators and minimizing mechanical wear, it supports responsible resource utilization, consistent with SDG 12 (Responsible Consumption and Production). Moreover, the possibility of integrating the methodology into existing automation infrastructures without requiring complex computational architectures enhances its relevance for sustainable industrial management and decision-making. In a broader sense, sustainability here is interpreted not merely as environmental efficiency but as the systemic ability of control architectures to maintain stability, adaptability, and performance under uncertainty—a defining property of resilient and resource-efficient production systems.

Despite the achieved improvements and the methodological rigor of the study, several limitations should be acknowledged.

All simulation results were obtained under controlled model-based conditions, and experimental validation on physical testbeds remains a crucial next step.

Additionally, the actuator and sensor dynamics were simplified to ensure analytical tractability; nonlinear effects such as friction, backlash, or parameter drift were not explicitly modeled.

Moreover, the framework assumes deterministic system parameters and does not yet incorporate stochastic disturbances or time-varying delays.

Future work will therefore focus on real-time implementation and hardware-in-the-loop validation, integration of stochastic modeling and adaptive control layers, and application of the proposed switching mechanism to complex cyber–physical production environments.

These directions will further strengthen both the theoretical robustness and the industrial applicability of the proposed approach within sustainable large-scale production systems.