Reducing Waste in Retail: A Mixed Strategy, Cost Optimization Model for Sustainable Dead Stock Management

Abstract

The retail sector is the most demand-sensitive echelon in the supply chain, where non-moving items accumulate and become dead stock. Existing inventory management studies focus on fast-moving products and income generation. This paper focuses on dead stock management and proposes a mixed strategy solution using a pure integer non-linear programming model that minimizes the dead stock management cost of a retail chain operator. The number of products and volume of product-related data in a retail chain system require big data analysis to ensure sustainable inventory practices that reduce waste generated from dead stock inventory. Through hypothetical data sets, the 3-store, 10-product run showed that discount percentage, expected sales success probability of a product in a store location, and disposition of unsold products were the main drivers of the decisions made by the model. The most significant cost contributors arising from these decisions were the unrecovered product cost (UPC), disposed product cost (PC), and salvage value from the successful sale of dead stock. Inventory managers must balance the effect on these cost components when they choose the strategies to use in managing dead stock.

1. Introduction

The presence of dead stock has been an underrated and widely ignored problem in the retail industry. This term refers to non-moving items that lay in the stockroom or warehouses and accumulate over time [1]. These items are also considered obsolete and unsaleable [2]. Moreover, dead stock accumulates because of slow-moving items, damaged items, incorrect product specifications, highly perishable goods, and expired items. Literature has tackled this problem and has presented several causes as to why this problem persists.

Dead stock is prevalent in the general manufacturing and retail industries, where 20–40% of inventory is typically classified as non-moving or dead stock inventory. Some of the distinguished reasons why and how dead stock occurs in retail stores are errors in forecasting [3], ordering inconsistencies [4], defective goods [5], and overall loss of customer interest or changes in market preference [6]. These impact the retail industry in terms of financial loss in capital investment, additional storage costs, depreciation of seasonal products, risk of damage to unsold products, and impacts on business analytics, which make it difficult to make business decisions. While these causes have evidently contributed to the presence of dead stock, the most controllable aspect of this problem is for management to apply intervention strategies in a timely manner to keep these non-moving items from accumulating in the warehouse, and likewise keep the slow-moving items from turning into non-moving stock. When the dead stock problem is ignored or managed late, retail chain operators incur huge losses in the form of unproductive warehouse space utilization, leading to unnecessary holding and inventory management costs [7] that impact the cash flow of the business. The longer a business holds on to excess, non-moving, and slow-moving inventories, the less it can utilize its financial resources towards fast-moving and highly saleable items, which leads to a potential loss of profit [8].

To mitigate the negative effects of dead stock on business profitability, this paper shifts its focus from the priority management of fast-moving products to the management of dead stock. Commonly applied strategies in the literature include (1) disposal strategy [9]; (2) price discount strategy [10]; (3) product bundling strategy [11]; and (4) lateral transshipment strategy [12].

The disposal strategy has been used in the management of pharmaceutical products [13], and biotechnology and bioengineering [1], among others. The product bundling strategy has been investigated in the garment industry with the use of data analysis [14] and has been effective as a means of pushing out dead stock and reducing the effect of excess inventory [11]. In the case of price markdowns or discount pricing, wholesalers and retailers alike use this strategy to manage inventory, maximize revenue, and avoid unsold products from going to waste [15]. Finally, the lateral transshipment strategy also proved to increase customer service levels and reduce backorder and inventory holding costs [16].

Despite the availability of various strategies that can be used to manage and control the occurrence of dead stock, the problem continues to hound many retailers across many industries. A deeper analysis of the persisting dead stock problem reveals the need to have an integrative perspective in using these strategies to manage dead stock through a mixed strategy solution approach. This involves the simultaneous application of the strategies to take advantage of the benefits that each strategy provides towards minimizing inventory management costs and reducing dead stock in a chain store inventory system context.

2. Literature Review

One of the most important aspects of any business is its inventory. Inventory management, therefore, has a big impact on a company’s bottom line. Effective inventory management practices produce higher service levels that increase both profitability and customer satisfaction. Inventory management prioritizes the monitoring of demand and movement of goods for replenishment decisions [17]. Management priority is given to inventory items based on their contribution to total sales [18]. Hence, existing inventory management theory revolves around the management of fast-moving products. In the manufacturing level, fast-moving goods are often prioritized since they have fewer changeovers and are therefore more efficient to produce [19]. In the retail level, inventories that have a constantly high consumer demand are prioritized so that they are actively offered in the market [20]. Fast-moving products also represent a significant part of demand forecasts [18,21], actual order volumes [18,21], and total sales [18].

With inventory management focused on fast-moving and high-value products, many businesses are seeing a rise in dead stock. Dead stock can be a major problem for businesses, as it can impact both short and long-term profitability [8]. Once this dead stock is identified, a business must decide what to do with it.

2.1. The Presence of Dead Stock in the Retail Industry

Retailers attempt to forecast demand and use it to determine the most economical order quantities that would satisfy their customers’ needs. However, due to the unpredictable changes in customers’ expectations and preferences [6], including the introduction of new and more saleable products, forecasting and traditional inventory management models fail to systematically and effectively prevent or address the occurrence of the dead stock problem [10]. Inventories that become slow or non-moving due to sudden changes in demand patterns accumulate and become dead stock, especially when they are not given management attention [22].

The domain of dead stock management remains to be underdeveloped, with little to no advancement on how such types of inventories should be treated. Nonetheless, the general inventory management scale has touched on how slow-moving inventory items, like dead stock, can be managed. These strategies involving disposal, price discount, product bundling, and lateral transshipment are discussed in the section that follows.

2.2. General Dead Stock Inventory Management Strategies

Despite the emergence of data science, which paved the way for more efficient forecasting systems and stock replenishment policies, companies still find themselves in an overstock situation due to the inability of these tools to predict and adjust to the dynamic preferences of modern-day consumers, resulting in the eventual disposal of these excess unsaleable inventories known as dead stock. Before this happens, reactive strategies are employed to minimize losses during or after the unanticipated accumulation of excess stocks. Studies that focused on reactive strategies included lateral transshipment, disposal of dead stock through scrapping, price markdowns, and product bundling.

2.2.1. Disposal Strategy

Disposal is a strategy for dead stock management if no other action is suitable or feasible for the dead stock. The studies of Kakarlamudi [23] and Yan et al. [9] both adopted scrapping to dispose of the accumulated dead stock. In the study of Kakarlamudi [23], a checklist that considers all possible options regarding the use of dead stock must be assessed first, since scrapping is considered the last resort. Historical data regarding the product’s demand was reviewed to check for potential demand in the future. However, historical demand is not an accurate indicator of future demand due to the dynamics of consumer preferences in the retail industry, especially for products that are prone to obsolescence. If future demand does not take place as projected, this dead stock stays in the warehouse and accumulates unnecessary costs. On the other hand, Yan et al.’s study utilized scrapping and adjusting order levels as the options for dead stock management. They developed a periodic review inventory model that considered a chance constraint having specified probabilities of meeting different profit targets per period. The objective of their model was to maximize expected profit. It was one of the very few management-based studies that focused on the early identification of dead stock in the inventory to avoid overproduction and excess inventories. However, the focus was on managing dead stock by ordering less to meet target profits rather than disposing of the dead stock to prevent the accumulation of dead stock management costs.

2.2.2. Price Discount Strategy

One of the most common strategies utilized in managing dead stock is the discount pricing strategy, where wholesalers and retailers alike use this strategy to manage inventory, maximize revenue, and avoid unsold products from going to waste [15]. The product pricing strategy has been integral to marketing [24]. Since this strategy is considered revenue-generating, it involves marking down the prices of products with the goal of maximizing sales. This strategy has been applied in the reduction in potential fresh food waste from retailers, as explored by Buisman [25] and as an intervention to save near-expired foods from being thrown out by Zhang et al. [26]. Moreover, an article by Collart et al. [27] highlighted the profitability and sustainability of this strategy due to its effectiveness in pushing the near-expired foods out of the retailer’s inventory system. These studies all focused on using the discount strategy for highly perishable products. Non-perishable products and products with longer shelf lives may also benefit from the application of the discount strategy. Furthermore, other sales and non-sales strategies may simultaneously be used alongside the discount strategy to maximize sales and dead stock reduction.

2.2.3. Product Bundling Strategy

Product bundling is mostly used to maximize profit [12], where the effect of overproduction may be mitigated, market reach may be increased, and dead stock pushing may be promoted [28]. Product bundling is also a good proposition to reduce dead stock since slow or non-moving products are bundled with faster-moving products to increase profit or manage unwanted excess inventory [29]. What makes product bundling an attractive strategy is that product bundles are beneficial from the customer’s perspective since a bundle offers the products at a price discount, making it cheaper than the summed price of the individual products [30]. However, the literature on dead stock reduction through product bundling is sparse. What is available in the literature is the formulation of optimization models in the retailer or manufacturer perspective, where both the pricing and bundling decisions are determined not for the purpose of dead stock management but primarily to maximize profits or reduce lost opportunities [31]. Most of the bundling and pricing models just considered reservation prices of different consumer groups in making the bundling and pricing decisions. It is important to note that product bundling of perishable products is quite different from non-perishable products since the quality of perishable products is subject to degradation. This means that the customers’ willingness to pay varied as the quality of goods deteriorated, such that the bundling model must include a deterioration rate and a total life cycle period [31]. Although there were some bundling and pricing studies that included inventory management costs in their objective [32,33], these studies did not consider dead stock pushing in developing their respective decision rules for bundling and pricing.

The study of Sugumaran and Sukumaran [14] proposed a system that determined the stocks that are highly unlikely to move and separated these stocks from those that are likely to be sold. The first part of their study used a combination of two classifier models, namely ID3 and AdaBoost ensemble, which determined the classification of a garment. The second part of their study shifted to mathematical modeling that was used to search for an optimal solution in terms of maximizing the profit from selecting fast and non-moving items to put together and sell in a product bundle. It determined the optimal discount for the dead stock to be sold. However, their study only considered the fast-moving and dead stock in the inventory system and applied a single strategy to manage the dead stock within a single store context. The study by Sugumaran and Sukumaran [14] is a good baseline for single strategy intervention and optimization. However, it is limited to a single store and forecasting as a decision tool for dead stock management. In contrast, the proposed research aimed to cover dead stock management in the whole retail chain store system using multiple strategy interventions in determining optimal strategy mixes to be applied to the dead stock in the inventory system.

2.2.4. Lateral Transshipment Strategy

Lateral transshipment is more commonly used to take advantage of backorder opportunities in stockout situations [34]. Adhering to the lateral transshipment policy is especially beneficial for networks that involve multiple warehouses or multiple retail stores at different locations. Not only does it have a positive impact in terms of reducing excess and dead stock, but it also augments customer service levels because of minimizing occurrences of backorder costs and holding costs [34]. Transshipment allows the flow of slow and non-moving products from one node of the network with unsaleable product inventory to another node that requires stocks of the same product. This strategy aims to control excess inventory and the accumulation of slow and non-moving products in one node and stockout in another node, thereby maintaining inventory balance and reducing dead stock across multiple nodes through the distribution or redistribution of inventory across nodes and networks [11].

The study by Nakandala et al. [35] developed a transshipment model consisting of decision rules based on the minimization of the inventory costs. In their study, unrealistic assumptions and limitations compromised the effectiveness of the transshipment model. Assumptions include instantaneous delivery of transshipped items, and partial orders from multiple wholesalers are not allowed. Instantaneous delivery of transshipped items implies that distance and time are irrelevant factors in the total transshipment cost. This means that a transshipment decision may be made even if the distance separating two locations is far from ideal. Restricting the placement of transshipment orders from a single wholesaler, on the other hand, also influences the total transshipment cost of the system. Since the transshipment models use decision rules that are based on the minimization of inventory costs, the assumptions made affect the transshipment decisions made as well as the costs associated with the decisions.

Li and Yu [12] developed a lateral transshipment model that incorporated the decisions of balancing inventories across different locations to reduce the waste generated by perished products and consequently increase the retailer’s profitability. Like Li and Yu [11], Naderi et al. [34] developed a transshipment model that aimed to maximize the profit for the allied retailers. The effectiveness of the results was validated as the transshipment solutions yielded higher profits as compared to solutions without it. However, selling prices and holding costs were the only drivers of the transshipment decisions made in Naderi et al’s model. For lateral transshipment models to successfully solve the problem of dead stock among the allied retailers, policies or rules that drive transshipment decisions should not just be based on inventory holding costs and the cost of waste. Rather, the transshipment decisions should also be driven by the inventory classification (i.e., fast, slow, or non-moving), inventory levels in both source and destination stores, and the saleability of the transhipped product in the receiving store location. Assumptions that will have an impact on inventory and dead stock management costs should also be avoided.

The strategies highlighted in this section show that there are multiple ways by which retailers can manage and control dead stock. The use of a single strategy management system to solve a specific dead stock scenario is noticeable across the reviewed papers in this field of research. This research explored the simultaneous application of multiple dead stock management strategies in each store to minimize total network dead stock management cost and reduce the quantity of dead stock in the inventory system of the retail network. The application of multiple strategies considers resources and constraints inherent in each store and capitalizes on the synergy produced by the collaboration among stores to maximize the benefits of dead stock management. Retailers can leverage the unique benefits provided by each strategy to control the occurrence and persistence of the dead stock problem.

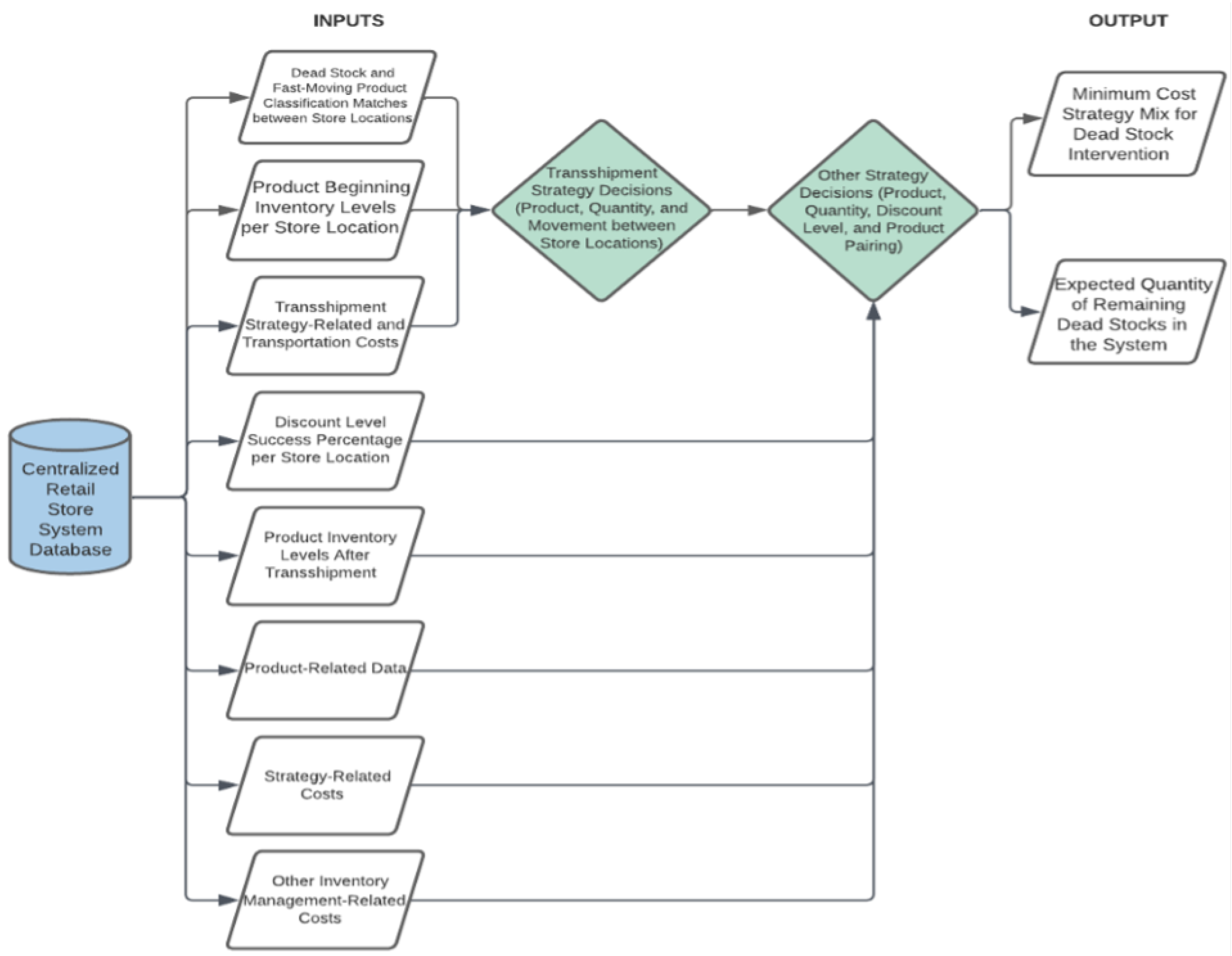
3. Methodology

To accomplish the research objectives, the study developed a pure integer non-linear programming model that yielded an optimal mixed strategy solution in managing dead stock in the retail chain store system. The study of Li et al. [36,37] highlighted the importance of timely recognition of dead stock (and recognizing even those that are likely to become dead stock, known as potential dead stock), through inventory classification and periodic monitoring of the transition in inventory classifications. According to Sebatjane and Adetunji [38], inventory classification and monitoring using decision rules and performance indicators were needed to objectively and accurately classify inventory. The proposed dead stock management process of Li et al. [22] consisted of two stages: (1) potential dead stock and dead stock identification through classification and monitoring, and (2) determination of the best dead stock intervention strategy mix that significantly reduced dead stock management costs through an optimization model. This study represents the second part of the two-phase approach suggested in the work of Li et al. [22], where the timely identification of potential dead stock and dead stock is a prerequisite in controlling the dead stock problem. The single-period, multi-product and multi-store mathematical model utilized the list of classified inventories from Li et al.’s [37] proposed classification method, expected sales success percentages associated with different discount levels, strategy-related costs, beginning inventories, and other product-specific details (e.g., weight, volume) as model inputs to yield the mixed strategy solution output that minimizes the total dead stock management cost of the system. The expected sales success percentages per location can be estimated based on the location of the stores and factoring in location-specific factors such as historical performance and distance [39].

In terms of implementation, the model can be run on a daily basis since planning and ordering are involved in terms of selling the products in the retail industry [40]. With this, the dead stock and potential dead stock items may be handled in a timely manner.

The model combined the application of lateral transshipment, individual price discounts, product bundle discounts, and disposal in each store to reduce the quantity of remaining dead stock in the chain store system. Figure 1 shows the flowchart for the inputs and outputs of the model.

The model considered a retailer that operates multiple stores in different locations within its network, where each store sells the same products that exhibit different consumption patterns across stores. Therefore, the same products in different store locations may be classified differently. Products in each store may fall under any one of the three classifications, namely fast-moving (i.e., non-dead stock or NDS), slow-moving (i.e., potential dead stock or PDS), or non-moving (i.e., unexpired dead stock or UDS). Expired dead stock (EDS) was automatically disposed of upon identification and was no longer included in the list of dead stock for management intervention.

In each store location, outbound transshipment decisions were made first. Only PDS and/or UDS with corresponding products classified as NDS in another store location may be transshipped out of any store. In transshipment, the sending store incurs strategy-related transportation cost (SRT) and operations cost (SRO) but generates savings in warehouse cost (SWC) due to the freed up space. The store receiving the transshipment generates savings in product purchase cost (SPC) and savings in ordering cost (SOC) because its NDS requirements were internally supplied and need not be purchased from an external supplier. The inventory level (IL) of each product in each store was then calculated by the model after the transshipment quantity decisions were made.

In each store location, the retailer has set a lower maintaining inventory level (LMIL), expected maintaining inventory level (EMIL), and upper maintaining inventory level (UMIL) for each product. In all store locations, each dead stock may be sold at a discount level that depends on its actual inventory level relative to LMIL, EMIL, and UMIL. The model provides four discount level options for all store locations. Each of the four discount level options has an associated expected sales success percentage that varies per store location according to the overall historical sales performance of the store. Successfully sold dead stock (i.e., PDS and UDS) generates revenue or salvage value (SV) but incurs unrecovered product purchase cost (UPC) for the chain store system. On the other hand, unsold PDS are kept in the warehouse for another period of management intervention, while unsold UDS are automatically collected at the end of the period and transported to the centralized disposal facility for proper disposal. Unsold PDS incurs warehouse cost (WC) for the entire period under consideration, while unsold UDS incurs both disposal cost (i.e., labor and overhead costs) and disposed product cost (PC). There is a disposal facility to receive the unexpired dead stock that is disposed of.

4. Mathematical Model

A typical retail setting includes various products, dynamic transactions, and challenges such as perishability, limited shelf space, product lifecycles, and costs [41]. Products revolve around different categories that are either fast, slow, or non-moving. The typical retail setting has multiple stores, and there are regular operations; hence, there are regular replenishment practices, store capacity, and inter-store activities to manage inventory. The model developed was coded using Matlab version 23.2.0.2380103 (R2023b) Update 1 (see Appendix A for Matlab code). The following were the assumptions made in formulating the model:

• Fast-moving items may not be transshipped to other stores in the chain store system. Only slow-moving (potential dead stock) and non-moving items (unexpired dead stock) are allowed to be transshipped from one store to another store if these items belong to the fast-moving product classification in the store that they will be transshipped to.
• There are dedicated trucks for dead stock management. The number of trucks in the retail chain store system and the capacity per truck are enough to transport products from one store to another as needed.
• Transportation cost is a function of a product’s store-to-store distance. It does not consider travel time, vehicle speed, and vehicle routing.
• All fast-moving products for the given period are equally desirable for bundling. The success in selling the bundles is not dependent on the fast-moving product that a dead stock or potential dead stock is bundled with.
• Product bundling strategy success is a function of bundle discount % level and sales throughput of the store.
• Unlimited additional warehouse space is maintained for potential dead stock and unexpired dead stock.
• Stockout costs of fast-moving products are not considered in the total inventory cost.

4.1. Decision Variables

The main decisions made by the model, together with the factors considered in making these decisions, are described and summarized in

Table 1. System variables.

P	set of all products or item codes
p’i	set of all potential dead stock (slow-moving items) in store location i
dni	set of all unexpired dead stock (non-moving items) in store location i
fi	set of all fast-moving stocks in store location i, where p’i ⊆ P; dni⊆ P; fi⊆ P
p’i ⋀ fj	set of all products classified as potential dead stock (slow-moving items) in store location i but classified as fast-moving stocks in store location j
dni ⋀ fj	set of all products classified as unexpired dead stock (non-moving items) in store location i but classified as fast-moving stocks in store location j
fi ⋀ fj	set of all products classified as fast-moving stocks in store location i and also classified as fast-moving stocks in store location j
i,j	indices of retail store location i, j = 0, 1, 2, …, M
p	index of retail store products p = 1, 2, …, N
s	index of retail store strategy s = 1, 2, …, S
o	index of product discount levels for p’ o = 1, 2, …, O
o’	index of product discount levels for dn o’ = 1, 2, …, O’
o"	index of product bundle discount levels for p’ and f bundle o” = 1, 2, …, O”
o’”	index of product bundle discount levels for dn and f bundle o” ’ = 1, 2, …, O” ’
copi	fixed product ordering cost (paperwork and communications) in store location i
dcoi	discount factor level o of product p (belonging to product category set p’i) in store location i
dc’o’i	discount factor level o’ of product p (belonging to product category set dni) in store location i
disppi	disposal cost (variable labor cost of collecting, unbundling and loading the unsold product into the truck for disposal) per unit of product p (belonging to product category set dni) in store location i
E(pbs%o”)	expected product bundle discount success % based on discount level o” for product p (belonging to product category set p’i)
E(pbs%’o” ’)	expected product bundle discount success % based on discount level o” ’ for product p (belonging to product category set dni)
E(pds%o)	expected price discount success % based on discount level o for product p (belonging to product category set p’i)
E(pds%’o’)	expected price discount success % based on discount level o’ for product p (belonging to product category set dni)
pbdco”i	product bundle discount factor level o” of product p (belonging to product category set p’i) in store location i
pbdc’o” ’i	product bundle discount factor level o” ’ of product p (belonging to product category set dni) in store location i
pbci	variable product bundling strategy cost (variable labor and supplies cost to bundle and reprice the bundled products) per bundled unit of product (belonging to product category sets p’i and dni) in store location i
pbcfi	fixed product bundling strategy cost (fixed cost of visual or print collaterals placed in both primary and secondary shelves plus system registration cost) per product (belonging to product category sets p’i and dni) in store location i
pdcfi	cost (fixed cost of visual or print collaterals placed in both primary and secondary shelves plus system registration cost) of discount offer strategy per product belonging to product category sets p’i and dni in store location i
tp,i,j	transportation cost (truck operations and fuel cost) per unit of product p (belonging to product category sets p’i and dni) transshipped from store location i to store location j
tpi	transportation cost (logistics provider cost) per unit of product p (belonging to product category set dni) from store location i to centralized disposal facility location
tspi	transshipment cost (labor, material and overhead cost to retrieve and handle products from the warehouse, inspect and load them into the truck, and process necessary paperwork) per unit of product p (belonging to product category sets p’i and dni) in store location i
wpi	warehouse cost (labor cost and holding cost) per unit of product p in the warehouse of store location i
cp	total cost of purchasing and making each unit of product p available for sale in the retail store
spp	original selling price per unit of product p
BIpi	beginning inventory of product p (belonging to product category sets p’i, dni and fi) in store location i
LMILpi	lower maintaining inventory level for product p in store location i
EMILpi	expected maintaining inventory level for product p in store location i
UMILpi	upper maintaining inventory level for product p in store location i
ILpi	inventory level of product p (belonging to product category sets p’i, dni and fi) in store location i after transshipment to or from the store has been carried out at the beginning of the single period
Qpis	quantity of product p from store location i to manage using strategy s · Qpi(ts)—quantity of product p from store location i to manage using transshipment (ts) strategy · Qpi(pd)—quantity of product p from store location i to manage using price discount (pd) strategy · Qpi(pb)—quantity of product p from store location i to manage using product bundling (pb) strategy
QTSpij	quantity of product p transshipped from store location i to store location j
PBQp$\epsilon$p’i,p$\epsilon$fi	quantity of product p from set p’i to bundle with product p from set fi
PBQp$\epsilon$dni,p$\epsilon$fi	quantity of product p from set dni to bundle with product p from set fi
STpis	=1 if strategy s is selected for product p in store location i =0 otherwise · STpi(ts) = 1 if transshipment strategy is selected for product p in store location i where p$\epsilon${p’i, dni} =0 otherwise · STpi(pd) = 1 if price discount strategy is selected for product p in store location i where p$\epsilon${p’i, dni} =0 otherwise · STpi(pb) = 1 if product bundling strategy is selected for product p in store location i where p$\epsilon${p’i, dni, fi} =0 otherwise
TQpij	=1 if product p where p$\epsilon${p’i, dni} is transshipped from store location i to store location j =0 otherwise
DLopi	=1 if price discount level o is applied to product p in store location i where p$\epsilon$p’i =0 otherwise
DLo=1,p,i	=1 if price discount level o = 1 is applied to product p in store location i where p$\epsilon$p’i (i.e., ILpi-LMILpi ≤ 0) =0 otherwise
DLo=2,p,i	=1 if price discount level o = 2 is applied to product p in store location i where p$\epsilon$p’i (i.e., LMILpi< ILpi ≤ EMILpi) =0 otherwise
DLo=3,p,i	=1 if price discount level o = 3 is applied to product p in store location i where p$\epsilon$p’i (i.e., EMILpi< ILpi ≤ UMILpi) =0 otherwise
DLo=4,p,i	=1 if price discount level o = 4 is applied to product p in store location i where p$\epsilon$p’i (i.e., ILpi-UMILpi > 0) =0 otherwise
DL’o’pi	=1 if price discount level o’ is applied to product p in store location i where p$\epsilon$dni =0 otherwise
DL’o’=1,p,i	=1 if price discount level o’ = 1 is applied to product p in store location i where p$\epsilon$dni (i.e., ILpi-LMILpi ≤ 0) =0 otherwise
DL’o’=2,p,i	=1 if price discount level o’ = 2 is applied to product p in store location i where p$\epsilon$dni (i.e., LMILpi< ILpi ≤ EMILpi) =0 otherwise
DL’o’=3,p,i	=1 if price discount level o’ = 3 is applied to product p in store location i where p$\epsilon$dni (i.e., EMILpi< ILpi ≤ UMILpi) =0 otherwise
DL’o’=4,p,i	=1 if price discount level o’ = 4 is applied to product p in store location i where p$\epsilon$dni (i.e., ILpi-UMILpi > 0) =0 otherwise
Ypi	=1 if UMILpi –BIpi> 0 where p$\epsilon$fi in store location i where product transshipment will be received =0 if UMILpi –BIpi ≤ 0 where p$\epsilon$fi in store location i where product transshipment will be received
PBp$\epsilon$p’i,p$\epsilon$fi	=1 if product p$\epsilon$p’i is bundled with product p$\epsilon$fi =0 otherwise
PBp$\epsilon$dni,p$\epsilon$fi	=1 if product p$\epsilon$dni is bundled with product p$\epsilon$fi =0 otherwise
PBSp1$\epsilon$fi,p2$\epsilon$fi	=1 if p1$\epsilon$ fi is to be bundled ahead of p2$\epsilon$ fi in store location i where p1 ≠ p2 =0 if p2$\epsilon$ fi is to be bundled ahead of p1$\epsilon$ fi in store location i where p1 ≠ p2
BDLo”,p,i	=1 if product bundle discount level o” is applied to product p bundle in store location i where p$\epsilon$p’i =0 otherwise
BDLo”=1,p,i	=1 if product bundle discount level o” = 1 is applied to product p bundle in store location i where p$\epsilon$p’i (i.e., ILpi-LMILpi ≤ 0) =0 otherwise
BDLo”=2,p,i	=1 if product bundle discount level o” = 2 is applied to product p bundle in store location i where p$\epsilon$p’i (i.e., LMILpi< ILpi ≤ EMILpi) =0 otherwise
BDLo”=3,p,i	=1 if product bundle discount level o” = 3 is applied to product p bundle in store location i where p$\epsilon$p’i (i.e., EMILpi< ILpi ≤ UMILpi) =0 otherwise
BDLo”=4,p,i	=1 if product bundle discount level o” = 4 is applied to product p bundle in store location i where p$\epsilon$p’i (i.e., ILpi-UMILpi > 0) =0 otherwise
BDL’o” ’, p,i	=1 if product bundle discount level o” ’ is applied to product p bundle in store location i where p$\epsilon$dni =0 otherwise
BDL’o” ’=1,p,i	=1 if product bundle discount level o” ’ = 1 is applied to product p bundle in store location i where p$\epsilon$dni (i.e., ILpi-LMILpi ≤ 0)
BDL’o” ’=2,p,i	=1 if product bundle discount level o” ’ = 2 is applied to product p bundle in store location i where p$\epsilon$dni (i.e., LMILpi< ILpi ≤ EMILpi)
BDL’o” ’=3,p,i	=1 if product bundle discount level o” ’ = 3 is applied to product p bundle in store location i where p$\epsilon$dni (i.e., EMILpi< ILpi ≤ UMILpi)
BDL’o” ’=4,p,i	=1 if product bundle discount level o” ’ = 4 is applied to product p bundle in store location i where p$\epsilon$dni (i.e., ILpi-UMILpi > 0)

.

Decision Variable	Definition	Factors Considered by the Model in Deciding
Qpi(ts)	quantity of product p in store location i to manage using transshipment (ts) strategy	Inventory Classification: Only slow (PDS) or non-moving (UDS) items in a store are allowed to be transshipped. There should be at least one receiving store where the same product to be transshipped is classified as fast-moving (NDS).
QTSpij	quantity of product p transshipped from store location i to store location j	Inventory level (IL) of NDS in the receiving store must not exceed its UMIL after transshipment. Inventory classification of the product (PDS or UDS) to be transshipped from the sending store should be considered. The cost profile of the sending store should be considered.
Qpi(pd)	quantity of product p in store location i to manage using price discount (pd) strategy	IL, Discount %, Expected Sales Success % Inventory Classification: Unsold PDS are kept in the warehouse for another period, while unsold UDS are automatically disposed of. The realizable salvage value factor of a product should be considered.
Qpi(pb)	quantity of product p from store location i to manage using product bundling (pb) strategy	IL, Discount %, Expected Sales Success % Inventory Classification: Unsold PDS are kept in the warehouse for another period, while unsold UDS are automatically disposed of. The realizable salvage value factor of a product should be considered.
PBQp$\epsilon$p’i,p$\epsilon$fi PBQp$\epsilon$dni,p$\epsilon$fi	quantity of product p from set p’i to bundle with product p from set fi quantity of product p from set dni to bundle with product p from set fi	IL of NDS should be higher than its EMIL. The max. qty. of NDS that can be assigned for pairing is IL-EMIL. Priority is given to the NDS with the highest % excess over its EMIL.

The complete list and definition of sets, indices, parameters, binary variables, and decision variables used in the model are enumerated as follows:

Sets

4.2. Objective Function

The objective function of the model aimed to minimize the total system dead stock management cost. It is given by the equation:

$$\begin{array}{c}\hfill Min.Z=A1+B1+C1+D1+E1+A2+B2+C2+\\ \hfill D2+E2+A3+B3-F1-F2-C3-D3-E3\end{array}$$

(1)

$$\begin{array}{c}\hfill CostofProductBundlingIntervention=A1+B1+C1+D1+E1-F1\end{array}$$

(2)

$$\begin{array}{c}\hfill CostofPriceDiscountIntervention=A2+B2+C2+D2+E2-F2\end{array}$$

(3)

$$\begin{array}{c}\hfill CostofTransshipmentIntervention=A3+B3-C3-D3-E3\end{array}$$

(4)

The objective function cost and “savings” components were organized into the cost and “savings” contributed by the product bundling strategy (A1 to F1), price discount strategy (A2 to F2), and lateral transshipment strategy (A3 to E3). The contribution of the disposal strategy to total dead stock management cost is embedded in the product bundling (C1 and D1) and price discount strategy costs (C2 and D2). The objective function components of each dead stock management strategy are defined and summarized in

Table 2. Mathematical model objective function components.

Dead Stock Management Strategy	Objective Function Component	Definition
Product Bundling/Price Discount	A1/A2—Strategy Related Cost (SRC)	Semi-fixed and variable costs that are incurred in carrying out the strategy
Product Bundling/Price Discount	B1/B2—Unrecovered Product Purchase Cost (UPC)	Difference between the product cost and discounted selling price of successfully sold dead stock
Product Bundling/Price Discount	C1/C2—Disposal Cost (DC)	Labor and other operational costs associated with product disposal
Product Bundling/Price Discount	C1/C2—Disposed Product Cost (PC)	Totally unrecovered purchase cost of a disposed product
Product Bundling/Price Discount	D1/D2—Transport Cost (TC)	Variable cost of transporting a disposed product to the disposal facility
Product Bundling/Price Discount	E1/E2—Warehouse Cost (WC)	Cost of holding inventory for one full period including risk of obsolescence
Product Bundling/Price Discount	F1/F2—Salvage Value (SV)	Revenue derived from the sale of discounted products
Lateral Transshipment	A3—Strategy Related Transportation Cost (SRT)	Variable cost of transporting a product from one store to another store
Lateral Transshipment	B3—Strategy Related Operations Cost (SRO)	Labor and other operational costs associated with product transshipment
Lateral Transshipment	C3—Savings in Purchase Cost (SPC)	Purchase cost savings realized by the chain store system because the product requirement of the receiving store was internally supplied through transshipment
Lateral Transshipment	D3—Savings in Ordering Cost (SOC)	Savings arising from not having to order the product with an external supplier
Lateral Transshipment	E3—Savings in Warehouse Cost (SWC)	Savings in holding and obsolescence risk cost arising from the transshipment of the dead stock

.

Equation (1) shows the total system dead stock management cost, where the negative terms (F1, F2, C3, D3, and E3) represent savings arising from strategy application that are deducted from the total dead stock management cost. Equations (2)–(4), on the other hand, show the contribution of each dead stock management strategy to the total system cost.

Referring to Table 2: For the product bundling and price discount strategies, respectively, Equations (5) and (11) represent the SRC while Equations (6) and (12) represent the UPC. Equations (7), (8), (13) and (14) represent the disposal costs of all unsold unexpired dead stock. The first term of Equations (7) and (13) represents DC, while the second term represents PC. Equations (8) and (14) represent the TC, Equations (9) and (15) represent the WC, while Equations (10) and (16) represent the SV of the product bundling and price discount strategies, respectively. For the transshipment strategy, Equation (17) represents the SRT, Equation (18) represents the SRO, Equation (19) represents the SPC, Equation (20) represents the SOC and Equation (21) represents the SWC. What each Equation computes for is defined in Table 2.

$$A1=\sum _{p\in {\mathcal{P}}_i}pb{c}_i·Q_{p\left(i\right)}\left(pb\right)+\sum _{p\in {\mathcal{P}}_i}pb{c}_i·Q_{p\left(i\right)}\left(pb\right)+\sum _{p\in {\mathcal{P}}_i}pb{c}_f·S{T}_{p\left(i\right)}\left(pb\right)+\sum _{p\in {\mathcal{P}}_i}pb{c}_f·S{T}_{p\left(i\right)}\left(pb\right)$$

(5)

$$\begin{array}{c}\hfill B_1=\sum _i\sum _{p\in p_{e_i^{\prime }}}\sum _{o\in l}\left\{max\left[(pbd{c}_{o^{\prime \prime }i}·spp)-(spp-c_p),⌀\right]·E(pbs·\left(BD{L}_{o^{\prime \prime },p,i}\right)·\left(Q_{p\left(i\right)\left(pb\right)}\right)\right\}\\ \hfill +\sum _i\sum _{p\in e{d}_{n_i}}\sum _{o\in l}\left\{max\left[(pbd{c}_{o^{\prime \prime \prime }i}·spp)-(spp-c_p),⌀\right]·E(pbs·\left(BD{L}_{o^{\prime \prime \prime },p,i}\right)·\left(Q_{p\left(i\right)\left(pb\right)}\right)\right\}\end{array}$$

(6)

$$\begin{array}{c}\hfill C_1=\sum _i\sum _{p\in e{d}_{n_i}}\sum _{o\in l}\left\{disp{p}_i\sum _{o\in l}\left[(1-E(pbs·\left(BD{L}_{o^{\prime \prime \prime },p,i}\right)·\left(Q_{p\left(i\right)\left(pb\right)}\right)\right]\right\}\\ \hfill +\sum _i\sum _{p\in e{d}_{n_i}}\sum _{o\in l}\left\{c_p·(1-E(pbs·\left(BD{L}_{o^{\prime \prime \prime },p,i}\right)·\left(Q_{p\left(i\right)\left(pb\right)}\right)\right\}\end{array}$$

(7)

$$D_1=\sum _i\sum _{p\in e{d}_{n_i}}\left\{t{p}_i\sum _{o\in l}\left[(1-E(pbs·\left(BD{L}_{o^{\prime \prime \prime },p,i}\right)·\left(Q_{p\left(i\right)\left(pb\right)}\right)\right]\right\}$$

(8)

$$E_1=\sum _i\sum _{p\in p_{e_i^{\prime }}}\sum _{o\in l}\left\{W_p\sum _{o\in l}\left[(1-E(pbs·\left(BD{L}_{o^{\prime \prime },p,i}\right)·\left(Q_{p\left(i\right)\left(pb\right)}\right)\right]\right\}$$

(9)

$$\begin{array}{cc}\hfill F_1& =\sum _i\sum _{p\in p_{e_i^{\prime }}}\sum _{o\in l}\left\{spp\sum _{o\in l}\left[(1-pbd{c}_{o^{\prime \prime }i})·E(pbs·\left(BD{L}_{o^{\prime \prime },p,i}\right)·\left(Q_{p\left(i\right)\left(pb\right)}\right)\right]\right\}\hfill \\ \hfill & +\sum _i\sum _{p\in e{d}_{n_i}}\sum _{o\in l}\left\{spp\sum _{o\in l}\left[(1-pbd{c}_{o^{\prime \prime \prime }i})·E(pbs·\left(BD{L}_{o^{\prime \prime \prime },p,i}\right)·\left(Q_{p\left(i\right)\left(pb\right)}\right)\right]\right\}\hfill \end{array}$$

(10)

$$A_2=\sum _i\sum _{p\in p_{e_i^{\prime }}}pdc{f}_i·S{T}_{p\left(i\right)\left(pd\right)}+\sum _i\sum _{p\in e{d}_{n_i}}pdc{f}_i·S{T}_{p\left(i\right)\left(pd\right)}$$

(11)

$$\begin{array}{cc}\hfill B2& =\sum _i\sum _{p\in p_i}\sum _o\left\{max\left[(d{c}_{oi}\ast s{p}_p)-(s{p}_p-c_p),⌀\right]\ast E\left(pds{\%}_{oi}\right)\ast \left(D{L}_{opi}\right)\right.\hfill \\ \hfill & \left.\ast \left(Q_{p\left(i\right)\left(pd\right)}\right)\right\}\hfill \\ \hfill & +\sum _i\sum _{p\in d{n}_i}\sum _{o^{\prime }}\left\{max\left[(d{c}_{o^{\prime }i}^{\prime }\ast s{p}_p)-(s{p}_p-c_p),⌀\right]\ast E\left(pds{\%}_{o^{\prime }i}\right)\right.\hfill \\ \hfill & \left.\ast \left(D{L}_{o^{\prime }pi}^{\prime }\right)\ast \left(Q_{p\left(i\right)\left(pd\right)}\right)\right\}\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill C2& =\sum _i\left\{\sum _{p\in d{n}_i}dis{p}_{pi}\sum _{o^{\prime }}\left[(1-E\left(pds{\%}_{o^{\prime }i}\right))\ast \left(D{L}_{o^{\prime }pi}^{\prime }\right)\ast \left(Q_{p\left(i\right)\left(pd\right)}\right)\right]\right\}\hfill \\ \hfill & +\sum _i\left\{\sum _{p\in d{n}_i}\sum _{o^{\prime }}\left[c_p\ast (1-E\left(pds{\%}_{o^{\prime }i}\right))\ast \left(D{L}_{o^{\prime }pi}^{\prime }\right)\ast \left(Q_{p\left(i\right)\left(pd\right)}\right)\right]\right\}\hfill \end{array}$$

(13)

$$D2=\sum _i\left\{\sum _{p\in d{n}_i}{t}_{pi}\sum _{o^{\prime }}\left[(1-E\left(pds{\%}_{o^{\prime }i}\right))\ast \left(D{L}_{o^{\prime }pi}^{\prime }\right)\ast \left(Q_{p\left(i\right)\left(pd\right)}\right)\right]\right\}$$

(14)

$$E2=\sum _i\left(\sum _{p\in p_i}{W}_{pit}\sum _o(1-E\left(pds{\%}_{oi}\right))\ast D{L}_{opi}\ast Q_{p\left(i\right)\left(pd\right)}\right)$$

(15)

$$\begin{array}{cc}\hfill F2& =\sum _i\sum _{p\in p_i}s{p}_{pt}\left\{\sum _o\left[(1-d{c}_{oi})\ast E\left(pds{\%}_{oi}\right)\ast D{L}_{opi}\ast Q_{p\left(i\right)\left(pd\right)}\right]\right\}\hfill \\ \hfill & +\sum _i\sum _{p\in d{n}_i}s{p}_{pt}\left\{\sum _{o^{\prime }}\left[(1-d{c}_{o^{\prime }i}^{\prime })\ast E\left(pds{\%}_{o^{\prime }i}\right)\ast D{L}_{o^{\prime }pi}^{\prime }\right]\right.\hfill \\ \hfill & \left.\ast Q_{p\left(i\right)\left(pd\right)}\right\}\hfill \end{array}$$

(16)

$$A3=\sum _{j\ne i}\sum _i\sum _{p\in p_i}{t}_{pij}\ast QT{S}_{pij}+\sum _{j\ne i}\sum _i\sum _{p\in d{n}_i}{t}_{pij}\ast QT{S}_{pij}$$

(17)

$$B3=\sum _{j\ne i}\sum _i\sum _{p\in p_i}{t}_{spi}\ast QT{S}_{pij}+\sum _{j\ne i}\sum _i\sum _{p\in d{n}_i}{t}_{spi}\ast QT{S}_{pij}$$

(18)

$$C3=\sum _{j\ne i}\sum _i\sum _{\begin{array}{c}p\in p_i\wedge f_j\\ p\in d{n}_i\wedge f_j\end{array}}{c}_p\ast QT{S}_{pij}$$

(19)

$$D3=\sum _i\sum _{p\in f_i}{c}_{opi}\ast Y_{pi}$$

(20)

$$E3=\sum _{j\ne i}\sum _l\sum _{\begin{array}{c}p\in e{p}_i\wedge f_j\\ p\in ed{n}_i\wedge f_j\end{array}}{w}_{pi}\ast QT{S}_{pij}$$

(21)

4.3. Model Constraints

The constraints section of the model specifies the strategy and policy restrictions imposed on decision-making. For each dead stock management strategy,

Table 3. Mathematical model constraints.

Dead Stock Management Strategy	Constraints	Description
	General constraints	Involve the selection/activation of a strategy and the determination of inventory quantities in each store to be managed using a specific strategy
	Binary and integer constraints	Specify which decision variables are 0–1 variables and which variables are integers
Lateral Transshipment	Post-transshipment inventory level calculation constraints	Calculate the IL of all products in the sending and receiving stores after transshipment
Lateral Transshipment	Allowable outbound and inbound transshipment quantity constraints	Ensure that the quantities transshipped from the sending stores do not exceed the requirement of products in the receiving stores
Product Bundling	Product bundle pairing constraints	Determine which NDS and how much of each NDS should be bundled with each dead stock
Product Bundling	Bundling strategy discount level determination constraints	Determine the bundle discount % to offer based on the IL of the dead stock
Product Bundling	NDS sequencing constraints	Determine which among many NDS should be prioritized for bundle pairing based on the % by which an NDS exceeds its expected maintaining inventory level (EMIL)
Price Discount	Price discount strategy discount level determination constraints	Determine the price discount % to offer based on the IL of the dead stock

identifies and describes each set of constraints formulated in the model.

$$I{L}_{pi}=B{L}_{pi}-\sum _{j\ne i}QT{S}_{pij}\forall p\in [(p_i^{\prime }\wedge f_j),(d{n}_i\wedge f_j)],\forall i$$

(22)

$$I{L}_{pi}=B{L}_{pi}+\sum _{j\ne i}\sum _{\begin{array}{c}p\in f_i\wedge p_j^{\prime }\\ p\in f_i\wedge d{n}_j\end{array}}QT{S}_{pji}\forall p\in [(f_i\wedge p_j^{\prime }),(f_i\wedge d{n}_j)],\forall i$$

(23)

$$\sum _{j\ne i}\sum _{\begin{array}{c}p\in (p_j^{\prime }\wedge f_i)\\ p\in (d{n}_j\wedge f_i)\end{array}}QT{S}_{pji}\le (UMI{L}_{pi}-B{L}_{pi})\ast Y_{pi}\forall p\in [(f_i\wedge p_j^{\prime }),(f_i\wedge d{n}_j)],\forall i$$

(24)

$$Q_{pi\left(ts\right)}=\sum _{j\ne i}QT{S}_{pij}\forall p\in [(p_i^{\prime }\wedge f_j),(d{n}_i\wedge f_j)],\forall i$$

(25)

$$QT{S}_{pij}\le M\ast T{Q}_{pij}\forall p\in [(p_i^{\prime }\wedge f_j),(d{n}_i\wedge f_j)],\forall i,\forall j\ne i$$

(26)

$$Q_{pi\left(ts\right)}\le B{L}_{pi}\ast S{T}_{p\left(i\right)\left(ts\right)}\forall p\in [(p_i^{\prime }\wedge f_j),(d{n}_i\wedge f_j)],\forall i$$

(27)

$$S{T}_{p\left(i\right)\left(ts\right)}=0\forall p\in f_i,\forall i$$

(28)

$$T{Q}_{pij}=0\forall p\in f_i,\forall i,\forall j$$

(29)

$$Q_{p\left(i\right)\left(pb\right)}\le M\ast S{T}_{p\left(i\right)\left(pb\right)}\forall p\in [p_i^{\prime },d{n}_i],\forall i$$

(30)

$$Q_{p\left(i\right)\left(pb\right)}\le I{L}_{pi}\forall p\in [p_i^{\prime },d{n}_i],\forall i$$

(31)

$$I{L}_{pi}-EMI{L}_{pi}\le M\ast S{T}_{p\left(i\right)\left(pb\right)}\forall p\in f_i,\forall i$$

(32)

$$I{L}_{pi}-EMI{L}_{pi}\ge -M\ast [1-S{T}_{p\left(i\right)\left(pb\right)}]\forall p\in f_i,\forall i$$

(33)

$$Q_{p\left(i\right)\left(pb\right)}\le (I{L}_{pi}-EMI{L}_{pi})\ast S{T}_{p\left(i\right)\left(pb\right)}\forall p\in f_i,\forall i$$

(34)

$$PB{Q}_{pep{i}^{\prime },pe{f}_i}\le M\ast P{B}_{pep{i}^{\prime },pe{f}_i}\forall p\in [p_i^{\prime },f_i],\forall i$$

(35)

$$PB{Q}_{ped{n}_i,pe{f}_i}\le M\ast P{B}_{ped{n}_i,pe{f}_i}\forall p\in [p_i^{\prime },f_i],\forall i$$

(36)

$$\sum _{p\in f_i^{\prime }}PB{Q}_{pep{i}^{\prime },pe{f}_i}=Q_{p\left(i\right)\left(pb\right)}\forall p\in p_i^{\prime },\forall i$$

(37)

$$\sum _{p\in f_i^{\prime }}PB{Q}_{ped{n}_i,pe{f}_i}=Q_{p\left(i\right)\left(pb\right)}\forall p\in d{n}_i,\forall i$$

(38)

$$\sum _{p\in f_i^{\prime }}PB{Q}_{pep{i}^{\prime },pe{f}_i}-\sum _{p\in ed{n}_i}PB{Q}_{ped{n}_i,pe{f}_i}=Q_{p\left(i\right)\left(pb\right)}\forall p\in f_i,\forall i$$

(39)

$$\sum _{p\in ed{n}_i}{Q}_{p\left(i\right)\left(pb\right)}=\sum _{p\in f_i^{\prime }}{Q}_{p\left(i\right)\left(pb\right)}\forall i$$

(40)

$$I{L}_{lpi}-LMI{L}_{lpi}\le M\ast (1-BD{L}_{o^{\prime \prime }=1,p,i})\forall p\in p_l^{\prime },\forall i$$

(41)

$$I{L}_{lpi}-LMI{L}_{lpi}\ge -M\ast (1-BD{L}_{o^{\prime \prime }=2,p,i})\forall p\in p_l^{\prime },\forall i$$

(42)

$$I{L}_{lpi}-EMI{L}_{lpi}\le M\ast (1-BD{L}_{o^{\prime \prime }=2,p,i})\forall p\in p_l^{\prime },\forall i$$

(43)

$$I{L}_{lpi}-EMI{L}_{lpi}\ge -M\ast (1-BD{L}_{o^{\prime \prime }=3,p,i})\forall p\in p_l^{\prime },\forall i$$

(44)

$$I{L}_{lpi}-UMI{L}_{lpi}\le M\ast (1-BD{L}_{o^{\prime \prime }=3,p,i})\forall p\in p_l^{\prime },\forall i$$

(45)

$$I{L}_{lpi}-UMI{L}_{lpi}\ge -M\ast (1-BD{L}_{o^{\prime \prime }=4,p,i})\forall p\in p_l^{\prime },\forall i$$

(46)

$$\sum _{o\prime \prime =1}^{4}BD{L}_{o\prime \prime ,p,i}=1\forall p\in p_l^{\prime },\forall i$$

(47)

$$I{L}_{lpi}-LMI{L}_{lpi}\le M\ast (1-BD{L}_{o^{\prime \prime \prime }=1,p,i}^{\prime })\forall p\in d{n}_l,\forall i$$

(48)

$$I{L}_{lpi}-LMI{L}_{lpi}\ge -M\ast (1-BD{L}_{o^{\prime \prime \prime }=2,p,i}^{\prime })\forall p\in d{n}_l,\forall i$$

(49)

$$I{L}_{lpi}-EMI{L}_{lpi}\le M\ast (1-BD{L}_{o^{\prime \prime \prime }=2,p,i}^{\prime })\forall p\in d{n}_l,\forall i$$

(50)

$$I{L}_{lpi}-EMI{L}_{lpi}\ge -M\ast (1-BD{L}_{o^{\prime \prime \prime }=3,p,i}^{\prime })\forall p\in d{n}_l,\forall i$$

(51)

$$I{L}_{lpi}-UMI{L}_{lpi}\le M\ast (1-BD{L}_{o^{\prime \prime \prime }=3,p,i}^{\prime })\forall p\in d{n}_l,\forall i$$

(52)

$$I{L}_{lpi}-UMI{L}_{lpi}\ge -M\ast (1-BD{L}_{o^{\prime \prime \prime }=4,p,i}^{\prime })\forall p\in d{n}_l,\forall i$$

(53)

$$\sum _{o\prime \prime \prime =1}^{4}BD{L}_{o\prime \prime \prime ,p,i}^{\prime }=1\forall p\in d{n}_l,\forall i$$

(54)

$$\begin{array}{c}\hfill {\displaystyle \frac{max\left([I{L}_{p_2ϵf_i}-EMI{L}_{p_1ϵf_i}],⌀\right)}{EMI{L}_{p_2ϵf_i}}}-{\displaystyle \frac{max\left([I{L}_{p_1ϵf_i}-EMI{L}_{p_2ϵf_i}],⌀\right)}{EMI{L}_{p_1ϵf_i}}}\\ \hfill \le M\ast PB{S}_{p_1ϵf_i,p_2ϵf_i}\forall p_1\in f_i,\forall p_2\in f_i,p_1\ne p_2\end{array}$$

(55)

$$\begin{array}{c}\hfill {\displaystyle \frac{max\left([I{L}_{p_2\in f_i}-EMI{L}_{p_2\in f_i}],⌀\right)}{EMI{L}_{p_2\in f_i}}}-{\displaystyle \frac{max\left([I{L}_{p_1\in f_i}-EMI{L}_{p_1\in f_i}],⌀\right)}{EMI{L}_{p_1\in f_i}}}\\ \hfill \le M·(1-PB{S}_{p_1\in f_i,p_2\in f_i})\forall p_1\in f_i,\forall p_2\in f_i,p_1\ne p_2\end{array}$$

(56)

$$\begin{array}{c}\hfill P{B}_{p\in p_l^{\prime },p_1ϵf_i}\ge P{B}_{pϵp_l^{\prime },p_2ϵf_i}\ast PB{S}_{p_1ϵf_i,p_2ϵf_i}\\ \hfill \forall p\in p_l^{\prime },\forall p_1\in f_i,\forall p_2\in f_i,p_1\ne p_2\end{array}$$

(57)

$$P{B}_{pϵp_l^{\prime },p_2ϵf_i}\ge P{B}_{pϵp_l^{\prime },p_1ϵf_i}\ast (1-PB{S}_{p_1ϵf_i,p_2ϵf_i})\forall p\in p_l^{\prime },\forall p_1\in f_i,\forall p_2\in f_i,p_1\ne p_2$$

(58)

$$P{B}_{pϵd{n}_l,p_1ϵf_i}\ge P{B}_{pϵd{n}_l,p_2ϵf_i}\ast PB{S}_{p_1ϵf_i,p_2ϵf_i}\forall p\in d{n}_l,\forall p_1\in f_i,\forall p_2\in f_i,p_1\ne p_2$$

(59)

$$P{B}_{p2dni,p2\in f_i}\ge P{B}_{p1dni,p1\in f_i}\ast \left(1-PB{S}_{p1\in f_i,p2\in f_j}\right)\forall p\in dni,\forall p_1\in f_i,\forall p_2\in f_j,\forall p_1\ne p_2$$

(60)

$$Q_{p\left(i\right)\left(pd\right)}\le M\ast S{T}_{p\left(i\right)\left(pd\right)}\forall p\in [p_i^{\prime },dn{i}_i],\forall i$$

(61)

$$Q_{p\left(i\right)\left(pd\right)}\le I{L}_{pi}\forall p\in [p_i^{\prime },dn{i}_i],\forall i$$

(62)

$$I{L}_{pi}-LMI{L}_{pi}\le M\ast (1-D{L}_{o=1,p,i})\forall p\in p_i^{\prime },\forall i$$

(63)

$$I{L}_{pi}-LMI{L}_{pi}>-M\ast (1-D{L}_{o=2,p,i})\forall p\in p_i^{\prime },\forall i$$

(64)

$$I{L}_{pi}-EMI{L}_{pi}\le M\ast (1-D{L}_{o=2,p,i})\forall p\in p_i^{\prime },\forall i$$

(65)

$$I{L}_{pi}-EMI{L}_{pi}>-M\ast (1-D{L}_{o=3,p,i})\forall p\in p_i^{\prime },\forall i$$

(66)

$$I{L}_{pi}-UMI{L}_{pi}\le M\ast (1-D{L}_{o=3,p,i})\forall p\in p_i^{\prime },\forall i$$

(67)

$$I{L}_{pi}-UMI{L}_{pi}>-M\ast (1-D{L}_{o=4,p,i})\forall p\in p_i^{\prime },\forall i$$

(68)

$$\sum _{o=1}^{4}D{L}_{o,p,i}=1\forall p\in p_i^{\prime },\forall i$$

(69)

$$I{L}_{pi}-LMI{L}_{pi}\le M\ast (1-D{L}_{o=1,p,i}^{\prime })\forall p\in dni,\forall i$$

(70)

$$I{L}_{pi}-LMI{L}_{pi}>-M\ast (1-D{L}_{o=2,p,i}^{\prime })\forall p\in dni,\forall i$$

(71)

$$I{L}_{pi}-EMI{L}_{pi}\le M\ast (1-D{L}_{o=2,p,i}^{\prime })\forall p\in dni,\forall i$$

(72)

$$I{L}_{pi}-EMI{L}_{pi}>-M\ast (1-D{L}_{o=3,p,i}^{\prime })\forall p\in dni,\forall i$$

(73)

$$I{L}_{pi}-UMI{L}_{pi}\le M\ast (1-D{L}_{o=3,p,i}^{\prime })\forall p\in dni,\forall i$$

(74)

$$I{L}_{pi}-UMI{L}_{pi}>-M\ast (1-D{L}_{o=4,p,i}^{\prime })\forall p\in dni,\forall i$$

(75)

$$\sum _{o=1}^{4}D{L}_{o,p,i}^{\prime }=1\forall p\in dni,\forall i$$

(76)

$$Q_{p\left(i\right)\left(pb\right)}+Q_{p\left(i\right)\left(pd\right)}=I{L}_{pi}\forall p\in [p_i^{\prime },dn{i}_i],\forall i$$

(77)

Equations (22) to (29) represent the transshipment strategy constraints. Equations (22) and (23) represent the post-transshipment inventory level calculation constraints. Equation (24) represents the allowable outbound and inbound transshipment quantity constraint, while Equations (25) to (29) represent the general transshipment strategy activation and quantity constraints. Equations (30) to (60) represent the product bundling strategy constraints. Equations (30) to (31) represent the general product bundling strategy activation and quantity constraints. Equations (32) to (34) require that the inventory level of a fast-moving product exceeds its expected maintaining inventory level (EMIL) for it to be paired with a dead stock in a product bundle to accelerate turnover and ensure slower moving inventory move with the fast-moving inventory. Equations (35) to (40) represent the product bundle pairing activation and quantity constraints involving one fast-moving product and one dead stock. Equations (41) to (54) represent the bundling strategy discount level determination constraints. Equations (55) to (60) represent the fast-moving product (NDS) bundling sequence constraints.

Equations (61) to (76) represent the price discount strategy constraints. Equations (61) to (62) represent the general price discount strategy activation and quantity constraints. Equations (63) to (76) represent the price discount strategy discount level determination constraints. Lastly, Equation (77) represents the general constraint that all dead stock in each store should be managed using the available strategies.

4.4. Non-Negativity, Integer and Binary Constraints

The following constraints specify the non-negativity and integer requirements of the decision variables used in the formulation of the mathematical model.

$$\begin{array}{c}\hfill Q_{p\left(i\right)\left(ts\right)}\ge 0;Q_{p\left(i\right)\left(pb\right)}\ge 0;Q_{p\left(i\right)\left(pd\right)}\ge 0\end{array}$$

(78)

$$\begin{array}{c}\hfill QT{S}_{pij}\ge 0;PB{Q}_{p\in p_i^{\prime },p\in f_i}\ge 0;PB{Q}_{p\in d{n}_i,p\in f_i}\ge 0\end{array}$$

(79)

$$\begin{array}{c}\hfill Q_{p\left(i\right)\left(ts\right)};Q_{p\left(i\right)\left(pb\right)};Q_{p\left(i\right)\left(pd\right)}\mathrm{are}\mathrm{integers}\end{array}$$

(80)

$$\begin{array}{cc}\hfill QT{S}_{pij};PB{Q}_{p\in p_i^{\prime },p\in f_i};PB{Q}_{p\in d{n}_i,p\in f_i}& \mathrm{are}\mathrm{integers}\hfill \end{array}$$

(81)

The following constraints specify the integer requirement as well as the (0,1) requirement of the binary variables used in the formulation of the mathematical model.

$$\begin{array}{c}\hfill S{T}_{\pi \left(ts\right)}·S{T}_{\pi \left(pb\right)}·S{T}_{\pi \left(pd\right)}·T{Q}_{pij}·D{L}_{opi}·D{L}_{o^{\prime }pi}·PD{L}_{opi}·PD{L}_{o^{\prime }pi}·Y_{pi}·P{B}_{p\in {\mathcal{P}}_i,p\in {\mathcal{F}}_i}\ge 0\end{array}$$

(82)

$$\begin{array}{c}\hfill S{T}_{\pi \left(ts\right)}·S{T}_{\pi \left(pb\right)}·S{T}_{\pi \left(pd\right)}·T{Q}_{pij}·D{L}_{opi}·D{L}_{o^{\prime }pi}·PD{L}_{opi}·PD{L}_{o^{\prime }pi}·Y_{pi}·P{B}_{p\in {\mathcal{P}}_i,p\in {\mathcal{F}}_i}\le 1\end{array}$$

(83)

$$\begin{array}{c}\hfill S{T}_{\pi \left(ts\right)}·S{T}_{\pi \left(pb\right)}·S{T}_{\pi \left(pd\right)}·T{Q}_{pij}·D{L}_{opi}·D{L}_{o^{\prime }pi}\\ \hfill ·PD{L}_{opi}·PD{L}_{o^{\prime }pi}·Y_{pi}·P{B}_{p\in {\mathcal{P}}_i,p\in {\mathcal{F}}_i}\mathrm{where}P{B}_{p\in {\mathcal{P}}_i,p\in {\mathcal{F}}_i}\in \mathbb{Z}\end{array}$$

(84)

5. Results

A hypothetical dataset that replicated a real-life retail chain store system was used to validate the logic and analyze the effectiveness of the model. The system that was analyzed was a chain store system having three store locations and 10 products. All the stores have the same products. The 10 products consist of fast-moving (NDS), slow-moving (PDS), and non-moving (UDS) items.

Table 4. Store and system quantity and percentage of each inventory classification.

Inventory Classification	Store 1 Qty.	% of Store 1 Invty.	Store 2 Qty.	% of Store 2 Invty.	Store 3 Qty.	% of Store 3 Invty.	System Total Qty.	% of System Invty.
PDS	94	13	375	41.1	282	40.6	751	32.2
UDS	96	13.3	154	16.9	324	46.7	574	24.6
NDS	534	73.7	384	42	88	12.7	1006	43.2
Store Total Qty.	724	100	913	100	694	100	2331	100
Total Dead Stock (PDS + UDS)	190	26.3	529	58	606	87.3	1325	56.8

shows the complete inventory profile of the system that was analyzed in terms of the store and system quantity of each inventory classification and the quantity of each inventory classification as a percentage of total store and system inventory quantity.

The dead stock problem is characterized by the presence of PDS and UDS in each store. Table 4 shows that the total dead stock in the chain store system accounts for an average of 56.8% of total system inventory, broken down into 32.2% PDS and 24.6% UDS. This represents a good approximation of the current industry problem (Warchol, 2021). The PDS needs to be managed in each store to prevent it from becoming UDS, while UDS needs to be managed in each store to prevent it from becoming expired dead stock (EDS). The results of the mixed strategy model are shown in

Table 5. Mixed strategy model results summary.

Obj. Function Component	Store 1	Store 2	Store 3	Total
Strategy Related Cost (SRC)	-	651.50	111.00	762.50
Unrecovered Product Cost (UPC)	-	6062.76	-	6062.76
Disposal Cost (DC)	-	-	68.73	68.73
Product Cost (PC)	-	-	309.06	309.06
Transportation Cost (TC)	-	-	46.24	46.24
Warehouse Cost (WC)	-	563.83	-	563.83
Salvage Value (SV)	-	42,965.72	296.94	43,262.66
Total Net Product Bundling Strategy Cost	-	−35,687.63	238.10	−35,449.54
Strategy Related Cost (SRC)	60.00	120.00	120.00	300.00
Unrecovered Product Cost (UPC)	73,570.56	147,810.30	47,526.89	268,907.75
Disposal Cost (DC)	426.95	707.73	-	1134.69
Product Cost (PC)	73,920.00	83,545.00	-	157,465.00
Transportation Cost (TC)	320.09	378.10	-	698.20
Warehouse Cost (WC)	643.17	2,481.43	1504.18	4628.77
Salvage Value (SV)	24,299.52	47,353.14	103,549.74	175,202.40
Total Net Price Discount Strategy Cost	124,641.25	187,689.42	−54,398.68	257,932.00
Strategy Related—Transpo (SRT)	-	2646.50	10,861.00	13,507.50
Strategy Related—Operations (SRO)	-	163.90	461.73	625.63
Savings in Purchase Cost (SPC)	50,289.75	33,804.55	-	84,094.30
Savings in Ordering Cost (SOC)	360.00	400.00	-	760.00
Savings in Warehouse Cost (SWC)	-	1817.99	5445.26	7263.25
Total Net Transshipment Strategy Cost	−50,649.75	−33,212.14	5877.47	−77,984.42
Total System Dead Stock Management Cost	73,991.50	118,789.65	−48,283.11	144,498.04
Total Remaining Qty. of Dead Stock	49.00	133.00	138.00	320.00
Dead Stock as a % of Total Inventory	6.77	14.57	19.88	13.73

.

Based on Table 5, the mixed strategy model yielded the minimum system dead stock management cost of Php 144,498.08. There was a total of 1325 units of potential dead stock (PDS) and unexpired dead stock (UDS) across the three stores at the beginning of the period. The transshipment strategy alone reduced the total dead stock from 1325 units to 928 units, equivalent to a 30% reduction. These dead stock were further reduced to 320 units by the end of the period after applying the product bundling and price discount strategies. This 76% reduction in the dead stock quantity demonstrates the logic and potential of the proposed mixed strategy model.

The model decisions on the total quantity of PDS and total quantity of UDS transshipped, sold at a price discount, and sold as a product bundle in each store are shown in

Table 6. Mixed strategy model decisions on transshipment, price discount and product bundling.

Integrated Model Decision	Store 1	Store 2	Store 3	System Total Qty.
Qty. of PDS Transshipped	0	67	21	88
Qty. of UDS Transshipped	0	0	309	309
Total PDS + UDS Qty. Transshipped	0	67	330	397
Qty. of PDS Discounted	94	217	261	572
Qty. of UDS Discounted	96	154	0	250
Total PDS + UDS Qty. Discounted	190	371	261	822
Qty. of PDS Sold as a Bundle	0	91	0	91
Qty. of UDS Sold as a Bundle	0	0	15	15
Total PDS + UDS Qty. Sold as a Bundle	0	91	15	106
Total Qty. of PDS + UDS Managed	190	529	606	1325

.

Referring to Table 5, store 2 was the largest contributor to total system dead stock management cost (i.e., 118,769.65), followed by store 1 (73,991.50) and then store 3 (−48,283.11). Table 6 shows that store 2 transshipped only 67 out of 529 dead stock, leaving it with the largest quantity (462 units) of dead stock for sales strategy management. The large quantity of dead stock meant more units sold compared to the other stores, which caused store 2 to have the highest unrecovered product cost (UPC) among the three stores. Store 2 also had the highest quantity of UDS, which were automatically disposed of when unsold, causing it to have the highest disposed product purchase cost (PC) among the three stores. In contrast, store 3 transshipped a large quantity of its dead stock, including all its UDS which resulted in zero disposed PC. The fewer dead stock in store 3 for sales management also resulted in a lower UPC. This explained why store 3 even had a negative cost contribution to the system cost.

Table 5 shows that the major contributors to total system cost are UPC and PC. An analysis of the results produced by the mixed strategy model shows that the selected sales discount level for both PDS and UDS was the main driver of UPC and PC.

Table 7. Summary of relationships between parameter drivers and major objective function cost components.

Relationship Item Number	Cost of UDS	Discount Offer %	Selling Price of UDS	% of Unsold UDS	Selling Price of Dead Stock	% of Unsold Dead Stock	PC	UPC
1	↑						↑
2				↑			↑
3		↑		↓			↓
4		↓	↑	↑
5						↑		↓
6		↑				↓		↑
7		↓			↑	↑
8		↓			↑			↓

summarizes the relationships between the different parameter drivers and major objective function cost components.

Relationship item number 1 to number 4 showed that lower discount % led to higher discounted UDS selling price and higher % of unsold UDS, resulting in higher PC. Relationship item number 5 to number 8, on the other hand, showed that lower discount % led to higher discounted dead stock selling price and higher % of unsold dead stock, resulting in lower UPC. PC and UPC therefore behave in opposite directions in terms of their contribution to the total system dead stock management cost. Moreover, the selected discount % is an important variable in minimizing the total dead stock management cost. The contrasting effects of discount % on the objective function cost components must be carefully considered and balanced by inventory managers to achieve minimum dead stock management cost. The quantity, location, and classification of dead stock managed using the product bundling or price discount strategy are important decision variables as they determine the magnitude of sold/unsold quantities, which consequently determine the magnitude of the objective function cost and “savings” components. An integrated mixed strategy model is therefore necessary to recommend strategy and quantity decisions that balance the impact of these cost components on total dead stock management cost. In addition, the application of big data analytics allows sustainable practices to be implemented.

Results in Table 5 showed that the proposed integrated mixed strategy model produced the lowest system dead stock management cost of Php144,498.04. Potential dead stock (PDS) and unexpired dead stock (UDS) that totaled 1325 units across the three stores at the beginning of the period were also reduced to just 320 units at the end of the period. This 76% reduction in system dead stock quantity was also the best when compared to the results of the two base models, namely the price-discount-strategy-only model and the product-bundling-strategy-only model (refer to

Table 8. Inventory cost breakdown of product bundling and price discount model results.

Inventory Cost Component	Product Bundling Model	Price Discount Model
Strategy Related (SR)	1512.70	480.00
Unrecovered Product Cost (UPC)	150,904.44	284,518.44
Disposal Cost (DC)	5571.24	3168.55
Product Cost (PC)	321,515.70	166,948.55
Transportation Cost (TC)	3448.74	2066.60
Warehouse Cost (WC)	12,775.47	6157.38
Salvage Value (SV)	42,317.56	234,763.81
Grand Total Cost for all Stores	453,410.73	228,575.70
Total Qty. of Remaining Potential Dead Stock for all Stores	651.00	375.00

). The superior performance of the integrated mixed strategy model proposed in this research was due to the presence of alternative dead stock management strategies that enabled decisions for maximizing total system salvage value while minimizing total system disposal cost of UDS and warehouse cost of PDS.

6. Discussion

In the case of the product bundling model, stores that did not have enough fast-moving (NDS) inventory were unable to pair their PDS and UDS with fast-moving products. In the absence of alternative dead stock management strategies, these unpaired PDS and UDS automatically incurred warehouse and disposal costs, respectively. Furthermore, Table 8 shows that if these unpaired PDS and UDS have high warehouse costs and high unit product costs, respectively, the salvage value obtained from sold product bundles will be outweighed by total warehouse and product disposal costs, which increase total net system dead stock management costs.

In the case of the price discount model, all PDS and UDS were constrained to be sold individually at a price discount regardless of discount percentage and expected sales success percentage in each store outlet. The absence of alternative strategies such as product bundling and transshipment hindered the model from trading off the major cost contributors in the different stores to minimize total system cost. In both the product bundling and price discount models, the store outlets also did not have the opportunity to push out and reduce the inventory level of their respective PDS and UDS through lateral transshipment. This took away the possibility of purchase cost savings in the receiving stores, which hindered the minimization of system dead stock management costs.

It is worth noting that between the two base models, the price discount model produced a lower system dead stock management cost of Php228,575.69 due to lower discount levels used in selling the dead stocks. It also produced a lower quantity of remaining dead stock of 375 units, which was equivalent to a 72% decrease from the initial quantity of dead stock. The comparison summary among the results of the integrated strategy mix model and the two base models is shown in

Table 9. Comparative summary of model results.

	Integrated Model		Product Bundling Only		Price Discount Only
Store	Cost (Php)	Qty. of Remaining Dead Stock (Units)	Cost (Php)	Qty. of Remaining Dead Stock (Units)	>Cost (Php)	Qty. of Remaining Dead Stock (Units)
1	73,991.50	48.88	166,279.17	30.08	124,641.25	48.88
2	118,789.65	133.02	276,757.99	363.78	151,159.71	173.65
3	−48,283.11	137.69	10,373.58	255.12	−47,225.27	151.98
Total System Cost (Php)	144,498.04	319.59	453,410.74	648.98	228,575.69	374.51

, clearly suggesting the potential effectiveness of the integrated strategy mix model. In addition, carbon emissions can be prevented using the current integrated model wherein using the same data from the study of Li et al. [37], it will yield about 1,020,759.33 g of Carbon emissions prevented. This was computed based on the number of transitions for PDS and DS multiplied by the total weight and carbon emission per gram of a generic retail product. This implies that the integrated model not only potentially saves costs but also prevents carbon emissions.

Several practical insights were drawn from the analysis of the model results. Counter-intuitive decisions made by the model produced the most interesting insights.

(1) In choosing between two or more transshipment sources, lower transportation cost (TC) and higher savings in warehouse cost (SWC) are not always favored. Although it may seem counter-intuitive, the manager should opt for the transshipment source with higher TC and/or lower SWC because if dead stock is not pushed out from this source through transshipment, the lower historical sales performance of this source when sales strategies are applied results in more unsold dead stock in the system that increases total inventory management costs.

(2) It is also better to transship an unexpired dead stock (UDS) from a source with higher TC and lower SWC over a source that transships a potential dead stock (PDS) with lower TC and higher SWC. This counter-intuitive decision enables the inventory manager to avoid the higher disposed product cost (PC) contribution of unsold UDS while absorbing the lower additional warehouse cost of unsold PDS.

(3) The realizable salvage value factor represents the fraction of the dead stock selling price that is realizable as revenue when it is successfully sold. Results show that the sales strategy with the higher realizable salvage value factor is generally selected because it decreased the number of unsold PDS/UDS (increased SV), which consequently decreased PC, although it increased the UPC of sold dead stock. However, the inventory manager should choose the sales strategy with a lower realizable salvage value factor if the decrease in UPC outweighs the lower SV and higher PC, because this decision produced a net decrease in total dead stock management cost.

(4) Offering higher discount percentages typically increases inventory management costs. However, the model showed that offering larger discounts on high-margin, unexpired dead stocks did not raise costs. In fact, inventory management costs decreased when these dead stocks were managed in stores with stronger past sales performance.

(5) Higher percentage discounts should be offered in low-performing stores to increase the quantity and percentage of sold dead stock, but this also increases the total inventory management costs. However, the model showed surprising results: offering low-percentage discounts in low-performing stores where selling prices and purchase costs of dead stock are significantly lower than in other stores does not increase total inventory management costs.

6.1. Scalability of the Model

The number of stores and products affected the decisions made by the model. The consideration of only a few stores and products in the chain store system (i.e., 3 stores, 10 products) limited the transshipment, bundling, and discount quantity decisions that the model made, and this prevented the model from achieving its full potential in managing dead stock profitably. This analysis was performed to evaluate the performance (i.e., in terms of dead stock management cost) of the integrated mixed strategy model when it is applied to more realistic chain store systems (i.e., more stores and products).

Four separate runs of the integrated mixed strategy model were performed to determine the scalability of the proposed model. The four runs, each with a varying number of stores and products, also sought to determine the effect of bigger store systems on total dead stock management cost and percentage of unresolved dead stock. The first run of the integrated mixed strategy model involved 3 stores and 10 products. This was increased to 4 stores and 15 products in the second run. The third and fourth runs involved 5 stores and 20 products, and 7 stores and 30 products, respectively.

Table 10. Effect of increasing number of stores and products on integrated model performance.

	Total Dead Stock Management Cost	Qty. of Remaining Dead Stock	% of Unresolved Dead Stock
3 stores 10 products	144,498.04	320.00	24%
4 stores 15 products	125,702.02	427.00	24%
5 stores 20 products	(472,046.94)	782.00	25%
7 stores 30 products	(1,109,978.52)	1448.00	19%

shows the effect of increasing the number of stores and products on the total net dead stock management cost, quantity of remaining dead stock, and percentage of unresolved dead stock. It shows that as the quantity of remaining dead stock increased, the total dead stock management cost decreased, consistent with earlier results. Results also showed that as the available alternatives within (i.e., more products) and outside a store (i.e., more stores in the system) increased, the performance of the model improved in terms of total net dead stock management cost (refer to Figure 2) and percentage of unresolved dead stock.

Three types of variation in the dataset were also introduced to determine the effect of each variation on the scalability of the proposed integrated model. These variations included increasing the number of products in each store while holding the number of stores constant, increasing the number of stores in the chain store system while holding the number of products in each store constant, and increasing the number of stores and products simultaneously.

Table 11. Effect of increasing number of stores and products on the scalability of the proposed integrated model.

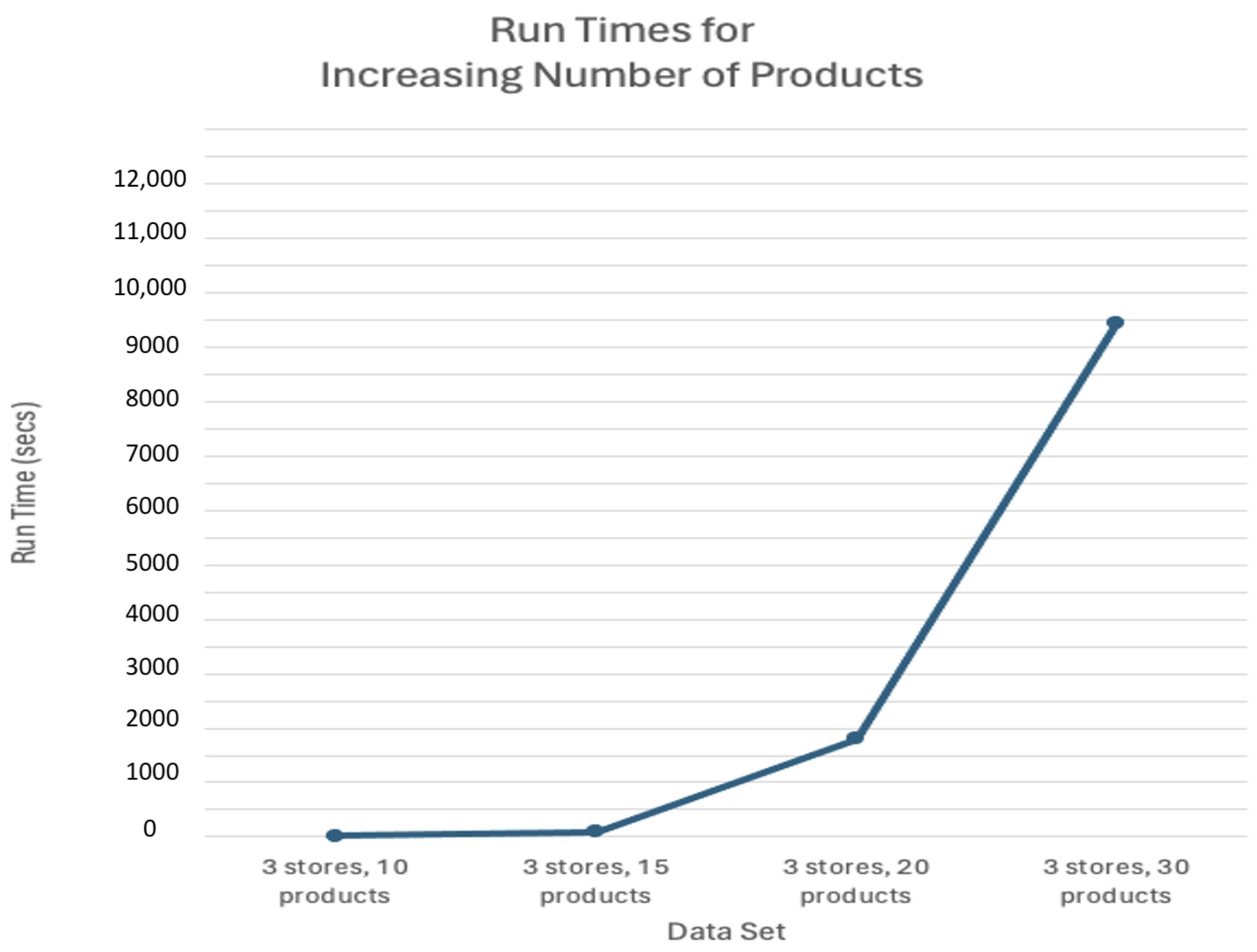
Scenario	Data Set	Run Time (s)	Number of Variables	Number of Constraints
Increasing Number of Products	3 stores 10 products	20.70	14,479	66,919
	3 stores 15 products	95.03	44,854	214,414
	3 stores 20 products	1803.37	102,679	497,959
	3 stores 30 products	9453.62	336,679	1,653,199
Increasing Number of Stores	3 stores 10 products	20.70	14,479	66,919
	4 stores 10 products	37.54	19,378	89,338
	5 stores 10 products	119.59	24,317	111,817
	7 stores 10 products	270.87	34,315	156,955
Increasing Number of Stores and Number of Products	3 stores 10 products	20.70	14,479	66,919
	4 stores 15 products	161.30	59,918	286,058
	5 stores 20 products	7826.55	171,517	830,517
	7 stores 30 products	12,968.29	787,235	3,859,955

shows the effect of increasing the number of stores and products using the proposed integrated model across different scenarios, as well as the run times for each type of variation in the dataset.

Table 12. Effect of increasing number of stores and products on the objective function component.

	Total Net Dead Stock Management Cost	Total Net Dead Stock Management Cost	Total Net Dead Stock Management Cost	Total Net Dead Stock Management Cost
Objective Function Components	3 stores 10 products	4 stores 15 products	5 stores 20 products	7 stores 30 products
Bundling Strategy Related Cost (BSRC)	762.50	1879.00	3494.00	4785.00
Unrecovered Product Purchase Cost (UPC)	6062.76	33,244.87	172,443.04	28,307.48
Disposal Cost (DC)	68.73	616.64	1427.17	239.07
Disposed Product Purchase Cost (PC)	309.06	37,119.04	140,277.48	5189.00
Transportation Cost TC)	46.24	365.12	848.45	135.39
Warehouse Cost (WC)	563.83	874.28	995.25	4288.68
Salvage Value (SV)	43,262.66	78,022.65	202,689.24	82,013.03
Total Bundling Management Cost	(35,449.54)	(3923.70)	116,796.15	(39,067.91)
Discount Strategy Related Cost (DSRC)	300.00	450.00	630.00	1470.00
Unrecovered Product Purchase Cost (UPC)	268,907.75	293,260.76	88,229.60	284,505.24
Disposal Cost (DC)	1134.69	1211.34	238.80	3555.33
Disposed Product Purchase Cost (PC)	157,465.00	157,652.46	2144.68	351,919.70
Transportation Cost TC)	698.20	743.58	141.40	2157.02
Warehouse Cost (WC)	4628.77	4798.11	10,057.89	22,139.92
Salvage Value (SV)	175,202.40	210,498.25	213,891.86	388,660.52
Total Discount Management Cost	257,932.00	247,617.99	(112,449.51)	277,086.68
Strategy Related-Transpo (SRT)	13,507.50	20,382.00	36,329.50	168,123.00
Strategy Related-Operations (SRO)	625.63	1575.59	3126.26	12,183.18
Savings in Purchase Cost (SPC)	84,094.30	126,819.90	490,828.65	1,430,113.70
Savings in Ordering Cost (SOC)	760.00	1920.00	3170.00	7490.00
Savings in Warehouse Cost (SWC)	7263.25	11,209.96	21,850.70	90,699.78
Total Transshipment Management Cost	(77,984.42)	(117,992.28)	(476,393.58)	(1,347,997.30)
Net Total Dead Stock Management Cost	144,498.04	125,702.02	(472,046.94)	(1,109,978.52)
Total Qty. of Potential Dead Stocks	751.00	1354.00	2328.00	5589.00
Total Qty. of Unexpired Dead Stocks	574.00	437.00	787.00	1891.00
Total Qty. of Dead Stocks	1325.00	1791.00	3115.00	7480.00
Qty. of Remaining Potential Dead Stocks	320.00	427.00	782.00	1448.00
Percentage of Unresolved Dead Stocks	24%	24%	25%	19%

, on the other hand, shows the effect of increasing the number of stores and products on the different components of the objective function and their collective effect on the percentage of unresolved dead stocks in the system.

The effect of each type of dataset variation on the run time of the model is also shown in Figure 3, Figure 4 and Figure 5.

6.2. Practical Application

The retail system inventory managers then use the outputs of this research in the following manner:

• Run the Inventory Classification Module of the ERP system and generate Inventory Classification Report per store.
• Consolidate all store-level product classification results, product-related, and sales-strategy-related data into an Excel file with specific data formatting (i.e., separate sheet per parameter where rows represent products and columns represent stores) that an optimization software will read.
• Run the mixed strategy cost optimization model code and generate the dead stock management decision report for each dead stock per store.
• Examine the transshipment, price discount, and product bundling results per store and check for sudden operational, logistical, and resource constraints that need to be considered. Discount percentage levels selected by the model for each dead stock should also be checked against the most recent product demand patterns and forecasts, if available.
• Finalize the dead stock management decision report per store.

At the beginning of the following period, the inventory managers should carry out the following:

• Prepare the labor, material, marketing, logistical, and other operational resources needed per store in carrying out the dead stock management strategies prescribed by the optimization model.
• Prepare a transshipment routing plan and perform the prescribed transshipment decisions in the final dead stock management decision report first.
• Update and verify the inventory level of each product after transshipment to see if it matches the inventory level used by the model in making the sales strategy decisions.
• Execute the sales strategy decisions in the final dead stock management decision report.
• Monitor the sales performance of each dead stock during the period and adjust strategies to reduce dead stock management costs if necessary.
• If possible, and with the help of people from the finance and accounting department, record and monitor actual costs and benefits of strategy implementation.

At the end of the period, the inventory managers should carry out the following:

• Prepare the labor, material, logistical, and other operational resources needed per store to collect the unsold unexpired dead stock (UDS) from the store and return them to the warehouse.
• Prepare the unsold UDS for disposal. Judgement should be exercised in deciding whether to dispose of the unsold UDS or not based on the actual sales strategy’s success during the period.
• Consolidate the unsold UDS for disposal from each store and prepare a truck routing plan to transport these to the centralized disposal facility.
• Prepare the labor and other operational resources needed per store to transfer the unsold PDS back to the warehouse.
• If possible, and with the help of people from the finance and accounting department, record the actual disposal and warehouse costs for the period. Compute the total actual dead stock management costs and benefits incurred for the period, and compare this cost against the total cost computed by the optimization model.
• The cycle repeats itself in the following period.

7. Conclusions

In the retail industry, dead stock accumulates due to management’s failure to control the accumulation of non-moving inventory. Priority attention given to the management of fast-moving products has resulted in the rise in dead stock costs that severely impacted the retailers’ profitability. Studies have considered single-strategy solutions to manage the dead stock problem, but mixed-strategy solutions remain unexplored in the literature. This research formulated a mixed strategy model that considered the simultaneous application of product bundling, price discount, and transshipment in minimizing total dead stock management cost and reducing the quantity of dead stock in the inventory system of the retail chain operator. Conclusions drawn from the results were as follows:

(1) Lateral transshipment was mostly used in the literature to proactively balance inventory levels and reactively respond to stockout situations in retail chain stores. This research showed that lateral transshipment is a “profitable” strategy in the management of dead stock of a retail chain store system.

(2) The profit of retail chain operators improves significantly (because of minimized dead stock management costs) by adopting a balanced inventory management approach that gives attention to the management and control of both fast-moving products and dead stock.

(3) For the sales strategies used in pushing out the dead stock, higher discount percentages generally increased dead stock management costs and decreased the quantity of remaining dead stock.

(4) The proposed optimization model is a better dead stock management tool compared to single strategy models because it provides strategy options for the decision maker in cases where internal or external constraints favor the selection of one strategy over another.

Limitations of the Proposed Integrated Mixed Strategy Model and Future Research

The mixed strategy model developed in this research may be used to manage dead stock in retail chain store contexts, including but not limited to fast-fashion, medicines, books, toys, electronic gadgets, etc., as long as economic and marketing parameters that determine highly stochastic demand functions accurately reflect the relationship between discount percentage and expected product sales success. The model also promoted the use of sustainable inventory management practices in the retail chain system through the reduction in dead stock waste. However, there are assumptions and limitations that may compromise some realities of the problem situation that is being modeled and affect the level of significance of the results. The limitations of the Proposed Integrated Mixed Strategy model include the following:

• Discount levels are not treated as decision variables in the model. Hence, the selection of discount % is limited to only four possible values in all store locations.
• Stockout cost of fast-moving products was not considered in the optimization model. The consideration of stockout cost can alter the product bundling decisions and total inventory management cost.
• The single-period model formulated in this research was unable to show the effect of changes in product classifications on dead stock management. Consequently, it was unable to determine the degree of accumulation or elimination of dead stock over time.
• The formulated model is limited to only three dead stock management strategies. Consideration of other strategies, such as return to vendor and donation of dead stock, provides an opportunity for management to consider tradeoffs between social and environmental costs.
• The use of hypothetical data in determining the effectiveness of the results limited the realism and strength of validity of the stated results.

Since the discount percentage was found to be the main factor that drove the values of the major cost contributors to total dead stock management cost, future studies should focus on developing a model that uses discount percentage as a sales strategy decision variable. The mixed strategy model is also expected to produce better results for any chain store operator if more strategy options are considered in a multi-period setting. More strategy options potentially produce better results because of the increased trade-off opportunities for inventory management decision-making. Furthermore, a multi-period model can better demonstrate how the accumulation of dead stock can be prevented as product classifications that change over time are managed and pushed out of the system in a timely manner. The developed model will also benefit from using big data analysis in deriving a demand and obsolescence forecasting model that is able to accurately relate the product pricing and product sales success variables. Lastly, the result of this research is most useful if validation is carried out with real-world, anonymized data from a retail chain partner.