Water Quality Prediction Model Based on Temporal Attentive Bidirectional Gated Recurrent Unit Model
Abstract
1. Introduction
2. Study Area and Data
2.1. Study Area Profile
2.2. Data and Processing
2.2.1. Dataset Condition
2.2.2. Data Processing
3. Model Construction
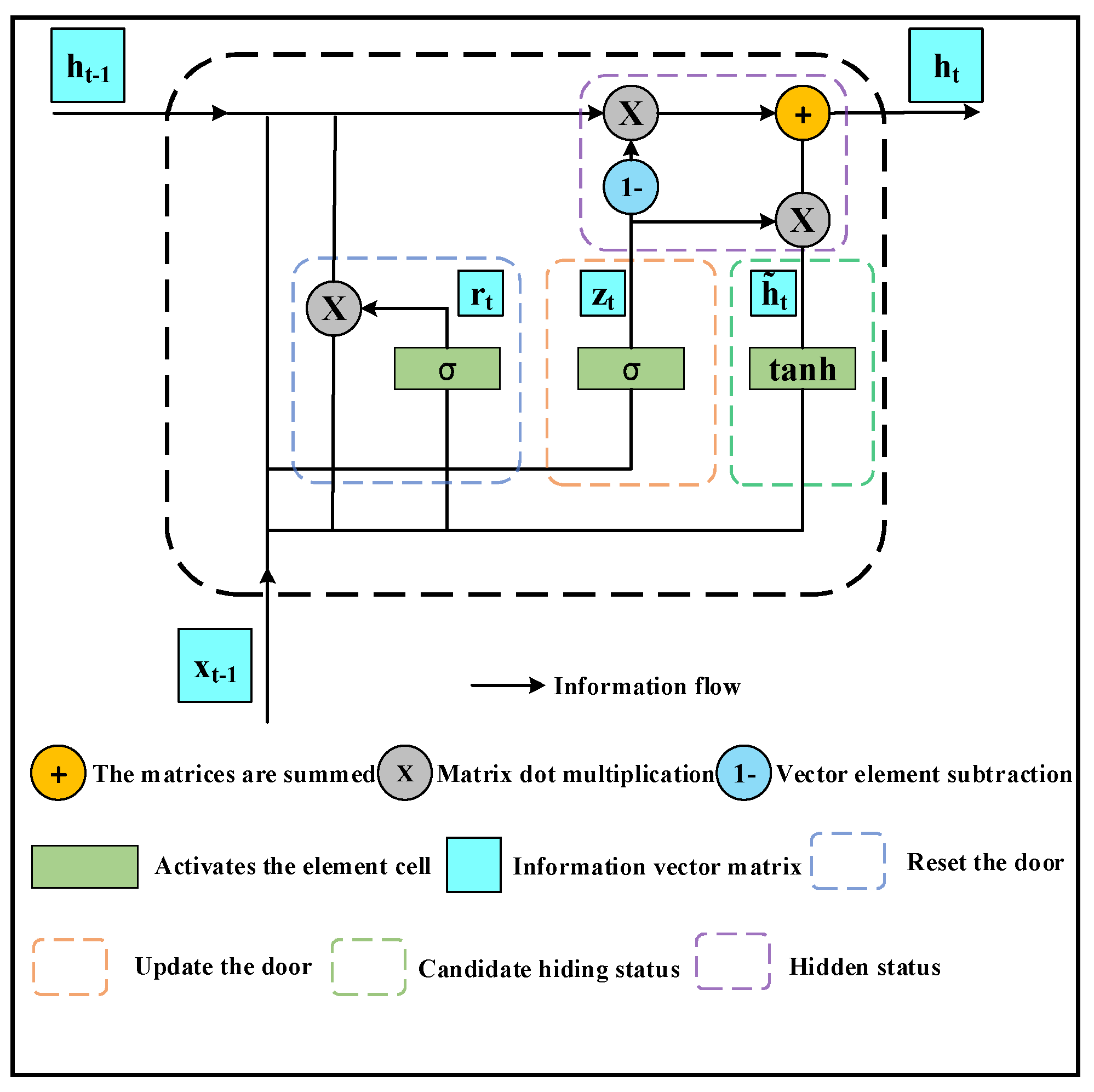
3.1. Gated Recurrent Unit (GRU)
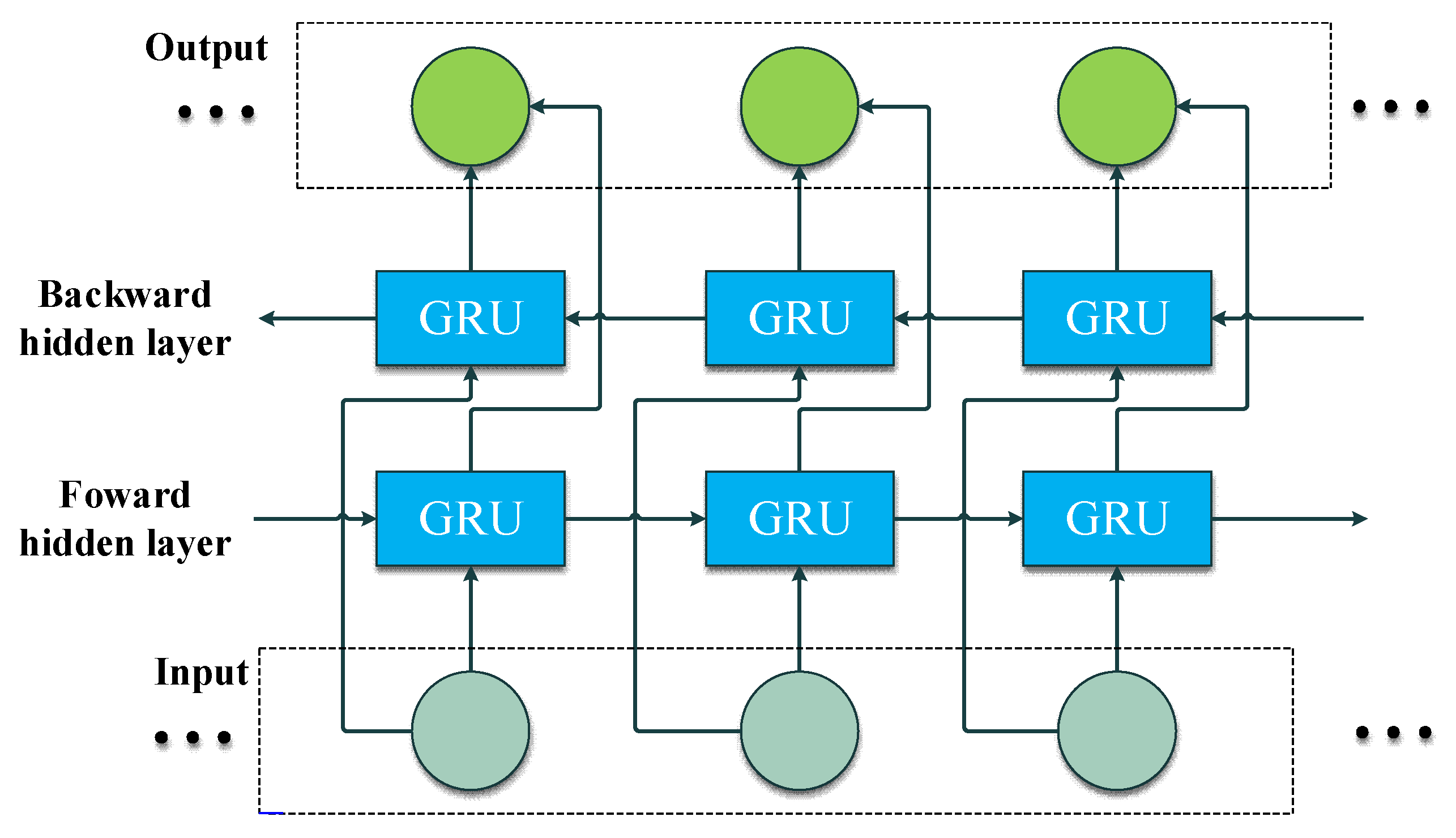
3.2. Bi-Directional GRU (Bi-GRU)
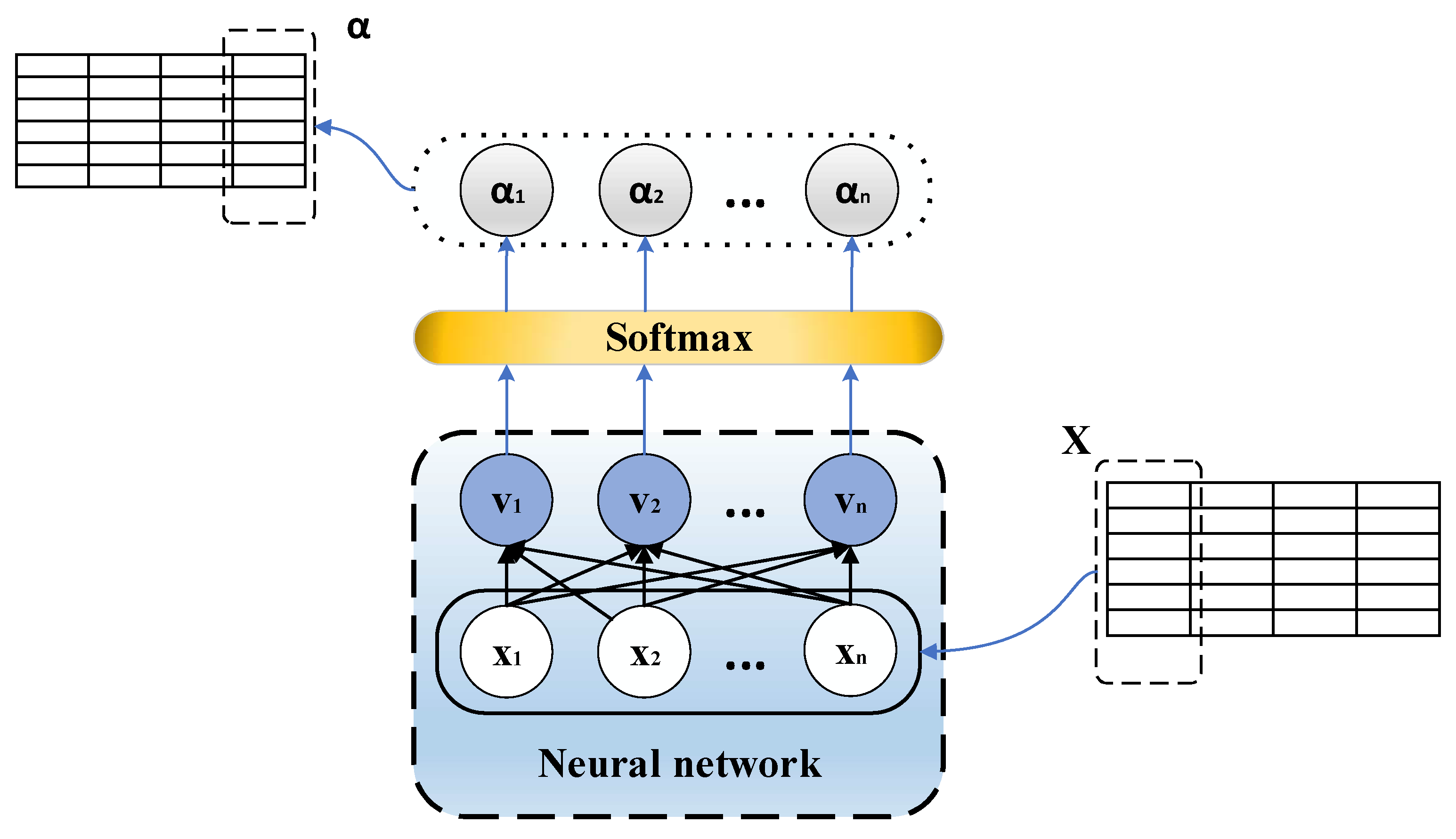
3.3. Temporal Attention Mechanism (TA)
- (1)
- First, the similarity of the query vector (usually the hidden state from the previous time step, denoted Q) to each element in the sequence is calculated by the formula:
- (2)
- The similarity is normalized to obtain the attention weight (denoted as α). The calculation formula of attention weight is as follows:
- (3)
- Finally, the attention weight is weighted and summed with each element in the sequence to obtain the output of the attention mechanism. The formula for calculating attention output is:
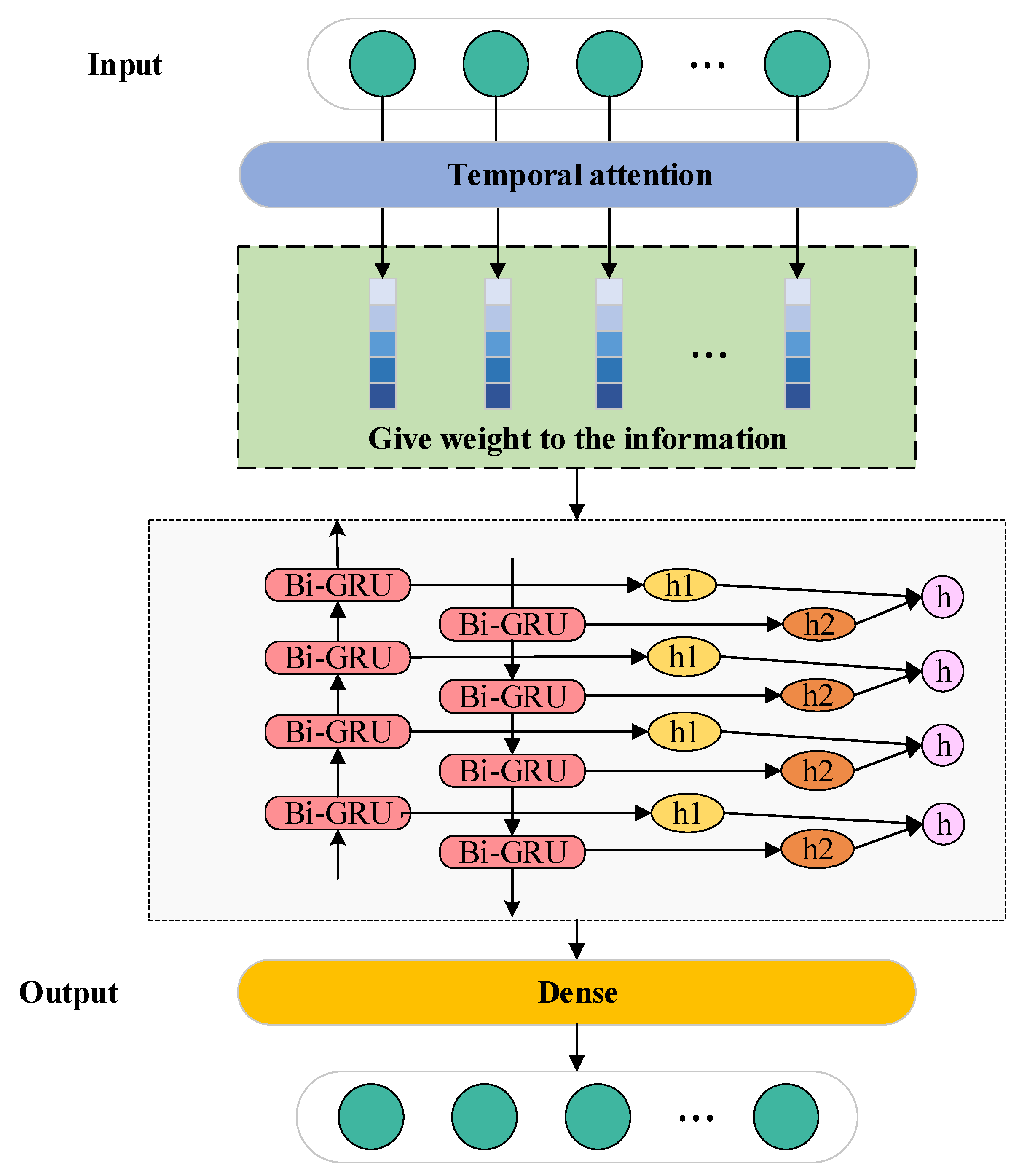
3.4. Temporal Attentive Bidirectional Gated Recurrent Unit (TA-Bi-GRU)
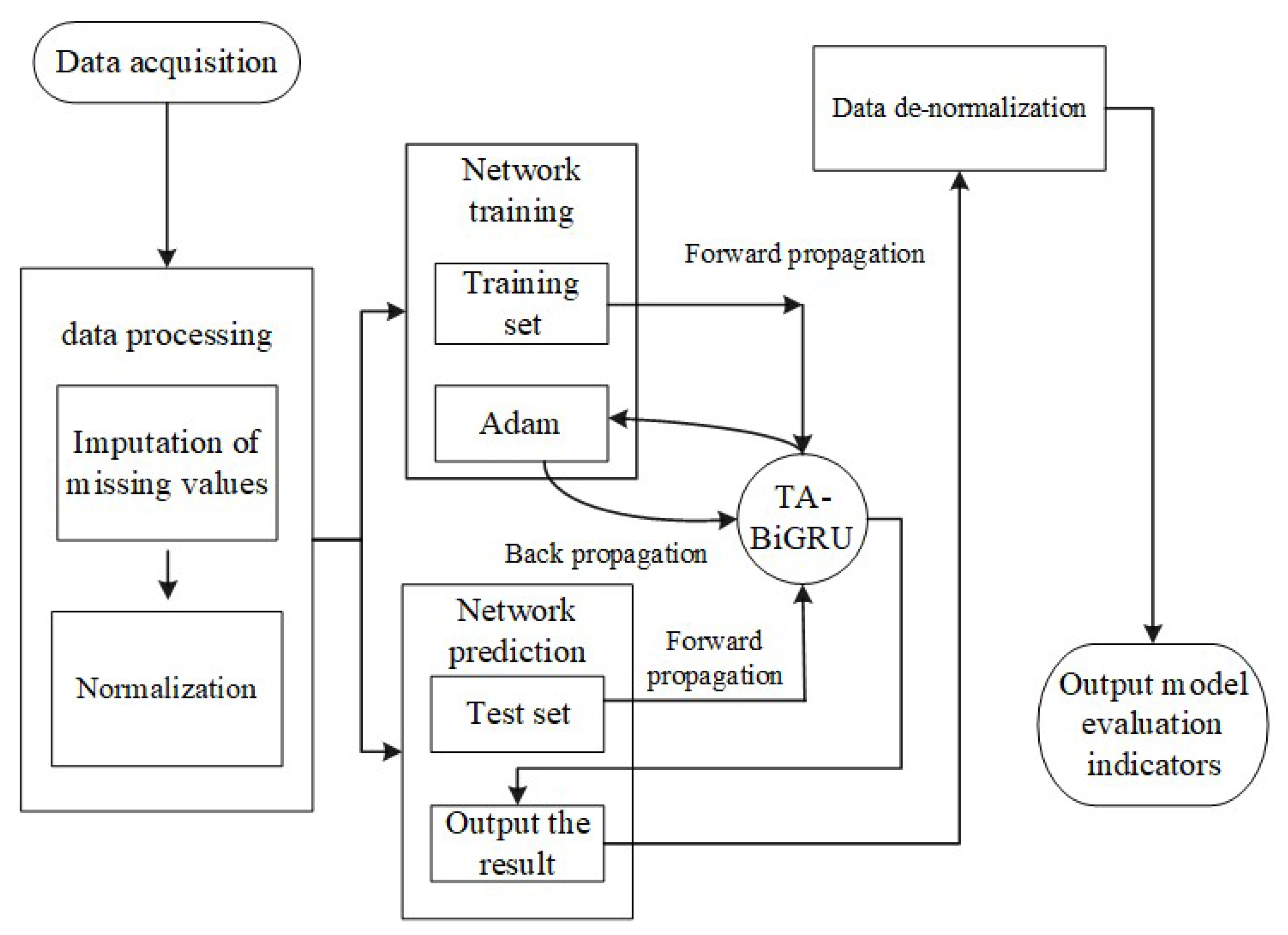
3.5. Prediction Steps for TA-Bi-GRU
4. Case Verification
4.1. Evaluation Index
4.2. Model Parameters and Experimental Environment
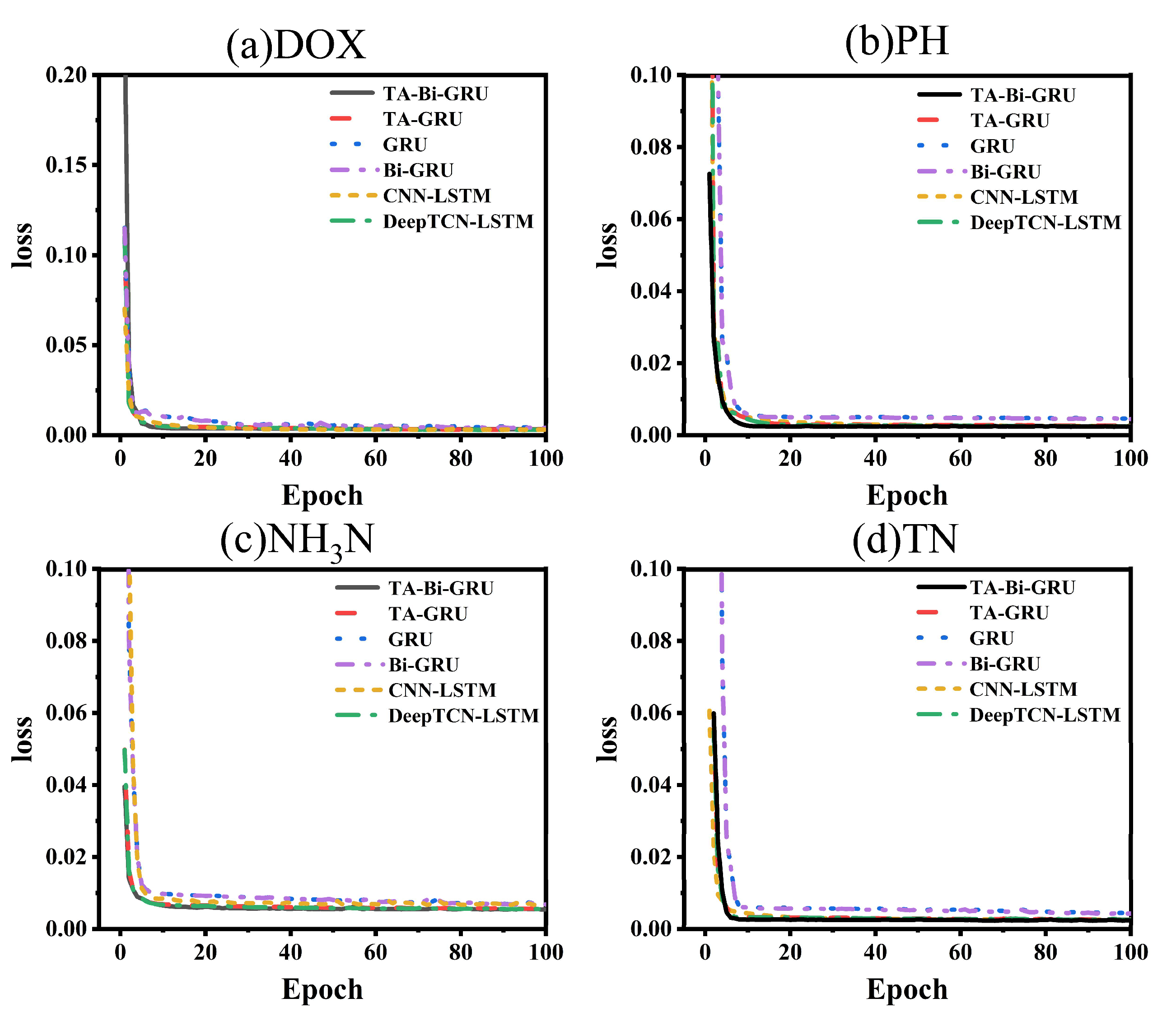
4.3. Training Loss
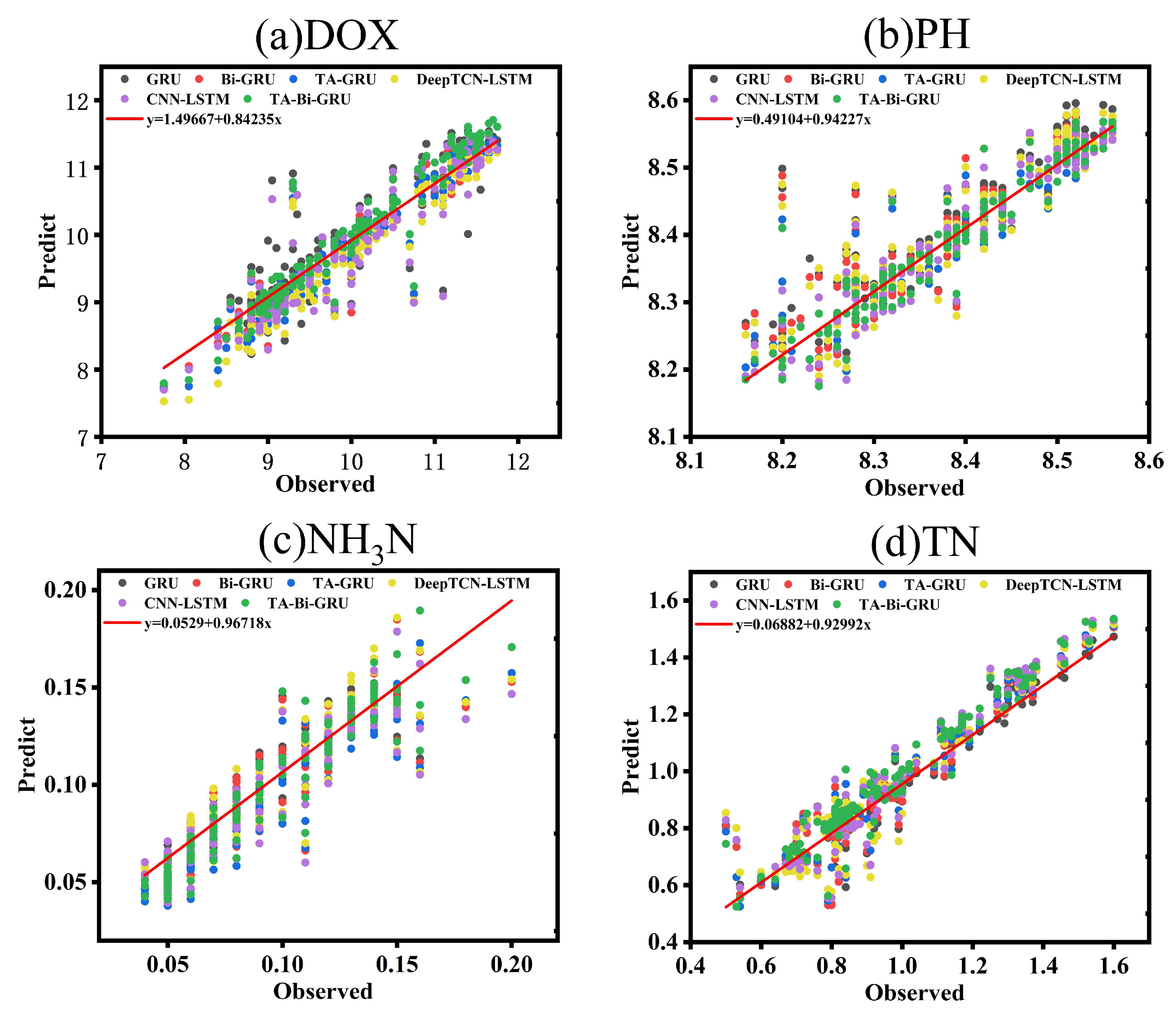
4.4. Analysis of Experimental Results
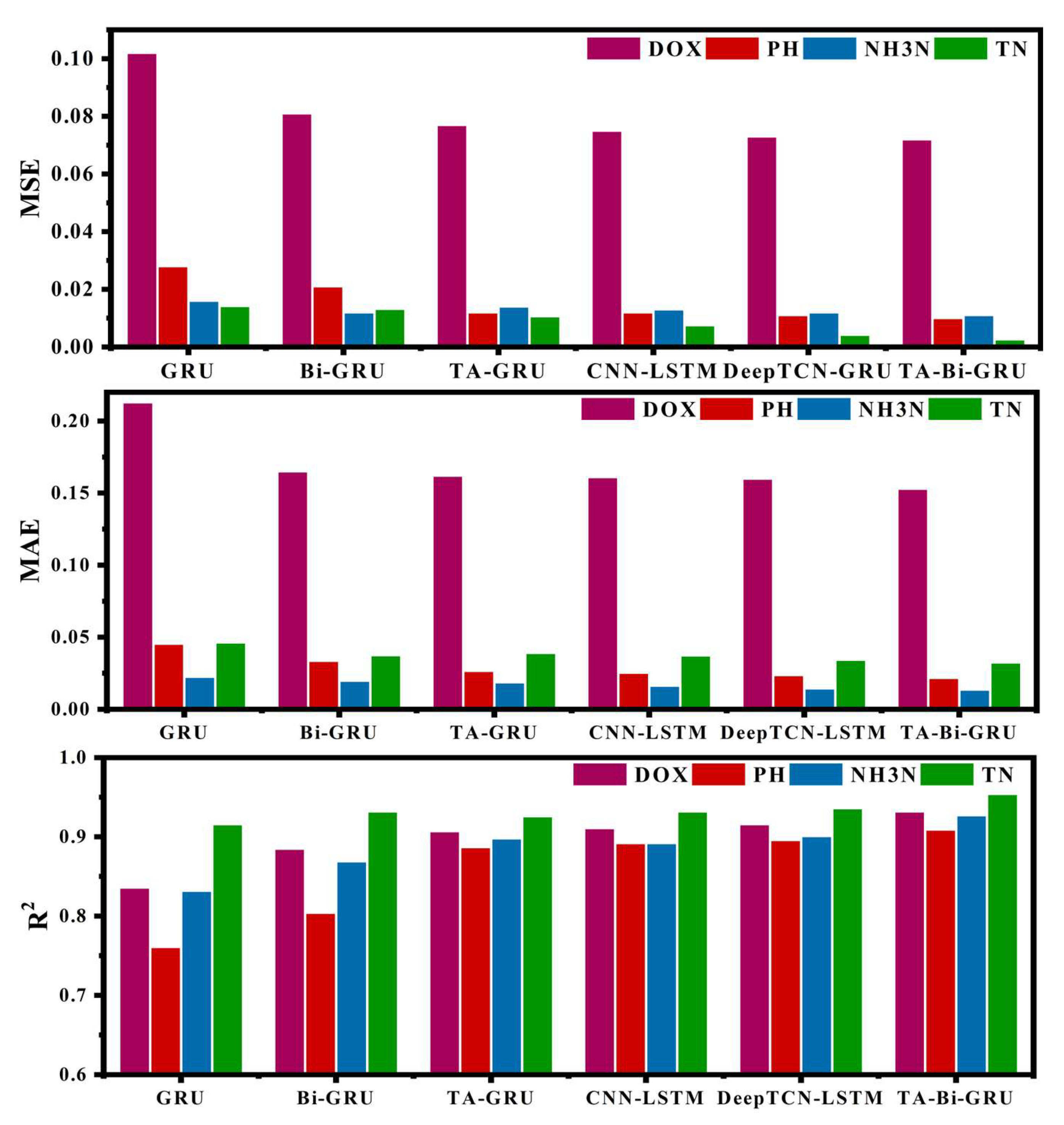
4.4.1. Performance Verification and Analysis of the Model
4.4.2. Experiment on the Influence of Training Set Size on Model Performance
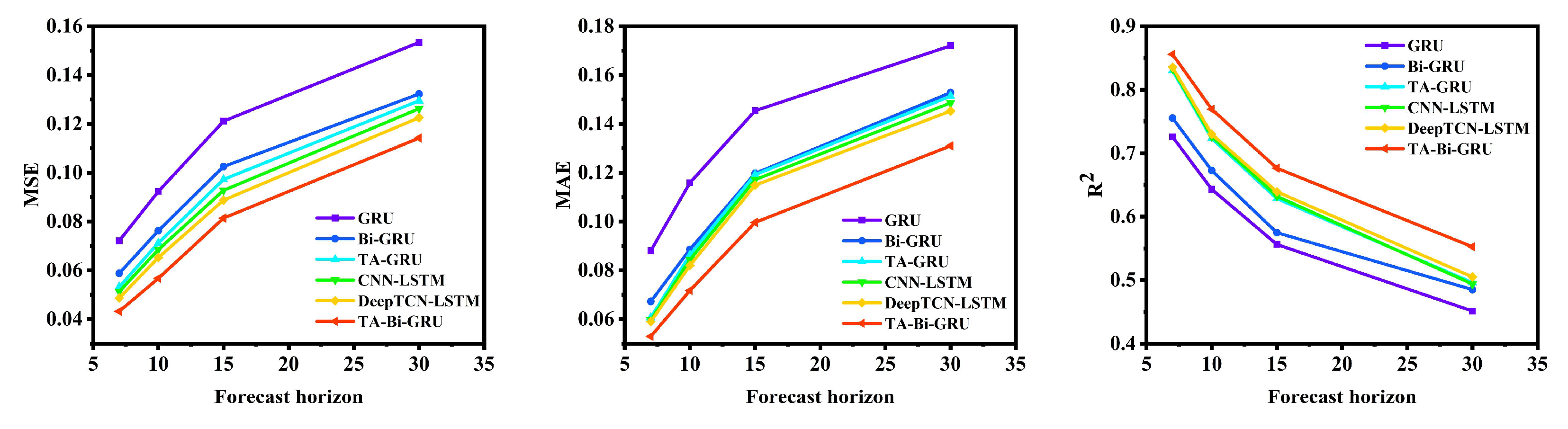
4.4.3. Performance Verification and Analysis of the Model Under Multiple Prediction Periods
5. Discussion
5.1. Significance of the Research Results: Comparison with Similar Studies
5.2. The Adaptability of TA-Bi-GRU to Environmental Time Series Data
- (1)
- For strong nonlinearity: The Bi-GRU module collaboratively models the causal relationship of water quality changes through forward and reverse GRUs, while the TA mechanism amplifies the weight of the time step of extreme events. This is in sharp contrast to fixed-core models such as DeepTDN-GRU, which cannot dynamically adapt to nonlinear mutations. The MSE of 30-day TN reaches 0.0665, which is 4.3% higher than that of TA-Bi-GRU (0.0638).
- (2)
- For dual time scales: TA-Bi-GRU employs a two-layer stacked Bi-GRU (forward + reverse), which can fully extract the dicircadian fluctuations of DOX (short-term) and the seasonal accumulation of TN (long-term) features. The TA mechanism further distinguishes the importance of the two. In contrast, for the one-way model TA-GRU [23], due to the absence of future time series information (such as ignoring the influence of subsequent dry seasons when predicting TN), the TN R2 at 180 days was only 0.469, which was 14.7% lower than that of TA-Bi-GRU (0.550).
- (3)
- For high interference: The TA mechanism can filter out noise at non-critical time steps and focus on signals of significant ecological importance. This is particularly evident in the highly volatile metric pH: The 30-day pH R2 of TA-Bi-GRU reaches 0.520, which is 14.3% higher than that of CNN-LSTM (0.455), because the convolutional layer of the latter is prone to overfitting the short-term noise of pH.
5.3. The Practical Application Value of Water Pollution Prevention and Control
- (1)
- Early prevention and control of eutrophication: The average TN of Xiduan Village Reservoir (0.982 mg/L) has approached the limit of Class III water (Section 2.1), and the 15-day TN prediction R2 of TA-Bi-GRU can still reach 0.68 (Table 6), which can accurately predict the cumulative trend of TN. Therefore, managers can start measures such as reducing the use of chemical fertilizers in upstream farmlands and ecological water replenishment for reservoirs 7 to 15 days in advance to avoid passive emergency response after TN exceeds the standard. Compared with traditional post-event management, this proactive prevention and control model can reduce the economic cost of emergency water treatment by 30% to 40%.
- (2)
- Rainy season pollution warning: The peak of NH3N in the reservoir during the rainy season reaches 0.55 mg/L (Section 2.1), threatening the safety of drinking water. The 7-day NH3N prediction MAE of TA-Bi-GRU is only 0.0151 and the R2 reaches 0.845 (Table 6). It can identify high-risk periods in advance and trigger pre-control measures such as pre-interception of drainage channels and inspection of sewage outlets. It is expected that the peak concentration of NH3N during the rainy season can be reduced by 15% to 20%.
- (3)
- Long-term ecological water replenishment dispatching: The reservoir undertakes the ecological water replenishment function of the downstream river channel (Section 2.1). The 30-day DOX prediction R2 of TA-Bi-GRU reaches 0.585 (Table 6), which can predict the risk of DOX decline during the dry season in advance. Based on this, adjust the water extraction volume of the Yellow River to maintain DOX above 5 mg/L and ensure the stability of the aquatic ecosystem downstream.
5.4. The Limitations and Prospects of the Model
6. Conclusions
- (1)
- This model, through the collaborative design of the TA mechanism and Bi-GRU, effectively makes up for the deficiencies of the traditional model: Bi-GRU bidirectionally captures the time series dependency relationship, solving the problem of “history-future” information fragmentation; The TA mechanism dynamically focuses on the key time steps, significantly improving the prediction accuracy and stability. In the one-day short-term prediction, the average R2 of the four indicators reached 0.932, and the MAE and MSE decreased by 15% to 35% and 25% to 45%, respectively, compared with the other comparison models. Moreover, in the small-sample scenario with only 30% of the training set (236 samples), its average R2 still reached 0.692, which was 34.4% and 18.7% higher than that of GRU (0.515) and Bi-GRU (0.583), respectively, and the performance degradation was much lower than that of other models. The strong adaptability of bidirectional temporal perception and dynamic attention structure to small sample data has been verified, which can meet the actual needs of insufficient data accumulation in newly built monitoring stations.
- (2)
- The model is adapted to the characteristics of water quality data and can accurately capture multi-scale water quality changes. TA-Bi-GRU demonstrates strong adaptability to the characteristics of strong nonlinearity and dual time scales of water quality data: for the highly volatile NH3N, the 30-day prediction MAE is only 0.0372 (5.8% lower than that of DeepTCN-LSTM); For TN accumulated over a long period, the 7-day prediction R2 reached 0.893 (3.8% higher than CNN-LSTM), and the 15-day prediction could still accurately predict the cumulative trend of TN (R2 = 0.680), which could effectively support the early prevention and control of eutrophication and avoid passive emergency response after water quality exceeded the standard. The 7-day prediction of NH3N (R2 = 0.845, MAE = 0.0151) can provide early warnings of pollution risks during the rainy season, and the 30-day DOX prediction (R2 = 0.585) can guide the ecological water replenishment scheduling during the dry season, contributing to the balance of water supply for “life-production-ecology”.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ahmed, U.; Mumtaz, R.; Anwar, H.; Shah, A.A.; Irfan, R.; García-Nieto, J. Efficient Water Quality Prediction Using Supervised Machine Learning. Water 2019, 11, 2210. [Google Scholar] [CrossRef]
- Shah, M.I.; Javed, M.F.; Alqahtani, A.; Aldrees, A. Environmental assessment based surface water quality prediction using hyper-parameter optimized machine learning models based on consistent big data. Process Saf. Environ. Prot. 2021, 151, 324–340. [Google Scholar] [CrossRef]
- Jamshidzadeh, Z.; Ehteram, M.; Shabanian, H. Bidirectional Long Short-Term Memory (BILSTM)-Support Vector Machine: A new machine learning model for predicting water quality parameters. Ain Shams Eng. J. 2024, 15, 102510. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, D.; Liu, Z.; Liu, Z.; Wang, L.; Tan, J. A novel robotic grasping method for moving objects based on multi-agent deep reinforcement learning. Robot. Comput.-Integr. Manuf. 2024, 86, 102644. [Google Scholar] [CrossRef]
- Kang, Y.; Song, J.; Lin, Z.; Huang, L.; Zhai, X.; Feng, H. Water Quality Prediction Based on SSA-MIC-SMBO-ESN. Comput. Intell. Neurosci. 2022, 2022, 1264385. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Liu, T.; Liu, Z.; Luo, H.; Pei, H. A novel deep learning ensemble model based on two-stage feature selection and intelligent optimization for water quality prediction. Environ. Res. 2023, 224, 115560. [Google Scholar] [CrossRef] [PubMed]
- Afan, H.A.; El-shafie, A.; Mohtar, W.H.M.W.; Yaseen, Z.M. Past, present and prospect of an Artificial Intelligence (AI) based model for sediment transport prediction. J. Hydrol. 2016, 541, 902–913. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; Trajkovic, S.; Zounemat-Kermani, M.; Li, B.; Kisi, O. Daily streamflow prediction using optimally pruned extreme learning machine. J. Hydrol. 2019, 577, 123981. [Google Scholar] [CrossRef]
- Najwa Mohd Rizal, N.; Hayder, G.; Mnzool, M.; Elnaim, B.M.; Mohammed, A.O.Y.; Khayyat, M.M. Comparison between regression models, support vector machine (SVM), and artificial neural network (ANN) in river water quality prediction. Processes 2022, 10, 1652. [Google Scholar] [CrossRef]
- Li, T.; Lu, J.; Wu, J.; Zhang, Z.; Chen, L. Predicting Aquaculture Water Quality Using Machine Learning Approaches. Water 2022, 14, 2836. [Google Scholar] [CrossRef]
- Najah, A.A.; El-Shafie, A.; Karim, O.A.; Jaafar, O. Water quality prediction model utilizing integrated wavelet-ANFIS model with cross-validation. Neural Comput. Appl. 2012, 21, 833–841. [Google Scholar] [CrossRef]
- Tiwari, S.; Babbar, R.; Kaur, G. Performance evaluation of two ANFIS models for predicting water quality index of River Satluj (India). Adv. Civ. Eng. 2018, 2018, 8971079. [Google Scholar] [CrossRef]
- Dong, Y.; Ren, Z.; Li, L.H. Forecast of Water Structure Based on GM (1, 1) of the Gray System. Sci. Program. 2022, 2022, 8583959. [Google Scholar] [CrossRef]
- Adebiyi, A.A.; Adewumi, A.O.; Ayo, C.K. Comparison of ARIMA and artificial neural networks models for stock price prediction. J. Appl. Math. 2014, 2014, 614342. [Google Scholar] [CrossRef]
- Kabir, S.; Patidar, S.; Pender, G. Investigating capabilities of machine learning techniques in forecasting stream flow. Proc. Inst. Civ. Eng.-Water Manag. 2020, 173, 69–86. [Google Scholar] [CrossRef]
- Mei, P.; Li, M.; Zhang, Q.; Li, G. Prediction model of drinking water source quality with potential industrial-agricultural pollution based on CNN-GRU-Attention. J. Hydrol. 2022, 610, 127934. [Google Scholar] [CrossRef]
- Ostad-Ali-Askari, K.; Shayan, M. Subsurface drain spacing in the unsteady conditions by HYDRUS-3D and artificial neural networks. Arab. J. Geosci. 2021, 14, 1936. [Google Scholar] [CrossRef]
- Yang, Y.; Xiong, Q.; Wu, C.; Zou, Q.; Yu, Y.; Yi, H.; Gao, M. A study on water quality prediction by a hybrid CNN-LSTM model with attention mechanism. Environ. Sci. Pollut. Res. 2021, 28, 55129–55139. [Google Scholar] [CrossRef]
- Hochreiter, S. The vanishing gradient problem during learning recurrent neural nets and problem solutions. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 1998, 6, 107–116. [Google Scholar] [CrossRef]
- Yang, B.; Yin, K.; Lacasse, S.; Liu, Z. Time series analysis and long short-termmemory neural network to predict landslide displacement. Landslides 2019, 16, 677–694. [Google Scholar] [CrossRef]
- Li, L.; Jiang, P.; Xu, H.; Lin, G.; Guo, D.; Wu, H. Water quality prediction based on recurrent neural network and improved evidence theory: A case study of Qiantang River, China. Environ. Sci. Pollut. Res. 2019, 26, 19879–19896. [Google Scholar] [CrossRef] [PubMed]
- Lei, D.; Liu, H.; Le, H.; Huang, J.; Yuan, J.; Li, L.; Wang, Y. Ionospheric TEC Prediction Base on Attentional Bi-GRU. Atmosphere 2022, 13, 1039. [Google Scholar] [CrossRef]
- Wongburi, P.; Park, J.K. Prediction of Wastewater Treatment Plant Effluent Water Quality Using Recurrent Neural Network (RNN) Models. Water 2023, 15, 3325. [Google Scholar] [CrossRef]
- Gupta, U.; Bhattacharjee, V.; Bishnu, P.S. StockNet—GRU based stock index prediction. Expert Syst. Appl. 2022, 207, 117986. [Google Scholar] [CrossRef]
- Mahjoub, S.; Chrifi-Alaoui, L.; Marhic, B.; Delahoche, L. Predicting Energy Consumption Using LSTM, Multi-Layer GRU and Drop-GRU Neural Networks. Sensors 2022, 22, 4062. [Google Scholar] [CrossRef]
- Li, W.; Wu, H.; Zhu, N.; Jiang, Y.; Tan, J.; Guo, Y. Prediction of dissolved oxygen in a fishery pond based on gated recurrent unit (GRU). Inf. Process. Agric. 2021, 8, 185–193. [Google Scholar] [CrossRef]
- Niu, Z.; Yu, Z.; Tang, W.; Wu, Q.; Reformat, M. Wind power forecasting using attention-based gated recurrent unit network. Energy 2020, 196, 117081. [Google Scholar] [CrossRef]
- Eze, E.; Kirby, S.; Attridge, J.; Ajmal, T. Aquaculture 4.0: Hybrid Neural Network Multivariate Water Quality Parameters Forecasting Model. Sci. Rep. 2023, 13, 16129. [Google Scholar] [CrossRef]
- Xu, Z.; Zhou, Q.; Yan, Z. Special Section on Recent Advances in Artificial Intelligence for Smart Manufacturing–Part I Intelligent Automation & Soft Computing. Intell. Autom. Soft Comput. 2019, 25, 693–694. [Google Scholar]
- Li, X.; Ma, X.; Xiao, F.; Xiao, C.; Wang, F.; Zhang, S. Time-series production forecasting method based on the integration of Bidirectional Gated Recurrent Unit (Bi-GRU) network and Sparrow Search Algorithm (SSA). J. Pet. Sci. Eng. 2022, 208, 109309. [Google Scholar] [CrossRef]
- Liang, R.; Chen, X.; Jia, P.; Xu, C. Mine Gas Concentration Forecasting Model Based on an Optimized Bi-GRU Network. ACS Omega 2020, 5, 28579–28586. [Google Scholar] [CrossRef]
- Yuan, Q.; Wang, J.; Zheng, M.; Wang, X. Hybrid 1D-CNN and attention-based Bi-GRU neural networks for predicting moisture content of sand gravel using NIR spectroscopy. Constr. Build. Mater. 2022, 350, 128799. [Google Scholar] [CrossRef]
- Zhao, L.; Luo, T.; Jiang, X.; Zhang, B. Prediction of soil moisture using BiGRU-LSTM model with STL decomposition in Qinghai–Tibet Plateau. PeerJ 2023, 11, e15851. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q.; Zhang, F.; Liu, S.; Wu, Y.; Wang, L. A hybrid VMD–BiGRU model for rubber futures time series forecasting. Appl. Soft Comput. 2019, 84, 105739. [Google Scholar] [CrossRef]
- Wu, L.; Kong, C.; Hao, X.; Chen, W. A short-term load forecasting method based on GRU-CNN hybrid neural network model. Math. Probl. Eng. 2020, 2020, 1428104. [Google Scholar] [CrossRef]
- Franke, T.; Buhler, F.; Cocron, P.; Neumann, I.; Krems, F.J. Enhancing sustainability of electric vehicles: A field study approach to understanding user acceptance and behavior. In Advances in Traffic Psychology; CRC Press: Boca Raton, FL, USA, 2012; Volume 1, pp. 295–306. [Google Scholar]
- Gao, X.; Li, X.; Zhao, B.; Ji, W.; Jing, X.; He, Y. Short-term electricity load forecasting model based on EMD-GRU with feature selection. Energies 2019, 12, 1140. [Google Scholar] [CrossRef]
- Luo, H.; Wang, M.; Wong, P.K.Y.; Tang, J.; Cheng, J.C. Construction machine pose prediction considering historical motions and activity attributes using gated recurrent unit (GRU). Autom. Constr. 2021, 121, 103444. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, W. Shale content prediction of well logs based on CNN-BiGRU-VAE neural network. J. Earth Syst. Sci. 2023, 132, 139. [Google Scholar] [CrossRef]
- Dai, Z.; Li, P.; Zhu, M.; Zhu, H.; Liu, J.; Zhai, Y.; Fan, J. Dynamic prediction for attitude and position of shield machine in tunneling: A hybrid deep learning method considering dual attention. Adv. Eng. Inform. 2023, 57, 102032. [Google Scholar] [CrossRef]
- Tian, T.; Luo, W.; Guo, L. Water quality prediction in the Yellow River source area based on the DeepTCN-GRU model. J. Water Process Eng. 2024, 59, 2214–7144. [Google Scholar] [CrossRef]
- Chen, Z.F.; Li, X.F. Water Quality Prediction Model for the Pearl River Estuary Based on BiLSTM Improved with Attention Mechanism. Environ. Sci. 2023, 45, 3205–3213. [Google Scholar]
- Sheng, C.; Yang, L.; Yang, W. Dissolved oxygen concentration prediction model based on Bi-GRU helped river. New Technol. New Prod. China 2025, 14, 122–124. [Google Scholar]
- Liao, X.; Deng, W. Combined Model Based on Two-stage Decomposition and Long-short-term Memory Network for Short-term Wind Speed Multi-step. Prediction. Inf. Control 2021, 50, 470–482. [Google Scholar]


| Index | Min | Max | Mean | SD |
|---|---|---|---|---|
| DOX | 5.5 | 12.05 | 8.933 | 1.320 |
| NH3N | 0.03 | 0.55 | 0.158 | 0.078 |
| pH | 6.79 | 8.94 | 8.25 | 0.420 |
| TN | 0.38 | 2.21 | 0.982 | 0.251 |
| Chi-Square Value | Degrees of Freedom | p-Value | Accept/Reject the Null Hypothesis |
|---|---|---|---|
| 0.0556 | 6561 | 1.0 | Accept |
| Model | Argument | Selection Basis and System Adjustment Process |
|---|---|---|
| Time Distributed activation (inputs) | Tanh | It is more stable than Sigmoid, ADAPTS to the feature transmission of water quality data, and alleviates the impact of extreme value fluctuations. |
| Time Distributed activation (attention) | Softmax | The standard normalization method of the temporal attention mechanism ensures that the sum of the attention weights is 1. |
| Weighted_inputs axis | 2 | Match the characteristic dimensions of four core water quality indicators. |
| Weighted_sum axis | 1 | Align the time step dimension and test that the temporal correlation breaks when axis = 0, so set it to 1. |
| Bi-GRU layer activation function | ReLU | It can alleviate gradient vanishing better than Sigmoid and Leaky ReLU and improve the capture accuracy of key temporal correlation. |
| Optimizer | Adam | Compared with SGD and RMSprop, it achieves a better balance between convergence speed and stability, adapting to the heterogeneity of exponential fluctuations. |
| Loss function | MSE | Amplifying the errors related to water quality safety is more in line with the early warning requirements of water sources than MAE. |
| Learning rate | 0.001 | [0.01, 0.001, 0.0001] In the test, 0.001 has the best generalization. |
| batch_size | 32 | [16, 32, 64] In the test, 32 training stability and data diversity. |
| Epoch | 100 | In the tests of [100, 200, 300], the training loss for 100 years was stable and there was no overfitting. |
| Weight attenuation | 1 × 10−5 | In the [1 × 10−4, 1 × 10−5, 1 × 10−6] tests, 1 × 10−5 can optimally increase R2 by 0.02 to 0.03. |
| Model | MSE | MAE | R2 | |
|---|---|---|---|---|
| DOX | GRU | 0.102 | 0.213 | 0.836 |
| Bi-GRU | 0.081 | 0.165 | 0.885 | |
| TA-GRU | 0.077 | 0.162 | 0.907 | |
| CNN-LSTM | 0.075 | 0.161 | 0.911 | |
| DeepTCN-LSTM | 0.073 | 0.160 | 0.916 | |
| TA-Bi-GRU | 0.072 | 0.159 | 0.932 | |
| pH | GRU | 0.028 | 0.0454 | 0.761 |
| Bi-GRU | 0.021 | 0.0336 | 0.804 | |
| TA-GRU | 0.012 | 0.0266 | 0.887 | |
| CNN-LSTM | 0.012 | 0.0253 | 0.892 | |
| DeepTCN-LSTM | 0.011 | 0.0237 | 0.896 | |
| TA-Bi-GRU | 0.010 | 0.0217 | 0.909 | |
| NH3N | GRU | 0.016 | 0.0104 | 0.882 |
| Bi-GRU | 0.012 | 0.0082 | 0.899 | |
| TA-GRU | 0.014 | 0.0102 | 0.908 | |
| CNN-LSTM | 0.013 | 0.0093 | 0.902 | |
| DeepTCN-LSTM | 0.012 | 0.0082 | 0.901 | |
| TA-Bi-GRU | 0.011 | 0.0072 | 0.917 | |
| TN | GRU | 0.0142 | 0.0463 | 0.916 |
| Bi-GRU | 0.0132 | 0.0375 | 0.932 | |
| TA-GRU | 0.0106 | 0.0391 | 0.926 | |
| CNN-LSTM | 0.0075 | 0.0372 | 0.932 | |
| DeepTCN-LSTM | 0.0042 | 0.0343 | 0.936 | |
| TA-Bi-GRU | 0.0026 | 0.0325 | 0.964 |
| Training Set Ratio | Model | Average MAE | Average MSE | Average R2 |
|---|---|---|---|---|
| 30% | GRU | 0.122 | 0.108 | 0.515 |
| Bi-GRU | 0.107 | 0.088 | 0.583 | |
| TA-GRU | 0.102 | 0.083 | 0.613 | |
| CNN-LSTM | 0.100 | 0.082 | 0.622 | |
| DeepTCN-LSTM | 0.096 | 0.079 | 0.645 | |
| TA-Bi-GRU | 0.087 | 0.073 | 0.692 | |
| 50% | GRU | 0.104 | 0.087 | 0.605 |
| Bi-GRU | 0.085 | 0.069 | 0.672 | |
| TA-GRU | 0.080 | 0.065 | 0.704 | |
| CNN-LSTM | 0.079 | 0.064 | 0.714 | |
| DeepTCN-LSTM | 0.076 | 0.061 | 0.731 | |
| TA-Bi-GRU | 0.073 | 0.058 | 0.775 | |
| 70% | GRU | 0.086 | 0.073 | 0.685 |
| Bi-GRU | 0.074 | 0.056 | 0.751 | |
| TA-GRU | 0.068 | 0.051 | 0.785 | |
| CNN-LSTM | 0.066 | 0.050 | 0.794 | |
| DeepTCN-LSTM | 0.063 | 0.048 | 0.810 | |
| TA-Bi-GRU | 0.058 | 0.044 | 0.839 |
| Forecast Horizon | Index | Model | MSE | MAE | R2 |
|---|---|---|---|---|---|
| 7 d | DOX | GRU | 0.185 | 0.302 | 0.768 |
| Bi-GRU | 0.142 | 0.248 | 0.812 | ||
| TA-GRU | 0.131 | 0.235 | 0.835 | ||
| CNN-LSTM | 0.127 | 0.231 | 0.84 | ||
| DeepTCN-LSTM | 0.122 | 0.226 | 0.845 | ||
| TA-Bi-GRU | 0.115 | 0.218 | 0.858 | ||
| pH | GRU | 0.045 | 0.0628 | 0.692 | |
| Bi-GRU | 0.036 | 0.0515 | 0.736 | ||
| TA-GRU | 0.021 | 0.0382 | 0.816 | ||
| CNN-LSTM | 0.02 | 0.0375 | 0.815 | ||
| DeepTCN-LSTM | 0.019 | 0.0368 | 0.827 | ||
| TA-Bi-GRU | 0.017 | 0.0342 | 0.830 | ||
| NH3N | GRU | 0.028 | 0.0215 | 0.808 | |
| Bi-GRU | 0.022 | 0.0168 | 0.825 | ||
| TA-GRU | 0.024 | 0.0198 | 0.832 | ||
| CNN-LSTM | 0.023 | 0.0189 | 0.826 | ||
| DeepTCN-LSTM | 0.022 | 0.0168 | 0.825 | ||
| TA-Bi-GRU | 0.019 | 0.0151 | 0.845 | ||
| TN | GRU | 0.0285 | 0.0638 | 0.835 | |
| Bi-GRU | 0.0268 | 0.0598 | 0.850 | ||
| TA-GRU | 0.0252 | 0.0572 | 0.862 | ||
| CNN-LSTM | 0.0249 | 0.0567 | 0.860 | ||
| DeepTCN-LSTM | 0.0241 | 0.0551 | 0.875 | ||
| TA-Bi-GRU | 0.0218 | 0.0502 | 0.893 | ||
| 10 d | DOX | GRU | 0.248 | 0.365 | 0.692 |
| Bi-GRU | 0.182 | 0.302 | 0.738 | ||
| TA-GRU | 0.195 | 0.288 | 0.763 | ||
| CNN-LSTM | 0.176 | 0.282 | 0.765 | ||
| DeepTCN-LSTM | 0.17 | 0.275 | 0.772 | ||
| TA-Bi-GRU | 0.158 | 0.263 | 0.762 | ||
| pH | GRU | 0.062 | 0.0735 | 0.615 | |
| Bi-GRU | 0.052 | 0.0638 | 0.658 | ||
| TA-GRU | 0.032 | 0.0478 | 0.725 | ||
| CNN-LSTM | 0.031 | 0.047 | 0.731 | ||
| DeepTCN-LSTM | 0.03 | 0.0461 | 0.735 | ||
| TA-Bi-GRU | 0.026 | 0.0435 | 0.740 | ||
| NH3N | GRU | 0.038 | 0.0278 | 0.725 | |
| Bi-GRU | 0.034 | 0.0258 | 0.748 | ||
| TA-GRU | 0.031 | 0.0244 | 0.756 | ||
| CNN-LSTM | 0.032 | 0.0249 | 0.745 | ||
| DeepTCN-LSTM | 0.031 | 0.0225 | 0.748 | ||
| TA-Bi-GRU | 0.027 | 0.0208 | 0.783 | ||
| TN | GRU | 0.0392 | 0.0765 | 0.740 | |
| Bi-GRU | 0.0378 | 0.0702 | 0.755 | ||
| TA-GRU | 0.0358 | 0.0731 | 0.763 | ||
| CNN-LSTM | 0.0358 | 0.0702 | 0.775 | ||
| DeepTCN-LSTM | 0.0345 | 0.0681 | 0.782 | ||
| TA-Bi-GRU | 0.0305 | 0.0658 | 0.804 | ||
| 15 d | DOX | GRU | 0.325 | 0.428 | 0.605 |
| Bi-GRU | 0.268 | 0.372 | 0.652 | ||
| TA-GRU | 0.251 | 0.355 | 0.672 | ||
| CNN-LSTM | 0.243 | 0.348 | 0.678 | ||
| DeepTCN-LSTM | 0.235 | 0.34 | 0.685 | ||
| TA-Bi-GRU | 0.22 | 0.328 | 0.715 | ||
| pH | GRU | 0.085 | 0.0862 | 0.523 | |
| Bi-GRU | 0.075 | 0.0785 | 0.565 | ||
| TA-GRU | 0.048 | 0.0592 | 0.617 | ||
| CNN-LSTM | 0.047 | 0.0583 | 0.615 | ||
| DeepTCN-LSTM | 0.046 | 0.0572 | 0.622 | ||
| TA-Bi-GRU | 0.041 | 0.0548 | 0.647 | ||
| NH3N | GRU | 0.052 | 0.0352 | 0.620 | |
| Bi-GRU | 0.048 | 0.0338 | 0.642 | ||
| TA-GRU | 0.045 | 0.0305 | 0.653 | ||
| CNN-LSTM | 0.046 | 0.0329 | 0.659 | ||
| DeepTCN-LSTM | 0.045 | 0.0305 | 0.667 | ||
| TA-Bi-GRU | 0.039 | 0.0285 | 0.693 | ||
| TN | GRU | 0.0538 | 0.0926 | 0.585 | |
| Bi-GRU | 0.0502 | 0.0875 | 0.592 | ||
| TA-GRU | 0.0521 | 0.0902 | 0.613 | ||
| CNN-LSTM | 0.0502 | 0.0875 | 0.620 | ||
| DeepTCN-LSTM | 0.0485 | 0.0848 | 0.638 | ||
| TA-Bi-GRU | 0.0458 | 0.0825 | 0.680 | ||
| 30 d | DOX | GRU | 0.412 | 0.495 | 0.482 |
| Bi-GRU | 0.352 | 0.442 | 0.525 | ||
| TA-GRU | 0.331 | 0.42 | 0.54 | ||
| CNN-LSTM | 0.322 | 0.412 | 0.545 | ||
| DeepTCN-LSTM | 0.311 | 0.401 | 0.557 | ||
| TA-Bi-GRU | 0.295 | 0.385 | 0.585 | ||
| pH | GRU | 0.118 | 0.0985 | 0.384 | |
| Bi-GRU | 0.105 | 0.0921 | 0.427 | ||
| TA-GRU | 0.072 | 0.0735 | 0.452 | ||
| CNN-LSTM | 0.07 | 0.0723 | 0.455 | ||
| DeepTCN-LSTM | 0.068 | 0.0708 | 0.465 | ||
| TA-Bi-GRU | 0.062 | 0.0682 | 0.520 | ||
| NH3N | GRU | 0.07 | 0.0438 | 0.494 | |
| Bi-GRU | 0.062 | 0.0395 | 0.515 | ||
| TA-GRU | 0.065 | 0.0418 | 0.519 | ||
| CNN-LSTM | 0.064 | 0.0409 | 0.525 | ||
| DeepTCN-LSTM | 0.062 | 0.0395 | 0.527 | ||
| TA-Bi-GRU | 0.055 | 0.0372 | 0.545 | ||
| TN | GRU | 0.0725 | 0.1128 | 0.455 | |
| Bi-GRU | 0.0682 | 0.1075 | 0.462 | ||
| TA-GRU | 0.0705 | 0.1102 | 0.469 | ||
| CNN-LSTM | 0.0682 | 0.1075 | 0.470 | ||
| DeepTCN-LSTM | 0.0665 | 0.1048 | 0.480 | ||
| TA-Bi-GRU | 0.0638 | 0.1025 | 0.550 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Guo, L.; Tian, Q. Water Quality Prediction Model Based on Temporal Attentive Bidirectional Gated Recurrent Unit Model. Sustainability 2025, 17, 9155. https://doi.org/10.3390/su17209155
Yang H, Guo L, Tian Q. Water Quality Prediction Model Based on Temporal Attentive Bidirectional Gated Recurrent Unit Model. Sustainability. 2025; 17(20):9155. https://doi.org/10.3390/su17209155
Chicago/Turabian StyleYang, Hongyu, Lei Guo, and Qingqing Tian. 2025. "Water Quality Prediction Model Based on Temporal Attentive Bidirectional Gated Recurrent Unit Model" Sustainability 17, no. 20: 9155. https://doi.org/10.3390/su17209155
APA StyleYang, H., Guo, L., & Tian, Q. (2025). Water Quality Prediction Model Based on Temporal Attentive Bidirectional Gated Recurrent Unit Model. Sustainability, 17(20), 9155. https://doi.org/10.3390/su17209155


_Li.png)


