Incentive-Based Peak Demand Regulation with Intelligent Parking Management for Enhanced Sustainability
Abstract
1. Introduction
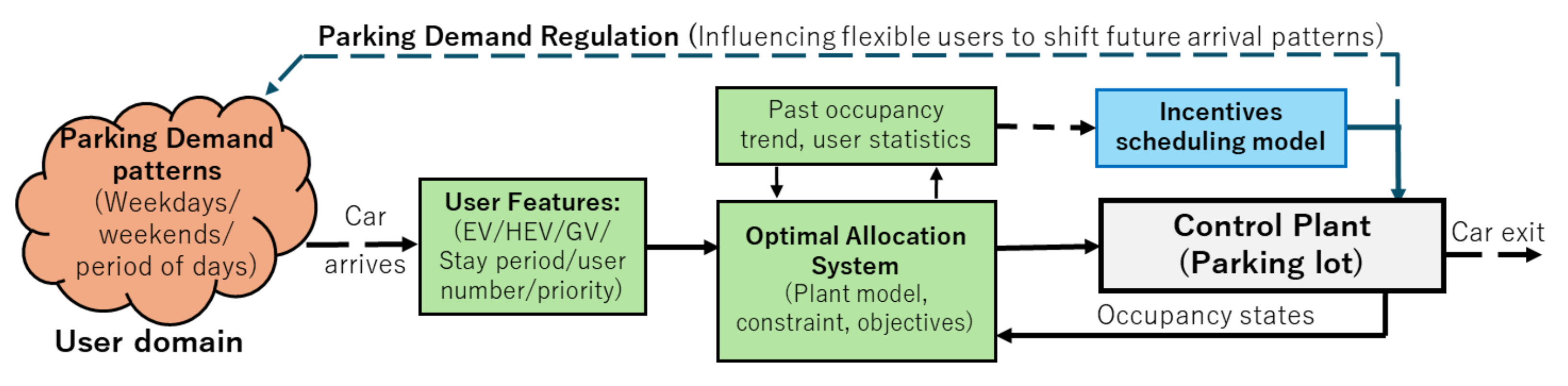
2. Incentive-Based Parking Management System
2.1. Formulation of Incentive Model
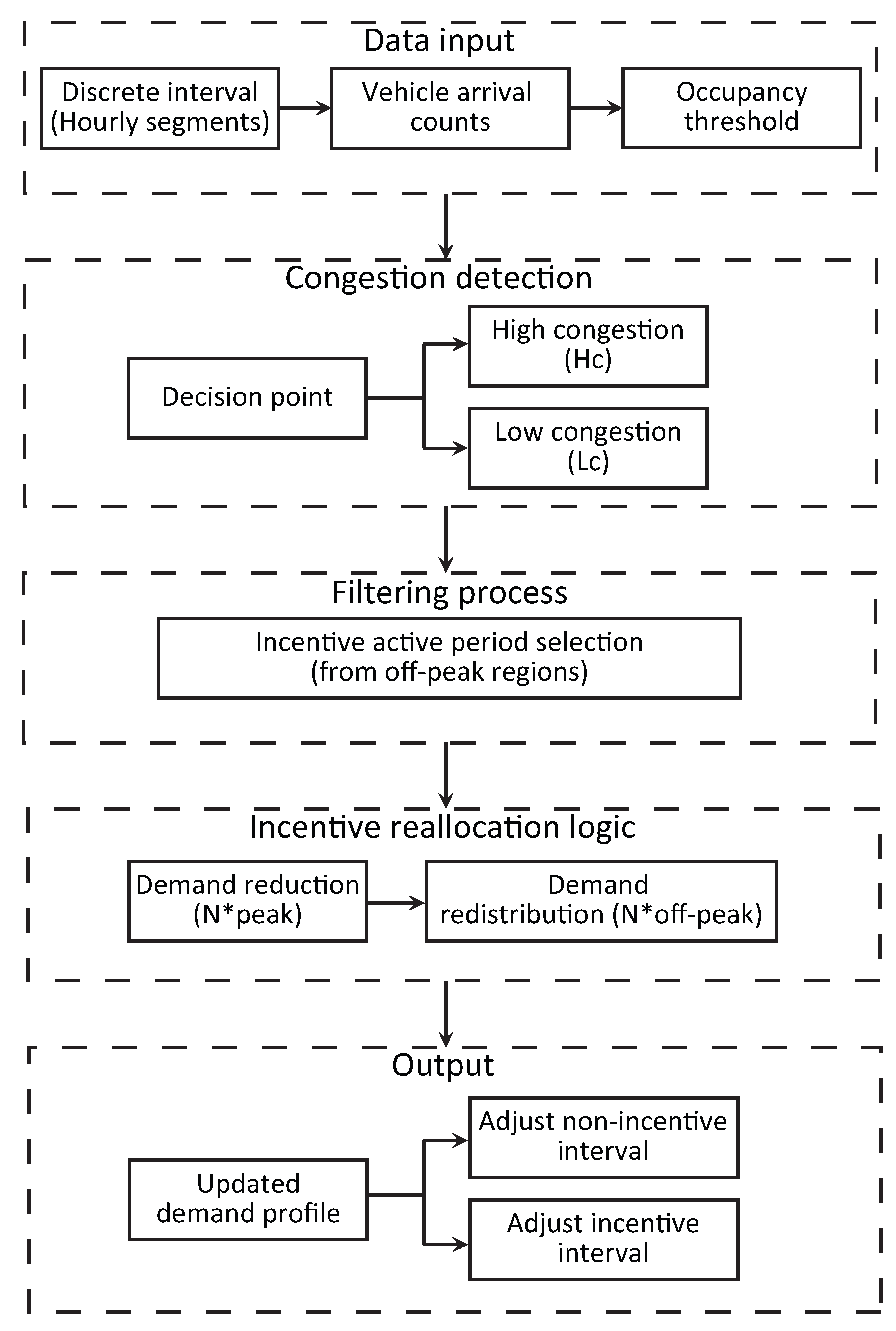
2.1.1. Data Input
- (i)
- Vehicle Arrival Counts: The number of vehicles entering the parking system during each interval. The arrival vehicle count is as follows,Here, Equation (1) defines the incoming vehicles within a discrete time step . Specifically, it includes all users n whose arrival times fall within the interval bounded by the start time and the finish time . In other words, the system divides vehicles into time segments based on when they enter the parking facility, allowing time-dependent demand modeling.
- (ii)
- Occupancy Threshold: A predefined upper limit of acceptable parking utilization, beyond which the system considers the lot to be congested (e.g., percentage (%) of total capacity).
2.1.2. Congestion Detection
- (i)
- High congestion: If the measured occupancy exceeds the threshold , the interval is flagged as a high congestion region .
- (ii)
- Low congestion: represents the off-peak regions where parking occupancy remains below the congestion threshold. These intervals are candidates for applying incentives to shift demand.
2.1.3. Filtering Process
2.1.4. Incentive Reallocation Logic
- (i)
- Ratio of flexible users (): This parameter represents the overall proportion of flexible users within the total population over all days. It quantifies how many users in the system, on average, have the potential to adjust their parking time or behavior. A higher value of indicates a greater share of users who could be responsive to incentive-based interventions.
- (ii)
- Fraction of incentive-responsive flexible users (): This parameter measures the percentage increase in flexible user participation on incentive days compared to the overall average. It captures the behavioral shift caused by the incentive, indicating how many additional flexible users responded positively (i.e., shifted their behavior) due to the presence of an incentive. A higher value of reflects the greater effectiveness of the incentive mechanism in influencing user decisions.
- (i)
- Demand reduction :
- (ii)
- Demand redistribution :
2.1.5. Output
2.2. Optimization System
2.2.1. Primary Optimization
- (i)
- Greedy (Walk-Minimizing) Method: Each arriving car is assigned to the available parking spot that minimizes THE walking distance to the destination entrance (i.e., the spot closest to the entrance). This method prioritizes user comfort by minimizing walking, effectively employing a greedy strategy for convenience.
- (ii)
- Random (Uncontrolled) Method: Each arriving car is assigned to a randomly chosen available spot. This approach does not optimize any particular objective but can serve as a neutral baseline; in practice, it may help avoid the competitive behavior of everyone aiming for the same preferred spots.
- (iii)
- Balanced Objective Method: Each arriving car is assigned to a spot by considering a combination of driving distance and walking distance, giving both factors equal (or at least significant) weight. In this approach, neither driving nor walking distance is ignored; the goal is to strike a compromise between minimizing travel distance within the lot (for lower emissions) and minimizing walking distance (for higher user comfort).
- (a)
- In the greedy method (i), we set (ignoring driving distance entirely). The cost then reduces to just , and the allocation decision for car n is to choose the spot with the minimum walking distance:Here, denotes the set of available parking spaces for allocation. The shortcomings of this method are that it can lead to many drivers converging on the few closest spots, potentially causing conflicts and localized congestion near the entrance during peak periods.
- (b)
- The random method (ii) does not use the cost function ; instead, is selected uniformly at random from the available spots. This method serves as a control case that avoids the biased use of particular spots. Notably, a random allocation can, in some situations, outperform a naive greedy approach by distributing vehicles more evenly, thereby preventing excessive crowding in any one area of the lot.
- (c)
- For the balanced method (iii), we choose an intermediate (for instance, for equal weighting) to account for both driving and walking distances. In this case, the assignment for car n is based on minimizing the combined cost:This method avoids the extreme biases of the purely greedy approach; however, it still does not differentiate between different types of vehicles or the number of passengers.
2.2.2. Proposed Optimization Scheme with Incentive Benefit
2.3. Parking Allocation System
3. Simulation Results
3.1. Simulation Framework and Setup
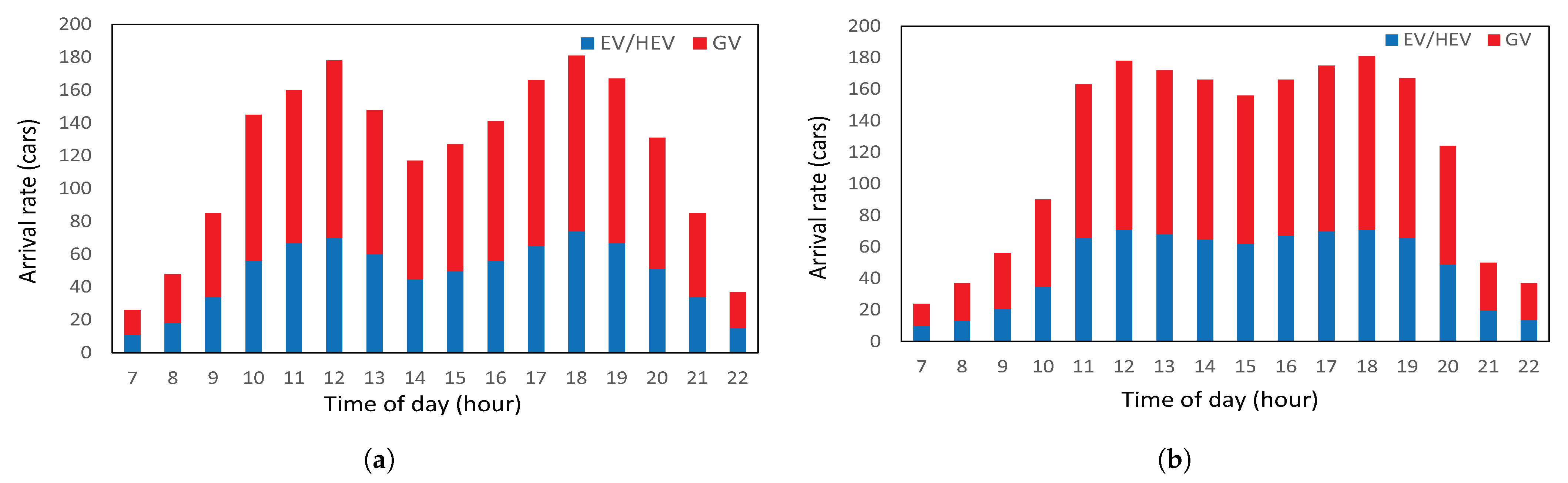
3.2. Demand (Arrival) Pattern Characteristics in Simulation
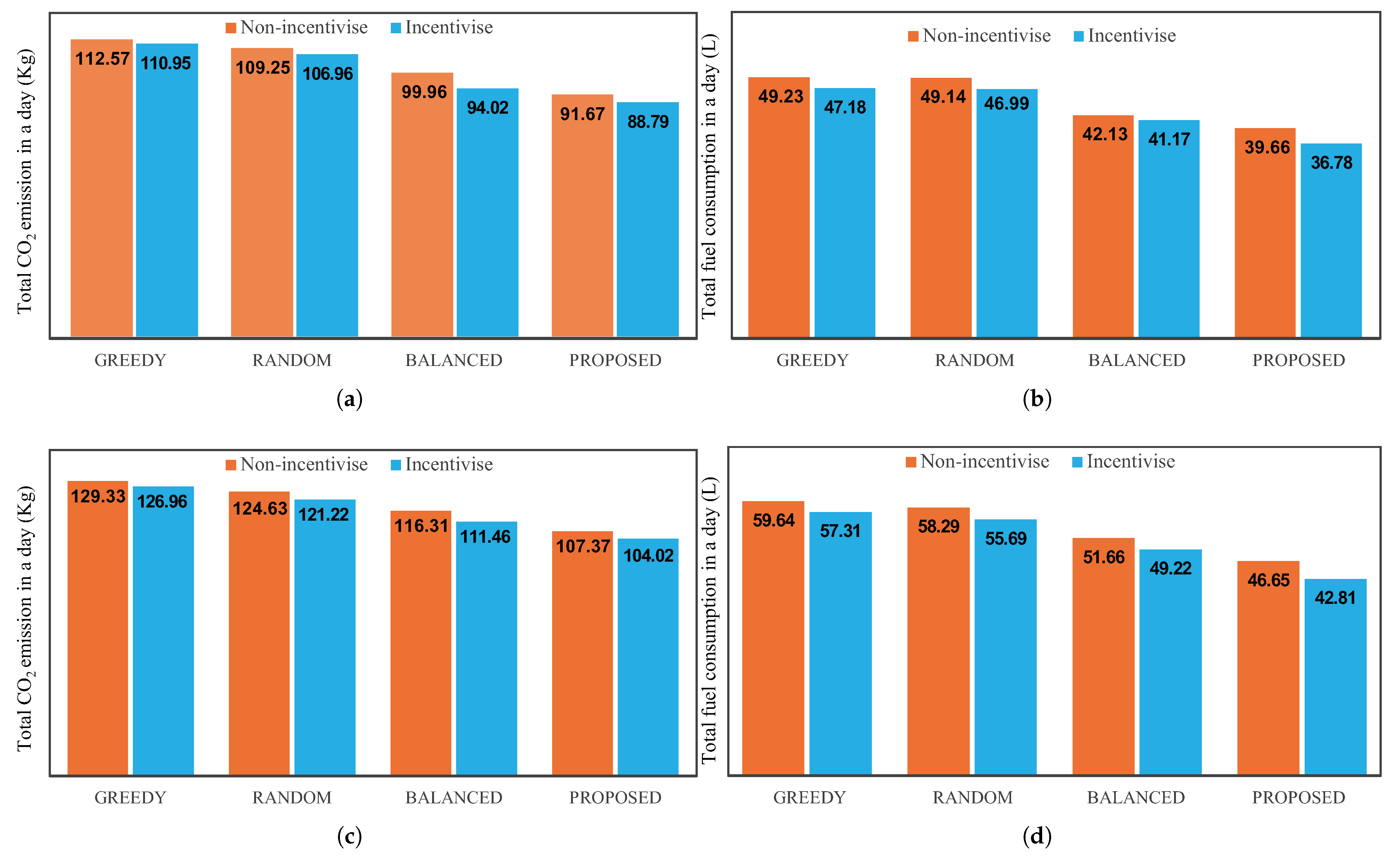
3.3. Calculation of Emission and Fuel Consumption
3.4. Real Parking Survey and Influence of Incentive Model
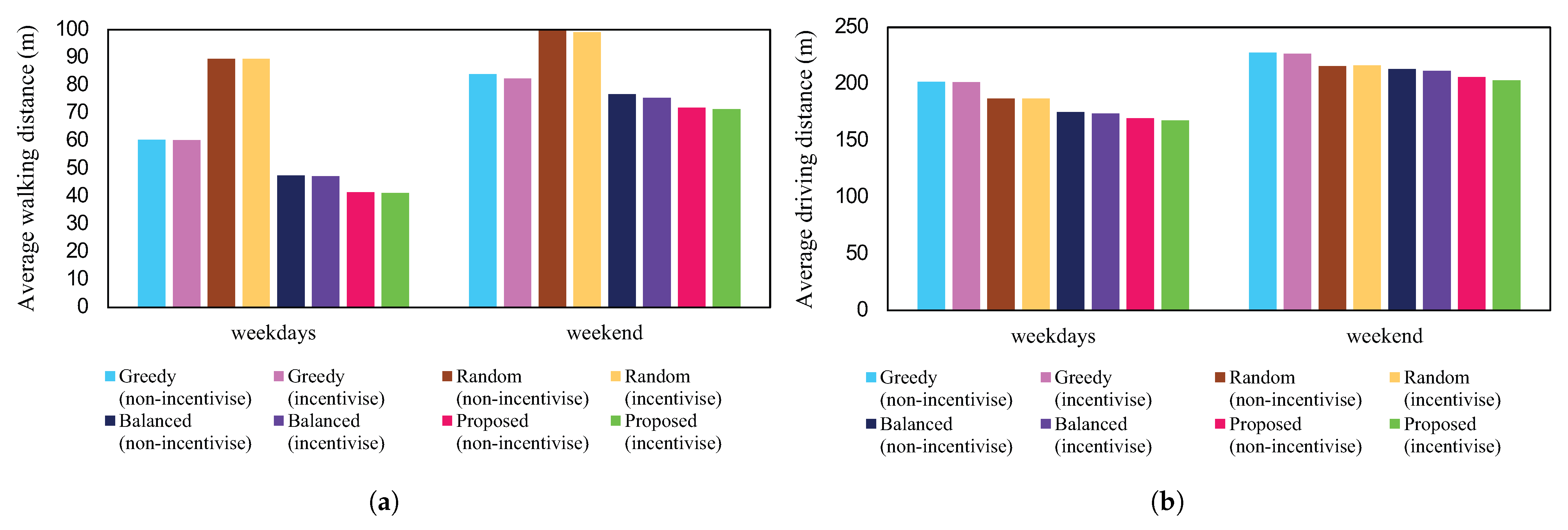
3.5. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, S.; Sun, C.; Liu, N. Road congestion and air pollution -analysis of spatial and temporal congestion effects. Sci. Total Environ. 2024, 945, 173896. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Feng, W.; Yuan, H. Multimode Traffic Travel Behavior Characteristics Analysis and Congestion Governance Research. J. Adv. Transp. 2020, 2020, 1–8. [Google Scholar] [CrossRef]
- Zang, J.; Jiao, P.; Liu, S.; Zhang, X.; Song, G.; Yu, L. Identifying traffic congestion patterns of urban road network based on Traffic Performance index. Sustainability 2023, 15, 948. [Google Scholar] [CrossRef]
- Meena, K.K.; Goswami, A.K. A review of air pollution exposure impacts on travel behaviour and way forward. Transp. Policy 2024, 154, 48–60. [Google Scholar] [CrossRef]
- Ajayi, S.A.; Adams, C.A.; Dumedah, G.; Adebanji, O.A.; Ababio-Donkor, A.; Ackaah, W.; Kehinde, A. Public perceptions of vehicular traffic emissions on Health Risk in Lagos metropolis nigeria: A critical survey. Heliyon 2023, 9, e15712. [Google Scholar] [CrossRef]
- Paiva, S.; Ahad, M.; Tripathi, G.; Feroz, N.; Casalino, G. Enabling Technologies for Urban Smart Mobility: Recent trends, opportunities and challenges. Sensors 2021, 21, 2143. [Google Scholar] [CrossRef]
- Kirschner, F.; Lanzendorf, M. Parking management for promoting sustainable transport in urban neighbourhoods. A review of existing policies and challenges from a German perspective. Transp. Rev. 2019, 40, 54–75. [Google Scholar] [CrossRef]
- Chen, R.; Gao, G.; Kang, L.-J.; Zhang, L.-Y. Efficiency and equity analysis on Parking Reservation. Transp. Res. Part E Logist. Transp. Rev. 2024, 187, 103606. [Google Scholar] [CrossRef]
- Liu, W.-J.; Li, Z.-C.; Yang, H. Gasoline and electric vehicle ownership rationing over time: Lottery vs. first-come-first-served schemes. Transp. Res. Part B Methodol. 2024, 186, 102995. [Google Scholar] [CrossRef]
- Verma, S.K.; Verma, R.; Singh, B.K.; Sinha, R.S. Management of Intelligent Transportation Systems and Advanced Technology. In Intelligent Transportation System and Advanced Technology; Energy, Environment, and Sustainability; Springer: Berlin/Heidelberg, Germany, 2024; pp. 159–175. [Google Scholar]
- Elassy, M.; Al-Hattab, M.; Takruri, M.; Badawi, S. Intelligent Transportation Systems for Sustainable Smart Cities. Transp. Eng. 2024, 16, 100252. [Google Scholar] [CrossRef]
- Shen, T.; Hua, K.; Liu, J. Optimized public parking location modelling for Green Intelligent Transportation System using genetic algorithms. IEEE Access 2019, 7, 176870–176883. [Google Scholar] [CrossRef]
- Musa, A.A.; Malami, S.I.; Alanazi, F.; Ounaies, W.; Alshammari, M.; Haruna, S.I. Sustainable Traffic Management for smart cities using internet-of-things-oriented intelligent transportation systems (ITS): Challenges and recommendations. Sustainability 2023, 15, 9859. [Google Scholar] [CrossRef]
- Luque-Vega, L.F.; Michel-Torres, D.A.; Lopez-Neri, E.; Carlos-Mancilla, M.A.; González-Jiménez, L.E. IOT smart parking system based on the visual-aided smart vehicle presence sensor: Spin-V. Sensors 2020, 20, 1476. [Google Scholar] [CrossRef]
- Jabbar, W.A.; Wei, C.W.; Azmi, N.A.; Haironnazli, N.A. An IOT raspberry pi-based parking management system for Smart Campus. Internet Things 2021, 14, 100387. [Google Scholar] [CrossRef]
- Al-Turjman, F.; Malekloo, A. Smart parking in IOT-enabled cities: A survey. Sustain. Cities Soc. 2019, 49, 101608. [Google Scholar] [CrossRef]
- Xu, D.; Shi, Y.; Ji, Z. Model-free adaptive discrete-time integral sliding-mode-constrained-control for autonomous 4WMV Parking Systems. IEEE Trans. Ind. Electron. 2018, 65, 834–843. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, C.-Y.; Wei, H.-Y. Parking reservation auction for parked vehicle assistance in Vehicular Fog Computing. IEEE Trans. Veh. Technol. 2019, 68, 3126–3139. [Google Scholar] [CrossRef]
- Lin, T.; Rivano, H.; Le Mouel, F. A survey of Smart Parking Solutions. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3229–3253. [Google Scholar] [CrossRef]
- Lu, K.; Zheng, B.; Shi, J.; Xu, Y. Automated optimal parking slot prediction using Deep Learning and digital twin technology aided parking space management for Material Science Application. Alex. Eng. J. 2025, 122, 229–242. [Google Scholar] [CrossRef]
- Su, Z.; Liu, X.; Li, H.; Zhang, T.; Liu, X.; Jiang, Y. A vehicle trajectory-based parking location recognition and inference method: Considering both travel action and intention. Sustain. Cities Soc. 2025, 119, 106088. [Google Scholar] [CrossRef]
- Tsiropoulou, E.E.; Baras, J.S.; Papavassiliou, S.; Sinha, S. RFID-based Smart Parking Management System. Cyber-Phys. Syst. 2017, 3, 22–41. [Google Scholar] [CrossRef]
- Abdulkader, O.; Bamhdi, A.M.; Thayananthan, V.; Jambi, K.; Alrasheedi, M. A novel and secure smart parking management system (SPMS) based on integration of WSN, RFID, and IOT. In Proceedings of the 15th Learning and Technology Conference (L&T), Jeddah, Saudi Arabia, 25–26 February 2018; pp. 102–106. [Google Scholar]
- Chen, H.; Wu, H.; Li, H.; Chen, F.; Shui, S.; Li, Z. Bi-level optimal scheduling of Integrated Energy Systems considering incentive-based demand response and Green Certificate-Carbon Trading Mechanisms. Energy Rep. 2025, 13, 330–344. [Google Scholar] [CrossRef]
- Gao, W.; Liang, X.; Zhao, F.; Wang, Z. Research on demand response mechanism based on Price Incentive Driven Directrix Load. In Proceedings of the 4th New Energy and Energy Storage System Control Summit Forum (NEESSC), Hohhot, China, 9–31 August 2024; pp. 231–235. [Google Scholar]
- Bakibillah, A.S.M.; Paw, Y.F.; Kamal, M.A.S.; Susilawati, S.; Tan, C.P. An incentive based dynamic ride-sharing system for Smart Cities. Smart Cities 2021, 4, 532–547. [Google Scholar] [CrossRef]
- Tang, Q.; Hu, X. Triggering behavior changes with information and incentives: An active traffic and demand management-oriented review. In The Evolving Impacts of ICT on Activities and Travel Behavior; Advances in Transport Policy and Planning; Elsevier: Amsterdam, The Netherlands, 2019; pp. 209–250. [Google Scholar]
- Tian, Y.; Li, Y.; Sun, J.; Ye, J. Characterizing favored users of incentive-based Traffic Demand Management Program. Transp. Policy 2021, 105, 94–102. [Google Scholar] [CrossRef]
- Metropia Mobility as a Service. Available online: https://www.metropia.com/ (accessed on 26 August 2025).
- Sakib, N.; Bakibillah, A.S.M.; Kamal, M.A.S.; Yamada, K. An incentive-based parking management system for reducing congestion during peak demands. In Proceedings of the SICE International Symposium on Control Systems (SICE ISCS), Osaka, Japan, 3–5 March 2025; pp. 113–118. [Google Scholar]
- Sakib, N.; Bakibillah, A.S.M.; Kamal, M.A.S.; Yamada, K. Intelligent parking management for sustainable society: A data-driven demand elasticity incentive model. Sustain. Cities Soc. 2025, 106864. [Google Scholar] [CrossRef]
- Asitha, K.S.; Khoo, H.L. Incentivised travel and mobile application as multiple policy intervention for Mode Shift. KSCE J. Civ. Eng. 2020, 24, 3074–3091. [Google Scholar] [CrossRef]
- Sakib, N.; Bakibillah, A.S.M.; Susilawati, S.; Kamal, M.A.S.; Yamada, K. Eco-friendly smart car parking management system with enhanced sustainability. Sustainability 2024, 16, 4145. [Google Scholar] [CrossRef]
- Japan Electric Vehicles. International Trade Administration. Available online: https://www.trade.gov/market-intelligence/japan-electric-vehicles (accessed on 25 August 2025).
- Rakha, H.; Ahn, K.; Trani, A. Development of VT-micro model for estimating Hot Stabilized Light Duty Vehicle and truck emissions. Transp. Res. Part D Transp. Environ. 2004, 9, 49–74. [Google Scholar] [CrossRef]
- Bakibillah, A.S.M.; Kamal, M.A.S.; Tan, C.P.; Hayakawa, T.; Imura, J. Optimal eco-driving scheme for reducing energy consumption and carbon emissions on curved roads. Heliyon 2024, 10, e23586. [Google Scholar] [CrossRef]
- Lu, C.; Liu, C. Ecological control strategy for cooperative autonomous vehicle in mixed traffic considering linear stability. J. Intell. Connect. Veh. 2021, 4, 115–124. [Google Scholar] [CrossRef]
- Makarova, I.; Mavrin, V.; Sadreev, D.; Buyvol, P.; Boyko, A.; Belyaev, E. Rational organization of urban parking using microsimulation. Infrastructures 2022, 7, 140. [Google Scholar] [CrossRef]
| Method | Period | Walking | Distance (m) | Driving | Distance (m) |
|---|---|---|---|---|---|
| Weekdays | Weekend | Weekdays | Weekend | ||
| Greedy | Peak | 61.55 | 85.69 | 204.94 | 229.16 |
| (non-incentivize) | Off-peak | 59.16 | 82.39 | 198.69 | 226.21 |
| Greedy | Peak | 58.89 | 80.67 | 201.02 | 224.86 |
| (incentivize) | Off-peak | 61.48 | 84.31 | 202.11 | 228.22 |
| Random | Peak | 91.20 | 101.33 | 189.62 | 216.00 |
| (non-incentivize) | Off-peak | 87.66 | 98.06 | 184.65 | 215.60 |
| Random | Peak | 88.23 | 97.36 | 187.25 | 214.81 |
| (incentivize) | Off-peak | 90.90 | 100.79 | 186.63 | 217.65 |
| Balanced | Peak | 50.15 | 77.61 | 188.94 | 214.23 |
| (non-incentivize) | Off-peak | 45.04 | 75.92 | 161.68 | 212.45 |
| Balanced | Peak | 47.57 | 74.08 | 183.17 | 210.00 |
| (incentivize) | Off-peak | 46.83 | 76.95 | 164.55 | 213.26 |
| Proposed | Peak | 43.26 | 71.33 | 171.69 | 207.83 |
| (non-incentivize) | Off-peak | 39.81 | 72.68 | 167.63 | 204.44 |
| Proposed | Peak | 40.83 | 68.26 | 166.38 | 200.31 |
| (incentivize) | Off-peak | 41.55 | 74.55 | 169.35 | 205.91 |
| Method | Walking | Distance (m) | Driving | Distance (m) |
|---|---|---|---|---|
| Weekdays | Weekend | Weekdays | Weekend | |
| Greedy | 60.36 | 84.04 | 201.81 | 227.69 |
| (non-incentivize) | (Base) | (Base) | (Base) | (Base) |
| Proposed | 41.54 | 72.00 | 169.66 | 206.14 |
| (non-incentivize) | (−31.18%) | (−14.33%) | (−15.93%) | (−9.46%) |
| Proposed | 41.19 | 71.41 | 167.86 | 203.11 |
| (incentivize) | (−31.76%) | (−15.03%) | (−16.83%) | (−10.80%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakib, N.; Bakibillah, A.S.M.; Kamal, M.A.S.; Yamada, K. Incentive-Based Peak Demand Regulation with Intelligent Parking Management for Enhanced Sustainability. Sustainability 2025, 17, 9093. https://doi.org/10.3390/su17209093
Sakib N, Bakibillah ASM, Kamal MAS, Yamada K. Incentive-Based Peak Demand Regulation with Intelligent Parking Management for Enhanced Sustainability. Sustainability. 2025; 17(20):9093. https://doi.org/10.3390/su17209093
Chicago/Turabian StyleSakib, Nazmus, A. S. M. Bakibillah, Md Abdus Samad Kamal, and Kou Yamada. 2025. "Incentive-Based Peak Demand Regulation with Intelligent Parking Management for Enhanced Sustainability" Sustainability 17, no. 20: 9093. https://doi.org/10.3390/su17209093
APA StyleSakib, N., Bakibillah, A. S. M., Kamal, M. A. S., & Yamada, K. (2025). Incentive-Based Peak Demand Regulation with Intelligent Parking Management for Enhanced Sustainability. Sustainability, 17(20), 9093. https://doi.org/10.3390/su17209093








