1. Introduction
With the depletion of traditional fossil fuels and the advancement of renewable energy technologies, countries worldwide are actively reshaping their energy mix to diminish their reliance on conventional fossil-based energy sources. The development of integrated energy systems (IES), enhancing energy efficiency, and boosting the capacity to integrate intermittent renewable sources via heterogeneous energy networks, represents pivotal pathways towards achieving a low-carbon, sustainable energy future [
1,
2].
Certain power grids in China’s “Three North” regions feature a high penetration of distributed renewable energy and are coupled with intricate gas and heat networks, forming a typical multi-energy flow integrated energy system. Power-to-gas (P2G) technology converts surplus wind power or off-peak electricity into hydrogen, which can be further synthesized into methane. This enables a two-way interaction between the power grid and the gas grid, offering a novel pathway for renewable energy integration [
3]. Ref. [
4] proposed a two-stage joint operation strategy involving P2G and Hydrogen fuel cells (HFCs) to promote wind power utilization while reducing energy losses and carbon emissions. Ref. [
5] introduced P2G and carbon capture technologies, proposing an optimized scheduling strategy for an IES with carbon capture-electricity-to-gas coupling, which enhanced the renewable energy absorption rate. Addressing photovoltaic (PV) uncertainty, Ref. [
6] demonstrated that the joint operation of hydrogen fuel cells and cogeneration units improves the rationality of PV consumption and equipment output. Ref. [
7] utilized the thermal energy storage characteristics of heating pipelines to improve the operational flexibility of combined heat and power (CHP) systems and constructed a flexibility evaluation method for generalized thermal energy storage models to quantitatively analyze the flexibility of district heating networks.
The primary problem facing the integrated energy system is the coordinated optimization and scheduling of multi-energy flows. Ref. [
8] established a comprehensive optimization model, which was solved by the non-dominated ranking genetic algorithm (NSGA-II) with the goals of operating cost, carbon emissions, and energy efficiency utilization, and the Pareto optimal frontier solution set was output. Ref. [
9] established a steady-state energy flow and carbon flow calculation model for the integrated electricity–gas–hydrogen energy system and performed iterative calculations using the Newtonian method. Ref. [
10] applied the fully distributed internal point conjugate gradient method to the problem of correcting equations in the distributed optimal scheduling of integrated electrical energy systems. Ref. [
11] studied the scheduling strategy of the integrated electrical–gas–thermal energy system at multiple time scales and constructed a data-driven optimization model for the split-brud rod. Ref. [
12] used an improved multi-objective optimization algorithm to enhance the operational economy and energy efficiency and to reduce the carbon emission level of the integrated electric–heat–hydrogen–cooling energy system. Ref. [
13] addressed the uncertainty and correlation between wind power and electricity/gas loads by calculating the probabilistic optimal power flow model of the electric-gas interconnection system using the three-point estimation method of Nataf transformation. Ref. [
14] considered the influence of wind and solar uncertainty and constructed a stochastic scheduling model for integrated energy virtual power plants. This model couples “coal-fired” power generation with electricity–carbon–hydrogen–chemical coupling, aiming to maximize benefits.
In the establishment of the optimal scheduling model, the stochastic programming method shows obvious advantages in reducing the operating cost of the system compared with the deterministic method. Ref. [
15] considered adding hydrogen vehicle emission reductions to carbon trading and used the Monte Carlo algorithm to generate scenarios for wind and solar output uncertainty. Stochastic programming uses random sampling, chance constraint generation, and other methods to convert uncertainty problems into deterministic models and calculate the operating status of the system through multiple scenarios. However, the large number of scenarios increases both the computational burden and solving difficulty. Therefore, it is necessary to balance calculation accuracy with computational load. Robust optimization is mainly aimed at optimizing the operation of the system in extreme scenarios. Ref. [
16] used stochastic optimization and robust optimization to deal with the uncertainty of load-side power generation measurement. It also added a coordination strategy to the second-stage optimization objectives, bringing the real-time optimization results closer to the global optimization value. However, the former faces a bottleneck in computational efficiency due to its heavy reliance on scenario generation, while the latter suffers from model complexity and a difficult trade-off between economic efficiency and conservatism. More importantly, these traditional methods belong to “static” optimization—once the model or parameters are determined, they struggle to adaptively learn new uncertainty patterns online, demonstrating limited capability in coping with continuously dynamic real-world environments.
In recent years, artificial intelligence technology has flourished, with reinforcement learning (RL) as a model-free approach. It does not need to understand environmental changes in advance, has strong adaptability to many uncertainties and interferences, makes optimal decisions through continuous learning and interaction, and has good generalization ability, so it is more and more important in the optimal control of the power system. Ref. [
17] used a deep Q-network (DQN) to adaptively respond to random fluctuations in power generation and demand, solving the energy management problem. Ref. [
18] used the Nash equilibrium Q-learning algorithm to enable the coordinated scheduling of integrated energy microgrids. Ref. [
19] used the double deep expected Q-network (DDEQN) algorithm to efficiently solve the real-time stochastic economic scheduling problem of microgrids. However, the above reinforcement learning methods often discretize actions, which not only reduces the accuracy of optimization decisions but also increases the number of discrete actions exponentially due to the increase in action dimensions, causing “dimensional disasters” that are difficult to solve. At present, some studies have begun to explore continuous control deep reinforcement learning models. Ref. [
20] used the deep deterministic policy gradient (DDPG) algorithm to enable dynamic regulation of the integrated electrical–heat–gas energy system. Ref. [
21] used the DDPG algorithm to solve the continuous control problem in the coordinated and optimized operation of active distribution networks. However, existing studies still exhibit two main limitations: Firstly, at the algorithmic level, the DDPG algorithm itself suffers from issues such as hypersensitivity to hyperparameters, limited exploration efficiency, and Q-value overestimation, which may lead to training instability and suboptimal policy performance; secondly, at the system modeling level, most existing works focus on traditional electricity–heat–gas-coupled systems, failing to deeply integrate hydrogen energy as a key low-carbon carrier with carbon capture, utilization, and trading mechanisms, thereby restricting the system’s deep decarbonization and operational flexibility under the “dual-carbon” goals.
Based on the Soft Actor–Critic (SAC) framework, this paper constructs a deep reinforcement learning method for the operation of the hydrogen-coupled electrothermal integrated energy system (HCEH-IES). This method enables the algorithm to adaptively learn the characteristics of uncertain variations in wind power, photovoltaics, and various loads, thereby realizing optimal system scheduling under multiple scenarios.
(1) An HCEH-IES model is constructed, with the optimization objective being the minimization of the sum of the system’s comprehensive operating costs, carbon capture and utilization costs, and carbon trading costs.
(2) The optimal scheduling of the integrated energy system is formulated as a Markov Decision Process (MDP), and the system’s state space, action space, and reward function are defined.
(3) The SAC algorithm is utilized to optimize the dynamic energy scheduling of the system. The feasibility and effectiveness of the proposed optimal scheduling strategy and model are verified by comparing results obtained using different optimization algorithms and scenarios.
2. Hydrogen-Coupled Electro-Thermal Integrated Energy System Architecture
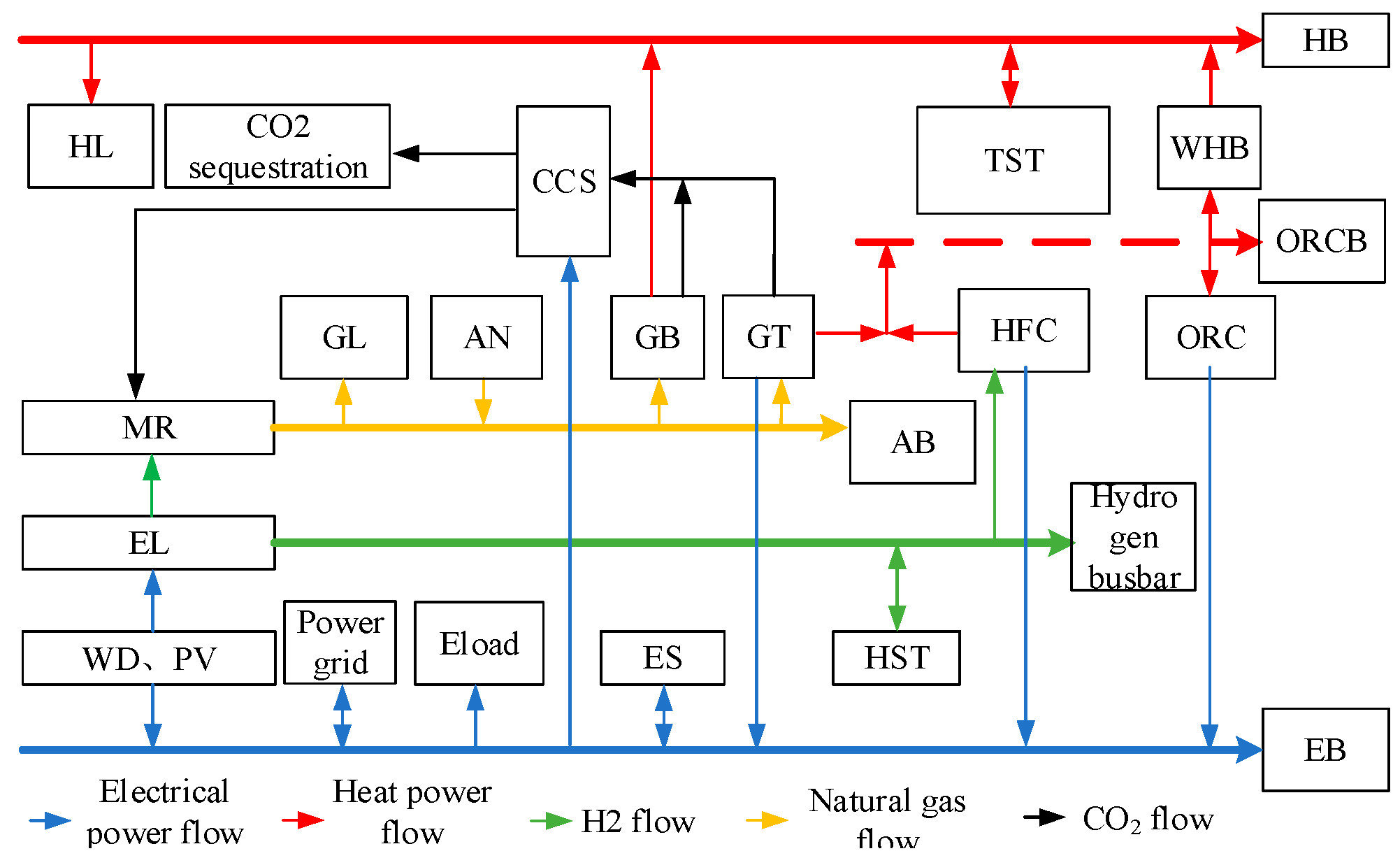
The system structure is shown in
Figure 1 and is mainly composed of energy supply, energy conversion, energy storage, and load. The supply side mainly includes the upper gas grid, wind turbine photovoltaic, and upper gas network. The conversion side is mainly composed of an electrolyzer (EL), methane reactor (MR), gas turbine (GT), gas boiler (GB), hydrogen fuel cell (HFC), waste heat power generation device based on organic Rankine cycle (ORC), and waste heat boiler (waste heat boiler, WHB); the energy storage end is mainly the electricity storage (ES), thermal storage tank (TST), and hydrogen storage tank (HST). On the energy load side, users are aggregated and uniformly characterized as electrical loads, gas loads, and heat loads.
Flow of energy and matter. We explicitly describe the core flows: electrical flow: from PV/WT/Grid, through converters (P2G, EL), to electrical loads and storage (ES). Gas flow: from the superior gas grid and the methane reactor (MR), through gas turbines (GT) and gas boilers (GB), to gas loads. Hydrogen flow: from electrolyzers (AWE, PEM) to storage (HST) and then to hydrogen fuel cells (HFC) or the methane reactor (MR). Heat flow: from cogeneration units (GT, HFC, GB), waste heat recovery (WHB, ORC), to heat loads and storage (TST). CO2 flow: from the gas turbine’s flue gas to the carbon capture system (CCS) and then to the methane reactor for utilization or to storage.
5. Examples
5.1. Example Description
Simulation analysis is performed for the HCEH-IES built in
Figure 1. This paper verifies the ability of reinforcement learning for offline training and online optimization of the model in this paper and conducts a comparative analysis of the three designed scenarios, as well as compares the ability of different optimization algorithms to solve the model. Under the premise of giving priority to meeting load demand, making full use of renewable energy sources, choosing appropriate optimal scheduling strategies, reducing the comprehensive operation cost and carbon control cost of the system, and finally planning the output of each unit. The parameters of each unit within HCEH-IES are shown in
Appendix A.
5.2. Training Convergence Analysis
A total of 4000 cycles are trained in this simulation. In offline training, the SAC algorithm has the highest reward function value and the fastest convergence speed. The SAC reward curve gradually stabilizes in 3000 training cycles and converges to the reward value interval of −3.2 × 10
7–3.22 × 10
7, while the DDPG algorithm stabilizes only in 3500 training cycles, and the training results are poor. For detailed specifications, see
Appendix B.
5.3. Analysis of Scheduling Results
After training the algorithmic network using historical data, the resulting network is saved and applied to the dynamic economic scheduling of the system. The results of scheduling actions are shown in
Figure 2,
Figure 3,
Figure 4 and
Figure 5.
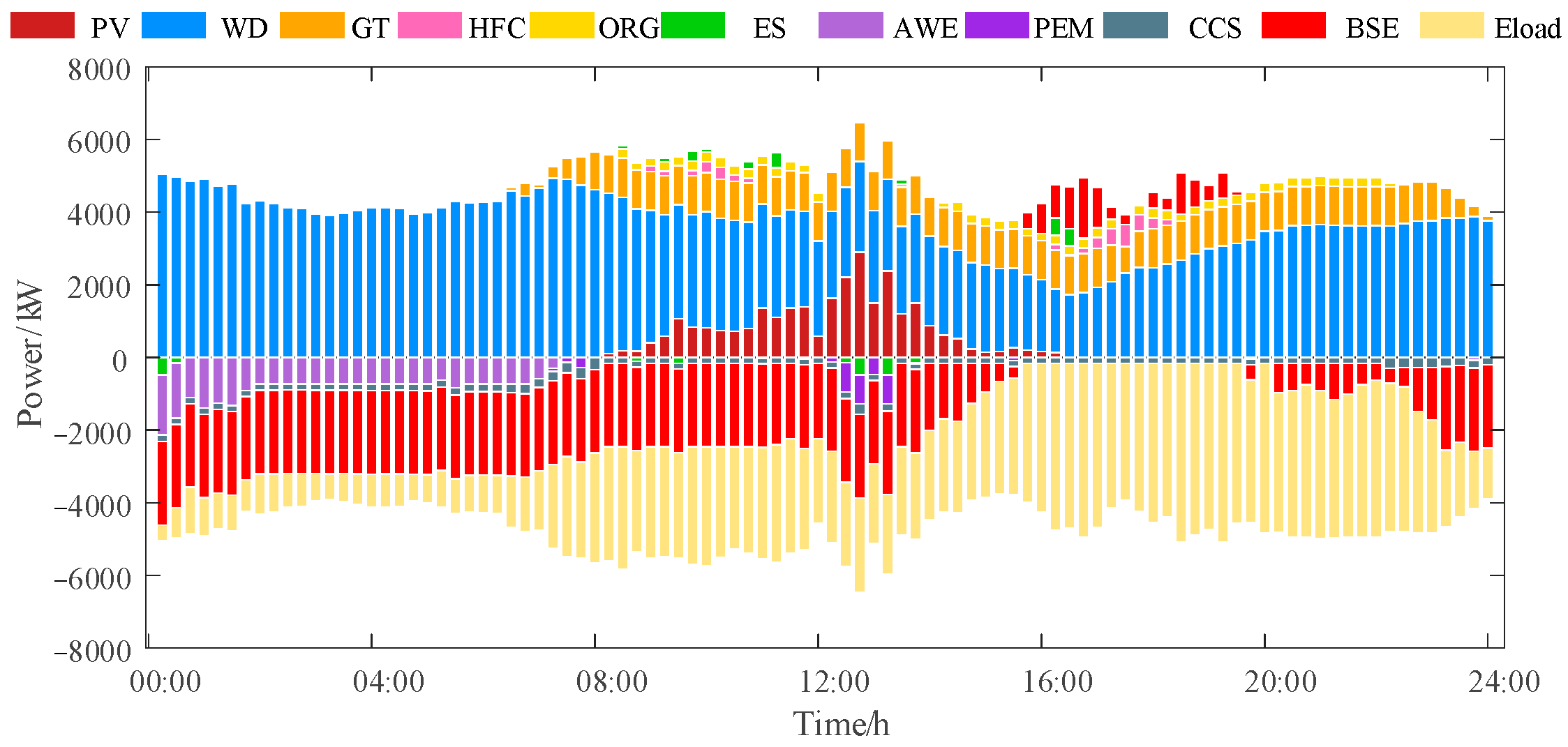
As shown in
Figure 2, power dispatch exhibits characteristics of multi-timescale collaborative optimization. During 00:00–04:00, there is PV plant shutdown, wind turbine as the main power supply of renewable energy, gas turbine low power operation to fill the gap between wind power and electric load, and hot standby maintained. Due to wind power overcapacity, the system sells power to the grid. During 04:00–06:00, wind turbine power drops and gas turbine power increases to ensure the stability of the electric load. From 06:00 onwards, the increase in light makes the power of photovoltaic power generation rise, and the system continues to optimize the dispatch to maintain electric balance. After 6:00, solar power generation increases but experiences a timing mismatch with peak electricity demand. At this time, the system coordinates gas turbines, hydrogen fuel cells, and low-temperature waste heat power generation units to form a diversified, complementary power supply structure. Notably, during the 18:00 to 20:00 peak load period, the system achieved peak shaving and valley filling by preemptively discharging stored energy, adjusting P2G operation strategies, and promptly activating hydrogen fuel cells. This demonstrates that the SAC algorithm has mastered forward-looking decision-making capabilities in power dispatch, effectively mitigating renewable energy fluctuations through multi-energy flow conversion.
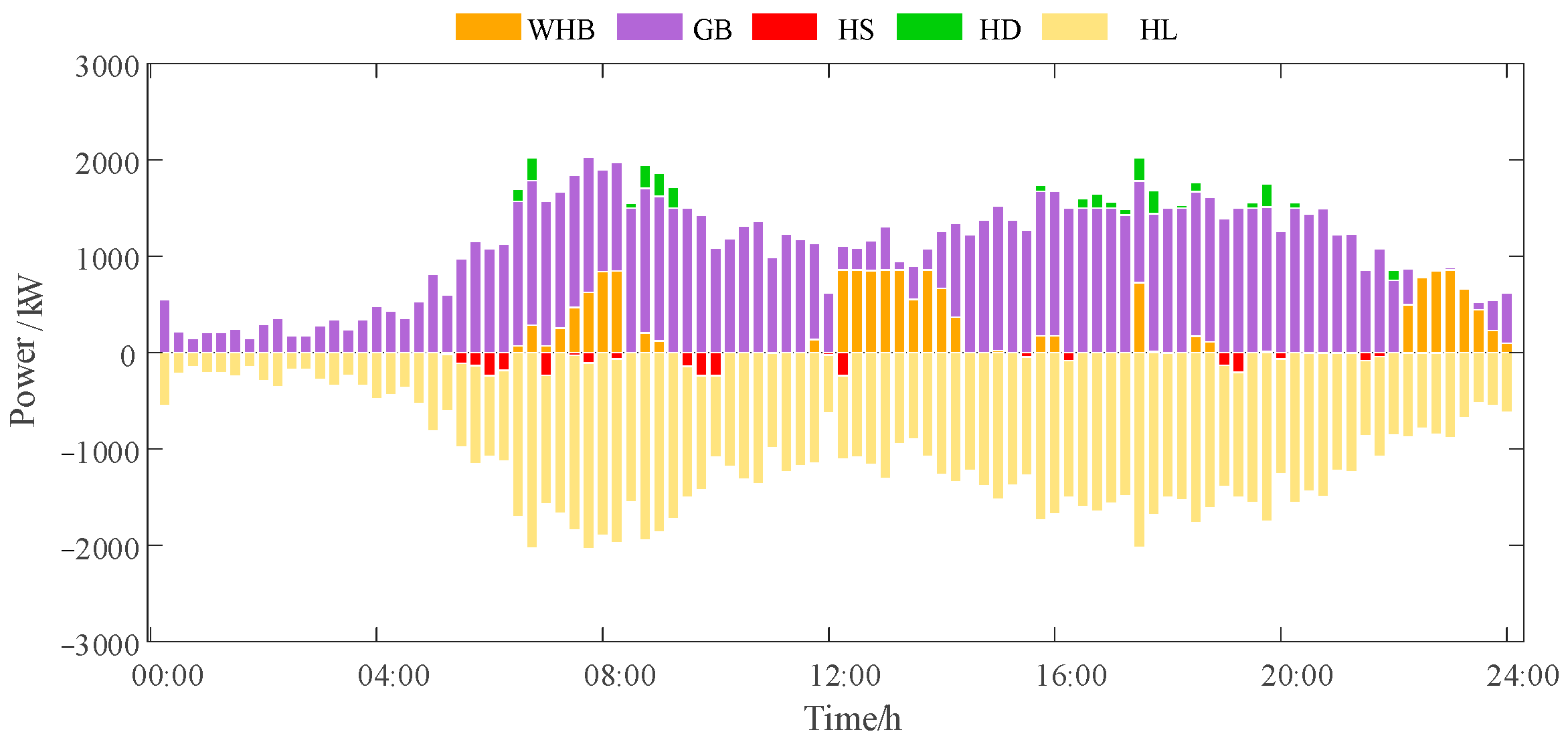
The thermal load scheduling in
Figure 3 clearly demonstrates the system’s full utilization of thermal inertia. From 00:00 to 04:00, during low-load periods, the system maintains baseline heating solely through fluctuating operation of gas boilers, while thermal storage units perform intermittent heat storage. This “valley-filling” operation reserves capacity for subsequent adjustments. From 06:00 onwards, as thermal load increases, the system synchronously boosts output from both gas and waste heat boilers while activating thermal storage units for heat release, establishing a “storage-supply” coordination mode. During the high-load period from 08:00 to 20:00, the gas boiler, waste heat boiler, and thermal storage units operate in a coordinated state. Through multi-heat-source control, this achieves a balance between heating reliability and economic efficiency. This optimized scheduling, based on the thermal system’s spatiotemporal characteristics, demonstrates the unique advantages of integrated energy systems in thermal energy management.
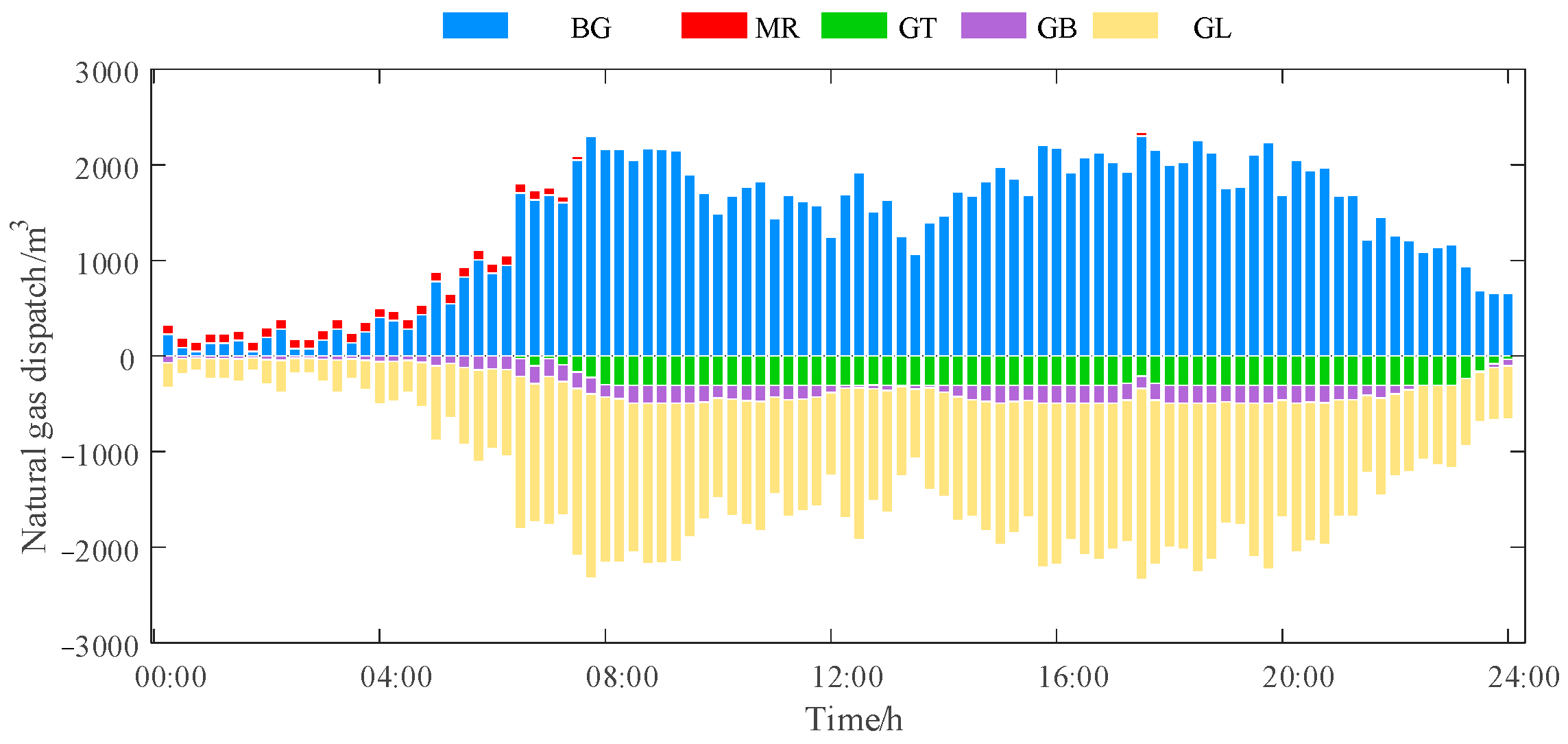
Figure 4 illustrates the pivotal role of the gas network in multi-energy conversion. During 00:00–04:00, due to the low heat demand for production and life, the gas boiler maintains the basic heat supply in a fluctuating mode, the power of the waste heat boiler is small, and the heat storage device intermittently carries out heat storage with small power. From 06:00 onwards, the heat load starts to rise, the power of the gas boiler increases significantly, the power of the waste heat boiler increases synchronously, and the heat storage tank participates in heat storage during part of the time period. During 08:00–20:00, accompanied by a continuous growth or fluctuation of the heat from 08:00 to 20:00, along with the continuous growth or fluctuation of heat load, gas boilers, waste heat boilers, and heat storage tanks operate synergistically to increase the heat supply. The methane reactor increased its output around 20:00. This strategic arrangement responded to the anticipated growth in gas load while leveraging its time-varying operational characteristics to participate in system regulation. Throughout the entire scheduling process, the natural gas system ensured gas volume balance and operational safety for the multi-energy system through the dual safeguards of “purchased gas + P2G gas production”.
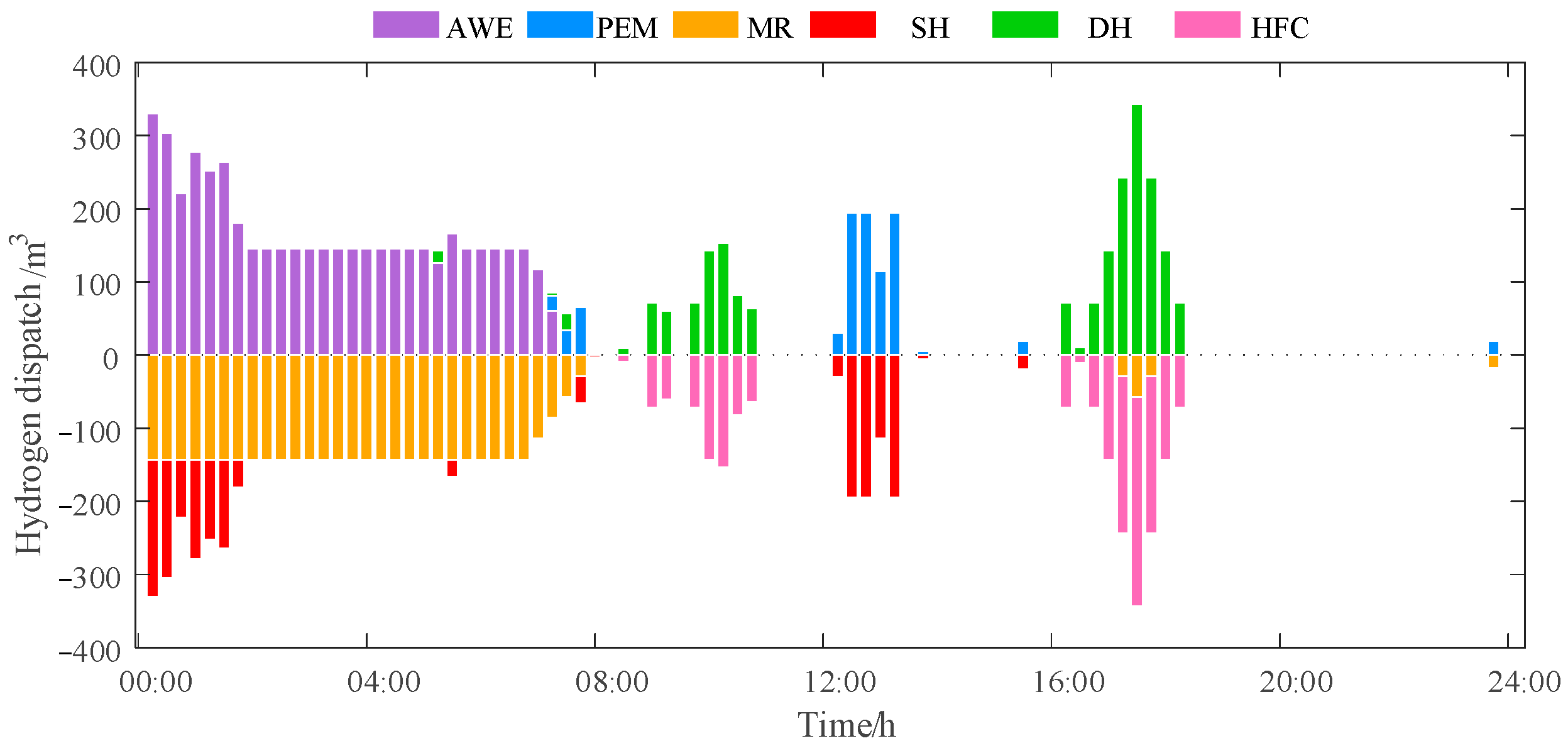
Figure 5 illustrates the core value of hydrogen energy dispatch in energy conversion. Between 00:00 and 04:00, alkaline electrolyzers maximize low-cost wind power for large-scale hydrogen production while proton exchange membrane electrolyzers remain on standby. This differentiated operation demonstrates the system’s precise control over hydrogen production economics. Simultaneously, methane reactors continuously consume hydrogen to synthesize natural gas, while hydrogen storage tanks handle surplus storage, forming a complete “production-storage-consumption” hydrogen management chain. Between 14:00 and 16:00, PEM electrolyzers significantly increase output—aligned with their rapid response characteristics—to smooth power fluctuations during this period. During the peak hydrogen consumption period from 18:00 to 20:00, the system achieved precise matching of hydrogen supply and demand by coordinating electrolyzer load reduction, hydrogen fuel cell power generation, and hydrogen tank release. This multi-timescale hydrogen management strategy fully demonstrates hydrogen’s critical role in enhancing system flexibility and facilitating renewable energy integration.
5.4. Comparison of Methods
- (1)
Model Comparison
The following scenarios are set up to verify the superiority of this paper’s model:
Scenario 1: Introducing gas-fired units and a carbon trading mechanism, without adding hydrogen fuel cells to form a cogeneration system, and without carbon capture utilization technology.
Scenario 2: Based on scenario 1, carbon capture technology is added, and electrolytic hydrogen is converted to natural gas for utilization.
Scenario 3: Based on scenario 2, two-stage P2G is used, and hydrogen fuel cells and ORC low-temperature power generators are introduced to form a cogeneration system.
From
Table 1, it can be seen that scenario 1 only deploys gas units, does not build a cogeneration system, and lacks technical means such as electricity-to-gas, resulting in significantly high gas grid interaction costs. Scenario 2 integrates carbon capture technology on the basis of scenario 1 and directly converts electrolyzed hydrogen into natural gas for utilization, which effectively reduces natural gas procurement expenditure by supplementing gas sources, reducing the gas grid interaction cost to 108,204.95 CNY. However, due to the constraints of the carbon trading mechanism, the additional carbon purchase cost was 1576.83 CNY. Scenario 3 uses two-stage power-to-gas (P2G) technology to introduce hydrogen fuel cells and ORC cryogenic power generation devices to build a cogeneration system, although the complexity of the system increases and changes the natural gas demand structure, resulting in the gas grid interaction cost rising to 113,808.10 CNY, however, its grid interaction cost is −59,777.26 CNY, achieving significant benefits, which is attributed to the fact that the cogeneration system improves energy utilization efficiency and grid interaction benefits through energy allocation optimization and interactive collaboration.
Carbon control cost analysis: Scenario 1 does not involve carbon capture technology, so both carbon purchase costs and carbon capture and storage costs are zero. Scenario 2 introduces carbon capture technology, generating carbon purchase costs of 1576.83 CNY, carbon capture and storage costs of 866.22 CNY, and carbon trading costs of 18,116.87 CNY, initiating carbon emission control through technological and market-based measures. Scenario 3 continues relevant mechanisms and technologies, with carbon purchase costs of CNY 1246.84, carbon capture and storage costs of CNY 836.31, and carbon trading costs of CNY 17,551.39. Due to system optimization, some costs have been adjusted, but overall, carbon emission control and management continue.
- (2)
Algorithm comparison
To comprehensively evaluate the effectiveness of the proposed optimization scheduling strategy, this study employs both mathematical programming and deep reinforcement learning (DRL) methods for comparative analysis. Specifically, the commercial solver CPLEX (IBM ILOG CPLEX Optimization Studio) is introduced to solve the deterministic day-ahead optimization problem of the HCEH-IES model, providing a theoretical optimal solution as a benchmark under idealized forecasting conditions. Meanwhile, two representative DRL algorithms—deep Q-network (DQN) and deep deterministic policy gradient (DDPG)—are also optimized and applied to solve the same model.
From
Table 2, the computational costs for the SAC, DDPG, and DQN algorithms are CNY 95,601.14, CNY 97,629.78, and CNY 99,287.60, respectively. Calculations show that the operational cost increases relative to CPLEX for the SAC, DDPG, and DQN algorithms are approximately 2.76%, 4.94%, and 6.72%, respectively. Among these, the SAC algorithm exhibits a lower total operational cost than both DDPG and DQN, and its results are closer to those of CPLEX’s current optimal scheduling method. It is important to emphasize that CPLEX achieves theoretical optimal solutions under ideal conditions where all source-load data is fully known. In contrast, the SAC algorithm develops scheduling strategies adaptable to uncertainty through interactive learning in dynamic environments. CPLEX’s marginally superior economic performance in deterministic settings validates its theoretical advantage while highlighting SAC’s effectiveness and robustness in scenarios closer to real-world operations. Compared to DDPG and DQN, SAC’s operational costs were CNY 75,846.92, CNY 76,957.37, and CNY 77,633.45, respectively, demonstrating cost advantages that indicate greater efficiency in resource utilization or computational logic. Regarding carbon control costs, SAC incurred CNY 19,493.30, lower than DDPG’s CNY 20,672.41 and DQN’s CNY 21,654.15, demonstrating greater effectiveness in carbon emission control strategies.
This study adopts the SAC algorithm primarily based on the following considerations: First, this algorithm can adaptively learn the random fluctuation characteristics of wind and solar power generation and multi-energy loads through interaction with the environment without relying on precise predictive models; second, it possesses online learning and real-time adjustment capabilities, making it better suited for dynamic scheduling scenarios.
6. Conclusions
In this paper, an optimization method for the scheduling and operation of a hydrogen-coupled electrothermal integrated energy system is proposed. The source-side structure of the system is optimized by integrating carbon trading policies with low-carbon technology to improve the renewable energy consumption rate and system decarbonization level. Furthermore, to address the uncertainties in system source-load and the insufficient exploration in existing reinforcement learning algorithms, a deep reinforcement learning method based on Soft Actor–Critic (SAC) is proposed. The adaptive learning control strategy is obtained through interactions between agents and the energy system. The following conclusions are drawn:
(1) The proposed HCEH-IES framework and its optimization methodology, which synergizes carbon trading mechanisms with low-carbon technologies like P2G-CCS, increased the renewable energy consumption rate to over 85%. This architecture effectively matches the energy consumption of carbon capture and electrolytic hydrogen production with renewable generation profiles, resulting in a 12.7% reduction in total carbon emissions in scenario 3 compared to scenario 1, empirically demonstrating its significant effectiveness in enhancing the system’s carbon reduction capability.
(2) The hybrid hydrogen production system, comprising AWE and PEM electrolyzers, operated in a complementary manner to meet hydrogen demand while effectively utilizing low-cost wind power and surplus PV generation, contributing approximately 15% to the system’s flexibility regulation potential. The diversified utilization of hydrogen through power generation in fuel cells, methanation, and direct storage fully unlocks its potential as a cross-seasonal storage medium and a coupling hub for multi-energy flows, proving crucial for the system’s low-carbon and economic operation.
(3) Based on the deep reinforcement learning method of soft SAC, the adaptive optimization of control strategies is realized through the interaction learning between agents and energy systems. Compared with traditional reinforcement learning algorithms, this method can reduce the total cost of HCEH-IES and effectively improve the low-carbon and economic efficiency of the system.