Sustainability-Oriented Furnace Temperature Prediction for Municipal Solid Waste Incineration Using IWOA-SAGRU

Abstract

Municipal solid waste incineration promotes sustainable development by reducing waste, recovering resources, and minimizing environmental impact, with furnace temperature control playing a key role in maximizing efficiency. Accurate real-time temperature prediction is crucial in developing countries to optimize incineration, re-duce emissions, and enhance energy recovery for global sustainability. To address this, we propose a method integrating an improved whale optimization algorithm (IWOA) with a self-attention gated recurrent unit (SAGRU). Using the maximal information coefficient (MIC) to identify key factors, we optimize SAGRU parameters with IWOA, enhancing prediction accuracy by capturing temporal dependencies. Experimental validation from an MSWI plant in China demonstrates that the proposed model significantly enhances prediction accuracy under complex conditions. When compared with the Elman and LSTM models, the error is reduced by 0.7146 and 0.4689, respectively, highlighting its strong potential for practical applications in waste incineration temperature control.

1. Introduction

Municipal solid waste incineration (MSWI) directly contributes to the achievement of sustainable development goals, such as “clean environment,” “clean energy,” and “sustainable cities,” through reduction (decreasing the waste volume by 60–90%), resource recovery (converting thermal energy into electricity), and harmless treatment (eliminating pathogens at high temperatures). This process not only enables effective waste disposal but also facilitates resource recycling. However, to ensure that MSWI is both efficient and environmentally friendly, furnace temperature control plays a pivotal role. Accurate prediction and maintenance of the incineration temperature within the range of 850–1000 °C can maximize energy conversion efficiency (increasing power generation by 10–15% per 10,000 tons of waste), while simultaneously preventing dioxin formation at low temperatures and equipment damage at excessively high temperatures. Therefore, furnace temperature control is the key to ensuring a green, low-carbon, and harmless incineration process, and it significantly enhances the overall efficiency of waste-to-energy systems [1].

Although many studies have investigated combustion parameters in waste incineration, developed countries such as those in Europe and North America have already implemented waste classification systems. For example, in France, municipal solid waste (MSW) is primarily incinerated, and recent studies have provided comprehensive data on technological, environmental, and energy aspects across 90 MSW incineration plants, highlighting common air pollution control techniques, emissions, and energy recovery efficiency [2]. In these regions, public awareness of environmental protection is relatively strong, the calorific value of classified combustible components is relatively stable, and advanced temperature control technologies have been developed and supported by well-established expertise. In contrast, in developing countries, waste classification policies and regulations are still in the process of improvement and promotion [3]. As a result, the composition of municipal solid waste (MSW) in developing countries remains highly uncertain, with relatively low and fluctuating calorific values, making it difficult to directly apply the mature control technologies developed in developed countries [4]. Taking China as an example, waste incineration in many developing countries still relies heavily on operating engineers to anticipate changes in operating conditions based on experience, predict possible temperature fluctuations, and manually adjust temperature control. However, this experience-dependent approach cannot fully cope with the complex and dynamic nature of the incineration process, which often results in unstable temperature control [5].

Nevertheless, the heterogeneous and variable composition of solid waste leads to fluctuations in its physical and chemical properties, which in turn cause dynamic changes and uncertainties in furnace temperature. These factors make it difficult for traditional mathematical models to provide accurate descriptions of the process [6]. Consequently, developing advanced prediction models capable of handling such complexity has become a research priority. These models are designed to improve incineration efficiency, reduce pollutant emissions, and enhance resource recovery [7], which are all directly aligned with global sustainability objectives in terms of energy efficiency, circular economy, and environmental protection. Moreover, waste incineration can effectively reduce harmful factors associated with electricity generation and phosphate fertilizer production, thereby minimizing environmental impacts [8].

In the field of modeling for solid waste incineration processes, early studies primarily focused on mechanism-based approaches to establish temperature models. For example, Ref. [9] developed a comprehensive mathematical model by dividing the movement of solid waste into zones and constructing mass and energy balance equations for the fuel bed. Simulation results showed that the model was consistent with the operating characteristics of an incinerator. Similarly, Ref. [10] proposed different combustion modes of volatile matter based on its release and combustion processes inside the furnace, and constructed a combustion model using chemical reaction equations. However, the MSWI process is characterized by intricate physical and chemical reactions. Furnace temperature is influenced by multiple factors, such as air supply, fuel composition, and reaction rate. Due to the strong complexity and non-stationary nature of MSWI, furnace temperature exhibits dynamic and nonlinear characteristics, making it extremely difficult to establish accurate mechanism-based mathematical models.

With the rapid advancement of machine learning and deep learning technologies, data-driven modeling approaches have emerged as a prominent area of research in the field of solid waste incineration processes. For instance, references [8,11] employed back-propagation techniques to establish nonlinear relationships between key process parameters, such as energy consumption and pollutant emissions, and their influencing factors. Experimental results demonstrated that these methods significantly outperformed linear regression models. In reference [12], a T-S fuzzy neural network was used to model the temperature during the solid waste incineration process, with a parameter learning mechanism incorporated to enhance adaptability under varying conditions. Reference [13] introduced a novel time-span input neural network, considering the time factor in input variables, to predict trends in the main steam temperature during the incineration process. Furthermore, a temperature model for the incinerator was established in [14] using the Tikhonov regularization–least regression decision tree (TR-LRDT) algorithm. To improve the model’s generalization ability, reference [15] developed an explainable Bayesian support vector regression (E-BSVR) model for generalized prediction and optimization of operating parameters, including PCDD/F emissions. However, these methods often face limitations when handling complex, multivariable, and high-dimensional data.

On the other hand, in order to cope with the strong nonlinearity and dynamic temporal features of the incineration process, reference [16] proposes a heterogeneous feature ensemble modeling method for furnace temperature prediction in municipal solid waste incineration. This approach enhances accuracy, generalization, stability, and training efficiency by combining multiple base models and employing a negative correlation learning strategy. In reference [17], a model for predicting gas concentration is proposed by combining convolutional neural networks (CNN) with long short-term memory (LSTM) networks. However, the accuracy of the model is influenced by manually set key parameters, such as the number of neurons and the learning rate. Therefore, despite some progress, challenges remain, including the lack of a systematic approach for selecting input variables and insufficient model generalization capability.

In recent years, research on complex process modeling in industrial applications has mainly evolved along three directions. First, in the traditional modeling stage, researchers employed methods such as multiple linear regression [18] and partial least squares [19], as well as shallow machine learning approaches including support vector machines [20] and backpropagation neural networks [21]. These methods perform reliably when dealing with linear or weakly nonlinear problems. However, they face limitations in capturing the dynamic temporal features and strong nonlinear relationships inherent in the complex MSWI process [22,23].

With the rapid development of deep learning, modeling techniques have entered the deep learning stage. Typical models include recurrent neural networks (RNN) and LSTM networks have significantly improved the prediction accuracy of nonlinear dynamic processes by deeply exploiting temporal dependencies. Among them, the gated recurrent unit (GRU) simplifies the structure of LSTM while maintaining comparable predictive performance, thereby improving computational efficiency. GRU has been widely applied in areas such as chemical reaction modeling and energy forecasting [24]. However, the hyperparameters of GRU are typically set empirically, which often leads to fluctuations in prediction results. To tackle this problem, heuristic methods like genetic algorithms and artificial bee colony optimization have been applied by researchers to tune GRU hyperparameters [25,26]. Experimental studies have shown that incorporating intelligent optimization algorithms can substantially improve the predictive accuracy of single models. Nevertheless, when dealing with long input sequences, GRU-based models may still suffer from information loss across time steps, reducing their predictive reliability. Consequently, as industrial processes become increasingly complex, the generalization ability of single models has become limited. This has given rise to the stage of intelligent optimization and algorithm integration, where hybrid models combining attention mechanisms, ensemble learning, and intelligent optimization algorithms—such as whale optimization and particle swarm optimization—have emerged as a new research trend [27]. However, there is still a lack of studies explicitly linking advanced modeling methods with sustainability-oriented objectives, such as enhancing energy efficiency, improving combustion stability, and supporting more efficient resource recovery in municipal solid waste incineration.

Based on the above analysis, the primary goal of this study is to develop an accurate and robust furnace temperature prediction model for municipal solid waste incineration (MSWI) that can effectively handle the nonlinear, dynamic, and complex characteristics of the process. To achieve this goal, we propose a model integrating a Self-Attention Gated Recurrent Unit (SAGRU) with an Improved Whale Optimization Algorithm (IWOA) to address the limitations of traditional temperature prediction methods. First, the Maximal Information Coefficient (MIC) is employed to evaluate the correlation between different features and temperature, thereby selecting appropriate input variables. Next, a temperature prediction model is constructed using GRU and an attention mechanism. The attention mechanism assigns adaptive weights across different time steps, which enhances the modeling accuracy. To overcome the shortcomings of the conventional Whale Optimization Algorithm (WOA), including slow convergence and a propensity to become trapped in local optima during the later stages of training, this study improves the algorithm by incorporating Latin hypercube sampling, an adaptive threshold strategy, and Gaussian perturbation. Finally, the improved IWOA is applied to optimize the key parameters of the SAGRU model, including the learning rate (η), the number of hidden nodes (n) and the dropout rate ($p$), thereby establishing a more accurate prediction model. Experimental validation is conducted using real operating data from a MSWI plant in China. The results demonstrate that the proposed furnace temperature prediction model achieves superior accuracy, generalization, and robustness compared with other networks, while also contributing to the broader sustainability agenda, reducing operational risks, and supporting the transition toward low-carbon waste management systems.

2. Description of the MSWI Process and Problem Formulation for Furnace Temperature Modeling

2.1. Process Description

As shown in Figure 1 [28], a typical MSWI process consists of several stages, including pretreatment, drying, combustion, and grate handling. First, a grab crane delivers the pretreated solid waste into the incinerator, where it is subjected to drying, combustion, and burnout. During this process, the combustible components of the waste are fully oxidized, and the organic matter is converted into carbon dioxide, water vapor, and other gases. To ensure efficient combustion, primary and secondary air is supplied through blowers, injected from the bottom of the grate and the middle of the furnace chamber. The incineration residues are discharged by a slag conveyor, while the high-temperature flue gas is directed into a waste heat boiler for energy recovery and subsequently treated by a flue gas purification system before being released into the atmosphere.

In this process, conventional temperature measurement instruments often exhibit slow response under dynamic operating conditions, which becomes a critical factor limiting the efficiency of temperature control. The temperature in MSWI processes typically fluctuates significantly, as both the composition of the waste and the combustion state are constantly changing. These factors make real-time monitoring of furnace temperature highly challenging. Traditional measurement methods suffer from considerable lag and cannot capture rapid or transient temperature variations with sufficient accuracy. Particularly under conditions of sharp or frequent fluctuations, sensors are unable to respond promptly. This time lag prevents the recorded data from fully reflecting the actual furnace temperature dynamics, reducing the effectiveness of real-time combustion regulation. Consequently, the accuracy of temperature control is compromised, which may even result in inadequate control strategies, thereby threatening the safety and stability of the entire incineration process. Therefore, the development of an accurate furnace temperature model is a prerequisite for effective furnace temperature control.

2.2. Problem Formulation for Furnace Temperature Prediction Modeling

The municipal solid waste incineration (MSWI) process is a complex thermochemical reaction involving multiple physical and chemical transformations. During this process, furnace temperature is influenced by various factors, which are usually characterized by complex nonlinear relationships. Moreover, temperature often fluctuates significantly under different operating conditions.

From a mechanistic perspective, the combustion of municipal solid waste involves complex physical and chemical transformations.

(1) The mechanistic model of the moisture evaporation process can be expressed as follows [29]:

$$m_w={\displaystyle \frac{d{R}_{air}+d{R}_{rad}}{R_{water}}}$$

(1)

$m_w$ represents the change in moisture mass of a single waste module, $d{R}_{air}$ represents the change in the thermal energy of the waste module. $d{R}_{rad}$ represents the change in radiative heat of the waste module, $R_{\mathit{water}}$ represents the heat absorbed for the evaporation of each kilogram of water, which is taken as 2571.4 kJ/kg.

(2) After the moisture has evaporated to a certain extent, the waste undergoes pyrolysis reactions under high-temperature conditions.

The release of volatile matter corresponds to the pyrolysis process of the waste. The mechanistic model for the release of volatile matter can be expressed as follows [9]:

$$m_T=m_{vol}{\displaystyle {\int }_0^T{A}_V{e}^{-\frac{E_V}{R{y}_V}}}{(1-\alpha )}^{n}d\tau$$

(2)

$m_T$ represents the amount of volatile matter released over a period $T$, $m_{vol}$ represents the initial amount of volatile matter, $A_V$ refers to the pre-exponential factor. $E_V$ represents the activation energy, The volatile conversion occurs only when the activation energy of the molecules reaches a certain threshold. $R$ is the universal gas constant, and $y_v$ is the temperature of the waste in the material layer. $\alpha$ represents the conversion rate of volatile matter during the pyrolysis process. $n$ represents the reaction order.

(3) The combustion performance can be classified into three states based on the ratio of oxygen to the mass of volatile matter: oxygen-limited combustion, incomplete combustion, and complete combustion [30].

Assuming that the ratio of oxygen mass in the air to the mass of volatile matter is less than $k_1$, the combustion is in an oxygen-limited state, and the products formed are CO, CO₂, and CH₄:

$$C_x{H}_y{O}_z+({\displaystyle \frac{3x}{4}}-{\displaystyle \frac{3y}{16}}-{\displaystyle \frac{z}{2}})O_2\to ({\displaystyle \frac{x}{2}}-{\displaystyle \frac{y}{8}})C{O}_2+({\displaystyle \frac{x}{2}}-{\displaystyle \frac{y}{8}})CO+{\displaystyle \frac{y}{4}}C{H}_4$$

(3)

When the ratio of oxygen mass in the air to the mass of volatile matter is greater than $k_1$ but less than $k_2$, the combustion is in an incomplete state, and the products formed are CO, CH₄, CO₂ and H₂O:

$$\left\{\begin{array}{l}{C}_x{H}_y{O}_z+({\displaystyle \frac{3x}{4}}-{\displaystyle \frac{3y}{16}}-{\displaystyle \frac{z}{2}})O_2\to ({\displaystyle \frac{x}{2}}-{\displaystyle \frac{y}{8}})C{O}_2+({\displaystyle \frac{x}{2}}-{\displaystyle \frac{y}{8}})CO+{\displaystyle \frac{y}{4}}C{H}_4\\ 2CO+C{H}_4+3O_2\to 3C{O}_2+2H_{2}O\end{array}\right.$$

(4)

When the ratio of oxygen mass in the air to the mass of volatile matter is greater than $k_2$, the combustion is in a complete state, and the products formed areCO₂ and H₂O.

$$2CO+C{H}_4+3O_2\to 3C{O}_2+2H_{2}O$$

(5)

The combustion process involves complex physical and chemical reactions. In practice, the furnace temperature is influenced by multiple operational parameters, which collectively determine the stability and efficiency of the incineration process. These parameters include primary air volume, primary air temperature, secondary air volume, secondary air temperature, main steam flow rate, grate temperature, left-side furnace temperature, furnace negative pressure, and inlet temperature of the combustion zone.

Specifically, primary air volume directly determines oxygen supply: a higher primary air volume enhances combustion reactions and raises the furnace temperature, whereas insufficient air supply leads to incomplete combustion and lowers the temperature. Similarly, primary air temperature plays a vital role in the combustion process; higher temperatures improve combustion efficiency, reduce heat loss, and increase furnace temperature, while lower temperatures may weaken combustion and reduce temperature. A moderate increase in secondary air volume enhances airflow and combustion uniformity, whereas excessive supply can lead to incomplete combustion and impair temperature regulation. Secondary air temperature also influences combustion efficiency: hot secondary air accelerates combustion and raises furnace temperature, while cooler air may slow down combustion and reduce temperature.

In addition, the main steam flow rate is closely related to heat output. Excessive steam flow may cause rapid heat loss in the furnace, lowering the temperature, while a moderate flow rate helps maintain temperature stability. Grate temperature reflects the combustion conditions at the furnace bottom: a higher grate temperature indicates efficient combustion, contributing to an overall increase in furnace temperature, whereas a lower grate temperature suggests incomplete combustion and reduced furnace temperature. The left-side furnace temperature is linked to airflow distribution; uneven temperature distribution may result in non-uniform combustion and hinder temperature rise, while uniform distribution contributes to stability. Furnace negative pressure regulates airflow and combustion efficiency: higher negative pressure increases oxygen supply and enhances combustion, thereby raising furnace temperature, whereas insufficient negative pressure may cause poor airflow and weaken combustion performance. Finally, the inlet temperature of the combustion zone, as the initial airflow temperature entering the furnace, has a direct effect on furnace heating. A higher inlet temperature accelerates combustion reactions and promotes an increase in furnace temperature.

In summary, the furnace temperature can be represented as being influenced by multiple variables, with complex nonlinear relationships existing between the temperature and these influencing factors, as shown in Equation (6).

$$Y(i)=F(x_1(i),x_2(i),x_3(i)\cdots x_9(i))$$

(6)

In the equation, $Y(i)$ represents the furnace temperature, $F\left(\right)$ indicates the unknown nonlinear relationship, and $i$ refers to the sampling time. The input vector $x_1\sim x_9$ consists of primary air volume, secondary air volume, main steam flow rate, grate speed, primary air temperature, secondary air temperature, left-side furnace temperature, furnace negative pressure, and inlet temperature of the combustion zone. Therefore, in essence, furnace temperature prediction is achieved by indirectly measuring these influencing variables and applying data-driven methods to establish a nonlinear model of the furnace temperature.

3. Furnace Temperature Prediction Model Based on IWOA-SAGRU

To address the challenges of accurately measuring furnace temperature and constructing reliable prediction models, this study proposes a data-driven IWOA-SAGRU furnace temperature prediction model for MSWI. As shown in Figure 2, the model consists of three modules: the MIC feature selection module, the SAGRU-based furnace temperature prediction module, and the IWOA-based parameter optimization module.

In the MIC feature selection module, the maximal information coefficient (MIC) method is employed to screen the influencing factors of furnace temperature, balancing model accuracy with complexity reduction [31]. Based on expert knowledge, nine key variables—including the left-side temperature, combustion section inlet temperature, primary air flow, secondary air flow, primary air temperature, secondary air temperature, main steam flow, flue gas temperature, and furnace pressure—are identified as key temperature-influencing factors. These nine factors are further screened using MIC. Based on the MIC analysis results, four feature variables—Primary air flow, Main steam flow, Primary air temperature, and Left-side furnace temperature—are finally selected as inputs for the SAGRU-based furnace temperature prediction module, with the furnace temperature serving as the model output.

The SAGRU-based module integrates a self-attention (SA) mechanism with a gated recurrent unit (GRU) network to model the temporal dynamics of furnace temperature. In the IWOA-based parameter optimization module, the IWOA is used to optimize network parameters, including the learning rate ($\eta$), the number of hidden nodes ($n$), and the dropout rate (p), thereby improving the model’s prediction performance.

3.1. Furnace Temperature Prediction Model Based on SAGRU

The Gated Recurrent Unit (GRU) effectively captures temporal dependencies of varying lengths in time-series data, rendering it well-suited for dynamic temperature forecasting. However, relying solely on GRU to extract sequence features is insufficient to address the complexity of furnace temperature prediction. To better capture the nonlinear relationships between measurable variables and furnace temperature, this study combines GRU with a SA mechanism and proposes the SAGRU model. In this model, the GRU processes the input furnace temperature time-series data, effectively memorizing and updating historical temperature information, while the self-attention mechanism adaptively assigns weights to different time steps, thereby highlighting critical operating variables and key points of temperature variation.

As shown in Figure 3, the structure of the model is provided. When the self-attention mechanism is combined with the GRU, four feature variables selected by the MIC analysis are used as inputs and processed by the GRU encoder to generate a series of hidden state $h_t=[h_1,h_2,h_3,\cdots h_t]$. The self-attention mechanism then assigns weights to these hidden states by generating queries ($Q$), keys ($K$), and values ($V$) to capture the critical features at different time steps within the sequence. The dot product between the queries and keys is computed to measure the similarity or relevance between the current state (query) and the historical states (keys), resulting in attention weights. These weights are then used to calculate a weighted average of the input sequence, which ultimately produces the predicted furnace temperature output from the model.

3.1.1. GRU-Based Furnace Temperature Prediction Model Structure

Since furnace temperature exhibits strong temporal dependence and dynamic characteristics, and is influenced by multiple factors such as feed rate, waste composition, and combustion air supply, the GRU, an improved architecture of the RNN [32], introduces a gating mechanism that effectively alleviates the vanishing gradient problem encountered by traditional RNNs when processing long sequences. This advantage makes GRU highly suitable for furnace temperature prediction, as it can efficiently handle temperature data with reduced risk of overfitting during training, while accurately capturing both short-term fluctuations and long-term trends in temperature variation. Compared with the LSTM [33] network, GRU has a simpler structure and fewer parameters. The GRU architecture contains two core gating mechanisms: the update gate and the reset gate. The update gate dynamically adjusts the balance between historical temperature memory and current operating information, which is particularly effective for handling abrupt temperature transitions caused by sudden changes in waste calorific value. The reset gate selectively discards irrelevant historical states, thereby filtering out sensor noise and improving the robustness of prediction results.

The reset gate $r_t$ and update gate $z_t$ are influenced by the previous hidden state $h_{t-1}$ and the current furnace temperature $Y_t$. The calculation formulas for $r_t$ and $z_t$ are given in Equation (7) [34]:

$$\begin{array}{l}{r}_t=\sigma (w_{xr}{Y}_t+w_{hr}{h}_{t-1}+b_r)\\ z_t=\sigma (w_{xr}{Y}_t+w_{hz}{h}_{t-1}+b_z)\end{array}$$

(7)

For the calculation of the candidate hidden state ${\tilde{h}}_t$ the update relies on the current furnace temperature input together with part of the preceding hidden state. The reset gate $r_t$ determines the extent to which historical furnace temperature information is retained:

$${\tilde{h}}_t=\tanh (w_{xh}{Y}_t+r_t\otimes (w_{hh}{h}_{t-1})+b_h)$$

(8)

Finally, the update gate $z_t$ updates the hidden state $h_t$ at the current time step, which incorporates the furnace temperature information, as shown in Equation (9):

$$h_t=z_t\otimes h_{t-1}+(1-z_t)\otimes {\tilde{h}}_t$$

(9)

In the equation, $\sigma$ represents the Sigmoid function; $w_{xr}$, $w_{hr}$, $w_{hz}$, $w_{xh}$, $W_{hh}$ denotes the weight parameters; and $b_r$, $b_h$, $b_z$ refers to the bias parameters.

3.1.2. Self-Learning of Influence Weight Coefficients Based on the Self-Attention Mechanism

When processing long-sequence incineration data, the GRU can effectively capture short-term dependencies in temperature fluctuations. However, it still faces limitations in modeling long-range dependencies, particularly under abnormal operating conditions that lead to significant furnace temperature variations. To address this issue, this study introduces the SA mechanism to enhance feature learning in long sequences and accurately capture complex long-range dependencies [35]. The core advantage of the self-attention mechanism lies in its ability to dynamically assign different weights to historical temperature data according to the current operating parameters. Specifically, the current operating state is encoded as a query, which is compared with historical states represented as keys to compute similarity scores. These scores are then normalized via a softmax function to produce attention weights, allowing the model to focus more on the most relevant past temperature data when predicting the current furnace temperature. In this way, the model can automatically learn the influence of each operating parameter on the present furnace temperature, effectively identifying and strengthening critical features while ignoring redundant or noisy information. Compared with traditional GRU networks, the self-attention mechanism is more suitable for handling complex data with significant temporal dependencies. In furnace temperature prediction tasks, it enables more precise weighting across different time steps, thereby not only capturing short-term fluctuations but also reinforcing long-term trends in temperature variation. This provides more accurate prediction performance under complex operating conditions. The specific implementation is as follows:

A series of hidden states ($h_t=[h_1,h_2,h_3,\cdots h_t]$) generated by the GRU model are linearly transformed to produce three matrices: the query (Q) matrix, key (K) matrix, and value (V) matrix. The query vectors are generated using the operating parameters at the current time step, and these operating conditions are compared with historical temperature data to determine their influence on the current temperature prediction. The specific equations are as follows [36]:

$$Q={\mathit{h}}_t{W}^q$$

(10)

The key matrix is constructed from the historical temperature data, where each time step of the historical sequence is mapped to a key vector. These key vectors are then compared with the query vector to calculate their similarity, which reflects the relevance of each historical moment to the current prediction.

$$K={\mathit{h}}_t{W}^k$$

(11)

The value matrix corresponds to the measured values or feature data of the historical temperature, aligned with the historical key vectors. After the attention weights are calculated, these weights are applied to the value matrix to compute a weighted average of the historical temperature data, thereby generating the result for the current temperature prediction.

$$V={\mathit{h}}_t{W}^v$$

(12)

In the equation: $Q$, $K$, $V$ represent matrices obtained from the same input through different linear transformations; and $W^q$, $W^k$, $W^V$ are the learned weight matrices.

$$a=\mathrm{softmax}({\displaystyle \frac{Q{K}^T}{\sqrt{d}}})$$

(13)

$$Y_t=aV$$

(14)

$Y_t$ represents the weighted temperature obtained from the historical temperature data, $a$ denotes the attention weight, $\sqrt{d}$ indicates the vector dimension, and softmax is the normalization activation function.

3.2. IWOA-Based Parameter Optimization Algorithm

The IWOA optimization algorithm is employed to tune parameters of the GRU model, such as the learning rate, the number of hidden nodes (n) and the dropout rate ($p$), thereby reducing the tedious process of manual adjustment and improving parameter tuning efficiency. These parameters have a direct impact on the performance of the GRU model: the learning rate determines the step size of parameter updates during training, while the number of hidden nodes influences the model’s representation and memory capacity, The dropout rate is used to prevent overfitting during training. By optimizing these parameters, IWOA enables the GRU to better adapt to complex datasets, thereby enhancing training efficiency and improving prediction accuracy.

The Whale Optimization Algorithm (WOA), inspired by the foraging behavior of humpback whales, is a swarm intelligence optimization method that mainly involves three stages: encircling prey, spiral hunting, and prey searching [37]. We selected WOA for this study because it offers strong global search capability, fast convergence, and relatively simple implementation with few parameters, making it well-suited for optimizing the parameters of our GRU-based furnace temperature prediction model. Compared with other algorithms such as Particle Swarm Optimization (PSO) or Genetic Algorithms (GA), WOA has demonstrated more stable and efficient performance in similar optimization tasks. WOA is adopted to optimize the parameters of the GRU model. First, a set of candidate initial parameters is randomly generated and used to train the GRU model. The training loss corresponding to each parameter configuration is then calculated and regarded as its fitness value. Next, whales simulate the behavior of encircling prey by approaching the current best solution and updating their positions according to the fitness of the candidate solutions. Guided by the global best solution, the whale individuals iteratively adjust their positions and gradually converge toward the global optimum through contraction behaviors. During the search process, the individuals update their positions based on training errors and fitness evaluations, and the population is updated accordingly. This iterative process continues until the predefined termination condition is satisfied. Finally, the optimized GRU parameters are output, ensuring that the GRU model achieves optimal performance in time-series prediction or other tasks. When new datasets or task requirements arise, the optimization process can be repeated to re-adjust the parameters.

(1) Encircling prey: In the WOA, the encircling phase simulates the process in which whales gradually approach their prey through a contraction behavior, and eventually converge to the global optimum in the later stage. This behavior is governed by the value of parameter $A$. When $\left|A\right|<1$, the algorithm enters the encircling phase, and the whale individuals are updated according to the position of the current best solution. The mathematical model is given in Equation (15) [37].

$$L\left(t+1\right)=L^{*}\left(t\right)-A\left|C{L}^{*}\left(t\right)-L\left(t\right)\right|$$

(15)

In the equation: $t$ denotes the indicates how many iterations are performed. $L\left(t\right)$, $L^{*}\left(t\right)$ represent the position vectors of the whale individual and the prey, respectively; $A$ denotes the coefficient vector, defined a $A=2d{r}_1-d$; $C$ denotes the coefficient vector, $C=2r_2$ ($r$ is a random vector within [0, 1]), and d is a parameter linearly decreasing from 2 to 0.

$$d=2\times {\displaystyle \frac{t_{\max }-t}{t_{\max }}}$$

(16)

(2) Spiral hunting: In the WOA, during the spiral hunting phase, the process of whales moving around the prey along a spiral route is simulated. The corresponding mathematical model is given in Equation (17).

$$L\left(t+1\right)=\left|L^{*}-L\left(t\right)\right|\cdot {\mathrm{e}}^{bl}\cos \left(2\pi l\right)+L^{*}\left(t\right)$$

(17)

In the equation: $b$ is used to define the logarithmic spiral shape, and $l$ denotes a random number within the range [−1, 1].

During the optimization process, the contraction-based encircling strategy and the spiral updating strategy of whale individuals are performed simultaneously. The selection between the two strategies is controlled by a probability $p$, and the position update is expressed as in Equation (18).

$$L\left(t+1\right)\left\{\begin{array}{l}{L}^{*}\left(t\right)-A\left|C{L}^{*}\left(t\right)-L\left(t\right)\right|,p<0.5\\ \left|L^{*}-L\left(t\right)\right|\cdot {\mathrm{e}}^{bl}\cos \left(2\pi l\right)+L^{*}\left(t\right),p\ge 0.5\end{array}\right.$$

(18)

In the equation: $p$ represents a random number between 0 and 1.

(3) Prey Search: In order to strengthen the global search ability and prevent convergence to local optima at an early stage, whale individuals randomly explore new prey positions within the search space. The corresponding mathematical model is expressed in Equation (19).

$$L\left(t+1\right)=L_{rand}\left(t\right)-A\cdot \left|C{L}_{rand}\left(t\right)-L\left(t\right)\right|$$

(19)

In the equation: $L_{rand}$ denotes the position vector of a randomly selected whale individual.

When $\left|A\right|\ge 1$, the whale does not move toward the current prey. Instead, it randomly selects another position $L_{rand}$ in the search space and uses it as a reference point to perform global exploration.

To improve the traditional WOA’s capability to avoid local optima and increase search efficiency, this study introduces three improvements to the algorithm.

(1)

Population diversity enhancement based on Latin Hypercube Sampling (LHS).

During the population initialization stage, the LHS strategy is introduced to enhance population diversity. In the traditional WOA, the initial population is generated randomly, which may result in uneven distribution of individuals and overlaps among them [38]. Such issues can negatively affect the optimization performance of the algorithm [39]. Therefore, it is necessary to improve and optimize the population initialization method to strengthen the algorithm’s search capability.

The specific implementation is as follows: let the initial population size of WOA be $N$, where each individual represents a solution and its position consists of $v$ variables. For each variable $l_j(j=1,2,\cdots v)$, its domain $[l_j^{\min },l_j^{\max }]$ is divided into $M$ intervals, each with a length of $(l_j^{\max }-l_j^{\min })/M$. Within each interval, a random point is selected as the sampling value of the variable, ensuring that each interval contains one sampling point. The $N$ sampled points are then randomly recombined to form the individuals of the initial population. The position vector of an individual $L_{pos}$ is represented as $L_{pos}=(l_{i1},l_{j=i2},\cdots ,l_{iv})$, where $l_{ij}$ denotes the $i$-th variable value in the $j$-th sample combination. This sampling method provides a more uniform and efficient exploration of the search space, which not only improves search efficiency but also facilitates the identification of the optimal hyperparameter combination.

(2)

Adaptive Threshold Selection Strategy

In the traditional WOA, during the prey-hunting phase, a random number within the range of [0, 1] is generated and compared with 0.5 to determine whether the whale chooses an encircling behavior or a spiral motion. However, this equal-probability selection strategy lacks reliability, as it does not allow whales to adaptively choose the most suitable movement pattern for the current individual. To address this limitation, this study introduces an adaptive threshold selection strategy to replace the fixed threshold in the conventional WOA. This method automatically adjusts the threshold according to the problem characteristics during the search process, thereby facilitating the identification of the optimal hyperparameter combination for the GRU model. The calculation formula for the adaptive threshold is given in Equation (20) [40].

$$p_a=1-\left[{\displaystyle \frac{1}{\lambda +\xi }}\cdot \left(\lambda \cdot {\displaystyle \frac{t^{\lambda }}{{t_{\max }}^{\lambda }}}+\xi \cdot {\displaystyle \frac{t^{\xi }}{{t_{\max }}^{\xi }}}\right)\right]$$

(20)

In the equation: $t$ denotes the current iteration number; $t_{\max }$ represents the maximum number of iterations; and $\lambda$, $\xi$ are the control parameters, with $\lambda =2$, $\xi =4$.

As shown in Equation (19), the adaptive selection threshold decreases gradually with the increase in iteration number. This indicates that, in the early stage of the algorithm, the adaptive probability threshold is relatively large, and whales tend to prioritize the encircling strategy. With the increase in iterations, the adaptive probability threshold gradually decreases, making it more likely for whales to adopt the spiral updating strategy. Accordingly, Equation (18) is updated to Equation (21).

$$L\left(t+1\right)\left\{\begin{array}{l}{L}^{*}\left(t\right)-A\left|C{L}^{*}\left(t\right)-L\left(t\right)\right|,p<p_a\\ \left|L^{*}-L\left(t\right)\right|\cdot {\mathrm{e}}^{bl}\cos \left(2\pi l\right)+L^{*}\left(t\right),p\ge p_a\end{array}\right.$$

(21)

(3)

Population Resetting Based on Gaussian Disturbance

In the later stages of the search, swarm intelligence algorithms often encounter population aggregation, which reduces the diversity of the search population and makes the algorithm more prone to being trapped in local optima. To address this issue, Gaussian disturbance is introduced to implement population resetting. This strategy enhances diversity during the search process, prevents the algorithm from stagnating around local optima, improves global search efficiency, and ultimately enhances the quality of the optimization results.

The probability density function is given by [41]:

$$f\left(x\right)={\displaystyle \frac{1}{\sqrt{2\pi }\sigma }}\exp \left(-{\displaystyle \frac{{\left(l-\mu \right)}^2}{2{\sigma }^2}}\right)$$

(22)

In Equation (17), when the value of $\sigma$ is relatively large, the probability value at position $l$ becomes lower, indicating that the curve is relatively flat and the probability distribution is more dispersed. In contrast, when the value of $\sigma$ is smaller, the curve becomes steeper and the probability distribution is more concentrated. In the IWOA, the Gaussian perturbation applied to the optimal individual is formulated as Equation (23).

$$F\left(\mathrm{x}\right)=l_{*}\left(t\right)+l_{*}\left(t\right)\cdot normrnd\left(0,1\right)$$

(23)

In the equation, $normrnd\left(0,1\right)$ denotes a random number produced from a Gaussian distribution with a mean of 0 and variance of 1.

To evaluate the optimization capability of the improved IWOA, the objective function $f_{object}$ and the fitness function $f_{fit}(IWOA)$ are defined as follows.

$$f_{object}={\displaystyle \frac{{\displaystyle \sum _{i=1}^{200}\sqrt{{(b_i-{\widehat{b}}_i)}^2}}}{200}}$$

(24)

$$f_{fit}(IWOA)={\displaystyle \frac{1}{1+f_{object}}}$$

(25)

In the equation, $b_i$ and ${\widehat{b}}_i$ denote the measured temperature of the i-th sample and the temperature value calculated based on the optimized parameters in [42].

The correspondence between the IWOA and the parameter optimization problem is summarized in

Table 1. Correspondence between the IWOA and the Parameters Optimization Problem.

IWOA Parameter	Parameter Optimization Problem
Position of a whale	$\mathrm{Potential} \mathrm{feasible} \mathrm{solution} \mathrm{of} \mathrm{the} \mathrm{optimized} \mathrm{parameters} (\eta$$,n$$,p)$
Positions of the whale population	$\mathrm{Set} \mathrm{of} \mathrm{potential} \mathrm{feasible} \mathrm{solutions} \mathrm{of} \mathrm{the} \mathrm{optimized} \mathrm{parameters} (\eta$$,n$$,p)$
Movement of whales	$\mathrm{Search} \mathrm{process} \mathrm{for} \mathrm{the} \mathrm{optimal} \mathrm{solution} \mathrm{of} \mathrm{parameters} (\eta$$,n$$,p)$
Bubble-net attack	$\mathrm{Update} \mathrm{strategy} \mathrm{for} \mathrm{candidate} \mathrm{solutions} \mathrm{of} \mathrm{parameters} (\eta$$,n$$,p)$
Encircling prey	$\mathrm{Convergence} \mathrm{process} \mathrm{to} \mathrm{the} \mathrm{optimal} \mathrm{solution} \mathrm{of} \mathrm{parameter} (\eta$$,n$$,p)$
Position of prey	$\mathrm{Global} \mathrm{optimal} \mathrm{solution} \mathrm{of} \mathrm{parameter} (\eta$$,n$$,p)$

. In this framework, the position of a whale represents a potential feasible solution for the optimized parameters ($\eta$,$n$,$p$); the position of the prey represents the global optimal solution of the parameters ($\eta$,$n$,$p$).

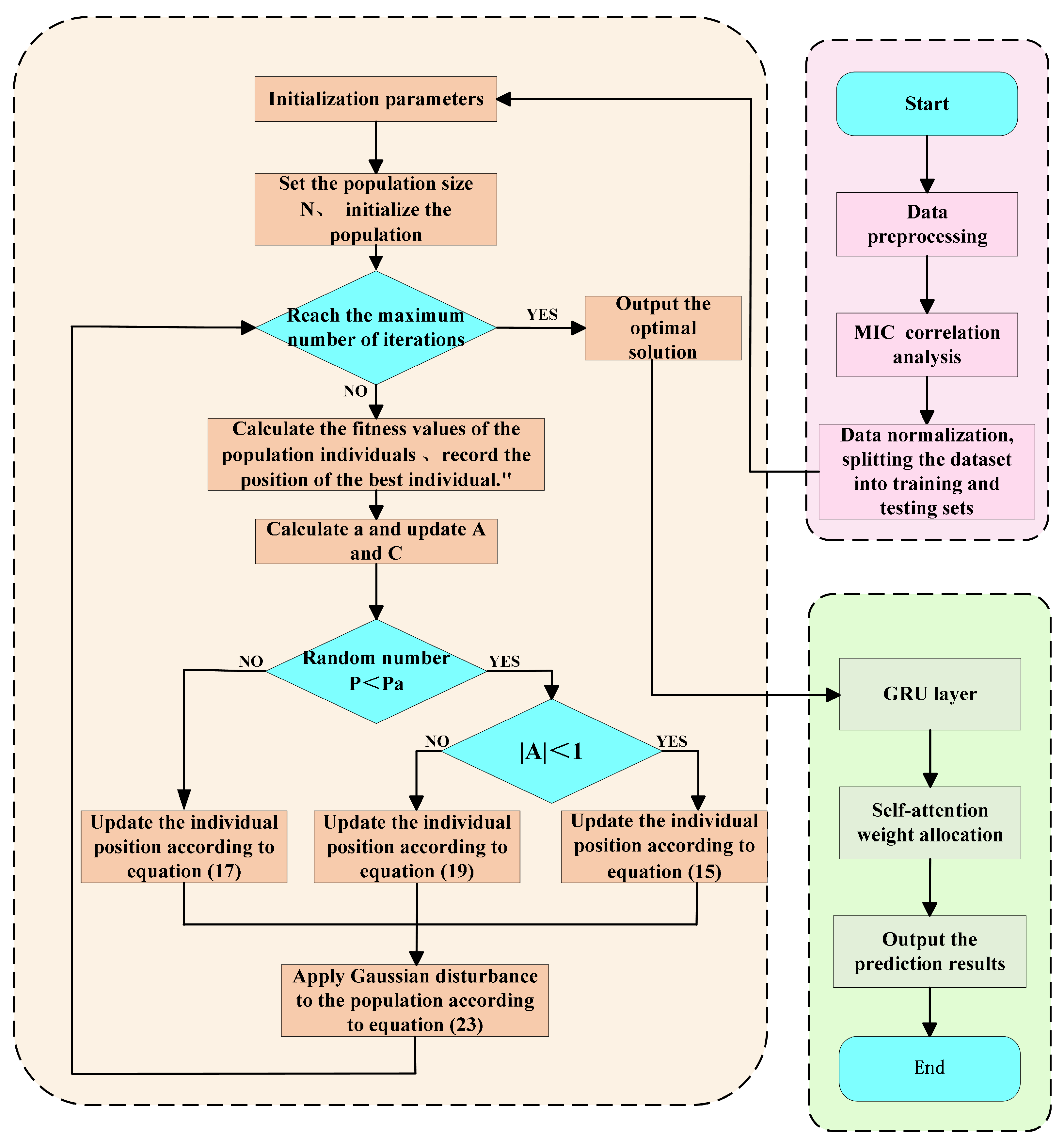
3.3. IWOA-SAGRU-Based Furnace Temperature Prediction: Algorithmic Workflow

The workflow of the IWOA-SAGRU-based furnace temperature prediction model is illustrated in Figure 4, The key steps are outlined as follows:

(1) According to MIC analysis results, the main variables influencing the furnace temperature are identified. The dataset is subsequently split into training and testing subsets, and the obtained data are normalized using the formula given in Equation (26).

$$s^{\ast }={\displaystyle \frac{s-s_{\min }}{s_{\max }-s_{\min }}}$$

(26)

In the equation, $s^{\ast }$ represents the normalized data, $s_{\max }$ and $s_{\min }$ denote the maximum and minimum values of the dataset, respectively.

(2) Construct the basic framework of the GRU-based network model and integrate the attention mechanism to improve the model’s ability to generalize.

(3) Initialize the SAGRU model and employ the IWOA to update the learning rate ($\eta$), the number of hidden nodes ($n$) and dropout rate ($p$). The model parameters are iteratively updated until the error converges or the maximum number of iterations is reached, at which point the training process terminates.

(4) Output the prediction results and evaluate the model performance by comparing different evaluation metrics with those of other models.

4. Experimental Study

To verify the effectiveness of the IWOA-SAGRU model for furnace temperature prediction in MSWI, historical measured data from a municipal solid waste incineration plant in Beijing were used for case analysis. The municipal solid waste incineration (MSWI) plant adopts a moving grate combustion technology and mainly treats urban solid waste, with a daily treatment capacity of approximately 1600 tons. Electricity is primarily generated through waste incineration. The composition of the MSW treated in this plant is shown in

Table 2. MSW properties.

Proximate (as a Received Basis, wt%)		Ultimate (as a Dry Ash-Free Basis, wt%)
Moisture	48	C	65.2
Volatile matter	33.31	H	8.09
Fixed carbon	8.08	O	24.93
Ash	10.61	N	1.12
		S	0.24

[43]. From the perspective of waste components, the moisture content is 48%, volatile matter is 33.31%, fixed carbon is 8.08%, and ash is 10.61%. In terms of elemental composition, carbon accounts for 65.2%, hydrogen for 8.09%, oxygen for 24.93%, nitrogen for 1.12%, and sulfur for 0.24%. These characteristics indicate a certain combustibility of the waste, but also highlight the necessity of pollutant control. At present, the operation of the plant relies mainly on manual control rather than full automation. From waste feeding and furnace combustion to waste heat recovery and power generation, the entire process depends on manual operation. Experienced operators perceive the changing operating conditions, predict temperature variations during combustion, and then adjust the manipulated variables to achieve temperature control.

The plant is equipped with a comprehensive monitoring and control system that can record furnace temperatures and related operating parameters in real time. A sampling interval of one second was adopted to continuously collect temperature data from key areas of the incinerator (from 08:00 to 24:00), covering the full production cycle. The core purpose of this design was to establish a raw temperature database with high temporal resolution. Considering the different requirements of data time scales in subsequent research applications, high-frequency sampling (1 s interval) was first used to preserve both the instantaneous fluctuations and the complete variation process of the temperature parameters. Then, targeted down-sampling was conducted according to specific research objectives (e.g., optimization of control algorithms and analysis of operating stability). This approach ensured the completeness and validity of the original data, while also providing flexible data support for studies at different levels, thus avoiding limitations in research scenarios caused by a fixed initial sampling interval.

In this experiment, 3000 sets of furnace temperature data and their related influencing factors were collected. After preprocessing, the dataset was divided into training and testing sets in a 4:1 ratio. The testing set was then used to evaluate the rationality of the proposed algorithm.

4.1. The MIC Feature Selection Module Algorithm

As previously mentioned, during the MSWI combustion process, there are numerous variables that are related to the furnace temperature. To guarantee accurate temperature prediction while simultaneously lowering model complexity, it is essential to select the relevant features associated with temperature. The MIC is a statistical method used to measure the degree of association between variables and can effectively capture the nonlinear relationships between them [44]. Compared to the Pearson linear correlation measure, MIC offers better stability and universality, enabling deeper analysis of the relationships between variables. In this study, a comparison between the Pearson and MIC analysis methods is performed. By calculating the correlation coefficients between different variables and the furnace temperature, variables with high correlation coefficients are selected as inputs, which helps reduce the number of input features and lower the model’s dimensionality.

The correlation formula for the MIC analysis method is shown in Equation (27) [44]:

$$MIC(x,y)=\underset{a·b<B}{\max }{\displaystyle \frac{I(x,y)}{{\log }_2\min (a,b)}}$$

(27)

In the equation, $a$ represents the number of horizontal grid divisions, $b$ denotes the number of vertical grid divisions, and $B$ refers to the variable, typically set to approximately 0.6 times the total data size. $x$ is the feature variable, and y represents the furnace temperature.

The left-side temperature, combustion section inlet temperature, primary air flow, secondary air flow, primary air temperature, and secondary air temperature are identified as key temperature-influencing factors based on expert knowledge. The value ranges of each variable are presented in

Table 3. Table of Temperature-Influencing Factors Variables.

Serial Number	Variable Name	Unit	Range of Variation
1	Primary air flow	m3/s (N)	153.609–439.860
2	Primary air temperature	K	435.860–460.342
3	Main steam flow	kg/s	9191.778–9526.580
4	Left-side furnace temperature	K	1224.089–1301.078
5	Secondary air flow	m3/s (N)	0.776–32.574
6	Inlet temperature of the combustion zone	K	461.757–502.531
7	Secondary air temperature	K	295.744–300.461
8	Combustion grate temperature	K	451.638–598.742
9	Furnace negative pressure	Pa	−108.614–104.073

.

The correlation of the above-mentioned influencing variables was calculated to determine their effect on furnace temperature. The results were then compared with the Pearson correlation coefficient method, as detailed in Equation (28):

$$\rho = {\displaystyle \frac{Cov(X,Y)}{{\sigma }_X {\sigma }_Y }}$$

(28)

In the equation, $Cov(X,Y)$ represents the covariance between $X$ and $Y$; ${\sigma }_X$ denotes the standard deviation of $X$, ${\sigma }_Y$ represents the standard deviation of $Y$. $X$ refers to the influencing factor variable, while $Y$ represents the furnace temperature.

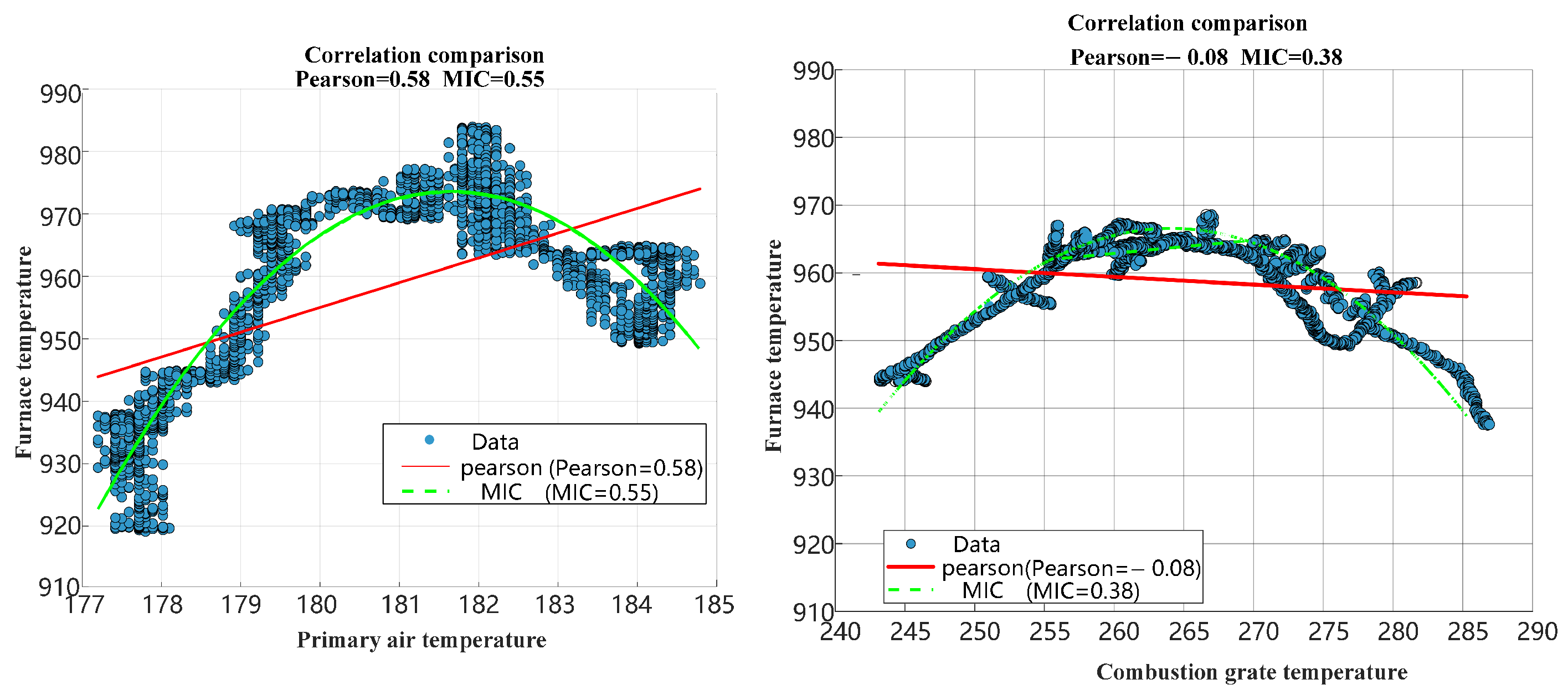
To enhance the understanding of the influence of the above-mentioned variables on furnace temperature, visualizations were created. The results are shown in Figure 5 and Figure 6.

Figure 5 and Figure 6 clearly reflect the correlation between the influencing variables and the output variable, furnace temperature. However, there are differences in the correlation among the variables.

In

Table 4. Analysis of Pearson correlation.

Variable Name	Correlation Coefficient
Left-side furnace temperature	0.80
Primary air flow	0.60
Main steam flow	0.59
Primary air temperature	0.58
Secondary air temperature	0.39
Secondary air flow	0.37
Inlet temperature of the combustion zone	0.34
Furnace negative pressure	−0.20
Combustion grate temperature	−0.08

, variables showing a correlation above 0.5 with the output variable are presented, in order, are the furnace left-side temperature, primary air flow, main steam flow, and primary air temperature.

In

Table 5. Analysis of MIC correlation.

Variable Name	Correlation Coefficient
Primary air flow	0.67
Main steam flow	0.61
Primary air temperature	0.55
Left-side furnace temperature	0.47
Combustion grate temperature	0.38
Furnace negative pressure	0.32
Inlet temperature of the combustion zone	0.26
Secondary air flow	0.19
Secondary air temperature	0.13

, the four variables with the highest correlation identified by the MIC analysis method are, in descending order, the primary air volume, the main steam flow, the primary air temperature, and the left-side furnace temperature.

There are differences in the correlation results of feature variables obtained by the two analysis methods. To verify the superiority of the MIC over the Pearson correlation coefficient in detecting nonlinear relationships, this study conducts a comparative analysis of the primary air temperature and the grate temperature in the combustion section using scatter plots combined with fitted curves, as shown in Figure 7.

In Figure 7, the Pearson correlation coefficient can only capture linear relationships, and its fitted curve deviates significantly from the actual data distribution. In contrast, the MIC, through dynamic binning and mutual information maximization, successfully identifies the quadratic relationship embedded in the data. Its nonlinear fitted curve shows a markedly higher consistency with the data points. This finding confirms that, for complex nonlinear relationships, MIC provides a more comprehensive quantification of statistical dependence between variables. Therefore, four feature variables—primary air flow, main steam flow, primary air temperature, and left-side furnace temperature—are selected as inputs, with the furnace temperature as the output.

4.2. Performance Evaluation of the IWOA

To validate the optimization capability of the IWOA, this study selects the Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and the standard WOA as comparison benchmarks. Six test functions with different characteristics are used for evaluation, as listed in

Table 6. Test Functions.

Test Functions	Range
$F_1(x)={\displaystyle \sum _{i=1}^n}{x}_i^2$	[−100, 100]
$F_2\left(x\right)={\displaystyle \sum _{i=1}^n}\left|x_i\right|+{\displaystyle \prod _{i=1}^n}\left|x_i\right|$	[−10, 10]
$F_3\left(x\right)={\displaystyle \sum _{i=1}^n}{\left({\displaystyle \sum _{j-1}^i}{x}_j\right)}^2$	[−100, 100]
$F_4\left(x\right)={\displaystyle \sum _{i=1}^n}i{x}_i^4+random[0,1)$	[−1.28, 1.28]
$F_5\left(x\right)=\left[x_i^2-10\cos \left(2\pi x_i\right)+10\right]$	[−5.12, 5.12]
$F_6\left(x\right)=-20\exp \left(-0.2\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}{x}_i^2}\right)-\exp \left[{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}\cos \left(2\pi x_i\right)\right]+20+e$	[−32, 32]

. The algorithm is configured with a maximum of 500 iterations and a population size of 30. To eliminate errors caused by randomness, each of the four algorithms is independently executed multiple times on the six test functions, and the average optimal value is taken as the optimization result. The comparative results of different algorithms are summarized in

Table 7. Results Comparison of Optimization Algorithms.

Test Functions	Evaluation Metrics	GA	PSO	WOA	IWOA
F1	Mean	3.62 × 103	3.52 × 10−2	7.20 × 10−10	1.46 × 10−19
	Best	1.45 × 103	1.41 × 10−3	3.32 × 10−13	1.17 × 10−24
F2	Mean	2.11 × 101	3.20 × 101	5.16 × 10−8	1.74 × 10−13
	Best	1.39 × 101	8.14 × 10−2	5.12 × 10−9	2.24 × 10−15
F3	Mean	3.48 × 103	1.00 × 103	8.98 × 10−10	4.16 × 10−20
	Best	1.77 × 103	1.75 × 10−3	1.86 × 10−12	1.40 × 10−22
F4	Mean	1.43 × 100	5.17 × 100	1.48 × 10−2	7.48 × 10−4
	Best	4.08 × 10−1	6.53 × 10−2	3.29 × 10−3	1.42 × 10−4
F5	Mean	9.18 × 101	1.27 × 102	4.61 × 10−1	0.00 × 100
	Best	6.48 × 101	6.92 × 101	6.78 × 10−11	0.00 × 100
F6	Mean	1.13 × 101	2.03 × 100	3.93 × 100	1.49 × 10−11
	Best	9.19 × 100	2.32 × 10−2	8.06 × 10−7	1.35 × 10−12

.

As shown in Table 7, when the average of the optimal values is used as the evaluation metric, the optimization results obtained by the IWOA outperform those of the other three algorithms across all six test functions. In particular, for the F(5) test function, both the average value and the optimal value found by the IWOA are equal to zero. Overall, the results indicate that the average values achieved by IWOA in multiple optimization runs are consistently smaller than those of the other algorithms, demonstrating that IWOA possesses superior global search capability.

4.3. Model Evaluation Metrics

To evaluate the performance of the IWOA-SAGRU temperature prediction model, this study employs the mean absolute error $S_{\mathrm{MAE}}$, root mean square error $S_{\mathrm{RMSE}}$, mean absolute percentage error $S_{\mathrm{MAPE}}$, and coefficient of determination $S_{{\mathrm{R}}^2}$ as performance metrics. The corresponding formulas are given in Equations (29)–(32).

$$S_{\mathrm{MAE}}={\displaystyle \frac{1}{n_s}}{\displaystyle \sum _{i=1}^n\left|\stackrel{\wedge }{(y_i}-y_i)\right|}$$

(29)

$$S_{\mathrm{RMSE}}=\sqrt{{\displaystyle \frac{1}{n_s}}{\displaystyle \sum _{i=1}^n{\left(y_i-\stackrel{\wedge }{y_i}\right)}^2}}$$

(30)

$$S_{\mathrm{MAPE}}={\displaystyle \frac{1}{n_s}}{\displaystyle \sum _{i=1}^n\left|\frac{y_i-\stackrel{\wedge }{y_i}}{y_i}\right|}\times 100\%$$

(31)

$$S_{{\mathrm{R}}^2}=1-{\displaystyle \frac{{\displaystyle \sum _{i=1}^n{(\stackrel{\wedge }{y_i}-y_i)}^2}}{{\displaystyle \sum _{i=1}^n{(y_i-\overline{y_i})}^2}}}$$

(32)

In the equations, $n_s$ denotes the number of samples; ${\stackrel{\wedge }{y}}_i$ and $y_i$ represent the predicted temperature value and measured temperature value, respectively; $\overline{y_i}$ is the mean of measured temperature values. Parameters $S_{\mathrm{MAE}}$, $S_{\mathrm{RMSE}}$ and $S_{\mathrm{MAPE}}$ reflect the error between the prediction and the measured values, where a smaller error indicates higher prediction accuracy of the model. Moreover, the closer $S_{{\mathrm{R}}^2}$ is to 1, the better the model fitting performance.

4.4. Experimental Analysis

The optimal parameter settings of the IWOA-SAGRU model are presented in

Table 8. Setting of model hyperparameters.

Hyperparameters	Initial Value	Optimized Value
Learning rate	0.001	0.039
Number of hidden nodes	20	32
dropout rate	0.13	0.25

. To compare the characteristics of the SAGRU prediction model, a GRU prediction model was also established. The key parameters of the GRU model were determined using IWOA. The calculation results and error comparisons are shown in Figure 8 and

Table 9. Comparison of model errors.

Model	${\mathit{S}}_{\mathbf{RMSE}}$	${\mathit{S}}_{\mathbf{MAE}}$	${\mathit{S}}_{\mathbf{MAPE}}$	${\mathit{S}}_{{\mathbf{R}}^2}$
GRU	2.1312	1.4367	0.1492	0.9717
SAGRU	1.8627	1.0022	0.1044	0.9789
IOWA-SAGRU	1.7275	0.8855	0.0927	0.9815

.

As shown in Figure 8, the single network model exhibits larger deviations in prediction results when the temperature data fluctuate significantly. In contrast, the IWOA-optimized SAGRU model captures the variation trend of the temperature data more effectively, resulting in a predicted curve that nearly overlaps with the measured data.

As shown in Table 9, the IWOA-SAGRU model achieves higher prediction accuracy and demonstrates better forecasting performance. The comparative experimental results indicate that, compared with the SAGRU model, the IWOA-SAGRU model reduces the errors by 7.82%, 12.62%, and 13.18%, respectively. This confirms that integrating the attention mechanism with the optimization algorithm can effectively improve prediction accuracy. The attention mechanism improves the forecasting accuracy of the GRU model by assigning suitable weights according to the inherent correlations between different variables. Meanwhile, the introduction of the IWOA optimization algorithm allows the determination of optimal values for key network parameters, leading to higher prediction accuracy compared with the trial-and-error method.

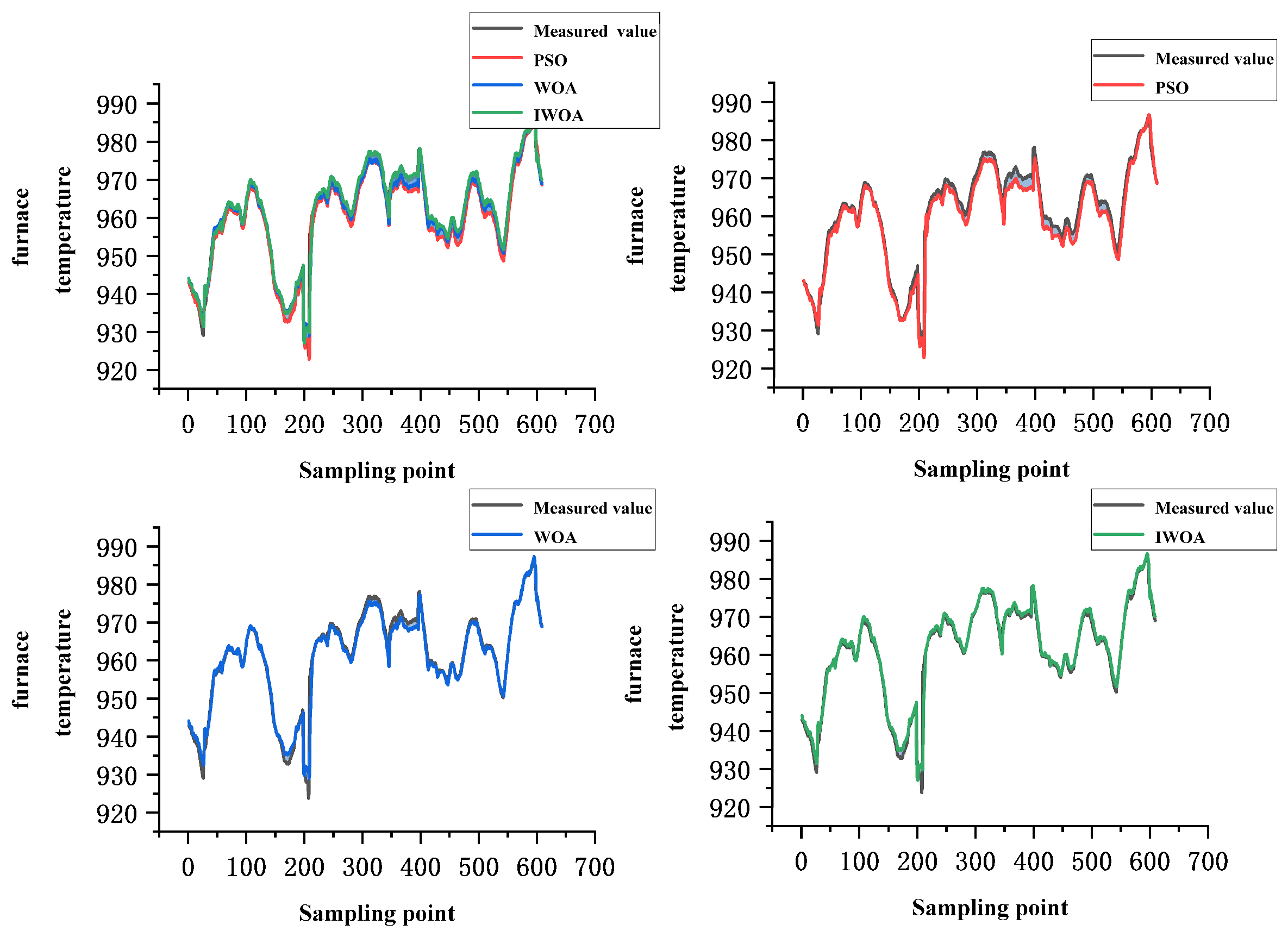
To further investigate the impact of different optimization algorithms on the performance of the SAGRU model, A population size of 10 and a maximum of 200 iterations were used. Under the same conditions, the proposed model was compared with the PSO-SAGRU and WOA-SAGRU models. The corresponding prediction results and errors are presented in Figure 9 and

Table 10. Comparison of algorithm errors.

Model	${\mathit{S}}_{\mathbf{RMSE}}$	${\mathit{S}}_{\mathbf{MAE}}$	${\mathit{S}}_{\mathbf{MAPE}}$	${\mathit{S}}_{{\mathbf{R}}^2}$
PSO	1.9229	1.0897	0.1138	0.9771
WOA	1.7833	0.9660	0.1010	0.9802
IWOA	1.7275	0.8855	0.0927	0.9815

.

As shown in Figure 9 and Table 10, the prediction curve of the proposed IWOA-SAGRU model is closer to the measured furnace temperature variation curve compared with models optimized by other algorithms. The error metrics of the IWOA-optimized model are reduced by 11.31% and 3.23%, and by 22.76% and 8.95%, respectively, relative to the other models. This indicates that the IWOA can better identify the optimal combination of key parameters (learning rate $\eta$, number of hidden nodes $n$ and dropout rate $p$), thereby reducing the prediction error of the SAGRU model and improving its accuracy. These results verify the superiority of the IWOA-SAGRU model.

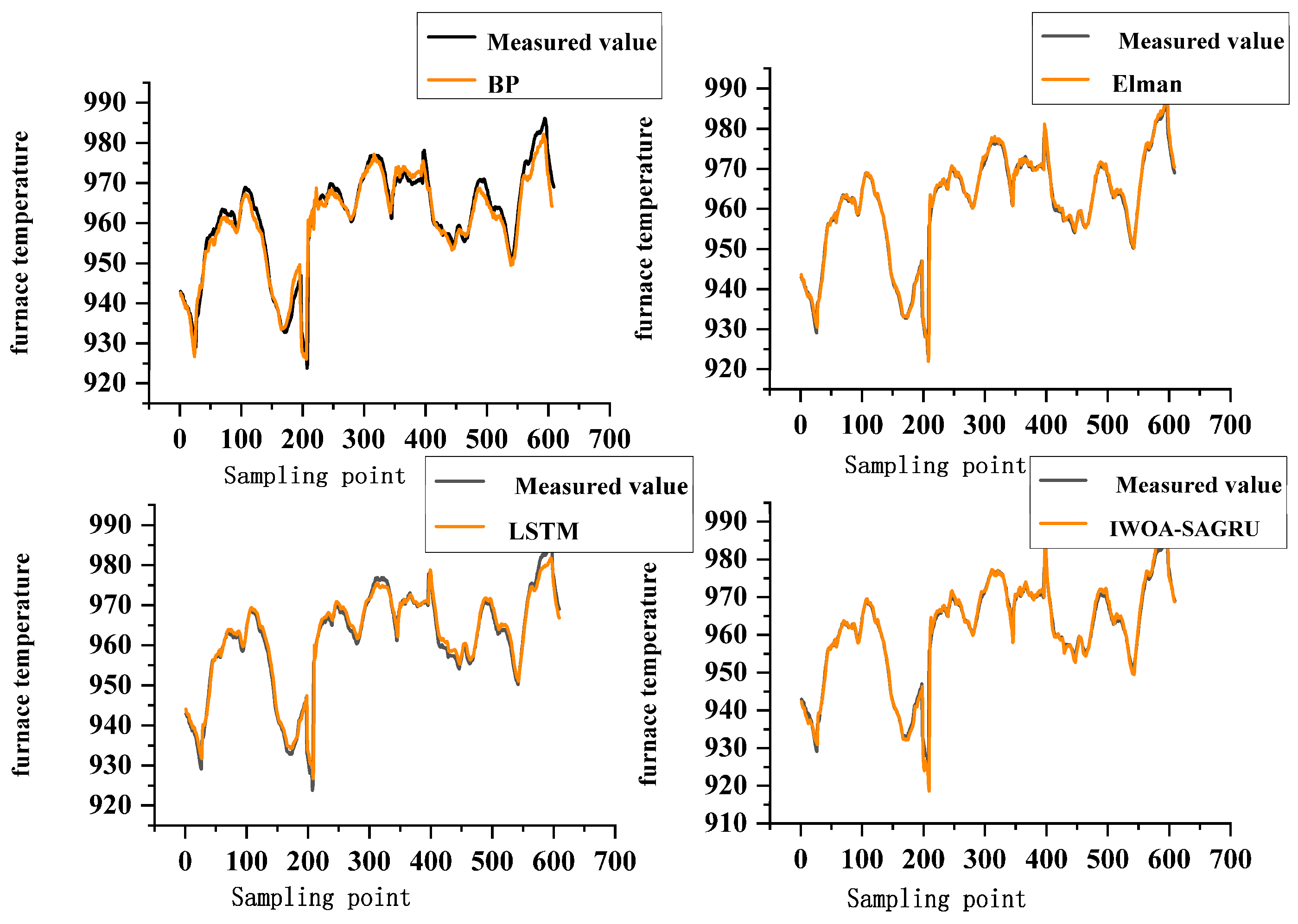
To further assess the performance advantage of the IWOA-SAGRU model in temperature prediction, comparative tests were carried out using the BP neural network, Elman neural network, and LSTM network. To ensure fairness, the parameters of the BP, Elman, and LSTM models were standardized: each network contained 10 neurons, trained for 100 epochs, with a learning rate of 0.001 and a batch size of 64. The prediction outcomes of all models are illustrated in Figure 10 and summarized in

Table 11. Comparison of error metrics for forecasting models.

Model	${\mathit{S}}_{\mathbf{RMSE}}$	${\mathit{S}}_{\mathbf{MAE}}$	${\mathit{S}}_{\mathbf{MAPE}}$	${\mathit{S}}_{{\mathbf{R}}^2}$
BP	3.0976	1.9128	0.1981	0.9406
Elman	2.4421	1.5139	0.1576	0.9628
LSTM	2.1964	1.4533	0.1519	0.9701
IWOA-SAGRU	1.7275	0.8855	0.0927	0.9815

.

From Figure 10, Table 11, it can be observed that the IWOA-SAGRU model achieves the best prediction performance, with the lowest values of $S_{\mathrm{RMSE}}$, $S_{\mathrm{MAPE}}$, and $S_{\mathrm{MAE}}$. In contrast, the BP and Elman neural network models, as classical deep learning algorithms, have limited ability to capture long-term temporal patterns. Although the LSTM network addresses the issue of long-term dependency to some extent, its complex structure results in low computational efficiency. Moreover, the absence of an attention mechanism limits its ability to focus on key features in complex tasks. By integrating the IWOA optimization algorithm, the IWOA-SAGRU model is able to identify optimal parameter combinations more effectively than the traditional gradient descent method. When compared with the Elman and LSTM models, the proposed model reduces error $S_{\mathrm{RMSE}}$ by 0.7146 and 0.4689, respectively, while errors $S_{\mathrm{MAE}}$ and $S_{\mathrm{MAPE}}$ are minimized to 0.8855 and 0.0927%. Furthermore, $S_{{\mathrm{R}}^2}$ is closer to 1, indicating superior fitting and generalization ability. Analysis of the prediction results indicates that the proposed furnace temperature prediction model attains high forecasting accuracy, enabling early detection of temperature anomalies and contributing to the reduction in harmful substance emissions.

5. Conclusions

This study proposes an IWOA-optimized SAGRU model for predicting the furnace temperature in municipal solid waste incineration (MSWI), aiming to overcome the limitations of conventional temperature measurement methods under complex operating conditions. By introducing a self-attention mechanism into the GRU network and optimizing key parameters such as learning rate, number of hidden nodes, and dropout rate using IWOA, the proposed approach significantly improves prediction accuracy, generalization capability, and computational efficiency. The results indicate that the model can more effectively capture both short-term dynamics and long-term trends of furnace temperature, thereby enabling stable and efficient combustion control.

From a sustainability perspective, this study has important practical significance. Accurate furnace temperature prediction not only helps optimize the municipal solid waste incineration process and improve energy recovery efficiency but also reduces reliance on fossil fuels and promotes the clean utilization of waste-derived thermal energy. In addition, by enabling more precise combustion control, harmful gas emissions can be effectively reduced, contributing to the achievement of emission reduction targets. These outcomes provide strong technical support for advancing low-carbon waste management and the development of a circular economy.

Nevertheless, this study has certain limitations. First, the model validation data are primarily derived from a specific MSWI plant in China, and variations in waste composition, equipment conditions, and operational modes across different regions may affect its generalizability and applicability. Second, potential equipment malfunctions or extreme environmental conditions during actual incineration processes have not been fully incorporated into the prediction framework. Future research could focus on expanding the collection and utilization of multi-source data to enhance the model’s applicability and robustness. In addition, integrating equipment condition monitoring and environmental factors into the prediction system could improve the model’s adaptability to complex operating conditions. Furthermore, exploring the combination of advanced techniques such as reinforcement learning and edge computing may further enhance the model’s real-time performance and self-adaptive capabilities.

Overall, the proposed IWOA-SAGRU model not only offers a new technical approach for furnace temperature prediction and combustion optimization in MSWI processes but also provides theoretical support and practical value for achieving efficient energy utilization, emission reduction, and low-carbon waste management. It holds important reference significance for promoting intelligent and green urban solid waste management systems. Moreover, the findings of this study can provide data support and decision-making guidance for governments and management authorities in formulating emission reduction policies for waste incineration, optimizing energy utilization strategies, and developing low-carbon cities, thereby further advancing the achievement of sustainability goals.