Abstract
The article addresses the problem of increasing the capacity of the Baikal–Amur Mainline, which is part of the Northern Eurasian Corridor and provides the shortest route from Europe to the countries of the Asia-Pacific region via the ports of the Russian Far East. A key focus of the study is the Severobaikalsk section, which currently operates as a single-track system and is located in a specially protected natural area. In this regard, it is a limiting element since its reconstruction projects require environmental expertise. To tackle this issue, we develop a mathematical model based on semi-open queuing networks as a research tool. This modeling apparatus allows us to describe the features of the considered transport system, including single-track traffic, long sections between stations, which leads to the appearance of additional sidings, the presence of through and ring routes, and the significant influence of random factors on train operation. Based on the results of a numerical study of the model, we evaluate the current and maximum permissible section loads and point out bottlenecks in its structure. We compare two alternative ways of increasing the section capacity: creating a double-track connection on the most problematic sections and using a partially batch train schedule. Based on the results of the calculations, we conclude about the possibility and conditions of their implementation.
1. Introduction
Rail transport provides a high level of mobility with a relatively low environmental impact, making it an effective alternative to air and road transport [1,2]. According to the International Energy Agency (IEA), the CO2 emissions from moving one passenger per kilometer on a train are six and eight times lower than those associated with air and road transport, respectively [2,3]. At the same time, rail transport is advantageous in terms of price/speed and price/volume of cargo for long-distance transportation within the continent. These factors contribute to the growth of rail transportation and the development of the corresponding infrastructure, primarily in Eurasia, which has the longest railway network.
Five main international transport corridors operate on the continent (see Figure 1), providing connectivity between European and Asian regions. The total volume of cargo flows on them reached 260 million tons in 2023 and, according to forecasts, will increase by 50% by 2030 [4]. Among them, the largest cargo flow falls on the Northern Eurasian Corridor. On the routes running through it, the cargo volume reached 173.9 million tons in 2023 (67% of the total). At the same time, 73.8% of this cargo follows from the European part of the continent (EU, Belarus, and western regions of Russia) to the ports of the Russian Far East and back via the Trans-Siberian Railway and Baikal–Amur Mainline [4]. In 2023, the Trans-Siberian Railway transported 138.4 million tons, reaching its maximum capacity [5]. As a result, there has been a significant focus on developing its alternative trunk—the Baikal–Amur Mainline (BAM) [4,5].
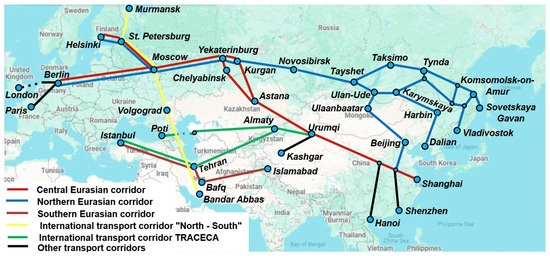
Figure 1.
Railway corridors of the Eurasian transport carcass.
The decision to modernize the BAM is based on the following key points. Firstly, it is the shortest railway route from the central regions of Russia to the ports of the Russian Far East. Secondly, the BAM could potentially increase the volume of transported cargo on the Northern Eurasian Corridor by up to 50% (according to various estimates) in the next five years [4,6]. Additionally, the BAM region contains deposits of minerals, particularly coal, oil, and iron ore, whose extraction necessitates a well-developed transportation infrastructure.
A new stage of the BAM construction began in 2021 [5]. According to the project passport, it is planned to fully electrify the trunk and almost double the carrying capacity of its sections by 2025 [4,6]. To implement such large-scale plans successfully, it is necessary to assess the current load, maximum capacity of sections, and the effectiveness of possible measures for their reconstruction, taking into account the negative impact on the environmental situation in the influenced areas. The last point is especially significant since 500 species of animals live in the BAM area, among which 19 species of mammals and 74 species of birds are listed in the Red Book. There are six large nature conservation areas along the highway, including Lake Baikal, listed as a UNESCO World Heritage Site. It is practically impossible to solve the problem without using mathematical and computer modeling methods.
This study aims to develop a mathematical model of train traffic along sections of the BAM to analyze its capacity, determine bottlenecks, and assess the effectiveness of measures to eliminate them. It is the first step in developing plans for the BAM reconstruction, considering the negative impact on adjacent areas.
We deal with the Severobaikalsk section of the BAM, which has some peculiar properties. It provides a single-track traffic system, which is not typical for railroads. The distance between stations is longer than on other large single-track railways. Therefore, up to five sidings may be located on a stretch of this section to allow oncoming trains to pass. For comparison, on the Trans-Mongolian Railway, the sections have no more than three sidings, and, in most cases, there is only one. The modeling is also complicated by two ring routes of freight trains that run between adjacent large stations within the section, and their number is fixed for each route. All listed points do not allow for the direct use of previously developed modeling methods [7,8], require more flexible mathematical apparatuses, and assume the creation of a new model.
We propose a mathematical model of a train running along a section of the BAM railway based on a specific queuing network (QN), that is, a set of interconnected queuing systems [9,10]. The model utilizes a semi-open QN (SOQN) to describe the movements of trains on several routes, including ring ones. SOQNs allow us to take into account the complex structure of the section, in particular, the different number of sidings between stations, several train routes within the section, and the fixed number of trains operating on ring routes. We also employ the Batch Marked Markovian Arrival Process (BMMAP) to simulate the arrival of several categories of trains, which have different speeds and come from various directions. To the best of our knowledge, SOQNs with BMMAP are applied for the first time in the context of railway transportation.
The paper is organized as follows. Section 2 presents the literature review and justification for choosing QNs as a tool for mathematical modeling. Section 3 describes the object under consideration. Section 4 and Section 5 present the methodology for modeling train traffic on a railway sections and the construction of the mathematical model. Section 6 and Section 7 focus on the results of the numerical study and their interpretation. The Section 8 includes a discussion and outlines possible directions for further research.
2. Literature Review
Deterministic models based on the theories of mathematical programming and graph theory have traditionally been used in the field of railway transportation [11,12]. These models allow us to determine the optimal performance parameters of railway facilities, including optimizing routes [13], train scheduling [14], and calculating the required fleet of cars [12,15]. This approach is also used in alignment optimization for railways and rail transit lines [16], including for ring lines [17]. In the context of reducing adverse effects on the environmental condition of adjacent territories, the tasks of increasing energy efficiency and reducing CO2 emissions are considered [18,19].
As a rule, models of this class yield meaningful results if the object’s operation is not significantly affected by random factors. Otherwise, stochastic (probabilistic) models [19,20], including dynamic simulation [21,22] and agent-based [23,24] models, become reasonable options. The agent-based approach, along with the known advantages [22,23], has a significant limitation—high complexity of development, which requires considerable time to study the tools and to create models of a specific object. Additionally, it is hard to apply the available models to another research object.
Due to the specific properties of transport systems, such as the regular performance of the same technical operations, their non-deterministic duration, and the limited system capacity, it is possible to reduce the complexity of models compared with general-type simulation by applying queuing theory [25,26,27].
Queuing systems have been utilized in the field of rail transportation since the 1970s [25]. This mathematical apparatus is most often used to describe the operation of small railway stations and their components [25,28]. However, these models have also been used to analyze delay propagation on railway tracks and routes [29]. Currently, this approach is still relevant. For example, works [26,27] estimate the throughput of individual railway sections and stations using single-channel queuing systems. The scheduling problem for single-track railway lines is addressed in [30], while [31] predicts the waiting time for track release. Paper [32] presents a methodology for modeling the operation of a single-track segment and a railway junction.
To describe the operation of larger objects with complex branch structures and complex, including ring routes, we need an advanced tool—queuing networks (QNs). Based on QN, models of urban passenger [33,34], freight [35,36,37], and marshalling [38,39], as well as seaport [40] railway stations have been developed. They allow us to take into account both the infrastructure of the entire station and the operating of its individual elements. QNs also fit to model railway corridors, including single-track ones [7,41,42], as well as describing the operation of railway network sections and assessing their capacity with changes in train traffic volumes in [8,43].
To describe ring and through train routes, we propose using a more general type of QNs—a SOQN [9]. The main feature of SOQNs is that some of the requests come from the external environment (external requests) and leave the system after servicing, while the other part (internal requests) circulates within the system. As a rule, SOQNs are used to model telecommunication and computer networks [44]. In the field of transport, SOQNs have been applied to describe the operation of sea container terminals but not for ground transportation systems [45].
Section 3 presents a description of the BAM and its key features that are essential for modeling.
3. Object of Study
3.1. General Characteristics of Baikal–Amur Mainline
The BAM is a unique and one of the most complex engineering structures in the world. It separates from the Trans-Siberian Railway in Tayshet and passes through Severobaikalsk, skirting Lake Baikal from the north. Then, it crosses six large rivers and seven mountain ranges, finally ending on the shores of the Pacific Ocean in Sovetskaya Gavan. The trunk has 2230 bridges, with a total length of over 400 km, and ten tunnels. One of these tunnels is 15.3 km long (see Figure 2). The majority of the BAM lies in the permafrost area. The tunnels are in a mountainous and inaccessible region and can withstand −40 °C and seismic activity of 8–9 on the Richter scale.
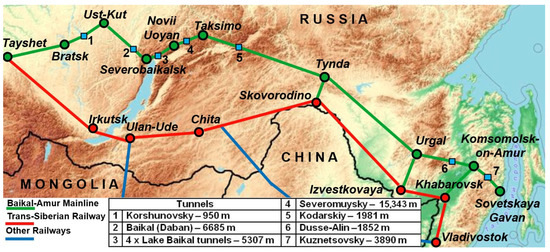
Figure 2.
The BAM scheme with tunnels.
Since the BAM runs near Lake Baikal, projects for its reconstruction within the Baikal Natural Territory should be evaluated from an economic and environmental point of view. The main difficulty lies in developing solutions that significantly increase the capacity of the railway section and, at the same time, have a local impact on the environmental situation.
From Tayshet to Ust-Kut, the trunk is double-track and electrified; then to Taksimo, it is single-track with double-track sections. From Taksimo, it is single track, and diesel locomotives carry out the running. Incomplete electrification and rugged terrain lead to significant fuel consumption. In particular, 2.5 million tons of diesel fuel were consumed in 2019. According to the Environmental Protection Agency (see https://www.epa.gov, accessed on 7 November 2024), burning one liter of diesel fuel produces 2.7 kg of CO2. Consequently, in 2019 alone, 6.75 million tons of greenhouse gases were emitted into the atmosphere, which corresponds (according to various estimates) to 18–22.5% of the volume of CO2 emitted by Russian rail transport (see [46] and https://sr2023.rzd.ru, accessed on 7 November 2024).
3.2. Severobaikalsk Section of the Baikal–Amur Mainline
We consider the BAM railway section between Kirenga and Novii Uoyan, which is 351 km long. Firstly, it is one of the most problematic sections [5]. In particular, it runs through mountainous terrain, which is why there are four tunnels on it, and the creation of double-track traffic is arduous. Secondly, this section runs along the shore of Lake Baikal, so its reconstruction projects require an assessment of the environmental impact and public discussion.
The Severobaikalsk section has seven stations and sixteen sidings for passing oncoming trains when there is single-track traffic. Figure 3 shows a diagram of the section. White circles mark the stations, and black circles show the sidings.
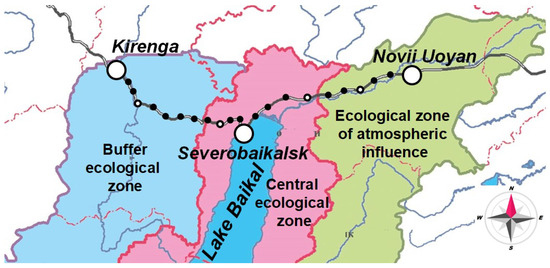
Figure 3.
Scheme of the Severobaikalsk section.
4. Methodology of Modeling of Train Traffic in a Railway Section
4.1. Key Features of the Railway Section
A section of the railway system means a complex of railway stations on a relatively small territory that jointly perform operations for servicing transit and local (within the section) transportation of goods and passengers. Many factors affect the capacity of railway sections, such as the number and category of arriving trains, the number of stations and their track development, the length of lines, the train schedule, the reliability of the infrastructure, the efficiency of the power supply system, the signaling, centralization, and blocking devices used.
It is not possible to consider all these factors within one model. Therefore, we focus on the elements and characteristics of the railway section that directly influence its capacity. Firstly, it is the number and types of trains arriving at the section, as they determine the technical operations carried out with trains at stations, the ratio of trains in freight and passenger traffic, and their routes. Secondly, it is the infrastructure of the railway network: the number of stations, lines, and sidings. Thirdly, the duration of performing the same type of technical operations at stations plays a key role. They include changing crews, parking the train, inspecting and reorganizing it (maintenance time), and for sidings and lines—the time of passing them (running time). Fourthly, we take into account forced train stops due to busy tracks further along their route.
We reckon the following elements indirectly. The work of staff is taken into account when determining the duration of technical operations at stations. The running time depends on the locomotive type. The efficiency of signaling, centralization, and blocking devices (train control systems) affect the number of trains that can simultaneously run along the section in one direction, the duration of the interval between trains, and the number of forced stops due to a prohibiting traffic light signal. The number of batches and their sizes in a partially batched train schedule depends on the power supply system.
As a rule, the schedule sets the arrival time of trains at a railway station, siding, or line. However, significant deviations from the schedule occur due to the long length of the railway network and the influence of weather conditions [41,42]. Additionally, the same type of operations with trains are regularly performed at stations. Their duration is regulated [11] but is affected by various, usually non-deterministic factors. Therefore, it is considered a random variable [33,38,39]. The number of trains at a single station is limited and can be only positive integers. Then, a random process with continuous time and a discrete number of states can describe the station (siding or line) operation.
4.2. The Methodology and Mathematical Apparatus
To construct the mathematical model, we distinguish three groups of components: the incoming train flows, the procedure for their handling within the facility’s structural elements, and the routes along which these trains move. In contrast to the previously proposed modeling technique [7], we utilize the following mathematical apparatus to account for the features of the BAM.
Incoming flows. We use the Batch Marked Markovian Arrival Process to describe an incoming train flow [10]. It allows us to consider the arrival of various train types with different parameters and routes within one model.
BMMAP is defined by a Markov chain with continuous time and state space . The intensity of arrival request groups depends on the state number of the Markov chain. The residence time in each state is exponentially distributed. With probability , the chain can go to state w, with probability generating a group of random size , and with probability , the requests in the group have the type . The normalization condition is satisfied:
It is convenient to collect all this information in matrices , which are set according to the formulas
As a rule, trains come from two or more directions. We use a separate BMMAP flow for each direction, the sub-flows describe the arrival of passenger and freight trains. It allows us to consider the difference in arriving intensity for each category of trains, which, in turn, implicitly takes into account the difference in their speeds. If a single train is one request, then a batch of trains is a group of requests.
Functioning of structural elements. To model the process of a train running along a railway section with several routes, including loop ones, we use a set of interconnected QSs. Some of the requests come to these QSs from an external source and leave them after servicing, and the second part circulates within the system. The number of internal requests at time t is fixed, while the number of external ones is variable. According to [45], such a set of servicing systems is a semi-open queuing network.
SOQN consists of a finite set of nodes S, containing elements. A node is a queuing system that includes homogeneous channels and spots in the queue [9]. The external source is considered an additional (dummy) node. The route of request movement between nodes is given by the route matrix P having dimensions . Its elements are as follows:
- is the probability that a request serviced at node y will go to node u;
- is the probability that a request arrives from the source at node u, ;
- is the probability that a request will leave the SOQN immediately after completion of service in node y.
The elements of the route matrix satisfy the condition .
The stations and sidings service the trains; along the lines, trains move without stops. Both operations are of the single type and regularly repeated, and random factors affect their duration. The mathematical model of the structural element operations is constructed depending on their number and type according to the following rules.
Four multi-channel QSs (nodes) with finite queue lengths model large stations (6 or more tracks). The QSs describe the operation of tracks for passenger trains, freight transit trains, loading/unloading trains (cargo yard), and departure local trains after servicing. Small stations (from 3 to 5 tracks) are described by one multi-channel QS with a finite queue. The number of tracks determines the number of channels, and the queue capacity is the number of trains that can temporarily stop before the station if there is no free space for receiving. The queue service discipline is FIFO.
There are four typical configurations of lines and sidings in the BAM sections.
(A) A double-track line with a siding or a siding between two double-track lines.
(B) A single-track line without sidings.
(C) A single-track line–siding–single-track line. Such a section is considered standard for the BAM.
(D) A single-track line–siding–single-track line–siding–single-track line.
We employ pairs of single-channel QS without a queue to describe A, B, and C, and we use two pairs for D. The service time depends on the type of structural elements and their technological parameters.
Train routes. Requests coming from an external source and circulating within the system have different types i and separate route matrices
The union of the constructed BMMAP flows, QSs, and the route matrices brings us to the SOQN.
The purpose of the simulation is to find the performance indicators of the SOQN, such as the loss probability; residence time of a request in the system and separately in each node; average number of busy channels; average queue length; and channel blocking time in the node. These indicators allow us to draw conclusions about the efficiency of the system and point out “bottlenecks” in its structure.
5. Structural and Parametric Identification of the Model
This section outlines the railway section characteristics that are taken into account when simulating its operation. Based on these, we construct a model of a train running along the section of the Baikal–Amur Mainline.
5.1. Characteristic of Severobaikalsk Section
The Severobaikalsk section includes seven stations, sixteen sidings, and seven double-track and fifteen single-track lines. Figure 4 presents a diagram of the section as a graph. Circles represent stations and sidings, while arcs show the lines connecting them. Weights in the format indicate the average travel time for passenger/freight trains on the line, considering acceleration and braking. These data are obtained based on an analysis of the train schedule for the East Siberian Railway in 2023.
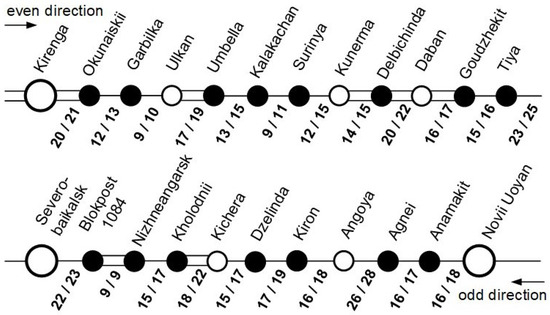
Figure 4.
Diagram of the Severobaikalsk section and travel time of the train by sidings.
District stations Kirenga, Severobaikalsk, and Novii Uoyan are aimed at performing the following operations: receiving, technical inspection, dispatching and transit of all types of trains; changing locomotives and crews; and forming and disbanding local freight trains, and performing freight operations with them. These stations include a receiving and departure yard, which has tracks for passenger trains, tracks for transit freight trains, and tracks for handling local freight trains (waiting, disbanding and forming trains, and shunting operations). Each station also has a cargo yard that can accommodate trains. Table 1 shows the number of tracks at the stations; the minimum and maximum processing time for passenger () and transit freight () trains in minutes, according to the station operating regulations.

Table 1.
Parameters of the district stations.
Intermediate stations facilitate the passing, overtaking, and crossing of trains, as well as the boarding and disembarking of passengers. Ulkan and Kichera have five tracks each, while Daban and Angoya have four. The travel time for passenger and freight trains passing through these stations ranges from 1 to 5 min.
Sidings Kunerma, Nizhneangarsk, Kholodnii, Dzelinda, Kiron, Agney, and Anamakit have three tracks each, and the rest include two tracks each. It takes from 1 to 5 min to pass through them.
The train flow consists of transit freight, local freight, and passenger trains, including suburban trains. Field observations were conducted over a 60-day period from 17 June to 16 August 2024. It was established that, on average, 13 passenger and 17 freight trains pass through the Kirenga per day in both directions. From Severobaikalsk, the train flow decreases to 21 trains per day. There are two ring routes for local freight trains: Kirenga–Severobaikalsk and Severobaikalsk–Novii Uoyan.
The maximum estimated capacity of the section is determined by the train schedule. The schedule for 2023 is currently available, according to which 56 trains (28 pairs) can pass through the Kirenga station and 44 trains (22 pairs) from the Severobaikalsk station and further. Figure 5 shows a train flow diagram, where pairs of numbers indicate the number of trains per day in 2024 (actual data) and according to the plan in 2023. Directed arcs indicate the train turn.
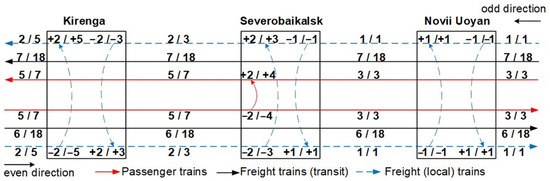
Figure 5.
Train flows.
The Severobaikalsk section does not currently use batch train traffic, as its capacity is sufficient to handle the current level. However, it is technically possible to implement a partial batch schedule.
5.2. Mathematical Model
The model encompasses three components: a depiction of incoming train flows, the procedure for their handling within the facility’s structural elements, and the routes along which these requests move.
5.2.1. Incoming Train Flows
Thirteen trains per day arrive from the west (east direction), and eleven trains per day arrive from the east (west direction). These train flows are described by two Batch Marked Markovian Arrival Processes: BMMAP1 and BMMAP2. Each direction includes three categories of trains. The routes of passenger and transit freight trains do not have significant differences (see Figure 5). Then, there are four routes in the section:
- 1.
- Passenger and transit freight trains running in the eastern direction;
- 2.
- Passenger and transit freight trains running in the western direction;
- 3.
- Local freight trains heading east;
- 4.
- Local freight trains heading west.
Let us first construct BMMAP1. Based on field observations, we find that the average speed of freight trains in the section is 14% less than that of passenger ones. Then, the Markov chain has two states 1, 2 with different intensities of requests per hour (freight) and (passenger), as well as the probabilities of transitions between states (freight) and (passenger). The probabilities of the arriving requests of different types in state 1 of the Markov chain are and for state 2 they are . Trains arrive one at a time; therefore, . Thus, BMMAP1 includes 5 matrices of size , which are constructed according to Formula (1):
The construction of BMMAP2 is similar. It also includes five matrices:
5.2.2. Structural Elements
According to the presented methodology we employ three nodes to describe the operation of Kirenga and Novii Uoyan stations and four nodes for Severobaikalsk since one of the receiving and departure tracks is used to form and dispatch trains after processing at the cargo yard.
At these stations, a variety of train operations are carried out, which are regulated, but a large number of unpredictable factors influences the timing of these operations. Furthermore, the number of required operations varies for each train. Therefore, according to the Central Limit Theorem, the service time at these nodes can be regarded as a random variable obeying a normal distribution . For nodes describing the tracks for passenger and transit freight trains, the average number of operations determines the mathematical expectation , and standard deviation is the possible deviation from the average (see Table 1). These parameters for a cargo yard are chosen based on expert assessments and the train schedule (Figure 5).
We introduce five separate nodes to model Ulkan, Daban, Kichera, Angoya, and Kunerma siding. The service time in the channels has an exponential distribution since it is the most suitable for describing the time intervals between the arrival of trains [41,42]. Based on the train schedule, we find that 96% of trains have a stopover or travel time through stations of less than 5 min. Therefore, we specify the exponential distribution parameter so that 96% of the values of this random variable fall within the interval [0, 5] minutes.
The Severobaikalsk section includes eight A-type combinations, two B-type and C-type combinations each, and three D-type combinations. The average travel time of passenger () and freight () trains depends on the configuration and is calculated using the data presented in Figure 4. In case (A), the average travel time coincides with the schedule; for (B), it doubles due to the single-track section, and for (C) and (D), the travel times of each component are added up.
We employ pairs of single-channel QS without a queue to describe A, B, and C, and we use two pairs for D. The service time in these nodes obeys a normal distribution, which is chosen by analogy with the duration of operations at large stations. Its parameters are calculated as , , .
Thus, the model for the Severobaikalsk section takes the form of a SOQN with two BMMAP flows, and 51 nodes, to which we must also add 2 dummy nodes that represent the external sources. Table 2 presented the formal descriptions of nodes in terms of queuing theory (N, Kendall’s notation) and the laws of service time distribution (T). If the parameters of the arriving flow to the node are unknown, then we put the symbol “∗”. Here, exp is the exponential distribution, is the intensity, is the normal distribution, is the mathematical expectation, and is the standard deviation.

Table 2.
Node parameters of the SOQN.
5.2.3. Train Routes
On the Severobaikalsk section, trains follow four routes (see Section 5.1). We introduce four types of requests with separate route matrices to take them into consideration. The matrix elements are the probabilities of transitions between nodes (lines and stations). They are calculated as a relative frequency: the ratio of the train number arriving at a specific element to the total number of trains for one direction. These matrices are sparse and uninformative; therefore, Figure 6 shows non-zero transition probabilities as weights of the graph edges.
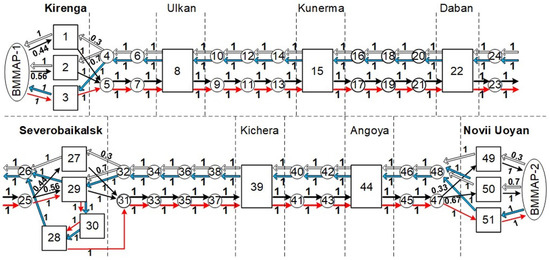
Figure 6.
Scheme of SOQN.
After being serviced at node y (station), a request can change its type i to type j with probability , which allows describing U-turns. Requests of type 1 change the route at Node 27 with probability .
We describe the loop routes of local freight trains in the model as follows. Initially, Nodes 8, 15, and 39 have two requests each (types 3 and 4), corresponding to four local trains on the Kirenga–Severobaikalsk route and two on the Severobaikalsk–Novii Uoyan route. The requests change their routes at Nodes 3, 30, and 51 with probabilities , , , respectively. Thus, requests of types 3 and 4, which are present in the SOQN at the beginning of the simulation, cannot leave it, while requests arriving from an external source immediately leave the system after being serviced in Nodes 3 and 51.
Figure 6 shows the SOQN scheme. Squares correspond to stations and their parts, circles indicate lines, and weights of the black, white, red, and blue arrows set the non–zero elements of the route matrices , , , and , respectively.
The resulting BMMAP flows, QSs, and routing matrices form the SOQN. It is hardly possible to determine the performance indicators of the constructed SOQN using analytical methods. Therefore, we develop a simulation model implemented as software in the Object Pascal programming language [7,8]. The next section presents the results of the numerical experiments.
6. Numerical Experiments
The most obvious way to increase the capacity of the BAM radically is to create a double-track connection along its entire length [5]. The economic feasibility of such a decision is justified [4,47,48]. The work [4] shows that demand for cargo transportation from the European part of the continent to the Asia-Pacific countries via the ports of the Russian Far East significantly increases. Moreover, building the capacity of the Eastern Range (including the BAM) will lead to a sharp rise in the volume of cargo transported on the Northern Eurasian Corridor. Paper [47] discusses the necessity of advanced transport infrastructure for the mining of large mineral deposits located in the BAM zone. In [48], the authors estimate the positive effect on the socio-economic situation of the regions of Northeastern Siberia.
However, large-scale railway reconstruction is associated with significant environmental damage, which should be considered in specially protected natural areas where the Severobaikalsk section lies. In this regard, we examine below two alternative ways of increasing capacity with less negative impact: creating a double-track connection only on problematic sections and using a partially batch train schedule.
Four computational experiments are carried out using the developed software to evaluate the effectiveness of these measures:
- The first experiment aims to check the adequacy of the constructed model and assess the current load of the section under consideration based on field observation.
- The second experiment addresses determining bottlenecks in system structure and evaluating its maximum capacity.
- The third analyzes the throughput capacity of the Severobaikalsk section when eliminating the identified bottlenecks.
- The fourth studies an alternative method for increasing the capacity of the railway section by using a partial batch train schedule.
The following tables and figures show the average performance characteristics of SOQN obtained for ten program runs (one series of calculations). The duration of each experiment (model time) equals 60 virtual days and corresponds to the duration of field observation. We use the following notation:
- V is the total number of requests arrived at the system in 60 days;
- is the loss probability;
- and are average sojourn time of a request in the SOQN, which describe the running of passenger and transit freight trains in one direction, respectively;
- is an average total time (in minutes) of blocking one request when passing all nodes in one direction, i.e., the total waiting time for departure for an individual passenger or transit freight train on the entire section;
- is a number of requests arrived at node y during the simulation;
- is a channel occupancy rate at node y;
- is an average queue length at node y;
- is an average sojourn time of a request at node y;
- is an average time (in minutes) for one request to stay in a blocked channel at node y (hereinafter referred to as the average blocking time).
6.1. Experiment 1
Recall that this experiment aims to verify the model and assess the current load based on field observations. Table 3 presents the results of the numerical study of the obtained SOQN (see Section 5.2). Matrices (2) and (3) specify the incoming request flow corresponding to the current volume of train flows.

Table 3.
The results of Experiment 1.
We assess the correctness of the model by two key indicators. The first is the number of daily trains passing through a separate station. This value for each station is compared with the number of requests received at the corresponding nodes () from Table 3. As a result, the average relative deviation is 1.15%, and the maximum is 2.51%. The second indicator is the average running time from station Kirenga to Novii Uoyan, including the handling at all stations and sidings except for Kirenga and Novii Uoyan. It is calculated based on the train schedule and an analysis of station operating technologies. For passenger trains, it is 471 min, for freight trains, 463.5 min. The sojourn time of a request in the corresponding nodes is min and min. Therefore, the relative deviation is 0.3% and 0.7%, respectively.
Let us interpret the calculation results (Table 3) in terms of the Severobaikalsk section. The cargo yards at the Kirenga and Severobaikalsk stations are the most loaded since the corresponding Nodes 3 and 30 have the highest channel occupancy rates and . However, no more than four trains arrive at the cargo yards daily, so their occupancy does not significantly influence the operation of the system as a whole. The potential bottlenecks are the single-track sections Goudzhekit–Severobaikalsk (Nodes 25 and 26) and Severobaikalsk–Blokpost (Nodes 31 and 32). For Goudzhekit–Severobaikalsk, the channel occupancy rate is , and for Severobaikalsk–Blokpost, . Such values are typical for yards but too big for lines. The preceding Nodes 24, 27, 28, 29, and 34 have the highest average blocking time . This fact indicates an increased load on Nodes 25, 26, 31, and 32.
In this study, the loss probability means the ratio of the number of trains temporarily taken out of running (‘postponed’ trains) at preceding stations due to the occupancy of the current node to the total number of trains. After some time, they receive an adjusted schedule and continue the route. The model considers them to be newly arrived requests. Logistics specialists at Russian railways suggest that the key indicator of whether the system can handle the load is . For the BAM, such a means that, on average, no more than one train per two days becomes ‘postponed’ at the maximum estimated load of the section. In our case, corresponds to 11.2 ‘postponed’ trains in 60 days or 1.31 per week. This number of unaccepted trains does not significantly affect the system operation as a whole. This means the current train volume can be handled, but its increase can lead to an emergency. The following experiments aim to evaluate the consequences of such an increase.
6.2. Experiment 2
The estimated capacity of the Severobaikalsk section, according to the train schedule 2023, is 52 trains per day. Let us evaluate the section’s load with such a train flow (see Figure 5) and find its maximum capacity. To do this, we modify the constructed model as follows:
- 1.
- The BMMAP1 matrices describing the arrival of 30 trains from the west arewhile the BMMAP2 matrices corresponding to the arrival of 22 trains from the east are
- 2.
- Initially, at Node 22, there is one request of type 3 and one request of type 4. Thus, the number of circulating requests between Nodes 3 and 30 increases to six, corresponding to the number of local freight trains running between Kirenga and Severobaikalsk.
- 3.
- The probabilities of arrival of type 1 requests at Nodes 1, 2, 27, 29, 49 and 50 are , , , , and those of type 2 requests are , , , , respectively. These changes are necessary to reflect the new ratio of passenger and transit freight trains.
Table 4 and Figure 7 show the simulation results for the modified SOQN. In Case 1, matrices (4) and (5) define the request flows. In Case 2, the elements of the first rows in matrices (4) are increased by 6.5%, and those in matrices (5), by 9%, corresponding to the arrival of two additional transit freight trains.

Table 4.
The results of Experiment 2.
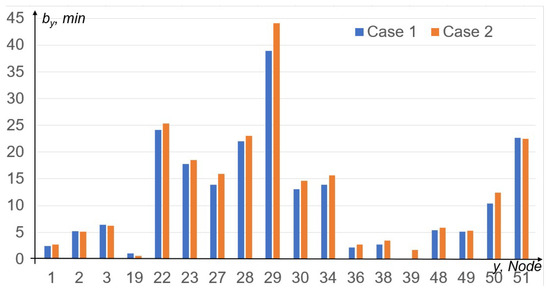
Figure 7.
Experiment 2. Average blocking time of one request.
Here and below, D is the average number of arrived requests per day, , , which is reached at Node 29.
During the computational experiment, we observe so-called ‘collisions’—situations where counter request flows overflow neighboring nodes and block each other, which causes overflow and approaches 1. In Case 1, there are 3 collisions of 10 runs, and in Case 2, there are 5 of 10. We do not consider the results of these runs and instead conduct new ones. In practice, dispatch control can correct such situations in advance if they are not permanent.
Collisions occur between Nodes 22 and 27 (Goudzhekit–Severobaikalsk section), Nodes 30 and 33 (Severobaikalsk–Blokpost section), and Nodes 44 and 47 (Angoya–Agnei section), indicating bottlenecks in the system. It is impossible to conduct such an experiment with a higher intensity of incoming flows since a collision occurs in each run. We can interpret this situation as the section reaching its maximum load.
Thus, the Severobaikalsk section has a capacity reserve of 6.5% more than the estimated one, which allows 27 pairs of trains to pass through it in normal mode. Three bottlenecks in the section are the Goudzhekit–Severobaikalsk, Severobaikalsk–Blokpost, and the Angoya–Agnei. They cause significant idle time for trains observed at the Severobaikalsk station, which for transit freight trains, averages over 39 min, and for passenger trains, over 15 min. Such delays are significant for the system.
6.3. Experiment 3
Let us evaluate the capacity of the Severobaikalsk section, eliminating the identified bottlenecks and increasing the volume of arriving train flows. We assume that double-track lines have been built on the problematic sections. Then, compared to Experiment 2, we modify the model as follows:
- 1.
- Nodes 25, 26, 45, and 46 model the original Goudzhekit–Severobaikalsk and Angoya–Agnei sections, which, recall, consist of two lines and one siding. With double-track traffic, up to three trains can simultaneously run in the same direction, so the number of channels in Nodes 25, 26, 45, and 46 should be increased to three.
- 2.
- Nodes 31 and 32 describe the train running along the Severobaikalsk–Blokpost without a siding. With double-track traffic, the travel time along it in each direction is, on average, 22 min. Then, the service time at Nodes 31 and 32 is reduced by half and obeys .
- 3.

Table 5.
The results of Experiment 3.
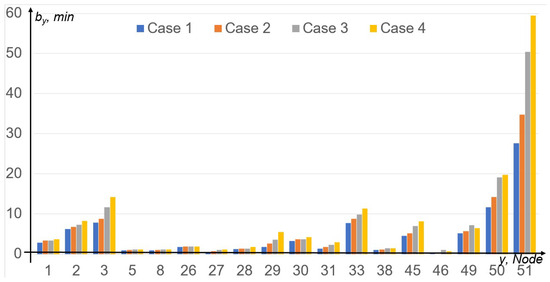
Figure 8.
Experiment 3. Average blocking time of one request.
Based on the results obtained, we conclude the following. With a train flow of 68 trains per day and more, the average number of postponed trains exceeds the permissible value (). With an arrival of 64 trains per day, the highest value of is at Node 51, which describes the cargo yard at Novii Uoyan station. Nevertheless, its load does not significantly affect the system. In other parts of Novii Uoyan station, the waiting time for departure is min and min, which is permissible. For Severobaikalsk station, , , , and do not exceed 4 min. Thus, after eliminating bottlenecks in the Severobaikalsk section, the maximum train flow can reach 32 pairs of trains daily.
It is possible to introduce a partial package schedule in the section under consideration. However, this requires a notable change in the schedule and modernization of some elements of the railway network, in particular, increasing the number of tracks at all sidings to at least three, allowing two batches of trains to run on one section simultaneously. The following experiment evaluates the effectiveness of employing a partial batch schedule.
6.4. Experiment 4
Let us modify the mathematical model to take into account the partial batch schedule. First, we assume that a quarter of freight trains arrive in batches (groups). This value is the maximum possible given the availability of three tracks at sidings and the current energy efficiency of the power supply devices equipment in the section. This recommendation is based on an expert analysis of the 2023 train schedule. For the same reasons, the maximum batch size is two trains. Passenger and local freight trains are not included in the batches. The train traffic volumes correspond to the train schedule for 2023. Then, the incoming train flow from the west is described by BMMAP1:
and from the east, by BMMAP2:
Secondly, we make the following changes to the models of lines and sidings (see Table 2). In the nodes that describe the operation of lines, we introduce group servicing of requests (Nodes 4–7, 9–14, 16–21, 23–26, 31–38, 40–42, and 45–48)—. In the first channel of the nodes that model the Ulkan, Kunerma, Daban, Kichera, and Angoya stations, requests are also serviced in groups. This is necessary to pass a batch through the station without stopping. The maximum size of groups is two. The service time at these nodes depends on the size of the group serviced. For one request, the service time parameters for the corresponding node are set according to the data in Table 2. For two requests, we add to this time the minimum inter-train interval, which is eight minutes for sections with automatic blocking. The operation models of large stations are kept. The initial number of requests of types 3 and 4 in the SOQN and the route matrices are the same as in Experiment 2.
Table 6 shows the simulation results for the modified SOQN with different volumes of incoming flows. In Case 1, matrices (6) and (7) define the request flows, corresponding to an arrival of 50 trains per day, of which 8–10 trains arrive as batches. In Case 2, the elements of matrices (6) are increased by 6.5%, and in matrices (7), by 7%, corresponding to 52 trains daily.

Table 6.
The results of Experiment 4.
Let us compare and analyze the results of Experiments 2 and 4. It can be seen that the introduction of a partial batch schedule allows us to reduce the blocking time, in particular, if , the and values in Table 6 are 29.8% and 59.5% lower than in Table 4, respectively. However, the loss probability, on the contrary, is significantly higher. The reason is the insufficient capacity of Nodes 1, 2, 49, and 50, i.e., a lack of tracks at the Kirenga and Novii Uoyan stations. As a result, with the arrival of 52 trains per day, which corresponds to the schedule for 2023, the average number of ’postponed’ trains exceeds the permissible value. Thus, the introduction of a partial batch schedule leads to a decrease in the throughput capacity of the Severobaikalsk section.
6.5. Overall Numerical Results
The results of computational experiments show the following points. The capacity of the Severobaikalsk section is sufficient to handle 26 pairs of trains per day in normal mode and up to 27 pairs per day with significant delays in the departure of trains from stations. These delays arise due to the lack of capacity of three sections: Goudzhekit–Severobaikalsk, Severobaikalsk–Blokpost, and Angoya–Agnei. They are the longest compared to other single-track sections. At the same time, there are four tunnels on the Severobaikalsk–Blokpost section, which is why it is the most problematic.
A partial batch schedule allows for a reduction in the average delay in train departures from stations, which, in turn, decreases the average travel time along the section by 2%. However, this positive effect is offset by several factors. First, the average speed of a batch is lower than that of a single train. Second, when the train flow exceeds 26 pairs of trains per day, there may not be enough available tracks to accommodate an incoming batch at stations like Ulkan and Angoya. In this case, the trains stop at neighboring stations and lines, leading to the overflowing at large stations such as Kirenga and Novii Uoyan. Consequently, as the volume of train flows increases, the number of ‘postponed’ trains increases faster with batch traffic than without.
The most suitable option seems to be the organization of double-track lines in problematic sections, increasing the system’s capacity to 32 pairs of trains per day. It is necessary to lay 65 km of new tracks, build 10 bridges and overpasses, and extend four tunnels along Lake Baikal shore. These changes would affect an area of approximately 1.3 square kilometers. However, this solution is temporary since the capacity of the Severobaikalsk section should be increased to 43 pairs of trains per day in 2025 [5].
7. Discussion
The single-track traffic system and the relatively small size of stations on the BAM limit the effectiveness of introducing innovative alternatives to the measures discussed above to increase the section’s capacity. The virtual coupling technology, which is currently being implemented on the Trans-Siberian Railway, is, in fact, an improvement in batch train running. Accordingly, this technology has the same advantages and disadvantages, in particular, the need to increase the size of stations and the capacity of the railway power system. Dynamic scheduling algorithms or hybrid solutions do not allow one to eliminate the existing physical restrictions on the capacity of a single-track railway line; therefore, their application will have limited effect. Thus, it is advisable to consider scenarios that include innovative alternatives on the BAM after organizing a full-fledged double-track connection.
Thus, the only effective way to significantly increase the capacity of the Severobaikalsk section of the BAM is to build a full-fledged double-track railway. However, the implementation of such a project carries certain environmental risks [48]. In particular, a significant increase in the intensity of train traffic accelerates the spread of aggressive invasive organisms to new territories: insects, plant parasites, and pathogens [48,49]. This problem is especially relevant for Baikal, where there are 1455 species and subspecies of endemics. In this regard, it is necessary to develop and evaluate the effectiveness of appropriate measures, in particular, the regular monitoring and analysis of the correlation between the dispersal of invasive species and climatic and other factors, the installation of barriers that prevent parasites from going beyond the boundaries of the railway, the use of chemical and biological protection of plants and animals, and the study of the patterns of transformation and recovery of biological systems.
The results obtained are the first step in developing plans for the BAM reconstruction, considering the negative impact on adjacent areas. This study focuses on the transport aspect when choosing reconstruction measures for the railway section. The environmental component is considered indirectly, in particular, by taking into account the areas of the affected territories when implementing the measures. Nevertheless, during the research, we collected data on the spread of invasive organisms in the area of the Severobaikalsk station. However, the data obtained are insufficient to extrapolate to the entire section. In order to develop specific proposals to reduce negative environmental impacts, additional field observations are required, which can be carried out only during the warm season.
We conducted the model verification based on field data and the official train schedules for a specific section of the BAM. The relative error of the obtained results is acceptable for transportation systems. Nevertheless, it looks promising to compare the presented model-algorithmic tool with alternative modeling techniques to assess its competitiveness and further development. To date, we have not managed to find ready-made solutions in the known simulation modeling software that adequately consider the specifics of the BAM operation. Adapting it requires substantial effort, meaning constructing a new model from scratch.
8. Conclusions
In the study carried out within the framework of the project “Fundamental research of the Baikal natural territory based on a system of interconnected basic methods, models, neural networks and a digital platform for environmental monitoring of the environment”, we evaluate the current throughput capacity and conduct a scenario analysis of possible ways to increase it for the Severobaikalsk section of the BAM. It is located on the Baikal natural territory, passes near specially protected natural areas, and therefore requires special attention. As a research tool, we have developed a mathematical model based on the queuing theory, which takes into account the influence of random factors on the running and maintenance of trains at stations. The latter is necessary due to the peculiarities of the existing single-track traffic on the section and the complexity of natural and climatic conditions.
Based on the results of the numerical study of the constructed model, we found that the Severobaikalsk section is capable of handling up to 27 pairs of trains per day in normal mode. It was shown that a partial batch schedule is inappropriate since it does not increase the capacity significantly. The organization of a double-track connection on three problematic sections, although it allows up to 32 pairs of trains per day, is a temporary solution since, following plans, the capacity of the Severobaikalsk section should reach 43 pairs of trains per day in 2025 [5]. Thus, the only effective way to achieve the planned indicators is to create a full-fledged double-track connection on the entire section.
The proposed model generalizes the model of the Trans-Mongolian Railway [7], which has a structure and operating technology similar to the BAM. When constructing the model, we distinguished several typical combinations of elements that describe the operation of single-track and double-track lines, stations, and their parts. These typical combinations in different variants can help model other railway sections, in particular, Mongolian [7], Russian, and European railways [8].
Thus, the model can help identify bottlenecks in the structure of various railway sections, evaluate the effectiveness of measures to eliminate them, and reduce the forced downtime of trains at stations. Additionally, it provides the scientific justification for the infrastructure facilities on the railway, such as tracks, tunnels, and new yards at stations. Such justification is necessary for railway operators and local authorities to develop environmental protection measures and build a constructive dialogue between railway management, local authorities, environmental agencies, and indigenous communities. Therefore, the obtained results can be employed to optimize construction work on the BAM, including minimizing their negative impact on the environment.
Let us point out the relevant directions for further research. First, we can refine the proposed model and apply it to optimize train running along the BAM sections, which, in particular, will reduce the volume of greenhouse gas emissions on the railway [15,18]. The next is to take into account in the model the dependence of the spread of aggressive invasive organisms on the intensity of train traffic and the time they spend at stations or sections to predict zones of the highest concentration of such organisms [48]. Finally, a life cycle analysis of the BAM sections can help assessing the environmental costs for their reconstruction, which is urgent for railway operators and local authorities to develop appropriate environmental protection measures.
Author Contributions
Conceptualization, I.B. and A.K.; methodology, M.Z. and A.L.; software, M.Z.; validation, I.B., A.K. and A.L.; formal analysis, M.Z.; investigation, A.K. and M.Z.; resources, I.B.; data curation, A.K. and M.Z.; writing—original draft preparation, A.K. and M.Z.; writing—review and editing, I.B. and A.L.; visualization, M.Z.; supervision, I.B.; funding, I.B. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the Ministry of Science and Higher Education of the Russian Federation, the grant No. 075-15-2024-533 for implementation of Major scientific projects on priority areas of scientific and technological development (the project «Fundamental research of the Baikal natural territory based on a system of interconnected basic methods, models, neural networks and a digital platform for environmental monitoring of the environment»).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are not publicly available, though the data may be made available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BAM | Baikal–Amur Mainline |
| BMMAP | Batch Marked Markovian Arrival Process |
| SOQN | Semi-open queuing network |
| QN | Queuing network |
| QS | Queuing system |
References
- Fonseca-Soares, D.A.; Eliziario, S.A.; Galvincio, J.D.; Ramos-Ridao, A.F. Greenhouse Gas Emissions in Railways: Systematic Review of Research Progress. Buildings 2024, 14, 539. [Google Scholar] [CrossRef]
- Tostes, B.; Henriques, S.T.; Brockway, P.E.; Heun, M.K.; Domingos, T.; Sousa, T. On the right track? Energy use, carbon emissions, and intensities of world rail transportation, 1840–2020. Appl. Energy 2024, 367, 123344. [Google Scholar] [CrossRef]
- World Energy Outlook 2023. Available online: https://www.iea.org/reports/world-energy-outlook-2023 (accessed on 7 November 2024).
- Vinokurov, E.; Amangeldy, S.; Ahunbaev, A.; Zaboev, A.; Kuznetsov, A.; Malakhov, A. The Eurasian Transport Network, Reports 24/6; Eurasian Development Bank: Almaty, Kazakhstan, 2024; 142p. [Google Scholar]
- Order of the Government of the Russian Federation dated 04/28/2021 N 1100-p: On Approval of the Passport of the Investment Project “Modernization of the Railway Infrastructure of the Baikal-Amur and Trans-Siberian Railway with the Development of Capacity and Carrying Capacity (Second Stage)” [Rasporyazhenie Pravitel’stva RF ot 28.04.2021 № 1100-r: Ob Utverzhdenii Pasporta Investicionnogo Proekta «Modernizaciya Zheleznodorozhnoj Infrastruktury Bajkalo-Amurskoj i Transsibirskoj Zheleznodorozhnyh Magistralej s Razvitiem Propusknyh i Provoznyh Sposobnostej (Vtoroj Etap)»]. Available online: https://base.garant.ru/400726399/ (accessed on 7 November 2024). (In Russian).
- Shcherbanin, Y.A. Transport in Russia: Nine Years of Economic Sanctions. Stud. Russ. Econ. Dev. 2023, 34, 592–600. [Google Scholar] [CrossRef]
- Kazakov, A.; Lempert, A.; Zharkov, M. Modeling a Section of a Single-Track Railway Network Based on Queuing Networks. In Information Technologies and Mathematical Modelling. Queueing Theory and Applications; Dudin, A., Nazarov, A., Moiseev, A., Eds.; ITMM 2022. CCIS, 1803; Springer: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Kazakov, A.; Lempert, A.; Zharkov, M. An approach to railway network sections modeling based on queuing networks. J. Rail Transp. Plan. Manag. 2023, 27, 100404. [Google Scholar] [CrossRef]
- Bolch, G.; Greiner, S.; de Meer, H.; Trivedi, K.S. Queueing Networks and Markov Chains: Modeling and Performance Evaluation with Computer Science Applications; John Wiley & Sons, Inc.: New York, NY, USA, 2006; 878p. [Google Scholar] [CrossRef]
- Dudin, A.; Klimenok, V.; Vishnevsky, V. The Theory of Queuing Systems with Correlated Flows; Springer Nature: Cham, Switzerland, 2019; 431p. [Google Scholar] [CrossRef]
- Pyrgidis, C.N. Railway Transportation Systems. Design, Construction and Operation; CRC Press: Boca Raton, FL, USA, 2016; 500p. [Google Scholar] [CrossRef]
- Milenkovic, M.; Bojovic, N. Optimization Models for Rail Car Fleet Management; Elsevier Inc.: Amsterdam, The Netherlands, 2019; 282p. [Google Scholar]
- Sun, Y.; Cao, C.; Wu, C. Multi-objective optimization of train routing problem combined with train scheduling on a high-speed railway network. Transp. Res. Part C Emerg. Technol. 2014, 44, 1–20. [Google Scholar] [CrossRef]
- Kozlov, P.; Osokin, O.; Timukhina, E.; Tushin, N. Optimization of fleet size and structure while serving given freight flows. Adv. Intellegent Syst. Comput. 2020, 1116, 1064–1075. [Google Scholar] [CrossRef]
- Alfieri, L.; Battistelli, L.; Pagano, M. Energy efficiency strategies for railway application: Alternative solutions applied to a real case study. IET Electr. Syst. Transp. 2018, 8, 122–129. [Google Scholar] [CrossRef]
- Song, T.; Schonfeld, P.; Pu, H. A Review of Alignment Optimization Research for Roads, Railways and Rail Transit Lines. IEEE Trans. Intell. Transp. Syst. 2023, 24, 4738–4757. [Google Scholar] [CrossRef]
- Owais, M.; Ahmed, A.S.; Moussa, G.S.; Khalil, A.A. An Optimal Metro Design for Transit Networks in Existing Square Cities Based on Non-Demand Criterion. Sustainability 2020, 12, 9566. [Google Scholar] [CrossRef]
- Zhang, H.; Pu, H.; Schonfeld, P. Multi-objective railway alignment optimization considering costs and environmental impacts. Appl. Soft Comput. 2020, 89, 106105. [Google Scholar] [CrossRef]
- Kerner, B.S. Introduction to Modern Traffic Flow Theory and Control; Springer: Berlin/Heidelberg, Germany, 2009; 265p. [Google Scholar]
- Lefebvre, M. Basic Probability Theory with Applications; Springer: New York, NY, USA, 2009; 267p. [Google Scholar]
- Hu, W.; Dong, J.; Hwang, B.-G.; Ren, R.; Chen, Y.; Chen, Z. Using system dynamics to analyze the development of urban freight transportation system based on rail transit: A case study of Beijing. Sustain. Cities Soc. 2019, 53, 101923. [Google Scholar] [CrossRef]
- Ghisolfi, V.; Tavasszy, L.A.; Correia, G.H.d.A.; Chaves, G.d.L.D.; Ribeiro, G.M. Freight Transport Decarbonization: A Systematic Literature Review of System Dynamics Models. Sustainability 2022, 14, 3625. [Google Scholar] [CrossRef]
- Huang, J.; Cui, Y.; Zhang, L.; Tong, W.; Shi, Y.; Liu, Z. An Overview of Agent-Based Models for Transport Simulation and Analysis. J. Adv. Transp. 2022, 17, 1252534. [Google Scholar] [CrossRef]
- Cunha, J.; Reis, V.; Teixeira, P. Development of an agent-based model for railway infrastructure project appraisal. Transportation 2022, 49, 1649–1681. [Google Scholar] [CrossRef]
- Potthoff, G. Verkehrs Stromungs Lehre; TRANSPRESS-VEB: Berlin, Germany, 1970. [Google Scholar]
- Huisman, T.; Boucherie, R.J. Running times on railway sections with heterogeneous train traffic. Transp. Res. B 2001, 35, 271–292. [Google Scholar] [CrossRef]
- Weik, N. Long-term Capacity Planning of Railway Infrastructure: A Stochastic Approach Capturing Infrastructure Unavailability. Ph.D. Thesis, Rheinisch-Westfalische Technische Hochschule Aachen University, Aachen, Germany, 2020. [Google Scholar] [CrossRef]
- Daganzo, C.F.; Dowling, R.G.; Hall, R.W. Railroad classification yard throughput: The case of multistage triangular sorting. Transp. Res. Part A Gen. 1998, 17, 95–106. [Google Scholar] [CrossRef]
- Higgins, A.; Kozan, E. Modelling train delays in urban networks. Transp. Sci. 1998, 32, 346–357. [Google Scholar] [CrossRef]
- Fatnes, J.N. Flow-Times in an M/G/1 Queue under a Combined Preemptive/Non-preemptive Priority Discipline: Scheduled Waiting Time on Single Track Railway Lines; Norwegian University of Science and Technology: Trondheim, Norway, 2010; 81p. [Google Scholar]
- Wendler, E. The scheduled waiting time on railway lines. Transp. Res. Part B Methodol. 2007, 41, 148–158. [Google Scholar] [CrossRef]
- Emunds, T.; Nieben, N. Evaluating railway junction infrastructure: A queueing-based, timetable-independent analysis. Transp. Res. Part C Emerg. Technol. 2024, 165, 104704. [Google Scholar] [CrossRef]
- Wang, W.; Ji, Y.; Zhao, Z.; Yin, H. Simulation Optimization of Station-Level Control of Large-Scale Passenger Flow Based on Queueing Network and Surrogate Model. Sustainability 2024, 16, 7502. [Google Scholar] [CrossRef]
- Kazakov, A.; Vu, G.; Zharkov, M. A Stochastic Model of a Passenger Transport Hub Operation Based on Queueing Networks. In Information Technologies and Mathematical Modelling. Queueing Theory and Applications; Dudin, A., Nazarov, A., Moiseev, A., Eds.; ITMM 2023. CCIS, 2163; Springer: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]
- Bychkov, I.V.; Kazakov, A.L.; Lempert, A.A.; Bukharov, D.S.; Stolbov, A.B. An intelligent management system for the development of a regional transport logistics infrastructure. Autom. Remote Control 2016, 77, 332–343. [Google Scholar] [CrossRef]
- Bychkov, I.; Kazakov, A.; Lempert, A.; Zharkov, M. Modeling of Railway Stations Based on Queuing Networks. Appl. Sci. 2021, 11, 2425. [Google Scholar] [CrossRef]
- Zharkov, M.L.; Kazakov, A.L.; Lempert, A.A. Transient process modeling in micrologistic transport systems. IOP Conf. Ser. Earth Environ. Sci. 2021, 629, 012023. [Google Scholar] [CrossRef]
- Marinov, M.; Viegas, J. A simulation modelling methodology for evaluating flat-shunted yard operations. Simul. Model. Pract. Theory 2009, 17, 1106–1129. [Google Scholar] [CrossRef]
- Zharkov, M.; Lempert, A.; Pavidis, M. Simulation of Railway Marshalling Yards Based on Four-Phase Queuing Systems. In Information Technologies and Mathematical Modelling. Queueing Theory and Applications; Dudin, A., Nazarov, A., Moiseev, A., Eds.; ITMM 2020. CCIS, 2163; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Kazakov, A.; Lempert, A.; Zharkov, M. Modeling of a Coal Transshipment Complex Based on a Queuing Network. Appl. Sci. 2024, 14, 6970. [Google Scholar] [CrossRef]
- Wilson, N.; Fourie, C.J.; Delmistro, R. Mathematical and simulation techniques for modelling urban train networks. S. Afr. J. Ind. Eng. 2016, 27, 109–119. [Google Scholar] [CrossRef]
- Weik, N.; Nieben, N. Quantifying the effects of running time variability on the capacity of rail corridors. J. Rail Transp. Plan. Manag. 2020, 15, 100203. [Google Scholar] [CrossRef]
- Huisman, T.; Boucherie, R.J.; Van Dijk, N.M. A solvable queueing network model for railway networks and its validation and applications for the Netherlands. Eur. J. Oper. Res. 2002, 142, 30–51. [Google Scholar] [CrossRef]
- Kim, C.; Dudin, S.; Dudin, A.; Samouylov, K. Analysis of a Semi-Open Queuing Network with a State Dependent Marked Markovian Arrival Process, Customers Retrials and Impatience. Mathematics 2019, 7, 715. [Google Scholar] [CrossRef]
- Roy, D. Semi-open queuing networks: A review of stochastic models, solution methods and new research areas. Int. J. Prod. Res. 2015, 54, 1735–1752. [Google Scholar] [CrossRef]
- Klepikov, V.P.; Klepikova, L.V. Distribution of fugitive emissions in the energy complex of Russia during the supply of oil to refineries. Energy Rep. 2023, 9, 72–78. [Google Scholar] [CrossRef]
- Rasskazov, I.Y.; Arkhipova, Y.A.; Kryukov, V.G.; Volkov, A.F. Mining Industry in the Russian Far East: Balancing the Interests of Subsoil Use and the State. J. Min. Sci. 2023, 59, 481–489. [Google Scholar] [CrossRef]
- Povoroznyuk, O.; Vincent, W.F.; Schweitzer, P.; Laptander, R.; Bennett, M.; Calmels, F.; Sergeev, D.; Arp, C.; Forbes, B.C.; Roy-Leveillee, P.; et al. Arctic roads and railways: Social and environmental consequences of transport infrastructure in the circumpolar North. Arct. Sci. 2023, 9, 297–330. [Google Scholar] [CrossRef]
- Lemke, A.; Buchholz, S.; Kowarik, I.; Starfinger, U.; von der Lippe, M. Interaction of traffic intensity and habitat features shape invasion dynamics of an invasive alien species (Ambrosia artemisiifolia) in a regional road network. NeoBiota 2021, 64, 55–175. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).