Abstract
Gross primary productivity (GPP), the primary driver of carbon accumulation, governs the sequestration of atmospheric CO2 into biomass. However, GPP cannot be measured directly, as photosynthesis and respiration are simultaneous. At canopy level in plot-scale studies, GPP can be estimated through the closed chamber-based measurements of net ecosystem exchange (NEE) and ecosystem respiration (Reco). This technique is cost-effective and widely used in small-scale studies with short vegetation, but measurements are periodic-based and require temporal interpolations. The rectangular hyperbolic model (RH) was the basis of this study, developing two temperature-dependent factors following a linear and exponential shift in GPP when the temperature oscillates from the optimum for vegetation performance. Additionally, a water table depth (WTD)-dependent model and an exponential model were tested. In the peak season, modified RH models showed the best performance, while for the rest of the year, the best model varied for each subplot. The statistical results demonstrate the limitations of assuming the light-use efficiency as a fixed shape mechanism (using only one model). Therefore, a multi-model approach with the best performance model selected for each period is proposed to improve GPP estimations for peatlands.
1. Introduction
Peatlands sustain the global carbon cycle by acting as reservoirs, accumulating up to 40% of the soil carbon (C) stored globally [1]. The accumulation of C in peat is attributed to the slow decomposition rates of organic matter (OM), driven by waterlogged conditions that inhibit decomposer activity, as well as to gross primary productivity (GPP), which represents the amount of atmospheric CO2 assimilated by plants [2].
Vegetation productivity is estimated with GPP flux calculations, based on the assumption that the amount of CO2 fixed in photosynthesis reflects the quantity of biomass produced [3]. However, GPP cannot be directly measured. During the daytime, respiration and photosynthesis occur simultaneously, and the coupled processes are measured as net ecosystem exchange (NEE). Therefore, the CO2 emission rate, or ecosystem respiration (Reco), must be subtracted from NEE to determine GPP [4].
One of the most widespread techniques to measure short-vegetation CO2 fluxes (NEE and Reco) at canopy level are closed dynamic chambers, a non-expensive and easy-to-operate technique used for over a century [5]. In the chamber technique, opaque and transparent chambers are used to measure Reco and NEE fluxes, respectively [6]. The main advantages of chamber systems are their relatively low costs and suitability for use on small plots with short and heterogenous vegetation, enabling determination of plot-specific fluxes. However, they have disadvantages, primarily related to their labour-intensive nature (particularly when using manual chambers) and their limited spatial (restricted to plot-scale) and temporal (dependent on measurement frequency) resolutions [5]. The spatial limitation can also be an advantage, as the chamber’s technique is frequently employed in experimental studies where subareas are manipulated with induced WTD, precipitation and/or temperature changes. When manual chambers are used instead of automatic systems, the gap-filling of fluxes between campaigns is needed [7]. Multiple environmental variables, such as soil and air temperatures, water table depth (WTD), or photosynthetically active radiation (PAR), and their relationship with GPP are employed as gap-filling approaches [8,9]. Consequently, a modelled GPP can be obtained with using the same timestamp as the variable used for its estimation, with PAR being the most commonly used for this purpose.
Light-response models are based on the relationship between the photon flux density and the photosynthetic rate as described by the light-response photosynthetic curve. Numerous equations have been developed to explain this connection. Among them, the most commonly employed are the rectangular hyperbolic (RH), the non-rectangular hyperbolic (NRH), and the exponential (EXP) models [10]. The accuracy of these models was recently evaluated in drip-irrigated maize regions, where an improved version of the RH model, including the leaf area index (LAI), demonstrated the best performance [10]. Similarly, an overview of the strategies for fluxes time-integration in peatlands has been compiled as a review by Baird et al. [8]. Therefore, comparing modelling strategies for either fluxes or gap-filling in CO2 exchange is not a new concept. However, our objective was to develop a new approach to identify the most suitable model for peatlands.
Temperature controls numerous metabolic processes linked to photosynthesis, e.g., an increase in temperature can stimulate enzyme activity and accelerate the photosynthesis rate or indirectly increase vapour pressure deficit (VPD), thereby reducing the photosynthetic rate [11,12]. Therefore, classical approaches (RH, EXP, NRH) that do not consider the stress caused by too low or too high of a temperature in vegetation may overestimate GPP fluxes during frozen or heatwave periods. This paper presents two temperature-based factors that can improve the RH model during overheated periods over summer heatwaves or during frost events in spring and winter when plants are under stress. Empirical observations revealed a shift in the light curve during winter and early spring, related to the low, near-zero-degree temperatures typical for frost events. Additionally, when temperatures exceeded 28 °C, non-fitting values were observed in the classical RH model. Based on these observations, we developed a temperature factor to detect temperature-related changes over shorter time spans instead of daily intervals.
The usual assumptions include a fixed-shape type of the light-use efficiency curves independently of the vegetation stage, status, or distribution of species abundances when applying it to heterogeneous vegetation covers. In this research, we intend to present the limitations of these assumptions, demonstrating how, depending on the conditions of each period, a different model may perform better, and there is a need to combine them to accomplish the best possible results. We conducted a comparison of the accuracy of classical models and the improved RH model that includes temperature factors against a water-table-depth-based GPP model in a peatland ecosystem, where WTD and temperature significantly influence its dynamics, to demonstrate how the performances of the models change within the year. Moreover, beyond the classical performance analysis and oscillations in yearly cumulative fluxes, we estimated the growing seasons for each model to compare them with the classical thermal growing season, providing deeper insides into implications of modifying the modelling strategy. Henceforth, the novelty of this work lies not only in the creation of a multi-model framework and gathering the best performances of each model, but also in the development of two new parameters to enhance GPP estimations in peatlands, along with an analysis of the implications of these models for phenology estimations.
No two peatlands are identical; each is unique in its vegetation, water table regimes, and climate, which are the main factors defining peatland carbon flux dynamics and the shape of the photosynthetic light-response curve. Different models are expected to show the best performance in each different site. For instance, the presence or dominance of Sphagnum mosses is known for shifting the RH fit when growing in full light (open peatlands) as the photoinhibition plays a major role in lowering GPP values [8]. The results presented in this study will also be affected by the site dependency; thus, the extrapolation of the conclusions for different peatlands and sites is not their intended application. The algorithm should be applied in each case study to determine the best approach. However, no considerable variances in their trend are expected. GPP is the most significant carbon flux in the terrestrial system; thus, improving its estimation is essential for understanding the global dynamics and reducing uncertainty [13].
2. Methodology
2.1. Experimental Site
Manual chamber measurements were conducted in the Rzecin peatland (52°45′41″ N, 16°18′35″ E), an ecosystem included in the Natura 2000 European Union habitat protection network (Area code: PLH300019; [14]). The peatland area is classified as a poor-rich fen with high vegetation heterogeneity. Measurements were conducted at two experimental sites (CR and CL), located 50 m apart, to represent stable and variable water table depth (WTD) conditions (Figure 1). The sites are equipped with meteorological stations providing continuous data, like the nearby tower continuously providing PAR with 30 min time steps [15]. The CR site is located on a floating Sphagnum mat, and its surface oscillates within the range of 15–25 cm, depending on the year. The CL site is located close to the border between the floating mat and the part of the peatland underlined with 4–5 m of lake sediments. Hence, both locations present differences in their WTD regimes, which eventually developed into, among others, two distinct vegetation species dominating each site. The dominant species in CR are Sphagnum spp. and Carex rostrata with the presence of Oxycoccus palustris, while the CL site is a poor fen dominated by Sphagnum spp. and Carex lasiocarpa with the presence of O. palustris, Equisetum palustre, and Comarum palustre [13]. The names of the sites are derived from the dominant vascular plant species: C. rostrata for CR and C. laciocarpa for CL [14]. CR and CL sites are divided into plots, and three replicates are used per site.
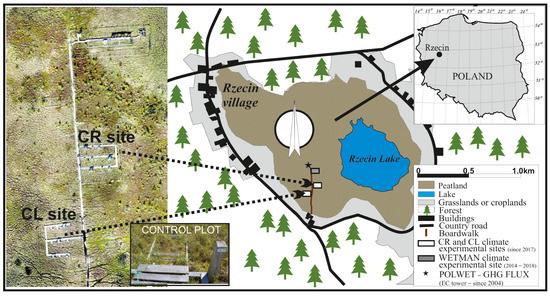
Figure 1.
Location of Rzecin peatland as well as CR and CL sites with climate manipulation experiments.
2.2. Meteorological and Hydrological Measurements
PAR, air temperature, and WTD measurements were used with 30 min timestamps. PAR was measured by BF5 Sunshine Sensor (Delta-T Devices Ltd., Burwell Cambridge, UK) installed on a tower 3 m above the peatland surface, separated 70 m from CR and 120 m from CL sites. The temperature was measured in each sub-site/plot by radiation-sheltered thermohygrometers HygroVue5 (Campbell Sci., Logan, UT, USA) installed 30 cm above the surface [15]. WTD was measured using TD-divers (Royal Eijkelkamp, Giesbeek, The Netherlands) installed at three locations at each site within PVC piezometers permanently fixed to the wooden platforms. These measurements are combined with the peatland surface level oscillation data, using the wooden platforms as the reference point. Further details about the hydrometeorological conditions’ measurements are provided by Antala et al. [15].
2.3. CO2 Flux Measurements and Flux Calculation
The closed dynamic portable chamber system was used to manually measure carbon dioxide fluxes, following methodology described in Acosta et al. [16]. The system measures Reco and NEE by combining an opaque and a transparent chambers, including measurements of relative humidity and temperature within each chamber and PAR in the transparent one; detailed information can be found in Antala et al. [15]. Both sites, CL and CR, utilize preinstalled 20 cm high white PVC soil frames with outside dimensions of 0.75 × 0.75 m inserted 15 cm deep into the peat (three frames per each treatment per site). These frames enable a complete sealing of the chamber headspace, complemented by the elastic rubber installed along the bottom edge of each chamber’s walls.
Chamber campaigns were conducted every 3–5 weeks (overall, five campaigns were organized in 2020 and ten in 2021) under sunny and cloudless conditions from early morning until late afternoon. The measurement duration was 1.5 min for NEE and 2.5 min for Reco, with these measurements taken sequentially with a maximum interval of one minute between them. Here, Reco flux rates are assumed to represent CO2 emissions corresponding to the time of NEE measurements. Hence, GPP flux rates were calculated for each plot as a sum of consecutively measured NEE and Reco fluxes [17]. The CO2 concentrations measured in the chamber headspace during the closure time were corrected for the water dilution effect [18] and were used to calculate the flux rates of NEE and Reco as described by Hoffmann et al. [7]. The flux of GPP is defined as negative in this research using the atmospheric sciences point of view, atmosphere is the reference point, hence GPP is a reduction in the CO2, expressed as negative.
The above approach enabled the measurements of NEE and Reco fluxes on the same plot with no more than a 2 h interval between successive measurements. However, due to the reduced sun hours, only three complete rounds of measurements were taken per site during winter, while summer conditions allowed five rounds per site. The chamber system was designed to operate manually, resulting in significant gaps between measurement campaigns and a limited number of replicates per campaign due to the need for physical presence and operation in the field. Consequently, a gap-filling procedure is required to estimate CO2 fluxes with the highest possible temporal resolution during the periods between campaigns.
As described in the following sub-section, multiple models have been used to estimate GPP values for each plot during the campaign dates based on the calculated plot-specific GPP rates and PAR measured during NEE measurements. Subsequently, the estimated model parameters were employed to calculate GPP based on the PAR measured with 30 min time steps; the sum of 24 h of half-hourly GPP fluxes cumulated over the campaign day was considered as the daily GPP. When fewer than four measurements of NEE and Reco fluxes per plot were available for a campaign, data from two consecutive campaigns were merged using a moving window (e.g., first + second campaign, second + third campaign). Then, the median date of the combined dataset was selected as the reference point for the estimated model parameters.
2.4. Parametrisation and Models’ Implementation
The RH model was selected as the base photosynthetic light response curve used in this study. Within the rectangular hyperbolas, the selected variations include the original formulation, which follows the enzyme kinetic curve of Michaelis–Menten (Equation (1)), along with two modified rectangular hyperbolic models that incorporate the average temperature from the previous hours (Equations (2) and (3)). These models were used for comparison.
The classical hyperbolic light response model (Equation (1)) estimates GPP (called here GPPRH) in µmol−1 m−2 s−1 based on the measured photon flux density of PAR (µmol−1 m−2 s−1), maximum rate of carbon fixation at infinitive PAR (GPmax; µmol−1 m−2 s−1), and the light-use efficiency (α, mol CO2 mol−1 photons).
Due to the observed shift in the light response curve during winter and early spring—associated with near-freezing temperatures typical for frost events—and during extremely hot summer days, modifications of RH modelling approach were implemented to better capture the effects of stressed conditions on GPP. The temperature factors are calculated based on the previous hours’ air temperature average, and the length of the moving average is altered depending on the time of the day (Figure 2). Before 11:00, the average temperature is calculated over three hours to account for the possible effect of night frost periods. Conversely, after 11:00, the span is reduced to 1.5 h to detect the possible heat stress in summer.
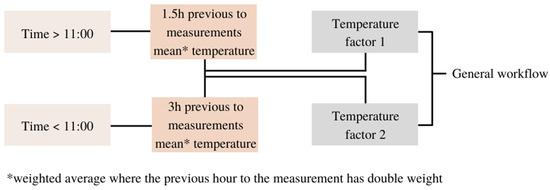
Figure 2.
Scheme of the temperature factors calculation where the general workflow is the reference for Figure 4 scheme, and the temperature factors are secondary variables introduced at the start.
The first temperature-adjusted model, TRH, applies a linear factor that only shifts to the left of the RH curve when the temperature is displaced from the optima (Topt; defined by Huang et al. [19] in this case) for photosynthetic activity. Temperatures below 0 °C are considered limiting for plants with highly reduced active photosynthesis. Consequently, when the average temperature is below zero, the maximum displacement of the first temperature factor (Tf1) is applied: GPP = GPPRH − 2. In the same way, when the temperature average is above 45 °C, the Tf1 factor is set to saturate (Tf1 = 2) and again GPP = GPPRH − 2. In order to have the same displacement penalizing too-cold and too-warm temperatures, the Tf1 calculation is split in two: (i) it decreases from 0 to −2 from Tf1 = optimum temperature − x2 °C until Tf1 = 0 °C; (ii) it increases from 0 to 2 from Tf1 = optimum temperature + x1 °C until Tf1 = 45 °C; and lastly to obtain the new GPPTf1, the computed factors are subtracted from the RH result (Equation (2)).
The second model adjusting temperature uses the temperature factor (Tf2) to decrease the light-use efficiency (α) value exponentially when the temperature is displaced from the optima, assuming that the effect of too-high or too-low temperature results in reducing the efficiency of photosynthetic activity (Equation (3)). In this case, the penalization for conditions below 0 °C is set to reduce a maximum of 85% of the GPP expected at the same PAR with an optimum temperature. At the same time, when the temperature average is above 45 °C, the Tf2 is fixed to a rate reducing ~70% of the GPP expected at the same PAR with an optimum temperature (both reduction percentages established based on empirical results). Hence, the Tf2 reduces α exponentially when temperatures decrease from the optima to 0 or increase from the optima until 45 °C, and in the same way as the Tf1, Tf2 calculation is split (Equation (3)). In both cases, the optimum temperature range is between Topt − x2 and Topt + x1, where no penalization of the light-use efficiency or GPP reduction is applied. Lastly, the parameters x1 and x2 are calculated for each plot, choosing the temperatures in which the model performs the best, ranging from ±6.5 °C to ±11.5 °C.
The non-rectangular hyperbola proposed by Gilmanov et al. [20] and the exponential model of Bassman and Zwier [21] are also tested (Equations (4) and (5), respectively) to compare the performance of the rectangular hyperbolic models with some alternatives.
For the non-rectangular hyperbolic and exponential models, GPmax, α and PAR are defined as in the previous equations, and θ determines the convexity of the curve for the non-rectangular hyperbola with the value ranging between 0–1.
Finally, a WTD-based GPP model developed by Tuittila et al. [22] is included in the set of models compared (Equation (6)), where uP is the optimum WTD, tP the tolerated range of the oscillation of WTD from the optimum (uP), and GPmax also considers a WTD optimal for photosynthetic activity. In this case, the model is applied two times, using the measurement of WTD in 30 min time steps and the last 15 days’ WTD average values. In both cases, the same equation is applied (Equation (6)).
Before the parametrisation of the final fixed variables for the WTD-based model, a Gaussian relationship between GPP and WTD oscillations from the optimum (uP) and tolerated positions (tP) is assumed, applying Equation (7) to obtain the fixed parameters of optimum and tolerated WTD as Tuittila et al. [22] developed and based on the Sphagnum spp. response to WTD changes.
The models are used with the chamber flux measurements of GPP (NEE-Reco) for parametrising the campaign’s fixed variables: GPmax, α, and θ. The sole exception occurs with the WTD-based model where a previous step is required (Figure 3, Equation (7)), as earlier described. A general workflow is followed, and the best fit for every single model is selected for the two campaign moving windows (Figure 4).
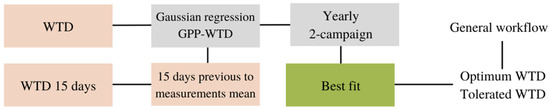
Figure 3.
Optimum and tolerated water table depth (WTD) calculation scheme. The general workflow is the reference for Figure 4 scheme, and WTD parameters are secondary variables introduced at the start.
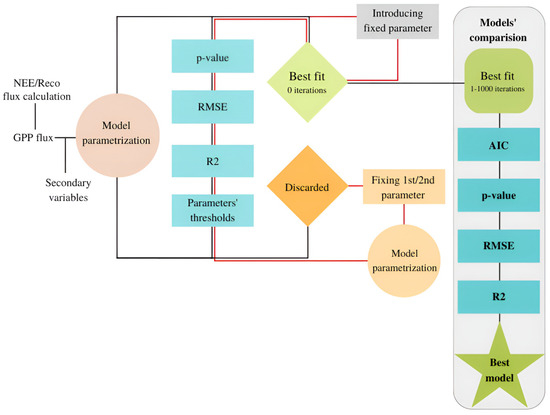
Figure 4.
Algorithm workflow to choose the best fit for each model and the best model out of them. Net ecosystem exchange (NEE) and ecosystem respiration (Reco) fluxes are the fluxes calculated from manual chamber campaigns following the Hoffmann et al. approach [7].
The resulting parameters are interpreted as the output for the median date between the campaigns analyzed for every two campaign moving windows when the number of measurements in a campaign is lower than eight. Once all the campaigns are processed, the parameters are compiled and interpolated daily to model the inter-campaign GPP values using these parameters, tower-based PAR, and air temperature or WTD, if applied. Subsequently, as the final output, the whole time-series GPP with 30 min time steps, daily cumulative values, and yearly cumulative values are generated together with all statistical results from each model.
2.5. Models’ Statistical Evaluation
The GPP data were analyzed using the Lilliefors test to determine their normality. Once the normality and no homoscedasticity are assured (Supplementary Tables S1 and S2), the goodness of fit to select the best performance of each model is evaluated with the p-value, adjusted R2, and root mean square error (RMSE). For each parameter, the results in which their values are outside the bounds are discarded. For instance, in case of the convexity parameter for Gilmanov et al. [20] fit, the parametrisation cannot trespass below zero or above one. Moreover, all parameters should present p-values < 0.05, if possible. The p-value filter is modified to select the most significant results (not below 0.05) only when no possible combination retrieves all parameters with significance levels below 0.1. Lastly, the fit with the lowest RMSE, highest adjusted R2, and the most significant result based on the p-value is selected.
In order to compare the performance of the models, RMSE, p-value, Akaike information criterion (AIC), and the correlation (R2) from the best fit are considered. The AIC indicates the amount of information that the model has lost concerning the original dataset and the efficiency of the model. In large datasets when an extra predictor is not efficient, the input would be avoided and the calculations would be faster, this is the reason why AIC presents the highest weight. Simultaneously, RMSE evaluates the differences between the modelled and measured values, the R2 measures the relationship, and the p-value evaluates the significance of this relationship and, consequently, the fit. High accuracies can mask low probabilities to estimate the predicted value, and the combination of statistics allow us to discard these cases. The best performance for each combined two campaigns is selected based on them, with the highest weight of AIC (indicating the likelihood and efficiency of the model), followed by p-value and RMSE (revealing the significance and error of the estimations), and finally, R2 is considered. The R2 has the lowest weight since, for a good correlation, just a similar trend between variables is needed; thus, R2 is not always an indicator of a good or the best fit.
The selection of the best performing model involves creating a multi-model output and identifying the best performance separately. Within each two-campaigns-moving-windows, the models are ranked based on the AIC, p-value, RMSE, and R2 outputs rescaled from 0 to 1 and multiplied by the weights presented in Table 1. The model with the lowest weighted statistics output is then chosen. Once the computations are completed for all the campaign values, the parameters obtained from the models are interpolated daily using the best ones. The strategy is applied for all models as the predicted parameters are equivalent. Lastly, a moving average (span = 12) is applied to the model’s last three and the first three days for the multi-model consistency. The output with the smoothed sections represents the final thirty-minute multi-model result, from which daily and yearly cumulative values are computed.

Table 1.
Values of the weighting factors used to select the best model based on their performance.
2.6. Changes in Vegetation Seasonality Estimations
In order to evaluate the implications of changing the modelling strategy, the length, amplitude, start and end of the growing season were calculated using DATimeS [23]. For each model, including the multi-model approach, the phenological variables mentioned were calculated using the GPP estimated from November 2020 to December 2021, selecting the upper 40% of the values in terms of average daily PAR and hours of sun and applying a moving average with a four-day span. The data filter was used to exclude cloudy and partially cloudy days to minimize the PAR effect on the oscillations. The percentage selected (40%) was based on the experimental testing performed (the one adjusting best to keeping only sunny days). In parallel, the thermal growing season was computed considering the start of the season as the start of a continuous average soil temperature above 5 °C and the end of the season as the first days below this temperature [24]. Lastly, the results were compared per model to check the changes in these parameters’ estimation based on the modelling strategy chosen. The year 2020 was excluded from this analysis due to an insufficient number of chamber campaigns.
3. Results
3.1. Measured Data and Climatology
The models’ performance has been analyzed based on the outputs of the 2020/2021 campaigns. During 2021, ten field campaigns collected chamber data from 25 February to 30 October while, due to COVID restrictions, only 5 field campaigns collected data in 2020 from 15 March to 14 September (Table 2). Each campaign included between two and five measurements of NEE and Reco fluxes per plot, excluding the winter campaign of February due to the reduced hours of light. The scarcity of data per plot forced the grouping of measurements every two campaigns as defined in the methodology. Considering only control plots, the average campaign values per site show a Gaussian distribution of PAR, GPP, and temperature peaking in July for both CL and CR for both years (Table 2). A continuous decreasing trend of WTD can also be observed from February/May to September/October, with a slight increase in May 2021 (Table 2) matching with the highest cumulative precipitation of the year (Figure 5).

Table 2.
Conditions and results for plots 1, 2, and 3 averaged per site: Carex rostrata (CR) and Carex lasiocarpa (CL) dominated sites during the campaign for 2020 (A) and 2021 (B). Temperature is the average air temperature (°C) measured at the sites, PAR is the average photosynthetically active radiation (µmol m−2 s−1) from the tower, GPP is the average of gross primary productivity fluxes results (with standard deviation) from the subtraction of consecutively measured net ecosystem exchange and ecosystem respiration averaged for all replications (µmol CO2 m−2 s−1)—all fluxes measured during each campaign were used for calculation. SD—stands for standard deviation. WTD represents the daily average water table depth (cm), and “Nr.” represents the number of measurements per plot/site.
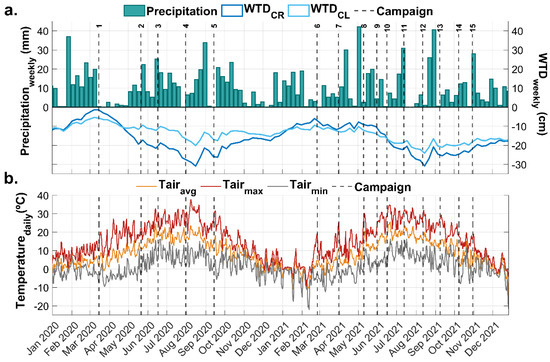
Figure 5.
Hydrometeorological conditions for CR and CL sites in the Rzecin peatland during 2020–2021. Conditions are presented in a weekly timestep for the averaged water table depth (WTD) and cumulative precipitation (a) and in daily timesteps for air temperature (b). Dashed lines indicate dates of CO2 chamber campaigns (from 1 to 5 in 2020 and from 6 to 16 in 2021).
Compared to previous years, a progressive drawdown of WTD was observed in CR, reflected in the annual average dropping from −12.4 cm (2018) to −15.8 cm (2021). Although this may appear to be a slight change, it represents a significant variation within the intra-annual oscillations of WTD. Between the second half of January and the first one of February, a rise in the WTD is observed within previous years (2018–2019) in CR, with the WTD reaching near-surface values (−1–−7 cm). This peak was displaced in 2020 to the second week of May, and it became hard to identify during 2021, a year with relatively stable values of WTD from January to May (Figure 5). The drawdown during summer is present in all years (2018–2021), reaching its lowest WTD value in 2021 at 25 cm below the surface. Meanwhile, the CL site’s annual average WTD was lower in 2020 (−20.3 cm) and increased in 2021 to −16.7 cm. The high 2021 average was thanks to a not-so-low WTD value from January to July, oscillating between −5 and −14 cm. The same was recorded for 2019, with WTD values always higher than −10 cm. The rise in WTD during winter–spring seasons, while it reached the surface level in 2020, only lasted one month that year; 2021 WTD did not reach the surface, but the near-surface levels were maintained during the first five months, explaining the higher annual average (Figure 5). In 2021, WTD recovered the 2019 behaviour and levels for the CL site.
The year 2020 was a warm year with 9.4 °C due to a warmer winter (Figure 5b). Over the previous 21 years (2000–2021), the winter season of December 2019 to February 2020 was the warmest for the entire country, with temperatures 3.6 °C higher than the 2000–2021 average [25]. Moreover, the year was dry during the start of the growing season; between 15 March and 17 May, only 34.1 mm of precipitation was accumulated. In the case of 2021, it was thermally a usual average year when comparing annual air temperature to the standard period 1991–2020 [25], with an 8.0 °C average temperature. However, the same year presents unusually dry periods during the temperatures’ peak, between June and August (Figure 5). Antala et al. [15] identified that heat and drought waves occurred during this period, from 18 July until 22 August, when just 13.3 mm of precipitation was recorded. This drought wave was immediately followed by a relatively dry period between 30 August and 11 October, with 12 days accumulating only 32.5 mm. However, the yearly accumulated precipitation for CL and CR (535 mm) was within the range of ±10% of the average for Poland, based on measurements from 1991 to 2020 [25].
3.2. Performance of the Temperature Factors
The improvement in the performance of the rectangular hyperbolic approach, due to the addition of the temperature effect, solved the problem observed during measurements of the displaced light curve when temperatures are too low. For example, this displacement can be observed in CL_3 and CR_2 during the first campaigns modelled (25 February and 31 March of 2021, merged as 14 March), with air temperatures ranging from 6.5 °C to 20.2 °C in February and from 9.5 °C to 26.8 °C in March during measurements after the nighttime frost when the peatland surface was frozen (the minimum air temperature on 25 February and 31 March 2021 was −3.7 °C and −2.7 °C, respectively). In Figure 6, it can be observed that the RH model in CL_3 and CR_2 fails to predict the low GPP values measured early in the morning under low PAR (~340 µmol m−2 s−1 and ~500 µmol m−2 s−1) and low air temperatures (11.2 °C and 15.2 °C). Conversely, the adapted models displace the curve to fit these values, reaching 0 GPP with PAR < 300 µmol m−2 s−1 due to the constraint in photosynthesis produced by low temperatures and vegetation not yet recovered after the frozen night periods.
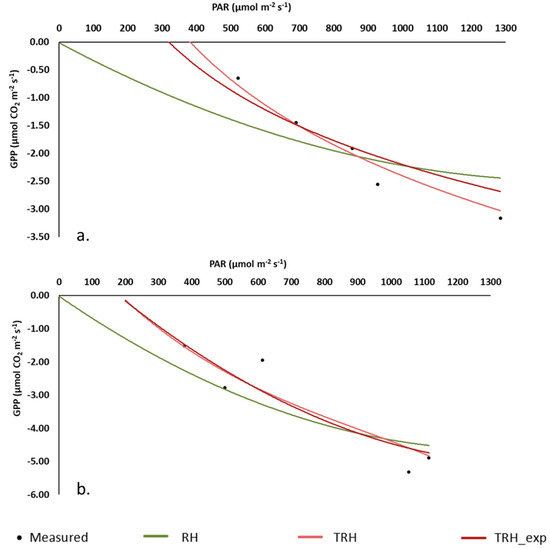
Figure 6.
The light response curve of photosynthesis with the Michaelis–Menten rectangular hyperbolic approach (RH) and the modified RH with temperature factors (TRH, TRH_exp) for the first campaigns of the year (25 February and 31 March) in CL_3 (a) and CR_2 (b) plots.
Generally, adding temperature to the rectangular hyperbola increased the model’s accuracy, decreasing the average BIAS from 77% to 92% of the time and RMSE from 54% to 77% (Figure 7). The thresholds of optimal temperatures for GPP were calculated for each plot’s best performance based on the average optimal temperature reported for the peatland area studied. Despite this adjustment for each particular case instead of a generalization of the thresholds, the vegetation coverage differences and distinct WTD regimes between CL and CR sites generate different performances between plots and sites. Furthermore, the seasonal distribution of the effectiveness of the temperature factors also oscillates between plots (Supplementary Tables S3–S7).
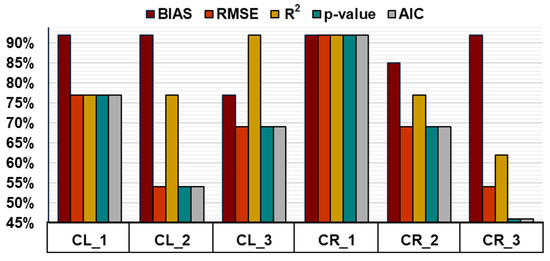
Figure 7.
Percentage of 2020/21 campaigns in which including one of the temperature factors benefited the statistical results or resulted in an equally precise output. In the case of BIAS, RMSE, p-value, and AIC, a benefit is considered when the addition of temperature factor decreases these values and, in the case of R2, when it increases them. Statistics are shown for each plot of the CL (1–3) and CR (1–3) sites.
In the case of CL_1 and CR_2 plots, the statistics show how adding temperatures does not improve the RH model during the start and end of the growing season (April–May, October), while it only occurs for the start of the season (April–May) in CL_3 (Supplementary Tables S3–S7). At the same time, CL_2 displays no improvement of RH with temperature during the early middle of the season (June). The temperature addition to the model did not increase the performance during the late-mid-season for CR_1 and CR_2, and CR_3 showed the weakest performance. The results in the CR site can be due to the higher coverage of Sphagnum spp.; mosses can desiccate during hot months, reducing their GPP and the changes in the shape of the light-response curve.
3.3. Models’ General Performance
In general, the models have shown reliable values; however, when using the WTD-based approach [22] with short-term measurements (30 min time steps), some unusual drops of GPP values were observed, e.g., during June and July 2021 for CL_2 and CR_2 plots. The same model applied with the fifteen-day average WTD provided more continuous and reliable results along the time series, although some unusual drops remain (WTD_15). The reason behind this can be the response time from vegetation; the effect of WTD is not immediate, and a continuous rise or drop is needed to modify vegetation productivity without a limited effect [26]. Thus, thirty-minute WTD measurements cannot correctly predict the effect of WTD on GPP and the optimal WTD estimated during a campaign is not necessarily reliable for the rest of that period if the oscillations are significant.
The exponential model from Bassman and Zwier [21], the non-rectangular hyperbolic function proposed by Gilmanov et al. [20], together with the Michaelis–Menten rectangular hyperbolic model with and without the addition of the created temperature factors, have displayed a consistent trend of outputs through the time series as it can be observed in Figure 8 for the year 2021. In the case of the WTD-based approach [22], some punctual periods during low WTD levels resulted in drops in the GPP trend not observed for the rest of the models (e.g., July–August CL_3, October CR_3). For this reason, during those periods, this model was not considered for the multi-model choice. As expected, a Gaussian distribution of GPP values with a peak between June and July marks the middle of the vegetation season. Each plot presents a different maximum and length of the GPP peak. Unquestionably, CL and CR sites report considerable differences in the daily cumulative GPP due to the differences in vegetation coverage and WTD regimes (Figure 8).
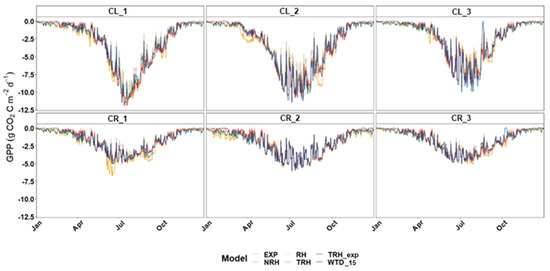
Figure 8.
Modelled diurnal rates of gross primary productivity (GPP) for each plot of CL (1–3) and CR (1–3) sites for 2021 for all compared models; GPP is expressed in daily cumulative values (g CO2 m−2 d−1). Note that the GPP models abreviations stand for EXP—exponential model [21], NRH—non-rectangular hyperbolic model [20], RH—rectangular hyperbolic model, TRH and TRH_exp—linear and exponential temperature adjusted RH, and WTD_15—water table depth based model [22].
These differences affect the performance of the models and the final output accuracy. The biggest residuals, or differences between the models and the measured data, happened in the June and July campaigns for the CL and CR sites. Although considering the average GPP measured during the winter campaign in February (Table 2), the values remain below ±0.2 times the average GPP (Figure 9). Hence, considering the relative difference between modelled and measured data, the winter measurements, including February and March or October campaigns, present the highest errors. It is also important to mention how, in CL sites, generally, all models overestimate the measured values (negative relative BIAS), with particular attention to WTD_15, which has the highest general overestimation.
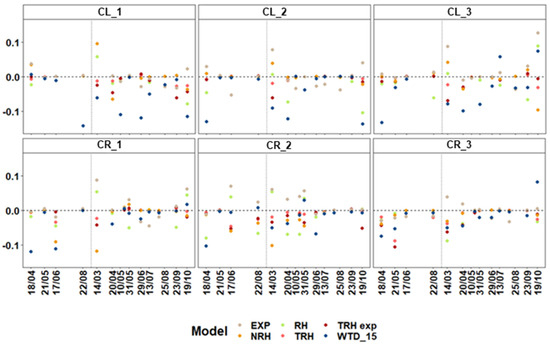
Figure 9.
Seasonal distribution of the average gross primary productivity (GPP) relative error per campaign (), being 0 the minimum and ±1 the highest error. The exponential model (EXP) during the March 14th-merged campaign is not shown; the value is outside the bounds (0.17). Note that the GPP models abreviations stand for EXP—exponential model [21], NRH—non-rectangular hyperbolic model [20], RH—rectangular hyperbolic model, TRH and TRH_exp—linear and exponential temperature adjusted RH, and WTD_15—water table depth based model [22].
Additionally, half of them underestimated the measurements during the first campaigns of the year (WTD, NRH, and EXP—18 April 2021, and RH, NRH, and EXP—14 March 2021, Figure 9). In the case of CR sites, the patterns are not that clear, though generally, the measured GPP values are overestimated except in the exponential model. The exponential model shows the underestimation of GPP during the first half of the measurement season and their overestimation during the next half. In this case, the first campaigns of the year are only underestimated by the NRH and EXP models in CR_1 and CR_2 and only by the EXP model in CR_3. Overall, modelled values in CR and CL sites show errors below ±10% (±0.1, Figure 9). Other statistics, such as R2, follow the same trend where the year’s first and last campaigns show the lowest correlations (Supplementary Table S3), possibly due to lower vegetation productivity and cold temperatures effect plus a lower number of measurements per campaign.
Generally, the RH, NRH, TRH, TRH_exp, and WTD_15 model’s statistical results note their reliability as in almost all campaigns; each presents a significant result indicated by the model’s p-value, with relatively small errors and an acceptable adjusted R2 value with CR plots presenting better performances than CL (Supplementary Table S8). As mentioned, the performances of every model were much better in CR; this is observed with higher correlation, lower errors, and higher significance levels than in the CL site. The CR site WTD values reached lower levels during the second half of the year compared to CL. The Sphagnum spp. coverage is higher in CR, and the cumulative GPP is inferior, facts that can partially explain the differences in statistics.
If instead of a multi-model approach using different models for each inter-campaign period only one model were chosen based on Table 3’s weighted statistics average over the whole year, the rectangular hyperbolic model adjusted with the temperature factor (TRH) and the exponential temperature factor (TRH_exp) would be the ones exhibiting the best performance in CL and CR sites, while the WTD-based model would show the poorest performance (Table 3). Despite the poor average performance of the WTD-based model, it presents in CR_3 the highest R2 and lowest RMSE (Supplementary Table S8). However, the lower p-value and higher AIC highly penalize the overall result. The WTD_15 model is thus not chosen in this case because the AIC statistic penalizes the number of predictors needed to choose the most optimal. Despite the low errors and high correlations, the WTD_15 model is not the most significant and efficient in predicting GPP. The AIC and p-value are crucial, as these metrics help ensure that the WTD model is excluded during periods when it is observed to fail.

Table 3.
Values of the average performance per model, estimated via weighted statistics from Table 1, where eight is the weakest and zero is the most robust performance. Note that the GPP models abreviations stand for EXP—exponential model [21], NRH—non-rectangular hyperbolic model [20], RH—rectangular hyperbolic model, TRH and TRH_exp—linear and exponential temperature adjusted RH, and WTD_15—water table depth based model [22].
3.4. Multi-Model Results and Performance
In general, the distribution of GPP followed the same trends for every model; not surprisingly, the multi-model results show a Gaussian distribution with a peak between June and August (Figure 10). The use of multiple statistics to choose the best performance in each inter-campaign period, the exclusion of the WTD_15 model when non-reliable results were provided, and the smoothing during the first and last days of the model have generated a continuous trend where no apparent jump or significant trend change in between models is observed (Figure 10). Hence, it is assumed that the strategy proposed has provided an excellent synergy/combination of the models, capable of showing the seasonality of fluxes without any interference due to the multi-model approach.
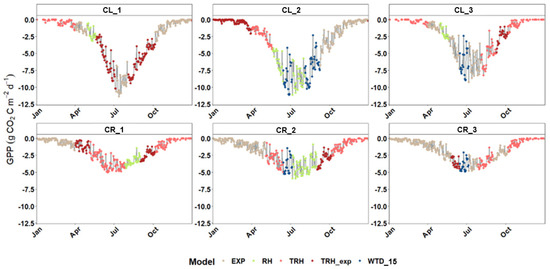
Figure 10.
Modelled diurnal rates of gross primary productivity (GPP) for each plot of CL (1–3) and CR (1–3) sites for 2021 determined based on the multi-model approach; GPP is expressed in daily cumulative values (g CO2 m−2 d−1). Note that the GPP models abreviations stand for EXP—exponential model [21], NRH—non-rectangular hyperbolic model [20], RH—rectangular hyperbolic model, TRH and TRH_exp—linear and exponential temperature adjusted RH, and WTD_15—water table depth based model [22].
Implementing the multi-model to obtain the best performance in each period generated a reliable model with R2 over 0.85, p-value below 0.001, BIAS lower than ±0.1 µmol CO2 m−2 s−1, and RMSE below 1.1 µmol CO2 m−2 s−1 except for CL_1 (Table 4). The highest average errors and lowest mean correlation are found in CL_1; however, for most of the year, CL_1’s statistical performance is comparable to the rest of the plots. The drop in its average values is due to the 29 July campaign with RMSE values above five and R2 values below 0.5 (Supplementary Table S9). In general, the 29 July campaign also shows the weakest performance for all CR plots, with the highest weighted statistic and, hence, with the worst combination of statistics. In the case of CL_2, the weakest performance takes place on 20 April, while for CL_3 occurs on 23 September; however, in both plots, these campaigns are closely followed by 29 July with also a weak performance, following the general trend (Supplementary Table S10). Once again, the performance in CR plots is more robust than in CL plots (Table 4) with higher correlations, lower errors, and more information preserved (AIC), and yet, it has to be considered that the absolute errors are lower also because the vegetation productivity is much lower at this site.

Table 4.
Average statistics per plot for the multi-model choice, including the weighted statistics factor calculated from Table 1 (first column) vs. best statistic result from individual models (second column). RMSE and BIAS are expressed with µmol CO2 m−2 s−1.
3.5. Changes in Vegetation Seasonality Estimations
The most significant CO2 uptake by vegetation occurs when their physiological status is the most optimal—coinciding with the highest photosynthetic efficiency—essentially, the peak of the growing season. This makes GPP a suitable variable for estimating the timing of the vegetation’s growing season within the year. As previously observed, the shape of the yearly distribution of GPP did not differ significantly by model due to the effect of PAR. Hence, it could be assumed that the estimation of the phenological variables will not differ much between models. However, phenology indicators have to be located based on stable conditions (sunny days); when these conditions are isolated, some displacements and minor changes can be identified in the trends. Starting with the length of the growing season, the displacements between models range between ±1–30 days, and CL_1 and CR_3 show the least significant displacements. In the CL site, the RH and WTD’s models results, in most cases, predict the shortest growing season, while the NRH model estimates the longest. In contrast, for the CR site, the NRH model estimates the shortest growing season, while the multi-model and the EXP model predict the longest growing season (Table 5). The most similar length of the season to the thermal growing season on average at the CL site is determined by the multi-model results, while for CR, it is the WTD-based model.

Table 5.
Length of the 2021 growing season (days) and, in brackets, the amplitude of the 2021 GPP (g CO2-C m−2 d−1) during the vegetation growing season per plot and model strategy generated by DATimeS [23] and the classical temperature approach. Note that the GPP models abreviations stand for EXP—exponential model [21], NRH—non-rectangular hyperbolic model [20], RH—rectangular hyperbolic model, TRH and TRH_exp—linear and exponential temperature adjusted RH, and WTD_15—water table depth based model [22].
The length of the season is not the only critical factor for determining and indicating changes between model predictions; the amplitude of the GPP seasonal curve is equally important. The amplitude of the season indicates the height of the GPP curve during the growing season or, what is the same, the difference between the median peak values and the median values at the start and end of the season. The rectangular hyperbola modified with temperature factors (TRH and TRH_exp) plus the non-rectangular hyperbola (NRH) present the highest amplitude and, therefore, a steeper curve, while the EXP model estimates the lowest amplitudes and shortest curves for both CR and CL (Table 5).
The changes in the shape of the GPP during the growing season per model are the first indication of the possible oscillation of the cumulative GPP of the growing and non-growing seasons. Depending on the model chosen to estimate the annual distribution of GPP, the cumulative values differ by ±4–5% in CL and CR sites except for CR_C1, with a standard deviation of ±7% of the average cumulative GPP (Table 6). The same occurs in the GPP growing season for CL_1, CL_2, and CR_1 with deviations of ±4–5%, while in CL_3, CR_2, and CR_3, the models only differ ±2–3%. In most of the plots, the models using a hyperbola to fit the light-response curve (RH, NRH, TRH_exp), except TRH, present the highest cumulative values while the exponential approach shows the lowest (Table 6). Considering the multi-model approach as the nearest to reality based on the statistical performance, all models overestimate the yearly cumulative GPP with two exceptions: the exponential model, which underestimates this value in CL_1 and CL_2, and the TRH model underestimates it in all plots excluding CL_1 (Table 6). Hence, the modelling strategy can affect the distribution of the growing season, its shape, and the cumulative uptake of CO2 by vegetation throughout the year and the growing season.

Table 6.
Cumulative gross primary productivity (GPP; g CO2-C m−2) during the growing season (GS) defined by DATimeS, and for the year (Total), calculated for each model estimations with the relative standard deviation (SD = SD/mean). Note that the GPP models abreviations stand for EXP—exponential model [21], NRH—non-rectangular hyperbolic model [20], RH—rectangular hyperbolic model, TRH and TRH_exp—linear and exponential temperature adjusted RH, and WTD_15—water table depth based model [22].
4. Discussion
4.1. Gap-Filling Temporal Approach and Measurements
In this article, we employed multiple models to fit the photosynthetic light response curve and used it as a gap-filling method for GPP fluxes for full-day periodic chamber campaigns on a campaign-wise basis. Compared to year-wise approaches, the campaign-wise gap-filling strategy has been identified as the most robust for peatland areas [4]. Additionally, the campaign-wise approach has demonstrated a better performance with full-day measurements compared to midday values [27]. However, the reliability of the campaign-wise approach depends on the number of measurements and the range of temperatures and PAR measured during the CO2 fluxes measurements [7,27]. It is not always possible to capture enough PAR and temperature conditions when the number of replicates and sites is considerable while the hours of sun are limited. Due to the previously mentioned constraints, the campaign-wise gap-filling approach was modified in this article. The modification involves applying a conditional order whenever the number of measurements is fewer than eight (four NEE and four Reco). In such cases, a two-campaign moving window was implemented. Merging two campaigns, especially during winter, has partially solved the problem of lack of variability in PAR and temperature, allowing the retrieval of reliable results during the period with less than 10% error. However, the eight-measurement threshold is not always sufficient for a reliable fit (e.g., March and April campaigns), and the number of measurements selected as the limit should probably be increased to catch the saturation points of the light response curve.
4.2. WTD-Based Model
The differences between sites are visible in the yearly cumulative GPP values. Lower GPP fluxes in the areas with higher presence of mosses are consistently reported for peatland [11], and CR presents the highest abundance of Sphagnum spp. Despite the greater presence of mosses, the WTD-based model was still not selected as the best overall model for the CR site. This approach was developed for Sphagnum-dominated peatlands, assuming that water saturation of Sphagnum spp. governs its photosynthetic capacity [22]. However, other authors have indicated that, with stable moisture in Sphagnum spp., the GPP is governed by PAR [28]. Vascular plants, the most abundant in the study area, also present a GPP driven mainly by PAR when conditions are not extreme, which is generally the case in the study area. Additionally, although mosses are more abundant in CR, the site is situated in a floating mat area. As a result, the oscillations of WTD are accompanied by surface oscillations, which reduce the impact of WTD changes on vegetation, making less relevant to incorporate WTD into GPP modelling.
The inclusion of WTD in the Tuittila et al. [22] approach has shown some unusual drops with the deepest WTDs. Usually, including environmental parameters increases the complexity of the model and its performance with more accurate results, but they can also induce outliers when abrupt changes occur [4]. Instead of the short-term WTD values, this article proposes using the average WTD of the fifteen previous days to avoid sudden drops in the GPP trend. With this simplification of the values, we can account for the legacy effect of WTD, and it has solved most of the drops present when the model was used for thirty minutes and daily WTDs. The number of campaigns during the 2021 year (10) can induce the remaining outliers from the WTD-based model. Possibly, the estimated optimum and tolerated WTD levels cannot adequately reflect the vegetation thresholds during the periods between campaigns and induce the worst performance of this model and this was further amplified during 2020 with even less data. Similar limitations have been observed in seasonal approaches with other environmental variables [4].
4.3. Displacement of the Rectangular Hyperbolic Model and Temperature Factors
The photosynthetic response to light, as represented by the light-response-curve models, is influenced by factors such as vapour pressure deficit and temperature. Cold temperatures limit photosynthesis; during winter, the GPP fluxes can switch from PAR to temperature-driven. This phenomenon is well-known in boreal areas where, despite the high photosynthetic potential, GPP fluxes are not significant even during spring [29]. Hence, the determined cold season is often assumed to be negligible when there is a combination of light and temperature limitations [30]. The effect of the cold temperatures is visible in the light curves presented in Section 3.2; instead of reaching no uptake of CO2 when no PAR is available, the temperature limitation induces a displacement, and 0 GPP is already reached with PAR ranging from 200 to 400 µmol m−2 s−1. Higher light intensities are needed to jumpstart photosynthesis; consequently, the RH can often overestimate GPP [10].
The effect of high temperatures on GPP fluxes is similar, as it can also limit photosynthetic capacity. However, the reasons behind this can be different, and apart from the decrease in electron transport and Rubisco activity, the stomatal closing also induces a reduction in GPP [19]. High temperatures can be accompanied by an elevated vapour pressure deficit when humidity is inadequate; this combination induces stomatal closing to prevent water loss and limits the assimilation of CO2 [31]. While there is a displacement at the start of the photosynthetic light curve response due to low-temperature limitations, high temperatures induce a constant decrease in GPP, lowering the curve, especially near the saturation point. At canopy scale during short-term low water content—induced by high temperatures—the canopy conductance and GPP are strongly coupled and the lowest the conductance, the highest the decrease in GPP in a continuous pattern [32]. Adding temperature to the photosynthetic light curves is a widespread technique generally used to adapt the models to the stressful conditions of elevated temperatures and reduce the overestimations of the classical approaches [33,34], though in our case, it has been applied to account for both hot and cold limitations. Generally, the temperature factors employed to correct classical GPP models include hourly, thirty minutes or daily temperatures, and estimated optimal and tolerated temperatures. In our study, it was assumed that there is a legacy effect of the previous hours’ temperature and the plants under frozen conditions before sunrise will not react the same way to the immediate temperature oscillations as those under non-frozen conditions or hot conditions will not affect the same way if they are punctual (30 min measurements) than if they are constantly high (1.5 h average). Hence, the temperature factors have been calculated based on the 3 h and 1.5 h averages, as described in the Methodology section.
The simplest displacement of the RH model adding an intercept (TRH) has shown the most remarkable improvement of the RH estimates during winter, estimating the limitations of cold temperatures at the CL site. In the case of the CR site, the adjustments enhance the performance of the models at the end of the year, while at the start of the year, both adjustments seem to increase the model’s error (TRH, TRH_exp). During June and July, when overheating is most frequent, both temperature models performed similarly, with less than a 1% difference in statistical performance. Both models improved upon the RH model by reducing GPP based on temperature constraints. It is uncertain why the performance of the models worsens at the start of the year, though, during this period, the relationship between GPP and PAR seems to be exponential and not a rectangular hyperbola. An exponential light curve can be induced by the more significant role of species with a low light saturation point and high photosynthetic potential once air temperature is above 0 °C and PAR is still primarily low, e.g., Sphagnum spp. Some indications of this assumption can be interpreted from the study by Lagergren et al. [35], which reported the lowest correlation of the exponential relationship of GPP-PAR at the site with a lower average temperature and no moss presence. The higher moss presence in CR could be the factor inducing the difference in performance of CR and CL sites.
4.4. Variations in Yearly Cumulative Values and Determination of the Growing Season
The comparison between models resulted in differences in the yearly cumulative value and the shape of GPP distribution, leading to oscillations in the growing season estimations. These oscillations in the yearly cumulative values have been observed in other studies, where the NRH model is frequently reported to overestimate GPP [10]. The RH model is often reported to underestimate or overestimate actual GPP values depending on the temperature and season [9,36], potentiality leading to compensation effects in GPP flux rates when annual cumulative GPP is calculated. However, in our case, there is a general overestimation of GPP from RH when compared to the multi-model results. The models with temperature factors (TRH and TRH_exp) improve the RH when the temperature plays a significant role. However, when used for the overall year, the TRH model presents a slight underestimation and TRH_exp overestimation compared to the multi-model. Ultimately, both models are RH-based, and as the results indicate, the RH fit does not always produce the best result. Adding temperature factors adjusts the fit by either reducing or augmenting the curve without altering its shape. The WTD-based model mainly presents a higher cumulative value than the multi-model, while it is the contrary for the exponential model. Hence, we see how the oscillations of the yearly cumulative GPP values are highly dependent on the fit of the light response curve.
In addition to comparing cumulative GPP values—a widely used approach for model evaluation—we also analyzed the differences between models based on phenology oscillations. The interpretation of the growing season changes depending on the focus of the study [37]. The thermal growing season approach defines “the period during which plants could potentially grow based on meteorological criteria (meteorological season)” [38], while with GPP, the goal is to define the actual period of vegetation growth based on the carbon uptake [38]. Despite the differences, the period in which the plants can potentially grow based on temperature should be the actual period of growth if there is no other limitation. In “normal” waterlogged conditions (no drainage, drying, etc.), peatland areas do not suffer water availability limitations [39]. Therefore, in the study area, it was assumed that there is an equivalency between these types of growing seasons. The approach could not be applied to other environments with vegetation growth limitations where the temperature and GPP growing season would not be comparable. Each GPP model presented a different annual value and distribution shape, finally producing variances in the length and amplitude of the growing seasons. These oscillations prove the importance of the right choice of strategy and how a multi-model approach can accomplish results that are more similar to reality; that is why the multi-model GPP growing season is more similar to the results obtained from the thermal growing season in CL. However, CR presents a growing season that is more similar to the WTD-based approach. The reasons for the higher similarity of the determined length of the growing season are unknown. We can only hypothesize that the higher presence of mosses and the surface oscillations in the floating mat area following WTD change, maybe, are creating more convenient set of conditions for the WTD-based model to work in CR. Hence, due to the penalization applied in the AIC to the use of more predictor variables, the WTD model is not selected on enough occasions in CR. The AIC evaluates the efficiency of the model, balancing the best results and the number of predictors to have those results. The WTD has additional parameters for tolerated and optimal WTD, hence, if another model has close results that are good enough without these extra two parameters, it is ranked as better.
5. Conclusions
Based on the results from Rzecin peatland in 2021, the usefulness of a multi-model approach is proven to be more accurate in GPP estimation than single-model approaches with a better statistical performance. Additionally, the main conclusions can be listed as follows:
- The use of a multi-model approach increases the statistical performance during the year, increasing the significance, reducing errors and information lost (in CL—RMSE: −12.3%, AIC: −11.4%, p-value: −52.2%; in CR—RMSE: −13.6%, AIC: −13.8%, p-value: −48.3%). Further improvement can be accomplished with a higher frequency of chamber campaigns or a greater number of replicates per campaign.
- The rectangular hyperbolas plus temperature factors (TRH and TRH_exp) increase the reliability of winter GPP at the start and the exponential models at the end of the year in the site with a non-floating mat (CL). While, for the CR site—floating-mat area with higher presence of mosses—the reliability of the estimated GPP increased using the exponential model at the start of the year and the TRH model at the end of the year.
- Using different models to estimate the annual distribution of GPP can change the distribution and the annual cumulative values, with higher oscillations in the case of the Sphagnum-dominated floating mat area (CR: ±5.23%; CL: ±4.56%). These oscillations can change our interpretation of peatlands’ sink or source potential, making the correct selection of modelling strategy necessary.
- The growing season determined from GPP is displaced for each model approach. Using the classical RH instead of a multi-model approach displaces the start and end of the season by 2 and 3 days, respectively, and shortens the growing season length up to a week. Hence, selecting the best statistical performance is crucial for phenological analysis.
Nonetheless, it must be stated that there is no possible way to prove which model retrieved the most accurate annual GPP value or defined the proper growing season, and the conclusions are based on the assumption that the best statistical performance implies the most reliable results.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/su17020393/s1, Table S1: p-value results from the Lilliefors test; Table S2: p-value results from the Barlett test; Table S3: Correlation results of models per campaign and plot; Table S4: RMSE results of models per campaign and plot; Table S5: BIAS results of models per campaign and plot; Table S6: p-value results of models per campaign and plot; Table S7: AIC results of models per campaign and plot; Table S8: Average statistic results of each model per plot; Table S9: Multimodel statisical results per campaign and plot; Table S10: Weighted statistics for the multi-model result during each campaign per plot.
Author Contributions
M.A.-S.: conceptualization, investigation, data curation, formal analysis, methodology, visualization, and writing—original draft. M.S.: data curation, investigation, supervision, and writing—review and editing. A.R.: funding acquisition, project administration, supervision, and writing—review and editing. R.J.: conceptualization, formal analysis, investigation, methodology, visualization, resources, funding acquisition, project administration, supervision, and writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Science Centre of Poland (NCN) under projects No. 2016/21/B/ST10/02271 (Sun-Induced fluorescence and photosynthesis of peatland vegetation response to stress caused by water deficits and increased temperature under conditions of climate manipulation experiment) and 2020/37/B/ST10/01213 (Assessment of the impact of warming and drier conditions on photosynthetic efficiency, productivity, spectral characteristics and morphology of peatland vegetation under the controlled in situ conditions of climate manipulation experiment).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Jungkunst, H.F.; Krüger, J.P.; Heitkamp, F.; Erasmi, S.; Fiedler, S.; Glatzel, S.; Lal, R. Accounting More Precisely for Peat and Other Soil Carbon Resources. In Recarbonization of the Biosphere; Springer: Dordrecht, The Netherlands, 2012; Volume 4, pp. 127–157. ISBN 9789400741584. [Google Scholar]
- Peichl, M.; Gažovič, M.; Vermeij, I.; de Goede, E.; Sonnentag, O.; Limpens, J.; Nilsson, M.B. Peatland Vegetation Composition and Phenology Drive the Seasonal Trajectory of Maximum Gross Primary Production. Sci. Rep. 2018, 8, 8012. [Google Scholar] [CrossRef] [PubMed]
- Fennessy, M.S.; Cronk, J.K. Primary Production and Respiration: Ecological Processes in Wetlands. In The Wetland Book; Finlayson, C.M., Everard, M., Irvine, K., McInnes, R.J., Middleton, B.A., van Dam, A.A., Davidson, N.C., Eds.; Springer: Dordrecht, The Netherlands, 2018; pp. 315–322. ISBN 978-90-481-9659-3. [Google Scholar]
- Liu, W.; Fritz, C.; Weideveld, S.T.J.; Aben, R.C.H.; van den Berg, M.; Velthuis, M. Annual CO2 Budget Estimation from Chamber-Based Flux Measurements on Intensively Drained Peat Meadows: Effect of Gap-Filling Strategies. Front. Environ. Sci. 2022, 10, 803746. [Google Scholar] [CrossRef]
- Pavelka, M.; Acosta, M.; Kiese, R.; Altimir, N.; Brümmer, C.; Crill, P.; Darenova, E.; Fuß, R.; Gielen, B.; Graf, A.; et al. Standardisation of Chamber Technique for CO2, N2O and CH4 Fluxes Measurements from Terrestrial Ecosystems. Int. Agrophysics 2018, 32, 569–587. [Google Scholar] [CrossRef]
- Kandel, T.P.; Laerke, P.E.; Hoffmann, C.C.; Elsgaard, L. Complete Annual CO2, CH4, and N2O Balance of a Temperate Riparian Wetland 12 Years after Rewetting. Ecol. Eng. 2019, 127, 527–535. [Google Scholar] [CrossRef]
- Hoffmann, M.; Jurisch, N.; Albiac Borraz, E.; Hagemann, U.; Drösler, M.; Sommer, M.; Augustin, J. Automated Modeling of Ecosystem CO2 Fluxes Based on Periodic Closed Chamber Measurements: A Standardized Conceptual and Practical Approach. Agric. For. Meteorol. 2015, 200, 30–45. [Google Scholar] [CrossRef]
- Baird, A.J.; Green, S.M.; Brown, E.; Dooling, G.P. Modelling Time-Integrated Fluxes of CO2 and CH4 in Peatlands: A Review. Mires Peat 2019, 24, 1–15. [Google Scholar] [CrossRef]
- Couwenberg, J.; Thiele, A.; Tanneberger, F.; Augustin, J.; Bärisch, S.; Dubovik, D.; Liashchynskaya, N.; Michaelis, D.; Minke, M.; Skuratovich, A.; et al. Assessing Greenhouse Gas Emissions from Peatlands Using Vegetation as a Proxy. Hydrobiologia 2011, 674, 67–89. [Google Scholar] [CrossRef]
- Guo, H.; Li, S.; Kang, S.; Du, T.; Liu, W.; Tong, L.; Hao, X.; Ding, R. Comparison of Several Models for Estimating Gross Primary Production of Drip-Irrigated Maize in Arid Regions. Ecol. Modell. 2022, 468, 109928. [Google Scholar] [CrossRef]
- Li, Q.; Gogo, S.; Leroy, F.; Guimbaud, C.; Laggoun-Défarge, F. Response of Peatland CO2 and CH4 Fluxes to Experimental Warming and the Carbon Balance. Front. Earth Sci. 2021, 9, 631368. [Google Scholar] [CrossRef]
- Fu, Z.; Ciais, P.; Bastos, A.; Stoy, P.C.; Yang, H.; Green, J.K.; Wang, B.; Yu, K.; Huang, Y.; Knohl, A.; et al. Sensitivity of Gross Primary Productivity to Climatic Drivers during the Summer Drought of 2018 in Europe: Sensitivity of GPP to Climate Drivers. Philos. Trans. R. Soc. B Biol. Sci. 2020, 375, 20190747. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.; Wang, J.; Zeng, N.; Sitch, S.; Tang, W.; McGrath, M.J.; Cai, Q.; Liu, D.; Lombardozzi, D.; Tian, H.; et al. Divergent Historical GPP Trends among State-of-the-Art Multi-Model Simulations and Satellite-Based Products. Earth Syst. Dyn. 2022, 13, 833–849. [Google Scholar] [CrossRef]
- Górecki, K.; Rastogi, A.; Stróżecki, M.; Gąbka, M.; Lamentowicz, M.; Łuców, D.; Kayzer, D.; Juszczak, R. Water Table Depth, Experimental Warming, and Reduced Precipitation Impact on Litter Decomposition in a Temperate Sphagnum-Peatland. Sci. Total Environ. 2021, 771, 145452. [Google Scholar] [CrossRef]
- Antala, M.; Rastogi, A.; Cogliati, S.; Stróżecki, M.; Colombo, R.; Juszczak, R. Sun-Induced Fluorescence Spectrum as a Tool for Assessing Peatland Vegetation Productivity in the Framework of Warming and Reduced Precipitation Experiment. Remote Sens. Environ. 2024, 301, 113921. [Google Scholar] [CrossRef]
- Acosta, M.; Juszczak, R.; Chojnicki, B.; Pavelka, M.; Havránková, K.; Lesny, J.; Krupková, L.; Urbaniak, M.; Machačová, K.; Olejnik, J. CO2 Fluxes from Different Vegetation Communities on a Peatland Ecosystem. Wetlands 2017, 37, 423–435. [Google Scholar] [CrossRef]
- Sakowska, K.; Alberti, G.; Genesio, L.; Peressotti, A.; Delle Vedove, G.; Gianelle, D.; Colombo, R.; Rodeghiero, M.; Panigada, C.; Juszczak, R.; et al. Leaf and Canopy Photosynthesis of a Chlorophyll Deficient Soybean Mutant. Plant Cell Environ. 2018, 41, 1427–1437. [Google Scholar] [CrossRef] [PubMed]
- Hubb, J. The Importance of Water Vapour Measurements and Corrections LI-COR Biosciences Inc. Appl. Note 2012, 129, 8. [Google Scholar]
- Huang, M.; Piao, S.; Ciais, P.; Peñuelas, J.; Wang, X.; Keenan, T.F.; Peng, S.; Berry, J.A.; Wang, K.; Mao, J.; et al. Air Temperature Optima of Vegetation Productivity across Global Biomes. Nat. Ecol. Evol. 2019, 3, 772–779. [Google Scholar] [CrossRef] [PubMed]
- Gilmanov, T.G.; Soussana, J.F.; Aires, L.; Allard, V.; Ammann, C.; Balzarolo, M. Partitioning European Grassland Net Ecosystem CO2 Exchange into Gross Primary Productivity and Ecosystem Respiration Using Light Response Function Analysis. Agric. Ecosyst. Environ. 2007, 121, 93–120. [Google Scholar] [CrossRef]
- Bassman, J.H.; Zwier, J.C. Gas Exchange Characteristics of Populus Trichocarpa, Populus Deltoides and Populus Trichocarpa x P. Deltoides Clones. Tree Physiol. 1991, 8, 145–159. [Google Scholar] [CrossRef] [PubMed]
- Tuittila, E.-S.; Vasander, H.; Laine, J. Sensitivity of C Sequestration in Reintroduced Sphagnum to Water-Level Variation in a Cutaway Peatland. Restor. Ecol. 2004, 12, 483–493. [Google Scholar] [CrossRef]
- Belda, S.; Pipia, L.; Morcillo-Pallarés, P.; Rivera-Caicedo, J.P.; Amin, E.; De Grave, C.; Verrelst, J. DATimeS: A Machine Learning Time Series GUI Toolbox for Gap-Filling and Vegetation Phenology Trends Detection. Environ. Model. Softw. 2020, 127, 104666. [Google Scholar] [CrossRef]
- Carter, T.R. Changes in the Thermal Growing Season in Nordic Countries during the Past Century and Prospects for the Future. Agric. Food Sci. 1998, 7, 161–179. [Google Scholar] [CrossRef]
- Miętus, M. Climate of Poland 2021. Polish Climate Monitoring Bulletin, 2021. [Google Scholar]
- Gatis, N.; Luscombe, D.J.; Benaud, P.; Ashe, J.; Grand-Clement, E.; Anderson, K.; Hartley, I.P.; Brazier, R.E. Drain Blocking Has Limited Short-Term Effects on Greenhouse Gas Fluxes in a Molinia Caerulea Dominated Shallow Peatland. Ecol. Eng. 2020, 158, 106079. [Google Scholar] [CrossRef]
- Huth, V.; Vaidya, S.; Hoffmann, M.; Jurisch, N.; Günther, A.; Gundlach, L.; Hagemann, U.; Elsgaard, L.; Augustin, J. Divergent NEE Balances from Manual-Chamber CO2 Fluxes Linked to Different Measurement and Gap-Filling Strategies: A Source for Uncertainty of Estimated Terrestrial C Sources and Sinks? J. Plant Nutr. Soil Sci. 2017, 180, 302–315. [Google Scholar] [CrossRef]
- Leroy, F.; Gogo, S.; Guimbaud, C.; Bernard-Jannin, L.; Yin, X.; Belot, G.; Shuguang, W.; Laggoun-Défarge, F. CO2 and CH4 Budgets and Global Warming Potential Modifications in Sphagnum-Dominated Peat Mesocosms Invaded by Molinia Caerulea. Biogeosciences 2019, 16, 4085–4095. [Google Scholar] [CrossRef]
- Korrensalo, A.; Alekseychik, P.; Hájek, T.; Rinne, J.; Vesala, T.; Mehtätalo, L.; Mammarella, I.; Tuittila, E.-S. Species-Specific Temporal Variation in Photosynthesis as a Moderator of Peatland Carbon Sequestration. Biogeosciences 2017, 14, 257–269. [Google Scholar] [CrossRef]
- Strilesky, S.L.; Humphreys, E.R. A Comparison of the Net Ecosystem Exchange of Carbon Dioxide and Evapotranspiration for Treed and Open Portions of a Temperate Peatland. Agric. For. Meteorol. 2012, 153, 45–53. [Google Scholar] [CrossRef]
- Goodrich, J.P.; Campbell, D.I.; Clearwater, M.J.; Rutledge, S.; Schipper, L.A. High Vapor Pressure Deficit Constrains GPP and the Light Response of NEE at a Southern Hemisphere Bog. Agric. For. Meteorol. 2015, 203, 112–123. [Google Scholar] [CrossRef]
- Fu, Z.; Ciais, P.; Prentice, I.C.; Gentine, P.; Makowski, D.; Bastos, A.; Luo, X.; Green, J.K.; Stoy, P.C.; Yang, H.; et al. Atmospheric Dryness Reduces Photosynthesis along a Large Range of Soil Water Deficits. Nat. Commun. 2022, 13, 989. [Google Scholar] [CrossRef] [PubMed]
- June, T.; Evans, J.R.; Farquhar, G.D. A Simple New Equation for the Reversible Temperature Dependence of Photosynthetic Electron Transport: A Study on Soybean Leaf. Funct. Plant Biol. 2004, 31, 275. [Google Scholar] [CrossRef]
- McCallum, I.; Franklin, O.; Moltchanova, E.; Merbold, L.; Schmullius, C.; Shvidenko, A.; Schepaschenko, D.; Fritz, S. Improved Light and Temperature Responses for Light-Use-Efficiency-Based GPP Models. Biogeosciences 2013, 10, 6577–6590. [Google Scholar] [CrossRef]
- Lagergren, F.; Lindroth, A.; Dellwik, E.; Ibrom, A.; Launiainen, S.; Mölder, M.; Kolari, P.; Pilegaard, K.; Lagergren, F.; Lindroth, A.; et al. Biophysical Controls on CO2 Fluxes of Three Northern Forests Based on Long-Term Eddy Covariance Data. Tellus B Chem. Phys. Meteorol. 2017, 0889, 143–152. [Google Scholar]
- Wang, F.; Chen, J.M.; Gonsamo, A.; Zhou, B.; Cao, F.; Yi, Q. A Two-Leaf Rectangular Hyperbolic Model for Estimating GPP across Vegetation Types and Climate Conditions. J. Geophys. Res. Biogeosci. 2014, 119, 1385–1398. [Google Scholar] [CrossRef]
- Körner, C. Concepts in Empirical Plant Ecology. Plant Ecol. Divers. 2018, 11, 405–428. [Google Scholar] [CrossRef]
- Körner, C.; Möhl, P.; Hiltbrunner, E. Four Ways to Define the Growing Season. Ecol. Lett. 2023, 26, 1277–1292. [Google Scholar] [CrossRef]
- Stirling, E.; Fitzpatrick, R.W.; Mosley, L.M. Drought Effects on Wet Soils in Inland Wetlands and Peatlands. Earth-Sci. Rev. 2020, 210, 103387. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).