Predictive Energy Storage Management with Redox Flow Batteries in Demand-Driven Microgrids
Abstract
1. Introduction
1.1. Literature Review
1.2. Research Problem
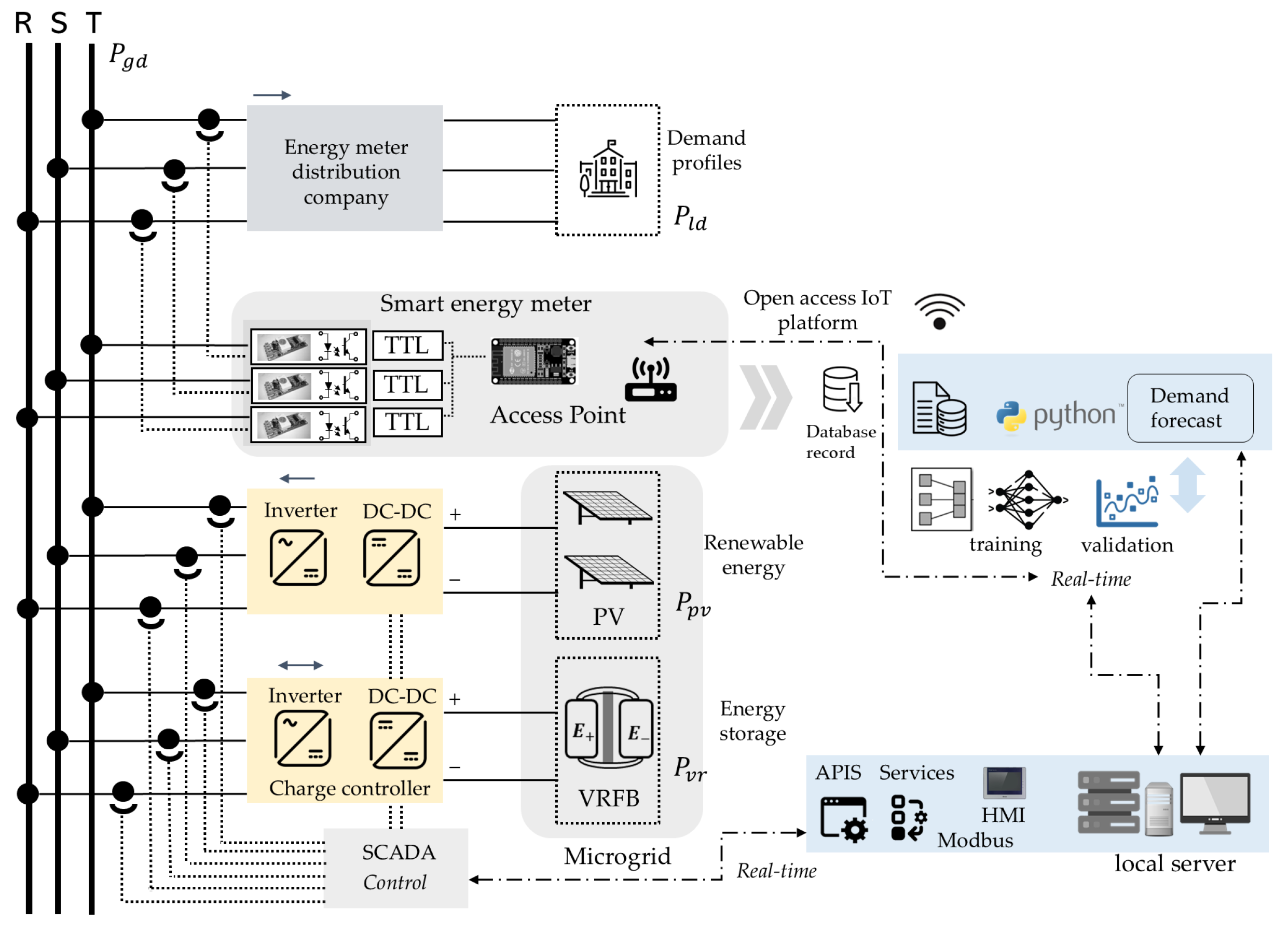
2. System Architecture
- Data Collection:
- Smart energy meters are strategically placed at specific points in the main distribution panels to collect real-time data. This ensures continuous demand monitoring based on the current energy landscape.
- Microgrid Monitoring and Control:
- The use of MODBUS over TCP/IP platforms enables demand and microgrid monitoring through Application Programming Interfaces (APIS) and a local server. This allows for dynamic analysis of PV production and energy consumption demand, with access to management of the VRFB (Remote Power Storage Facility).
- Remote Demand Monitoring:
- The proposed system uses ThingSpeak ©2025 and Python v3.10.0 servers to establish a Remote Monitoring Unit (RMU) in the cloud. This facilitates real-time remote communication with the microgrid.
- Real-Time Demand Forecasting:
- After data collection, a training model is established based on demand profiles from previous days to predict the next day based on deep learning models. This allows for real-time monitoring of current energy consumption and predictions.
- Automatic control algorithm:
- The study incorporates a storage system control model in predictive IoT environments. This improves the system’s predictive capacity and decision-making processes in optimizing the storage system’s state of charge for future demand events.
3. Methods and Materials
3.1. Demand Forecast
3.1.1. Smart Meter
3.1.2. Data Recording and Preprocessing
3.1.3. Architecture of the Prediction Neural Network Model
- be the input matrix with d features,
- be the target output matrix with m output variables,
- and be the weights and biases of the hidden layer,
- and be the weights and biases of the output layer.
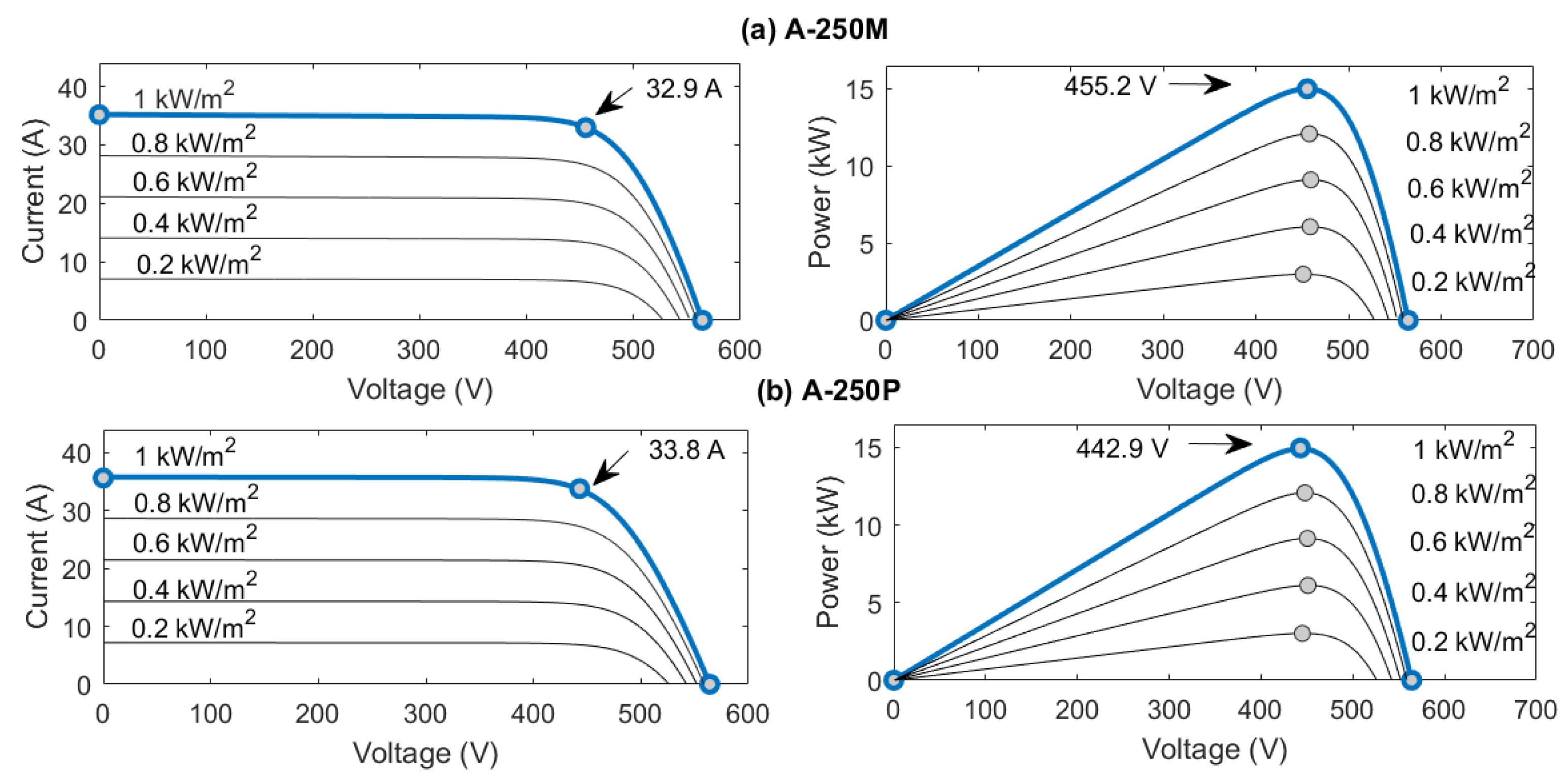
3.2. Photovoltaic Systems
3.3. Vanadium Redox Flow Battery
3.4. Automatic Control Algorithm
3.4.1. Predictive Analytics
3.4.2. Real-Time Processing
4. Case Study
5. Results and Discussion
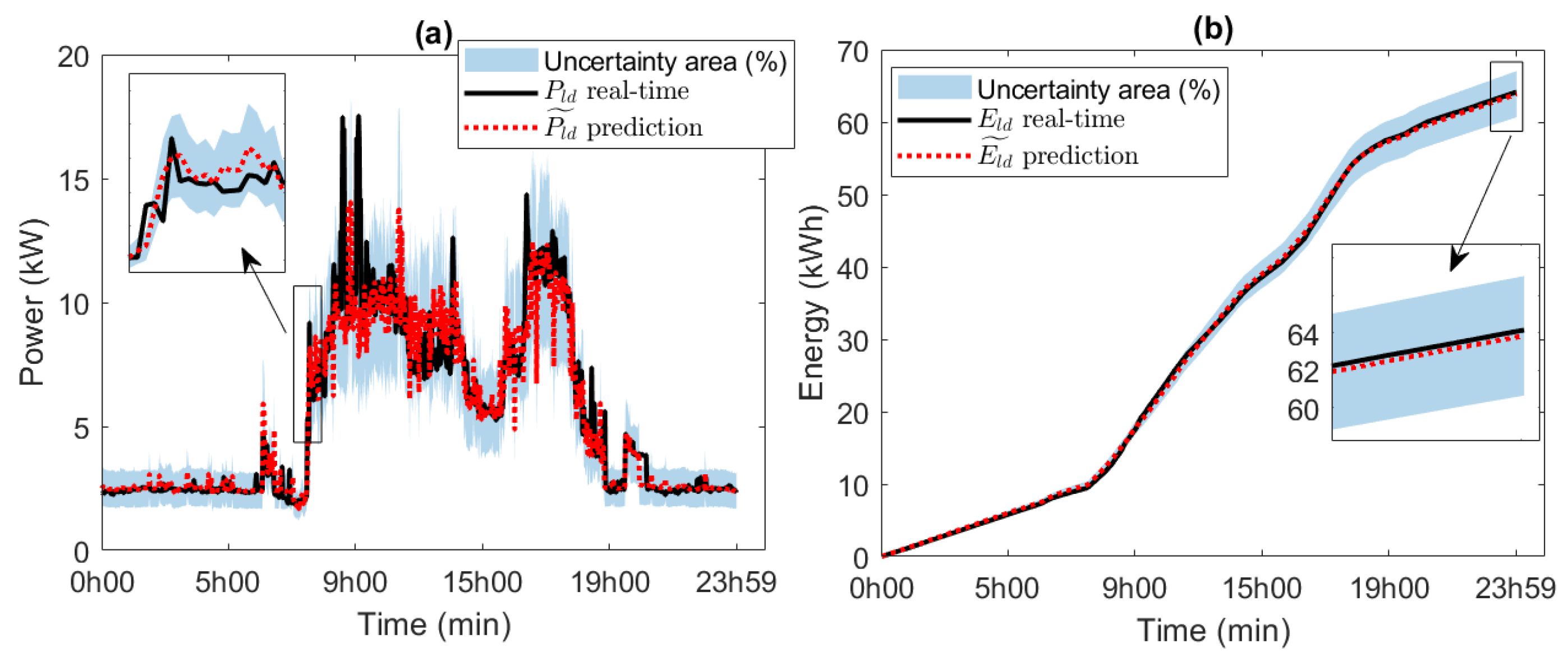
5.1. Data Acquisition
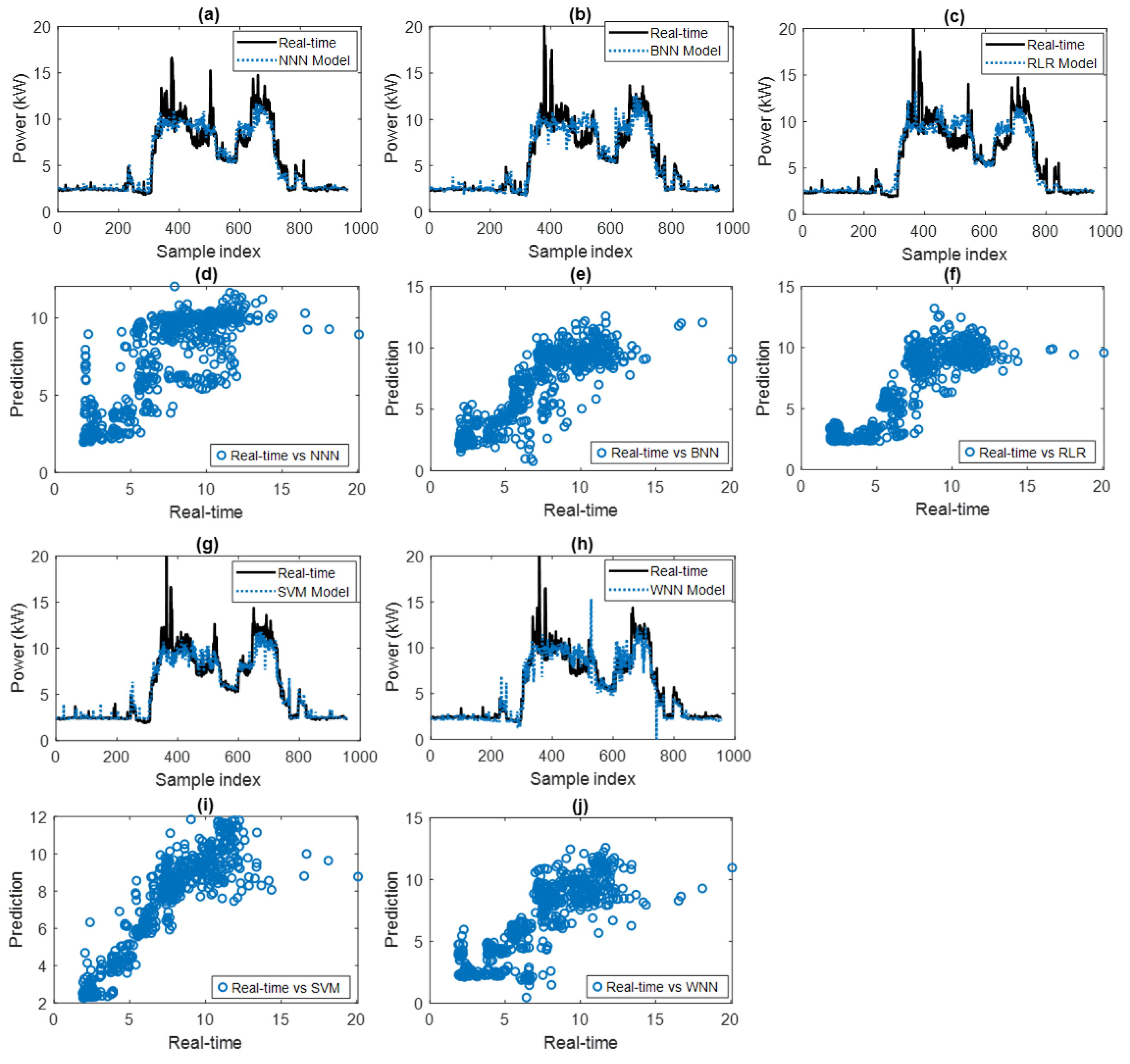
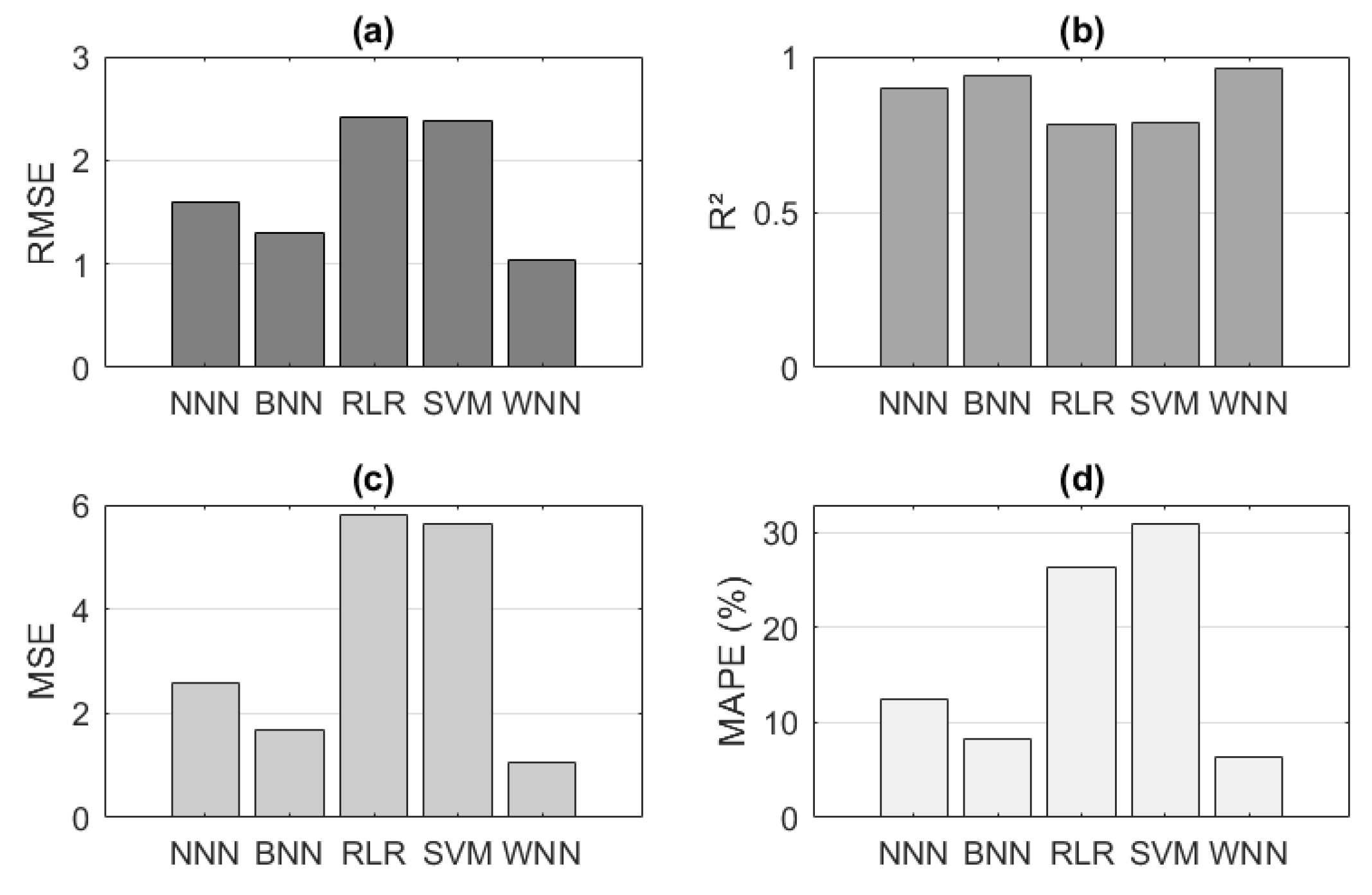
5.2. Evaluation of Predictive Models
5.3. Results Evaluation Indices
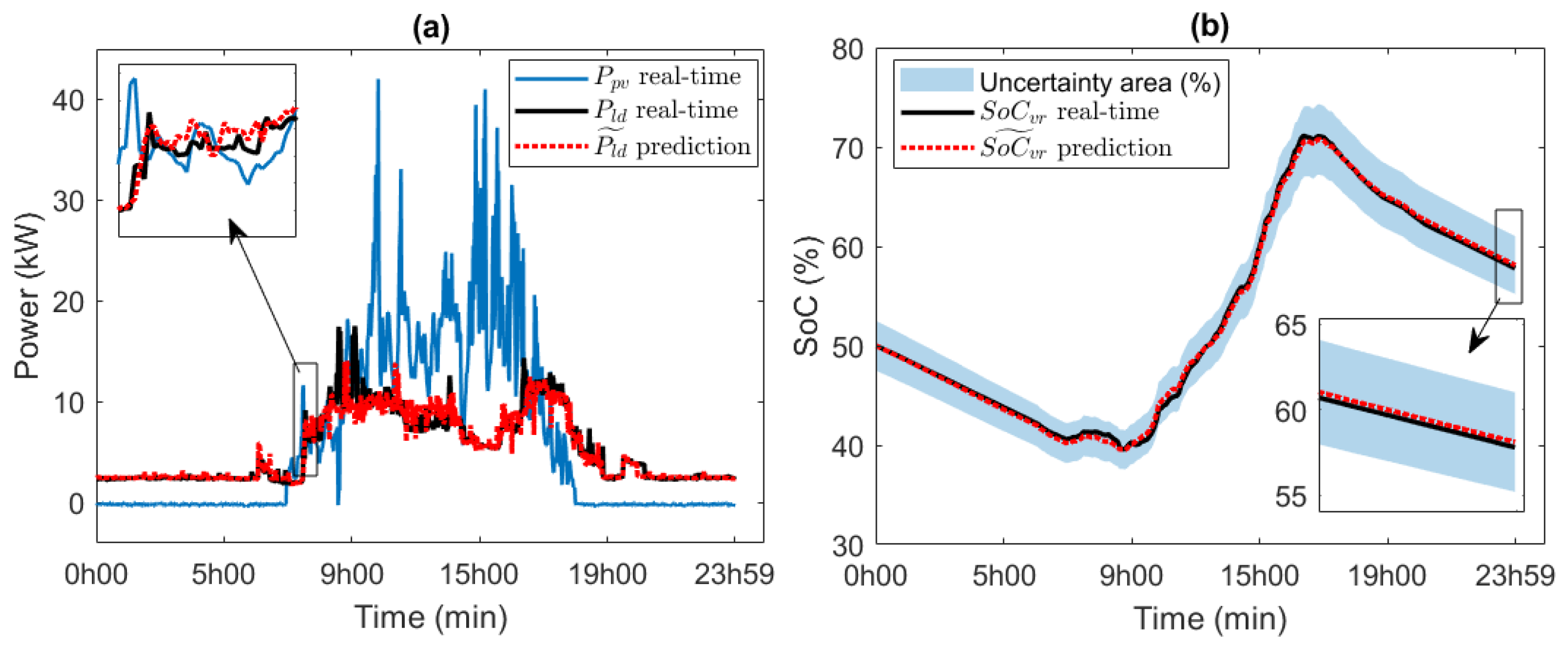
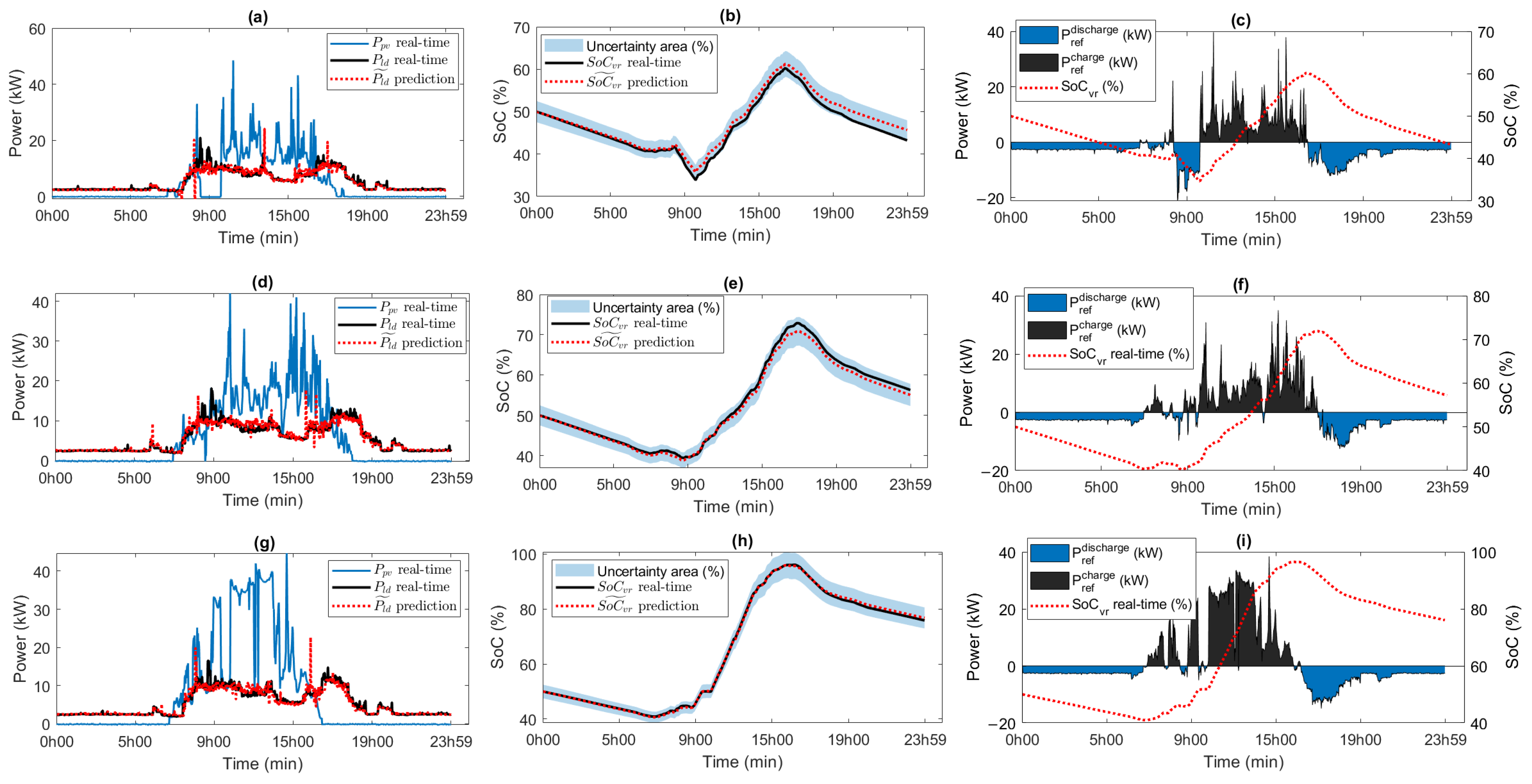
5.4. Experimental Evaluation of VRFB
5.5. Energy Analysis
5.6. Sensitivity Analysis of System Power and Load
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Selvarasu, U.; Amirabadi, M.; Li, Y.; Crow, C.; Lehman, B. BESS Sizing for PV Power Smoothing. In Proceedings of the 2024 IEEE Energy Conversion Congress and Exposition (ECCE), Phoenix, AZ, USA, 20–24 October 2024; pp. 546–552. [Google Scholar] [CrossRef]
- Apribowo, C.H.B.; Sarjiya; Hadi, S.P.; Wijaya, F.D.; Setyonegoro, M.I.B. Optimal Allocation of Vanadium Redox Flow Battery Storage Systems With Integrated Variable Renewable Energy. In Proceedings of the 2023 15th International Conference on Information Technology and Electrical Engineering (ICITEE), Chiang Mai, Thailand, 26–27 October 2023; pp. 375–380. [Google Scholar] [CrossRef]
- Zhang, Q.; Gao, Y.; Mo, W.; Han, F.; Zhang, L. Load Forecasting Considering Demand Response Mechanism. In Proceedings of the 2023 Panda Forum on Power and Energy (PandaFPE), Chengdu, China, 27–30 April 2023; pp. 1172–1177. [Google Scholar] [CrossRef]
- Ruiz-Abellón, M.C.; Fernández-Jiménez, L.A.; Guillamón, A.; Gabaldón, A. Applications of Probabilistic Forecasting in Demand Response. Appl. Sci. 2024, 14, 9716. [Google Scholar] [CrossRef]
- Sharifhosseini, S.M.; Niknam, T.; Taabodi, M.H.; Aghajari, H.A.; Sheybani, E.; Javidi, G.; Pourbehzadi, M. Investigating Intelligent Forecasting and Optimization in Electrical Power Systems: A Comprehensive Review of Techniques and Applications. Energies 2024, 17, 5385. [Google Scholar] [CrossRef]
- Wang, X.; Wang, H.; Bhandari, B.; Cheng, L. AI-Empowered Methods for Smart Energy Consumption: A Review of Load Forecasting, Anomaly Detection and Demand Response. Int. J. Precis. Eng.-Manuf.-Green Technol. 2024, 11, 963–993. [Google Scholar] [CrossRef]
- Tushar, M.H.K.; Zeineddine, A.W.; Assi, C. Demand-Side Management by Regulating Charging and Discharging of the EV, ESS, and Utilizing Renewable Energy. IEEE Trans. Ind. Inform. 2018, 14, 117–126. [Google Scholar] [CrossRef]
- Alvarado-Barrios, L.; Rodríguez del Nozal, Á.; Boza Valerino, J.; García Vera, I.; Martínez-Ramos, J.L. Stochastic Unit Commitment in Microgrids: Influence of the Load Forecasting Error and the Availability of Energy Storage. Renew. Energy 2020, 146, 2060–2069. [Google Scholar] [CrossRef]
- Sharrma, S.; Prasad, A.; Pajany, M. A Scheduling System for an Energy Storage Device Using Photovoltaic and Demand Forecasting. In Proceedings of the 2021 2nd International Conference on Advances in Computing, Communication, Embedded and Secure Systems (ACCESS), Ernakulam, India, 2–4 September 2021; pp. 291–296. [Google Scholar] [CrossRef]
- Lyu, C.; Jia, Y.; Xu, Z. Tube-Based Model Predictive Control Approach for Real-Time Operation of Energy Storage System. In Proceedings of the 2020 International Conference on Smart Grids and Energy Systems (SGES), Perth, Australia, 23–26 November 2020; pp. 493–497. [Google Scholar] [CrossRef]
- Mary, N.; Dessaint, L.A. Robust Model Predictive Control of Battery Energy Storage with Neural Network Forecasting for Peak Shaving in University Campus. J. Build. Eng. 2025, 107, 112445. [Google Scholar] [CrossRef]
- Arévalo, P.; Benavides, D.; Aguado, J.A.; Jurado, F. Advanced wind/photovoltaic power smoothing using LSTM neural networks and machine learning. Soft Comput. 2025, 29, 5193–5211. [Google Scholar] [CrossRef]
- Kim, K.; Ko, D.; Jung, J.; Ryu, J.O.; Hur, K.J.; Kim, Y.J. Real-Time AI-Based Power Demand Forecasting for Peak Shaving and Consumption Reduction Using Vehicle-to-Grid and Reused Energy Storage Systems: A Case Study at a Business Center on Jeju Island. Appl. Sci. 2025, 15, 3050. [Google Scholar] [CrossRef]
- Wang, C.; Cheng, B.; He, X.; Xi, L.; Yang, N.; Zhao, Z.; Lai, C.S.; Lai, L.L. Integrated Underfrequency Load Shedding Strategy for Islanded Microgrids Integrating Multiclass Load-Related Factors. IEEE Trans. Smart Grid 2025, 1. [Google Scholar] [CrossRef]
- Sadeghi, S.; Jahangir, H.; Vatandoust, B.; Golkar, M.A.; Ahmadian, A.; Elkamel, A. Optimal Bidding Strategy of a Virtual Power Plant in Day-Ahead Energy and Frequency Regulation Markets: A Deep Learning-Based Approach. Int. J. Electr. Power Energy Syst. 2021, 127, 106646. [Google Scholar] [CrossRef]
- Abedi, S.; Kwon, S. Rolling-Horizon Optimization Integrated with Recurrent Neural Network-Driven Forecasting for Residential Battery Energy Storage Operations. Int. J. Electr. Power Energy Syst. 2023, 145, 108589. [Google Scholar] [CrossRef]
- Promasa, N.; Songkoh, E.; Phonkaphon, S.; Sirichunchuen, K.; Ketkaew, C.; Unahalekhaka, P. Optimization of Sizing of Battery Energy Storage System for Residential Households by Load Forecasting with Artificial Intelligence (AI): Case of EV Charging Installation. Energies 2025, 18, 1245. [Google Scholar] [CrossRef]
- Wang, C.; Wang, M.; Wang, A.; Zhang, X.; Zhang, J.; Ma, H.; Yang, N.; Zhao, Z.; Lai, C.S.; Lai, L.L. Multiagent deep reinforcement learning-based cooperative optimal operation with strong scalability for residential microgrid clusters. Energy 2025, 314, 134165. [Google Scholar] [CrossRef]
- Morsali, R.; Thirunavukkarasu, G.S.; Seyedmahmoudian, M.; Stojcevski, A.; Kowalczyk, R. A relaxed constrained decentralised demand side management system of a community-based residential microgrid with realistic appliance models. Appl. Energy 2020, 277, 115626. [Google Scholar] [CrossRef]
- Venkata Pavan Kumar, Y.; Naga Venkata Bramareswara Rao, S.; Kannan, R. Islanding Detection in Grid-Connected Urban Community Multi-Microgrid Clusters Using Decision-Tree-Based Fuzzy Logic Controller for Improved Transient Response. Urban Sci. 2023, 7, 72. [Google Scholar] [CrossRef]
- Algburi, S.; Abed Al Kareem, S.S.; Sapaev, I.B.; Mukhitdinov, O.; Hassan, Q.; Khalaf, D.H.; Jabbar, F.I. The Role of Artificial Intelligence in Accelerating Renewable Energy Adoption for Global Energy Transformation. Unconv. Resour. 2025, 8, 100229. [Google Scholar] [CrossRef]
- Mughees, N.; Mughees, A.; Mughees, A.; Ejsmont, K. Optimizing Electrical and Thermal Energy Storage Systems for Hour-Ahead Integrated Demand Response in Industries. Energy Rep. 2025, 13, 4441–4458. [Google Scholar] [CrossRef]
- Filho, E.M.L.; Silveira, A.B.; Ferreira, A.M.; Marques, J.A.L.; Batista, J.G.; Guimarães, G.D.F.; De Alexandria, A.R.; Rodrigues, J.J.P.C. Optimization of Energy Storage Systems with Renewable Energy Generation and Consumption Data. In Proceedings of the 2024 IEEE 7th Student Conference on Electric Machines and Systems (SCEMS), Macao, China, 6–8 November 2024; pp. 1–9. [Google Scholar] [CrossRef]
- Dong, J.; Zang, T.; Li, X.; Bao, P. Research on Energy Management and Scheduling Algorithm of Lithium Battery Energy Storage System Based on Artificial Intelligence. In Proceedings of the 2025 International Conference on Electrical Drives, Power Electronics & Engineering (EDPEE), Athens, Greece, 26–28 March 2025; pp. 1079–1084. [Google Scholar] [CrossRef]
- Sanan, O.; Sperling, J.; Greene, D.; Greer, R. Forecasting Weather and Energy Demand for Optimization of Renewable Energy and Energy Storage Systems for Water Desalination. In Proceedings of the 2024 IEEE Conference on Technologies for Sustainability (SusTech), Portland, OR, USA, 14–17 April 2024; pp. 175–182. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Y.; Zhang, Y.; Xi, L.; Yang, N.; Zhao, Z.; Lai, C.S.; Lai, L.L. Strategy for optimizing the bidirectional time-of-use electricity price in multi-microgrids coupled with multilevel games. Energy 2025, 323, 135731. [Google Scholar] [CrossRef]
- Nguyen-Duc, T.; Nguyen-Duc, H.; Le-Viet, T.; Takano, H. Single-Diode Models of PV Modules: A Comparison of Conventional Approaches and Proposal of a Novel Model. Energies 2020, 13, 1296. [Google Scholar] [CrossRef]
- Abdulrazzaq, A.K.; Bognár, G.; Plesz, B. Enhanced single-diode model parameter extraction method for photovoltaic cells and modules based on integrating genetic algorithm, particle swarm optimization, and comparative objective functions. J. Comput. Electron. 2025, 24, 44. [Google Scholar] [CrossRef]
- Hao, X.; Liu, P.; Deng, Y.; Meng, X. A MIC-LSTM based parameter extraction method for single-diode PV model. Front. Energy Res. 2024, 11, 1349887. [Google Scholar] [CrossRef]
- Criollo, A.; Minchala-Avila, L.I.; Benavides, D.; Ochoa-Correa, D.; Tostado-Véliz, M.; Meteab, W.K.; Jurado, F. Green Hydrogen Production—Fidelity in Simulation Models for Technical–Economic Analysis. Appl. Sci. 2024, 14, 10720. [Google Scholar] [CrossRef]
- Espinoza, J.L.; González, L.G.; Sempértegui, R. Micro grid laboratory as a tool for research on non-conventional energy sources in Ecuador. In Proceedings of the 2017 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 8–10 November 2017; pp. 1–7. [Google Scholar] [CrossRef]
- CellCube Energy Storage GmbH. Products–CellCube. 2025. Available online: https://www.cellcube.com/products/ (accessed on 22 August 2025).
- Gu, F.C.; Chen, H.C. Modelling and control of vanadium redox flow battery for smoothing wind power fluctuation. IET Renew. Power Gener. 2021, 15, 3552–3563. [Google Scholar] [CrossRef]
- Benavides, D.; Villa-Ávila, E.; Criollo, A.; Aguado, J.A. 17—Optimal energy management of energy storage and electric vehicles in power systems. In Towards Future Smart Power Systems with High Penetration of Renewables; Tostado-Véliz, M., Rezaee Jordehi, A., Mansouri, S.A., Ramos Galán, A., Melguizo, F.J., Eds.; Academic Press: New York, NY, USA, 2025; pp. 413–434. [Google Scholar] [CrossRef]
- Turker, B.; Arroyo Klein, S.; Hammer, E.M.; Lenz, B.; Komsiyska, L. Modeling a vanadium redox flow battery system for large scale applications. Energy Convers. Manag. 2013, 66, 26–32. [Google Scholar] [CrossRef]
- Benavides, D.; Arévalo, P.; Villa-Ávila, E.; Aguado, J.A.; Jurado, F. Predictive power fluctuation mitigation in grid-connected PV systems with rapid response to EV charging stations. J. Energy Storage 2024, 86, 111230. [Google Scholar] [CrossRef]








| Reference | Scope/Objective | Methods/Models | Technology Focus | Key Contributions | Identified Limitations |
|---|---|---|---|---|---|
| Tushar et al. (2018) [7] | Decentralized DSM for EVs and ESS | Game theory, mixed strategies | EVs, ESS, DSM | Adaptive load control, day-ahead correction | No experimental platform, limited to simulations |
| Wang et al. (2025) [26] | Coordination between multiple microgrids | Multilevel game theory | PV, WT, ESS, Users | bidirectional time-of-use electricity price | Simulated environments |
| Alvarado-Barrios et al. (2020) [8] | Stochastic unit commitment in microgrids | ARMA + stochastic optimization | WT, PV, BESS | Dispatch under forecast uncertainty | No real-time feedback, 24 h horizon only |
| Sharrma et al. (2021) [9] | Peak shaving using PV + BESS | Week-ahead time series | PV, BESS | Coordinated forecast and storage scheduling | No online updates or adaptive models |
| Lyu et al. (2020) [10] | Battery operation under uncertainty | Tube-based MPC | Li-ion BESS | Forecast-bounded SoC control | No forecasting module, simulated validation only |
| Kim et al. (2025) [13] | AI-based load prediction and peak shaving | MC-LSTM + clustering | V2G, reused ESS | Real-world deployment, 21% reduction | Focused on commercial buildings, no SoC tracking |
| Sadeghi et al. (2021) [15] | VPP bidding with forecasting | Bidirectional LSTM | VPP, RES, EVs | Participation in regulation markets | Economic optimization only, not microgrid-based |
| Zhang et al. (2023) [3] | DR-aware forecasting | GA-LSTM hybrid | Interruptible loads, DR, ESS | Improved accuracy via DR signals | No storage dynamics modeled |
| Ruiz-Abellón et al. (2024) [4] | Probabilistic DR coverage planning | Quantile regression methods | DR programs | Uncertainty range quantification | City-scale data, not microgrid-specific |
| Apribowo et al. (2023) [2] | Optimal VRFB allocation on grid | GAMS optimization (IEEE 39-bus) | Grid-scale VRFB | Cost-efficient VRFB placement | No forecasting integration |
| Selvarasu et al. (2024) [1] | Sizing BESS for PV smoothing | Empirical sizing approach | PV, BESS | Ramp-rate control strategy | No forecast-based operation |
| Abedi & Kwon (2023) [16] | BESS operation in residential context | RNN + rolling-horizon optimization | PV, BESS | Adaptive BESS scheduling | No experimental validation |
| Mary & Dessaint (2025) [11] | Peak shaving with MPC + NN forecast | NN + robust MPC | Institutional BESS | Forecast-aware peak management | Generic load scenarios only |
| Sharifhosseini et al. (2024) [5] | Review of AI in power systems | Literature survey | General AI methods | Comprehensive taxonomy | No implementation case |
| Wang et al. (2024) [6] | AI in smart energy systems | Review of ML/DL models | Forecasting, DR, anomaly detection | Practical guidance and model comparison | No validation or deployment |
| This work | Forecast-based VRFB operation in microgrid | WNN + adaptive SoC control | Smart meters, VRFB, PV | Real lab validation, forecasting + control integration | Limited storage capacity, university-scale |
| PV System | |
| Model: | ATERSA A-250M/ATERSA A-250P |
| Peak nominal power: | 15 kW (×2) |
| Number of modules: | 60 units (×2) |
| Max. DC Voltage: | 553 (A-250M)/563 (A-250P) |
| Max. AC Voltage: | 230 (60 Hz) |
| MPPT: | Perturb and observe (P&O) |
| DC/AC Inverter: | GPTech Two Level |
| VRFB System | |
| Model: | Gildemeister/CellCube FB 20 |
| Nominal charge output/input | 20 kW |
| Capacity of the energy storage system | 100 kWh |
| Battery and system voltage: | 48 (x2) |
| Output voltage: | 230 (60 Hz) |
| Charge/discharge cycle DC: | up to 80% |
| Charge and discharge cycles: | practically unlimited cycling |
| Depth of Discharge (DoD): | 100% |
| Number of cells: | 12 cells per string |
| Number of clusters: | 2 units (A and B) |
| Metric | Description | Equation | Model Evaluation |
|---|---|---|---|
| RMSE | Root Mean Squared Error. Measures the standard deviation of prediction errors. Penalizes large deviations more heavily. | If the RMSE is low, it ensures that predictions do not deviate drastically from actual demand. | |
| R2 | Coefficient of determination. Indicates how well the model fits the actual data. Values close to 1 imply a better fit. | An R2 close to 1 indicates that the model captures daily demand variability well. | |
| MSE | Mean Squared Error. Evaluates the average of squared prediction errors. Sensitive to outliers. | A low MSE indicates stability in demand predictions and will improve their efficiency. | |
| MAPE | Mean Absolute Percentage Error. Measures relative error in percentage. Useful for comparing models across different scales. | A low MAPE facilitates model integration in environments with daily demand variability. |
| Reference Power | Charge | Discharge | ||||||
|---|---|---|---|---|---|---|---|---|
| 5 kW | 10 kW | 15 kW | 20 kW | 5 kW | 10 kW | 15 kW | 20 kW | |
| Autonomy Time (h) | 27 | 12 | 7.5 | 7 | 15 | 7.5 | 5 | 5 |
| Avg. DC Current (A) | 82.57 | 165.08 | 241.38 | 297.89 | 104.63 | 216.4 | 344.79 | 480.33 |
| Avg. DC Voltage (V) | 57.74 | 58.25 | 58.72 | 59.435 | 53.71 | 51.705 | 49.35 | 55.115 |
| Active Power (kW) | 4.76 | 9.61 | 17.65 | 18.18 | 5.6 | 11.16 | 17 | 21.62 |
| Energy (kWh) | 128.61 | 115.71 | 118 | 122.01 | 83.56 | 85.5 | 83.57 | 79.28 |
| Event | Parameter | |||
|---|---|---|---|---|
| (kWh) | (kWh) | (kWh) | ||
| 1 | Generation | 115.52 | 40.53 | −51.96 |
| Mon | Demand | 167.49 | 93.57 | Energy usage |
| 2 | Generation | 145.34 | 44.32 | −44.42 |
| Tue | Demand | 189.76 | 89.74 | Energy usage |
| 3 | Generation | 162.19 | 83.65 | −7.00 |
| Wed | Demand | 169.20 | 91.70 | Energy usage |
| 4 | Generation | 219.79 | 127.67 | 42.01 |
| Thur | Demand | 177.78 | 86.71 | Energy production |
| 5 | Generation | 178.75 | 99.87 | 29.46 |
| Fri | Demand | 149.29 | 71.66 | Energy production |
| 6 | Generation | 118.89 | 95.43 | 63.04 |
| Sat | Demand | 55.84 | 33.36 | Energy production |
| 7 | Generation | 232.64 | 208.85 | 178.03 |
| Sun | Demand | 54.60 | 31.86 | Energy production |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benavides, D.; Arévalo-Cordero, P.; Ochoa-Correa, D.; Torres, D.; Ríos, A. Predictive Energy Storage Management with Redox Flow Batteries in Demand-Driven Microgrids. Sustainability 2025, 17, 8915. https://doi.org/10.3390/su17198915
Benavides D, Arévalo-Cordero P, Ochoa-Correa D, Torres D, Ríos A. Predictive Energy Storage Management with Redox Flow Batteries in Demand-Driven Microgrids. Sustainability. 2025; 17(19):8915. https://doi.org/10.3390/su17198915
Chicago/Turabian StyleBenavides, Dario, Paul Arévalo-Cordero, Danny Ochoa-Correa, David Torres, and Alberto Ríos. 2025. "Predictive Energy Storage Management with Redox Flow Batteries in Demand-Driven Microgrids" Sustainability 17, no. 19: 8915. https://doi.org/10.3390/su17198915
APA StyleBenavides, D., Arévalo-Cordero, P., Ochoa-Correa, D., Torres, D., & Ríos, A. (2025). Predictive Energy Storage Management with Redox Flow Batteries in Demand-Driven Microgrids. Sustainability, 17(19), 8915. https://doi.org/10.3390/su17198915










