Performance Comparison of Metaheuristic and Hybrid Algorithms Used for Energy Cost Minimization in a Solar–Wind–Battery Microgrid
Abstract
1. Introduction
2. Problem Definition
2.1. System Components
- G(t): Energy drawn from the grid at time t (kWh);
- S(t): Energy produced from solar at time t (kWh);
- W(t): Wind energy production at time t (kWh);
- D(t): Battery discharge amount at time t (kWh);
- L(t): Load demand at time t (kWh);
- C(t): Battery charging requirement at time t (kWh).
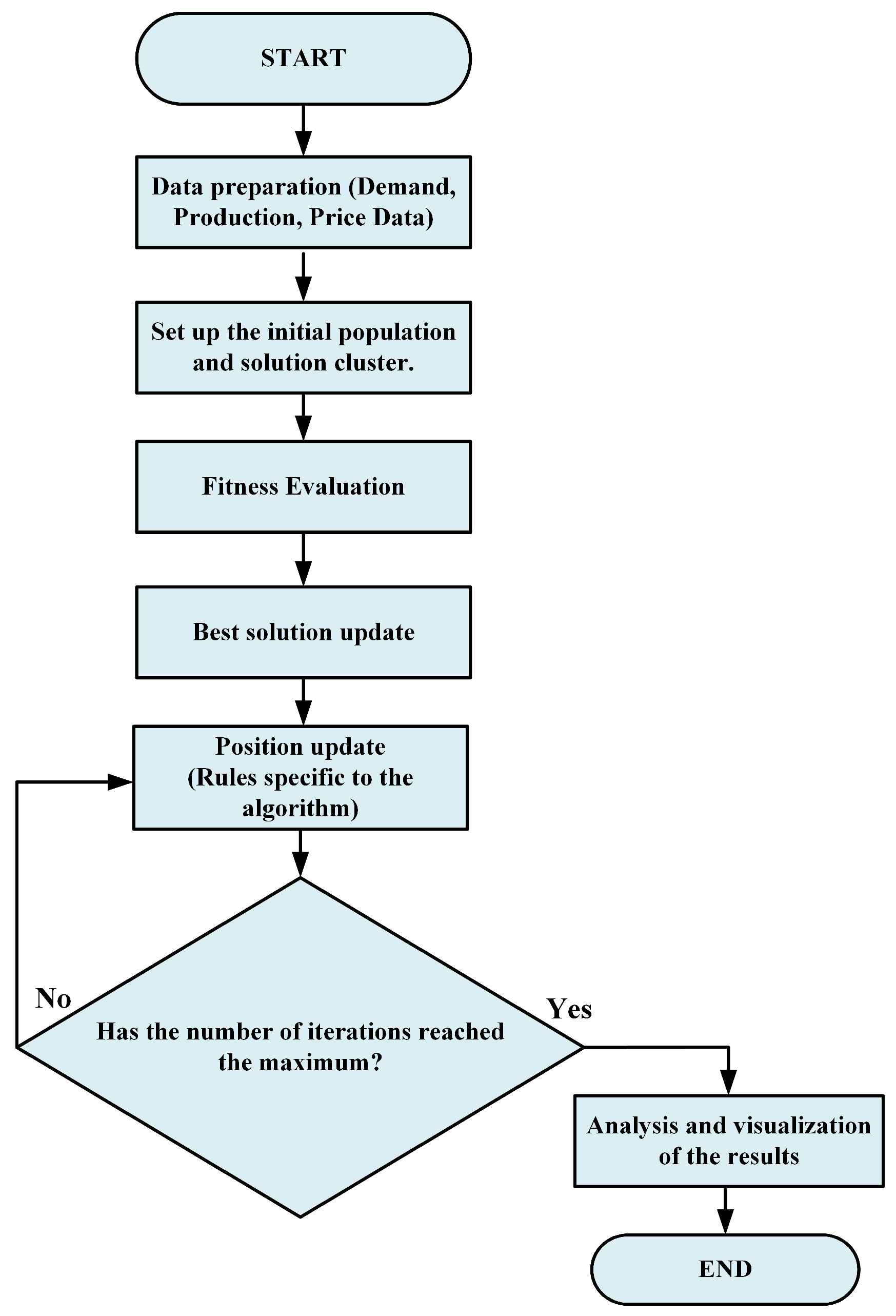
2.2. Energy Optimization Flow Diagram
2.3. Decision Variables
2.4. Objective Function
- Grid(t): Energy purchased from the grid at time t (kWh);
- Price(t): Unit price of grid electricity at time t (TL/kWh);
- Solar(t), Wind(t): Renewable generation from solar and wind at time t (kWh);
- Charge(t), Discharge(t): Battery charging and discharging amounts at time t (kWh);
- Demand(t): System energy demand at time t (kWh);
- PenaltySOC(d): Daily penalty function for the battery SOC at the end of day d;
- λ1: Weight coefficient for penalizing supply–demand imbalance (set to 10);
- λ2: Weight coefficient for penalizing end-of-day SOC violation (set to 100).
2.5. Constraints
3. Method
3.1. Setting up the Dataset
3.2. Algorithms Used in the Simulation Study
3.3. Performance Parameters
4. Simulation Results and Discussion
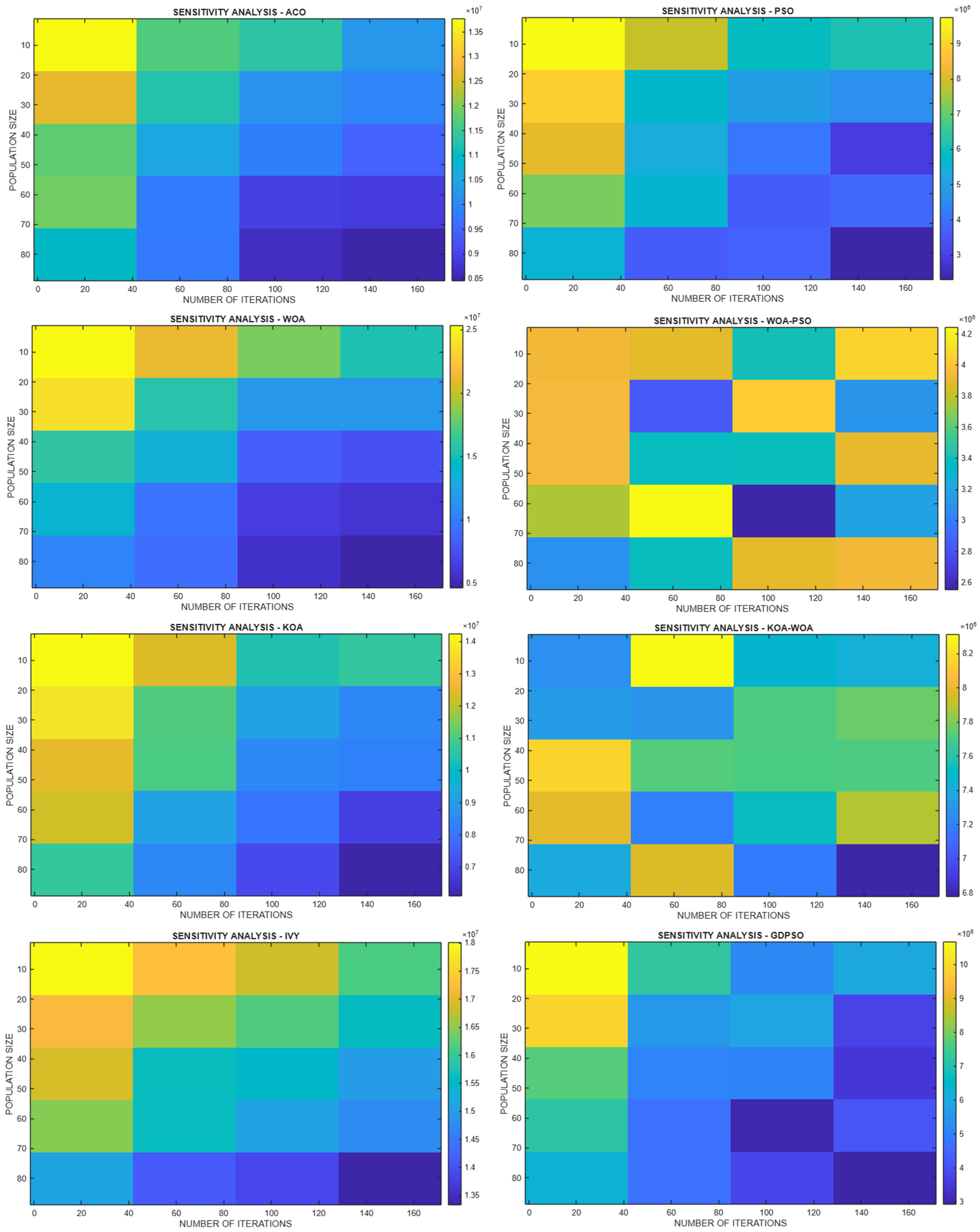
4.1. Sensitivity Analysis
- ACO exhibited a strong dependence on iteration count, with stable yet significant improvements at higher iterations, while being largely insensitive to population size.
- PSO demonstrated rapid improvements within the first 80–100 iterations, after which the benefits plateaued, and showed moderate dependence on population size.
- WOA displayed gradual improvements but was highly sensitive to both iterations and population size, performing better with larger populations.
- KOA revealed iteration-dominant behavior with moderate effects from population size.
- KOA-WOA showed balanced behavior, improving consistently with higher iterations but stabilizing around medium population sizes (~50).
- IVY was sensitive to iteration increases and moderately responsive to population size, though its performance was less stable compared to others.
- WOA-PSO achieved its best performance around 100 iterations and a population size of ~50, demonstrating efficient convergence.
- GD-PSO benefited from both parameters, though improvements diminished beyond 100 iterations and 50–60 agents.
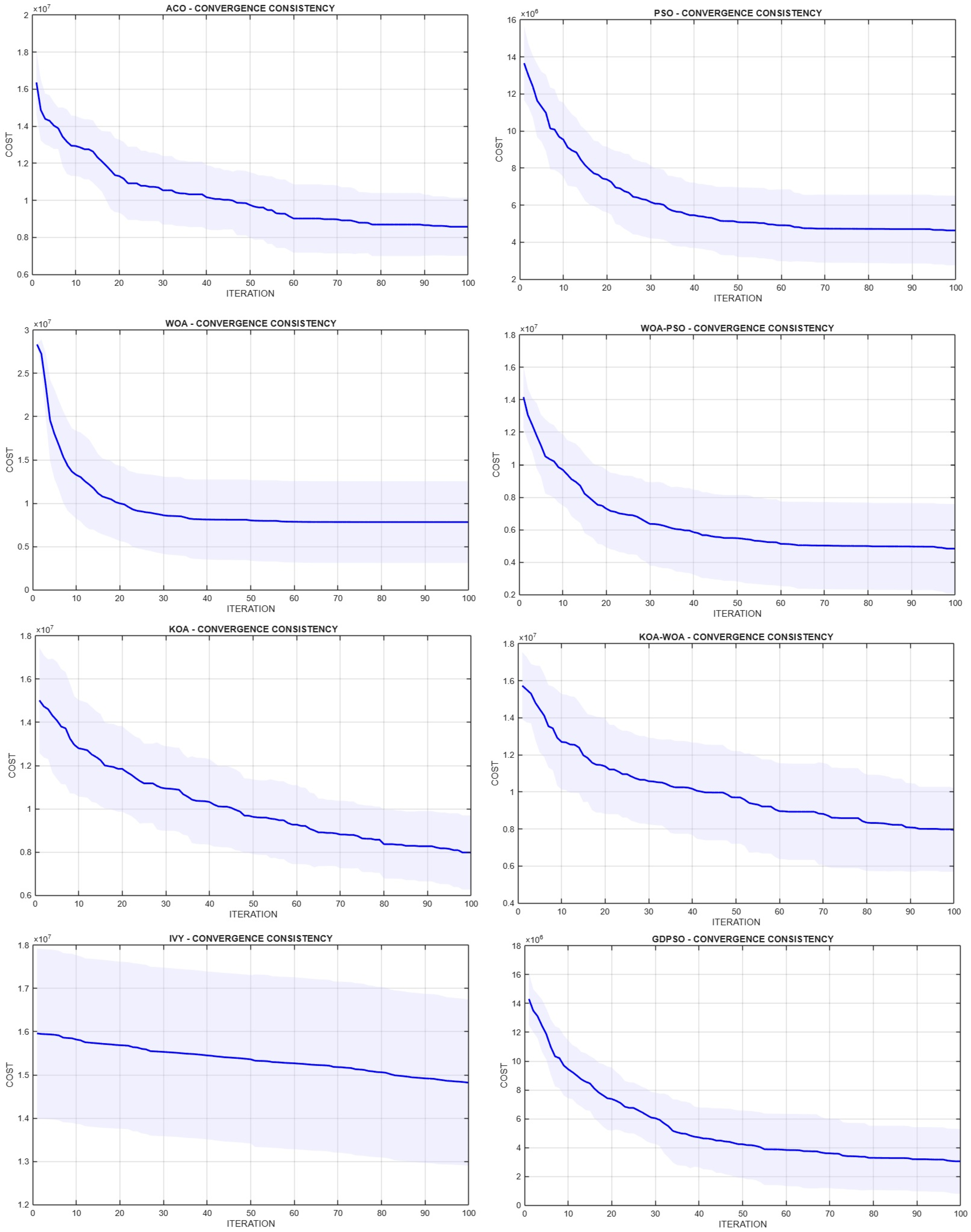
4.2. Convergence Consistency
- PSO demonstrates rapid initial convergence but tends to stagnate in later iterations, indicating strong exploitation capability yet limited exploration depth over time.
- GD-PSO, as a dynamic and gradient-guided variant of PSO, maintains the early convergence strength of PSO while slightly improving stability throughout the optimization process.
- WOA shows a smoother but slower convergence pattern, with gradual improvements becoming more evident in later iterations.
- In contrast, WOA–PSO, a hybrid approach combining the exploration mechanisms of WOA and the exploitation efficiency of PSO, significantly enhances convergence performance. It achieves faster early improvements compared to WOA and avoids premature stagnation, resulting in a steeper and more consistent trajectory.
- ACO and KOA also exhibit moderate convergence, with ACO showing a more gradual descent and KOA achieving steady improvement across iterations.
- The KOA–WOA hybrid outperforms both individual components by accelerating early convergence and demonstrating lower variance, suggesting improved robustness and balance.
- IVY, while biologically inspired and capable of navigating the search space, displays the slowest convergence, and its performance curve remains relatively flat throughout the iterations. This indicates limited capacity for both exploration and exploitation in the con-text of the tested problem.
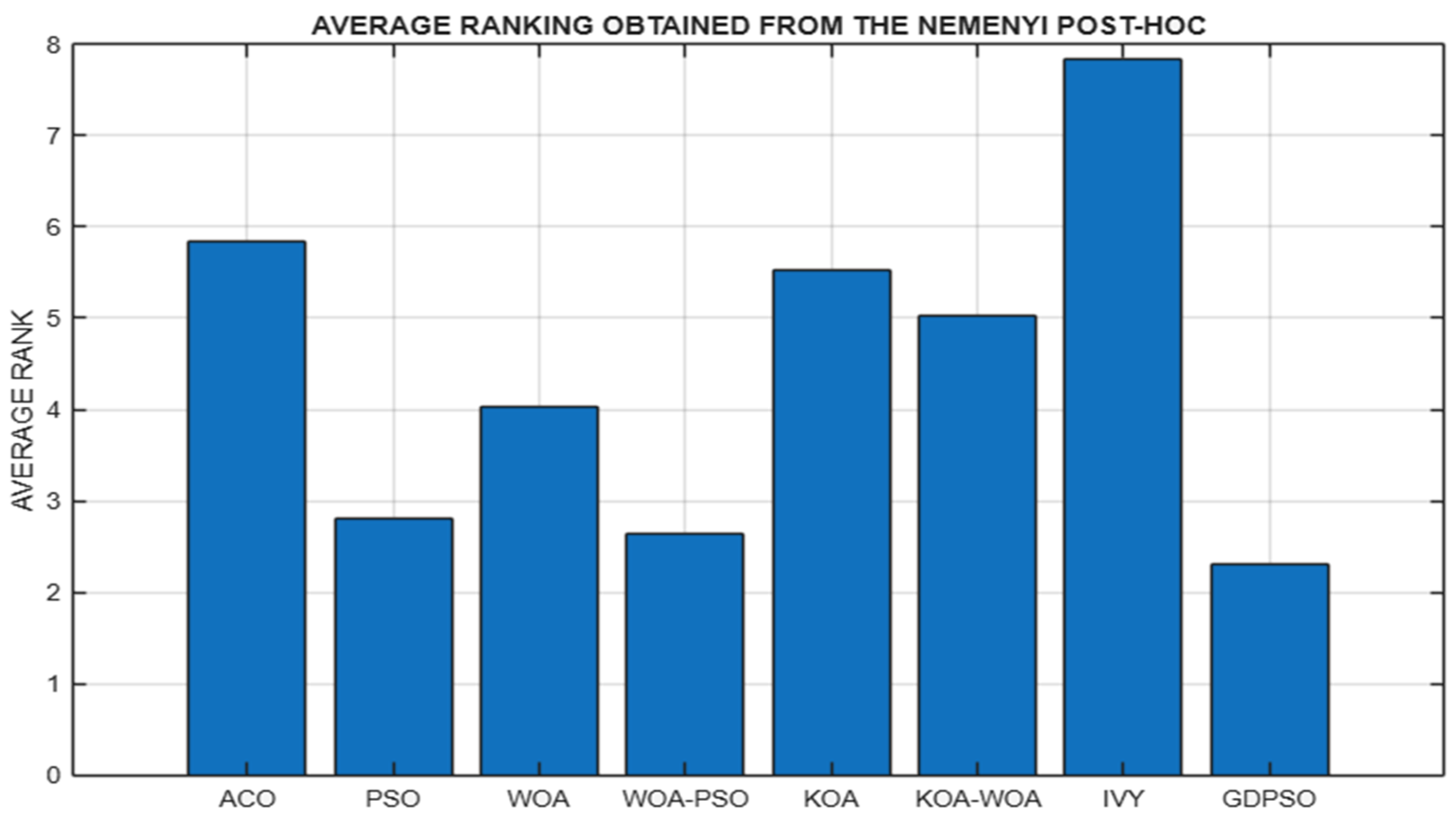
4.3. Statistical Performance Comparison
- : Critical value obtained from the Studentized range distribution. For a significance level of α = 0.05, the critical value is approximately ≈ 2.728 for large sample sizes.
- k: The number of algorithms being compared. In this study, k = 8.
- N: The number of independent executions or problems. In this case, N = 30.
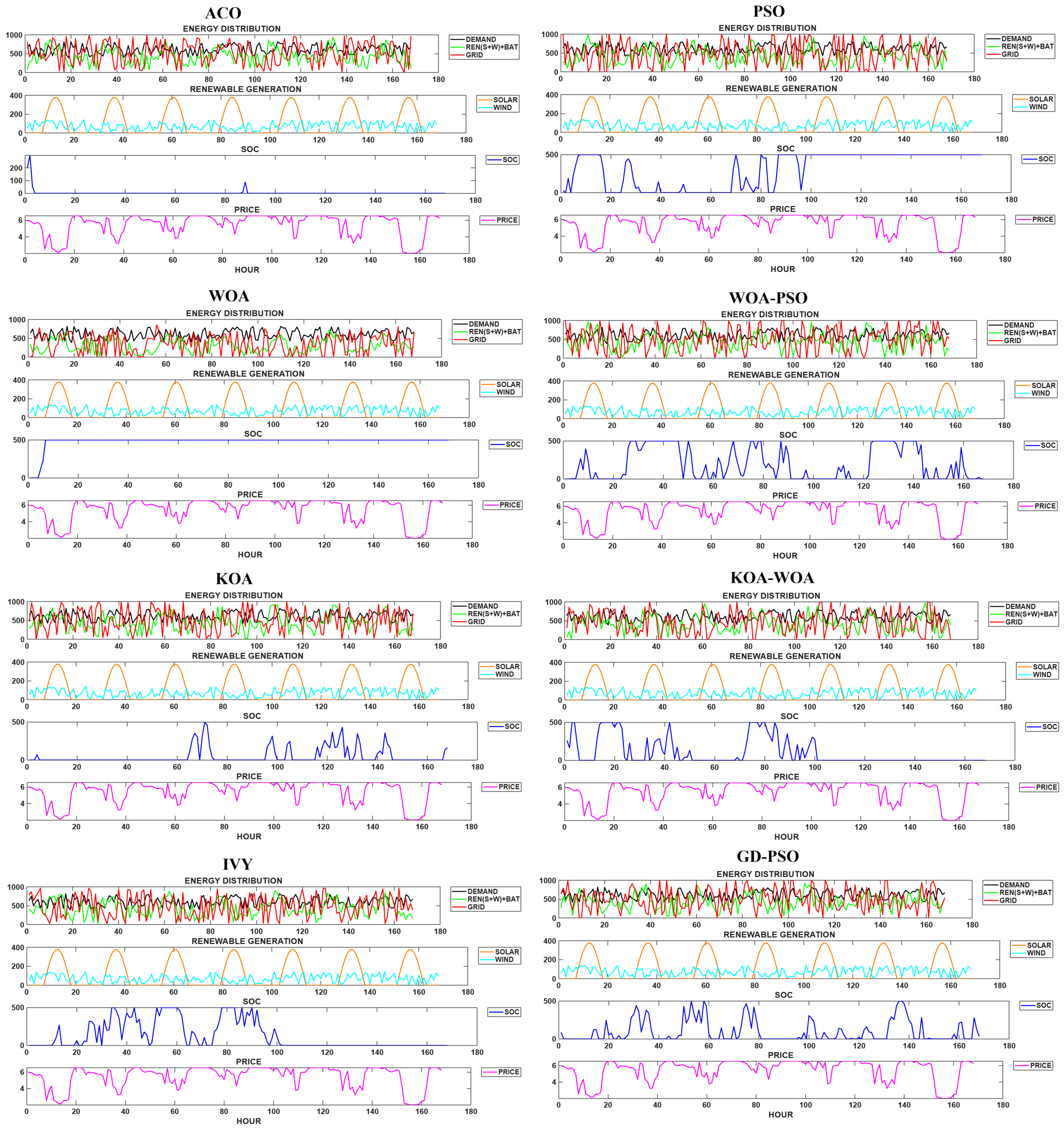
- GD-PSO and WOA-PSO maintain SOC within efficient operating zones, indicating advanced energy arbitrage strategies that align with market dynamics.
- KOA-WOA and PSO show moderately adaptive SOC profiles, occasionally failing to exploit low-price periods or renewable surpluses fully.
- In contrast, ACO and IVY display inconsistent SOC behaviors and greater reliance on grid energy, which leads to higher operating costs.
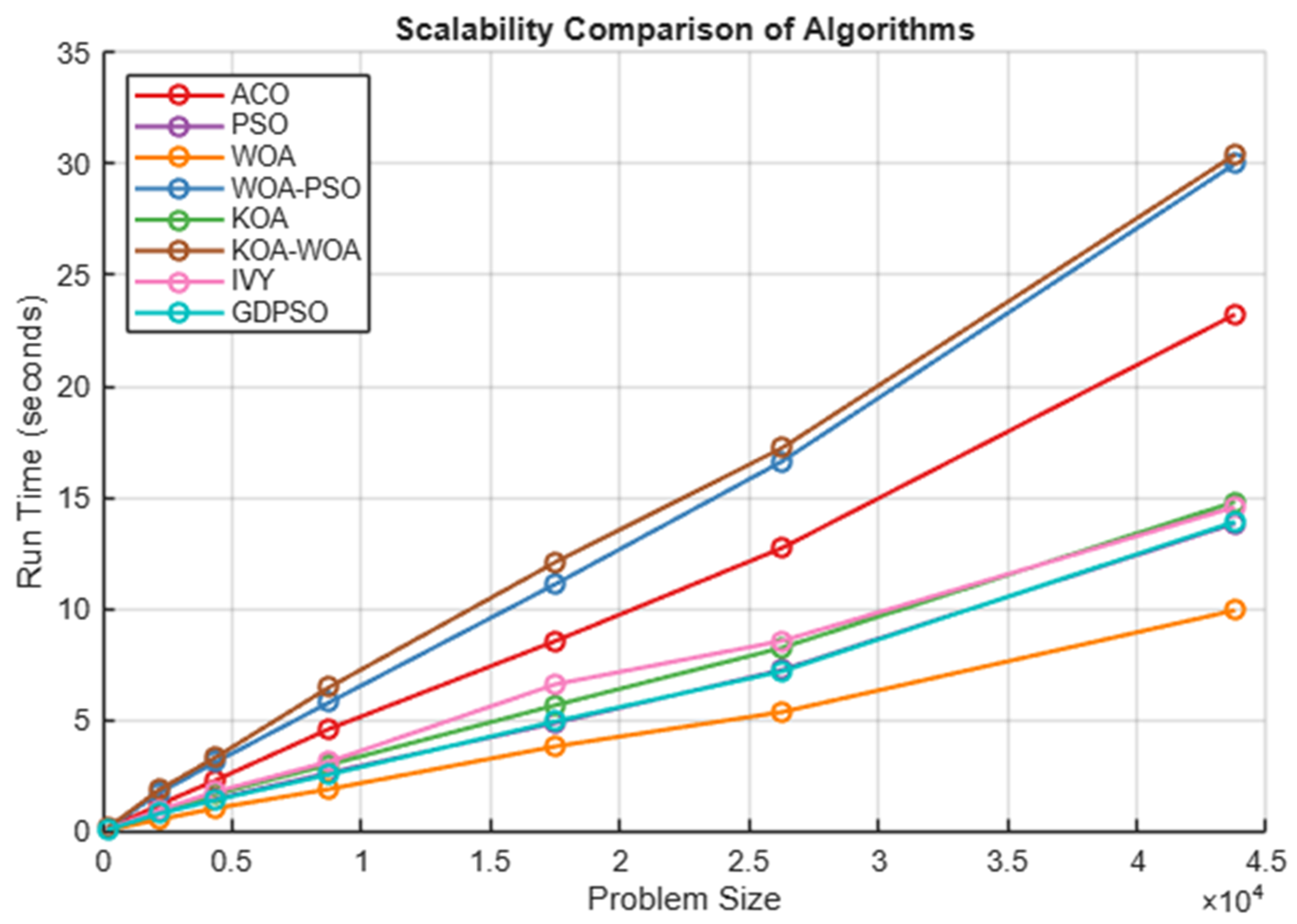
4.4. Scalability Comparison of Algorithms
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN‘95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Siano, P. Demand response and smart grids—A survey. Renew. Sustain. Energy Rev. 2014, 30, 461–478. [Google Scholar] [CrossRef]
- Abido, M. Optimal power flow using particle swarm optimization. Int. J. Electr. Power Energy Syst. 2002, 24, 563–571. [Google Scholar] [CrossRef]
- Deb, K. Multi-objective optimisation using evolutionary algorithms: An introduction. In Multi-Objective Evolutionary Optimisation for Product Design and Manufacturing; Springer: London, UK, 2011; pp. 3–34. [Google Scholar]
- Coello, C.C. Evolutionary multi-objective optimization: A historical view of the field. IEEE Comput. Intell. Mag. 2006, 1, 28–36. [Google Scholar] [CrossRef]
- Farhangi, H. The path of the smart grid. IEEE Power Energy Mag. 2009, 8, 18–28. [Google Scholar] [CrossRef]
- Singh, S.; Singh, M.; Kaushik, S.C. A review on optimization techniques for sizing solar-wind hybrid energy systems. Int. J. Green Energy 2016, 13, 1564–1578. [Google Scholar] [CrossRef]
- Krueasuk, W.; Ongsakul, W. Optimal placement of distributed generation using particle swarm optimization. In Proceedings of the Australasian Universities Power Engineering Conference (AUPEC), Melbourne, Australia, 10–13 December 2006. [Google Scholar]
- Khan, S.A.; Tao, Z.; Agyekum, E.B.; Fahad, S.; Tahir, M.; Salman, M. Sustainable rural electrification: Energy-economic feasibility analysis of autonomous hydrogen-based hybrid energy system. Int. J. Hydrogen Energy 2024, 141, 460–473. [Google Scholar] [CrossRef]
- Şenel, F.A.; Gökçe, A.; Yüksel, M.; Yiğit, E. A novel hybrid PSO–GWO algorithm for optimization problems. Eng. Comput. 2019, 35, 1359–1373. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhang, L.; Liu, X.; Wang, J. Metaheuristic techniques in microgrid management: A survey. Swarm Evol. Comput. 2023, 78, 101256. [Google Scholar] [CrossRef]
- Dey, B.; Bhattacharyya, B.; Márquez, F.P.G. A hybrid optimization-based approach to solve environment constrained economic dispatch problem on microgrid system. J. Clean. Prod. 2021, 307, 127196. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, X.; Wang, X.; Xu, Y. Modelling and optimal energy management for battery energy storage systems in renewable energy systems: A review. Renew. Sustain. Energy Rev. 2022, 167, 112671. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Abdelhamid, A.M.; Sultan, H.M. Comprehensive analysis of optimal power flow using recent metaheuristic algorithms. Sci. Rep. 2024, 14, 13422. [Google Scholar] [CrossRef]
- Nandish, B.M.; Pushparajesh, V. Efficient power management based on adaptive whale optimization technique for residential load. Electr. Eng. 2024, 106, 4439–4456. [Google Scholar] [CrossRef]
- Rajagopalan, A.; Sundar, K.R.; Sivanesan, S.M.; Kumar, M. Multi-objective optimal scheduling of a microgrid using oppositional gradient-based grey wolf optimizer. Energies 2022, 15, 9024. [Google Scholar] [CrossRef]
- Ali, S.; Rehman, A.U.; Wadud, Z.; Khan, I.; Murawwat, S.; Hafeez, G.; Albogamy, F.R.; Khan, S.; Samuel, O. Demand response program for efficient demand-side management in smart grid considering renewable energy sources. IEEE Access 2022, 10, 53832–53853. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y.; Liu, M.; Chen, H. Integrated energy management of smart grids in smart cities based on PSO scheduling models. Adv. Civ. Eng. 2023, 2023, 5794002. [Google Scholar] [CrossRef]
- Al-Maqaleh, M.A.; El-Sawy, A.M.; Shaheen, A.M. Hybrid swarm intelligence models for renewable-based microgrid optimization. Sustain. Energy Technol. Assess. 2023, 56, 103–115. [Google Scholar]
- Akopov, A.S. MBHGA: A Matrix-Based Hybrid Genetic Algorithm for Solving an Agent-Based Model of Controlled Trade Interactions. IEEE Access 2025, 13, 26843–26863. [Google Scholar] [CrossRef]
- Şen, G.; Bilgin, M.Z. Optimal power flow using kepler optimization algorithm for active power loss analysis in island mode: A case study. Heliyon 2025, 11, e41915. [Google Scholar] [CrossRef]
- Ghasemi, M.; Zare, M.; Trojovský, P.; Rao, R.V.; Trojovská, E.; Kandasamy, V. Optimization based on the smart behavior of plants with its engineering applications: Ivy algorithm. Knowl.-Based Syst. 2024, 295, 111850. [Google Scholar] [CrossRef]
- İzmir Development Agency, Investment in the Solar Energy. Sector in İzmir, Jan. 2016. Available online: https://www.kalkinmakutuphanesi.gov.tr/assets/upload/dosyalar/zmirde-gunes-enerjisi-sektorunde-yatirim.pdf (accessed on 19 August 2025).
- İzmir Development Agency. Investment in the Wind Energy Sector in İzmir, Jan. 2016. Available online: https://www.kalkinmakutuphanesi.gov.tr/assets/upload/dosyalar/zmirde-ruzgar-enerjisi-sektounde-yatirim.pdf (accessed on 19 August 2025).
- EPİAŞ (Energy Markets Operation Inc.). EPİAŞ Transparency Platform. Available online: https://seffaflik.epias.com.tr/home (accessed on 19 September 2025).
- EMRA (Energy Market Regulatory Authority). Electricity Tariff Tables. Available online: https://www.epdk.gov.tr/Detay/Icerik/3-1327/elektrik-faturalarina-esas-tarife-tablolari (accessed on 19 September 2025).
- Oloyede, M.O.; Akpakwu, G.A.; Myburgh, H.C.; De Freitas, A.; Kunatsa, T. A review on state-of-charge estimation methods, energy storage technologies and state-of-the-art simulators: Recent developments and challenges. World Electr. Veh. J. 2024, 15, 381. [Google Scholar] [CrossRef]
- Zhao, X. Optimal allocation of wind power hybrid energy storage capacity based on ant colony optimization algorithm. Eng. Optim. 2024, 57, 1873–1889. [Google Scholar] [CrossRef]
- Khan, A.M.; Hekmati, A.; Bagheri, M. Enhancing cost-effectiveness in residential microgrids: An optimization for energy management with proactive electric vehicle charging. Front. Energy Res. 2025, 13, 1454448. [Google Scholar] [CrossRef]
- Wang, H.; Xie, G.; Zhan, Y. Optimal power flow of power systems using hybrid whale and particle swarm optimization technique. In Proceedings of the 2024 IEEE International Conference on Energy Internet (ICEI), Guangzhou, China, 22–24 November 2024. [Google Scholar]
- Liu, W.; Rui, C.; Liu, Z.; Chen, J. Energy management for microgrids integrating renewable sources and hybrid electric vehi-cles. Case Stud. Therm. Eng. 2025, 69, 105937. [Google Scholar] [CrossRef]
- Zhang, C.; Lin, W.; Hu, G. An enhanced ivy algorithm fusing multiple strategies for global optimization problems. Adv. Eng. Softw. 2025, 203, 103862. [Google Scholar] [CrossRef]
- Fahad, S.; Khan, S.A.; Yang, S.; Khan, S.U.; Tahir, M.; Salman, M. Optimizing multi-modal electromagnetic design problems using quantum particle swarm optimization with differential evolution. IEEE Access 2023, 11, 101760–101775. [Google Scholar] [CrossRef]
- Uzer, M.S.; Inan, O. Application of improved hybrid whale optimization algorithm to optimization problems. Neural Comput. Appl. 2023, 35, 12433–12451. [Google Scholar] [CrossRef]
- Varaee, H.; Naser, S.H.; Mahsa, S. A hybrid generalized reduced gradient-based particle swarm optimizer for constrained engineering optimization problems. J. Soft Comput. Civ. Eng. 2021, 5, 86–119. [Google Scholar]


| Reference | Method | Result | Explanation |
|---|---|---|---|
| [7] | GA, PSO | The system efficiency has increased by 20%. | Optimization techniques have been used to improve efficiency in distributed production. |
| [8] | PSO | Energy losses have decreased by 20%. | The DG placement problem has been solved, and system losses have been reduced. |
| [11] | Hybrid GWO | There has been a 20% reduction in costs and an 18% increase in renewable usage. | The economic load distribution in the microgrid has been optimized. |
| [12] | EMS + Metaheuristics | A 25% increase in battery life has been achieved. | It has been shown how optimization affects battery strategies. |
| [13] | Different Metaheuristic Methods | The increase in efficiency is in the range of 5–15%. | Algorithms have been tested comparatively. |
| [14] | Adaptive WOA | The system response time has been reduced by 23%. | In smart grids, adaptive WOA has been used for load forecasting. |
| [15] | Improved GWO | A 15.7% reduction in energy losses has been achieved. | Multi-purpose optimization has been provided for hybrid microgrids. |
| Algorithm | Iteration Sensitivity | Population Sensitivity | Observation |
|---|---|---|---|
| ACO | High | Low | Iteration-dominant; performance improves mainly with more iterations |
| PSO | High (early stage) | Moderate | Rapid gains up to 80–100 iterations; diminishing returns afterward |
| WOA | Moderate | High | Sensitive to both parameters; larger populations improve outcomes |
| KOA | High | Moderate | Iteration-driven improvements; moderate impact of population size |
| KOA-WOA | Moderate | Moderate | Balanced performance; stable at ~100 iterations and ~50 population |
| IVY | High | Moderate | Strong iteration sensitivity; moderate effect of population size |
| WOA-PSO | Moderate | Moderate | Efficient convergence; best at ~100 iterations and ~50 agents |
| GD-PSO | Moderate | Moderate | Benefits from both parameters; limited gains beyond 100 iterations and 50–60 agents |
| Algorithm | Average Value (₺) | Standard Deviation (₺) | Minimum Value (₺) | Maximum Value (₺) |
|---|---|---|---|---|
| ACO | 8,416,626.31 | 1,411,978.81 | 5,623,892.68 | 10,711,552.45 |
| PSO | 3,785,255.37 | 2,961,357.74 | 966,419.20 | 9,050,530.72 |
| WOA | 6,827,950.15 | 4,798,082.67 | 644,556.85 | 16,786,284.37 |
| WOA-PSO | 3,771,291.93 | 2,827,135.40 | 973,943.77 | 9,107,438.97 |
| KOA | 7,892,183.37 | 1,865,770.93 | 5,234,181.02 | 11,327,106.65 |
| KOA-WOA | 7,296,357.91 | 2,103,747.94 | 2,723,651.00 | 10,729,949.80 |
| IVY | 14,750,985.52 | 2,485,039.90 | 9,075,607.57 | 17,749,640.73 |
| GD-PSO | 2,903,637.51 | 2,018,626.38 | 1,006,536.46 | 5,936,622.93 |
| Algorithm Pair | Mean Rank Difference | Significance |
|---|---|---|
| ACO vs. PSO | 3.03 > 1.73 | Significant |
| ACO vs. WOA | 1.80 > 1.73 | Significant |
| ACO vs. WOA-PSO | 3.20 > 1.73 | Significant |
| ACO vs. KOA | 0.30 ≤ 1.73 | Not Significant |
| ACO vs. KOA-WOA | 0.80 ≤ 1.73 | Not Significant |
| ACO vs. IVY | 2.00 > 1.73 | Significant |
| ACO vs. GD-PSO | 3.53 > 1.73 | Significant |
| PSO vs. WOA | 1.23 ≤ 1.73 | Not Significant |
| PSO vs. WOA-PSO | 0.17 ≤ 1.73 | Not Significant |
| PSO vs. KOA | 2.73 > 1.73 | Significant |
| PSO vs. KOA-WOA | 2.23 > 1.73 | Significant |
| PSO vs. IVY | 5.03 > 1.73 | Significant |
| PSO vs. GD-PSO | 0.50 ≤ 1.73 | Not Significant |
| WOA vs. WOA-PSO | 1.40 ≤ 1.73 | Not Significant |
| WOA vs. KOA | 1.50 ≤ 1.73 | Not Significant |
| WOA vs. KOA-WOA | 1.00 ≤ 1.73 | Not Significant |
| WOA vs. IVY | 3.80 > 1.73 | Significant |
| WOA vs. GD-PSO | 1.73 > 1.73 | Significant |
| WOA-PSO vs. KOA | 2.90 > 1.73 | Significant |
| WOA-PSO vs. KOA-WOA | 2.40 > 1.73 | Significant |
| WOA-PSO vs. IVY | 5.20 > 1.73 | Significant |
| WOA-PSO vs. GD-PSO | 0.33 ≤ 1.73 | Not Significant |
| KOA vs. KOA-WOA | 0.50 ≤ 1.73 | Not Significant |
| KOA vs. IVY | 2.30 > 1.73 | Significant |
| KOA vs. GD-PSO | 3.23 > 1.73 | Significant |
| KOA-WOA vs. IVY | 2.80 > 1.73 | Significant |
| KOA-WOA vs. GD-PSO | 2.73 > 1.73 | Significant |
| IVY vs. GD-PSO | 5.53 > 1.73 | Significant |
| Algorithm | The Best Cost (₺) | Renewable Energy + Battery (kWh) | Renewable Energy Ratio (%) | Grid Usage at High Price (kWh) |
|---|---|---|---|---|
| ACO | 9,595,899.37 | 72,764.24 | 70.67% | 61,390.80 |
| PSO | 9,077,786.24 | 70,657.33 | 68.63% | 61,106.24 |
| WOA | 12,799,272.40 | 50,207.44 | 48.76% | 37,570.89 |
| WOA-PSO | 1,062,846.26 | 72,670.28 | 70.58% | 59,324.24 |
| KOA | 9,246,023.88 | 73,358.95 | 71.25% | 58,830.96 |
| KOA-WOA | 5,244,023.95 | 72,889.37 | 70.80% | 51,800.61 |
| IVY | 14,244,386.21 | 72,464.98 | 70.38% | 58,009.07 |
| GD-PSO | 1,031,950.12 | 71,900.54 | 69.83% | 61,016.14 |
| Algorithm | Execution Time (s) |
|---|---|
| ACO | 0.1141 |
| PSO | 0.0993 |
| WOA | 0.0447 |
| WOA-PSO | 0.1605 |
| KOA | 0.1096 |
| KOA-WOA | 0.1724 |
| IVY | 0.1084 |
| GD-PSO | 0.0948 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vadi, S.; Bildirici, M.; Kaplan, O. Performance Comparison of Metaheuristic and Hybrid Algorithms Used for Energy Cost Minimization in a Solar–Wind–Battery Microgrid. Sustainability 2025, 17, 8849. https://doi.org/10.3390/su17198849
Vadi S, Bildirici M, Kaplan O. Performance Comparison of Metaheuristic and Hybrid Algorithms Used for Energy Cost Minimization in a Solar–Wind–Battery Microgrid. Sustainability. 2025; 17(19):8849. https://doi.org/10.3390/su17198849
Chicago/Turabian StyleVadi, Seyfettin, Merve Bildirici, and Orhan Kaplan. 2025. "Performance Comparison of Metaheuristic and Hybrid Algorithms Used for Energy Cost Minimization in a Solar–Wind–Battery Microgrid" Sustainability 17, no. 19: 8849. https://doi.org/10.3390/su17198849
APA StyleVadi, S., Bildirici, M., & Kaplan, O. (2025). Performance Comparison of Metaheuristic and Hybrid Algorithms Used for Energy Cost Minimization in a Solar–Wind–Battery Microgrid. Sustainability, 17(19), 8849. https://doi.org/10.3390/su17198849







