Machine Learning-Aided Supply Chain Analysis of Waste Management Systems: System Optimization for Sustainable Production

Abstract

Electronic-waste (e-waste) management is a key challenge in engineering smart cities due to its rapid accumulation, complex composition, sparse data availability, and significant environmental and economic impacts. This study employs a bespoke machine learning infrastructure on an Indian e-waste supply chain network (SCN) focusing on the three pillars of sustainability—environmental, economic, and social. The economic resilience of the SCN is investigated against external perturbations, like market fluctuations or policy changes, by analyzing six stochastically perturbed modules, generated from the optimal point of the original dataset using Monte Carlo Simulation (MCS). In the process, MCS is demonstrated as a powerful technique to deal with sparse statistics in SCN modeling. The perturbed model is then analyzed to uncover “hidden” non-linear relationships between key variables and their sensitivity in dictating economic arbitrage. Two complementary ensemble-based approaches have been used—Feedforward Neural Network (FNN) model and Random Forest (RF) model. While FNN excels in regressing the model performance against the industry-specified target, RF is better in dealing with feature engineering and dimensional reduction, thus identifying the most influential variables. Our results demonstrate that the FNN model is a superior predictor of arbitrage conditions compared to the RF model. The tangible deliverable is a data-driven toolkit for smart engineering solutions to ensure sustainable e-waste management.

1. Introduction

The last decade has witnessed an overwhelming surge in electronic waste, popularly called e-waste generation due to high rates of product desuetude [1]. The combination of digital dependency and digital necessity in the modern world has driven complex sustainability challenges [2]. As the fastest growing urban waste stream, e-waste poses high environmental risk but also presents an untapped opportunity of repurposing secondary raw materials [3]. Resilient supply chain systems are key to responsible resource recovery from secondary materials, reducing environmental impact, and in highlighting a circular economy, which directly aligns with SDG 12 (Responsible Consumption and Production) and SDG 11 (Sustainable Cities and Communities) [4].

Supply Chain Network (SCN) refers to the dynamic network system of interconnected organizations and entities enabling optimal flow of goods, information, and finances, a nebulous and complex interlinked pathway representing the performance chain of an industrial plant. Each SCN consists of a supply side, a demand side, and internal operations. This study explicitly focuses on the internal operations part, which is responsible for the dynamical evolution of the plant’s performance. All variables used pertain to the operations of the plant. Traditional SCN models often rely on equilibrium optimization techniques that focus only on static equilibrium properties and hence are inadequate in capturing the time-sensitive, non-linear, and feedback-driven behavior typical of real-world systems. To address this limitation, Debnath et al. [5] developed a novel supply chain network analysis framework, pioneering an altogether different modeling approach, drawn from the lexicon of classical mechanics, that treats supply chain logistics analogous to chemical reaction kinetics where the key features are seen as evolutionary, that is, time-dependent, rather than time-morphed with an unchangeable (and hence unphysical) arbitrage point. The mathematical infrastructure was based on the established Euler–Lagrange formalism [6] which led to a paradigm shift enabling the dynamic mapping of material, information, and value flows across supply chain nodes, analyzing the temporal evolution and systemic feedback loops.

The existing literature chronicling machine learning (ML) and deep learning (DL) applications on supply chain management and optimization evidence major advancements in logistics and inventory management, demand forecasting, etc. ML has been proved to add to efficiency and resilience in wide ranging supply chains, in various industries and regions [7]. Pasupuleti et al. [8] implemented a robust combination of ML and statistical techniques, including regression, classification, clustering, and time series analysis, on historical real-world data of an MNC aiming at enhancing logistics and inventory management systems. The results highlight a 15% boost in demand forecasting, 10% reduction in overstock and stock-outs, and 95% on-time order fulfillment. The overall lead-time efficiency improvement by 12% underscores the success of the implementation of ML techniques. Zhu et al. [9] combined forecasting, anomaly detection, and resource optimization to enhance supply chain sustainability and resilience. The framework achieved significant results, including a reduction in transportation costs of 18.2% and a 26.5% improvement in inventory turnover. The enhanced Long Short-Term Memory (LSTM) network incorporated an attention mechanism, leading to a reduction in Root-Mean-Square-Error (RMSE) by 18.8%, which largely enhances the demand forecasting accuracy while reducing the stockout and overstocking risks. Lin and Lu [10] presented an innovative framework that combines inverse Data Envelopment Analysis (DEA) towards supplier performance predictions. They implemented Random Forest and a Neural Network (k-NN) on historical data for revaluation of supplier benchmarks, while enabling provisions of carbon reduction by 30–50% for data-centric decision making. Further economic aspects such as earning persistence and market recognition were also analyzed. Yan et al. [11] utilized a time series Convoluted Neural Network (CNN) towards inventory replenishment, ending with efficiency improvement up to 93.5%. Similarly, Zhao et al. [12] employed analogous architecture to achieve high efficiency in predicting inventory replenishment. The robustness of ML in supply chain analytics, especially in forecasting, has been demonstrated in the literature. Wang et al. [13] implemented variational autoencoders for prediction of shipping delays in diverse practical conditions, which led to an accuracy of 90% or more. Fatorachian et al. [14] studied a mixed-methods case involving food SCN to reduce waste, enhance logistic efficiency, and support circular economy in smart cities. ML techniques were used to model complicated and non-linear relationships between waste generation and factors driving waste. A comprehensive review of ML/DL applications in SCN can be found in [15].

The dynamic mapping of supply chain nodes has recently been successfully accomplishing a ubiquitous Lagrange–Euler framework [16]. Building on this foundational framework, the study optimized an e-waste Supply Chain Network (SCN) using machine learning tools. This model successfully explained system-wide (i.e., dynamic) equilibrium behavior and supported sustainable production planning by aligning economic efficiency against environmental objectives [17]. However, a critical question remained unexplored: This understanding will be key to business and environmental sustainability, as the saddle point zones can identify key operation windows for supply chain analysts and managers to act upon for strategic decision making [16].

The literature is replete with studies focusing on supply chain analytics that utilize ML as a core tool to improve efficiency, reduce overstock, manage stock replenishment, accurate demand forecasting, minimize shipping delay, etc. As mentioned earlier, these studies focus specifically on aspects of supply chains which are either related to operational aspects or to inventory management. In addition, some studies on e-waste use ML that is prioritized towards material recovery efficiency [18], classification [19], strategic approaches [20], and business model approaches [21], but not primed for process prediction. Dedicated research that delves deeper into the e-waste supply chain dynamics with focus on uncertainties are scant. The key variables inflicting uncertainties are often labeled as ‘sensitivity’ while the underlying interaction is often overlooked. In addition, dynamic systems such as e-waste SCNs are often prone to uncertainty due to random fluctuations (stochasticity) of the said variables. The response of SCNs under dynamically evolving stochastic perturbations thus remains a key challenge.

The present study addresses this knowledge gap by stochastically perturbing the original dynamic model [5] within a Monte Carlo framework [22] and then studying whether the perturbed equilibrium can eventually converge to its previously predicted (deterministic) equilibrium state [20]. This study explicitly focuses on the internal operations part of the SCN which is responsible for the operation of the plant. All variables are pertaining to the operations of the plant. To analyze, we simulate 4 datasets (1 key dataset and 3 perturbed datasets) for each variable from the original model, identify “irrelevant” parameters (i.e., parameters which do not cause any major fluctuation in the supply chain performance), and then perturb only the relevant parameters using Monte Carlo simulations to ascertain system robustness [23]. The incorporation of controlled randomness enables us to test the sensitivity and structural resilience of the modeled e-waste supply chain, examining whether the system returns to equilibrium or transitions away along unstable saddle trajectories [24].

To analyze the complexity of the emergent system and pinpoint the latent drivers of instability, we deploy a state-of-the-art deep learning (Neural Network) and a machine learning (Random Forest) tool: (a) a Feedforward Neural Network (FNN), capable of capturing non-linear dependencies in addition to features [25], and (b) a Random Forest Network (RFN) [26], which excels at ranking feature importance via ensemble learning.

This article targets three key objectives:

• Explore whether the stochastically perturbed kinetic system converges to a stable equilibrium or exhibits metastable saddle behavior [5] under stochastic perturbations. Convergence to a stable equilibrium will point to a resilient economic SCN while a saddle point will point to probabilistically unreliable SCNs.
• Extract embedded and latent features using established Machine and Deep Learning algorithms (Deep Neural Network and Random Forest). This will identify the key variables within the e-waste supply chain network from a much wider set of potential contributors. The eventual minimalist model will use these key variables only.
• Generate and analyze four alternative scenarios beyond the base case (original dataset). This will allow us to design and predict parametric spaces within which the system will converge to a resilient SCN (point 1 above).

Such Artificial Intelligence (AI)-driven predictions on supply chains, analyzing dynamic, real-world scenarios, are expected to pave the way for a resilient, adaptive, and intelligent e-waste management systems [27].

2. Methodology

2.1. Baseline Model

The base structure of this study is contemplated in the framework developed by Debnath et al. [5], where SCNs are modeled as interconnected dynamic reaction networks analogous to chemical systems. The model utilizes a cost function that encompasses all key nodes of a supply chain based on three pillars of sustainability, i.e., environmental, economic and social, including supply chain uncertainties. Time-evolving performance of this SCN, modeled as an Euler–Lagrange framework, is then undertaken to identify key players, and then extract a minimalist model from the starting generalized framework as in the original study [5,28].

This study is structured on three key remits:

• Introduction of stochasticity via Monte Carlo simulations in quasi-static variables.
• Application of Machine Learning (ML) to assess the sensitivity and relevance of individual features.
• Exploring multiple simulation scenarios to test the robustness of the originally observed equilibria.

By revisiting the baseline model through a lens of stochastic resilience and feature-driven complexity analysis, this study aims to both challenge and refine the conclusions drawn from the original kinetic modeling effort.

2.2. Dataset Management

Initially, anonymous SCN performance data for a month was collected from a multi-award-winning Indian e-waste company in 2023 (details cannot be disclosed due to IP rights). To ensure unambiguous data with minimized outliers, we engaged in phased discussions with the company. These discussions enabled us to identify key variables from the industrial perspectives. To analyze whether these experience-based assertions match with data modeled deductions, we gathered data for another 1.5 years. Overall, considering each month’s data as a singular entry, we recorded 18 entries, translating into a 24 × 18 data matrix. Missing data were cloned from previous trend lines and the authors’ experience of analyzing industrial data that typically compiles quantitative information with qualitative inputs from the practitioners. To ensure objectivity and reproducibility, each Monte Carlo dataset that has been used for modeling has been generated by ensemble-averaging over 24 stochastic realizations (additive noise within the Ito manifold). This comprised the core dataset for the benchmark case.

2.3. Data Preprocessing

The data collected comprises a total of 21 variables, of which 5 are dependent variables, each of which depends on 16 independent variables. Six datasets were generated from the original (cannot be disclosed due to copyrights) dataset using Monte Carlo Simulation (MCS). The first 5 columns of each dataset represent the dependent variables, the remaining 16 being independent. The dependent variables are Volume of CO₂ generated (VCO₂), Energy Consumed (Ec), Water Consumed (Wp), Wastewater Produced (Ww), and number of awareness activities and marketing per year (N₃). The independent variables are as follows: number of labors (N1), number of recycled materials (N4), number of operations (N5), number of logistics (N7), number of waste materials going to TSDF (N8), number of tax units (N9), unit cost of CO₂ recovery (F1), unit cost of energy used (F2), unit cost of water used (F3), unit cost of wastewater treatment (F4), salary of one labor (F5), average cost of awareness activity and marketing (F6), unit revenue earned from recycled product sold (F7), unit cost of each operation (F8), unit cost of logistics (F10), and unit cost of disposal in TSDF (F11) [16].

Variable nomenclature:

• V_CO2 = Volume of CO₂ generated
• E_C = Energy Consumption in the processes involved
• W_p = Water used due to the processes involved
• W_w = Wastewater generated in the process
• N₁ = Number of laborers
• N₃ = Number of awareness activities, e.g., adaptation to information, invisible e-waste, repair substituting new
• N₄ = Number of recycled products sold
• N₅ = Number of operations involved
• N₇ = Number of Logistics involved
• N₈ = Number of waste materials sent for Treatment, Storage and Disposal Facility (TSDF)
• N₉ = Number of Taxes to be paid
• F₁ = Unit cost for CO₂ recovery
• F₂ = Unit cost of energy used
• F₃ = Unit cost for water used
• F₄ = Unit cost of wastewater treatment
• F₅ = Salary of one labor
• F₆ = Average cost of awareness activity
• F₇ = Unit revenue earned from product sold
• F₈ = Unit cost of each operation
• F₁₀ = Unit cost of logistics
• F₁₁ = Unit cost for disposal in TSDF

As shown in

Table 1. Summary statistics of the MCS datafiles (representing the original data).

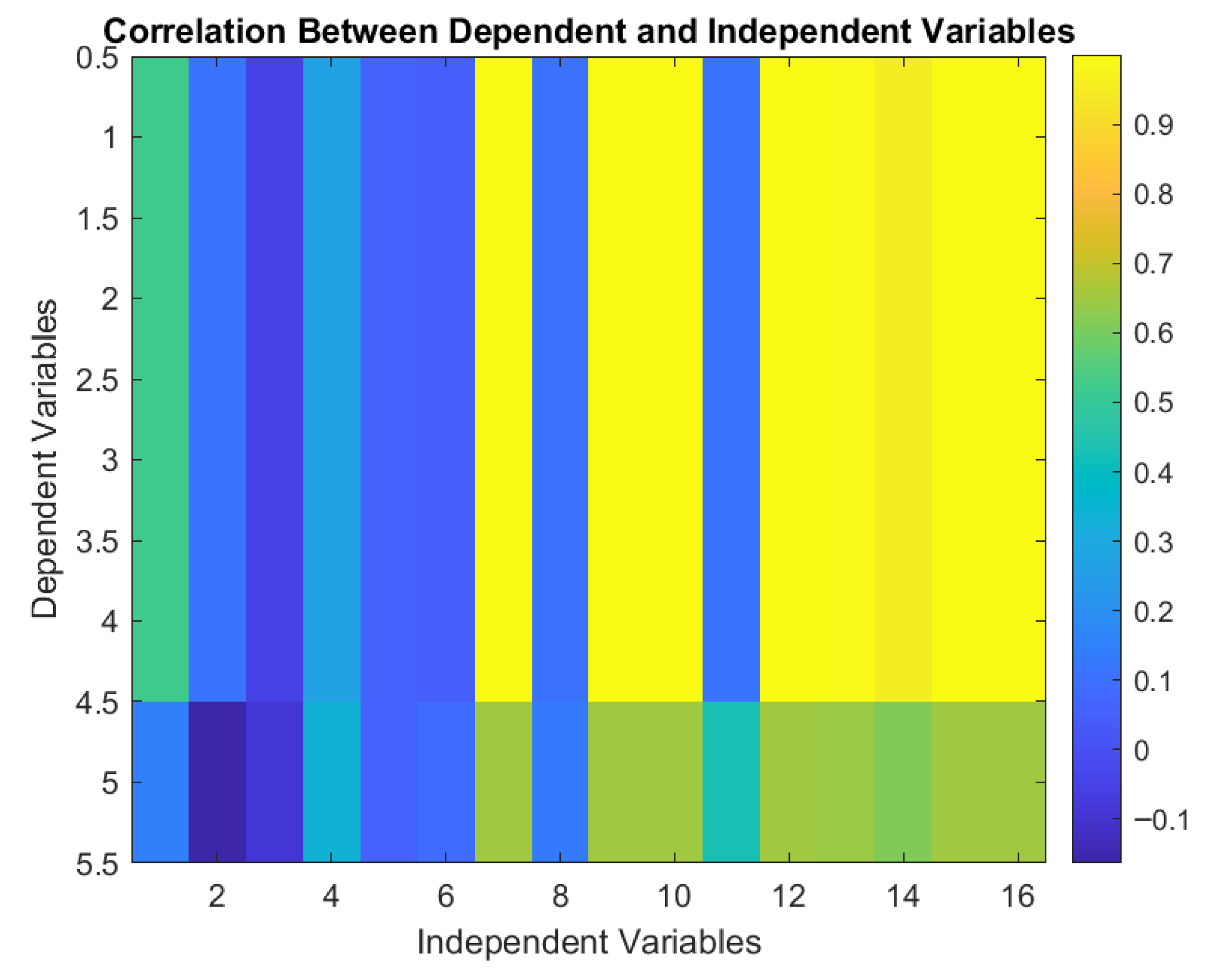
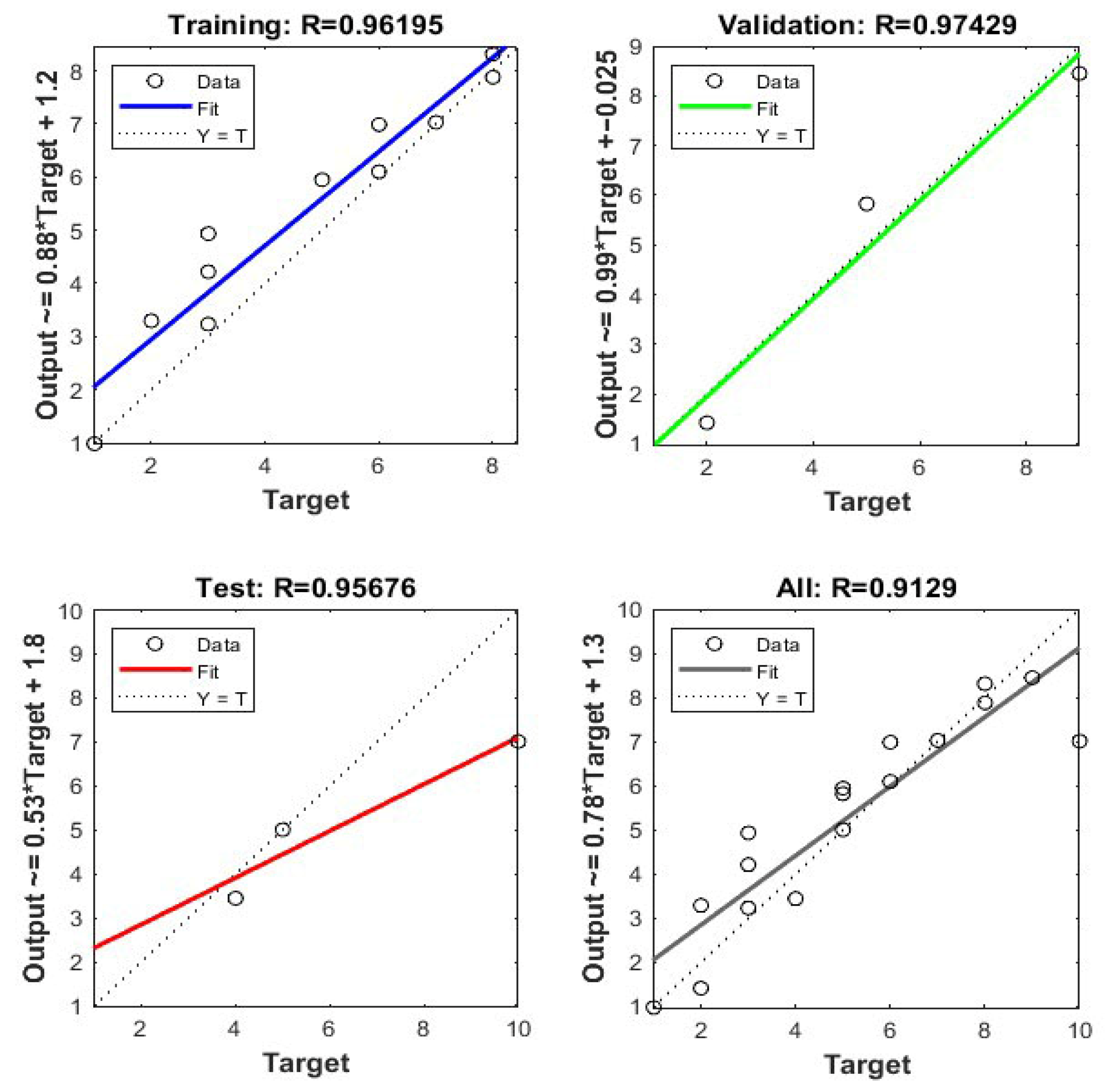
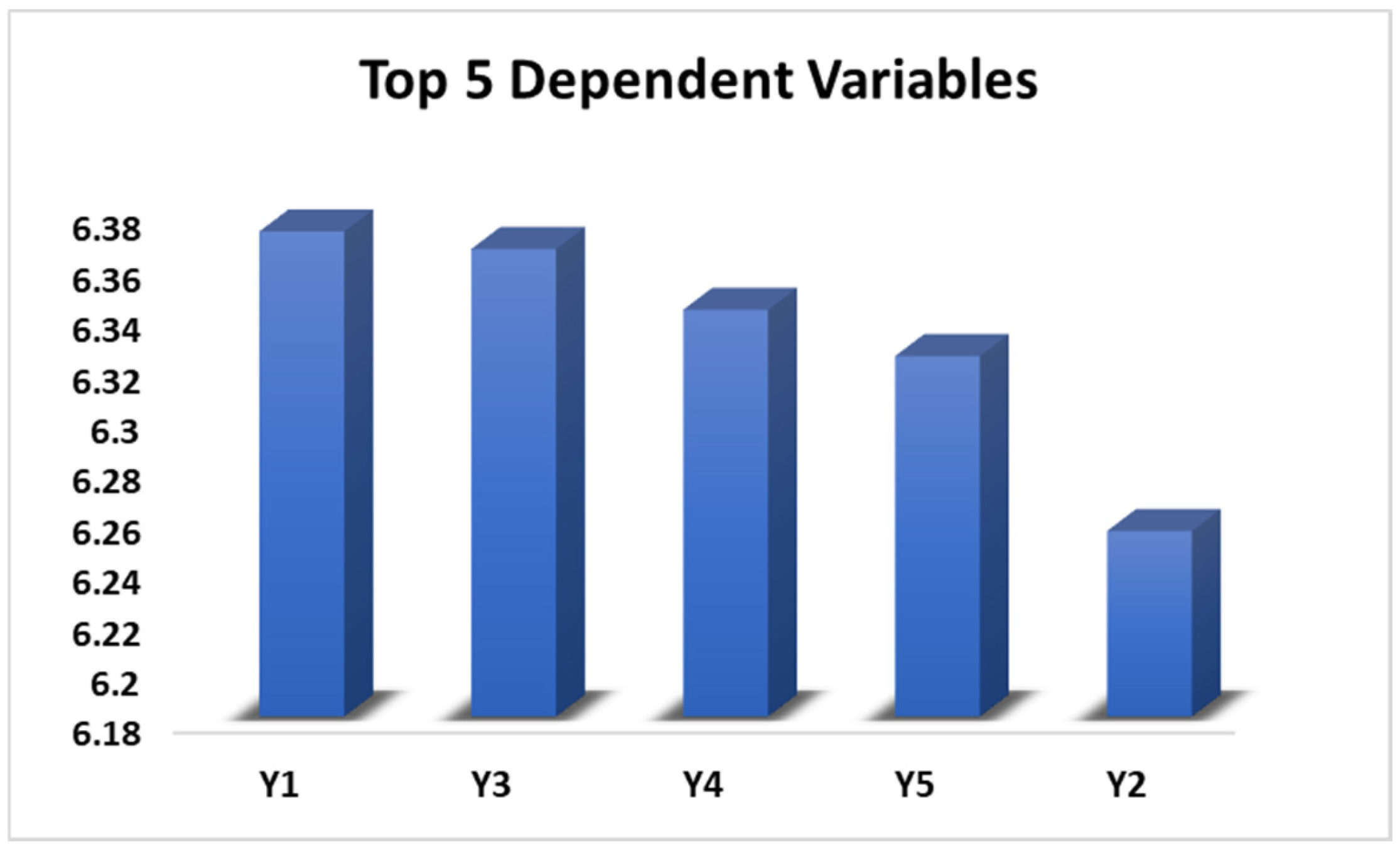
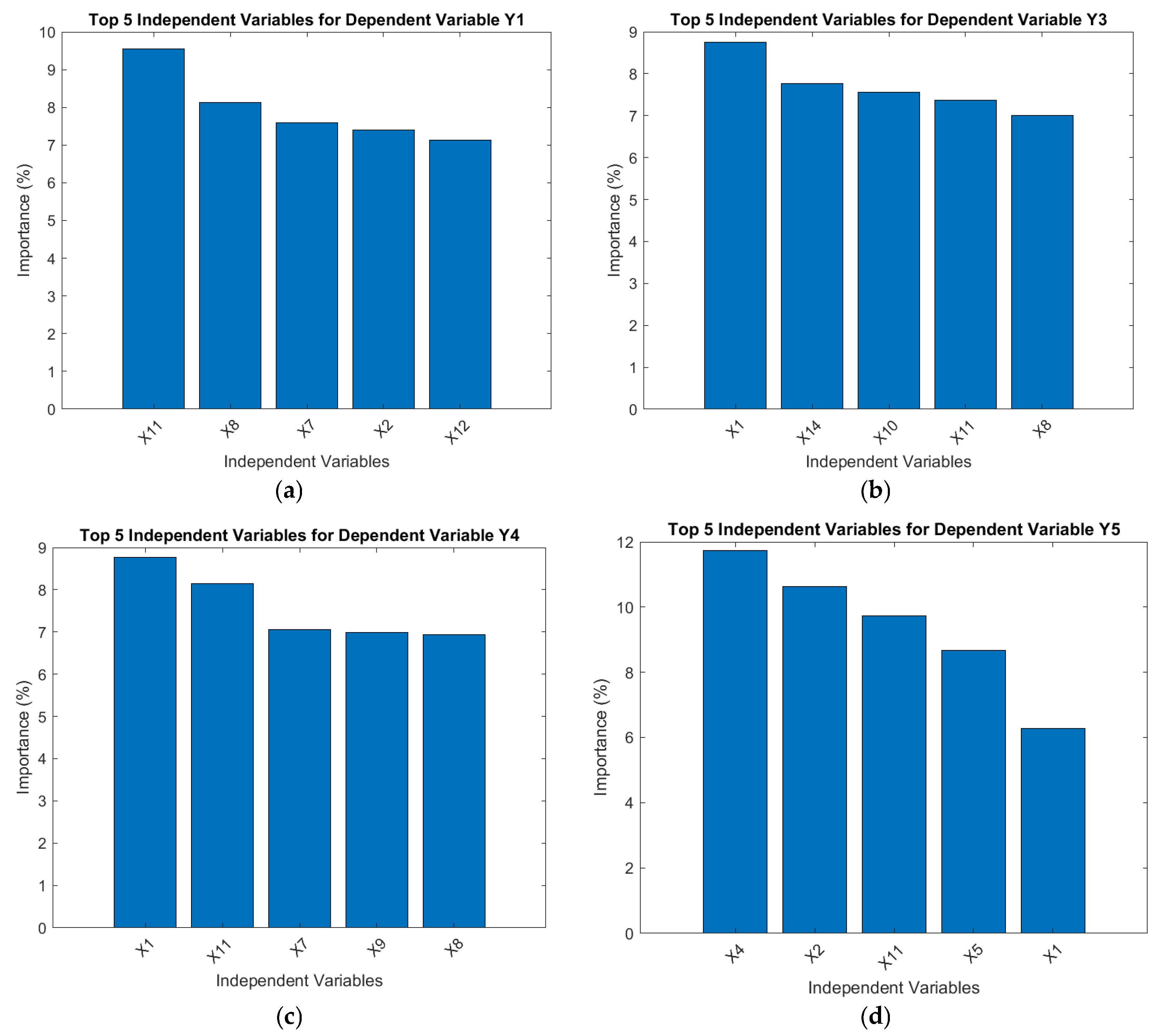
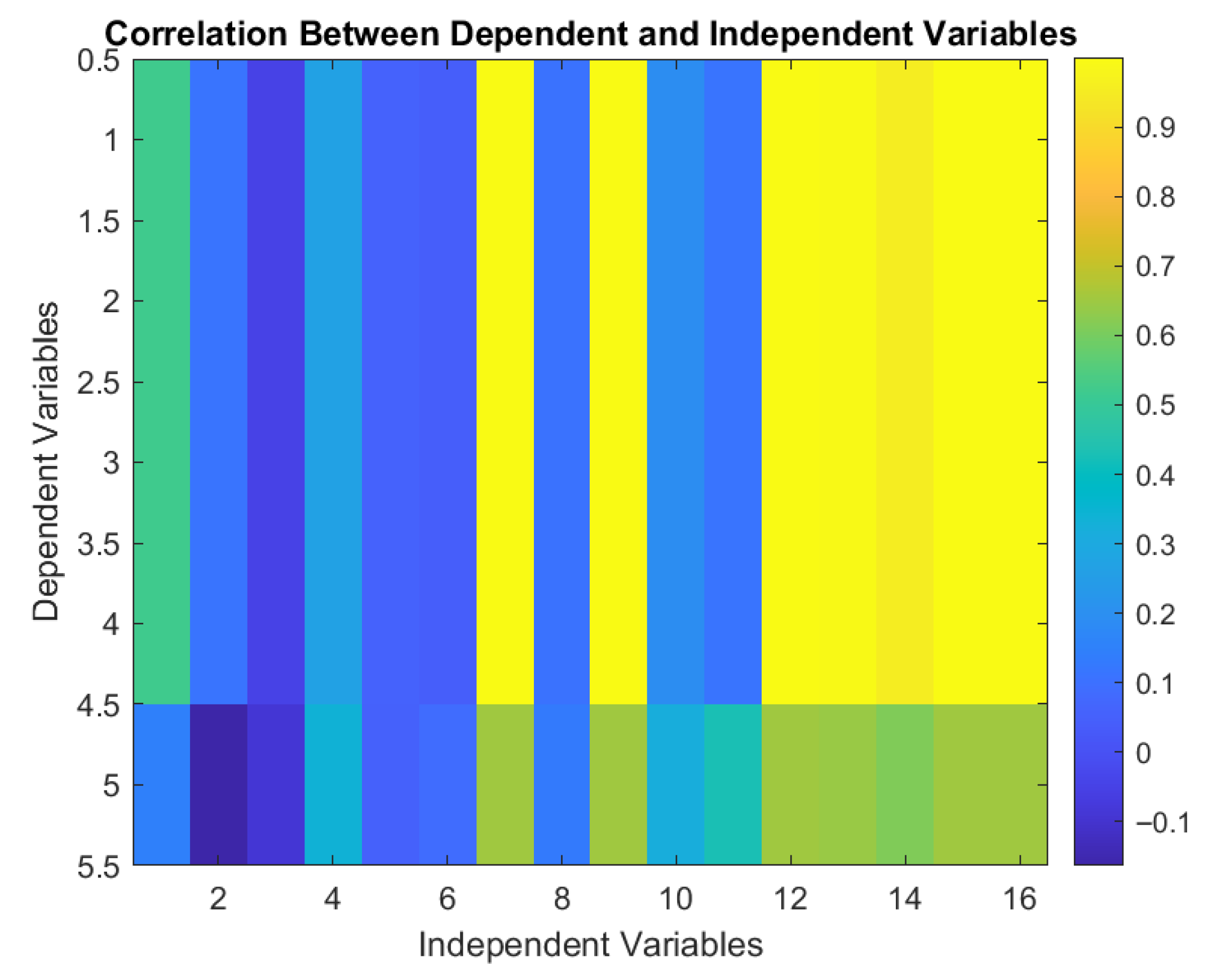
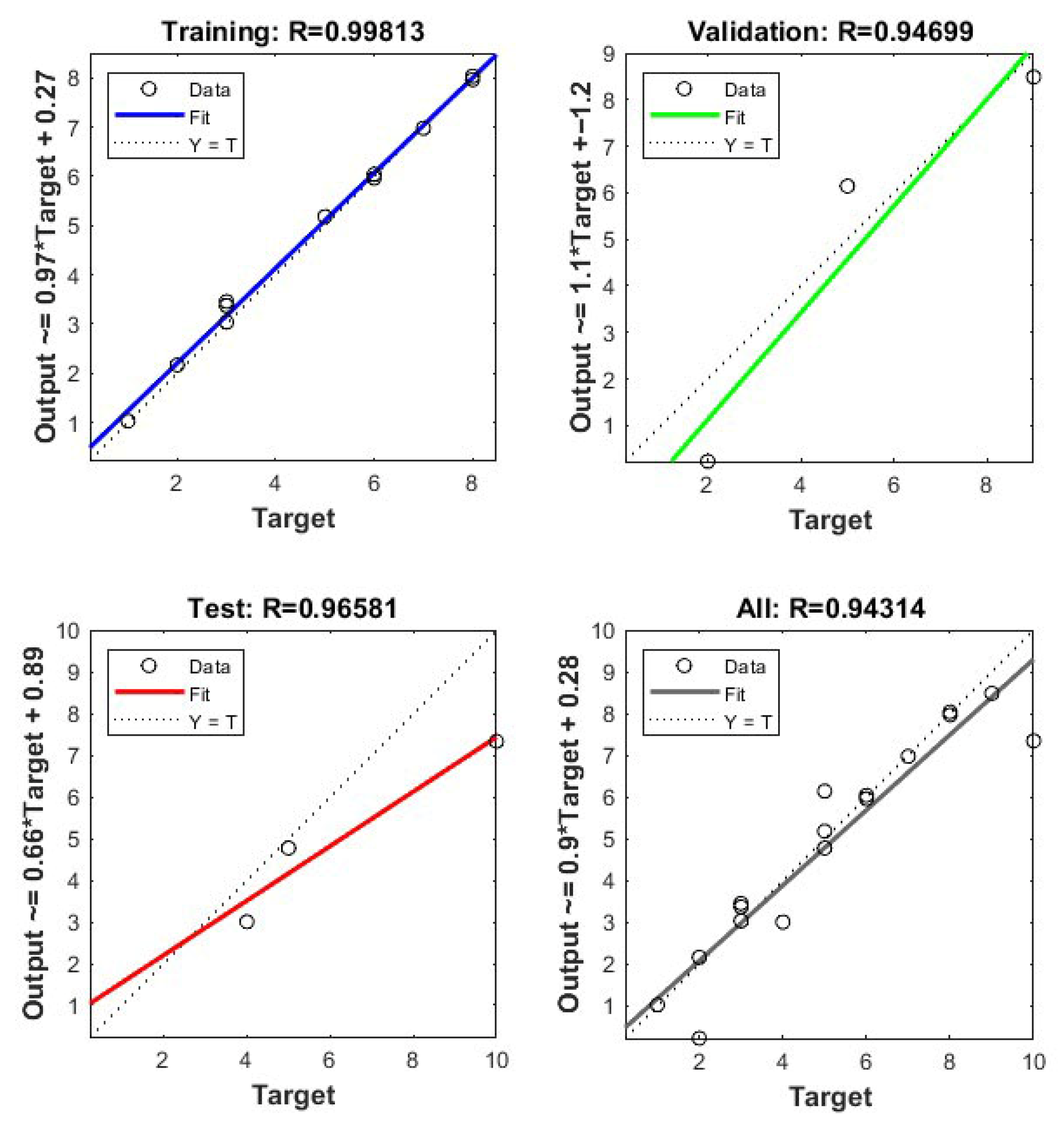
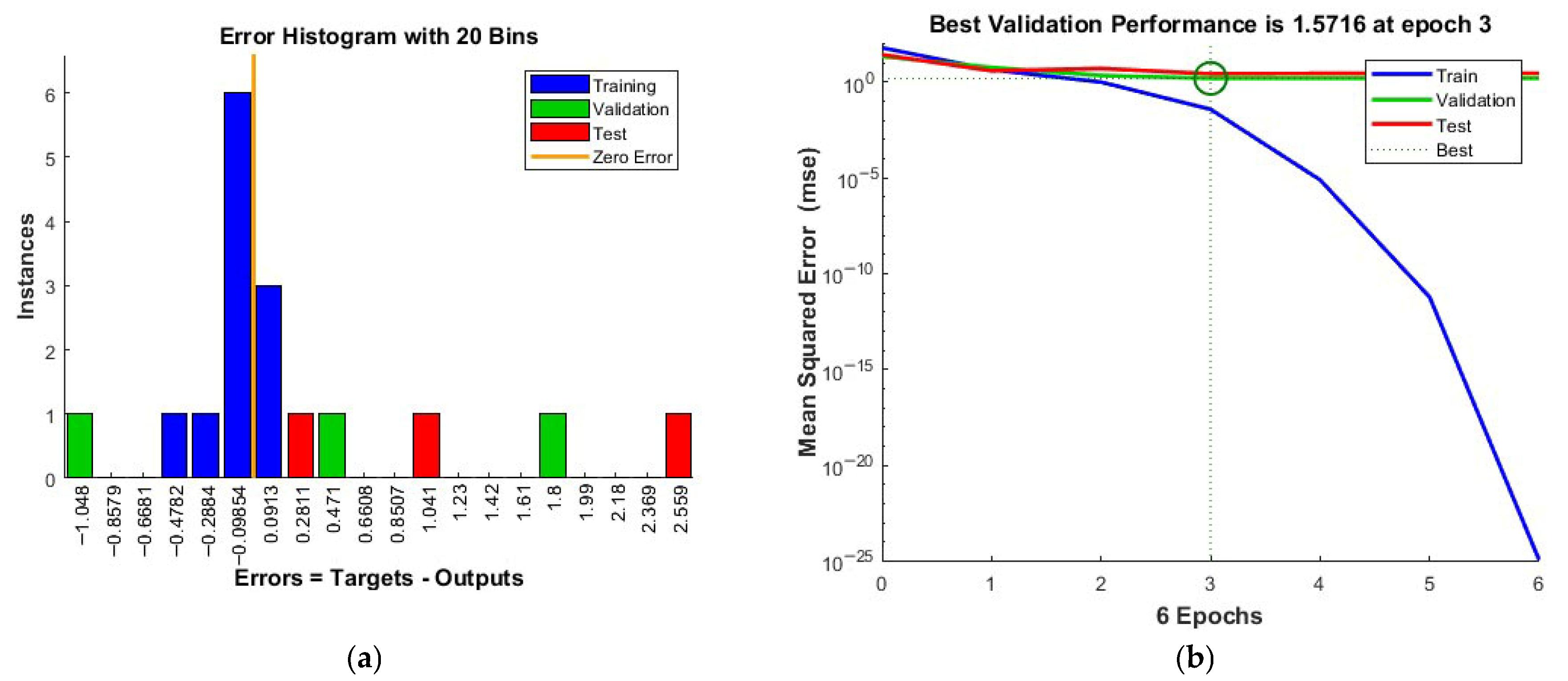
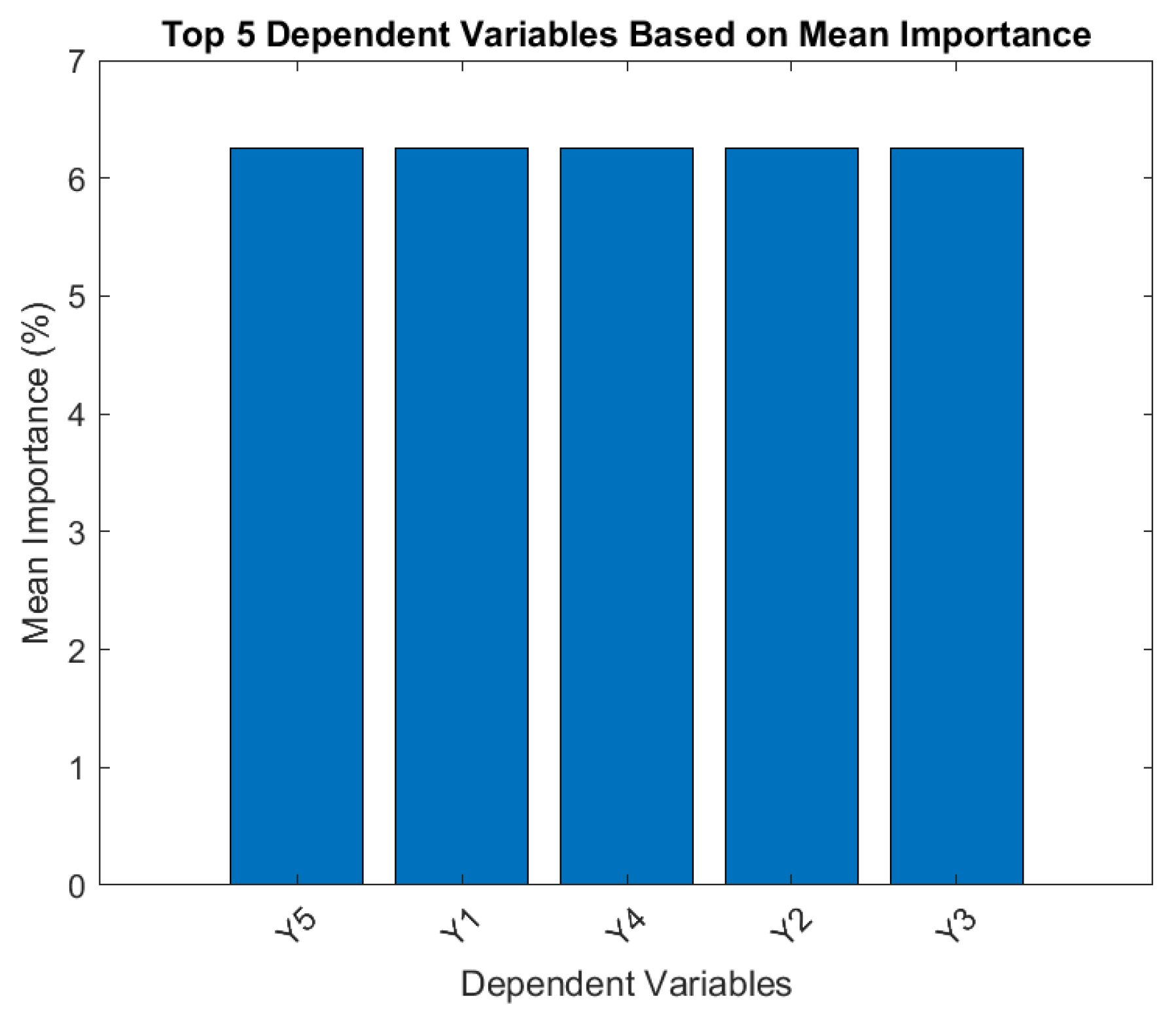
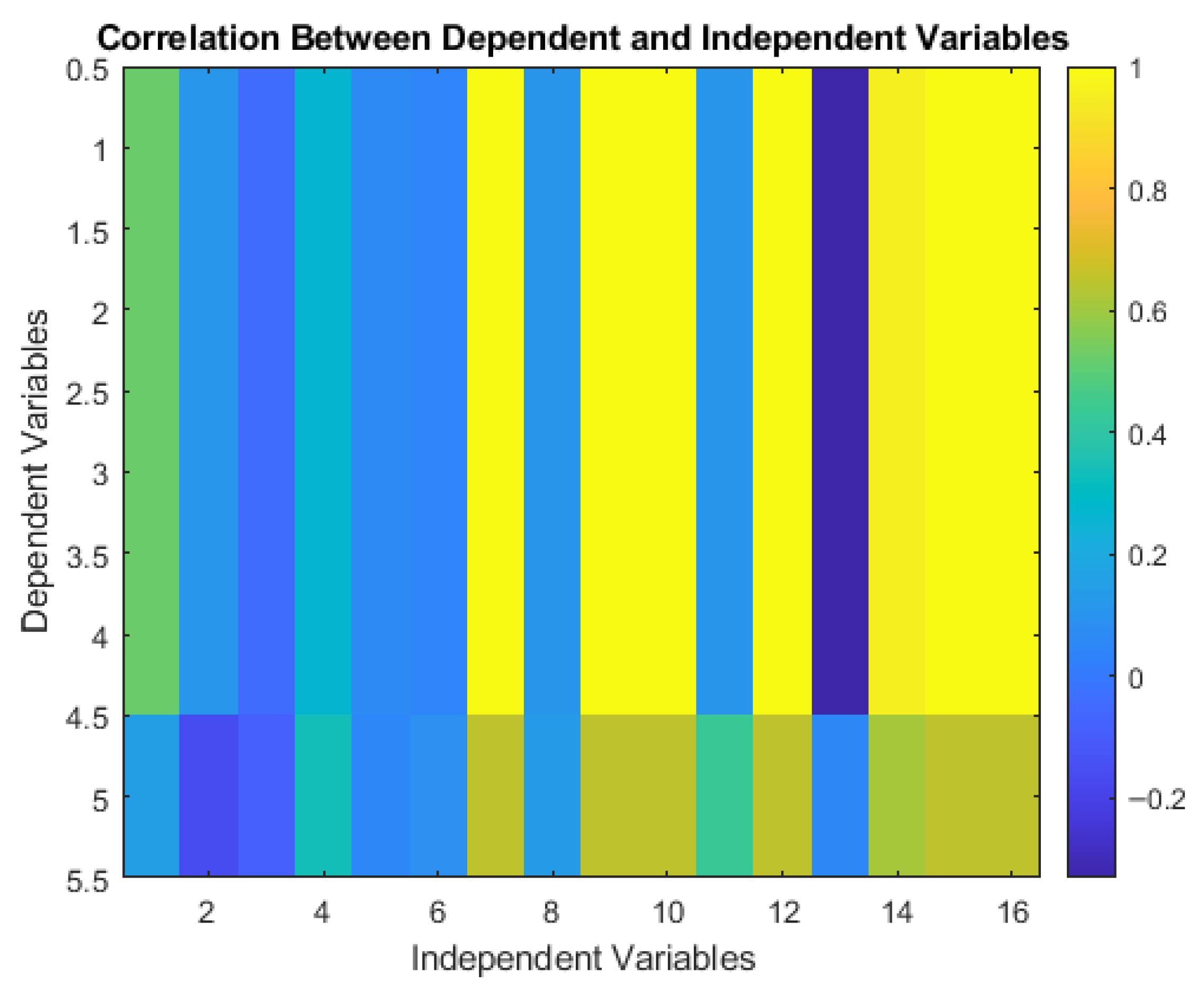
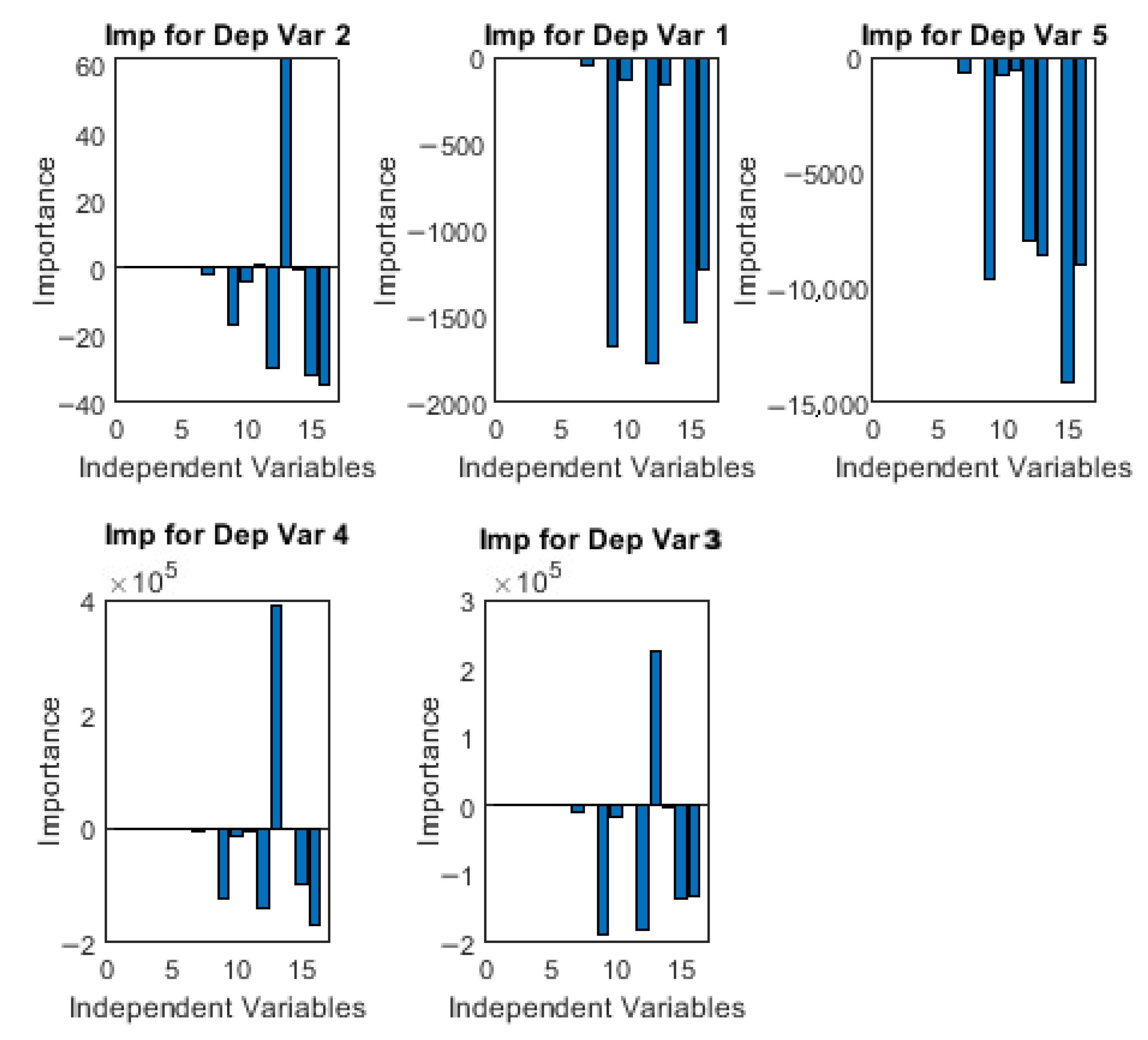
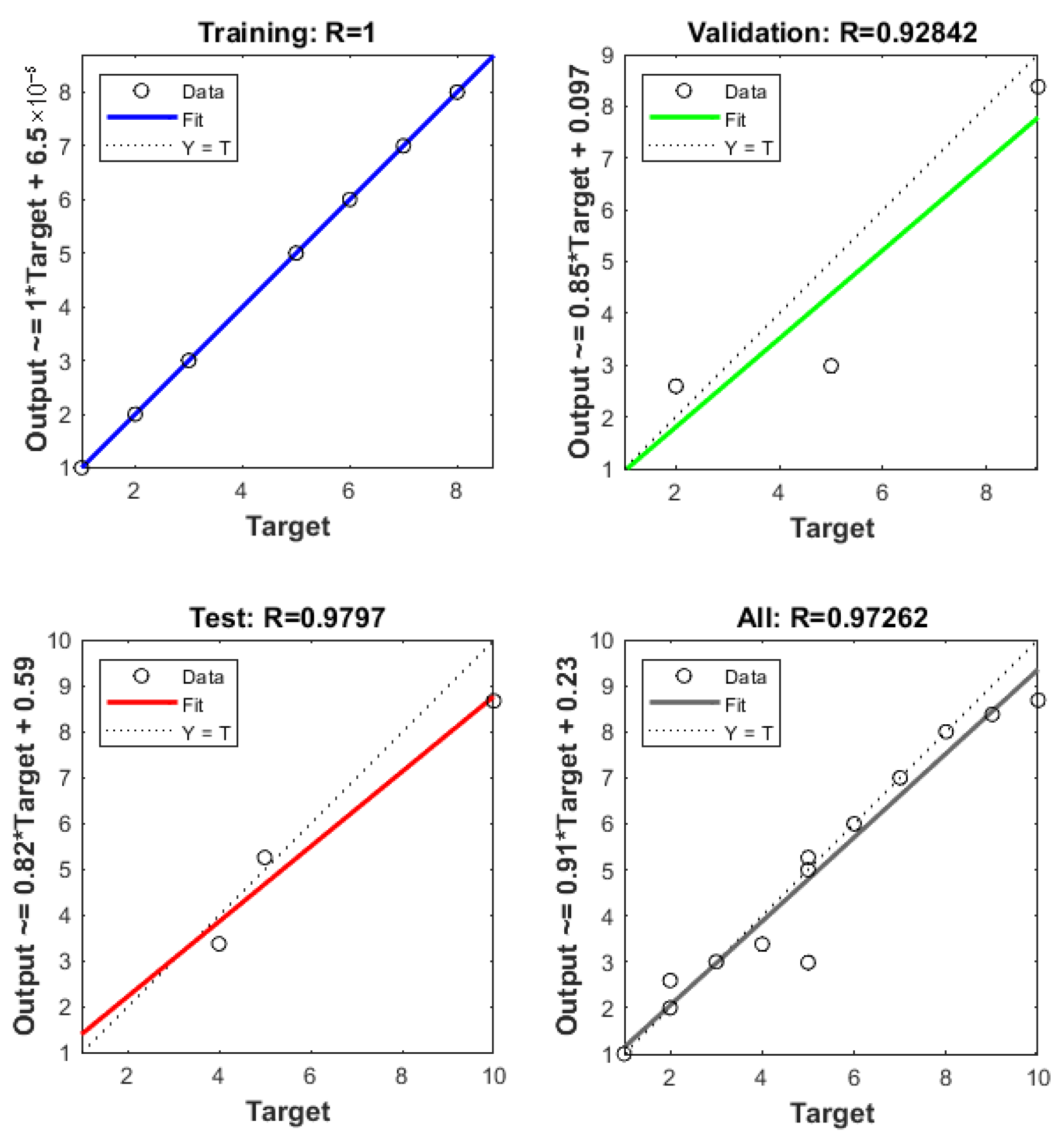
Dependent Variables
Variable	Mean	Standard Deviation
VCO2	1.575	0.238
Ec	0.0095	0.0053
Ww	82.5	9.014
Wp	77.5	9.014
N3	4.5	2.739
Independent Variables
N1	29.33	11.832
N4	4.333	2.146
N5	6.0	0.816
N7	2.667	1.155
N8	2.667	1.155
N9	2.0	0.816
F1	14,250	2752.6
F2	34.167	9.072
F3	1,575,000	45,984
F4	609,796	4249
F5	108,778	2540
F6	171,667	45,038
F7	4,500,000	250,551
F8	4600	545.9
F10	269,474	62,339
F11	174,000	38,720

, the variances amongst independent variables are substantial, reflecting the large range of values in the dataset. For instance, F1’s variance is 6,666,666.7, and F3’s is $6.67\times {10}^3$. Analysis of the two-point correlation reveals a strong positive correlation among most of the first four dependent variables (VCO₂, EC, WW, WP). Table 1 lists the original data provided by the industry.

The first step that we followed in preprocessing this dataset was to check for and handle missing values. Although the provided data appears to be complete, in a real-world scenario, techniques like mean imputation or row deletion to handle any missing entries are often required and we have used these in outlining the original dataset that was MC-simulated. Next, because the variables have vastly different scales (e.g., VCO₂ ranges from 1.2 to 2.0, while F3 ranges from 1.5 M to 1.66 M), it was crucial to standardize the data. We have used the standard process of subtracting each data from the mean and dividing by the standard deviation. Eventual dimension reduction to converge to the top 5 independent variables defining each dependent variable was performed through Random Forest, which was preferred to the Principal Component Analysis due to its better ability to deal with collinearity and non-linearity of the data involved.

2.4. Variable Behavior Analysis

Starting from all possible contributors to the e-waste SCN, after consultation with the industry, many of these were later retracted as “irrelevant” or “redundant” variables for the industry in question, an input based on real-life experiences of the industrial exponents. Once the core set of potential variables (and parameters) were identified, we extracted three stochastically perturbed datasets starting from the original dataset using Monte Carlo Simulations (MCSs). Addressing the stability aspect of the emergent model and risk validation through MCS is the key novelty of this study. If the perturbed states converge to the stable fixed points of the original dataset [3,4], the SCN is regarded as generically stable; if not, we analyze points of instability as functions of specific variables.

2.5. Monte Carlo Simulation (MCS)

Monte Carlo (MC) simulation is a powerful computational technique that is structured on random sampling to model the behavior of complex systems and estimate the probability of different outcomes. The idea relies on identifying an equilibrium system as a maximally chaotic system, a “high temperature” state in the physics parlance, where all concerned atoms and molecules become hyperactive. The probability of finding any such (hyperactive) particle is obtained by weighing the corresponding state with a probability function that is drawn from a Boltzmann distribution [29].

In supply chain modeling, MCS is widely used in quantifying and mitigating the inherent uncertainties that characterize modern global logistics networks. Instead of relying on single-point estimates, Monte Carlo simulations generate a vast number of potential scenarios by sampling from (Boltzmann) probability distributions for key variables, such as customer demand, supplier lead times, transportation delays, and even production yields. The highest temperature state is popularly identified as the steady state when the SCN performance is expected to bear a probabilistic connection to past statistical performance of the SCN. This is the premise on which we build.

Monte Carlo for E-Waste SCN

We used Monte Carlo simulation to perturb the original multidimensional e-waste data from a spreadsheet to introduce stochastic perturbations, enabling the exploration of uncertainty and the generation of perturbed manifolds [30,31]. This was performed using MSExcel Macro and then compared against a MATLAB 2024b code that we wrote for the purpose (available through the GitHub link). The choice was guided by easy accessibility (Macro through the Developer module embedded within Microsoft Excel). While MATLAB is undeniably more robust, it is not so freely available as MSExcel. The approach comprised defining variable probability distributions (we checked both normal and uniform; results were not much different and hence the eventual analysis was performed on normal distribution) for key input variables within Excel (or MATLAB) cells through the NORM.INV(RAND()) operator, then randomizing the input data structure around the mean and standard deviation of the real data distribution function to generate cognate statistics but through varying numerical representations [32]. Each iteration generated a slightly varied dataset, effectively creating a “stochastically perturbed” version of the original. A template MATLAB code is made available through a GitHub link shared under the Data Availability Statement.

This process is particularly useful when the data represents points on a manifold (a high-dimensional surface or structure) and one wishes to understand how noise or uncertainty in the input measurements propagates to the shape or features of that manifold. For our e-waste data that is often sparse or contains inherent measurement errors, perturbing the Excel-based input data through Monte Carlo can generate numerous slightly different manifolds. Analyzing this ensemble of perturbed manifolds allowed for the quantification of uncertainty in the manifold’s geometry, the robustness of features extracted from it, or the sensitivity of downstream analyses to input variability. Apart from providing a more comprehensive risk assessment and a deeper understanding of the system’s behavior under noisy conditions, we used MCS to validate our supply chain kinetic predictions. This is the second novelty of this study.

2.6. Machine Learning Framework

• Feedforward Neural Network (FNN)

Feedforward Neural Networks (FNNs) are a class of artificial neural networks characterized by multiple hidden layers between the input and output layers, enabling them to learn intricate patterns and hierarchical representations from complex data [33]. Each neuron within these layers processes input signals by applying a weighted sum of its inputs, augmented by a bias term, which is then passed through a non-linear activation function. This layered architecture allows FNNs to model highly complex, non-linear relationships that single-layer networks cannot [34]. For a single neuron in a hidden layer, its output, $A_j^{\left(l\right)}$, can be expressed as:

$$A_j^{\left(p\right)}=\sigma {\sum }_{k=1}^{n_{p-1}}{w}_{jk}^{\left(p\right)}{A}_k^{(p-1)}+B_j^{\left(p\right)}$$

(1)

Here $A_k^{(p-1)}$ represents the activations from the kth neuron in the preceding layer (p − 1), $w_{jk}^{\left(p\right)}$ are the synaptic weights connecting the kth neuron in layer (l − 1) to the j-th neuron in layer l, $B_j^{\left(p\right)}$ is the bias term for the jth neuron in layer l, and $\sigma$ denotes the non-linear activation function (e.g., ReLU, sigmoid, tanh).

The “deep” aspect comes from stacking many such layers, where the output of one layer serves as the input to the next. The entire network’s feed-forward process involves sequentially computing activations from the input layer through all hidden layers to the output layer [35]. This is the key reason for our choice. With a complex networked system involving multidimensional variables and parameters comprising an e-waste SCN [21,36], an FNN is perhaps better placed to analyze the nuance and extract the hidden features of the system. During training, the network learnt optimal weights and biases by minimizing a loss function, typically through backpropagation and gradient descent, which adjusts these parameters to reduce the discrepancy between predicted and actual outputs [37].

In the present study, we have used a Feedforward neural network (FNN) characterized by 3 layers in total. There are two hidden layers in the feedforward network, including an input and an output layer. The two hidden layers each have 10 neurons. The number of neurons in the input and output layers depends on the data: for the input layer, the number of neurons equals the number of independent variables, while there is only 1 neuron in the output layer since it is trained on one dependent variable at a time. The infrastructure (code rank_nn.m, available from the GitHub link provided) uses the default activation functions for feedforwardnet, which are a hyperbolic tangent sigmoid transfer function (tansig) for the hidden layers and a linear transfer function (purelin) for the output layer.

Albeit without an explicit optimizer, the network reverts to the Levenberg–Marquardt backpropagation algorithm (trainlm), which is a form of an optimizer. The learning rate is set to 0.01 using net.trainParam.lr = 0.01. The code does not explicitly set a batch size. By default, trainlm uses a full batch training approach, meaning the entire dataset is used for each training iteration. The training has a hard stop after 100 epochs.

b.

Random Forest Network (RFN)

The Random Forest (RF) was chosen as the only Machine Learning module to compare the FNN predictions as it stands out for its inherent robustness, enhanced interpretability, and exceptional proficiency in discerning intricate, non-linear relationships within data [38]. As an ensemble learning paradigm, RF operates by constructing a multitude of decision trees during its training phase. For a given input, the final prediction is derived by aggregating the individual predictions from each of these constituent trees, typically by averaging them [39]. This collective wisdom approach significantly mitigates the perennial problem of overfitting, which is particularly prevalent in high-dimensional datasets, thereby ensuring the model’s strong generalization capabilities [40]. Furthermore, RF offers a reliable mechanism for assessing the importance of individual features, primarily through the permutation importance method. Mathematically, the prediction of an RF model for a given input ‘x’ can be expressed as:

$$\widehat{y}={\displaystyle \frac{1}{B}}{\sum }_{b=1}^B{T}_b\left(x\right),$$

(2)

where B is the number of trees defining the interacting nodes, and $T_b\left(x\right)$ is the prediction of the bth tree. The variable importance score for a feature $X_j$ was calculated as

$$\mathrm{I}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\left(X_j\right)={\displaystyle \frac{1}{B}}{\sum }_{b=1}^B\left(MS{E}_b-MS{E}_{b,j}\right)$$

(3)

Here $MS{E}_b$ is the mean squared error of the bth tree, and $MS{E}_{b,j}$ is the MSE obtained from permuting $X_j$. Variable importance score in RFs enhances the model predictions and interpretability, helps in feature selection, and reduces dimensionality, thus improving the overall performance through identification of the key significant variables for accurate predictions. This method ensures the suitability of RF in identifying key economic players in the analysis of the SCN.

3. Results and Discussions

We have used two major ML algorithms, FNN and RF, for our analysis. We present one Benchmark Case and two perturbed cases in this study. For each case study, the first four figures are obtained from FNN, and the last two figures are obtained from RF.

3.1. Case 1: Benchmark Dataset

Figure 1 represents the correlation between dependent and independent variables of the e-waste supply chain system. A key outcome of this study is the ability to first identify key independent variables controlling the dynamical process and then to quantify their individual and collective contributions. Towards that, independent variables 7 (F1), 9 (F3), 10 (F4), and 12–16 (F6–F8, F10 and F11) are highly sensitive, having most of the complex effects on the dependent variables, except no. 5 which is N3. This means that the correlation between these variables is the strongest, contributing to high system entropy. These are basically the cost variables associated with the largest domino effect on SCN. This points to complexity in the economic sustainability of the business. On the other hand, independent variables 1–6 (N1, N4, N5, N7–N9), 8 (F2), and 12 (F6) are least affected. Despite seasonal dependence, these variables are the least affected because the numbers are often sector independent, that is, they remain the same whatever the choice of company may be. Figure 1 displays correlation strength between variables.

To enumerate the distribution of the independent variables and their strengths, we now implement FNN to identify that the top four dependent variables are VCO₂, Ec, Ww, and Wp (Figure 1 and Figure 2). Further analysis of Figure 2 suggests the same. Although the overall importance of direction is negative, the magnitude conforms to the initial analysis of Figure 1. These results imply that the environmental parameters are highly interconnected as dependent variables that affect the stability of the supply chain system.

The independent variables show mixed correlations with both dependent and other independent variables (Figure 2). For example, F1 is strongly correlated with the dependent variables. The regression analysis obtained from the different phases of FNN (Figure 3) suggests that the model successfully translates the data to a validation point with a regression co-efficient (R²) valued at 0.97, while the same for training, test, and overall process are 0.96, 0.956, and 0.91, respectively. This highlights the efficiency of the algorithm that captures the maximum dimensionality of the dataset and reproduces the same.

Several outliers are visible in Figure 4, which are shown in the error histogram (Figure 4a). The figure is skewed on the right. This suggests that the inherent stochastic nature of the system is prone to shifting its equilibrium from the current stable state with the slightest perturbation, and, hence, is metastable. A similar outcome has been found in our previous work [5].

A key objective of using multiple learning platforms is to compare and optimize their performances. As can be seen, the Random Forest (RF) outputs (Figure 5) are in partial agreement with the FNN results. While the top three dependent variables in this case are Y1, Y3, and Y4, i.e., VCO₂, Ww, and Wp, Y2 here is the least important, which is Ec and Y5 is the second least important, i.e., N3. These results are somewhat the result of overestimation of the Random Forest algorithm, as in reality, Y2, i.e., energy consumption, is one of the sensitive parameters in the system [16]. However, given that the e-waste recycling plant considered was primarily engaged in mechanical recycling, they will experience a largely consistent consumption of energy. Our evaluation points to RF as a valid optimizing platform. In addition, the identification of the key environmental parameters as tuning parameters gives a strong operational handle to the SCN.

The RF algorithm takes things one step further with the estimation of the highest contributors (independent variables) to the top dependent variables. This is elucidated in Figure 6a–d. In other words, RFN determines the interdependence between the variables. This highlights the degree of complexity of the SCN. For Y1, i.e., VCO₂, the top contributors are X11 (F5), X8 (F2), X7 (F1), X2 (N4), and X12 (F6), respectively. These are labor salaries, unit cost of energy used, CO₂ recovery, recycled items, and awareness activities. In other words, these are environmental, economic, and social parameters, which highlight that CO₂ recovery is co-dependent on recycling efficiency, technological advancements (corroborating to the economic parameters), and awareness level. As ESG reporting has become mandatory for most large corporations, this is expected to be a critical component in identifying and measuring scope 1 and scope 3 emissions of the supply chain network [41]. For Y3, i.e., Ww, the top contributors are X1 (N1), X14 (F8), X10 (F4), X11 (F5), and X8 (F2), respectively. These are labor count, operation cost, cost of water treatment, labor cost, and energy cost. These cost variables are primarily linked to the operational aspects of the dependent variable Ww, which is the wastewater treatment. This suggests that the operational efficiency of the processes dictates sustainability. In case of Y4, i.e., Wp, the top contributors are X1 (N1), X11 (F5), X7 (F1), X9 (F3), and X8 (F2), respectively. These are labor count, labor salary, cost of CO₂ recovery, cost of water, and cost of energy. The significance is that the associated top variables are social and economic parameters that directly affect operations related to water as Wp is water consumed. On the other hand, for Y5, i.e., N3, the top contributors are X4 (N7), X2 (N4), X11 (F5), X5 (N8), and X1 (N1), respectively. These refer to the logistics involved, recycled items, labor cost, waste materials going to TSDF, and labor count. As N₃ identifies awareness and marketing activities, the emergence of cost components related to labor and logistics are justified. Although the emergence of N4 and N8 was unexpected, their dependency in terms of environmental sustainability is somewhat justified. As can be seen, other than N₃, the energy cost is common to all top dependent variables. This irrevocably points to the fact that all these operations consume a minimum (not nonzero) amount of energy. These results differ from FNN outputs while revealing more intricate details.

3.2. Case 2: Perturbation in F4

While Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 give us a quantitative handle on individual contributions from the dimensionally reduced model, since many of these are interrelated variables, their mutual correlations could offset the equilibria. Figure 7 represents the correlation between dependent and independent variables of the considered e-waste supply chain system with F4 inducing fluctuations. Independent variables 7 (F1), 9 (F3), and 12–16 (F6–F8, F10 and F11) are highly sensitive, having most of the complex effect to the dependent variables, except no. 5 which is N3. These independent variables are cost components that are similar to the base case, suggesting the dependence of economic sustainability on the business. On the other hand, independent variables 1–6 (N1, N4, N5, N7–N9), 8 (F2), 10 (F4), and 11 (F6) are least affected. Although inherently time-dependent, these variables are least affected by perturbations because for most companies, the unit numbers remain unchanged. Surprisingly, the results suggest that F4, which is the variable we have perturbed here, is the least affected. However, in the benchmark case, F4 was a sensitive variable. This change in the system is pushing the SCN towards a more equilibrium state rather than forcing it out of it, as one would expect.

From Figure 8, the top four dependent variables are clearly seen as Ww, N3, Wp, and Ec. Although the overall importance of direction is negative, the magnitude confirms this initial analysis. These results imply that not only the environmental parameters, but also social parameters are highly interconnected dependent variables that determine the equilibria of the supply chain system.

The regression analysis obtained from the different phases of FNN (Figure 9) suggests that the model successfully translates data to a validation point with a regression co-efficient (R²) of 0.95 while the same for training, test and overall process are 0.99, 0.96, and 0.94, respectively, which are not too different from Figure 4. Once again, the efficiency remains unaltered.

Some outliers are visible in Figure 10 which are outlined in the error histogram, depicted in Figure 10a, which is right-skewed. This suggests that the inherent stochastic nature of the system is prone to shifting its equilibrium from the current stable state with the slightest nudge. A similar outcome has been found in our previous work and consistent with the benchmark case [5]. Figure 10b illustrates a successful training process with the model achieving its best performance on validation data at epoch 3.

As can be seen from Figure 11, the Random Forest (RF) outputs, all dependent variables have equal mean importance, which means either the algorithm is overpredicting or the system is exceptionally stable. The latter represents a utopian scenario and hence it is more legitimate to consider the overpredictive nature of the RF algorithm. A similar case of overprediction was found in our previous work with PCA [16].

As demonstrated in Figure 12a–e, the RF algorithm takes things one step further with the estimation of the highest contributors (independent variables) to the top dependent variables. In other words, RFN determines the interdependence between the variables. For Y1, i.e., VCO₂, the top contributors are X11 (F5), X14 (F7), X1 (N1), X10 (F4), and X8 (F2), respectively. These variables represent the number of operations, revenue earned from recycled materials, labor count, cost of wastewater treatment, and cost of energy. As can be seen, this is a mixture of environmental, economic, and social parameters, which highlights that CO₂ recovery is dependent on both operational efficiency as well as costs of operations. For Y2, i.e., Ec, the top contributors are X11 (F5), X14 (F7), X15 (F10), X10 (F4), and X13 (F6), respectively. As before, these represent the number of operations, revenue earned from recycled materials, cost of logistics, cost of wastewater treatment, and cost of awareness activity and marketing. These are mostly cost variables associated with energy consumption. For Y3, i.e., Ww, the top contributors are X10 (F4), X1 (N1), X16 (F11), X11 (F5), and X7 (F1), respectively. These are recycled materials, labor count, cost of disposal in TSDF, labor salaries, and cost of CO₂ recovery. This highlights that economics plays the key role in case of wastewater treatment. For Y4, i.e., Wp, the top contributors are X1 (N1), X11 (F5), X10 (F4), X9 (F3), and X8 (F2), respectively. These are labor count, labor salaries, cost of wastewater treatment, cost of water used, and cost of energy. As can be seen, these are mixtures of social and cost parameters. This is logically supported as water usage will always be linked to both water treatment as well as the cost of energy. On the other hand, for Y5, i.e., N3, the top contributors are X4 (N7), X10 (F4), X11 (F5), X1 (N1), and X2 (N4), respectively. These represent logistics, cost of wastewater treatment, labor salaries, labor count, and recycled items. As can be noticed, these are socio-economic parameters suggesting their effect on awareness level. As can be seen, other than Ec, the labor count or the labor cost is common in top dependent variables. This is achieved with a perturbed F4, and wastewater treatment is labor-intensive.

3.3. Case 3: Perturbation in F7

Figure 13 represents the correlation between dependent and independent variables of the considered e-waste supply chain system. Independent variables 7 (F1), 9 (F3), 10 (F4), 12 (F6), and 14–16 (F8, F10 and F11) are highly sensitive, having most of the complex effect on the dependent variables, except no. 5 which is N3. These independent variables represent cost components like the two previous cases confirming the role of economics in business sustenance. On the other hand, independent variables 1–6 (N1, N4, N5, N7–N9), 8 (F2), 10 (F4), and 12 (F6) are least affected. However, the green bar suggests that variable 1, i.e., N1 (labor count), has significant effect on lead dependent variables. This not only confirms that social parameters such as N1 may affect business sustainability, which is in line with the inaugural study [5,28], this also tells us how much their relative contributions are.

Figure 14 compares the relative contributions of the dependent variables in the composition of the model. The top 3 dependent variables are Ec, Ww, and Wp. Positive values for these three dependent variables suggest that they have a significant effect on the e-waste supply chain. Considering a Material Recovery from E-waste (MREW) plant aimed at recovering metals both via mechanical and chemical route [42], energy consumption is going to be the most important parameter [16]. In this case, the perturbed variable is F7, which is the revenue earned from selling the recycled materials recovered via e-waste treatment. Since the majority of the economic sustenance of any e-waste recycling plant is plowed upon the material recovery efficiency and its market price, the results reconfirm the need for analyzing the stability of the model against market fluctuations in energy usage. As the results clearly depict that E_c is the most important variable here and the perturbed variable being F7, which is linked to the economic sustainability of the system, the need for optimization emerges as the most important variable. These findings are consistent with the other experimental literature [28].

The regression analysis (Figure 15) obtained from the different phases of FNN suggests that the model successfully translates the data to a validation point with a regression co-efficient (R²) of 0.93 while the same for training, test, and overall process are 1, 0.98, and 0.97, respectively. Once again, the error margins follow Figure 4 and Figure 9.

A few outliers can be found in Figure 15 and are captured in the error histogram and depicted in Figure 16a, which is right-skewed. This suggests the inherent stochastic nature of the system, which is prone to shifting its equilibrium from the current stable state. A similar outcome has been found in our previous work [5]. Figure 16b illustrates a successful training process with the model achieving its best performance on validation data at epoch 4.

As can be seen in the Random Forest (RF) outputs (Figure 17), all dependent variables have equal mean importance, which means either the algorithm is overpredicting or the system is exceptionally stable. The latter being another utopian scenario, it is more appropriate to consider the overpredictive nature of the RF algorithm. A similar case of overprediction was found in our previous work using PCA [16]. Surprisingly, this configuration apparently suggests greater system stability. This is unlikely, though, because probabilistically, unless the system is close to a global attractor, a perturbation is more likely to throw a system away from (metastable or unstable) equilibrium. A recent study has identified such a state as a pseudo steady state [43]. This can be treated analogous to the concept of steady state multiplicity existing in the chemical engineering discipline, where multiple steady states can coexist [44,45].

The RF algorithm takes things one step further with the estimation of the highest contributors (independent variables) to the top dependent variable (Figure 17 and Figure 18a–e). For Y1, i.e., VCO₂, the top contributors are X11 (F5), X14 (F7), X1 (N1), X10 (F4), and X8 (F2), respectively. For Y2, i.e., Ec, the top contributors are X11 (F5), X14 (F7), X15 (F10), X10 (F4), and X13 (F7), respectively. For Y3, i.e., Ww, the top contributors are X10 (F4), X1 (N1), X16 (F11), X11 (F5), and X7 (F1), respectively. In the case of Y4, i.e., Wp, the top contributors are X1 (N1), X11 (F5), X10 (F4), X9 (F3), and X8 (F2), respectively. On the other hand, for Y5, i.e., N3, the top contributors are X4 (N7), X10 (F4), X11 (F5), X1 (N1), and X2 (N4), respectively. These RF results differ from FNN outputs while revealing more intricate details.

4. Conclusions

This study combined the deep learning recess of Deep Neural Network (DNN) with a Random Forest Network (RFN) for extraction of relevant features from the dataset. Both models were effective in unmasking underlying patterns within the perturbed supply chain system, which our earlier approaches [5,16] were unable to predict. For the benchmark case, both FNN and RFN extracted identical patterns; however, in most cases, FNN outperformed RFN. The superior performance of FNN can be attributed to its ability to associate latent interactions and stratify information across kernels which are beyond the capability of RFN. This enables a nuanced dimension for deciphering and understanding the supply chain behavior. However, direct interpretability was sometimes overshadowed due to outliers leading to poor regression co-efficients.

On the contrary, the RFN was unable to clearly capture the effect of the dependent variables. Despite this, RFN could provide insights into the independent variables in the simulated uncertainty scenarios. Specifically, the effect of perturbing quasi-steady variables was more clearly captured in some cases. However, there were multiple scenarios where RFN overpredicted due to complex interdependencies among the variables.

The juxtaposition of these two models reveals a trade-off between predictive power and interpretability. While the FNN served as a potent tool for uncovering hidden complexity and emergent behaviors, the RFN proved invaluable for feature engineering, scenario simplification, and system pruning. This complementary use reinforces the importance of hybrid modeling approaches in supply chain analytics—particularly in domains characterized by uncertainty, feedback, and evolving equilibria, such as e-waste management networks. Note, the platform outlined is sufficiently generic to be repurposed beyond the present data regime and can be used to analyze different SCNs. With the help of the developed methodology, the uncertainties along the supply chain can be identified along with their contributions in system perturbation, more in the form of predictive analytics, which will be essential for strategic decision making.

This study had the challenge of sparse data: only 18 samples against 21 variables. To address this, first, we trial-tested a feedforward neural network against a Random Forest prediction. The second risk validation was ensured through the Monte Carlo procedure itself. While the GitHub link will show only six datasets for each ML/DL algorithm, each of these datasets were obtained using stochastic ensemble-averaging over 24 realizations, thus largely obfuscating the dependence on skewed statistics. Admittedly, extremal values may still exhibit “finite sized effects”, but given basic conformity between the two independent ML/DL approaches, we are reasonably confident about the results.

Despite this long list of positives, the study has certain limitations, specifically concerning the trade-off between predictivity and interpretability. While FNN dominates the predictivity aspect, it displays poor interpretability performance. Conversely, RFN is more interpretable for independent variables but fails to provide relevant information about complex interdependencies of the e-waste SCN, often overpredicting. Another problem is the sensitivity towards the outliers, which needs to be tackled individually and subjectively. There is no generic panacea, but some of these issues could be better handled through enhanced hybrid models, a future target spanning multiple diverse datasets.