Vertical Vibration Analysis in Metro-Adjacent Buildings: Influence of Structural Height, Span Length, and Plan Position on Maximum Levels
Abstract
1. Introduction
2. Methodology
3. Field Measurement of Metro-Induced Vibration
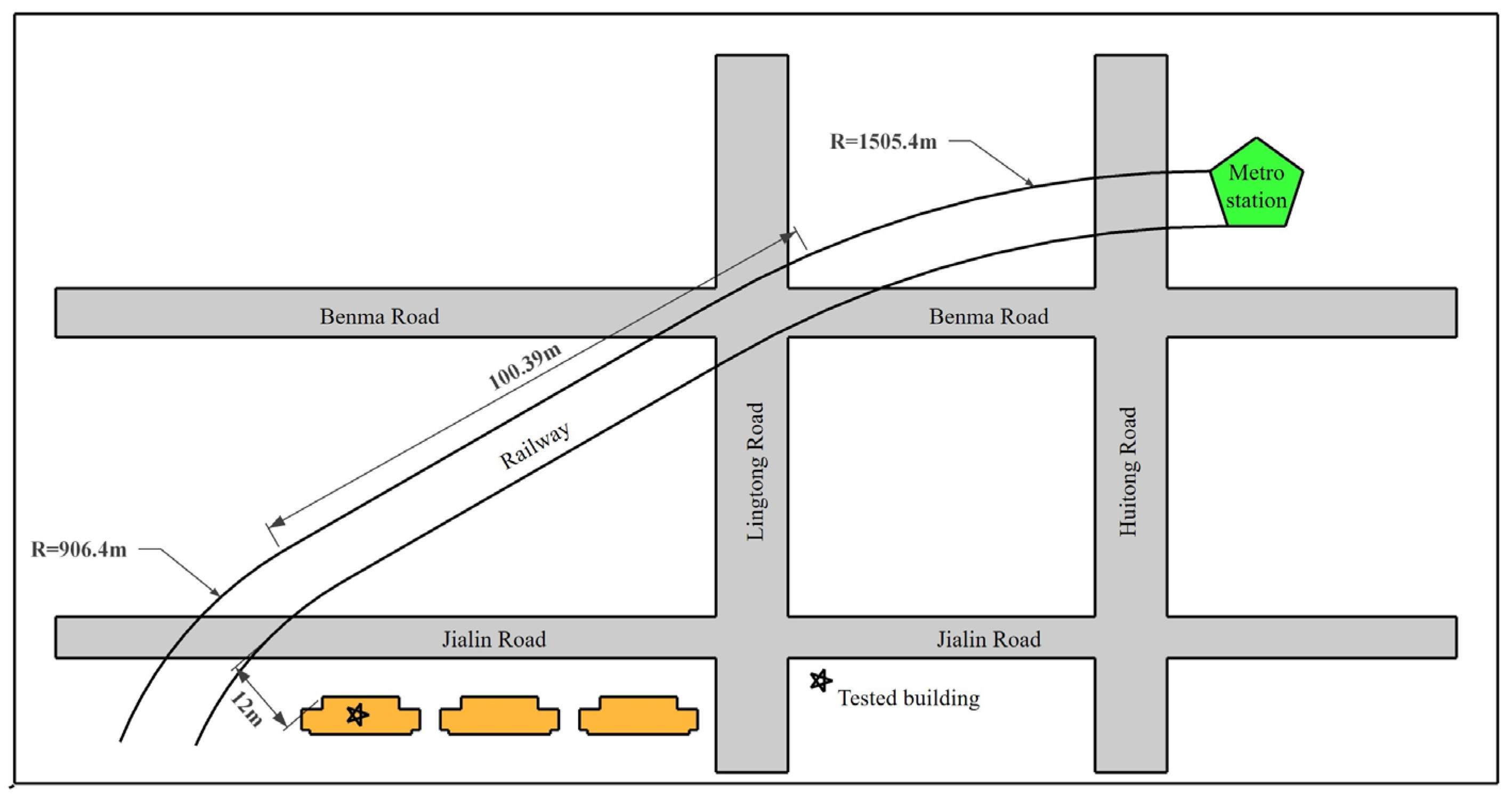
3.1. Geological Conditions
3.2. Instrumentations and Signal Processing
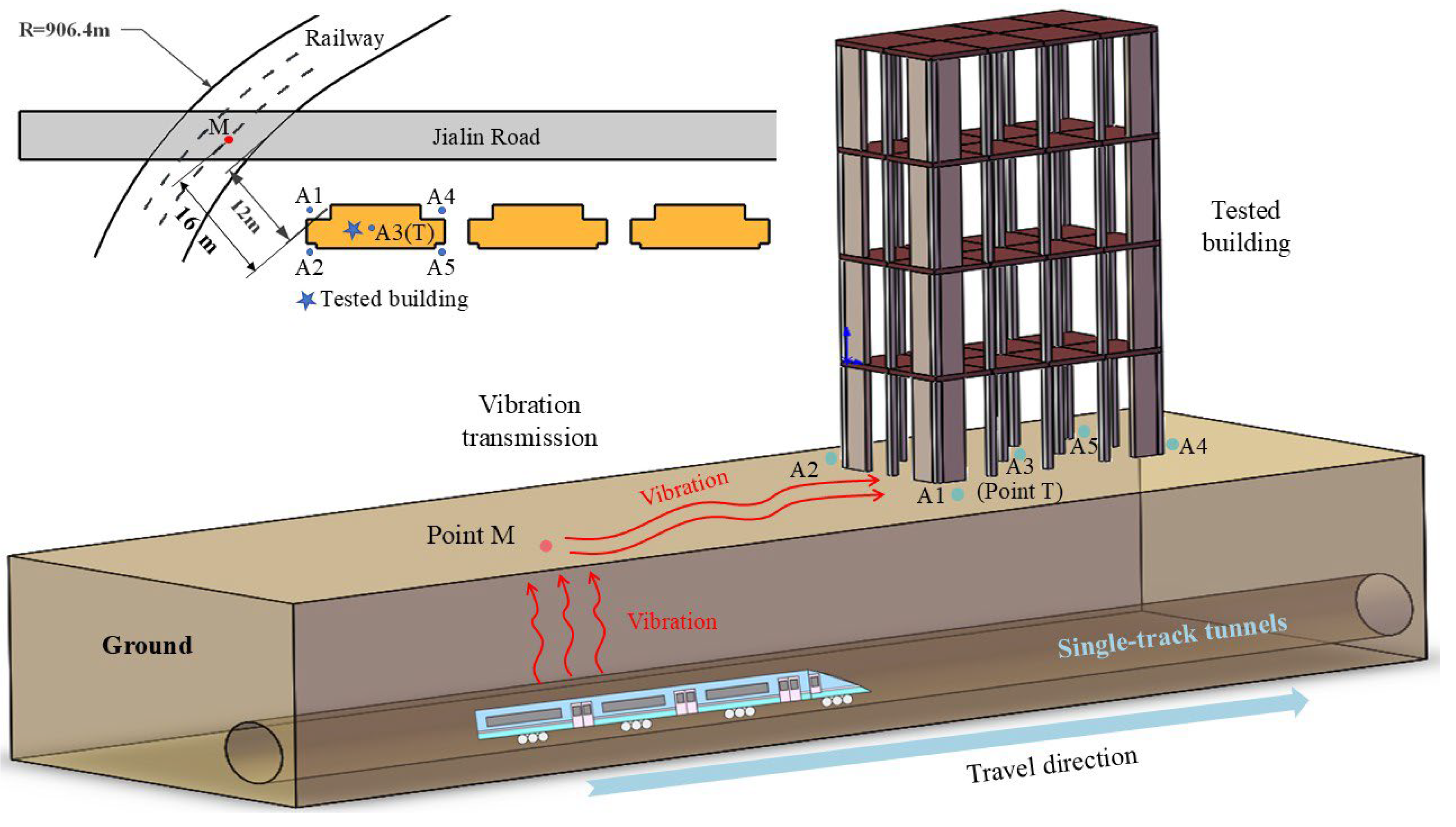
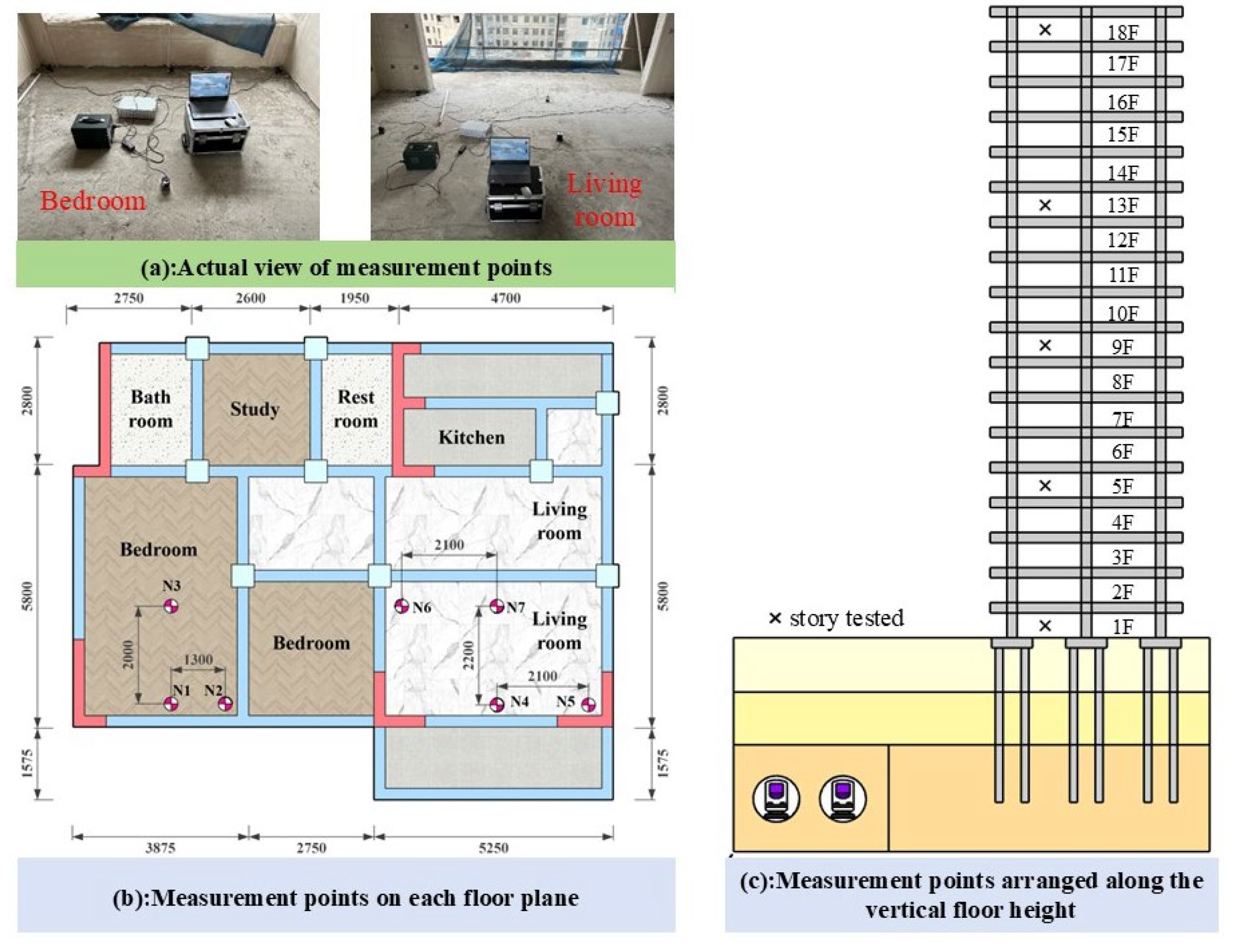
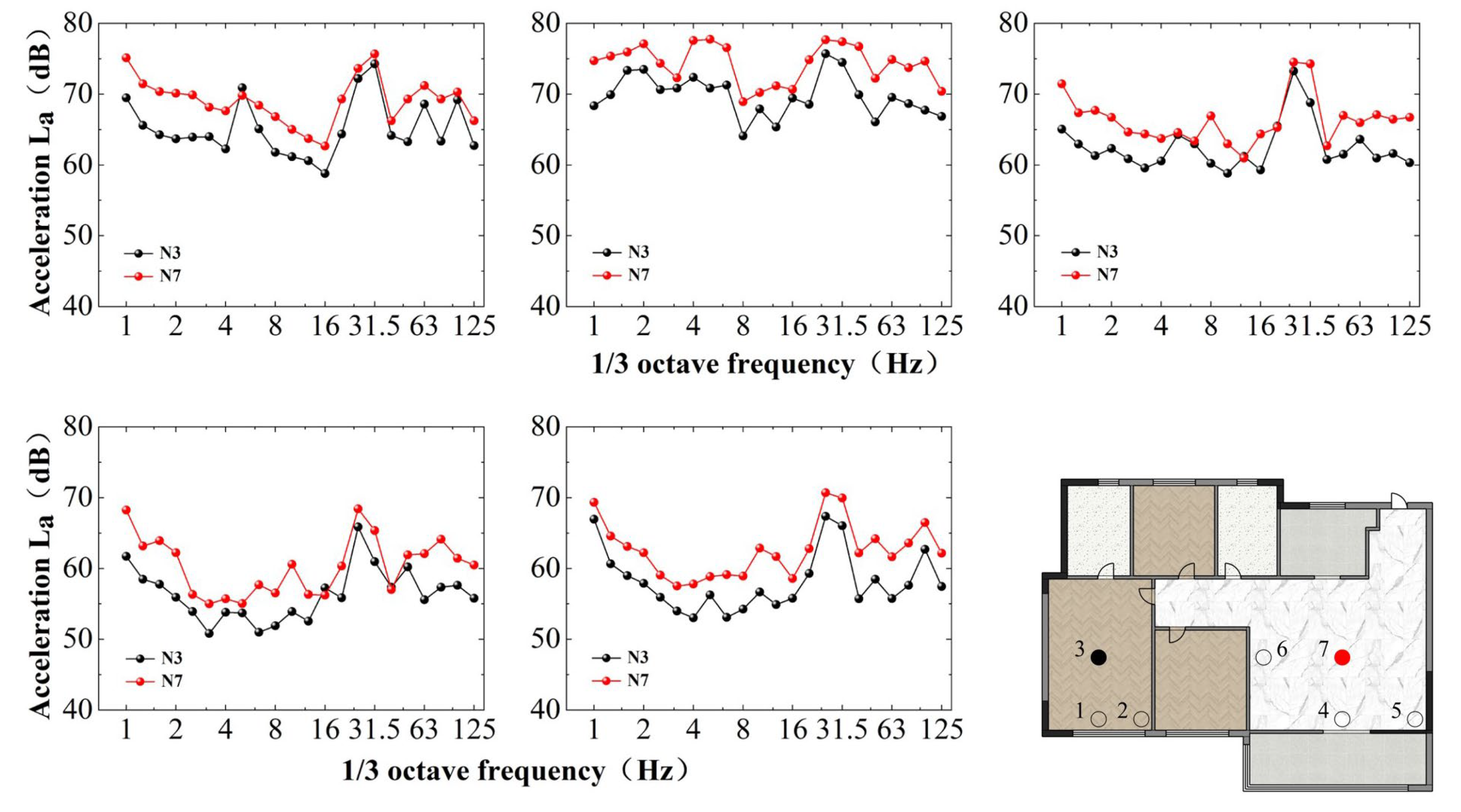
3.3. Measuring Points
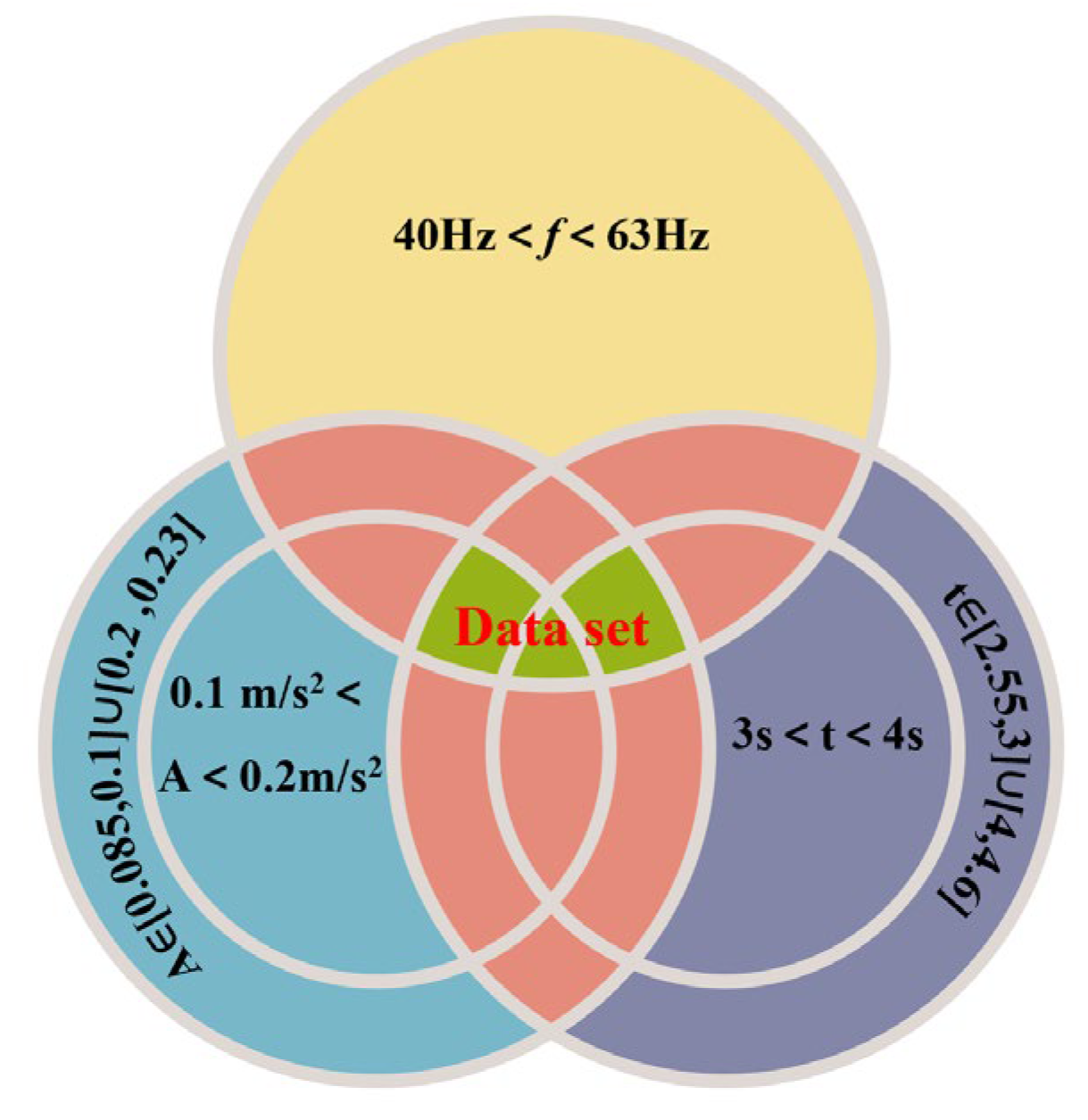
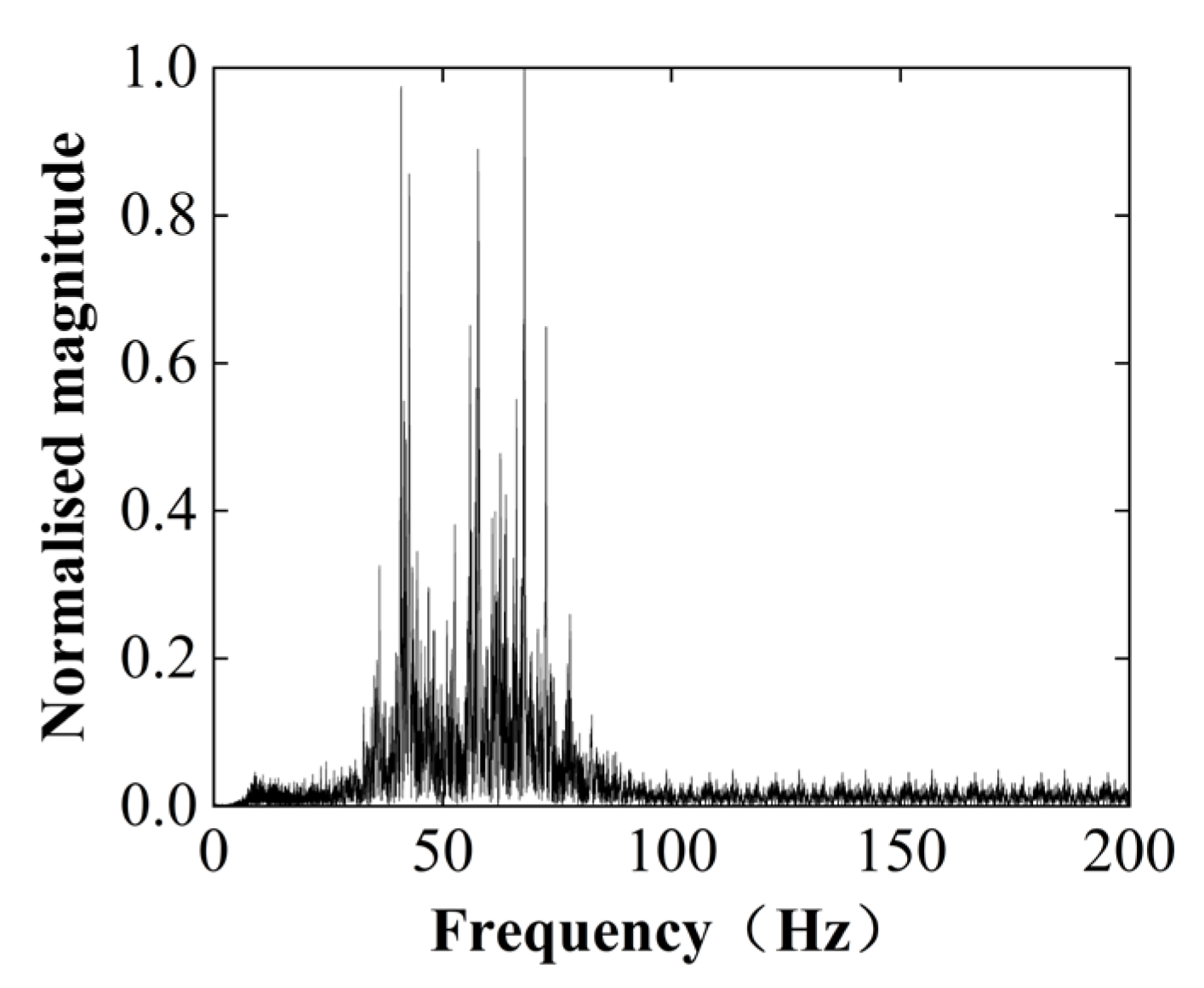
3.4. Characteristics of Vibrations Obtained by Machine Learning
4. Maximum Vertical Vibration Levels
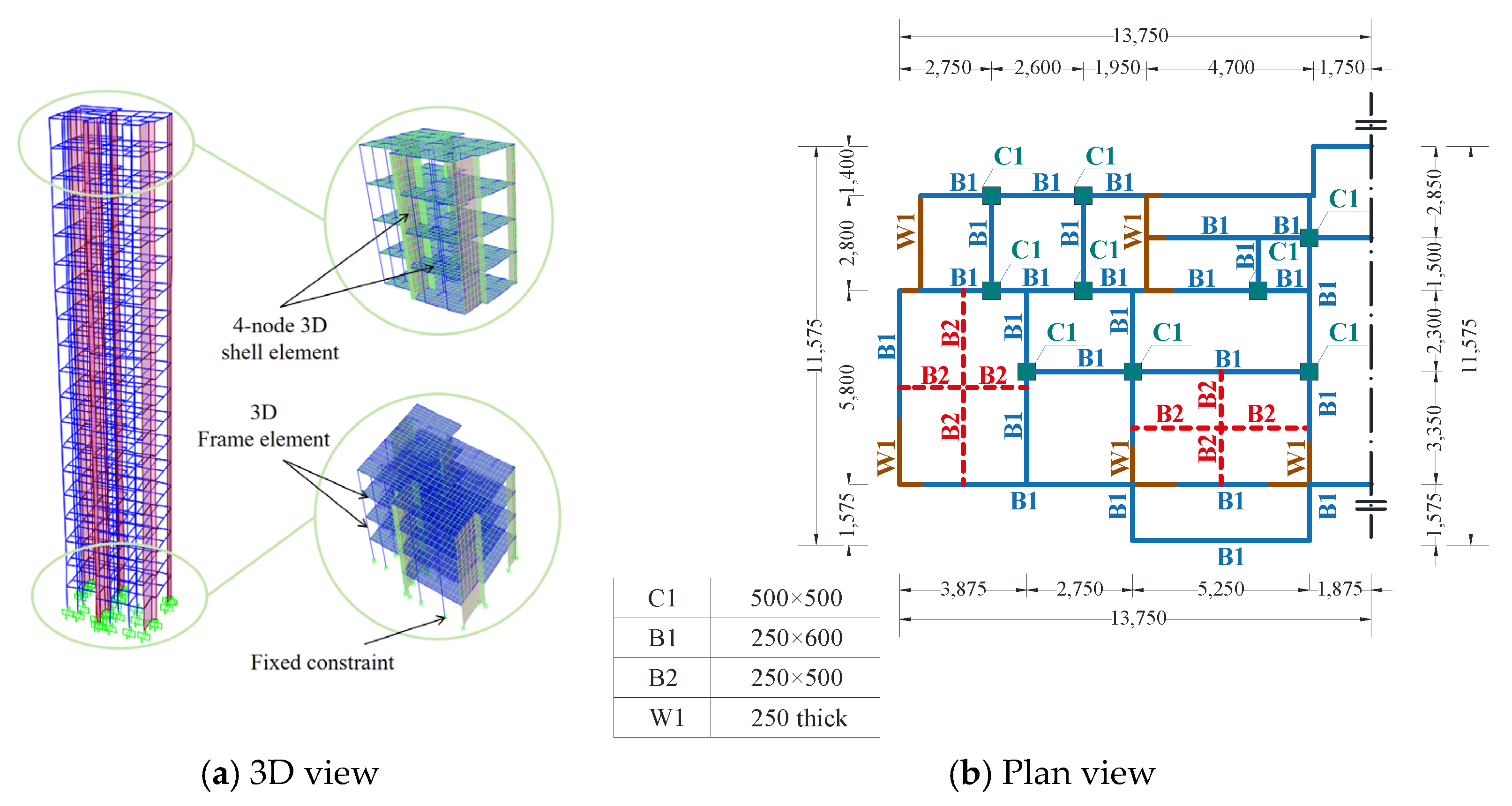
4.1. Finite Element Modeling
4.2. Validation of the Model
4.3. Evaluation of Vibration Input
4.4. Results and Analysis
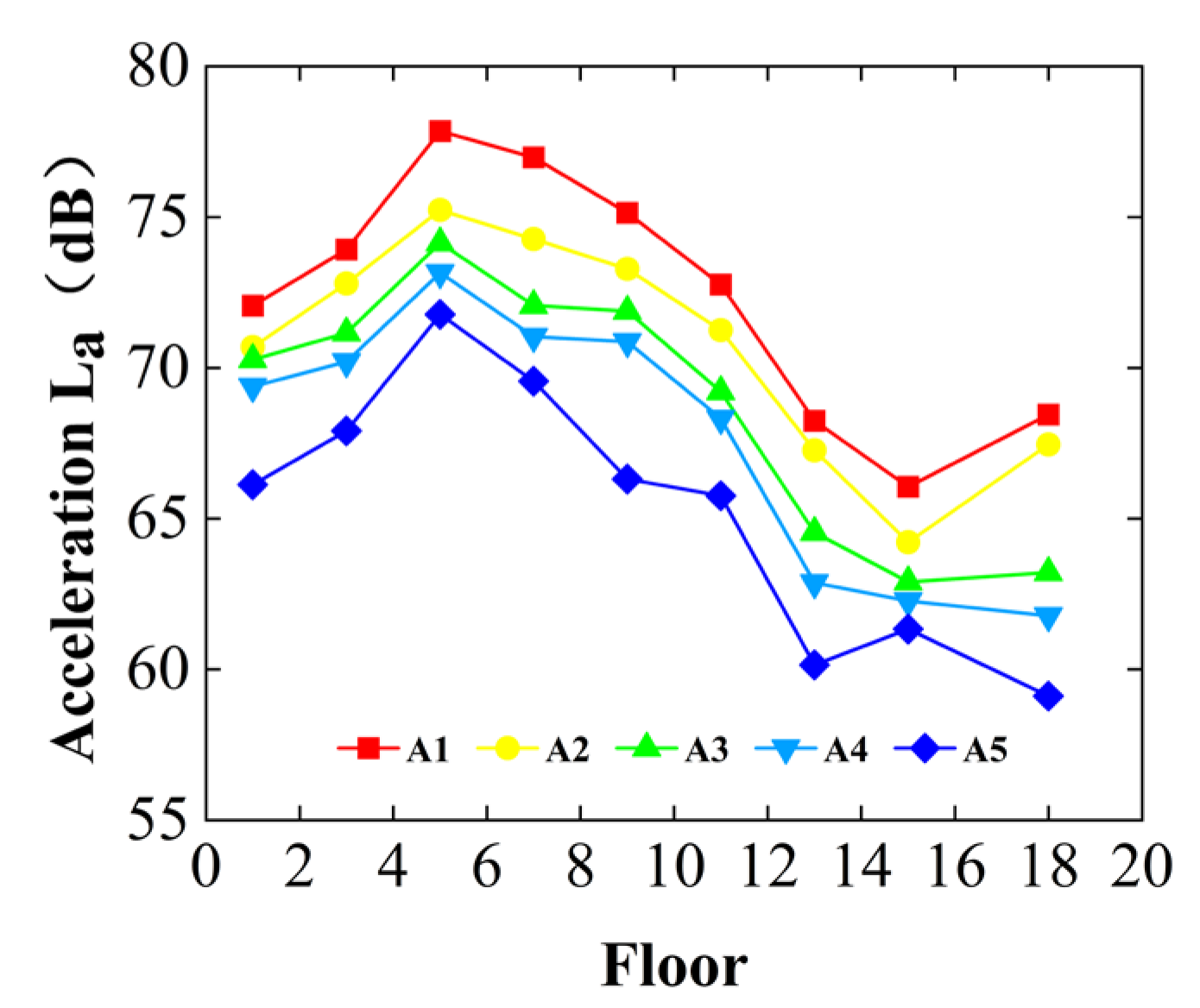
4.4.1. Vertical Vibration Level Results for Different Heights
4.4.2. Vertical Vibration Level Results for Different Structural Members
4.4.3. Vertical Vibration Level Results for Different Spans
5. Validation of Factors Affecting Maximum Vertical Vibration Levels
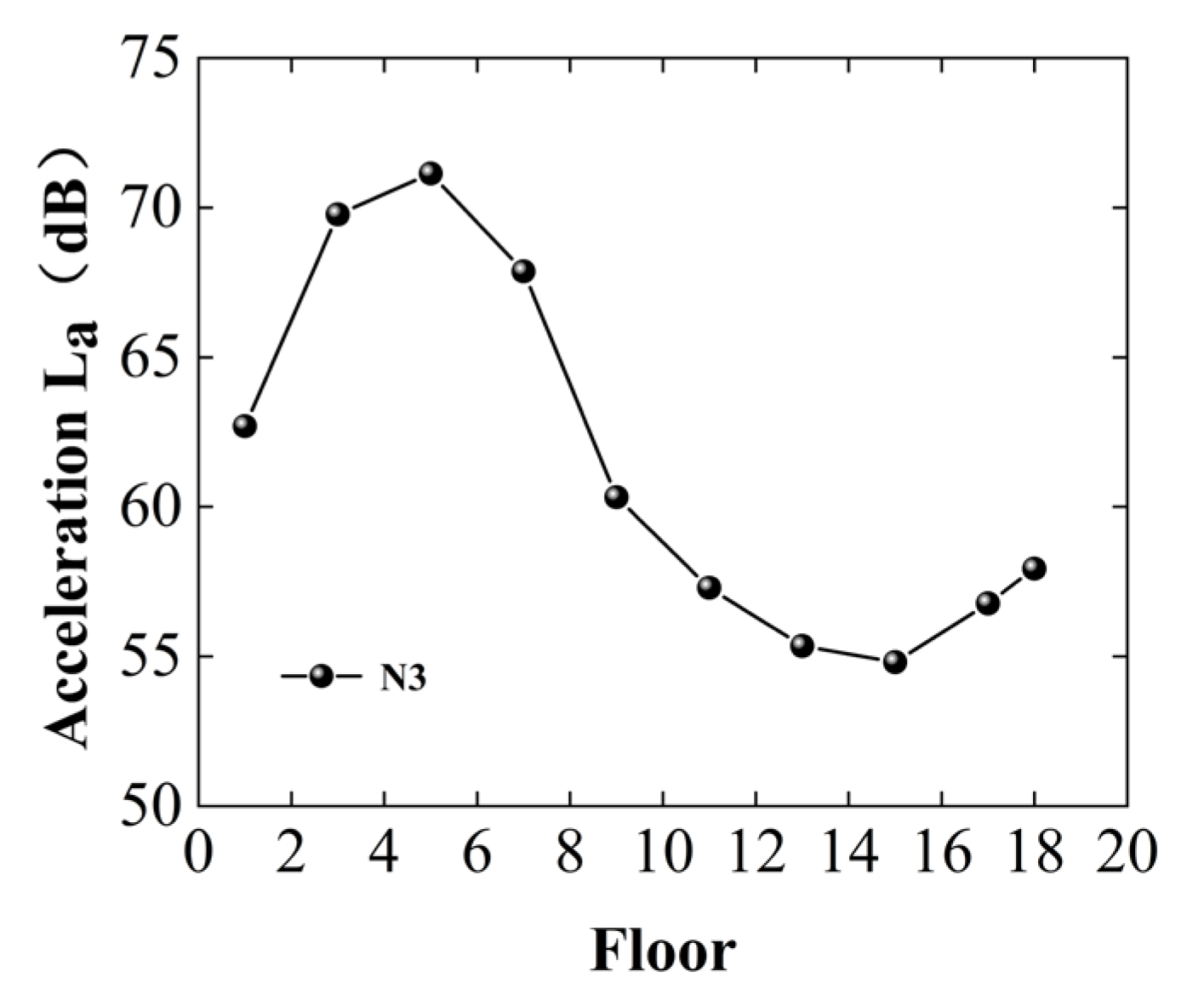
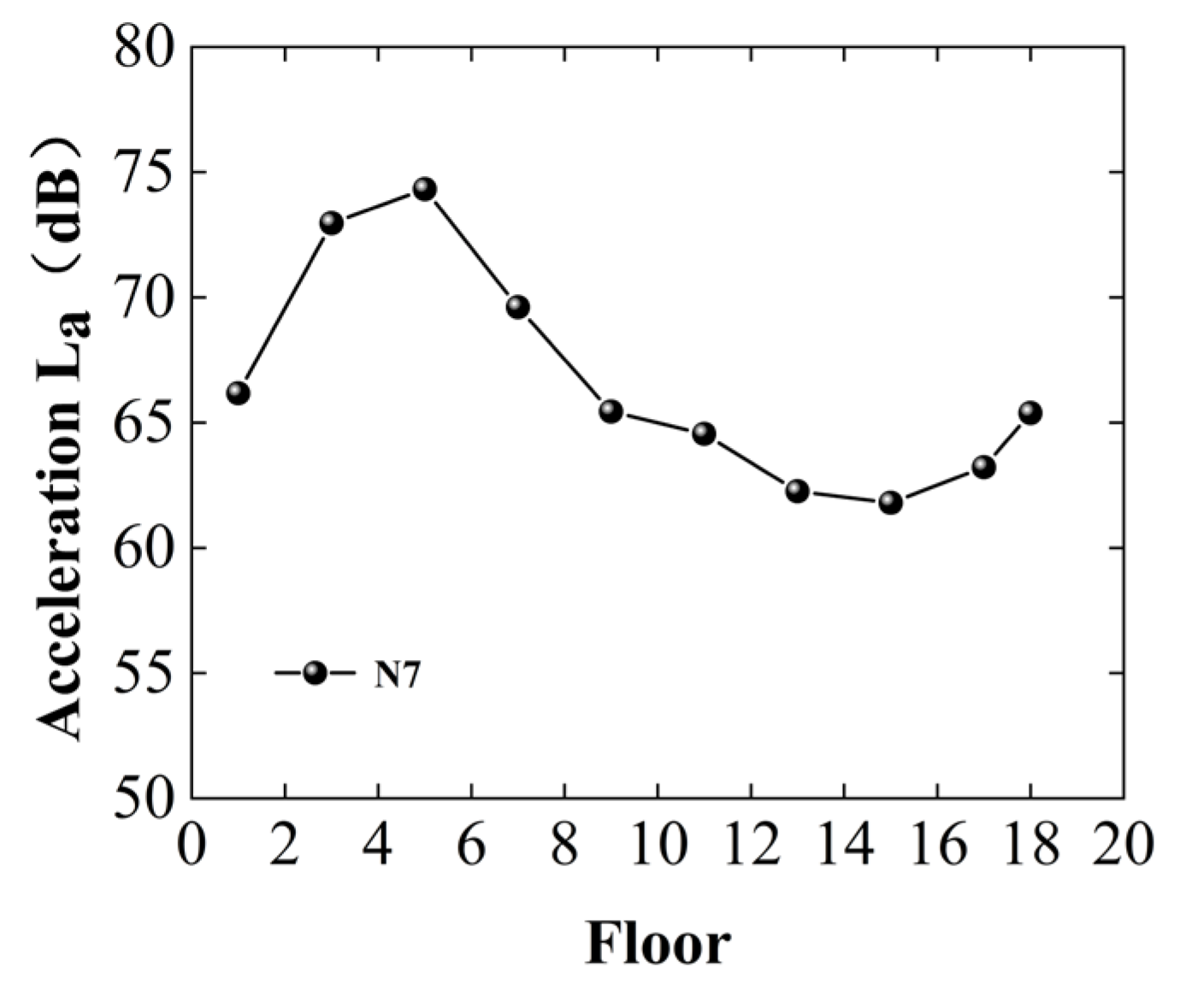
5.1. Influence of Height on Vertical Vibration Levels
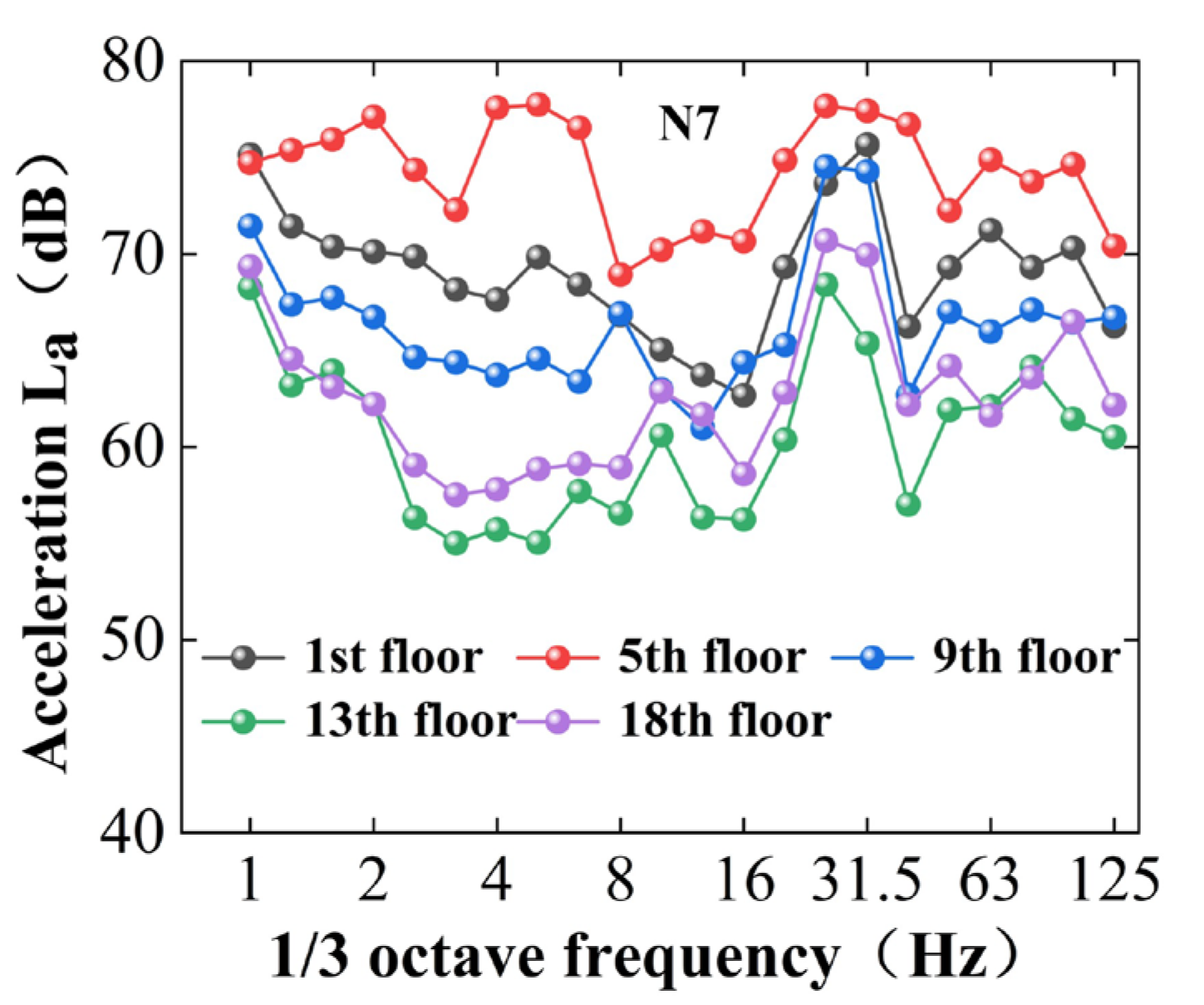
5.2. Influence of Structural Component Types on Vertical Vibration Levels
5.3. Influence of Span Length on Vertical Vibration Levels
6. Conclusions
- (1)
- A novel vibration filtering method based on machine learning is proposed to efficiently and accurately capture representative data that reflects the ground vibration characteristics. The decision tree thresholds (40–63 Hz, 0.1–0.2 m/s2, 3–4 s) were statistically validated against field data. Future work will optimize thresholds for varied soil types. The method first filters out data exhibiting significant anomalies by analyzing the vibration characteristics. It then removes abnormal vibration data caused by irregularities in the propagation path. The results of finite element simulations using the filtered data demonstrate strong agreement with actual measurements.
- (2)
- The maximum vertical vibration level in a tall building typically increases initially with height and then decreases. The location of the highest vibration levels typically occurs at approximately one-quarter to one-third of the total height of the building. Additionally, a localized amplification phenomenon is observed on the top two floors. However, the study’s conclusions are based on measured and simulated data from an 18-story shear wall–frame structure under specific geological conditions. The site geology primarily consists of highly and moderately weathered quartz diorite conglomerate, which exhibits high stiffness and vibration sensitivity. Furthermore, the observed vibration patterns, such as amplification effects at specific heights, may differ in other structural systems, including steel frames and composite structures.
- (3)
- Different structural components exhibit varying maximum vertical vibration levels within the same floor. Compared to shear walls, floor slabs have a more significant effect on vibration levels. Vibration levels are higher at the center of the slab than at the edges. Furthermore, the effect of metro-induced vibrations on buildings is strongly correlated with the span length of structural elements, with larger span elements exhibiting more pronounced vibration levels at their measurement points. For critical structural points, targeted renovations should be implemented to extend the building’s service life. This is key to creating a city that conserves resources.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zou, C.; Wang, Y.; Wang, P.; Guo, J. Measurement of ground and nearby building vibration and noise induced by trains in a metro depot. Sci. Total Environ. 2015, 536, 761–773. [Google Scholar] [CrossRef] [PubMed]
- Sheng, T.; Liu, G.B.; Bian, X.C.; Shi, W.X.; Chen, Y. Development of a three-directional vibration isolator for buildings subject to metro-and earthquake-induced vibrations. Eng. Struct. 2022, 252, 113576. [Google Scholar] [CrossRef]
- Liang, Q.; Luo, W.; Zhou, Y.; Lu, Z.; Li, J.; He, Z. Vibration filtering effect of a novel three-dimensional isolation bearing on metro vibration isolation. Eng. Struct. 2024, 301, 117304. [Google Scholar] [CrossRef]
- Xie, W.; Hua, Y. Structural Vibration Comfort: A Review of Recent Developments. Buildings 2024, 14, 1592. [Google Scholar] [CrossRef]
- Farahani, M.V.; Sadeghi, J.; Jahromi, S.G.; Sahebi, M.M. Modal based method to predict subway train-induced vibration in buildings. Structures 2023, 47, 557–572. [Google Scholar] [CrossRef]
- ISO 2631-2:1989; Evaluation of Human Exposure to Whole-Body Vibration—Part 2: Continuous and Shock-Induced Vibration in Buildings (1 to 80 Hz). International Organization for Standardization: Geneva, Switzerland, 1989.
- Ministry of the Environment Government of Japan. Vibration Regulation Law. Japan. 1997. Available online: https://www.env.go.jp/en/laws/air/vibration/index.html (accessed on 17 September 2024).
- Liao, Y.; Zhang, P.; Wu, Q.; Zhang, H. A case study on structural serviceability subjected to railway-induced vibrations at TOD developed metro depot. Buildings 2022, 12, 1070. [Google Scholar] [CrossRef]
- Zou, C.; Wang, Y.; Moore, J.A.; Sanayei, M. Train-induced field vibration measurements of ground and over-track buildings. Sci. Total Environ. 2017, 575, 1339–1351. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y. Impact of Subway Train Vibrations in Curved Tunnels on Adjacent Buildings and Control Technology. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2022. Available online: https://link.cnki.net/doi/10.26944/d.cnki.gbfju.2022.002026 (accessed on 17 September 2024).
- Xia, H.; Chen, J.; Wei, P.; Jia, C.; De Roeck, G.; Degrande, G. Experimental investigation of railway train-induced vibrations of surrounding ground and a nearby multi-story building. Earthq. Eng. Eng. Vib. 2009, 8, 137–148. [Google Scholar] [CrossRef]
- Cao, Z.; Guo, T.; Zhang, Z.; Li, A. Measurement and analysis of vibrations in a residential building constructed on an elevated metro depot. Measurement 2018, 125, 394–405. [Google Scholar] [CrossRef]
- Qian, X.; Wen-Jun, Q. Experimental and numerical studies of metro train-induced vibrations on adjacent masonry buildings. Int. J. Struct. Stab. Dyn. 2016, 16, 1550067. [Google Scholar] [CrossRef]
- Chen, Z.; Wan, F.; He, C. Field Test and Numerical Study of Train-Induced Vibration of Over-Track Buildings Above Metro Depot. Urban Rail Transit 2024, 10, 361–375. [Google Scholar] [CrossRef]
- Pranno, A.; Greco, F.; Lonetti, P.; Luciano, R.; De Maio, U. An improved fracture approach to investigate the degradation of vibration characteristics for reinforced concrete beams under progressive damage. Int. J. Fatigue 2022, 163, 107032. [Google Scholar] [CrossRef]
- Liu, L.; Chen, R.C.; Zhao, Q.; Zhu, S. Applying a multistage of input feature combination to random forest for improving MRT passenger flow prediction. J. Ambient. Intell. Humaniz. Comput. 2019, 10, 4515–4532. [Google Scholar] [CrossRef]
- Yao, J.; Xia, H.; Zhang, N.; Yu, B. Prediction on building vibration induced by moving train based on support vector machine and wavelet analysis. J. Mech. Sci. Technol. 2014, 28, 2065–2074. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, L.; Fu, X. Time series prediction of tunnel boring machine (TBM) performance during excavation using causal explainable artificial intelligence (CX-AI). Autom. Constr. 2023, 147, 104730. [Google Scholar] [CrossRef]
- Rajalakshmi, V.; Ganesh Vaidyanathan, S. Hybrid time-series forecasting models for traffic flow prediction. Promet Traffic Transp. 2022, 34, 537–549. [Google Scholar] [CrossRef]
- AlKhereibi, A.H.; Wakjira, T.G.; Kucukvar, M.; Onat, N.C. Predictive machine learning algorithms for metro ridership based on urban land use policies in support of transit-oriented development. Sustainability 2023, 15, 1718. [Google Scholar] [CrossRef]
- ISO 2631; Mechanical Vibration and Shock—Evaluation of Human Exposure to Whole-Body Vibration—Part 2: Vibration in Buildings (1 Hz to 80 Hz). International Organization for Standardization: Geneva, Switzerland, 2003.
- ISO 8041:2005; Human Response to Vibration—Measuring Instrumentation. International Organization for Standardization: Geneva, Switzerland, 2005.
- Zhi, G.; Xu, X.; Guo, T.; Chen, Z.; Zhang, M. Experimental and numerical investigation of vibrations in over-track scale model buildings. J. Build. Eng. 2023, 77, 107538. [Google Scholar] [CrossRef]









| Soil Type | Thickness d (m) | Water Content W (%) | Volumetric Weight γ (kN/m3) | Porosity Ratio e | Density (g/cm3) | Elasticity Modulus (MPa) | Poisson Ratio ν | Vp | Vs |
|---|---|---|---|---|---|---|---|---|---|
| Plain Fill | 3.5 | 25.8 | 19.3 | 0.762 | 1.87 | 125 | 0.34 | 301 | 148 |
| Silty Clay | 10.70 | 25.8 | 19.6 | 0.724 | 1.86 | 290 | 0.33 | 315 | 159 |
| Completely Weathered Diorite | 23.3 | / | / | / | 2.287 | 2375 | 0.32 | 472 | 243 |
| Moderately Weathered Diorite | 10.4 | / | / | / | 2.536 | 5077 | 0.24 | 1106 | 647 |
| Name and Characteristics of Foundation Soil | Thickness | Engineering Properties |
|---|---|---|
| Highly Weathered Quartz Monzonite Porphyry | 2.5 m | High strength, low compressibility, most of the rock mass structure is damaged, classified as extremely soft rock |
| Moderately Weathered Quartz Monzonite Porphyry | 12.3 m | Classified as extremely soft to soft rock, the rock mass is relatively intact, with a basic quality rating of Grade IV to V |
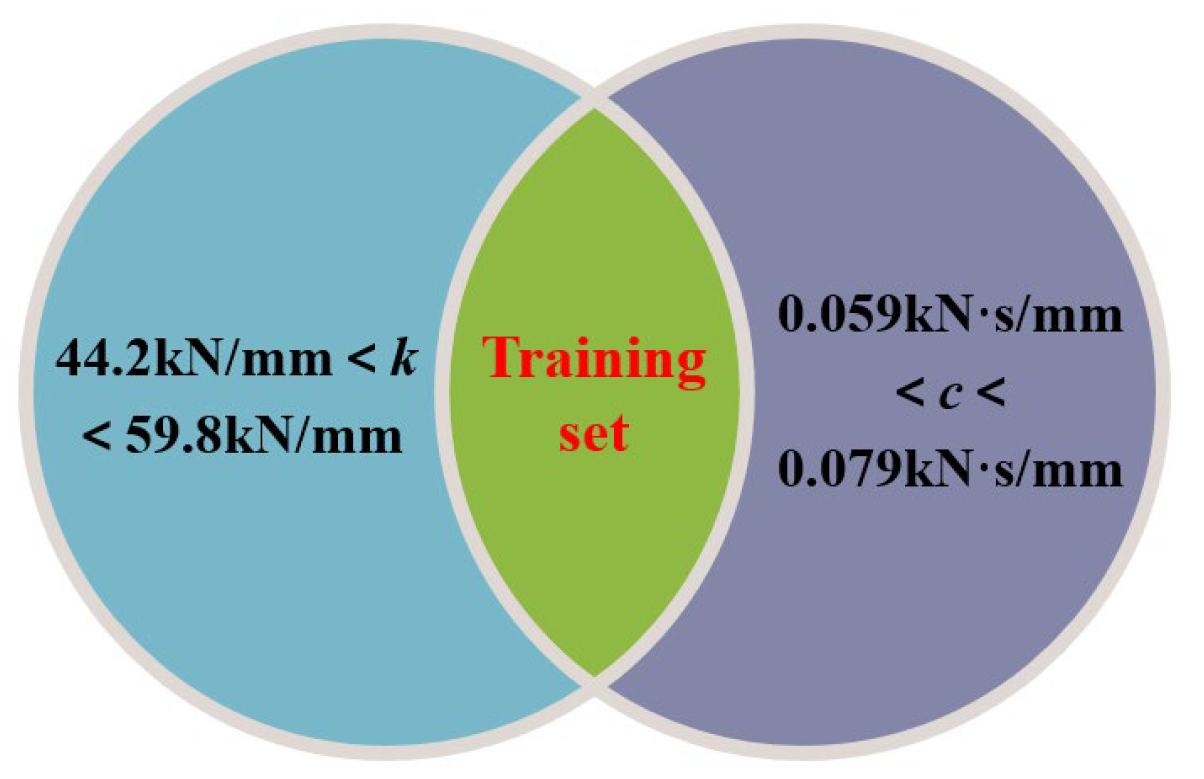
| Number | k (kN/mm) | c (kN·s/mm) |
|---|---|---|
| 1 | 50 | 0.08 |
| 2 | 20 | 0.06 |
| 3 | 30 | 0.1 |
| 4 | 90 | 0.09 |
| … | … | … |
| 58 | 80 | 0.07 |
| 59 | 30 | 0.05 |
| 60 | 60 | 0.08 |
| Average value | 52 | 0.069 |
| Vertical Mode | Period/s | Frequency/Hz |
|---|---|---|
| 1st Order | 1.91 | 0.52 |
| 2nd Order | 1.74 | 0.57 |
| 3rd Order | 1.27 | 0.79 |
| 4th Order | 0.54 | 1.85 |
| Floor | Category | Point N2 | Point N6 | ||
|---|---|---|---|---|---|
| Maximum Acceleration (m/s2) | Maximum Frequency-Weighted Vibration Level (dB) | Maximum Acceleration (m/s2) | Maximum Frequency-Weighted Vibration Level (dB) | ||
| 1F | Measured Value | 0.0735 | 107.23 | 0.0943 | 109.49 |
| Simulated Value | 0.0715 | 104.08 | 0.0924 | 108.31 | |
| Relative Error | 2.72% | 2.94% | 2% | 1.07% | |
| 9F | Measured Value | 0.0453 | 102.12 | 0.0735 | 107.23 |
| Simulated Value | 0.0450 | 100.49 | 0.0712 | 105.04 | |
| Relative Error | 0.66% | 1.6% | 3% | 2.04% | |
| 18F | Measured Value | 0.0333 | 98.95 | 0.0644 | 104.17 |
| Simulated Value | 0.0323 | 98.55 | 0.0637 | 103.08 | |
| Relative Error | 3% | 0.4% | 1% | 1.04% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Su, Y.; Zhang, H. Vertical Vibration Analysis in Metro-Adjacent Buildings: Influence of Structural Height, Span Length, and Plan Position on Maximum Levels. Sustainability 2025, 17, 8764. https://doi.org/10.3390/su17198764
Wang J, Su Y, Zhang H. Vertical Vibration Analysis in Metro-Adjacent Buildings: Influence of Structural Height, Span Length, and Plan Position on Maximum Levels. Sustainability. 2025; 17(19):8764. https://doi.org/10.3390/su17198764
Chicago/Turabian StyleWang, Jiashuo, Yi Su, and Hengyuan Zhang. 2025. "Vertical Vibration Analysis in Metro-Adjacent Buildings: Influence of Structural Height, Span Length, and Plan Position on Maximum Levels" Sustainability 17, no. 19: 8764. https://doi.org/10.3390/su17198764
APA StyleWang, J., Su, Y., & Zhang, H. (2025). Vertical Vibration Analysis in Metro-Adjacent Buildings: Influence of Structural Height, Span Length, and Plan Position on Maximum Levels. Sustainability, 17(19), 8764. https://doi.org/10.3390/su17198764





