Rethinking Evaluation Metrics in Hydrological Deep Learning: Insights from Torrent Flow Velocity Prediction

Abstract

Accurate estimation of flow velocities in torrents and steep rivers is essential for flood risk assessment, sediment transport analysis, and the sustainable management of water resources. While deep learning models are increasingly applied to such tasks, their evaluation often depends on statistical metrics that may yield conflicting interpretations. The objective of this study is to clarify how different evaluation metrics influence the interpretation of hydrological deep learning models. We analyze two models of flow velocity prediction in a torrential creek in Taiwan. Although the models differ in architecture, the critical distinction lies in the datasets used: the first model was trained on May–June data, whereas the second model incorporated May–August data. Four performance metrics were examined—root mean square error (RMSE), Nash–Sutcliffe efficiency (NSE), Willmott’s index of agreement (d), and mean absolute percentage error (MAPE). Quantitatively, the first model attained RMSE = 0.0471 m/s, NSE = 0.519, and MAPE = 7.78%, whereas the second model produced RMSE = 0.0572 m/s, NSE = 0.678, and MAPE = 11.56%. The results reveal a paradox. The first model achieved lower RMSE and MAPE, indicating predictions closer to the observed values, but its NSE fell below the 0.65 threshold often cited by reviewers as grounds for rejection. In contrast, the second model exceeded this NSE threshold and would likely be considered acceptable, despite producing larger errors in absolute terms. This paradox highlights the novelty of the study: model evaluation outcomes can be driven more by data variability and the choice of metric than by model architecture. This underscores the risk of misinterpretation if a single metric is used in isolation. For sustainability-oriented hydrology, robust assessment requires reporting multiple metrics and interpreting them in a balanced manner to support disaster risk reduction, resilient water management, and climate adaptation.

1. Introduction

In recent years, deep learning has become a cornerstone of hydrological modeling, with applications extending from streamflow prediction to water quality assessment and sustainable basin management. Hao et al. [1] demonstrated that causal recurrent neural networks can improve spring discharge forecasts while supporting sustainable groundwater management. Yin et al. [2] introduced a Temporal–Periodic Transformer for monthly streamflow forecasting, emphasizing the role of the Nash–Sutcliffe efficiency (NSE) as a central performance metric in water-scarce basins. Wi et al. [3] applied long short-term memory (LSTM)-based approaches to reconstruct streamflow in ungauged basins of the Great Lakes, directly linking NSE-based evaluation to regional water sustainability. Similarly, Yin et al. [4] proposed a Transformer–XAJ model, combining deep learning with a process-based hydrological model to enhance runoff prediction and flood risk reduction. Beyond runoff forecasting, Lu et al. [5] explored turbidity prediction using multiple deep learning models, highlighting implications for rural water ecosystem management. Tang et al. [6] advanced cross-regional LSTM transfer to ungauged basins in Brazil and the Lancang–Mekong River, using NSE as a benchmark for transboundary sustainability. Xu et al. [7] developed a hybrid convolutional neural network (CNN)–BiLSTM–attention framework with probabilistic forecasting in the Yangtze River Basin, linking improved NSE performance to sustainable flood control and water allocation. Ampas et al. [8] combined a physical rainfall–runoff model with a temporal fusion Transformer in Greece, demonstrating that bias correction and NSE-based evaluation can enhance forecasting in irrigation-driven watersheds. Collectively, these studies show that recent advances in deep learning consistently rely on metrics such as NSE for model evaluation, and increasingly frame their contributions in terms of sustainability.

Reliable knowledge of river flow velocity underpins a wide range of hydrological and engineering applications, from assessing flood hazards and sediment transport to ensuring the sustainable management of reservoirs and related infrastructure [9,10]. Nowhere is this need more acute than in Taiwan, where torrential streams are shaped by steep terrain, intense rainfall, and frequent typhoons. Yet direct field measurements in such environments remain difficult, as unstable flow conditions and hazardous settings often limit the deployment of conventional monitoring systems.

Traditional in situ instruments, including Doppler radar and current meters, can deliver accurate point measurements [11,12]. However, the expense, limited coverage, and maintenance demands of these devices have curtailed their use in many mountainous catchments. To overcome these constraints, researchers have increasingly turned to image-based, non-intrusive approaches. Particle Image Velocimetry (PIV) [13], Large-Scale PIV (LSPIV) [14,15,16,17], and Space–Time Image Velocimetry (STIV) [18,19,20,21] have all been adapted for river applications, while optical flow algorithms that track pixel motion have become a versatile alternative [22,23,24,25]. Despite their promise, these methods continue to face obstacles related to image quality, flow variability, and seeding requirements.

Building on these advances, recent progress in artificial intelligence (AI) and deep learning has opened new possibilities for video-based velocity monitoring. Deep neural networks have been coupled with PIV frameworks [26,27,28,29,30], while state-of-the-art optical flow models are increasingly capable of capturing the complex structures of turbulent surface currents [31,32,33]. In our own work, we have demonstrated that combining deep learning with optical flow provides a powerful means to estimate river velocities under field conditions in Taiwan, offering a pathway toward more resilient and sustainable hydrological observation systems [34].

While these developments highlight the promise of deep learning for river monitoring, a crucial challenge remains largely overlooked: the choice of performance metrics for evaluating model accuracy. In hydrology, root mean square error (RMSE) and mean absolute percentage error (MAPE) are widely used to quantify error magnitudes, while the NSE and Willmott’s index of agreement (d) are frequently applied as variance-based efficiency measures. However, these metrics do not always lead to consistent conclusions. For example, a model may yield lower RMSE but also lower NSE compared with an alternative, reflecting differences in how each statistic accounts for variance in the observed data. Such discrepancies complicate model interpretation and risk misguiding both academic reporting and practical decision-making.

Few studies have systematically examined the implications of relying on different performance metrics in the evaluation of hydrological deep learning models. This gap is particularly important in sustainability-focused research, where reliable flow predictions are vital for disaster preparedness, sediment management, and climate adaptation strategies. Misinterpretation of model performance may translate into flawed risk assessments or inadequate design measures, undermining the goal of resilient water management.

In this study, we compare two deep learning architectures applied to video-based velocity estimation in a torrential creek in Taiwan: a three-dimensional convolutional neural network (3D CNN, hereafter referred to as the first model) and a hybrid convolutional neural network with long short-term memory (CNN+LSTM, hereafter referred to as the second model). Both models were trained on optical flow inputs and validated against Doppler radar measurements. Their performance was evaluated using four widely cited metrics: RMSE, NSE, Willmott’s d, and MAPE. The results reveal a paradox. The first model achieved an NSE below 0.65, a threshold often cited in academic publishing as grounds for rejection, whereas the second model produced an NSE above 0.65 and would likely be considered acceptable. However, the first model also yielded lower errors according to RMSE and MAPE, meaning its predictions were actually closer to the observations. Why does such a contradiction arise? By analyzing this discrepancy, we aim to clarify the interpretation of evaluation metrics in hydrological deep learning and discuss the implications for sustainable flood risk management and river monitoring. This work contributes methodological insights that are essential for balancing academic rigor with practical reliability in sustainability-oriented hydrological research.

2. Materials and Methods

This study establishes an experimental framework to evaluate the performance of deep learning models for surface flow velocity estimation in a torrential creek in Taiwan. The framework combines optical-flow-derived inputs with supervised training against Doppler radar measurements, which provide the reference velocities. 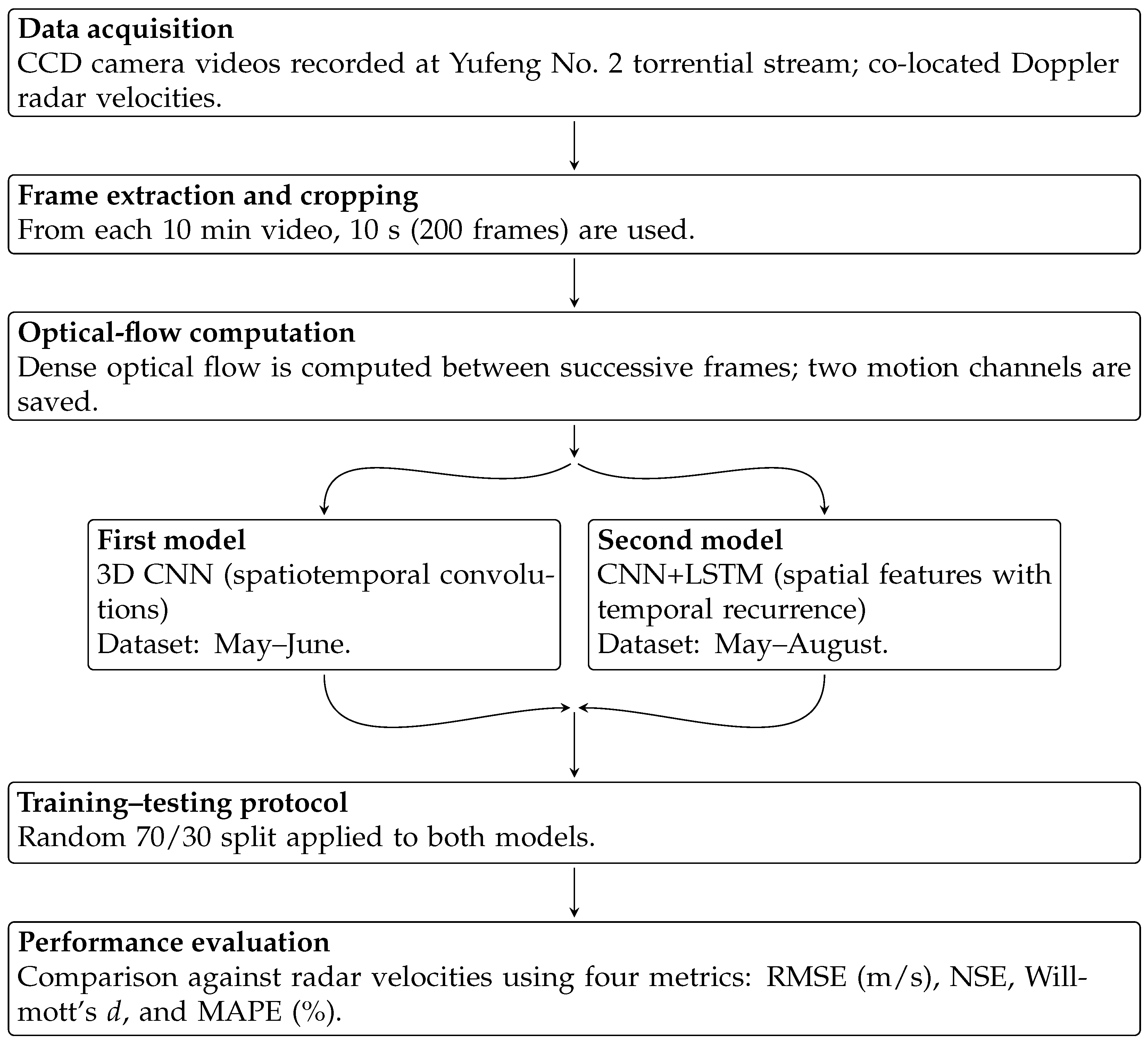In contrast to prior work that emphasized architectural design and input configurations, the present study focuses on comparing four evaluation metrics—RMSE, NSE, Willmott’s d, and MAPE—and analyzing their implications for interpreting model quality. An overview of the workflow is given in Figure 1.

Figure 1 summarizes the workflow. CCD videos recorded at the Yufeng No. 2 torrential stream were paired with Doppler radar velocities serving as reference data. From each video, 200 frames were extracted and processed with dense optical flow to generate motion fields. These optical flow inputs were supplied to two alternative model architectures: 3D CNN and CNN+LSTM. The first model used data collected from May to June, whereas the second model extended the dataset to cover May through August. For both models, training and testing followed a 70/30 random split. Performance was evaluated against Doppler radar observations using RMSE, NSE, Willmott’s d, and MAPE. The subsequent subsections provide detailed descriptions of the study area, model structures, and evaluation procedures.

2.1. Study Area and Data

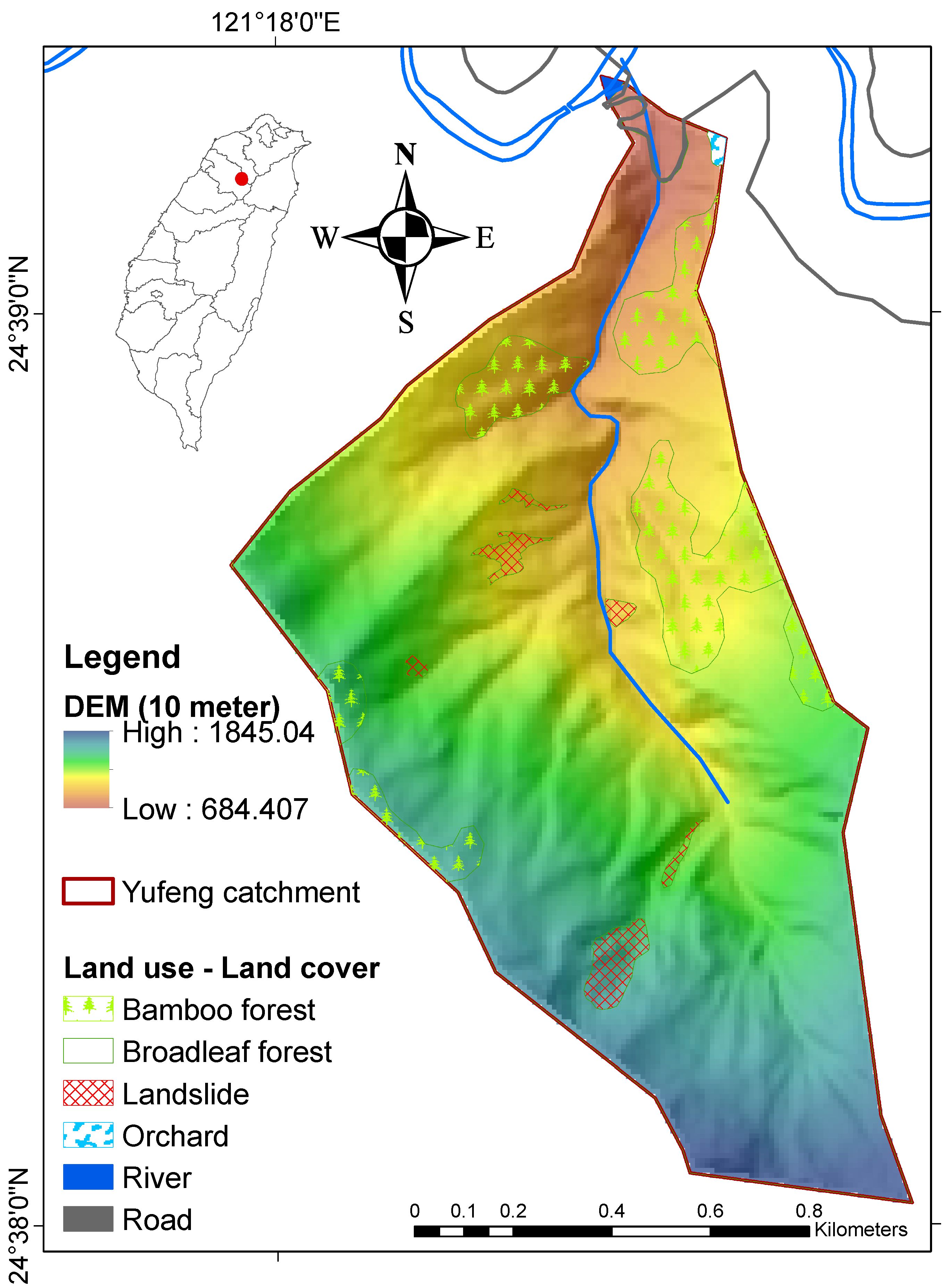
The case study was conducted at the Yufeng No. 2 torrent in northern Taiwan, a steep mountain stream prone to rapid hydrological responses during typhoon rainfall events. Sediment check dams and grade-control structures (bed stabilization works) have been constructed along the stream to mitigate sediment-related hazards and prevent excessive bed material from entering the main channel. The basin area is approximately 1.52 km² and is characterized by shallow soils, rapidly weathering sedimentary formations, and predominantly forested land cover. These features contribute to flash flood hazards, frequent sediment transport, and high spatial variability of surface flows. The catchment context is shown in Figure 2.

Continuous monitoring was implemented at the outlet of the torrent using a CCD (Charge-Coupled Device) camera system paired with a co-located Doppler radar, which provided reference flow velocities at 10 min intervals. Details of the equipment setup and site photographs are available in our previous study [34]. During May and June 2025, a total of 3263 videos were recorded, each lasting 10 min at 4K resolution (3840 × 2160 pixels). A second batch of videos was collected in July and August 2025, comprising approximately 3432 recordings of similar duration and resolution. Together, these datasets capture both daytime and nighttime conditions, reflecting diverse illumination and flow states.

For this study, two model-specific datasets were derived. The first model (3D CNN) was trained and evaluated exclusively on the May–June dataset, while the second model (CNN+LSTM) was trained and evaluated on the combined May–August dataset. Both models relied only on daytime videos for training and testing. Although the data originated from the same monitoring campaign, the definition of daytime differed between the two approaches. Model 1 applied an average brightness threshold to separate daytime and nighttime videos, based on the clearly bimodal brightness distribution of all recordings. In contrast, Model 2 defined daytime as the period from 6:00 a.m. to 6:00 p.m. As a result, the videos used by the two models for May–June are not identical. It should be noted that the two models were developed by different co-authors. As a result, their data preprocessing steps (e.g., defining daytime conditions) and training datasets are not identical, which contributes to the contrasting evaluation outcomes. In both cases, the videos were paired with Doppler radar velocity measurements, providing robust ground truth for supervised learning. The availability of real-world, high-frequency velocity data makes this case study directly relevant to sustainability-oriented research on flood risk reduction, sediment management, and resilient water resource monitoring.

2.2. Model Architectures

Two deep learning architectures were applied to estimate flow velocity from video sequences: 3D CNN and CNN+LSTM. Both models were implemented in PyTorch 2.7.1+cu118 and trained to predict a single continuous value of surface velocity (m/s) from 200-frame video clips paired with Doppler radar observations. The 3D CNN captures spatiotemporal features directly through three-dimensional convolutions, whereas the CNN+LSTM first extracts spatial features and then models their temporal evolution. A detailed comparison of the two models is provided in [34].

It is important to emphasize that the subsequent analysis does not depend on the specific details of these architectures. Once predictions are obtained, the comparison with observed velocities is carried out solely using four performance metrics—RMSE, NSE, d, and MAPE. Thus, the interpretation of model performance in this study is based entirely on the relationship between predicted and observed values, independent of how the models internally process the data.

2.3. Performance Metrics

Model performance was evaluated using four widely applied statistical measures: RMSE [35,36], NSE [37], Willmott’s d [38], and MAPE [39]. These metrics capture different aspects of predictive performance and must be interpreted with care, as they vary in their treatment of scale, variance, and error magnitude versus variance-based efficiency.

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{(v_i-{\widehat{v}}_i)}^2}$$

(1)

$$\mathrm{NSE}=1-{\displaystyle \frac{{\sum }_{i=1}^N{(v_i-{\widehat{v}}_i)}^2}{{\sum }_{i=1}^N{(v_i-\overline{v})}^2}}$$

(2)

$$d=1-{\displaystyle \frac{{\sum }_{i=1}^N{(v_i-{\widehat{v}}_i)}^2}{{\sum }_{i=1}^N{\left(\left|{\widehat{v}}_i-\overline{v}\right|+\left|v_i-\overline{v}\right|\right)}^2}}$$

(3)

$$\mathrm{MAPE}={\displaystyle \frac{100}{N}}\sum _{i=1}^N\left|{\displaystyle \frac{v_i-{\widehat{v}}_i}{v_i}}\right|$$

(4)

where:

$$\begin{array}{cc}\hfill v_i& =\mathrm{observed}\mathrm{velocity}\mathrm{at}\mathrm{instance}i;\hfill \\ \hfill {\widehat{v}}_i& =\mathrm{predicted}\mathrm{velocity}\mathrm{at}\mathrm{instance}i;\hfill \\ \hfill \overline{v}& =\mathrm{mean}\mathrm{of}\mathrm{observed}\mathrm{velocities};\hfill \\ \hfill N& =\mathrm{total}\mathrm{number}\mathrm{of}\mathrm{observations}.\hfill \end{array}$$

Conceptually, RMSE and MAPE serve as error magnitude metrics, with RMSE being scale-dependent (expressed in m/s) and MAPE providing error percentages relative to observed values. In contrast, NSE and d are variance-based efficiency metrics that assess predictive performance relative to the variability of the observed data. NSE ranges from $-\infty$ to 1, where a value of 1 indicates perfect agreement, a value of 0 corresponds to performance equal to the mean of the observations, and negative values indicate that the mean outperforms the model. NSE is sensitive to variance and penalizes deviations from the mean more strongly, while d provides a more robust measure of agreement by bounding values strictly between 0 and 1. Taken together, these four metrics offer complementary perspectives on model performance, underscoring the importance of multi-metric evaluation.

3. Results

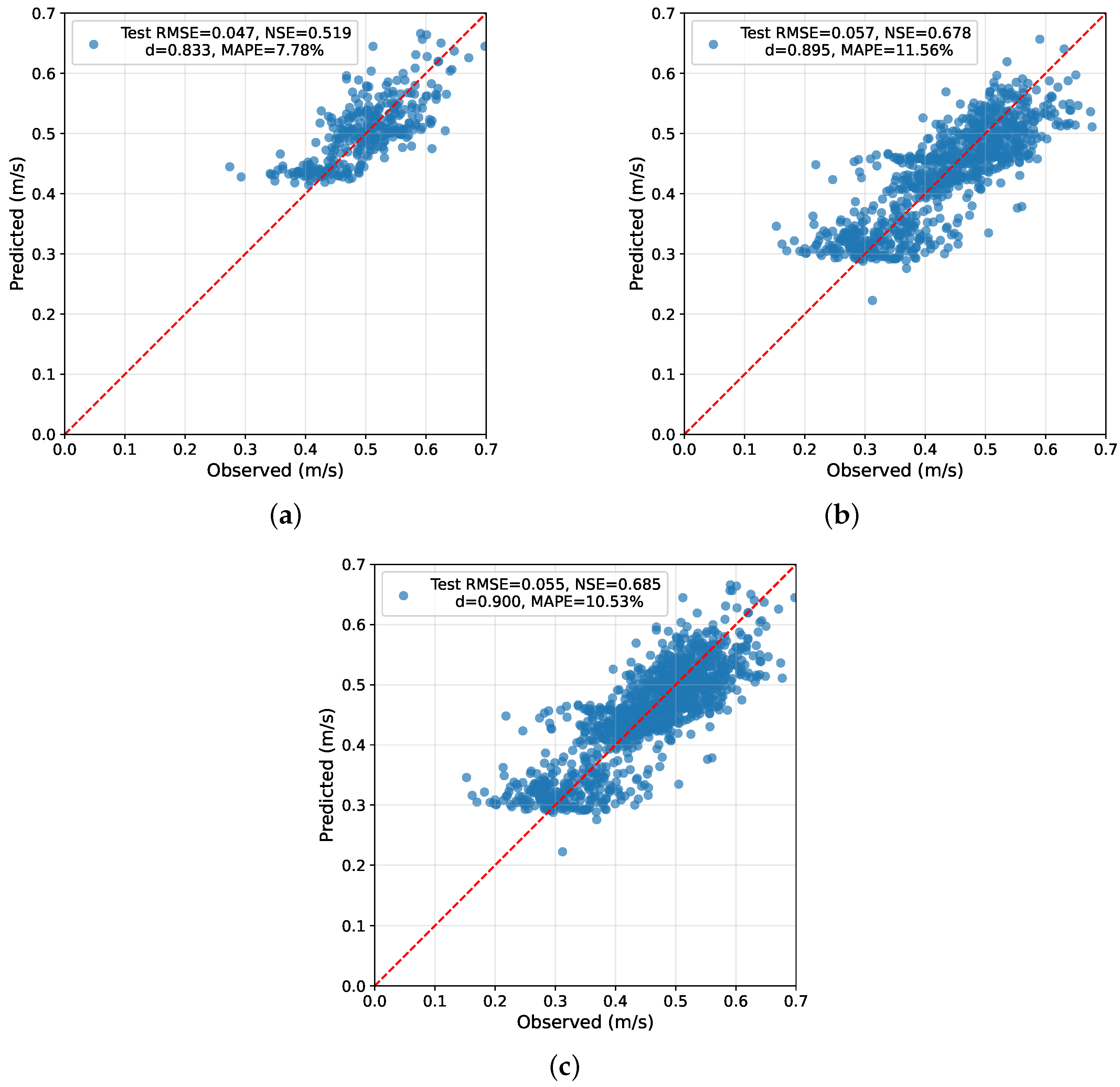
The performance of the two models was first examined through scatter plots of predicted versus observed velocities. The scatter plots in Figure 3 illustrate these contrasting tendencies. Predictions from the first model, trained on May–June data, are concentrated in the upper right-hand corner and align closely with the 1:1 line. By contrast, the second model, trained on the extended May–August dataset, shows an additional cluster of points in the lower left-hand corner corresponding to the July–August period. It should be noted that the data points representing the May–June period are not exactly the same between the two models, as explained earlier, due to the different methods used to separate daytime and nighttime videos. As will be shown later, this broader distribution substantially alters the four metrics used to evaluate model performance. Visually, the second model exhibits a wider spread around the 1:1 line, indicating inferior performance compared to the first model. However, the NSE suggests the opposite. This provides the first indication that reliance on a single indicator may lead to incomplete or even misleading conclusions. For completeness, panel (c) of Figure 3 further illustrates the case when the two datasets are combined, an issue discussed later in this section.

Table 1. Comparison of evaluation metrics between the first model (3D CNN), the second model (CNN+LSTM), and the combined dataset (Models 1 + 2). Lower RMSE and MAPE indicate better absolute/percentage accuracy; higher NSE and Willmott’s d indicate better variance-based efficiency and agreement.

Model/Dataset	RMSE (m/s)	NSE	Willmott’s d	MAPE (%)
First model (3D CNN)	0.0471	0.519	0.833	7.78
Second model (CNN+LSTM)	0.0572	0.678	0.895	11.56
Combined dataset (Models 1 + 2)	0.0547	0.685	0.900	10.53

summarizes the performance of the two models across four evaluation metrics. The first model (3D CNN) achieved the lowest RMSE (=0.0471 m/s) and the lowest MAPE (=7.78%), indicating superior error magnitude accuracy. In contrast, the second model (CNN+LSTM) produced a slightly higher RMSE (0.0572 m/s) and MAPE (11.56%), reflecting larger error magnitudes. When the two datasets were combined (Models 1 + 2), the RMSE (=0.0547 m/s) and MAPE (=10.53%) fell between those of the individual models, which is consistent with the expectation that combining datasets would yield intermediate performance in error magnitude metrics.

When evaluated using variance-based efficiency indices, however, the second model outperformed the first. Specifically, the CNN+LSTM achieved higher values of NSE (=0.678) and Willmott’s d (=0.895) compared with the 3D CNN (NSE = 0.519; $d=0.833$). This suggests that although less accurate in terms of error magnitudes, the second model better reproduced the variance structure of the observed velocities and exhibited stronger overall concordance with the ground-truth data. Even more striking, the combined dataset (Models 1 + 2) further improved these variance-based efficiency metrics, reaching NSE = 0.685 and $d=0.900$, despite no change in the underlying models. This counterintuitive result contrasts sharply with the expected intermediate values observed for RMSE and MAPE.

This situation presents a dilemma: how should one determine which model is superior? On the one hand, the first model achieves smaller error magnitudes, but on the other hand, the second model attains higher variance-based efficiency scores. A second issue further complicates interpretation: why do variance-based metrics such as NSE and Willmott’s d improve simply by combining datasets, even though the model architectures themselves remain unchanged? This counterintuitive behavior, first noted by [40], raises fundamental questions about the reliability of these indices. The NSE is among the most commonly used metrics in hydrological and hydraulic model evaluation, particularly for calibration, model comparison, and verification purposes [40,41,42,43,44,45,46]. Surveys and recent studies even describe NSE as “perhaps the most used metric in hydrology” [40], underscoring its widespread acceptance in the field. More recently, NSE has also been adopted in the evaluation of machine learning and deep learning models for other applications, owing to its convenient, dimensionless form that enables straightforward comparison across sites and contexts.

Nevertheless, this popularity has also contributed to the emergence of widely cited threshold values. For example, one reviewer of our previous work emphasized that “a generally accepted threshold of 0.65” is often used as a benchmark for satisfactory performance in environmental and spatial models. Such cutoff values are consistent with guidelines that classify performance as “satisfactory” when NSE $>0.50$ and “good” when NSE $>0.65$ [43]. Applying this criterion, the first model would be judged as inadequate and therefore rejected, whereas the second model would be considered acceptable. However, such a conclusion is paradoxical: despite its lower NSE, the first model actually produces smaller absolute and relative errors, and therefore should arguably be regarded as the more accurate model. Together with the artificial enhancement of NSE observed when datasets are combined, these findings highlight the risk of placing undue trust in a single metric and motivate a deeper examination of its limitations, a theme we will pursue in the discussion section.

4. Discussion

The results reveal that the two deep learning models demonstrate contrasting strengths depending on the evaluation metric applied. While the first model achieved lower error magnitudes, the second model attained higher variance-based efficiency and agreement scores. These discrepancies highlight a broader issue in hydrological model assessment: different metrics emphasize different aspects of performance, and reliance on a single indicator may lead to misleading conclusions. The following subsections first use $R^2$ as a cautionary example, then turn to the central focus of this paper—the interpretation paradox between NSE and RMSE—and conclude with implications for sustainability.

4.1. The Pitfalls of $R^2$ and the Analogy to NSE

The coefficient of determination ($R^2$) is frequently reported in hydrological and environmental modeling studies, as well as in machine learning and deep learning, largely because of its apparent simplicity as a measure of explained variance. However, $R^2$ is not a reliable indicator of predictive accuracy. As shown in [47], $R^2$ evaluates the fit of predictions to a regression line, which is not necessarily the 1:1 line that represents perfect agreement between observations and predictions. Consequently, a model can achieve a very high $R^2$, even approaching unity, while still producing biased predictions or systematic deviations from the 1:1 line. In such cases, $R^2$ reflects correlation rather than true accuracy, and its use as a primary evaluation metric can be misleading. This problem persists because many readers and practitioners who are less familiar with statistical nuances continue to interpret $R^2$ as a gold standard for model performance.

A similar problem arises with the NSE. Although NSE and $R^2$ share the same mathematical formula, their ranges differ because of how they are applied. Under ordinary least squares (OLS) regression, the residual sum of squares is always less than or equal to the total sum of squares, ensuring $0\le R^2\le 1$. In contrast, NSE is used more generally to evaluate predictive models, which can yield residual errors larger than the variance of the observations; therefore, its range extends from $-\infty$ to 1. As discussed by Melsen et al. [46], this historical conflation of NSE with $R^2$ has led to persistent confusion in the hydrological literature, with some studies treating them as equivalent and others clearly distinguishing between the two. Like $R^2$, NSE has gained widespread popularity in hydrology and hydraulic modeling, and it is often treated as a decisive indicator of model adequacy. Yet, as demonstrated in this study, NSE can present a distorted view of performance by rewarding models that reproduce variance even if their error magnitudes are larger. In this sense, NSE has become the “new $R^2$”: a metric that is widely used and frequently reported, but whose limitations are not always recognized. Drawing this analogy situates our findings within a broader critique of evaluation practices in hydrology, highlighting the need for careful selection and interpretation of performance metrics.

4.2. The RMSE–NSE Paradox

Table 2. Comparison of evaluation metrics for the two models. Although the second model has a higher RMSE, it attains a higher NSE because of the larger denominator in the NSE formulation.

Dataset	RMSE	NSE	Variance of Observed	NSE Denominator
First	0.0471	0.519	0.0046	1.48
Second	0.0572	0.678	0.0102	8.65
Combined	0.0547	0.685	0.0095	11.09

illustrates the paradoxical relationship between RMSE and NSE. Mathematically, the RMSE expression is similar to the numerator of the second term in the NSE formula. This similarity may give the false intuition that a smaller RMSE should always correspond to a larger NSE. However, the results here demonstrate the opposite: the first model yielded the lowest RMSE (0.0471) and, thus, more accurate predictions in terms of error magnitude, yet it produced a lower NSE (0.519). By contrast, the second model had a higher RMSE (0.0572), indicating larger errors, but attained a much higher NSE (0.678).

NSE has long been valued in hydrology as a convenient tool for assessing how well models reproduce temporal trends and variability. From this perspective, higher NSE values are often interpreted as evidence of better model performance. However, the present study shows that such reliance can be misleading: the second model achieved a higher NSE despite exhibiting larger error magnitudes than the first model. In this case, NSE rewarded variance reproduction while misrepresenting true predictive accuracy.

This contradiction arises because NSE depends not only on the numerator (prediction errors) but also on the denominator, which represents the total variability of the observed data around its mean and, therefore, reflects both the variance of the observations and the sample size. As shown in Table 2, the denominator for the second model (8.65) was substantially larger than that of the first model (1.48), inflating the NSE value despite greater errors. Importantly, the second model achieved this higher NSE not by changing the architecture, but simply by incorporating additional July–August data. This broader dataset increased the total variability of the observed data around its mean and, in turn, raised the NSE. When the two datasets were combined, the corresponding denominator (11.09) became larger than both. This produced an NSE of 0.685 that exceeded the values of either individual model, even though the RMSE (0.0547) and MAPE (10.53%) merely fell between them. The comparison underscores how NSE can shift dramatically with changes in data variability, even when model performance in terms of error magnitude remains inferior. This sensitivity to the choice of reference average has long been recognized, with early work showing that alternative definitions of the mean discharge can yield substantially different efficiency values and sometimes mask poor performance [48].

An additional perspective is offered by the well-known classification of MAPE thresholds proposed by Lewis [39]. According to this interpretation, MAPE values below 10% indicate “highly accurate forecasting,” values between 10–20% represent “good forecasting,” 20–50% correspond to “reasonable forecasting,” and values above 50% are considered “inaccurate forecasting.” Within this framework, the first model ($\mathrm{MAPE}=7.78\%$) qualifies as highly accurate, whereas the second model ($\mathrm{MAPE}=11.56\%$) is merely good. Despite this, the second model achieved a substantially higher NSE, which would often be cited in the literature as evidence of superior performance. This discrepancy underscores the paradox emphasized in this study: while MAPE highlights the practical accuracy of predictions in intuitive terms, NSE can elevate models that reproduce variance at the expense of error magnitude. The contrast between these two interpretations reinforces the need to evaluate models using multiple complementary metrics rather than relying solely on NSE.

4.3. Implications of the RMSE–NSE Paradox

Building on the analogy to $R^2$, a central finding of this study is the divergence between RMSE and NSE when assessing deep learning models of flow velocity. Although both metrics are derived from squared residuals, they are normalized differently. RMSE provides an error-magnitude measure expressed in physical units (m/s), whereas NSE is a variance-based index that compares squared prediction errors to the total variability of the observed data around its mean. Mathematically, if the observed velocities exhibit high variability, the denominator in the NSE formulation (Equation (2)) becomes large. This can yield relatively high NSE values even when prediction errors remain non-negligible. Conversely, when variability is small, the same magnitude of error has a stronger impact on NSE, potentially driving it to negative values even when error magnitudes are acceptable.

This paradox implies that two models can produce nearly identical prediction errors, but their NSE scores may differ substantially depending on the variability of the observed dataset. In the present study, the second model achieved higher NSE despite producing larger error magnitudes, reflecting its better reproduction of variability rather than superior pointwise accuracy. Such behavior demonstrates that RMSE and NSE, though mathematically related, emphasize different aspects of model performance. As shown by [49], NSE can be further decomposed into contributions from correlation, bias, and relative variability, which clarifies why the metric may appear favorable even when error magnitudes are large. Researchers and practitioners must, therefore, interpret them together rather than treating one as a universal indicator of model quality.

4.4. The Dataset Combination Effect and Divide-And-Measure Nonconformity

Building on the RMSE–NSE paradox discussed above, an even more striking issue arises when datasets are combined. As shown in Table 1, the RMSE (0.0547) and MAPE (10.53%) of the combined dataset fall between those of the individual models, which is consistent with expectations for error-magnitude metrics. Yet, counterintuitively, both NSE (0.685) and Willmott’s d (0.900) exceed the values obtained by either model alone. This outcome reflects a more general property of the NSE recently identified by [40], who demonstrated that the combined NSE is always greater than or equal to the worst of the individual NSEs and, in many cases, greater than both.

This divide-and-measure nonconformity (DAMN) highlights a statistical paradox: the act of aggregating evaluation datasets can artificially inflate variance-based indices, even though no improvement has been made to the underlying model architectures or learning process. In our study, the combined NSE improved solely because the aggregation altered the variance structure of the denominator in the NSE formula, not because of enhanced predictive accuracy.

The implications of this behavior extend beyond our case study. In principle, one could train separate models for different seasons or months of the year and then combine their outputs to report a deceptively higher overall NSE. More generally, other types of data partitioning or selective aggregation strategies could be devised to exploit the same weakness, artificially boosting variance-based indices without improving model skill. Such practices risk presenting inflated evaluation scores that do not reflect genuine advances in modeling. For this reason, DAMN-susceptible metrics such as NSE should be interpreted with caution, particularly when model performance is reported across aggregated datasets.

4.5. Academic Perspective: Strengths and Pitfalls of NSE

NSE has become a standard performance indicator in hydrological research because it offers a dimensionless scale, with 1 representing perfect prediction, 0 equivalent to the mean-observed benchmark, and negative values indicating performance worse than the mean. This straightforward interpretation makes it attractive for cross-comparison across sites and methods. Moreover, because it is a variance-based index that emphasizes variability reproduction, NSE can reveal whether models capture fluctuations in flow rather than merely matching mean values. In academic contexts, this is valuable for studies seeking to evaluate the realism of hydrological simulations.

Nevertheless, the sensitivity of NSE to the variability of the observed dataset can also exaggerate model skill under certain conditions. For catchments with high variability in flow velocities, models may achieve seemingly strong NSE values even if error magnitudes remain large. This can lead to overly optimistic conclusions about predictive skill. On the other hand, in basins with stable flows, even small discrepancies may sharply reduce NSE, giving the impression of poor model performance. For this reason, academic reporting should treat NSE as a complementary measure, interpreted in conjunction with error-magnitude metrics such as RMSE.

4.6. Practical Perspective: Intuitive Accuracy from RMSE and MAPE

For practitioners tasked with operational decisions, RMSE and MAPE provide error-magnitude metrics that are both interpretable and actionable. RMSE quantifies prediction error in the same units as the observed variable, directly informing thresholds used in river engineering, sediment management, and flood preparedness. For example, an RMSE of 0.05 m/s can be evaluated against acceptable tolerances for hydraulic design or early warning thresholds. In this sense, RMSE provides a direct link between statistical evaluation and real-world decision-making.

MAPE further enhances interpretability by expressing errors as percentages relative to observed values. This makes it accessible to decision makers and stakeholders without technical backgrounds, who may find percentage-based indicators easier to relate to performance expectations. MAPE also facilitates comparisons across sites or studies with different velocity magnitudes. However, it should be interpreted with caution when observed velocities are very small, as division by small values can inflate percentage errors. Together, RMSE and MAPE provide intuitive measures of predictive reliability that are better suited to guiding practical interventions than variance-based indices alone.

4.7. Implications for Sustainability and Risk Reduction

The choice of evaluation metric has direct consequences for sustainability-oriented water management. Although NSE is sometimes cited as useful for assessing whether models reproduce flow variability, relying on it in isolation risks overstating predictive skill. Our findings confirm the necessity of balancing NSE with error-magnitude metrics. Overreliance on NSE alone may foster overconfidence in model skill, particularly in basins with high flow variability where large errors can be masked by variance scaling. This could result in under-preparedness for extreme flood events, inappropriate design of hydraulic infrastructure, or misguided sediment transport modeling. Such misinterpretations can undermine disaster risk reduction efforts and expose communities to greater vulnerability. A balanced view that integrates error-magnitude metrics such as RMSE and MAPE is, therefore, critical for ensuring robust flood prediction and management strategies. Beyond reporting NSE, robust model evaluation requires comparison against benchmark models to ensure meaningful performance assessment and cross-study comparability. This perspective, highlighted by Schaefli and Gupta [50], underscores the necessity of interpreting NSE as an improvement over a baseline rather than in isolation.

From a broader sustainability perspective, transparent reporting of multiple performance indicators supports accountable and evidence-based decision-making. Water resource planning increasingly requires interdisciplinary collaboration, where stakeholders from engineering, environmental management, and policy must rely on understandable and credible model assessments. Presenting both error-magnitude metrics (e.g., RMSE and MAPE) and variance-based indices (e.g., NSE and d) avoids misleading conclusions and enhances trust in predictive tools. Ultimately, sustainability depends not only on developing powerful models but also on evaluating them with metrics that are meaningful, transparent, and aligned with the goals of disaster resilience, river engineering, and long-term water resource management.

5. Conclusions

This study compared two deep learning models for flow velocity estimation in a torrential creek in Taiwan and revealed a paradox in performance evaluation. The first model (3D CNN) produced lower error magnitudes, as reflected by RMSE and MAPE, while the second model (CNN+LSTM) achieved higher variance-based efficiency and agreement scores, as indicated by NSE and Willmott’s d. These contrasting outcomes demonstrate that metric choice can fundamentally alter the interpretation of model quality, with NSE and RMSE often telling different stories.

The findings emphasize the need for careful selection and interpretation of evaluation metrics in hydrological applications. NSE, although widely reported, should be interpreted with caution, particularly when observed variance and dataset definitions differ, as it may overstate model performance. RMSE and MAPE, by contrast, provide intuitive measures of error magnitude that are directly actionable for engineering and risk management purposes. For example, the first model attained RMSE = 0.0471 m/s and MAPE = 7.78%, results that directly convey predictive accuracy relevant to disaster risk reduction. For sustainability-related water resource management, a balanced evaluation framework should combine both error-magnitude metrics (RMSE, MAPE) and variance-based indices (NSE, d) to ensure transparent and meaningful assessment. The contributions clarify the RMSE–NSE paradox, highlight the practical value of multi-metric evaluation, and underline the risks of overreliance on a single index.

This work has some limitations, including the use of a single case study, differences in dataset coverage, and the exclusion of alternative indices such as the Kling–Gupta efficiency. Future research should extend this analysis to other rivers and hydrological settings to test the generality of the observed paradox. Replication across diverse hydrological contexts and the integration of additional evaluation frameworks will help establish more robust best practices. Ultimately, sustainable water management requires not only advanced predictive models but also the consistent use of evaluation metrics that align with the dual goals of scientific rigor and practical decision-making.