Development of Evaluation Model for Building Energy Usage: Methodology Development and Case Study on Day-Care Centers in South Korea
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
1.2.1. Metacognition Based Energy Saving
1.2.2. Modeling Methods
1.3. Research Gap and Objectives
- Inapplicability of detailed models for nationwide energy policy applications: simplified models are required for generalization and large-scale implementation.
- Unfair evaluation methods for user behavior in building energy consumption: simple yet robust models that account for building performance and weather impacts are required.
- Limited use of real-world data in model development: large-scale datasets from actual buildings should be collected and utilized.
- Expensive metacognition systems requiring hardware for specific buildings and occupants: a general framework that enables metacognitive evaluation through simplified modeling approaches is needed.
- To develop a methodology for evaluating building energy usage levels for inducing savings with potential metacognition.
- To develop machine learning-based evaluation models using large-scale datasets from actual day-care centers.
- To exemplarily demonstrate the methodology with developed models.
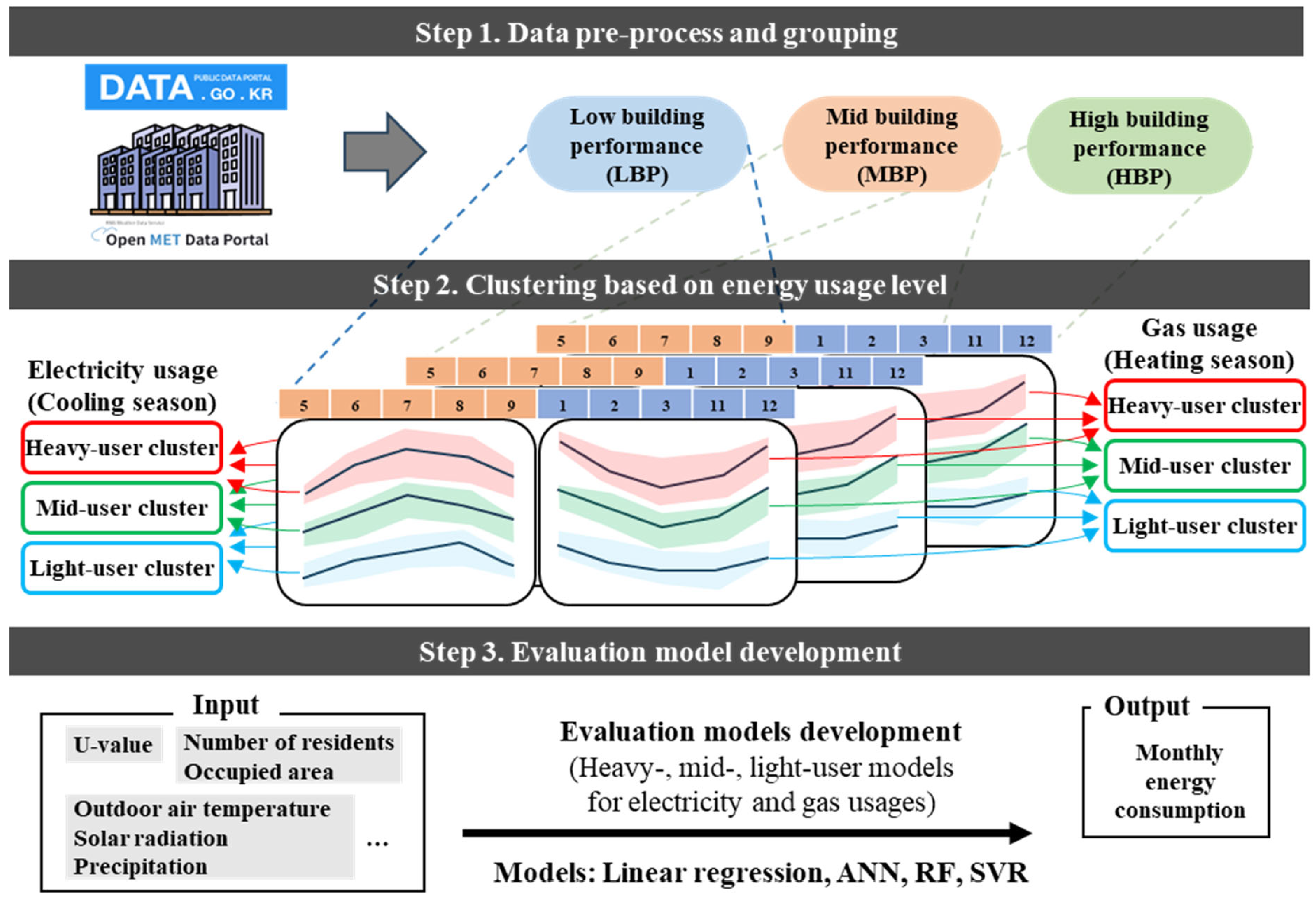
2. Methodology
3. Demonstration of Framework: Case Study on Day-Care Centers
3.1. Data Preprocessing and Grouping
3.1.1. Data Collection
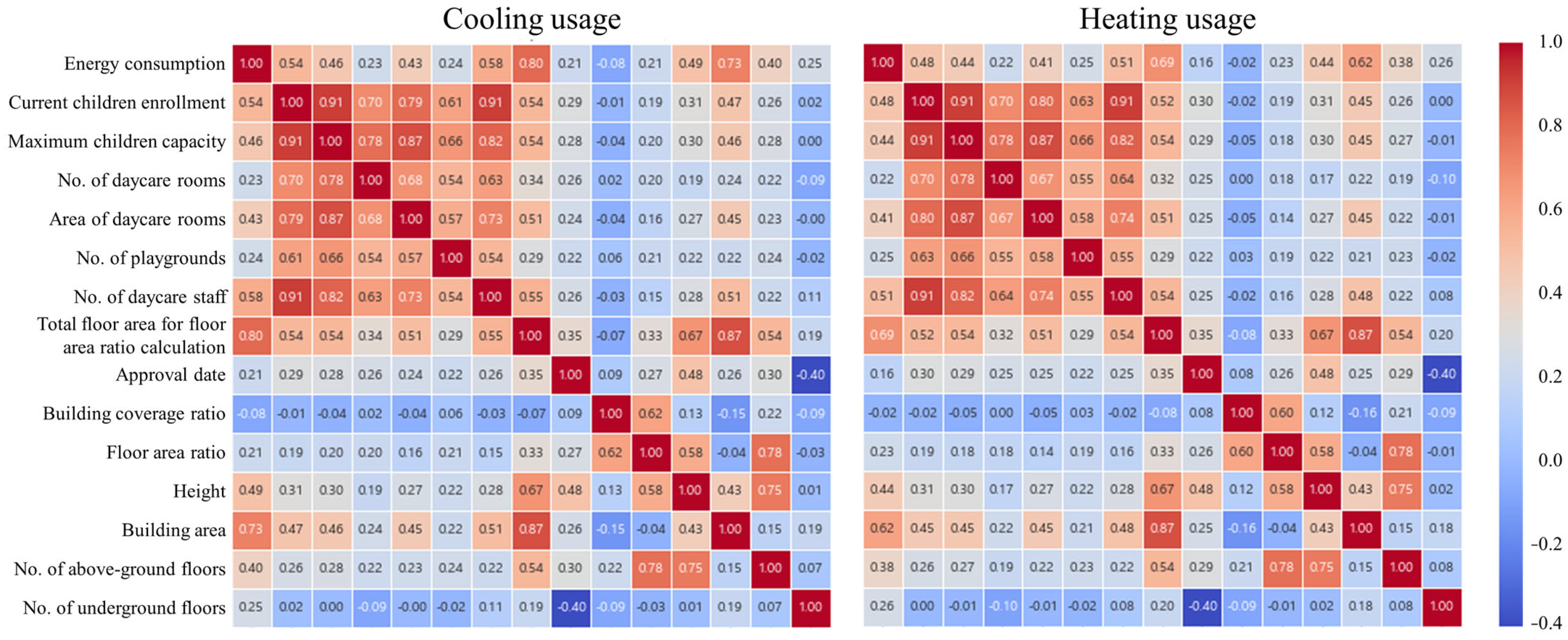
3.1.2. Data Analysis and Normalization
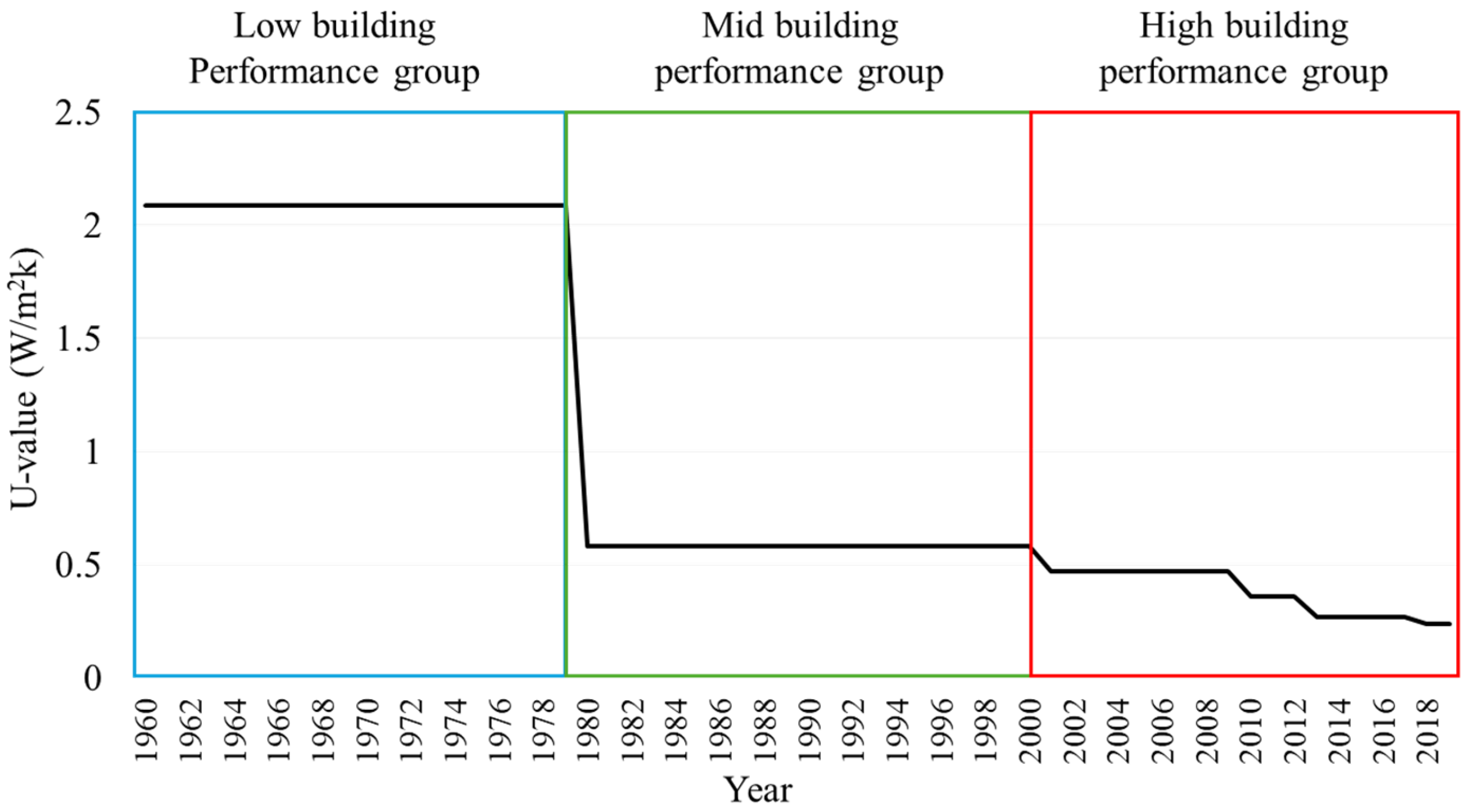
3.1.3. Data Grouping
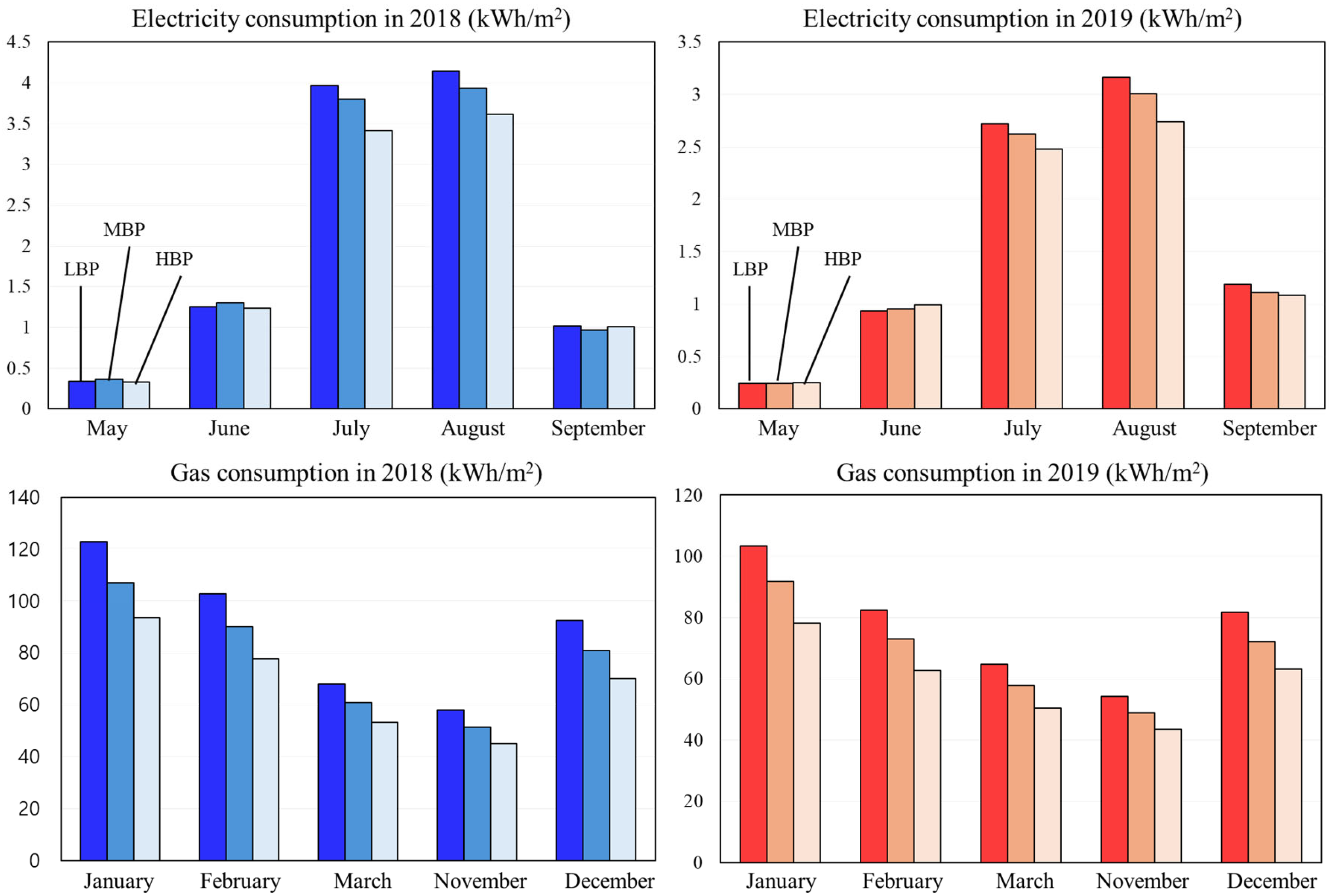
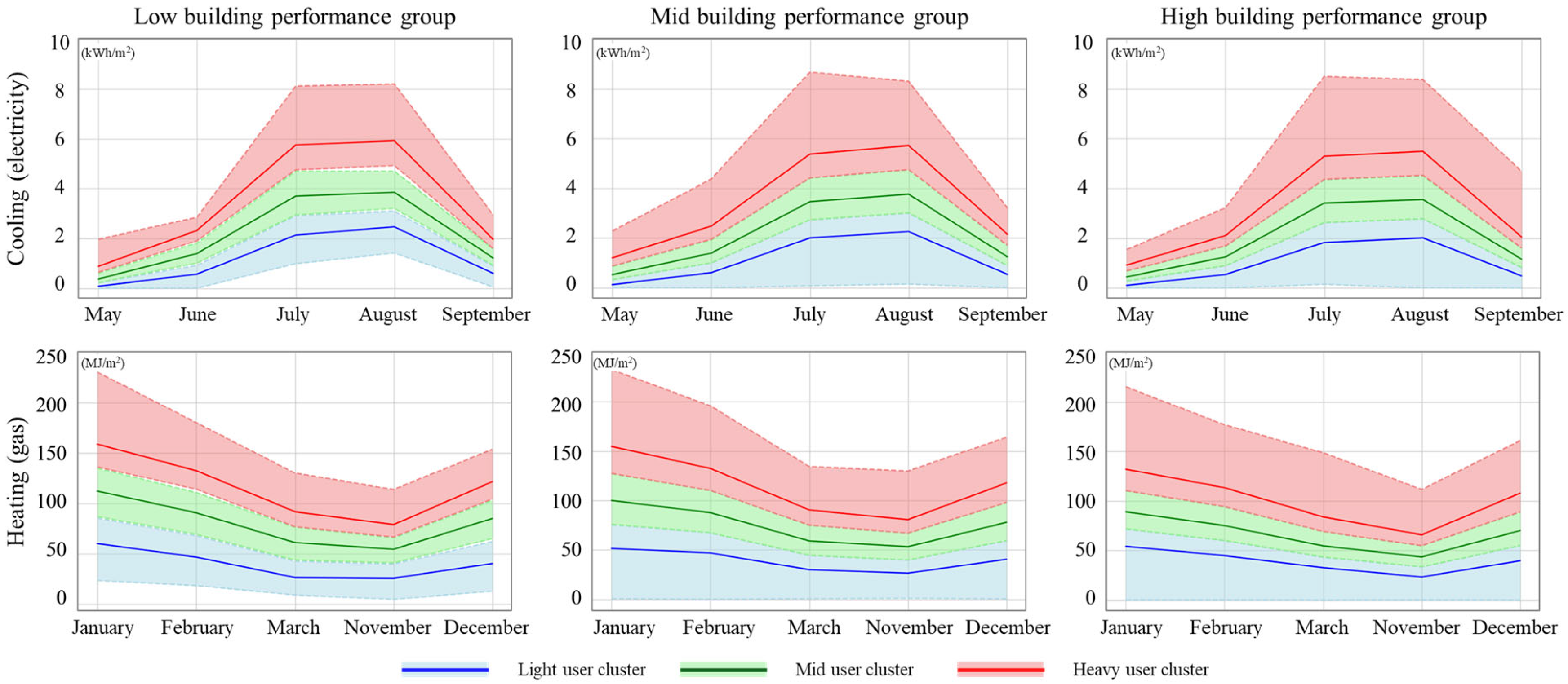
3.2. K-Means Clustering for Three Energy Usage Levels: Light, Mid, and Heavy Users
- Initialization Step: The first step in k-means clustering involves selecting k initial centroids. In this study, the k-means++ method was adopted with k fixed at 3; this minimizes the performance degradation caused by the randomness in centroid selection.
- Assignment Step: In this step, for each data point xi, the distance to each centroid μk is calculated, and the data point is assigned to the cluster with the nearest centroid. The Euclidean distances between each data point and the centroids are computed to identify the closest centroid, and the point is assigned accordingly, as expressed in Equation (1).
- 3.
- Update Step: A new centroid is determined based on the mean position of the data points assigned to each cluster. Specifically, the new centroid for each cluster k is set to the mean of the data points within that cluster, as expressed in Equation (2).
- 4.
- Iteration Step: The assignment and update steps are repeated until the centroid positions no longer change or a predefined number of iterations is reached. This iterative process continues until either the convergence criteria are met or the maximum number of iterations is reached.
3.3. Evaluation Model Development
3.3.1. Linear Regression
3.3.2. Artificial Neural Networks (ANN) Model
3.3.3. Random Forest Model
3.3.4. Support Vector Regression Model
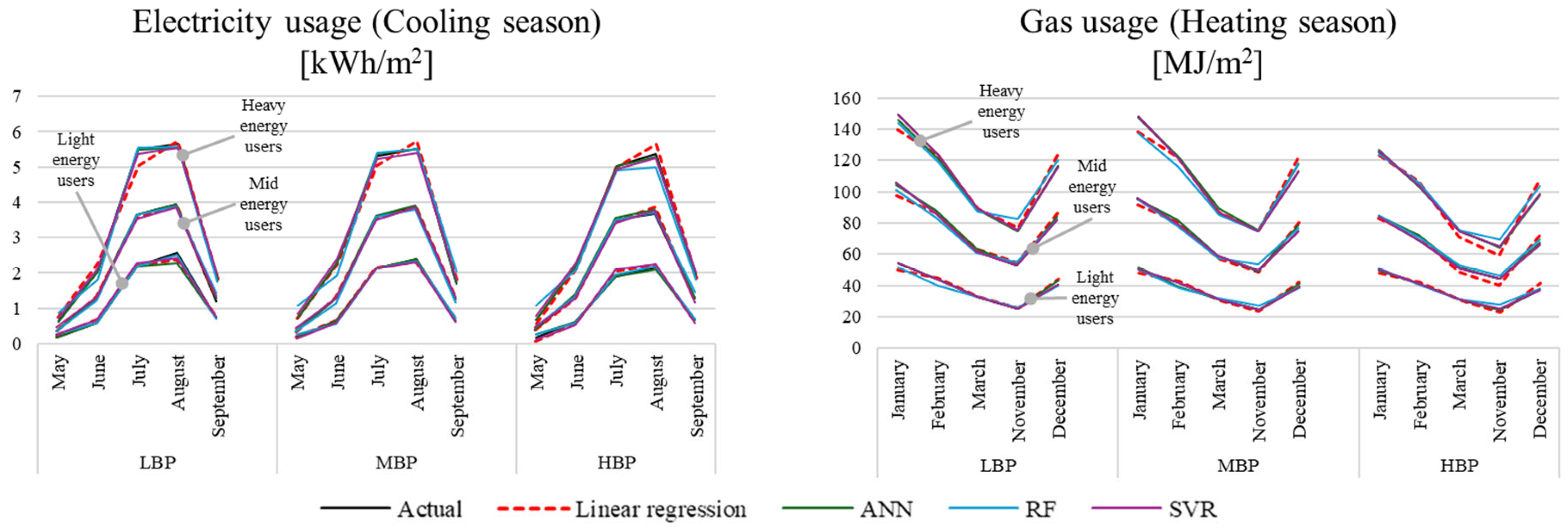
3.3.5. Modeling Performance Analysis
3.4. Virtual Demonstration with Example Cases
4. Conclusions
- Clustering for building energy usage levels was carried out based on actual energy consumption data from day-care center buildings. Heavy user, mid user, and light user groups were identified with reasonable reliability by using the k-means clustering method.
- Regression and machine-learning-based models were developed for each cluster, with inputs including building performance (U-value), weather, building characteristics, and output of monthly energy consumption. All models showed reasonable performance (12% cv(RMSE) in the worst case); the LR model is recommended for practical use owing to its simplicity and applicability to policy and decision-making.
- The evaluation process was demonstrated through virtual examples. To this end, three trajectories of building energy usage levels, calculated using the input variables and the coefficients of the linear model, were compared with the actual monthly energy consumption trajectory.
5. Discussion and Limitations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description | Unit |
| Coefficient derivation | - | |
| Number of data points in cluster k | - | |
| i | Index | - |
| K | Thermal transmittance | W/m2°C |
| n | Total number of data points | - |
| P | Precipitation | Mm |
| Silhouette coefficient score | - | |
| S | Solar radiation | w/m2 |
| T | Outdoor air temperature | ℃ |
| Distance from the centroid | - | |
| Position of a data point | - | |
| X | Independent variable matrix | - |
| Y | Dependent variable matrix | - |
| y | Measured data values | kWh, MJ |
| Maximum children enrollment | No. | |
| Day-care room area | m2 | |
| Estimated regression coefficients | - | |
| Number of day-care staff | No. |
Abbreviations
| ANN | Artificial neural network |
| FAR | Floor area ratio |
| GFA | Gross floor area |
| HVAC | Heating, ventilation, and air-conditioning |
| HBP | High building performance |
| LBP | Low building performance |
| MBP | Mid building performance |
| RF | Random forest |
| RMSE | Root mean square error |
| SVR | Support vector regression |
| TOU | Time of use |
| OAT | Outdoor air temperature |
Subscripts and Superscripts
| elec | Electricity |
| gas | Gas |
| — | Mean function |
| T | Inverse function |
| ⌃ | Predicted/estimated function |
Appendix A
| Institution | Platform Name | Provided Data |
|---|---|---|
| Korea Energy Agency | Building Energy Service Total Platform | -Explanation of building energy systems and civil complaint services -Statistics on building attributes, energy sources -Total energy consumption assessment, building operation efficiency |
| Ministry of Land, Infrastructure and Transport | Architectural Data Open System | -Monthly electricity and gas energy consumption by lot number |
| Apartment Complex Management Information System | -Monthly and yearly statistics on heating, hot water, gas, electricity, water energy usage costs, and energy consumption by apartment complex | |
| Public Building Energy Consumption Information Management System | -Monthly energy consumption of public buildings | |
| Building Energy Consumption Map | -Annual energy consumption by energy source and detailed use for each city and province | |
| Korea Electric Power Corporation | Energy Integrated Platform | -Status of electricity, water, gas, heating energy by district in the pilot city, and renewable energy generation status |
| Ministry of the Interior and Safety | Public Data Portal | -Greenhouse gas emissions from local government buildings -Building energy efficiency rating information -Energy consumption by building (electricity, gas) by lot number -Energy usage information of apartment complexes -Energy consumption by energy source, energy statistics |
| Korea Institute of Energy Technology Evaluation and Planning | Development and Establishment of a Housing Energy Big Data Platform | -Data under development |
| 2018 Electricity | 2019 Electricity | 2018 Gas | 2019 Gas | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| May. | Jun. | Jul. | Aug. | Sep. | May. | Jun. | Jul. | Aug. | Sep. | Jan. | Feb. | Mar. | Nov. | Dec. | Jan. | Feb. | Mar. | Nov. | Dec. | |
| Current children enrollment | 0.48 | 0.49 | 0.55 | 0.52 | 0.53 | 0.47 | 0.51 | 0.54 | 0.5 | 0.54 | 0.43 | 0.45 | 0.5 | 0.3 | 0.43 | 0.39 | 0.43 | 0.5 | 0.2 | 0.48 |
| Maximum children enrollment | 0.41 | 0.41 | 0.47 | 0.45 | 0.48 | 0.4 | 0.43 | 0.46 | 0.43 | 0.47 | 0.41 | 0.47 | 0.47 | 0.28 | 0.4 | 0.38 | 0.47 | 0.47 | 0.14 | 0.44 |
| Number of day-care rooms | 0.17 | 0.18 | 0.24 | 0.2 | 0.22 | 0.17 | 0.2 | 0.23 | 0.2 | 0.22 | 0.17 | 0.25 | 0.26 | 0.08 | 0.19 | 0.14 | 0.24 | 0.23 | 0 | 0.22 |
| Area of day-care rooms | 0.4 | 0.4 | 0.45 | 0.43 | 0.45 | 0.38 | 0.4 | 0.43 | 0.4 | 0.43 | 0.37 | 0.45 | 0.45 | 0.28 | 0.39 | 0.34 | 0.43 | 0.43 | 0.13 | 0.41 |
| Number of playgrounds | 0.22 | 0.23 | 0.27 | 0.24 | 0.27 | 0.21 | 0.23 | 0.24 | 0.2 | 0.25 | 0.17 | 0.24 | 0.24 | 0.12 | 0.21 | 0.18 | 0.25 | 0.24 | 0.02 | 0.25 |
| Number of day-care staff | 0.5 | 0.52 | 0.57 | 0.55 | 0.56 | 0.53 | 0.55 | 0.58 | 0.55 | 0.57 | 0.45 | 0.49 | 0.52 | 0.36 | 0.47 | 0.43 | 0.49 | 0.52 | 0.26 | 0.51 |
| GFA for FAR calculation | 0.77 | 0.76 | 0.77 | 0.78 | 0.77 | 0.81 | 0.81 | 0.8 | 0.81 | 0.8 | 0.69 | 0.72 | 0.73 | 0.57 | 0.69 | 0.68 | 0.72 | 0.76 | 0.46 | 0.69 |
| Approval date | 0.23 | 0.22 | 0.24 | 0.23 | 0.24 | 0.21 | 0.22 | 0.21 | 0.2 | 0.22 | 0.2 | 0.21 | 0.27 | 0.14 | 0.18 | 0.13 | 0.17 | 0.24 | 0.04 | 0.16 |
| Building coverage ratio | −0.08 | −0.06 | −0.05 | −0.05 | −0.07 | −0.1 | −0.09 | −0.08 | −0.09 | −0.07 | −0.03 | −0.01 | −0.04 | −0.05 | −0.02 | −0.01 | −0.04 | −0.06 | −0.01 | −0.02 |
| Floor area ratio | 0.19 | 0.2 | 0.23 | 0.21 | 0.2 | 0.18 | 0.2 | 0.21 | 0.2 | 0.21 | 0.18 | 0.23 | 0.18 | 0.12 | 0.2 | 0.22 | 0.22 | 0.2 | 0.17 | 0.23 |
| Building height | 0.45 | 0.44 | 0.48 | 0.46 | 0.44 | 0.48 | 0.48 | 0.49 | 0.49 | 0.47 | 0.44 | 0.48 | 0.48 | 0.35 | 0.45 | 0.44 | 0.46 | 0.5 | 0.33 | 0.44 |
| Building area | 0.75 | 0.72 | 0.71 | 0.74 | 0.74 | 0.76 | 0.75 | 0.73 | 0.74 | 0.75 | 0.67 | 0.67 | 0.71 | 0.55 | 0.64 | 0.63 | 0.64 | 0.7 | 0.41 | 0.62 |
| No. of above-ground floor | 0.33 | 0.35 | 0.39 | 0.36 | 0.33 | 0.36 | 0.38 | 0.4 | 0.39 | 0.37 | 0.35 | 0.38 | 0.35 | 0.26 | 0.35 | 0.38 | 0.41 | 0.39 | 0.26 | 0.38 |
| No. of underground floors | 0.25 | 0.25 | 0.24 | 0.26 | 0.23 | 0.28 | 0.26 | 0.25 | 0.28 | 0.27 | 0.22 | 0.19 | 0.17 | 0.25 | 0.24 | 0.25 | 0.24 | 0.22 | 0.27 | 0.26 |
References
- IEA. Energy Efficiency 2023; IEA: Paris, France, 2023; Available online: https://www.iea.org/reports/energy-efficiency-2023 (accessed on 14 September 2025).
- IRENA. World Energy Transitions Outlook; IRENA: Abu Dhabi, United Arab Emirates, 2023; Available online: https://www.iea.org/reports/world-energy-outlook-2023 (accessed on 14 September 2025).
- European Commission. European Green Deal: Energy Efficiency Directive Adopted, Helping Make the EU ‘Fit for 55′; European Commission: Brussels, Belgium, 2023; Available online: https://energy.ec.europa.eu/news/european-green-deal-energy-efficiency-directive-adopted-helping-make-eu-fit-55-2023-07-25_en (accessed on 14 September 2025).
- US Environmental Protection Agency. Energy Star Program Overview; US Environmental Protection Agency: Washington, DC, USA, 2023.
- Laaroussi, Y.; Bahrar, M.; el Mankibi, M.; Draoui, A.; Si-Larbi, A. Occupant presence and behavior: A major issue for building energy performance simulation and assessment. Sustain. Cities Soc. 2020, 63, 102420. [Google Scholar] [CrossRef]
- Crawley, D.B.; Lawrie, L.K.; Winkelmann, F.C.; Buhl, W.F.; Huang, Y.J.; Pedersen, C.O.; Strand, R.K.; Liesen, R.J.; Fisher, D.E.; Witte, M.J.; et al. EnergyPlus: Creating a new-generation building energy simulation program. Energy Build. 2001, 33, 319–331. [Google Scholar] [CrossRef]
- TRNSYS (A TRaNsient SYstems Simulation Program). Available online: https://trnsys.org/ (accessed on 14 September 2025).
- Prototype Building Models. Available online: https://www.energycodes.gov/prototype-building-models (accessed on 14 September 2025).
- BPD (Building Performance Database). Department of Energy, United States. 2014. Available online: https://bpd.lbl.gov (accessed on 14 September 2025).
- Granderson, J.; Lin, G.; Chen, Y.; Casillas, A.; Wen, J.; Chen, Z.; Im, P.; Huang, S.; Ling, J. A labeled dataset for building HVAC systems operating in faulted and fault-free states. Sci. Data 2023, 10, 342. [Google Scholar] [CrossRef] [PubMed]
- Na, W.; Liu, S. Benchmarking building energy consumption for space heating using an empirical Bayesian approach with urban-scale energy model. Energy Build. 2024, 320, 114581. [Google Scholar] [CrossRef]
- Yoon, Y.; Jung, S.; Im, P.; Gehl, A. Datasets of a Multizone Office Building under Different HVAC System Operation Scenarios. Sci. Data 2022, 9, 775. [Google Scholar] [CrossRef] [PubMed]
- Arjunan, P.; Poolla, K.; Miller, C. BEEM: Data-driven building energy benchmarking for Singapore. Energy Build. 2022, 260, 111869. [Google Scholar] [CrossRef]
- Li, T.; Bie, H.; Lu, Y.; Sawyer, A.O.; Loftness, V. MEBA: AI-powered precise building monthly energy benchmarking approach. Appl. Energy 2024, 359, 122716. [Google Scholar] [CrossRef]
- Park, H.S.; Lee, M.; Kang, H.; Hong, T.; Jeong, J. Development of a new energy benchmark for improving the operational rating system of office buildings using various data-mining techniques. Appl. Energy 2016, 173, 225–237. [Google Scholar] [CrossRef]
- Luo, N.; Wang, Z.; Blum, D.; Weyandt, C.; Bourassa, N.; Piette, M.A.; Hong, T. A three-year dataset supporting research on building energy management and occupancy analytics. Sci. Data 2022, 9, 156. [Google Scholar] [CrossRef]
- Lee, K.; Lim, H.; Hwang, J.; Lee, D. Development of building benchmarking index for improving gross-floor-area-based energy use intensity. Energy Build. 2025, 328, 115103. [Google Scholar] [CrossRef]
- Piscitelli, M.S.; Giudice, R.; Capozzoli, A. A holistic time series-based energy benchmarking framework for applications in large stocks of buildings. Appl. Energy 2024, 357, 122550. [Google Scholar] [CrossRef]
- Piscitelli, M.S.; Razzano, G.; Buscemi, G.; Capozzoli, A. An interpretable data analytics-based energy benchmarking process for supporting retrofit decisions in large residential building stocks. Energy Build. 2025, 328, 115115. [Google Scholar] [CrossRef]
- Roth, J.; Lim, B.; Jain, R.K.; Grueneich, D. Examining the feasibility of using open data to benchmark building energy usage in cities: A data science and policy perspective. Energy Policy 2020, 139, 111327. [Google Scholar] [CrossRef]
- Liu, C.; Li, Y.; Chen, H.; Xing, L.; Zhang, S. Energy-saving potential benchmarking method of office buildings based on probabilistic forecast. J. Build. Eng. 2024, 95, 110282. [Google Scholar] [CrossRef]
- Zheng, P.; Zhou, H.; Liu, J.; Nakanishi, Y. Interpretable building energy consumption forecasting using spectral clustering algorithm and temporal fusion transformers architecture. Appl. Energy 2023, 349, 121607. [Google Scholar] [CrossRef]
- Piselli, C.; Pisello, A.L. Occupant behavior long-term continuous monitoring integrated to prediction models: Impact on office building energy performance. Energy 2019, 176, 667–681. [Google Scholar] [CrossRef]
- Nazeriye, M.; Haeri, A.; Haghighat, F.; Panchabikesan, K. Understanding the influence of building characteristics on enhancing energy efficiency in residential buildings: A data mining based study. J. Build. Eng. 2021, 43, 103069. [Google Scholar] [CrossRef]
- Kim, H.; Ham, S.; Promann, M.; Devarapalli, H.; Bihani, G.; Ringenberg, T.; Kwarteng, V.; Bilionis, I.; Braun, J.E.; Rayz, J.T.; et al. MySmartE—An eco-feedback and gaming platform to promote energy conserving thermostat-adjustment behaviors in multi-unit residential buildings. Build. Environ. 2022, 221, 109252. [Google Scholar] [CrossRef]
- Kim, H.; Bilionis, I.; Karava, P.; Braun, J.E. Human decision making during eco-feedback intervention in smart and connected energy-aware communities. Energy Build. 2023, 278, 112627. [Google Scholar] [CrossRef]
- Zhu, J.; Shen, Y.; Song, Z.; Zhou, D.; Zhang, Z.; Kusiak, A. Data-driven building load profiling and energy management. Sustain. Cities Soc. 2019, 49, 101587. [Google Scholar] [CrossRef]
- Trotta, G. An empirical analysis of domestic electricity load profiles: Who consumes how much and when? Appl. Energy 2020, 275, 115399. [Google Scholar] [CrossRef]
- Ciulla, G.; D’Amico, A. Building energy performance forecasting: A multiple linear regression approach. Appl. Energy 2019, 253, 113500. [Google Scholar] [CrossRef]
- Olu-Ajayi, R.; Alaka, H.; Sulaimon, I.; Sunmola, F.; Ajayi, S. Building energy consumption prediction for residential buildings using deep learning and other machine-learning techniques. J. Build. Eng. 2022, 45, 103406. [Google Scholar] [CrossRef]
- Shi, Z.; Wu, L.; Zhou, Y. Predicting household energy consumption in an aging society. Appl. Energy 2023, 352, 121899. [Google Scholar] [CrossRef]
- Tang, W.; Wang, H.; Lee, X.L.; Yang, H.T. Machine-learning approach to uncovering residential energy consumption patterns based on socioeconomic and smart meter data. Energy 2022, 240, 122500. [Google Scholar] [CrossRef]
- Li, X.; Yao, R. A machine-learning-based approach to predict residential annual space heating and cooling loads considering occupant behaviour. Energy 2020, 212, 118676. [Google Scholar] [CrossRef]
- Kamel, E.; Sheikh, S.; Huang, X. Data-driven predictive models for residential building energy use based on the segregation of heating and cooling days. Energy 2020, 206, 118045. [Google Scholar] [CrossRef]
- Konstantakopoulos, I.C.; Barkan, A.R.; He, S.; Veeravalli, T.; Liu, H.; Spanos, C. A deep learning and gamification approach to improving human-building interaction and energy efficiency in smart infrastructure. Appl. Energy 2019, 237, 810–821. [Google Scholar] [CrossRef]
- Wei, P.; Xia, S.; Chen, R.; Qian, J.; Li, C.; Jiang, X. A Deep-Reinforcement-Learning-Based Recommender System for Occupant-Driven Energy Optimization in Commercial Buildings. IEEE Internet Things J. 2020, 7, 6402–6413. [Google Scholar] [CrossRef]
- Motlagh, O.; Berry, A.; O’Neil, L. Clustering of residential electricity customers using load time series. Appl. Energy 2019, 237, 11–24. [Google Scholar] [CrossRef]
- Zhang, X.; Ramírez-Mendiola, J.L.; Li, M.; Guo, L. Electricity consumption pattern analysis beyond traditional clustering methods: A novel self-adapting semi-supervised clustering method and application case study. Appl. Energy 2022, 308, 118335. [Google Scholar] [CrossRef]
- Wang, C.; Du, Y.; Li, H.; Wallin, F.; Min, G. New methods for clustering district heating users based on consumption patterns. Appl. Energy 2019, 251, 113373. [Google Scholar] [CrossRef]
- Duan, J.; Li, N.; Peng, J.; Liu, Q.; Peng, T.; Wang, S. Clustering and prediction of space cooling and heating energy consumption in high-rise residential buildings with the influence of occupant behaviour: Evidence from a survey in Changsha, China. J. Build. Eng. 2023, 76, 107418. [Google Scholar] [CrossRef]
- Wang, S.; Liu, H.; Pu, H.; Yang, H. Spatial disparity and hierarchical cluster analysis of final energy consumption in China. Energy 2020, 197, 117195. [Google Scholar] [CrossRef]
- Yilmaz, S.; Chambers, J.; Patel, M.K. Comparison of clustering approaches for domestic electricity load profile characterisation—Implications for demand side management. Energy 2019, 180, 665–677. [Google Scholar] [CrossRef]
- Park, S.H.; Lee, S.M.; Ahn, N.H. A Case Study on Pilot Application of Building Diagnosis Evaluation Method Considering Architectural and Mechanical Elements. J. Korean Inst. Archit. Sustain. Environ. Build. Syst. 2020, 14, 439–450. [Google Scholar] [CrossRef]
- Ministry of Land Infrastructure and Transport. Open Service Sector. Available online: https://www.hub.go.kr/portal/main.do (accessed on 14 September 2025).
- Korea Meteorological Administration, Automated Synoptic Observing System. Available online: https://data.kma.go.kr/data/grnd/selectAsosRltmList.do;jsessionid=ES0sOzyo9y0irTs93l8JXjm7aCYA6wRNl8Yf7tBbNgzkFavt7C0kRv6ChttkH4Fl.was01_servlet_engine5?pgmNo=36 (accessed on 14 September 2025).
- Tahmasebinia, F.; He, R.; Chen, J.; Wang, S.; Sepasgozar, S.M.E. Building Energy Performance Modeling through Regression Analysis: A Case of Tyree Energy Technologies Building at UNSW Sydney. Buildings 2023, 13, 1089. [Google Scholar] [CrossRef]
- Saxena, A.; Prasad, M.; Gupta, A.; Bharill, N.; Patel, O.P.; Tiwari, A.; Er, M.J.; Ding, W.; Lin, C.T. A review of clustering techniques and developments. Neurocomputing 2017, 267, 664–681. [Google Scholar] [CrossRef]
- Alzubi, J.; Nayyar, A.; Kumar, A. Machine Learning from Theory to Algorithms: An Overview. J. Phys. Conf. Ser. 2018, 1142, 012012. [Google Scholar] [CrossRef]
- Jung, S.H.; Kim, J.C.; Kim, C.Y.; Yoo, K.S.; Shim, C.B. A Study on Cluster-based Classification Evaluation Prediction Model for Measuring the Accuracy of Unsupervised Learning Data. J. Korea Multimed. Soc. 2018, 21, 779–786. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Chong, A.; Augenbroe, G.; Yan, D. Occupancy data at different spatial resolutions: Building energy performance and model calibration. Appl. Energy 2021, 286, 116492. [Google Scholar] [CrossRef]
- Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): When to use them or not. In Geoscientific Model Development; Copernicus GmbH: Göttingen, Germany, 2022; Volume 15, pp. 5481–5487. [Google Scholar] [CrossRef]
- Ruiz, G.R.; Bandera, C.F. Validation of calibrated energy models: Common errors. Energies 2017, 10, 1587. [Google Scholar] [CrossRef]





| Category | Data Name | Data Scope | Data Content |
|---|---|---|---|
| Ministry of Land, Infrastructure and Transport (Architectural Data Open System) | Building register | Basic overview General title section | General title section PK *, Title section PK *, Land address, Approval date, Building area, Gross floor area (GFA) for floor area ratio (FAR) calculation, Building coverage ratio, Gross floor area (GFA), Number of above-ground floors, Number of underground floors, Main use code, Other use code, Number of households, etc. |
| Monthly energy usage | Electricity usage Gas usage | Usage year and month, Usage purpose code, Supply institution code, Monthly energy consumption | |
| Ministry of Health and Welfare (Day-care Centers) | Day-care center information disclosure portal | Seoul, South Korea | Day-care center type, Address, Number of day-care rooms, Area of day-care rooms, Number of playgrounds, Number of staff, Maximum children enrollment, Current children enrollment, School bus operation status |
| Korea Meteorological Administration | Weather data | Seoul, South Korea | Monthly average outdoor temperature, Outdoor solar radiation, Precipitation |
| Year | Public | Social Welfare Corporation | Corporate Organizations | Workplace Based | Home Based | Cooperative | Private | Total |
|---|---|---|---|---|---|---|---|---|
| 2018 | 442/1825 | 8/20 | 26/82 | 0/304 | 0/1362 | 10/26 | 490/1006 | 976/4625 |
| 2019 | 442/1825 | 8/20 | 26/82 | 0/304 | 0/1362 | 10/26 | 490/1006 | 976/4625 |
| 2018 | 2019 | ||||||
|---|---|---|---|---|---|---|---|
| Outdoor Air Temperature (℃) | Solar Radiation (MJ/m2) | Precipitation (mm) | Outdoor Air Temperature (℃) | Solar Radiation (MJ/m2) | Precipitation (mm) | ||
| Cooling season | min | 7.00 | 0 | 0 | 8.50 | 0 | 0 |
| max | 39.40 | 35.00 | 3.52 | 36.70 | 20.40 | 3.59 | |
| avg | 23.95 | 1.47 | 1.22 | 23.62 | 1.19 | 1.16 | |
| Heating season | min | −17.80 | 0 | 0 | −10.80 | 0 | 0 |
| max | 21.80 | 2.99 | 18.00 | 22.00 | 3.05 | 12.40 | |
| avg | 1.97 | 0.84 | 1.39 | 3.26 | 0.88 | 1.11 | |
| Group | Public | Social Welfare Corporation | Corporate Organizations | Cooperative | Private | Total |
|---|---|---|---|---|---|---|
| Low building performance (LBP) group | 58/33.0% | 2/1.1% | 8/4.5% | 4/2.3% | 104/59.1% | 176/100% |
| Mid building performance (MBP) group | 410/43.4% | 8/0.8% | 36/3.8% | 8/0.8% | 482/51.1% | 944/100% |
| High building performance (HBP) group | 416/50.0% | 6/0.7% | 8/1.0% | 8/1.0% | 394/47.4% | 832/100% |
| Parameter | Value |
|---|---|
| Number of clusters | 3 |
| Initialization | k-means++ |
| Maximum number of iterations | 300 |
| Tolerance | 1 × 10−4 |
| Electricity | Light User Cluster | Mid User Cluster | Heavy User Cluster | |
|---|---|---|---|---|
| Electricity usage (Heating season) | Low building performance group | 0.61 | 0.56 | 0.65 |
| Mid building performance group | 0.60 | 0.55 | 0.59 | |
| High building performance group | 0.63 | 0.54 | 0.53 | |
| Gas usage (Cooling season) | Low building performance group | 0.56 | 0.54 | 0.59 |
| Mid building performance group | 0.58 | 0.56 | 0.53 | |
| High building performance group | 0.56 | 0.57 | 0.52 |
| Coefficient | Electricity (Cooling Season) | Gas (Heating Season) | ||||
|---|---|---|---|---|---|---|
| Light Energy Users | Mid Energy Users | Heavy Energy Users | Light Energy Users | Mid Energy Users | Heavy Energy Users | |
| −5.26536 | −6.92537 | −9.11922 | 39.95922 | 77.37089 | 116.2422 | |
| 0.088502 | 0.030367 | 0.015953 | 1.403744 | 8.030171 | 6.582097 | |
| 0.241582 | 0.368555 | 0.495517 | −1.25577 | −2.38423 | −4.23574 | |
| 0.00222 | 0.002569 | 0.003773 | −0.16026 | −0.21441 | −0.22728 | |
| 0.000477 | −0.00038 | −0.0005 | 0.004554 | −0.00473 | 0.002597 | |
| 0.000493 | −0.00018 | −0.00372 | 0.07374 | 0.002679 | −0.08007 | |
| −0.00024 | −0.00024 | 0.000053 | 0.002433 | −0.00533 | 0.012607 | |
| 0.007898 | 0.005787 | 0.023746 | −0.17032 | 0.134137 | 0.184771 | |
| Artificial Neural Network | Hidden Layer Size (2:2:30) | Num Hidden Layer (1:3) | |
|---|---|---|---|
| Electricity | Light energy users | 20 | 1 |
| Mid energy users | 2 | 1 | |
| High energy users | 6 | 3 | |
| Gas | Light energy users | 6 | 1 |
| Mid energy users | 4 | 1 | |
| High energy users | 2 | 1 | |
| Random Forest | Number of Trees (2:2:30) | Leaf Size (1:5) | Number of Splits (10:50) | |
|---|---|---|---|---|
| Electricity | Light energy users | 22 | 1 | 20 |
| Mid energy users | 12 | 1 | 20 | |
| High energy users | 10 | 1 | 10 | |
| Gas | Light energy users | 12 | 1 | 20 |
| Mid energy users | 20 | 1 | 10 | |
| High energy users | 24 | 1 | 10 | |
| Support Vector Regression | Kernel Function | Box Constraints (10:100) | Kernel Scales (1:10) | Epsilon Values (0.1:0.5) | |
|---|---|---|---|---|---|
| Electricity (Cooling season) | Light energy users | Linear | 10 | 1 | 0.1 |
| Mid energy users | Linear | 10 | 1 | 0.1 | |
| High energy users | Gaussian | 10 | 1 | 0.1 | |
| Gas (Heating season) | Light energy users | Gaussian | 100 | 10 | 0.1 |
| Mid energy users | Gaussian | 100 | 10 | 0.1 | |
| High energy users | Gaussian | 100 | 10 | 0.1 | |
| R2 | RMSE [kWh/m2] | cv(RMSE) [%] | R2 | RMSE [kWh/m2] | cv(RMSE) [%] | R2 | RMSE [kWh/m2] | cv(RMSE) [%] | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Low energy users | Mid energy users | Heavy energy users | ||||||||
| LBP | Linear regression | 0.994118 | 0.104826 | 8.5% | 0.998948 | 0.063719 | 5.2% | 0.989753 | 0.231576 | 18.7% |
| ANN | 0.990533 | 0.13388 | 10.8% | 0.999623 | 0.031558 | 2.6% | 0.999765 | 0.043285 | 3.5% | |
| RF | 0.997805 | 0.06163 | 5.0% | 0.993981 | 0.115851 | 9.4% | 0.993475 | 0.167057 | 13.5% | |
| SVR | 0.994299 | 0.098917 | 8.0% | 0.998838 | 0.103214 | 8.4% | 0.999859 | 0.099985 | 8.1% | |
| avg | 0.994189 | 0.099813 | 8.1% | 0.997847 | 0.078585 | 6.4% | 0.995713 | 0.135476 | 11.0% | |
| Low energy users | Mid energy users | Heavy energy users | ||||||||
| MBP | Linear regression | 0.999305 | 0.029281 | 2.4% | 0.999503 | 0.035736 | 2.9% | 0.992428 | 0.169729 | 13.7% |
| ANN | 1 | 6.68 × 10−11 | 0.0% | 0.999998 | 0.017767 | 1.4% | 0.999914 | 0.024576 | 2.0% | |
| RF | 0.996162 | 0.0652 | 5.3% | 0.998489 | 0.084114 | 6.8% | 0.982708 | 0.272112 | 22.0% | |
| SVR | 0.998885 | 0.05428 | 4.4% | 0.999595 | 0.070633 | 5.7% | 0.999821 | 0.09985 | 8.1% | |
| avg | 0.998588 | 0.03719 | 3.0% | 0.999396 | 0.052063 | 4.2% | 0.993718 | 0.141567 | 11.5% | |
| Low energy users | Mid energy users | Heavy energy users | ||||||||
| HBP | Linear regression | 0.998373 | 0.097285 | 7.9% | 0.996031 | 0.102991 | 8.3% | 0.997322 | 0.147886 | 12.0% |
| ANN | 0.997925 | 0.048298 | 3.9% | 0.999881 | 0.061612 | 5.0% | 0.999759 | 0.040015 | 3.2% | |
| RF | 0.99645 | 0.05545 | 4.5% | 0.997087 | 0.095503 | 7.7% | 0.99154 | 0.256596 | 20.8% | |
| SVR | 0.996552 | 0.1154 | 9.3% | 0.994711 | 0.097816 | 7.9% | 0.999744 | 0.100017 | 8.1% | |
| avg | 0.997325 | 0.079108 | 6.4% | 0.996927 | 0.089481 | 7.2% | 0.997091 | 0.136129 | 11.0% | |
| R2 | RMSE [MJ/m2] | cv(RMSE) [%] | R2 | RMSE [MJ/m2] | cv(RMSE) [%] | R2 | RMSE [MJ/m2] | cv(RMSE) [%] | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Light energy users | Mid energy users | Heavy energy users | ||||||||
| LBP | Linear regression | 0.94701 | 2.44818 | 6.3% | 0.95967 | 4.47853 | 11.6% | 0.95658 | 5.68368 | 14.7% |
| ANN | 0.99284 | 0.98321 | 2.5% | 0.99566 | 1.58536 | 4.1% | 0.99837 | 1.88102 | 4.9% | |
| RF | 0.98868 | 2.23891 | 5.8% | 0.99469 | 2.55713 | 6.6% | 0.97710 | 4.95031 | 12.8% | |
| SVR | 0.99998 | 0.09309 | 0.2% | 0.99999 | 0.09974 | 0.3% | 1.00000 | 0.09807 | 0.3% | |
| avg | 0.98213 | 1.44085 | 3.7% | 0.98750 | 2.18019 | 5.6% | 0.98301 | 3.15327 | 8.1% | |
| Light energy users | Mid energy users | Heavy energy users | ||||||||
| MBP | Linear regression | 0.96270 | 1.76793 | 4.6% | 0.95564 | 3.47618 | 9.0% | 0.94656 | 6.13855 | 15.8% |
| ANN | 0.97312 | 1.52985 | 3.9% | 0.98765 | 2.14162 | 5.5% | 0.99552 | 2.24808 | 5.8% | |
| RF | 0.96755 | 1.90482 | 4.9% | 0.98755 | 2.22949 | 5.8% | 0.96780 | 5.84998 | 15.1% | |
| SVR | 0.99996 | 0.09995 | 0.3% | 0.99999 | 0.10041 | 0.3% | 1.00000 | 0.10070 | 0.3% | |
| avg | 0.97583 | 1.32564 | 3.4% | 0.98271 | 1.98692 | 5.1% | 0.97747 | 3.58432 | 9.2% | |
| Light energy users | Mid energy users | Heavy energy users | ||||||||
| HBP | Linear regression | 0.92854 | 2.42215 | 6.2% | 0.95784 | 3.76364 | 9.7% | 0.95725 | 5.36451 | 13.8% |
| ANN | 0.99843 | 0.38428 | 1.0% | 0.99447 | 1.72604 | 4.5% | 0.99936 | 0.55318 | 1.4% | |
| RF | 0.98893 | 1.29992 | 3.4% | 0.99684 | 2.23679 | 5.8% | 0.98631 | 3.64071 | 9.4% | |
| SVR | 0.99996 | 0.09991 | 0.3% | 0.99999 | 0.09964 | 0.3% | 1.00000 | 0.09852 | 0.3% | |
| avg | 0.97897 | 1.05157 | 2.7% | 0.98729 | 1.95653 | 5.0% | 0.98573 | 2.41423 | 6.2% | |
| May | June | July | August | September | RMSE Between Actual Usage and Example | ||
|---|---|---|---|---|---|---|---|
| Example 1 | Heavy users | 1.35 | 2.80 | 5.58 | 6.02 | 2.19 | 3.81 |
| Mid users | 0.51 | 1.08 | 3.61 | 3.89 | 1.46 | 0.96 (√) | |
| Light users | 0.15 | 0.66 | 2.21 | 2.53 | 0.55 | 2.19 | |
| Actual usage | 0.25 | 1.05 | 4.00 | 3.72 | 0.63 | ||
| Example 2 | Heavy users | 1.17 | 2.53 | 5.64 | 5.90 | 2.16 | 2.88 (√) |
| Mid users | 0.54 | 1.07 | 3.54 | 3.77 | 1.40 | 4.37 | |
| Light users | 0.14 | 0.62 | 2.10 | 2.34 | 0.47 | 6.35 | |
| Actual usage | 0.01 | 0.73 | 5.34 | 7.70 | 1.55 | ||
| Example 3 | Heavy users | 1.21 | 2.58 | 5.63 | 5.91 | 2.09 | 5.61 |
| Mid users | 0.52 | 1.03 | 3.54 | 3.76 | 1.39 | 2.25 | |
| Light users | 0.13 | 0.64 | 2.17 | 2.42 | 0.49 | 0.99 (√) | |
| Actual usage | 0.01 | 0.00 | 2.66 | 2.71 | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Choi, K.; Mo, C.-H.; Talib, A.; Park, S.; Kim, D.-W.; Joe, J. Development of Evaluation Model for Building Energy Usage: Methodology Development and Case Study on Day-Care Centers in South Korea. Sustainability 2025, 17, 8339. https://doi.org/10.3390/su17188339
Park J, Choi K, Mo C-H, Talib A, Park S, Kim D-W, Joe J. Development of Evaluation Model for Building Energy Usage: Methodology Development and Case Study on Day-Care Centers in South Korea. Sustainability. 2025; 17(18):8339. https://doi.org/10.3390/su17188339
Chicago/Turabian StylePark, Jinhyung, Kwangwon Choi, Chan-Hyuk Mo, Abu Talib, Semi Park, Deuk-Woo Kim, and Jaewan Joe. 2025. "Development of Evaluation Model for Building Energy Usage: Methodology Development and Case Study on Day-Care Centers in South Korea" Sustainability 17, no. 18: 8339. https://doi.org/10.3390/su17188339
APA StylePark, J., Choi, K., Mo, C.-H., Talib, A., Park, S., Kim, D.-W., & Joe, J. (2025). Development of Evaluation Model for Building Energy Usage: Methodology Development and Case Study on Day-Care Centers in South Korea. Sustainability, 17(18), 8339. https://doi.org/10.3390/su17188339






