Biodiversity Resilience in Terms of Evolutionary Mass, Velocity and Force
Abstract
1. Introduction
2. Materials and Methods
2.1. The Relationship of Characters and Their Evolutionary Vehicles
2.2. The Models
3. Results
3.1. Units of Measurement
3.1.1. Process
3.1.2. Mass
3.1.3. Distance
3.1.4. Time
- (1)
- Microgenera are inferred as originating in a burst of speciation, on the order of 22 million years (my) in extent from data on the recent West Indies diversification [8], but there are also arguments for 27 my evolution-modifying intervals [41] and 32 my cycles [42]. In a massive molecular phylogenetic analysis of the bryophytes [43], with 29 fossil calibrations, the crown age of the Pottiaceae (77 genera, ca. 1209 species) was estimated at 133.3 (115–150) mya, while the majority of bryophyte families diversified during the Cretaceous terrestrial revolution. There would then be an estimated 133/(22–32) or 4 to 5 caulon units for Pottiaceae in that time. Timewise anchorage is also provided by a study of the pottiaceous genus Syntrichia by [44] who used the late Cretaceous fossil Cynodontium luthii for calibration.
- (2)
- Two microgenera of extant Pottiaceae, Chionoloma and Tainoa are largely restricted to the West Indies where their estimated age of origination is 22 mya [8], about halfway through the existence of this area. One has a species of secondary ancestry. This period here is assigned to each caulon unit (caulogram distance between serial microgenus progenitors) as a morphological clock.
- (3)
- Ignatov and Maslova [46] described fossils of mosses prior to late Cretaceous as having a quite different morphology from that of modern species, implying a vastly different set of morphological characters—a set different than that in the present study serving as evolutionary mass. The earliest fossils of modern genera (Campylopodium and Cynodontium) are, according to Ignatov and Maslova, from the late Cretaceous. Thus, the species and genera in the present study (Pottiaceae and its segregate Streptotrichaceae) are estimated to be between 22 and 110 my in age. The results of this study found 5 caulon units in Streptotrichaceae and 3 in Pleuroweisieae, each unit considered circa 22 my in duration, which fit the above scales.
3.1.5. Velocity
3.1.6. Equilibrium
3.1.7. Momentum
3.1.8. Acceleration
3.1.9. Force
3.2. Simplification of Calculations
3.3. The Streptotrichaceae Caulogram
3.4. The Pottiaceae Tribe Pleuroweisieae Caulogram
3.5. Comparison of Caulograms
3.6. Comparison of Species per Genus and Traits per Species
3.7. Graphs Limited to Immediate Descendants
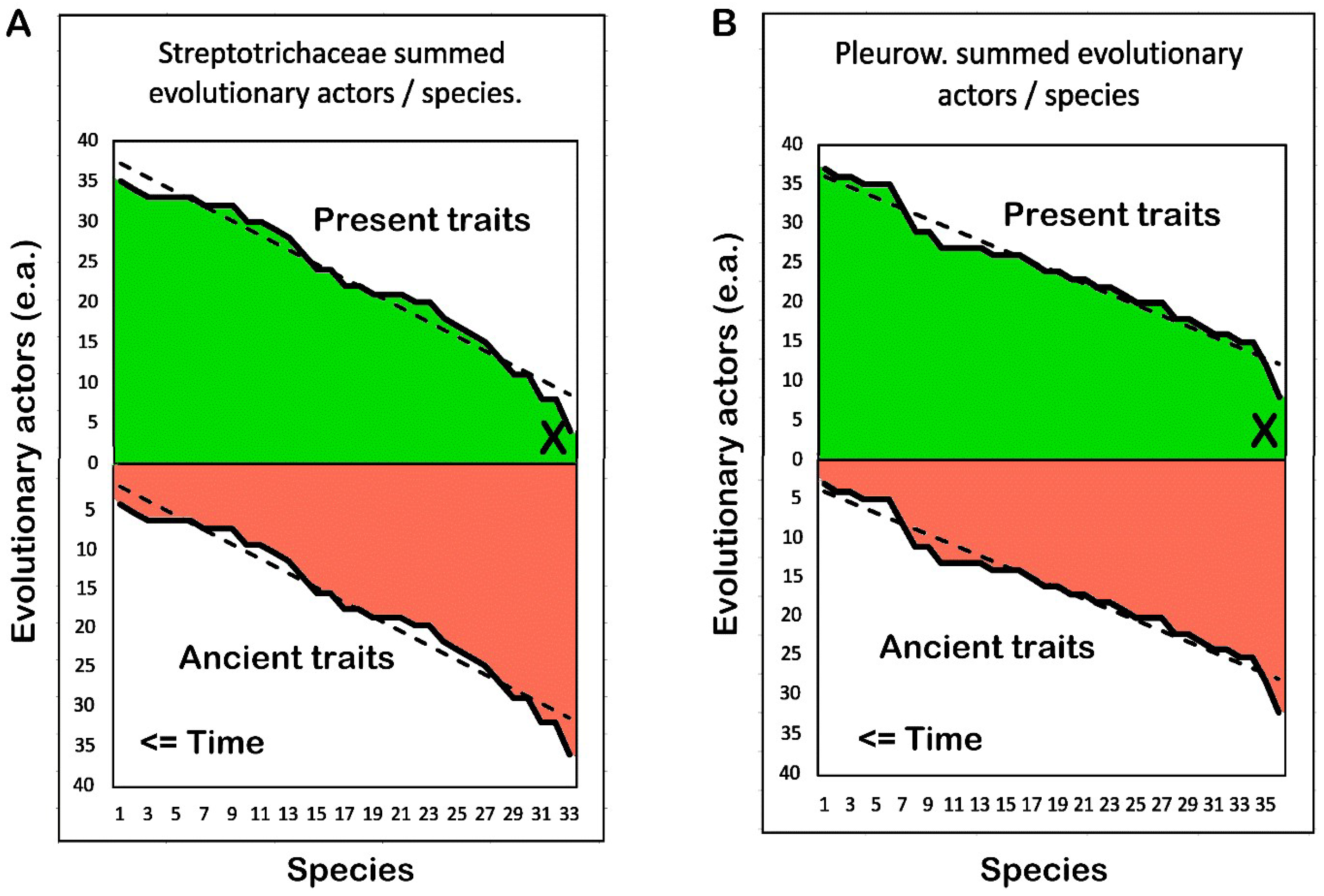
3.8. Comparison of Summed Evolutionary Actors per Species
3.9. Combined Streptotrichaceae and Pleuroweisieae Data
3.10. Streptotrichaceae and Pleuroweisieae Through 220 MY
4. Discussion
4.1. Inferred Speciation over 220 MY
4.2. Heuristic Parallels
4.3. Why Not Use Molecular Techniques?
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Currie, D.J. Energy and large-scale patterns of animal- and plant-species richness. Am. Nat. 1991, 137, 27–49. [Google Scholar] [CrossRef]
- Fagenblat, M.; De Meester, L.; Urban, M.C. Dispersal evolution alters evolution-mediated priority effects in a metacommunity. Philos. Trans. R. Soc. B Biol. Sci. 2024, 379, 20230129. [Google Scholar] [CrossRef]
- Lynch, M. Methods for the analysis of comparative data in evolutionary biology. Evolution 1991, 45, 1065–1080. [Google Scholar] [CrossRef] [PubMed]
- Watts, A.A.; Birks, H.J.B.; Willis, K.J.; Birks, H.H. What drives biodiversity patterns? Using long-term environmental datasets to understand recent biodiversity trends. J. Ecol. 2020, 108, 1365–2745. [Google Scholar]
- Willig, M.R.; Kaufman, D.M.; Stevens, R.D. Latitudinal gradients of biodiversity: Pattern, process, scale, and synthesis. Ann. Rev. Ecol. Evol. Syst. 2003, 34, 273–309. [Google Scholar] [CrossRef]
- Lai, J.; Ye, M.; Hou, M.; Zhang, A.; Wang, G.; Mao, L. Evaluating the relative importance of phylogeny and predictors in phylogenetic generalized linear models using the phylolm.hp R package. Plant Divers. 2025; in press. [Google Scholar] [CrossRef]
- Uyeda, J.C.; Zenil-Ferguson, R.; Pennell, M.W. Rethinking phylogenetic comparative methods. Syst. Biol. 2018, 67, 1091–1109. [Google Scholar] [CrossRef]
- Zander, R.H. Fractal Evolution, Complexity and Systematics; Zetetic Publications: St. Louis, MO, USA, 2023. [Google Scholar]
- Zander, R.H. Integrative systematics with structural monophyly and ancestral signatures: Chionoloma (Bryophyta). Acad. Biol. 2024, 2, 1–14. [Google Scholar] [CrossRef]
- Camp, W.H. The concept of genus: V. Our changing generic concepts. Bull. Torrey Bot. Club 1940, 67, 381–389. [Google Scholar] [CrossRef]
- Humphreys, A.; Linder, H.P. Concept versus data in delimitation of plant genera. Taxon 2009, 58, 1054–1074. [Google Scholar] [CrossRef]
- Malik, V. The genus: A natural or arbitrary entity. Plant Arch. 2017, 17, 251–257. [Google Scholar]
- Gingerich, P.D. Rates of evolution on the time scale of the evolutionary process. Genetica 2001, 112–113, 127–144. [Google Scholar] [CrossRef]
- Haldane, J.B.S. Suggestions as to quantitative measurement of rates of evolution. Evolution 1949, 3, 51–56. [Google Scholar] [CrossRef] [PubMed]
- Lynch, M.; Lande, R. Evolution and extinction in response to environmental change. Evol. Ecol. 1993, 7, 318–339. [Google Scholar]
- Moutinho, M.; Amorim, M.; Campos, P. Gene expression and the rate of adaptive and nonadaptive evolution. Genome Biol. Evol. 2019, 11, 522–532. [Google Scholar]
- Ogburn, N.D.; Edwards, E.J. Rates of morphological evolution are heterogeneous in Early Cretaceous angiosperms. Proc. Roy. Soc. B Biol. Sci. 2016, 283, 20160214. [Google Scholar]
- Rabosky, D.L.; Santini, F.; Eastman, J.; Smith, S.A.; Sidlauskas, B.; Chang, J.; Alfaro, M.E. Rates of speciation and morphological evolution are correlated across the largest vertebrate radiation. Nat. Comm. 2013, 4, 1958. [Google Scholar] [CrossRef] [PubMed]
- Sanderson, M.J. Estimating absolute rates of molecular evolution and divergence times: A penalized likelihood approach. Mol. Biol. Evol. 2002, 19, 101–109. [Google Scholar] [CrossRef]
- Wicke, S.; Müller, K.F.; de Pamphilis, C.W.; Quandt, D.; Bellot, S.; Schneeweiss, G.M. Mechanistic model of evolutionary rate variation en route to a nonphotosynthetic lifestyle in plants. Proc. Nat. Acad. Sci. USA 2016, 113, 9045–9050. [Google Scholar] [CrossRef]
- Evans, K.L.; Gaston, K.J. Can the evolutionary-rates hypothesis explain species–energy relationships? J. Biogeogr. 2005, 19, 899–915. [Google Scholar] [CrossRef]
- García-Pintos, L.P. Limits on the evolutionary rates of biological traits. Nat. Sci. Rep. 2024, 14, 11314. [Google Scholar] [CrossRef]
- Simpson, G.G. Tempo and Mode in Evolution; Columbia University Press: New York, NY, USA, 1944. [Google Scholar]
- Niklas, K. Theoretical evolutionary rates in plant groups and the fossil record. Brittonia 1977, 29, 241–254. [Google Scholar] [CrossRef]
- Zander, R.H. Macroevolutionary Systematics of Streptotrichaceae of the Bryophyta and Application to Ecosystem Thermodynamic Stability, 2nd ed.; Zetetic Publications: St. Louis, MO, USA, 2018. [Google Scholar]
- Zander, R.H. Genera of the Pottiaceae: Mosses of harsh environments. Bull. Buffalo Soc. Nat. Sci. 1993, 32, 216. [Google Scholar]
- Zander, R.H. Evolutionary leverage of dissilient genera of Pleuroweisieae (Pottiaceae) evaluated with Shannon-Turing analysis. Hattoria 2021, 12, 9–25. [Google Scholar]
- Alonso, M.; Jiménez, J.A.; Cano, M.J. Taxonomic revision of Chionoloma (Pottiaceae, Bryophyta). Ann. Mo. Bot. Gard. 2019, 104, 563–632. [Google Scholar] [CrossRef]
- Köckinger, H.; Kučera, J. Hymenostylium xerophilum, sp. nov., and H. gracillimum, comb. nov., two neglected European mosses and their molecular affinities. J. Bryol. 2011, 33, 195–209. [Google Scholar]
- Kučera, J.; Košnar, J.; Werner, O. Partial generic revision of Barbula (Musci: Pottiaceae): Re-establishment of Hydrogonium and Streblotrichum, and the new genus Gymnobarbula. Taxon 2013, 62, 21–39. [Google Scholar] [CrossRef]
- Werner, O.; Ros, R.M.; Grundmann, M. Molecular phylogeny of Trichostomoideae (Pottiaceae, Bryophyta) based on nrITS sequence data. Taxon 2005, 54, 361–368. [Google Scholar] [CrossRef]
- Zander, R.H. On the origin of taxa. J. Theor. Phys. Math. Res. 2025, 3, 1–20. [Google Scholar] [CrossRef]
- Zander, R.H. Lineages of fractal genera comprise the 88-million-year steel evolutionary spine of the Ecosphere. Plants 2024, 13, 1559. [Google Scholar] [CrossRef]
- Gavrilets, S.; Losos, J.B. Adaptive radiation: Contrasting theory with data. Science 2009, 323, 732–737. [Google Scholar] [CrossRef]
- Quental, L.B.; Marshall, C.R. Diversity dynamics: Molecular and fossil data reveal contrasting patterns of diversification. Philos. Trans. R. Soc. B Biol. Sci. Biol. Sci. 2010, 365, 2537–2545. [Google Scholar]
- Hanisch, S.; Eirdosh, D.; González Galli, L.; Hartelt, T.; Pérez, G.; Cupo, B. Understanding agency in evolutionary explanations: An assessment tool for biology education. J. Biol. Educ. 2025, 1–30. [Google Scholar] [CrossRef]
- Rosslenbroich, B.; Kümmell, S.; Bembé, B. Agency as an inherent property of living organisms. Biol. Theory 2024, 19, 224–236. [Google Scholar] [CrossRef]
- Nei, M.; Kumar, S. Molecular Evolution and Phylogenetics; Oxford University Press: New York, NY, USA, 2000. [Google Scholar]
- Diaz, L.F.H.; Harmon, L.J.; Sugawara, M.T.C.; Miller, E.T.; Pennell, M.W. Macroevolutionary diversiication rates show time dependency. Proc. Natl. Acad. Sci. USA 2019, 116, 7403–7408. [Google Scholar] [CrossRef]
- Lovejoy, S.; Spiridonov, A. The Fractional MacroEvolution Model: A simple quantitative scaling macroevolution model. Paleobiology 2024, 50, 376–400. [Google Scholar] [CrossRef]
- Melott, A.L.; Bambach, R.K. Analysis of periodicity of extinction using the 2012 geological timescale. Paleobiology 2014, 40, 177–196. [Google Scholar] [CrossRef] [PubMed]
- Rampino, M.R.; Caldeira, K. A 32-million year cycle detected in sea-level fluctuations over the last 545 Myr. Geosci. Front. 2020, 11, 2061–2065. [Google Scholar] [CrossRef]
- Bechteler, J.; Peñaloza-Bojacá, G.; Bell, D.; Burleigh, J.G.; McDaniel, S.F.; Davis, E.C.; Sessa, E.B.; Bippus, A.; Cargill, D.C.; Chantanoarrapint, S.; et al. Comprehensive phylogenomic time tree of bryophytes reveals deep relationships and uncovers gene incongruences in the last 500 million years of diversification. Am. J. Bot. 2023, 110, e16249. [Google Scholar] [CrossRef] [PubMed]
- Jauregui-Lazo, J.; Brinda, J.C.; GoFlag Consortium; Mishler, B.D. The phylogeny of Syntrichia, an ecologically diverse clade of mosses with an origin in South America. Am. J. Bot. 2023, 110, e16103. [Google Scholar] [CrossRef]
- A Rensing, S.; Ick, J.; A Fawcett, J.; Lang, D.; Zimmer, A.; Van de Peer, Y.; Reski, R. An ancient genome duplication contributed to the abundance of metabolic genes in the moss Physcomitrella patens. BMC Evol. Biol. 2007, 7, 130. [Google Scholar] [CrossRef]
- Ignatov, M.S.; Maslova, E.V. Fossil mosses, what do they tell us about moss evolution? Bryophyt. Divers. Evol. 2021, 43, 72–97. [Google Scholar] [CrossRef]
- Wigner, E.P. The unreasonable effectiveness of mathematics in the natural sciences. Commun. Pure Appl. Math. 1960, 13, 1–14. [Google Scholar] [CrossRef]
- Rabosky, D.L.; Adams, D.C. Rates of morphological evolution are correlated with species richness in salamanders. Evolution 2012, 66, 384–398. [Google Scholar] [CrossRef]
- Eldredge, N.; Thompson, J.N.; Brakefield, P.M.; Cavrilets, S.; Jablonski, D.; Jackson, J.B.C.; Lenski, R.E.; Lieberman, B.S.; McPeek, M.A.; Miller, W., III. The dynamics of evolutionary stasis. Paleobiology 2005, 31, 133–145. [Google Scholar] [CrossRef]
- Hardy, G.H. Mendelian proportions in a mixed population. Science 1908, 28, 49–50. [Google Scholar] [CrossRef] [PubMed]
- Rominger, A.J.; Overcast, I.; Krehenwinkel, H.; Gillespie, R.G.; Harte, J.; Hickerson, M.J. Linking evolutionary and ecological theory illuminates non-equilibrium biodiversity. arXiv 2017, arXiv:1705.04725. [Google Scholar] [CrossRef]
- Goldbeter, A. Dissipative structures in biological systems: Bistability, oscillations, spatial patterns and waves. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2018, 376, 20170376. [Google Scholar] [CrossRef] [PubMed]
- Kondepudi, D.K.; De Bari, B.; Dixon, J.A. Dissipative structures, organisms and evolution. Entropy 2020, 22, 1305. [Google Scholar] [CrossRef]
- Nicolis, G.; Prigogine, I. Exploring Complexity: An Introduction; W.H. Freeman and Company: New York, NY, USA, 1989. [Google Scholar]
- Erwin, D.H. Extinction as the loss of evolutionary history. Proc. Natl. Acad. Sci. USA 2008, 105, 11453–11457. [Google Scholar] [CrossRef]
- Raup, D.M. Extinction: Bad Genes or Bad Luck? WW Norton & Company: New York, NY, USA, 1991. [Google Scholar]
- Carroll, S. The Biggest Ideas in the Universe: Space, Time, and Motion; Dutton Press: New York, NY, USA, 2022. [Google Scholar]
- Zander, R.H. Minimally monophyletic genera are the cast-iron building blocks of evolution. Ukr. Bot. J. 2024, 81, 87–99. [Google Scholar] [CrossRef]
- Zander, R.H. A new rugose-leaved Anoectangium (Pottiaceae) from Mexico. Bryologist 2023, 126, 457–460. [Google Scholar] [CrossRef]
- Zander, R.H. Synopsis of Ozobryum (Pottiaceae, Bryophyta), and sequential Bayes evaluation of genus integrity. Ann. Mo. Bot. Gard. 2021, 106, 458–468. [Google Scholar] [CrossRef]
- Zander, R.H.; Toren, D.; Eckel, P.M. Gymnostomum aeruginosum, G. calcareum and G. viridulum (Pottiaceae, Bryopsida) in California. J. Bryol. 2007, 29, 27–32. [Google Scholar] [CrossRef]
- McPeek, M.A. The macroevolutionary consequences of ecological differences among species. Palaeontaology 2007, 50, 111–129. [Google Scholar] [CrossRef]
- Pearse, I.S.; McIntyre, P.; Cacho, N.I.; Strause, S.Y. Fitness homeostasis across an experimental water gradient predicts species’ geographic range and climatic breadth. Ecology 2022, 103, e3827. [Google Scholar] [CrossRef]
- Pimm, S.L. The complexity and stability of ecosystems. Nature 1984, 307, 321–326. [Google Scholar] [CrossRef]
- Huss, J. The Shape of Evolution: The MBL Model and Clade Shape. In The Paleobiological Revolution: Essays on the Growth of Modern Paleontology; Sepkoski, D., Ruse, M., Eds.; University of Chicago Press: Chicago, IL, USA, 2009; pp. 326–345. [Google Scholar] [CrossRef]
- Raup, D.M.; Gould, S.J.; Schopf, T.J.M.; Simberloff, D. Stochastic models of phylogeny and the evolution of diversity. J. Geol. 1973, 81, 525–542. [Google Scholar] [CrossRef]
- Uyeda, J.C.; Hansen, T.F.; Arnold, S.J.; Pienaar, J. The million-year wait for macroevolutionary bursts. Proc. Nat. Acad. Sci. USA 2011, 108, 15908–15913. [Google Scholar] [CrossRef] [PubMed]
- Grunert, K.; Holden, H.; Jakobsen, E.R.; Stenseth, N.C. Evolutionarily stable strategies in stable and periodically fluctuating populations: The Rosenzweig-MacArthur predator-prey model. Proc. Nat. Acad. Sci. USA 2021, 118, e2017463118. [Google Scholar] [CrossRef] [PubMed]
- McKelvey, B. Self-organization, complexity catastrophe, and microstate models at the edge of chaos. In Variations in Organization Science: In Honor of Donald T. Campbell; Baum, J.A.C., McKelvey, B., Eds.; SAGE: Thousand Oaks, CA, USA, 1999; pp. 279–307. [Google Scholar][Green Version]
- Weibull, J.W. Evolutionary Game Theory; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar][Green Version]
- Stockwell, D.R.B.; Peters, D.P. The GARP modelling strategy for species distribution prediction. Ecol. Model. 1999, 114, 1–15. [Google Scholar]
- Stauffer, D. Evolutionary ecology in silico: Does mathematical modeling help in understanding ‘generic’ trends? J. Biosci. 2005, 30, 277–287. [Google Scholar] [CrossRef]
- Van Valen, L. A new evolutionary law. Evol. Theory 1973, 1, 1–30. [Google Scholar]
- Barnosky, A.D. Distinguishing the effects of the Red Queen and Court Jester on Miocene mammal evolution in the northern Rocky Mountains. J. Vertebr. Paleontol. 2001, 21, 172–185. [Google Scholar] [CrossRef]
- Bowring, S.A.; Erwin, D.H.; Sozaki, Y. The tempo of mass extinction and recovery: The end-Permian example. Proc. Nat. Acad. Sci. USA 1999, 96, 8827–8828. [Google Scholar] [CrossRef] [PubMed]
- Shen, S. The Permian-Triassic extinction event: Causes, consequences and contemporary relevance. Trans. Mater. Biotechnol. Life Sci. 2024, 4, 242–248. [Google Scholar] [CrossRef]
- Xu, Z.; Yu, J.; Yin, H.; Merdith, A.S.; Hilton, J.; Allen, B.J.; Gurung, K.; Wignall, P.B.; Dunhill, A.M.; Shen, J.; et al. Early Triassic super-greenhouse climate driven by vegetation collapse. Nat. Commun. 2025, 16, 5400. [Google Scholar] [CrossRef]
- Fitz-Palacios, O.; Schneider, H.; Heinrichs, J.; Savolainen, V. Diversification of land plants: Insights from a family-level phylogenetic analysis. BMC Evol. Biol. 2011, 11, 341. [Google Scholar] [CrossRef] [PubMed]
- Zander, R.H. Structural monophyly analysis allows estimation of self-sustainability at the supraspecific level over 88 million years in mosses. Sustainability 2025, 17, 3657. [Google Scholar] [CrossRef]
- Zander, R.H. Infraspecific molecular trees are associated with serial macroevolution in Pottiaceae (Bryophyta). Ukr. Bot. J. 2019, 76, 390–405. [Google Scholar] [CrossRef]
- Stevens, P.F. The genus concept in practice: But for what practice? Kew Bull. 1985, 40, 457–465. [Google Scholar] [CrossRef]
- Stevens, P.F. Why do we name organisms? Some reminders from the past. Taxon 2002, 51, 11–26. [Google Scholar] [CrossRef]
- Mishler, B.D. What, If Anything, Are Species? CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Flores, J.R.; Suárez, G.M.; Hyvönen, J. Reassessing the role of morphology in bryophyte phylogenetics: Combined data improves phylogenetic inference despite character conflict. Mol. Phyl. Evol. 2020, 143, 10662. [Google Scholar] [CrossRef] [PubMed]
- Scotland, R.W.; Olmstead, R.G.; Bennett, J.R. Phylogeny reconstruction: The role of morphology. Syst. Biol. 2003, 52, 539–548. [Google Scholar] [CrossRef]
- Schwartz, J.H. Barking up the wrong ape—Austalopiths and the quest for chimpanzee characters in hominid fossils. Colllegium Antropol. 2004, 28 (Suppl. S2), 87–101. [Google Scholar]
- Ford, I.J.; Spinney, R.E. Entropy production from stochastic dynamics in discrete full phase space. arXiv 2012, arXiv:1204.4822. [Google Scholar] [CrossRef]
- Tomé, T.; de Oliveira, M.J. Stochastic motion in phase space on a surface of constant energy. Phys. Rev. E 2022, 106, 034129. [Google Scholar] [CrossRef]
- Gould, S.J. Smooth curve of evolutionary rate: A psychological and mathematical artifact. Science 1984, 226, 994–995. [Google Scholar] [CrossRef] [PubMed]
- Gingerich, P.D. Smooth curve of evolutionary rate: A psychological and mathematical artifact—Reply to Gould. Science 1984, 226, 994–996. [Google Scholar] [CrossRef]
- Huang, S. The maximum genetic diversity theory: A comprehensive framework for understanding evolutionary processes. BioCosmos 2025, 1, 41–61. [Google Scholar] [CrossRef]
- Kopp, M. Speciation and the neutral theory of biodiversity. Bioessays 2010, 32, 564–570. [Google Scholar] [CrossRef] [PubMed]
- Roopnarine, P.D. Analysis of rates of evolution. Ann. Rev. Ecol. Syst. 2003, 34, 605–632. [Google Scholar] [CrossRef]
- Lenton, T. Gaia Hypothesis. In Encyclopedia of Atmospheric Sciences; Holton, J.R., Ed.; Academic Press: Cambridge, MA, USA, 2003; pp. 815–820. [Google Scholar] [CrossRef]
- Lovelock, J.E.; Margulis, L. Atmospheric homeostasis by and for the biosphere: The Gaia Hypothesis. Tellus 1974, 26, 2–10. [Google Scholar] [CrossRef]
- Doolittle, W.F. Darwinizing Gaia. J. Theor. Biol. 2017, 434, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Odifreddi, P. The Mathematical Century: The 30 Greatest Problems of the Last 100 Years; Princeton University Press: Princeton, NY, USA; Oxford, UK, 2000. [Google Scholar]
- Von Neumann, J. Theory of Self-Reproducing Automata; Burke, A.W., Ed.; University of Illinois Press: Urbana, IL, USA; London, UK, 1966. [Google Scholar]

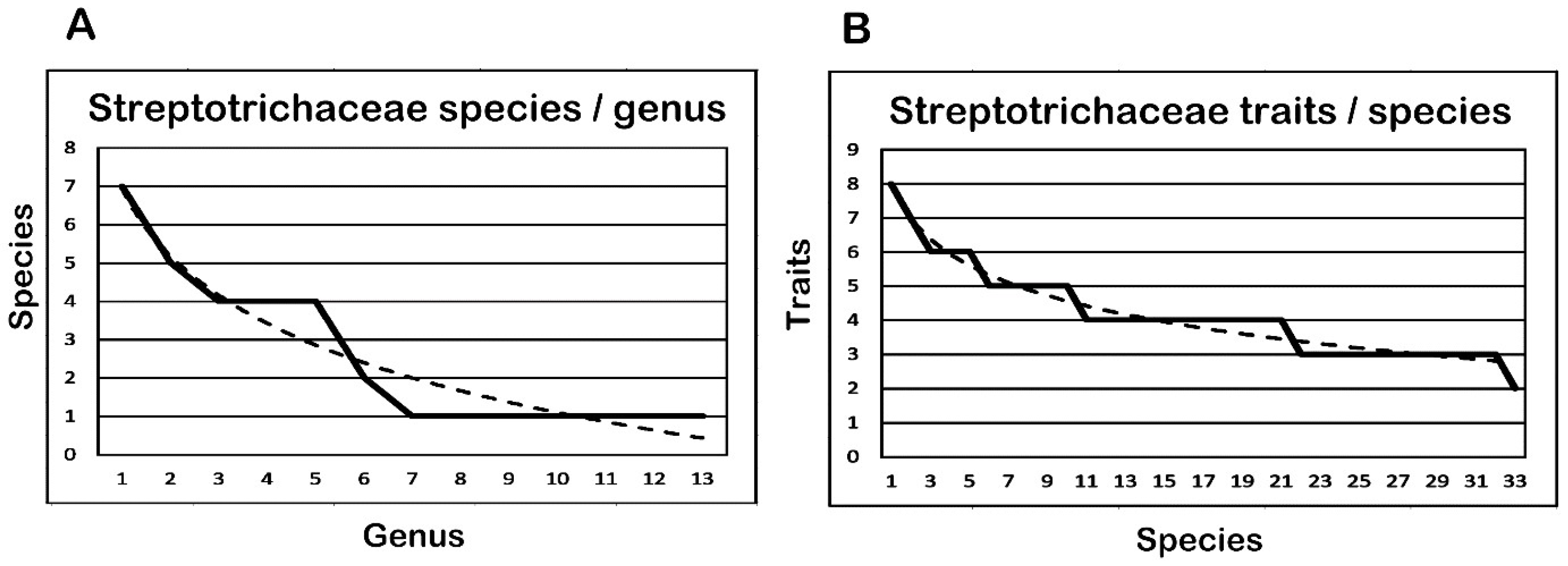
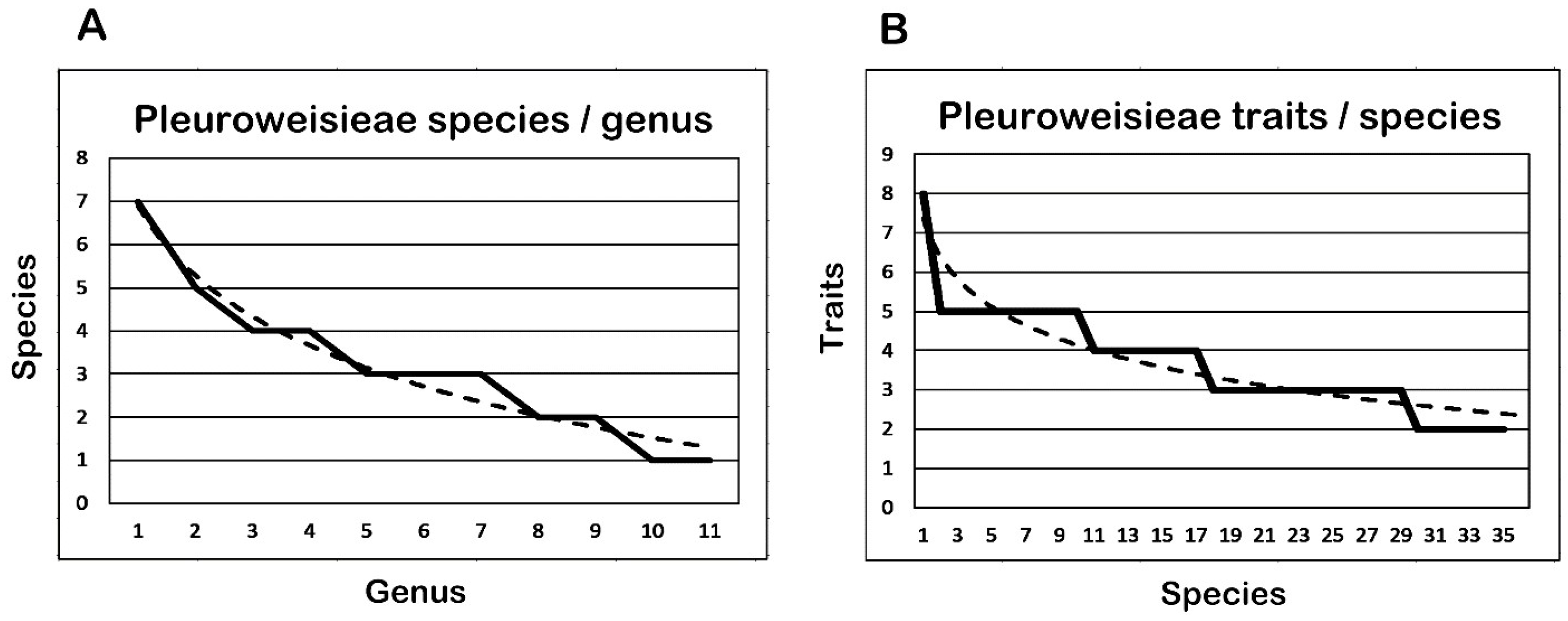

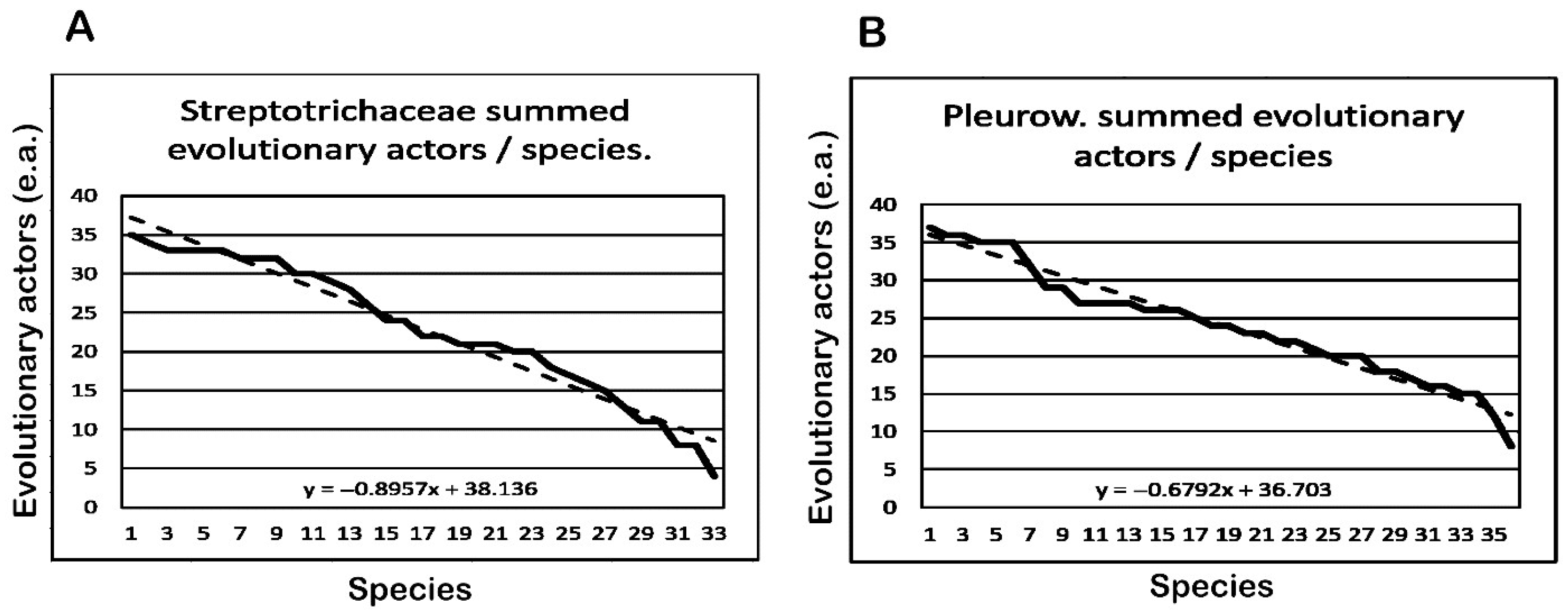


| Genus | S/G | Fm | Cu | Species | Speciation Events (e.a./s.e.) | F | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||||||
| IEG 1 | 1 | 4 | 5 | unknown | 4 | 4 | ||||||
| IEG 2 | 1 | 8 | 4 | unknown | ╠> | 4 | 8 | |||||
| Trachyodontium | 2 | 11 | 3 | unknown | ║ | ╠> | 3 | 11 | ||||
| zanderi | ║ | ║ | ╚> | 4 | 15 | |||||||
| Crassileptodontium | 4 | 17 | 2 | pungens | ║ | ╚> | 6 | 17 | ||||
| wallisii | ║ | ╚> | 3 | 20 | ||||||||
| erythroneuron | ║ | ╠> | 4 | 21 | ||||||||
| subintegrifolium | ║ | ╚> | 3 | 20 | ||||||||
| Streptotrichum | 1 | 8 | 4 | ramicola | ╚> | 4 | 8 | |||||
| Austroleptodontium | 1 | 16 | 3 | interruptum | ╠> | 8 | 16 | |||||
| Leptodontiella | 1 | 11 | 3 | apiculata | ╠> | 3 | 11 | |||||
| Microleptodontium | 5 | 18 | 2 | unknown | ║ | ╚> | 7 | 18 | ||||
| flexifolium | ║ | ╠> | 3 | 21 | ||||||||
| gemmascens | ║ | ║ | ╠> | 4 | 22 | |||||||
| umbrosum | ║ | ║ | ╠> | 4 | 22 | |||||||
| stellaticuspis | ║ | ║ | ╚> | 3 | 21 | |||||||
| Rubroleptodontium | 1 | 24 | 1 | stellatifolium | ║ | ╚> | 5 | 24 | ||||
| IEG 3 | 1 | 13 | 3 | unknown | ╚> | 5 | 13 | |||||
| Williamsiella | 4 | 24 | 2 | araucarieti | ╚> | 6 | 24 | |||||
| tricolor | ╠> | 4 | 28 | |||||||||
| aggregata | ╠> | 6 | 30 | |||||||||
| lutea | ║ | ╠> | 2 | 26 | ||||||||
| Leptodontium | 4 | 30 | 1 | unknown | ║ | ╚> | 5 | 30 | ||||
| excelsum | ║ | ╠> | 3 | 33 | ||||||||
| viticulosoides | ║ | ╠> | 3 | 33 | ||||||||
| scaberrimum | ║ | ╚> | 5 | 35 | ||||||||
| Stephanoleptodontium | 7 | 29 | 1 | longicaule | ╚> | 4 | 29 | |||||
| syntrichioides | ╠> | 4 | 33 | |||||||||
| brachyphyllum | ╠> | 3 | 32 | |||||||||
| filicola | ║ | ╚> | 5 | 34 | ||||||||
| capituligerum | ╚> | 3 | 32 | |||||||||
| latifolium | ╠> | 3 | 32 | |||||||||
| stoloniferum | ╚> | 4 | 33 | |||||||||
| Total | 33 | 213 | 26 | 4 | 8 | 25 | 20 | 29 | 28 | 23 | 756 | |
| Average | 2.5 | 16.3 | 3.3 | 4.0 | 4.0 | 5.0 | 5.0 | 4.0 | 3.5 | 3.8 | 22.9 | |
| Genus | S/G | Fm | Cu | Species | Speciation Events (e.a./s.e.) | F | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||||||
| IEG | 1 | 8 | 3 | unknown | 8 | 8 | ||||
| Tuerckheimia | 3 | 16 | 2 | guatemalensis | ╠> | 4 | 16 | |||
| svihlae | ║ | ╠> | 2 | 18 | ||||||
| valeriana | ║ | ╚> | 2 | 18 | ||||||
| Eobryum | 3 | 24 | 2 | anoectangioides | ╚> | 5 | 15 | |||
| hildebrantii | ╠> | 3 | 21 | |||||||
| xeerophilum | ╠> | 2 | 20 | |||||||
| Anoectangium | 7 | 32 | 1 | aestivum | ╠> | 5 | 32 | |||
| euchloron | ║ | ╠> | 5 | 37 | ||||||
| radulans | ║ | ║ | ╚> | 3 | 35 | |||||
| clarum | ║ | ╠> | 4 | 36 | ||||||
| incrassatum | ║ | ║ | ╚> | 4 | 36 | |||||
| stracheyanum | ║ | ╚> | 3 | 35 | ||||||
| sikkimense | ║ | ╚> | 3 | 35 | ||||||
| Ardeuma | 5 | 23 | 1 | gracillimum | ╠> | 4 | 23 | |||
| recurvirostum | ║ | ╚> | 2 | 25 | ||||||
| crassinervium | ║ | ╠> | 3 | 26 | ||||||
| annotinum | ║ | ╠> | 3 | 26 | ||||||
| aurantiacum | ║ | ╚> | 3 | 26 | ||||||
| Gymnostomum | 4 | 20 | 1 | aeruginosum | ╠> | 5 | 20 | |||
| viridulum | ║ | ╠> | 2 | 22 | ||||||
| calcareum | ║ | ╚> | 3 | 23 | ||||||
| mosis | ║ | ╚> | 2 | 22 | ||||||
| Hymenostyliella | 2 | 15 | 1 | llanosii | ╠> | 5 | 15 | |||
| alata | ║ | ╚> | 2 | 17 | ||||||
| Hymenostylium | 2 | 16 | 1 | xanthocarpum | ╠> | 4 | 16 | |||
| townsendii | ║ | ╚> | 4 | 20 | ||||||
| Molendoa | 4 | 24 | 1 | sendtneriana | ╠> | 5 | 24 | |||
| hornschuchiana | ║ | ╠> | 5 | 29 | ||||||
| peruviana | ║ | ╚> | 3 | 27 | ||||||
| handelii | ║ | ╚> | 3 | 27 | ||||||
| Ozobryum | 4 | 24 | 1 | warburgii | ╠> | 5 | 24 | |||
| missing link | ║ | ╚> | 5 | 29 | ||||||
| ogalalense | ║ | ╠> | 3 | 27 | ||||||
| mexicanum | ║ | ╚> | 3 | 27 | ||||||
| Reimersia | 1 | 12 | 1 | inconspicua | ╚> | 4 | 12 | |||
| Total | 36 | 214 | 12 | 8 | 9 | 46 | 38 | 30 | 869 | |
| Average | 3.3 | 19.5 | 1.3 | 8.0 | 4.5 | 3.8 | 3.4 | 3.0 | 24.1 | |
| Streptotrichaceae 13 Genera | S/G | Fm | Cu | Speciation Events (e.a./s.e.) | F | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||||
| Total | 33 | 213 | 26 | 4 | 8 | 25 | 25 | 24 | 28 | 23 | 756 |
| Average | 2.5 | 16.3 | 3.3 | 4.0 | 4.0 | 5.0 | 5.0 | 4.0 | 3.5 | 3.8 | 22.9 |
| Pleuroweisieae 11 Genera | S/G | Fm | Cu | Speciation Events (e.a./s.e.) | F | ||||||
| 1 | 2 | 3 | 4 | 5 | |||||||
| Total | 36 | 214 | 12 | 8 | 9 | 46 | 38 | 30 | 869 | ||
| Average | 3.3 | 19.5 | 1.3 | 8.0 | 4.5 | 3.8 | 3.4 | 3.0 | 24.1 | ||
| Total combined e.a. | 4 | 8 | 33 | 34 | 70 | 66 | 53 | ||||
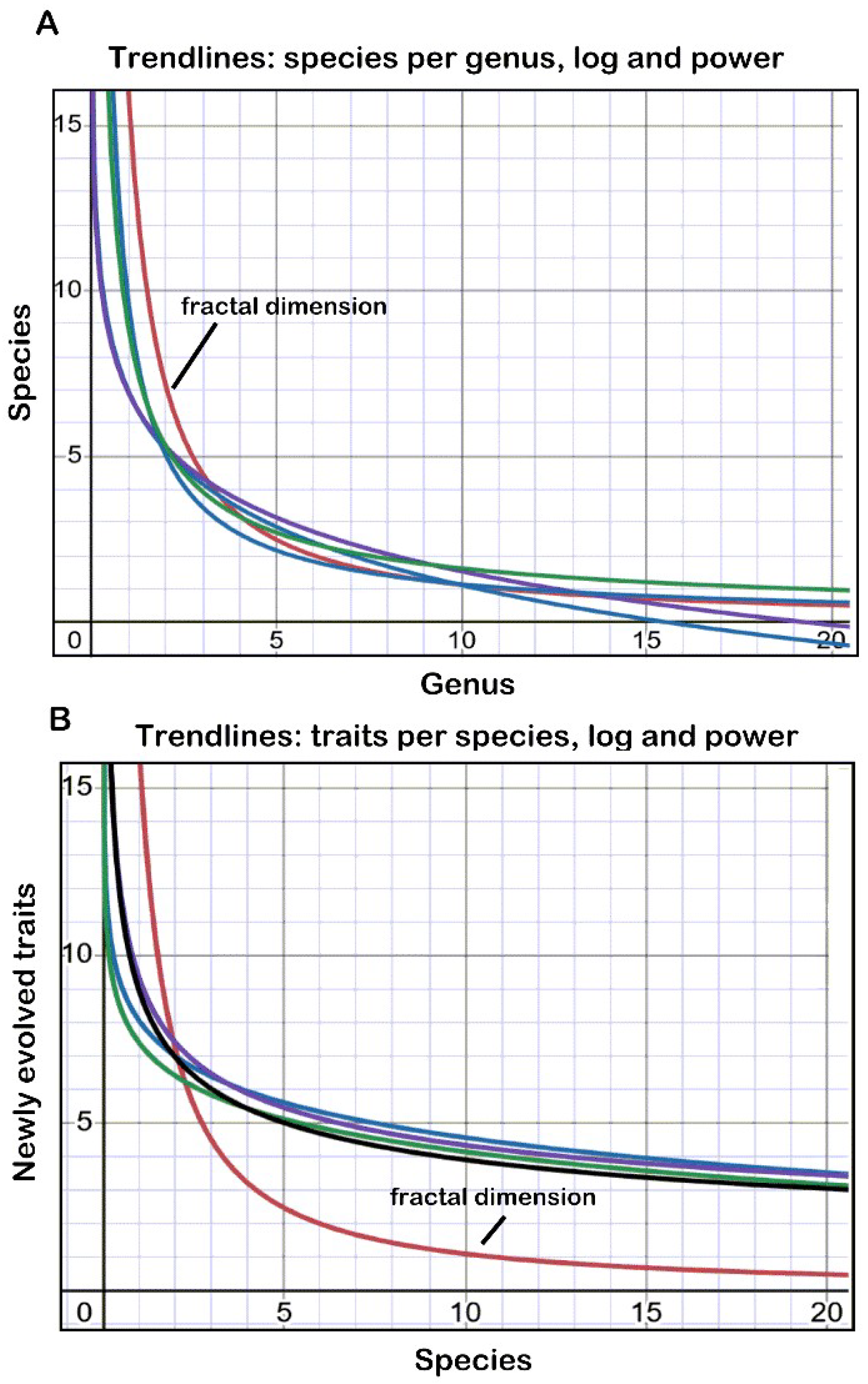
| Taxon | Species per Genus | Traits per Species | ||
|---|---|---|---|---|
| Logarithmic | Power Law | Logarithmic | Power Law | |
| Streptotrichaceae | y = −2.539 ln(x) + 6.9424 | y = 9.6142 x−0.932 | y = −1.504 ln(x) + 8.0292 | y = 9.2839 x−0.33 |
| Pleuroweisieae | y = −2.340 ln(x) + 6.9042 | y = 8.859 x−0.742 | y = −1.4 ln(x) + 7.3699 | y = 8.8937 x−0.357 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zander, R.H. Biodiversity Resilience in Terms of Evolutionary Mass, Velocity and Force. Sustainability 2025, 17, 8272. https://doi.org/10.3390/su17188272
Zander RH. Biodiversity Resilience in Terms of Evolutionary Mass, Velocity and Force. Sustainability. 2025; 17(18):8272. https://doi.org/10.3390/su17188272
Chicago/Turabian StyleZander, Richard H. 2025. "Biodiversity Resilience in Terms of Evolutionary Mass, Velocity and Force" Sustainability 17, no. 18: 8272. https://doi.org/10.3390/su17188272
APA StyleZander, R. H. (2025). Biodiversity Resilience in Terms of Evolutionary Mass, Velocity and Force. Sustainability, 17(18), 8272. https://doi.org/10.3390/su17188272






