Hybrid Forecasting for Sustainable Electricity Demand in The Netherlands Using SARIMAX, SARIMAX-LSTM, and Sequence-to-Sequence Deep Learning Models

Abstract

Accurate forecasting is essential for effective energy management, particularly in evolving and data-driven electricity markets. To address the increasing complexity of national energy planning in The Netherlands, this study proposes a hybrid multi-stage forecasting framework to improve both short- and long-term electricity demand predictions. We compare three model types, classical statistical (SARIMAX), hybrid statistical–deep learning (SARIMAX–LSTM), and deep learning (sequence-to-sequence), across forecasting horizons from 1 to 180 days. The models are trained on daily load data from ENTSO-E (2009–2023), incorporating exogenous variables such as weather conditions, energy prices, and socioeconomic indicators, as well as engineered temporal features such as calendar effects, seasonal patterns, and rolling demand statistics. Three feature configurations were tested: exogenous-only, generated-only, and a combined set. Internally generated features consistently outperformed exogenous inputs, especially for long-term forecasts. The sequence-to-sequence model achieved the highest accuracy at the 180-day horizon, with a mean absolute percentage error (MAPE) of approximately 1.88%, outperforming both SARIMAX and the SARIMAX–LSTM hybrid models. An additional SARIMAX-based analysis assessed the individual effects of renewable and socioeconomic indicators. Renewable energy production improved short-term accuracy (MAPE reduced from 2.13% to 1.09%) but contributed little to long-term forecasting. Socioeconomic variables had limited predictive value and, in some cases, slightly reduced accuracy, particularly over long-term horizons.

1. Introduction

Electricity is the backbone of modern economies, driving industries, businesses, and households alike. It powers essential infrastructure, fuels technological advancements, and plays a pivotal role in the global transition toward sustainable energy systems [1,2]. Globally and locally, electricity demand has steadily risen, influenced by economic growth, increased electrification in transport and heating, and the expansion of energy-intensive industries such as data centers [3,4]. However, as the country shifts away from coal and natural gas in favor of weather-dependent renewables, maintaining a stable electricity supply has become a significant challenge [5]. According to The Netherlands’ National Energy System Plan, electricity supply is expected to increase fourfold by 2050. Achieving this target will require a significant scale-up of renewable energy deployment, leveraging the country’s established strengths in solar PV and wind energy [6]. Grid operators like TenneT have warned that energy shortages could emerge in regions such as Noord-Holland as early as 2026 [7]. Consequently, accurate electricity demand forecasting is critical for energy system stability, efficient resource allocation, and policy planning [8].

Energy demand forecasting serves multiple purposes. Accurate predictions optimize energy distribution, reduce operational costs, and prevent supply and demand imbalances [9,10]. Underestimating demand can lead to power shortages, disruptions in economic activity, and grid instability, whereas overestimating demand can result in unnecessary investments and financial inefficiencies. With global electricity demand projected to increase at an average annual rate of 4% through 2027 [3], improving forecasting techniques is essential for ensuring a reliable, cost-effective, and sustainable energy transition.

Electricity consumption is shaped by a complex interplay of factors [11]. While historical consumption patterns provide a baseline for prediction, exogenous variables introduce fluctuations that complicate forecasting. Weather and climate conditions, such as temperature, humidity, and wind speed, directly impact heating, cooling, and overall electricity usage. Socioeconomic trends, including population growth and economic activity, shape long-term demand patterns, while the transition to renewable energy introduces new uncertainties due to the variability of wind and solar generation [12]. Additionally, fluctuations in energy prices play a crucial role in shaping consumer behavior, particularly among low-income households. For example, in 2020, energy consumption reached its lowest point, largely due to rising costs, underscoring the strong relationship between price increases and reduced demand [13].

Classical statistical models, such as time series approaches, have often outperformed AI-based models in long-term forecasting, particularly when trends and seasonality remain stable. These models offer strong interpretability and consistency over time [14]. However, AI models, especially deep learning techniques like LSTM and sequence to sequence, have excelled in capturing complex, nonlinear relationships, making them highly accurate for short-term forecasts [14,15]. Despite their advantages, AI-based models have struggled with long-term dependencies due to issues such as vanishing gradients, and they are heavily reliant on data quality, computational resources, and careful tuning [16,17]. This reliance can obscure variable relationships and complicate model interpretation. To effectively forecast energy demand while addressing both long-term trends and short-term fluctuations, a hybrid modeling approach is recommended.

This paper presents a novel approach to forecasting national electricity demand in The Netherlands by evaluating and comparing classical statistical, hybrid, and deep learning models. The baseline model, SARIMAX, was selected due to its widespread use in energy forecasting and its well-documented ability to model seasonality, trends, and autocorrelation with transparency [18,19]. Its interpretability and robustness made it a strong reference point for evaluating the added value of more complex models. To improve on this benchmark, two alternative models were proposed: a hybrid SARIMAX–LSTM model that combines linear and nonlinear forecasting capabilities, and a deep learning-based sequence-to-sequence (Seq2Seq) model designed to capture complex temporal dependencies. By incorporating key exogenous predictors, such as climate variability, energy prices, and socioeconomic indicators, together with engineered temporal features, each model was evaluated for its ability to capture short-term fluctuations and long-term trends. Unlike previous studies focused on small-scale or regional forecasting, this work applied these methods at the national level and investigated the role of energy source composition and socioeconomic factors in shaping forecast accuracy.

This study aimed to evaluate how the integration of heterogeneous feature sets influenced the performance of statistical, hybrid, and deep learning models in forecasting electricity demand across short- and long-term horizons. Specifically, we examined the added predictive value of renewable energy production data and assessed the role of socioeconomic indicators such as GDP and population. Three models were compared, SARIMAX, a hybrid SARIMAX–LSTM model, and a sequence-to-sequence deep learning model, across different feature configurations to determine their effectiveness in capturing temporal dynamics and improving forecast accuracy at the national level.

2. Related Work

Energy demand forecasting is a critical area of research, especially as global energy systems face increasing complexities due to climate targets and shifts toward renewable sources [20]. Since the 1950s, a wide range of methodologies have emerged to address the intricate patterns of energy consumption, from traditional statistical models to advanced machine learning and hybrid techniques. Despite these advancements, a key research gap remains: few models adequately capture the effects of rising green energy adoption on natural gas demand and electricity [14]. This study seeks to fill this gap by developing adaptable forecasting models that respond to the dynamics of energy transitions.

2.1. Influencing Factors in Energy Load Forecasting

2.1.1. Socioeconomic Factors

Gross Domestic Product (GDP) strongly influences energy demand [14,21]. Economic growth drives industrial production, commercial services, and household consumption, increasing energy use. Industrialized economies rely on energy-intensive manufacturing, while service-based economies require substantial energy for infrastructure. In developed nations, efficiency improvements and renewables have reduced the link between GDP and energy use, whereas developing countries still see rising demand due to urbanization and industrial expansion. In The Netherlands, GDP grew by 0.9% in 2024 [22].

Population growth is a key driver of rising energy demand, as expanding populations lead to greater residential energy consumption for housing, appliances, and transportation [8,14]. This effect is further intensified by urbanization, which fuels energy demand in commercial buildings, public transport, and infrastructure. In The Netherlands, the population has grown rapidly, reaching approximately 18 million in 2024—an increase of about 1.1 million over the past decade. This growth is largely driven by high life expectancy, economic expansion, and job opportunities. Major cities such as Amsterdam, Rotterdam, and The Hague continue to see rising demand, with Amsterdam alone home to nearly 800,000 residents [23].

Energy prices have a significant impact on energy demand, influencing both consumer behavior and industrial operations. In 2022, rising energy costs, driven by inflation, led to a noticeable decline in energy consumption as households and businesses sought to reduce expenses through energy-saving measures. In response, the Dutch government has introduced additional policies to cushion the effects of inflation and surging energy prices, particularly for low- and middle-income households. Inflation is expected to rise further, potentially reaching 5.2% this year, primarily due to increased energy costs. Consequently, average purchasing power is projected to decline by 2.7% [24].

Together, GDP, population, and energy prices form a complex relationship that drives energy consumption trends. While economic growth and population expansion generally lead to higher energy demand, energy prices act as a balancing factor, influencing how individuals and businesses respond to changes in supply and affordability. The interplay of these factors, alongside technological advancements and sustainability policies, determines the long-term trajectory of energy demand across different regions and economies. Although GDP and population data are available only at a yearly resolution, they provide valuable structural context for long-term energy consumption patterns. In larger daily forecasting horizons, where short-term seasonality becomes less dominant, incorporating such stable indicators helps capture the broader socioeconomic trends that influence aggregate demand levels [25].

2.1.2. Weather and Renewable Energy

Weather variables such as temperature, humidity, and wind speed significantly influence energy demand patterns by affecting heating and cooling requirements. For instance, a study conducted in The Netherlands shows that energy demand peaks during colder months due to increased heating needs [26]. Similarly, research in Prague has demonstrated that warmer weather reduces heating demand while simultaneously increasing the need for cooling infrastructure [27].

In parallel, renewable energy sources, especially solar and wind, have become critical components of modern energy systems. Their outputs are inherently weather-dependent, introducing new levels of variability into the grid. The Netherlands aims to deploy more renewables in order to quadruple its electricity supply [6]. Therefore, integrating weather and renewable energy variables into prediction models is essential. These features not only capture the direct influence of environmental conditions on consumption patterns but also reflect fluctuations in supply due to the intermittent nature of renewables. This dual impact makes them key predictors in short-term forecasting models [4].

2.2. Classical Statistical Models for Long-Term Forecasting

Classical statistical models, particularly time series (TS) methods, have long been effective in long-term forecasting scenarios, especially where seasonal patterns and trends remain relatively stable [14,28]. These models leverage historical data to identify patterns and generate forecasts, making them valuable tools for understanding the influence of past trends on future outcomes. A widely used model, ARIMA, is known for its strong interpretability and robustness in low-volatility environments. It has been commonly applied to forecast total gas demand as well as specific subsectors like households and industries, often utilizing confidence intervals to assess the reliability of predictions [29,30]. Variants of ARIMA, such as seasonal ARIMA (SARIMA), incorporate seasonal and external factors, further enhancing their predictive capabilities for energy demand forecasting [14]. Research indicates that these models frequently outperform AI techniques in long-term forecasts due to their reliance on well-established patterns rather than extensive datasets. However, they exhibit notable limitations when faced with complex, nonlinear relationships or significant short-term demand fluctuations, where more adaptive and data-driven approaches may be required [8]. While SARIMA-type models are highly effective for capturing long-term periodicity, they struggle with short-term nonlinearities and abrupt changes, often present in high-frequency energy data.

2.3. Applications of Machine Learning and Deep Learning in Energy Forecasting

AI-based forecasting techniques, encompassing both machine learning and deep learning, have become essential tools for improving the accuracy and adaptability of energy demand predictions. These methods excel at capturing complex and nonlinear relationships, which are challenging for traditional statistical models.

ML methods, such as Support Vector Regression (SVR) and Stochastic Gradient Descent (SGD), have demonstrated strong potential in short-term forecasting tasks [31,32]. SVR, leveraging linear and Radial Basis Function (RBF) kernels, effectively captures both linear and nonlinear data patterns. Meanwhile, SGD optimizes gradient descent by using random subsets, offering computational efficiency and fast convergence, particularly in large-scale scenarios. Among these models, SGD has achieved the highest prediction accuracy, showcasing its scalability and precision in forecasting tasks like predicting peak natural gas production trends [33].

DL techniques, particularly Artificial Neural Networks (ANNs) such as Multilayer Perceptron (MLP) and Long Short-Term Memory (LSTM) networks, have shown exceptional performance in long-term forecasting tasks [34,35]. For instance, in studies on gas consumption in Poland, MLP and LSTM networks significantly outperformed traditional statistical methods. While LSTM excelled in capturing sequential dependencies in time series data, MLP demonstrated superior computational efficiency, achieving comparable accuracy with less processing time. Notably, the multivariate MLP model performed best in scenarios involving noisy lower-level hierarchical data, further solidifying the role of ANNs in energy demand forecasting [36]. Recent research in Sustainability demonstrates enhanced Seq2Seq effectiveness when integrating renewable awareness and temporal feature fusion—for instance, a short-term residential load forecasting model achieved improved accuracy by embedding renewable energy signals alongside Seq2Seq learning [37].

Despite their advantages, ML and DL models rely heavily on high-quality data, and some models require significant computational resources [34]. Besides this, they lack interpretability, complicating efforts to understand variable relationships and model structures. In terms of applicability, deep learning models such as LSTM and Seq2Seq are especially well-suited for short- to medium-term forecasts where data are abundant and nonlinear patterns dominate. However, they often require extensive hyperparameter tuning, are less interpretable, and are sensitive to input noise and data quality. In contrast, classical statistical models like ARIMA or SARIMAX offer superior interpretability and tend to perform better over long horizons in systems where seasonality and trends are relatively stable. Therefore, the selection of a forecasting method should depend on both the prediction horizon and the complexity of the system being modeled—statistical models excel in long-term policy planning, while deep learning approaches are advantageous in dynamic, data-rich environments such as real-time grid management.

3. Methodology

This research focuses on multivariate time series forecasting for energy consumption. The process involves five key steps: data collection, exploratory data analysis (EDA), data cleaning and preparation, model implementation, and performance evaluation.

3.1. Data Collection

3.1.1. Target Variable

In this study, the energy consumption in The Netherlands is the target variable. To analyze this, load consumption data from the European Network of Transmission System Operators for Electricity (ENTSO-E) is used. ENTSO-E defines load as the total power consumed by end-users connected to the electricity grid [38]. The dataset covers the period from 2009 to 2023 and provides hourly load measurements in megawatts (MW) for The Netherlands. The Netherlands represents a mature, high-density, and renewables-integrated electricity market, making it a relevant testbed for forecasting approaches applicable to many European countries. The ENTSO-E dataset used is a standardized, quality-assured source used widely in academic and regulatory forecasting studies across the EU. Moreover, the 14-year duration (2009–2023) captures seasonal cycles, climate fluctuations, economic shifts (e.g., post-2008 recovery and COVID-19), and changes in energy policy, making it representative of real-world energy demand dynamics.

3.1.2. Predictors

Long-term energy demand forecasting requires integrating predictors that reflect both socioeconomic trends and energy market dynamics. As illustrated in Figure 1, this study incorporates a diverse set of variables, including GDP, population, energy prices, weather data, and renewable energy production. This comprehensive approach enables the modeling of structural patterns and evolving consumption behavior over extended periods.

The key predictors include the following:

Socioeconomic Indicators:

• GDP (quarterly, in Euro) [39] Serves as a primary measure of economic activity and growth, with higher GDP generally indicating increased energy demand.
• Population (annual, number of inhabitants) [40]: Reflects demographic trends, influencing energy usage in residential, commercial, and industrial sectors.

Energy Market Factors:

• Average energy price for households and non households (EUR/KWh) [41]: Aggregates various household and non-household categories.

Production of Renewable Energy:

• TotalWindEnergy (MWh): Quantifies electricity generated from offshore wind farms, marking the growing role of wind power.
• TotalSolarEnergy (MWh): Measures solar power output, indicating the expansion of solar energy capacity.
• TotalRes (incl. Stat.Transfer) (MWh): Represents the aggregate renewable energy production, including policy-driven adjustments.

3.2. EDA

Exploratory Data Analysis (EDA) was conducted on individual datasets as well as the combined dataset to uncover patterns, trends, and correlations among variables. This process provided critical insights into the relationships between electricity demand and influencing factors such as weather conditions, socioeconomic indicators, and energy prices. By analyzing datasets both independently and in aggregate, the study identified dependencies, anomalies, and temporal patterns essential for informed feature selection and model development.

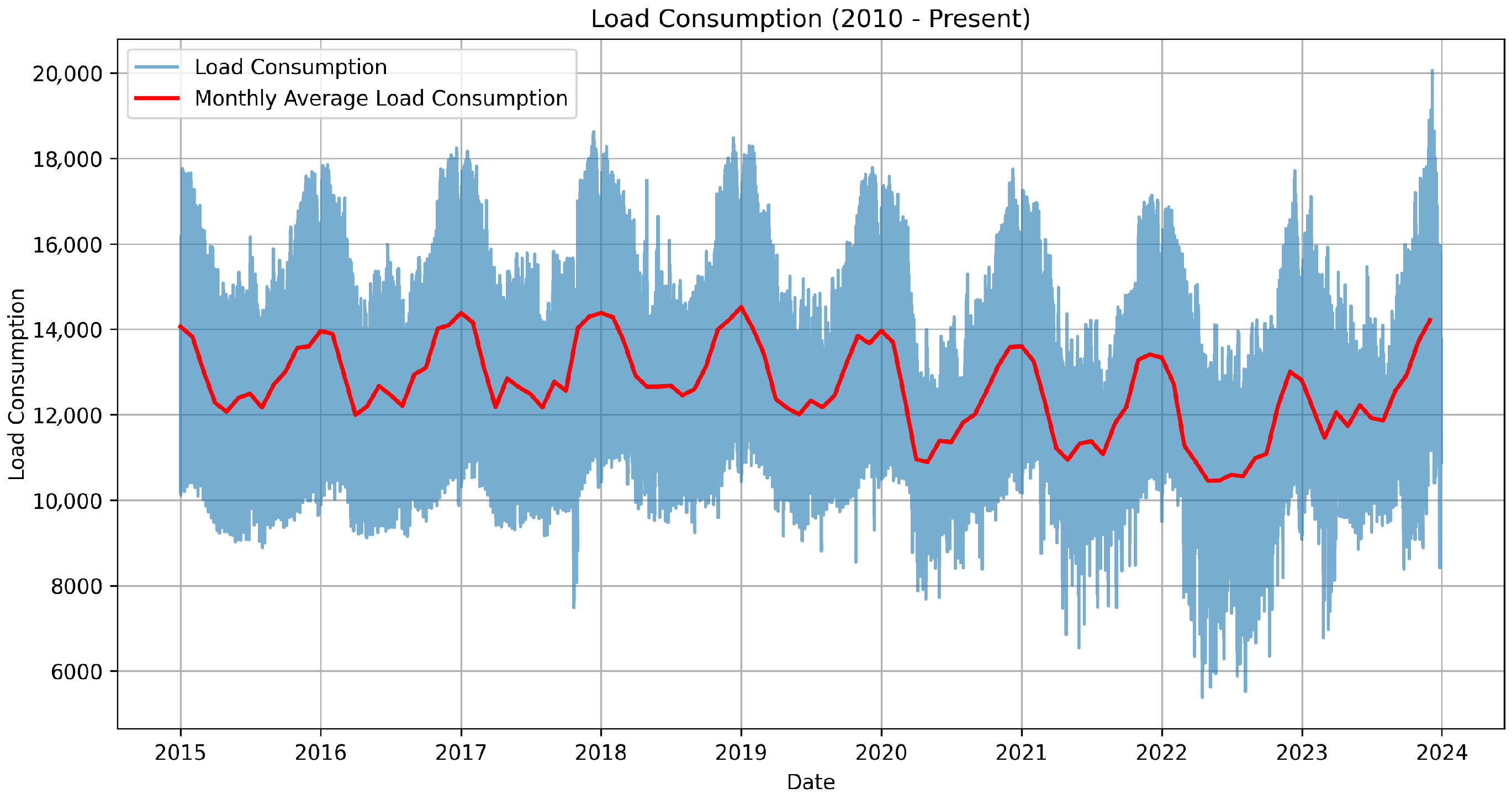
As shown in Figure 2, monthly electricity consumption in The Netherlands exhibits strong seasonality across the study period (2015–2023). To assess whether these time series are stationary, the Augmented Dickey–Fuller (ADF) test was applied, confirming stationarity [19,42].

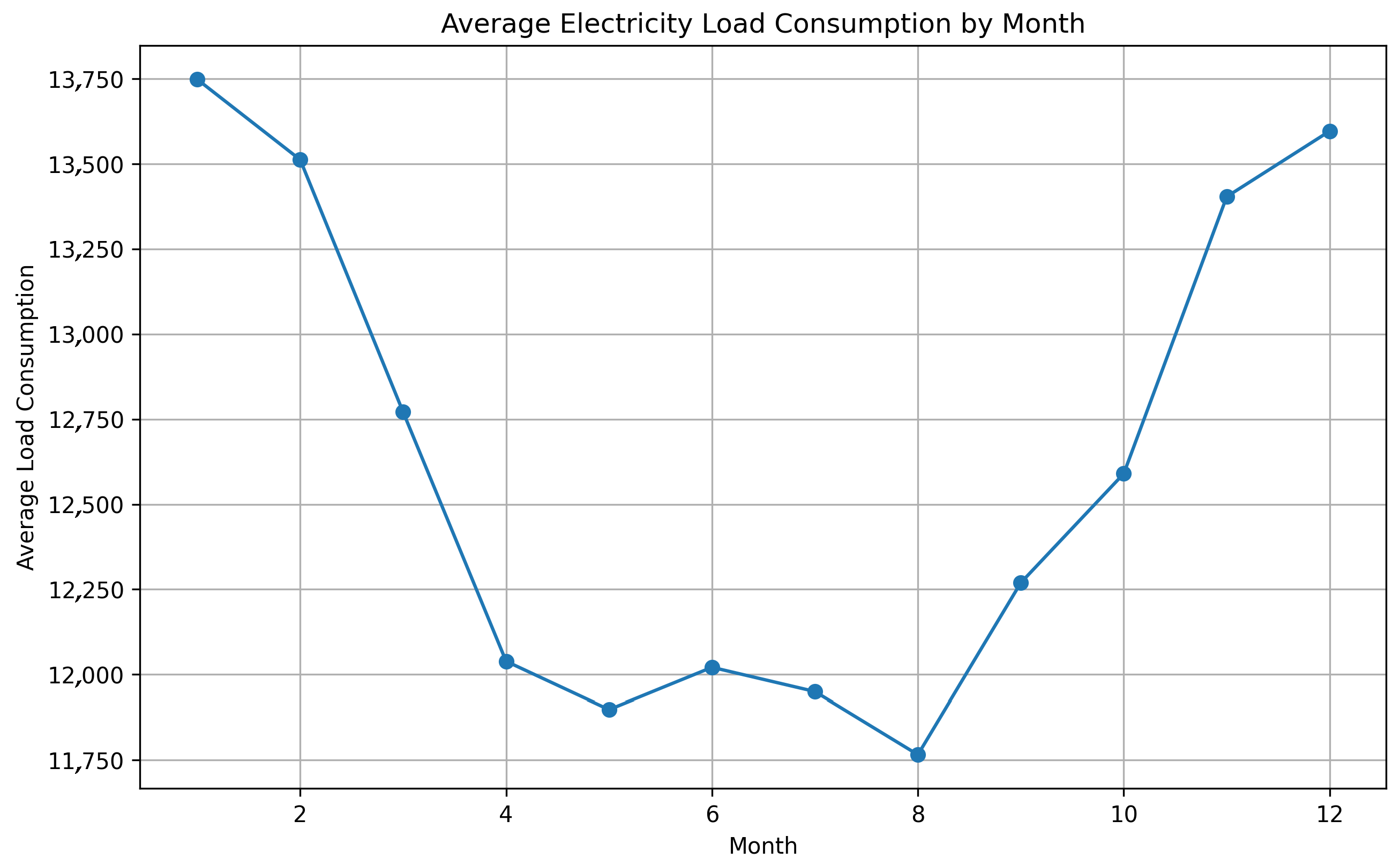
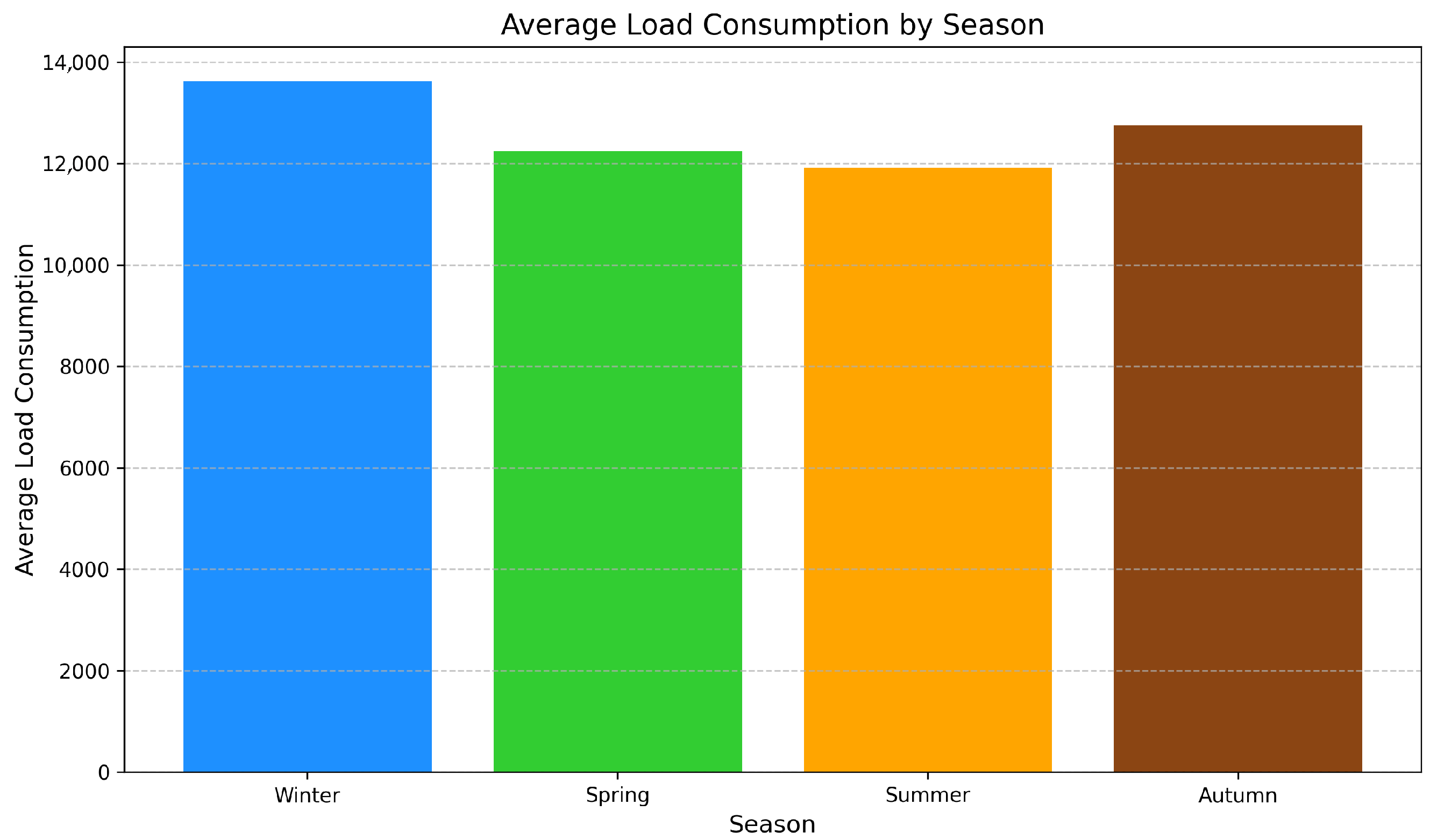
Figure 3 highlights annual electricity demand trends, revealing how seasonality evolves across different years. Seasonal-level aggregation in Figure 4 further confirms consistent demand peaks during the winter months.

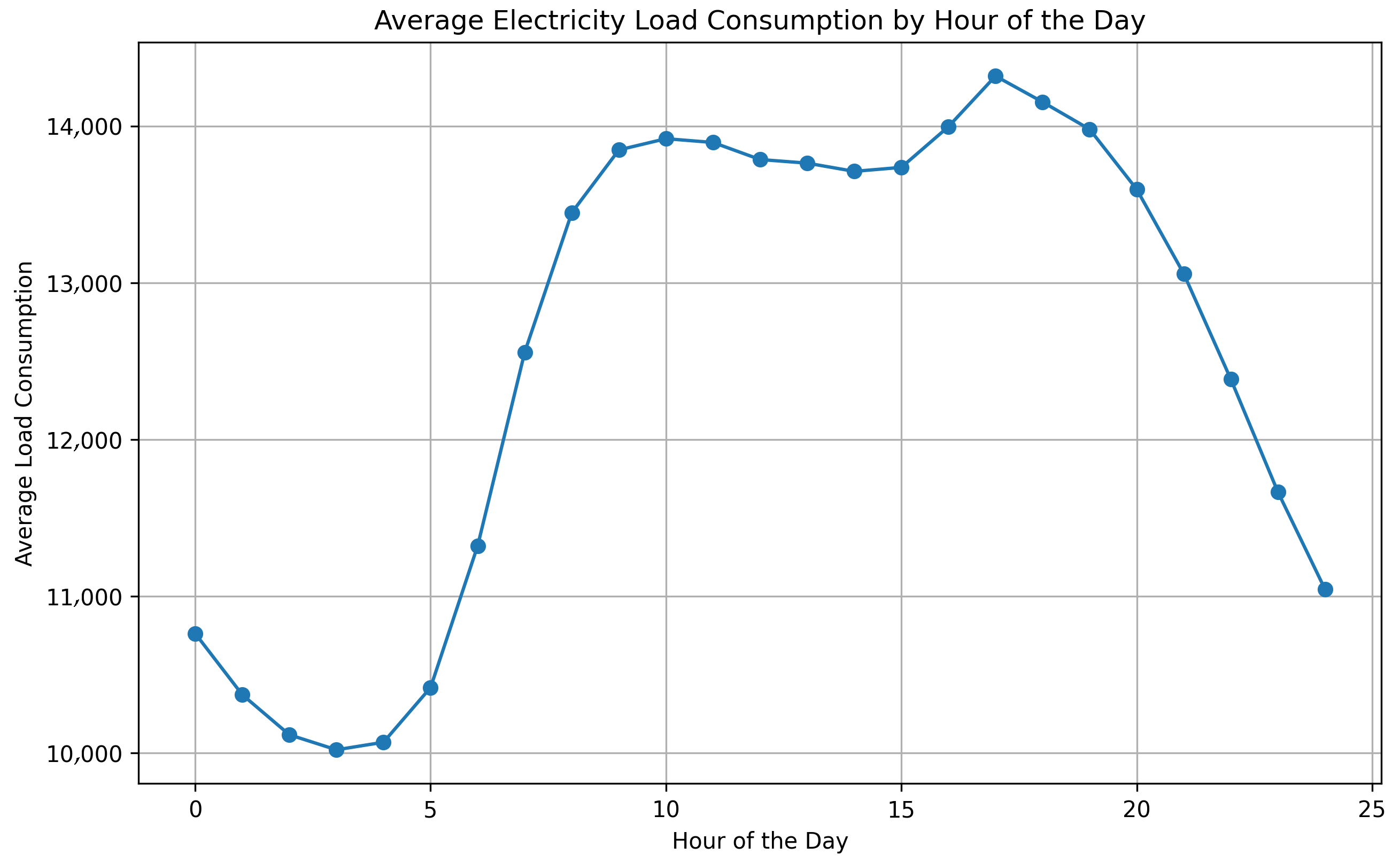
The typical daily demand cycle is visualized in Figure 5, which shows energy usage rising sharply during morning hours and peaking during daytime periods.

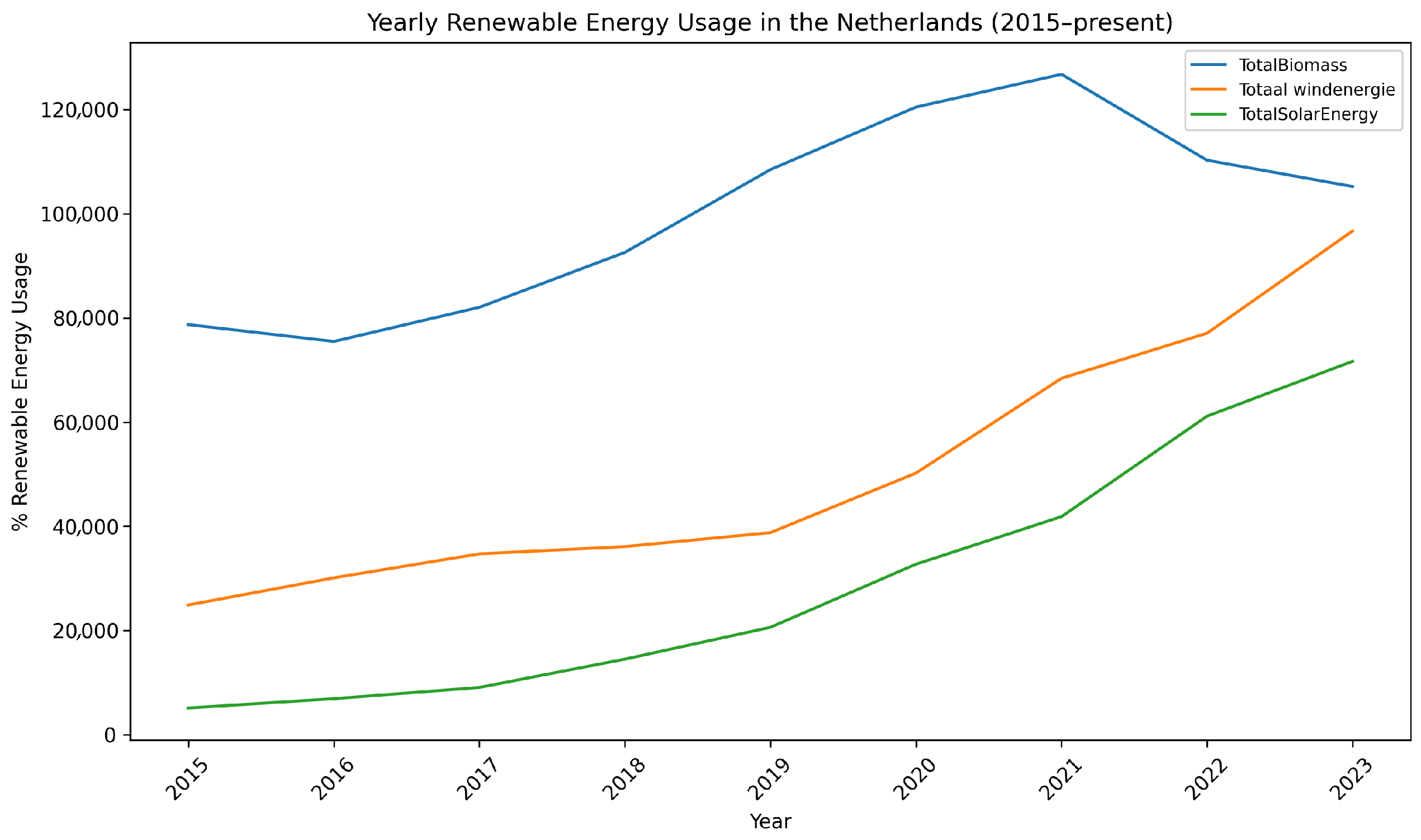
In terms of energy production, Figure 6 illustrates the steady growth of renewable energy generation in The Netherlands from 2009 to 2023. Solar, wind, and biomass energy sources all show increasing contributions over time, with wind energy representing the largest share of renewable output in recent years.

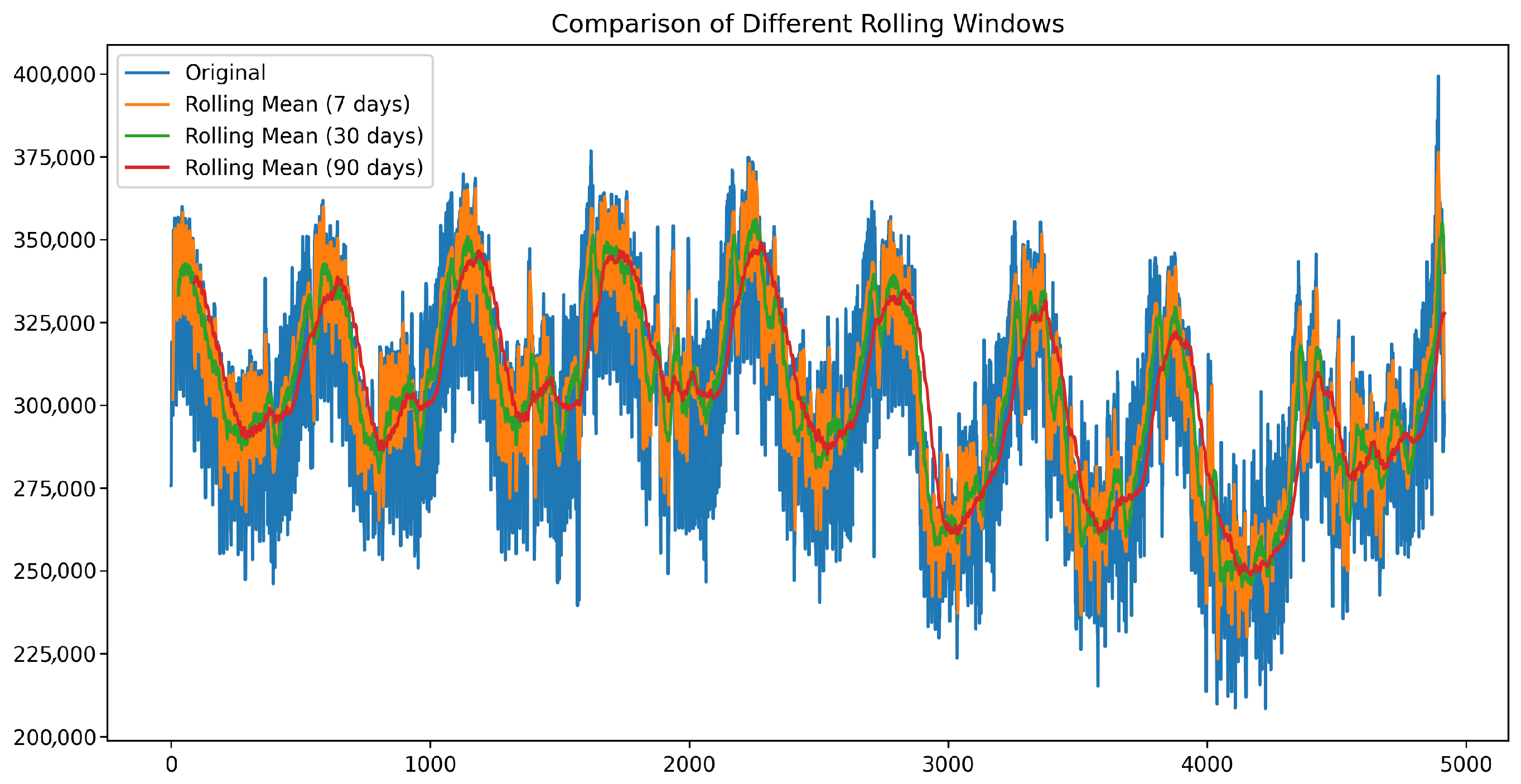
To further analyze short- and long-term variability in electricity demand, smoothing techniques were applied to daily consumption data. As shown in Figure 7, applying 7-day, 30-day, and 90-day rolling mean windows progressively reduces short-term fluctuations, enabling a clearer understanding of broader demand trends.

4. Experimental Setup

This section outlines the procedures used to prepare the data, engineer relevant features, and configure inputs for model training. It includes details on data cleaning, dimensionality reduction, feature scaling, and the setup of various predictor configurations, all of which ensure that the forecasting models are trained on consistent, high-quality input.

4.1. Data Cleaning and Preparation

Following the exploratory data analysis, the data were refined to ensure consistency and reliability for modeling. This process involved identifying and handling outliers, addressing missing values, standardizing measurement units, and aligning data granularity across different sources.

A total of 26 features were used to model electricity demand, categorized into weather variables, renewable generation, socioeconomic indicators, temporal flags, and engineered demand metrics. A detailed breakdown of these input features is presented in

Table 1. Summary of 26 input features grouped by type (e.g., weather, socioeconomic, temporal flags, and rolling demand), prior to dimensionality reduction.

Feature Group	Features
Weather (5)	Temperature (min, max, avg), Wind Speed, Humidity
Renewable Generation (3)	Wind Generation, Solar Generation, Total Renewables
Temporal Flags (6)	Hour of Day, Day of Week, Month, Season, Weekend Indicator, Holiday Indicator
Lag/Rolling Demand (5)	Previous Hour Load, Previous Day Load, Previous Week Load, 7-day Rolling Mean, 30-day Rolling Mean
Socioeconomic (5)	GDP, Population, Electricity Price, Gas Price, Industrial Activity Index
Other Indicators (2)	COVID-19 Lockdown Flag, Energy Import Ratio

. While some of these features were later transformed or reduced via dimensionality reduction techniques, this table reflects the original preprocessed feature set used for model training.

4.1.1. Handling Missing Values

The dataset was highly complete, with only 6 missing hourly entries out of over 15,000 records. These were imputed using a forward-fill method, which preserves temporal continuity. Additionally, Winsorization was applied to mitigate outliers, capping extreme values at the 1st and 99th percentiles, ensuring robustness without distorting underlying demand trends. These steps ensured that the model was trained on high-integrity, noise-resistant data.

4.1.2. Handling Outliers

Outliers were identified using the Interquartile Range (IQR) method, with any data point exceeding 1.5 times the IQR flagged as an outlier. Given their minimal presence relative to the dataset, these outliers were addressed through Winsorization, capping values at the 1st and 99th percentiles to preserve data integrity while mitigating extreme variations.

4.1.3. Combining Data

The datasets were merged based on the date attribute. To address differences in temporal granularity, yearly data were upsampled to a daily frequency by forward-propagating the annual values across all days within the corresponding year.

4.1.4. Predictor Selection

Initially, 26 features were available for modeling. To refine the feature set, a three-step approach was applied:

• Correlation Matrix: Used to identify highly correlated variables and reduce redundancy, minimizing multicollinearity and ensuring diverse informational input.
• Variance Inflation Factor (VIF): Applied to quantify multicollinearity among predictors. Features with high VIF scores were removed to enhance model interpretability and prevent unstable coefficients.

  $${\mathrm{VIF}}_j={\displaystyle \frac{1}{1-R_j^2}}$$

  where $R_j^2$ is the coefficient of determination obtained by regressing $X_j$ on all other predictors.
• Principal Component Analysis (PCA): PCA was used to reduce dimensionality and mitigate multicollinearity among economic and renewable energy features. GDP and Population were standardized and combined into a principal component, EconomicComponent, which explained approximately 93.8% of the variance. Similarly, TotalSolarEnergy, TotalWindEnergy, TotalBiomass, and TotalResIncludingStatTransfer were combined into RenewableEnergyComponent, which captured 92.6% of variance. The explained variance of these principal components is summarized in

  Table 2. Variance explained by principal components for economic and renewable energy features after PCA transformation.

  Principal Component	Input Features	Explained Variance (%)
  Economic Component	GDP, Population	93.8
  Renewable Energy Component	Total Solar Energy, Total Wind Energy, Total Biomass, Total ResIncluding Stat Transfer	92.6

  .

4.1.5. Incorporating Rolling Mean Features

Rolling mean features were introduced to capture temporal trends and reduce noise in demand data. By averaging past values over specified time windows, these features preserve seasonal and trend components while improving model stability.

Two window sizes were used: a 7-day rolling average to capture weekly patterns (e.g., weekend–weekday variation), and a 30-day rolling average to model broader monthly trends. These choices align with typical operational cycles in energy forecasting literature.

4.1.6. Feature Set Configurations

Three feature configurations were evaluated: (1) exogenous features including weather, price, economic, and renewable indicators; (2) generated features such as rolling means and calendar flags; and (3) a combined set integrating both types. This setup facilitated comparison of how each feature group impacts forecasting performance.

4.1.7. Scaling Data

Because LSTM models are sensitive to feature magnitudes, all inputs were scaled using Min–Max normalization:

$$X_{\mathrm{scaled}}={\displaystyle \frac{X-X_{min}}{X_{max}-X_{min}}}$$

Values were normalized within the range [0,1] to enhance convergence during training and ensure efficient gradient descent.

4.2. Model Implementation: Baseline Model SARIMAX

The Seasonal Autoregressive Integrated Moving Average with Exogenous Variables (SARIMAX) model was selected as the baseline for energy demand forecasting due to its effectiveness in capturing underlying trends, seasonal structures, and the influence of external covariates in time series data. As an extension of the classical ARIMA model, SARIMAX introduces seasonal components and allows for the incorporation of exogenous variables, making it particularly suitable for modeling electricity consumption patterns influenced by weather and socioeconomic factors.

SARIMAX captures temporal dependencies through autoregressive (AR) and moving average (MA) terms, stabilizes non-stationary trends via differencing (I), and accounts for recurring patterns through seasonal terms (S). The integration of exogenous regressors (X), such as weather and economic indicators, enables the model to enhance predictive performance by leveraging additional sources of information beyond the intrinsic time series behavior.

Hyperparameter Selection ($p,d,q$) and Seasonal Components

Model hyperparameters $(p,d,q)$ and seasonal components $(P,D,Q,m)$ were identified through a combination of statistical testing, diagnostic plotting, and empirical evaluation:

• Stationarity: The Augmented Dickey–Fuller (ADF) test was conducted to assess stationarity. Since the test statistic rejected the null hypothesis of a unit root, the series was deemed stationary, and the differencing order was set to $d=0$.
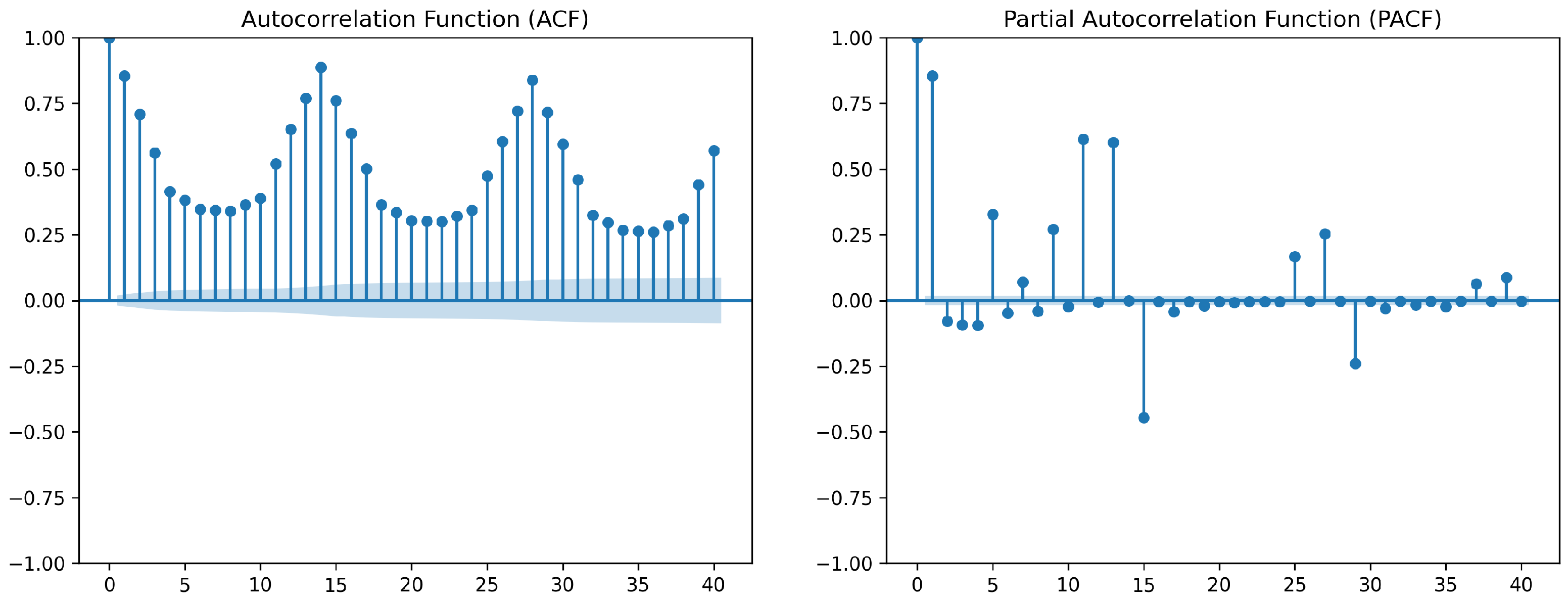
• Short-Term Dynamics: The autocorrelation (ACF) and partial autocorrelation (PACF) functions were analyzed to determine p and q. The PACF exhibited significant lags at 1 and 2, suggesting $p=1$, while the ACF revealed significant lags up to order 3, indicating $q=1$ (Figure 8).
• Seasonal Structure: Weekly seasonality was detected in the load patterns, motivating the choice of a seasonal period $m=7$. Seasonal AR and MA terms were set to $P=1$ and $Q=1$, respectively. As the data was already stationary, seasonal differencing was not required, and $D=0$.

A grid-based search was used to fine-tune the model hyperparameters, evaluating multiple combinations within the identified ranges. The optimal configuration was selected based on the lowest forecasting error on a validation subset of the training data.

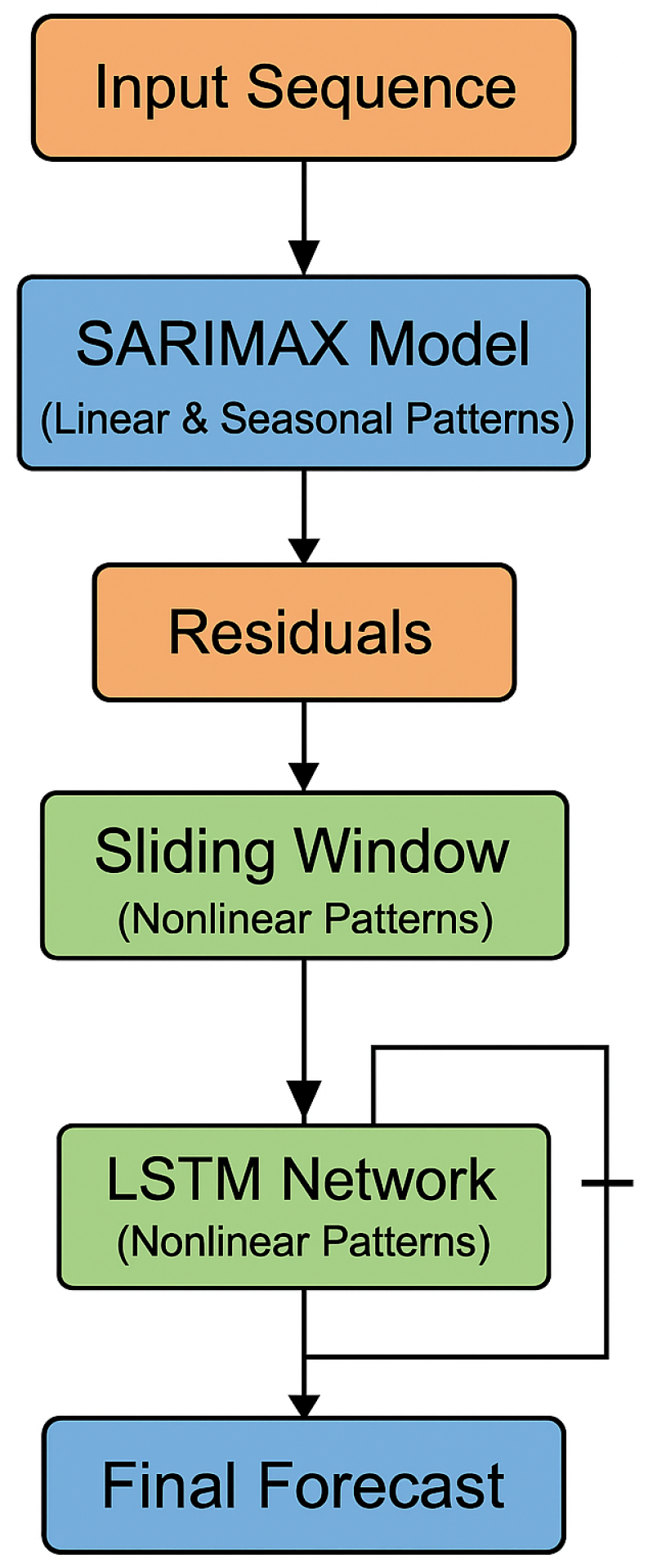
4.3. Hybrid Multi-Stage Forecasting Model

This study implemented a hybrid multi-stage forecasting framework combining a SARIMAX model with a Long Short-Term Memory (LSTM) network. The rationale behind this hybrid approach is to leverage the complementary strengths of statistical modeling and deep learning: SARIMAX excels at modeling linear trends and seasonality, while LSTMs are adept at capturing complex nonlinear patterns [43].

The methodology is divided into two sequential stages. In Stage 1, the SARIMAX model is trained to capture the dominant linear and seasonal structure in the time series. The residuals from this stage, representing the nonlinear components not explained by SARIMAX, are passed to Stage 2, an LSTM network designed to learn and forecast these residual patterns.

Figure 9 provides a schematic of the two-stage model architecture, showing how the input sequence is first processed by SARIMAX and then refined through the LSTM using a residual learning approach.

• Stage 1: SARIMAX Model (Linear and Seasonal Modeling)

The SARIMAX model, discussed in detail in earlier sections, is used here to model linear relationships and seasonal fluctuations in electricity demand. Once trained, it generates a baseline forecast and a corresponding residual sequence, i.e., the portion of the signal not captured by the SARIMAX framework.

• Stage 2: LSTM Network (Residual Modeling)

In the second stage, an LSTM network is employed to model the complex nonlinear dependencies embedded in the residuals produced by SARIMAX. These residuals represent forecast errors from the first stage, and modeling them enables the hybrid framework to improve overall forecasting accuracy.

To effectively model residual dynamics, a sliding window technique is applied to transform the one-dimensional residual time series into supervised sequences. Specifically, for each time step t, the input to the LSTM is a sequence of the previous 30 residuals:

$$X_t=[r_{t-30},r_{t-29},\dots ,r_{t-1}]$$

and the target output is the residual at time t: $y_t=r_t$. This approach preserves temporal dependencies and enables the LSTM to capture lagged nonlinear patterns.

Unlike feedforward networks that process independent inputs, LSTMs retain sequential memory. Each sliding window is shaped as a two-dimensional input of size $(\mathrm{window\_length},1)$, where each row corresponds to a lagged residual.

The LSTM architecture comprises:

• A single LSTM layer with 50 units and ReLU activation
• A dense output layer for one-step-ahead residual prediction

A shallow architecture was chosen to balance learning capacity with generalizability, as deeper configurations showed no notable improvement.

The network is trained using the Mean Squared Error (MSE) loss function and optimized via the Adam optimizer. After training, the LSTM generates residual forecasts recursively, which are then added to the SARIMAX predictions to form the final output:

$${\widehat{y}}_t={\widehat{y}}_t^{SARIMAX}+{\widehat{r}}_t^{LSTM}$$

This composite formulation enables the model to handle both structured linear dynamics and unstructured nonlinear variations.

Key advantages of the SARIMAX–LSTM hybrid model:

• Decomposes time series into interpretable linear and nonlinear components.
• Exploits SARIMAX for structured temporal modeling (seasonality, trend).
• Uses LSTM for residual correction and fine-grained forecast refinement.
• Facilitates modular, stage-wise model training and evaluation.

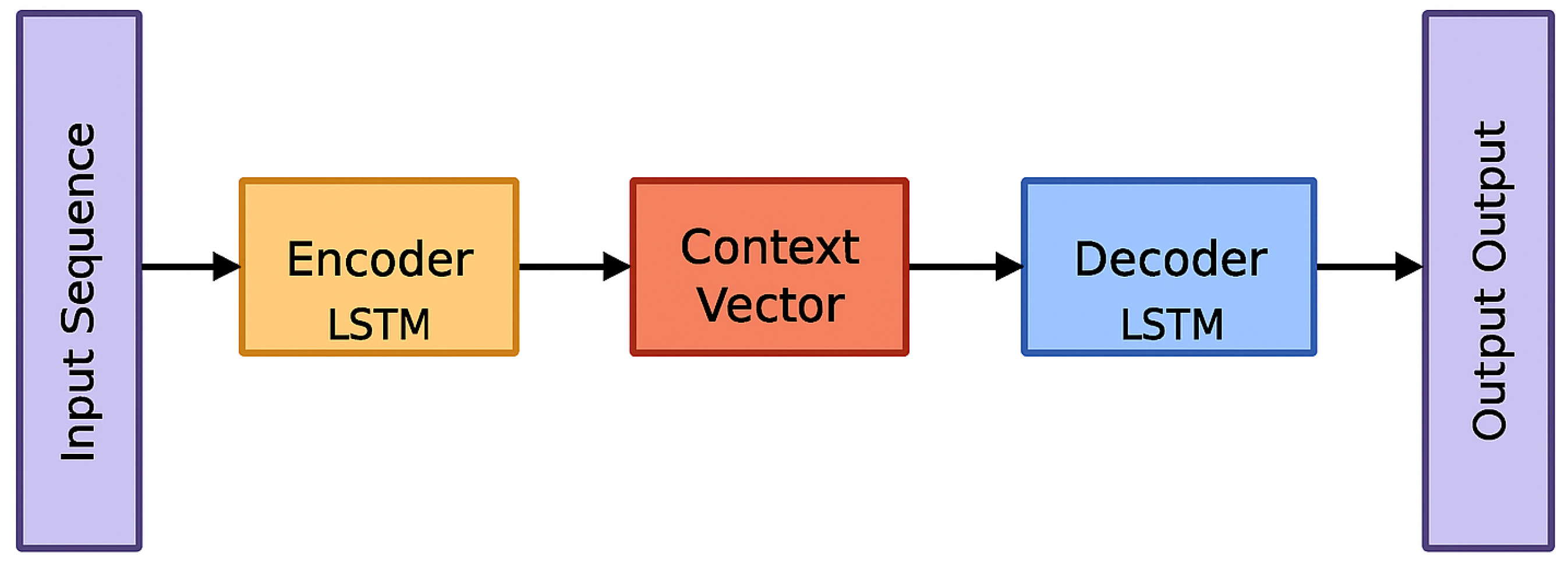
4.4. Sequence-to-Sequence Forecasting Model

To complement the hybrid approach, a seq-to-seq model architecture was implemented to directly forecast energy consumption over multiple time horizons. This model leverages two separate Long Short-Term Memory (LSTM) networks to form an encoder–decoder structure, enabling it to capture complex temporal dependencies in multivariate time series data. seq-to-seq models are particularly suited for forecasting tasks where both input and output sequences can vary in length, offering flexibility for short-term and long-term predictions.

Figure 10 provides a high-level overview of the Seq2Seq architecture, where the encoder compresses historical information into a context vector and the decoder transforms it into a multi-step forecast. This flow enables the model to handle variable-length sequences and preserve temporal structure across time horizons.

4.4.1. Encoder

The encoder processes the historical input features and summarizes them into a fixed-length context vector. The input to the encoder is a 3D tensor of shape (samples, input_length, num_encoder_feature), where each sample represents a sequence of multivariate past observations.

The encoder architecture consists of a single LSTM layer with 64 units. This layer outputs the final hidden state ($h_t$) and cell state ($C_t$), which encapsulate the temporal context of the input sequence. These states are then passed to the decoder to initialize its internal memory.

4.4.2. Decoder

The decoder receives a sequence of lagged target values as input, shaped as (samples, output_length, num_decoder_feature). These values are scaled using Min–Max normalization. During training, teacher forcing is employed, which means the true previous target values are used as decoder inputs to guide the learning process and reduce error accumulation. Similar to the hybrid LSTM model, a single-layer design was adopted to maintain model simplicity and mitigate overfitting.

The decoder also uses a single LSTM layer with 64 units, initialized with the encoder’s hidden and cell states. Its outputs are passed through a TimeDistributed(Dense(1)) layer, which applies a fully connected layer to each time step individually, producing one forecasted value per future time step.

4.4.3. Training Configuration and Model Details

The model was built using the Keras functional API, enabling distinct inputs for the encoder and decoder. The following hyperparameters and training settings were used:

• Input length: 30 days;
• Output length: 7 days;
• LSTM units: 64 for both encoder and decoder;
• Number of LSTM layers: 1 in both encoder and decoder;
• Training technique: Teacher forcing;
• Batch size: 16;
• Epochs: 20;
• Loss function: Mean Squared Error (MSE);
• Optimizer: Adam;
• Decoder input during training: Lagged target values (scaled).

All features, including the target variable, were scaled to the range $[0,1]$ using Min–Max scaling to enhance model convergence. After prediction, inverse transformation is applied to return the forecasted values to their original scale.

4.5. Model Evaluation

Model performance was assessed using four evaluation metrics: Root Mean Squared Error (RMSE), Mean Absolute Percentage Error (MAPE), Mean Absolute Error (MAE), and normalized versions of RMSE and MAE. These metrics offer complementary insights into the magnitude and relative scale of prediction errors, which are essential in the context of energy demand forecasting.

Table 3. Definitions and formulas for model evaluation metrics (RMSE, MAPE, and MAE) used throughout the analysis.

Metric	Formula	Interpretation
RMSE	$\sqrt{{\displaystyle \frac{1}{n}}\sum {(y_{\mathrm{true}}-y_{\mathrm{pred}})}^2}$	Measures average error magnitude; penalizes larger deviations more heavily.
MAPE	$\left({\displaystyle \frac{1}{n}}\sum \left|{\displaystyle \frac{y_{\mathrm{true}}-y_{\mathrm{pred}}}{y_{\mathrm{true}}}}\right|\right)\times 100$	Measures average percentage error; enables comparisons across time periods or scales.
MAE	${\displaystyle \frac{1}{n}}\sum |y_{\mathrm{true}}-y_{\mathrm{pred}}|$	Measures average absolute deviation; treats all errors equally.

summarizes the definitions and mathematical formulas of the three primary metrics used in this study.

Root Mean Squared Error (RMSE): RMSE is calculated as the square root of the average squared differences between predicted and actual values [44]. Because it squares the errors before averaging, it penalizes larger deviations more strongly. In energy demand forecasting, where sudden large errors (e.g., unexpected demand spikes) can have significant operational consequences, RMSE helps highlight these critical deviations. Since its units match those of the target variable (e.g., megawatts), it provides an intuitive sense of the error magnitude.

Mean Absolute Percentage Error (MAPE): MAPE represents the average absolute difference between actual and predicted values, expressed as a percentage of the actual values [44]. This percentage-based error measure is useful because it normalizes the error, allowing for comparisons across different scales or time periods. In energy demand forecasting, where values can vary widely depending on time and context, MAPE provides stakeholders with an easily understandable measure of relative error.

Mean Absolute Error (MAE): MAE computes the average absolute difference between predicted and actual values [44]. Unlike RMSE, MAE treats all errors equally without disproportionately penalizing larger errors. This makes it a robust indicator of average model performance and is particularly useful when understanding the typical deviation is more important than identifying extreme cases.

Normalized RMSE and MAE: To ensure meaningful interpretation and fair comparison across models and forecast horizons, both RMSE and MAE were normalized by dividing them by the mean of the actual load values for each forecast horizon. This yields scale-independent metrics—normalized RMSE (nRMSE) and normalized MAE (nMAE)—which express the average error as a proportion of the typical energy demand [45].

This normalization is particularly important in energy forecasting contexts, where the absolute magnitude of load values can vary significantly across seasons, time periods, or scenarios. Without normalization, RMSE and MAE may appear deceptively large due to the high numerical scale of the target variable. Presenting normalized metrics therefore allows for a clearer understanding of model performance relative to the demand level and facilitates more equitable comparisons across models and feature sets.

Using these metrics in combination allows for a comprehensive evaluation of model performance. RMSE and MAE offer insights into the magnitude of forecasting errors, while MAPE provides a normalized, intuitive measure that aids in communicating results to non-technical stakeholders. This multi-faceted evaluation is critical in energy demand prediction, where both absolute error magnitudes and relative percentages have direct implications for grid management and planning.

5. Results

This section presents the results of the three models evaluated in this study across different feature configurations. It also addresses the impact of renewable and socioeconomic features on forecasting accuracy.

5.1. Performance of Baseline SARIMAX

The performance of the SARIMAX model using different feature sets is summarized in

Table 4. Forecast accuracy of SARIMAX model using exogenous, generated, and combined feature sets.

Metric	Exog. Features	Gen. Features	Both
nRMSE%	11.14	4.00	3.96
MAPE	8.81	3.09	3.01
nMAE%	9.16	3.01	2.94

.

Overall, using only exogenous features led to poor performance, with an nRMSE of 11.14% and a MAPE of 8.81%, indicating that the model struggled to capture meaningful patterns. Generated features improved predictive accuracy substantially (nRMSE = 4.00%, MAPE = 3.09%), while combining both feature types led to a slight improvement (nRMSE = 3.96%, MAPE = 3.01%).

5.2. SARIMAX-LSTM: Hybrid Model Performance

The SARIMAX-LSTM model exhibited improved and stable performance over the baseline SARIMAX, particularly with generated and combined feature sets.

Table 5. Forecast accuracy of SARIMAX–LSTM hybrid model (180-day horizon) across three feature configurations.

Metric	Exog. Features	Gen. Features	Both
nRMSE%	12.13	4.18	3.84
MAPE%	9.89	3.38	3.13
nMAE%	10.73	3.33	3.09

outlines the performance at the 180-day prediction horizon.

Using only exogenous features yielded poor results (nRMSE = 12.13%, MAPE = 9.89%). Generated features enhanced accuracy significantly (nRMSE = 4.18%, MAPE = 3.38%), while the combined set slightly improved further (nRMSE = 3.84%, MAPE = 3.13%).

5.3. Sequence to Sequence Performance

The Seq2Seq model consistently outperformed the other models across all feature configurations, particularly at the 180-day horizon.

Table 6. Forecast performance of the Seq2Seq model (180-day horizon) using exogenous, generated, and combined feature sets.

Metric	Exog. Features	Gen. Features	Both
nRMSE%	3.66	2.86	3.19
MAPE%	2.617	1.88	2.29
nMAE%	2.55	2.29	2.22

summarizes these results. Generated features yielded the best accuracy (nRMSE = 2.86%, MAPE = 1.88%). Exogenous features resulted in higher errors (nRMSE = 3.66%, MAPE = 2.61%), while combining both feature types slightly worsened performance (nRMSE = 3.19%, MAPE = 2.29%).

5.4. Summary of Model Results

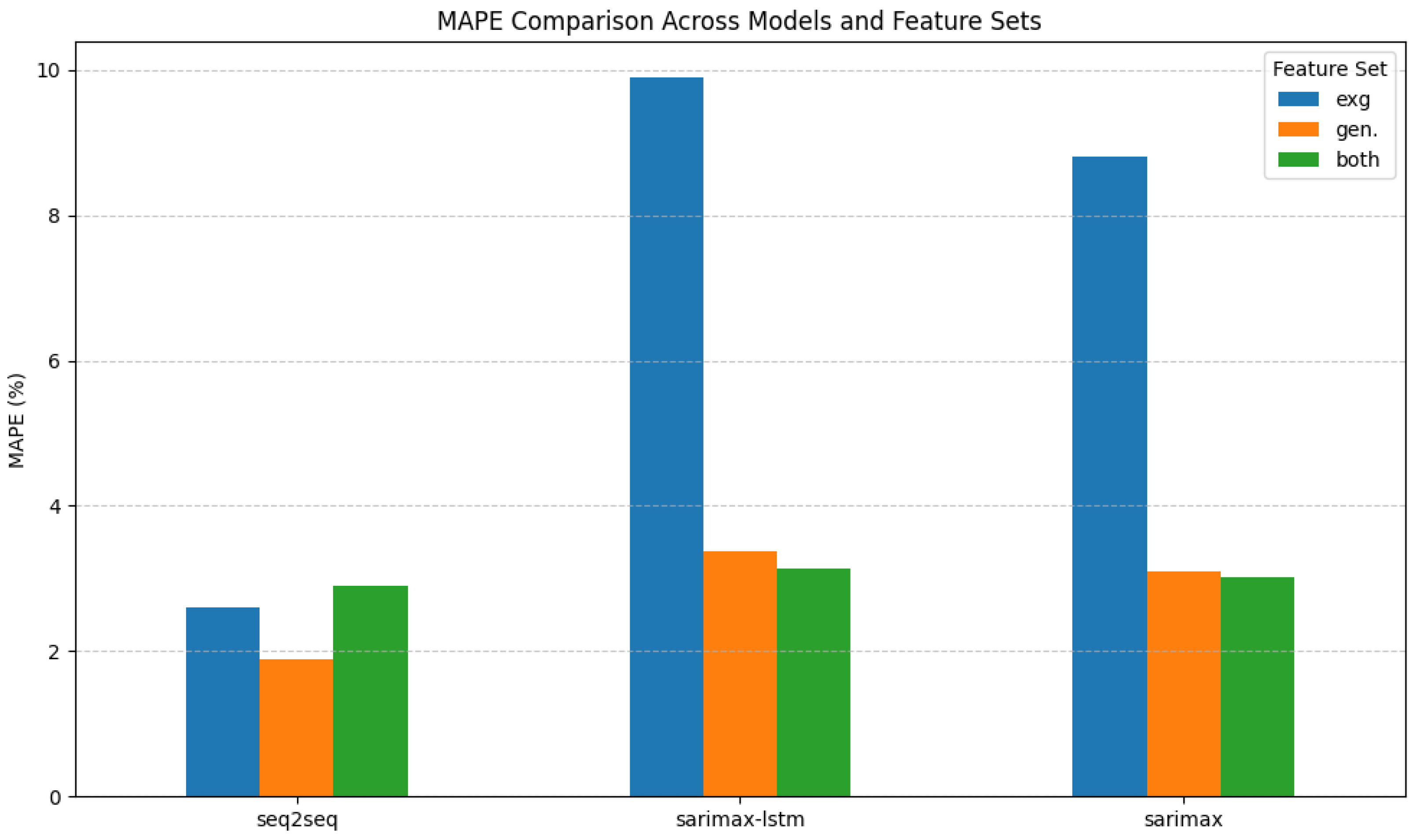
Among the evaluated models, the Seq2Seq model with generated features achieved the best performance, highlighting the effectiveness of deep learning in capturing complex sequential patterns. It consistently outperformed the classical and hybrid models in both short- and long-term horizons.

To further illustrate the performance differences, Figure 11 shows a side-by-side comparison of MAPE across all three models and feature sets.

Robustness of Model Comparison

Although formal significance testing was not performed, the evaluation was designed to ensure meaningful and fair model comparison. All models were trained and tested on the same data splits, using consistent preprocessing and feature scaling pipelines. Furthermore, each model was tested under multiple feature configurations and forecast horizons, enabling a multidimensional comparison of predictive performance. The performance metrics (RMSE, MAPE, and nRMSE) were selected to reflect both absolute and relative error magnitudes, offering complementary perspectives on model behavior. These measures collectively contribute to a robust and reproducible comparison framework.

5.5. Impact of Exogenous Feature Sets

To assess the contribution of different exogenous variables to forecasting performance, we conducted additional SARIMAX experiments using two key feature groups: renewable energy indicators and socioeconomic variables. The evaluation was performed across both short-term (1-day) and long-term (180-day) forecasting horizons.

As summarized in

Table 7. SARIMAX model accuracy comparison with and without renewable and socioeconomic feature groups across 1-day and 180-day horizons.

Horizon	Feature Group	nRMSE (%)	nMAE (%)	MAPE (%)
1 day	Without Exogenous	2.18	2.18	2.18
1 day	With Renewables	1.09	1.09	1.09
1 day	With Socioeconomic	2.48	2.48	2.48
180 days	Without Exogenous	7.85	6.67	6.90
180 days	With Renewables	9.07	7.54	7.93
180 days	With Socioeconomic	8.72	7.34	7.26

, renewable energy features substantially improved short-term forecast accuracy. Specifically, at the 1-day horizon, incorporating renewables reduced the MAPE from 2.18% to 1.09%. In contrast, adding socioeconomic indicators led to a slight increase in error, with MAPE rising to 2.48%.

However, the results at the 180-day horizon suggest limited utility of these features for long-term forecasting. Both renewable and socioeconomic groups increased forecasting error compared to the baseline SARIMAX model without exogenous inputs. This indicates that while real-time exogenous data may be helpful for capturing short-term fluctuations, their relevance diminishes over extended prediction windows.

To provide a concise overview of model performance across all feature sets,

Table 8. Comparative summary of nRMSE, MAPE, and nMAE across SARIMAX, SARIMAX–LSTM, and Seq2Seq models for three feature set configurations.

Metric	Model	Exog. Features	Gen. Features	Both
nRMSE%	SARIMAX	11.14	4.00	3.96
	SARIMAX–LSTM	12.13	4.18	3.84
	Seq2Seq	3.66	2.86	3.19
MAPE%	SARIMAX	8.81	3.09	3.01
	SARIMAX–LSTM	9.89	3.38	3.13
	Seq2Seq	2.62	1.88	2.29
nMAE%	SARIMAX	9.16	3.01	2.94
	SARIMAX–LSTM	10.73	3.33	3.09
	Seq2Seq	2.55	2.29	2.22

presents an aggregated comparison of nRMSE, MAPE, and nMAE for the SARIMAX, SARIMAX–LSTM, and Seq2Seq models.

6. Discussion

This section critically reflects on this study’s findings, comparing them with previous work, analyzing the strengths and weaknesses of the models and features explored, and addressing limitations and ethical implications of energy demand forecasting.

Performance Comparison and Insights

• Exogenous Features Only. Models trained exclusively on exogenous variables, such as weather, energy prices, and socioeconomic indicators, consistently underperformed across all forecast horizons. For example, SARIMAX yielded a MAPE of 8.81% and SARIMAX-LSTM scored 9.89%, while Seq2Seq slightly improved at 2.61%. These results indicate that while these features provide contextual insight, they fail to capture internal demand dynamics on their own.
• Generated Features Only. Internally generated features, such as calendar-based variables and rolling demand windows, led to significantly improved accuracy across all models. SARIMAX achieved a MAPE of 3.09%, SARIMAX-LSTM reached 3.38%, and Seq2Seq performed best at 1.88%. This highlights the dominant role of historical patterns and temporal structure in determining energy demand.
• Combined Feature Set. Combining generated and exogenous features provided marginal improvements over generated features alone in some cases (e.g., SARIMAX: 3.01%, SARIMAX-LSTM: 3.13%), but slightly worsened Seq2Seq performance (MAPE increased from 1.88% to 2.29%). This suggests that while combining signals may be beneficial for statistical models, deep learning architectures may become more sensitive to noise introduced by less predictive external features.
• Deep Learning Performance. Among the evaluated models, Seq2Seq demonstrated the most robust and consistent performance, particularly at the 180-day forecast horizon. With the lowest nRMSE (2.86%) and MAPE (1.88%) when using generated features, it significantly outperformed SARIMAX (3.96%, 3.01%) and SARIMAX-LSTM (3.84%, 3.13%). This supports the strength of deep learning in modeling long-term temporal dependencies when fed clean, structured input data.
• Feature Importance Across Time Horizons. The performance differences between generated and exogenous features reflect both their data characteristics and their interaction with specific model types. Generated features, such as rolling means, lagged windows, and calendar-based indicators, tend to encode stable seasonal patterns and long-term structure. These patterns persist over time and are particularly useful in long-horizon models like Seq2Seq, which benefit from consistent temporal signals. In contrast, exogenous features (e.g., weather and energy prices) are more dynamic and provide high short-term explanatory power, especially when recent observations are available. Their predictive utility is strongest over short horizons (e.g., 1–7 days), where models like SARIMAX can leverage immediate fluctuations in external conditions. These insights help explain why generated features outperform in long-term forecasts while exogenous variables improve short-term predictions.

7. Conclusions

The findings demonstrate that combining exogenous and engineered features substantially improves forecasting accuracy, particularly when tailored to the strengths of each model architecture. The SARIMAX model captured seasonal trends effectively, while the SARIMAX–LSTM hybrid improved short-term accuracy by modeling nonlinear fluctuations. The sequence-to-sequence (Seq2Seq) deep learning model offered robust long-range forecasting performance, especially when trained with calendar-based and smoothed historical features.

Experiments confirmed that including renewable energy variables, such as wind and solar production, led to substantial improvements in short-term (1-day) forecasts. For longer horizons, the benefits were less consistent, reflecting the time-sensitive nature of renewable energy patterns. Socioeconomic indicators like GDP and population also contributed modest improvements, especially when forecasting over multi-month horizons.

The results of this study have direct implications for energy system planning and operation. The Seq2Seq deep learning model’s superior long-term performance makes it well-suited for forecasting horizons relevant to energy policy, infrastructure investment, and capacity planning. This can aid national regulators and utilities in anticipating seasonal surges, renewable variability, and long-term trends in electrification. Conversely, the SARIMAX model’s strength in short-term forecasting makes it highly valuable for operational applications, such as grid balancing, day-ahead scheduling, and short-term dispatch. The SARIMAX–LSTM hybrid, meanwhile, bridges the gap between interpretability and flexibility, offering an option for medium-horizon planning in dynamic environments. Together, these models offer complementary tools for multi-scale energy management and forecasting strategies.

Beyond quantitative improvements, this work illustrates the value of feature engineering and model layering in building scalable, adaptable forecasting systems. These insights are particularly relevant for grid operators and policymakers, as they transition toward a decentralized and renewables-driven energy landscape.

This study developed and evaluated a hybrid multi-stage forecasting framework to enhance short- and long-term electricity demand prediction in The Netherlands. By integrating statistical (SARIMAX), hybrid (SARIMAX–LSTM), and deep learning (sequence-to-sequence) models with diverse data sources, including weather, energy prices, socioeconomic indicators, and engineered temporal features, this research sought to overcome the limitations of single-model forecasting systems.

The results showed that engineered time series features (e.g., rolling averages and calendar effects) consistently improved model performance across different architectures. Among the evaluated models, the sequence-to-sequence architecture, trained with generated features, achieved the best forecasting accuracy (MAPE = 1.88% at the 180-day horizon), outperforming both classical and hybrid approaches.

While this study is constrained by its focus on one country and specific modeling choices, it provides evidence that engineered temporal features combined with appropriate model architectures can meaningfully improve energy demand forecasting. These findings may support future research and practical forecasting efforts as energy systems grow more dynamic and data-driven.

Future work could extend this approach using transformer-based models and real-time data integration to improve long-horizon accuracy and adaptability