Demand Information Sharing in Building Material Supply Chain Considering Competing Manufacturers’ Greening Efforts

Abstract

The environmental pollution problem caused by the construction industry has been paid attention to by scholars. However, few existing studies on supply chain management explore the interplay between information-sharing strategies and green-effort strategies in a green building materials supply chain. This study explores green building materials design and information-sharing dynamics in a supply chain consisting of a common building enterprise and two competing building materials manufacturers. The building enterprise decides whether to share demand information with manufacturers, who then determine product greenness, while the building enterprise determines the retail price. The findings reveal that information sharing has dual effects on manufacturers’ profitability, depending on competitive dynamics and demand sensitivity to building materials greenness. Additionally, the interplay between information sharing and green design strategies highlights the importance of aligning product design decisions with optimal information-sharing practices. While information sharing consistently improves environmental performance in a bilateral monopoly system where a single manufacturer provides building materials to a single building enterprise, it can induce adverse environmental outcomes in competitive scenarios. These results provide actionable guidance for developing green supply chain strategies that balance economic and environmental goals.

1. Introduction

Traditional building materials (TBMs), including concrete, glass, and steel, are associated with significant environmental pollution during both production and operational phases, posing substantial risks to both environment and human health [1,2,3,4]. In contrast, green building materials (GBMs) have the advantages of environmental protection and energy conservation, playing a leading and supporting role in reducing carbon emissions [5]. Driven by the growing environmental consciousness and social responsibility of consumers, more and more BM manufacturers are beginning to transform into the production of GBMs, and construction enterprises and developers are also increasingly inclined to use GBMs [6].

However, the upstream BM manufacturers rely more on historical data or industry reports to plan BM production, and it is difficult to accurately predict demand information. Therefore, inventory backlogs caused by insufficient green research and development investment or inaccurate pricing are likely to occur. For example, in 2022, the bitter lesson of Beijing Oriental Yuhong, which suffered a backlog of RMB 1.26 billion worth of waterproof materials inventory due to misjudging the demand fluctuations in the Yangtze River Delta, exposed the huge cost of information silos [7]. This lesson underscores the critical importance of information management in the green building materials supply chain.

Downstream construction enterprises play a key role by leveraging their direct market insights. In practice, downstream construction enterprises directly participate in the construction and delivery of projects such as real estate and infrastructure construction. They can perceive the changes in the demand of the terminal market in time and adjust the BM procurement plan according to the project progress, the availability of funds, and customer preferences. There are actual cases of construction enterprises sharing demand information through WeChat groups and information-sharing platforms for the supply and demand of raw materials for construction projects. For example, the Jinan Housing and Urban–Rural Development Bureau has set up WeChat groups and an information-sharing platform for the supply and demand of raw materials for construction projects to ensure that ready-mixed concrete, mortar, sand and gravel, and cement production enterprises resume work and production as soon as possible and guarantee the timely supply of raw materials [8]. The BIM data sharing platform established by Vanke and Beijing New Building Materials Public Limited Company has created an industry miracle with 300% improvement in the R&D response speed. However, despite these benefits, construction enterprises may hesitate to share demand information due to potential risks.

Although construction enterprises can feed back terminal developers’ preferences for GBMs to the production side the recognition of GBMs by terminal developers, helping building materials manufacturers make effective decisions on green research and development investment, construction enterprises may lose their own advantages in information acquisition. After obtaining the demand information, BM manufacturers will quickly adjust wholesale prices, which will undoubtedly exacerbate the double-marginalization effect and greatly compress the profit margins of downstream construction enterprises [9]. More seriously, in order to expand their business, some building materials manufacturers may engage in self-operated construction business, forming a direct vertical competition relationship with construction enterprises. Therefore, whether construction enterprises are willing to share information is crucial for BM manufacturers and also affects the realization of the overall green performance of the BM supply chain.

2. Literature Review

We focus on the demand information-sharing problem of BM supply chains with competitive manufacturers’ greening efforts. Hence, our work is mainly related to two streams: (1) green building supply chain management and (2) demand information sharing in the supply chain under competitive environment.

2.1. Green Building Supply Chain Management

Sustainable supply chain management is attracting more and more attention in academic and practical communities [10,11]. Some research indicates that consumer environmental consciousness and social responsibility can motivate sustainable initiatives among stakeholders, ultimately improving overall supply chain performance [12,13]. For example, Heydari et al. consider demand is affected by green level of product and study the manufacturer’s greening decisions in a three-tier dual channel supply chain [14]. Liang and Fu study the influence of factors such as consumers’ green preferences, building greenness on profits, and comparatively analyze developers’ evolutionary stable strategies under the government’s static and dynamic subsidy mechanisms [15].

Some research focuses on the impact of government policies on green production. For example, He et al. construct a differential game model composed of developers and contractors under government participation and consider how non-government subsidies (NGS), lump-sum government subsidies (LGS), and unit government subsidies (UGS) influence building green [16]. Qian et al. construct a two-level supply chain composed of two building materials manufacturers and a contractor to study the influence of the government’s subsidy mechanism on the green innovation investment decision of the building materials supply chain [17]. Ning et al. construct an evolutionary game model between real-estate developers and consumers to analyze the guiding role of government regulations on real-estate developers’ green construction when the market mechanism fails [18]. Fu et al. study the key driving factors of low-carbon practices in the construction industry based on institutional theory, relational view theory and self-determination theory [19]. Li et al. analyze the effect of competition intensity between building materials manufacturers and consumer green preference on the profit of the green supply chain of building materials under the duopoly competition model [6]. Xia et al. study the effect of public–private partnership on rural residential environments and analyze the effect of policy benefits and incentive expenditures of local governments on evolutionary stable strategy [20]. Yang and Xiao analyze how channel leadership and governmental interventions affect prices, green levels and expected profits [21].

The above studies mainly consider the effect of consumer environmental consciousness, consumers’ sensitivity to product greenness, and government policy on manufacturers’ green effort. On the one hand, few scholars pay attention to the information asymmetry in the building material production supply chain considering the manufacturers’ effort to improve the environmental protection level of products. On the other hand, most studies consider encouraging developers to carry out green construction to achieve low-carbon emission reductions, ignoring the incentive mechanism design of improving the green level of building materials products at the production source. Our paper extends the research perspective to the building materials production. And we study how construction enterprises’ information-sharing strategies, developers’ sensitivity to green building materials, and market competition affect building materials manufacturers’ greening effort levels under asymmetric information.

2.2. Demand Information Sharing in the Green Supply Chain

Our work is also related to the literature on vertical demand information sharing in supply chains. Some research considers the effect of information sharing on supply chain and carbon emissions. For example, Yu et al. study the influence of information sharing on carbon emission reduction effects and the profits of supply chains, considering the impacts of consumers’ low-carbon awareness and enterprises’ risk aversion on players’ decisions [22]. Cao et al. construct a green agricultural product supply chain composed of cooperatives, agricultural enterprises, and consumers and find that the greater consumers’ sensitivity to the greenness of agricultural products, the more inclined agricultural enterprises are to actively share information [23]. Ma et al. study the impact of information superiority and power structures on equilibrium decisions, consumer benefits, and the environment in the situation that the manufacturer or retailer has information on consumer preferences [24]. Li et al. find information disclosure has a positive impact on the environment [9], while Yu et al. highlight the benefits of information sharing for both environmental and supply chain efficiency are not always guaranteed [22]. Huang et al. find that there may be negative environmental impacts when third-party manufacturers do not share cost information [25].

Some research considers supply chain competition. For example, Yu et al. study the carbon reduction capabilities of manufacturers under incumbent retailer’s different information-sharing formats, including no information sharing, partial information sharing, and public information sharing, in a supply chain consisting of one manufacturer, one incumbent retailer, and an entrant retailer [26]. Guan et al. consider the influence of manufacturers’ provision of green services on retailers’ information-sharing strategies in two competing green supply chains [27]. Similarly, Quadir et al. analyze the impact of information sharing on the manufacturer’s green decisions in two competing supply chains and compare the retailer’s information-sharing strategy and the manufacturer’s green decision under Bertrand and Cournot competition [28]. Li et al. study retailers’ motivation for information sharing and the impact of information sharing on green supply chains with horizontal competition [29]. Different from the above literature, this paper considers that developers’ demand is affected by the greenness of building materials. Under demand uncertainty, it discusses the influence of different market structures, product substitutability, and developers’ sensitivity to the greenness of building materials on building material manufacturers’ green R&D investment decisions and information-sharing decisions.

Based on the above research background, we specifically focus on the following research questions: (1) How will the competition among building materials manufacturers and construction enterprises’ demand information-sharing strategies affect building manufacturers’ green innovation investment levels? (2) In a supply chain with competing manufacturers and under information asymmetry, will construction enterprise actively share information with building materials manufacturers? If not, how should building materials manufacturers formulate corresponding information contracts to motivate construction enterprise to share information and achieve a “win-win” situation?

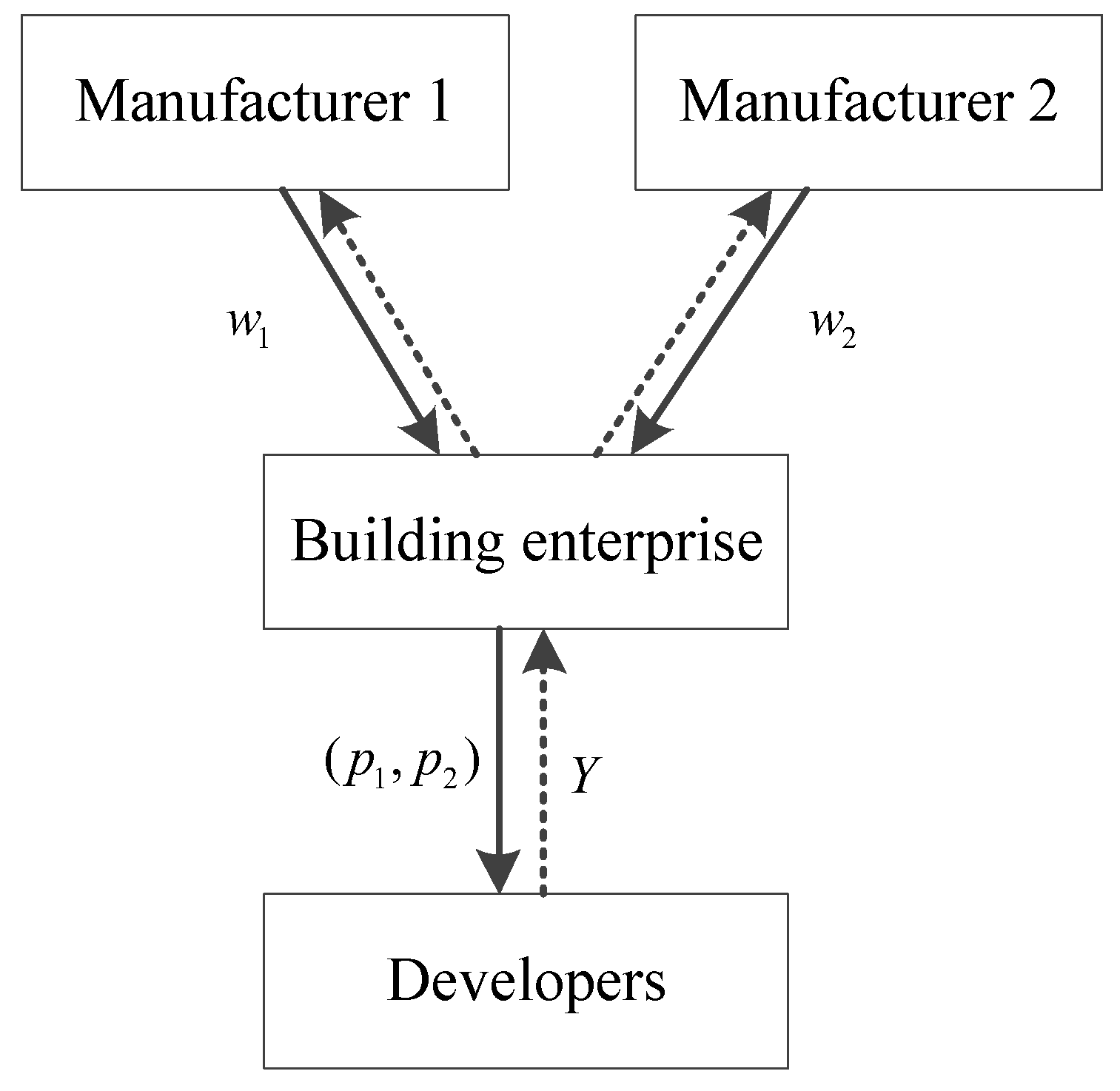
3. Model Assumptions

Consider a two-tier green building materials supply chain with two identical green building materials manufacturers (indexed by 1 or 2) selling substitute green building materials through a common construction enterprise. Manufacturer $i$ produces green building materials with cost given by ${\displaystyle \frac{{g_i}^2}{2}}$. The quadratic form of the effort cost function accounts for the diminishing return of effort, which is widely used in the literature (e.g., [30,31]). Figure 1 illustrates the channel structure, where a dotted arrow indicates signal flow and a solid arrow indicates product flow. The demand function of products $i$ is given by

$$d_i=a+\theta -(1+\varphi )p_i+\varphi p_{3-i}-\lambda g_{3-i}+(1+\lambda )g_i$$

where $a$ is the average level of demand that is known to both firms, and the random variable $\theta$, with zero mean and variance ${\sigma }^2$, represents demand uncertainty. $p_i$ is the retail price of product $i$, $g_i>0$ represents the greenness of manufacturer $i$’s building material, $\lambda >0$ represents the sensitivity of developers to the greenness of building materials, and $\varphi >0$ represents competition intensity. Linear demand functions have been extensively used in operations management literature (e.g., [32,33]). Assume that $\varphi >{\displaystyle \frac{1}{4}}({\lambda }^2+2\lambda -3)$; this assumption ensures that building materials manufacturers will not refrain from making R&D investments due to the excessively high costs of green research.

Affected by policies and construction schedules, the demand for building materials is significantly volatile. As the construction party of the project, the construction enterprise has a grasp of the fluctuations in the demand for building materials. In contrast, the building materials manufacturer relies on historical data or industry reports to plan the production of building materials, and it is difficult for them to accurately predict the dynamic demand of the downstream. So we assume that the construction enterprise has access to demand signal $Y$, which is an unbiased estimator of $\theta$ (i.e., $E[Y | \theta ]=\theta$), and decides whether to share it with manufacturer $i$ before the demand is observed. Define signal accuracy as $s\triangleq 1/E[Var(Y | \theta )]$, which can be interpreted as the construction enterprise’s ability in demand forecasting. Assume that the conditional expectation of $\theta$ with respect to $Y$ is a linear function of $Y$ [34,35,36], and we can obtain $E[\theta | Y]=s{\sigma }^2{(1+s{\sigma }^2)}^{-1}Y$, $\mathrm{\eta }(s,\sigma )\triangleq E[{(E[\theta | Y])}^2]=$$s{\sigma }^4{(1+s{\sigma }^2)}^{-1}$.

The sequence of events for the multi-stage game problem considered is as follows: Firstly, the construction enterprise decides whether to share this information with the manufacturers and both manufacturers determine whether to pay for the information. Secondly, the construction enterprise learns the private demand information $Y$ and shares it with the manufacturers based on information-sharing decisions made in Stage 1. Thirdly, manufacturers determine the greenness of building materials. Subsequently, the construction enterprise determines the retail price.

The information-sharing strategies in the green supply chain can be categorized into three cases, defined as follows:

(1)

$(0,0)$: Neither of the manufacturers acquire information.

(2)

$(0,1)$ or $(1,0)$: Only one manufacturer obtains information from the construction enterprise (i.e., either manufacturer $i$ or manufacturer $j$ acquires information). Without loss of generality, we assume that it is manufacturer $i$ who obtains the information.

(3)

$(1,1)$: Both manufacturers obtain information (i.e., both manufacturers $i$ and $j$ acquire information from the construction enterprise).

4. One Building Materials Manufacturer

To examine the impact of manufacturer competition on optimal strategies, we initially simplify our model to a non-competitive scenario where one building material manufacturer sells products through a construction enterprise in the supply chain. The results obtained from this serve as benchmarks for the competitive case, after which we proceed to analyze the strategies employed by a green supply chain with two competing manufacturers. So the demand function of building material is given by $d=a+\theta -p+\lambda g$, where $p$ is the retail price of product, $\lambda >0$ represents the sensitivity of developers to the green level of building materials, and $g$ is the greenness of product.

4.1. Equilibrium Decisions in Non-Competitive Scenario

Knowing the wholesale prices $w$ and $g$ as well as the demand signal $Y$, the construction enterprise’s optimization problem is to determine $p$ to maximize their expected profit.

$$\underset{p}{\max } {\mathrm{\Pi }}_R=(p-w)(a+E[\theta | Y]-p+\lambda g)$$

where $E[\theta | Y]=s{\sigma }^2{(1+s{\sigma }^2)}^{-1}Y$. Because ${\mathrm{\Pi }}_R$ is concave in $p$, by solving the first-order condition ${\displaystyle \frac{\mathit{\partial }{\mathrm{\Pi }}_R}{\mathit{\partial }p}}=0$, the construction enterprise’s best-response retail price is

$$p(w,g)={\displaystyle \frac{1}{2\mathrm{\varphi }}}\left(a+E[\mathrm{\theta } | Y]+w+\lambda g\right)$$

Thus, the resulting demand for building material is

$$d(w,g)={\displaystyle \frac{1}{2}}\left[a+2\theta -E[\mathrm{\theta } | Y]-w+\lambda g\right]$$

Next, we show how the manufacturer of building materials determines their wholesale price in anticipation of the construction enterprise’s response.

If the construction enterprise does not share information, then the manufacturer can only determine the wholesale price $w$ and the green-effort level $g$ based on $E[\theta ]$, and the expected profit of the manufacturer is

$${\mathrm{\Pi }}_M=wE[d(w,g)]-{\displaystyle \frac{g^2}{2}}$$

If the construction enterprise shares the demand information, then the manufacturer makes decisions to maximize its expected profit based on $E[\theta | Y]$, and the expected profit of the manufacturer is

$${\mathrm{\Pi }}_M=wE[d(w,g) | Y]-{\displaystyle \frac{g^2}{2}}$$

It can be shown that the manufacturer’s expected profit function is concave. An uninformed manufacturer maximizes their expected profit by choosing the optimal wholesale price and green-effort level.

$$w^N={\displaystyle \frac{2a}{4-{\lambda }^2}}, g^N={\displaystyle \frac{a\lambda }{4-{\lambda }^2}}$$

An informed manufacturer maximizes his expected profit by choosing the optimal wholesale price and green-effort level.

$$w^S={\displaystyle \frac{2(a+E[\mathrm{\theta } | Y])}{4-{\lambda }^2}}, g^S={\displaystyle \frac{\lambda (a+E[\mathrm{\theta } | Y])}{4-{\lambda }^2}}$$

Condition 1 shows, in equilibrium, the optimal decision-making of the supply chain in the situation of (no) information sharing.

Condition 1.

(a) When the construction enterprise does not share information, the equilibrium wholesale price and green-effort level are as follows: $w^N={\displaystyle \frac{2a}{4-{\lambda }^2}}$, $g^N={\displaystyle \frac{a\lambda }{4-{\lambda }^2}}$; the equilibrium retail price is$p^N={\displaystyle \frac{(4-{\lambda }^2)E[\mathrm{\theta } | Y]+6a}{2(4-{\lambda }^2)}}$.

(b) When the construction enterprise shares the demand information, the equilibrium wholesale price and green-effort level are as follow: $w^S={\displaystyle \frac{2(a+E[\mathrm{\theta } | Y])}{4-{\lambda }^2}}$, $g^S={\displaystyle \frac{\lambda (a+E[\mathrm{\theta } | Y])}{4-{\lambda }^2}}$; the equilibrium retail price is$p^S={\displaystyle \frac{3(a+E[\mathrm{\theta } | Y])}{4-{\lambda }^2}}$.

Compare and analyze the optimal decision of the manufacturer under the condition that the construction enterprise shares and does not share demand information and take derivatives with respect to parameters $\lambda$; we have Corollary 1.

Corollary 1.

(a) $w^S>w^N$, $g^S>g^N$; (b) ${\displaystyle \frac{\mathit{\partial }\mathrm{\Delta }w}{\mathit{\partial }\lambda }}>0$, ${\displaystyle \frac{\mathit{\partial }\mathrm{\Delta }g}{\mathit{\partial }\lambda }}>0$, where$\mathrm{\Delta }w=w^S-w^N$, $\mathrm{\Delta }g=g^S-g^N$ are presented in Appendix A.

Firstly, Corollary 1 shows that the information sharing of the construction enterprise makes the responsiveness of the wholesale price of the manufacturer and the greenness of the product as well as the sales price of the building materials to $Y$ stronger. As shown in Figure 2, on the one hand, information sharing intensifies the double-marginalization effect. On the other hand, the building material manufacturer that obtains demand information sharing can improve the greenness of the product and the utilization efficiency of resources according to the demand.

Secondly, Corollary 1 shows that the more sensitive the developers are to the greenness of building materials, the greater the double-marginalization effect. When developers pay more attention to the green level of building material products, the manufacturer needs to improve the greenness of products. Because of the high cost of green production, the building material manufacturer is more inclined to increase the wholesale price to compensate for excessive costs.

Thirdly, Corollary 1 demonstrates that the more sensitive developers are to the greenness of building material products, the more responsive the greenness of the product is to demand information and the more inclined the building materials manufacturer is to increase the greenness of the product. When the preference of developers for green building materials increases, the sensitivity of market demand to green level increases, so the building material manufacturer will improve the greenness of the product to enhance product competitiveness and gain greater market share and premium space.

4.2. Firms’ Ex Ante Profits in Non-Competitive Scenario

Based on the equilibrium pricing and greenness of product decisions, for given strategy of information sharing, we take expectation with respect to the demand signal $Y$ to obtain the firms’ ex ante profits before the demand signal is observed. Condition 2 shows, in equilibrium, the more optimal firm’s ex ante profit in the situation of (no) information sharing.

Condition 2.

(a) When the construction enterprise does not share information, the firms’ ex ante profits are given by

$${\mathrm{\Pi }}_M^N={\displaystyle \frac{a^{2}k}{8k-2{\lambda }^2}}, {\mathrm{\Pi }}_R^N={\displaystyle \frac{4a^2{k}^2+{(4k-{\lambda }^2)}^2\mathrm{\eta }(s,\sigma )}{4{(4k-{\lambda }^2)}^2}.}$$

(b) When the construction enterprise shares the demand information, the firms’ ex ante profits are given by

$${\mathrm{\Pi }}_M^S={\displaystyle \frac{k(a^2+\mathrm{\eta }(s,\sigma ))}{2(4k-{\lambda }^2)}}, {\mathrm{\Pi }}_R^S={\displaystyle \frac{k^2(a^2+\mathrm{\eta }(s,\sigma ))}{{(4k-{\lambda }^2)}^2}.}$$

By comparing the profit of the building material manufacturer, construction enterprise, and supply chain in different information-sharing strategies, we explore the value of information sharing and attempt to design an information-sharing incentive mechanism. In the following Proposition 1, we show the information-sharing strategy of the construction enterprise under conditions without competition.

Proposition 1.

The construction enterprise’s expected profit under different information-sharing strategies satisfies

(a) If $0<\lambda <\sqrt{2}$, then ${\mathrm{\Pi }}_R^S<{\mathrm{\Pi }}_R^N$;

(b) If $\sqrt{2}<\lambda <2$, then ${\mathrm{\Pi }}_R^S>{\mathrm{\Pi }}_R^N$.

Proposition 1 demonstrates that information sharing does not always increase the profits of the construction enterprise. According to Figure 3, when developers are less sensitive to greenness ($0<\lambda <\sqrt{2}$), the revenue improvement effect brought by the improvement of product greenness is relatively low, so the construction enterprise does not share information. But when developers show high green sensitivity ($\sqrt{2}<\lambda <2$), construction enterprise shares information. This is because (1) information transparency enables more effective improvement of product greenness by material manufacturers, creating greater value enhancement, and (2) the revenue-boosting effect of green effort becomes more pronounced when developer willingness to pay for eco-friendly materials is high. In this case, the benefits of coordinated green innovation outweigh the potential drawbacks of information sharing, leading to higher overall supply chain efficiency and profitability.

Furthermore, by comparing the expected profits of the building material manufacturer and building material supply chain under different information-sharing strategies, we have Proposition 2.

Proposition 2.

(a) ${\mathrm{\Pi }}_M^S>{\mathrm{\Pi }}_M^N$;

(b) If$0<\lambda <\sqrt{3-\sqrt{5}}$, then${\mathrm{\Pi }}_M^S+{\mathrm{\Pi }}_R^S<{\mathrm{\Pi }}_M^N+{\mathrm{\Pi }}_R^N$; If$\sqrt{3-\sqrt{5}}<\lambda <2$, then ${\mathrm{\Pi }}_M^S+{\mathrm{\Pi }}_R^S>{\mathrm{\Pi }}_M^N+{\mathrm{\Pi }}_R^N$.

Figure 4a,b visually show the changes in manufacturer and supply chain profits under different information-sharing strategies. According to Proposition 2, the manufacturer always prefers receiving information from the construction enterprise. Therefore, when information sharing is not beneficial to the construction enterprise but can increase the revenue of the building material supply chain, the manufacturer can provide information fees to incentivize the construction enterprise to share information, achieving a Pareto improvement among the supply chain members. Therefore, consider that the manufacturer provides a transfer payment to the construction enterprise, and only when the total profit levels obtained by the construction enterprise and the building material manufacturer after information sharing are not lower than their revenues before information sharing will the manufacturer provide information fees to encourage the construction enterprise to share information. According to Proposition 1, when $\sqrt{2}<\lambda <2$, the construction enterprise will actively share information, and the manufacturer can obtain the information without providing an information fee, while when $0<\lambda <\sqrt{2}$, if the manufacturer does not provide an information fee, the construction enterprise will not share the information. Thus, we have Proposition 3.

Proposition 3.

If$\sqrt{3-\sqrt{5}}<\lambda <\sqrt{2}$, the building material manufacturer can provide information fee$M\in [M_{\min },M_{\max }]$ to the construction enterprise to encourage the construction enterprise to share information, where$M_{\min }=M_R^N-M_R^S>0$, $M_{\max }=M_M^S-M_M^N>0$.

Proposition 3 shows that if the information-sharing motives of the manufacturer and construction enterprise are different, only when the sensitivity of developers to the greenness of products meets the corresponding parameter conditions can the building materials manufacturer effectively stimulate information sharing of construction enterprises through the economic compensation mechanism. Therefore, scientific design of information-sharing incentive contracts based on developers’ sensitivity to the greenness of building materials products is helpful to build a stable information cooperation mechanism between building materials manufacturer and construction enterprise. This mechanism can not only improve the accuracy of market demand response but also significantly optimize the overall performance level of the supply chain, providing theoretical basis and practical guidance for the collaborative development of the building materials supply chain.

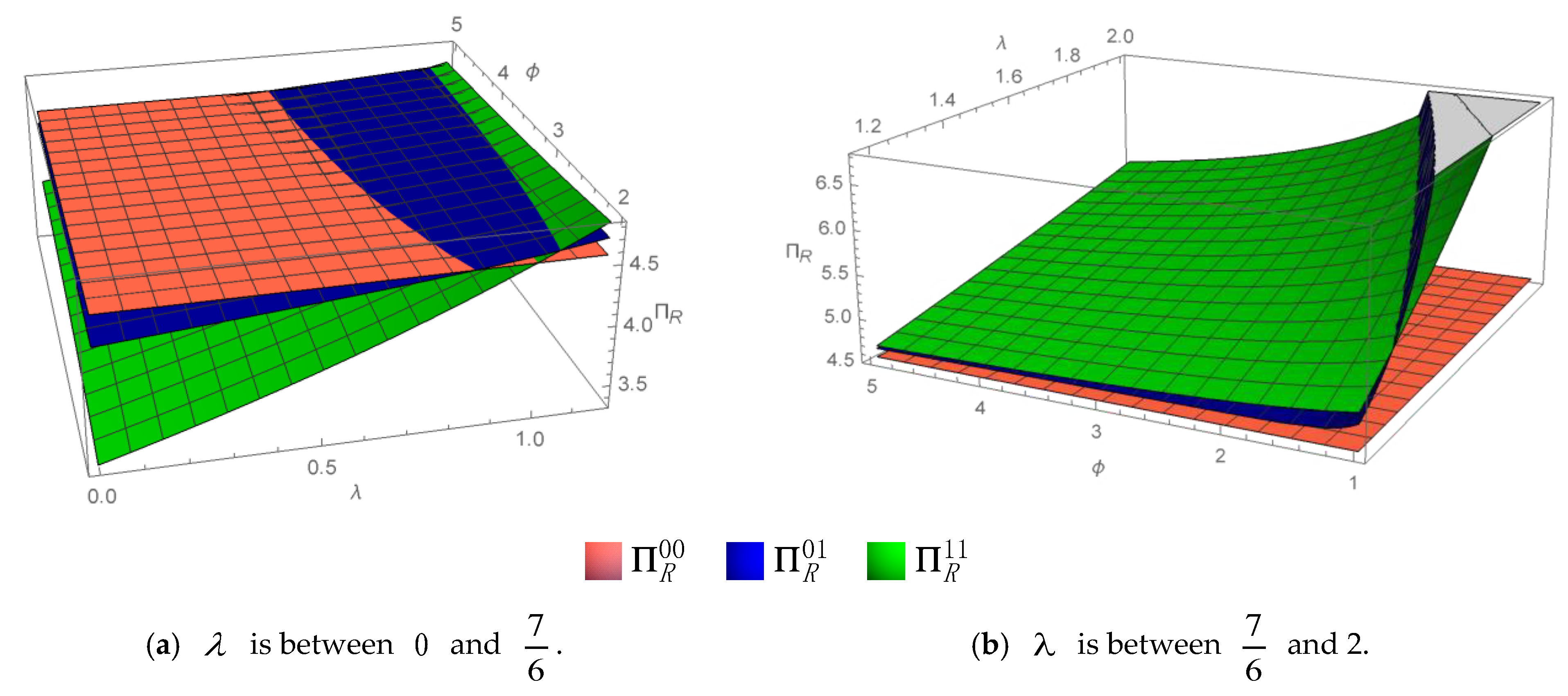
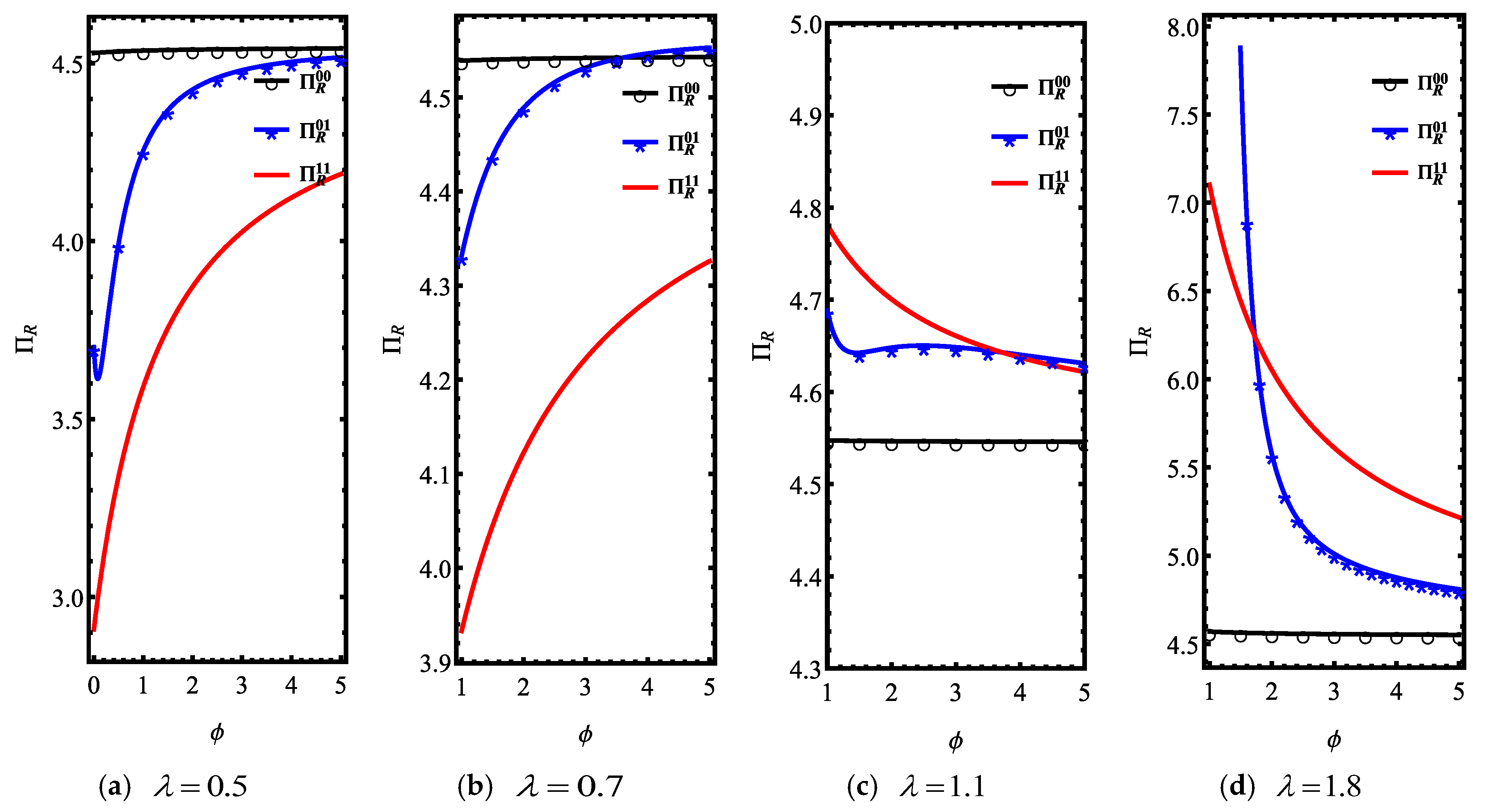
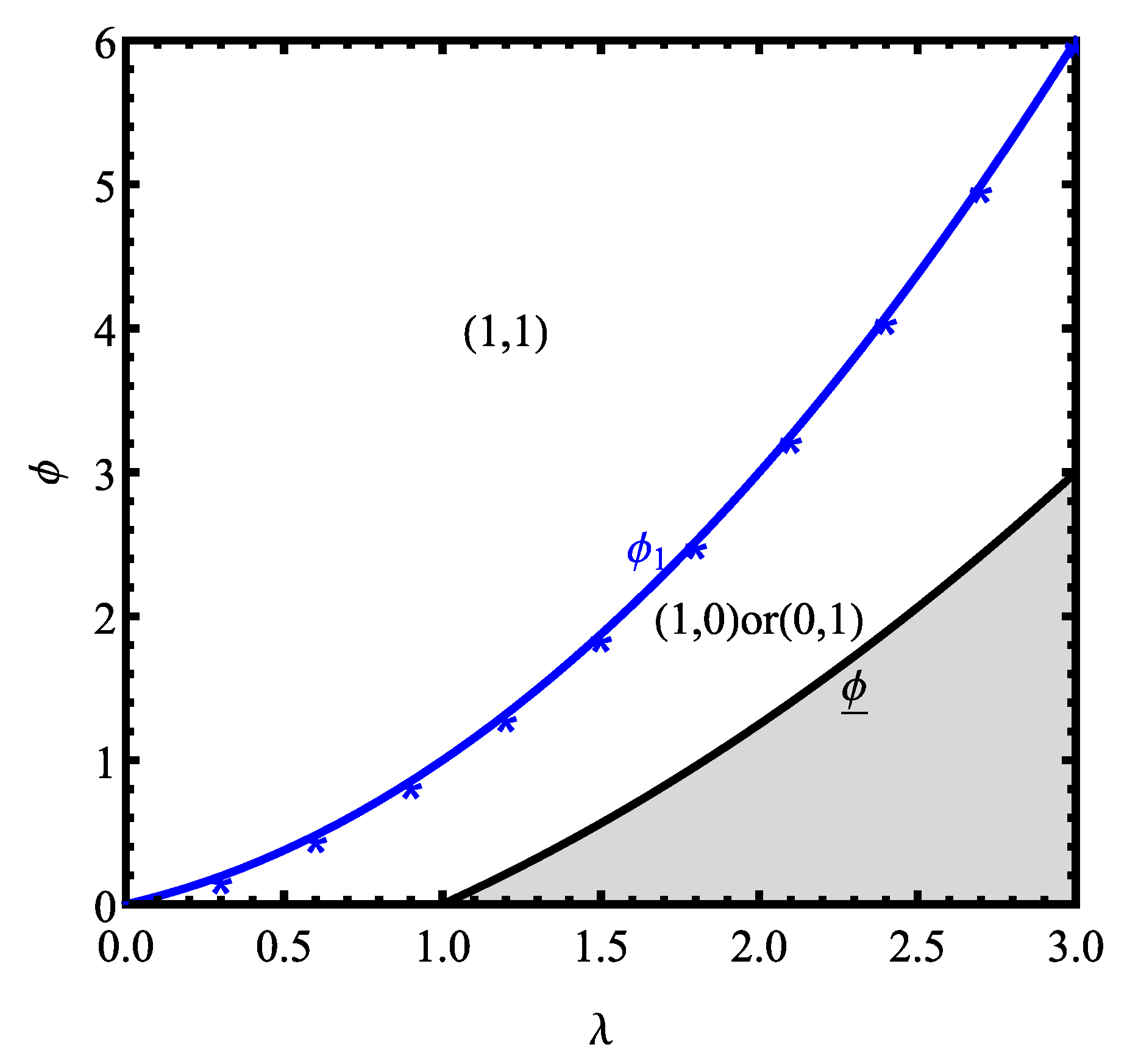
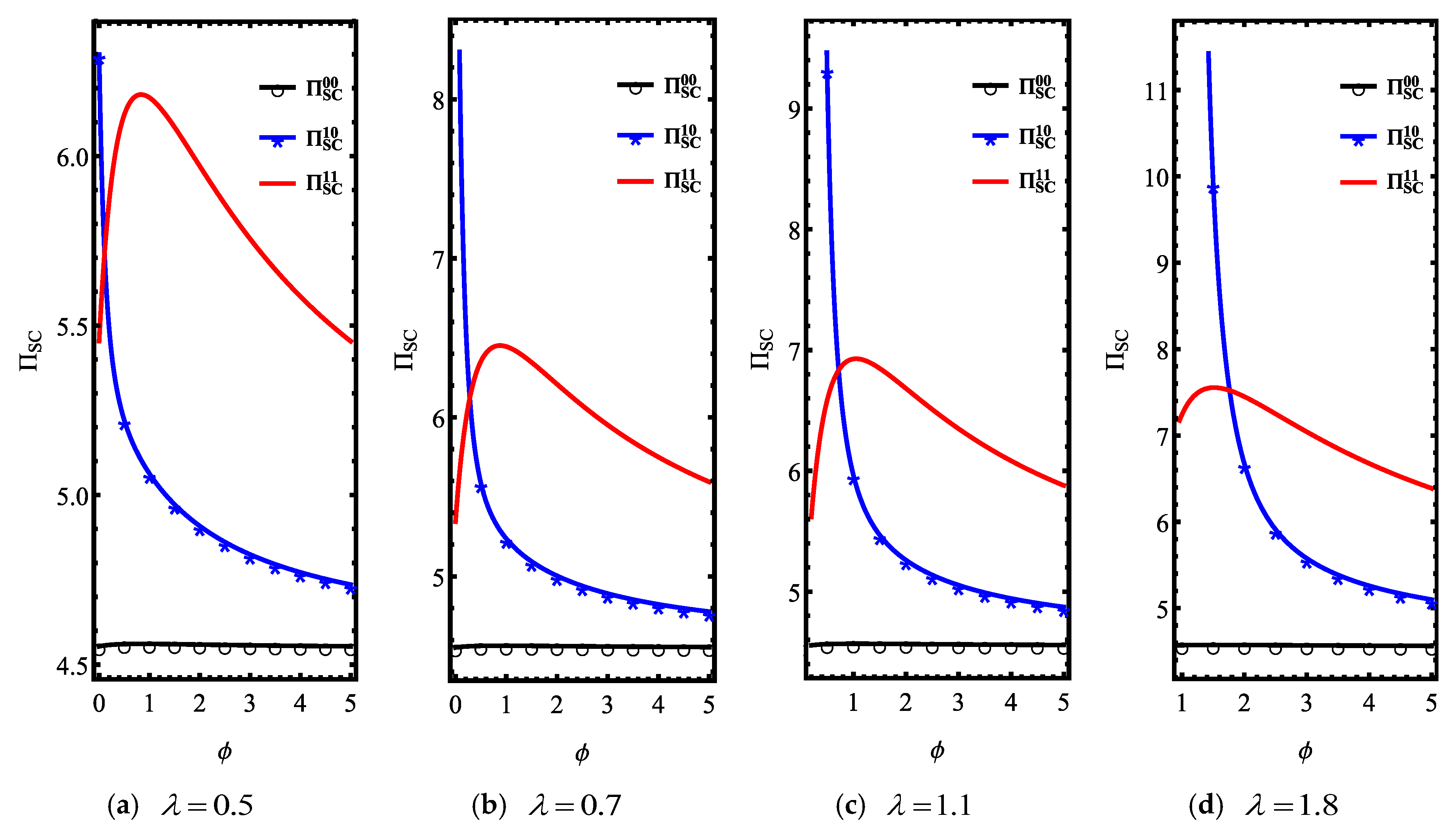
5. Two Building Materials Manufacturers

In this section, we explore the effect of manufacturer competition on information-sharing strategies of construction enterprise.

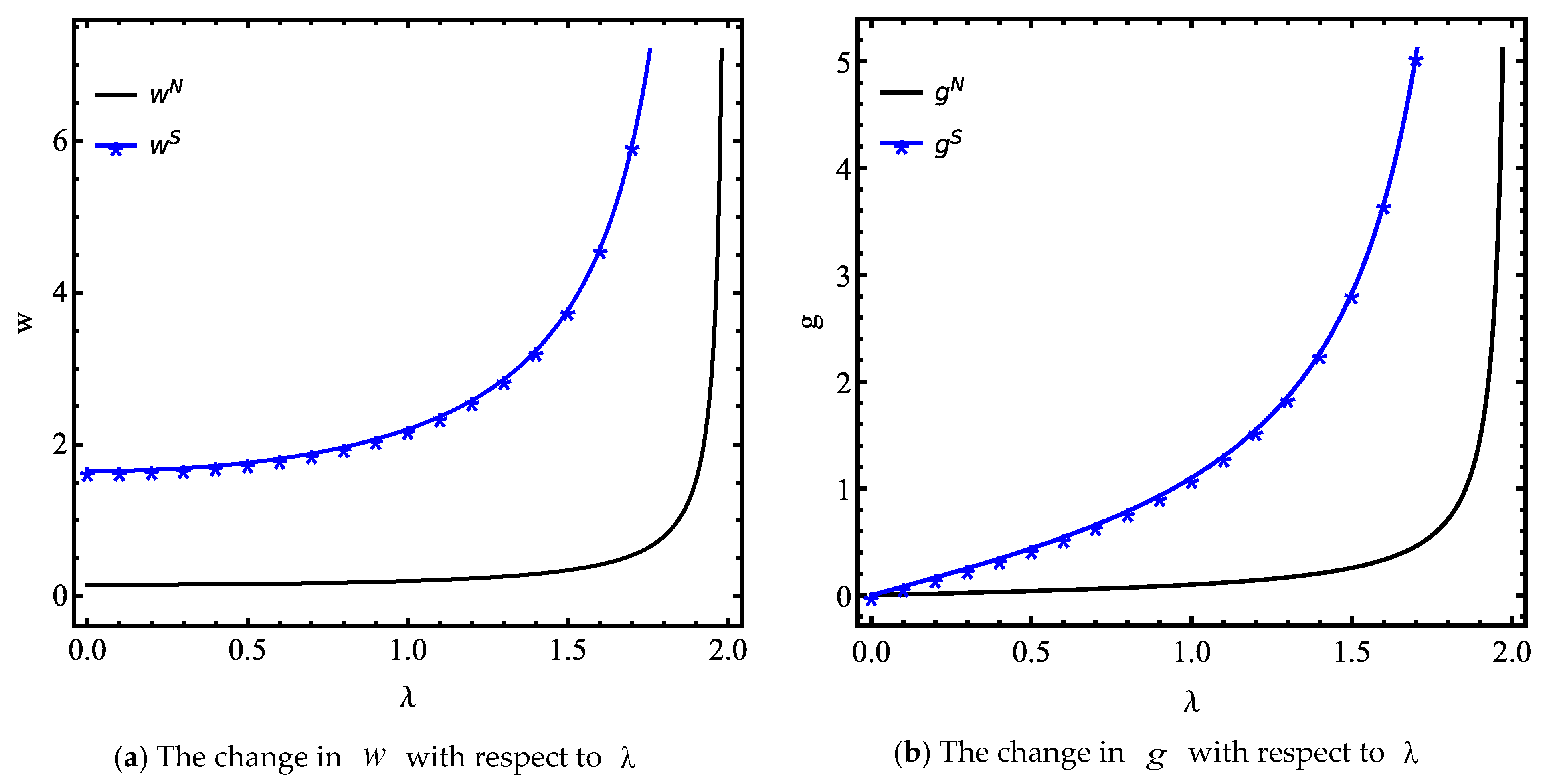
5.1. Equilibrium Decisions in Competitive Scenario

Knowing the wholesale prices $w_i$ and $g_i$ as well as the demand signal $Y$, the construction enterprise’s optimization problem is to determine $p_i$ and $p_j$ to maximize their expected profit

$${\mathrm{\Pi }}_R={\displaystyle \sum _{i=1}^2(p_i-w_i)}(a+E[\theta | Y]-(1+\varphi )p_i+\varphi p_{3-i}-\lambda g_{3-i}+(1+\lambda )g_i)$$

It is easy to prove that it is a joint concave function with respect to $p_i$ and $p_j$. Thus, by the first-order condition ${\displaystyle \frac{\mathit{\partial }{\mathrm{\Pi }}_R}{\mathit{\partial }{p}_i}}=0$ and ${\displaystyle \frac{\mathit{\partial }{\mathrm{\Pi }}_R}{\mathit{\partial }{p}_j}}=0$, the optimal pricing of building material $i$ ($i=1,2$) is

$$p_i(w_i,g_i)={\displaystyle \frac{1}{2}}\left(a+E[\mathrm{\theta } | Y]+w_i+{\displaystyle \frac{(1+\lambda +\mathrm{\varphi })g_i}{(1+2\mathrm{\varphi })}}-{\displaystyle \frac{(\lambda -\mathrm{\varphi })g_{3-i}}{1+2\mathrm{\varphi }}}\right)$$

(1)

Thus, the resulting demand for building materials is

$$d_i(w_i,w_{3-i},g_i,g_{3-i})={\displaystyle \frac{1}{2}}\left[a+2\mathrm{\theta }-E[\mathrm{\theta } | Y]+\mathrm{\varphi }{w}_{3-i}-(1+\mathrm{\varphi })w_i+(1+\lambda )g_i-\lambda g_{3-i}\right]$$

If the construction enterprise does not share information with building material manufacturer $M_i$ ($i=1,2$), then the expected profit of the building material manufacturer is

$${\mathrm{\Pi }}_i=w_{i}E[d_i(w_i,w_{3-i},g_i,g_{3-i})]-{\displaystyle \frac{1}{2}}{g}_i^2$$

Since building materials manufacturer $i$ is unaware of the demand information, regardless of whether building materials manufacturer $3-i$ knows the information or not, building materials manufacturer $i$ can only make decisions based on $E[w_{3-i}]$ and $E[g_{3-i}]$ to maximize its own expected profit.

$$\underset{w_i,g_i}{\max }{\mathrm{\Pi }}_i={\displaystyle \frac{1}{2}}{w}_i\left[a+E[\theta ]+\varphi w_{3-i}-(1+\varphi )w_i+(1+\lambda )g_i-\lambda g_{3-i}\right]-{\displaystyle \frac{1}{2}}{g}_i^2$$

It is easy to obtain the expected profit of the building materials manufacturer $i$ who is unaware the information is a joint concave function with respect to $w_i$ and $g_i$. Then, its optimal green-effort level ${\widehat{g}}_i$ and optimal wholesale price ${\widehat{w}}_i$ are, respectively,

$${\widehat{g}}_i={\displaystyle \frac{(1+\lambda )(a+\mathrm{\varphi }E[w_{3-i}]-\lambda E[g_{3-i}])}{3+4\mathrm{\varphi }-{\lambda }^2-2\lambda }, {\widehat{w}}_i=\frac{2(a+\mathrm{\varphi }E[w_{3-i}]-\lambda E[g_{3-i}])}{3+4\mathrm{\varphi }-{\lambda }^2-2\lambda }}$$

(2)

If the construction enterprise shares information with building material manufacturer $M_i$ ($i=1,2$), then the expected profit of the building material manufacturer is

$${\mathrm{\Pi }}_i=w_{i}E[d_i(w_i,w_{3-i},g_i,g_{3-i})|Y]-{\displaystyle \frac{1}{2}}{g}_i^2$$

Since the building material manufacturer $i$ is aware of the demand information, regardless of whether building materials manufacturer $3-i$ knows the information or not, building materials manufacturer $i$ can only make decisions based on $w_{3-i}$ and $g_{3-i}$ to maximize its own expected profit:

$$\underset{w_i,g_i}{\max }{\mathrm{\Pi }}_i={\displaystyle \frac{1}{2}}{w}_i\left[a+E[\theta | Y]+\varphi w_{3-i}-(1+\varphi )w_i+(1+\lambda )g_i-\lambda g_{3-i}\right]-{\displaystyle \frac{1}{2}}{g}_i^2$$

Therefore, the optimal green effort ${\widehat{g}}_i$ and the optimal wholesale price ${\widehat{w}}_i$ of the building materials manufacturer $M_i$ who is aware of the information are, respectively,

$${\widehat{g}}_i={\displaystyle \frac{(1+\lambda )(a+\mathrm{\varphi }{w}_{3-i}-\lambda g_{3-i})}{3+4\mathrm{\varphi }-{\lambda }^2-2\lambda }}, {\widehat{w}}_i=\frac{2(a+\mathrm{\varphi }{w}_{3-i}-\lambda g_{3-i})}{3+4\mathrm{\varphi }-{\lambda }^2-2\lambda }$$

(3)

When $n=(0,0)$, both building material manufacturers are unaware of the information. At this time, $E[w_i]=w_i$ and $E[g_i]=g_i$. When $n=(1,1)$, both building material manufacturers have the same information. At this time, $E[w_i | Y]=w_i$ and $E[g_i | Y]=g_i$. When $n=(1,0)$ or $(0,1)$, the wholesale price $w_i$ of the manufacturer that has not obtained the demand information is independent of $Y$. According to Equations (2) and (3), the optimal green-effort level and the optimal wholesale price of the building materials manufacturer $M_i$ can be obtained. Substituting them into Equation (1), the optimal retail price of the construction enterprise can be obtained. Condition 3 shows that, in equilibrium, the equilibrium decisions of the supply chain in four situations of $(0,0)$, $(0,1)$, $(1,0)$, $(1,1)$.

Condition 3.

The optimal retail price of construction enterprise and wholesale price and greenness of building material are as follows (

Table 1. The equilibrium decisions of construction enterprise and building materials manufacturers.

Information-Sharing Strategy	Retail Price of Construction Enterprise	Wholesale Price and Greenness of Building Material
(0,0)	$p_1^{(0,0)}=p_2^{(0,0)}=\overline{p}+{\displaystyle \frac{1}{2}}E[\theta |Y]$	$g_1^{(0,0)}=g_2^{(0,0)}=\overline{g}$ $w_1^{(0,0)}=w_2^{(0,0)}=\overline{w}$
(1,0)	$p_1^{(1,0)}=\overline{p}+\left[{\displaystyle \frac{1}{2}}+{\displaystyle \frac{{\lambda }^2+\lambda (2+\varphi )+5\varphi +3}{2(3+4\varphi -{\lambda }^2-2\lambda )(1+2\varphi )}}\right]E[\theta |Y]$ $p_2^{(1,0)}=\overline{p}+\left[{\displaystyle \frac{1}{2}}-{\displaystyle \frac{(1+\lambda )(\lambda -\varphi )}{2(3+4\varphi -{\lambda }^2-2\lambda )(1+2\varphi )}}\right]E[\theta |Y]$	$g_1^{(1,0)}=\overline{g}+{\displaystyle \frac{(1+\lambda )E[\theta |Y]}{3+4\varphi -{\lambda }^2-2\lambda }}$ $w_1^{(1,0)}=\overline{w}+{\displaystyle \frac{2E[\theta |Y]}{3+4\varphi -{\lambda }^2-2\lambda }}$ $g_2^{(1,0)}=\overline{g}$ $w_2^{(1,0)}=\overline{w}$
(0,1)	$p_1^{(0,1)}=\overline{p}+\left[{\displaystyle \frac{1}{2}}-{\displaystyle \frac{(1+\lambda )(\lambda -\varphi )}{2(3+4\varphi -{\lambda }^2-2\lambda )(1+2\varphi )}}\right]E[\theta |Y]$ $p_2^{(0,1)}=\overline{p}+\left[{\displaystyle \frac{1}{2}}+{\displaystyle \frac{{\lambda }^2+\lambda (2+\varphi )+5\varphi +3}{2(3+4\varphi -{\lambda }^2-2\lambda )(1+2\varphi )}}\right]E[\theta |Y]$	$g_1^{(0,1)}=\overline{g}$ $w_1^{(0,1)}=\overline{w}$ $w_2^{(0,1)}=\overline{w}+{\displaystyle \frac{2E[\theta |Y]}{3+4\varphi -{\lambda }^2-2\lambda }}$ $g_2^{(0,1)}=\overline{g}+{\displaystyle \frac{(1+\lambda )E[\theta |Y]}{3+4\varphi -{\lambda }^2-2\lambda }}$
(1,1)	$p_1^{(1,1)}=p_2^{(1,1)}=\overline{p}+{\displaystyle \frac{(3+\varphi )E[\theta |Y]}{3+2\varphi -\lambda }}$	$g_1^{(1,1)}=g_2^{(1,1)}=\overline{g}+{\displaystyle \frac{(1+\lambda )E[\theta |Y]}{3+2\varphi -\lambda }}$ $g_1^{(1,1)}=g_2^{(1,1)}=\overline{g}+{\displaystyle \frac{2E[\theta |Y]}{3+2\varphi -\lambda }}$

The first letter in the superscript indicates whether building materials manufacturer 1 is aware of the information, and the second letter indicates whether building materials manufacturer 2 is aware of the information. For example, (1,0) represents that manufacturer 1 is aware of the information while manufacturer 2 is not aware of the information. $\overline{w}={\displaystyle \frac{2a}{3+2\mathrm{\varphi }-\lambda }}$, $\overline{g}={\displaystyle \frac{a(1+\lambda )}{3+2\mathrm{\varphi }-\lambda }}$ and $\overline{p}={\displaystyle \frac{a(3+\mathrm{\varphi })}{3+2\mathrm{\varphi }-\lambda }}$, respectively, represent the optimal wholesale price of the building material, the green investment, as well as the optimal sales price of the construction enterprise under deterministic demand when $\theta =0$.

):

Corollaries 2 and 3, respectively, present the influence $\mathrm{\varphi }$ and $\lambda$ on the wholesale prices and greenness of building materials under different information-sharing strategies.

Corollary 2.

(a) If$\varphi >{\displaystyle \frac{(2+\sqrt{2}){\lambda }^2+2\lambda +3\sqrt{2}}{4}}$, then${\displaystyle \frac{\mathit{\partial }{w}_1^{(1,1)}}{\mathit{\partial }\mathrm{\varphi }}}<{\displaystyle \frac{\mathit{\partial }{w}_1^{(1,0)}}{\mathit{\partial }\mathrm{\varphi }}}<{\displaystyle \frac{\mathit{\partial }{w}_1^{(0,0)}}{\mathit{\partial }\mathrm{\varphi }}}<0$ and${\displaystyle \frac{\mathit{\partial }{g}_1^{(1,1)}}{\mathit{\partial }\mathrm{\varphi }}}<{\displaystyle \frac{\mathit{\partial }{g}_1^{(1,0)}}{\mathit{\partial }\mathrm{\varphi }}}<{\displaystyle \frac{\mathit{\partial }{g}_1^{(0,0)}}{\mathit{\partial }\mathrm{\varphi }}}<0$; (b) If$\max \{0,{\displaystyle \frac{1}{4}}(-3+2\lambda +{\lambda }^2)\}<\varphi <{\displaystyle \frac{(2+\sqrt{2}){\lambda }^2+2\lambda +3\sqrt{2}}{4}}$, then${\displaystyle \frac{\mathit{\partial }{w}_1^{(1,0)}}{\mathit{\partial }\mathrm{\varphi }}}<{\displaystyle \frac{\mathit{\partial }{w}_1^{(1,1)}}{\mathit{\partial }\mathrm{\varphi }}}<{\displaystyle \frac{\mathit{\partial }{w}_1^{(0,0)}}{\mathit{\partial }\mathrm{\varphi }}}<0$ and${\displaystyle \frac{\mathit{\partial }{g}_1^{(1,0)}}{\mathit{\partial }\mathrm{\varphi }}}<{\displaystyle \frac{\mathit{\partial }{g}_1^{(1,1)}}{\mathit{\partial }\mathrm{\varphi }}}<{\displaystyle \frac{\mathit{\partial }{g}_1^{(0,0)}}{\mathit{\partial }\mathrm{\varphi }}}<0$.

According to Corollary 2, firstly, the wholesale price decreases with the increase in market competition. In order to gain a greater advantage in the competitive market, manufacturers will continuously lower the wholesale prices. Secondly, when $\varphi$ and $\lambda$ meet different conditions, the reduction effect of competition on the wholesale prices will vary under different information-sharing strategies. Thirdly, since consumer demand is influenced by the greenness of building material products, in a competitive environment, manufacturers will continuously improve their products in order to obtain market share, thereby promoting the continuous enhancement of the greenness of the products.

Corollary 3.

(a) If$\varphi >{\displaystyle \frac{\sqrt{2}\sqrt{1+\lambda }(3+{\lambda }^2)}{4(1-\lambda )}}+{\displaystyle \frac{2\lambda }{1-\lambda }}$, then${\displaystyle \frac{\mathit{\partial }{w}_1^{(1,1)}}{\mathit{\partial }\lambda }}>{\displaystyle \frac{\mathit{\partial }{w}_1^{(1,0)}}{\mathit{\partial }\lambda }}>{\displaystyle \frac{\mathit{\partial }{w}_1^{(0,0)}}{\mathit{\partial }\lambda }}>0$ and${\displaystyle \frac{\mathit{\partial }{g}_1^{(1,1)}}{\mathit{\partial }\lambda }}>{\displaystyle \frac{\mathit{\partial }{g}_1^{(1,0)}}{\mathit{\partial }\lambda }}>{\displaystyle \frac{\mathit{\partial }{g}_1^{(0,0)}}{\mathit{\partial }\lambda }}>0$; (b) If$0<\varphi <{\displaystyle \frac{\sqrt{2}\sqrt{1+\lambda }(3+{\lambda }^2)}{4(1-\lambda )}}+{\displaystyle \frac{2\lambda }{1-\lambda }}$, or$\lambda \ge 1$ and$\varphi >{\displaystyle \frac{1}{4}}(-3+2\lambda +{\lambda }^2)$, then${\displaystyle \frac{\mathit{\partial }{w}_1^{(1,0)}}{\mathit{\partial }\lambda }}>{\displaystyle \frac{\mathit{\partial }{w}_1^{(1,1)}}{\mathit{\partial }\lambda }}>{\displaystyle \frac{\mathit{\partial }{w}_1^{(0,0)}}{\mathit{\partial }\lambda }}>0$ and${\displaystyle \frac{\mathit{\partial }{g}_1^{(1,0)}}{\mathit{\partial }\lambda }}>{\displaystyle \frac{\mathit{\partial }{g}_1^{(1,1)}}{\mathit{\partial }\lambda }}>{\displaystyle \frac{\mathit{\partial }{g}_1^{(0,0)}}{\mathit{\partial }\lambda }}>0$.

According to Corollary 3, firstly, the more consumers pay attention to the greenness of products, the more significant the marginal revenue increase effect of green research and development will be. Thus, manufacturers will have greater motivation to produce green products. Secondly, the wholesale price increases with the sensitivity of developers to the greenness of building materials products. When consumers pay attention to the greenness of building materials products, manufacturers will actively improve the greenness of their products, increase research and development costs, and transfer the costs by raising the wholesale prices.

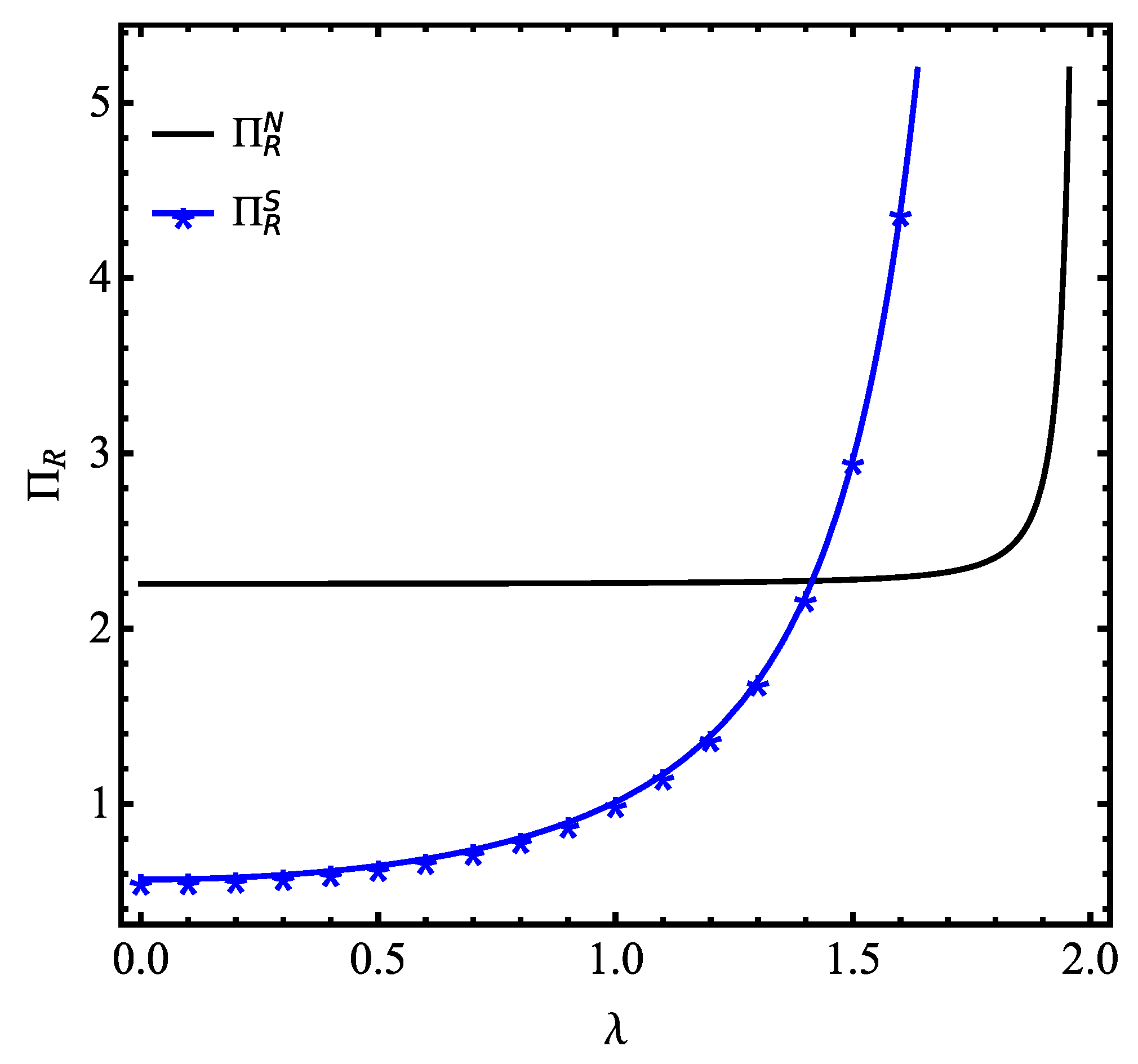
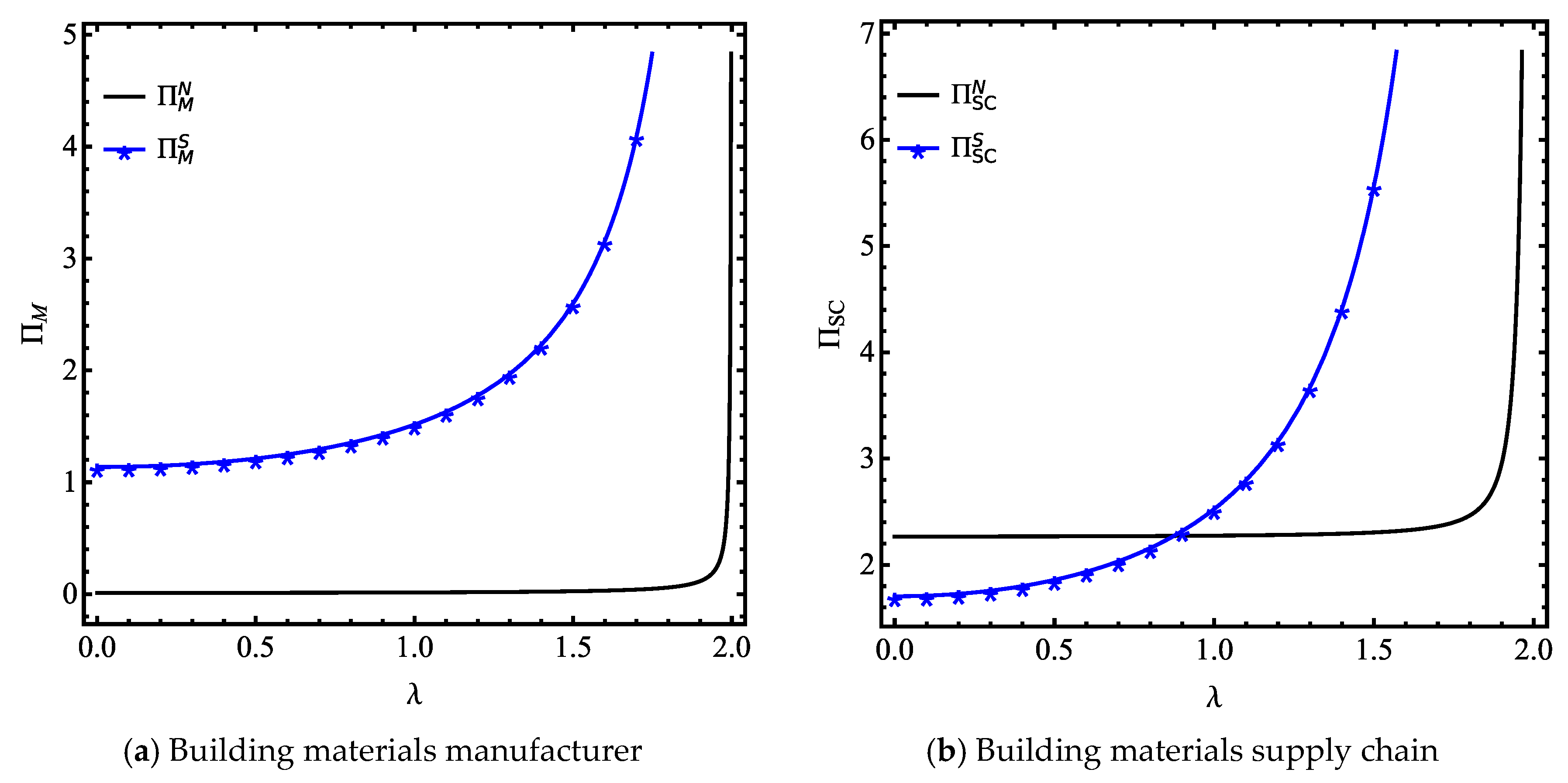
5.2. Firms’ Ex Ante Profits in Competitive Scenario

Substitute the equilibrium results in Table 1 into the profit expressions of the building material manufacturers and construction enterprise and calculate the firms’ ex ante profits. Condition 4 shows the ex ante expected profits of building material manufacturers under different information-sharing strategies.

Condition 4.

Under different information-sharing strategies, the ex ante expected profits of building materials manufacturers are respectively:

$$\begin{gathered} {\mathrm{\Pi }}_{M1}^{(0,0)}={\mathrm{\Pi }}_{M2}^{(0,0)}={\overline{\pi }}_M, {\mathrm{\Pi }}_{M1}^{(0,1)}={\mathrm{\Pi }}_{M2}^{(1,0)}={\overline{\pi }}_M, {\mathrm{\Pi }}_{M1}^{(1,0)}={\mathrm{\Pi }}_{M2}^{(0,1)}={\overline{\pi }}_M+{\displaystyle \frac{\eta (s,\sigma )}{8\varphi -2{\lambda }^2-4\lambda +6}}, \\ {\mathrm{\Pi }}_{M1}^{(1,1)}={\mathrm{\Pi }}_{M2}^{(1,1)}={\overline{\pi }}_M+{\displaystyle \frac{(3+4\varphi -{\lambda }^2-2\lambda )\eta (s,\sigma )}{2{(3+2\varphi -\lambda )}^2}} \end{gathered}$$

the ex ante expected profits of construction enterprises are, respectively,

$$\begin{gathered} {\mathrm{\Pi }}_R^{(0,0)}={\overline{\pi }}_R+\frac{1}{2}\eta (s,\sigma ), {\mathrm{\Pi }}_R^{(1,1)}={\overline{\pi }}_R+\frac{2{(1+\varphi )}^2\eta (s,\sigma )}{{(3+2\varphi -\lambda )}^2} \\ {\mathrm{\Pi }}_R^{(1,0)}={\mathrm{\Pi }}_R^{(0,1)}={\overline{\pi }}_R+\frac{(1+\varphi )\left(13+12{\lambda }^3+4{\lambda }^4+56\varphi +64{\varphi }^2-6\lambda (3+8\varphi )-{\lambda }^2(3+32\varphi )\right)\eta (s,\sigma )}{4{(3+4\varphi -{\lambda }^2-2\lambda )}^2(1+2\varphi )}, \end{gathered}$$

where${\overline{\pi }}_M={\displaystyle \frac{a^2(3+4\varphi -{\lambda }^2-2\lambda )}{2{(3+2\varphi -\lambda )}^2}}$and${\overline{\pi }}_R={\displaystyle \frac{4a^2{(1+\varphi )}^2}{2{(3+2\varphi -\lambda )}^2}}$are the profits in the deterministic model.

Further, we explore the information-sharing preferences of construction enterprise and the impact of information sharing on the profits of building material manufacturers and building material supply chain. In order to more intuitively show the information-sharing strategy of construction enterprise, the numerical analysis method is used to summarize all possible information sharing strategies by drawing the ex ante expected revenue of construction enterprises under different parameter values.

Figure 5a shows the change in profits of construction firms with respect to $\lambda$ and $\varphi$ when $\lambda$ is between $0$ and ${\displaystyle \frac{7}{6}}$. Figure 5b shows the change in profits of construction firms with respect to $\lambda$ and $\varphi$ when $\lambda$ is between ${\displaystyle \frac{7}{6}}$ and 2. By observing Figure 5, it can be found that when $\lambda$ is fixed, the information sharing strategy of construction enterprises will show different rules with respect to $\varphi$. Thus, $\lambda =0.5$, $\lambda =0.7$, $\lambda =1.1$, $\lambda =1.8$ is taken to draw the change in the ex ante expected profit of construction enterprises, as shown in Figure 6.

When the sensitivity of developers to the greenness of building material products is extremely small, such as $\lambda =0.5$, the construction enterprise does not share information with both manufacturers. As the developer’s sensitivity to the greenness of the building material product slightly increases, such as $\lambda =0.7$, the construction firm shares information with only one manufacturer when the market competition is strong. If the sensitivity of developers to the greenness of building materials continues to increase, such as $\lambda =1.1$, the construction enterprise shares information with both manufacturers when the market competition is low, while the construction enterprise shares information with only one of them when the market competition is high. When the developer is very concerned about the greenness of building materials, such as $\lambda =1.8$, under fierce competition, it becomes an equilibrium strategy for the developer to share information with both manufacturers of building materials.

Therefore, when deciding whether to share information with building materials manufacturers, construction enterprises should pay close attention to the sensitivity of developers to the greenness of building material products and the degree of market competition. When the developer’s sensitivity is extremely low, no information sharing can avoid resource waste. With a slight increase in sensitivity, sharing information with one manufacturer is optional to optimize cooperation in the presence of strong market competition. If the sensitivity continues to increase, it is necessary to make differentiated decisions based on the level of competition. When the competition is low, information should be shared with two manufacturers to promote diversified cooperation, and when the competition is high, one manufacturer should be focused to maintain the advantage. When developers are very concerned about greenness and the market competition is fierce, sharing information with both manufacturers can help meet the demand of high green standards and improve the collaborative efficiency of the supply chain so as to occupy a favorable position in the green building materials market and achieve a win-win situation for all parties.

Furthermore, Proposition 4 presents the influence rules of information sharing on building material manufacturers and the building material supply chain.

Proposition 4.

If$0<\lambda \le 1$and$0<\mathrm{\varphi }<{\mathrm{\varphi }}_1$, or$\lambda >1$and$\underset{\_}{\mathrm{\varphi }}<\mathrm{\varphi }<{\mathrm{\varphi }}_1$hold, then${\mathrm{\Pi }}_{M1}^{(1,0)}>{\mathrm{\Pi }}_{M1}^{(1,1)}>{\mathrm{\Pi }}_{M1}^{(0,0)}$; If$\mathrm{\varphi }>{\mathrm{\varphi }}_1$, then${\mathrm{\Pi }}_{M1}^{(1,1)}>{\mathrm{\Pi }}_{M1}^{(1,0)}>{\mathrm{\Pi }}_{M1}^{(0,0)}$, where$\underset{\_}{\mathrm{\varphi }}={\displaystyle \frac{1}{4}}({\lambda }^2+2\lambda -3)$, ${\mathrm{\varphi }}_1={\displaystyle \frac{1}{2}}({\lambda }^2+\lambda )$.

As shown in Figure 7, sharing information with both manufacturers at the same time does not always benefit the manufacturers. Specifically, with the decrease in the developer’s sensitivity to the green level of building materials and the increase in market competition, it is more beneficial for the developer to share information with both manufacturers simultaneously. On the contrary, when the developer is very concerned about the green level of building materials and the market competition is weak, it is more beneficial for the construction enterprise to share with only one of them.

Further, Figure 8 shows that the change in the profits of building materials supply chain with respect to $\varphi$ when $\lambda =0.5$, $\lambda =0.7$, $\lambda =1.1$, $\lambda =1.8$. According to Figure 8, when the market competition is low, sharing information with only one of manufacturers is beneficial to the whole building material supply chain. However, when the market competition is high, it is more beneficial for the whole building material supply chain to share information with two building material manufacturers simultaneously. Therefore, construction enterprises should fully consider the degree of market competition and implement differentiation strategies when formulating an information-sharing strategy for the building material supply chain. When the market competition degree is low, choosing to share information with a single manufacturer is helpful to improve the synergy efficiency of supply chain and form a stable supply/demand relationship to enhance overall competitiveness. However, when the market competition is high, sharing information with two manufacturers can stimulate the enthusiasm of both manufacturers by introducing a competition mechanism and encourage them to optimize their products and services.

6. Conclusions

This paper explores the interplay between information-sharing strategies and green-effort strategies in a building material supply chain. Firstly, we solve optimal wholesale price, green-effort, and retail price decisions. Then, we identify the optimal strategies for the building enterprise to share information and analyze the impact of information sharing on equilibrium strategies, profit of manufacturers, and the whole supply chain. The specific conclusions are as follows.

(1) This paper also analyzes the impact of information sharing on the building material supply chain’s environmental performance. Analytical findings indicating that although information sharing can improve product greenness in a non-competitive supply chain, it may have negative effects in the situation of manufacturer competition. The competition between the two manufacturers and the sensitivity of developers to the greenness of building materials products affect the promotion effect of product greenness.

(2) We find that information sharing is not always conducive to improving the manufacturer’s profit and its level of green innovation. In a non-competitive supply chain, information sharing is always conducive to increasing the manufacturer’s profit and promoting green production. However, in the competitive environment of manufacturers, the impact of information sharing on manufacturers’ profits and their green innovation level depends on the intensity of market competition and consumers’ sensitivity to product greenness.

(3) Information sharing is an effective means of cooperation to improve both the manufacturers’ and construction enterprise’s profits. However, it cannot eliminate the adverse effects of double marginalization in the supply chain. In the competitive and non-competitive environments of manufacturers, the construction enterprise is not always willing to share information, and their information-sharing strategy is affected by consumers’ preference level for product greenness and market competition intensity. Specifically, we find that the building enterprise can transmit demand information of green building materials to the manufacturers and receive transfer payments in return; meanwhile, the manufacturers benefit from access to this valuable information.

The research is limited by some necessary assumptions which provide opportunities for future research. Future work could also explore additional complexities involved in information-sharing decisions, including risk profiles and temporal aspects. Additionally, we study a green supply chain model consisting of a single retailer and more than two manufacturers, while other supply chain structures motivated by practical applications could be explored in future research on information sharing.