Operational Evaluation of Mixed Flow on Highways Considering Trucks and Autonomous Vehicles Based on an Improved Car-Following Decision Framework
Abstract
1. Introduction
2. Data Collection
2.1. Data Presentation
2.2. Data Preprocessing
3. Material Results of Driving Characterization Based on Car-Following Combination
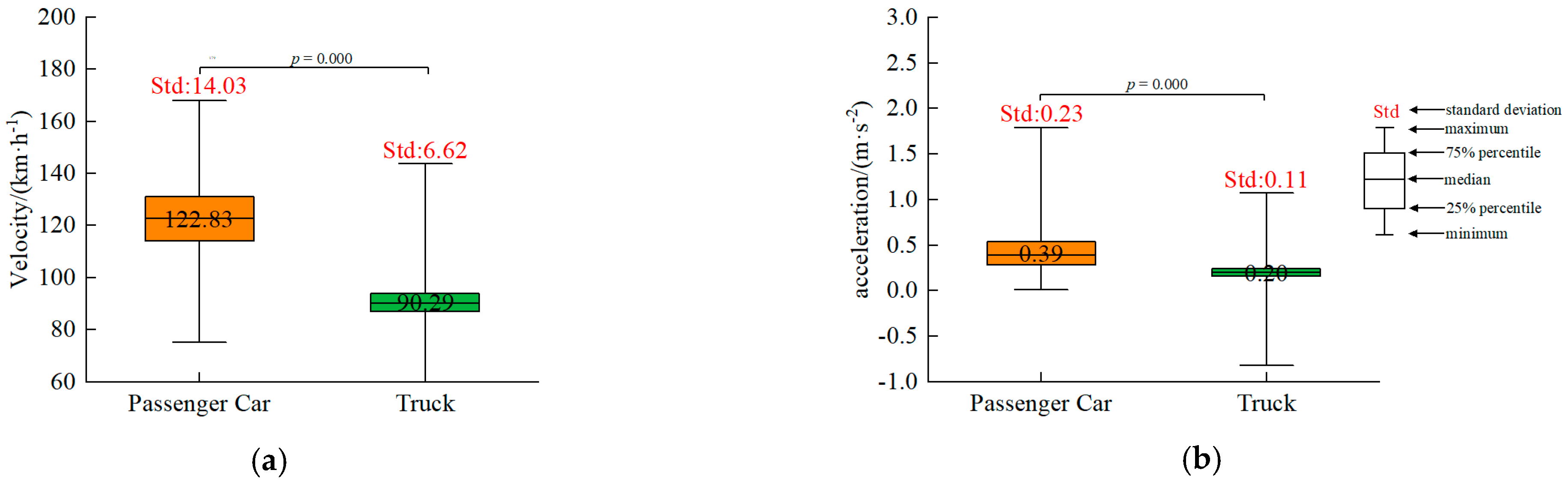
3.1. Free-Flow Condition
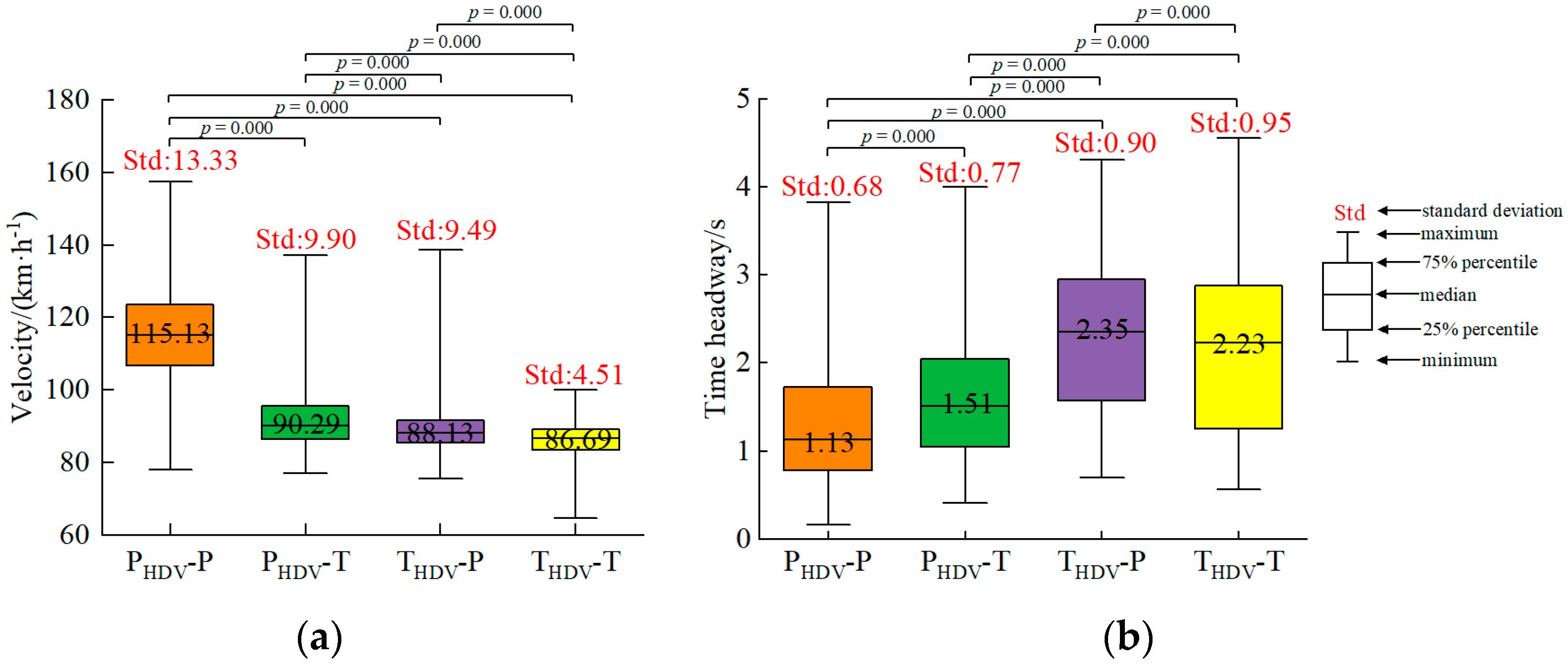
3.2. Car-Following Condition
4. Optimization of Model Parameters Based on Following Combinations
4.1. Scenario Introduction
4.2. Model Introduction
4.2.1. Free-Flow Acceleration Model
4.2.2. Car-Following Model for HDV—IDM Model
4.2.3. Car-Following Model for AV (Accelerating/Uniform Behavior)—CACC Model
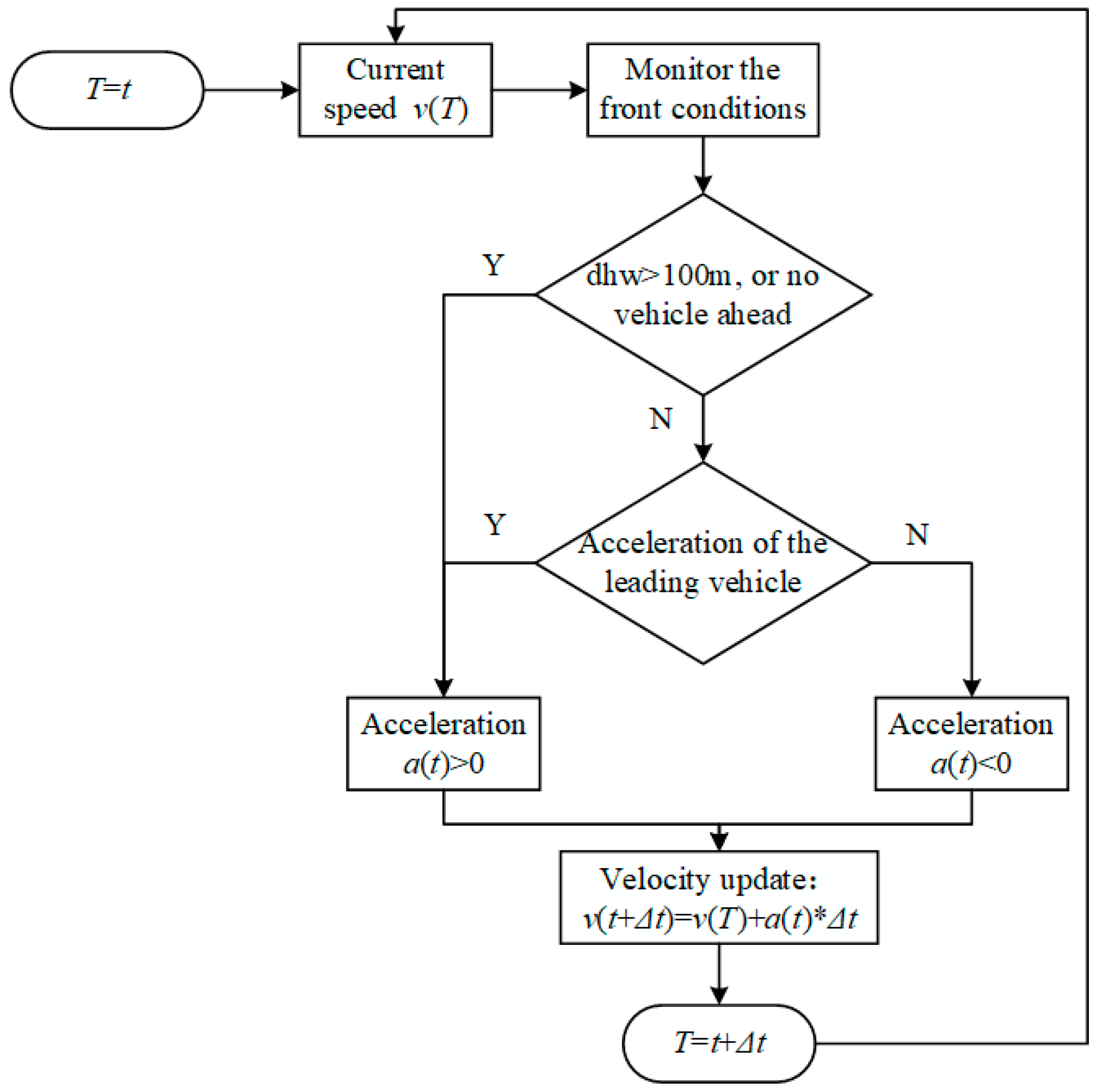
4.2.4. Car-Following Model for AV (Decelerating)
4.3. Parameter Optimization
4.3.1. Optimization Algorithm
4.3.2. Parameter Calibration Results
4.3.3. Model Validation Based on TM and EM Parameters
5. Optimization Numerical Simulation
5.1. Overview of the Simulation Environment
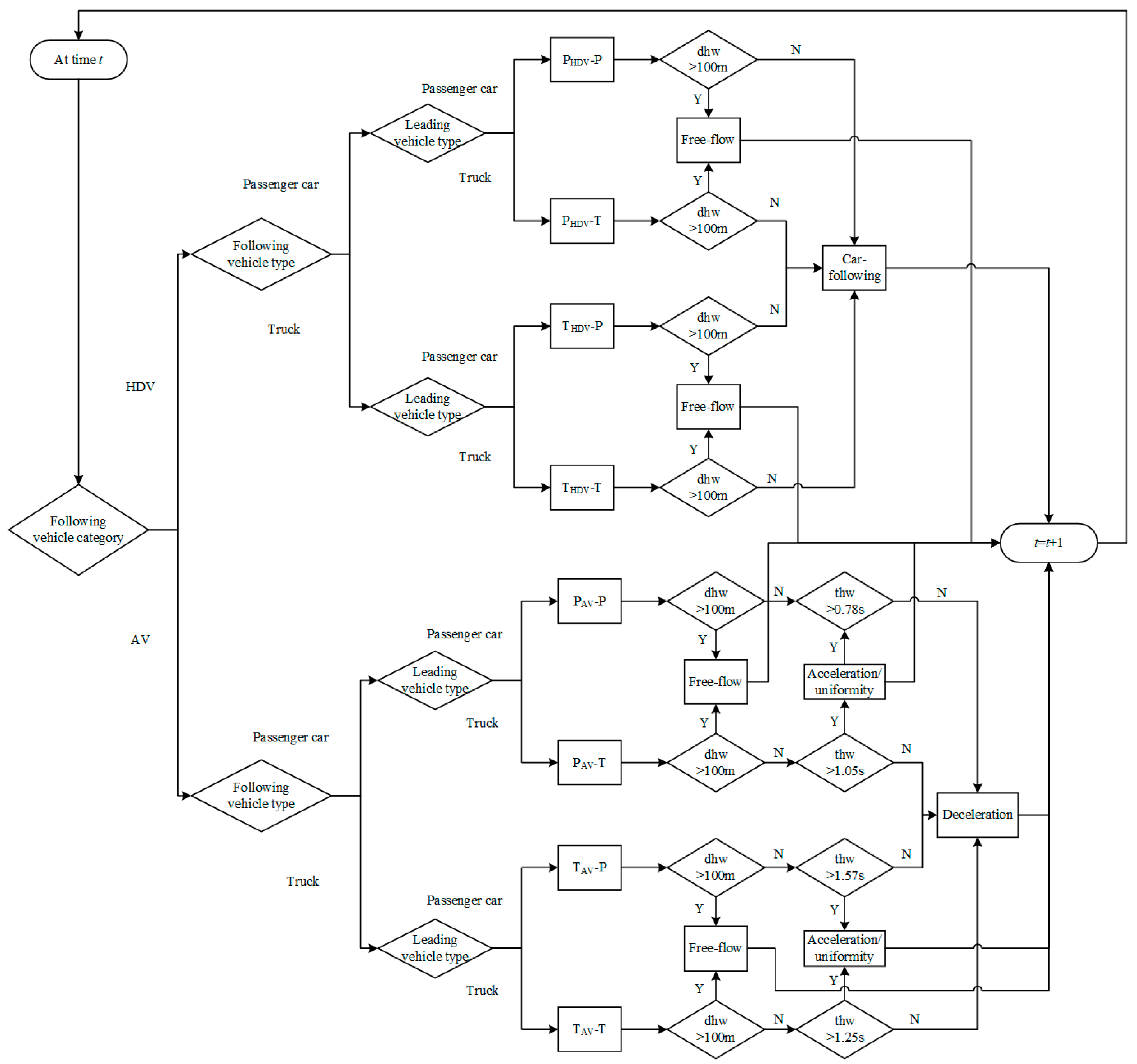
5.2. Overview Threshold for Decision of Car-Following Behavior
6. Optimization Results and Analysis
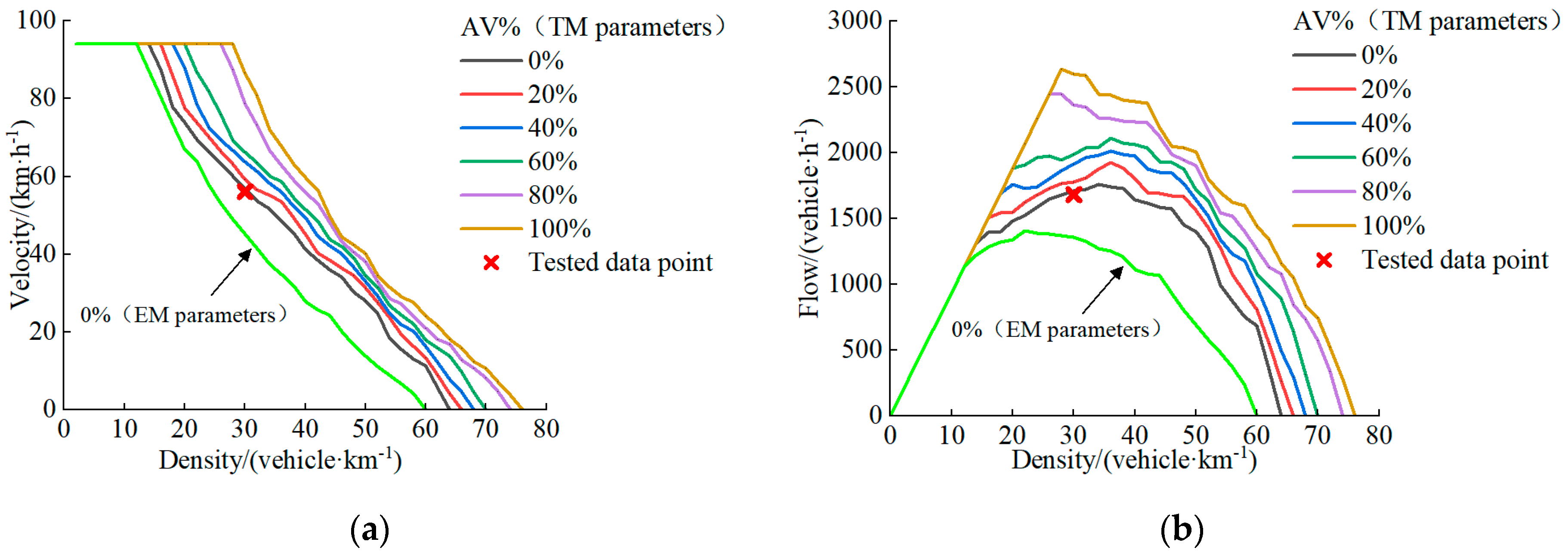
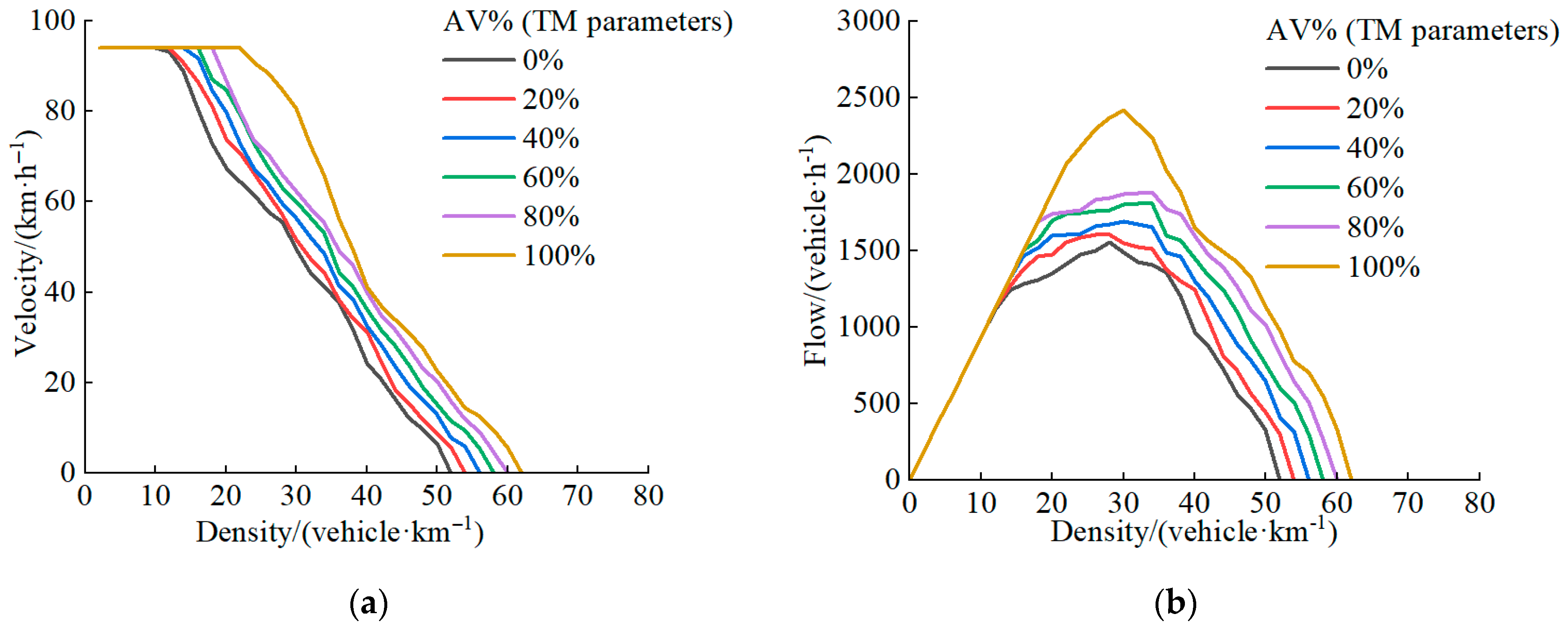
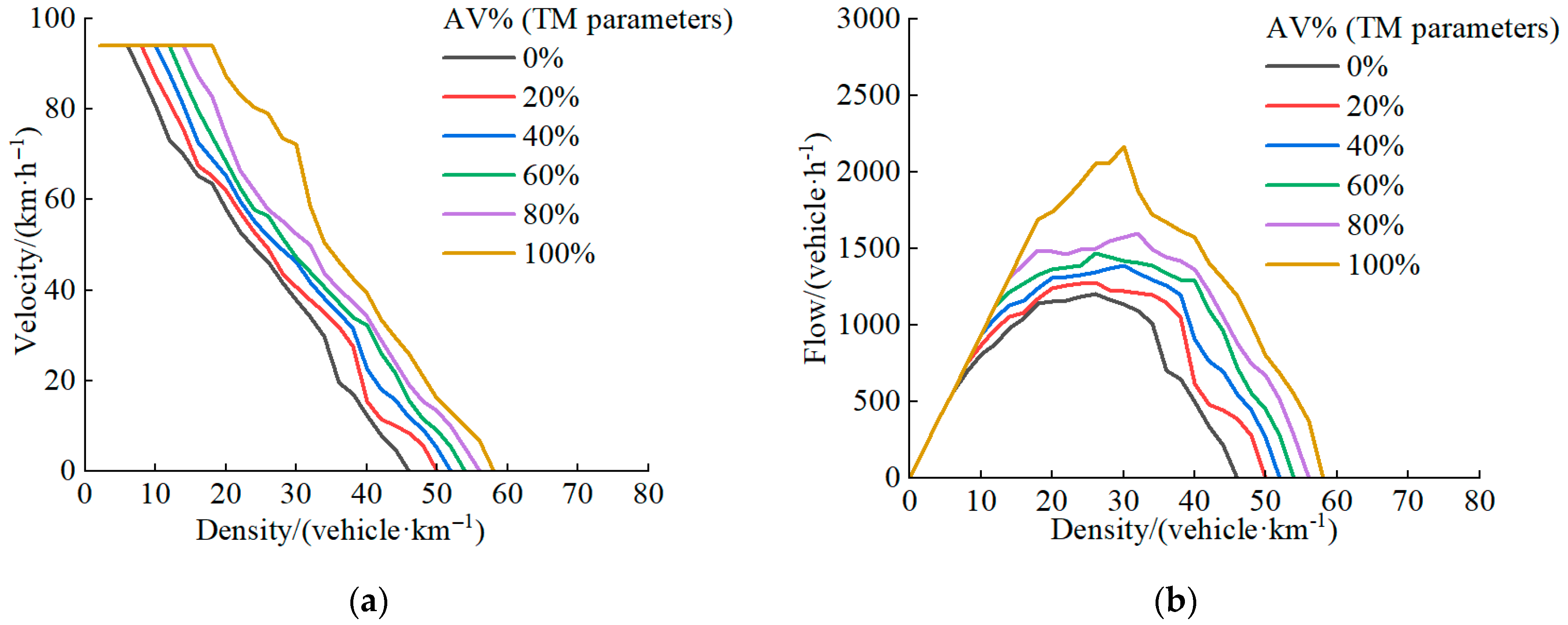
6.1. Traffic Flow Characteristics at Different Levels of T% and AV%
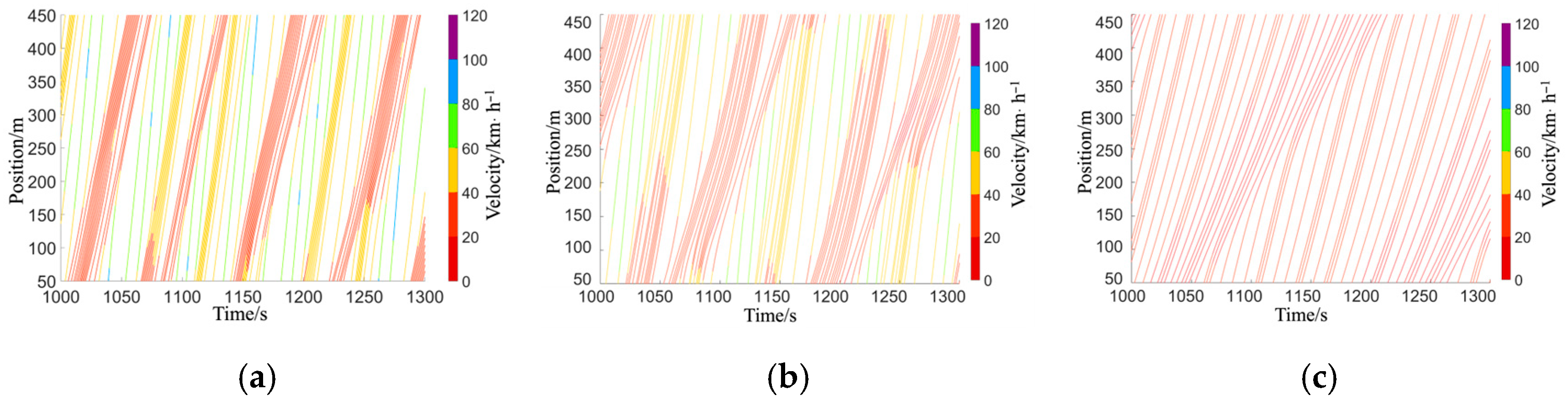
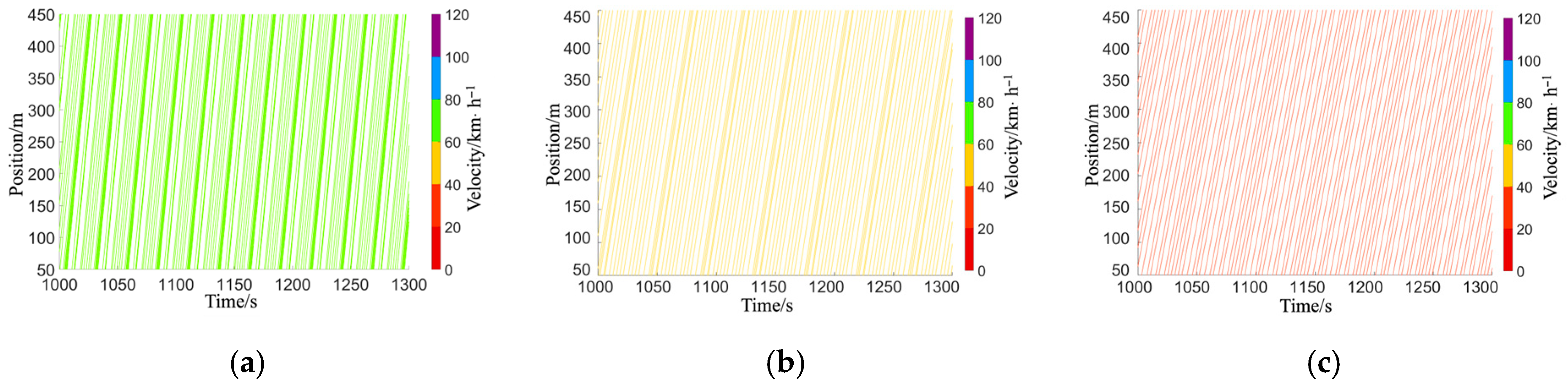
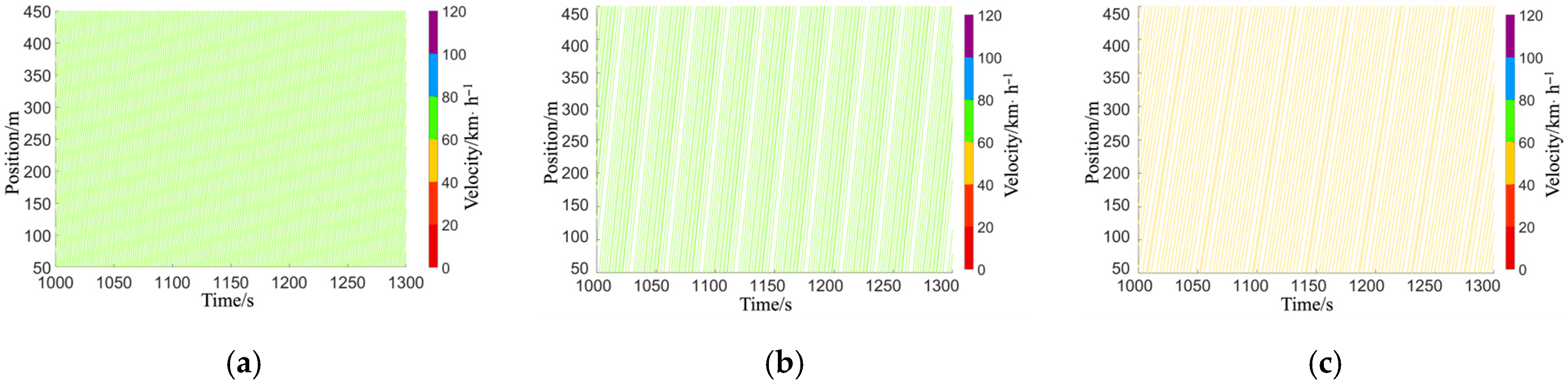
6.2. Time–Space Results at Different T% and AV%
6.3. Mean Speed Heatmaps Under Varying T% and AV% Conditions
7. Discussion
- (1)
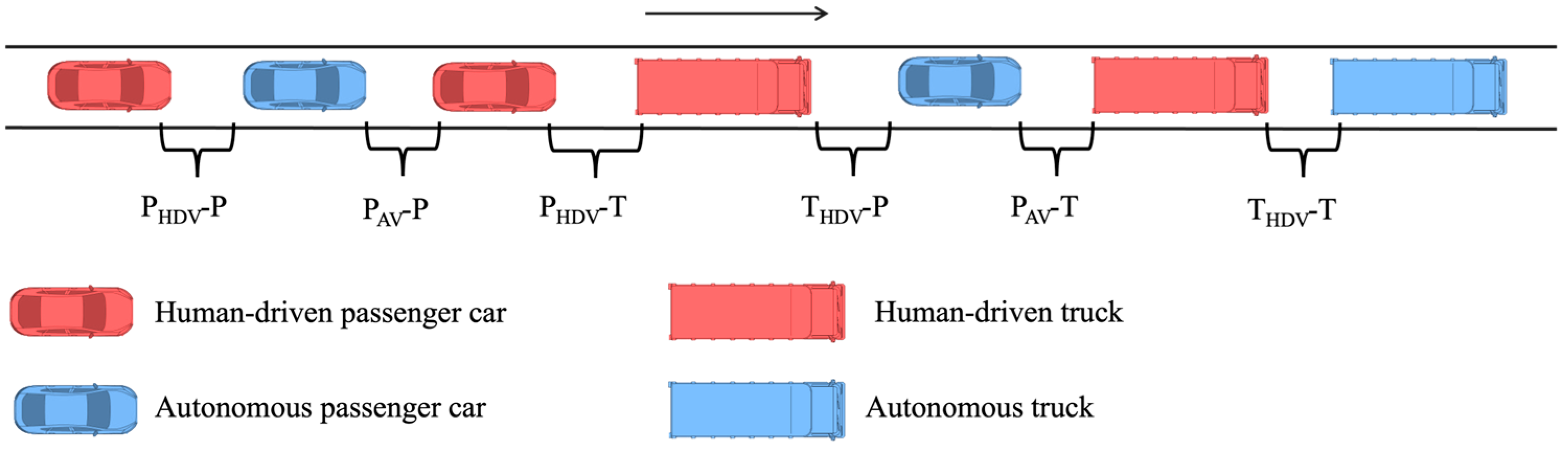
- This study analyzes driving behaviors, including the speed and acceleration of cars and trucks, under various traffic flow conditions using the HighD dataset, specifically focusing on the free-flow and follow-me datasets. Additionally, within the following dataset, which includes both HDVs and AVs, the following combinations are categorized into eight types: PHDV-P, PHDV-T, THDV-P, THDV-T, PAV-P, PAV-T, TAV-P, and TAV-T. The analysis of driving behaviors, such as speed, acceleration, and headway time, revealed notable differences in vehicle conditions across various following combinations.
- (2)
- This study presents the calibration of the following behavior model parameters using the simulated annealing method with measured data. The calibrated parameter model was subsequently compared with the empirical model. The results show that the parameter optimization method, which accounts for different follower combinations, enhances the accuracy of the model in capturing the driving behavior characteristics of various vehicle type and category combinations within the traffic flow. Specifically, the calibrated model achieves an average improvement of 85.31% in MAPE, 79.19% in MAE, and 77.02% in RMSE compared to the empirical model. Consequently, it can be concluded that this method significantly improves the accuracy of traffic flow predictions.
- (3)
- This study developed a cellular automaton model to simulate mixed passenger and goods traffic flow in both AV and HDV environments. The results show that AV% and T% significantly influence the efficiency and stability of traffic flow. Increasing the AV% improves road capacity, enhances traffic flow stability, and raises the overall average speed. As AV penetration increases, traffic volume rises by 50%. In contrast, a higher T% reduces traffic flow stability and lowers the average speed. In the case of full truck penetration, the average speed decreases by 75.37%. However, traffic stability at T% = 100% is more favorable than in mixed passenger and freight scenarios. Increased stability from higher AV penetration helps reduce fluctuations in traffic speed, leading to lower emissions by minimizing unnecessary acceleration and deceleration. In contrast, higher truck percentages tend to degrade traffic flow, leading to higher emissions.
- (4)
- This study primarily focuses on car-following behavior in a single-lane highway scenario, assuming that automated vehicles (AVs) strictly follow the CACC model during acceleration and deceleration, while neglecting real-world factors such as communication delays, perception errors, and control execution deviations. The type of lead vehicle (AV or HDV) and the vehicle connectivity environment are also not considered. Future research will build upon this model by incorporating more complex vehicle interactions, such as lane-changing behavior, and exploring its application in diverse driving environments like highway weaving zones.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bansal, P.; Kockelman, M.K. Forecasting Americans’ Long-Term Adoption of Connected and Autonomous Vehicle Technologies. Transp. Res. Part A 2017, 95, 49–63. [Google Scholar] [CrossRef]
- Gipps, P.G. A Behavioural Car-Following Model for Computer Simulation. Transp. Res. Part B Methodol. 1981, 15, 105–111. [Google Scholar] [CrossRef]
- Jiang, R.; Wu, Q.; Zhu, Z. Full Velocity Difference Model for a Car-Following Theory. Phys. Rev. E 2001, 64, 017101. [Google Scholar] [CrossRef]
- Bando, M.; Hasebe, K.; Nakayama, A.; Shibata, A.; Sugiyama, Y. Dynamical Model of Traffic Congestion and Numerical Simulation. Phys. Rev. E 1995, 51, 1035–1042. [Google Scholar] [CrossRef]
- Helbing, D.; Tilch, B. Generalized Force Model of Traffic Dynamics. Phys. Rev. E 1998, 58, 133–138. [Google Scholar] [CrossRef]
- Nagel, K.; Schreckenberg, M. A Cellular Automaton Model for Freeway Traffic. J. Phys. I 1992, 2, 2221–2229. [Google Scholar] [CrossRef]
- Takayasu, M.; Takayasu, H. 1/f Noise in a traffic model. Fractals 1993, 04, 860–866. [Google Scholar] [CrossRef]
- Barlovic, R.; Santen, L.; Schadschneider, A.; Schreckenberg, M. Metastable States in Cellular Automata for Traffic Flow. Eur. Phys. J. B Condens. Matter Complex Syst. 1998, 5, 793–800. [Google Scholar] [CrossRef]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested Traffic States in Empirical Observations and Microscopic Simulations. Phys. Rev. E 2000, 62, 1805–1824. [Google Scholar] [CrossRef]
- Milanés, V.; Shladover, S.E. Modeling Cooperative and Autonomous Adaptive Cruise Control Dynamic Responses Using Experimental Data. Transp. Res. Part C Emerg. Technol. 2014, 48, 285–300. [Google Scholar] [CrossRef]
- Jia, B.; Jiang, R.; Gao, Z.-Y.; Zhao, X.-M. The effect of mixed vehicles on traffic flow in two lane cellular automata model. Int. J. Mod. Phys. C 2005, 16, 1617–1627. [Google Scholar] [CrossRef]
- Ebersbach, A.; Schneider, J.; Morgenstern, I.; Hammwöhner, R. The Influence of Truck on Traffic Flow: An Investigation on the Nagel-Schreckenber-Model. Int. J. Mod. Phys. C 2000, 11, 837–842. [Google Scholar] [CrossRef]
- Meng, Q.; Weng, J. An Improved Cellular Automata Model for Heterogeneous Work Zone Traffic. Transp. Res. Part C Emerg. Technol. 2011, 19, 1263–1275. [Google Scholar] [CrossRef]
- Moridpour, S.; Mazloumi, E.; Mesbah, M. Impact of Heavy Vehicles on Surrounding Traffic Characteristics. J. Adv. Transp. 2015, 49, 535–552. [Google Scholar] [CrossRef]
- Dewen, K.; Xiucheng, G.; Bo, Y. Analyzing the Impact of Trucks on Traffic Flow Based on an Improved Cellular Automaton Model. Discret. Dyn. Nat. Soc. 2016, 2016, 1–14. [Google Scholar]
- Yang, D.; Qiu, X.; Yu, D.; Sun, R.; Pu, Y. A Cellular Automata Model for Car–Truck Heterogeneous Traffic Flow Considering the Car–Truck Following Combination Effect. Phys. A Stat. Mech. Appl. 2015, 424, 62–72. [Google Scholar] [CrossRef]
- Baikejuli, M.; Shi, J. A Cellular Automata Model for Car–Truck Heterogeneous Traffic Flow Considering Drivers’ Risky Driving Behaviors. Int. J. Mod. Phys. C 2023, 34, 2350154. [Google Scholar] [CrossRef]
- Liu, L.; Zhu, L.; Yang, D. Modeling and Simulation of the Car-Truck Heterogeneous Traffic Flow Based on a Nonlinear Car-Following Model. Appl. Math. Comput. 2016, 273, 706–717. [Google Scholar] [CrossRef]
- Yunze, W.; Ranran, X.; Ke, Z. A Car-Following Model for Mixed Traffic Flows in Intelligent Connected Vehicle Environment Considering Driver Response Characteristics. Sustainability 2022, 14, 11010. [Google Scholar] [CrossRef]
- Liu, H.; Kan, X.; Shladover, S.E.; Lu, X.-Y.; Ferlis, R.E. Modeling Impacts of Cooperative Adaptive Cruise Control on Mixed Traffic Flow in Multi-Lane Freeway Facilities. Transp. Res. Part C Emerg. Technol. 2018, 95, 261–279. [Google Scholar] [CrossRef]
- Xie, H.; Ren, Q.; Lei, Z. Influence of Lane-Changing Behavior on Traffic Flow Velocity in Mixed Traffic Environment. J. Adv. Transp. 2022, 1, 1–26. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, J.; Xie, L.; Ding, H. Analysis on the characteristics of traffic flow in expressway weaving area under mixed connected and autonomous environment. J. Southeast Univ. (Nat. Sci. Ed.) 2023, 53, 156–164. [Google Scholar]
- Zhang, W.; Liu, J.; Xie, L.; Ding, H. Lane-Changing Model of Autonomous Vehicle in Weaving Area of Expressway in Intelligent and Connected Mixed Environment. J. Jinlin Univ. (Eng. Technol. Ed.) 2023, 54, 469–477. [Google Scholar] [CrossRef]
- Wu, D.; Chen, R. Characteristics of passenger-cargo mixed traffic flow in intelligent network and agglomeration lane-change strategy. J. Jilin Univ. (Eng. Technol. Ed.) 2024, 1–9. [Google Scholar] [CrossRef]
- Wang, Y.; Gan, H.; Wang, K.; Cheng, Z. Dedicated lane management and control strategy of intelligent heavy trucks based on cellular automata. Univ. Shanghai Sci. Technol. 2024, 47, 100–107. [Google Scholar] [CrossRef]
- Zhou, J.; He, Y.; Tian, J. Speed Characteristic Analysis Based on NGSIM Trajectory Data. Technol. Econ. Areas Commun. 2019, 21, 45–48+61. [Google Scholar]
- Gu, H. Research on Freeway Car-Following Modeling and Simulation in Connected Vehicle Environment. Ph.D. Thesis, Southeast University, Nanjing, China, 2017. [Google Scholar]
- Guo, X.; Xiao, Z.; Zhang, Y.; Zhang, Y.; Xu, P. Variable Speed Limit Control Method in Work Zone Area of Eight-lane Highway Considering Effects of Connected Automated Vehicles. J. Southeast Univ. (Nat. Sci. Ed.) 2024, 54, 353–359. [Google Scholar]
- Wu, S.; Zou, Y.; Liu, D.; Chen, X.; Wang, Y. Investigating Traffic Characteristics at Freeway Merging Areas in Heterogeneous Mixed-Flow Environments. Sustainability 2025, 17, 2282. [Google Scholar] [CrossRef]



| Car-Following Model | Model Concept | Relevant Model | Advantages of the Model | Disadvantages of the Model |
|---|---|---|---|---|
| Safety Distance Model | Assume that the driver of the following vehicle expects to maintain a desired distance from the leading vehicle | Gipps model [2] | The model parameter calibration is relatively simple and can accurately simulate various traffic flow phenomena on the road | There is a discrepancy between the vehicle time headway and actual traffic conditions |
| Optimal Velocity Model | Assume that the vehicle aims to maintain an ideal safe velocity based on the difference in distance | FVD model [3], OV model [4], and GF model [5] | A relatively realistic representation of car-following behavior | When there is a significant velocity difference, it becomes difficult to ensure a safe time headway |
| NaSch Model | Simulate the dynamic behavior of vehicles on the road through simple rules and interactions between individuals | NaSch model [6], TT model [7], and VDR model [8] | The model is simple to understand, flexible to expand, and naturally captures phase transitions in traffic flow | The model imposes strict safety distance constraints but overlooks the impact of relative velocity |
| Intelligent Driving Model | It is assumed that the driver has a certain level of perception ability and aims to eliminate the difference from the desired velocity | IDM model [9] | The simulation results exhibit a small error compared to actual traffic data | The model has a large number of parameters |
| Autonomous Driving Model | Information sharing and cooperative control enhance the efficiency and safety of car following | CACC model [10] | The model has a simple structure, allowing for faster and more accurate responses based on the lead vehicle’s velocity and distance headway | Ignores communication delays and failures between vehicles |
| Name | Value | Unit | Description |
|---|---|---|---|
| frame | 534 | 0.05 s | Frame count for this data (1 frame = 0.05 s) |
| ID | 22 | —— | Vehicle ID |
| x | 81.47 | m | Horizontal distance relative to the road’s starting point |
| y | 25.36 | m | Vertical distance relative to the road’s starting point |
| width | 10.91 | m | Vehicle length |
| heigh | 2.83 | m | Vehicle width |
| x speed | 20.97 | m·s−1 | Vehicle speed at the current moment |
| x acceleration | 0.11 | m·s−2 | Vehicle acceleration at the current moment |
| dhw (distance headway) | 25.03 | m | —— |
| thw (time headway) | 1.19 | s | —— |
| ttc (time to collision) | −70.51 | s | —— |
| preceding x speed | 21.31 | m·s−1 | Speed of the leading vehicle at the current moment |
| preceding ID | 21 | —— | Preceding vehicle ID |
| lane ID | 6 | —— | Vehicle travel lane |
| Dataset | Training Data Volume | Validation Data Volume | |
|---|---|---|---|
| Free Flow | Passenger Car | 57,868 | 24,801 |
| Truck | 29,754 | 12,752 | |
| HDV Car Following | PHDV-P | 104,461 | 44,769 |
| PHDV-T | 13,779 | 5905 | |
| THDV-P | 7384 | 3165 | |
| THDV-T | 20,286 | 8694 | |
| Notion | Explanation |
|---|---|
| k | the coefficient of the free-flow acceleration model |
| vf | the desired speed of the vehicle |
| ai(t) | the acceleration of vehicle i at time t |
| vi(t) | the speed of vehicle i at time t |
| si(t) | the actual gap between vehicle i and its preceding vehicle at time t |
| δ | the free-flow acceleration exponent |
| s0 | the minimum gap when the vehicle is stationary |
| h | the safe time headway |
| Δvi(t) | the speed difference between vehicle i and its preceding vehicle at time t |
| amax | the maximum acceleration of the vehicle |
| b | the maximum comfortable deceleration |
| kp | the coefficient of position error |
| kd | the coefficient of speed error |
| Model | Parameters | TM | EM | ||||||
| Passenger Car | Truck | Passenger Car | Truck | ||||||
| Free-flow acceleration modeling | k | 0.032 | 0.028 | 0.4 | |||||
| vf/(km·h−1) | 131.18 | 93.85 | 120 | 100 | |||||
| Model | Parameters | TM | EM | ||||||
| PHDV-P | PHDV-T | THDV-P | THDV-T | PHDV-P | PHDV-T | THDV-P | THDV-T | ||
| IDM | amax/(m·s−2) | 0.24 | 0.13 | 0.44 | 0.03 | 1 | |||
| vf/(km·h−1) | 131.18 | 93.85 | 120 | 100 | |||||
| s0/m | 2.93 | 1.39 | 2.95 | 1.48 | 2 | ||||
| b/(m·s−2) | 3.60 | 1.73 | 0.57 | 1.00 | 2 | ||||
| h/s | 0.16 | 0.40 | 1.05 | 3.08 | 1.5 | 2 | |||
| δ | 8.41 | 2.71 | 0.77 | 2.56 | 4 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, N.; Qian, C.; Zhou, Y.; Luo, W. Operational Evaluation of Mixed Flow on Highways Considering Trucks and Autonomous Vehicles Based on an Improved Car-Following Decision Framework. Sustainability 2025, 17, 6450. https://doi.org/10.3390/su17146450
Kang N, Qian C, Zhou Y, Luo W. Operational Evaluation of Mixed Flow on Highways Considering Trucks and Autonomous Vehicles Based on an Improved Car-Following Decision Framework. Sustainability. 2025; 17(14):6450. https://doi.org/10.3390/su17146450
Chicago/Turabian StyleKang, Nan, Chun Qian, Yiyan Zhou, and Wenting Luo. 2025. "Operational Evaluation of Mixed Flow on Highways Considering Trucks and Autonomous Vehicles Based on an Improved Car-Following Decision Framework" Sustainability 17, no. 14: 6450. https://doi.org/10.3390/su17146450
APA StyleKang, N., Qian, C., Zhou, Y., & Luo, W. (2025). Operational Evaluation of Mixed Flow on Highways Considering Trucks and Autonomous Vehicles Based on an Improved Car-Following Decision Framework. Sustainability, 17(14), 6450. https://doi.org/10.3390/su17146450





