A Sustainable Solution for High-Standard Farmland Construction—NGO–BP Model for Cost Indicator Prediction in Fertility Enhancement Projects

Abstract

High-standard farmland fertility enhancement projects can lead to the sustainable utilization of arable land resources. However, due to difficulties in project implementation and uncertainties in costs, resource allocation efficiency is constrained. To address these challenges, this study first analyzes the impact of geography and engineering characteristics on cost indicators and applies principal component analysis (PCA) to extract key influencing factors. A hybrid prediction model is then constructed by integrating the Northern Goshawk Optimization (NGO) algorithm with a Backpropagation Neural Network (BP). The NGO–BP model is compared with the RF, XGBoost, standard BP, and GA–BP models. Using data from China’s 2025 high-standard farmland fertility enhancement projects, empirical validation shows that the NGO–BP model achieves a maximum RMSE of only CNY 98.472 across soil conditioning, deep plowing, subsoiling, and fertilization projects—approximately 30.74% lower than those of other models. The maximum MAE is just CNY 88.487, a reduction of about 32.97%, and all R² values exceed 0.914, representing an improvement of roughly 5.83%. These results demonstrate that the NGO–BP model offers superior predictive accuracy and generalization ability compared to other approaches. The findings provide a robust theoretical foundation and technical support for agricultural resource management, the construction of projects, and project investment planning.

1. Introduction

Food security represents a critical national strategy, with farmland serving as the foundation of agricultural production and a vital resource. Soil fertility plays a decisive role in determining both crop yield and quality and functions as the core carrier for implementing the strategies of “storing grain in the land, storing grain in technology” [1,2]. At present, traditional farmland production relies heavily on inputs such as labor, fertilizers, pesticides, and plastic mulch. The complex pattern of high input and output has intensified the conflict between production efficiency and quality demands [3,4,5,6]. High-quality farmland fertility enhancement projects, such as those centered on soil conditioning, deep plowing and loosening, optimized fertilization, and straw return, have emerged as key approaches to improving soil structure and nutrient use efficiency. The systematic implementation of such projects can protect arable land, reduce environmental risks, and provide long-term support for sustainable agricultural development [7,8,9].

Significant gaps remain in current research regarding the economic evaluation and technological dissemination of farmland fertility enhancement projects. In particular, the lack of scientifically supported cost estimation models poses substantial challenges, including high investment risks and difficulties in controlling fertilization costs [10,11,12,13]. The present study focuses on developing a predictive model for cost indicators in fertility enhancement projects, aiming to establish quantitative relationships between influencing factors and cost metrics. This model is intended to serve as a decision-making tool for optimizing resource allocation and formulating targeted investment strategies, thereby promoting the transformation of fertility enhancement efforts from technical implementation to system-level efficiency optimization in support of national food security goals.

Cost indicator prediction methods have been widely applied across various engineering domains, with numerous scholars proposing effective modeling approaches that have yielded notable results. These methods can generally be categorized into statistical prediction techniques and machine learning-based approaches.

Statistical prediction methods include the autoregressive (AR) model [14], multiple linear regression (MLR) analysis [15], and grey system prediction [16]. Lin et al. [17] proposed an MLR model to estimate product manufacturing costs, demonstrating through empirical analysis that the model achieves high fitting accuracy and predictive performance. Ottaviani et al. [18] applied MLR to develop an engineering management optimization model and introduced a novel EAC prediction formula with improved accuracy and reduced error. However, both AR and linear regression models are limited to capturing linear relationships in raw data. Grey system prediction, while theoretically flexible, exhibits low tolerance to data uncertainty and requires a large volume of samples. These limitations hinder its effectiveness in modeling nonlinear patterns, making it unsuitable for predicting cost indicators in fertility enhancement projects, where nonlinearity is a prominent feature.

With the rapid development of artificial intelligence, machine learning models have been increasingly adopted by researchers and engineers to address a range of predictive challenges in the engineering domain. Models such as support vector regression (SVR) [19,20], backpropagation (BP) neural networks, random forests (RFs) [21,22], and convolutional neural networks (CNNs) [23] have been widely applied in construction management, cost estimation, and soil fertility assessment [24,25,26,27]. For example, Khanal et al. [28] integrated remote sensing imagery to build six predictive models, including linear regression, RF, and XGBoost, and demonstrated that the RF model outperformed the others in predicting maize yield and soil characteristics with higher accuracy and robustness. Hu et al. [29] considered both natural and anthropogenic drivers of soil nutrient variation and developed an RF model to estimate nutrient levels. The model outperformed XGBoost in mapping nitrogen, phosphorus, and potassium concentrations, confirming its superior predictive capability. Zhang et al. 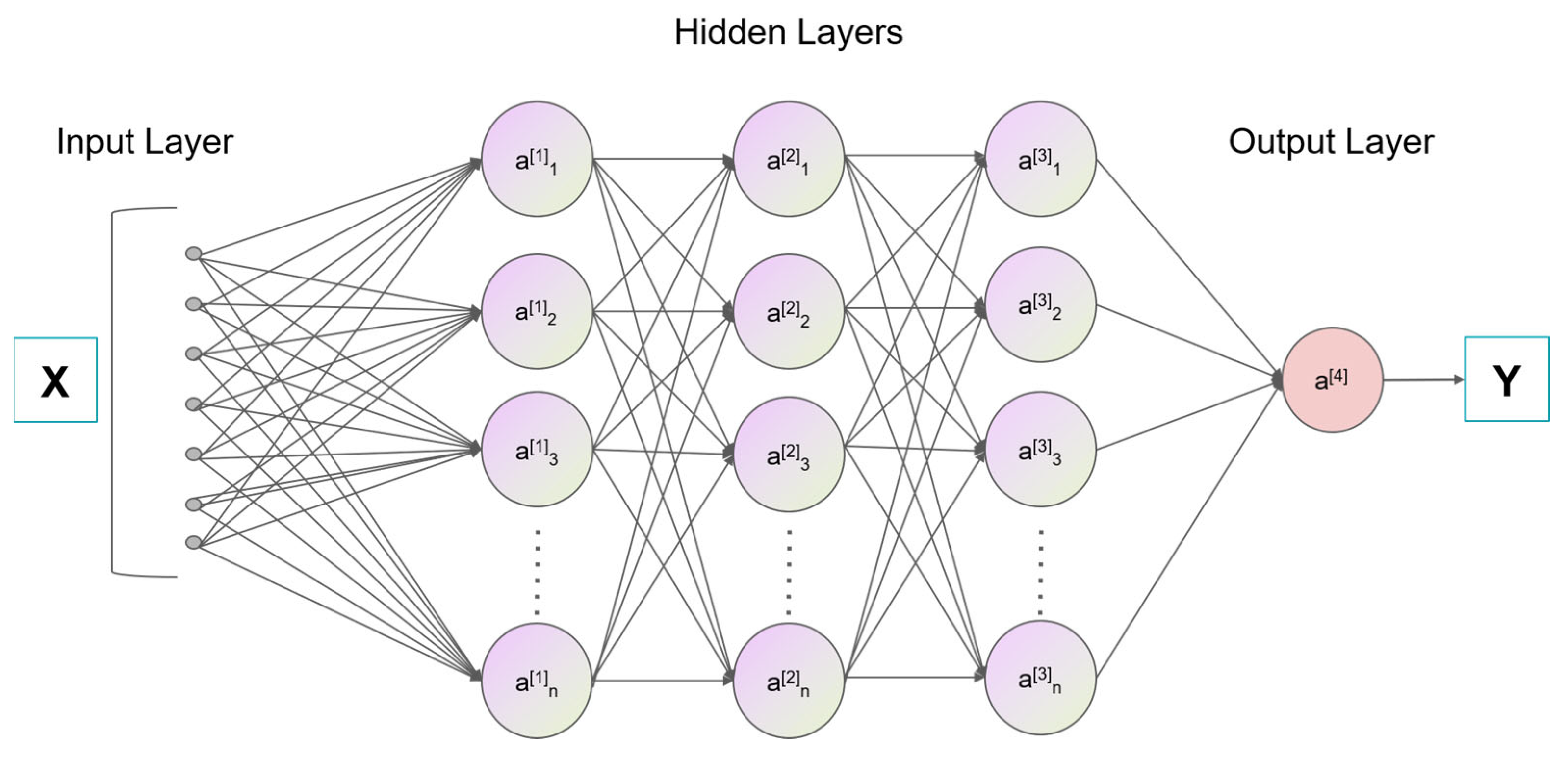[30] employed principal component analysis (PCA) and Pearson correlation to identify key logging parameters for coalbed methane prediction. A BP neural network model constructed using these variables achieved approximately 61% higher prediction accuracy compared to RF, XGBoost, and k-nearest neighbor (KNN) models. This model demonstrated high efficiency and precision in estimating gas content, offering strong applicability in coal seam exploration and resource evaluation. Among existing machine learning approaches, BP neural networks are particularly effective in modeling nonlinear relationships between variables, making them well-suited for predicting cost indicators in farmland fertility enhancement projects [31].

Redundant information increases the computational burden and compromises both the robustness and generalization capability of predictive models. The accuracy of model predictions is highly dependent on the quality of input data, underscoring the importance of feature selection to reduce the dimensionality of raw datasets. Wyke et al. [32] utilized PCA to eliminate redundancy in high-dimensional data and to ensure variable independence, thereby enhancing compatibility with predictive modeling [33]. In addition to data preprocessing, model performance is critically influenced by hyperparameter selection. Recent studies have increasingly adopted optimization algorithms to improve prediction accuracy through automated hyperparameter tuning [34,35]. Li et al. [36] employed a genetic algorithm (GA) to optimize the weights and thresholds of a BP neural network, developing a GA–BP model for construction cost prediction in Guangdong Province that achieved a coefficient of determination of 0.94, validating its effectiveness. Chang et al. [37] constructed a BP neural network model. To improve predictive performance, they applied the Northern Goshawk Optimization (NGO) algorithm for parameter optimization and demonstrated that the NGO–BP model outperformed the DBO–BP model in accuracy. Among various optimization methods, NGO has demonstrated a strong global search capacity and rapid convergence toward near-optimal solutions [38,39], making it well-suited for hyperparameter tuning in BP neural networks. Given the non-temporal and nonlinear nature of the engineering cost data in this study, four widely used models (RF, XGBoost, BP, and GA–BP) were selected for comparative analysis against the proposed NGO–BP model.

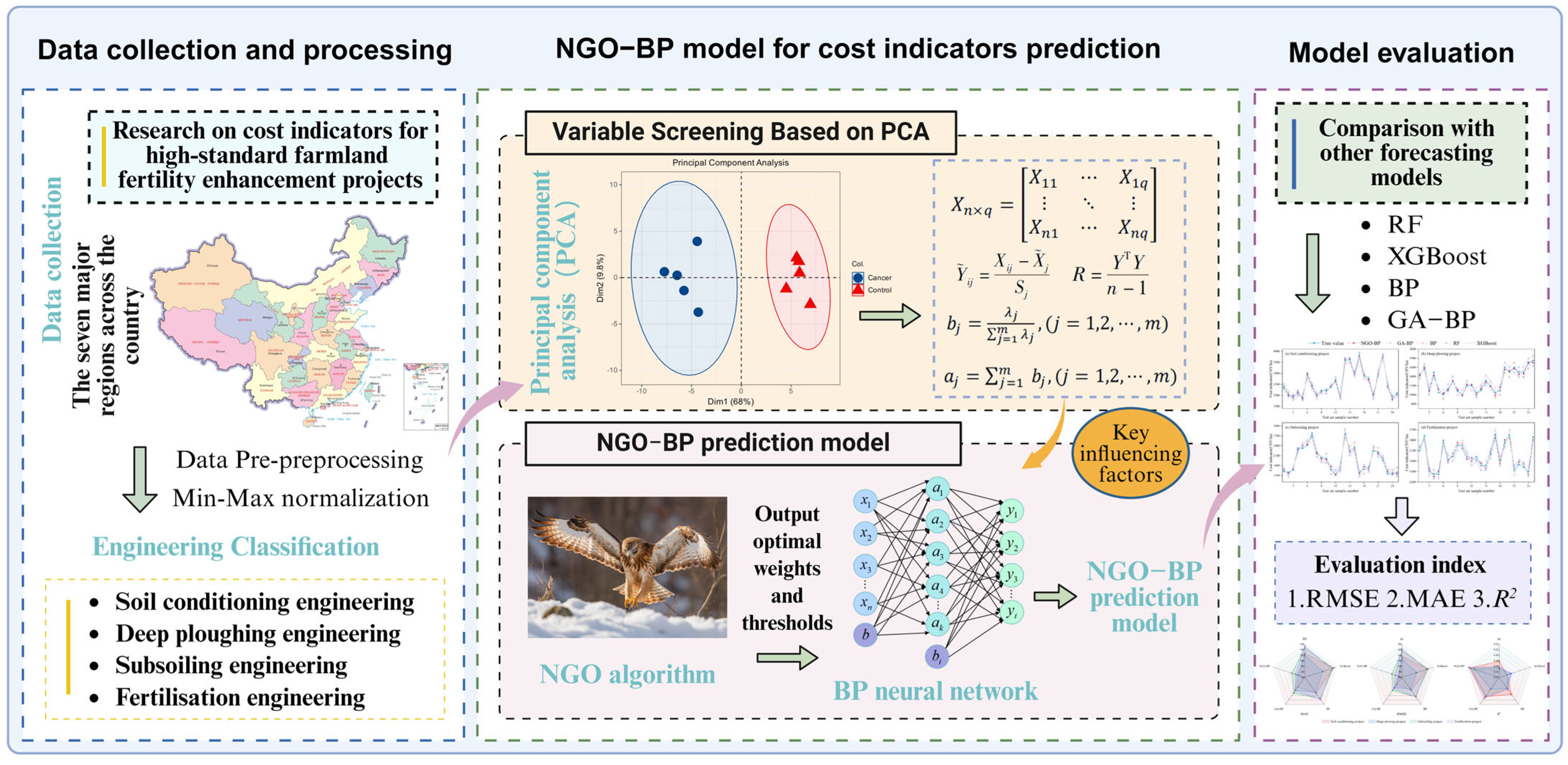
The construction of farmland fertility enhancement projects serves as a fundamental strategy for improving soil structure and increasing nutrient use efficiency, underscoring the necessity of accurate cost prediction models. A review of the literature on cost indicator modeling shows that most existing models are applied in sectors such as building construction, water conservancy, and power transmission [40,41,42], while research specifically addressing cost prediction in fertility enhancement projects remains limited. In this study, PCA was applied to identify and reduce the dimensionality of relevant influencing factors, isolating the key variables associated with project costs. Qualitative variables were subsequently quantified, and a BP neural network optimized by the NGO algorithm was developed. The proposed NGO–BP model enables cost indicator prediction across diverse engineering types and environmental conditions. This modeling approach provides a practical reference for regional investment planning, promotes more refined cost management throughout the entire lifecycle of high-standard farmland construction, and supports optimal resource allocation and evidence-based investment decisions. Accordingly, this study offers not only a theoretical framework for cost prediction in fertility enhancement projects but also a technical foundation to advance the sustainable development of agricultural production.

The innovation of this study lies in constructing a cost indicator prediction model for fertility enhancement projects. Based on PCA screening, an indicator system of influencing factors for fertility enhancement project costs is established. The NGO algorithm optimizes the BP model to establish a combined NGO–BP prediction model. This algorithm outperforms others in parameter optimization. Simultaneously, the prediction model precisely captures nonlinear variations among different soil fertility improvement project data. The overall model performance surpasses other prediction models. Through variable screening and algorithm optimization, it aims to enhance prediction accuracy and generalization capability.

The remainder of this paper is organized as follows: Section 2 introduces the study area and data sources, along with the principal component analysis, BP neural network model, and NGO algorithm. Specific steps for predicting fertility enhancement project cost indicators are also presented. Section 3 screens and reduces the dimensions of influencing factors using the PCA method, constructs five different prediction models to compare their accuracy and stability, and ultimately demonstrates the optimal performance of the NGO–BP model in predicting fertility enhancement project cost indicators. Section 4 discusses the results. Section 5 contains conclusions and future work.

2. Data and Methods

2.1. Data Sources and Preprocessing

The dataset used in this study was obtained from cost indicators of high-standard farmland fertility enhancement projects implemented across provinces and municipalities in China’s seven major geographic regions in 2025. These projects are designed to improve the ecological condition of farmland, reduce the impact of flood-related disasters on crop production, and enhance local agricultural productivity. Sample data were collected through a combination of field investigations and official project acceptance documents. The seven geographic regions include Northeast China, North China, Central China, South China, East China, Northwest China, and Southwest China. Specifically, surveyed provinces and cities include Northeast China (Heilongjiang, Jilin, Liaoning); North China (Hebei, Shanxi, Tianjin); Central China (Henan, Hubei, Hunan); South China (Guangdong, Guangxi Zhuang Autonomous Region); East China (Anhui, Jiangsu); Northwest China (Gansu, Shaanxi); and Southwest China (Yunnan, Sichuan). Data preprocessing involved handling missing values, removing outliers, and normalizing the data. Missing values were imputed using the average and proportional values of similar projects. Outliers were removed based on constraints related to the cost structure and rationality of project quantities. Normalization was applied to eliminate the effects of differing data scales by transforming all values into the [0, 1] range, as calculated by Equation (1). The dataset includes 500 records, comprising 125 samples each from four project types: soil conditioning, deep plowing, subsoiling, and fertilization. Each category was randomly divided into a training set and a testing set in an 80:20 ratio.

$$x_i^{\ast }={\displaystyle \frac{x_i-x_{min}}{x_{max}-x_{min}}},$$

(1)

where $x_{max}$ and $x_{min}$ represent the maximum and minimum values in the sample data, respectively; $x_i$ denotes the original value; and $x_i^{\ast }$ denotes the normalized value.

2.2. Analysis of Influencing Factors for Cost Indicators in Farmland Fertility Enhancement Projects

2.2.1. Selection of Influencing Factors

The cost indicators of farmland fertility enhancement projects are influenced by a wide range of variables, often characterized by complex interdependencies [43,44]. The selection of comprehensive and rational influencing factors forms the foundation for constructing accurate cost prediction models. Based on an extensive review of the relevant literature and practical considerations in engineering implementation, a set of key variables affecting cost indicators was identified. Farmland fertility enhancement projects generally include four major components: soil conditioning, deep plowing, subsoiling, and fertilization. Influencing factors were classified into three main categories—geographical and environmental factors, engineering-related factors, and cost-related factors [45,46]—and further divided into qualitative and quantitative types. To enable model integration, qualitative variables were numerically encoded based on standardized criteria: topography was assigned values of 1 for plains, 2 for hills, 3 for mountains, and 4 for plateaus; the application method of fertilizers or conditioners was coded as 1 for manual, 2 for mechanical, and 3 for drone-based operations; plot shape was encoded as 1 for rectangular, 2 for triangular, and 3 for polygonal; soil classification was assigned values of 1 for Class I–II soils, 2 for Class III, and 3 for Class IV; and fertilizer type was coded as 1 for conventional chemical fertilizers, 2 for organic fertilizers, and 3 for bio-organic fertilizers. The complete set of influencing factors for each project type is summarized in

Table 1. Summary of factors influencing the cost indicators for farmland fertility enhancement projects.

No.	Influencing Factors
	Soil Conditioning Project	Deep Plowing Project	Subsoiling Project	Fertilization Project
1	Plot area/ha (S1)	Plot area/ha (E1)	Plot area/ha (L1)	Plot area/ha (F1)
2	Application amount/kg (S2)	Plowing depth/cm (E2)	Subsoiling depth/cm (L2)	Slope gradient/(F2)
3	Soil layer thickness/m (S3)	Slope gradient/(E3)	Slope gradient/(L3)	Fertilizer amount/kg (F3)
4	Slope gradient/(S4)	Land leveling accuracy/cm (E4)	Land leveling accuracy/cm (L4)	Land leveling accuracy/cm (F4)
5	Land leveling accuracy/cm (S5)	Plot length/m (E5)	Plot length/m (L5)	Plot length/m (F5)
6	Plot length/m (S6)	Plot width/m (E6)	Plot width/m (L6)	Plot width/m (F6)
7	Plot width/m (S7)	Labor cost/CNY (E7)	Labor cost/CNY (L7)	Labor cost/CNY (F7)
8	Plot elevation/m (S8)	Machinery cost/CNY (E8)	Machinery cost/CNY (L8)	Machinery cost/CNY (F8)
9	Labor cost/CNY (S9)	Material cost/CNY (E9)	Material cost/CNY (L9)	Material cost/CNY (F9)
10	Machinery cost/CNY (S10)	Contingency cost/CNY (E10)	Contingency cost/CNY (L10)	Contingency cost/CNY (F10)
11	Material cost/CNY (S11)	Indirect cost/CNY (E11)	Indirect cost/CNY (L11)	Indirect cost/CNY (F11)
12	Contingency cost/CNY (S12)	Construction duration/day (E12)	Construction duration/day (L12)	Construction duration/day (F12)
13	Indirect cost/CNY (S13)	Topography (E13)	Topography (L13)	Topography (F13)
14	Construction duration/day (S14)	Soil type (E14)	Soil type (L14)	Fertilizer type (F14)
15	Topography (S15)	Plot shape (E15)	Plot shape (L15)	Soil type (F15)
16	Conditioner application method (S16)			Fertilizer application method (F16)
17	Plot shape (S17)			Plot shape (F17)

.

2.2.2. Principal Component Analysis

To eliminate the influence of redundant variables and ensure the feasibility of model construction, it is necessary to screen and reduce the dimensionality of the selected influencing factors. Common dimensionality reduction techniques include grey relational analysis and PCA. Given the non-temporal nature of the dataset used in this study, PCA was selected to identify the key influencing factors for predicting cost indicators in farmland fertility enhancement projects [47]. PCA is a statistical method that extracts and transforms multiple correlated variables into a smaller set of uncorrelated composite indicators through dimensionality reduction. The goal is to retain as much information from the original dataset as possible while reducing the number of input variables [48]. The specific steps are as follows:

• Suppose the dataset contains n samples, each with m variables, forming an n × m sample matrix X, expressed as

$$X_{n\times m}=\left[\begin{array}{ccc}{X}_{11}& \dots & X_{1m}\\ ⋮& \ddots & ⋮\\ X_{n1}& \dots & X_{nm}\end{array}\right],$$

(2)

2.

Calculate the correlation coefficient matrix R, and obtain its eigenvalues ${\lambda }_1$ ≥ ${\lambda }_2$ ≥ … ${\lambda }_m$ ≥0 along with the corresponding eigenvectors $u_1$, $u_2$,…, $u_m$, where $u_j$ = ($u_{1j}$,$u_{2j}$,…,$u_{mj}$)^T. These eigenvectors form the new uncorrelated principal component variables.

3.

Determine the principal components. After data standardization, calculate the variance contribution rate $b_j$ and the cumulative contribution rate $a_j$ for each influencing factor, as shown in Equations (3) and (4). Only components with eigenvalues greater than or equal to 1 and a cumulative contribution rate exceeding 80% are retained as principal components.

$$b_j={\displaystyle \frac{{\lambda }_j}{{\sum }_{j=1}^m {\lambda }_j}},\hspace{1em}(j=\mathrm{1,2},\dots ,m),$$

(3)

$$a_j={\sum }_{j=1}^m b_j,\hspace{1em}(j=\mathrm{1,2},\dots ,m),$$

(4)

4.

Compute the composite score. Based on the factor loading matrix, obtain the score coefficients of each influencing factor on the principal components. A composite score is calculated for each sample, followed by normalization and ranking.

2.3. NGO–BP Neural Network Model

The BP neural network is one of the most widely used multilayer feedforward models in machine learning. Its core mechanism involves training sample data through an error backpropagation algorithm, which iteratively optimizes the network’s parameters. Owing to its distinctive computational architecture, the BP neural network demonstrates strong fault tolerance and memory capacity, making it particularly effective in addressing nonlinear problems and small-sample learning scenarios [49]. As illustrated in Figure 1, the BP network typically consists of three parts: an input layer, one or more hidden layers, and an output layer. During training, weights and thresholds are randomly initialized. The learning process comprises two stages: forward propagation and backward propagation. In the forward stage, normalized input data, filtered via PCA, are fed into the input layer. These data are processed by the hidden layer and propagated forward to generate predicted values of cost indicators for farmland fertility enhancement projects. In the backward phase, the error between the predicted and actual values is computed and propagated backward through the network to update the weights and thresholds. This iterative adjustment process, guided by the error backpropagation algorithm, aims to minimize prediction errors and improve the model’s accuracy and robustness. The weight update formula is given in Equation (5).

$${\omega }^{\prime }=\omega -\eta {\displaystyle \frac{\mathsf{\partial }E}{\mathsf{\partial }\omega }}$$

(5)

where $\omega$ is the weight between neurons at iteration; ${\omega }^{\prime }$ is the updated weight; E denotes the prediction error; and $\eta$ is the learning rate.

In conventional BP neural networks, the random assignment of initial weights and thresholds often results in parameter sensitivity, which can lead the network into local optima. Such limitations cause slow convergence and low computational efficiency and hinder the achievement of global optimization. To improve the global search ability and predictive performance of BP neural networks, the NGO algorithm is introduced for parameter optimization. Incorporating NGO enables the model to escape local minima and enhances prediction accuracy. The NGO algorithm, proposed by Mohammad Dehghani in 2021, is a population-based optimization algorithm. It simulates the hunting process of the Northern Goshawk, which involves two phases, prey search and identification, followed by pursuit and evasion, to find high-performance hyperparameter combinations [50]. The NGO algorithm offers faster convergence and higher search precision than other optimization algorithms, such as the GA. It effectively addresses the limitations of manually assigned hyperparameters in BP neural networks, often leading to suboptimal accuracy and weak generalization. The step-by-step procedure of the NGO algorithm is outlined as follows:

• First phase: Prey search and identification (exploration phase).

$$X_{i,j}^{new,P1}=\left\{\begin{array}{c}{x}_{i,j}+q \left(p_{i,j}-E{x}_{i,j}\right),\hspace{1em}{F}_{P_i}<F_i\\ \\ x_{i,j}+q \left(x_{i,j}-p_{i,j}\right),\hspace{1em}{F}_{P_i}\ge F_i\end{array}\right.,$$

(6)

where P₁ represents the first measurement stage, F_pi is the target function value of the position of the i-th Northern Goshawk in the first hunting stage, and $X_{i,j}^{new,P1}$ represents the updated position of the i-th Northern Goshawk in the j-th dimension during the first measurement stage. The variable q is a random number within the range [0, 1], and E is an integer, either 1 or 2, representing the type of random number.

2.

Second phase: Pursuit and evasion (exploitation phase).

$$x_{i,j}^{new,P2}=x_{i,j}+R \left(2q-1\right){ x}_{i,j},$$

(7)

$$R=0.02\left(1-{\displaystyle \frac{t}{T}}\right),$$

(8)

3.

Assume that the attack range of this hunting activity has a radius of R.

In the formula, $X_{i,j}^{new,P2}$ represents the new position of the i-th Northern Goshawk in the j-th dimension during the second exploitation phase; t is the current iteration number, and T is the maximum iteration number; and R is the attack radius.

The process of optimizing the BP neural network using the NGO is illustrated in Figure 2.

2.4. Cost Indicator Prediction for Farmland Fertility Enhancement Projects

The overall process of predicting cost indicators for farmland fertility enhancement projects is illustrated in Figure 3. The procedure consists of the following steps: First, engineering data were collected through field investigations from high-standard farmland fertility enhancement projects across China’s seven major regions, including soil conditioning, deep plowing, subsoiling, and fertilization. The collected data underwent preprocessing, including data cleaning and normalization. Principal component analysis (PCA) was then applied to perform dimensionality reduction and select key influencing factors, which were used as the input variables of the prediction model. The unit cost of each sample project was defined as the model output. Based on the scale of the dataset and to ensure a balance between sufficient model training and reliable evaluation, the data were randomly divided into training and testing sets in a ratio of 8:2. A NGO–BP prediction model was constructed by optimizing the weights and thresholds of the BP neural network using the NGO algorithm. Finally, the predictive performance and feasibility of the proposed model were validated through comparisons with other machine learning models and optimization algorithms.

3. Results

3.1. Key Influencing Factor Selection Based on PCA

PCA was applied to the collected dataset, which consists of 125 samples for each of the four project types (soil conditioning, deep plowing, subsoiling, and fertilization). PCA was used to identify the key influencing factors affecting cost indicators in farmland fertility enhancement projects. Eigenvalues and variance contribution rates for the principal components were calculated according to Equations (3) and (4), and the results are presented in

Table 2. Principal component eigenvalues and variance contributions.

Engineering Category	Principal Component	Eigenvalue	Variance Contribution (%)	Cumulative Contribution (%)
Soil conditioning project	1	6.807	40.043	40.043
	2	2.747	16.158	56.201
	3	1.865	10.971	67.172
	4	1.624	9.554	76.726
	5	1.058	6.222	82.948
Deep plowing project	1	4.004	35.694	35.694
	2	2.747	18.314	54.008
	3	1.535	10.233	64.241
	4	1.469	9.793	74.034
	5	1.330	8.866	82.900
Subsoiling project	1	4.895	32.633	32.633
	2	3.897	25.977	58.610
	3	2.441	16.271	74.881
	4	1.550	10.336	85.217
Fertilization project	1	5.009	39.464	39.464
	2	2.967	17.451	56.915
	3	2.253	13.251	70.166
	4	1.376	8.097	78.262
	5	1.184	6.965	85.227

.

Principal components with eigenvalues greater than 1 and cumulative variance contribution rates exceeding 80% were selected for subsequent analysis. As shown in Table 2, the first five principal components of the soil conditioning project account for a cumulative contribution rate of 82.948%, with the fifth eigenvalue reaching 1.058. These results suggest that the first five components sufficiently capture most of the information in the original dataset and are retained as the principal components. Similarly, in the deep plowing project, the first five components yield a cumulative contribution rate of 82.900%, with the fifth eigenvalue reaching 1.330, thus satisfying the selection criteria. For the subsoiling and fertilization projects, the first four and five principal components were retained following the same rule. Using the selected principal components and the corresponding component matrix, comprehensive scores for the influencing factors on cost indicators were calculated for each type of farmland fertility enhancement project.

As shown in

Table 3. Composite scores of influencing factors.

Influencing Factor No.	Soil Conditioning Project		Deep Plowing Project		Subsoiling Project		Fertilization Project
	Composite Score	Normalize	Composite Score	Normalize	Composite Score	Normalize	Composite Score	Normalize
1	0.203	0.993	0.186	0.896	0.212	0.930	0.183	0.957
2	0.201	0.987	0.183	0.887	0.231	1.000	0.078	0.560
3	0.202	0.989	0.039	0.284	0.142	0.678	0.121	0.720
4	0.001	0.280	0.147	0.735	0.192	0.860	0.162	0.875
5	0.170	0.877	0.052	0.339	0.108	0.554	0.114	0.696
6	0.047	0.443	0.107	0.567	0.098	0.518	0.066	0.514
7	0.084	0.574	0.202	0.964	0.202	0.893	0.146	0.817
8	0.063	0.499	0.209	0.994	0.156	0.729	0.138	0.787
9	0.203	0.993	0.211	1.000	0.157	0.730	0.174	0.921
10	0.205	1.000	−0.030	0.000	−0.046	0.000	0.190	0.981
11	0.203	0.992	0.183	0.886	0.143	0.681	0.107	0.669
12	−0.079	0.000	0.146	0.733	0.153	0.718	0.195	1.000
13	0.003	0.290	0.092	0.506	0.022	0.243	0.047	0.440
14	0.164	0.857	0.062	0.383	0.057	0.371	0.123	0.728
15	0.018	0.343	0.055	0.351	0.077	0.444	0.085	0.585
16	0.091	0.599					−0.070	0.000
17	−0.002	0.270					0.075	0.547

, influencing factors with normalized composite scores exceeding 0.7 were selected as key variables for subsequent modeling. For the soil conditioning project, eight critical factors were identified: soil conditioning area (S1), conditioner application amount (S2), soil layer thickness (S3), surface leveling degree (S5), labor cost (S9), machinery cost (S10), material cost (S11), and construction period (S14). For the deep plowing project, the selected factors included deep plowing area (E1), plowing depth (E2), surface leveling degree (E4), labor cost (E7), machinery cost (E8), material cost (E9), indirect cost (E11), and construction period (E12). In the subsoiling project, seven key variables were retained: subsoiling area (L1), depth (L2), surface leveling degree (L4), labor cost (L7), machinery cost (L8), material cost (L9), and construction period (L12). For the fertilization project, nine key factors were identified: fertilization area (F1), fertilization amount (F3), surface leveling degree (F4), labor cost (F7), machinery cost (F8), material cost (F9), contingency cost (F10), construction period (F12), and fertilizer type (F14). These variables were subsequently used as inputs in the cost prediction model for farmland fertility enhancement projects.

3.2. Cost Prediction Based on the NGO–BP Model

3.2.1. Parameter Configuration and Model Evaluation

The influencing factors selected via PCA for each project type were used as input variables in the prediction model, with the cost indicator serving as the output variable. Eighty percent of the dataset was allocated to the training set, and the remaining 20% to the test set. Since the data are non-temporal, the entire dataset was shuffled prior to splitting. Accordingly, the datasets for the soil conditioning, deep plowing, subsoiling, and fertilization projects were each divided into 100 training samples and 25 test samples.

To evaluate the predictive performance of the NGO–BP model, four benchmark models (RF, XGBoost, BP, and GA–BP) were constructed using the same dataset for comparison. The BP network requires the specification of the number of hidden layer nodes. Based on an empirical formula and trial-and-error approach, the optimal range was between 6 and 16. The best performance was obtained with 13 hidden nodes.

Both population size and the number of iterations influence the performance of the NGO. Although larger values enhance the global search capability, they may also lead to overfitting or convergence to local optima. The optimal settings were determined using the mean squared error (MSE) from the training set as the fitness function. As shown in

Table 4. Comparison of algorithm errors under different population sizes and iteration numbers.

No.	Population		Iteration
	Population Size	Algorithm Error	Number of Iterations	Algorithm Error
1	10	0.01936	80	0.00426
2	20	0.01753	90	0.00216
3	30	0.01309	100	0.00914
4	40	0.01422	110	0.00176
5	50	0.01848	120	0.00104
6	60	0.01704	130	0.00114
7	70	0.01926	140	0.00136
8	80	0.02352	150	0.00175

, the minimum error occurred when the population size was set to 30 and the number of iterations to 100, indicating that the NGO algorithm had converged. The upper and lower bounds for the optimization problem were 3 and −3.

In addition, RF and XGBoost were selected as baseline machine learning models for comparison. RF constructs an ensemble of decision trees and averages their outputs, effectively reducing overfitting and improving prediction stability. XGBoost, a gradient-boosting framework, integrates multiple weak learners to achieve high prediction accuracy and is particularly suited for large-scale datasets. These characteristics justify their selection for benchmarking purposes. The specific parameter settings for all models and algorithms are summarized in

Table 5. Parameter settings for each model.

Model	Hyperparameterization	Value
BP	Number of iterations	1000
	Learning rate	0.01
	Number of hidden layer nodes	13
	Minimum training error target	0.00001
	Training function	trainlm
RF	Number of decision trees	100
	Maximum depth	5
XGBoost	Number of decision trees	500
	Maximum depth	3
	Learning rate	0.01
NGO	Initial learning rate	0.01
	Population size	30
	Maximum number of iterations	100
	Upper bound for weights/thresholds	3
	Lower bound for weights/thresholds	−3

.

Three evaluation metrics were employed to assess the predictive accuracy of the cost indicator model for farmland fertility enhancement projects: root mean square error (RMSE), mean absolute error (MAE), and the coefficient of determination (R²). Smaller RMSE and MAE values, along with R² values closer to 1, indicate better model performance, lower prediction error, and higher reliability of the results. The corresponding calculation formulas are defined as follows:

$$RMSE=\sqrt{{\displaystyle \frac{1}{\mathrm{n}}}{\sum }_{i=1}^n {\left(Y_i-Y_i^{\mathrm{\prime }}\right)}^2},$$

(9)

$$MAE={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n \left|Y_i-Y_i^{\prime }\right|,$$

(10)

$$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^n {\left(Y_i^{\mathrm{\prime }}-\overline{Y_i}\right)}^2}{\sum _{i=1 }^n {\left(Y_i-\overline{Y_i}\right)}^2}},$$

(11)

where $Y_i$ denotes the actual cost indicator value for the i-th sample; $Y_i^{\mathrm{\prime }}$ represents the predicted value, and $\overline{Y_i}$ is the mean of the actual values across n prediction samples.

3.2.2. Comparative Analysis of Different Prediction Models

None of the five predictive models exhibited signs of overfitting during the training and testing phases. For the cost indicator predictions in the soil conditioning, deep plowing, subsoiling, and fertilization projects, predicted values from each model were compared against actual values. The results are presented in Figure 4, and the performance evaluation metrics of each model are summarized in

Table 6. Comparison of evaluation metrics for different models.

Engineering Category	Model	MAE (CNY/ha)	RMSE (CNY/ha)	R2
Soil conditioning project	RF	126.752	135.761	0.878
	XGBoost	149.124	157.193	0.850
	BP	109.595	117.539	0.894
	GA–BP	83.616	92.661	0.905
	NGO–BP	61.054	71.054	0.931
Deep plowing project	RF	120.070	128.097	0.851
	XGBoost	108.283	115.079	0.863
	BP	106.947	113.132	0.869
	GA–BP	98.502	105.542	0.872
	NGO–BP	67.873	74.167	0.914
Subsoiling project	RF	145.268	155.225	0.856
	XGBoost	148.429	158.414	0.852
	BP	134.158	144.143	0.870
	GA–BP	108.409	118.454	0.902
	NGO–BP	88.487	98.472	0.927
Fertilization project	RF	152.143	162.685	0.858
	XGBoost	143.429	153.712	0.867
	BP	136.109	146.034	0.874
	GA–BP	99.286	109.675	0.911
	NGO–BP	75.369	85.791	0.935

and Figure 5.

As illustrated in Figure 4, a comparison of the prediction outcomes across the four cost indicator models for farmland fertility enhancement projects shows that the deviations between predicted and actual values are significantly larger in the RF and XGBoost models than in the BP model. These results indicate that the BP neural network better fits the characteristics and sample size of the current dataset, offering improved predictive accuracy. Despite larger deviations, the predicted trends from the RF and XGBoost models generally align with the actual trends, indicating that PCA effectively extracted key influencing factors, reduced dimensionality, and eliminated redundant information, thereby enhancing model performance to a certain extent. Further evaluation of the NGO algorithm’s role in parameter optimization reveals that the NGO–BP model produces the prediction curve most closely aligned with the actual values, with minimal deviation across samples. In addition, the residual plot in Figure 6 shows that the NGO–BP model is closest to the zero-level line in terms of residuals compared to the other models, which suggests that the predicted values of the model are the closest to the actual values and have the highest prediction accuracy. Consequently, the NGO–BP hybrid model demonstrates superior performance compared to the standalone BP neural network, RF, and XGBoost models regarding simulation accuracy.

As shown in Table 6, the NGO–BP prediction model achieved the lowest RMSE and MAE and the highest R² across all project types, consistently outperforming the other models. Under the same conditions, the BP neural network exhibited superior predictive accuracy compared to traditional machine learning models such as RF and XGBoost, particularly in handling nonlinear feature relationships in cost prediction. In the soil conditioning project, the BP model reduced the RMSE and MAE by 13.42% and 13.54%, respectively, compared to RF, with a 2% increase in R². Relative to XGBoost, the reductions in RMSE and MAE were 25.23% and 26.51%, with a 5% gain in R². In the deep plowing project, BP achieved RMSE and MAE reductions of 11.68% and 10.93% over RF and 1.69% and 1.23% over XGBoost, with corresponding R² improvements of 2% and 1%, respectively. These results confirm that the BP neural network effectively captures the nonlinear relationships among input features while mitigating the influence of data randomness, thereby achieving higher prediction accuracy and computational efficiency. Furthermore, the integration of PCA for dimensionality reduction helped eliminate redundant input variables, improved the effectiveness of training samples, and enhanced overall model precision.

The BP neural network model demonstrates considerable improvement when enhanced with optimization algorithms to address hyperparameter tuning challenges. Compared with the standard BP model, the GA–BP model showed significant gains in the subsoiling project, reducing the RMSE and MAE by 17.82% and 19.19%, respectively, and increasing R² by 4%. In the fertilization project, the RMSE and MAE decreased by 24.90% and 27.05%, with an R² improvement of 4%. These results highlight that optimizing hyperparameters can substantially improve both prediction accuracy and computational efficiency. In contrast, random initialization in conventional BP networks often leads to instability, weak generalization, and suboptimal performance. Further comparison shows that the NGO–BP model outperforms GA–BP. In the subsoiling project, NGO–BP reduced RMSE and MAE by 16.87% and 18.38%, respectively, and improved R² by 3%. In the fertilization project, the reductions in RMSE and MAE were 21.78% and 24.09%, with a 3% increase in R². These findings suggest that the NGO algorithm offers more effective optimization of weights and thresholds in BP networks compared to GA. The superior performance is attributed to the NGO’s behavioral simulation of dung beetles, which improves coverage of the hyperparameter search space and reduces convergence iterations. This behavior enhances robustness and optimization capacity, particularly in high-dimensional parameter spaces.

Based on the overall results, the proposed NGO–BP prediction model exhibited markedly better performance in terms of MAE, RMSE, and R² compared to conventional machine learning models, demonstrating strong applicability and high predictive accuracy. The incorporation of PCA and the NGO algorithm into the BP neural network substantially enhanced both prediction efficiency and effectiveness while reducing the subjectivity involved in the manual selection of weights and thresholds. Consequently, the NGO–BP model surpasses the standalone BP neural network in both precision and generalization ability. In the absence of standardized construction guidelines for high-standard farmland development, the NGO–BP model yields more stable and accurate predictions of cost indicators for fertility enhancement projects. The model supports project evaluation with both theoretical grounding and empirical evidence. It also functions as an effective tool for dynamically refining investment benchmarks and improving capital allocation strategies in future project planning and implementation.

4. Discussion

High-standard farmland fertility enhancement projects play a vital role in improving soil structure and ensuring stable, high crop yields. By enhancing soil physicochemical properties and promoting nutrient cycling, these projects support the sustainable use of arable land, reduce dependence on chemical fertilizers and pesticides, and contribute to both food security and ecological balance. However, the absence of accurate and scientific cost prediction during project implementation constrains resource allocation efficiency, increases investment risk, and impedes the translation of technology into practical benefits. Establishing a dynamic and robust cost prediction model is essential to guide decision-making throughout project planning and execution.

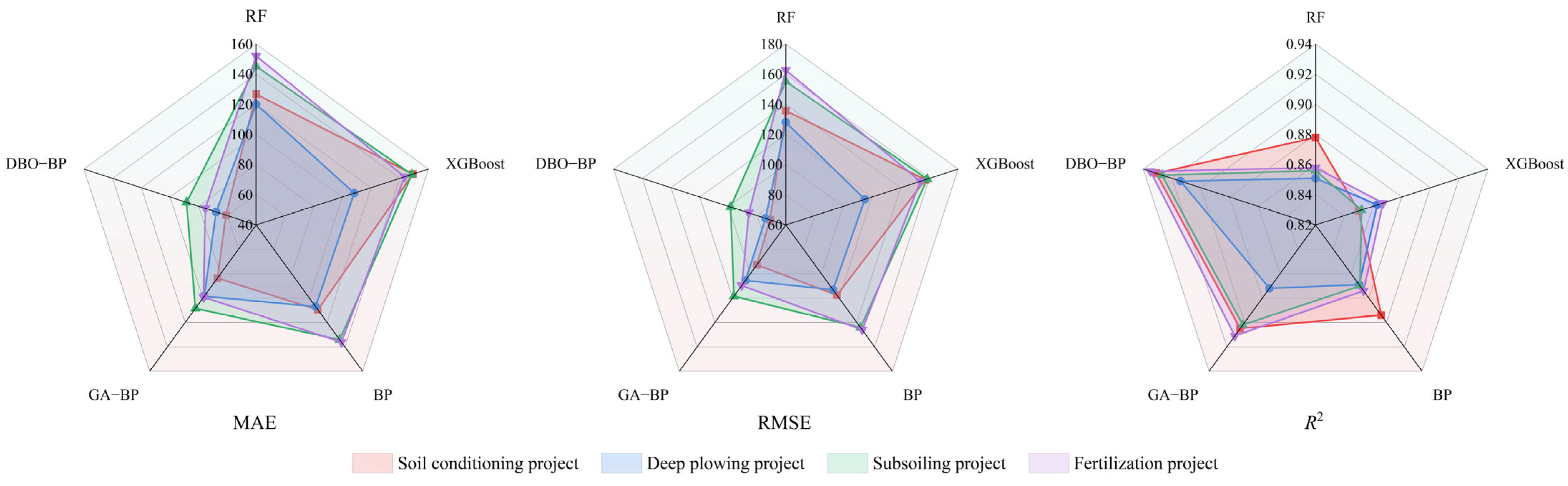
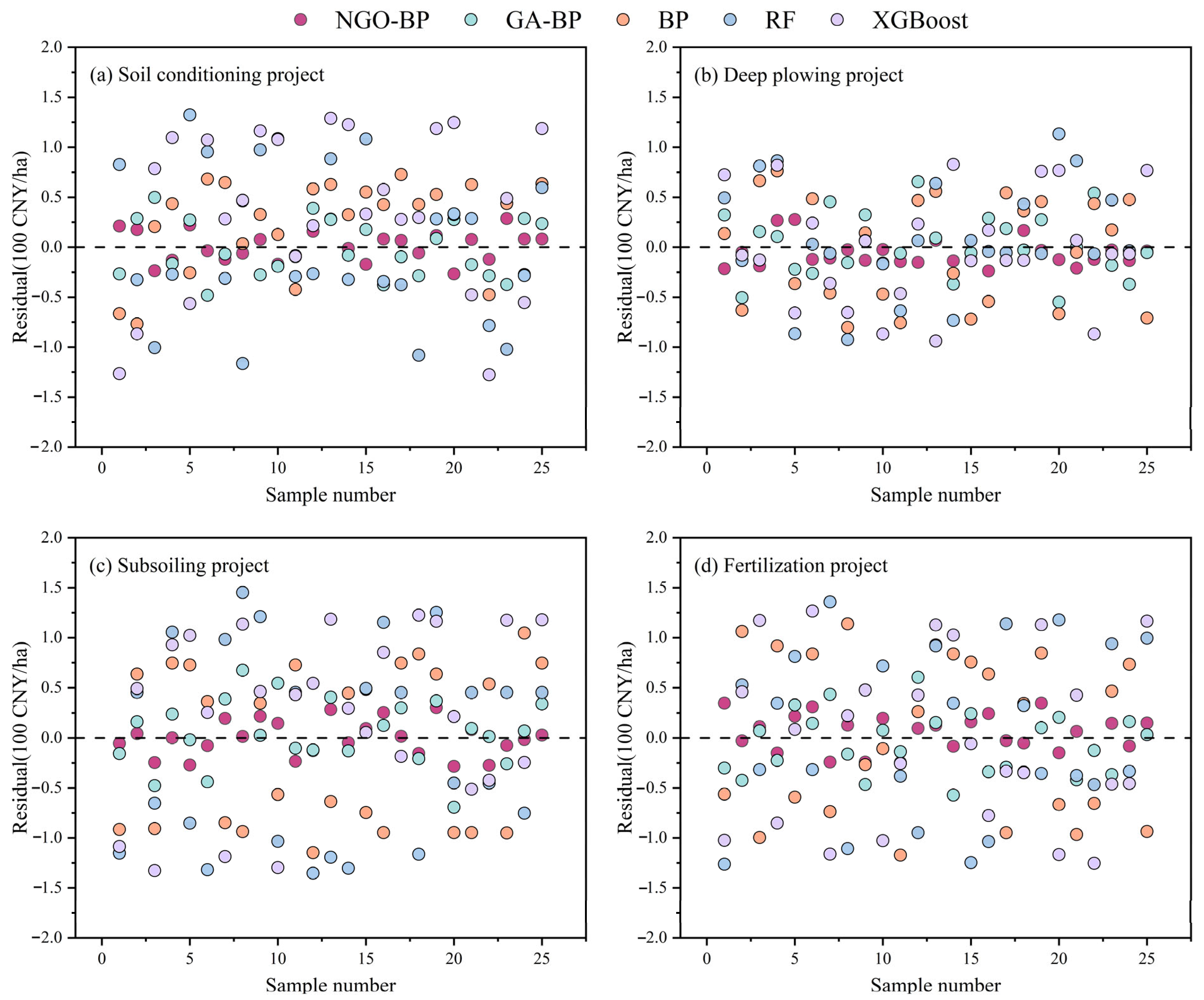
The NGO–BP prediction model developed in this study demonstrated significantly better performance in terms of MAE, RMSE, and R² compared to conventional machine learning models, indicating strong applicability and predictive accuracy. Elmousalami et al. [45] selected factors such as project characteristics, construction location, and duration when designing a cost-influencing factor system. Drawing from similar methodological principles, the present study established a quantifiable framework of cost indicators based on geographic, engineering, and financial dimensions. Due to the initially large number of influencing factors, dimensionality reduction was required to minimize redundancy, reduce computational time, and maintain model accuracy. Zhang et al. [30] developed a BP neural network model to predict coalbed methane content by analyzing the correlation between logging parameters using principal component analysis and Pearson correlation and constructing composite input variables. Their findings confirmed that targeted parameter transformation enhances model efficiency and precision. The application of PCA in the present study similarly improved prediction performance by identifying the most relevant variables. Experimental outcomes confirmed that PCA-based preprocessing substantially increased the accuracy of the NGO–BP model.

Zhang et al. [30] evaluated several prediction models, including KNN, Ridge regression, RF, XGBoost, and BP neural networks, for estimating coalbed methane content. The models were assessed using the coefficient of determination, root mean square error, and relative error. Among these, the BP neural network exhibited the highest prediction accuracy, achieving a relative error of 4.5% and improving prediction precision by approximately 61%. These results demonstrate the BP model’s strong capability to capture variations in coalbed methane content and deliver rapid, accurate predictions. Based on this evidence, the present study adopted BP neural networks [30,36,37], RF [21,22,28], XGBoost [28,30], GA–BP [36], and NGO–BP models for comparative analysis. The results confirm that the NGO–BP model is more suitable for predicting cost indicators in farmland fertility enhancement projects.

In terms of optimization strategies, Li et al. [36] applied a GA to optimize the weights and thresholds of a BP neural network for predicting construction costs in Guangdong Province. The optimized model exhibited a significant performance gain, with an approximate 8% increase in the coefficient of determination, validating the use of GA in enhancing BP models. To further improve predictive accuracy, Chang et al. [37] employed Northern Goshawk Optimization (NGO) to optimize BP neural network parameters and compared its results with those of the GA–BP model. The findings indicated the superior performance of the NGO–BP model, with a 1.6% increase in R² and reductions of 11.6% and 6.34% in RMSE and MAE, respectively. These comparisons validate the advantage of using NGO for optimizing BP neural networks, justifying the selection of GA–BP and NGO–BP models in the present study.

The proposed NGO–BP model enables accurate prediction of differentiated cost indicators for high-standard farmland fertility enhancement projects by incorporating regional and project-specific characteristics. This approach supports evidence-based project management, improves resource allocation, and enhances overall efficiency. By providing reliable cost estimates, the model contributes to national food security goals while promoting ecological sustainability and agricultural modernization. During feasibility assessments, key influencing factors can be entered into the model to generate real-time cost predictions, supporting design optimization and strategic financial planning throughout the construction process.

5. Conclusions and Future Work

5.1. Conclusions

To address the absence of unified standards and the low predictive accuracy of cost indicators in high-standard farmland development projects across regions, this study focused on fertility enhancement projects as a representative case. PCA was applied to identify key influencing factors, forming the basis for constructing a cost prediction model using a NGO–BP neural network. Through systematic factor selection, model comparison, and algorithmic optimization, the NGO–BP model demonstrated high prediction accuracy and strong generalization capabilities. The main conclusions are as follows:

(1)

Based on the engineering characteristics of high-standard farmland construction, influencing factors were selected from the dimensions of project features, geography conditions, and management variables. PCA was employed to extract the most relevant factors, thereby establishing a cost indicator system tailored to fertility enhancement projects. This process significantly contributed to improving the precision of the subsequent predictive modeling.

(2)

Empirical validation indicated that, among the five models tested, including RF, XGBoost, BP, GA–BP, and NGO–BP, the NGO–BP model achieved the lowest error metrics and the highest prediction accuracy. In soil conditioning, deep plowing, subsoiling, and fertilization projects, the NGO–BP model yielded a maximum RMSE of only 98.472 CNY and a maximum MAE of 88.487 CNY, with all R² values exceeding 0.914. The model integrated PCA-based feature selection with NGO-based parameter optimization, resulting in superior predictive performance.

(3)

The NGO–BP prediction model provides a robust tool for estimating the cost of high-standard farmland fertility enhancement projects. It enhances cost control, reduces investment risks, and supports data-driven decision-making. The model offers theoretical and practical value for project evaluation and resource planning, contributing to the realization of agricultural modernization and sustainable rural development.

5.2. Future Work

However, this work has several limitations. Currently focusing on cost indicator prediction for high-standard farmland fertility enhancement projects nationwide, it was validated in soil conditioning, deep plowing, deep loosening, and fertilization projects but has not covered other projects such as residual film removal, straw returning, and green manure rotation. The model emphasizes static engineering parameters, though its architecture supports dynamic expansion. In future research, we will increase project type diversity, integrate time-related variables into the prediction model to further improve model rationality and universality, while enhancing the collection and organization of project-related data, and establish multi-year sample databases to develop cross-year generalization capability, thereby providing theoretical support for the dynamic adjustment of national investment standards.