Machine Learning Prediction of Urban Heat Island Severity in the Midwestern United States
Abstract
1. Introduction
2. Relevant Studies
2.1. Exploring Influential Indicators on UHI
2.2. UHI Intensity Prediction
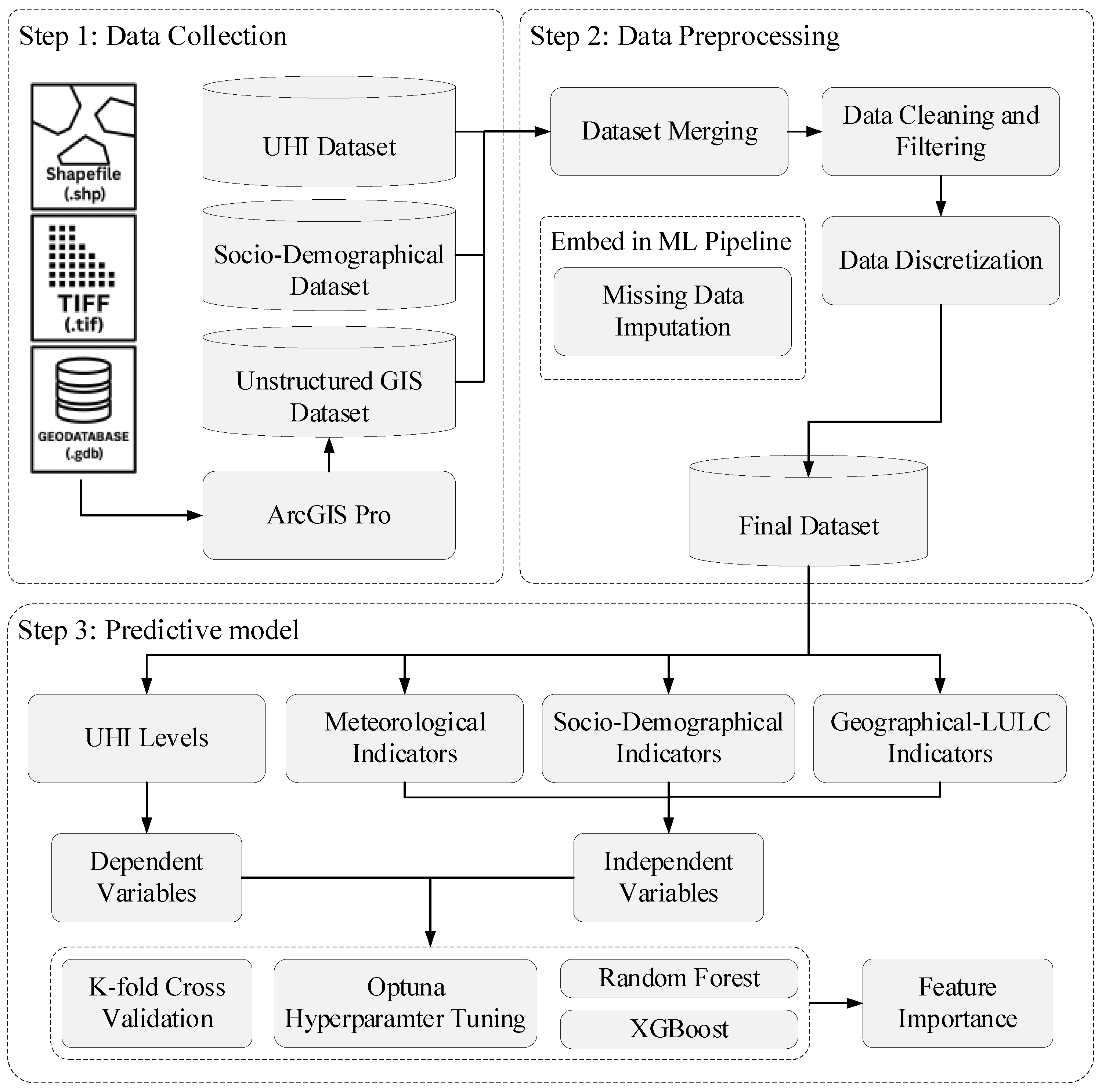
3. Materials and Methods
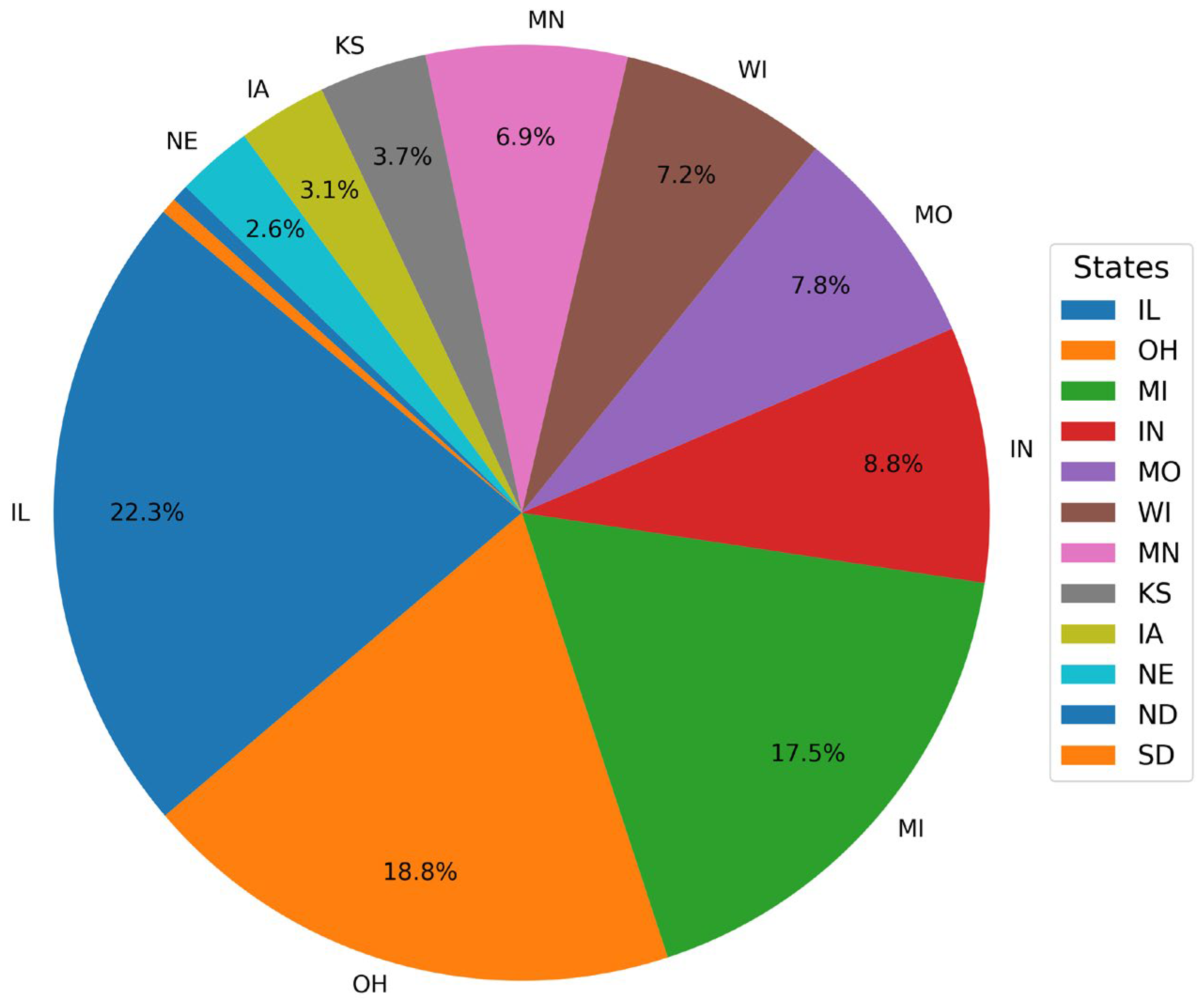
3.1. Data Collection
3.1.1. UHI Dataset
3.1.2. Socio-Demographical Dataset
3.1.3. Unstructured Dataset
- DTC: To calculate DTC, the shapefile of the Earth’s coastline was first imported into the software. Then, geometric centroids of the census tracts were derived based on their polygonal boundaries. Lastly, using the Proximity tool, the closest distance from the centroids to the coastline was calculated.
- IMP and TC: These factors are in TIFF format. After importing them into the software, the Zonal Statistics tool was used to calculate the mean value of their pixels intersecting with the census tracts.
- BA: This factor is in TIFF form and each state had a separate file. After importing the state files, the Zonal Statistics tool was applied to each to calculate the sum of pixel values intersecting the census tracts. These outputs were then merged and added to the Midwestern census tracts layer.
- AR and AT: These factors were in tabular format, containing longitude and latitude of data points. The spatial resolution of these data was coarser than that of census tracts. To address this difference in spatial resolution, we employed the Spatial Join tool within ArcGIS. For the join operation, the CLOSEST match option was selected. This method identifies the single closest AR or AT data point to each census tract polygon and assigns its value accordingly. This technique is functionally a nearest neighbor assignment, chosen for its directness in linking each census tract to the most proximate available measurement.
- BH: These data were obtained in (GDB) format. Like other factors, the data were imported into the software. These data are at the block group level, which is a finer resolution than census tracts. Therefore, the Spatial Join tool was first utilized to assign values from intersecting block groups to each census tract. Second, the Summary Statistics tool was used to average these values for each census tract.
3.2. Data Preprocessing
3.2.1. Dataset Merging
3.2.2. Data Cleaning and Filtering
3.2.3. Data Discretization
3.2.4. Missing Data Handling and Imputation
3.3. Predictive Model and Feature Importance
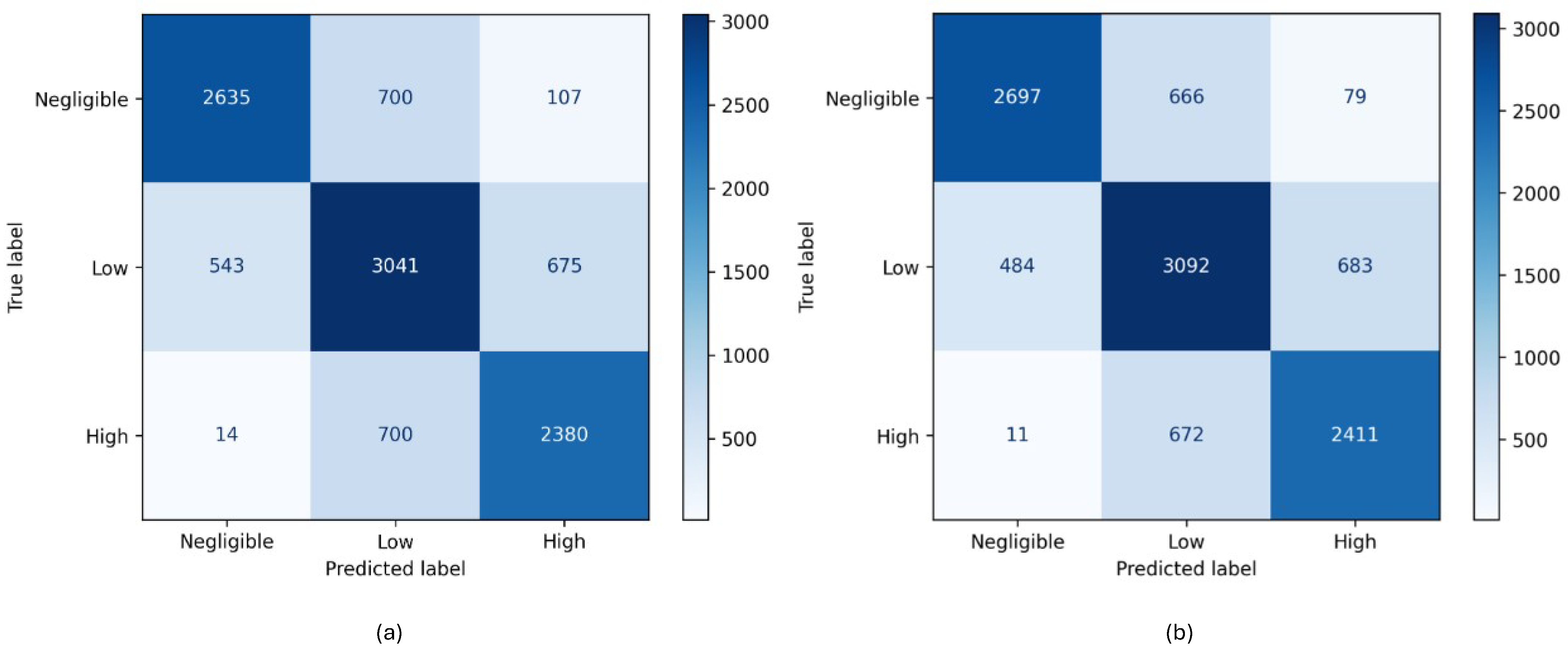
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Hyperparameter Ranges of Models
| Model | Hyperparameter | Range/Values | Distribution/Type |
|---|---|---|---|
| Random Forest | n_estimators | [100, 300] | Integer |
| max_depth | [10, 30] | Integer (Logarithmic) | |
| min_samples_split | [2, 10] | Integer | |
| min_samples_leaf | [1, 10] | Integer | |
| max_features | [‘sqrt’, ‘log2’, None] | Categorical | |
| class_weight | [‘balanced’, ‘balanced_subsample’, None] | Categorical | |
| XGBoost | n_estimators | [50, 500] | Integer (Step: 50) |
| max_depth | [3, 15] | Integer | |
| learning_rate | [0.001, 0.3] | Float (Logarithmic) | |
| subsample | [0.5, 1.0] | Float | |
| colsample_bytree | [0.5, 1.0] | Float | |
| gamma | [0, 5] | Float | |
| min_child_weight | [1, 20] | Integer | |
| reg_alpha (L1) | [1 × 10−8, 1.0] | Float (Logarithmic) | |
| reg_lambda (L2) | [1 × 10−8, 1.0] | Float (Logarithmic) |
Appendix A.2. Label Definitions
| Labels | Definition |
|---|---|
| AR | Mean Annual Rainfall |
| AT | Mean Annual Temperature |
| BH | Average building height |
| DTC | The shortest distance between the centroid of a census tract to its ocean shoreline |
| TC | Tree canopy coverage proportion |
| Impreviousness | Proportion of impervious surface in a census tract |
| LAND_AREA | The tract’s land area, measured in square miles |
| DEM_rur | Mean elevation of the surrounding rural area |
| DEM_urb_CT_act | Mean elevation of urban areas within a census tract |
| DelDEM | Urban–rural elevation difference |
| NDVI_rur | Mean NDVI of the surrounding rural area |
| NDVI_rur_summer | Mean summer NDVI of the rural area |
| NDVI_rur_winter | Mean winter NDVI of the rural area |
| NDVI_urb_CT_act | Mean NDVI of urban areas within a census tract |
| NDVI_urb_CT_act_summer | Mean summer NDVI of urban areas within a census tract |
| NDVI_urb_CT_act_winter | Mean winter NDVI of urban areas within a census tract |
| DelNDVI_annual | Annual urban–rural NDVI difference |
| DeINDVI_summer | Urban–rural NDVI difference in summer |
| DeINDVI_winter | Urban–rural NDVI difference in winter |
| PD | Population density |
| pct_Hispanic_CEN_2020 | Percentage of population identifying as Hispanic or Latino |
| pct_MLT_U10p_ACS_17_21 | Percentage of housing in buildings with 10+ units |
| pct_NH_Asian_alone_CEN_2020 | Percentage of non-Hispanic population identifying as Asian alone |
| pct_NH_Blk_alone_CEN_2020 | Percentage of non-Hispanic population identifying as Black alone |
| pct_NH_White_alone_CEN_2020 | Percentage of non-Hispanic population identifying as White alone |
| pct_RURAL_POP_CEN_2020 | Percentage of population in low-density rural areas |
| pct_URBAN_POP_CEN_2020 | Percentage of population in high-density urban areas |
References
- Du, H.; Wang, D.; Wang, Y.; Zhao, X.; Qin, F.; Jiang, H.; Cai, Y. Influences of Land Cover Types, Meteorological Conditions, Anthropogenic Heat and Urban Area on Surface Urban Heat Island in the Yangtze River Delta Urban Agglomeration. Sci. Total Environ. 2016, 571, 461–470. [Google Scholar] [CrossRef] [PubMed]
- Erfani, A.; Tavakolan, M. Risk Evaluation Model of Wind Energy Investment Projects Using Modified Fuzzy Group Decision-Making and Monte Carlo Simulation. Arthaniti J. Econ. Theory Pract. 2023, 22, 7–33. [Google Scholar] [CrossRef]
- Yang, K.; Zhang, J.; Cui, D.; Ma, Y.; Ye, Y.; He, X.; Zhang, Y. Multi-Scale Study of the Synergy Between Human Activities and Climate Change on Urban Heat Islands in China. Sustain. Cities Soc. 2025, 125, 106341. [Google Scholar] [CrossRef]
- Li, D.; Hu, X.; Rollo, J.; Luther, M.; Lu, M.; Liu, C. Spatial Cluster Characteristics of Land Surface Temperatures. Sustainability 2025, 17, 2653. [Google Scholar] [CrossRef]
- Li, H.; Meier, F.; Lee, X.; Chakraborty, T.; Liu, J.; Schaap, M.; Sodoudi, S. Interaction Between Urban Heat Island and Urban Pollution Island During Summer in Berlin. Sci. Total Environ. 2018, 636, 818–828. [Google Scholar] [CrossRef]
- Piracha, A.; Chaudhary, M.T. Urban Air Pollution, Urban Heat Island and Human Health: A Review of the Literature. Sustainability 2022, 14, 9234. [Google Scholar] [CrossRef]
- Aboelata, A. Vegetation in Different Street Orientations of Aspect Ratio (H/W 1:1) to Mitigate UHI and Reduce Buildings’ Energy in Arid Climate. Build. Environ. 2020, 172, 106712. [Google Scholar] [CrossRef]
- Wang, S.Y.; Ou, H.Y.; Chen, P.C.; Lin, T.P. Implementing Policies to Mitigate Urban Heat Islands: Analyzing Urban Development Factors with an Innovative Machine Learning Approach. Urban Clim. 2024, 55, 101868. [Google Scholar] [CrossRef]
- Rizwan, A.M.; Dennis, L.Y. A Review on the Generation, Determination and Mitigation of Urban Heat Island. J. Environ. Sci. 2008, 20, 120–128. [Google Scholar] [CrossRef]
- U.S. Environmental Protection Agency. Climate Change Indicators: Heat Waves. Available online: https://www.epa.gov/climate-indicators/climate-change-indicators-heat-waves (accessed on 2 May 2025).
- Bao, Y.; Li, Y.; Gu, J.; Shen, C.; Zhang, Y.; Deng, X.; Ran, J. Urban Heat Island Impacts on Mental Health in Middle-Aged and Older Adults. Environ. Int. 2025, 199, 109470. [Google Scholar] [CrossRef]
- He, B.J.; Wang, J.; Liu, H.; Ulpiani, G. Localized Synergies Between Heat Waves and Urban Heat Islands: Implications on Human Thermal Comfort and Urban Heat Management. Environ. Res. 2021, 193, 110584. [Google Scholar] [CrossRef]
- Heaviside, C.; Macintyre, H.; Vardoulakis, S. The Urban Heat Island: Implications for Health in a Changing Environment. Curr. Environ. Health Rep. 2017, 4, 296–305. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Siri, J.G.; Remais, J.V.; Cheng, Q.; Zhang, H.; Chan, K.K.; Gong, P. The Tsinghua–Lancet Commission on Healthy Cities in China: Unlocking the Power of Cities for a Healthy China. Lancet 2018, 391, 2140–2184. [Google Scholar] [CrossRef] [PubMed]
- Foroutan, E.; Hu, T.; Li, Z. Revealing Key Factors of Heat-Related Illnesses Using Geospatial Explainable AI Model: A Case Study in Texas, USA. Sustain. Cities Soc. 2025, 122, 106243. [Google Scholar] [CrossRef]
- Assaf, G.; Hu, X.; Assaad, R.H. Mining and Modeling the Direct and Indirect Causalities Among Factors Affecting the Urban Heat Island Severity Using Structural Machine Learned Bayesian Networks. Urban Clim. 2023, 49, 101570. [Google Scholar] [CrossRef]
- Han, D.; Zhang, T.; Qin, Y.; Tan, Y.; Liu, J. A Comparative Review on the Mitigation Strategies of Urban Heat Island (UHI): A Pathway for Sustainable Urban Development. Clim. Dev. 2023, 15, 379–403. [Google Scholar] [CrossRef]
- Aslani, A.; Sereshti, M.; Sharifi, A. Urban Heat Island Mitigation in Tehran: District-Based Mapping and Analysis of Key Drivers. Sustain. Cities Soc. 2025, 125, 106338. [Google Scholar] [CrossRef]
- Cai, P.; Li, R.; Guo, J.; Xiao, Z.; Fu, H.; Guo, T.; Song, X. Multi-Scale Spatiotemporal Patterns of Urban Climate Effects and Their Driving Factors Across China. Urban Clim. 2025, 60, 102350. [Google Scholar] [CrossRef]
- Petrou, I.; Kassomenos, P. Estimating the Importance of Environmental Factors Influencing the Urban Heat Island for Urban Areas in Greece: A Machine Learning Approach. J. Environ. Manag. 2024, 368, 122255. [Google Scholar] [CrossRef]
- Xu, J.; Jin, Y.; Ling, Y.; Sun, Y.; Wang, Y. Exploring the Seasonal Impacts of Morphological Spatial Pattern of Green Spaces on the Urban Heat Island. Sustain. Cities Soc. 2025, 125, 106352. [Google Scholar] [CrossRef]
- Xu, D.; Wang, Y.; Zhou, D.; Wang, Y.; Zhang, Q.; Yang, Y. Influences of Urban Spatial Factors on Surface Urban Heat Island Effect and Its Spatial Heterogeneity: A Case Study of Xi’an. Build. Environ. 2024, 248, 111072. [Google Scholar] [CrossRef]
- Mathew, A.; Arunab, K.S.; Sharma, A.K. Revealing the Urban Heat Island: Investigating Spatiotemporal Surface Temperature Dynamics, Modeling, and Interactions with Controllable and Non-Controllable Factors. Remote Sens. Appl. Soc. Environ. 2024, 35, 101219. [Google Scholar] [CrossRef]
- Ghorbany, S.; Hu, M.; Yao, S.; Wang, C. Towards a Sustainable Urban Future: A Comprehensive Review of Urban Heat Island Research Technologies and Machine Learning Approaches. Sustainability 2024, 16, 4609. [Google Scholar] [CrossRef]
- Adilkhanova, I.; Ngarambe, J.; Yun, G.Y. Recent Advances in Black Box and White-Box Models for Urban Heat Island Prediction: Implications of Fusing the Two Methods. Renew. Sustain. Energy Rev. 2022, 165, 112520. [Google Scholar] [CrossRef]
- Mansouri, A.; Naghdi, M.; Erfani, A. Machine Learning for Leadership in Energy and Environmental Design Credit Targeting: Project Attributes and Climate Analysis Toward Sustainability. Sustainability 2025, 17, 2521. [Google Scholar] [CrossRef]
- Koc, M.; Acar, A. Investigation of Urban Climates and Built Environment Relations by Using Machine Learning. Urban Clim. 2021, 37, 100820. [Google Scholar] [CrossRef]
- Erfani, A.; Cui, Q. Predictive Risk Modeling for Major Transportation Projects Using Historical Data. Autom. Constr. 2022, 139, 104301. [Google Scholar] [CrossRef]
- Oh, J.W.; Ngarambe, J.; Duhirwe, P.N.; Yun, G.Y.; Santamouris, M. Using Deep-Learning to Forecast the Magnitude and Characteristics of Urban Heat Island in Seoul, Korea. Sci. Rep. 2020, 10, 3559. [Google Scholar] [CrossRef]
- Tanoori, G.; Soltani, A.; Modiri, A. Machine Learning for Urban Heat Island (UHI) Analysis: Predicting Land Surface Temperature (LST) in Urban Environments. Urban Clim. 2024, 55, 101962. [Google Scholar] [CrossRef]
- Assaf, G.; Hu, X.; Assaad, R.H. Predicting Urban Heat Island Severity on the Census-Tract Level Using Bayesian Networks. Sustain. Cities Soc. 2023, 97, 104756. [Google Scholar] [CrossRef]
- Tehrani, A.A.; Veisi, O.; Delavar, Y.; Bahrami, S.; Sobhaninia, S.; Mehan, A. Predicting Urban Heat Island in European Cities: A Comparative Study of GRU, DNN, and ANN Models Using Urban Morphological Variables. Urban Clim. 2024, 56, 102061. [Google Scholar] [CrossRef]
- Hoang, N.D.; Nguyen, Q.L. Geospatial Analysis and Machine Learning Framework for Urban Heat Island Intensity Prediction: Natural Gradient Boosting and Deep Neural Network Regressors with Multisource Remote Sensing Data. Sustainability 2025, 17, 4287. [Google Scholar] [CrossRef]
- Dong, X.; Yu, Z.; Cao, W.; Shi, Y.; Ma, Q. A Survey on Ensemble Learning. Front. Comput. Sci. 2020, 14, 241–258. [Google Scholar] [CrossRef]
- Lyu, F.; Wang, S.; Han, S.Y.; Catlett, C.; Wang, S. An Integrated CyberGIS and Machine Learning Framework for Fine-Scale Prediction of Urban Heat Island Using Satellite Remote Sensing and Urban Sensor Network Data. Urban Inform. 2022, 1, 6. [Google Scholar] [CrossRef]
- Hashemi, F.; Najafian, P.; Salahi, N.; Ghiasi, S.; Passe, U. The Impact of the Urban Heat Island and Future Climate on Urban Building Energy Use in a Midwestern US Neighborhood. Energies 2025, 18, 1474. [Google Scholar] [CrossRef]
- Kim, M.; Lee, K.; Cho, G.H. Temporal and Spatial Variability of Urban Heat Island by Geographical Location: A Case Study of Ulsan, Korea. Build. Environ. 2017, 126, 471–482. [Google Scholar] [CrossRef]
- Acosta, M.P.; Vahdatikhaki, F.; Santos, J.; Hammad, A.; Dorée, A.G. How to Bring UHI to the Urban Planning Table? A Data-Driven Modeling Approach. Sustain. Cities Soc. 2021, 71, 102948. [Google Scholar] [CrossRef]
- Singh, M.; Sharston, R.; Murtha, T. Critical Evaluation of the Spatiotemporal Behavior of UHI, Through Correlation Analyses Based on Multi-City Heterogeneous Dataset. Sustain. Cities Soc. 2024, 110, 105576. [Google Scholar] [CrossRef]
- Ngarambe, J.; Oh, J.W.; Su, M.A.; Santamouris, M.; Yun, G.Y. Influences of Wind Speed, Sky Conditions, Land Use and Land Cover Characteristics on the Magnitude of the Urban Heat Island in Seoul: An Exploratory Analysis. Sustain. Cities Soc. 2021, 71, 102953. [Google Scholar] [CrossRef]
- Zheng, Z.; Lin, X.; Chen, L.; Yan, C.; Sun, T. Effects of Urbanization and Topography on Thermal Comfort During a Heat Wave Event: A Case Study of Fuzhou, China. Sustain. Cities Soc. 2024, 102, 105233. [Google Scholar] [CrossRef]
- Hidalgo-García, D.; Arco-Díaz, J. Modeling the Surface Urban Heat Island (SUHI) to Study Its Relationship with Variations in the Thermal Field and with the Indices of Land Use in the Metropolitan Area of Granada (Spain). Sustain. Cities Soc. 2022, 87, 104166. [Google Scholar] [CrossRef]
- Xu, Z.; Rui, J. The Mitigating Effect of Green Space’s Spatial and Temporal Patterns on the Urban Heat Island in the Context of Urban Densification: A Case Study of Xi’an. Sustain. Cities Soc. 2024, 117, 105974. [Google Scholar] [CrossRef]
- Patel, S.; Indraganti, M.; Jawarneh, R.N. Land Surface Temperature Responses to Land Use Dynamics in Urban Areas of Doha, Qatar. Sustain. Cities Soc. 2024, 104, 105273. [Google Scholar] [CrossRef]
- Deilami, K.; Kamruzzaman, M.; Liu, Y. Urban Heat Island Effect: A Systematic Review of Spatio-Temporal Factors, Data, Methods, and Mitigation Measures. Int. J. Appl. Earth Obs. Geoinf. 2018, 67, 30–42. [Google Scholar] [CrossRef]
- Cetin, M.; Ozenen Kavlak, M.; Senyel Kurkcuoglu, M.A.; Bilge Ozturk, G.; Cabuk, S.N.; Cabuk, A. Determination of Land Surface Temperature and Urban Heat Island Effects with Remote Sensing Capabilities: The Case of Kayseri, Türkiye. Nat. Hazards 2024, 120, 5509–5536. [Google Scholar] [CrossRef]
- Yoo, S. Investigating Important Urban Characteristics in the Formation of Urban Heat Islands: A Machine Learning Approach. J. Big Data 2018, 5, 2. [Google Scholar] [CrossRef]
- Mehmood, M.S.; Rehman, A.; Sajjad, M.; Song, J.; Zafar, Z.; Shiyan, Z.; Yaochen, Q. Evaluating Land Use/Cover Change Associations with Urban Surface Temperature via Machine Learning and Spatial Modeling: Past Trends and Future Simulations in Dera Ghazi Khan, Pakistan. Front. Ecol. Evol. 2023, 11, 1115074. [Google Scholar] [CrossRef]
- Thambawita, T.K.C.N.; Munasinghe, D.S.; Yapa, L.K.K. Identification of Urban Heat Island Effect on Land Use Land Cover Changes. J. Geospat. Surv. 2023, 3, 43–53. [Google Scholar] [CrossRef]
- Ullah, S.; Khan, M.; Qiao, X. Evaluating the Impact of Urbanization Patterns on LST and UHI Effect in Afghanistan’s Cities: A Machine Learning Approach for Sustainable Urban Planning. Environ. Dev. Sustain. 2025, 1–42. [Google Scholar] [CrossRef]
- Hickey, P.J.; Erfani, A.; Cui, Q. Use of LinkedIn Data and Machine Learning to Analyze Gender Differences in Construction Career Paths. J. Manag. Eng. 2022, 38, 04022060. [Google Scholar] [CrossRef]
- Chaturvedi, V.; de Vries, W.T. Machine Learning Algorithms for Urban Land Use Planning: A Review. Urban Sci. 2021, 5, 68. [Google Scholar] [CrossRef]
- Casali, Y.; Aydin, N.Y.; Comes, T. Machine Learning for Spatial Analyses in Urban Areas: A Scoping Review. Sustain. Cities Soc. 2022, 85, 104050. [Google Scholar] [CrossRef]
- Equere, V.; Mirzaei, P.A.; Riffat, S.; Wang, Y. Integration of Topological Aspect of City Terrains to Predict the Spatial Distribution of Urban Heat Island Using GIS and ANN. Sustain. Cities Soc. 2021, 69, 102825. [Google Scholar] [CrossRef]
- O’Malley, C.; Piroozfar, P.; Farr, E.R.; Pomponi, F. Urban Heat Island (UHI) Mitigating Strategies: A Case-Based Comparative Analysis. Sustain. Cities Soc. 2015, 19, 222–235. [Google Scholar] [CrossRef]
- Mohammad, P.; Goswami, A.; Chauhan, S.; Nayak, S. Machine Learning Algorithm Based Prediction of Land Use Land Cover and Land Surface Temperature Changes to Characterize the Surface Urban Heat Island Phenomena Over Ahmedabad City, India. Urban Clim. 2022, 42, 101116. [Google Scholar] [CrossRef]
- Lin, J.; Qiu, S.; Tan, X.; Zhuang, Y. Measuring the Relationship Between Morphological Spatial Pattern of Green Space and Urban Heat Island Using Machine Learning Methods. Build. Environ. 2023, 228, 109910. [Google Scholar] [CrossRef]
- Guo, L.; Du, S.; Sun, W.; Fan, D.; Wu, Y. Multi-Scale Impact of Urban Building Function and 2D/3D Morphology on Urban Heat Island Effect: A Case Study in Shanghai, China. Energy Build. 2025, 338, 115719. [Google Scholar] [CrossRef]
- Hong, T.; Yim, S.H.; Heo, Y. Interpreting Complex Relationships Between Urban and Meteorological Factors and Street-Level Urban Heat Islands: Application of Random Forest and SHAP Method. Sustain. Cities Soc. 2025, 126, 106353. [Google Scholar] [CrossRef]
- Qiao, Z.; Jia, R.; Liu, J.; Gao, H.; Wei, Q. Remote Sensing-Based Analysis of Urban Heat Island Driving Factors: A Local Climate Zone Perspective. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 17337. [Google Scholar] [CrossRef]
- Global Climate Monitor. Available online: https://www.globalclimatemonitor.org/ (accessed on 2 May 2025).
- Chakraborty, T.C.; Hsu, A.; Sheriff, G.; Manya, D. United States Surface Urban Heat Island Database. Mendeley Data 2020, V3. Available online: https://doi.org/10.17632/x9mv4krnm2.3 (accessed on 2 May 2025).
- Multi-Resolution Land Characteristics Consortium (MRLC). Dataset Type: Tree Canopy. Available online: https://www.mrlc.gov/data?f%5B0%5D=category%3ATree%20Canopy&f%5B1%5D=region%3Aconus&f%5B2%5D=year%3A2020 (accessed on 2 May 2025).
- Multi-Resolution Land Characteristics Consortium (MRLC). Dataset Type: Impervious Descriptor. Available online: https://www.mrlc.gov/data?f%5B0%5D=category%3AImpervious%20Descriptor&f%5B1%5D=region%3Aconus&f%5B2%5D=year%3A2020 (accessed on 2 May 2025).
- Heris, M.P.; Foks, N.; Bagstad, K.; Troy, A. A National Dataset of Rasterized Building Footprints for the U.S. U.S. Geological Survey Data Release 2020. Available online: https://doi.org/10.5066/P9J2Y1WG (accessed on 2 May 2025).
- Department of the Interior. U.S. National Categorical Mapping of Building Heights by Block Group from Shuttle Radar Topography Mission Data. Available online: https://catalog.data.gov/dataset/u-s-national-categorical-mapping-of-building-heights-by-block-group-from-shuttle-radar-top (accessed on 2 May 2025).
- Natural Earth. 1:10m Physical Vectors. 2023. Available online: https://www.naturalearthdata.com/downloads/10m-physical-vectors/ (accessed on 2 May 2025).
- U.S. Census Bureau. Planning Database. 2023. Available online: https://www.census.gov/topics/research/guidance/planning-databases.2023.html#list-tab-1219258324 (accessed on 2 May 2025).
- U.S. Census Bureau. TIGER/Line Shapefiles. 2023. Available online: https://www.census.gov/geographies/mapping-files/time-series/geo/tiger-line-file.2023.html#list-tab-790442341 (accessed on 2 May 2025).
- Lin, M.; Dong, J.; Jones, L.; Liu, J.; Lin, T.; Zuo, J.; Ye, H.; Zhang, G.; Zhou, T. Modeling Green Roofs’ Cooling Effect in High-Density Urban Areas Based on Law of Diminishing Marginal Utility of the Cooling Efficiency: A Case Study of Xiamen Island, China. J. Clean. Prod. 2021, 316, 128277. [Google Scholar] [CrossRef]
- Little, R.J.A.; Rubin, D.B. Statistical Analysis with Missing Data; John Wiley & Sons: Hoboken, NJ, USA, 2019; Available online: https://books.google.com/books?id=BemMDwAAQBAJ&lpg=PR11&ots=FCDO82DT1V&dq=Statistical%20Analysis%20with%20Missing%20Data%20(3rd%20ed.)&lr&pg=PR3#v=onepage&q=Statistical%20Analysis%20with%20Missing%20Data%20(3rd%20ed.)&f=false (accessed on 2 May 2025).
- Junninen, H.; Niska, H.; Tuppurainen, K.; Ruuskanen, J.; Kolehmainen, M. Methods for Imputation of Missing Values in Air Quality Data Sets. Atmos. Environ. 2004, 38, 2895–2907. [Google Scholar] [CrossRef]
- Adnan, T.; Erfani, A.; Cui, Q. Paving Equity: Unveiling Socioeconomic Patterns in Pavement Conditions Using Data Mining. J. Manag. Eng. 2025, 41, 04025041. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Wong, T.T.; Yeh, P.Y. Reliable Accuracy Estimates from k-Fold Cross Validation. IEEE Trans. Knowl. Data Eng. 2019, 32, 1586–1594. [Google Scholar] [CrossRef]
- Vujović, Ž. Classification Model Evaluation Metrics. Int. J. Adv. Comput. Sci. Appl. 2021, 12, 599–606. [Google Scholar] [CrossRef]
- Li, L.; Erfani, A.; Wang, Y.; Cui, Q. Anatomy into the Battle of Supporting or Opposing Reopening Amid the COVID-19 Pandemic on Twitter: A Temporal and Spatial Analysis. PLoS ONE 2021, 16, e0254359. [Google Scholar] [CrossRef]
- Erfani, A.; Cui, Q. Natural language processing application in construction domain: An integrative review and algorithms comparison. Comput. Civ. Eng. 2021, 2021, 26–33. Available online: https://ascelibrary.org/doi/abs/10.1061/9780784483893.004 (accessed on 2 May 2025).
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-Generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar] [CrossRef]
- Erfani, A.; Shayesteh, N.; Adnan, T. Data Augmented Explainable AI for Pavement Roughness Prediction. Autom. Constr. 2025, 176, 106307. [Google Scholar] [CrossRef]





| Factor Name | Frequency |
|---|---|
| Building Height | 10 |
| Imperviousness | 9 |
| Air Temperature | 9 |
| NDVI | 8 |
| Water Area Ratio | 7 |
| Building Area | 6 |
| Precipitation | 6 |
| Wind Speed | 6 |
| Elevation | 5 |
| Population Density | 5 |
| Building Density | 4 |
| Commercial Area | 4 |
| Night Lights | 4 |
| Population | 4 |
| Road Length | 4 |
| Humidity | 4 |
| Industrial Area | 4 |
| Tree Canopy | 4 |
| Land Area | 3 |
| Building Volume | 3 |
| Surface Roughness | 3 |
| Factor Category | Frequency |
|---|---|
| Land Use/Land Cover (LULC) | 104 |
| Meteorological | 41 |
| Socio-economic Demographical | 31 |
| Other | 30 |
| Geographical | 23 |
| Reference | Data Size | Geospatial Focus | Model |
|---|---|---|---|
| Guo et al. 2025 [58] | - | Shanghai, China | Random Forest—Regression |
| Hong et al. 2025 [59] | 568 | Seoul, South Korea | Random Forest—Regression |
| Xu et al. 2025 [21] | 7020 | Nanjing, China | Random Forest—Regression |
| Xu et al. 2024 [22] | 2732 | Xi’an, China | Random Forest—Regression |
| Wang et al. 2024 [8] | 1168 | Taichung City, Taiwan | Decision Tree—Classification |
| Mathew et al. 2024 [23] | - | Bangalore and Hyderabad, India | Random Forest/XGBoost—Regression |
| Yang et al. 2025 [3] | - | China | XGBoost—Regression |
| Aslani et al. 2025 [18] | - | Tehran, Iran | Random Forest—Regression |
| Petrou et al. 2024 [20] | 39,925 | Athens and Thessaloniki, Greece | Random Forest—Regression |
| Qiao et al. 2024 [60] | - | 369 Cities in China | XGBoost—Regression |
| Assaf et al. 2023 [16] | 1313 | New Jersey, United States | Tree-Augmented Bayesian Network—Classification |
| Assaf et al. 2023 [31] | 1457 | New Jersey, United States | Tree-Augmented Bayesian Network—Classification |
| Category | Group Name | Abbreviation | Number of Factors | Source |
|---|---|---|---|---|
| Meteorological factors | Mean Annual Temperature | AT | 1 | Global Climate Monitor, 2020 [61] |
| Mean Annual Rainfall | AR | 1 | Global Climate Monitor, 2020 [61] | |
| Geographical–LULC factors | Digital Elevation Model (Urban and Rural) | DEM | 2 | Chakraborty et al., 2020 [62] |
| Urban and Rural Digital Elevation Model Difference | DelDEM | 1 | Chakraborty et al., 2020 [62] | |
| NDVI (Urban and Rural) (Annual, Summer and Winter) | NDVI | 6 | Chakraborty et al., 2020 [62] | |
| Urban and Rural NDVI Difference (Annual, Summer and Winter) | DelNDVI | 3 | Chakraborty et al., 2020 [62] | |
| Tree Canopy | TC | 1 | Multi-Resolution Land Characteristics Consortium (MLRC), 2020 [63] | |
| Imperviousness | IMP | 1 | Multi-Resolution Land Characteristics Consortium (MLRC), 2020 [64] | |
| Building Area | BA | 1 | Heris et al. 2020 [65] | |
| Building Height | BH | 1 | Department of the Interior [66] | |
| Distance to Coast | DTC | 1 | Natural Earth. 2023 [67] | |
| Land Area | LA | 1 | U.S. Census Bureau [68] | |
| Socio-demographical factors | Population | P | 3 | U.S. Census Bureau [69] |
| Population Density | PD | 1 | U.S. Census Bureau [69] | |
| Age | AG | 7 | U.S. Census Bureau [69] | |
| Gender | G | 2 | U.S. Census Bureau [69] | |
| Ethnicity | ET | 8 | U.S. Census Bureau [69] | |
| Education level | EL | 3 | U.S. Census Bureau [69] | |
| Health Insurance Coverage | HIC | 3 | U.S. Census Bureau [69] | |
| Employment Status | ES | 2 | U.S. Census Bureau [69] | |
| Household Income | HI | 2 | U.S. Census Bureau [69] | |
| Housing Price | HP | 2 | U.S. Census Bureau [69] | |
| Housing Units | HU | 7 | U.S. Census Bureau [69] | |
| Access to Computers and the Internet | ACI | 7 | U.S. Census Bureau [69] | |
| Number of Persons per Household | NPH | 2 | U.S. Census Bureau [69] |
| UHI Level | Range | Distribution (%) |
|---|---|---|
| Negligible | −1 ≤ UHI < 1 | 31.9% |
| Low | 1 ≤ UHI < 3 | 39.4% |
| High | 3 ≤ UHI | 28.7% |
| Random Forrest | XGBoost | ||
|---|---|---|---|
| Parameter | Optimum Value | Parameter | Optimum Value |
| n_estimators | 151 | n_estimators | 150 |
| max_depth | 24 | max_depth | 9 |
| min_samples_split | 7 | learning_rate | 0.073 |
| min_samples_leaf | 2 | subsample | 0.857 |
| max_features | None | colsample_bytree | 0.666 |
| class_weight | None | gamma | 0.463 |
| imputer_n_neighbors | 12 | min_child_weight | 8 |
| reg_alpha | 3.31 × 10−3 | ||
| reg_lambda | 4.67 × 10−6 |
| Model | Class | Precision | Recall | F1-Score | Sample Count |
|---|---|---|---|---|---|
| Random Forrest | Negligible | 0.83 | 0.77 | 0.79 | 3442 |
| Low | 0.68 | 0.71 | 0.7 | 4259 | |
| High | 0.75 | 0.77 | 0.76 | 3094 | |
| Accuracy | - | - | 0.75 | 10,795 | |
| Macro avg | 0.75 | 0.75 | 0.75 | 10,795 | |
| Weighted avg | 0.75 | 0.75 | 0.75 | 10,795 | |
| Cohen’s Kappa * | - | - | 0.62 | - | |
| ROC-AUC * | - | - | 0.9 | - | |
| XGBoost | Negligible | 0.84 | 0.78 | 0.81 | 3442 |
| Low | 0.7 | 0.73 | 0.71 | 4259 | |
| High | 0.76 | 0.78 | 0.77 | 3094 | |
| Accuracy | - | - | 0.76 | 10,795 | |
| Macro avg | 0.77 | 0.76 | 0.76 | 10,795 | |
| Weighted avg | 0.76 | 0.76 | 0.76 | 10,795 | |
| Cohen’s Kappa * | - | - | 0.64 | - | |
| ROC-AUC * | - | - | 0.91 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mansouri, A.; Erfani, A. Machine Learning Prediction of Urban Heat Island Severity in the Midwestern United States. Sustainability 2025, 17, 6193. https://doi.org/10.3390/su17136193
Mansouri A, Erfani A. Machine Learning Prediction of Urban Heat Island Severity in the Midwestern United States. Sustainability. 2025; 17(13):6193. https://doi.org/10.3390/su17136193
Chicago/Turabian StyleMansouri, Ali, and Abdolmajid Erfani. 2025. "Machine Learning Prediction of Urban Heat Island Severity in the Midwestern United States" Sustainability 17, no. 13: 6193. https://doi.org/10.3390/su17136193
APA StyleMansouri, A., & Erfani, A. (2025). Machine Learning Prediction of Urban Heat Island Severity in the Midwestern United States. Sustainability, 17(13), 6193. https://doi.org/10.3390/su17136193






