Game Analysis Between Manufacturer and Retailer Under Carbon Tax Policy

Abstract

Considering consumers’ low-carbon preferences, this article analyzes a manufacturer’s price and carbon abatement strategies, as well as a retailer’s price and promotion strategies, in a centralized game, where the manufacturer and the retailer jointly make decisions, and a decentralized game, where the two parties each make decisions simultaneously. This study discusses the impact of the carbon abatement cost coefficient, promotion cost coefficient, sensitivity coefficient of consumer demand to carbon abatement rate or promotion rate, or carbon tax rate on the manufacturer’s carbon abatement rate, commodity’s retail price, and retailer’s promotion rate. This article also discusses the impact of any one of the main parameters on supply chain profit. Through comparisons of the above two games, this article concludes that the former is better than the latter for firms, consumers, and the environment. This article also concludes that a reduction in the carbon abatement cost coefficient, a rise in the sensitivity coefficient of consumer demand to the carbon abatement rate, or a rise in the carbon tax rate increases the manufacturer’s optimal carbon abatement rate. A relatively high carbon abatement rate means relatively low CO₂ emissions, which are environmentally friendly and conducive to sustainable development at the ecological level. The foregoing conclusions provide governments with references for making carbon tax policies and also offer firms references for making decisions.

1. Introduction

Since 1990, the Intergovernmental Panel on Climate Change (hereinafter referred to as IPCC) has conducted six assessments on the issue of global climate change successively and has published assessment reports. According to the AR6 Synthesis Report: Climate Change 2023, published by IPCC in March 2023, “Human activities, principally through emissions of greenhouse gases, have unequivocally caused global warming” [1]. Global warming may cause many kinds of climate issues, for example, a rise in sea level and frequent occurrences of extreme weather, which are detrimental to the sustainable development of human beings. To cope with these climate issues and realize the sustainable development goals of human beings, governments have made efforts and approved many contracts. The “United Nations Framework Convention on Climate Change” (hereinafter referred to as UNFCCC) has established the ultimate goal and the international cooperation principles responding to climate change, for instance, principles of sustainable development, equity, and so on. The “Kyoto Protocol” has set the greenhouse gas abatement goal of the countries of Annex B and proposed that the developed countries can use “emission trade”, “joint implementation”, as well as “clean development mechanism” as supplementary measures to fulfill carbon abatement obligations. The “Paris Agreement” has set the global long-term temperature rise target. The 29th Conference of the Parties of the UNFCCC, held from 11–22 November 2024, in Baku, Azerbaijan, has achieved the “Baku Climate Unity Pact”. In this context, carbon abatement actions are bound to have complex and far-reaching impacts on the world economic situation and international trade relations.

In countries with weaker environmental regulations, social marginal costs are greater than firms’ production costs, meaning that these production processes can lead to negative externalities. There are two main ways to solve the above problem: one is the Coase Theorem, and the other is the Pigouvian Taxes. The former is a quantity-based mechanism, such as a carbon trading policy. The latter is a price-based mechanism, for example, a carbon tax policy. Grubb et al. [2] conclude that there are multiple positive interactions between carbon pricing and low-carbon innovation. From the perspective of institutional economics, levying a carbon tax on firms based on the degree of harm caused by carbon emissions is helpful in internalizing environmental costs. From the perspective of ecological modernization, the levying of a carbon tax provides firms with opportunities for innovation.

With the acceleration of economic globalization, competition among firms continues to intensify. More and more firms tend to focus on their core businesses, outsource other businesses to other advantageous firms, and improve the competitiveness of their product. Competition exists in various firms as well as various supply chains. Upstream and downstream firms are supposed to work together with each other, exploit their advantages, and make their supply chain more competitive. Due to the concern about climate change, more and more attention is paid to low-carbon supply chain management.

The research on low-carbon supply chain management is mainly based on different low-carbon policies, such as the carbon tax policy [3,4], carbon trading policy [5], carbon subsidy policy [6], and the hybrid policy [7], to study the strategy choices [8] and contract optimization [9,10] of upstream and downstream firms. Some researchers take into account consumers’ low-carbon preferences [11,12] and fairness preferences of upstream and downstream firms [13,14], and other research has focused on the optimal carbon tax [15], the dynamic carbon tax policy [16], carbon verification mechanisms [17], and the impact of carbon tax policy [18,19]. Yu et al. [20] studied the low-carbon supply chain strategy choices based on carbon tax policy and found that policymakers could guide firms to make better emission abatement decisions through reasonable carbon tax policy, which is an effective solution to reduce the negative externalities. Xia et al. [21] considered the impact of the carbon trading policy on different products. Chen et al. [22] found that compared with subsidies, imposing a carbon tax is more effective.

In summary, most of the existing literature does not consider low-carbon policies. Some scholars consider low-carbon policies, but most of them are based on carbon trading policies, and there are relatively few studies on carbon tax policies.

Building upon prior research, the article here delves into the research of the supply chain composed of two parties: a manufacturer and a retailer. Consumers’ low-carbon preferences and carbon tax policy are taken into account in this study. It compares the equilibrium strategies of both parties in a centralized game, where both parties jointly make decisions, and in a decentralized game, where both parties each make decisions simultaneously, and discusses the relevant parameters’ impacts on the strategies of both parties. First, this article concludes that for the manufacturer, the retailer, the consumers and the environment, the centralized decision-making scenario is better than the decentralized decision-making scenario, resulting in a greater supply chain profit, a lower retail price of the commodity, and a greater carbon abatement rate. Second, this article concludes that a rise in the sensitivity coefficient of consumer demand to the manufacturer’s carbon abatement rate, a reduction in the manufacturer’s carbon abatement cost coefficient, or a rise in carbon tax rate increases the manufacturer’s optimal carbon abatement rate, indicating that the carbon abatement rate can be increased through decreasing the carbon abatement difficulty from the manufacturer, increasing consumers’ low-carbon preferences through the consumers, or raising the carbon tax rate imposed by the government. Therefore, the efforts of all these parties will bring about environmental improvement, which, in turn, will contribute to achieving sustainable development goals. Third, through numerical simulation, we conclude that a rise in the carbon tax rate leads to an increase in the retail price of the commodity and a decrease in the supply chain profit. The government’s carbon tax policy should balance the environmental and economic development aspects.

The remainder of this article proceeds as follows. Section 2 describes the problem. Section 3 solves the problem, compares the results, and provides a numerical simulation. Section 4 concludes the article.

2. Methodology

2.1. Problem Description and Symbol Explanation

Figure 1 shows the structure of the supply chain.

During the process of the manufacturer’s production, emissions such as CO₂ are brought about, causing negative externalities and deterring sustainable development. The manufacturer can reduce these externalities by increasing the carbon abatement rate. The retailer can achieve promotional goals by increasing advertising investment. The government levies a tax on the product for emission abatement. Consumers have low-carbon preferences. This article analyzes the equilibrium strategies of the manufacturer and the retailer and considers two game scenarios: one is a centralized game, where both parties jointly make decisions (represented by C), and the other is a decentralized game, where the manufacturer and retailer each make decisions simultaneously (represented by N).

Table 1. Explanation of symbols.

Variable Types	Decision Variables		Non-Decision Variables
Manufacturer	$w$: Wholesale price per unit product	$p=w+m$: Retail price per unit commodity	$C_M$: Manufacturer’s carbon abatement cost
			${\pi }_M$: Manufacturer’s profit
	$x$: Carbon abatement rate		$e$: The amount of CO2 per unit product before carbon abatement
			$t$: The carbon tax rate levied by the government on per unit CO2 emissions
Retailer	$m$: Marginal profit per unit commodity		$C_R$: Retailer’s promotion cost
			${\pi }_R$: Retailer’s profit
	$y$: Promotion rate		$Q$: Consumer demand
			${\pi }_{SC}$: Supply chain profit

shows an explanation of the symbols.

The centralized game and the decentralized game are both static games with complete information. The normal-form representation of a game specifies the following: (1) the players in the game, (2) the strategies available to each player, and (3) the payoff received by each player for each combination of strategies that could be chosen by the players [23]. First, regarding the players, there are two players in the centralized game: a manufacturer and a retailer. As the two players make decisions jointly, it could also be understood as there being one player in the centralized game, and the supply chain is composed of a manufacturer and a retailer. In the decentralized game, there are two players: a manufacturer and a retailer. Second, regarding the strategies, the manufacturer and the retailer jointly decide the retail price $p$, carbon abatement rate $x$, and promotion rate $y$ in the centralized game; in other words, the supply chain is composed of a manufacturer and a retailer who decide on $p$, $x$, and $y$. In the decentralized game, the manufacturer decides the wholesale price $w$ and carbon abatement rate $x$, and the retailer decides the marginal profit $m$ and promotion rate $y$. Third, regarding the payoffs, in the centralized game, the supply chain’s payoff is ${\pi }_{SC}$. In the decentralized game, the manufacturer’s payoff is ${\pi }_M$, and the retailer’s payoff is ${\pi }_R$.

We denote the centralized game as $G^C=\{S_{SC};{\pi }_{SC}\}$ and the decentralized game as $G^N=\{S_M,S_R;{\pi }_M,{\pi }_R\}$. Among them, $S_{SC}$ is the set of strategies available to the supply chain composed of a manufacturer and a retailer in the centralized game, $S_M$ is the set of strategies available to the manufacturer in the decentralized game, and $S_R$ is the set of strategies available to the retailer in the decentralized game.

2.2. Model Assumptions

For the convenience of model solving, the following assumptions are made:

• Consumer demand rises with the rise in the manufacturer’s carbon abatement rate or retailer’s promotion rate but decreases with the increase in retail price per unit commodity. And we have $Q=a-bp+\alpha x+\beta y$; among them, $a$ represents market capacity, $b$, $\alpha$, and $\beta$ represent the sensitivity coefficients of consumer demand to the commodity’s retail price, manufacturer’s carbon abatement rate, and retailer’s promotion rate, respectively, and $a>0$, $b>0$, $\alpha >0$, and $\beta >0$.
• The manufacturer implements carbon abatement measures to increase its carbon abatement rate, such as adopting efficient carbon abatement technologies, and pays the carbon abatement cost. This cost increases with the increase in $x$, that is $\mathsf{\partial }{C}_M/\mathsf{\partial }x>0$, and the increase shows an accelerating trend, that is ${\mathsf{\partial }}^2{C}_M/\mathsf{\partial }{x}^2>0$. The article here supposes that $C_M(x)=1/2h{x}^2$, where $h$ represents the manufacturer’s carbon abatement cost coefficient.
• The retailer increases their promotion rate by increasing advertising investment. Similarly to the carbon abatement cost of the manufacturer, the article here supposes that $C_R(y)=1/2n{y}^2$, where $n$ represents the retailer’s promotion cost coefficient.
• Within a sales cycle, the possible inventory cost and shortage cost of the product are out of consideration.
• The manufacturer and retailer have complete information, and both parties are rational players in the game.
• For the simplification of the model, the article here supposes that the manufacturer’s production cost equals 0.

In a word, the profits are given by Equation (1):

$$\left\{\begin{array}{l}{\pi }_M=[w-e(1-x)t]Q-C_M\\ {\pi }_R=mQ-C_R\\ {\pi }_{SC}={\pi }_M+{\pi }_R\end{array}\right.$$

(1)

3. Results and Discussion

3.1. Model Solutions

3.1.1. A Centralized Scenario

Assuming that in the market, a manufacturer and a retailer trust each other and jointly make carbon abatement, price, and promotion decisions to maximize ${\pi }_{SC}$. The optimization problem is to maximize ${\pi }_{SC}$ when $p$ is between 0 and $a/b$, $x$ is between 0 and 1, and $y$ is between 0 and 1.

And the first-order derivatives of the above optimization problem with $x$, $p$ and $y$ can be set to 0 to obtain the equilibrium solutions. For the simplification of expressions, we set $A_1=h({\beta }^2-2bn)+n{(\alpha +bet)}^2$, $A_2=\alpha +bet$, $A_3=bet-a$, $A_4={\beta }^2-bn$, $A_5=2\alpha et-h$, and $A_6=et$.

The Hessian matrix is $H_1=\left(\begin{array}{ccc}{A}_5& 2\alpha -A_2& \beta A_6\\ 2\alpha -A_2& -2b& \beta \\ \beta A_6& \beta & -n\end{array}\right)$. And when $A_5<0$, $2bh-A_2^2>0$ and $A_1<0$ are met, $H_1$ is negative definite. We have

$$\left\{\begin{array}{l}{x}^{C^{\ast }}={\displaystyle \frac{n{A}_2{A}_3}{A_1}}\\ p^{C^{\ast }}={\displaystyle \frac{an(A_2{A}_6-h)+A_6(h{A}_4+\alpha n{A}_2)}{A_1}}\\ y^{C^{\ast }}={\displaystyle \frac{\beta h{A}_3}{A_1}}\end{array}\right.$$

(2)

and

$${\pi }_{SC}^{C^{\ast }}=-{\displaystyle \frac{hn{A}_3^2}{2A_1}}$$

(3)

3.1.2. A Decentralized Scenario

When a manufacturer and a retailer each make decisions simultaneously, the manufacturer’s optimization problem is to maximize ${\pi }_M$ when $w$ is between 0 and $a/b-m$, and $x$ is between 0 and 1. The retailer’s optimization problem is to maximize ${\pi }_R$ when $m$ is between 0 and $a/b-w$, and $y$ is between 0 and 1.

The first-order derivatives of the manufacturer’s optimization problem and the retailer’s optimization problem with $w$, $x$, $m$, and $y$ can be set to 0 to obtain the equilibrium solutions.

The manufacturer’s optimization problem’s Hessian matrix is $H_2=\left(\begin{array}{cc}-2b& 2\alpha -A_2\\ 2\alpha -A_2& A_5\end{array}\right)$, and when $2bh-A_2^2>0$ is met, $H_2$ is negative definite. The Hessian matrix of the retailer’s optimization problem is $H_3=\left(\begin{array}{cc}-2b& \beta \\ \beta & -n\end{array}\right)$, and when $A_4-bn<0$ is met, $H_3$ is negative definite. For the simplification of expressions, we set $B_1=h({\beta }^2-3bn)+n{(\alpha +bet)}^2$. We have

$$\left\{\begin{array}{l}{w}^{N^{\ast }}={\displaystyle \frac{A_6[h(A_4-bn)+\alpha n{A}_2]+an(A_2{A}_6-h)}{B_1}}\\ x^{N^{\ast }}={\displaystyle \frac{n{A}_2{A}_3}{B_1}}\\ m^{N^{\ast }}={\displaystyle \frac{hn{A}_3}{B_1}}\\ y^{N^{\ast }}={\displaystyle \frac{h\beta A_3}{B_1}}\\ p^{N^{\ast }}=w^{N\ast }+m^{N^{\ast }}={\displaystyle \frac{an(A_2{A}_6-2h)+A_6(h{A}_4+\alpha n{A}_2)}{B_1}}\end{array}\right.$$

(4)

and

$$\left\{\begin{array}{l}{\pi }_M^{N^{\ast }}=-{\displaystyle \frac{h{n}^2{A}_3^2(A_2^2-2bh)}{2B_1^2}}\\ {\pi }_R^{N^{\ast }}=-{\displaystyle \frac{h^{2}n{A}_3^2(A_4-bn)}{2B_1^2}}\\ {\pi }_{SC}^{N^{\ast }}=-{\displaystyle \frac{hn{A}_3^2[h(A_4-3bn)+n{A}_2^2]}{2B_1^2}}\end{array}\right.$$

(5)

3.2. Model Analyses

3.2.1. The Comparisons of the Optimal Carbon Abatement Rates and Supply Chain Profits in the Two Games

Comparing Equations (2) and (4), there is

$$x^{N^{\ast }}-x^{C^{\ast }}={\displaystyle \frac{bh{n}^2{A}_2{A}_3}{A_1{B}_1}}<0$$

(6)

Thus, we obtain $x^{C^{\ast }}>x^{N^{\ast }}$. And thus, $p^{C^{\ast }}<p^{N^{\ast }}$, $y^{C^{\ast }}>y^{N^{\ast }}$, and ${\pi }_{SC}^{C^{\ast }}>{\pi }_{SC}^{N^{\ast }}$.

Proposition 1. 

In the decentralized game, the manufacturer’s optimal carbon abatement rate, the retailer’s optimal promotion rate, and the supply chain’s optimal profit are lower than those in the centralized game. The commodity’s optimal retail price in the decentralized game is higher than that in the centralized game. Thus, the centralized game is better for the firms, consumers, and the environment than the decentralized game.

Proposition 1 is consistent with Aust et al. [24], and it may be due to the effect of double marginalization [25]. The double marginalization effect generally exists in decentralized games and leads to higher prices and lower profits than those in centralized games. In the article here, the manufacturer and the retailer make decisions with the goal of maximizing their respective profits in the decentralized game, and they aim to maximize the supply chain profit in the centralized game. This is also the reason why the centralized game is better for the manufacturer, the retailer, and consumers with a lower retail price, greater supply chain profit, greater carbon abatement rate, and greater promotion rate than the decentralized game.

Proposition 1 suggests that the manufacturer and the retailer can cooperate to make decisions, resulting in increased profits for both parties compared to the decentralized game. Compared with the decentralized game, the carbon abatement rate is greater in the centralized game, which means lower CO₂ emissions in the production process, less damage to the environment, and more conducive to the realization of sustainable development of human beings.

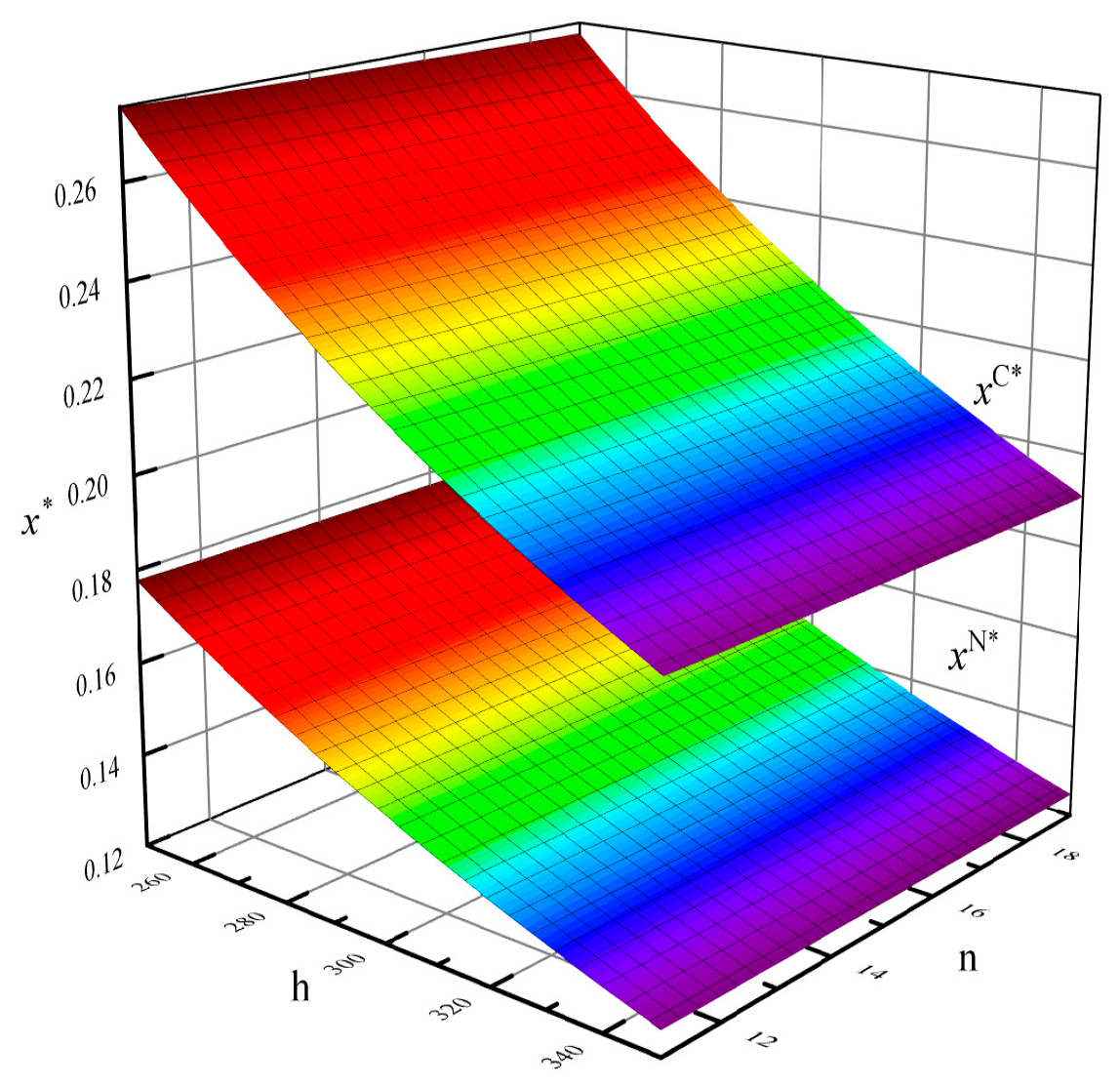
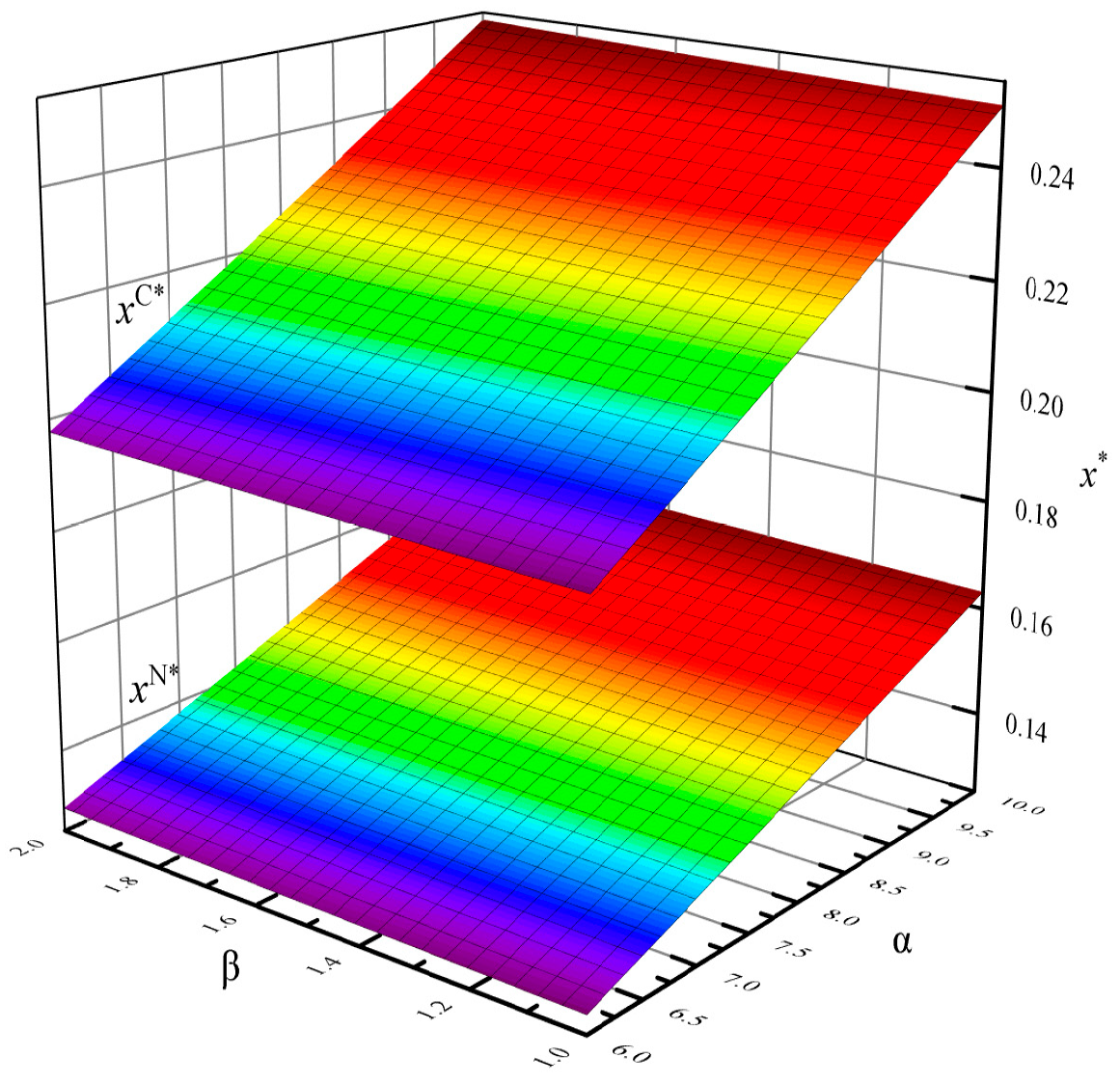
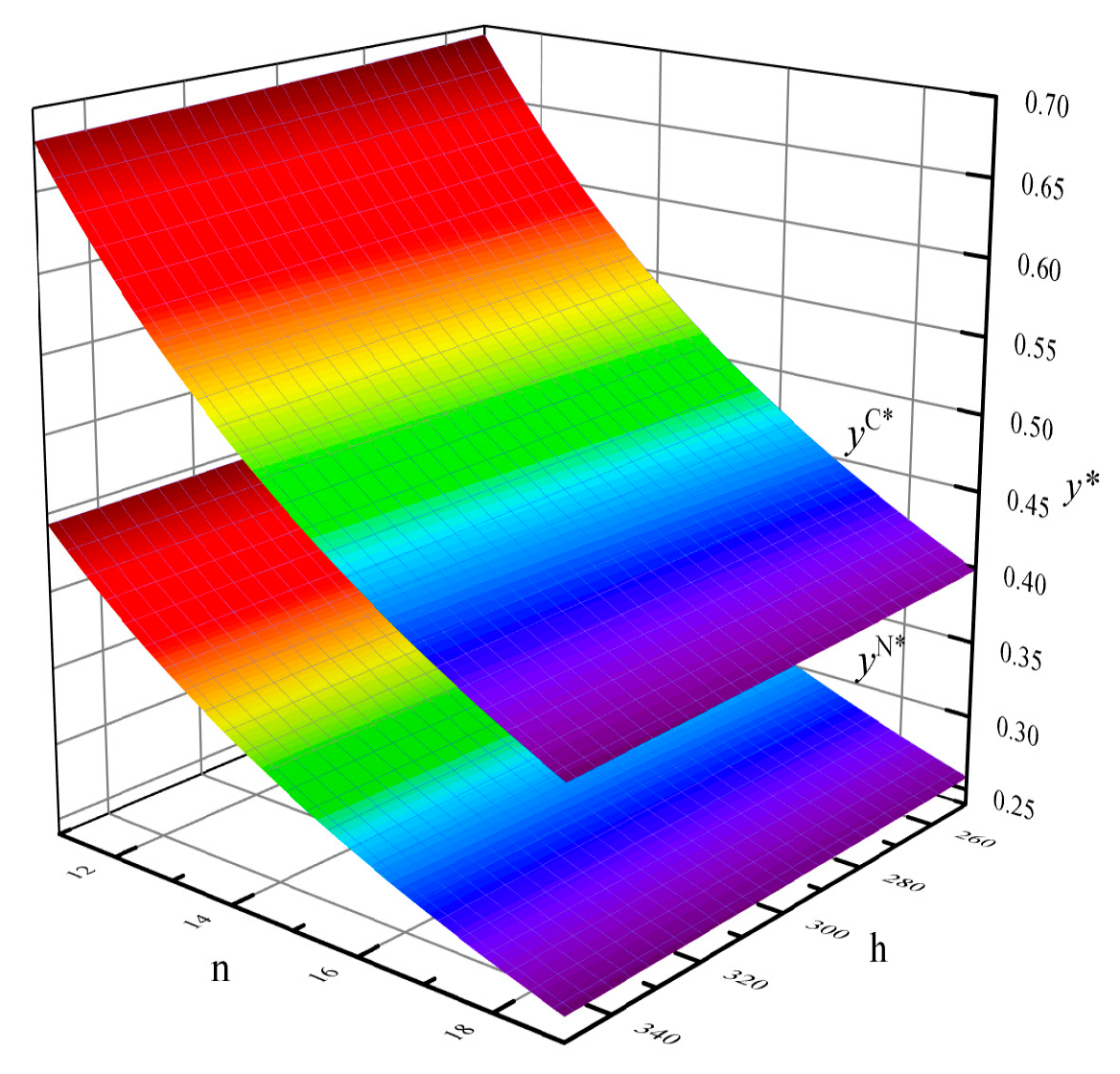
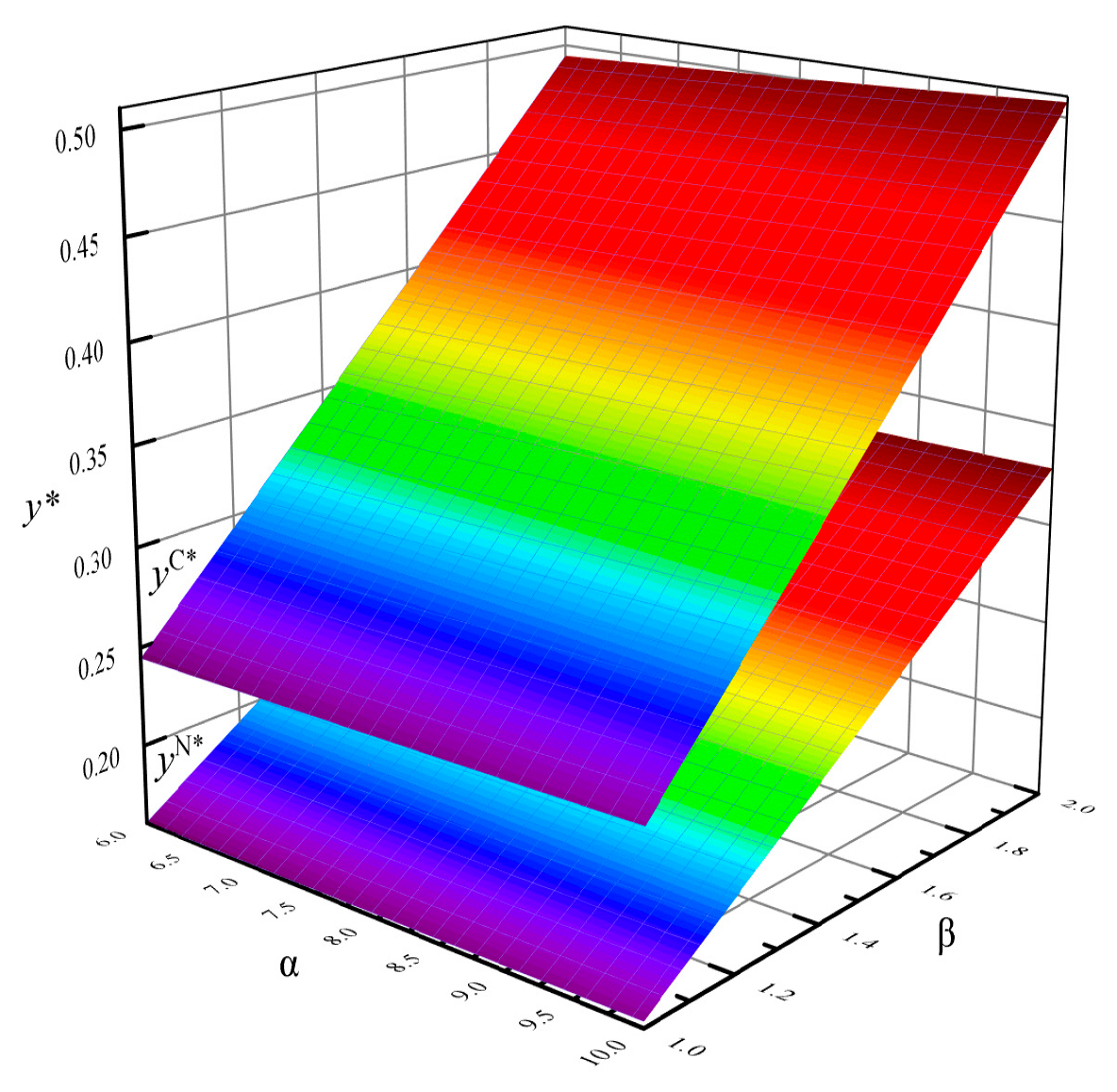
3.2.2. Sensitivity Analyses

(1)

The sensitivity analyses of the optimal carbon abatement rates

From Equation (2), we obtain

$$\mathsf{\partial }{x}^{C^{\ast }}/\mathsf{\partial }h=-{\displaystyle \frac{n(A_4-bn)A_2{A}_3}{A_1^2}}<0$$

(7)

And so, $\mathsf{\partial }{x}^{C^{\ast }}/\mathsf{\partial }n<0$, $\mathsf{\partial }{x}^{C^{\ast }}/\mathsf{\partial }\alpha >0$, and $\mathsf{\partial }{x}^{C^{\ast }}/\mathsf{\partial }\beta >0$. For the equilibrium solutions in the decentralized game, the same results can be obtained. In summary, we have $\mathsf{\partial }{x}^{\ast }/\mathsf{\partial }h<0$, $\mathsf{\partial }{x}^{\ast }/\mathsf{\partial }n<0$, $\mathsf{\partial }{x}^{\ast }/\mathsf{\partial }\alpha >0$, and $\mathsf{\partial }{x}^{\ast }/\mathsf{\partial }\beta >0$.

Because of the complicated expressions of the first-order derivatives of $x^{C^{\ast }}$ and $x^{N^{\ast }}$ to $t$, we will discuss the impact of $t$ on $x^{\ast }$ in Section 3.3.2, and so the impacts of $t$ on $p^{\ast }$, $y^{\ast }$, and ${\pi }_{SC}^{\ast }$.

Proposition 2. 

In the two games, the optimal carbon abatement rate decreases as the cost coefficient of carbon abatement or promotion increases, while it increases with the increase in the sensitivity coefficient of consumer demand to the carbon abatement rate or the promotion rate.

Proposition 2 suggests that the manufacturer can be encouraged to increase its carbon abatement rate by lowering the carbon abatement cost coefficient (for example, adopting new abatement technologies to improve efficiency or being provided with some preferential policies to continue reducing CO₂ emissions) and promoting low-carbon and environmental protection concepts to enhance consumers’ low-carbon preferences. When the manufacturer increases its carbon abatement rate, the CO₂ emissions from the process of production decrease. The lower the CO₂ emissions caused by human activities, the less harmful they are to the environment. This environmentally friendly behavior will promote the realization of the sustainable development goals of human beings.

(2)

The sensitivity analyses of the optimal retail prices

Because of the complicated expressions of the first-order derivatives of $p^{\ast }$ to $t$, we will discuss the impact of $t$ on $p^{\ast }$ in Section 3.3.2.

(3)

The sensitivity analyses of the optimal promotion rates

By solving the first-order derivatives of $y^{C^{\ast }}$ and $y^{N^{\ast }}$ to $h$, $n$, $\alpha$ and $\beta$, we obtain $\mathsf{\partial }{y}^{\ast }/\mathsf{\partial }h<0$, $\mathsf{\partial }{y}^{\ast }/\mathsf{\partial }n<0$, $\mathsf{\partial }{y}^{\ast }/\mathsf{\partial }\alpha >0$, and $\mathsf{\partial }{y}^{\ast }/\mathsf{\partial }\beta >0$.

Proposition 3. 

In the two games, a reduction in the cost coefficient of carbon abatement or promotion causes a rise in the retailer’s optimal promotion rate. A rise in the sensitivity coefficient of consumer demand to the carbon abatement rate or promotion rate also causes a rise in the retailer’s optimal promotion rate.

Proposition 3 suggests that the retailer can be encouraged to increase its promotion rate by lowering the promotion cost coefficient (for example, using effective ways to promote its commodity or being provided with some preferential measures to continue increasing promotion expenses). The more sensitive the consumer demand is to the promotion rate, the more likely the retailer is to raise it

(4)

The sensitivity analyses of the optimal supply chain profits

For equilibrium solutions, there are $\mathsf{\partial }{\pi }_{SC}^{\ast }/\mathsf{\partial }h<0$, $\mathsf{\partial }{\pi }_{SC}^{\ast }/\mathsf{\partial }n<0$, $\mathsf{\partial }{\pi }_{SC}^{\ast }/\mathsf{\partial }\alpha >0$, and $\mathsf{\partial }{\pi }_{SC}^{\ast }/\mathsf{\partial }\beta >0$. In the centralized game, we obtain $\mathsf{\partial }{\pi }_{SC}^{C^{\ast }}/\mathsf{\partial }t<0$.

Proposition 4. 

Within the two games, the cost coefficient of carbon abatement or promotion shows a negative influence on the supply chain profits, meaning that as one of the two coefficients increases, the supply chain profits decrease. The sensitivity coefficient of consumer demand to carbon abatement rate or promotion rate shows a positive influence on the supply chain profits, meaning that as one of the two sensitivity coefficients increases, the supply chain profits rise. In the centralized game, the carbon tax rate affects the optimal supply chain profit negatively.

Proposition 4 suggests that levying the carbon tax may hurt the optimal supply chain profit in the centralized game when a manufacturer and retailer jointly make decisions.

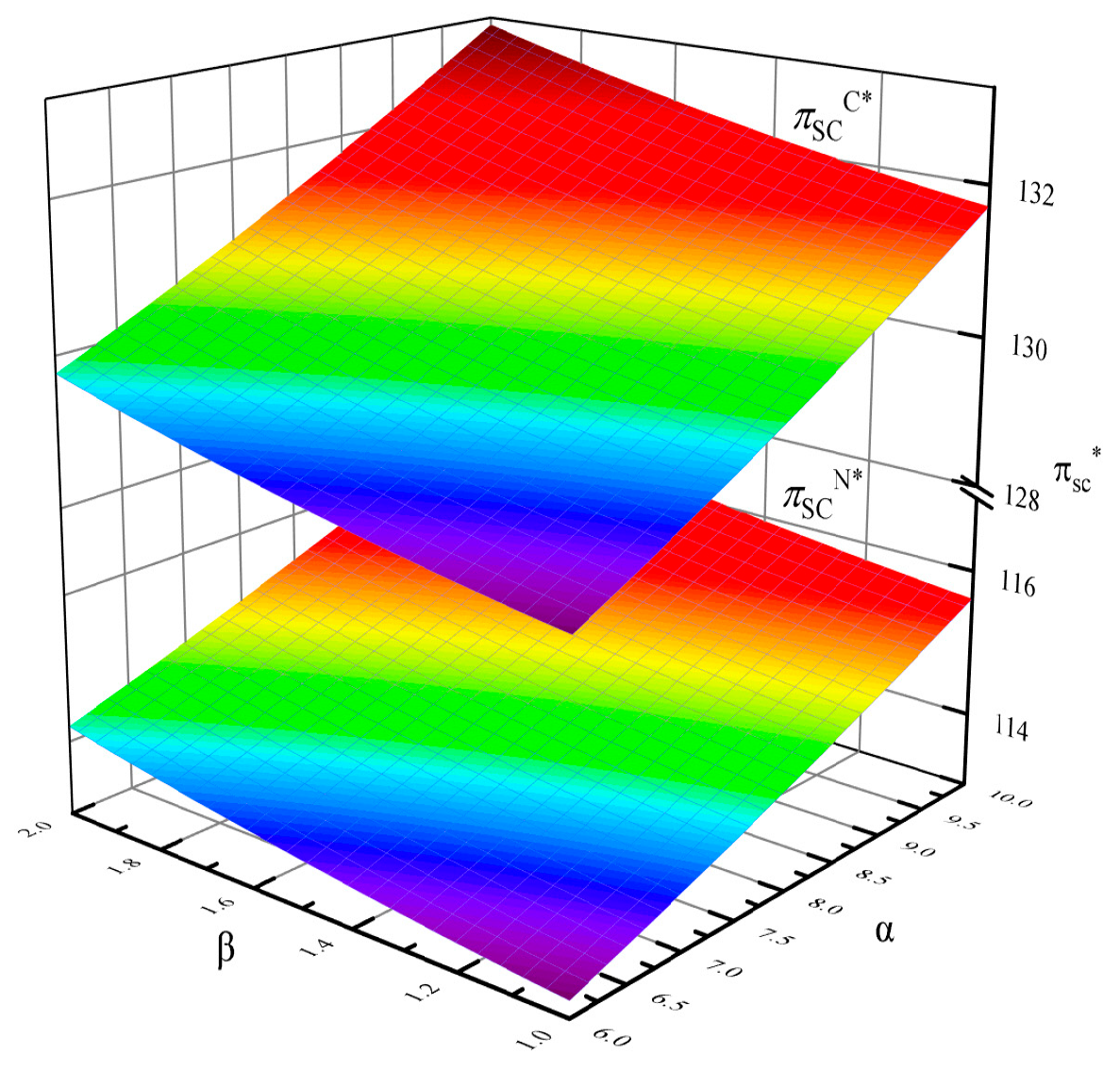
3.3. Numerical Simulations

To illustrate the above propositions graphically and analyze the impacts of carbon tax rates on the optimal carbon abatement rates, promotion rates, retail prices, and supply chain profits in the two games, we need to set the values of the parameters. There are two methods to set the parameters: first, according to the constraints, randomly valuing the parameters by using software or manually [24,26]. Second, according to the constraints, valuing some parameters by referring to the real-world data [27]. Carbon tax rates levied by countries have a broad range, between USD 0.08 per ton of CO₂ equivalent (CO₂e) in Poland and USD 129.89 in Sweden [19]. In the article here, we assume that $t=50$. Referring to the constraints, other parameters’ values are set as illustrated below.

3.3.1. The Comparisons of the Optimal Carbon Abatement Rates and Supply Chain Profits in the Two Games

For $a=80$, $b=10$, $\alpha =8$, $\beta =2$, $h=300$, $n=15$, $e=0.02$, and $t=50$, we compare the optimal carbon abatement rates, promotion rates, retail prices, and supply chain profits in the two scenarios, as shown in

Table 2. The comparisons of the optimal carbon abatement rates, promotion rates, retail prices, and supply chain profits in the two games.

Game Types	${\mathit{x}}^{\ast }$	${\mathit{p}}^{\ast }$	${\mathit{y}}^{\ast }$	${\mathit{\pi }}_{\mathit{S}\mathit{C}}^{\ast }$
The centralized game where the manufacturer and the retailer jointly make decisions (C)	0.22516	4.52752	0.500357	131.344
The decentralized game where the manufacturer and the retailer each make decisions simultaneously (N)	0.14658	5.73941	0.325733	115.346

.

3.3.2. Sensitivity Analyses

(1)

The sensitivity analyses of the optimal carbon abatement rates

When analyzing one or two specific parameters’ impact, the values of other parameters are the same as in Section 3.3.1.

As shown in Figure 2, it can be seen that when other parameters remain unchanged, the manufacturer’s optimal carbon abatement rates in the two games show downward trends as the cost coefficient of carbon abatement or promotion increases. As shown in Figure 3, it can be seen that when other parameters remain unchanged, the manufacturer’s optimal carbon abatement rates in the two games show upward trends as the sensitivity coefficient of consumer demand to carbon abatement rate or promotion rate increases.

As shown in Figure 4, when other parameters remain unchanged, the manufacturer’s optimal carbon abatement rates in the two games increase as the carbon tax rate increases. This indicates that imposing a certain proportion of carbon tax helps the manufacturer to be more proactive in carbon abatement decisions. The reason may be that the manufacturer’s CO₂ emission cost rises when the carbon tax rate rises. When the marginal cost of CO₂ emissions exceeds that of carbon abatement, the manufacturer finds it more beneficial to invest in carbon abatement research rather than to maintain high CO₂ emissions, and the manufacturer increases the carbon abatement rates. From Figure 2, Figure 3 and Figure 4, the manufacturer’s optimal carbon abatement rate in the centralized game is greater than that in the decentralized game.

In summary, there are three ways to increase the manufacturer’s carbon abatement rate: the first is decreasing the carbon abatement cost, the second is increasing the sensitivity coefficient of consumer demand to the carbon abatement rate, and the third is imposing a certain carbon tax rate. A high carbon abatement rate means a low amount of CO₂ emissions, and correspondingly, the greenhouse gas emissions decrease, reducing the negative impact on the environment and promoting sustainable development.

(2)

The sensitivity analyses of the optimal retail prices

From Figure 4, an increase in the carbon tax rate increases the commodity’s optimal retail prices in the two games.

(3)

The sensitivity analyses of the optimal promotion rates

As shown in Figure 5, a decrease in the carbon abatement or promotion cost coefficient increases the optimal promotion rates. As shown in Figure 6, a rise in the sensitivity coefficient of consumer demand to carbon abatement rate or promotion rate leads to increases in the optimal promotion rates. From Figure 4, as the carbon tax rate rises, the optimal promotion rates in the two games decrease.

(4)

The sensitivity analyses of the optimal supply chain profits

Figure 7 shows that a decrease in the carbon abatement or promotion cost coefficient causes a rise in the optimal supply chain profits. Figure 8 shows that a rise in the sensitivity coefficient of consumer demand to carbon abatement rate or promotion rate causes a rise in the optimal supply chain profits. Figure 4 shows that the optimal supply chain profits within the two games present downward trends when the carbon tax rate increases.

4. Conclusions

The main contribution of this article lies in analyzing the price, carbon abatement, and promotion strategies of one manufacturer and one retailer in a centralized game, where the manufacturer and the retailer make decisions jointly, and a decentralized game, where the manufacturer and the retailer each make decisions simultaneously. Carbon tax policy is taken into account in the article here. Because consumers pay more and more attention to climate change issues, consumers’ low-carbon preferences are also taken into consideration in the article here. After comparing the two games, the article here concludes that the centralized game is better than the decentralized game for firms, consumers, and the environment. This article also provides a detailed analysis of the main parameters’ impacts on the key decision variables. This article concludes that a certain amount of carbon tax levied by the government could encourage manufacturers to increase their optimal carbon abatement rates, thereby reducing the adverse impact of human activities on the environment, which is conducive to sustainable development. However, the increase in the carbon tax rate raises the retail price of the commodity and reduces the supply chain profit. The government should set an appropriate carbon tax rate to balance the impact on the environment and the economy. These findings provide theoretical support for carbon tax levying and offer another method to increase the manufacturer’s optimal carbon abatement rate. An increase in consumers’ low-carbon preferences can inspire the manufacturer to raise its optimal carbon abatement rate. Our research findings in this article can help firms with their decision-making and increase the international competitiveness of their products, which has a positive impact on export trade.

According to the conclusions drawn from the article here, the following suggestions are proposed: Firstly, referring to experiences of the international carbon tax levy, the government should start levying a certain rate of carbon tax on some heavily polluting industries to increase their CO₂ emission costs and encourage the manufacturer to increase carbon abatement rate. Secondly, the government can enhance the consumers’ preferences for low-carbon lifestyles to provide the manufacturer with incentives to reduce CO₂ emissions through some measures, such as popularizing environmental protection knowledge and raising public awareness of low-carbon development. Thirdly, the manufacturer and the retailer can improve the optimal supply chain profit by cooperating with each other.

The article here assumes that only the retailer has a promotion cost, but in reality, the manufacturer also uses promotion methods to make its product more attractive to consumers. Therefore, in the future, we can assume that the manufacturer also has a promotion cost and study the cooperation between the manufacturer and retailer on promotion. The article here only studies games under the carbon tax policy, and in the future, we can consider the game scenarios under the hybrid policy. Additionally, for the simplification of the model-solving process, we make some assumptions in the article here, such as consumers’ linear demand function, all consumers having the same low-carbon preferences, perfect rationality of the players, complete information of the games, and the like. In the future, we will break down these assumptions one by one to make the model more in line with the real economy.