Green Hydrogen Supply Chain Decision-Making and Contract Optimization Under Uncertainty: A Pessimistic-Based Perspective

Abstract

To address the issue of excessive pessimism caused by demand and supply uncertainties in the green hydrogen supply chain, this study develops a two-tier green hydrogen supply chain model comprising upstream hydrogen production stations and downstream hydrogen refueling stations. This research work investigates optimal ordering and production strategies under stochastic demand and supply conditions. Additionally, option contracts are introduced to share the risks associated with the stochastic output of green hydrogen. This study shows the following: (1) Under decentralized decision-making, the optimal ordering quantity when the hydrogen refueling station is excessively pessimistic is not necessarily lower than the optimal ordering quantity when it is in a rational state, and hydrogen production stations will only operate when the degree of excessive pessimism is relatively low. (2) The initial option ordering quantity is always larger than the minimum execution quantity under the option contract; higher first-order option prices and lower second-order option prices can help to increase the initial option ordering quantity. (3) The option contract is effective in circumventing the negative impact of excessive pessimism at hydrogen production stations on planned production quantities. This study addresses the gap in the existing research regarding excessively pessimistic behaviors and the application of option contracts within the green hydrogen supply chain, providing both theoretical insights and practical guidance for decision-making optimization. This advancement further promotes the sustainable development of the green hydrogen industry.

1. Introduction

As a zero-carbon secondary energy source made from renewable energy, green hydrogen has become a key factor in realizing China’s “dual-carbon” goal [1]. With the breakthroughs in key technologies such as proton exchange membrane electrolyzer technology and off-grid hydrogen system integration, green hydrogen is reshaping the pattern of China’s energy system [1]. In March 2022, the National Development and Reform Commission and the National Energy Administration jointly issued the “Medium- and Long-Term Plan for the Development of Hydrogen Industry (2021–2035)”, which clarifies the key tasks for China’s green hydrogen industry in terms of technological breakthroughs, industrial layout, infrastructure construction, application promotion, etc., and calls for the realization of a green hydrogen production capacity of 100,000–200,000 tons/year by 2025 [2]. The production of green hydrogen relies on renewable energy sources such as wind and solar energy and is widely recognized as an important trend in the future development of hydrogen energy [3]. Although green hydrogen has significant environmental advantages, the high price of electrolyzer equipment and the instability of renewable energy tariffs lead to its high cost (about USD 3–4/kg), while wind and solar energy are subject to weather and seasonal influences, which leads to unstable power supply and also affects the stability of the output of green hydrogen. In contrast, gray hydrogen, with its low cost (about USD 1.5–2.5/kg) and mature technology [4], is still the current mainstream form of hydrogen produced industrially; blue hydrogen, with its carbon capture technology (CCUS), reduces carbon emissions while maintaining a lower cost (about USD 2–3/kg), making it a transitional solution [5].

The high cost of green hydrogen means that it struggles to compete economically with gray and blue hydrogen, and although technological advances and policy support have provided the impetus for its development, uncertainty regarding its market acceptance and return on investment in the short term has led to excessive pessimism on the part of many green hydrogen producers and sellers [6]. This excessive pessimism stems from concerns about the commercialization of green hydrogen, especially with gray and blue hydrogen still holding a major market share [7]. Although the cost of green hydrogen is expected to decrease, meaning that it will gradually replace gray and blue hydrogen in the long run, this current dilemma causes some companies to be cautious about the future development of green hydrogen. This excessive pessimism may affect the ordering and production decisions of actors in the green hydrogen supply chain [8]. Taking the deviation index of production volume versus sales as an example, which is calculated as the difference between monthly production and monthly sales divided by monthly sales, a persistent negative deviation indicates that production consistently lags behind sales, reflecting a conservative market demand outlook and an excessively pessimistic mindset within the enterprise. Similarly, for the demand forecast conservativeness coefficient, defined as the ratio of the enterprise’s demand forecast to actual market demand, if it remains below 1 over an extended period and shows a declining trend, this suggests that the enterprise consistently underestimates market demand and maintains a pessimistic view of the commercial prospects for green hydrogen [6]. Furthermore, excessive pessimism among green hydrogen enterprises may lead to biased assessments of supply chain-related metrics such as safety stock redundancy ratios, investment decision lag cycles, market share contraction rates, risk reserve proportions, and decay rates of technological R&D investments, ultimately resulting in supply–demand imbalances.

Based on the above background, this paper focuses on the ordering and production decisions of upstream hydrogen production stations and downstream hydrogen refueling stations when the output and market demand of green hydrogen are uncertain and introduces the option contract into the green hydrogen supply chain, focusing on the following questions:

(1)

How do excessively pessimistic hydrogen production stations and hydrogen refueling stations make decisions under stochastic production and demand?

(2)

What is the impact of excessive pessimism on hydrogen production stations and hydrogen refueling stations in the green hydrogen supply chain?

(3)

How do excessively pessimistic hydrogen production stations and hydrogen refueling stations make decisions under an option contract?

(4)

How do hydrogen production stations and hydrogen refueling stations make decisions under an excessively pessimistic option contract?

This paper constructs a decentralized decision-making model in which hydrogen production stations independently bear the risk of stochastic output and an option contract model, and discusses how to make decisions when the subject of the green hydrogen supply chain is excessively pessimistic, as well as the impacts of excessive pessimism on decision-making.

2. Literature Review

This paper investigates the interactions between green hydrogen supply chain decision-making under stochastic production and demand, excessively pessimistic behavior, and option contracts; therefore, the literature review finds its basis in four aspects, namely option contracts, excessively pessimistic behavior, supply chain decision-making under stochastic production and demand, and green-hydrogen-supply-chain-related studies.

2.1. Option Contracts

A number of scholars have introduced option contracts into supply chains, mainly to study the supply chain coordination problem. For example, Wan et al. [9] identified explicit conditions under which a multi-period supply chain can be coordinated through put option contracts within two supply chain structures. Zhao [10] channeled synergy in the supply chain of elderly health services through loss-sharing contracts with embedded options. Wang et al. [11] found that option contracts can fully achieve Pareto-efficient coordination if they ensure that inventory costs are the same before and after coordination. Ding et al. [12] dealt with the problems of product shortages or surpluses and associated cost biases by introducing carbon option contracts (a new alternative mechanism to the traditional supply chain model) in an emissions-dependent supply chain involving carbon allowance suppliers and manufacturers. Chen et al. [13] explored a retailer-led supply chain, introducing option contracts to develop collaboration and sharing models to improve channel performance and enable supply chain coordination. Wang et al.’s [14] study yielded analytical results for decision-making and expected profits and proposed conditions for option prices and option strike prices for supply chain coordination.

In addition, other scholars have studied the impact of option contracts on subjects’ decision-making and corporate behavior. Yan et al. [15] studied the optimal decisions of supply chains based on two-period price, wholesale price, and option contracts. Zhao et al. [16] compared the performance of a two-stage decision-making model under three scenarios, namely centralized, decentralized, and option contracts, to explore the impact of preservation efforts on the supply chain and the coordination effect of option contracts on the supply chain. Li et al. [17] explored manufacturers’ optimal spot and option sourcing decisions and suppliers’ optimal physical reserve ratio decisions regarding option orders in a two-stage supply chain. Cai et al. [18] compared optimal decision-making under the VMI model and the Retailer Managed Inventory (RMI) model, introduced option contracts to coordinate SCs, and discussed possible allocation schemes for coordinating expected profits among SC members. Hou et al. [19] used a government-led Stackelberg game to analyze the risk of each link, model emergency procurement under option contracts, and derive optimal decisions.

2.2. Excessively Pessimistic Behavior

Excessively pessimistic behavior refers to supply chain decision makers’ excessively pessimistic expectations of future demand or market conditions, leading them to adopt excessively conservative strategies (e.g., reducing inventories, cutting production schedules, etc.) [20]. For example, Guo et al. [21] found that when both sides of the supply chain are in a pessimistic mood, the functional service provider remains optimistic and the retail service integrator remains pessimistic or rational, which can drive a synergistic improvement in the quality of the new RSSC. On the contrary, overconfident behavior leads to excessively aggressive strategies (e.g., expanding production). The existing research on limited-rationality behavior rarely studies excessively pessimistic behavior, instead mostly studying the impact of overconfident behavior on supply chains and firms. For example, Lang et al. [22] developed a pricing decision model to evaluate scenarios characterized by retailer overconfidence and scenarios without such bias. Chen et al. [23] studied how overconfidence influenced by reference prices affects green supply chain operations, which can provide an effective strategy for facilitating cooperation. Li [24] analyzed the investment behavior of retailers and showed that overconfidence leads to overinvestment in forecast accuracy. In addition to the investment decision itself, how overconfidence affects the performance of supply chain members and the system as a whole was examined. Liu et al. [25] investigated the optimal pricing strategies of manufacturers and retailers in a dual-channel supply chain under conditions of consumer overconfidence. Lu et al. [26] analyzed how retailers’ overconfidence affects the supply chain transparency of manufacturers who can encroach on the retail channel by paying a fixed cost of entry. Du et al. [27] studied the impact of manufacturer overconfidence on supplier innovation and supply chain profitability under wholesale price contract and cost-sharing contract settings.

2.3. Supply Chain Decision-Making Under Stochastic Production and Demand

Stochastic demand is usually caused by external factors (e.g., economic fluctuations, changes in consumer preferences, seasonal factors, etc.), and due to the uncertainty of demand, supply chain managers need to adopt appropriate strategies to cope with the risk of supply–demand imbalance. For example, Song et al. [28] investigated the impact of stochastic demand on an omni-channel supply chain, illustrating the effect of the mean and variance of stochastic demand on decision variables. Li et al. [29] compared two scenarios where market demand is stochastic versus deterministic. ESG-related cost-sharing contracts were found to be more profitable for the textile and apparel supply chain (TASC) in both deterministic and stochastic demand, thus effectively reducing the risk associated with unpredictable demand. Wu et al. [30] numerically compared optimal decisions under stochastic and deterministic scenarios and found that although demand uncertainty leads to inefficiencies in green supply chains, it may have a positive impact on the greenness and price of products. Bhosekar [31] considered the multi-cycle process and supply chain network design problem under demand uncertainty.

The downstream enterprises of the supply chain need to fully consider the stochastic output problem in the production process of the upstream enterprises when making decisions. Currently, the research on random output mainly focuses on the supply chain coordination and optimization problem under random output situations. Peng et al. [32] studied the impact of output uncertainty on supplier entry decisions and how it affects retailers’ profits and consumer surplus. Li et al. [33] investigated the loss of profits for supply chain members due to random yield supply, where present producers may benefit from this uncertainty in production yields, even though distributors and the supply chain as a whole suffer from impaired profits. Peng et al. [34] demonstrated that updating demand information in the presence of stochastic production improves supplier performance. Feng et al. [35] studied the effect of farmers’ equity concerns on planned output and maximum expected profit in the context of randomized output. Hosoda et al. [36] demonstrated that the parameters of stochastic yields play an important role in the benefits of advance notice programs.

A number of scholars have also studied the coordinated decision-making problem of supply chains under random output and random demand at the same time. For example, Zare et al. [37] explored the effects of stochastic production, stochastic demand, cost sharing, and wholesale price reduction on supply chain performance. Chen et al. [38] studied the buyer’s alternate purchasing strategy and the supplier’s production plan under stochastic production and stochastic demand. Luo et al. [39] studied the coordination of supply chains under put option contracts in the context of stochastic production and demand. Giri et al. [40] proposed price-only contracts and new revenue-sharing contracts to mitigate demand and supply uncertainty in decentralized models.

2.4. Research Related to the Green Hydrogen Supply Chain

Most of the existing studies on the green hydrogen supply chain are qualitative analyses of the current status of green hydrogen supply chain development and future trends, such as Azadnia et al. [41], who analyzed green hydrogen supply chain risk factors in the European region to develop comprehensive and supportive standards and regulations for green hydrogen supply chain implementation. Stoeckl et al. [42] suggested that energy modelers and system planners should consider the unique flexibility characteristics of the hydrogen supply chain in more detail when assessing the role of green hydrogen in future energy transition scenarios. Alexandrou et al. [43] used a case study to conclude that green hydrogen can replace traditional fossil fuels, resulting in carbon-free flight. Borge-Diez et al. [44] presented a methodology to quantify green hydrogen production and associated water demand and demonstrated that the current large-scale planning based on peaking generation will create significant uncertainty that will directly impact water supply security.

2.5. Research Gap

Based on the aforementioned literature, we summarize the research gaps in relevant studies, as shown in

Table 1. Research gaps in the relevant literature.

Literature	Stochastic Demand	Stochastic Output	Excessive Pessimistic Behavior	Supply Chain Decision-Making	Contract Optimization
Chen et al. [13]				√	√
Yan et al. [15]
Zhao et al. [16]
Wang et al. [14]	√				√
Hou et al. [19]
Li et al. [33]
Guo et al. [21]			√
Song et al. [28]	√			√
Li et al. [29]
Peng et al. [32]		√		√
Feng et al. [35]
Zare et al. [37]	√	√		√
Chen et al. [38]
Luo et al. [39]	√			√
Girir et al. [40]
Borge-Diez et al. [44]	√			√
Our study	√	√	√	√	√

. It is evident that scholars have extensively investigated supply chain decision-making and contract optimization under stochastic output or demand conditions. However, research on excessive pessimism remains scarce; Guo et al. [21] only examined the impact of excessive pessimism on supply chain decisions and performance in deterministic environments. This reflects static decision-making under specific conditions, whereas in real-world supply chains, both output and market demand are predominantly uncertain, and decision-making is inherently dynamic. To address this gap, this paper explores the influence of excessive pessimism on supply chain decision-making within the context of green hydrogen market demand and output uncertainties. We introduce option contracts to hedge against the risks associated with stochastic output and investigate the optimal contract design.

In general, the existing literature on the green hydrogen supply chain is very limited and focuses on qualitative research, while research on excessive pessimism/confidence is only reflected in excessive pessimism/confidence regarding the forecast value, with there being a lack of research on excessive pessimism/confidence regarding the forecast’s accuracy. Therefore, this paper considers the excessively pessimistic situation that exists in the green hydrogen supply chain against the background of stochastic production and demand and considers the ordering decision under two kinds of excessive pessimism, regarding forecast value and forecast accuracy. It shares the risk of the hydrogen production station due to the stochastic output of green hydrogen by introducing an option contract into the green hydrogen supply chain through the staggered ordering of the option. A decentralized decision-making model and an option contract model are constructed to investigate the optimal ordering and production decisions under the two decision-making models, and the effects of excessive pessimism, option price, and cost and salvage value parameters on the optimal decisions are analyzed.

3. Model Construction

3.1. Model Assumptions and Descriptions

This paper extends the traditional newsvendor model by focusing on the unique “excessive pessimism behavior” and “demand–supply stochasticity” inherent in the green hydrogen industry. Unlike the classical newsvendor assumption of fully rational decision makers, this study introduces a dual-layered over-pessimistic perception among supply chain participants regarding forecast accuracy and mean estimates. Additionally, an option contract mechanism is employed to share the risks associated with stochastic production outputs. The objective is to address irrational decision-making issues in the green hydrogen supply chain caused by high costs and technological uncertainties, such as overcapacity reduction by hydrogen production plants and conservative ordering by refueling stations, thereby providing a theoretical foundation for supply chain coordination in the green hydrogen sector. The specific hypotheses are as follows:

(1)

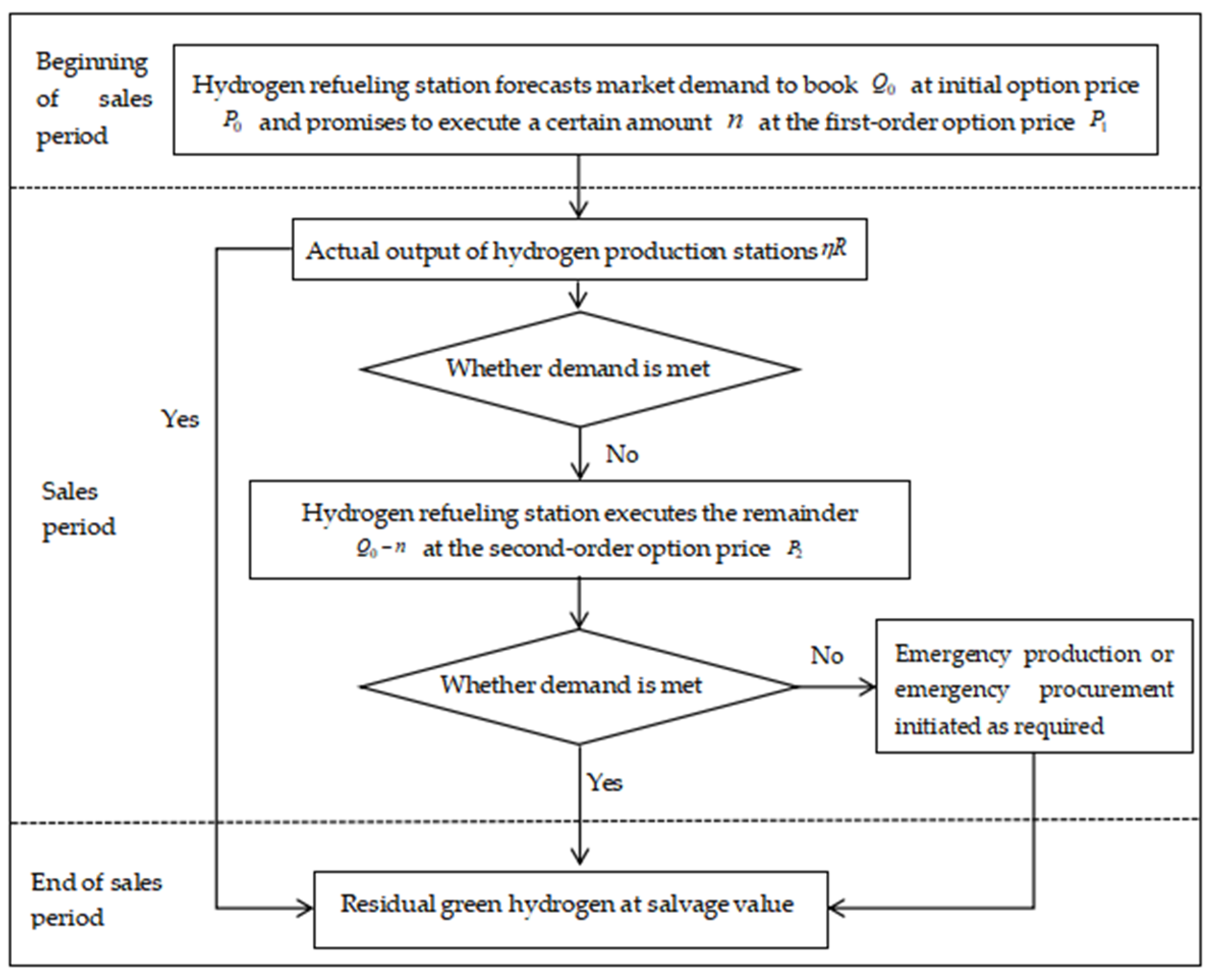
Consider a two-stage green hydrogen supply chain consisting of an upstream hydrogen production station and a downstream hydrogen refueling station, where the hydrogen refueling station forecasts the demand in advance during the planning period, determines the ordering quantity based on the forecast, and then sends an ordering request to the hydrogen production station. The hydrogen production station determines the planned production quantity based on the ordering request from the hydrogen refueling station to go into production and deliver the green hydrogen on time.

(2)

If the hydrogen refueling station faces a supply–demand imbalance, and if orders cannot be fulfilled on time due to insufficient inventory, it is necessary to urgently procure green hydrogen to meet the delayed demand, and it is also necessary to bear the loss of price discounts for delayed-delivery orders. Regarding the cost of adapting the hydrogen production station, if there is insufficient output, it is necessary to obtain power through the grid to produce hydrogen on an emergency basis, thus bearing the cost of emergency production [45].

(3)

Consider that the demand for green hydrogen follows a random distribution. There are two possible excessively pessimistic perceptions regarding green hydrogen market demand held by downstream hydrogen refueling stations: (1) they may underestimate the accuracy of their own demand forecasts for the green hydrogen market, where the variance of their perceived market demand is larger than the actual market demand variance; and (2) they may underestimate their own market share and marketing capabilities, where their perceived market expected demand is lower than the actual market demand value.

Previous studies have rarely considered this excessively pessimistic scenario. Zhang et al. [46] demonstrated through data from 200 renewable energy enterprises that when managers simultaneously hold pessimistic attitudes towards both “technological maturity” (accuracy aspect) and “market growth rate” (demand aspect), corporate R&D investments decline by more than 25%. Babai et al. [47] examined the variance amplification effect of demand forecast errors, finding that when managers overestimate demand variance, they tend to adopt “precautionary” inventory strategies, fearing that an excess inventory could result in order quantities 5% to 15% below the optimal level. In practice, the market space for green hydrogen is squeezed by high costs, technological bottlenecks, policy uncertainty, competitive pressures, investment risks, and a lack of public awareness, resulting in an unpromising demand for green hydrogen [42]. Therefore, both kinds of excessive pessimism have the possibility to exist. This paper investigates the optimal ordering decisions of downstream hydrogen refueling stations in the green hydrogen supply chain based on the two excessively pessimistic scenarios that exist in the reality of the green hydrogen market. For this purpose, it is assumed that the market demand for green hydrogen, denoted as $D$, follows a normal distribution, i.e., $D~N\left({\mu }_1,{\sigma }_1^2\right)$. Here, ${\mu }_1$ represents the actual mean demand for green hydrogen, reflecting the average market requirement; ${\sigma }_1$ signifies the actual standard deviation of demand, measuring the extent of fluctuation around the mean. A larger ${\sigma }_1$ indicates higher uncertainty in market demand. The over-pessimistic perception of green hydrogen demand held by hydrogen refueling stations is characterized by underestimating ${\mu }_1$ and ${\sigma }_1$: on one hand, they may underestimate the mean ${\mu }_1$ (believing the actual demand is lower), and on the other hand, they may overestimate the standard deviation ${\sigma }_1$ (believing demand fluctuations are more severe). These two cognitive biases jointly contribute to the stations’ excessively pessimistic expectations regarding market demand. We assume that the relationship between the perceived green hydrogen market demand $D$ and the actual demand $d$ of the downstream excessively pessimistic hydrogen refueling stations is $D=(1-\alpha )d+(\alpha +\beta -1){\mu }_1$, where $-1\le \alpha \le 0$ and $0\le \beta <1$. There are $E\left(D\right)=\beta {\mu }_1$, $\mathrm{var}\left(D\right)={(1-\alpha )}^2{\sigma }_1^2$. When $-1\le \alpha \le 0$, $\alpha$ denotes the level of excessive pessimism displayed by hydrogen refueling stations about the accuracy of forecasts. In particular, when $\alpha =0$, the hydrogen refueling station is rational in its perception of demand forecast accuracy in the green hydrogen market; when $\alpha =-1$, the hydrogen refueling station is extremely pessimistic, and the level of excessive pessimism increases as the value of $\alpha$ decreases. $\beta$ is the level of excessive pessimism displayed by hydrogen refueling stations about the expected demand. When $\beta =1$, the hydrogen refueling station’s perception of the expected demand in the hydrogen market is rational; when $0\le \beta <1$, the hydrogen refueling station’s perception of the expected demand in the green hydrogen market is lower than the actual demand value.

Referring to previous studies on overconfidence, both $\alpha$ and $\beta$ measure the level of over-pessimism of the same subject, so $\alpha$ and $\beta$ are not independent parameters and there is a certain functional relationship between them. With reference to previous studies, we consider the case that $\beta$ is a linear functional relationship of $\alpha$, i.e., $\beta ={\lambda }_1\alpha +k$. It is assumed that when the hydrogen refueling station’s perception of the accuracy of demand forecasting in the green hydrogen market is rational, i.e., $\alpha =0$, its perception of the expected demand in the green hydrogen market is also rational, i.e., $\beta =1$. Assume that $\beta ={\lambda }_1\alpha +1$, which yields an excessively pessimistic perception of the green hydrogen market demand of $D=(1-\alpha )d+({\lambda }_1+1)\alpha {\mu }_1$. When ${\lambda }_1=0$, it is consistent with the cognitive model of excessive pessimism or over-confidence in previous studies, i.e., $D=(1-\alpha )d+\alpha {\mu }_1$.

(4)

Consider that the green hydrogen output rate of hydrogen production stations follows a random distribution. There are two possible types of excessively pessimistic perceptions regarding hydrogen production output held by upstream hydrogen refueling stations: (1) they may underestimate the accuracy of their own predictions of the green hydrogen production rate of hydrogen production stations, where the variance of their perceived green hydrogen production rate is larger than that of the actual green hydrogen production rate; and (2) they may underestimate their own hydrogen production capacity, where their perceived green hydrogen production rate is lower than that of the actual green hydrogen production rate.

Hydrogen production at hydrogen production stations faces multiple challenges, such as high energy consumption, high cost, insufficient infrastructure, and resource dependence, and therefore, two excessively pessimistic scenarios can also exist at hydrogen production stations. In this paper, we consider these two excessively pessimistic scenarios of green hydrogen output to study the optimal input and output decisions of upstream hydrogen production stations in the green hydrogen supply chain [48]. To this end, it is assumed that the relationship between the perceived green hydrogen output rate and the actual green hydrogen output rate of the upstream excessively pessimistic hydrogen production stations is $\mathsf{\Phi }=(1-\gamma )\varphi +(\gamma +\delta -1){\mu }_2$, where $-1\le \gamma \le 0$,$0\le \delta <1$. There are $E\left(\mathsf{\Phi }\right)=\delta {\mu }_2$, $\mathrm{var}\left(\mathsf{\Phi }\right)={(1-\gamma )}^2{\sigma }_2^2$. When $-1\le \gamma \le 0$, $\gamma$ denotes the level of excessive pessimism of the hydrogen production station regarding the prediction accuracy. In particular, when $\gamma =0$, the hydrogen production station is rational in its perception of the prediction accuracy of the green hydrogen output rate; when $\gamma =-1$, the hydrogen production station is extremely pessimistic, and the level of excessive pessimism increases as the value of $\gamma$ decreases. $\delta$ is the excessive pessimism level regarding the hydrogen production rate of the hydrogen production station. When $\delta =1$, the hydrogen production station’s perception of green hydrogen output rate is rational; when $0\le \delta <1$, the hydrogen refueling plant’s perceived green hydrogen output rate is lower than the actual output rate.

As in point (3) of the hypothesis, consider the case where $\delta$ is a linear functional relationship of $\gamma$, i.e., $\delta ={\lambda }_2\gamma +m$. Assuming that when the hydrogen production station’s perception of the accuracy of the green hydrogen output rate prediction is rational, i.e., $\gamma =0$, its perception of the green hydrogen market output rate is also rational, i.e., $\delta =1$. It is then assumed that $\delta ={\lambda }_2\gamma +1$, which yields the green hydrogen output rate perceived under excessive pessimism as $\mathsf{\Phi }=(1-\gamma )\varphi +({\lambda }_2+1)\gamma {\mu }_2$. When ${\lambda }_2=0$, it is consistent with the cognitive modeling of excessive pessimism or over-confidence in previous studies, i.e., $\mathsf{\Phi }=(1-\gamma )\varphi +\gamma {\mu }_2$.

3.2. Parameter Definitions

In this paper, we construct a two-level green hydrogen supply chain consisting of an upstream hydrogen production station and a downstream hydrogen refueling station, where the green hydrogen market demand and green hydrogen output rate are randomized. We assume that the green hydrogen market demand is a continuous random variable $d$ with the probability density function and distribution function $f_d(\cdot )$ and $F_d(\cdot )$, respectively, and there are $E(d)=\mu$, $\mathrm{var}\left(d\right)={\sigma }_1^2$. The hydrogen production station is put into operation according to the planned output $R$, and the actual output is $\varphi R$. $\varphi$ is the green hydrogen output rate of the hydrogen production station, and its probability density function and distribution function are $g_{\varphi }(\cdot )$ and $G_{\varphi }(\cdot )$, respectively, and there are $E(\varphi )={\mu }_2$, $\mathrm{var}\left(\varphi \right)={\sigma }_2^2$. The related parameters in this paper are defined as shown in

Table 2. Parameter definitions.

Parameters	Parameter Definition	Parameters	Parameter Definition
$D$	Excessively pessimistic hydrogen refueling station perceptions of green hydrogen market demand	$\mathsf{\Phi }$	Excessively pessimistic about the perceived green hydrogen output rate of hydrogen production stations
$d$	Actual demand in the green hydrogen market	$\eta$	Green hydrogen actual output rate
$\alpha$	Hydrogen refueling stations’ level of excessive pessimism about the accuracy of demand forecasts in the green hydrogen market	$\gamma$	Hydrogen production stations’ level of excessive pessimism about the accuracy of predictions of green hydrogen output rates
$\beta$	Hydrogen refueling stations’ level of excessive pessimism about the green hydrogen market demand	$\delta$	Hydrogen production stations’ level of excessive pessimism about green hydrogen output rates
$Q$	Green hydrogen ordering quantity	$R$	Planned production of green hydrogen
$P$	Market price of green hydrogen	$w$	Wholesale price of green hydrogen units
$C_r$	Contingency procurement costs for hydrogen refueling stations	$C_o$	Unit production cost of green hydrogen
$\theta$	Green hydrogen delayed delivery price discount rate	$C_m$	Emergency production cost of green hydrogen
$S_r$	Residual value per unit of unsold green hydrogen at hydrogen refueling stations	$S_m$	Residual value per unit of excess green hydrogen produced at hydrogen production stations
$F_D(\cdot )$	Cumulative distribution function of green hydrogen market demand for excessively pessimistic hydrogen refueling station perceptions $D$	$G_{\mathsf{\Phi }}(\cdot )$	Cumulative distribution function of green hydrogen output rates for excessively pessimistic hydrogen production station perceptions $\mathsf{\Phi }$
$f_D(\cdot )$	Probability density functions of green hydrogen market demand for excessively pessimistic hydrogen refueling station perceptions $D$	$g_{\mathsf{\Phi }}(\cdot )$	Probability density functions of green hydrogen output rates for excessively pessimistic hydrogen production station perceptions $\mathsf{\Phi }$

.

4. Decentralized Decision-Making Models

At the beginning of the sales period, the hydrogen refueling station orders $Q$ from the hydrogen production station. Regarding the mismatch cost caused by the mismatch between supply and demand at the hydrogen refueling station, if the order is delayed due to a shortage of the initial sales stock, it needs to be urgently ordered from the hydrogen production station, and it bears a price discount for the delayed demand. Hydrogen stations plan to produce $R$ based on the amount ordered by the stations, and the actual output is $\varphi R$. If the actual output is not enough to meet the amount ordered by the stations, the shortfall will need to be obtained through emergency production in order to satisfy the demand for green hydrogen at the stations, which means that the stations need to independently bear the risk of a stochastic output of green hydrogen.

4.1. Optimal Ordering Decision for Hydrogen Refueling Stations Under Decentralized Decision Making

Although the green hydrogen output rate is stochastic, the hydrogen production station will satisfy the hydrogen refueling station’s ordering demand by means of emergency production. The profit function of the hydrogen refueling station in this case can be expressed as

$${\pi }_r=p\min \left\{D,Q\right\}+S_r{\left[Q-D\right]}^{+}-\left(C_r-\theta p\right){\left[D-Q\right]}^{+}-wQ$$

(1)

Its expected profit is

$$E\left(\pi \right)=P{\displaystyle {\int }_0^{Q}Df\left(z\right)}dz+P{\displaystyle {\int }_D^{\infty }Qf\left(z\right)}dz+S_r{\displaystyle {\int }_0^Q\left(Q-D\right)}f\left(z\right)dz-\left(C_r-\theta P\right){\displaystyle {\int }_Q^{\infty }\left(D-Q\right)f}\left(z\right)dz-wQ$$

(2)

Proposition 1. 

The optimal ordering quantity of the hydrogen refueling station under decentralized decision-making is

$$Q^{*}=\left(1-\alpha \right)F_d^{-1}\left({\displaystyle \frac{P+C_r-\theta P-w}{P-S_r-C_r+\theta P}}\right)+\left({\lambda }_1+1\right)\alpha {\mu }_1$$

(3)

Proof. 

Because $D=\left(1-\alpha \right)d+\left({\lambda }_1+1\right)\alpha {\mu }_1$,

$F_D\left(z\right)=P\left(\left(1-\alpha \right)d+\left({\lambda }_1+1\right)\alpha {\mu }_1\le x\right)=F_d\left({\displaystyle \frac{z-\left({\lambda }_1+1\right)\alpha {\mu }_1}{1-\alpha }}\right)$ and ${\displaystyle {\int }_0^{Q}F\left(z\right)dz}=$ ${\displaystyle {\int }_0^{\frac{Q-\left({\lambda }_1+1\right)\alpha {\mu }_1}{1-\alpha }}{F}_d\left(\left(1-\alpha \right)d+\left({\lambda }_1+1\right)\alpha {\mu }_1\right)}d\left(\left(1-\alpha \right)d+\left({\lambda }_1+1\right)\alpha {\mu }_1\right)=\left(1-\alpha \right){\displaystyle {\int }_0^{\frac{Q-\left({\lambda }_1+1\right)\alpha {\mu }_1}{1-\alpha }}{F}_d\left(z\right)}$.

Simplifying Equation (2),

$$\begin{array}{cc}E\left(\pi \right)& =P{\displaystyle {\int }_0^{Q}Df\left(z\right)}dz+P{\displaystyle {\int }_D^{\infty }Qf\left(z\right)}dz+S_r{\displaystyle {\int }_0^Q\left(Q-D\right)}f\left(z\right)dz-\left(C_r-\theta P\right){\displaystyle {\int }_Q^{\infty }\left(D-Q\right)f}\left(z\right)dz-wQ\\ & =\left(P+C_r-\theta P-w\right)Q-\left(P-S_r\right){\displaystyle {\int }_0^{Q}F\left(z\right)dz-\left(C_r-\theta P\right)}{\displaystyle {\int }_Q^{+\infty }F\left(z\right)dz}\\ & =\left(P+C_r-\theta P-w\right)Q-\left(P-S_r\right)(1-\alpha ){\displaystyle {\int }_0^{\frac{Q-({\lambda }_1+1)\alpha {\mu }_1}{1-\alpha }}{F}_d\left(z\right)dz}-\left(C_r-\theta P\right){\displaystyle {\int }_{\frac{Q-({\lambda }_1+1)\alpha {\mu }_1}{1-\alpha }}^{+\infty }{F}_d\left(z\right)dz}\end{array}$$

So ${\displaystyle \frac{\partial E\left(\pi \right)}{\partial Q}}=\left(P+C_r-\theta P-w\right)-\left(P-S_r\right)F_d\left({\displaystyle \frac{Q-({\lambda }_1+1)\alpha {\mu }_1}{1-\alpha }}\right)+\left(C_r-\theta P\right)F_d\left({\displaystyle \frac{Q-({\lambda }_1+1)\alpha {\mu }_1}{1-\alpha }}\right)$. Let ${\displaystyle \frac{\partial E\left(\pi \right)}{\partial Q}}=0$,$\left(P-S_r-C_r+\theta P\right)F_d\left({\displaystyle \frac{Q-({\lambda }_1+1)\alpha {\mu }_1}{1-\alpha }}\right)=P+C_r-\theta P-w$, so $Q^{*}=\left(1-\alpha \right)F_d^{-1}\left({\displaystyle \frac{P+C_r-\theta P-w}{P-S_r-C_r+\theta P}}\right)+\left({\lambda }_1+1\right)\alpha {\mu }_1$. □

Proposition 2. 

When ${\mu }_1\ge F_d^{-1}\left({\displaystyle \frac{P+C_r-\theta P-w}{P-S_r-C_r+\theta P}}\right)/\left({\lambda }_1+1\right)$ is excessively pessimistic, the optimal ordering quantity of a hydrogen refueling station is not less than its optimal ordering quantity when it is perfectly rational. When ${\mu }_1<F_d^{-1}\left({\displaystyle \frac{P+C_r-\theta P-w}{P-S_r-C_r+\theta P}}\right)/\left({\lambda }_1+1\right)$ is used, the optimal ordering quantity of a hydrogen refueling station when it is excessively pessimistic is lower than its optimal ordering quantity when it is perfectly rational.

Proof. 

Let the optimal ordering quantity when the hydrogen refueling station is perfectly rational be $Q^{\prime }$. The optimal ordering quantity when the station is perfectly rational at $\left(\alpha =0\right)$ is $Q^{\prime }=F_d^{-1}\left({\displaystyle \frac{P+C-\theta P-w}{P-S_r-C+\theta P}}\right)$. The difference between the optimal ordering quantity when excessively pessimistic and when perfectly rational is $Q^{*}-Q^{\prime }=\left(K+1\right)\alpha {\mu }_1-\alpha F_d^{-1}\left({\displaystyle \frac{P+C-\theta P-w}{P-S_r-C+\theta P}}\right)$. Let $Q^{*}-Q^{\prime }=\left(K+1\right)\alpha {\mu }_1-\alpha F_d^{-1}\left({\displaystyle \frac{P+C-\theta P-w}{P-S_r-C+\theta P}}\right)>0$, which leads to ${\mu }_1\ge F_d^{-1}\left({\displaystyle \frac{P+C-\theta P-w}{P-S_r-C+\theta P}}\right)/\left(K+1\right)$, when $Q^{*}\ge Q^{\prime }$; let $Q^{*}-Q^{\prime }=\left(K+1\right)\alpha {\mu }_1-\alpha F_d^{-1}\left({\displaystyle \frac{P+C-\theta P-w}{P-S_r-C+\theta P}}\right)<0$, which leads to ${\mu }_1<F_d^{-1}\left({\displaystyle \frac{P+C-\theta P-w}{P-S_r-C+\theta P}}\right)/\left(K+1\right)$, when $Q^{*}<Q^{\prime }$. □

Proposition 2 shows that the optimal ordering quantity when the hydrogen refueling station is excessively pessimistic is not necessarily lower than the optimal ordering quantity when it is rational. This is because if the expected mean value of the green hydrogen market demand is high, the hydrogen refueling station’s excessive pessimism about the accuracy of the green hydrogen market demand forecast exceeds the hydrogen refueling station’s blind pessimism about the green hydrogen market demand, and then the hydrogen refueling station will instead increase the ordering quantity; however, if the expected mean value of the green hydrogen market demand is low, the hydrogen refueling station’s excessive pessimism about the market demand will cause it to reduce the ordering quantity.

Proposition 3. 

When ${\mu }_1\ge F_d^{-1}\left({\displaystyle \frac{P+C-\theta P-w}{P-S_r-C+\theta P}}\right)/\left({\lambda }_1+1\right)$ is used, the optimal ordering quantity $Q^{*}$ decreases as the excessive pessimism factor $\alpha$ decreases; i.e., the optimal ordering quantity of a hydrogen refueling station decreases as the level of excessive pessimism increases. When ${\mu }_1<F_d^{-1}\left({\displaystyle \frac{P+C-\theta P-w}{P-S_r-C+\theta P}}\right)/\left({\lambda }_1+1\right)$ is used, the optimal ordering quantity $Q^{*}$ increases as the excessive pessimism factor $\alpha$ decreases; i.e., as the level of excessive pessimism of a hydrogen refueling station increases, its optimal ordering quantity gradually increases.

Proof. 

Taking the partial derivative of $Q^{*}=\left(1-\alpha \right)F_d^{-1}\left({\displaystyle \frac{P+C-\theta P-w}{P-S_r-C+\theta P}}\right)+\left({\lambda }_1+1\right)\alpha {\mu }_1$ with respect to the excessive pessimism factor $\alpha$ yields ${\displaystyle \frac{\partial Q^{*}}{\partial \alpha }}=\left(K+1\right){\mu }_1-F_d^{-1}\left({\displaystyle \frac{P+C-\theta P-w}{P-S_r-C+\theta P}}\right)$. Let ${\displaystyle \frac{\partial Q^{*}}{\partial \alpha }}=\left(K+1\right){\mu }_1-F_d^{-1}\left({\displaystyle \frac{P+C-\theta P-w}{P-S_r-C+\theta P}}\right)>0$, which gives ${\mu }_1\ge F_d^{-1}\left({\displaystyle \frac{P+C-\theta P-w}{P-S_r-C+\theta P}}\right)/\left(K+1\right)$ when $Q^{*}$ increases as $\alpha$ increases, and let ${\displaystyle \frac{\partial Q^{*}}{\partial \alpha }}=\left(K+1\right){\mu }_1-F_d^{-1}\left({\displaystyle \frac{P+C-\theta P-w}{P-S_r-C+\theta P}}\right)<0$, which gives ${\mu }_1<F_d^{-1}\left({\displaystyle \frac{P+C-\theta P-w}{P-S_r-C+\theta P}}\right)/\left(K+1\right)$ when decreases as $\alpha$ increases. □

Proposition 3 shows that the effect of excessive pessimism on the optimal ordering quantity of a hydrogen refueling station is not only related to its level of excessive pessimism $\alpha$, but also influenced by the expected demand of the green hydrogen market ${\mu }_1$. If the expected demand in the green hydrogen market is high, the optimal ordering quantity $Q^{*}$ of a hydrogen filling station decreases with the increase in its excessive pessimism level; if the expected demand in the green hydrogen market is low, the increase in the excessive pessimism level of a hydrogen filling station increases its accuracy in the prediction of the demand for green hydrogen, which may motivate the station to increase its ordering quantity in order to satisfy the demand. Through optimized ordering strategies, hydrogen refueling stations can more accurately align supply with market demand, thereby reducing operational costs and minimizing the additional expenditures associated with emergency procurement or inventory backlog. This approach not only enhances the economic efficiency of the stations but also strengthens the competitiveness of green hydrogen within the energy market, facilitating its large-scale adoption.

4.2. Optimal Production Decision for Hydrogen Production Station

The hydrogen production station independently bears the risk of a random green hydrogen output rate and needs to determine the optimal planned production decision based on the ordering quantity of the hydrogen refueling station. In the event that the actual green hydrogen output of the hydrogen production station does not coincide with the ordering quantity of the hydrogen refueling station, the portion of the actual output that does not meet the refueling station’s requirements needs to be met by emergency production, and the actual output of green hydrogen in excess of the actual green hydrogen can be obtained as a residual value. Therefore, the profit function of the hydrogen production station is

$${\pi }_m=w\min \left\{Q,\mathsf{\Phi }R\right\}+S_m{\left(\mathsf{\Phi }R-Q\right)}^{+}-\left(C_m-w\right){\left(Q-\mathsf{\Phi }R\right)}^{+}-C_{o}R$$

(4)

Its expected profit is

$$E\left({\pi }_m\right)=wR{\displaystyle {\int }_0^{Q/R}\mathsf{\Phi }g\left(z\right)}dz+wQ{\displaystyle {\int }_{Q/R}^{\infty }g\left(z\right)}dz+S_m{\displaystyle {\int }_{Q/R}^{\infty }\left(\mathsf{\Phi }R-Q\right)}g\left(z\right)dz-\left(C_m-w\right){\displaystyle {\int }_0^{Q/R}\left(Q-\mathsf{\Phi }R\right)}g\left(z\right)dz-C_{0}R$$

(5)

Proposition 4. 

The optimal planned production of the hydrogen production station $R^{*}$ is satisfied under decentralized decision-making: $A={\displaystyle \frac{\frac{Q}{R^{*}}-\left(m+1\right)\gamma {\mu }_2}{1-\gamma }}$,

$${\displaystyle \frac{Q}{R^{*}}}{G}_{\varphi }\left(A\right)-\left(1-\gamma \right){\displaystyle {\int }_0^A{G}_{\varphi }\left(z\right)}dz=\left(C_0-S_m{\mu }_2\right)/\left(C_m-S_m\right)$$

(6)

Proof. 

The first- and second-order derivatives with respect to $R$ for the expected profit function of the hydrogen production station can be obtained as follows, respectively:

$${\displaystyle \frac{\partial E\left({\pi }_m\right)}{\partial R}}=\left(C_m-S_m\right)\left[{\displaystyle \frac{Q}{R}}{G}_{\varphi }\left(A\right)\left(1-\gamma \right){\displaystyle {\int }_0^A{G}_{\varphi }\left(z\right)}dz\right]-\left(C_0-S_m{\mu }_2\right)$$

$${\displaystyle \frac{{\partial }^{2}E\left({\pi }_m\right)}{\partial R^2}}=-\left(C_m-S_m\right){\displaystyle \frac{Q^2}{R^3\left(1-\gamma \right)}}{g}_{\varphi }\left(A\right)<0$$

Thus, $E\left({\pi }_m\right)$ is a concave function of $R$, and the optimal planned production is obtained by making ${\displaystyle \frac{\partial E\left({\pi }_m\right)}{\partial R}}=0$, i.e., ${\displaystyle \frac{Q}{R^{*}}}{G}_{\varphi }\left(A\right)-\left(1-\gamma \right){\displaystyle {\int }_0^A{G}_{\varphi }\left(z\right)}dz=\left(C_0-S_m{\mu }_2\right)/\left(C_m-S_m\right)$. □

From Proposition 4, the optimal planned production of a hydrogen plant $R^{*}$ decreases as its level of excessive pessimism $\gamma$ decreases; i.e., the optimal planned production of a hydrogen plant decreases as its level of excessive pessimism increases. This is due to the fact that a hydrogen production station that is excessively pessimistic about its green hydrogen output rate tends to choose to reduce its production plan in order to cope with the problems of inefficiency in production, increases in the cost of production, wastage of resources, delays in delivery, and quality control of green hydrogen, and also to mitigate risks in the green hydrogen supply chain and market. Proposition 4 also shows that the optimal planned production of the hydrogen production station $R^{*}$ decreases as the unit production cost of green hydrogen $C_0$ increases, increases as the emergency production cost of green hydrogen $C_m$ increases, and increases as the mean value of the actual output rate of green hydrogen ${\mu }_2$ increases. This indicates that the optimal planned production of the hydrogen production station $R^{*}$ is influenced by a number of factors. With the increase in the cost of green hydrogen production, in order to control the cost, the hydrogen production station reduces its production quantity to avoid a decline in profits or losses; a higher emergency production cost of green hydrogen means that in the event where production is interrupted or there is a surge in demand, the cost to temporarily increase production will be very high. To avoid high emergency production costs, the hydrogen production process may increase planned production ahead of time to build up an inventory buffer to avoid being forced to pay higher costs in the future. Hydrogen stations that are excessively pessimistic may overestimate uncertainties or inefficiencies in production and generally adjust their plans to increase production to take advantage of higher production efficiencies if the actual rate of output is high, suggesting that the production process has been more efficient than expected afterward. Hydrogen production stations must also monitor market demand dynamics and adapt production strategies flexibly to mitigate excesses or shortages of green hydrogen. Such adjustments can significantly reduce resource consumption and environmental pollution throughout the entire lifecycle, thereby enhancing the overall environmental benefits of the green hydrogen supply chain and promoting the sustainable development of the green hydrogen industry.

5. Option Contract Modeling

With reference to previous studies, a new option contract design is introduced to construct a two-stage green hydrogen supply chain option contract model, where the hydrogen refueling station orders $Q_0$ at the initial option price $P_0$ during the planning period, and a certain quantity is executed at the first-order option price $P_1$, no matter how much demand for the eventual sale of green hydrogen there is $n$, and after the demand is satisfied, the station determines whether it is necessary to execute the remaining quantity and how much is executed at the second-order option price $P_2$ according to the residual demand situation [49,50,51]. The decision sequence is shown in Figure 1.

5.1. Optimal Ordering Decision for Hydrogen Refueling Stations Under Option Contracts

Within the option contract model, hydrogen refueling stations can effectively respond to fluctuations in the quantity demanded while committing to executing a certain number of purchases, which, to a certain extent, shares the risk of the random output of green hydrogen from hydrogen production stations. This model not only enhances the supply chain flexibility of the hydrogen refueling station but also provides a more stable demand expectation for the hydrogen production station, which helps it to optimize its production decisions and improve its overall operational efficiency. When the hydrogen refueling station is excessively pessimistic about green hydrogen market demand, the expression for its profit function is depicted below:

If $D>Q_0$, the demand for green hydrogen is higher than the initial ordering quantity, meaning the station may face the situation of insufficient inventory and hence need to pay the contingency purchase cost, and thus, the hydrogen refueling station’s profit function is ${\pi }_r=P{Q}_0-P_0{Q}_0-P_{1}n-P_2\left(Q_0-n\right)-\left(C_r-\theta P\right)\left(D-Q_0\right)$; if $Q_0>D>n$, it means that the demand for green hydrogen is higher than the initial ordering quantity but more than the minimum execution quantity, and the station does not need to pay the contingency purchase cost, meaning the hydrogen refueling station’s profit function is ${\pi }_r=PD-P_0{Q}_0-P_{1}n-P_2\left(D-n\right)$; if $n>D$, it means that the demand for green hydrogen is less than the minimum execution quantity, and the station does not need to pay the second-order option cost. In this case, the hydrogen refueling station’s profit function is ${\pi }_r=PD-P_0{Q}_0-P_{1}n+S_r\left(n-D\right)$.

In summary, the expected profit function of the hydrogen refueling station is

$$\begin{array}{cc}E\left({\pi }_r\right)& ={\displaystyle {\int }_{Q_0}^{\infty }\left[P{Q}_0-P_0{Q}_0-P_{1}n-P_2\left(Q_0-n\right)-\left(C_r-\theta P\right)\left(D-Q_0\right)\right]}f\left(z\right)dz+{\displaystyle {\int }_n^{Q_0}\left[PD-P_0{Q}_0-P_{1}n-P_2\left(D-n\right)\right]}f\left(z\right)dz\\ & +{\displaystyle {\int }_0^n\left[PD-P_0{Q}_0-P_{1}n+S_r\left(n-D\right)\right]}f\left(z\right)dz\end{array}$$

(7)

Proposition 5. 

The optimal initial option ordering quantity and minimum execution quantities for the hydrogen refueling station under the option contract are as follows, respectively:

$$Q_0^{*}=\left(1-\alpha \right){\overline{F_d}}^{-1}\left({\displaystyle \frac{P_0}{\left(1-\alpha \right)\left(P-P_2+C_r-\theta P\right)}}\right)+\left({\lambda }_1+1\right)\alpha {\mu }_1$$

(8)

$$n^{*}=\left(1-\alpha \right)F_d^{-1}\left({\displaystyle \frac{P_1-P_2}{S_r-P_2}}\right)+\left({\lambda }_1+1\right)\alpha {\mu }_1$$

(9)

Proof. 

The first-order and second-order derivatives of the expected profit function of the hydrogen refueling station with respect to the initial option ordering quantity $Q_0^{*}$ and the minimum execution quantity $n^{*}$ are obtained:

${\displaystyle \frac{\partial E\left({\pi }_r\right)}{\partial Q_0}}=\left(P-P_2+C_r-\theta P\right)\left(1-\alpha \right)\overline{F_d}\left({\displaystyle \frac{Q_0^{*}-\left({\lambda }_1+1\right)\alpha {\mu }_1}{\left(1-\alpha \right)}}\right)-P_0$, ${\displaystyle \frac{{\partial }^{2}E\left({\pi }_r\right)}{\partial Q_0^2}}=-\left(P-P_2+C_r-\theta P\right)f_d\left({\displaystyle \frac{Q_0^{*}-\left({\lambda }_1+1\right)\alpha {\mu }_1}{\left(1-\alpha \right)}}\right)<0$, ${\displaystyle \frac{\partial E\left({\pi }_r\right)}{\partial n}}=\left(P_1-P_2\right)-\left(S_r-P_2\right)F_d\left({\displaystyle \frac{n^{*}-\left({\lambda }_1+1\right)\alpha {\mu }_1}{1-\alpha }}\right)$, ${\displaystyle \frac{{\partial }^{2}E\left({\pi }_r\right)}{\partial n^2}}=-{\displaystyle \frac{S_r-P_2}{1-\alpha }}{f}_d\left({\displaystyle \frac{n^{*}-\left({\lambda }_1+1\right)\alpha {\mu }_1}{1-\alpha }}\right)<0$, ${\displaystyle \frac{{\partial }^{2}E\left({\pi }_r\right)}{\partial Q\partial n}}=0$${\displaystyle \frac{{\partial }^{2}E\left({\pi }_r\right)}{\partial n\partial Q}}=0$, first-order principal subequations ${\displaystyle \frac{{\partial }^{2}E\left({\pi }_r\right)}{\partial Q_0^2}}<0$, second-order principal subequations ${\displaystyle \frac{{\partial }^{2}E\left({\pi }_r\right)}{\partial Q_0^2}}\cdot {\displaystyle \frac{{\partial }^{2}E\left({\pi }_r\right)}{\partial n^2}}>0$. □

Therefore, $E\left({\pi }_r\right)$ is the joint concave function of the initial option ordering quantity $Q_0$ and the minimum execution quantity $n$, so that ${\displaystyle \frac{\partial E\left({\pi }_r\right)}{\partial Q_0}}=0$ and ${\displaystyle \frac{\partial E\left({\pi }_r\right)}{\partial n}}=0$ lead to the optimal initial option ordering quantity $Q_0^{*}$ and the optimal minimum option execution quantity $n^{*}$:

$$Q_0^{*}=\left(1-\alpha \right){\overline{F_d}}^{-1}\left({\displaystyle \frac{P_0}{\left(1-\alpha \right)\left(P-P_2+C_r-\theta P\right)}}\right)+\left({\lambda }_1+1\right)\alpha {\mu }_1,n^{*}=\left(1-\alpha \right)F_d^{-1}\left({\displaystyle \frac{P_1-P_2}{S_r-P_2}}\right)+\left({\lambda }_1+1\right)\alpha {\mu }_1$$

Proposition 6. 

When the excessive pessimism level at the hydrogen refueling station, denoted as $\alpha <1-{\displaystyle \frac{P_0\left(P-S_r+C_r-\theta P\right)}{\left(2\theta P+w-S_r-2C_r\right)\left(P-P_2+C_r-\theta P\right)}}$, is relatively low, the initial option purchase quantity under the option contract can exceed the optimal procurement quantity of the hydrogen station in the absence of an option contract.

Proof. 

Comparing the initial option ordering quantity $Q_0^{*}$ of the hydrogen station under the option contract with the optimal ordering quantity $Q_0^{*}$ of the hydrogen station without the option contract by making a difference, $Q_0^{*}-Q^{*}=\left(1-\alpha \right)\left[F_d^{-1}\left(1-{\displaystyle \frac{P_0}{\left(1-\alpha \right)\left(P-P_2+C_r-\theta P\right)}}\right)-F_d^{-1}\left({\displaystyle \frac{P+C_r-\theta P-w}{P-S_r-C_r+\theta P}}\right)\right]$, due to $\left(1-\alpha \right)>0$, it is then only necessary to compare the magnitudes of $1-{\displaystyle \frac{P_0}{\left(1-\alpha \right)\left(P-P_2+C_r-\theta P\right)}}$ and ${\displaystyle \frac{P+C_r-\theta P-w}{P-S_r-C_r+\theta P}}$, and to make a difference between the two, let $Q_0^{*}-Q^{*}>0$ yield $\alpha <1-{\displaystyle \frac{P_0\left(P-S_r+C_r-\theta P\right)}{\left(2\theta P+w-S_r-2C_r\right)\left(P-P_2+C_r-\theta P\right)}}$. Thus, the initial ordering quantity of hydrogen stations under the option contract can be greater than the optimal ordering quantity without the option contract when the level of excessive pessimism of hydrogen stations is low. □

Proposition 6 shows that the option contract mechanism can directly incentivize hydrogen refueling stations to increase their ordering volume when their level of excessive pessimism is low (i.e., a is less than a certain critical value). In addition, the critical value contains parameters such as cost, price, and residual value, reflecting the cost structure of the supply chain. When the production cost is lower or the wholesale price is higher, the incentive effect of the option contract is stronger, and the hydrogen refueling station is more motivated to expand the initial order. At the same time, hydrogen stations can further incentivize hydrogen refueling stations to increase the initial ordering quantity while enhancing supply chain synergies by designing a contractual combination of higher first-order option prices and lower second-order option prices.

Proposition 7. 

When $\left({\lambda }_1+1\right){\mu }_1\ge B+f^{\prime }{\left(B\right)}^{-1}/\left(1-\alpha \right)\left(P-P_2+C_r-\theta P\right)$, the initial option ordering quantity $Q_0^{*}$ increases with the increase in the excessive pessimism factor $\alpha$; i.e., the initial option ordering quantity $Q_0^{*}$ increases with the decrease in the excessive pessimism level of the hydrogen refueling station. When $\left({\lambda }_1+1\right){\mu }_1<B+f^{\prime }{\left(B\right)}^{-1}/\left(1-\alpha \right)\left(P-P_2+C_r-\theta P\right)$, the initial option ordering quantity $Q_0^{*}$ decreases as the excessive pessimism factor $\alpha$ increases; i.e., the initial option ordering quantity $Q_0^{*}$ decreases as the level of excessive pessimism at the hydrogen refueling station decreases.

Proof. 

Let $B={\overline{F_d}}^{-1}\left({\displaystyle \frac{P_0}{\left(1-\alpha \right)\left(P-P_2+C_r-\theta P\right)}}\right)$, the partial derivative of the initial option ordering quantity $Q_0^{*}$ with respect to the excessive pessimism factor $\alpha$, be obtained as follows: when $\left({\lambda }_1+1\right){\mu }_1\ge B+f^{\prime }{\left(B\right)}^{-1}/\left(1-\alpha \right)\left(P-P_2+C_r-\theta P\right)$, $\partial Q_0^{*}/\partial \alpha \ge 0$; when $\left({\lambda }_1+1\right){\mu }_1<B+f^{\prime }{\left(B\right)}^{-1}/\left(1-\alpha \right)\left(P-P_2+C_r-\theta P\right)$, $\partial Q_0^{*}/\partial \alpha <0$. □

Proposition 7 is similar to Proposition 3 in that the initial option subscription under the option contract is affected by the excessive pessimism of the hydrogen refueling station in addition to the expectation of the demand in the green hydrogen market. If the green hydrogen market demand expectation is high, the initial option ordering quantity $Q_0^{*}$ of the hydrogen refueling station increases as the degree of excessive pessimism decreases; if the green hydrogen market demand expectation is low and the hydrogen refueling station’s degree of excessive pessimism increases, the increase in the accuracy of the hydrogen refueling station’s green hydrogen demand prediction may result in the refueling station’s optimism about the green hydrogen market, and then the initial option ordering quantity $Q_0^{*}$ may instead increase.

Proposition 8. 

When $\left({\lambda }_1+1\right){\mu }_1\ge H$ is used, the minimum execution quantity $n^{*}$ increases as the excessive pessimism factor $\alpha$ increases; i.e., the minimum execution quantity $n^{*}$ increases as the level of excessive pessimism at the hydrogen refueling station decreases. When $\left({\lambda }_1+1\right){\mu }_1<H$ is used, the minimum execution quantity $n^{*}$ decreases as the excessive pessimism factor $\alpha$ increases; i.e., the minimum execution quantity $n^{*}$ decreases as the level of excessive pessimism at the hydrogen refueling station decreases.

Proof. 

Let $H=F_d^{-1}\left({\displaystyle \frac{P_1-P_2}{S_r-P_2}}\right)$, and find the partial derivative with respect to the excessive pessimism factor $\alpha$ for the minimum execution quantity $n^{*}$, which yields the following: when $\left({\lambda }_1+1\right){\mu }_1\ge H$, $\partial n^{*}/\partial \alpha \ge 0$; when $\left({\lambda }_1+1\right){\mu }_1<H$, $\partial n^{*}/\partial \alpha <0$. □

In Proposition 8, as above, the effect of minimum execution quantity under the option contract is also affected by the expectation of demand in the green hydrogen market. If the green hydrogen market demand expectation is high, the minimum execution quantity $n^{*}$ of hydrogen refueling stations increases as the level of excessive pessimism decreases; if the green hydrogen market demand expectation is low, the hydrogen refueling station’s increased degree of excessive pessimism makes it likely that its increased accuracy in forecasting green hydrogen demand will cause the hydrogen refueling station to become progressively more optimistic about the green hydrogen market, and then the minimum execution quantity $n^{*}$ will instead increase.

Proposition 9. 

$\partial Q_0^{*}/\partial P<0$, $\partial Q_0^{*}/\partial C_r<0$, $\partial Q_0^{*}/\partial P_0>0$, $\partial Q_0^{*}/\partial P_2>0$, $\partial Q_0^{*}/\partial \theta >0$.

Proof. 

The partial derivation can be obtained by solving for the initial period $P_2$ the optimal ordering quantity $Q_0^{*}$ with respect to the market selling price of green hydrogen $P$, the contingent purchasing cost $C_r$, the initial ordering price $P_0$, the second-order option price, and the delayed price discount $\theta$:

$\partial Q_0^{*}/\partial P={-\left(1-\theta \right)P_0{f}^{\prime }{\left(B\right)}^{-1}/\left(P-P_2+C_r-\theta P\right)}^2<0$; $\partial Q_0^{*}/\partial C_r=-{P_0{f}^{\prime }{\left(B\right)}^{-1}/\left(P-P_2+C_r-\theta P\right)}^2<0$; $\partial Q_0^{*}/\partial P_0=P_0{f}^{\prime }{\left(B\right)}^{-1}/\left(P-P_2+C_r-\theta P\right)>0$; $\partial Q_0^{*}/\partial P_2=P_0{f}^{\prime }{\left(B\right)}^{-1}/{\left(P-P_2+C_r-\theta P\right)}^2>0$; $\partial Q_0^{*}/\partial \theta =P{P}_0{f}^{\prime }{\left(B\right)}^{-1}/{\left(P-P_2+C_r-\theta P\right)}^2>0$. □

Proposition 9 shows that under the option contract, the initial option ordering quantity at the hydrogen refueling station $Q_0^{*}$ is affected by the green hydrogen market sales price $P$, the contingent purchase cost $C_r$, the initial ordering price $P_0$, the second-order option price $P_2$, and the deferred price discount $\theta$. The initial option subscription decreases as the green hydrogen market selling price $P$ and the contingency purchase cost $C_r$ of the hydrogen refueling station increase. The higher the market price of green hydrogen, the higher the price risk borne by the hydrogen refueling station, and in order to avoid the potential loss caused by the high price, the hydrogen refueling station will reduce the initial ordering quantity to minimize the risk. An increase in the cost of contingency purchases by the hydrogen refueling station will also motivate the station to reduce the initial ordering quantity, because the station needs to find a balance between initial option ordering and contingency purchases. The higher the cost of contingency procurement, the relatively less attractive the initial ordering is, and the hydrogen refueling station will reduce its initial ordering quantity to avoid paying too high an option fee. The initial option ordering quantity $Q_0^{*}$ increases as the initial ordering price $P_0$, the second-order option price $P_2$, and the delayed price discount $\theta$ increase. The higher the initial option price and the second-order option price, the higher or more volatile the market price of green hydrogen is expected to be in the future. In order to lock in the current price and avoid the risk of future price increases, hydrogen refueling stations often tend to increase the initial subscription quantity to ensure that they can satisfy future demand at a lower cost. An increase in deferred price discounts can similarly squeeze the margins of hydrogen fueling stations, causing them to increase their initial ordering quantities to avoid the deferred penalties associated with insufficient inventory. Through the strategic structuring of derivative contracts, such as dynamic adjustments of first- and second-order option premiums, supply chain participants are incentivized to collaboratively assume risk, optimize resource allocation, and enhance overall supply chain efficiency. This approach not only facilitates the reduction in green hydrogen production costs but also strengthens its competitiveness within the energy market, thereby promoting the sustainable development of the green hydrogen industry.

Proposition 10. 

$\partial n^{*}/\partial P_1>0$; $\partial n^{*}/\partial S_r<0$; if $P_1<S_r$, $\partial n^{*}/\partial P_2<0$; if $P_1>S_r$, $\partial n^{*}/\partial P_2>0$.

Proof. 

The partial derivatives of the minimum execution quantity $n^{*}$ with respect to the first-order option price $P_1$, the second-order option price $P_2$, and the residual value of a unit of green hydrogen $S_r$ are as follows:

$\partial n^{*}/\partial P_1=f^{\prime }{\left(H\right)}^{-1}/\left(S_r-P_2\right)>0$; $\partial n^{*}/\partial S_r=\left(P_1-P_2\right)f^{\prime }{\left(H\right)}^{-1}/{\left(S_r-P_2\right)}^2<0$; $\partial n^{*}/\partial P_2=\left(P_1-S_r\right)f^{\prime }{\left(H\right)}^{-1}/{\left(S_r-P_2\right)}^2$, if $P_1<S_r$, $\partial n^{*}/\partial P_2<0$; if $P_1>S_r$, $\partial n^{*}/\partial P_2>0$. □

Proposition 9 shows that under the option contract, the minimum execution quantity of a hydrogen refueling station is affected by the first-order option price $P_1$, the second-order option price $P_2$, and the residual value of a unit of green hydrogen $S_r$. The minimum execution quantity increases with the first-order option price $P_1$ because the hydrogen refueling station reduces the first-order ordering quantity and orders the remaining demand through the second-order option price, which reduces the option cost per unit of green hydrogen. The minimum execution quantity decreases as the residual value per unit of green hydrogen $S_r$ increases, and when the residual value per unit of green hydrogen $S_r$ exceeds the first-order option price $P_1$, the minimum execution quantity decreases as the second-order option price $P_2$ increases. This is because hydrogen refueling stations resort to increasing the initial option subscription to avoid executing more residual option executions at higher second-order option prices, while relying on higher residual values per unit to compensate for possible inventory backlogs.

5.2. Optimal Production Decisions for a Hydrogen Production Station

Under the option contract model, the hydrogen refueling station shares the risk of random green hydrogen output to a certain extent, which facilitates the optimal production decisions of the hydrogen production station based on the optimal ordering quantity from the upstream hydrogen refueling station, as well as the number of first-order option executions. When the hydrogen production station is excessively pessimistic about the green hydrogen output rate, the expression for its profit function is depicted as follows:

If $D>Q_0$, the hydrogen production station needs to meet the additional demand through emergency production, and the station’s profit function is ${\pi }_m=P_0{Q}_0+P_{1}n+P_2\left(Q_0-n\right)-\left(C_m-w\right){\left(Q_0-\mathsf{\Phi }R\right)}^{+}+S_m{\left(\mathsf{\Phi }R-Q_0\right)}^{+}-C_{0}R$. If $Q_0>D>n$, it means that the hydrogen production station earns revenue by selling the initial ordering quantity and the portion of emergency production while bearing the cost of green hydrogen production and emergency production, in which case the hydrogen production station’s profit function is ${\pi }_m=P_0{Q}_0+P_{1}n+P_2\left(D-n\right)-\left(C_m-w\right){\left(D-\mathsf{\Phi }R\right)}^{+}+S_m{\left(\mathsf{\Phi }R-D\right)}^{+}-C_{0}R$. If $n>D$, it means that the hydrogen refueling station does not have to pay the second-order option cost, and the hydrogen production station’s profit function is ${\pi }_m=P_0{Q}_0+P_{1}n-\left(C_m-w\right){\left(n-\mathsf{\Phi }R\right)}^{+}+S_m{\left(\mathsf{\Phi }R-n\right)}^{+}-C_{0}R$.

In summary, the expected profit function of the hydrogen production station is

$$\begin{array}{cc}E\left({\pi }_m\right)& ={\displaystyle {\int }_{Q_0}^{\infty }\left[P_0{Q}_0+P_{1}n+P_2\left(Q_0-n\right)-\left(C_m-w\right){\left(Q_0-\mathsf{\Phi }R\right)}^{+}+S_m{\left(\mathsf{\Phi }R-Q_0\right)}^{+}-C_{0}R\right]}f\left(z\right)dz\\ & +{\displaystyle {\int }_n^{Q_0}\left[P_0{Q}_0+P_{1}n+P_2\left(D-n\right)-\left(C_m-w\right){\left(D-\mathsf{\Phi }R\right)}^{+}+S_m{\left(\mathsf{\Phi }R-D\right)}^{+}-C_{0}R\right]}f\left(z\right)dz\\ & +{\displaystyle {\int }_0^{Q_0}\left[P_0{Q}_0+P_{1}n-\left(C_m-w\right){\left(n-\mathsf{\Phi }R\right)}^{+}+S_m{\left(\mathsf{\Phi }R-n\right)}^{+}-C_{0}R\right]}f\left(z\right)dz\end{array}$$

(10)

$$\begin{array}{cc}E\left({\pi }_m\right)& =P_0{Q}_0+P_{1}n-C_{0}R+P_2\left\{{\displaystyle {\int }_{Q_0}^{\infty }\left(Q_0-n\right)}f\left(z\right)dz+{\displaystyle {\int }_n^{Q_0}\left(D-n\right)f\left(z\right)dz}\right\}\\ & -\left(C_m-w\right)\left\{{\displaystyle {\int }_0^{\frac{Q_0}{R}}\left(Q_0-\mathsf{\Phi }R\right)g\left(z\right)dz+{\displaystyle {\int }_n^{Q_0}{\displaystyle {\int }_0^{\frac{Q_0}{R}}\left(D-\mathsf{\Phi }R\right)g\left(z\right)dzf\left(z\right)dz+{\displaystyle {\int }_0^{\frac{n}{R^{\prime }}}\left(n-\mathsf{\Phi }R\right)g\left(z\right)dz}}}}\right\}\\ & +S_m\left\{{\displaystyle {\int }_{\frac{Q_0}{R}}^{\infty }\left(\mathsf{\Phi }R-Q_0\right)g\left(z\right)dz+{\displaystyle {\int }_n^{Q_0}{\displaystyle {\int }_{\frac{Q_0}{R}}^{\infty }\left(\mathsf{\Phi }R-D\right)g\left(z\right)dzf\left(z\right)dz+{\displaystyle {\int }_{\frac{n}{R}}^{\infty }\left(\mathsf{\Phi }R-n\right)g\left(z\right)dz}}}}\right\}\end{array}$$

(11)

Proposition 11. 

The expected profit of the hydrogen production station $E\left({\pi }_m\right)$ under the option contract is a concave function about $R$ and there exists a unique optimal solution, which $R^{**}$ satisfies

$$\begin{array}{c}\left(1-\gamma \right)\left({\displaystyle {\int }_0^U{G}_{\varphi }\left(z\right)dz+{\displaystyle {\int }_0^V{G}_{\varphi }\left(z\right)dz}}\right)+{\displaystyle {\int }_{\frac{n-\left({\lambda }_1+1\right)\alpha {\mu }_1}{1-\alpha }}^{\frac{Q-\left({\lambda }_1+1\right)\alpha {\mu }_1}{1-\alpha }}{\displaystyle {\int }_0^W{G}_{\varphi }\left(z\right)dz{f}_d\left(z\right)dz}}\\ \hspace{1em}\hspace{1em}\hspace{1em}=\left(1-\gamma \right)R^{**}{G}_{\varphi }\left(W\right)\left(1-{\displaystyle \frac{P_1}{\left(1-\alpha \right)\left(P-P_2+C_r-\theta P\right)}}-{\displaystyle \frac{P_1-P_2}{S_r-P_2}}\right)+\left[G_{\varphi }\left(U\right)+G_{\varphi }\left(V\right)\right]/R^{**}\end{array}$$

(12)

where $U={\displaystyle \frac{\frac{Q}{R^{**}}-\left({\lambda }_2+1\right)\gamma {\mu }_2}{1-\gamma }}$, $V={\displaystyle \frac{\frac{n}{R^{**}}-\left({\lambda }_2+1\right)\gamma {\mu }_2}{1-\gamma }}$, and $W={\displaystyle \frac{\frac{d}{R^{**}}-\left({\lambda }_2+1\right)\gamma {\mu }_2}{1-\gamma }}$.

Proof. 

Simplifying Equation (11),

$$\begin{array}{cc}E\left({\pi }_m\right)& =P_0{Q}_0+P_{1}n-C_{0}R+P_2\left\{{\displaystyle {\int }_{Q_0}^{\infty }\left(Q_0-n\right)}{f}_D\left(z\right)dz+{\displaystyle {\int }_n^{Q_0}\left(D-n\right)f_D\left(z\right)dz}\right\}\\ & +\left(C_m-w\right)R\left({\displaystyle {\int }_0^{\frac{Q_0}{R}}{G}_{\eta }\left(z\right)dz+{\displaystyle {\int }_0^{\frac{n}{R}}{G}_{\eta }\left(z\right)dz}}\right)-S_{m}R\left({\displaystyle {\int }_{\frac{Q_0}{R}}^{+\infty }{G}_{\eta }\left(z\right)dz+{\displaystyle {\int }_{\frac{n}{R}}^{+\infty }{G}_{\eta }\left(z\right)dz}}\right)\\ & -R{\displaystyle {\int }_n^{Q_0}\left[\left(C_m-w\right){\displaystyle {\int }_0^{\frac{Q_0}{R}}{G}_{\eta }\left(z\right)dz+S_m{\displaystyle {\int }_{\frac{Q_0}{R}}^{+\infty }{G}_{\eta }\left(z\right)dz}}\right]}{f}_D\left(z\right)dz\end{array}$$

The derivative with respect to $R$ for $E\left({\pi }_m\right)$ is

${\displaystyle \frac{\partial E\left({\pi }_m\right)}{\partial R}}=\left(1-\gamma \right)\left({\displaystyle {\int }_0^U{G}_{\eta }\left(z\right)dz+{\displaystyle {\int }_0^V{G}_{\eta }\left(z\right)dz}}\right)-{\displaystyle {\int }_{\frac{n-\left({\lambda }_1+1\right)\alpha {\mu }_1}{1-\alpha }}^{\frac{Q-\left({\lambda }_1+1\right)\alpha {\mu }_1}{1-\alpha }}{\displaystyle {\int }_0^W{G}_{\eta }\left(z\right)dz{f}_d\left(z\right)dz}}$, $-\left(1-\gamma \right)R{G}_{\eta }\left(W\right)\left(1-{\displaystyle \frac{P_1}{\left(1-\alpha \right)\left(P-P_2+C_r-\theta P\right)}}-{\displaystyle \frac{P_1-P_2}{S_r-P_2}}\right)-\left[G_{\eta }\left(U\right)+G_{\eta }\left(V\right)\right]/R$. Let ${\displaystyle \frac{\partial E\left({\pi }_m\right)}{\partial R}}=0$, and the optimal planned production quantity $R^{**}$ can be satisfied as follows:

$$\left(1-\gamma \right)\left({\displaystyle {\int }_0^U{G}_{\varphi }\left(z\right)dz+{\displaystyle {\int }_0^V{G}_{\varphi }\left(z\right)dz}}\right)+{\displaystyle {\int }_{\frac{n-\left({\lambda }_1+1\right)\alpha {\mu }_1}{1-\alpha }}^{\frac{Q-\left({\lambda }_1+1\right)\alpha {\mu }_1}{1-\alpha }}{\displaystyle {\int }_0^W{G}_{\varphi }\left(z\right)dz{f}_d\left(z\right)dz}}$$

$$=\left(1-\gamma \right)R^{**}{G}_{\varphi }\left(W\right)\left(1-{\displaystyle \frac{P_1}{\left(1-\alpha \right)\left(P-P_2+C_r-\theta P\right)}}-{\displaystyle \frac{P_1-P_2}{S_r-P_2}}\right)+\left[G_{\varphi }\left(U\right)+G_{\varphi }\left(V\right)\right]/R^{**}$$

where $U={\displaystyle \frac{\frac{Q}{R^{**}}-\left({\lambda }_2+1\right)\gamma {\mu }_2}{1-\gamma }}$, $V={\displaystyle \frac{\frac{n}{R^{**}}-\left({\lambda }_2+1\right)\gamma {\mu }_2}{1-\gamma }}$, and $W={\displaystyle \frac{\frac{d}{R^{**}}-\left({\lambda }_2+1\right)\gamma {\mu }_2}{1-\gamma }}$. □

Proposition 11 shows that under the option contract, the optimal planned production of the hydrogen production station $R^{**}$ decreases as its excessive pessimism factor $\gamma$ decreases; i.e., the optimal planned production decreases as the hydrogen production station’s level of excessive pessimism increases. This is because excessive pessimism causes the hydrogen station to be more inclined to be risk-averse, worrying about over-production leading to stagnation and losses and resource wastage due to low output rates. At the same time, the optimal planned production of the hydrogen production station is also affected by the excessive pessimism of the hydrogen refueling station, because excessive pessimism of the hydrogen refueling station has a conservative attitude towards the green hydrogen market, and the expected lower demand makes the station more inclined to reduce the ordering quantity, and the hydrogen production station chooses to reduce the production quantity in order to avoid stagnation and loss of sales. In addition, the optimal planned production quantity increases as the emergency purchasing cost of the hydrogen refueling stations $C_r$ and the residual value of the green hydrogen unit $S_r$ increase. It decreases as the market price of green hydrogen $P$ increases. In option contract pricing, it increases only with the increase in the first-order option price. This is because the optimal initial option ordering quantity for the hydrogen refueling station decreases as the initial option price and the second-order option price increase, while the first-order option price does not affect it.

6. Arithmetic Analysis

6.1. Assessment of Excessively Pessimistic Bias

The magnitude of excessive pessimism levels is generally influenced by factors such as corporate personality traits, cognitive capabilities, risk preferences, market environment, organizational culture, and company performance. Multivariate regression analysis can be employed to examine the impact of internal and external factors on excessive pessimism levels and operational decision-making. This section primarily explores estimation methods for excessive pessimism levels and the relationship between two such levels using case company data. Taking hydrogen station excessive pessimism as an example, with the set $x_1,x_2,\cdot \cdot \cdot ,x_n$ representing a sample of $D$ observations, the maximum likelihood estimates for the excessive pessimism levels $\alpha$ and $\beta$ can be obtained accordingly.

$$\alpha ={\displaystyle \frac{1}{\sqrt{n}\sigma }}\left[1-\sqrt{{\displaystyle \sum _{i=1}^n{\left(x_i-\frac{1}{n}{\displaystyle \sum _{i=1}^n{x}_i}\right)}^2}}\right]$$

(13)

$$\beta ={\displaystyle \frac{1}{n\mu }}{\displaystyle \sum _{i=1}^n{x}_i}$$

(14)

Using the monthly production and sales volume data of the Inner Mongolia Shengyuan Energy Group from 2019 to 2024, sourced from the company’s annual reports, this analysis simplifies the market demand estimation by excluding the influence of comparable brands or similar hydrogen energy demands. Additionally, it disregards factors such as hydrogen refueling station inventory levels and delivery lead times. Monthly sales are treated as the actual market demand, while monthly production is considered a sample observation reflecting demand estimates based on overly conservative assumptions regarding hydrogen station capacity.

Based on the aforementioned assumptions, a significance level of 0.01 was adopted. The Kolmogorov–Smirnov test indicates that the green hydrogen market demand for the Inner Mongolia Shengyuan Energy Group from 2019 to 2024 follows a normal distribution. The annual normal distribution parameters are summarized in

Table 3. K-S test results for monthly sales data of Shengyuan Energy in Inner Mongolia.

Year	Case Count	Normal Distribution Parameters		Statistical Hypothesis Testing	Asymptotic Significance (Two-Tailed)
		Mean Value	Standard Deviation
2019	12	847.35	122.48	0.0682	0.200 a,b
2020	12	905.12	113.67	0.0721	0.200 a,b
2021	12	884.76	128.93	0.0593	0.200 a,b
2022	12	827.49	126.54	0.0814	0.050 a
2023	12	872.83	117.36	0.0635	0.035 a,b
2024	12	893.21	121.09	0.0756	0.200 a,b

^a. Lilliefors significance correction; ^b. Lower limit of true significance.

.

Assuming the excessive pessimism level at the hydrogen refueling station remains constant within the same year, and utilizing Table 2, the maximum likelihood estimation method is employed to determine the annual excessive pessimism levels. Consequently, the excessive pessimism coefficients for the Inner Mongolia Shengyuan Energy Group from 2019 to 2024 are derived, as presented in

Table 4. Excessively pessimistic coefficient of Shengyuan Energy in Inner Mongolia.

Year	α	β
2019	−0.147235	0.912874
2020	−0.092548	0.921736
2021	−0.218763	0.898125
2022	−0.305487	0.873652
2023	−0.119872	0.930258
2024	−0.187324	0.903821

.

The excessive pessimism level of the hydrogen refueling station’s impact on prediction accuracy, denoted as variable $\alpha$, and the excessive pessimism level of the station’s expected demand, denoted as variable $\beta$, are modeled using a linear regression framework $\beta =k\alpha +l+\epsilon$, with $\epsilon$ representing the residual error. Based on Table 3, at a significance level of 0.01, the derived linear regression equation is $\beta =0.086\alpha +1.002$, with the ratio of the regression sum of squares to the total sum of squares being $R^2=0.511$, indicating a statistically significant model fit. Empirical data analysis confirms the validity of the hypothesized relationship between the excessive pessimism levels $\alpha$ and $\beta$, demonstrating a significant linear correlation between these coefficients.

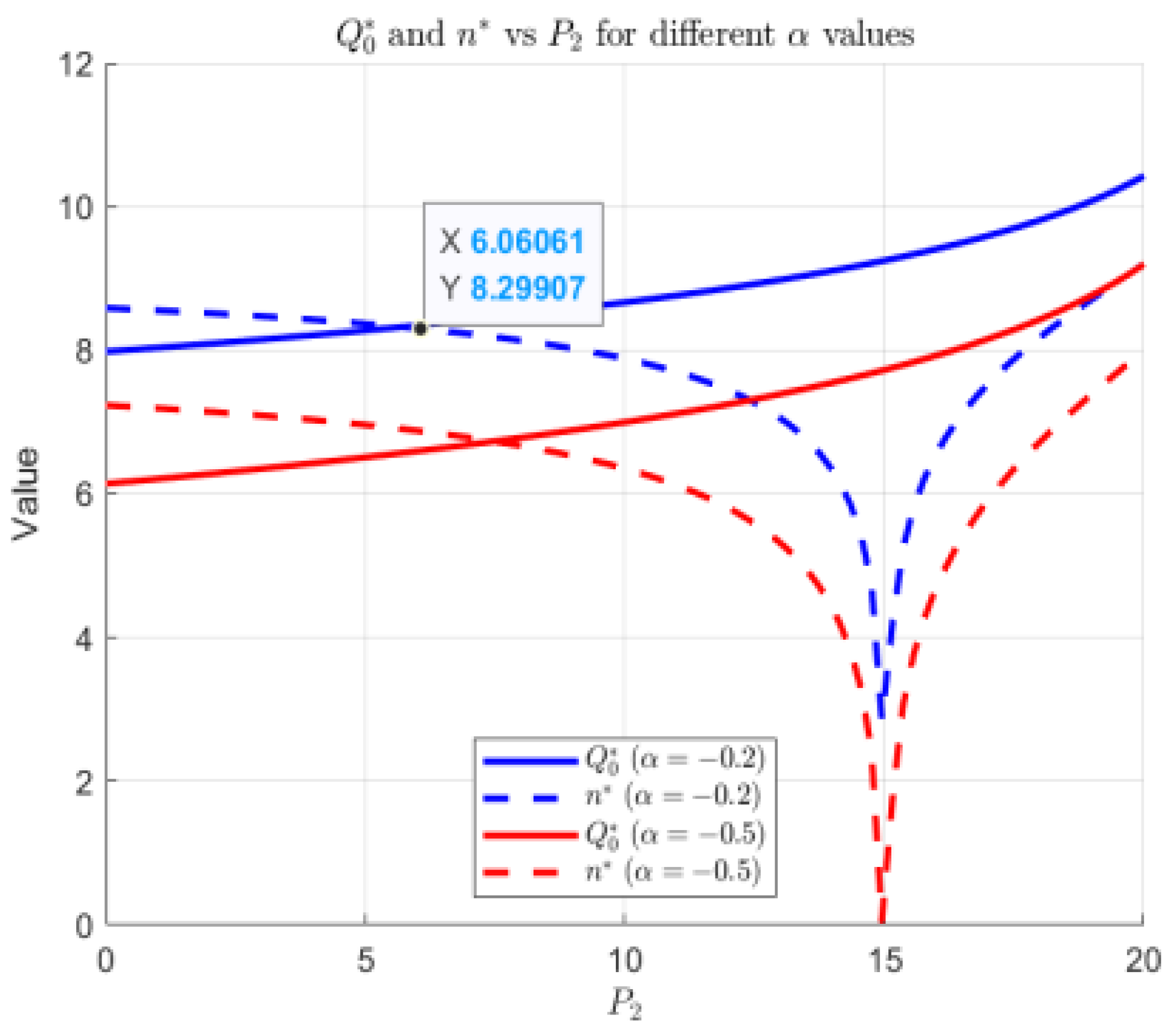
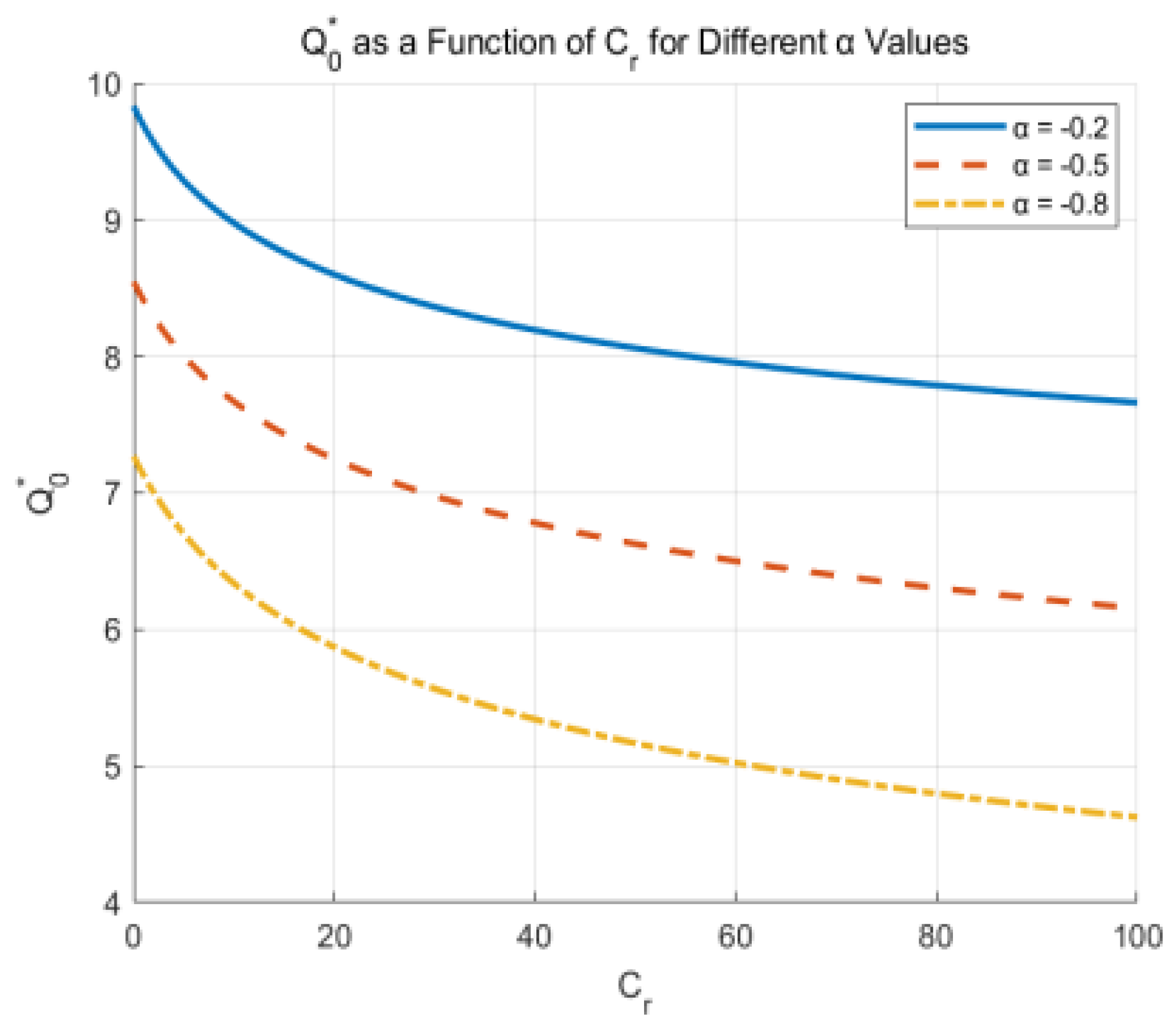
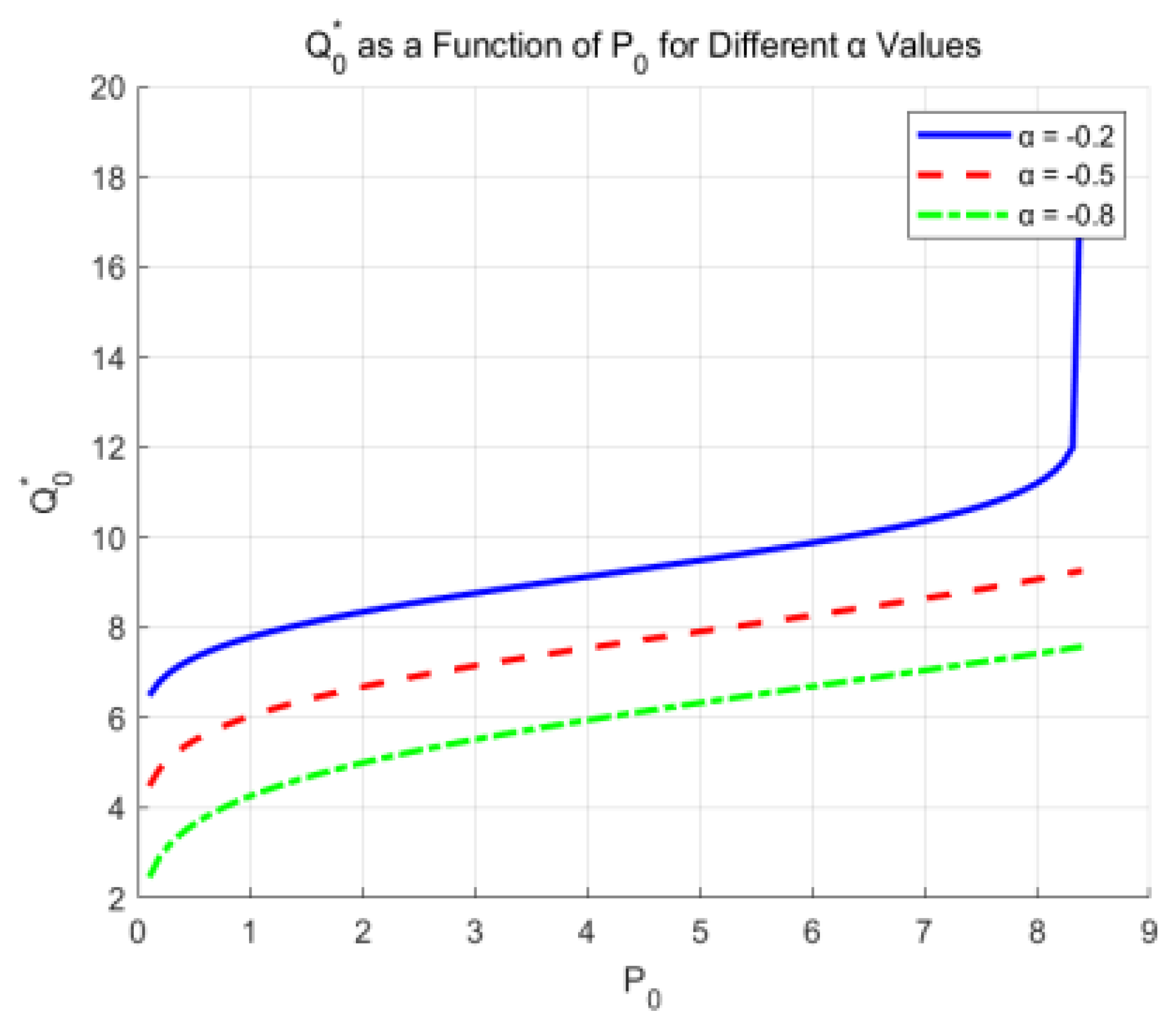
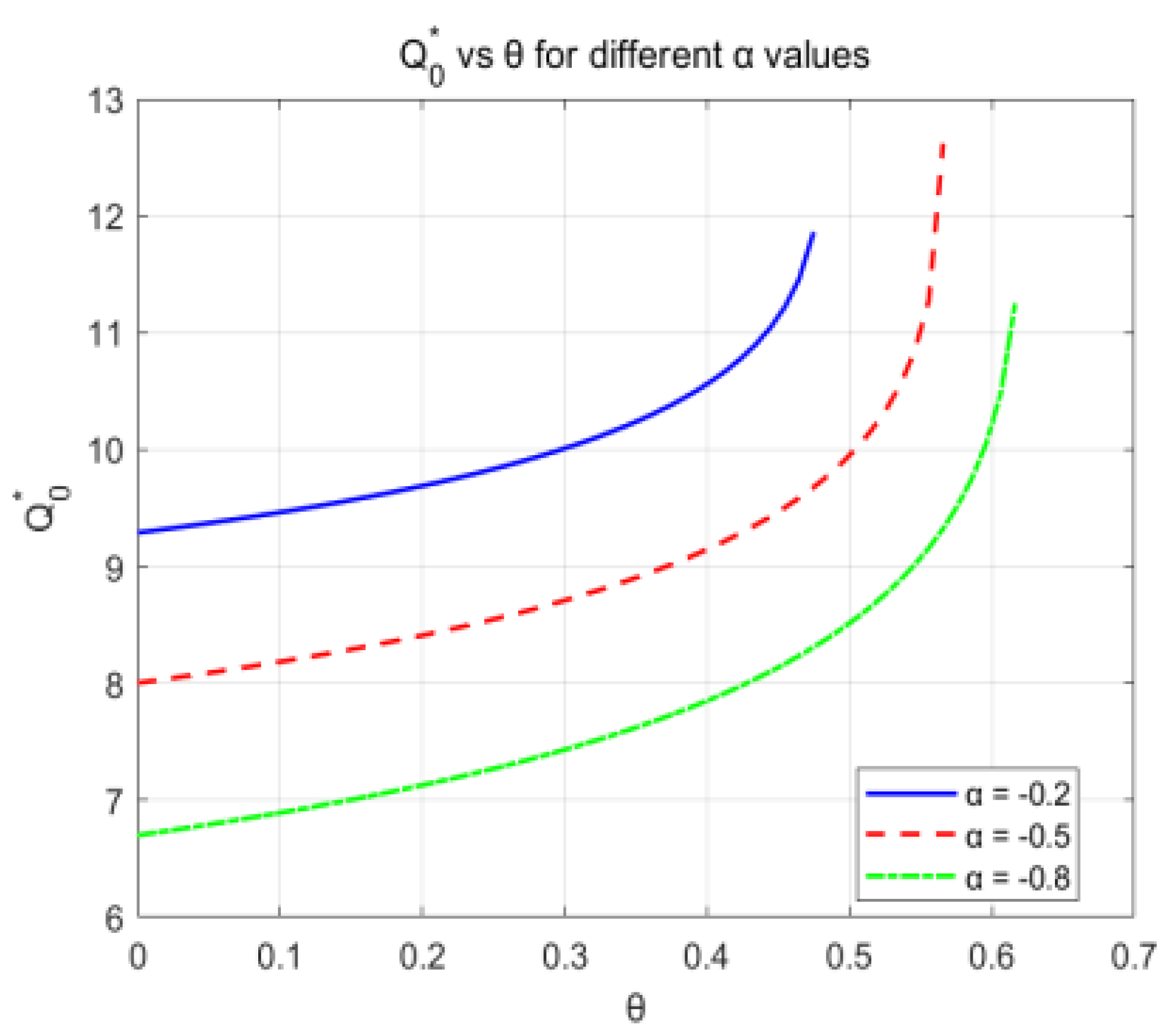
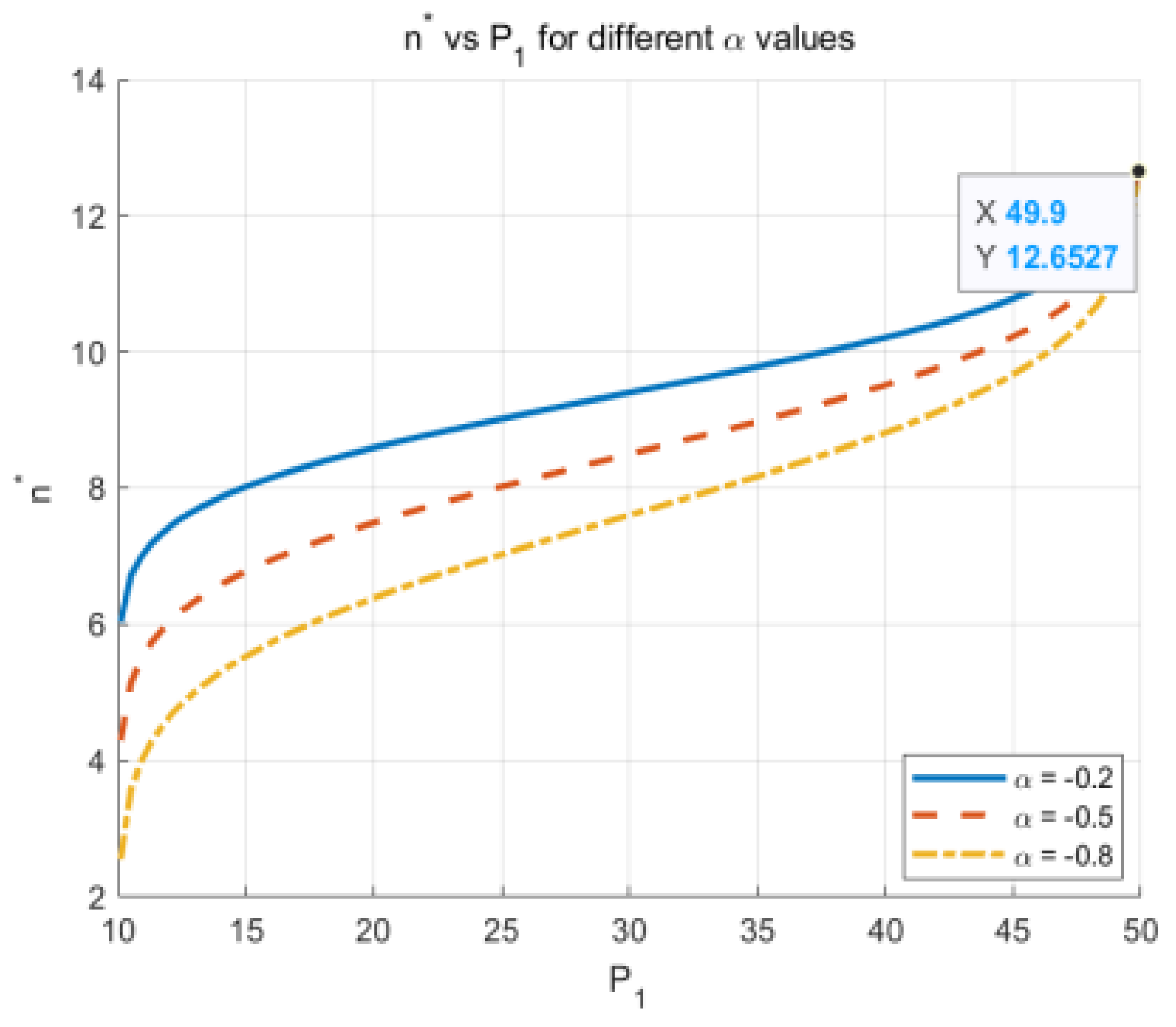
6.2. Analysis of Contributing Factors

This section employs numerical simulation to analyze the impact of excessive pessimism on decision-making processes at hydrogen refueling stations and hydrogen production facilities, validating the effects of option price fluctuations and parameters such as costs and residual values on procurement strategies for refueling stations and production strategies for hydrogen plants. In conjunction with China’s hydrogen energy development policies, such as the “Dalian Hydrogen Industry Development Special Fund Management Measures (2023–2025)”, which stipulate that the green hydrogen sales price at refueling stations should not exceed CNY 20 per kilogram, the terminal market price upper limit in the model is set at CNY 20 per kilogram, designated as $P=20$. Based on the “China Hydrogen Industry Development Report,” the cost of alkaline electrolysis for hydrogen production is estimated at approximately CNY 8–10 per kilogram [52]. Incorporating a reasonable profit margin of 15–20%, the wholesale price range is established at CNY 12–15 per kilogram (cost-plus pricing after subsidies). Consequently, the cost of green hydrogen via alkaline electrolysis is denoted as $C_0=10$, while the subsidized wholesale price is expressed as $w=10$, which is reduced by 30% compared to the unsubsidized scenario. Furthermore, the “China Hydrogen Market Trading Report” explicitly indicates that emergency transaction prices for hydrogen typically exceed the benchmark price by 20% to 40% [53]. Consequently, the emergency procurement cost for refueling stations and the emergency production cost for hydrogen production plants are designated as $C_r=10$ and $C_m=10$, respectively. Since neither the hydrogen production plants nor the refueling stations involve secondary processing or quality modification of green hydrogen, any unsold green hydrogen from the production plants can be directly resold to other purchasers, possessing an equivalent liquidity value to unsold green hydrogen from refueling stations. Referencing residual value ratios of comparable energy commodities (such as methanol and natural gas), generally ranging from 5% to 10%, the residual value $S_m=2$ and $S_r=2$ are adopted for an initial green hydrogen price $P=20$, conforming to the 5% to 10% proportional interval.

Regarding the definition of option prices within the option contract, this study references Chen’s research on option pricing under optimal supply chain conditions [13], Wang’s conditions for supply chain coordination involving option prices and strike prices [14], and other related studies [16,17]. The following assumptions are made: initial option price $P_0=5$, first-order option price $P_1=8$, second-order option price $P_2=10$, and a discount rate $\theta =0.6$ for delayed green hydrogen delivery. Additionally, drawing from the case study of Inner Mongolia Shengyuan Energy Group in Section 6.1, for computational convenience, monthly sales and production volumes are proportionally scaled down. It is assumed that the market demand for green hydrogen and the green hydrogen output rate follow a normal distribution: $X~N\left(20,2^2\right)$ and $\varphi ~N\left(0.8,2^2\right)$.

Figure 2 demonstrates the effect of the level of excessive pessimism on the optimal ordering quantity of a hydrogen refueling station by taking ${\mu }_1=20$ and ${\mu }_1=25$, which satisfy ${\mu }_1<F_d^{-1}\left({\displaystyle \frac{P+C_r-\theta P-w}{P-S_r-C_r+\theta P}}\right)/\left({\lambda }_1+1\right)$ and ${\mu }_1>F_d^{-1}\left({\displaystyle \frac{P+C_r-\theta P-w}{P-S_r-C_r+\theta P}}\right)/\left({\lambda }_1+1\right)$ in Proposition 2, respectively, and it can be seen that the optimal ordering quantity of a hydrogen refueling station under excessive pessimism is not necessarily lower than that of the optimal ordering quantity at the time of rationality, and it does not necessarily decrease with the increase in its excessive pessimism factor, verifying the conclusions of Proposition 2 and Proposition 3.

Figure 3 illustrates the relationship between the optimal ordering quantity of the hydrogen refueling station $Q^{*}$ and the excessive pessimism factor $\alpha$ and the green hydrogen market demand expectation ${\mu }_1$. It can be seen that when the green hydrogen market demand expectation is high, the optimal ordering quantity of the hydrogen refueling station decreases with the increase in the excessive pessimism degree. When the green hydrogen market demand expectation is low, it increases with the increase in the degree of excessive pessimism, which is due to the fact that the hydrogen refueling stations may choose to increase the ordering quantity to satisfy the market demand for the improvement of the accuracy of the green hydrogen market demand prediction. When hydrogen stations are extremely pessimistic, the greater the demand in the green hydrogen market, the smaller the stations’ ordering quantities become, because the extreme pessimism of hydrogen stations causes them to drastically reduce their ordering quantities in order to avoid the risks of capital being tied up in inventory and loss of market share.

The optimal ordering quantity of the hydrogen station under excessive pessimism, the optimal ordering quantity under rationality, and the initial ordering quantity under the option contract are calculated with the level of excessive pessimism measured in Section 6.1 and the relevant parameter settings of the enterprise, as shown in

Table 5. Comparison of optimal ordering quantities for hydrogen refueling stations.

Excessive Pessimism Level	Market Demand Expectation Value	Optimal Order Quantity Under Excessive Pessimism	Optimal Order Quantity Under Rational Conditions	Initial Option Order Quantity
−0.147235	40	38.5	35	41.8
−0.092548	35	34.2	32	39.2
−0.218763	20	19.8	22	20.9
−0.305487	15	14.5	16	13.7

. By comparing the optimal ordering quantities under different scenarios, it can be found that the optimal ordering quantity under excessive pessimism is not necessarily lower than the ordering quantity under rationality, and when the level of excessive pessimism is low, the option contract can effectively increase the ordering quantity of the hydrogen refueling station. The conclusions of Propositions 2–3 are verified.

Figure 4 shows the variation in the optimal planned production of the hydrogen production station $R^{*}$ with the excessive pessimism factor $\gamma$. When the degree of excessive pessimism is greater than a certain threshold, the hydrogen production station chooses not to produce hydrogen. It can be seen that the optimal planned production $R^{*}$ is affected only when the degree of excessive pessimism of the hydrogen production station is low, and in this event, the optimal planned production $R^{*}$ increases as the degree of excessive pessimism decreases. This indicates that the more pessimistic the station is about the green hydrogen output rate, the more it tends to reduce its planned production to avoid the waste of resources caused by the low output rate.

Figure 5a takes the market demand as ${\mu }_1=40$ and ${\mu }_1=35$, satisfying $\left({\lambda }_1+1\right){\mu }_1\ge B+f^{\prime }{\left(B\right)}^{-1}/\left(1-\alpha \right)\left(P-P_2+C_r-\theta P\right)$ in Proposition 6 and $\left({\lambda }_1+1\right){\mu }_1\ge H$ in Proposition 7, indicating that in this case, both the initial option ordering quantity $Q_0^{*}$ and the minimum execution quantity $n^{*}$ increase as the degree of excessive pessimism of the hydrogen refueling station decreases. Meanwhile, we take ${\mu }_1=20$ and ${\mu }_1=15$ in Figure 5b, which shows that in this case, both the initial option ordering quantity $Q_0^{*}$ and the minimum execution quantity $n^{*}$ decrease as the degree of excessive pessimism of the hydrogen refueling station decreases. The conclusions of Proposition 7 and Proposition 8 are verified. Figure 5a,b also show that the initial option ordering quantity $Q_0^{*}$ is always larger than the minimum execution quantity $n^{*}$, which also verifies the initial assumption of the option contract model. It can be seen that the ordering quantity under the option contract is affected by various factors, so the decision maker needs to pay attention to the expectation of the demand in the green hydrogen market while considering excessive pessimism in order to set a reasonable option price and other parameters to improve the ordering quantity.

From Figure 6, it can be clearly seen that the initial option ordering quantity $Q_0^{*}$ increases with the increase in the second-order option price $P_2$, while the minimum execution quantity $n^{*}$ decreases at first and then increases with the increase in the second-order option price $P_2$. At the same time, when the second-order option price $P_2$ is at a certain value, the initial option ordering quantity and the minimum execution quantity are equal, which is due to the fact that when the second-order option price increases, the hydrogen refueling station will take the action of raising the initial option ordering quantity to satisfy the demand quantity and reduce the potential loss caused by the high final execution price. When the potential loss caused by the second-order option price is too high, the hydrogen refueling station prefers to satisfy the green hydrogen demand through the minimum execution quantity.

Figure 7, Figure 8, Figure 9 and Figure 10 demonstrate the effect of the market selling price of green hydrogen $P$, the contingent purchase cost $C_r$, the initial ordering price $P_0$, and the delayed delivery discount rate $\theta$ on the initial option ordering quantity $Q_0^{*}$, verifying the conclusion of Proposition 9. Figure 11 and Figure 12 show the effects of the first-order option price $P_1$ and the residual value per unit of green hydrogen $S_r$ on the minimum execution quantity $n^{*}$, respectively, verifying the conclusions of Proposition 10.

Under the option contract, the level of excessive pessimism is taken as −0.2, and the initial option ordering quantity and the minimum execution quantity are derived by adjusting the green hydrogen market sales price and the option price, as shown in

Table 6. Impact of option prices on order quantity.

Selling Price of Green Hydrogen	First-Order Option Prices	Second-Order Option Prices	Initial Option Price	Excessive Pessimism Levels for Hydrogen Refueling Stations	Market Demand Expectation Value	Initial Option Order Quantity	Minimum Execution Quantity
20	8	15	5	−0.2	30	38.2	22.8
15 (−25%)	8	15	5	−0.2	30	44.4 (+16.2%)	22.8
25 (+25%)	8	15	5	−0.2	30	31.9 (−16.5%)	22.8
20	12 (+50%)	15	5	−0.2	30	38.2	25.6 (+12.3%)
20	14 (+75%)	15	5	−0.2	30	38.2	28.3 (+24.1%)
20	8	22.5 (+50%)	5	−0.2	30	49.6 (+29.8%)	17.5 (−23.2%)
20	8	25 (+67%)	5	−0.2	30	45.8 (+20.0%)	18.9 (−16.2%)
20	8	15	5.25 (+5%)	−0.2	30	42.6 (+11.5%)	22.8
20	8	15	6 (+20%)	−0.2	30	41.7 (+9.4%)	22.8

, which shows that the increase in the green hydrogen sales price negatively affects the initial option ordering quantity, whereas the increase in the initial option price and the second-order option price can increase the initial option ordering quantity. Meanwhile, the increase in the second-order option price decreases the minimum execution quantity, although the minimum execution quantity can be increased by increasing the first-order option price. The conclusions of Propositions 7–11 are verified.

Figure 13 shows that the optimal planned production of hydrogen production stations under the option contract is affected by both the excessive pessimism of hydrogen refueling stations and hydrogen production stations, and that the optimal planned production of hydrogen production stations increases with the degree of excessive pessimism regardless of the degree of pessimism of hydrogen refueling stations about the demand for green hydrogen in the market, and that the effect on the optimal planned production is more pronounced when hydrogen refueling stations tend to be rational. This is due to the fact that hydrogen refueling stations are more accurate in their forecasts of green hydrogen market demand and therefore need to order in large quantities, while hydrogen producers are more pessimistic about their own green hydrogen output rates and need to plan for higher production quantities to meet the orders of hydrogen refueling stations. In addition, optimal planned production increases as the level of excessive pessimism at hydrogen refueling stations decreases, and more optimism at hydrogen refueling stations about the green hydrogen market can lead to more demand for green hydrogen, which in turn can stimulate hydrogen production at hydrogen production stations to increase production.

7. Conclusions and Implications

7.1. Conclusions

In this paper, we construct a secondary green hydrogen supply chain consisting of upstream hydrogen production stations and downstream hydrogen refueling stations to explore the impact of excessively pessimistic behaviors of hydrogen refueling stations and hydrogen production stations on the ordering and production decisions under the uncertainty of the green hydrogen market demand and the green hydrogen output rate. An option contract model is immediately constructed to share the risk of stochastic green hydrogen output. Finally, numerical simulation reveals many factors affecting the ordering and production decisions in the green hydrogen supply chain. The main findings of this paper are as follows:

(1)

Under decentralized decision-making, the optimal ordering policy for hydrogen refueling stations operating under excessive pessimism may not necessarily be lower than that under rational expectations. Excessive pessimism among hydrogen refueling stations does not invariably exert a negative influence on ordering strategies; in fact, when the expected value of the green hydrogen market is low, it may lead to an increase in green hydrogen procurement volumes. Only when the hydrogen production plants exhibit a relatively mild degree of pessimism does this significantly impact the optimal production scheduling.

(2)

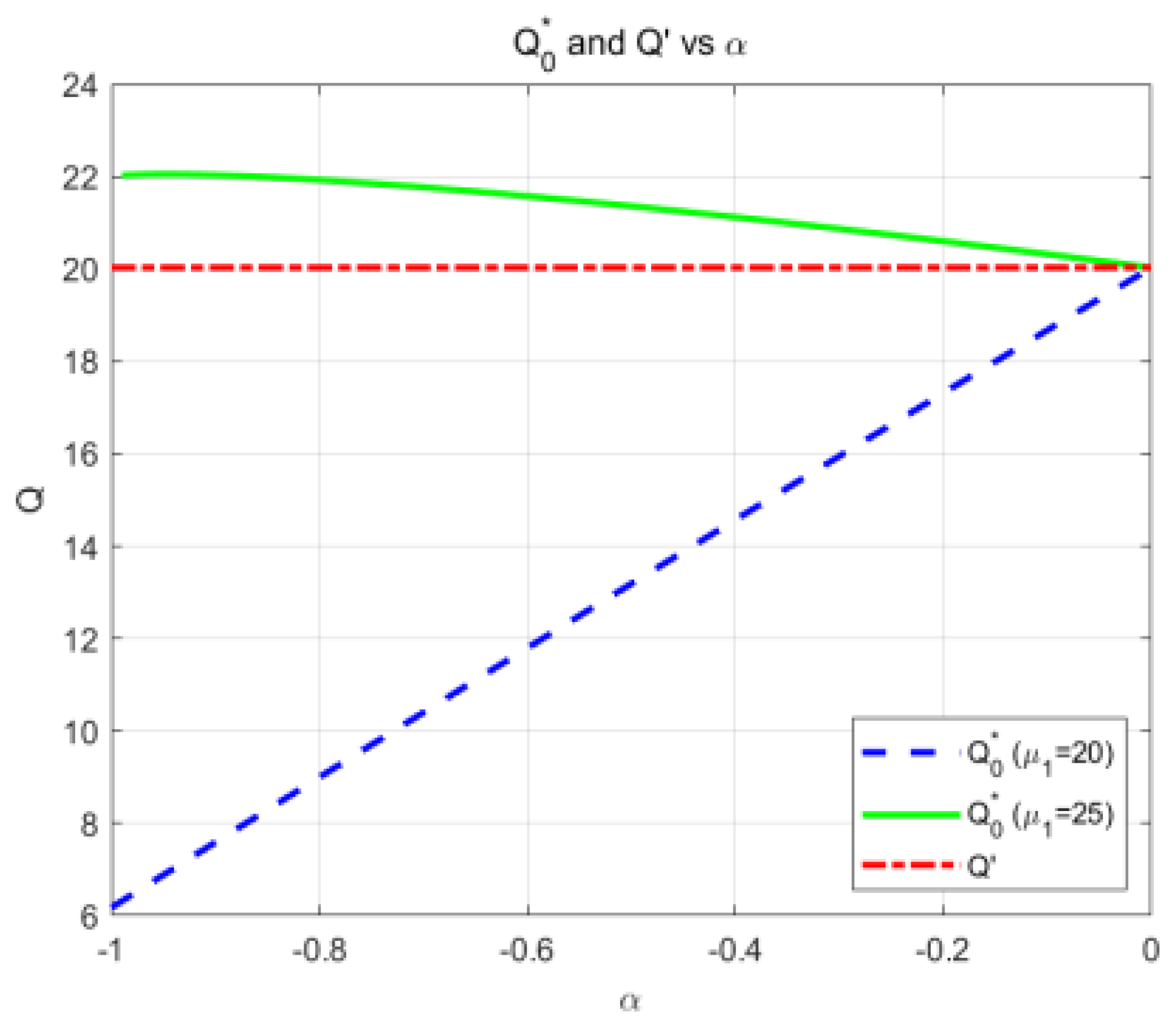
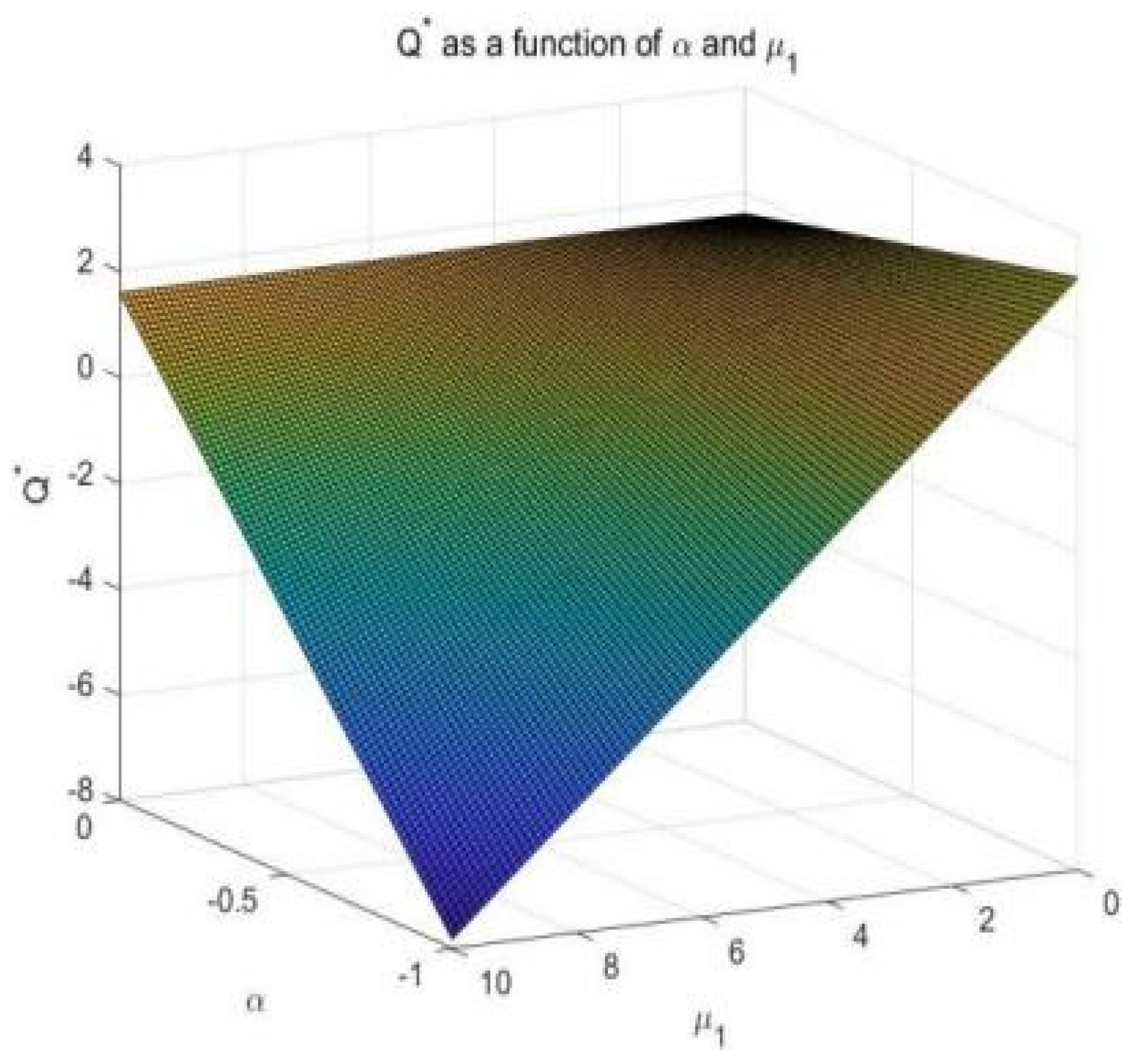
Under the option contract, initial option ordering and minimum execution quantity increase with decreasing levels of excessive pessimism and vice versa when green hydrogen market expectations are high. In addition, the initial option ordering quantity is always higher than the minimum execution quantity. Higher green hydrogen sales prices, contingency purchasing costs, and residual values of green hydrogen units all reduce the initial ordering quantity at hydrogen refueling stations.

(3)

The initial option ordering quantity and the minimum execution quantity are affected by the second-order option price at the same time. The initial option ordering quantity increases with the second-order option price, while the minimum execution quantity decreases with the second-order option price, and at the same time, the minimum execution quantity is only affected when the second-order option price is high enough. A design comprising a higher initial option price and first-order option price and a lower second-order option price design can effectively increase the ordering quantity in the green hydrogen supply chain.

(4)

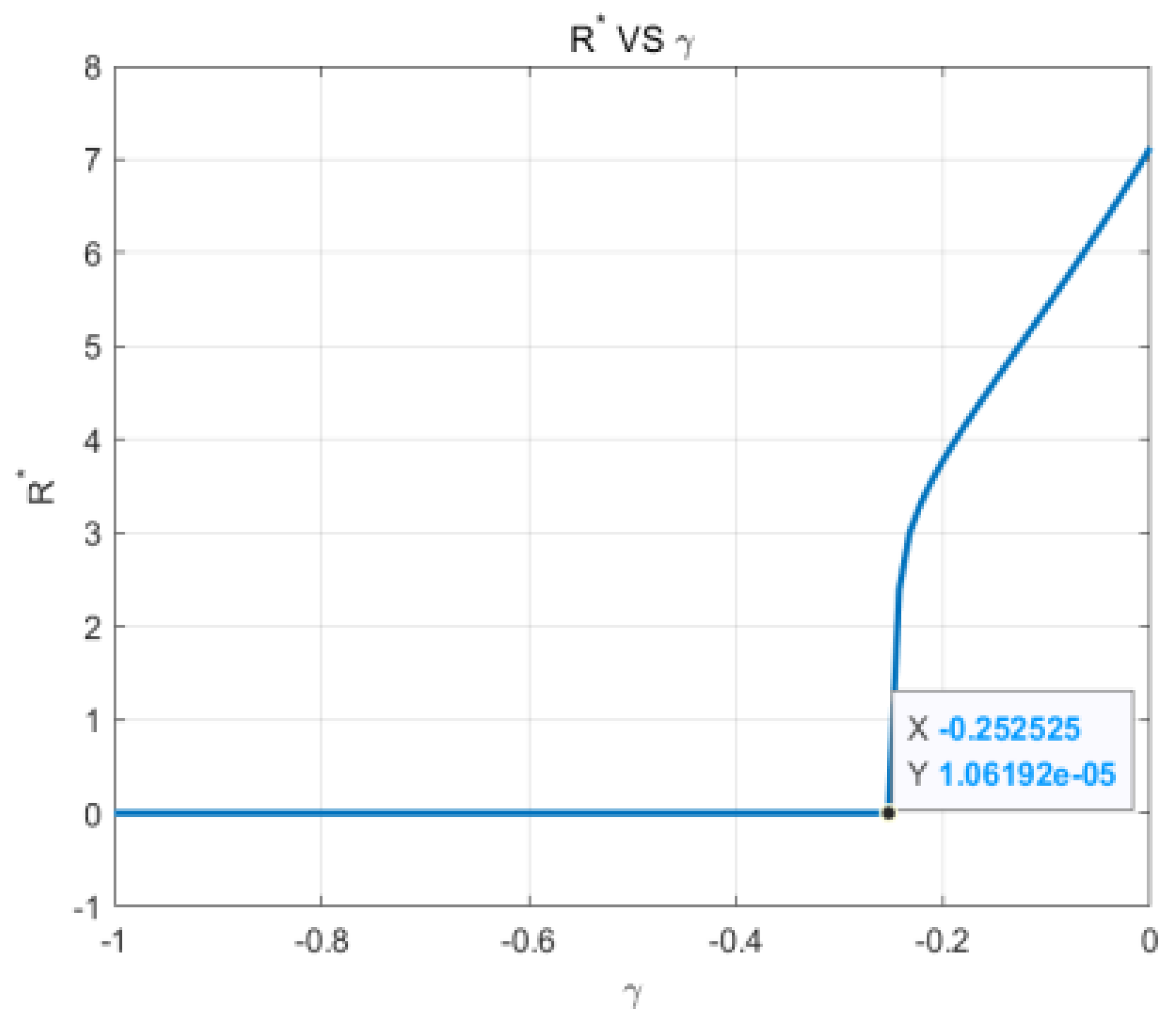
Under the option contract, the hydrogen station’s optimal planned production always increases with its own level of excessive pessimism, with the effect being most pronounced when the hydrogen station tends to be rational. Hydrogen stations’ excessive pessimism also reduces the optimal planned production.

7.2. Implications

Based on the findings of the above study, the management insights derived from this paper are as follows:

(1)

Hydrogen refueling stations need to rationally analyze the actual market demand data, flexibly use option contracts, and respond to demand fluctuations by dynamically adjusting the initial option ordering quantity and the minimum execution quantity. They also need to pay attention to the cost of emergency procurement and the residual value of green hydrogen utilization, weigh the pros and cons of initial ordering and emergency procurement, and optimize the inventory management strategy to reduce operational risks.

(2)

Hydrogen production facilities must develop optimized production schedules aligned with the procurement demands of refueling stations and their own manufacturing capacities. As market rationalization progresses, these facilities should scale up green hydrogen output to meet increasing demand. Through technological innovation and economies of scale, they can reduce green hydrogen production costs and enhance operational efficiency, thereby strengthening their competitiveness within the energy sector. Additionally, hydrogen production plants must monitor market demand fluctuations and adapt their production strategies flexibly to mitigate the risks associated with conservative procurement decisions by refueling stations.

(3)

An efficient information-sharing mechanism should be established between hydrogen production facilities and refueling stations to mitigate decision-making biases caused by information asymmetry. This will facilitate the better alignment of green hydrogen supply chain demand and supply, enabling joint responses to market uncertainties and reducing economic losses attributable to suboptimal decisions. The implementation of rational option contract designs, such as dynamic adjustments of first- and second-order option premiums, can incentivize supply chain participants to share risks collectively, thereby optimizing resource allocation and enhancing overall supply chain efficiency. Such measures not only contribute to lowering green hydrogen production costs but also to strengthening its competitiveness within the energy market, thus promoting the sustainable development of the green hydrogen industry.

(4)

Although the option contract model theoretically offers the effective optimization of supply chain decision-making and risk sharing, its practical implementation may encounter several challenges. To enhance the feasibility of this model within real-world green hydrogen supply chains, it is recommended to focus on the following aspects: firstly, simplifying the model design to improve comprehensibility and operational ease while maintaining its validity; secondly, establishing an efficient information-sharing mechanism to reduce asymmetries and bolster stakeholder trust; and thirdly, conducting pilot projects within limited scopes to accumulate experiential insights, refine the model, and facilitate gradual scaling. Finally, policymakers and industry associations should promote adoption through strategic policy guidance and incentive schemes, thereby fostering sustainable development within the green hydrogen sector. These measures are anticipated to enable the option contract model to play a more significant role in practical green hydrogen supply chains, supporting the industry’s healthy growth.

The results of this paper can provide guidance for green hydrogen supply chain decision-making and optimal coordination between hydrogen refueling stations and hydrogen production stations through option contracts, thus further promoting the development of the green hydrogen industry.

The main research contributions of this paper are as follows: considering the reality of excessive pessimism in the green hydrogen supply chain, improving the original model that only considers the perceived pessimism regarding market demand or output rate, constructing a model that reflects the two types of excessive pessimism, and optimizing the decision-making of the green hydrogen supply chain by sharing the risk of the stochastic output by applying the option contract to the green hydrogen supply chain. Future research can also study the following two aspects: during the green hydrogen sales period, the depletion of green hydrogen over time can be considered, and the optimization and coordination role of the option contract can be studied further. Research can use the actual operation data of green hydrogen enterprises and green hydrogen market data to estimate the degree of excessive pessimism of green hydrogen and its changes in different ways, and can continue to study the relationship between the two kinds of excessive pessimism in depth.