Enhancing Lithium-Ion Battery State-of-Health Estimation via an IPSO-SVR Model: Advancing Accuracy, Robustness, and Sustainable Battery Management

Abstract

Precise forecasting of lithium-ion battery health status is crucial for safe, efficient, and sustainable operation throughout the battery life cycle, especially in applications like electric vehicles (EVs) and renewable energy storage systems. In this study, an improved particle swarm optimization–support vector regression (IPSO-SVR) model is proposed for dynamic hyper-parameter tuning, integrating multiple intelligent optimization algorithms (including PSO, genetic algorithm, whale optimization, and simulated annealing) to enhance the accuracy and generalization of battery state-of-health (SOH) estimation. The model dynamically adjusts SVR hyperparameters to better capture the nonlinear aging characteristics of batteries. We validate the approach using a publicly available NASA lithium-ion battery degradation dataset (cells B0005, B0006, B0007). Key health features are extracted from voltage–capacity curves (via incremental capacity analysis), and correlation analysis confirms their strong relationship with battery capacity. Experimental results show that the proposed IPSO-SVR model outperforms a conventional PSO-SVR benchmark across all three datasets, achieving higher prediction accuracy: a mean MAE of 0.611%, a mean RMSE of 0.794%, a mean MSE of 0.007%, and robustness a mean R² of 0.933. These improvements in SOH prediction not only ensure more reliable battery management but also support sustainable energy practices by enabling longer battery life spans and more efficient resource utilization.

1. Introduction

Lithium-ion battery state-of-health (SOH) estimation is a critical function in a battery management system (BMS), especially for electric vehicles (EVs) and renewable energy storage, as it directly impacts operational safety and reliability [1]. Over time, lithium-ion batteries experience degradation in the form of capacity loss and increased internal resistance [2]. This degradation can lead to reduced performance, including decreased range and power [3]. In addition, aging batteries can pose serious safety hazards such as thermal runaway, which may lead to fire or explosion if not managed properly [4]. Therefore, obtaining accurate and timely SOH information enables predictive maintenance, optimizes energy use, and helps prevent unexpected failures [5]. However, SOH cannot be directly measured during battery operation, which makes SOH estimation challenging [6]. Therefore, it is necessary to develop stable estimation algorithms for SOH prediction by voltage, current, temperature and other signals, which has become an important research focus in recent years [7].

Currently, battery SOH estimation methods are mainly categorized into two main groups: modeling methods and data-driven methods. Modeling approaches for battery SOH estimation are generally categorized into equivalent circuit models (ECMs) and electrochemical models. ECMs simulate the dynamic behavior of batteries using combinations of resistors, capacitors, and voltage sources. These models are widely used due to their simplicity and low computational cost. However, they are empirical in nature, lack direct physical interpretability, and their parameters can drift significantly with aging and operating conditions, requiring frequent recalibration [8]. In contrast, electrochemical models, such as the pseudo two-dimensional model, are derived from fundamental principles of thermodynamics and electrochemistry. They can accurately capture internal states like lithium-ion concentration and reaction kinetics, offering high fidelity and predictive capability. However, these models are computationally demanding and rely on detailed knowledge of battery structure and material parameters, which limits their application in practical BMS implementations [9]. Due to the limitations of both model types, more studies have turned to more flexible data-driven methods to overcome the limitations of the modeling approach.

With the rapid development of artificial intelligence, SOH estimation with data-driven methods has attracted widespread attention. Data-driven methods extract features from battery data and utilize algorithms to explore the relationship between in features and capacity. Compared with other methods, data-driven approaches do not require complex experimental equipment or rely on an in-depth knowledge of the battery’s internal mechanical states. Furthermore, they can effectively improve the accuracy of SOH estimation in different application scenarios and battery charging and discharging modes, and show good adaptability and estimation capability, which is promising for a wide range of research. The two key steps of data-driven are feature extraction and model construction. Researchers usually extract features such as battery charging and discharging voltages, currents, and temperatures from battery databases, which respond to the health status such as battery capacity. Feature extraction is a key step in building SOH estimation models, and as research continues, various feature extraction strategies have emerged. For example, Deng et al. introduced a voltage-partitioning strategy to obtain the difference in discharge capacity between two cycles △Q(V) from a non-monotonic or impulse discharge voltage profile, and a filtering strategy to obtain a smoothed voltage profile under dynamic discharge conditions, and the standard deviation of the discharge capacity profile and △Q(V) were selected as the health features [10]. Li et al. At the same time, internal aging features, such as charge transfer resistance, solid-phase diffusion coefficient, and electrode volume fraction, are extracted by EM, and external health features are extracted from the voltage and temperature curves which are divided into multiple phases [11]. Tao et al. Based on the analysis of the aging mechanism of the batteries and the change rule of the curves, a total of 61 health indexes related to the degradation of the performance are extracted from the cycling curves. The Discrete Wavelet Transform (DWT) is used for noise reduction in the original metrics during preprocessing. A normalized mutual information (MI) feature selection algorithm based on maximum correlation and minimum common redundancy is introduced to select a set of optimized operating condition indicators [12].

Subsequently, algorithms are modeled to establish the relationship between these features and capacity, and commonly used algorithms include including linear regression (LR) [13], support vector machine (SVM) [14], random forest (RF) [15], decision tree (DT) [16] and others. In order to further improve the accuracy and efficiency of SOH estimation, many researchers have developed integrating intelligent optimization algorithms with data-driven models. In recent years, many high-level research results have proved the effectiveness of such methods. For example, Fu et al. proposed an improved Arithmetic Optimization–Backpropagation Neural Network (AO-BPNN) for state of charge (SOC) estimation, which achieved satisfactory results under dynamic conditions [17]. Chen et al. combined Particle Swarm Optimization (PSO) with Extreme Learning Machines (ELM) for SOH estimation, demonstrating enhanced predictive accuracy [18]. Li et al. use the PSO algorithm to optimize the parameter configuration of the group method of data handling (GMDH). The optimized GMDH was used for the SOH estimation. The results show that the error of the proposed PSO-GMDH estimation model in estimating the subsequent SOH of a battery using its historical data is kept within 0.89% [19]. Sheng et al., based on the MTR-GPR model, extracted the information from different datasets based on the distributional similarity to make full use of the aging data of batteries from multiple sources, and at the same time, reduce the negative impact of distributional differences [20]. Tong et al. proposed an SVR model optimized using the Dragon Beetle Optimizer (DBO) and conducted comparative experiments across different training data scales to validate the model in SOH estimation [21]. However, the performance of individual models may vary considerably on different datasets [22]. This suggests that different models may perform well in different data environments and that no single model consistently achieves optimal results in all scenarios [23]. To address this problem, increasing attention has been directed toward multiple model algorithms being collaboratively optimized into stacked integrated learning models for more accurate and reliable SOH estimation. For example, Zhi et al., proposed a genetic algorithm-particle swarm optimization (GA-PSO) algorithm to optimize the parameter values of SVR, improving the estimation accuracy and convergence speed of SVR [24]. Li et al. proposed a novel stacked-integrated model, which consists of five basic models, integrating LightGBM, XGBoost, random forest (RF), SVR, and GPR through LR fusion to ensure model diversity. and GPR to ensure model diversity and improve SOH estimation accuracy. The average SOH estimation error of the stacked integrated model is lower than that of the five basic models [25]. To further improve the performance of data-driven methods in SOH estimation, many researchers have focused on improving feature processing and optimizing algorithmic models. This paper also aims to contribute to this research area by exploring relevant improvement methods.

In addition, the estimation accuracy of SOH estimation models depends on the correlation between health features and battery SOH, and the adaptability of the algorithmic model’s own operation logic to the battery SOH. The selection of hyperparameters is a common challenge for most estimation models, and hyperparameter optimization plays a key role in improving the predictive performance and stability of the models [26]. However, the hyperparameters of most machine learning models still rely on offline adjustment or empirical selection and lack a mechanism to dynamically adjust with the battery operating conditions, which makes it difficult to ensure that the model maintains optimal performance under different operating conditions.

This study proposes the construction of the IPSO-SVR model for dynamic hyper-parameter tuning, integrating numerous intelligent optimization algorithms to address these issues. The method leverages the strengths of the genetic algorithm (GA), whale optimization algorithm (WOA), and simulated annealing algorithm (SA) to enhance PSO, while simultaneously incorporating dynamic optimization and adjustment of SVR hyperparameters. This approach aims to improve the model’s global optimization capability and convergence stability, thereby enhancing the accuracy, robustness, and generalization performance of SOH estimation. This research presents the training and validation of the proposed IPSO-SVR model utilizing a public battery aging experimental dataset and conducts a comparative analysis with classical PSO-SVR and other data-driven methodologies to assess the efficacy of the current approach. The primary objective of this paper is as follows:

• A health feature extraction method based on the value of the change in the voltage of a single point of the critical zone over the cycle period from the voltage profiles of different cycles of the battery is proposed to provide a more comprehensive description of the battery aging process. This approach permits a fast and flexible estimation of the battery capacity.
• In order to address the performance fluctuations of a single model on different datasets, this paper proposes the IPSO-SVR model for dynamic hyper-parameter tuning integrating multiple intelligent optimization algorithms, allowing us to take advantage of the complementary strengths of multiple models.
• The estimation results of the IPSO-SVR model in this paper are compared with the traditional model to confirm the model advantages with the help of relevant evaluation indexes, and the experimental results are analyzed and discussed at the same time.

The rest of the paper is organized as follows: Section 2 describes the dataset used in this study and the health factor extraction process. Section 3 describes the characteristics and structure of the estimated model. In Section 4, the estimation results of the model are analyzed and compared with the base model. Finally, Section 5 summarizes the paper.

2. Dataset and Health Feature Processing

2.1. Description of the Dataset

The aging dataset used in this study is from the NASA 18,650 lithium cobalt oxide battery dataset, with a nominal capacity of 2 Ah and a charge cutoff voltage of 4.2 V [27]. Based on different charge and discharge cycles, voltage, and current, three datasets B0005, B0006, and B007 from the NASA battery group were selected for cycling experiments. Their related parameters are listed in

Table 1. Relevant Parameters of Battery Experiment.

Battery	Charge (A)	Discharge (A)	Cutoff Current (A)	Cutoff Voltage (V)	Discharge Cutoff (V)	Temperature (°C)
B0005	1.5	2.0	0.1	4.2	2.7	24.0
B0006	1.5	2.0	0.1	4.2	2.2	24.0
B0007	1.5	2.0	0.1	4.2	2.5	24.0

. The lithium battery cycling experimental steps are as follows: the three batteries were charged using constant current-constant voltage (CC-CV) charging at 24 °C. A constant current of 1.5 A was applied to charge the lithium batteries to the cutoff voltage of 4.2 V. Then, charging continued with a constant voltage of 4.2 V until the current dropped to 0.02 A. After the batteries were left to rest for half an hour, they were discharged with a constant current of 2.0 A until the voltages of B0005, B0006, and B0007 dropped to 2.7 V, 2.2 V, and 2.5 V, respectively, at which point the discharge was stopped. The above charging and discharging procedures were repeated to accelerate battery aging. The experiments were terminated when the actual capacity of each experimental battery fell below 70% of its initial capacity.

This paper assesses SOH based on battery capacity, with the relationship between SOH and cycle count depicted in Figure 1, demonstrating the capacity degradation trends of the three battery packs as cycling progresses. All lithium-ion batteries exhibit three characteristic phases of capacity deterioration as cycle count increases: stable capacity decline, rapid capacity decay, and oscillation of capacity increase and decrease. This is related to the multiple chemical and physical changes involved in the aging process such as the loss of lithium and the loss of anode active material during the life cycle of lithium-ion batteries [28]. These internal changes are challenging to measure or quantify directly [29]. Therefore, this paper reflects these changes indirectly by plotting incremental capacity curves and observing the trend of the curves as the battery cycles proceed.

2.2. Extraction of Health Features

The health feature (HF) extraction is a critical step in data-driven battery capacity estimation and plays a major role in determining estimation accuracy [30]. During the operation of lithium-ion batteries, key operational data such as voltage and current can provide the necessary basis for battery aging [31]. In this study, based on the stability of the charging condition, the voltage-capacity data during the charging stage is selected for analysis. Using incremental capacity analysis (ICA), the voltage-capacity relationship during constant-current charging is differentially transformed to generate incremental capacity (IC) curves and extract aging characteristics.

The ICA method diagnoses battery degradation mechanisms without disassembling the battery, revealing subtle changes that are not apparent in the raw voltage and capacity curves. It is particularly effective in identifying changes in peak location and magnitude that can be linked to the state of health (SOH) of the battery [32,33]. The IC curve value can be obtained by calculating the differentiation of capacity against voltage, the specific formula is as follows:

$${\displaystyle \frac{dQ}{dV}}=I\cdot {\displaystyle \frac{dt}{dV}}$$

(1)

.

As shown in Figure 2, the IC curve of B0005 lithium-ion battery is plotted. Further analysis of the evolution of the IC curve under different cycle times reveals that the curve shows a trend of “peak decrease” and “right shift” as SOH decreases. This phenomenon is closely related to the loss of active lithium-ions and the loss of active material [34,35]. Through mechanistic and image analyses, it was determined that the 3.9 V to 3.98 V interval is the key voltage band that best characterizes SOH because of the significant and discriminatory capacity changes in this interval. Based on this, five IC feature points in this interval were uniformly extracted at 200 mV intervals for health characterization.

2.3. Correlation Analysis Between Health Characteristics and SOH

Following the plotting and analysis of the IC curves, five health features were derived from each battery dataset to serve as inputs for the estimation model, as previously described. To evaluate the correlation between these extracted features and battery capacity, Pearson’s correlation coefficient (PCC) was employed for the analysis. The PCC is a statistical metric that quantifies the linear correlation between two variables. This paper quantifies the linear association between each HF and battery capacity by computing the PCC, hence assessing the efficacy of these characteristics in determining battery capacity. A greater absolute value of PCC indicates a higher correlation between the feature and the capacity, thus providing more valuable information to enhance the model. The Pearson correlation coefficient formula and Spearman rank correlation coefficient formula can be expressed as

$$l_p={\displaystyle \frac{E\left(\mathrm{xy}\right)-E\left(x\right)E\left(y\right)}{\sqrt{E{\left(x\right)}^2-E^2\left(x\right)}\sqrt{E{\left(b\right)}^2-E^2\left(b\right)}}}.$$

(2)

In the formula, $l_p$ represents the Pearson correlation coefficient, $x=\left(x_1,x_2,\dots ,x_n\right)$, $y=\left(y_1,y_2,\dots ,y_n\right)$ They represent the feature values and SOH (state of health) of the lithium-ion battery, respectively. The closer the absolute value of Pearson’s correlation coefficient is to 1, the stronger the correlation between the two variables. A value close to 1 indicates a strong positive correlation, while a value close to −1 indicates a strong negative correlation.

$$l_s={\displaystyle \frac{{\displaystyle \sum _{i=1}^n\left(P_i-\overline{P}\right)\left(P_i-\overline{Q}\right)}}{\sqrt{{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{i=1}^n{\left(P_i-\overline{P}\right)}^2{\left(P_i-\overline{Q}\right)}^2}}}}}.$$

(3)

In the formula, $l_s$ represents the Spearman rank correlation coefficient, The vector $P=\left(P_1,P_2,\dots ,P_n\right)$ The vectoris transformed into a rank vector by assigning ranks to its elements based on their order. This rank-based representation is used to measure the monotonic relationship between variables, such as in Spearman correlation. The vectors $Q$ and $y$ have the same rank order, meaning their elements are ranked similarly. $\overline{P}$ and $\overline{Q}$ are the averages of $P$ and $Q$, respectively. Spearman is equivalent to the Pearson correlation coefficient between two new rank vectors obtained after converting the original vectors. The closer the absolute value of Spearman is to 1, the stronger the monotonic correlation.

The Pearson correlation coefficients and Spearman rank correlation coefficient between the five extracted HFs and battery capacity are presented in

Table 2. Correlation coefficient analysis of health factors between extracted HFs and SOH.

Battery	B0005		B0006		B0007
	Pearson	Spearman	Pearson	Spearman	Pearson	Spearman
HF1	0.9919	0.9826	0.9696	0.9888	0.9862	0.9829
HF2	0.9881	0.9802	0.9673	0.9895	0.9850	0.9780
HF3	0.9909	0.9740	0.9689	0.9913	0.9760	0.9531
HF4	0.9855	0.9771	0.9785	0.9922	0.9679	0.9802
HF5	0.9887	0.9863	0.9887	0.9948	0.9870	0.9801

and Figure 3 presents a heat map illustrating the absolute values of the Pearson coefficients and Spearman rank correlation coefficient between several battery health parameters and state of health for the NASA dataset, hence visualizing Table 2. A deeper orange hue in the heat map signifies a higher association, while a proximity to blue denotes a lesser correlation. The results suggest that the correlation coefficients of all the HFs exceed 0.95, signifying a robust association between the HFs and the SOH of the batteries.

3. IPSO-SVR Model Construction

The predictive efficacy of the identical model may fluctuate between batteries due to the varied aging trajectories of various batteries. These discrepancies result in inadequate estimation precision of individual models in conventional machine learning techniques. Numerous studies have employed methodologies like the implementation of advanced algorithms to assess SOH [36,37]. Nonetheless, traditional algorithms based on a singular model have specific benefits and intrinsic worth for reintegration and use, and they have previously been widely applied across various application scenarios. This study introduces the IPSO-SVR model for dynamic hyper-parameter tuning incorporating multiple intelligent optimization algorithms to enhance the resilience and generalization capacity of the SOH estimate process.

3.1. Algorithmic Principle

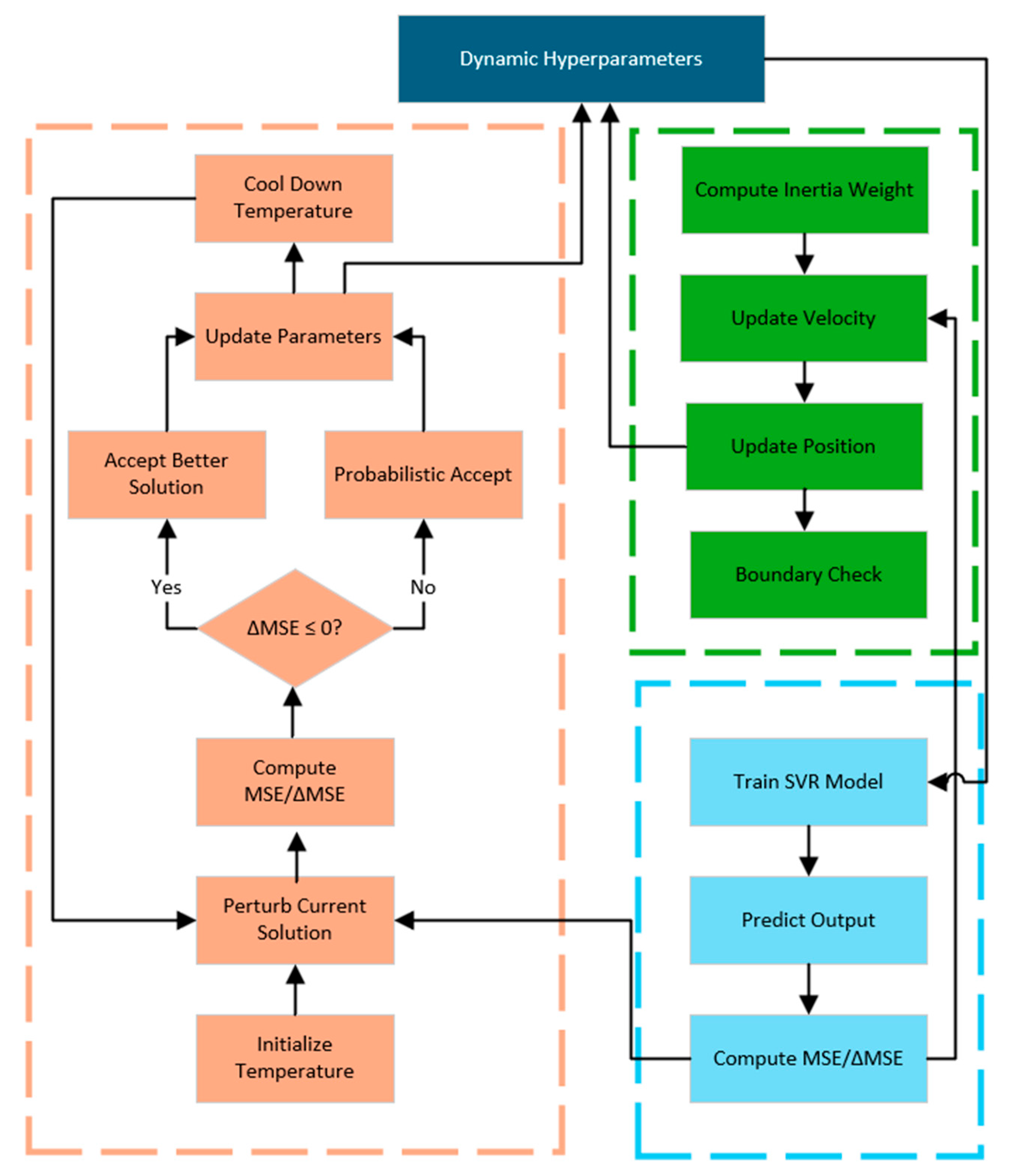
In SVR modeling for SOH estimation of lithium-ion batteries, optimizing hyperparameters presents challenges in balancing global optimization efficiency with local convergence accuracy when depending solely on a single intelligent algorithm. Consequently, this work proposes the development of the IPSO-SVR model for dynamic hyper-parameter tuning incorporating multiple intelligent optimization algorithms. The method leverages the strengths of WOA, GA, SA, and other algorithms to enhance PSO, while simultaneously incorporating dynamic hyperparameters to facilitate the adaptive optimization of SVR hyperparameters, thereby synergistically improving hyperparameter search efficacy and model performance.

3.2. Dynamic Hyper-Parameter Optimization

The selection of hyperparameters is vital for the efficacy of machine learning models, particularly in SVR models, where the choice of penalty coefficients and kernel function parameters directly influences generalization performance and predictive accuracy. The conventional fixed hyperparameter optimization method typically establishes hyperparameters during the training phase and maintains them constant throughout the optimization process, resulting in inflexibility when confronted with diverse datasets and variations in model complexity, potentially leading to suboptimal model performance.

The proposed dynamic hyperparameter optimization method modifies and calibrates hyperparameter values in real time throughout the model training process, allowing for adaptation to the evolving data features during training. This study demonstrates a fusion strategy, where hyperparameter adjustments are progressively refined during the program’s iterative phase by using dynamic inertia weights and adaptive cross-variation probabilities. Initially, elevated inertia weights and increased cross-variance probability enable the model to thoroughly investigate the hyperparameter space, thereby preventing premature convergence to local optima; as iterations progress, both inertia weights and cross-variance probability are systematically diminished, facilitating a transition to a more localized and refined search to accurately identify the optimal value within the hyperparameter space.

In contrast to the conventional fixed hyperparameter approach, this dynamic adjustment mechanism enhances the model’s generalization capability and predictive accuracy, while also markedly increasing the algorithm’s robustness, allowing for superior adaptation to diverse datasets and optimization requirements. The empirical results demonstrate that the fusion algorithm employing dynamic hyperparameter optimization exhibits significant advantages in the hyperparameter optimization search process of the SVR model, thereby validating its rationality and efficacy in real application.

3.3. Fusion Principle

The PSO algorithm, a conventional hyper-parameter optimization method, offers high computational efficiency and rapid convergence in optimizing parameters for the SVR model; however, it is also susceptible to limitations such as a tendency to converge to local optima and a swift decline in population diversity. This paper proposes three optimization strategies that integrate GA, SA and WOA with the PSO algorithm to leverage the strengths of each method and achieve synergistic benefits. Figure 4 shows the flowchart of the IPSO-SVR prediction process, using the SA-based fusion strategy as an example.

The GA-PSO fusion technique employs the selection, crossover, and mutation mechanisms of GA to successfully preserve population diversity and enhance search space coverage, thereby compensating for the limitations of PSO, which is susceptible to converging on local optima in the later stages.

The WOA-PSO fusion algorithm utilizes the WOA’s robust global search in the initial phase, remarkably enhancing the depth and precision of exploration while mitigating the risk of local optima.

The SA-PSO fusion algorithm is based on the SA, which enhances stability and accuracy during the later stages of convergence. This technique integrates the rapid convergence attributes of PSO to achieve the synchronized advancement of exploration and exploitation.

In essence, these three fusion algorithms leverage the strengths of several algorithms to enhance the standard PSO-SVR model and address the shortcomings of individual techniques. Practical experiments and subsequent calculations reveal that these fusion algorithms exhibit clear theoretical rationale and offer exceptional optimization performance in certain applications, thus validating their practical significance and superiority in the hyperparameter optimization of SVR models.

3.4. Indicators for Model Evaluation

In order to objectively and accurately assess the reliability of lithium-ion battery SOH estimation results, it is essential to select appropriate evaluation indicators. The evaluation indexes can quantify the difference between the model prediction and the actual data, which facilitates quantitative analysis and model performance comparison, and thus guides the optimization and improvement of the model. The evaluation indexes selected in this paper include mean absolute error (MAE), root mean square error (RMSE), mean square error (MSE), and coefficient of determination (R²).

(a)

MAE

The average absolute error can intuitively reflect the degree of absolute deviation between the predicted value and the real value, and the smaller its value indicates the better prediction performance of the model. The formula is as follows:

$$MAE={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}\left|y_i-\widehat{y_i}\right|$$

(4)

(b)

RMSE

The root mean square error averages the squares of the prediction errors before taking the square root, and can effectively reflect the overall degree of deviation in the prediction errors. Lower RMSE indicates better model accuracy. The calculation formula is as follows:

$$MSE=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}{\left(y_i-\widehat{y_i}\right)}^2}.$$

(5)

(c)

MSE

The mean square error, by averaging the squares of the prediction errors, can effectively penalize larger error values and thus reflect the accuracy of the model more sensitively. The calculation formula is as follows:

$$MSE={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}{\left(y_i-\widehat{y_i}\right)}^2$$

(6)

(d)

R²

The coefficient of determination is used to measure the degree of fit between the predicted and true values of the model, and its value ranges from 0 to 1, with values close to 1 indicating that the model has a good fit. The formula is as follows:

$$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}{{\sum }_{i=1}^n{\left(y_i-\overline{y}\right)}^2}}.$$

(7)

In the above four Formulas (4) to (6), $y_i$ is the true value, $\widehat{y_i}$ is the predicted value, $n$ is the number of samples, and $\overline{y}$ is the average value of the true value. Through the calculation and analysis of the above evaluation indexes, the performance of the SOH estimation model can be comprehensively and accurately assessed to ensure that the model has a high degree of reliability and stability when it is applied to practical problems.

4. Analysis and Comparison of Experimental Results

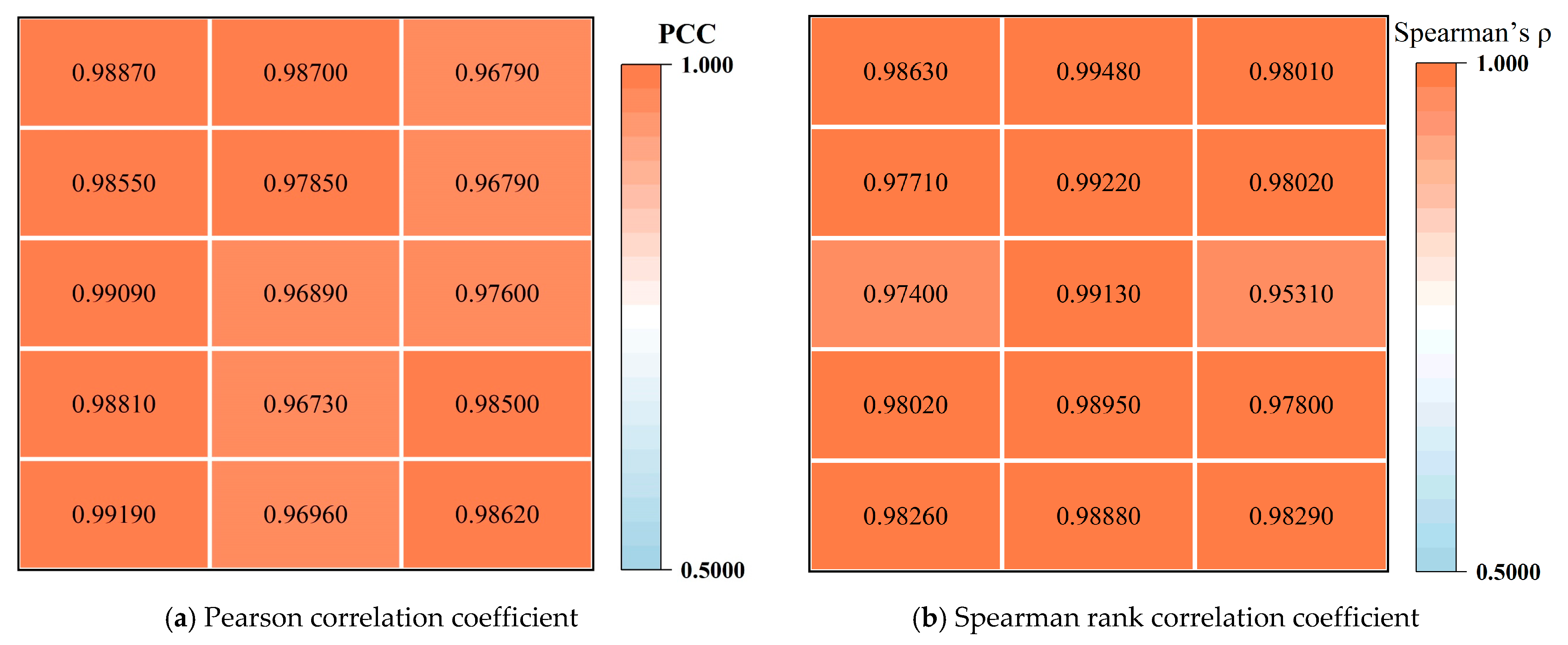
This part verifies the effectiveness of the IPSO-SVR model for dynamic hyper-parameter tuning incorporating multiple intelligent optimization algorithms in SOH estimation. Firstly, the health characteristics after Pearson’s correlation coefficient analysis are inputted into the IPSO-SVR model for SOH estimation, and the estimation results are visualized through graphs and charts, and the estimation results are evaluated through relevant evaluation indexes. The estimation results are also compared with those of traditional models to verify the superiority of the estimation model proposed in this paper.

4.1. Experimental Design

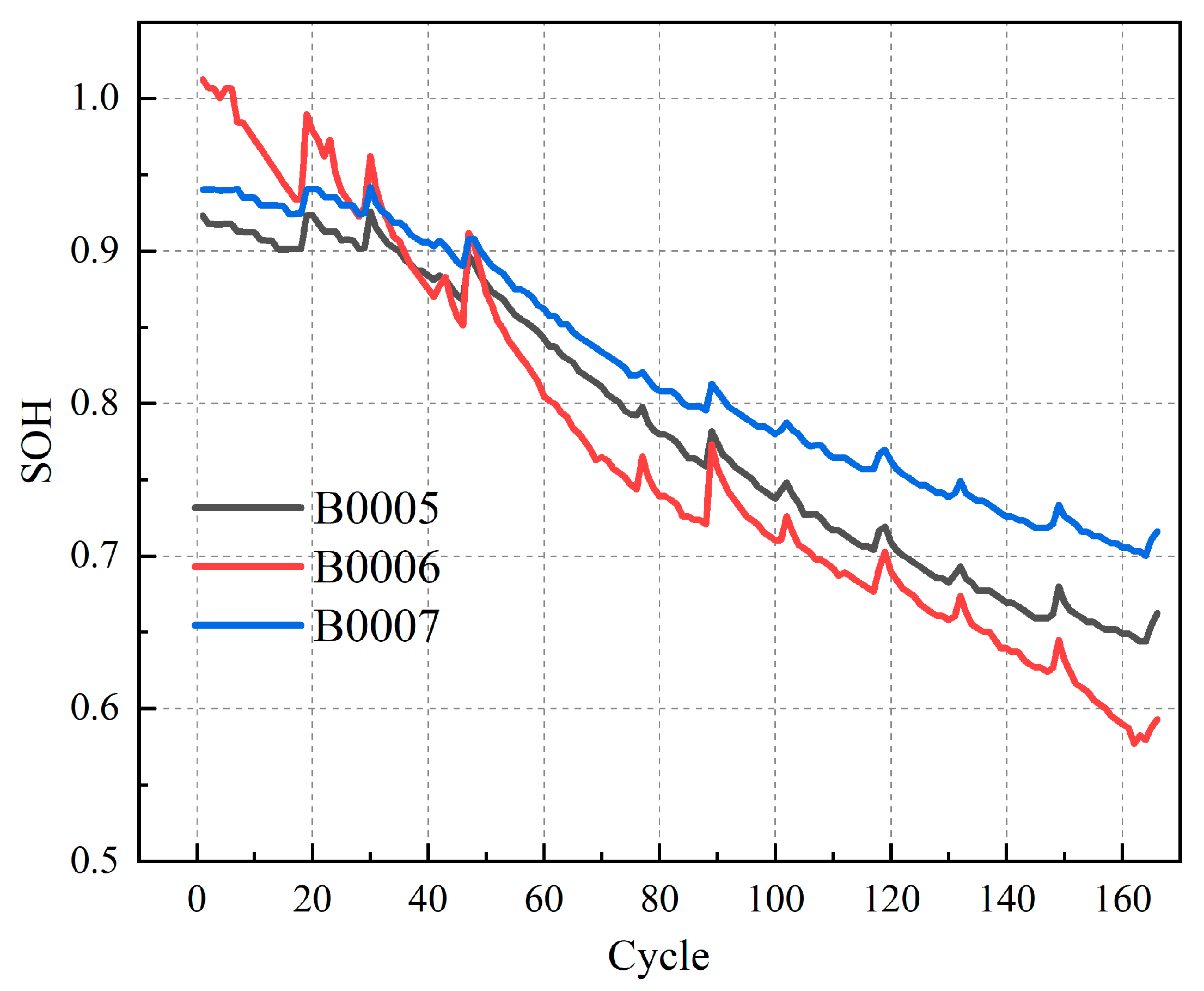
This paper utilizes B0005, B0006, and B0007 batteries from the NASA battery dataset for capacity estimation. The data concerning charge and discharge cycles throughout the lifespan of lithium-ion batteries serves as a critical foundation for constructing this estimation model, with a total of 166 cycles recorded in the dataset pertaining to the batteries’ cycle life. During model training, 60% of the data is used as training data, while 40% serves as test data; specifically, data pertaining to lithium-ion batteries from the initial 99 cycles constitute the training set, while data from the final 67 cycles comprise the test data.

To effectively validate the optimization effectiveness and stability of IPSO-SVR model, we selected an Intel® Core™ Ultra 9 185H CPU (2.50 GHz) and 32 GB of LPDDR5X memory, sourced from Intel Corporation (Santa Clara, CA, USA). The model was trained and tested using MATLAB R2024b software on the Windows 11 operating system.

4.2. IPSO-SVR Model Estimation Results

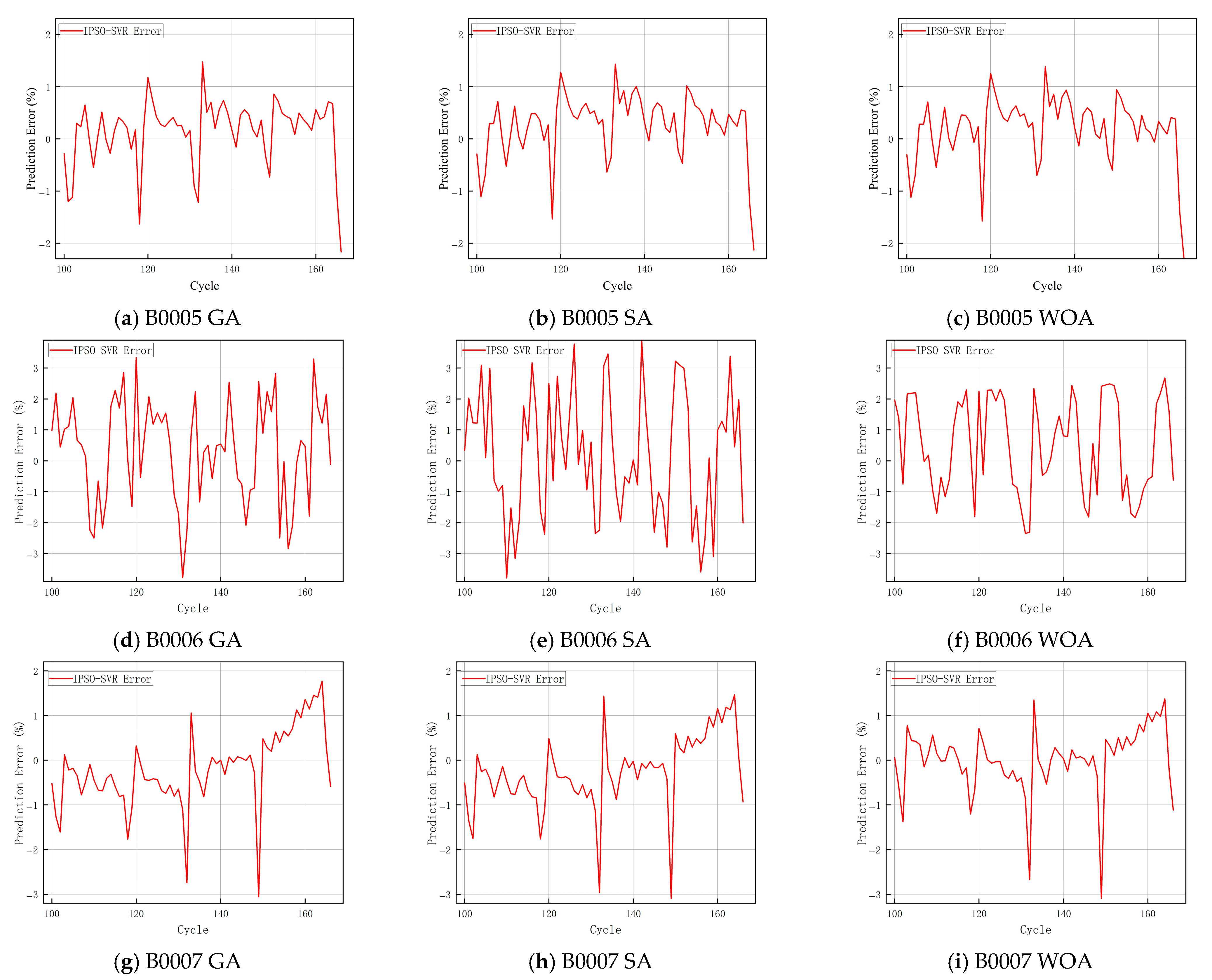
Figure 5 illustrates the error percentage curve derived from the capacity estimate outcomes of the IPSO-SVR model applied to the NASA dataset. The graphic distinctly illustrates the extent of the inaccuracy in SOH estimation by the IPSO-SVR model across various cells and fusion procedures, thus demonstrating the algorithm’s predictive ability. The absolute maximum error percentage is approximately 2% for cell B0005, indicating a little estimation error and precise prediction, whereas it is nearly 4% for cell B0006 and around 3% for cell B0007. The estimation errors of various batteries exhibit distinct variances and oscillations in accuracy while utilizing fusion GA, SA, and WOA, respectively. This may pertain to elements such as the intrinsic variations of lithium-ion batteries and the dataset, which could be associated with the inherent nonlinearity and uncertainty characteristics of lithium-ion batteries during the aging process. The degradation of battery capacity is not a straightforward linear decline but is influenced by various physicochemical phenomena, including the formation of solid electrolyte interfacial (SEI) membranes, structural alterations in electrode materials, and electrolyte decomposition. The strength and rate of these mechanisms among various battery monomers exhibit modest variations, resulting in a nonlinear, multi-stage capacity decline trajectory. Furthermore, minute variations in the production process of battery monomers, material imperfections, and internal structural discrepancies contribute to unpredictable alterations in the aging rate and pattern. Such nonlinearities and uncertainties are challenging to effectively represent using existing data-driven models, resulting in discrepancies in prediction accuracy across various battery datasets. Overall, the estimation findings indicate that the IPSO-SVR model exhibits high accuracy, particularly with the B0005 dataset, where various fusion procedures have yielded superior estimation outcomes.

Using the B0005 battery as an example, it is evident from Figure 6 that in the prediction set, the application of the three fusion strategies—fusion GA, SA, and WOA—yields prediction results with minimal volatility, all closely approximating the actual value. The dynamic hyper-parameter adjustment model design technique, which incorporates many intelligent optimization methods, demonstrates superior performance in the SOH estimate procedure.

The error data in

Table 3. SOH estimation errors of the IPSO-SVR algorithm with three fusion strategies on three NASA datasets.

Battery	Fusion Algorithm Type	Error Evaluation Metrics
		MAE (%)	RMSE (%)	MSE (%)	R2
B0005	GA	0.3821	0.5887	0.0035	0.9572
	SA	0.4143	0.5886	0.0035	0.9572
	WOA	0.3879	0.5847	0.0034	0.9577
B0006	GA	0.9186	1.0924	0.0119	0.9237
	SA	1.1359	1.3501	0.0182	0.8835
	WOA	0.9289	1.0514	0.0111	0.9293
B0007	GA	0.4809	0.6484	0.0042	0.9268
	SA	0.4864	0.6680	0.0045	0.9223
	WOA	0.3654	0.5758	0.0033	0.9422

indicates that the IPSO-SVR model demonstrates exceptional accuracy and stability for SOH estimate on the NASA dataset. The minimum R² value across all three datasets, utilizing various fusion strategies, is 0.8835, with the majority exceeding 0.9. The maximum MAE is 1.1359%, while most values are below 0.5%. The maximum RMSE is 1.3501%. And the maximum MSE is 0.0182%, with the majority remaining under 0.005%. The IPSO-SVR model exhibits low error values and high estimation capability across various evaluation metrics. The estimation models demonstrate superior results for B0005 and B0007 compared to B0006, potentially due to the inherent properties of the dataset. The estimation models, after implementing various fusion strategies, consistently yield low-error results, demonstrating that these strategies, leveraging the inherent characteristics of the fusion algorithms, effectively integrate with the PSO-SVR model to deliver precise estimations.

4.3. Comparison of the IPSO-SVR Model with Conventional Models

This research compares the IPSO-SVR model, which employs various fusion strategies for dynamic hyper-parameter tuning using numerous intelligent optimization algorithms, with the conventional PSO-SVR estimation model to further verify its superiority. To facilitate a more equitable comparison of each model’s performance, both the PSO-SVR model and the IPSO-SVR model utilize identical health features derived from the NASA dataset as inputs, employing the same top 60% of data as the training set, and implemented on the same experimental platform. Its construction process and performance objectives were designed based on existing models reported in previous studies, serving as a reference benchmark [38]. Figure 7 presents the estimation results of the various models for each battery set. The three estimation curves labeled WOA-PSO-SVR, SA-PSO-SVR, and GA-PSO-SVR in Figure 7 represent the estimation results of the IPSO-SVR model under different optimization strategies. Only the findings and errors of the test data are displayed for clarity.

Figure 7 illustrates the comparative estimation results of B0005, B0006, and B0007 across various estimation models. The visual representation facilitates the discernment of differences in estimation outcomes among the models, revealing that the IPSO-SVR exhibits superior estimation accuracy across all datasets. Particularly with the B0006 dataset, the inherent properties of the dataset result in significant estimation errors for the traditional model, with errors increasing progressively as the number of cycles increases. The estimation results of the IPSO-SVR model across the three fusion procedures closely align with the actual values, yielding superior estimation outcomes. This compellingly demonstrates the superiority of the proposed model in this study, which circumvents the prevalent severe errors found in traditional models, thus highlighting the high estimation accuracy and stability of the IPSO-SVR model across various datasets.

To further illustrate the superiority of the suggested model proposed in this study,

Table 4. SOH estimation errors of the PSO-SVR algorithm on three NASA datasets.

Battery	Error Evaluation Metrics
	MAE (%)	RMSE (%)	MSE (%)	R2
B0005	0.8251	0.9247	0.0086	0.8943
B0006	2.8494	3.7395	0.1398	0.1060
B0007	0.7419	0.9546	0.0091	0.8413

presents the error levels according to several error evaluation criteria for the classic PSO-SVR model. The findings across multiple error evaluation criteria indicate that the conventional PSO-SVR exhibits significant estimation errors for the NASA lithium-ion dataset in this study. Upon analyzing and computing data from Table 3 in the preceding section, the estimation outcomes exhibit significant errors across various fusion strategies for each evaluation metric: MAE is recorded at 0.4143%, RMSE at 0.5887%, MSE at 0.0035%, and R² at 0.9577 for B0005. Calculations indicate that the MAE decreased by around 50%, the RMSE by around 36%, the MSE by roughly 56%, and the R² increased by 7%. The error reduction for the remaining two datasets is comparable to the results for B0005. The IPSO-SVR model attains enhanced accuracy in capacity and SOH estimation by employing three distinct fusion optimization procedures alongside dynamic hyperparameter optimization.

4.4. Discussion

Although the proposed IPSO-SVR model demonstrates high accuracy and robustness in SOH estimation tasks, it still presents certain limitations in terms of model complexity, deployment adaptability, and general applicability, which warrant further discussion.

First, while the IPSO-SVR model enhances the capability of parameter optimization, it also introduces a significant computational burden during the training phase. Under the configuration of 100 maximum iterations and a population size of 20, the training and prediction process for a single battery over 166 cycles in the NASA dataset took approximately 15 to 40 s on our experimental platform, with an average of 23 s. Although this time consumption is acceptable for offline training and can be performed periodically, it may pose a potential bottleneck in resource-constrained scenarios or in cases requiring frequent model updates.

Despite its real-time prediction capabilities, deploying the IPSO-SVR model on embedded platforms may encounter challenges such as memory limitations and high algorithmic complexity. Future work will address these issues by exploring lightweight model variants, reducing redundant optimization stages, and tailoring algorithmic implementations to hardware specifications.

Moreover, the generalization ability of the model across different datasets and battery chemistries has not yet been fully verified. The experiments conducted in this study are based on the publicly available NASA dataset, which, although a widely accepted benchmark, differs from modern commercial batteries in terms of sample source and electrochemical characteristics. Therefore, the model’s stability and accuracy under alternative battery types, operating conditions, or charging/discharging strategies remain to be validated. In future work, we plan to incorporate multi-source datasets to further evaluate and improve the model’s practical robustness and reliability.

5. Conclusions

The assessment of state of health for lithium-ion batteries is a critical component in battery management, maintenance, and operation processes, particularly given the swift advancement of the global electric vehicle market and the extensive utilization of lithium-ion batteries as power sources [39]. This paper quantifies battery SOH, generates IC curves from the NASA dataset to extract health features, and develops the IPSO-SVR model for dynamic hyper-parameter tuning, integrating various intelligent optimization algorithms to address the inadequacies in SOH estimation accuracy of traditional models in complex and variable application scenarios. A more precise prediction of battery SOH is achieved, which successfully forecasts the variation in battery SOH. The primary conclusions of this paper are as follows:

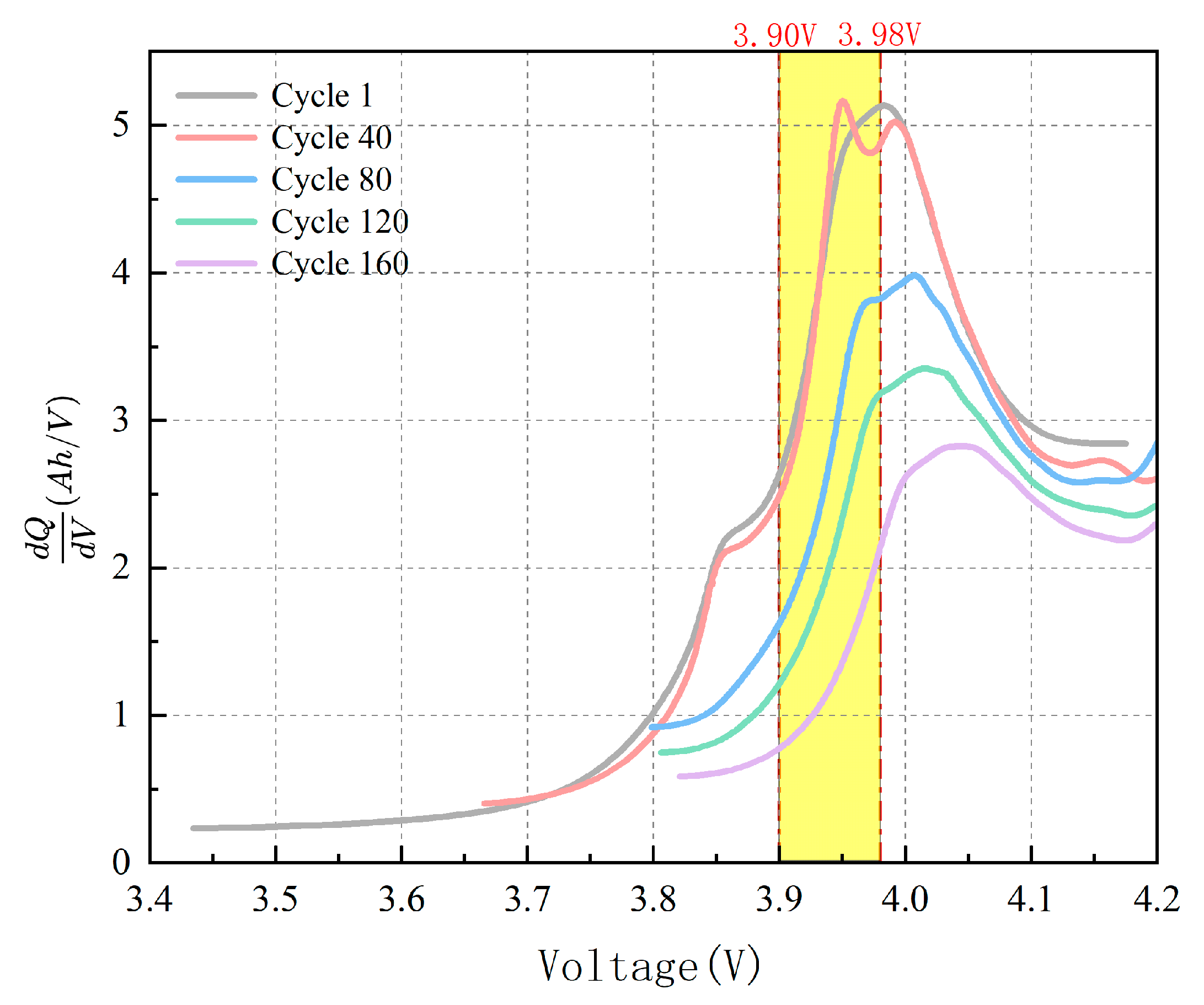
• The ICA method was used to generate IC curves. From these curves, five health-related features were extracted, and both Pearson and Spearman rank correlation analysis confirmed their strong association with SOH.
• This paper proposes the Improved Particle Swarm Optimization-Support Vector. Regression model for dynamic hyper-parameter tuning incorporating multiple intelligent optimization algorithms. Prediction results demonstrate that the IPSO-SVR model is both robust and generalizable. Across three battery packs, the minimum R² was 0.8835 (with the vast majority above 0.90), the maximum MAE was 1.1359% (most values below 0.50%), the maximum RMSE was 1.3501%, and the maximum MSE was 0.0182% (most values below 0.005%). Even in the worst-case fusion scenario, estimation accuracy remained high.
• Compared with the conventional PSO-SVR model, the proposed IPSO-SVR exhibits markedly stronger generalization: MAE was reduced by approximately 50%, RMSE by about 36%, MSE by around 56%, and R² increased by 7%.
• On the experimental platform used in this study, the average training time of the IPSO-SVR model was 23 s, with a maximum of 40 s. Although this represents an increase in time complexity relative to traditional models, it remains within an acceptable range.

In future work, we will validate the accuracy of the IPSO-SVR model on a broader range of battery datasets and devote efforts to continuously enhancing its generalization capability. We also plan to integrate the complementary strengths of traditional estimation models—leveraging their proven merits while further improving SOH prediction accuracy—and to explore the incorporation of emerging algorithms into SOH estimation, with the goal of developing models that deliver even better overall performance.

This research contributes to sustainable energy management by improving the accuracy of battery SOH estimation, which in turn enables more efficient and proactive battery management in applications like EVs and grid storage. By using the IPSO-SVR model to maintain batteries in optimal condition, the battery lifespan can be extended, delaying replacement needs and allowing each battery to deliver more service over its life. Extending battery life means fewer batteries need to be manufactured and discarded, which helps optimize resource utilization (reducing the demand for raw materials such as lithium and cobalt) and decreases waste. Consequently, the environmental impact associated with battery production and disposal is mitigated. Overall, the proposed approach supports the development of more sustainable energy storage systems and aligns with broader goals of sustainable development.