Spatial Prediction of Soil Organic Carbon Based on a Multivariate Feature Set and Stacking Ensemble Algorithm: A Case Study of Wei-Ku Oasis in China
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Research Methods
2.2.1. Soil Sample Collection and Processing
2.2.2. Extraction of Spectral Indices
2.2.3. Extraction of Environment Variables
2.2.4. Model Variable Screening and Feature Importance Analysis
2.2.5. Sample Partitioning Method
2.2.6. Machine Learning Ensemble Algorithmic Modeling
2.2.7. Model Estimation Evaluation Indicators
2.3. Research Framework
3. Results
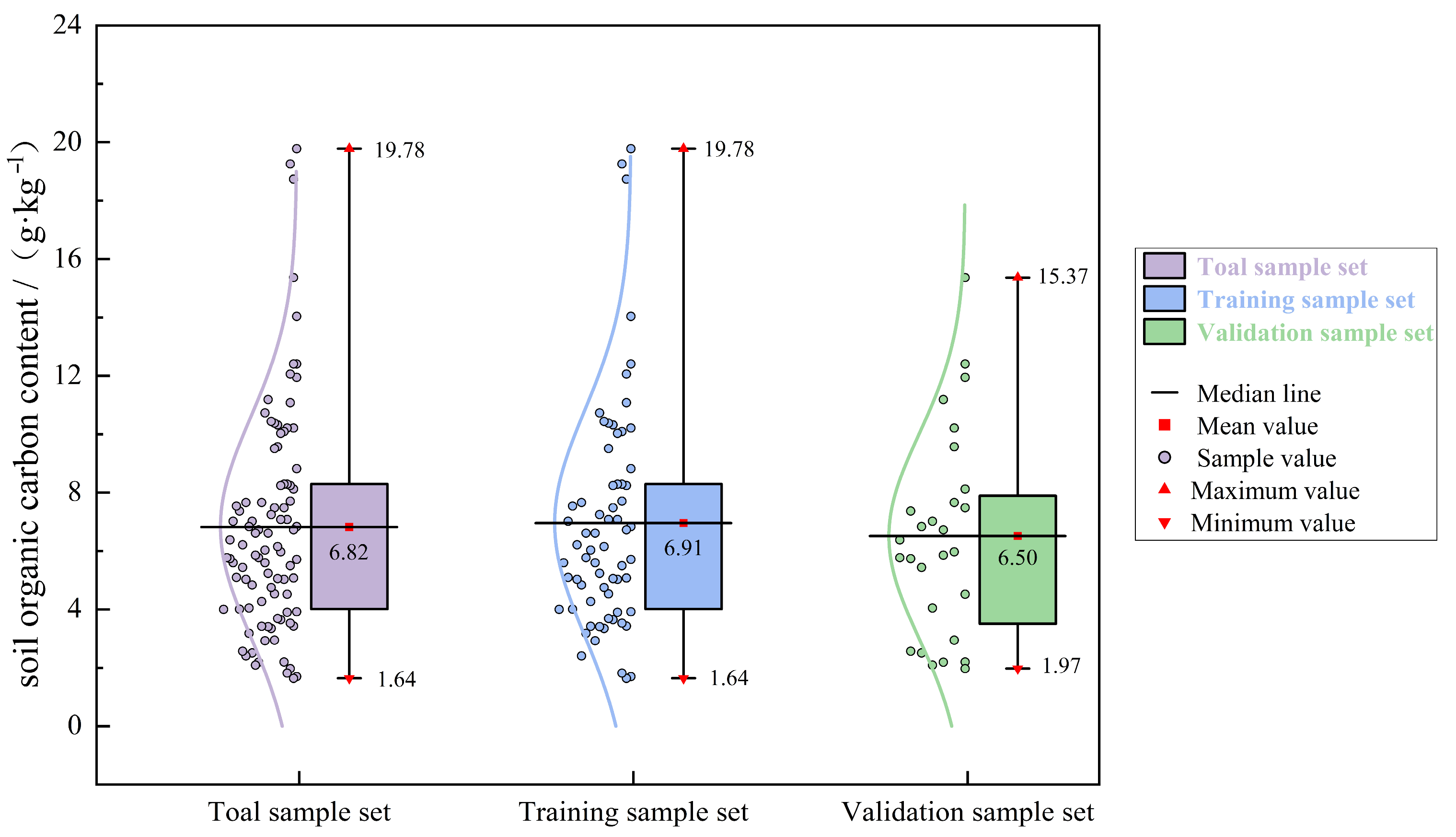
3.1. Soil Sample Characterization
3.2. Screening of Relevant Variables
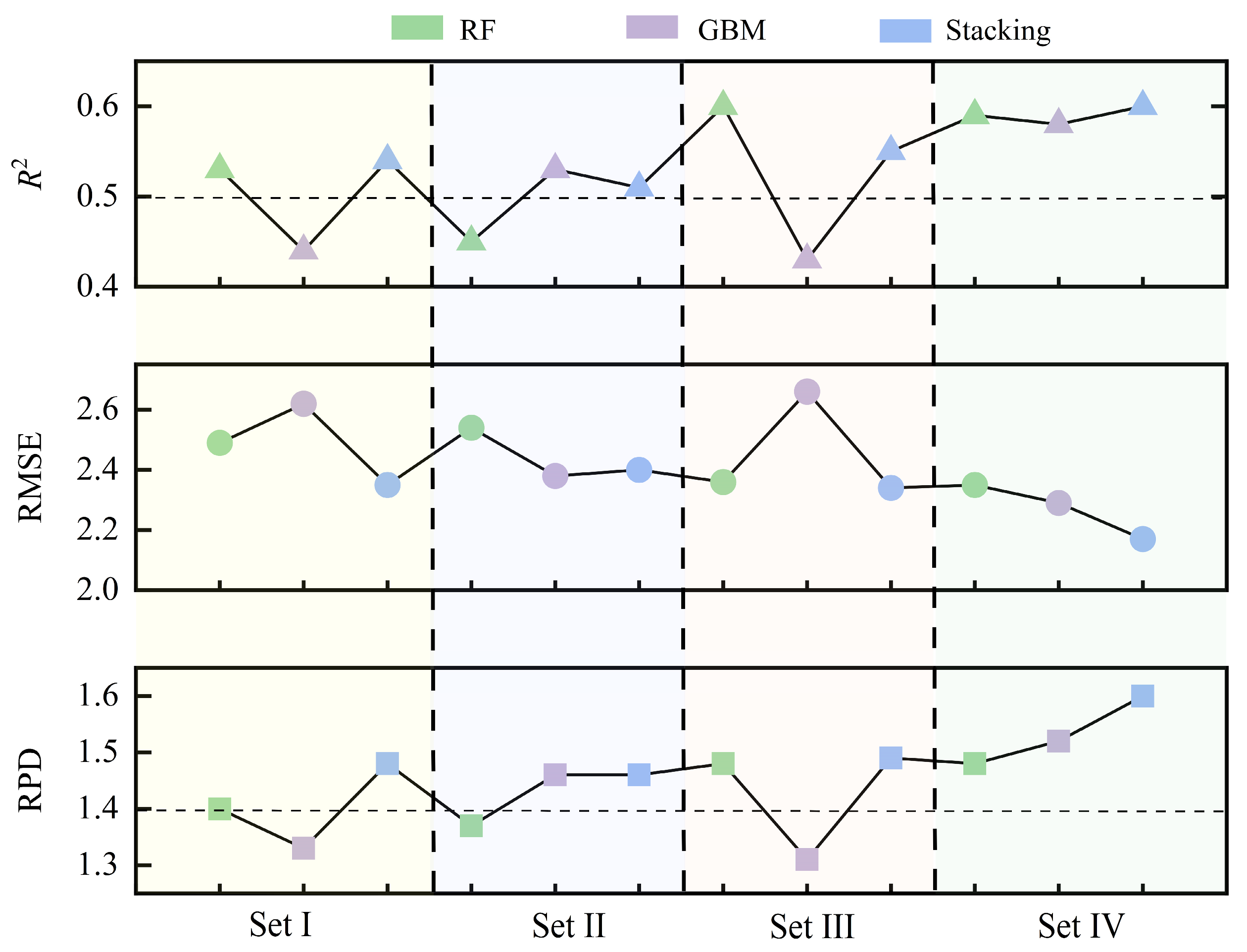
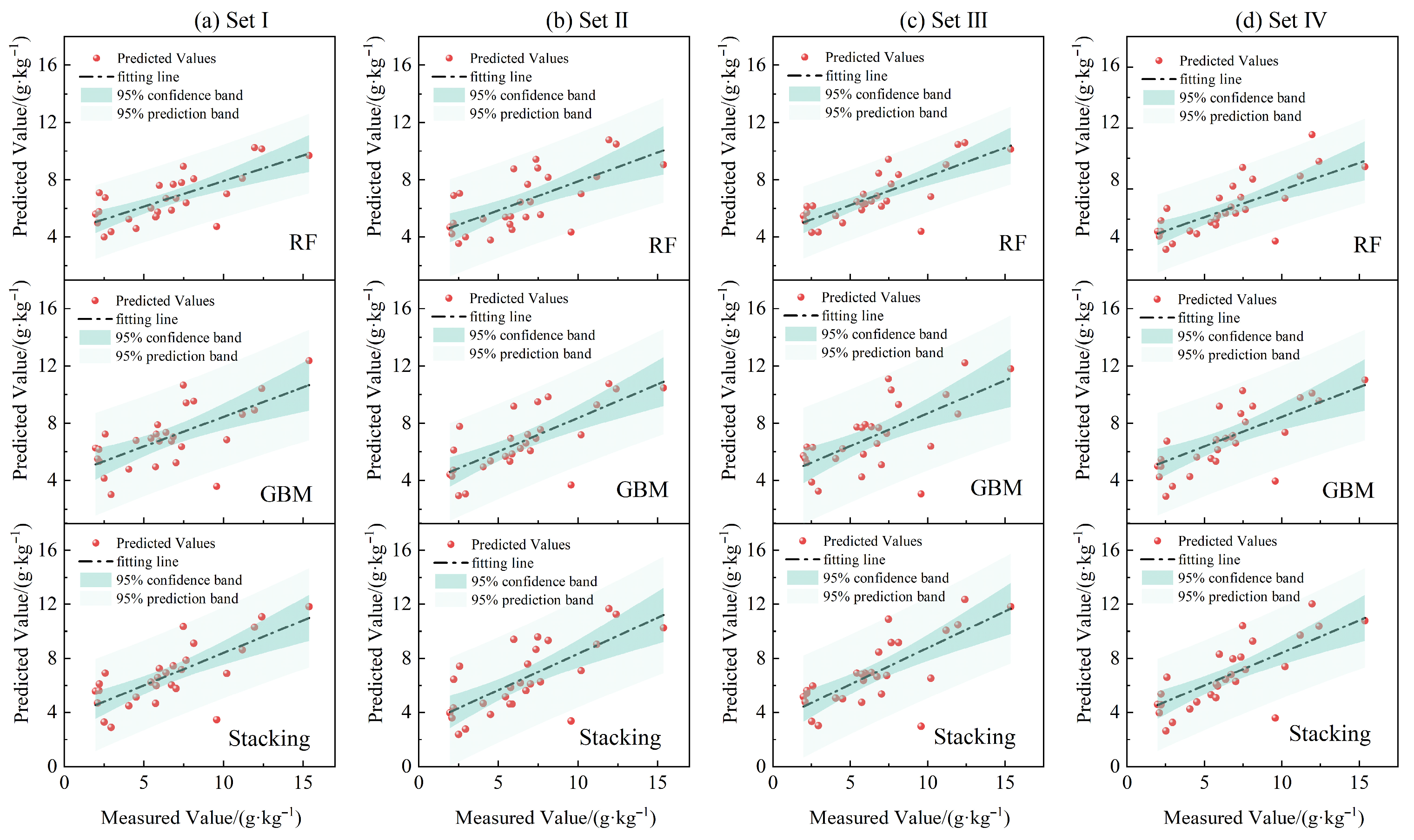
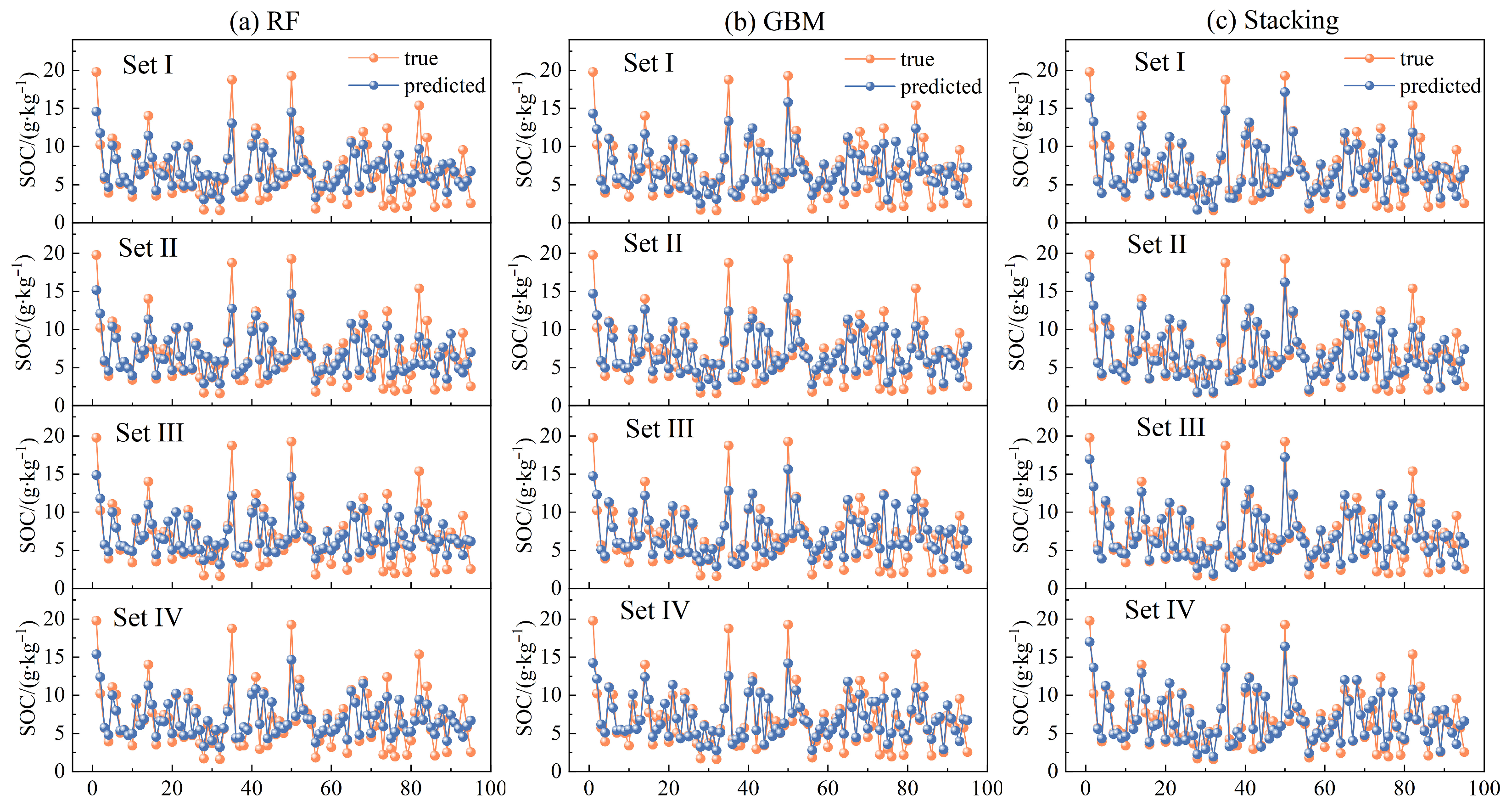
3.3. Estimation Modeling and Prediction Accuracy Evaluation
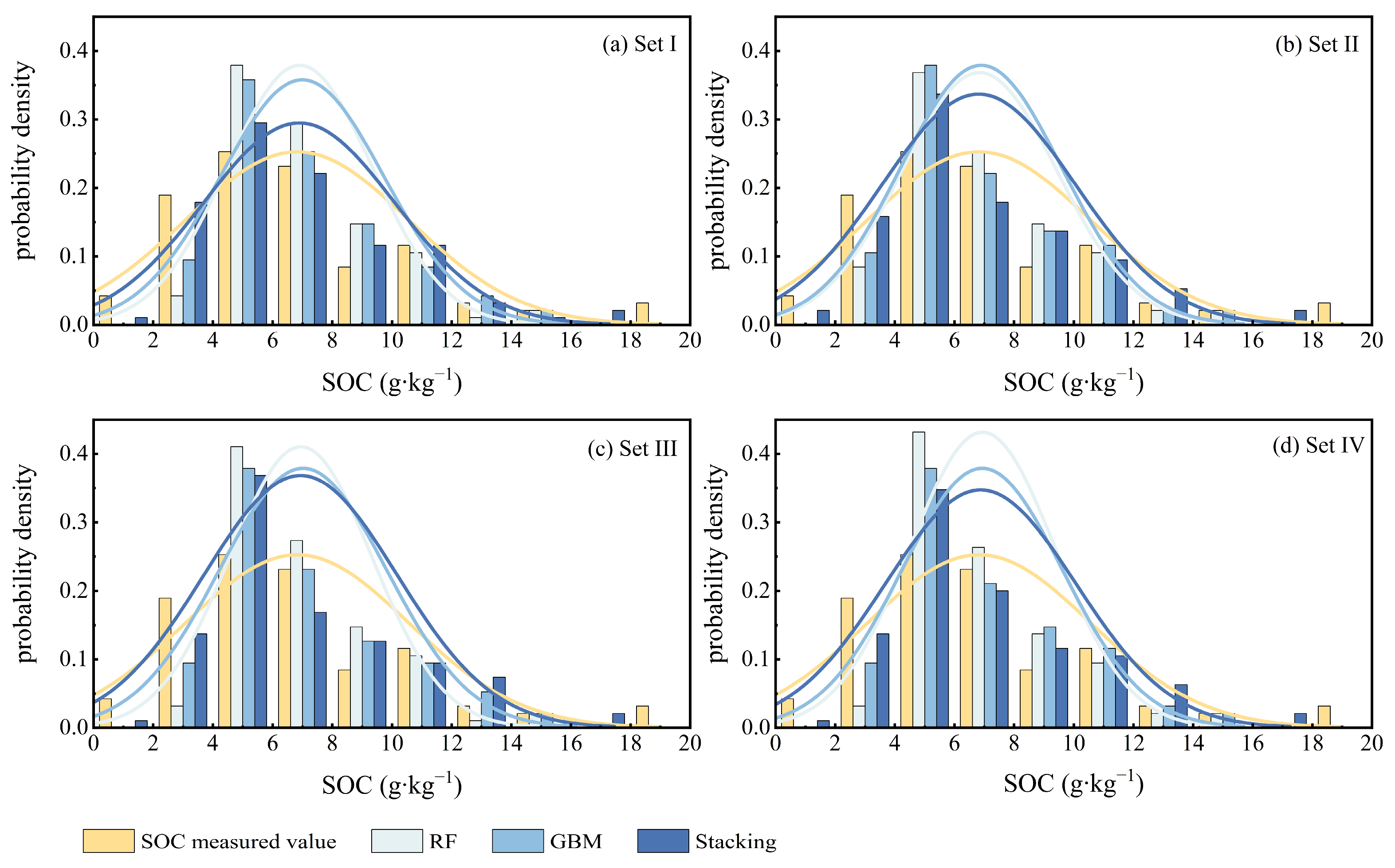
3.4. Comparison of SOC Spatial Prediction Results
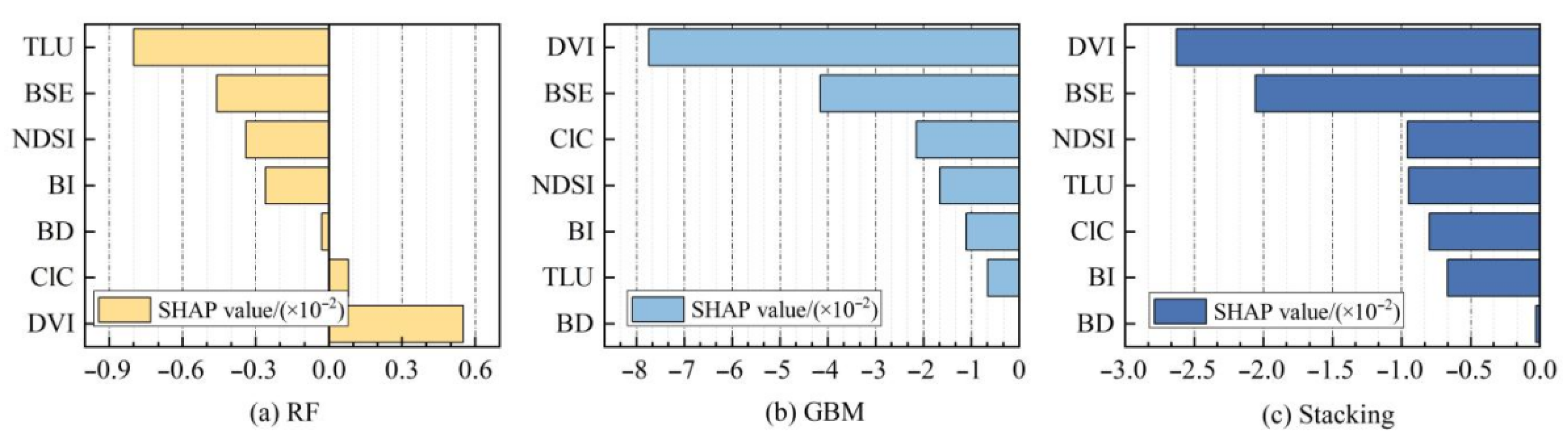
3.5. Importance Analysis of Characteristic Variables
4. Discussion
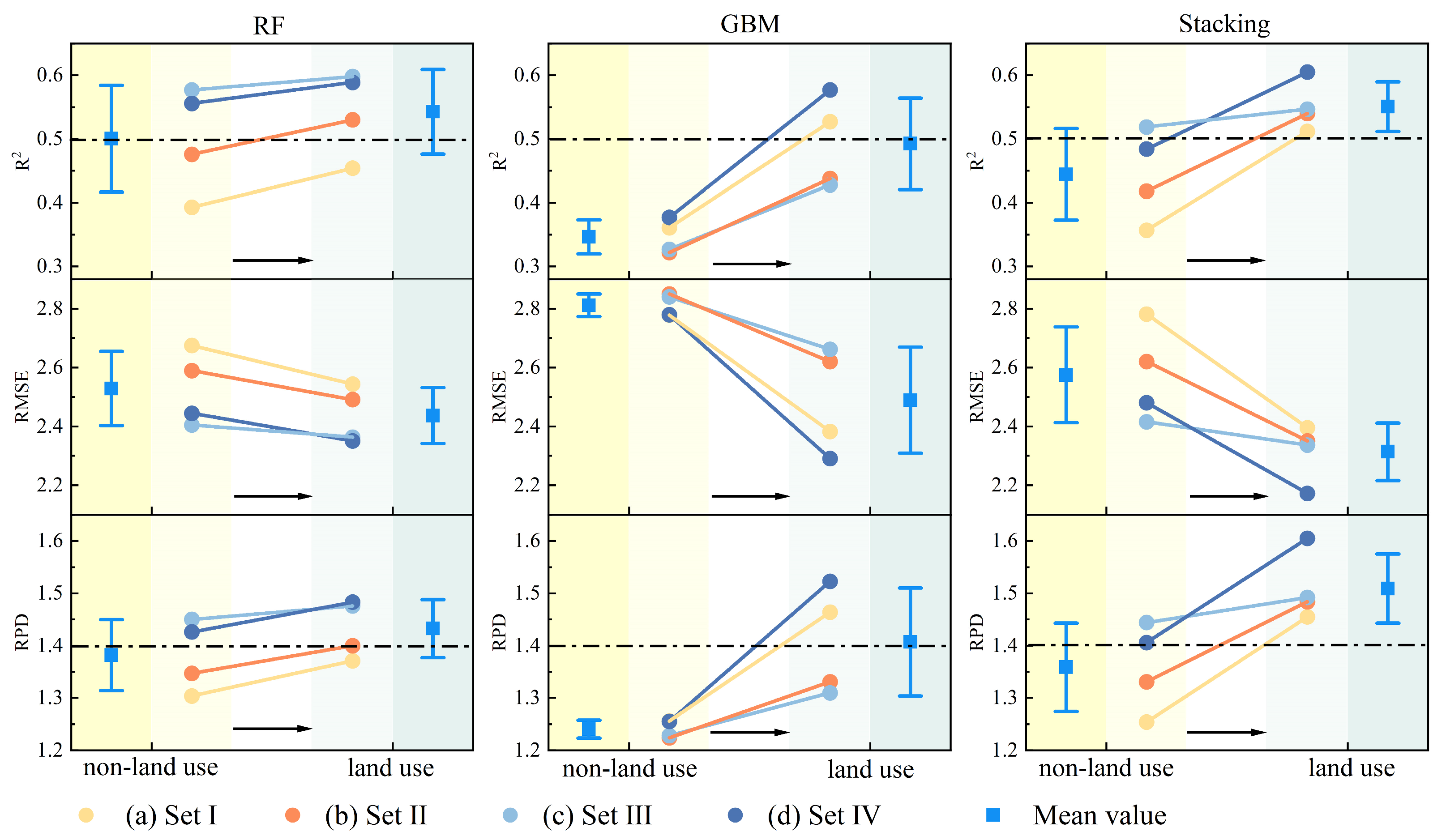
4.1. Integrated Assessment of Screening Methods and Model Performance
4.2. Impact of LU Data on Model Performance
4.3. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carvalhais, N.; Forkel, M.; Khomik, M.; Bellarby, J.; Jung, M.; Migliavacca, M.; Μu, M.; Saatchi, S.; Santoro, M.; Thurner, M.; et al. Global covariation of carbon turnover times with climate in terrestrial ecosystems. Nature 2014, 514, 213–217. [Google Scholar] [CrossRef]
- Bhattacharya, S.S.; Kim, K.H.; Das, S.; Uchimiya, M.; Jeon, B.H.; Kwon, E.; Szulejko, J.E. A review on the role of organic inputs in maintaining the soil carbon pool of the terrestrial ecosystem. J. Environ. Manag. 2016, 167, 214–227. [Google Scholar] [CrossRef] [PubMed]
- Nayak, A.K.; Rahman, M.M.; Naidu, R.; Dhal, B.; Swain, C.K.; Nayak, A.D.; Tripathi, R.; Mohammad Shahid, M.; Islam, M.R.; Pathak, H. Current and emerging methodologies for estimating carbon sequestration in agricultural soils: A review. Sci. Total Environ. 2019, 665, 890–912. [Google Scholar] [CrossRef]
- Abdulraheem, M.I.; Zhang, W.; Li, S.; Moshayedi, A.J.; Farooque, A.A.; Hu, J. Advancement of remote sensing for soil measurements and applications: A comprehensive review. Sustainability 2023, 15, 15444. [Google Scholar] [CrossRef]
- Lin, N.; Quan, H.; He, J.; Li, S.; Xiao, M.; Wang, B.; Chen, T.; Dai, X.; Pan, J.; Li, N. Urban vegetation extraction from high-resolution remote sensing imagery on SD-UNet and vegetation spectral features. Remote Sens. 2023, 15, 4488. [Google Scholar] [CrossRef]
- Li, T.; Cui, L.; Wu, Y.; McLaren, T.I.; Xia, A.; Pandey, R.; Liu, H.; Wang, W.; Xu, Z.; Song, X.; et al. Soil organic carbon estimation via remote sensing and machine learning techniques: Global topic modeling and research trend exploration. Remote Sens. 2024, 16, 3168. [Google Scholar] [CrossRef]
- Rodrigues, E.; Gomes, Á.; Gaspar, A.R.; Antunes, C.H. Estimation of renewable energy and built environment-related variables using neural networks–A review. Renew. Sustain. Energy Rev. 2018, 94, 959–988. [Google Scholar] [CrossRef]
- Vohland, M.; Besold, J.; Hill, J.; Fründ, H.C. Comparing different multivariate calibration methods for the determination of soil organic carbon pools with visible to near infrared spectroscopy. Geoderma 2011, 166, 198–205. [Google Scholar] [CrossRef]
- Tan, Q.; Geng, J.; Fang, H.; Li, Y.; Guo, Y. Exploring the impacts of data source, model types and spatial scales on the soil organic carbon prediction: A case study in the red soil hilly region of southern China. Remote Sens. 2022, 14, 5151. [Google Scholar] [CrossRef]
- Dos Santos, U.J.; De Melo Dematte, J.A.; Menezes, R.S.C.; Dotto, A.C.; Guimarães, C.C.B.; Alves, B.J.R.; Primo, D.C.; Sampaio, E.V.D.S.B. Predicting carbon and nitrogen by visible near-infrared (Vis-NIR) and mid-infrared (MIR) spectroscopy in soils of Northeast Brazil. Geoderma Reg. 2020, 23, e00333. [Google Scholar] [CrossRef]
- Cambou, A.; Barthès, B.G.; Moulin, P.; Chauvin, L.; Faye, E.H.; Masse, D.; Chevallier, T.; Chapuis-Lardy, L. Prediction of soil carbon and nitrogen contents using visible and near infrared diffuse reflectance spectroscopy in varying salt-affected soils in Sine Saloum (Senegal). Catena 2022, 212, 106075. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, H.; Gao, Q.; Zhao, L. Estimating soil organic carbon and pH in Jilin Province using Landsat and ancillary data. Soil Sci. Soc. Am. J. 2020, 84, 556–567. [Google Scholar] [CrossRef]
- Xiao, X.; He, Q.; Ma, S.; Liu, J.; Sun, W.; Lin, Y.; Yi, R. Environmental variables improve the accuracy of remote sensing estimation of soil organic carbon content. Sci. Rep. 2024, 14, 18964. [Google Scholar] [CrossRef]
- Ho, V.H.; Morita, H.; Bachofer, F.; Ho, T.H. Random forest regression kriging modeling for soil organic carbon density estimation using multi-source environmental data in central Vietnamese forests. Model. Earth Syst. Environ. 2024, 10, 7137–7158. [Google Scholar] [CrossRef]
- Cutler, A.; Cutler, D.R.; Stevens, J.R. Random forests. In Ensemble Machine Learning: Methods and Applications; Springer: New York, NY, USA, 2012; pp. 157–175. [Google Scholar] [CrossRef]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobotics 2013, 7, 21. [Google Scholar] [CrossRef] [PubMed]
- Healey, S.P.; Cohen, W.B.; Yang, Z.; Brewer, C.K.; Brooks, E.B.; Gorelick, N.; Hernandez, A.J.; Huang, C.; Hughes, M.J.; Kennedy, R.E.; et al. Mapping forest change using stacked generalization: An ensemble approach. Remote Sens. Environ. 2018, 204, 717–728. [Google Scholar] [CrossRef]
- Azizi, K.; Ayoubi, S.; Demattê, J.A. Controlling factors in the variability of soil magnetic measures by machine learning and variable importance analysis. J. Appl. Geophys. 2023, 210, 104944. [Google Scholar] [CrossRef]
- Keskin, H.; Grunwald, S.; Harris, W.G. Digital mapping of soil carbon fractions with machine learning. Geoderma 2019, 339, 40–58. [Google Scholar] [CrossRef]
- Xie, B.; Ding, J.; Ge, X.; Li, X.; Han, L.; Wang, Z. Estimation of soil organic carbon content in the Ebinur Lake wetland, Xinjiang, China, based on multisource remote sensing data and ensemble learning algorithms. Sensors 2022, 22, 2685. [Google Scholar] [CrossRef]
- Muñoz, A.S.M.; Alvis, Á.I.G.; Martínez, I.F.B. A random forest model to predict soil organic carbon storage in mangroves from Southern Colombian Pacific coast. Estuar. Coast. Shelf Sci. 2024, 299, 108674. [Google Scholar] [CrossRef]
- Wu, M.; Dou, S.; Lin, N.; Jiang, R.; Zhu, B. Estimation and mapping of soil organic matter content using a stacking ensemble learning model based on hyperspectral images. Remote Sens. 2023, 15, 4713. [Google Scholar] [CrossRef]
- Tang, K.; Zhao, X.; Xu, Z.; Sun, H. A stacking ensemble model for predicting soil organic carbon content based on visible and near-infrared spectroscopy. Infrared Phys. Technol. 2024, 140, 105404. [Google Scholar] [CrossRef]
- Bernardini, L.G.; Rosinger, C.; Bodner, G.; Keiblinger, K.M.; Izquierdo-Verdiguier, E.; Spiegel, H.; Retzlaff, C.O.; Holzinger, A. Learning vs. understanding: When does artificial intelligence outperform process-based modeling in soil organic carbon prediction? New Biotechnol. 2024, 81, 20–31. [Google Scholar] [CrossRef]
- Li, S.; Li, X.; Ge, X. Prediction and mapping of soil organic carbon in the Bosten Lake oasis based on Sentinel-2 data and environmental variables. Int. Soil Water Conserv. Res. 2025, 13, 436–446. [Google Scholar] [CrossRef]
- Li, Y.T.; Yang, R.M.; Zhang, X.; Xu, L.; Zhu, C.M. Understanding drivers of the spatial variability of soil organic carbon in China’s terrestrial ecosystems. Land Degrad. Dev. 2024, 35, 308–320. [Google Scholar] [CrossRef]
- An, B.; Wang, X.; Huang, X. Changing characteristics, driving factors and future predictions of land use in the Weigan-Kuqa River Delta Oasis, China. Sci. Rep. 2024, 14, 29318. [Google Scholar] [CrossRef]
- Adeniyi, O.D.; Maerker, M. Explorative analysis of varying spatial resolutions on a soil type classification model and its transferability in an agricultural lowland area of Lombardy, Italy. Geoderma Reg. 2024, 37, e00785. [Google Scholar] [CrossRef]
- Gutman, G.G. Vegetation indices from AVHRR: An update and future prospects. Remote Sens. Environ. 1991, 35, 121–136. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of leaf-area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Mangewa, L.J.; Ndakidemi, P.A.; Alward, R.D.; Kija, H.K.; Bukombe, J.K.; Nasolwa, E.R.; Munishi, L.K. Comparative assessment of UAV and sentinel-2 NDVI and GNDVI for preliminary diagnosis of habitat conditions in Burunge wildlife management area, Tanzania. Earth 2022, 3, 769–787. [Google Scholar] [CrossRef]
- Gurung, R.B.; Breidt, F.J.; Dutin, A.; Ogle, S.M. Predicting Enhanced Vegetation Index (EVI) curves for ecosystem modeling applications. Remote Sens. Environ. 2009, 113, 2186–2193. [Google Scholar] [CrossRef]
- Veraverbeke, S.; Gitas, I.; Katagis, T.; Polychronaki, A.; Somers, B.; Goossens, R. Assessing post-fire vegetation recovery using red–near infrared vegetation indices: Accounting for background and vegetation variability. ISPRS J. Photogramm. Remote Sens. 2012, 68, 28–39. [Google Scholar] [CrossRef]
- Purevdorj, T.S.; Tateishi, R.; Ishiyama, T.; Honda, Y. Relationships between percent vegetation cover and vegetation indices. Int. J. Remote Sens. 1998, 19, 3519–3535. [Google Scholar] [CrossRef]
- Vieira, A.S.; Do Valle Junior, R.F.; Rodrigues, V.S.; da Silva Quinaia, T.L.; Mendes, R.G.; Valera, C.A.; Fernandes, L.F.S.; Pacheco, F.A.L. Estimating water erosion from the brightness index of orbital images: A framework for the prognosis of degraded pastures. Sci. Total Environ. 2021, 776, 146019. [Google Scholar] [CrossRef]
- Li, S.; Yuan, F.; Ata-UI-Karim, S.T.; Zheng, H.; Cheng, T.; Liu, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cao, Q. Combining color indices and textures of UAV-based digital imagery for rice LAI estimation. Remote Sens. 2019, 11, 1763. [Google Scholar] [CrossRef]
- Mishra, M.; Singh, K.K.; Pandey, P.C.; Devrani, R.; Pandey, A.K.; Raju, K.P.; Ranjan, P.; Arora, A.; Costache, R.; Janizadeh, S.; et al. Spectral indices across remote sensing platforms and sensors relating to the three poles: An overview of applications, challenges, and future prospects. In Advances in Remote Sensing Technology and the Three Poles; Wiley & Sons: New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- Kandala, R.; Franssen, H.J.H.; Chaudhuri, A.; Sekhar, M. The value of soil temperature data versus soil moisture data for state, parameter, and flux estimation in unsaturated flow model. Vadose Zone J. 2024, 23, e20298. [Google Scholar] [CrossRef]
- Chen, W.; Zeng, J. Decoupling analysis of land use intensity and ecosystem services intensity in China. J. Nat. Resour. 2021, 36, 2853–2864. [Google Scholar] [CrossRef]
- Hu, Y.; Li, T. Forecasting Spatial Pattern of Land Use Change in Rapidly Urbanized Regions Based on SD-CA Model. Acta Sci. Nat. Univ. Pekin. 2022, 58, 372–382. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature selection with the Boruta package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Chen, J.; Shen, C.; Xue, H.; Yuan, B.; Zheng, B.; Shen, L.; Fang, X. Development of an early prediction model for vomiting during hemodialysis using LASSO regression and Boruta feature selection. Sci. Rep. 2025, 15, 10434. [Google Scholar] [CrossRef] [PubMed]
- Ekanayake, I.U.; Meddage, D.P.P.; Rathnayake, U. A novel approach to explain the black-box nature of machine learning in compressive strength predictions of concrete using Shapley additive explanations (SHAP). Case Stud. Constr. Mater. 2022, 16, e01059. [Google Scholar] [CrossRef]
- Chen, W.; Chen, H.; Feng, Q.; Mo, L.; Hong, S. A hybrid optimization method for sample partitioning in near-infrared analysis. Spectrochim. Acta Mol. Biomol. Spectrosc. 2021, 248, 119182. [Google Scholar] [CrossRef]
- Merabet, K.; Di Nunno, F.; Granata, F.; Kim, S.; Adnan, R.M.; Heddam, S.; Kisi, O.; Zounemat-Kermani, M. Predicting water quality variables using gradient boosting machine: Global versus local explainability using SHapley Additive Explanations (SHAP). Earth Sci. Inform. 2025, 18, 298. [Google Scholar] [CrossRef]
- Wang, W.C.; Gu, M.; Li, Z.; Hong, Y.H.; Zang, H.F.; Xu, D.M. A stacking ensemble machine learning model for improving monthly runoff prediction. Earth Sci. Inform. 2025, 18, 120. [Google Scholar] [CrossRef]
- Han, C.; Yang, G.; Wen, H.; Fu, M.; Peng, B.; Xu, B.; Yin, X.; Wang, P.; Zhu, L.; Feng, M. Development and validation of a quick screening tool for predicting neck pain patients benefiting from spinal manipulation: A machine learning study. Chin. Med. 2025, 20, 74. [Google Scholar] [CrossRef]
- Fu, Y.; Zhao, J.; Wang, Y. LASSO regression and Boruta algorithm to explore the relationship between neutrophil percentage to albumin ratio and asthma: Results from the NHANES 2001 to 2018. Clin. Exp. Med. 2025, 25, 149. [Google Scholar] [CrossRef]
- Cui, Z.; Chen, S.; Hu, B.; Wang, N.; Feng, C.; Peng, J. Mapping Soil Organic Carbon by Integrating Time-Series Sentinel-2 Data, Environmental Co-variates and Multiple Ensemble Models. Sensors 2025, 25, 2184. [Google Scholar] [CrossRef]
- Zhou, W.; Cao, X.; Wang, K.; Xiao, J.; Wang, T.; Li, H.; Ji, C. Hyperspectral modeling of soil organic carbon content-a case study of the Sanjiangyuan region of the Qinghai-Tibet Plateau. J. Glaciol. Geocryol. 2023, 45, 823–832. [Google Scholar] [CrossRef]
- Chai, X.; Li, S.; Liang, F. A novel battery SOC estimation method based on random search optimized LSTM neural network. Energy 2024, 306, 132583. [Google Scholar] [CrossRef]
- Guo, M.; Yang, L.; Zhang, L.; Shen, F.; Meadows, M.E.; Zhou, C. Hydrology, vegetation, and soil properties as key drivers of soil organic carbon in coastal wetlands: A high-resolution study. Environ. Sci. Ecotechnol. 2025, 23, 100482. [Google Scholar] [CrossRef]
- Luo, Z.; Wang, G.; Wang, E. Global subsoil organic carbon turnover times dominantly controlled by soil properties rather than climate. Nat. Commun. 2019, 10, 3688. [Google Scholar] [CrossRef]
- Yu, W.; Weintraub, S.R.; Hall, S.J. Climatic and geochemical controls on soil carbon at the continental scale: Interactions and thresholds. Glob. Biogeochem. Cycles 2021, 35, e2020GB006781. [Google Scholar] [CrossRef]
- Pei, Y.; Gong, S.; Zhang, X.; Zhang, Z.; Zhang, H.; Zha, T. What Is the Effect of Long-Term Revegetation on Soil Stoichiometry? Case Study Based on In Situ Long-Term Monitoring on the Loess Plateau, China. Land Degrad. Dev. 2025. [Google Scholar] [CrossRef]
- Wang, Q.; Le Noë, J.; Li, Q.; Lan, T.; Gao, X.; Deng, O.; Li, Y. Incorporating agricultural practices in digital mapping improves prediction of cropland soil organic carbon content: The case of the Tuojiang River Basin. J. Environ. Manag. 2023, 330, 117203. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Wang, J.; Zhang, D.; Cui, J.; Yuan, Y.; Bao, H.; Yang, M.; Guo, J.; Chen, F.; Zhou, W.; et al. Mapping surface soil organic carbon density of cultivated land using machine learning in Zhengzhou. Environ. Geochem. Health 2025, 47, 1. [Google Scholar] [CrossRef]
- Chen, S.; Xu, H.; Xu, D.; Ji, W.; Li, S.; Yang, M.; Hu, B.; Zhou, Y.; Wang, N.; Arrouays, D.; et al. Evaluating validation strategies on the performance of soil property prediction from regional to continental spectral data. Geoderma 2021, 400, 115159. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, J.; Xu, X. Machine learning in construction and demolition waste management: Progress, challenges, and future directions. Autom. Constr. 2024, 162, 105380. [Google Scholar] [CrossRef]
- Zhu, C.; Zhu, F.; Li, C.; Yan, Y.; Lu, W.; Fang, Z.; Li, Z.; Pan, J. Extracting Typical Samples Based on Image Environmental Factors to Obtain an Accurate and High-Resolution Soil Type Map. Remote Sens. 2024, 16, 1128. [Google Scholar] [CrossRef]
- Alalhareth, M.; Hong, S.C. Enhancing the internet of medical things (IoMT) security with meta-learning: A performance-driven approach for ensemble intrusion detection systems. Sensors 2024, 24, 3519. [Google Scholar] [CrossRef]
- Huang, J.; Peng, Y.; Hu, L. A multilayer stacking method base on RFE-SHAP feature selection strategy for recognition of driver’s mental load and emotional state. Expert Syst. Appl. 2024, 238, 121729. [Google Scholar] [CrossRef]




| Number | Index Type | Formulas | References |
|---|---|---|---|
| 1 | DVI | [29] | |
| 2 | RVI | [30] | |
| 3 | NDVI | [29] | |
| 4 | GNDVI | [31] | |
| 5 | EVI | [32] | |
| 6 | SAVI | [33] | |
| 7 | TSAVI | [34] | |
| 8 | MSAVI | [33] | |
| 9 | TVI | [33] | |
| 10 | BI | [35] | |
| 11 | CI | [36] | |
| 12 | NDCI | [37] | |
| 13 | NDSI | [37] |
| Number | Variable Name | Abbreviation | Number | Variable Name | Abbreviation |
|---|---|---|---|---|---|
| 1 | Elevation | ELEV | 10 | Gravel volume percentage | GVP |
| 2 | Slope | Slope | 11 | Sand content | SC |
| 3 | Aspect | Aspect | 12 | Silt content | SiC |
| 4 | 2 m air temperature | T2m | 13 | Clay content | ClC |
| 5 | Precipitation | PRCP | 14 | Bulk density | BD |
| 6 | Evapotranspiration | ET | 15 | pH | pH |
| 7 | Soil temperature | ST | 16 | Electrical conductivity | EC |
| 8 | Bare soil evaporation | BSE | 17 | Type of land use | TLU |
| 9 | Surface pressure | SP |
| Variable Set | Screening Methods | Model | R2 | RMSE | RPD |
|---|---|---|---|---|---|
| Set I | Unfiltered | RF | 0.91 | 1.50 | 2.57 |
| GBM | 0.90 | 1.41 | 2.75 | ||
| Stacking | 0.91 | 1.13 | 3.41 | ||
| Set II | Boruta | RF | 0.90 | 1.46 | 2.64 |
| GBM | 0.88 | 1.53 | 2.53 | ||
| Stacking | 0.90 | 1.21 | 3.18 | ||
| Set III | Lasso | RF | 0.91 | 1.57 | 2.45 |
| GBM | 0.88 | 1.47 | 2.62 | ||
| Stacking | 0.90 | 1.20 | 3.21 | ||
| Set IV | Boruta–Lasso | RF | 0.89 | 1.59 | 2.43 |
| GBM | 0.85 | 1.62 | 2.38 | ||
| Stacking | 0.89 | 1.31 | 2.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Z.; Luo, X.; Wang, X.; Li, D. Spatial Prediction of Soil Organic Carbon Based on a Multivariate Feature Set and Stacking Ensemble Algorithm: A Case Study of Wei-Ku Oasis in China. Sustainability 2025, 17, 6168. https://doi.org/10.3390/su17136168
Cao Z, Luo X, Wang X, Li D. Spatial Prediction of Soil Organic Carbon Based on a Multivariate Feature Set and Stacking Ensemble Algorithm: A Case Study of Wei-Ku Oasis in China. Sustainability. 2025; 17(13):6168. https://doi.org/10.3390/su17136168
Chicago/Turabian StyleCao, Zuming, Xiaowei Luo, Xuemei Wang, and Dun Li. 2025. "Spatial Prediction of Soil Organic Carbon Based on a Multivariate Feature Set and Stacking Ensemble Algorithm: A Case Study of Wei-Ku Oasis in China" Sustainability 17, no. 13: 6168. https://doi.org/10.3390/su17136168
APA StyleCao, Z., Luo, X., Wang, X., & Li, D. (2025). Spatial Prediction of Soil Organic Carbon Based on a Multivariate Feature Set and Stacking Ensemble Algorithm: A Case Study of Wei-Ku Oasis in China. Sustainability, 17(13), 6168. https://doi.org/10.3390/su17136168






