Abstract
Against the backdrop of global climate change and rapid urbanization, understanding the spatiotemporal dynamics and driving mechanisms of vegetation net primary productivity (NPP) is critical for ensuring regional ecological security and achieving carbon neutrality goals. This study focuses on the Yangtze River Delta Urban Agglomeration (YRDUA) and integrates multi-source remote sensing data with socioeconomic statistics. By combining interpretable machine learning (XGBoost-SHAP) with multiscale geographically weighted regression (MGWR), and incorporating Theil–Sen trend analysis and Mann–Kendall significance testing, we systematically analyze the spatiotemporal variations in NPP and its multiscale driving mechanisms from 2001 to 2020. The results reveal the following: (1) Total NPP in the YRDUA shows an increasing trend, with approximately 24.83% of the region experiencing a significant rise and only 2.75% showing a significant decline, indicating continuous improvement in regional ecological conditions. (2) Land use change resulted in a net NPP loss of 2.67 TgC, yet ecological restoration and advances in agricultural technology effectively mitigated negative impacts and became the main contributors to NPP growth. (3) The results from XGBoost and MGWR are complementary, highlighting the scale-dependent effects of driving factors—at the regional scale, natural factors such as elevation (DEM), precipitation (PRE), and vegetation cover (VFC) have positive impacts on NPP, while the human footprint (HF) generally exerts a negative effect. However, in certain areas, a dose–response effect is observed, in which moderate human intervention can enhance ecological functions. (4) The spatial heterogeneity of NPP is mainly driven by nonlinear interactions between natural and anthropogenic factors. Notably, the interaction between DEM and climatic variables exhibits threshold responses and a “spatial gradient–factor interaction” mechanism, where the same driver may have opposite effects under different geomorphic conditions. Therefore, a well-balanced combination of land use transformation and ecological conservation policies is crucial for enhancing regional ecological functions and NPP. These findings provide scientific support for ecological management and the formulation of sustainable development strategies in urban agglomerations.
1. Introduction
Under the dual pressures of global climate change and accelerating urbanization, NPP has emerged as a core for assessing ecosystem carbon sequestration capacity and ecological security, and as a research hotspot at the intersection of ecology and geography [1]. It has also become a central topic in understanding the coupled human–environment system [2,3]. As a key component of the terrestrial carbon cycle, NPP not only determines the carbon sink potential of ecosystems but also profoundly influences critical ecosystem services such as climate regulation, soil and water conservation, and biodiversity maintenance through the flow of energy and the cycling of materials [4,5]. According to the Intergovernmental Panel on Climate Change (IPCC) Sixth Assessment Report, terrestrial ecosystems globally absorbed approximately 29% of anthropogenic carbon emissions from 2001 to 2020, with urbanized areas identified as the most unstable carbon sink units due to intense human disturbances [6]. In rapidly urbanizing regions in particular, high-intensity land development leads to fragmentation of natural vegetation, industrial emissions exacerbate air pollution, and the urban heat island effect alters local climate conditions [7,8]. These multiple stressors interact nonlinearly, reshaping the spatiotemporal patterns of NPP [9]. Such changes not only threaten regional ecological security but also influence the trajectory of global climate change through carbon–climate feedback mechanisms [10,11]. For example, Chi Zhang et al. studied carbon dynamics across metropolitan areas in the southern United States from 1945 to 2007 and highlighted that pre-urbanization vegetation types and post-conversion land use patterns are the two primary determinants of urbanization-induced changes in carbon dynamics [12]. Cao et al. quantified the impacts of drought on net primary productivity (NPP) and further evaluated the contributions of climate change, land use change, rising CO2 concentrations, and nitrogen deposition to drought-induced NPP loss by integrating the MsTMIP carbon cycle model [13]. Against this backdrop, investigating the driving mechanisms of NPP in globally representative, rapidly urbanizing regions is not only crucial for regional sustainable development but also provides a scientific foundation for improving global carbon cycle models and optimizing climate governance strategies.
NPP not only directly reflects the capacity of vegetation to fix atmospheric carbon dioxide through photosynthesis [14], but is also closely linked to ecosystem services such as climate regulation [15], soil conservation [16,17], and biodiversity maintenance [18,19]. With the rapid development of remote sensing technologies and machine learning methods, the accuracy of NPP estimation has significantly improved [20,21]. Research approaches to understanding the driving mechanisms of NPP have undergone a paradigm shift from traditional statistical models to machine learning-based frameworks, with a concurrent evolution in research content—from single-factor analyses to the exploration of nonlinear interactions among multiple factors [22,23]. Early studies primarily relied on empirical statistical models (e.g., RUSLE) [24,25] or process-based models (e.g., CASA) [26] to quantify the effects of climatic [27] and topographic [28] factors on NPP using linear regression or principal component analysis. For instance, Potter et al. first simulated global NPP dynamics using the CASA model and identified the seasonal alignment of temperature and precipitation as a key driver of interannual variability in tropical rainforest NPP [29]. However, these models tend to oversimplify the parameterization of complex surface processes. This limitation is particularly evident in urbanized regions, where the stress effects of human activities on vegetation are difficult to capture through linear relationships.
With advances in machine learning, algorithms such as Random Forest (RF) [30,31] and Support Vector Machines (SVMs) [32] have been increasingly applied to NPP modeling, shifting the research paradigm toward data-driven nonlinear analysis. The rise of deep learning has further refined NPP research, particularly in understanding interaction effects among drivers. Interpretable machine learning techniques such as XGBoost-SHAP have been widely adopted in ecosystem service studies [33]. For example, Liu et al. developed an interpretable convolutional neural network (CNN) integrated with a long short-term memory (LSTM) framework to quantify the influence of climatic factors on NPP dynamics in the Yellow River source region. They found that temperature and precipitation were the dominant predictors affecting forecast accuracy [34]. These methods not only overcome the limitations of traditional models in nonlinear fitting but also provide new tools for visualizing multi-factor interactions. Despite these methodological advances, three major limitations persist in current research: (1) The first is a limited spatial scale, with most studies focusing only on regional or pixel-level analysis and lacking a multiscale framework connecting local, regional, and global perspectives. (2) The driving factor system remains incomplete. This is particularly true in highly urbanized regions, where intensive human activities and industrial production often lead to elevated CO2 emissions—one of the primary indicators of anthropogenic disturbance to natural ecosystems. However, in previous related studies, key urbanization-related factors such as atmospheric CO2 concentration and the human footprint have frequently been overlooked. (3) The third is a disconnect between model interpretability and ecological mechanisms, particularly in highly heterogeneous urban agglomerations, where the spatial variation in factor contributions remains poorly understood.
Multiscale research approaches have increasingly become a key direction in the study of NPP, as they are capable of revealing spatial heterogeneity in driving factors and cross-scale feedback mechanisms [35]. At the grid level, analytical methods have evolved from traditional geographically weighted regression (GWR) [36] to MGWR [37], which allows for more detailed exploration of localized relationships between NPP and its drivers [38]. As an extension of GWR, MGWR introduces variable-specific bandwidth [39], enabling the model to more accurately capture spatially non-stationary relationships and reflect the spatial variation in different factors influencing NPP at a local scale. In addition, multi-source data fusion techniques are frequently used in grid-based analysis, integrating meteorological, soil, and remote sensing data to provide a more comprehensive characterization of grid-scale drivers of NPP [40,41]. For instance, in studies examining the ecological impact of urban expansion, it has been found that while urbanization may lead to a decrease in local NPP, broader regional scales can show opposite trends due to vegetation restoration or improved management practices [42,43]. This reflects a “local loss–overall gain” phenomenon, emphasizing the importance of multiscale perspectives. Similarly, watershed-scale studies suggest that while certain land management practices may negatively impact NPP at small scales (e.g., through soil compaction), they may enhance NPP at larger scales via other mechanisms such as improved nutrient management [44]. These cases demonstrate that multiscale analysis not only helps to identify the spatial differentiation of dominant drivers but also uncovers cross-scale coupling mechanisms between natural processes and human interventions.
As one of the six globally recognized world-class urban agglomerations, the YRDUA, centered around Shanghai, is characterized by intense human activity and a fragile ecological foundation. Studying the spatiotemporal dynamics of NPP and its multiscale driving factors in this region is essential not only for providing scientific guidance on optimizing regional ecological security patterns but also for offering a reference model for sustainable development strategies in other rapidly urbanizing areas worldwide.
This study employs multi-source remote sensing data, ground-based observations, and socioeconomic statistics to construct a high-resolution spatiotemporal dataset of NPP for the YRDUA covering the period from 2001 to 2020. By integrating correlation analysis with the XGBoost-SHAP, we investigate the spatial and temporal dynamics of NPP and its driving mechanisms at both the grid and regional scales. The specific objectives of this research are as follows:
- (1)
- Utilizing MOD17A3H data, we investigated the spatiotemporal patterns of NPP across the YRDUA, with a particular focus on its long-term temporal trends and spatial heterogeneity;
- (2)
- We analyzed the characteristics of regional land use change during the urbanization process and its impacts on NPP;
- (3)
- By employing the XGBoost-SHAP model and the MGWR model at both regional and grid scales, we identified the mechanisms through which multiple driving factors influence NPP, with special emphasis on the nonlinear interactions among different drivers.
2. Materials and Methods
2.1. Study Area
The YRDUA is located in the lower reaches of the Yangtze River in eastern China, spanning from 115°46′ E to 123°25′ E longitude and 29°20′ N to 32°34′ N latitude. Situated at the confluence of the Yangtze River and the ocean, and adjacent to both the Yellow Sea and the East China Sea, the region lies on an extensive alluvial plain at the river’s estuary. It hosts numerous riverine and coastal ports and encompasses the entire administrative territories of Shanghai Municipality, Anhui Province, Zhejiang Province, and Jiangsu Province, with a total area of approximately 358,000 square kilometers. Topographically, the region features an elevation gradient that descends from the southwest to the northeast, with altitudes ranging from 0 to 1920 m. Climatically, the YRDUA belongs to the subtropical monsoon climate zone, characterized by warm and humid conditions, distinct seasonal variations, and abundant precipitation. The annual average temperature ranges between 18 °C and 23 °C, while the annual precipitation ranges from 1000 mm to 2000 mm, reflecting strong monsoonal and maritime influences. As one of the most economically developed and highly urbanized regions in China, the YRDUA plays a central role in driving national economic growth. In 2024, despite accounting for only 3.69% of China’s land area, the region generated a gross domestic product (GDP) of approximately USD 4.58 trillion—about 24.58% of the national total—and was home to roughly 16% of the country’s population. These characteristics make the YRDUA a critical engine of China’s modernization and a representative case for studying the ecological impacts of intensive urbanization [45]. (See Figure 1).
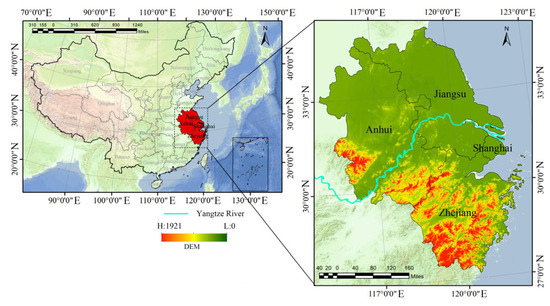
Figure 1.
The research is conducted based on China’s geographical location and the topography and landforms of the study area.
2.2. Data Sources
This study selected nine representative potential driving factors—CO2, DEM, land use/cover change (LUCC), normalized difference vegetation index (NDVI), PRE, soil organic matter (SOM), temperature (TEM), FVC, and HF (human footprint: a comprehensive quantitative indicator of the disturbances and impacts caused by human activities on the natural environment within a specific area) [46,47]—across five dimensions: topography, climate, vegetation, land use, and socioeconomic activities. The data sources and key attributes are summarized in Table 1. All spatial datasets were projected to the WGS_1984_UTM_Zone_50N coordinate system and resampled to a spatial resolution of 0.2 km × 0.2 km. Datasets originally provided at daily or monthly intervals were aggregated to annual values.

Table 1.
Summary of data products used in this study.
Land use data were extracted from the Annual China Land Cover Dataset and reclassified into six categories: cropland, forest, grassland, water bodies, built-up land, and unused land. The study area boundary was defined according to the official delineation of the YRDUA as defined in the Development Plan for the YRDUA issued by the Chinese government [48].
2.3. Research Methods
2.3.1. NPP Coefficient of Variation CV
The CV is often used to measure the relative stability (or fluctuation) of geographic data over time [49], and it is applied here to evaluate the stability of NPP in the YRDUA over the past 21 years. The calculation formula is as follows:
In the formula, Cv is the coefficient of variation; NPP is the value for year i; n is the width of the time series; is the average NPP in the Yangtze River Basin from 2001 to 2020. A larger Cv indicates greater fluctuations in NPP over the time series, while a smaller Cv indicates lesser fluctuations.
2.3.2. Theil–Sen Median Trend Analysis and the Mann–Kendall Test
Theil–Sen median trend analysis and the Mann–Kendall test are important methods for determining trends in long-term time series data [50]. These methods are particularly useful for assessing trends in data where the underlying distribution is unknown or not necessarily Gaussian [51,52]. They are used to evaluate the trends in NPP in the Yangtze River Basin over the past 20 years. The calculation formulas are as follows:
where β is the change trend and NPPi/j is the NPP value in years i/j. When β > 0, the NPP of the region shows an upward trend. When β < 0, the NPP of the region shows a downward trend.
In this study, the Mann–Kendall test is used to determine whether the changes in NPP trends in the region are statistically significant. The calculation formula is as follows:
where sgn denotes the sign function. Furthermore, the trend test was based on the null hypothesis H0: β = 0. The null hypothesis was rejected when |ZC| > Z1-a/2, where Z1-a/2 is the standard normal variance; α is the significance test level; and α < 0.05 passes the significance test when |ZC| ≥ 1.64, indicating a significant change in the change region.
2.3.3. Extreme Gradient Boosting (XGBoost)
XGBoost is an efficient ensemble learning algorithm built upon the gradient boosting framework. It incrementally improves prediction performance by sequentially training multiple decision trees [53]. The core idea is that each new tree is constructed to correct the errors made by the previous ones. At each iteration, the model evaluates the loss between the predicted values and the actual observations, using both first- and second-order derivatives of the loss function to determine the optimal way to construct a new tree and reduce residuals [54]. By leveraging second-order derivative information, XGBoost can more accurately approximate the minimum of the loss function, leading to faster convergence compared to traditional GBDT models, which rely solely on first-order gradients.
During the tree construction process, XGBoost uses a greedy strategy to select the optimal feature and split point. It evaluates all features and potential split thresholds to compute the “gain,” defined as the reduction in loss from splitting a node—calculated as the sum of losses in the left and right child nodes minus the loss of the original node—further adjusted by a regularization term to penalize complexity introduced by new leaf nodes. The split with the highest gain is selected, and this process continues until the predefined maximum tree depth is reached or no further improvement is possible. Additionally, the objective function explicitly incorporates a regularization term to control model complexity and prevent overfitting [55].
The XGBoost model is constructed through the following process: Initially, an initial tree is built using the training dataset to generate predictions and compute the residuals between predicted and actual values. In each subsequent iteration, a new tree is added to fit the residuals from the previous round. This process continues until the learning procedure is complete. Ultimately, an ensemble of multiple trees is formed to model the residuals, resulting in a robust and accurate predictive framework [56].
The objective function of the XGBoost model comprises a loss function and a regularization term and is formulated as follows:
where Obj(θ) denotes the overall objective function; l(yi,ŷi) represents the training loss, which measures the difference between the predicted value ŷi and the true value yi; and Ω(fk) is the regularization term used to control model complexity and prevent overfitting. The regularization term is defined as follows:
Here, T denotes the number of leaf nodes in the k-th tree, j represents the weight of the j-th leaf node in the k-th tree, γ is the penalty term for the number of leaf nodes, and is the L2 regularization term used to penalize large leaf weights.
In this study, an NPP prediction model was developed based on the selected driving factors using the dataset from the year 2020. The dataset was divided into a training set (70% of the data) and a testing set (30% of the data). The optimal model parameters were determined through 5-fold cross-validation on various parameter combinations. The best parameters were found to be as follows: colsample_bytree: 0.68, learning_rate: 0.14, max_depth: 9, n_estimators: 838, reg_alpha: 0.52, reg_lambda: 0.88, and subsample: 0.70. The main evaluation metrics of the optimized model are presented in Figure 2. The results indicate a coefficient of determination (R2) of 0.85, root mean square error (RMSE) of 63.418, mean absolute error (MAE) of 46.104, and residual error sum (RES) of −0.03. The residuals exhibited a relatively uniform spatial distribution and approximately normal frequency distribution, demonstrating good generalization performance of the model across different regions.
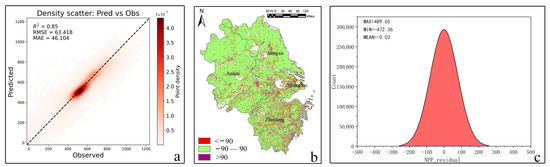
Figure 2.
(a) Accuracy evaluation of the XGBoost model in predicting NPP. MAE: mean absolute error; RMSE: root mean square error. (b) Spatial distribution of prediction residuals. (c) Histogram of residuals showing their distribution characteristics.
2.3.4. Shapley Additive exPlanations (SHAP)
SHAP is an interpretability method grounded in cooperative game theory and the principle of local explanations. It calculates the average marginal contribution of each feature to the model’s prediction, thereby determining the importance of that feature for the prediction outcome [57]. The SHAP interaction effect values, on the other hand, measure the average contribution of each feature to the model’s prediction under different feature combinations, thereby explaining the interaction between features. This approach incorporates feature attribution calculations based on Shapley values. The Shapley value calculation theory primarily involves two components: feature weights and marginal contributions, as described in the following formula:
In the formula, Φj represents the Shapley value of feature j; S denotes the subset of features used in the model; is the subset of features excluding {xj}; is the set of input feature vectors; P represents the number of features; represents the weight of subset S based on the concept of permutations; is the marginal contribution of the subset S, including {xj}; and val(S) represents the marginal contribution of subset S excluding {xj}.
The model’s predicted value is equivalent to the sum of the average value of the training samples and the Shapley values of the features, and f(x) represents the linear function of the feature variables’ Shapley values and can be expressed as
where represents the predicted output value; denotes the mean of predicted values for the training samples; and signifies a vector for the p features, where each element is 1 if the corresponding feature is present and 0 if it is absent.
Shapley values quantify the relative importance of each feature in driving NPP variation—the larger the Shapley value, the greater the feature’s contribution to changes in NPP. Computing exact Shapley values involves complex combinatorial and factorial operations. Therefore, we employ the Tree SHAP algorithm, a variant optimized for tree-based models, which efficiently traverses the tree structure to estimate each feature’s contribution to the model’s prediction.
2.3.5. Restricted Cubic Spline (RCS)
RCS is a type of piecewise polynomial regression used to flexibly model nonlinear relationships between independent and dependent variables. By fitting the SHAP values of each driving factor with RCS, we can accurately characterize the complex nonlinear dependencies between these drivers and NPP [58]. In this study, RCS fitting was implemented in Python (V 3.10) using the scikit-learn library.
2.3.6. MGWR
To further investigate the spatial heterogeneity of the influence of different factors on NPP, this study employs MGWR to analyze the varying degrees and directions (positive or negative) of impact that different driving factors exert on NPP at the grid scale [59,60]. The calculation is performed according to the following formula:
where yi represents the observed value of the dependent variable at location i; xij denotes the observed value of the j-th independent variable at location i; βj(ui,vi) is the regression coefficient of the j-th independent variable at location i, which is a function of geographic coordinates; and εi is the error term.
3. Results
3.1. Spatial and Temporal Variations in NPP
Figure 3 illustrates that the total NPP of the YRDUA exhibited a fluctuating upward trend from 2001 to 2020, with a mean annual value of 174.37 ± 8.12 TgC (1 TgC = 1012 gC). The total NPP increased from 168.77 TgC in 2001 to 186.51 TgC in 2020, representing an overall growth rate of 10.3%. Notably, the NPP peaked in 2014 at 192.69 TgC, marking the highest value over the 20-year period, while the lowest value occurred in 2005 (161.61 TgC), potentially due to extreme climatic events during that year.
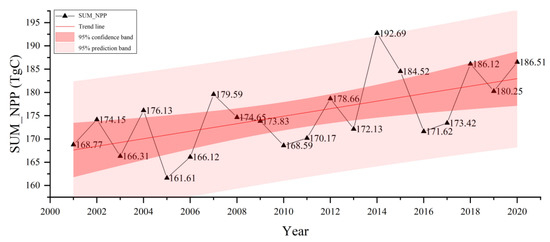
Figure 3.
The trend of NPP changes in the YRDUA from 2001 to 2020.
Figure 4 shows a clear spatial pattern of NPP across the study area, characterized by higher values in the south and lower values in the north. Regions with relatively high NPP values are primarily concentrated in the Wuyi Mountains of Zhejiang Province, whereas lower NPP values are predominantly found in Shanghai and the northern parts of Anhui and Jiangsu provinces. Comparing NPP in 2020 with that in 2001, approximately 25.72% of the area experienced a decrease in NPP, while around 5% showed no significant change—these areas are mainly composed of water bodies and built-up land as of 2001, and the spatial distribution of NPP changes exhibit a general pattern of increase in the north and decrease in the south. As shown in Figure 4c, the coefficient of variation (CV) of NPP in the YRDUA ranges from 0 to 1.7, with a mean value of 0.086, indicating relatively stable NPP overall. However, its spatial distribution exhibits notable variability. Areas with increased NPP fluctuations can be broadly categorized into two types: the first type is concentrated around urban fringes, particularly near the Yangtze River estuary and the Taihu Lake region; the second type is located in the hilly areas of Anhui Province.
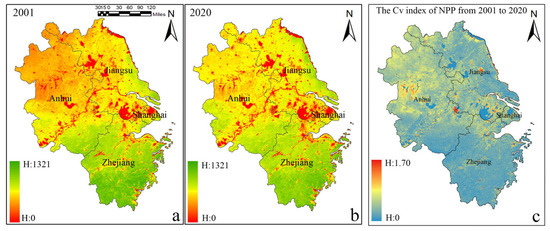
Figure 4.
Spatial distribution of NPP and spatial changes in NPP in the YRDUA in 2001 and 2020. (a) and (b) represent the spatial distribution of NPP in the study area in 2001 and 2020, respectively. (c) represents the CV of NPP changes from 2001 to 2020.
As shown in Figure 5a, the Theil–Sen slope (β) of NPP in the YRDUA ranges from –36.9 to 67.90. Only 5.06% of the region showed no change in NPP (β = 0), primarily corresponding to water bodies. Approximately 15.60% of the area experienced a decreasing trend (β < 0), mainly concentrated around urban fringes and in the southern coastal region of Zhejiang Province. In contrast, a substantial 79.34% of the region exhibited an increasing trend (β > 0), further confirming the overall upward trend in NPP.
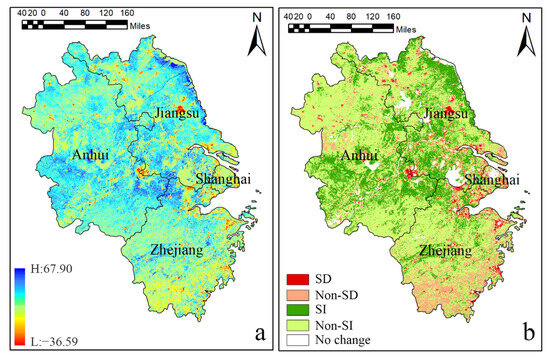
Figure 5.
Change trend map of NPP in the YRB, (a) spatial distribution of grid-scale β index; (b) spatial distribution of Mann–Kendall test results for change trends.
By integrating the Theil–Sen median trend analysis with the Mann–Kendall significance test, four trend categories were identified: significant increase (SI), significant decrease (SD), non-significant increase (Non-SI), and non-significant decrease (Non-SD) (Figure 5b). The results indicate that approximately 24.83% of the region experienced a significant increase in NPP over the past two decades, mainly located in the coastal areas of Jiangsu, mountainous areas in Anhui, and parts of Zhejiang. These improvements in ecosystem condition are likely attributable to policy interventions such as ecological restoration and land use optimization. The SD category accounts for only 2.75% of the region, suggesting that areas of ecological degradation are limited in extent. Nevertheless, these zones—often associated with urban expansion and intensified land use—should be closely monitored. The Non-SD category, covering 12.85% of the region, is primarily located adjacent to SD areas and in southern Zhejiang. Although these areas have not yet shown statistically significant degradation, their negative trend direction suggests potential ecological risks and thus warrants attention in future ecological planning and management. The Non-SI category comprises 54.51% of the region and is widely distributed, indicating a widespread but statistically non-significant trend of NPP improvement across most of the study area, albeit without reaching statistical significance.
3.2. Impacts of LUCC on NPP in the YRDUA
Between 2001 and 2020, the land use types in the YRDUA followed a consistent order in terms of areal extent: cultivated land > woodland > construction land > grassland > water > unused land. Woodland and cultivated land remained the dominant land use types, together accounting for over 76.34% of the total area; however, both types showed a declining trend over the two decades.
As shown in Table 2 and Figure 6, cultivated land experienced the largest outflow, with 19,545.36 km2 converted to other land use types, resulting in a net decrease of 16,613.2 km2. The primary conversion was to construction land, which accounted for 16,287.44 km2, or 83.33% of the total cropland loss. Woodland also saw significant conversion, with 2935.6 km2 transferred to other uses and a net decrease of 1225.48 km2. Construction land exhibited the greatest increase among all land use categories, growing from 31,203.04 km2 in 2001 to 49,364.68 km2 in 2020, an increase of 58.20%, with a net gain of 18,161.64 km2. The majority of this expansion came from cultivated land, which contributed 89.68% of the newly developed land.

Table 2.
Land use area and proportional changes in the YRDUA (2001–2020).
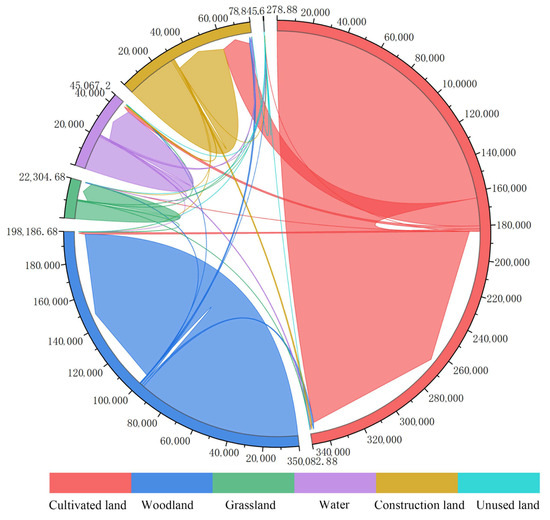
Figure 6.
String map of land use transfer between different types from 2001 to 2020.
As the study area is highly urbanized, the most typical land surface change during urbanization is the conversion of other land uses into construction land. Therefore, this study explores the impact of urbanization on NPP by analyzing the changes in construction land and their effects on NPP. As shown in Figure 7, the increase in construction land is primarily concentrated in the Yangtze River estuary region, centered around Shanghai, and in the central and northern parts of the study area. The expansion of construction land can be classified into two types. The first type is driven by urban expansion, characterized by a gradual outward extension along the edges of existing construction land, exhibiting block-like growth, mainly concentrated around the current urban areas, which experience the largest increase in construction land. The second type is characterized by a scattered, point-like distribution, with expansion mainly occurring in peri-urban and rural areas surrounding cities.
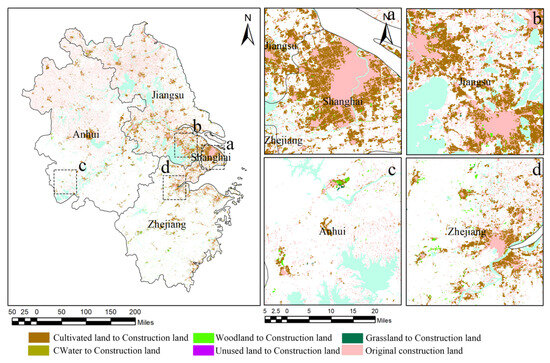
Figure 7.
Spatial distribution of changes in urban construction land in the YRDUA from 2001 to 2021. (a,b) are typical urban development areas; (c,d) are typical rural development areas.
In terms of NPP gains and losses caused by land use changes, the NPP in 2020 increased compared to 2001, but land use changes led to a decrease of approximately 2.67 TgC in NPP. As shown in Figure 8, the expansion of construction land due to urban development resulted in an annual NPP loss of 1.86 TgC from cropland, accounting for 69.80% of the net loss. The reduction in woodland contributed to an annual NPP loss of approximately 0.76 TgC. Additionally, cropland being converted to water bodies led to an NPP loss of 0.55 TgC. At the same time, certain land use changes contributed to increases in NPP. For instance, the conversion of cropland to woodland resulted in an NPP increase of 0.27 TgC, which was greater than the NPP decrease caused by the conversion of woodland to cropland. Similarly, the conversion of water bodies to cropland led to an NPP increase of 0.16 TgC, and the conversion of construction land to woodland resulted in an NPP increase of 0.11 TgC. Overall, the NPP changes caused by land use changes between non-construction land types in the study area were relatively balanced. However, the conversion of non-construction land to construction land resulted in a net NPP decrease of 2.28 TgC, accounting for 85.31% of the total decrease.
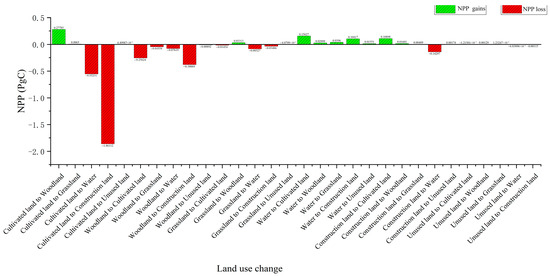
Figure 8.
The gains or losses of NPP caused by land use changes.
An analysis of the average NPP values for different land use types across various years reveals that the overall increase in NPP in the YRDUA is driven by the increase in the average NPP values of all land use types. As shown in Figure 9, the per-unit NPP of cultivated land, woodland, grassland, water bodies, and construction land all increased from 2001 to 2020. This indicates that during this period, the ecological environment of the YRDUA significantly improved. A better ecological environment provides more favorable conditions for plant growth, thereby promoting the increase in NPP.
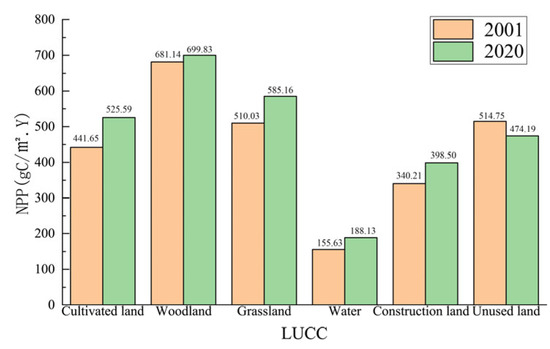
Figure 9.
The average changes in NPP for different land use types in 2001 and 2020.
3.3. Regional Influence and Interaction of Driving Factors Derived from XGBoost-SHAP
3.3.1. Importance of Driving Factors
To further quantify the contribution of each driving factor to NPP, SHAP analysis was performed on the NPP and driving factor datasets to assess the importance of each factor. As shown in Figure 10a, the factors are ranked by their contribution as follows: DEM > PRE > FVC > TEM > NDVI > HF > CO2 > SOM. Among them, the contribution of DEM is 51.2, and that of PRE is 42.42, while the contribution of SOM is only 9.9.
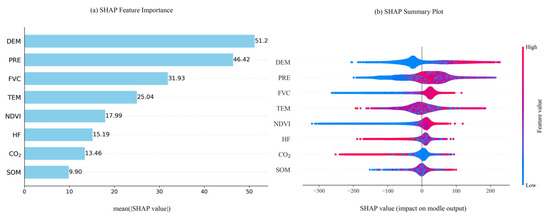
Figure 10.
(a) Bar plot showing the mean absolute SHAP values of each driving factor of NPP and (b) SHAP value impact plot of the XGBoost model.
As shown in Figure 10b, DEM at high elevations is mainly distributed within regions of positive SHAP values, indicating that NPP tends to increase with elevation within the study area. In contrast, low-elevation areas primarily contribute negative SHAP values, suppressing the predicted increase in NPP.
PRE exhibits a generally positive correlation with NPP. Areas with high precipitation are densely clustered on the positive SHAP value side, moderately promoting NPP, while regions with low precipitation are mainly located on the negative SHAP side, limiting NPP. Notably, some high-precipitation points also appear in the negative SHAP region, suggesting a nonlinear effect of precipitation on NPP.
FVC and NDVI both show positive driving effects on NPP. High values of FVC and NDVI are generally linked to positive SHAP values, enhancing NPP, whereas low values correspond to negative SHAP values, inhibiting NPP. In particular, low NDVI values are associated with strongly negative SHAP values, underscoring the significant adverse impact of poor vegetation conditions on NPP predictions.
TEM and SOM present more complex and less consistent patterns, without a clear positive or negative correlation. This indicates that their effects on NPP may vary depending on regional contexts or interactions with other variables.
HF exhibits a nonlinear relationship with NPP. Higher HF values tend to generate mildly negative SHAP values, suggesting a suppressive effect of intensified human activity on ecosystem productivity. Conversely, lower HF values are associated with slightly positive SHAP values. Notably, a considerable number of low-to-moderate HF values show a mild positive impact on NPP, which may reflect the potential benefits of moderate human interventions, such as sustainable land use or ecological restoration efforts.
Finally, atmospheric CO2 concentration exhibits a certain negative correlation with NPP. Excessively high CO2 concentrations negatively affect NPP, while appropriate CO2 levels positively promote NPP through the fertilization effect.
3.3.2. Interaction Effects Among Driving Factors
This study focuses on analyzing the interaction effects among six driving factors—DEM, PRE, FVC, TEM, NDVI, and HF—based on their importance. As shown in Figure 11a, a significant interaction trend exists between DEM and other factors. In areas with higher DEM, the negative impact on NPP diminishes as PER, VCF, and NDVI increase, gradually transitioning into a positive effect. In low-elevation areas, human activity is more frequent and disrupts the ecosystem more significantly, leading to a negative effect of the interaction between HF and DEM on NPP. As elevation increases and human activity decreases, HF also decreases, and the negative effect of the interaction between HF and DEM on NPP gradually weakens and turns positive. The effect of the interaction between DEM and TEM on NPP is more complex. In low-elevation areas, where the climate is hotter and plants are more sensitive to high temperatures, the interaction between TEM and DEM is negative. As elevation and temperature rise, the negative effect on NPP weakens and eventually transitions to a positive impact, reaching a peak. As elevation continues to increase and temperature drops, the impact on NPP weakens again.
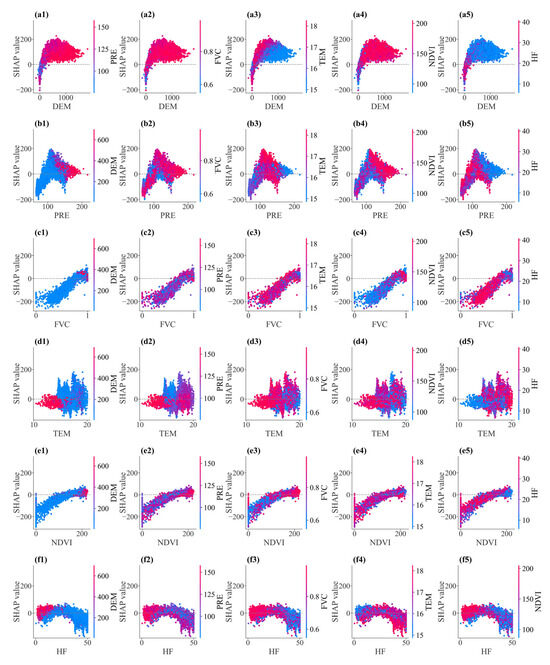
Figure 11.
The interaction effects of the main driving factors, each graph (a1–f5) represents the interaction effect of the horizontal axis (x-axis) and vertical axis (y-axis) factors on the SHAP values of NPP.
As shown in Figure 11b, there is a clear peak in the interaction between PRE and other factors, indicating that an appropriate amount of rainfall, when combined with other factors, is more conducive to plant growth and results in higher NPP in the region. Figure 11(c1) demonstrates that the interaction between low FVC and low DEM has a strong negative effect on NPP. Analyzing the low-elevation areas of the study region, which are mostly composed of construction and cropland, the per-unit NPP is relatively low. Meanwhile, Figure 11(c3) shows that the interaction between FVC and TEM significantly increases the SHAP value, indicating that the coupling of water and heat conditions plays a decisive role in the vegetation growth environment, thereby influencing the trend of NPP changes. Figure 11d reveals that the interaction between TEM and other factors has a more complex effect on NPP, with no obvious trend of change. This complexity can be attributed to urban development in the study area, which has altered land use patterns and introduced the urban heat island effect, leading to changes in geothermal conditions. As some ecological land uses have been converted to construction land, this suggests that the NPP changes are influenced by the combined effects of TEM and other factors.
Figure 11e shows that the interaction between NDVI and other variables remains relatively stable over time. Specifically, under the combination of NDVI and HF (e5), the SHAP value fluctuates significantly, with high-intensity human activities generally leading to lower NDVI and a negative impact on NPP. This indicates that NDVI, as a sensitive indicator of ecosystem health, is highly responsive to NPP changes under the combined influence of resource endowment and human disturbance.
The interaction between HF and various natural factors (Figure 11(f1–f5)) exhibits distinct characteristics of disturbance regulation, particularly in combinations such as HF and DEM (f1) and HF and NDVI (f5), where SHAP values show a nonlinear distribution trend. This suggests that in areas with intensified human activity, the effects of natural factors may be either amplified or suppressed, thereby influencing the spatial distribution of NPP.
3.4. Spatial Heterogeneity of Driving Factors at the Raster Scale Using MGWR
To explore the spatial relationships between NPP and the primary influencing factors, as well as the spatial heterogeneity of the driving factors, this study conducted an MGWR analysis of NPP and key driving factors in the YRDUA. The regression coefficients for FVC, TEM, NDVI, HF, and DEM were all found to be statistically significant at p < 0.05. As shown in Figure 10, the average regression coefficient (β) values for FVC, TEM, PRE, NDVI, HF, and DEM are 0.250, −0.332, 0.026, 0.228, −0.049, and 0.110, respectively. These results indicate that FVC, PRE, NDVI, and DEM exert a strong positive effect on NPP, while TEM and HF have a negative impact. These findings align closely with the results obtained from the SHAP model.
From a spatial distribution perspective (Figure 12 and Figure 13), approximately 90% of the study area shows a positive contribution of FVC and NDVI to NPP, with only a few localized regions exhibiting negative contributions. The contributions to NPP are most prominent in urbanized construction zones and mountainous areas, while regions with concentrated cropland exhibit slightly lower contributions. TEM contributes negatively to NPP in 69.56% of the area, with the most significant negative impacts observed in the low-elevation zones along the Yangtze River. However, in the higher-altitude regions of northern Jiangsu Province, TEM demonstrates a more substantial positive contribution to NPP. The contribution of PRE to NPP is characterized by a clear spatial division: the eastern coastal areas contribute negatively to NPP, covering approximately 50.71% of the study area, while inland areas show a positive contribution. Furthermore, the contribution of PRE to NPP increases the further inland one moves, likely due to the high-intensity rainfall associated with typhoons. HF has a detrimental effect on NPP in 68.52% of the study area, particularly in urban construction zones and southern mountainous regions, with the impact being more pronounced in the latter. This suggests that NPP in these regions is more sensitive to human activities. Additionally, areas where HF has a positive contribution to NPP largely overlap with regions of cropland distribution, indicating that human agricultural activities positively influence NPP in these areas.
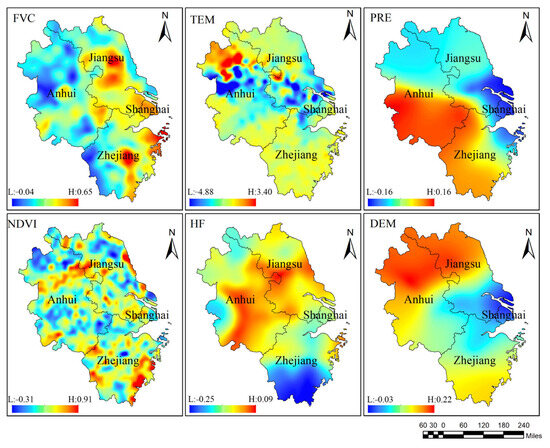
Figure 12.
Spatial distribution of the β value of the driving factors of the MGWR model.
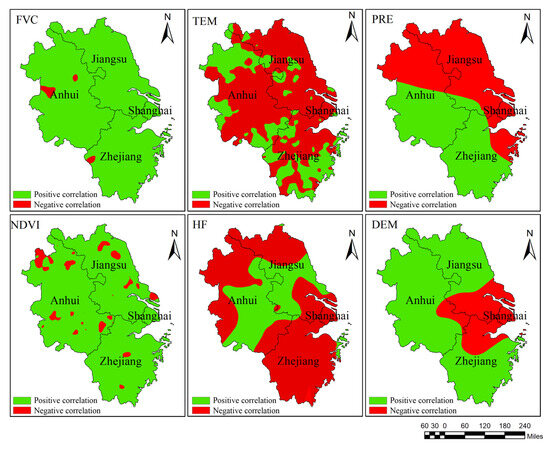
Figure 13.
The positive and negative spatial distribution of the β value of the driving factors of the MGWR model.
4. Discussion
4.1. Regional Mechanisms Underlying Trend Significance
The results of the Theil–Sen trend analysis and Mann–Kendall significance test reveal pronounced spatial heterogeneity in NPP changes within the YRDUA. This pattern reflects the complex interplay among natural ecological foundations, the intensity of human disturbance, and the capacity for ecological governance. Areas with a significant increase in NPP are primarily located along the Jiangsu coastline, the hilly regions of Anhui, and central Zhejiang. These regions share several key characteristics: on one hand, they possess relatively sound ecological conditions, dominated by forests and croplands with high vegetation cover and strong resilience. On the other hand, a number of large-scale ecological restoration initiatives have been implemented in recent years at both national and local levels—such as the “Grain for Green” reforestation program in the Anhui hills, Zhejiang’s “Thousand Villages Demonstration, Ten Thousand Villages Renovation” initiative, and coastal wetland restoration projects in Jiangsu. These efforts have directly enhanced vegetation quality and productivity. Additionally, advancements in agricultural technology (e.g., efficient water-saving irrigation, ecological farming) have significantly boosted NPP in cultivated lands.
In contrast, areas with significantly decreasing NPP are mostly located on the urban–rural fringe of rapidly expanding metropolitan areas, particularly around the Shanghai metropolitan region and the urban clusters in southern Jiangsu and northern Zhejiang. Intense urbanization has led to the continuous expansion of construction land, resulting in large-scale encroachment upon croplands and forests. This has caused drastic changes in land cover types and increased vegetation fragmentation, disrupting the original ecological continuity and productivity base. Furthermore, the combined effects of urban heat islands, localized air pollution, soil compaction, and altered hydrological processes have further constrained vegetation growth and the potential for NPP enhancement. Although urban green infrastructure has improved to some extent, its compensatory effect remains insufficient to reverse the overall downward trend in NPP. In addition, high-intensity construction activities may lead to long-term soil degradation and ecosystem deterioration, fundamentally weakening the region’s carbon sequestration capacity.
It is also noteworthy that over 50% of the region exhibited a non-significant increasing trend in NPP. These areas are mainly located in peri-urban zones and emerging secondary city belts, where the ecological foundation is moderate and human disturbance is relatively mild. Such areas hold significant potential for ecological improvement. Positioned near an “ecological tipping point,” these transitional zones could evolve in a positive direction if supported by targeted policies and dynamic monitoring. Conversely, without timely intervention, they may also be at risk of degradation due to latent ecological vulnerabilities. Therefore, proactive management and policy prioritization are essential to prevent ecological decline and promote sustainable development in these areas.
4.2. Analysis of the Similarities and Differences in the Mechanisms of Driving Factors from a Multiscale Perspective
From both the regional scale (based on the XGBoost-SHAP model) and the grid-level local scale (based on the MGWR model), the mechanisms by which driving factors influence NPP exhibit differences in intensity, direction, and spatial distribution. The regional scale emphasizes the average effect of factors, revealing the positive effects of natural factors such as DEM, PRE, and FVC on NPP, as well as the generally negative influence of HF on NPP. However, at the grid scale, the influence of each factor shows considerable spatial heterogeneity. For example, TEM does not show a significant impact in the overall model, but in the MGWR analysis, high temperatures suppress NPP in low-elevation areas, while promoting vegetation growth in mid- to high-elevation regions. Moreover, although HF is generally a negative driver factor, it collaborates with NDVI in some agricultural areas to produce a positive effect on NPP, reflecting the positive ecological impact of human activities and further revealing the complex interactions between topography, climate, and human activities.
The differences in scale also manifest in the precision of factor explanation. The regional-scale model is suitable for identifying the relative importance of key influencing factors but is limited in revealing the “heterogeneous effects” and “edge responses” at the local spatial level. On the other hand, the MGWR model, which introduces a bandwidth adjustment mechanism at the grid scale, allows for dynamic adjustment of the model according to the spatial scale of each factor’s influence, providing a more accurate depiction of the actual strength of different factors in different regions. For example, in coastal areas, PRE has a negative impact on NPP, while inland areas show a positive impact, suggesting that excessive rainfall (e.g., typhoon rainfall) may suppress NPP. However, this regional difference is not captured in the overall model. Thus, the analysis at different scales is complementary in identifying driving mechanisms. The regional scale helps grasp dominant trends, while the grid scale uncovers local specificity and spatial imbalance. The combination of both enhances the model’s explanatory power for complex ecological mechanisms and provides scientific support for “site-specific” regional ecological management strategies.
4.3. Nonlinear Response Mechanisms of NPP Change Under Multi-Factor Coupling
Changes in NPP are the result of a complex interplay between natural factors—including DEM, TEM, SOM, FVC, NDVI, and PRE—and anthropogenic factors such as CO2 and HF. These variables do not act independently; rather, they exhibit significant nonlinear interactions that jointly reshape the spatial and temporal patterns of NPP. This intricate coupling highlights the limitations of traditional linear cause–effect analytical frameworks, which are often inadequate for capturing the multifaceted mechanisms operating within complex ecological systems. Similar findings were reported by Li et al. in their study of the Amazon ecoregion [61]. For example, the interaction between DEM and climate variables demonstrates a clear “threshold response” pattern. In low-elevation regions, the combined stress of rising temperatures and intensified human activities significantly suppresses ecosystem productivity, resulting in marked declines in NPP. Conversely, in high-elevation zones where temperature and precipitation levels are moderate, conditions are more favorable for vegetation growth, leading to substantial increases in NPP. These nonlinear interaction effects suggest that the influence of each individual factor on NPP is not fixed but varies depending on the presence and intensity of other factors.
Such coupling effects are especially pronounced in areas where natural and human factors intersect—such as highly urbanized zones or regions with intensive agricultural activity. These findings underscore the necessity of evaluating NPP changes through a multi-factorial lens, rather than assessing each driver in isolation. Future research and modeling efforts should therefore prioritize the development of frameworks that can accommodate asymmetric and nonlinear response mechanisms. It is essential to incorporate the joint effects of topography, climate, and anthropogenic disturbance, as well as their complex interactions across multiple spatial scales. From a practical standpoint, these insights carry important implications for ecosystem management and conservation. Relying on single-factor projections of NPP is insufficient. Instead, it is crucial to consider the synergistic effects of multiple drivers and their spatial heterogeneity. For instance, in low-lying urban areas, strategies should focus on mitigating the ecological pressures caused by temperature rise and intense human activity, such as implementing urban cooling initiatives and ecological restoration projects to reduce negative impacts on NPP. In contrast, in high-altitude regions, leveraging favorable climatic conditions through scientifically informed vegetation restoration and sustainable land use practices may further enhance NPP, ultimately contributing to the sustainable development of regional ecosystems.
4.4. The Regulatory Role of Human Activities on NPP
Unlike natural factors, human activity intensity (HF) generally exhibits a negative influence on NPP, aligning with the widely accepted view of “urban expansion leads to ecosystem degradation.” As urbanization accelerates, large areas of cropland, forest, and grassland are converted into built-up land, resulting in reduced vegetation cover and disruption of ecosystem structure and function, ultimately leading to a decline in NPP. However, the findings are not entirely pessimistic. In some regions with low to moderate HF values, the interaction between HF and NDVI shows a slight positive trend. This suggests that under scenarios of moderate human intervention—such as urban green space construction or managed agricultural practices—rational and well-regulated human activities may enhance ecosystem service functions rather than degrade them.
These findings offer important implications for ecological planning in urban agglomerations. First, it is essential to recognize the “dose–response” mechanism of human activities—namely, that not all anthropogenic influences are inherently detrimental to ecosystems. The key lies in the intensity of intervention and whether spatial development aligns with local ecological baselines. In this regard, a zoned ecological regulation strategy is recommended. Ecologically sensitive and functionally critical areas should be subject to stricter construction controls, while urbanized zones should integrate well-planned green infrastructure. Expanding urban green spaces, establishing ecological corridors and pocket parks, and implementing context-sensitive vegetation design based on local climate and species composition can significantly enhance vegetation coverage and NPP, helping to offset the ecological impacts of urban development.
Second, in agricultural regions, promoting an ecological transition in farming is vital. This includes adopting precision agriculture, conservation tillage, and eco-friendly farming practices. Policies should also support non-point-source pollution control and soil conservation to improve the quality and resilience of agro-ecosystems. Introducing regional agri-ecological compensation schemes can incentivize farmers to adopt sustainable practices, achieving synergy between agricultural productivity and ecosystem conservation.
Finally, for high-altitude, plateau, and ecologically fragile regions, differentiated management strategies based on ecological zoning should be implemented. High-intensity human activities must be strictly limited in these areas, with priority given to ecological restoration and nature conservation. Policy measures such as delineating ecological redlines, enhancing ecological compensation mechanisms, and establishing robust monitoring systems can improve the precision and effectiveness of ecological governance.
4.5. Limitations and Future Directions
Although this study employs multiple methods and data sources to systematically analyze the spatiotemporal dynamics and driving mechanisms of NPP in the YRDUA, some limitations remain. Firstly, although the dataset incorporates multiple dimensions—including topography, climate, vegetation, land use, and socioeconomic activities—there may still be omissions of potentially influential factors, such as changes in soil fertility, nitrogen deposition, extreme climatic events, and the long-term impacts of land use policies. Secondly, while the model captures complex nonlinear relationships and threshold effects to some extent, further refinement is needed. Despite the strengths of SHAP and MGWR in revealing spatial heterogeneity and variable interactions, synergistic or antagonistic effects among key driving factor combinations under different contexts remain insufficiently explored. Finally, data quality issues—such as cloud contamination in remote sensing imagery and classification accuracy in LUCC datasets—can also affect model performance. In addition, parameter choices, including those in XGBoost (e.g., learning rate, tree depth) and bandwidth selection in MGWR, may further influence the robustness and reliability of the results.
Future research should aim to further refine the driving factor system by integrating more high-precision, long-term data resources, such as high-resolution soil data and multi-source satellite fusion data, to provide a more comprehensive understanding of the driving mechanisms of NPP. Additionally, it is important to combine ecological process models to validate the ecological plausibility of the interaction mechanisms.
5. Conclusions
By integrating multi-source remote sensing and socioeconomic data, this study systematically examined the spatiotemporal dynamics and multiscale driving mechanisms of NPP in the YRDUA from 2001 to 2020. This analysis employed a combination of interpretable machine learning (XGBoost-SHAP), the MGWR model, and Theil–Sen trend analysis with the Mann–Kendall test. The main findings are as follows:
Spatiotemporal Dynamics of NPP: From 2001 to 2020, the total NPP of the YRDUA exhibited a fluctuating upward trend, with an annual mean of 174.37 ± 8.12 TgC. The Theil–Sen slope estimates and Mann–Kendall test results indicate that approximately 24.83% of the region experienced a significant increase in NPP, while only 2.75% showed a significant decrease, reflecting an overall improvement in regional ecosystem conditions. However, areas undergoing rapid urban expansion still face ecological degradation risks and warrant close attention. Land use changes resulted in a net NPP loss of 2.67 TgC. However, improvements in ecological conditions and advances in agricultural technologies have helped offset these negative impacts and contributed to the overall NPP increase.
Scale-Dependent Differences in Driving Factors: The influence mechanisms of driving factors on NPP differed in intensity, direction, and spatial distribution at regional and local grid scales. Regionally, natural factors such as DEM, PRE, and FVC positively influenced NPP, whereas HF had a generally negative effect. Locally, however, driving factors showed substantial spatial heterogeneity. For instance, although HF typically negatively affected NPP, it interacted positively with NDVI in some agricultural regions, enhancing NPP there.
Nonlinear Response Mechanisms Under Multi-Factor Coupling: Significant nonlinear interactions between factors were observed, and these complex coupling effects profoundly reshaped the spatiotemporal pattern of NPP. The interaction effects were especially pronounced in areas where natural and human factors intersected, such as urbanized regions or areas with intensive agricultural activities.
Author Contributions
Y.Z.: Conceptualization, Data Curation, Formal Analysis, Writing—Original Draft, Writing—Review and Editing; W.Z.: Project Administration, Software, Supervision, Validation; J.Y.: Software, Supervision, Methodology. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (No. 42101275) and the Provincial Natural Science Foundation of Hubei, China (No. 2023AFB651).
Data Availability Statement
The data presented in this study are available upon request from the corresponding author. The data are not publicly available due to privacy restrictions.
Acknowledgments
The authors are grateful to the editor and reviewers for their valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NPP | net primary productivity |
| YRDUA | Yangtze River Delta Urban Agglomeration |
| MGWR | multiscale geographically weighted regression model |
| DEM | digital elevation model |
| PRE | precipitation |
| FVC | fractional vegetation cover |
| HF | human footprint |
| IPCC | Intergovernmental Panel on Climate Change |
| GWR | geographically weighted regression |
| LUCC | land use cover change |
| NDVI | normalized difference vegetation index |
| SOM | soil organic matter |
| TEM | temperature |
| XGBoost | Extreme Gradient Boosting |
| SHAP | Shapley Additive exPlanations |
| RCS | restricted cubic spline |
References
- Roxburgh, S.H.; Berry, S.L.; Buckley, T.N.; Barnes, B.; Roderick, M.L. What Is NPP? Inconsistent Accounting of Respiratory Fluxes in the Definition of Net Primary Production. Funct. Ecol. 2005, 19, 378–382. [Google Scholar] [CrossRef]
- Tian, G.; Qiao, Z. Assessing the impact of the urbanization process on net primary productivity in China in 1989–2000. Environ. Pollut. (1987) 2014, 184, 320–326. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Shen, H.; Wu, W.; Liu, Y.; Wang, Y. Net primary productivity (NPP) dynamics and associated urbanization driving forces in metropolitan areas: A case study in Beijing City, China. Landsc. Ecol. 2015, 31, 1077–1092. [Google Scholar] [CrossRef]
- Azhdari, Z.; Sardooi, E.R.; Bazrafshan, O.; Zamani, H.; Singh, V.P.; Saravi, M.M. Impact of climate change on net primary production (NPP) in south Iran. Environ. Monit. Assess 2020, 192, 409. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Running, S.W.; Zhao, M.; Costa, M.H.; Kirschbaum, A.A.; Ham, J.M.; Saleska, S.R.; et al. Evaluation of MODIS NPP and GPP products across multiple biomes. Remote Sens. Environ. 2006, 102, 282–292. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2021: The Physical Science Basis: Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Eigenbrod, F.; Bell, V.A.; Davies, H.N.; Heinemeyer, A.; Armsworth, P.R.; Gaston, K.J. The impact of projected increases in urbanization on ecosystem services. Proc. R. Soc. B Biol. Sci. 2011, 278, 3201–3208. [Google Scholar] [CrossRef]
- Delphin, S.; Escobedo, F.J.; Abd-Elrahman, A.; Cropper, W.P. Urbanization as a land use change driver of forest ecosystem services. Land Use Policy 2016, 54, 188–199. [Google Scholar] [CrossRef]
- Qin, Z.; Sha, Z. Modeling the impact of urbanization and climate changes on terrestrial vegetation productivity in China by a neighborhood substitution analysis. Ecol. Model. 2023, 482, 110405. [Google Scholar] [CrossRef]
- Hua, L.; Shao, G.; Zhao, J. A concise review of ecological risk assessment for urban ecosystem application associated with rapid urbanization processes. Int. J. Sustain. Dev. World Ecol. 2017, 24, 248–261. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, M.; Chen, H.; Adams, J. Global pattern of NPP to GPP ratio derived from MODIS data: Effects of ecosystem type, geographical location and climate. Glob. Ecol. Biogeogr. 2009, 18, 280–290. [Google Scholar] [CrossRef]
- Zhang, C.; Tian, H.; Chen, G.; Chappelka, A.; Xu, X.; Ren, W.; Hui, D.; Liu, M.; Lu, C.; Pan, S.; et al. Impacts of urbanization on carbon balance in terrestrial ecosystems of the Southern United States. Environ. Pollut. (1987) 2012, 164, 89–101. [Google Scholar] [CrossRef] [PubMed]
- Cao, D.; Zhang, J.; Han, J.; Zhang, T.; Yang, S.; Wang, J.; Prodhan, F.A.; Yao, F. Projected Increases in Global Terrestrial Net Primary Productivity Loss Caused by Drought Under Climate Change. Earths Future 2022, 10, e2022EF002681. [Google Scholar] [CrossRef]
- Pan, N.; Zhang, J.; Han, J.; Zhang, T.; Yang, S.; Wang, J.; Prodhan, F.A.; Yao, F. Inconsistent changes in NPP and LAI determined from the parabolic LAI versus NPP relationship. Ecol. Indic. 2021, 131, 108134. [Google Scholar] [CrossRef]
- Gang, C.; Odeh, I.; Groisman, P.Y. Comparative Assessment of Grassland NPP Dynamics in Response to Climate Change in China, North America, Europe and Australia from 1981 to 2010. J. Agron. Crop Sci. 2014, 201, 5–68. [Google Scholar] [CrossRef]
- Matamala, R.; Gonza, M.A.; Jastrow, J.D.; Norby, R.J.; Schlesinger, W.H. Impacts of Fine Root Turnover on Forest NPP and Soil C Sequestration Potential. Science 2003, 302, 1385–1387. [Google Scholar] [CrossRef]
- Zarei, A.; Chemura, A.; Gleixner, S.; Hoff, H. Evaluating the grassland NPP dynamics in response to climate change in Tanzania. Ecol. Indic. 2021, 125, 107600. [Google Scholar] [CrossRef]
- Costanza, R.; Fisher, B.; Mulder, K.; Liu, S.; Christopher, T. Biodiversity and ecosystem services: A multi-scale empirical study of the relationship between species richness and net primary production. Ecol. Econ. 2007, 61, 478–491. [Google Scholar] [CrossRef]
- Kicklighter, D.W.; Kicklighter, D.W.; Bondeau, A.; Schloss, A.L.; Kaduk, J.; Mcguire, A.D. The Participants of the Potsdam NPP Model Intercomparison. Comparing global models of terrestrial net primary productivity (NPP): Global pattern and differentiation by major biomes. Glob. Change Biol. 1999, 5, 16–24. [Google Scholar] [CrossRef]
- Chirici, G.; Chiesi, M.; Corona, P.; Puletti, N.; Mura, M.; Maselli, F. Prediction of forest NPP in Italy by the combination of ground and remote sensing data. Eur. J. For. Res. 2015, 134, 453–467. [Google Scholar] [CrossRef]
- Pachavo, G.; Murwira, A. Remote sensing net primary productivity (NPP) estimation with the aid of GIS modelled shortwave radiation (SWR) in a Southern African Savanna. Int. J. Appl. Earth Obs. Geoinf. 2014, 30, 217–226. [Google Scholar] [CrossRef]
- Yuan, X.; Guo, B.; Lu, M. The responses of vegetation NPP dynamics to the influences of climate–human factors on Qinghai–Tibet Plateau from 2000 to 2020. Remote Sens. 2023, 15, 2419. [Google Scholar] [CrossRef]
- Lv, Z.; Qiulin, D. Spatiotemporal variations and driving forces of regional-scale NPP based on a multi-method integration: A case study in the Beibu Gulf Economic Zone. Ecol. Indic. 2025, 174, 113453. [Google Scholar]
- Zhang, J.; Zhang, C.; Ma, W.; Wang, W.; Li, H. Improving the Model Performance of the Ecosystem Carbon Cycle by Integrating Soil Erosion–Related Processes. Atmosphere 2023, 14, 1724. [Google Scholar] [CrossRef]
- Gong, J.; Xie, Y.; Cao, E.; Huang, Q.; Li, H. Integration of InVEST-habitat quality model with landscape pattern indexes to assess mountain plant biodiversity change: A case study of Bailongjiang watershed in Gansu Province. J. Geogr. Sci. 2019, 29, 1193–1210. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, Y.; Sun, X.; Xu, Y. Estimation of NPP in Huangshan District Based on Deep Learning and CASA Model. Forests 2024, 15, 1467. [Google Scholar] [CrossRef]
- Chu, C.; Bartlett, M.; Wang, Y.; He, F.; Weiner, J.; Chave, J.; Sack, L. Does climate directly influence NPP globally? Glob. Change Biol. 2016, 22, 12–24. [Google Scholar] [CrossRef]
- Chen, S.; Ma, M.; Wu, S.; Tang, Q.; Wen, Z. Topography intensifies variations in the effect of human activities on forest NPP across altitude and slope gradients. Environ. Dev. 2023, 45, 100826. [Google Scholar] [CrossRef]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial ecosystem production: A process model based on global satellite and surface data. Glob. Biogeochem. Cycles 1993, 7, 811–841. [Google Scholar] [CrossRef]
- Yu, B.; Chen, F.; Chen, H. NPP estimation using random forest and impact feature variable importance analysis. J. Spat. Sci. 2019, 64, 173–192. [Google Scholar] [CrossRef]
- Zhou, T.; Hou, Y.; Yang, Z.; Laffitte, B.; Luo, K.; Luo, X.; Liao, D.; Tang, X. Reducing spatial resolution increased net primary productivity prediction of terrestrial ecosystems: A Random Forest approach. Sci. Total Environ. 2023, 897, 165134. [Google Scholar] [CrossRef]
- Yang, F.; Ichii, K.; White, M.A.; Hashimoto, H.; Michaelis, A.R.; Votava, P.; Zhu, A.-X.; Huete, A.; Running, S.W.; Nemani, R.R. Developing a continental-scale measure of gross primary production by combining MODIS and AmeriFlux data through Support Vector Machine approach. Remote Sens. Environ. 2007, 110, 109–122. [Google Scholar] [CrossRef]
- Li, L.; Xia, R.; Dou, M.; Zhang, K.; Chen, Y.; Jia, R.; Li, X.; Dou, J.; Li, X.; Hu, Q.; et al. Integrated machine learning reveals aquatic biological integrity patterns in semi-arid watersheds. J. Environ. Manag. 2024, 359, 121054. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Wu, T.; Lin, W.; Guo, Y. Spatiotemporal prediction of grassland net primary productivity using deep learning models integrating temporal decomposition and spatial clustering: A case study in source region of the Yellow River, China. Earth Sci. Inform. 2025, 18, 33. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, D.; Nan, Y.; Liu, Z.; Qi, D. Spatial patterns of net primary productivity and its driving forces: A multi-scale analysis in the transnational area of the Tumen River. Front. Earth Sci. 2020, 14, 124–139. [Google Scholar] [CrossRef]
- Wang, X.; He, W.; Huang, Y.; Wu, X.; Zhang, X.; Zhang, B. Exploring Spatial Non-Stationarity and Scale Effects of Natural and Anthropogenic Factors on Net Primary Productivity of Vegetation in the Yellow River Basin. Remote Sens. 2024, 16, 3156. [Google Scholar] [CrossRef]
- Wang, Z.; Dong, C.; Dai, L.; Wang, R.; Liang, Q.; He, L.; Wei, D. Spatiotemporal evolution and attribution analysis of grassland NPP in the Yellow River source region, China. Ecol. Inform. 2023, 76, 102135. [Google Scholar] [CrossRef]
- Wei, Z.; Chen, D.; Huang, Q.; Chen, Q.; Wei, C. Temporal–Spatial Evolution and Driving Mechanism for an Ecosystem Health Service Based on the GD-MGWR-XGBOOT-SEM Model: A Case Study in Guangxi Region. Sustainability 2025, 17, 3305. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Yang, W.; Kang, W. Multiscale Geographically Weighted Regression (MGWR. Ann. Am. Assoc. Geogr. 2017, 107, 1247–1265. [Google Scholar] [CrossRef]
- Xiaobin, G.; Shen, H.; Gan, W. A 33-Year NPP Monitoring Study in Southwest China by the Fusion of Multi-Source Remote Sensing and Station Data. Remote Sens. 2017, 9, 1082. [Google Scholar]
- Melser, R.; Coops, N.C.; Wulder, M.A.; Derksen, C. Multi-Source Remote Sensing Based Modeling of Vegetation Productivity in the Boreal: Issues & Opportunities. Can. J. Remote Sens. 2023, 49, 2256895. [Google Scholar]
- He, Y.; Lin, C.; Wu, C.; Pu, N.; Zhang, X. The urban hierarchy and agglomeration effects influence the response of NPP to climate change and human activities. Glob. Ecol. Conserv. 2024, 51, e02904. [Google Scholar] [CrossRef]
- Li, J.; Bi, M.; Wei, G. Investigating the Impacts of Urbanization on Vegetation Net Primary Productivity: A Case Study of Chengdu–Chongqing Urban Agglomeration from the Perspective of Townships. Land 2022, 11, 2077. [Google Scholar] [CrossRef]
- Cui, T.; Wang, Y.; Sun, R.; Qiao, C.; Fan, W.; Jiang, G.; Hao, L.; Zhang, L.; Yuan, W. Estimating Vegetation Primary Production in the Heihe River Basin of China with Multi-Source and Multi-Scale Data. PLoS ONE 2016, 11, e0153971. [Google Scholar] [CrossRef] [PubMed]
- Yin, H.; Xiao, R.; Fei, X.; Zhang, Z.; Gao, Z.; Wan, Y.; Tan, W.; Jiang, X.; Cao, W.; Guo, Y. Analyzing “economy-society-environment” sustainability from the perspective of urban spatial structure: A case study of the Yangtze River delta urban agglomeration. Sustain. Cities Soc. 2023, 96, 104691. [Google Scholar] [CrossRef]
- Leu, M.; Hanser, S.E.; Knick, S.T. Human Footprint in The West: A Large-Scale Analysis of Anthropogenic Impacts. Ecol. Appl. 2008, 18, 1119–1139. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, W.; Yao, Y.; Pereira, P. The rising human footprint in the Tibetan Plateau threatens the effectiveness of ecological restoration on vegetation growth. J. Environ. Manag. 2024, 351, 119963. [Google Scholar] [CrossRef]
- National Development and Reform Commission. Development Plan for the Urban Agglomeration of the Yangtze River Delta; National Development and Reform Commission: Beijin, China, 2016.
- Alharbi, S.; Raun, W.R.; Arnall, D.B.; Zhang, H. Prediction of maize (Zea mays L.) population using normalized-difference vegetative index (NDVI) and coefficient of variation (CV). J. Plant Nutr. 2019, 42, 673–679. [Google Scholar] [CrossRef]
- Gallardo, A. Spatial Variability of Soil Properties in a Floodplain Forest in Northwest Spain. Ecosystems 2003, 6, 564–576. [Google Scholar] [CrossRef]
- Diop, L.; Bodian, A.; Diallo, D. Spatiotemporal Trend Analysis of the Mean Annual Rainfall in Senegal. Eur. Sci. J. 2016, 12, 231. [Google Scholar] [CrossRef]
- Muia, V.K.; Opere, A.O.; Ndunda, E.; Amwata, D.A. Rainfall and Temperature Trend Analysis using Mann-Kendall and Sen′s Slope Estimator Test in Makueni County, Kenya. J. Mater. Environ. Sci. 2024, 15, 349–367. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting (With discussion and a rejoinder by the authors). Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Friedman, J. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Ma, M.; Zhao, G.; He, B.; Li, Q.; Dong, H.; Wang, S.; Wang, Z. XGBoost-based method for flash flood risk assessment. J. Hydrol. 2021, 598, 126382. [Google Scholar] [CrossRef]
- Omer, S.; Lior, R. Approximating XGBoost with an interpretable decision tree. Inf. Sci. 2021, 572, 522–542. [Google Scholar]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From Local Explanations to Global Understanding with Explainable AI for Trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Li, D.; Cao, W.; Dou, Y.; Wu, S.; Liu, J.; Li, S. Non-linear effects of natural and anthropogenic drivers on ecosystem services: Integrating thresholds into conservation planning. J. Environ. Manag. 2022, 321, 116047. [Google Scholar] [CrossRef]
- Shabrina, Z.; Buyuklieva, B.; Ng, M.K.M. Short-Term Rental Platform in the Urban Tourism Context: A Geographically Weighted Regression (GWR) and a Multiscale GWR (MGWR) Approaches. Geogr. Anal. 2021, 53, 686–707. [Google Scholar] [CrossRef]
- Furkova, A. Implementation of MGWR-SAR models for investigating a local particularity of European regional innovation processes. Cent. Eur. J. Oper. Res. 2022, 30, 733–755. [Google Scholar] [CrossRef]
- Li, L.; Zeng, Z.; Zhang, G.; Duan, K.; Liu, B.; Cai, X. Exploring the Individualized Effect of Climatic Drivers on MODIS Net Primary Productivity through an Explainable Machine Learning Framework. Remote Sens. 2022, 14, 4401. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).