Abstract
LiDAR-assisted wind turbine control holds strong potential for reducing structural loads and improving rotor speed regulation, thereby contributing to more sustainable wind energy generation. However, key research gaps remain: (i) the practical limitations of commercially available fixed beam LiDARs for large turbines, and (ii) the performance assessment of commonly used LiDAR assisted feedforward control methods. This study addresses these gaps by (i) analysing how the coherence of LiDAR estimated rotor effective wind speed is influenced by the number of beams, measurement locations, and turbulence box resolution, and (ii) comparing two established control strategies. Numerical simulations show that applying a low cut-off frequency in the low-pass filter can impair preview time compensation. This is particularly critical for large turbines, where reduced coherence due to fewer beams undermines the effectiveness of LiDAR assisted control compared to the smaller turbines. The subsequent evaluation of control strategies shows that the Schlipf method offers greater robustness and consistent load reduction, regardless of the feedback control design. In contrast, the Bossanyi method, which uses the current blade pitch measurements, performs well when paired with carefully tuned baseline controllers. However, using the actual pitch angle in the feedforward pitch rate calculation can lead to increased excitation at certain frequencies, particularly if the feedback controller is not well tuned to avoid dynamics in those ranges.
1. Introduction
As wind turbines increase in size, different control solutions are utilized to limit the structural loads. Nevertheless, one of the challenges when designing control systems for wind turbines is that the controller action happens after the wind inflow hits the turbine, which is known as the feedback mechanism. Feedforward control can overcome the challenge but it requires the knowledge of the incoming wind speed. The wind speed, generally obtained from nacelle-mounted anemometers, is disturbed by the rotor and only represents one point of measurement across the rotor. The application of Light Detection And Ranging (LiDAR) system technology for measuring upstream wind speed has shown promise in wind turbine control as it can remotely measure the velocity of the particles in the air, enabling estimation of the wind speed at a specific upstream distance from the wind turbine. These measurements then can be used to plan a control action to reduce structural fatigue loads and improve rotor speed regulation. Therefore, the advancement in LiDAR systems has motivated the study of LiDAR-assisted control for wind turbines.
One of the pioneering investigations into LiDAR-assisted feedforward control was undertaken by Harris et al. [1]. After this, a growing body of research has employed LiDAR systems to enhance collective pitch control, with the objective of refining rotor speed regulation and mitigating fatigue load, as documented in [2]. Moreover, various studies, such as [3], have concentrated on leveraging LiDAR technology for enhancing individual pitch control, thereby mitigating loads on blades and other turbine structures. Some research (e.g., [4]), has utilized LiDARs to optimize turbine power capture. In addition, the findings presented in [5,6] demonstrated the integration of wind measurements into a model predictive control (MPC) framework, resulting in enhanced load alleviation. In recent years, a few studies, including [7,8], have investigated the benefits of LiDAR-assisted control under varying turbulence conditions. Two further studies [9,10] explored LiDAR-assisted control retrofit applications, where LiDAR measurements were used to modify the rotor speed signal rather than directly influencing the pitch angle. Another study [11] examined LAC for floating wind turbines, while [12] applied a nonlinear output regulation approach to LiDAR-assisted control.
Numerous full-scale tests, including those outlined in [13], have been conducted to showcase and validate the efficacy of LiDAR-assisted control. More recently, an International Energy Agency (IEA) Wind task was established to endorse the adoption of LiDAR technology in wind energy applications, as highlighted in [14,15].
However, there is still a research gap. First, the applicability of current commercially available fixed-beam LiDAR systems in larger wind turbines has some potential limitations. Second, different feedforward control strategies would affect the benefit of using LiDARs in wind turbine control. The performance of two well-known LiDAR-assisted feedforward control approaches, developed by Schlipf [16] and Bossanyi [17] is evaluated, particularly regarding their implementation and uncertainties in the mapping between the wind speed to pitch angle used in the feedforward controller.
Therefore, the objective of this study is twofold: (i) to investigate how the coherence of the LiDAR-estimated rotor effective wind speed is influenced by the LiDAR configuration—specifically the number of beams, their measurement locations, and the resolution of the turbulence box; and (ii) to conduct a detailed analysis of two well-known feedforward LiDAR-assisted control approaches, namely those proposed by Schlipf [16] and Bossanyi [17]. Building on the simulation framework from our previous work [18], we extend that work significantly in both scope and analysis. In particular, this study examines variations in LiDAR configurations and coherence across different wind turbine sizes, the resulting effects on load reduction, and how the feedback control design influences both reference LiDAR-assisted strategies.
Wind energy plays a central role in the global transition towards a more sustainable and low-carbon energy system. This study contributes to that objective by investigating advanced control strategies that enable more efficient and reliable operation of wind turbines. By improving load mitigation and rotor speed regulation through LiDAR-assisted control, the findings support longer turbine lifetimes, reduced maintenance needs, and lower levelised cost of energy (LCOE). These improvements directly enhance the environmental and economic sustainability of wind power, especially as turbines grow larger and are deployed in more complex environments such as offshore and floating sites.
The structure of the paper is as follows. Section 2 presents the LiDAR-assisted control methodologies. Section 3 investigates how the LiDAR coherence is influenced by different LiDAR configuration and turbulence box resolution and followed by the validation of the proposed methods using simulation results in Section 4. Finally, conclusions and future work are presented in Section 5.
2. Overview of LiDAR-Assisted Control Methods
The LiDAR-assisted control design is typically decoupled into two key challenges: (i) determining the mapping from the LiDAR measurement to the rotor effective wind speed (REWS) experienced by the turbine, and (ii) translating the LiDAR-estimated REWS into an effective feedforward pitch action. The standard implementation of LiDAR-assisted control is illustrated in Figure 1.
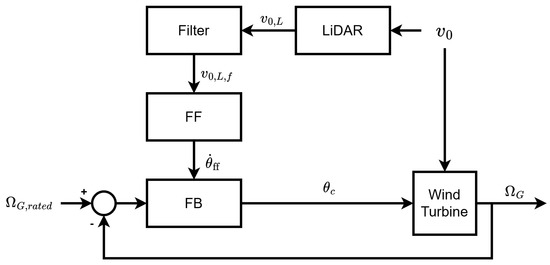
Figure 1.
Feedforward control implementation diagram where is the incoming wind speed, is the wind speed measured by the LiDAR measurements, is the filtered wind speed, is the rated generator speed, is the collective pitch angle and is the current generator speed. FF and FB denote the feedforward and feedback controllers respectively.
2.1. Wind Coherence
To address the first challenge, the identification of the transfer function mapping LiDAR measurements to the rotor effective wind speed is essential. Given the complexity of the evolution and the spatial averaging dynamics of a LiDAR, a common simplification is employed. Due to the low-pass effect inherent in LiDAR, the transfer function is typically modelled as an adaptive first-order Butterworth filter with some delay, and is defined as follows:
where is the time constant of the filter, and its cut-off frequency is computed based on the coherence bandwidth , where the magnitude-squared coherence . A more detailed discussion on coherence follows later in the text. The look-ahead time T is approximated with the following equation [4]:
where the first term is the time delay based on Taylor’s frozen turbulence hypothesis, in which the frozen turbulent structures are transported with the mean wind speed over the measured distance X. The time delay induced by the filter is accounted for by . The time is the modeling errors and is disregarded for simplicity ( = 0).
In this study, the rotor effective wind speed is defined as the rotor averaged wind speed, and the LiDAR-estimated rotor effective wind speed is computed as the average of all streamwise components of the line of sight measurements. LiDAR systems are particularly effective at measuring incoming wind speeds at low frequencies, where the coherence between the LiDAR signal and the rotor-effective wind speed is strongest [16]. However, at higher frequencies, this coherence diminishes due to the evolving nature of turbulence and the spatial separation between the measurement point and the rotor plane. To ensure that control actions are based on reliable data, it is essential to filter out these uncorrelated and unwanted frequency components. Failing to do so can lead to inappropriate control responses, potentially increasing structural loads or causing instability in the wind turbine [19]. Such filtering introduces a time delay in the signal, which must be considered alongside the look-ahead time.
The magnitude-squared coherence () is the key parameter used and it is commonly defined as follows [16]:
where is the cross-power spectral density between the rotor effective wind speed experienced by the wind turbine and the LiDAR measurement signals, while , are the power spectral densities of the rotor effective wind speed and the LiDAR measurement, respectively. The parameter k is the wavenumber.
The magnitude-squared coherence is a frequency-dependent function. A value of one indicates perfect correlation between wind speeds at two locations while a lower value reflects a weaker correlation. The results in the frequency domain can be translated into the wavenumber domain using Taylor’s frozen turbulence hypothesis. This is computed with Equation (4) [20]. The wavenumber (k) describes the size of a turbulence fluctuation. A small wavenumber indicates a spatially large fluctuation, while a larger wavenumber indicates a smaller fluctuation [21].
The coherent wavenumber, denoted as represents the frequency at which the magnitude-squared coherence () drops below 0.5. It is used as a performance indicator to quantify the correlation between the LiDAR measurement and the wind speed experienced by the rotor. Moreover, it serves as a parameter for determining the cut-off frequency of the Butterworth low pass filter, which is implemented to remove uncorrelated and undesired high frequencies in wind signals and improve the quality of the LiDAR preview.
2.2. Feedforward Methods
Next, to establish an effective mapping between the LiDAR-estimated REWS and the feedforward pitch angle, it is important to model the inverse of the rotor dynamics. This inverse model is typically linear but non-causal, making direct implementation impractical. As a result, static feedforward designs are commonly used, as seen in the approaches by Schlipf [16] and Bossanyi [17].
To keep the generator speed as close to rated as possible despite variations in wind speed, these controllers use a disturbance compensation model to compute the feedforward pitch angle. This is typically done using a lookup table that maps wind speeds to corresponding steady-state pitch values. The feedforward pitch angle based on the steady-state pitch curve with preview time T defined as:
where denotes the feedforward addition to the pitch command while is a function of the wind speed, represented by a one-to-one lookup table of the steady state pitch angles and the wind speeds.
Typically, there are two methods for implementing the feedforward signal into the system. The first method adds the feedforward pitch angle directly to the feedback signal. The second method differentiates the feedforward pitch angle and adds it to the integrator of the feedback controller. While both methods are mathematically equivalent, the second approach offers practical advantages from an industrial perspective. It allows the feedforward controller to be switched on and off without modifying the feedback controller and does not require changes to the existing anti-windup techniques [16]. When provided with an accurate wind preview, these methods can effectively compensate for wind disturbances, thereby reducing loads on key components such as the tower, the blades, and the shaft.
There is a distinct difference in how the feedforward pitch rate is computed in the Schlipf and Bossanyi approaches. Although both are similar in principle, they differ in key aspects, which is a central focus of this study. The following sections explore these two approaches in detail.
2.2.1. Schlipf Approach
Schlipf [16] uses a standard method to compute the feedforward pitch rate, which is calculated as the difference between the time-shifted steady-state pitch angle and its previous sample, divided by the sampling time, as shown below.
where corresponds to the sampling time. With this approach, the feedforward pitch angle can take over some low-frequency oscillations and improve the rotor speed regulation.
2.2.2. Bossanyi Approach
A similar approach proposed by Bossanyi et al. [17] is to implement the feedforward pitch rate considering the difference between the time-shifted steady-state feedforward pitch angle and the current measured pitch angle, , from the pitch actuator over the look-ahead time, T, as follows.
With this approach, it is possible to gradually move the current pitch angle to the target steady-state angle as mentioned in [4]. The feedforward pitch rate is also directly added to the feedback controller’s integrator. As suggested by [17], the feedforward approach allows the proportional-integral (PI) feedback controller to be re-optimized or detuned for maintaining good speed control while lowering thrust-related loads and pitch activity [17].
2.2.3. Implmentations
As previously explained, both LiDAR-assisted control approaches assumed that the pitch rate could be added to the feedback integrator. The typical feedback controller follows a Proportional-Integral (PI) structure, for example, the open-source DTU Wind Energy controller [22].
where and are the proportional and integral gains of the feedback controller, is the rotor speed, the rotor speed at rated and is the feedforward pitch rate for either Schlipf or Bossanyi approach.
For the implementation, the integral term of the feedforward approaches, , results in Equations (9) and (10) for the Schlipf and Bossanyi methods, respectively.
where corresponds to the time step.
Equations (9) and (10) underlines the differences between the two approaches. While Schlipf’s approach uses the time step, Bossanyi’s approach uses the overall look-ahead time. Moreover, Schlipf’s angle calculation will rely exclusively upon the steady state pitch angle provided by the lookup table at the current and previous time step while Bossanyi’s angle, will instead depend on the difference between and the current pitch angle of the wind turbine.
3. Result: Coherence Study
Before evaluating the two established LiDAR assisted control methods, it is important to identify the optimal LiDAR configuration that provides the highest coherence wavenumber. The analysis is based on simulations using the widely used aeroelastic software HAWC2 [23], which includes functionality for modelling LiDAR sensors, notably continuous wave (CW) LiDAR.
In this section, a sensitivity analysis is performed using the coherent wavenumber as the evaluation metric. The study investigates the influence of (i) the half cone angle, (ii) the number of LiDAR beams, (iii) wind speed, and (iv) turbulence grid resolution on the simulated LiDAR measurements, with the goal of identifying an optimal configuration.
The wind turbine used in the simulations is the IEA 10 MW reference turbine, which has a rotor diameter of 198 m [24]. A nacelle-mounted LiDAR model employing continuous wave (CW) technology and pointing directly upwind (zero mean yaw misalignment) is used. The LiDAR model parameters are based on a commercially available system developed by Windar Photonics A/S (More information can be found on the company websites: Windar Photonics A/S (http://www.windarphotonics.com/, last access: 2 July 2025)). The focus distance is set to be 100 m.
The proposed test bench scenarios include the following variations:
- Turbulence box grid dimensions of 32, 64, and 128 points in both width and height. The turbulence boxes are generated using the Mann model within the HAWC2 tool chain.
- Number of LiDAR beams set to either 4 or 8.
- Opening angles ranging from 5∘ to 40∘, in increments of 5∘.
- Two wind speeds above rated conditions: 14 m/s and 20 m/s, and 6 stochastic realisations (seeds).
The LiDAR opening angle can be translated into a percentage of the rotor radius covered by the circular measurement pattern, As illustrated in Figure 2, the focus distance, , is fixed and r represents the radius of the circular pattern. This percentage is computed as follows:
where R denotes the rotor radius. Furthermore, when the half-cone (opening) angle is changed while keeping the focus distance constant, the preview distance is also affected accordingly.
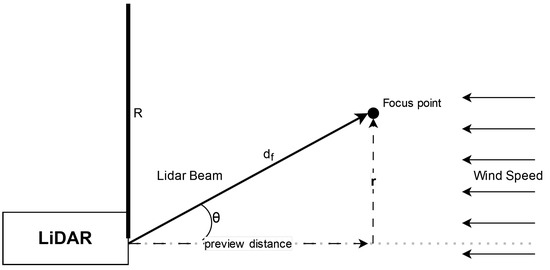
Figure 2.
LiDAR measurement for a 2-D wind vector at a single point.
3.1. Impact on Coherent Wavenumber Under Different LiDAR Configurations and Wind Conditions
The coherent wavenumber, , was calculated for each seed and averaged, as shown in Figure 3 for the configurations with 4 and 8 LiDAR beams, varying the turbulence grid box and half-cone angle. As the resolution of the turbulence box increases, the coherent wavenumber generally decreases. This trend is consistent for both wind speeds of 14 m/s and 20 m/s, and for both LiDAR configurations. Additionally, as the wind speed increases, the coherence wavenumber shows a similar decrease. However, an increase in the number of LiDAR beams leads to an upward trend in coherence, as more beams capture additional details of the rotor area, providing a more accurate representation of the incoming wind speed and improving rotor-equivalent wind speed (REWS) approximations.
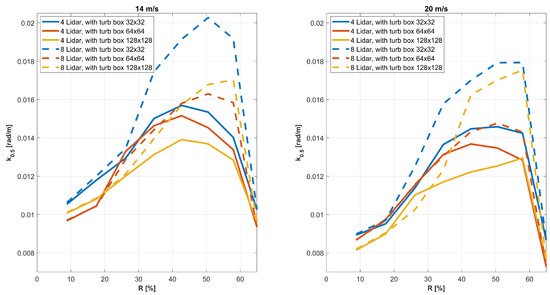
Figure 3.
Coherent bandwidth vs. LiDAR beam location at radius R. The results are averaged over six turbulence seeds for wind speeds of 14 and 20 m/s (left and right figures), using systems with four and eight LiDAR beams (solid and dash lines). The line colours distinguish the resolution of the turbulence box.
Furthermore, as the cone angle increases (with the focus length unchanged, see Figure 2), expanding the LiDAR coverage over the rotor radius, the coherence increases until it reaches peak points between 50% and 60% of the rotor radius. Beyond this, coherence decreases sharply. This behaviour holds for all simulated cases. The study suggests that for large wind turbines, the best correlation occurs when measurements are taken above 50% of the rotor radius, further supporting the coherence trends observed in this study. These results highlight the complex interplay between turbulence accuracy, wind speed, and the number of LiDAR beams on the coherent wavenumber.
3.2. Uncertainty in Coherence Under Different Realisations of Turbulent Fields
Next, the standard deviation is calculated for each case and presented as error bars, as shown in Figure 4. The findings of this study indicate that increasing the preview distance (by modifying the half-cone angle) of the LiDAR system leads to a significant rise in the standard deviation, reflecting a greater dispersion of data points around the mean. This effect is most pronounced within the range of 30% to 60% of the rotor radius, where the coherent wavenumber reaches its highest values. This range is particularly significant for simulations, as it is both operationally important and captivating.
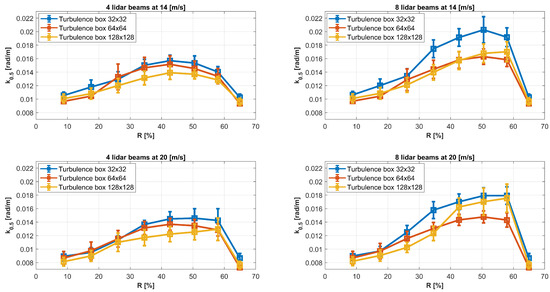
Figure 4.
Coherent bandwidth vs. LiDAR beam location at radius R. The results are averaged over six turbulence seeds for wind speeds of 14 and 20 m/s (upper and lower figures), using systems with four and eight LiDAR beams (left and right figures). The line colours distinguish the resolution of the turbulence box. The errors represent the standard deviation of results over six turbulence seeds.
Additionally, the data analysis revealed an interesting trend for shorter preview distances, specifically between 10% and 25% of the rotor radius, where greater dispersion of the coherent wavenumber was observed at lower wind speeds. As wind speed increased, the dispersion shifted towards larger preview distances, between 40% and 60% of the rotor radius. It was also noted that the turbulence box with dimensions 32 × 32 (height and width) exhibited higher deviations, likely due to fewer grid points providing less detailed information. Conversely, the turbulence box of 128 × 128 displayed less dispersion for shorter preview distances (10% to 40% of the rotor radius), while the 64 × 64 turbulence box showed less dispersion throughout simulations in the 40–60% range. This behaviour may explain the variations in coherence observed in Figure 3, as values between 40% and 60% of the rotor radius exhibit higher fluctuations. These factors should be considered when applying the coherent wavenumber and parameters to the filter to ensure an acceptable signal quality for predicting wind speed.
3.3. Summary of Coherence Study
The analysis reveals key insights regarding the turbulence box size, number of LiDAR beams, and opening angle in LiDAR configurations.
- Turbulence Box: Increasing the size of the turbulence box from 32 × 32 to 128 × 128 decreases the coherence wavenumber, suggesting that higher-resolution turbulence boxes might result in worse correlation due to higher fidelity simulations. The 64 × 64 turbulence box generally presents lower dispersion across different simulation seeds. It was observed that lower-resolution turbulence boxes (32 × 32) had higher variations and a larger standard deviation in the critical region, while 64 × 64 and 128 × 128 turbulence boxes were more consistent.
- Number of LiDAR Beams: Increasing the number of LiDAR beams leads to an increase in the coherence wavenumber, benefiting LiDAR-assisted control by capturing more information. However, further investigation is needed to determine how much the coherence can improve with additional LiDAR beams.
- Preview Distance: The coherence wavenumber increases with the preview distance up to 60% of the rotor radius, after which it decreases drastically. This highlights the importance of selecting the optimal preview distance to obtain the best signal quality and coherence. It is also noted that higher windspeeds lead to greater dispersion in coherence, underlining the significance of pre-evaluating parameters for optimal performance.
Based on the observations, the subsequent simulations will utilise a 64 × 64 turbulence box, offering a balance between accuracy and computational efficiency. While a 128 × 128 turbulence box would ideally provide higher resolution, its computational demands are substantial. Therefore, more powerful hardware should be considered before conducting such large-scale simulations.
4. Results: Study of Two Reference LiDAR-Assisted Methods
4.1. Simulation Set-Up
In this simulation study, the IEA 10MW reference wind turbine [24] with a rotor diameter of 198 m and, the NREL 5MW reference wind turbine [25] with a rotor diameter of 126 m, were used. The baseline setup of a turbulent wind box consists of a grid of 64 × 64 in the plane perpendicular to the flow direction using 8 LiDAR beams in a circular pattern with a minimum half-cone angle that covers 50% of the rotor radius. The preview distance results in 86.6 m. For Schlipf and Bossanyi approaches, the feedforward output pitch angle is extracted based on a steady-state pitch curve derived from HAWC2 steady-state simulations. An example of the steady-state pitch curve for the IEA 10MW reference wind turbine is shown in Figure 5.
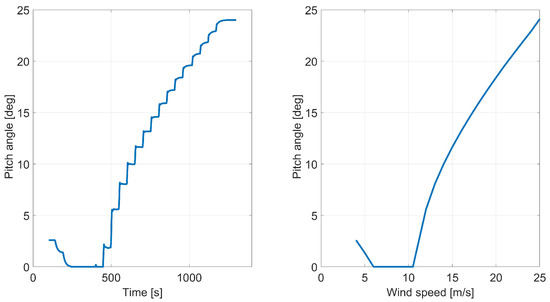
Figure 5.
Steady-state pitch curve for the IEA 10MW reference wind turbine. Left: Time-domain simulation. Right: Static pitch curve against the wind speeds.
Lastly, to evaluate the two approaches, short-term damage equivalent loads (DELs) averaged among different seeds based on the simulation time series are computed.
4.2. LiDAR-Assisted Control Coherence and Look-Ahead Time
Numerical simulations first showed the results of the coherence difference for the two wind turbines for a mean wind speed of 18 m/s. An example is exhibited in Figure 6. The coherence study considers six time series for each turbine. The coherent wavenumbers and for the IEA 10 MW and NREL 5 MW reference wind turbines respectively were found and utilized.
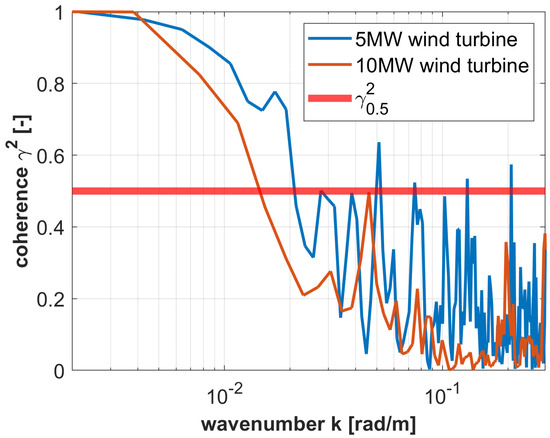
Figure 6.
Coherence aganist wavenumber for the NREL 5MW and IEA 10MW reference wind turbines for a wind speed of 18 m/s. The red line indicates where the magnitude-squared coherence equals 0.5.
The look-ahead time T can be computed using Equation (2), while the time delay introduced by the Butterworth filter can be approximated from K. Manal and W. Rose [26], and using the corresponding coherent.
When initially evaluating the case of the IEA 10 MW reference wind turbine, simulations revealed that the selected configuration resulted in the following:
This led to a preview time T of −0.25 s, which is clearly not feasible, as it suggests that the measured wind speed has already passed the wind turbine.
Upon further examination of the implementation, Equation (2) is divided into two main components. The first term depends on the LiDAR and the measurement distance (, where is the line-of-sight wind speed and is the half-cone angle). The second term is related to the LiDAR through the filter cut-off frequency. A smaller coherence bandwidth results in a larger , as indicated by Equation (12).
In the current results, the magnitude of the second term exceeds that of the first. This is due to the low cut-off frequency, which introduces a significant time delay in the filter. The delay is primarily a consequence of the low coherence bandwidth, , resulting from the limited number of LiDAR beams used in the current configuration.
The simplest solution to address the current issue is to increase the measurement distance X of the LiDAR system, thereby extending the look-ahead time and reducing the impact of the filter delay. However, practical considerations, such as the availability and accessibility of a customised LiDAR system, must also be taken into account.
4.3. Feedforward Method Analysis and Comparison
Results for the feedforward methods are presented in this section, based on (i) the recommended gain adjustments, and (ii) additional fine-tuning aimed at improving performance. The effectiveness of each method is evaluated through a comparison of Power Spectral Density (PSD) of key turbine signals and short-term Damage Equivalent Loads (DELs).
4.3.1. Results with Recommended Controller Tuning
When using the feedforward controllers, the gain adjustment of the feedback controller was performed, where the reduction in the integral gain () should be, in general, the square of the reduction in the proportional gain () [20]. For the Schlipf approach, adjustments are carried out as per the author’s recommendation to halve the proportional gain of the feedback controller [20]. Bossanyi’s approach followed the findings in Meng et al. [4], optimizing the gains to 90% of the original feedback signal [4].
Simulations were carried out for LiDAR-assisted control using both feedforward approaches on the NREL 5MW reference wind turbine. For comparison, the baseline controller used was the DTU open-source PI feedback controller. The simulations were performed under turbulent wind conditions at a mean wind speed of 18 m/s. The selected LiDAR configuration resulted in a preview time, T, of 1s. The results are shown in Figure 7a,b, which illustrate an example of the LiDAR-measured wind speed compared with the rotor effective wind speed (REWS), as well as the corresponding pitch angle response for the chosen coherence.
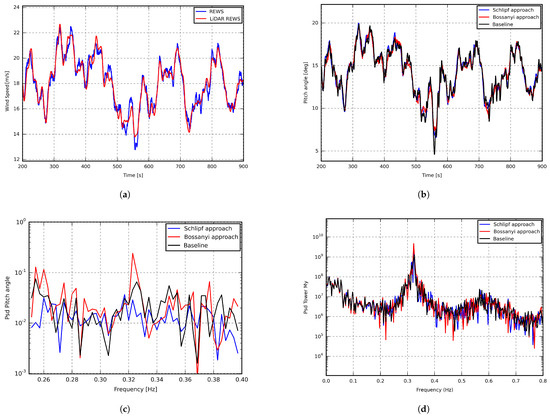
Figure 7.
NREL 5 MW reference wind turbine 700 s time series at 18 m/s for (a,b): LiDAR measured wind speed vs. REWS and the collective pitch angle and (c,d): PSD for zoom-in collective pitch angle and tower bottom side-side revealing frequency transfer/amplification from baseline controller.
To evaluate the approaches in terms of load reduction, short-term DELs were computed. Figure 8 shows the difference between the baseline and the studied methods, where a positive magnitude represents a load reduction.
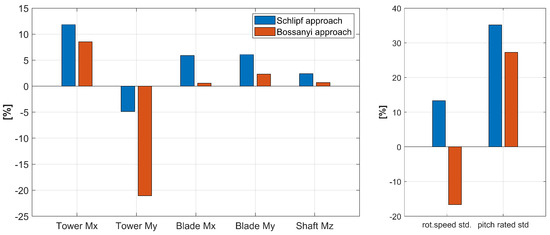
Figure 8.
Results for simulation at 18 m/s. Damage equivalent load reduction of tower bottom fore-aft (Tower Mx), tower bottom side-side (Tower My), blade flapwise (Blade Mx), blade edgewise (Blade My), and shaft torsion (Shaft Mz). Right: statistics of the standard deviation of rotor speed and pitch rate.
It is first revealed a decrease in the tower bottom fore-aft loads. This reduction is due to the diminished influence of wind disturbances on the rotor speed at lower frequencies, facilitated by the LiDAR. However, it is also noticed a clear increase in the tower bottom side-to-side loads particularly employing the Bossanyi approach. Minor load reductions are also appreciated on the blade loads.
To gain further insights into the increase in the tower load, the PSD of the pitch angle and tower side-to-side were computed (see Figure 7c,d). It is clearly visible a notable peak at the first tower side-to-side natural frequency (0.32 Hz) in both the baseline and the feedforward methods, mainly in the Bossanyi approach. This is due to the fact that the Bossanyi approach incorporates the actual pitch angle, allowing any baseline controller-induced frequencies to propagate into the feedforward design, as evidenced by the collective pitch angle PSD. As a result, this excitation is also noticeable in the PSD of the tower side-to-side moment, as illustrated in Figure 7d. The increased power spectral density at the first tower’s side-to-side natural frequency contributes to the increased loads experienced by the tower.
Furthermore, a frequency transport phenomenon is observed when using the Bossanyi approach, arising from both the use of the current pitch angle to calculate the feedforward pitch rate and the design implementation. In Bossanyi’s approach (Equation (10)), the actual pitch angle () contains components at the tower frequency, which are then fed back into the integrator through the feedforward design. As a result, Bossanyi’s approach imposes a higher requirement on the quality of the feedback design, demanding that the closed-loop system exhibits a low-frequency response at the tower frequency. This, in turn, influences the excited frequencies and ultimately impacts the Damage Equivalent Loads (DELs) in the tower side-to-side direction.
4.3.2. Results with Controller Fine-Tuning
Building on the previous findings, simulations were repeated in a scenario aimed at minimising the tower’s side-to-side moment. The controller was fine-tuned by reducing the frequency of the generator speed filter in the feedback loop from 0.4 Hz to 0.25 Hz. The results for the short-term DELs, alongside the previous DELs results, are presented in Figure 9.
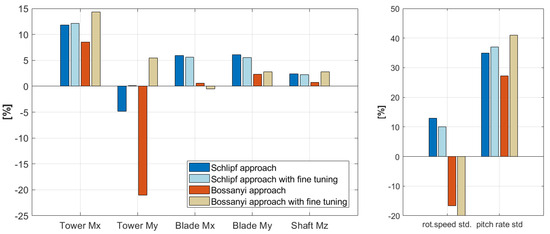
Figure 9.
Comparison between no fine-tuning and fine-tuning controller simulations at 18 m/s. Damage equivalent load reduction of tower bottom fore-aft (Tower Mx), tower bottom side-side (Tower My), blade flapwise (Blade Mx), blade edgewise (Blade My), and shaft torsion (Shaft Mz). Right: statistics of the standard deviation of rotor speed and pitch rate.
In this case, it is evident that the Schlipf approach achieves comparable load reduction in both scenarios, despite a 4% increase in the short-term tower side-to-side DELs. This increase is attributed to changes in the feedback loop filtering, specifically a reduction in the control bandwidth well below the tower frequency. As expected, this indicates that the Schlipf approach performs more robustly in low-frequency regulation, even when tower frequency components are present in the feedback controller.
Opposing this, the Bossanyi approach seems to be more sensitive to the performance of the baseline feedback controller. When the interaction with the tower side-to-side frequency is diminished in the feedback control design, Bossanyi’s approach has the potential to improve load reduction on tower bottom side-to-side moment.
5. Conclusions
This study initially focused on the effective use of wind measurements from commercially available LiDAR systems, evaluating how LiDAR configuration such as the number of beams, locations of the beams, and turbulence box resolution in HAWC2 simulations affects signal coherence. Results showed that improving the turbulence box resolution leads to lower coherent wavenumbers, while low-resolution boxes introduce greater variability across seeds. Overall, grids of 64 × 64 and 128 × 128 performed similarly, although the grid of 128 × 128 showed less dispersion for short preview distances. Increasing the number of LiDAR beams improved coherence, particularly when measurements were taken between 40–60% of the rotor radius; coherence dropped significantly outside this range. Wind speed increases were found to reduce coherence, suggesting a need for adaptive filters. Overall, for more accurate aeroelastic simulations, at least eight LiDAR beams should be used, with measurements taken at a minimum of 40% rotor radius, and a turbulence box grid of at least 64 × 64.
Next, the simulation results of the presented work initially revealed that larger wind turbines exhibit reduced coherence bandwidth when using the same LiDAR system compared to smaller sizes. Additionally, challenges were identified in correcting the time required to compensate for the filter time delay, . It was found that in larger wind turbines, such as the IEA 10MW reference wind turbine, the time needed to compensate for the time delay caused by the filter can exceed the available preview time from Equation (2). This phenomenon arises from the limited coherence bandwidth associated with the available LiDAR beams. As a consequence, the Butterworth filter exhibits a low cut-off frequency, leading to an increased value of .
These results underscore the critical importance of ensuring a sufficiently high coherence to effectively compensate for the time delay without compromising the available preview time due to the interplay between the measurement, coherence, and cut-off frequency of the filter. The specific threshold of coherence may vary depending on the particular setup and wind turbine size to guarantee a successful implementation when using LiDAR measurements. Addressing this issue may involve optimizing measurements to increase coherence bandwidth or increasing the preview time through the measurement distance. Notably, this phenomenon is not evident in simulations for smaller wind turbines, such as the NREL 5 MW reference wind turbine.
In the assessment of short-term DELs reduction, the Schlipf approach demonstrated overall better performance compared to the Bossanyi approach where deficiencies were observed including frequency propagation and higher excitation in existing natural frequency of the tower, as illustrated in Figure 7c,d. These issues resulted from utilizing the actual pitch angle for feedforward pitch rate calculation that might contains signal component at the tower frequency. Despite these challenges, fine-tuning of the the feedback controller allowed the Bossanyi approach to yield positive outcomes and outperform the Schlipf approach in terms of load reduction on tower side-to-side moment, as shown in Figure 9. In contrast, the Schlipf method demonstrated robustness and achieved its two primary objectives—reference signal tracking and disturbance compensation. Overall, the Schlipf approach exhibited a more robust and reliable performance in load reduction, regardless of the feedback controller design.
These insights point to several implications for future turbine control design. First, there is a clear need to co-design LiDAR systems and control algorithms to ensure sufficient coherence and preview quality. Second, the development of adaptive filtering techniques and improved scanning strategies could help mitigate coherence loss in large turbines. Finally, controller robustness must be a design priority to ensure safe and effective integration of feedforward control, particularly as rotor diameters and structural flexibility continue to increase in next-generation turbine designs.
In the future, this study will be extended to include a full design load case analysis. In the current work, the comparison of the two feedforward methods was limited to a wind speed of 18 m/s due to time constraints. This speed was selected as it represents above-rated conditions where pitch control is dominant. Six turbulence seeds were used to capture variability and provide averaged results. While only one wind speed was considered, we expect the relative trends in load impact between the two methods to remain consistent across other above-rated wind speeds.
Further work will also explore filtering strategies, such as applying a notch filter at the tower frequency to remove tower-induced components from the LiDAR signal. In addition, the study will investigate and optimise alternative LiDAR measurement patterns and configurations for larger wind turbines. The circular scan pattern used here serves as a baseline, and future efforts will explore new patterns and combinations with varying focal distances to improve the accuracy and effectiveness of LiDAR-assisted control.
Author Contributions
Conceptualization, C.D.S.P., A.W.H.L. and F.M.; methodology, C.D.S.P., A.W.H.L. and F.M.; software, C.D.S.P.; formal analysis, C.D.S.P., A.W.H.L. and F.M.; investigation, C.D.S.P.; writing—original draft preparation, C.D.S.P.; writing—review and editing, C.D.S.P., A.W.H.L. and F.M.; supervision, A.W.H.L. and F.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Dataset available on request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Harris, M.; Hand, M.; Wright, A. Lidar for Turbine Control; Technical Report, NREL Technical Report, NREL/TP-500-39154; National Renewable Energy Laboratory: Golden, CO, USA, 2005. [Google Scholar]
- Schlipf, D.; Kuhn, M. Prospects of a collective pitch control by means of predictive disturbance compensation assisted by wind speed measurements. In German Wind Energy Conference (DEWEK); Fraunhofer-Publica: Bremen, Germany, 2008. [Google Scholar]
- Dunne, F.; Schlipf, D.; Pao, L.Y.; Kelley, N.; Wright, A.D.; Simley, E.; Jonkman, B. Comparison of Two Independent Lidar-Based Pitch Control Designs; National Renewable Energy Laboratory: Golden, CO, USA, 2012. [Google Scholar]
- Meng, F.; Lio, W.H.; Larsen, G.C. Wind turbine LIDAR-assisted control: Power improvement, wind coherence and loads reduction. J. Phys. Conf. Ser. 2022, 2265, 022060. [Google Scholar] [CrossRef]
- Laks, J.; Pao, L.; Simley, E.; Wright, A.; Kelley, N.; Jonkman, B. Model Predictive Control Using Preview Measurements from LIDAR; American Institute of Aeronautics and Astronautics: Orlando, FL, USA, 2012. [Google Scholar] [CrossRef]
- Lio, W.H.; Jones, B.L.; Rossiter, J.A. Preview predictive control layer design based upon known wind turbine blade-pitch controllers. Wind Energy 2017, 20, 1207–1226. [Google Scholar] [CrossRef]
- Dong, L.; Lio, W.H.; Simley, E. On turbulence models and lidar measurements for wind turbine control. Wind Energy Sci. 2021, 6, 1491–1500. [Google Scholar] [CrossRef]
- Guo, F.; Schlipf, D.; Cheng, P.W. Evaluation of lidar-assisted wind turbine control under various turbulence characteristics. Wind Energy Sci. 2023, 8, 149–171. [Google Scholar] [CrossRef]
- Lio, W.H.; Meng, F.; Larsen, G.C. On LiDAR-assisted wind turbine retrofit control and fatigue load reductions. J. Phys. Conf. Ser. 2022, 2265, 032072. [Google Scholar] [CrossRef]
- Lio, A.W.; Meng, F.; Larsen, G.C. Performance similarities between standard and retrofit LiDAR-assisted control for wind turbines. J. Phys. Conf. Ser. 2024, 2265, 032046. [Google Scholar] [CrossRef]
- Russell, A.J.; Collu, M.; McDonald, A.S.; Thies, P.R.; Keane, A.; Quayle, A.R. LIDAR-assisted feedforward individual pitch control of a 15 MW floating offshore wind turbine. Wind Energy 2024, 27, 341–362. [Google Scholar] [CrossRef]
- Moldenhauer, R.H.; Schmid, R. LIDAR-assisted nonlinear output regulation of wind turbines. Wind Energ. Sci. Discuss. 2025. in review. [Google Scholar] [CrossRef]
- Schlipf, D.; Fleming, P.; Haizmann, F.; Scholbrock, A.; Hofsäß, M.; Wright, A.; Cheng, P.W. Field Testing of Feedforward Collective Pitch Control on the CART2 Using a Nacelle-Based Lidar Scanner. J. Phys. Conf. Ser. 2014, 555, 012090. [Google Scholar] [CrossRef]
- Clifton, A.; Clive, P.; Gottschall, J.; Schlipf, D.; Simley, E.; Simmons, L.; Stein, D.; Trabucchi, D.; Vasiljevic, N.; Würth, I. IEA Wind Task 32: Wind lidar identifying and mitigating barriers to the adoption of wind lidar. Remote Sens. 2018, 10, 406. [Google Scholar] [CrossRef]
- Simley, E.; Fürst, H.; Haizmann, F.; Schlipf, D. Optimizing lidars for wind turbine control applications-Results from the IEA Wind Task 32 workshop. Remote Sens. 2018, 10, 863. [Google Scholar] [CrossRef]
- Schlipf, D. Lidar-Assisted Control Concepts for Wind Turbines. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2016. [Google Scholar] [CrossRef]
- Bossanyi, E.A.; Kumar, A.; Hugues-Salas, O. Wind turbine control applications of turbine-mounted LIDAR. J. Phys. Conf. Ser. 2014, 555, 012011. [Google Scholar] [CrossRef]
- Steinmann Perez, C.D.; Lio, A.W.H.; Meng, F. Analysis and evaluation of two reference LiDAR-assisted control designs for wind turbines. In Proceedings of the The Science of Making Torque from Wind (TORQUE 2024), Florence, Italy, 29–31 May 2024; Institute of Physics: Bristol, UK, 2024; Volume 2767. [Google Scholar] [CrossRef]
- Schlipf, D.; Haizmann, F.; Cosack, N.; Siebers, T.; Cheng, P.W. Detection of Wind Evolution and Lidar Trajectory Optimization for Lidar Assisted Wind Turbine Control. Meteorol. Z. 2015, 24, 565–579. [Google Scholar] [CrossRef]
- Schlipf, D.; Bossanyi, E.; Carlo Enrico Carcangiu, T.F.; Maul, T.; Rossetti, M. LIDAR Assisted Collective Pitch Control; Technical Report Deliverable D5.1.3; Upwind: San Francisco, CA, USA, 2011. [Google Scholar]
- Held, D.P.; Mann, J. Lidar estimation of rotor-effective wind speed—An experimental comparison. Wind Energy Sci. 2019, 4, 421–438. [Google Scholar] [CrossRef]
- Meng, F.; Lio, W.H.; Barlas, T. DTUWEC: An open-source DTU Wind Energy Controller with advanced industrial features. J. Phys. Conf. Ser. 2020, 1618, 022009. [Google Scholar] [CrossRef]
- Larsen, T.; Hansen, A. How 2 HAWC2, the User’s Manual; Number 1597 (ver. 3-1) (EN); Forskningscenter Risø, Risø National Laboratory: Roskilde, Denmark, 2007. [Google Scholar]
- Bortolotti, P.; Tarrés, H.; Dykes, K.; Merz, K.; Sethuraman, L.; Verelst, D.; Zahle, F. IEA Wind TCP Task 37: Systems Engineering in Wind Energy-WP2.1 Reference Wind Turbines; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2019. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO USA, 2009. [Google Scholar] [CrossRef]
- Manal, K.; Rose, W. A general solution for the time delay introduced by a low-pass Butterworth digital filter: An application to musculoskeletal modeling. J. Biomech. 2007, 40, 678–681. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).