A Novel Method for Optimizing the Robustness and Carbon Emissions of Anchored Slopes
Abstract
1. Introduction
2. Methodology
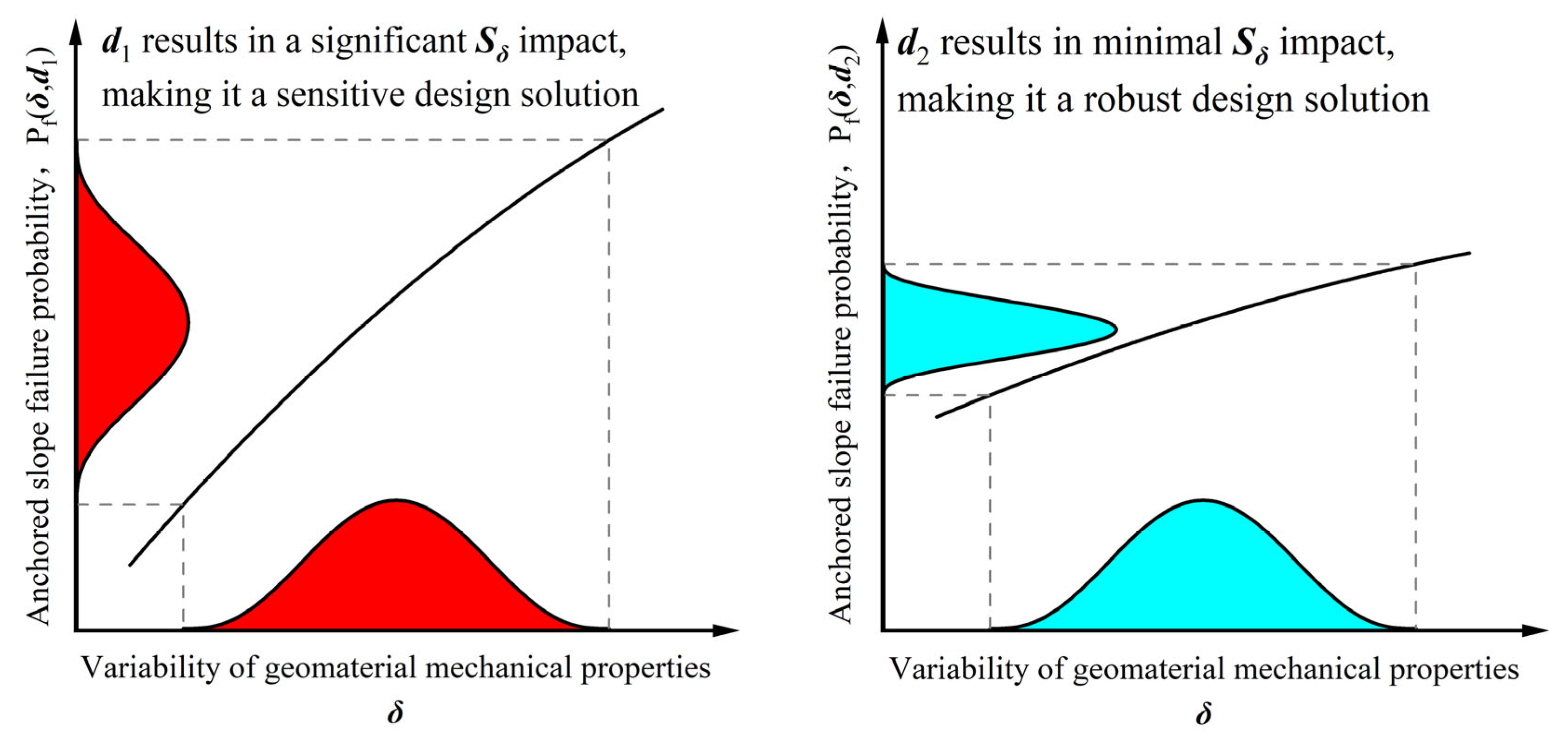
2.1. Design Robustness Analysis and MCS Implementation
2.2. Methods of Calculating Carbon Emissions for Anchored Slopes
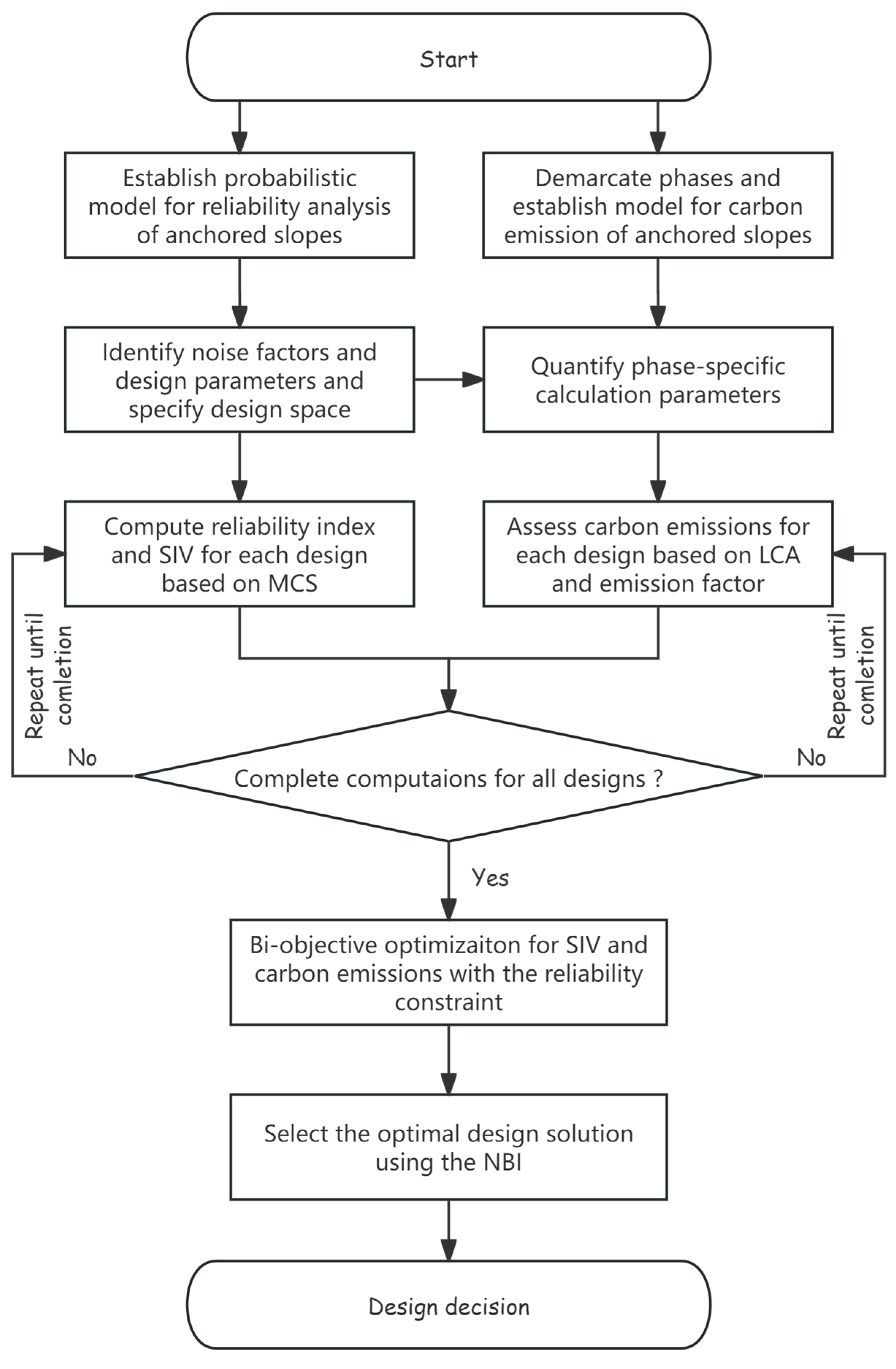
2.3. Framework for Robust Optimization Design
- (1)
- Construct the model of interest prior to design optimization. In this step, the probability computation for anchored slopes is established with physical and reliability models; the carbon emission phases and boundaries are demarcated, and the carbon emission models of various phases for anchored slopes are established.
- (2)
- Determine the diverse parameters and specify the design domain in computational analyses. The noise factors and their stochastic properties are identified; the typical ranges of the design parameters are specified according to the particular design situation at hand; these design parameters are modeled as discrete variables in the DS; and quantify the phase-specific calculation parameters such as building material consumed, energy consumption and emission factors.
- (3)
- Obtain the objective function and constraint function values for each design solution. The reliability index β can be computed by MCS; the SIV can be evaluated by the proposed method in the Section 2.1 which is more accurate than the SIV based on the first-order reliability method (FORM) according to the MCS theory; and the carbon emissions can be assessed based on the LCA and the carbon emission factor methods.
- (4)
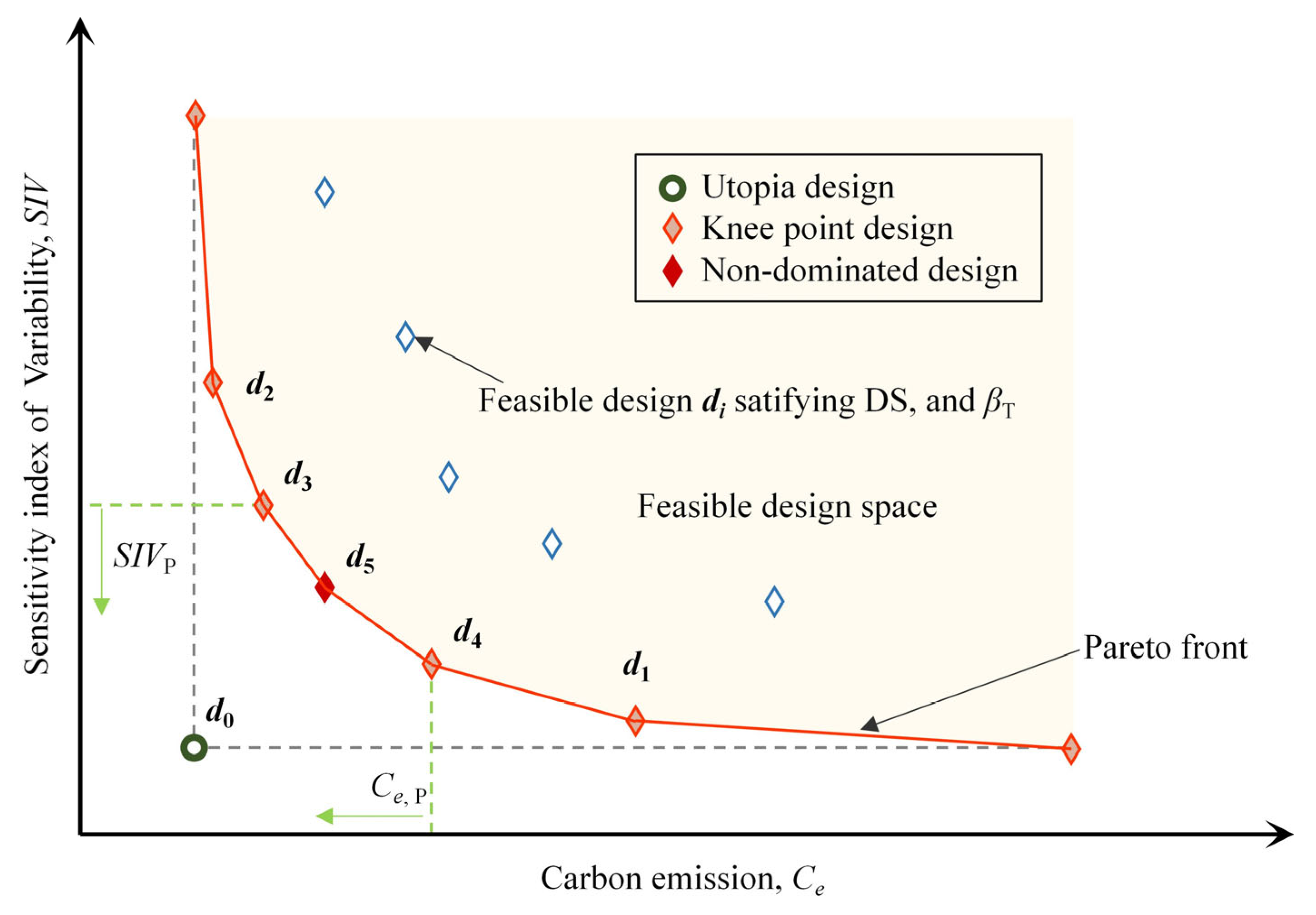
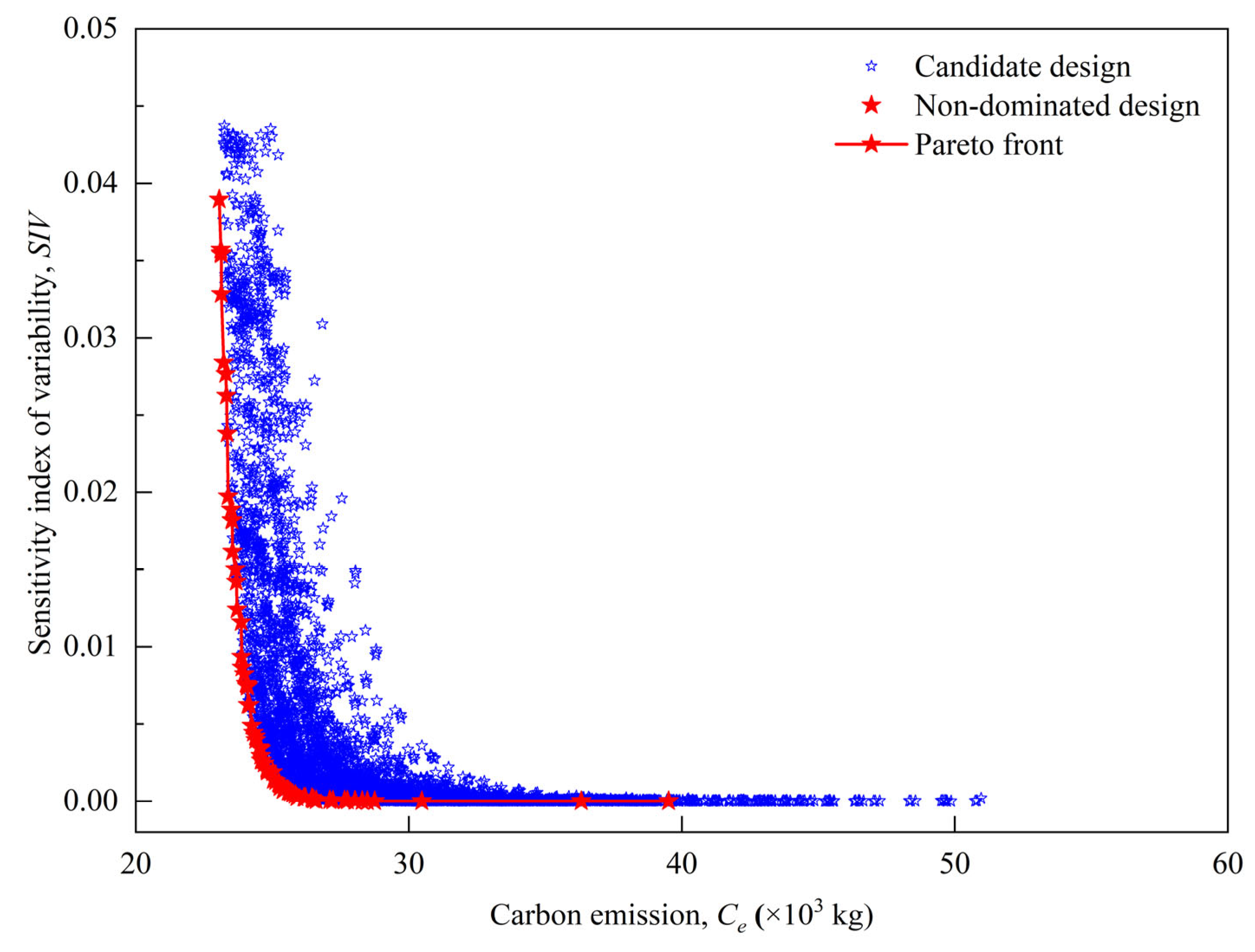
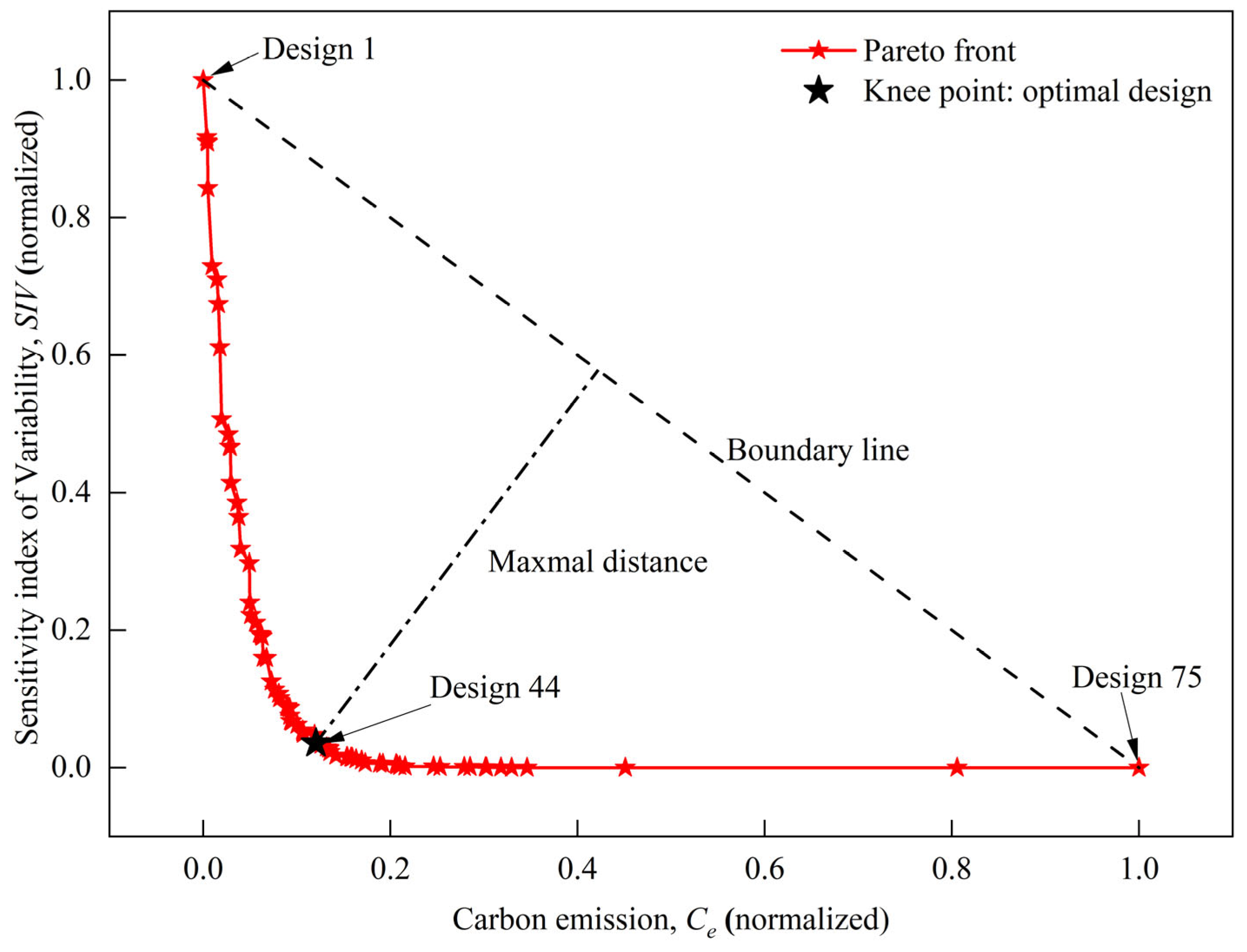
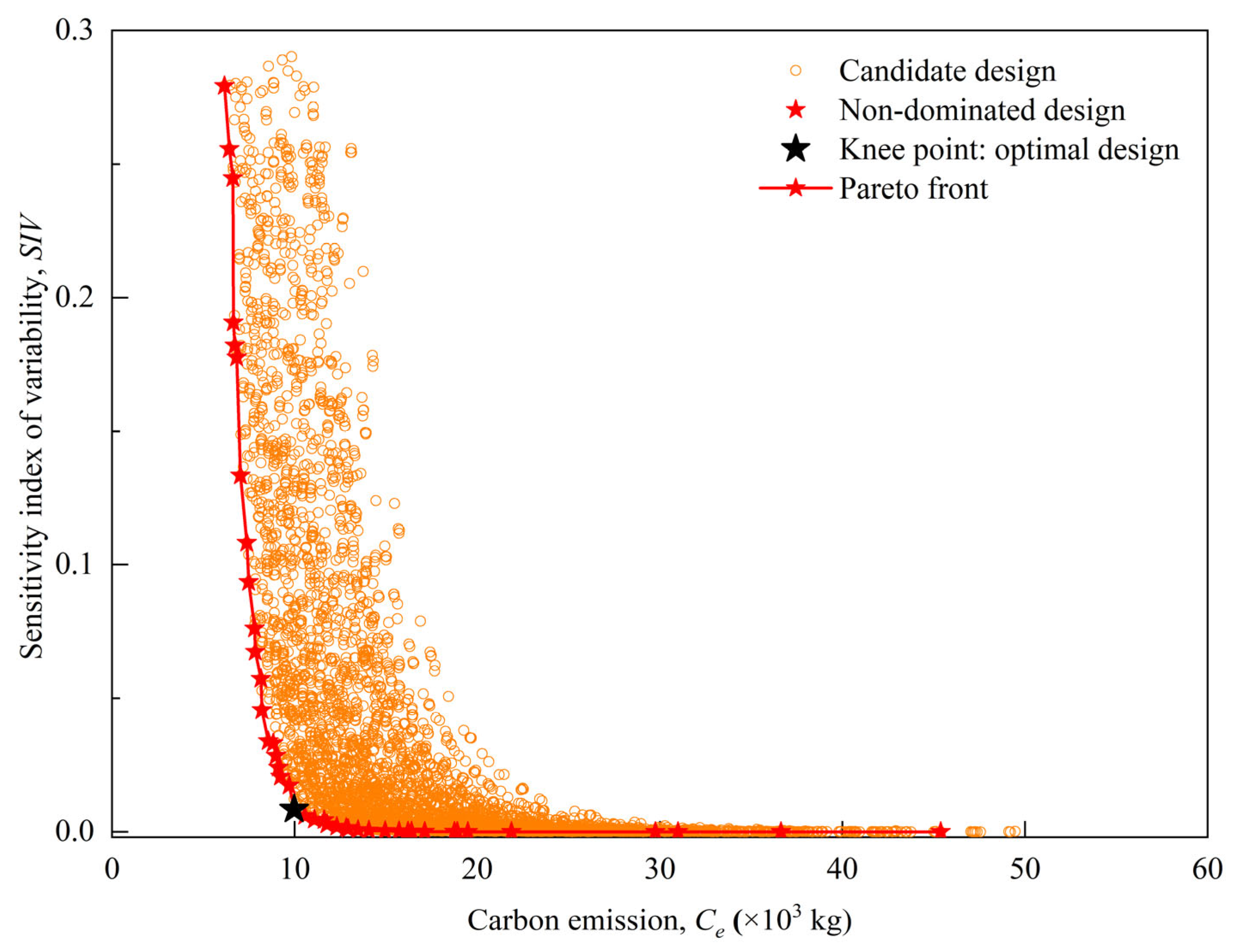
- Implement the bi-objective optimization using the non-dominated sorting genetic algorithm NSGA-II [39]. After applying Equation (14), numerous feasible design solutions are generated. Furthermore, by employing the NSGA-II [39], we obtain the warm-colored diamond-shaped scatter points as illustrated in Figure 3. During this process, the ideal scenario is often envisioned as a “utopian” design solution d0 (as shown in Figure 3) that simultaneously achieves optimal design robustness R and minimal carbon emissions Ce. However, in reality, maximizing design robustness R (i.e., minimizing SIV) and minimizing carbon emissions Ce are inherently conflicting objectives. Consequently, it is impossible to achieve a single optimal design solution that simultaneously fulfills both objectives. Instead, the optimization process yields a set of non-dominated design solutions. These solutions are such that, between the two objectives, no solution is simultaneously superior or inferior to another; rather, they are collectively superior to other feasible designs within the solution space di. For example, as shown in Figure 3, while the non-dominated design d2 offers higher carbon emissions, another non-dominated design d3 achieves a lower SIV value (indicating better robustness R), and vice versa. These non-dominated designs collectively form a Pareto front, which reveals the trade-offs between the two design objectives [23,39]. As mentioned above, the Pareto front can be obtained using the NSGA-II algorithm [39]. Although the optimization algorithm has been widely applied in fields such as industrial and electrical engineering, its application in geotechnical engineering, particularly in anchor design, differs due to the unique nature of the discipline.
- (5)
- Select the optimal design using the normal boundary intersection (NBI) method [40]. After identifying the Pareto front via NSGA-II, the algorithm can assist designers in making informed decisions tailored to specific project requirements. For instance, within DS, one may opt for a design solution that operates below a predefined carbon emission threshold Ce,P while minimizing SIV (as exemplified by design d4 in Figure 3) or select a solution that achieves a specified robustness level SIVP at the lowest level of carbon emissions Ce (as illustrated by design d3 in Figure 3). Such choices are typically made in response to the preferences of stakeholders or clients. However, in the absence of predefined priorities, the knee point of the Pareto front (as shown by design d5 in Figure 3) is often regarded as the most optimal solution, as it strikes the best balance between the two objectives. As Figure 3 demonstrates, selecting a design to the left of the knee point d5 on the Pareto front results in only marginal reductions in carbon emissions Ce, but significantly compromises robustness R, which is undesirable. Conversely, choosing a design to the right of the knee point achieves only modest improvements in robustness R but at the expense of substantially higher carbon emissions Ce, which is also impractical. Therefore, when no specific preferences are articulated by the stakeholders or clients, the knee point design serves as the most favorable option within the DS. The NBI method [40] is employed to identify the knee point design following the extraction of the Pareto front in geotechnical engineering.
3. Illustrative Example for a Framework with an Anchored Slope
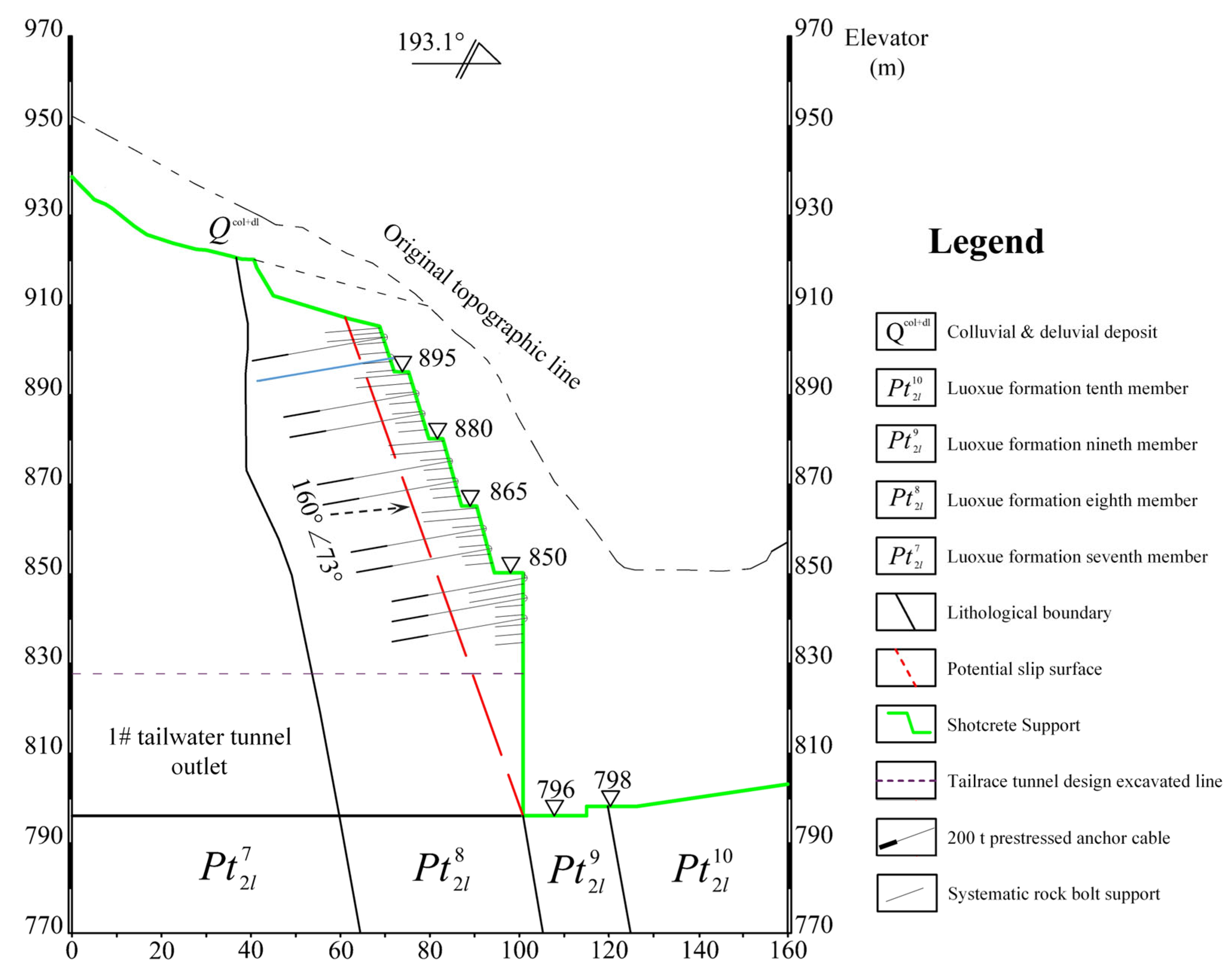
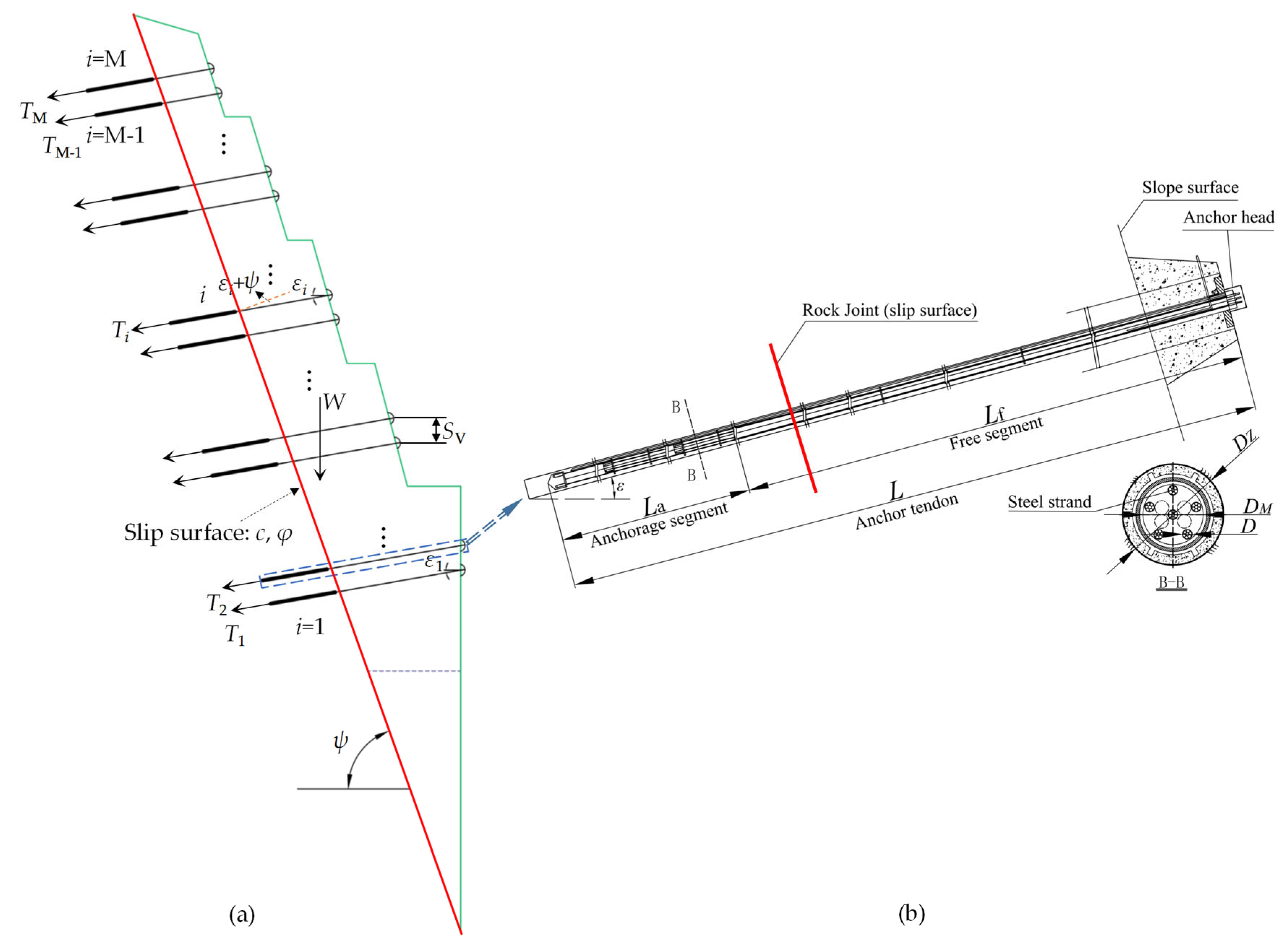
3.1. Engineering Overview
3.2. Reliability Analysis
- (1)
- Failure mode 1
- (2)
- Failure mode 2
- (3)
- Failure mode 3
3.3. Determining the Design Space
3.4. Carbon Emission Calculation
- (1)
- Calculating the carbon emissions of producing building materials
- (2)
- Calculating the carbon emissions of transporting building materials
- (3)
- Calculating the carbon emissions during the construction phase
- (4)
- Calculating the carbon emissions during the service phase
3.5. Bi-Objective Optimization Model for the Anchored Slope
3.6. Results and Analysis
4. Validation and Discussion
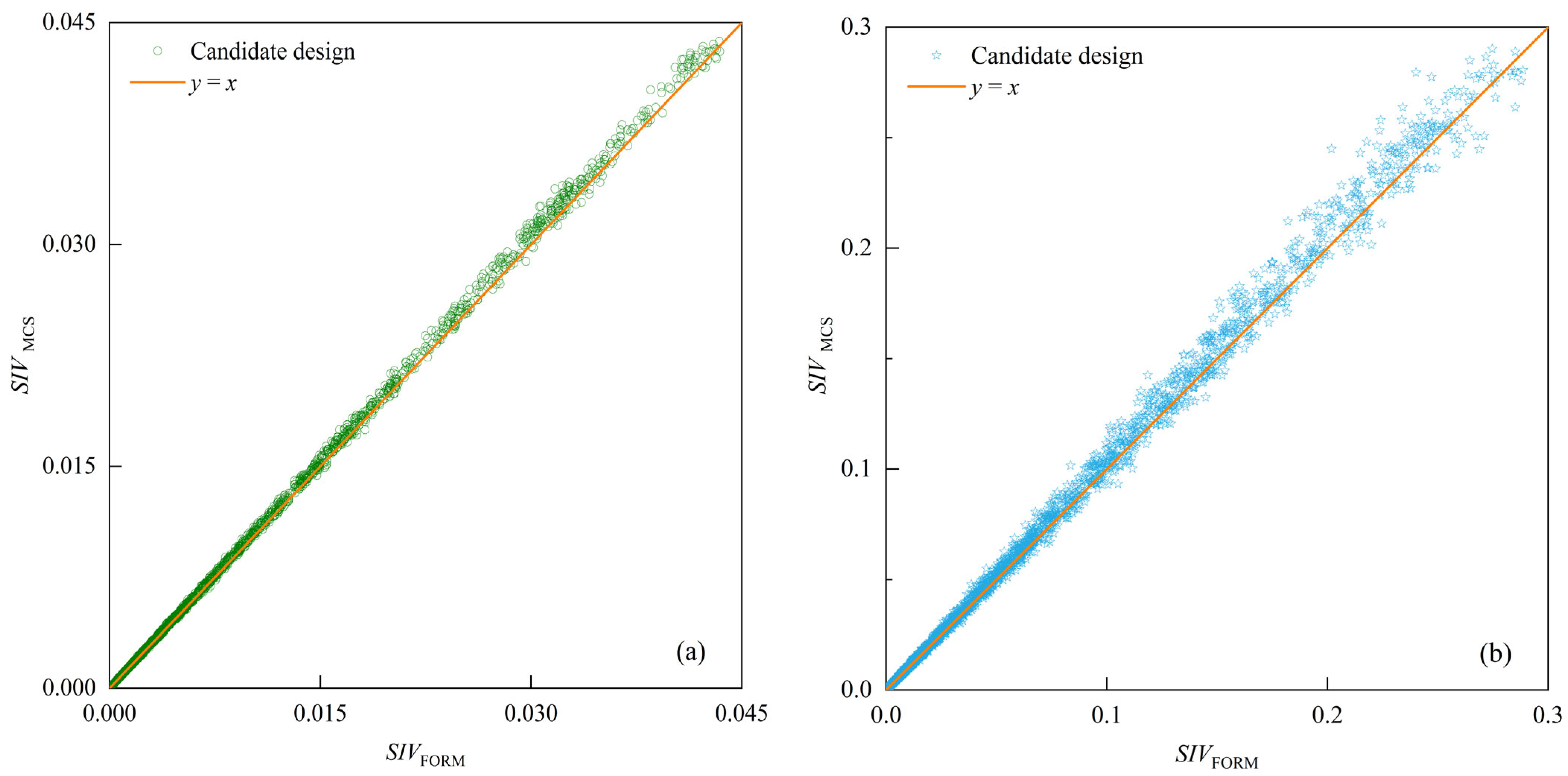
4.1. Validation of the SIV Based on MCS
4.2. Limitation of the Proposed Framework
- (1)
- Computational trade-offs between Monte Carlo simulation precision and runtime efficiency
- (2)
- Regional constraints of emission factors applied to global contexts
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SIV | Sensitivity index of variability |
| MCS | Monte carlo simulation |
| FS | Factor of safety |
| RGD | Robust geotechnical design |
| SNR | Signal-to-noise ratio |
| Probability density function | |
| CDF | Cumulative distribution function |
| DS | Design space |
| LCA | life cycle assessment |
| FORM | first-order reliability method |
| NSGA-II | Non-dominated sorting genetic algorithm-II |
| NBI | Normal boundary intersection |
| UAV | unmanned aerial vehicle |
| IoT | Internet of things |
References
- Hryciw, R.D. Anchor design for slope stabilization by surface loading. J. Geotech. Eng. 1991, 117, 1260–1274. [Google Scholar] [CrossRef]
- Yang, G.; Zhong, Z.; Zhang, Y.; Fu, X. Optimal design of anchor cables for slope reinforcement based on stress and displacement fields. J. Rock. Mech. Geotech. 2015, 7, 411–420. [Google Scholar] [CrossRef]
- Huang, Y.; He, Z.; Yashima, A.; Chen, Z.; Li, C. Multi-objective optimization design of pile-anchor structures for slopes based on reliability theory considering the spatial variability of soil properties. Comput. Geotech. 2022, 147, 104751. [Google Scholar] [CrossRef]
- Lin, D.; Zhang, Y.; Qiu, S.; Bai, M.; Xia, H.; Qiao, W.; Tang, Z. Landslide susceptibility assessment method during the construction of highways based on the index complexity algorithm. Sustainability 2024, 16, 6147. [Google Scholar] [CrossRef]
- Shi, G.; Gu, G.; Zhou, H.; Tao, Z.; Pan, H.; Tang, T. Stability monitoring and analysis of high and steep slope of a hydropower station. Geofluids 2020, 2020, 8840269. [Google Scholar] [CrossRef]
- Dai, F.; Li, B.; Xu, N.; Meng, G.; Wu, J.; Fan, Y. Microseismic Monitoring of the Left Bank Slope at the Baihetan Hydropower Station, China. Rock Mech. Rock Eng. 2017, 50, 225–232. [Google Scholar] [CrossRef]
- Khurshid, M.; Khan, A.; Rehman, Z.; Chaudhary, T. The evaluation of rock mass characteristics against seepage for sustainable infrastructure development. Sustainability 2022, 14, 10109. [Google Scholar] [CrossRef]
- Al-E’Bayat, M.; Guner, D.; Sherizadeh, T.; Asadizadeh, M. Numerical Investigation for the Effect of Joint Persistence on Rock Slope Stability Using a Lattice Spring-Based Synthetic Rock Mass Model. Sustainability 2024, 16, 894. [Google Scholar] [CrossRef]
- Li, B.; Li, T.; Xu, N.; Dai, F.; Chen, W.; Tan, Y. Stability assessment of the left bank slope of the Baihetan Hydropower Station, Southwest China. Int. J. Rock Mech. Min. 2018, 104, 34–44. [Google Scholar] [CrossRef]
- Wu, Y.; Cui, J.; Huang, J.; Zhang, W.; Yoshimoto, N.; Wen, L. Correlation of critical state strength properties with particle shape and surface fractal dimension of clinker ash. Int. J. Geomech. 2021, 21, 04021071. [Google Scholar] [CrossRef]
- Beyer, H.; Sendhoff, B. Robust optimization—A comprehensive survey. Comput. Methods Appl. Mech. Eng. 2007, 196, 3190–3218. [Google Scholar] [CrossRef]
- Phadke, M. Quality Engineering Using Robust Design; Prentice Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Taguchi, G. Introduction to Quality Engineering: Designing Quality into Products and Processes, Quality Resources; White Plains: New York, NY, USA, 1986. [Google Scholar]
- Juang, C.; Wang, L. Reliability-based robust geotechnical design of spread foundations using multi-objective genetic algorithm. Comput. Geotech. 2013, 48, 96–106. [Google Scholar] [CrossRef]
- Khoshnevisan, S.; Gong, W.; Juang, C.; Atamturktur, S. Efficient robust geotechnical design of drilled shafts in clay using a spreadsheet. J. Geotech. Geoenviron. Eng. 2014, 141, 4014092. [Google Scholar] [CrossRef]
- Wu, Y.; Li, N.; Wang, X.; Cui, J.; Chen, Y.; Wu, Y.; Yamamoto, H. Experimental investigation on mechanical behavior and particle crushing of calcareous sand retrieved from South China Sea. Eng. Geol. 2021, 280. [Google Scholar] [CrossRef]
- Dodigović, F.; Ivandić, K.; Kovačević, M.; Soldo, B. Modified, Reliability-Based Robust Geotechnical Design Method, in Accordance with Eurocode 7. Appl. Sci. 2021, 11, 8423. [Google Scholar] [CrossRef]
- Hong, L.; Wang, X.; Zhang, W. Reliability-based robust geotechnical design of braced excavations considering multiple failure modes. Undergr. Space 2023, 9, 43–52. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, L.; Xu, L.; Zhou, S.; Luo, B.; Ding, K. In-situ investigation on dynamic response of highway transition section with foamed concrete. Earthq. Eng. Eng. Vib. 2025, 24, 547–563. [Google Scholar] [CrossRef]
- Ding, X.; Luo, B.; Zhou, H.; Chen, Y. Generalized solutions for advection–dispersion transport equations subject to time- and space-dependent internal and boundary sources. Comput. Geotech. 2025, 178, 1069443. [Google Scholar] [CrossRef]
- Gong, W.; Tang, H.; Juang, C.; Wang, L. Optimization design of stabilizing piles in slopes considering spatial variability. Acta Geotech. 2020, 15, 3243–3259. [Google Scholar] [CrossRef]
- Wang, L.; Hwang, J.; Juang, C.; Atamturktur, S. Reliability-based design of rock slopes—A new perspective on design robustness. Eng. Geol. 2013, 154, 56–63. [Google Scholar] [CrossRef]
- Juang, C.; Wang, L.; Hsieh, H.; Atamturktur, S. Robust geotechnical design of braced excavations in clays. Struct. Saf. 2014, 49, 37–44. [Google Scholar] [CrossRef]
- Gong, W.; Khoshnevisan, S.; Juang, C.H. Gradient-based design robustness measure for robust geotechnical design. Can. Geotech. J. 2014, 51, 1331–1342. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, S.; Zhang, Y.; Zhou, Y.; Ji, J. Multi-objective reliability-based robust design for a rock tunnel support system using Pareto optimality. Int. J. Numer. Anal. Methods Geomech. 2024, 48, 3350–3368. [Google Scholar] [CrossRef]
- Fan, B.; Wang, L.; Gong, W.; Wang, C.; Jiang, Y.; Sun, Z. Improved robust design of rock wedge slopes with a new robustness measure. Comput. Geotech. 2020, 123, 103548. [Google Scholar] [CrossRef]
- Ang, A.; Tang, W. Probability Concepts in Engineering: Emphasis on Applications to Civil and Environmental Engineering, 2nd ed.; John Wiley and Sons Inc.: New York, NY, USA, 2007. [Google Scholar]
- Li, D.; Zhou, C.; Lu, W.; Jiang, Q. A system reliability approach for evaluating stability of rock wedges with correlated failure modes. Comput. Geotech. 2009, 36, 1298–1307. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Deng, F.; Zhao, D.; Wu, R. Impacts of built-environment on carbon dioxide emissions from traffic: A systematic literature review. Int. J. Environ. Res. Public Health 2022, 19, 16898. [Google Scholar] [CrossRef] [PubMed]
- Zhou, P.; Lv, Y.; Wen, W. The low-carbon transition of energy systems: A bibliometric review from an engineering management perspective. Engineering 2023, 29, 147–158. [Google Scholar] [CrossRef]
- Wu, T.; Tang, W.; Sangrey, D.; Baecher, G.B. Reliability of offshore foundations-State of the art. J. Geotech. Eng. 1989, 115, 157–178. [Google Scholar] [CrossRef]
- Juang, C.; Wang, L.; Atamturktur, S.; Luo, Z. Reliability-based robust and optimal design of shallow foundations in cohesionless soil in the face of uncertainty. J. Geoengin. 2012, 7, 75–87. [Google Scholar]
- Xiao, J.; Xie, W.; Wang, E.; Huang, Y.; Liu, Q.; Yan, M.; He, G. Carbon emission assessment system and model construction of loess slope protection project. J. Earth Environ. 2023, 14, 786–795. [Google Scholar]
- Bao, H.; Wang, G.; Yan, C.; Lan, H.; Xie, Y. Highway construction carbon emission assessment and low-carbon measures and carbon compensation for geotechnical engineering: A review. China J. Highw. Transp. 2025, 38, 46–72. [Google Scholar]
- Bao, X.; Shen, Z.; Liu, B.; Li, H.; Li, Z. Carbon emission reduction scheme of railway subgrade retaining wall and carbon reduction strategies. J. Railway Sci. Eng. 2024, 21, 3842–3853. [Google Scholar]
- Xu, H.; Yu, H.; Lv, Q.; Tan, J.; Zhu, Z.; Liu, C.; Chen, W. Research on accounting methods for road traffic carbon emissions. Chin. J. Automot. Eng. 2023, 13, 496–505. [Google Scholar]
- Jang, W.; You, H.; Han, S. Quantitative decision making model for carbon reduction in road construction projects using green technologies. Sustainability 2015, 7, 11240–11259. [Google Scholar] [CrossRef]
- Dalton, S.; Farajpour, I.; Juang, C.; Atamturktur, S. Robust design optimization to account for uncertainty in the structural design process. In Topics on the Dynamics of Civil Structures, Volume 1:Proceedings of the 30th IMAC, A Conference on Structural Dynamics; Springer: New York, NY, USA, 2012; pp. 341–351. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Deb, K.; Gupta, S. Understanding knee points in bicriteria problems and their implications as preferred solution principles. Eng. Optim. 2011, 43, 1175–1204. [Google Scholar] [CrossRef]
- Zhu, L. Study of Shear Mechanics Mechanism of Bolted Joint Rock Mass and Shearing Resistance Prediction Model of Bolt; China University of Geosciences: Wuhan, China, 2021. [Google Scholar]
- Zhao, S. Study on Stress Distribution of Prestressed Anchor (Cables) and Engineering Application in Rock Slope; Hohai University: Nanjing, China, 2007. [Google Scholar]
- Chen, C.; Cheng, X. Time-varying reliability analysis of anchor system of rock slopes with double slide blocks. Rock Soil Mech. 2012, 033, 197–203. [Google Scholar]
- Shukla, S.; Hossain, M. Stability analysis of multi-directional anchored rock slope subjected to surcharge and seismic loads. Soil Dyn. Earthq. Eng. 2011, 31, 841–844. [Google Scholar] [CrossRef]
- Jiang, S. A non-Intrusive Stochastie Method for Slope Reliability in Hydroelectricity Engineering; Wuhan University: Wuhan, China, 2014. [Google Scholar]
- Fan, Y.; Zheng, Q.; Wei, L. Research on failure mechanism and ultimate load carrying capacity of prestressed cable (in Chinese). Chin. J. Rock Mech. Eng. 2005, 15, 2765–2769. [Google Scholar]
- NB/T 10802-2021; National Energy Administration. Code for Design of Prestressed Anchorage for Hydropower Projects. China Water&Power Press: Beijing, China, 2022. (In Chinese)
- Hong, H. Study on Anchorage Properties of Slope Rockmass and Its Engineering Applications; Hohai University: Nanjing, China, 2007. [Google Scholar]
- Broding, W.; Diederich, F.; Parker, P. Structural optimization and design based on a reliability design criterion. J. Spacecraft Rockets 1964, 1, 56–61. [Google Scholar] [CrossRef]
- GB/T 51366-2019; Ministry of Housing and Urban Rural Development of the People’s Republic of China; State Administration for Market Regulation. Standard for Building Carbon Emission Calculation. China Architecture & Building Press: Beijing, China, 2019. (In Chinese)
- Database of National Greenhouse Gas Emission Factor. Available online: https://data.ncsc.org.cn/factoryes/index (accessed on 22 May 2025).
- Wen, K.; Wang, Y.; Bao, X.; Tian, Y. Study on carbon emission calculation and carbon reduction benefit of railway cutting project. Railw. Econ. Res. 2025, 1, 10–17. [Google Scholar]
- Cai, W.; Cai, Y. National construction carbon emission calculation method research and data analysis. Constr. Manag. Res. 2020, 1, 61–76. [Google Scholar]
- GB 50199-2013; Ministry of Housing and Urban Rural Development of the People’s Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China. Unified Standard for Reliability Design of Hydraulic Engineering Structures. China Planning Press: Beijing, China, 2014. (In Chinese)
- Hohenbichler, M.; Rackwitz, R. First-order concepts in system reliability. Struct. Saf. 1982, 1, 177–188. [Google Scholar] [CrossRef]
| Random Variables | Mean | COV | Distribution | |
|---|---|---|---|---|
| Rock mechanical parameters | ||||
| c | Layer cohesion, /MPa | 0.205 | 0.146 | Normal |
| φ | Layer internal friction angle, /° | 38 | 0.085 | Normal |
| Anchorage structure performance | ||||
| σu | Yield strength of anchor cable strands, /MPa | 1860 | 0.05 | Lognormal |
| τq | Bond strength between anchor cable and grout, /MPa | 2.92 | 0.12 | Lognormal |
| τs | Bond strength between grout and bore wall, /MPa | 1.54 | 0.2 | Lognormal |
| Limitation State Function | Interpretation |
|---|---|
| g1 = FSI − 1 | Block sliding due to failure mode 1 |
| g2 = FSII − 1 | Block sliding due to failure mode 2 |
| g3 = FSIII − 1 | Block sliding due to failure mode 3 |
| Design Resistance Td/t | Geometrical Parameter of Anchor Cable | Elasticity Modulus E/GPa | Yield Strength σu/MPa | Bond Strength with Grout τq/kPa | ||
|---|---|---|---|---|---|---|
| Strand Amount and Diameter D/mm | Length L/m | Length of Anchorage Segment La/m | ||||
| 100 | 6Φ15.24 | 40~120 | 8~12 | 180 | 1860 | 2920 |
| 150 | 9Φ15.24 | |||||
| 200 | 12Φ15.24 | |||||
| 250 | 16Φ15.24 | |||||
| 300 | 19Φ15.24 | |||||
| 350 | 23Φ15.24 | |||||
| 400 | 26Φ15.24 | |||||
| Design Parameters | Design Pool |
|---|---|
| Equivalent diameter of anchor cable, De/m | {0.037, 0.046, 0.053, 0.061, 0.066, 0.073, 0.078} |
| Length of anchorage segment, La/m | {8, 9, 10, 11, 12} |
| Vertical distance, SV/m | {3, 3.5, 4, 4.5, 5, 5.5, 6} |
| Horizontal distance, SH/m | {3, 3.5, 4, 4.5, 5, 5.5, 6} |
| Anchorage inclination, ε/° | {10, 15, 20, 25} |
| Types of Building Materials | Carbon Emission Factor | Unit | Transportation Distance/km |
|---|---|---|---|
| Concrete | 240 | kg/m3 | 20 |
| Cement mortar | 790 | kg/t | 21 |
| Steel strand | 2150 | kg/t | 24 |
| Reinforcement bar | 2150 | kg/t | 24 |
| Key Construction Process | Construction Machinery | Energy Consumption per Shift | Carbon Emissions per Shift/kg | |
|---|---|---|---|---|
| Diesel/kg | Electric Energy/kW·h | |||
| Prestressed anchor cable support | Rebar cutting machine | 32.1 | 3.98 | |
| Multi-functional anchoring drilling trolley | 106.5 | 390.86 | ||
| Electric single-drum slow-speed winch | 126 | 15.61 | ||
| Mortar mixer | 8.61 | 1.07 | ||
| Extrusion-type mortar conveying pump | 23.7 | 2.95 | ||
| Grout pump | 32.5 | 4.03 | ||
| Prestressed anchor cable tensioning machine | 54.25 | 6.72 | ||
| Systematic rock bolt support | Rebar cutting machine | 32.1 | 3.98 | |
| Multi-functional anchoring drilling trolley | 106.5 | 390.86 | ||
| Electric single-drum slow-speed winch | 126 | 15.61 | ||
| Mortar mixer | 8.61 | 1.07 | ||
| Extrusion-type mortar conveying pump | 23.7 | 2.95 | ||
| Grout pump | 32.5 | 4.03 | ||
| Shotcrete support | Rebar cutting machine | 32.1 | 3.98 | |
| Electric single-drum slow-speed winch | 126 | 15.61 | ||
| Concrete mixer | 34.1 | 4.22 | ||
| Concrete conveying pump | 243.46 | 30.15 | ||
| Wet-mix shotcrete machine | 15.4 | 1.91 | ||
| Condition (βT) | Design Solution | Anchor Design Parameters d | Design Safety | Carbon Emissions | Design Robustness, R | ||||
|---|---|---|---|---|---|---|---|---|---|
| Td (t) | L (m) | SV (m) | SH (m) | ε (°) | β | Ce (kg) | SIV | ||
| Natural (3.2) | RGD-1 | 100 | 8 | 3.5 | 3 | 10 | 4.19 | 2.50 × 104 | 1.39 × 10−3 |
| RGD-2 | 150 | 8 | 3.5 | 3.5 | 10 | 4.51 | 2.63 × 104 | 2.79 × 10−4 | |
| Initial | 200 | 8 | 4.5 | 4.5 | 10 | 3.46 | 2.52 × 104 | 1.85 × 10−2 | |
| Rainfall (2.7) | RGD-1 | 100 | 8 | 3.5 | 3 | 10 | 3.33 | 2.50 × 104 | 4.73 × 10−2 |
| RGD-2 | 150 | 8 | 3.5 | 3.5 | 10 | 3.87 | 2.63 × 104 | 6.06 × 10−3 | |
| Initial | 200 | 8 | 4.5 | 4.5 | 10 | 2.66 | 2.52 × 104 | 0.297 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, B.; Ma, Y. A Novel Method for Optimizing the Robustness and Carbon Emissions of Anchored Slopes. Sustainability 2025, 17, 5889. https://doi.org/10.3390/su17135889
Fan B, Ma Y. A Novel Method for Optimizing the Robustness and Carbon Emissions of Anchored Slopes. Sustainability. 2025; 17(13):5889. https://doi.org/10.3390/su17135889
Chicago/Turabian StyleFan, Binqiang, and Yongzheng Ma. 2025. "A Novel Method for Optimizing the Robustness and Carbon Emissions of Anchored Slopes" Sustainability 17, no. 13: 5889. https://doi.org/10.3390/su17135889
APA StyleFan, B., & Ma, Y. (2025). A Novel Method for Optimizing the Robustness and Carbon Emissions of Anchored Slopes. Sustainability, 17(13), 5889. https://doi.org/10.3390/su17135889





