CO Emission Prediction Based on Kernel Feature Space Semi-Supervised Concept Drift Detection in Municipal Solid Waste Incineration Process
Abstract
1. Introduction
2. Materials and Methods
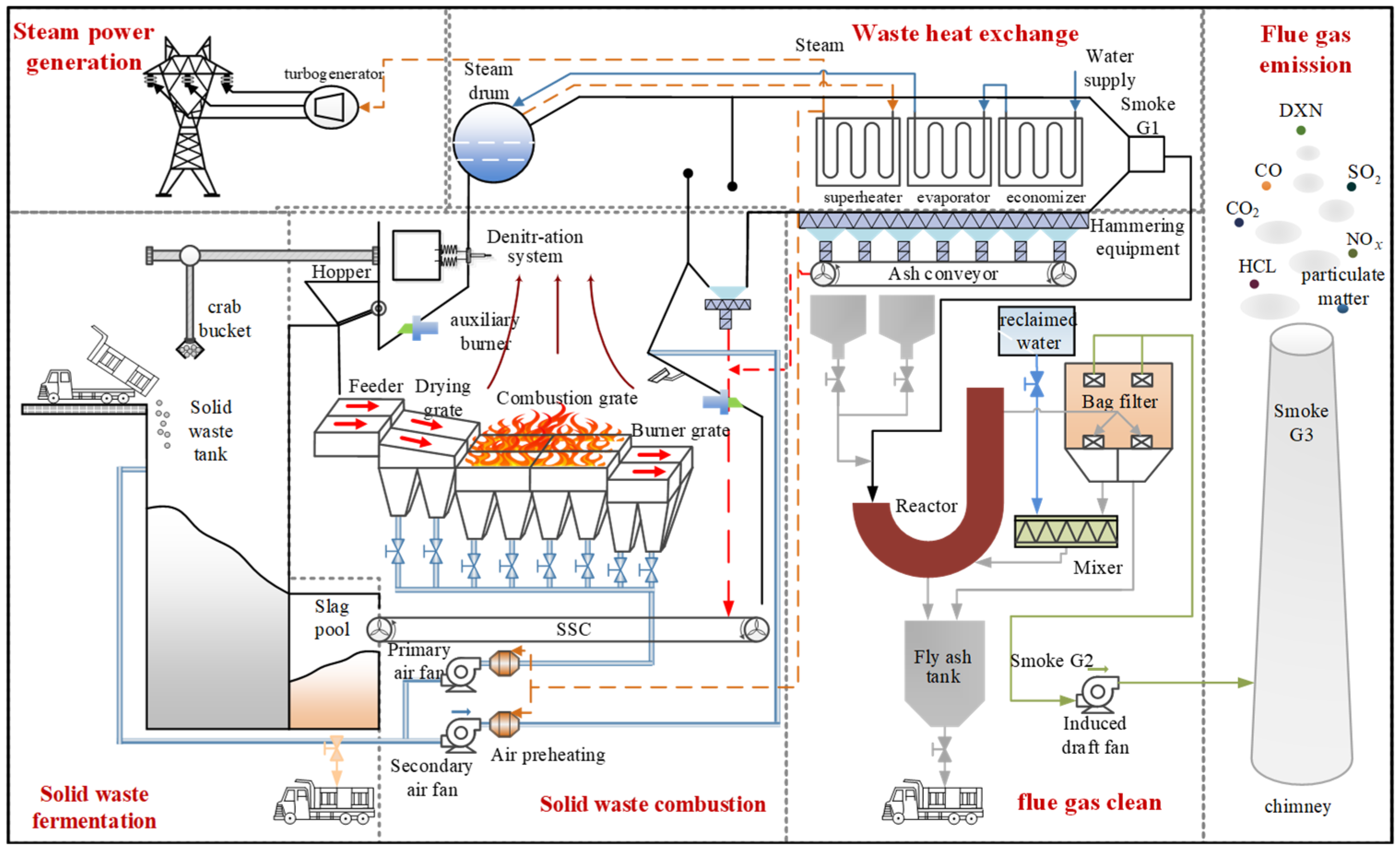
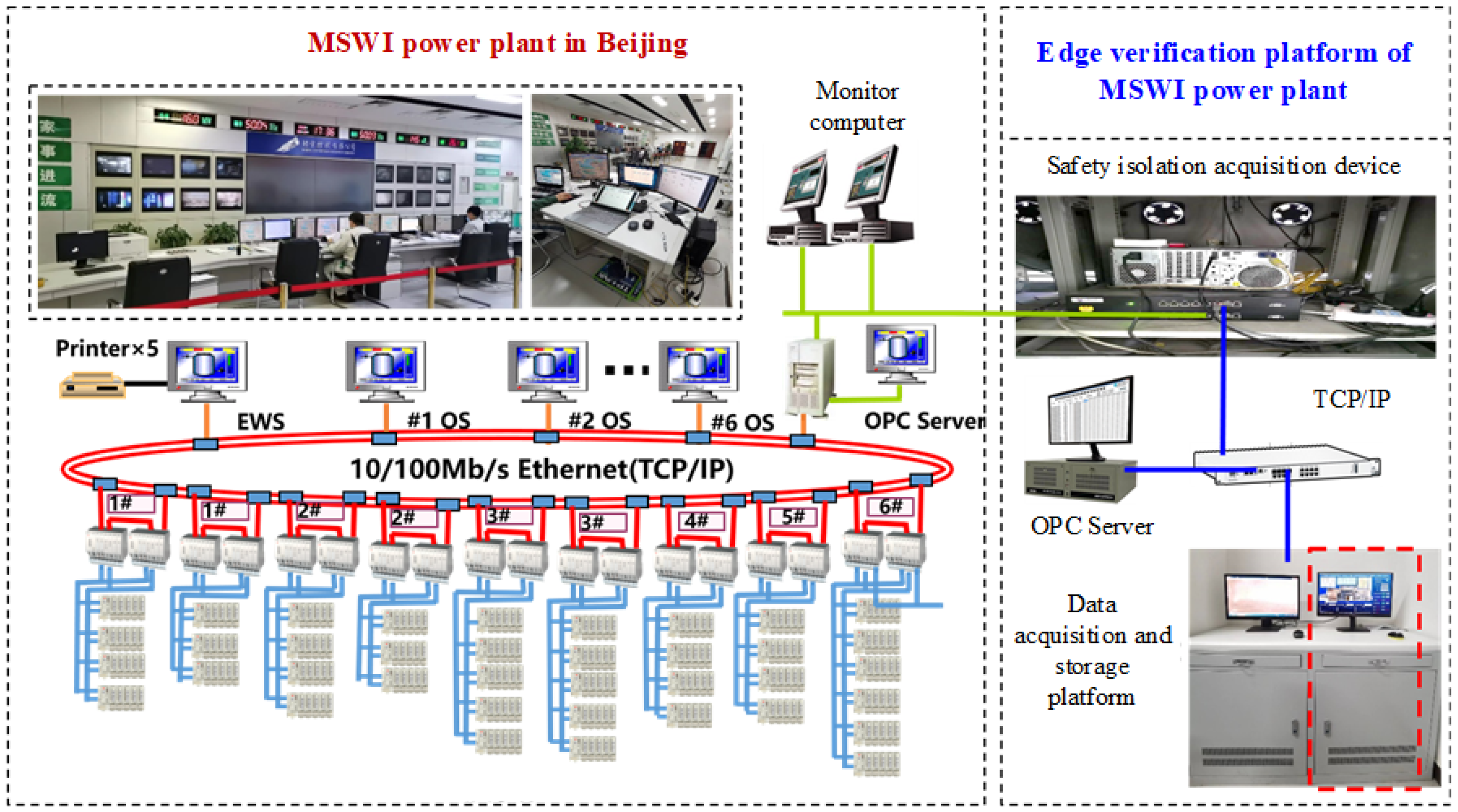
2.1. Materials
2.2. Methods
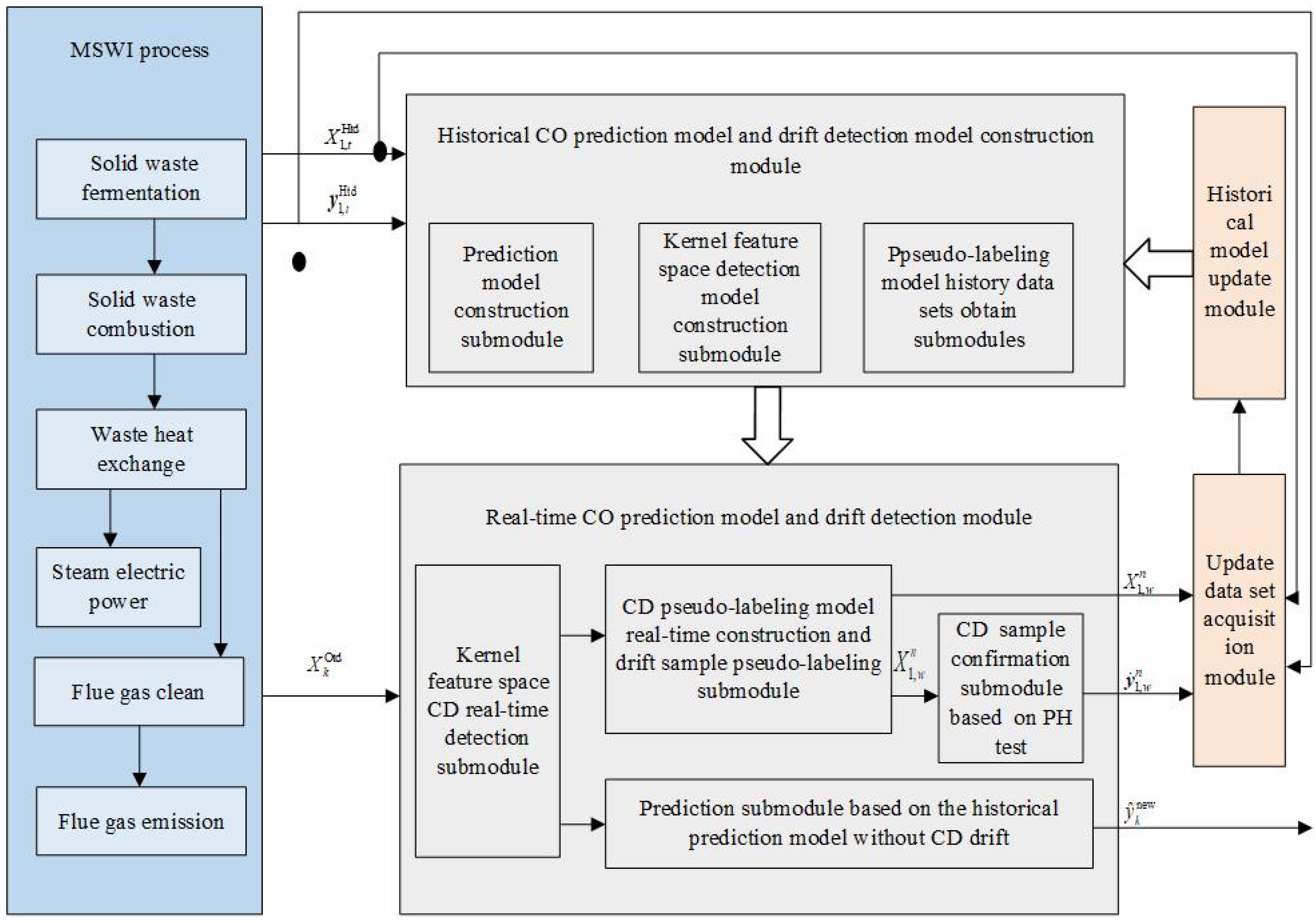
- (1)
- Historical CO prediction model and drift detection model construction module: historical samples are used to build prediction models and kernel feature space detection models and to obtain historical data sets to support pseudo-labeling model construction.
- (2)
- Real-time CO prediction model and drift detection module: When the CD detected value exceeds the KPCA control limit, it is considered that the sample has a drifting possibility. At this time, the sample is stored in the cache window to be labeled. When the number of samples in the window reaches the preset window capacity, a pseudo-labeling model is constructed in real time, and the drift samples are marked with pseudo-truth values. For the pseudo-truth values after labeling, the PH test method was used to determine whether the samples were drifting. If no CD occurs, the CO emission concentration is predicted based on the historical prediction model.
- (3)
- Update data set acquisition module: the samples confirmed to drift in the current cache window are recorded as the drift sample data set, and the historical data set is determined according to experience for the model update.
- (4)
- Historical model update module: The acquired updated data set is retrained for the CO prediction model and kernel feature space detection model, and the historical data set of the pseudo-labeling model is updated. At the same time, the cache window to be labeled is reset.
2.2.1. Historical CO Prediction Model and Drift Detection Model Construction Module
Prediction Model Construction Submodule
Kernel Feature Space Detection Model Construction n Submodule
Pseudo-Labeling Model History Data Sets Obtain Submodules
2.2.2. Real-Time CO Prediction Model and Drift Detection Module
Kernel Feature Space CD Real-Time Detection Submodule
Prediction Submodule Based on the Historical Prediction Model without CD Drift
CD Pseudo-Labeling Model Real-Time Construction and Drift Sample Pseudo-Labeling Submodule
CD Sample Confirmation Submodule Based on PH Test
2.2.3. Update Data Set Acquisition Module
2.2.4. Historical Model Update Module
2.3. Pseudo-Code
3. Results and Discussion
3.1. Performance Metrics
3.2. Experimental Results
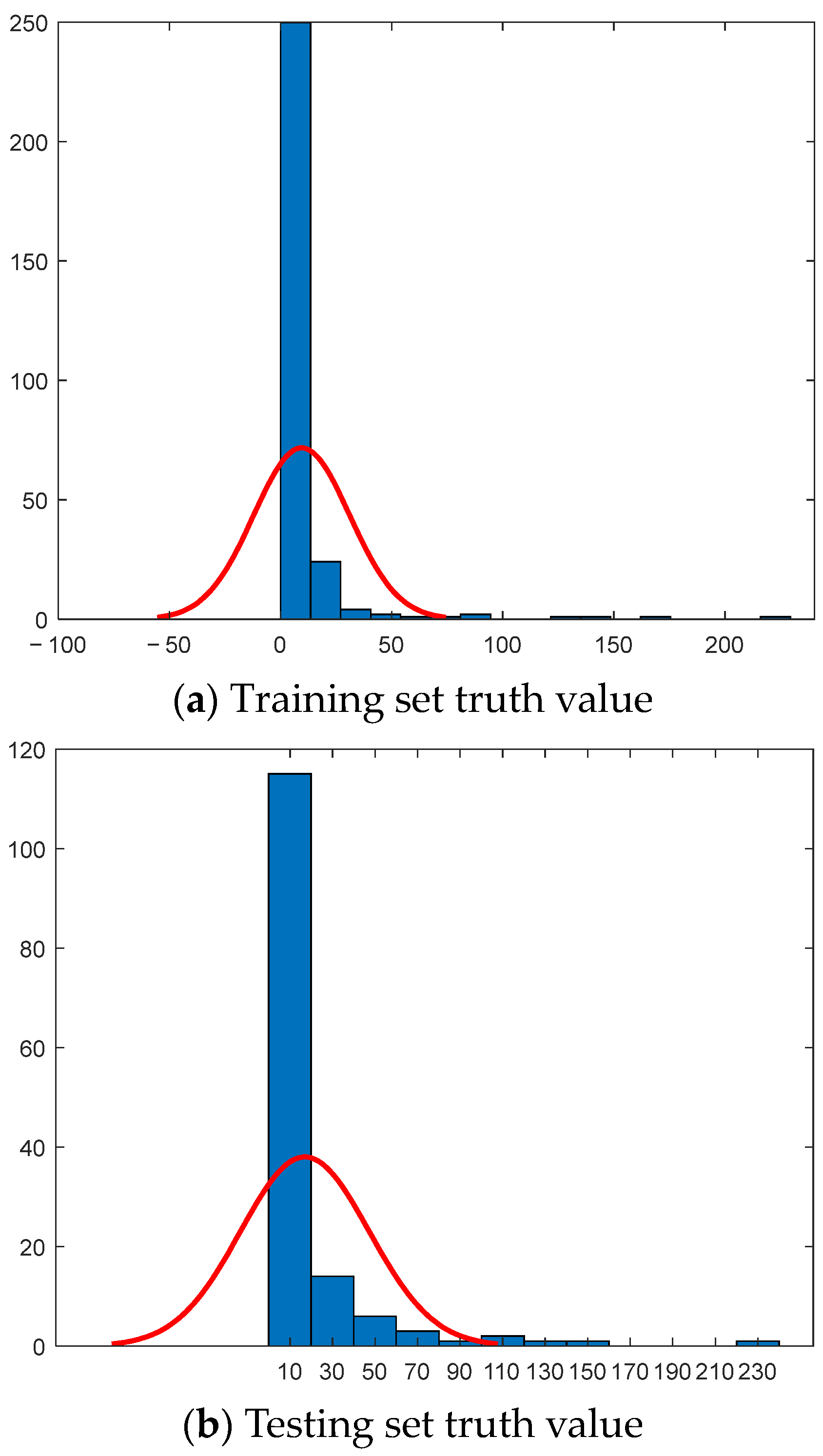
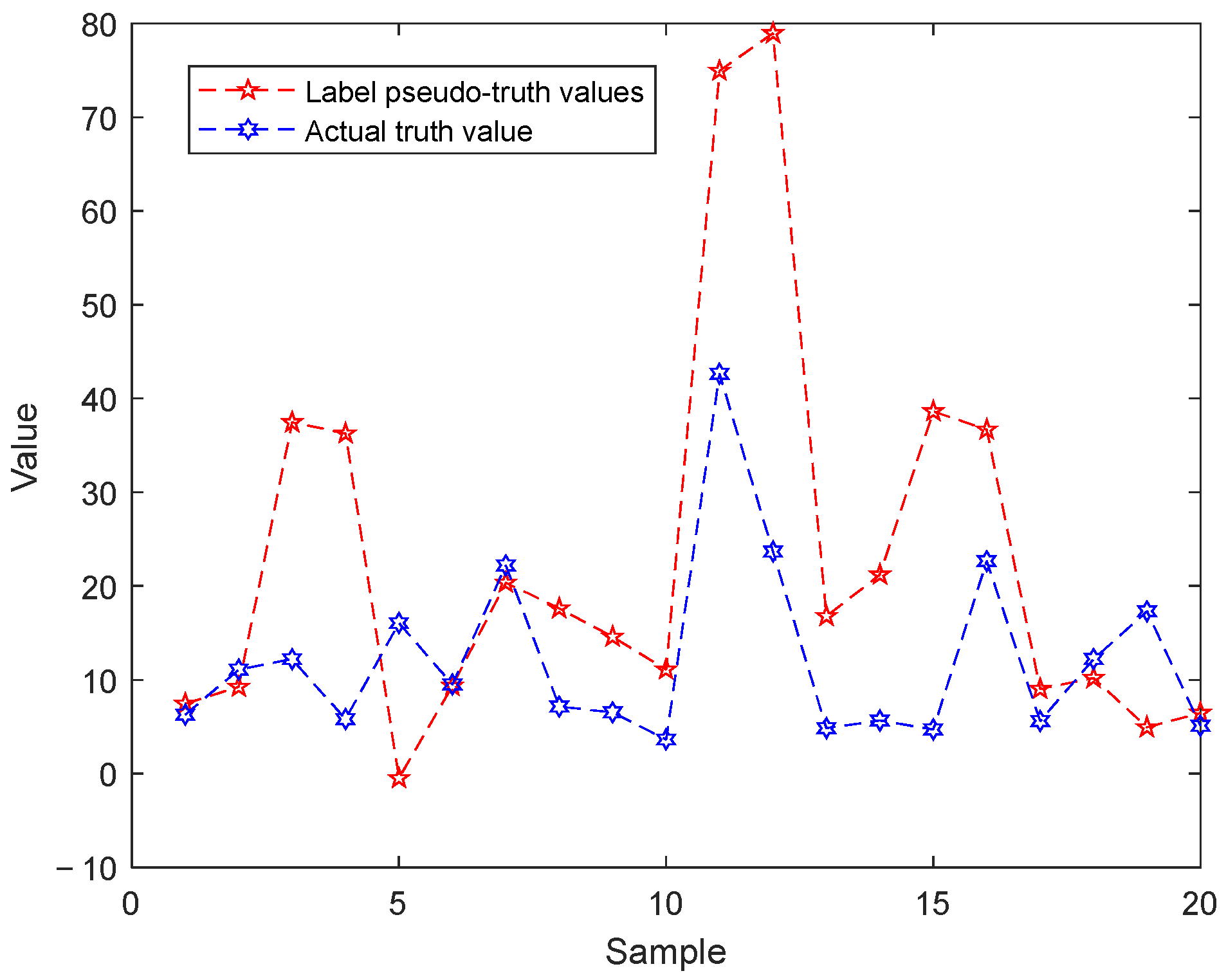
3.2.1. Historical Model Construction
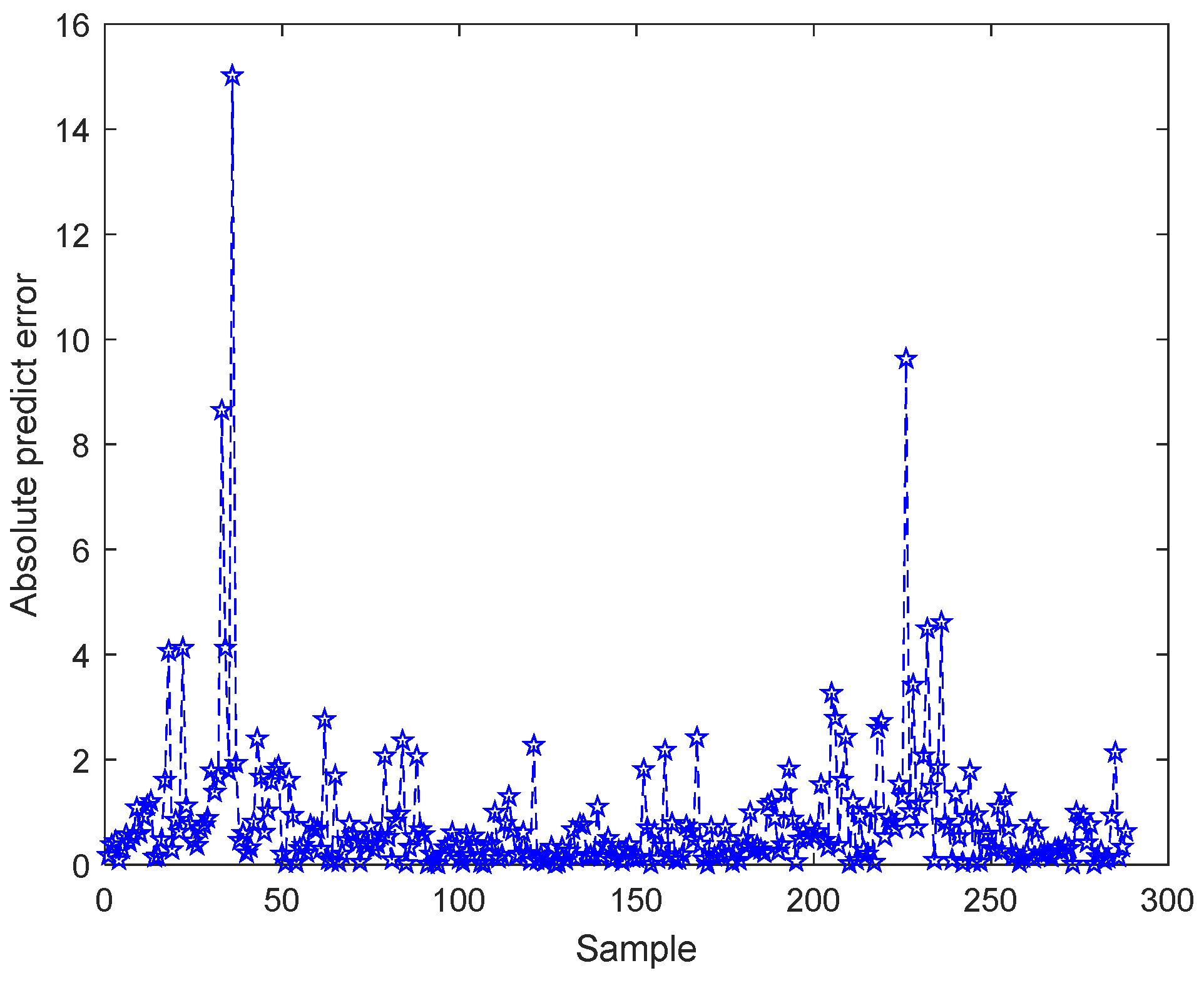
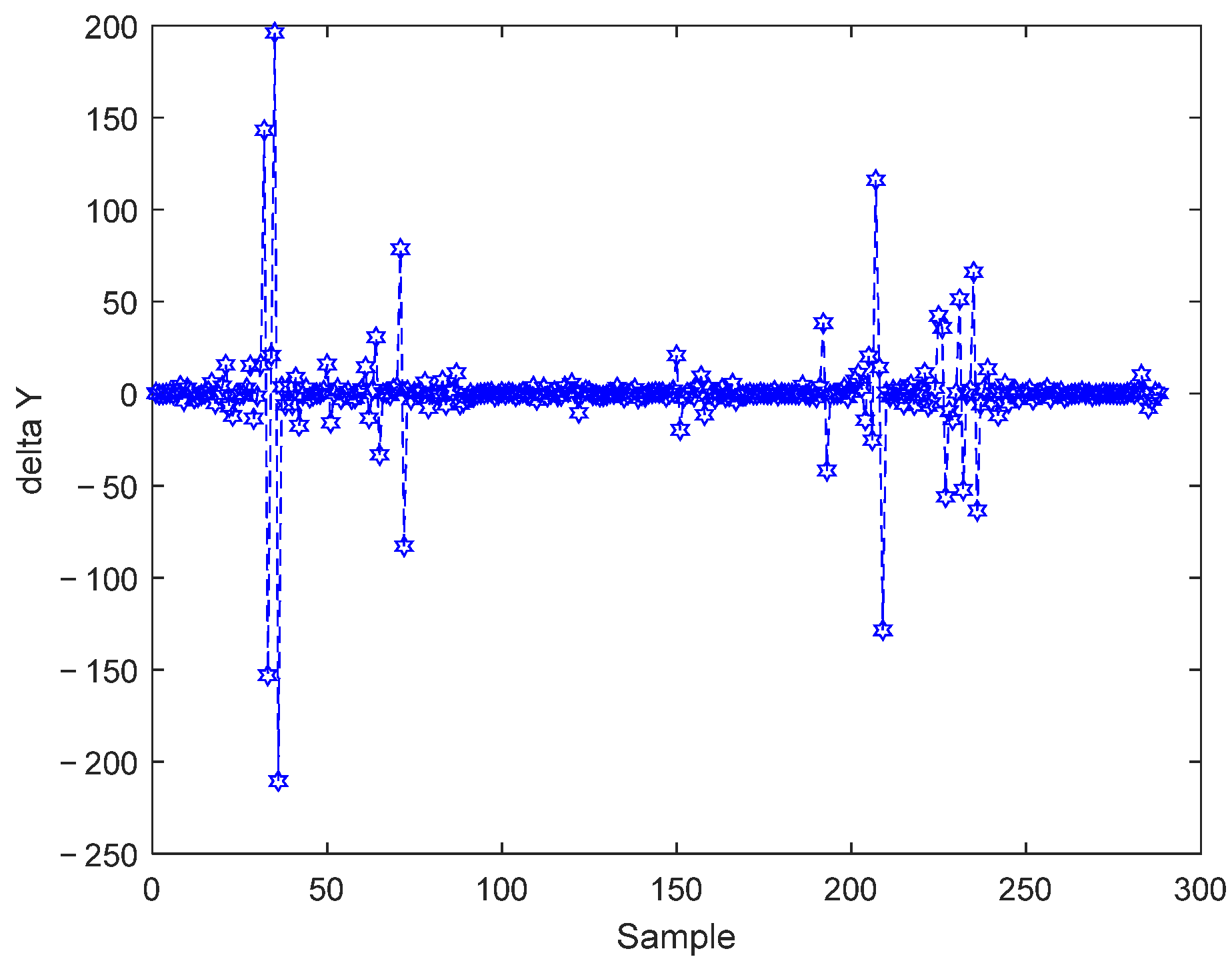
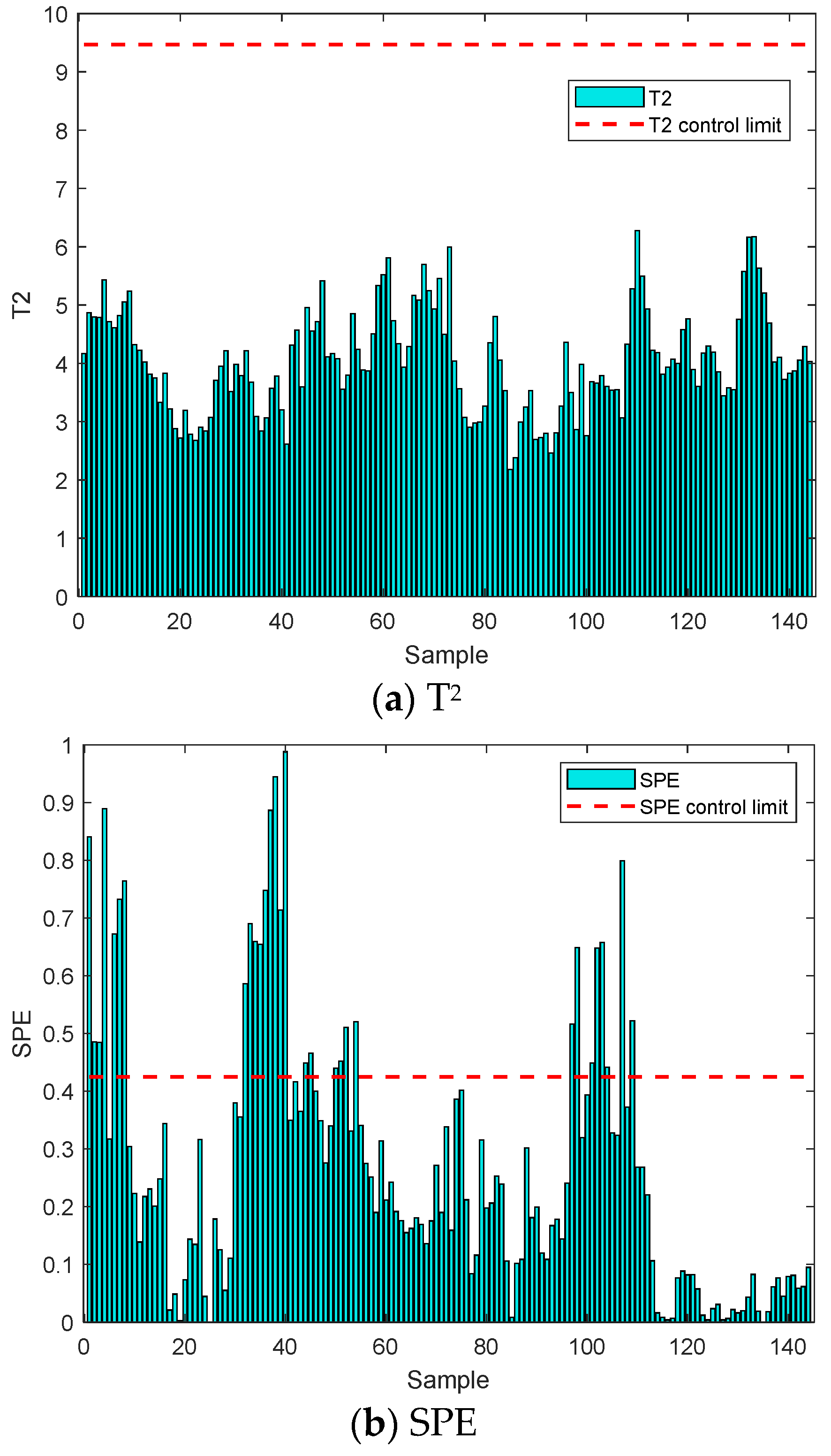
3.2.2. Real-Time Prediction and CD Detection
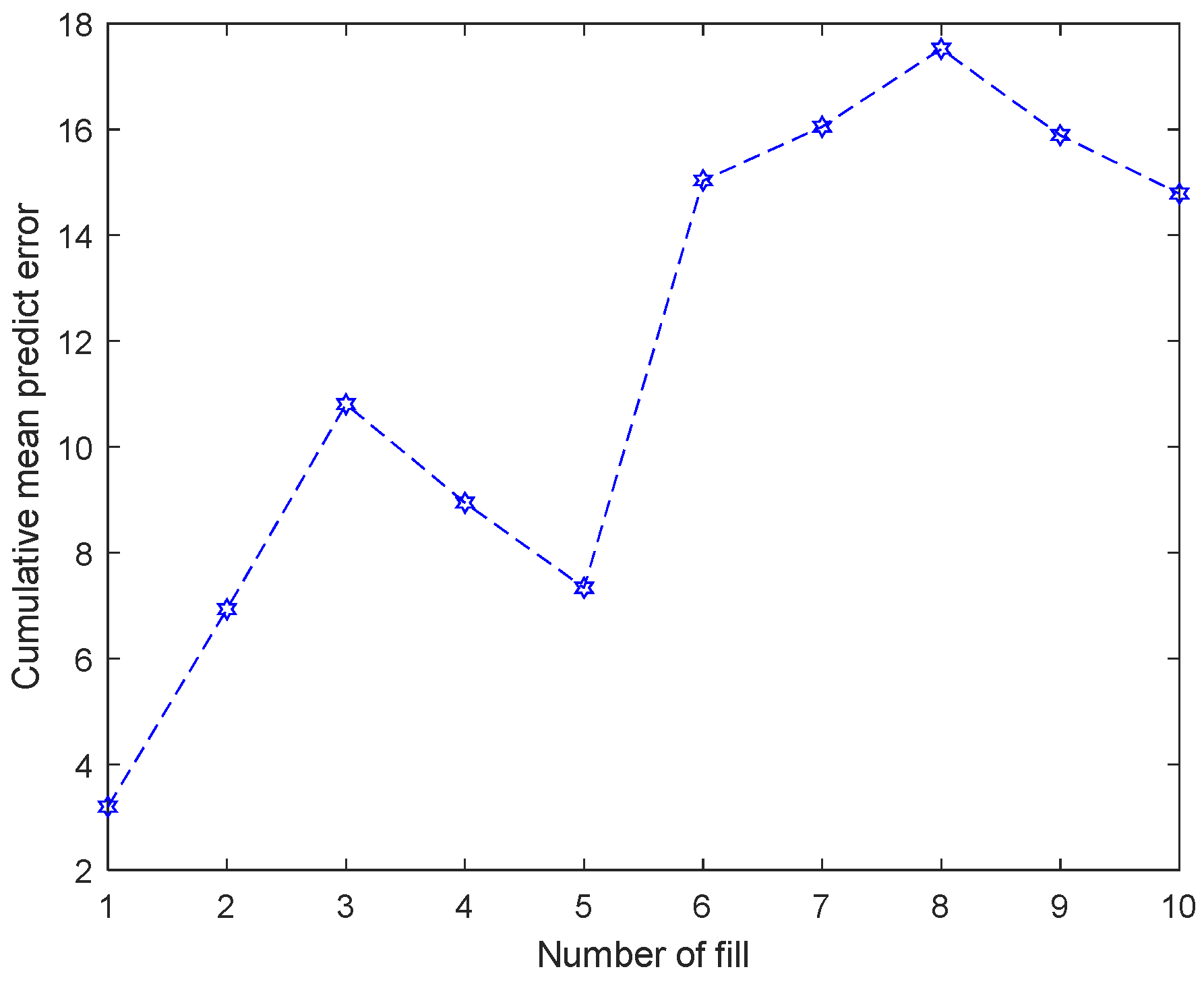
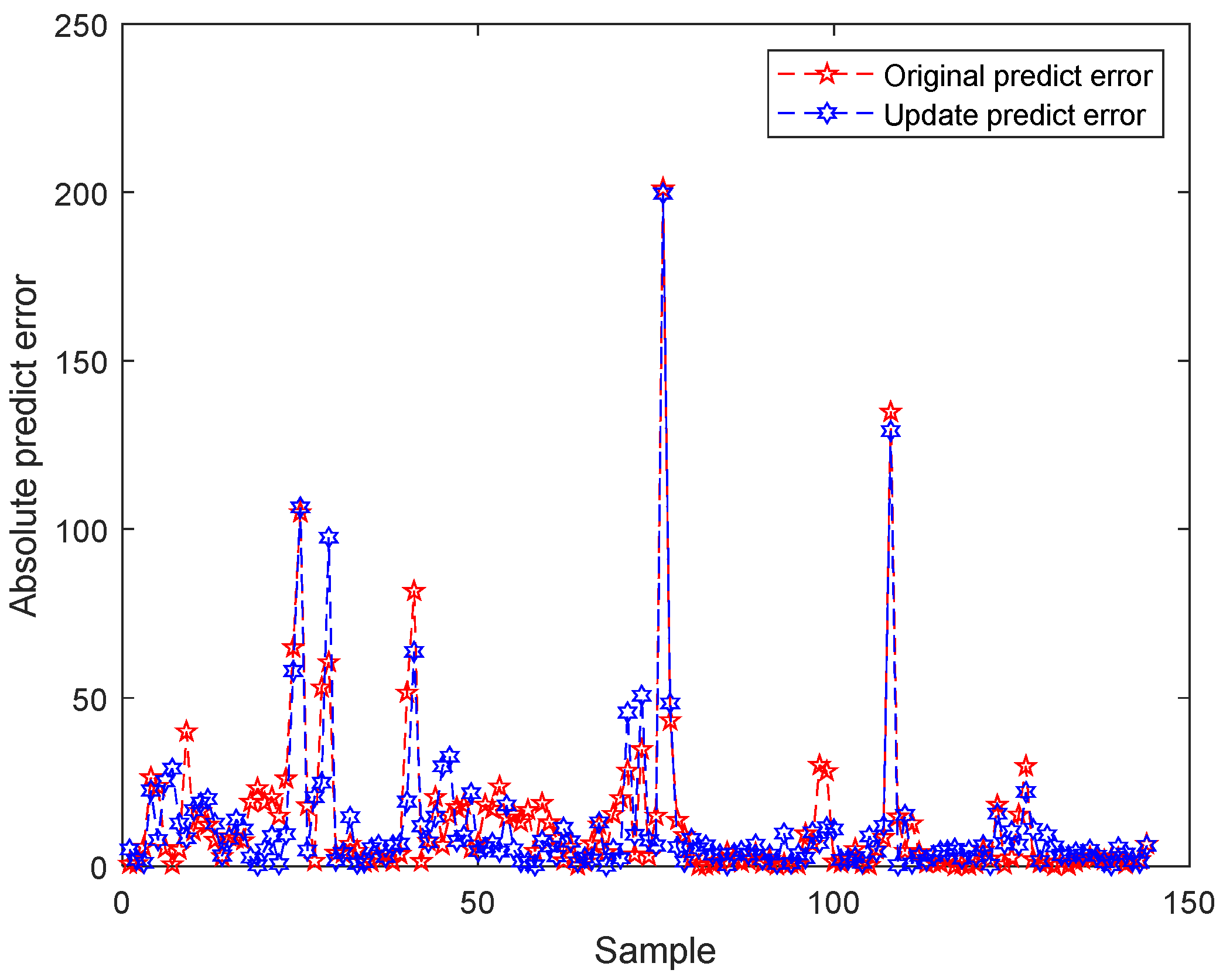
3.2.3. Data Set and Model Update
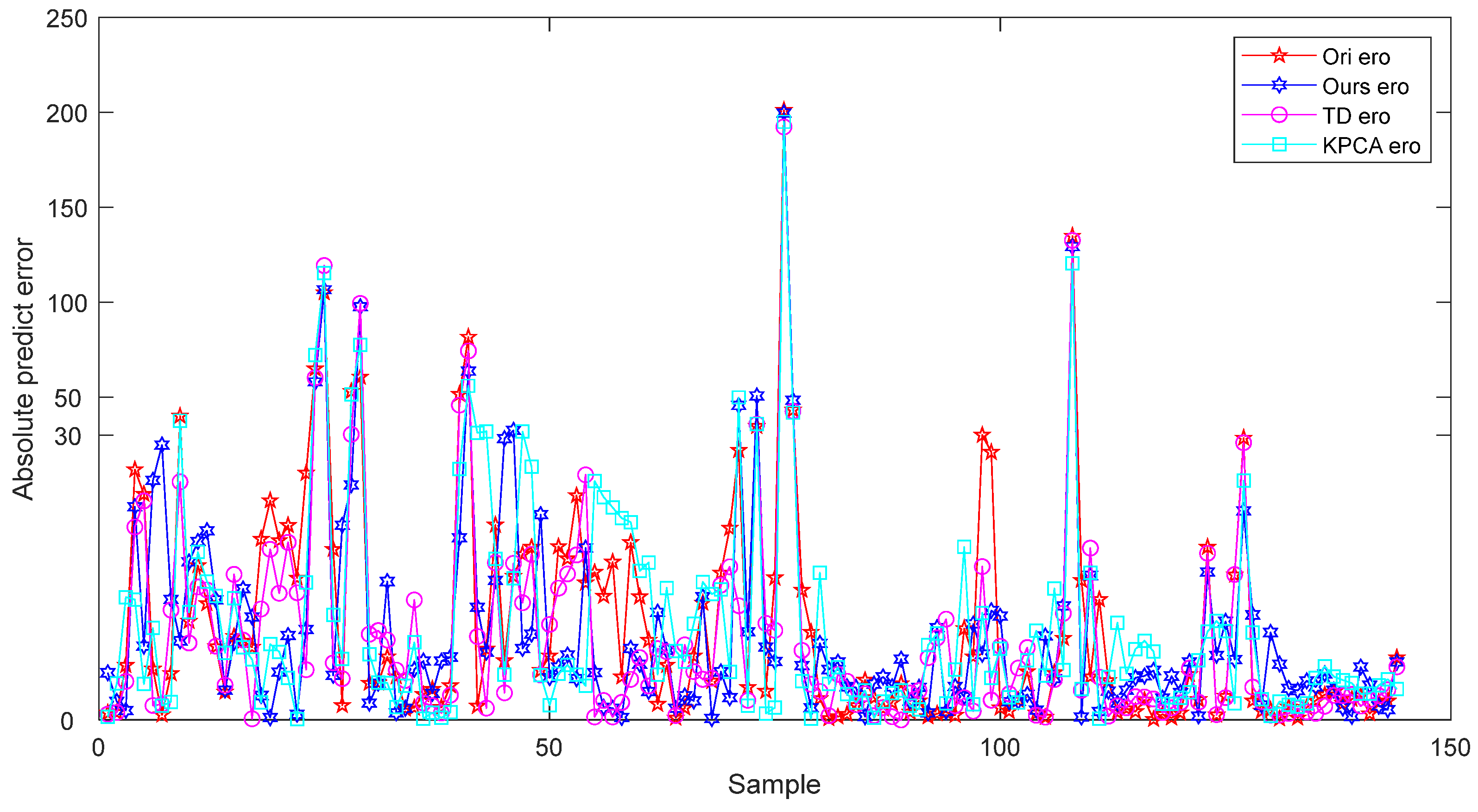
3.3. Method Comparison
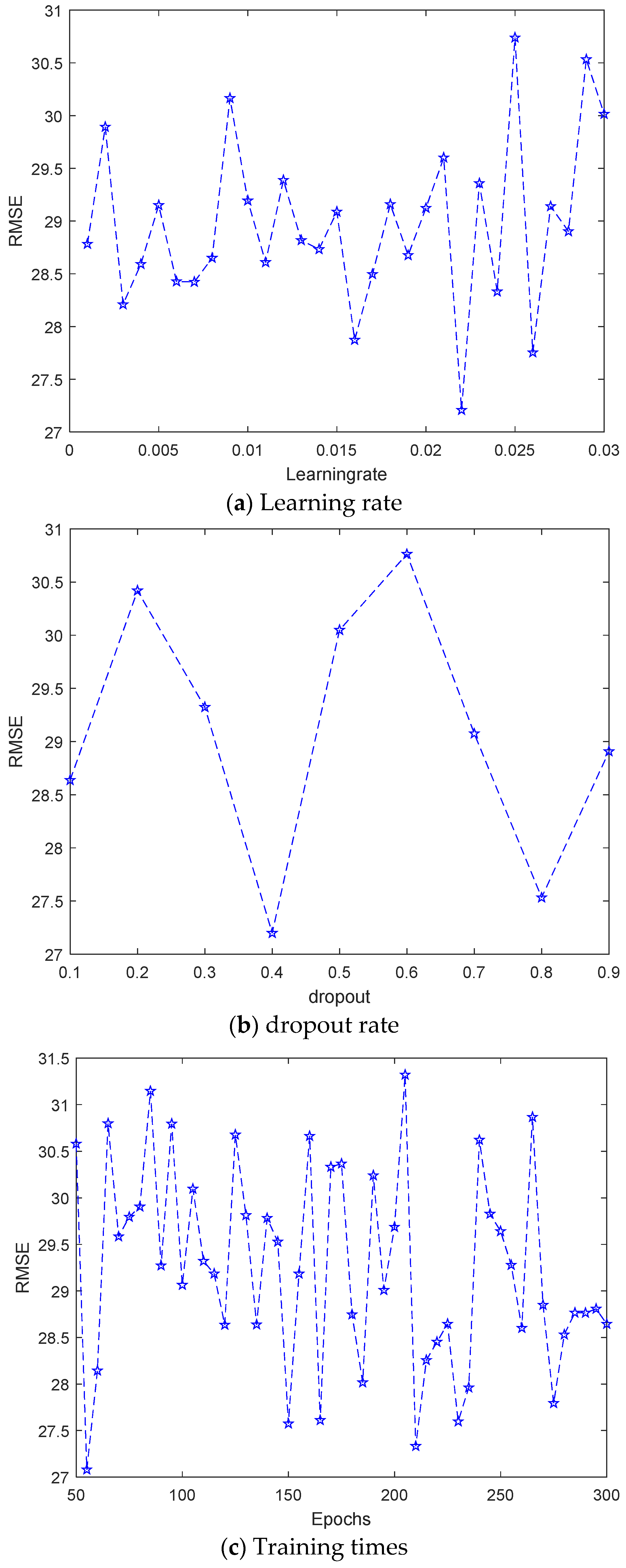
3.4. Hyperparameter Analysis
- (1)
- Learning rate: increasing this value can make the prediction model better fit the training data, and its change will cause fluctuations in the model performance, and 0.022 is preferable;
- (2)
- Dropout rate: both the training and test accuracy fluctuate within a small range with the change in this value, which is set to 0.4 in this article;
- (3)
- Training times: the predictive performance of the model is slightly worse with the increase in this value, and the model has the best performance when its value is 210;
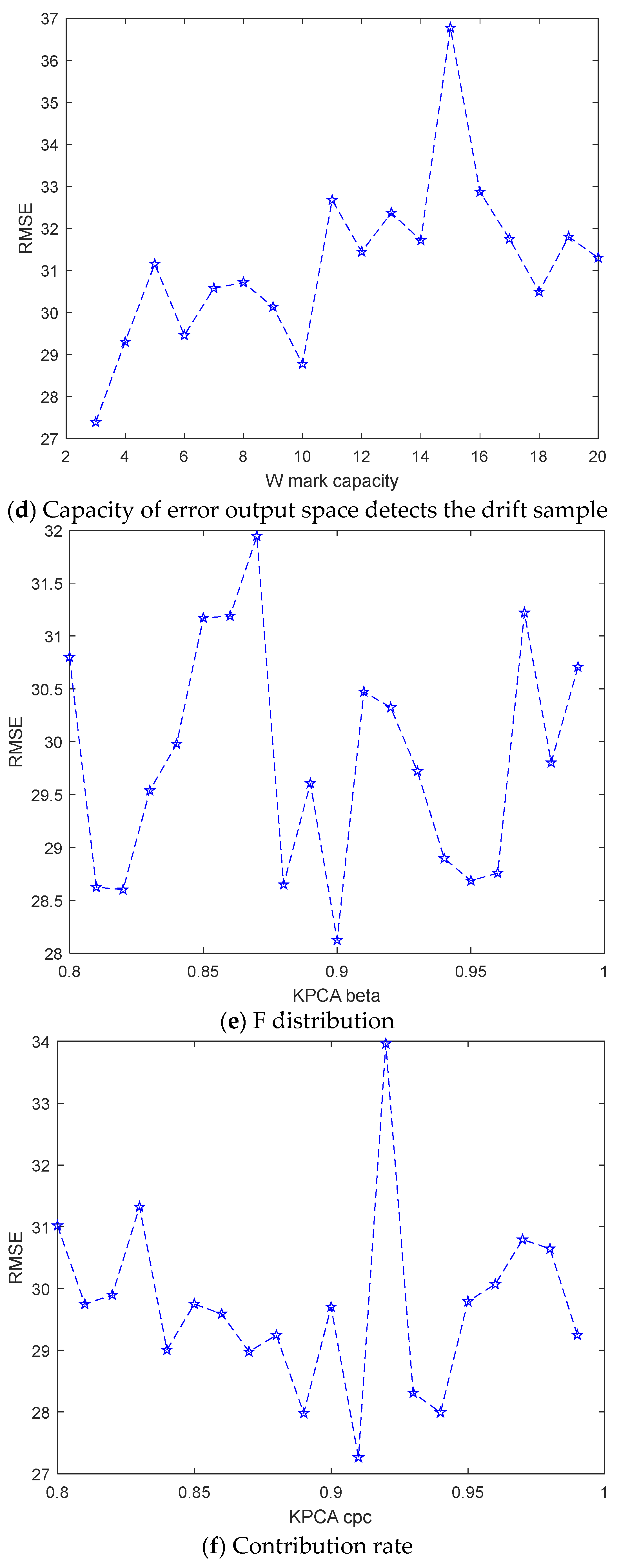
- (4)
- The capacity of error output space detects the drift sample: the prediction performance of the model is slightly worse with the increase in this value, which is set to 3 in this article;
- (5)
- F distribution: With the setting of the F distribution rate, the model performance fluctuates greatly. In order to ensure the modeling performance, 0.9 is preferred;
- (6)
- Contribution rate: the smaller the number of selected features, the more appropriate contribution rate should be selected, which is 0.91 in this article.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbol | Meaning |
| LSTM model built on the basis of historical data is also the prediction model used when there is no drift | |
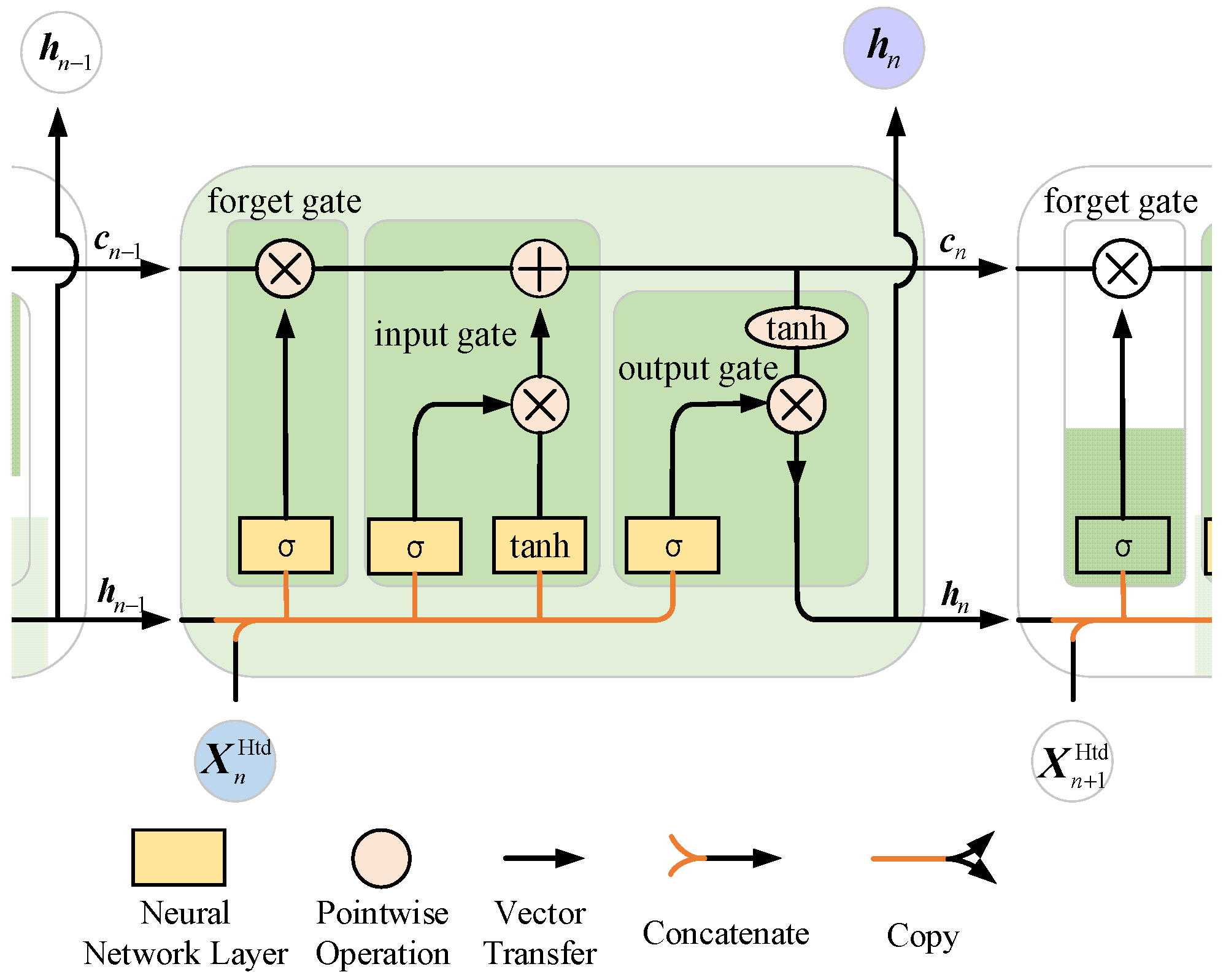
| The sample serves as the input to the LSTM | |
| LSTM hidden layer output of the sample | |
| LSTM output status information of the sample | |
| Sigmoid activation function | |
| Hadamard product | |
| Tanh activation function | |
| , , , | Weights of the forgetting gate, input gate and output gate correspond to , respectively |
| , , , | Weights of the forgetting gate, input gate and output gate correspond to , respectively |
| , , , | Corresponding offset of the forgetting gate, input gate, and output gate, respectively |
| , , | Output vector value of the sample forgetting gate, input gate and output gate |
| , | Output of the sample input gate and forget gate |
| Input status information for the sample | |
| Weight corresponding to | |
| Error of feedback | |
| Actual value of the sample | |
| Predicted value of the output of the sample | |
| Learning rate of LSTM model | |
| , | Loss function corresponds to finding the partial derivative of and |
| LSTM updated output gate weights | |
| LSTM offline model for CO concentration prediction results | |
| Number of data dimensions after high-dimensional mapping | |
| KPCA trains the kernel function of the model | |
| Tanh function | |
| , | Sigmoid parameter in the kernel function |
| 1 matrix of size | |
| Kernel matrix after centralizing | |
| Eigenvector matrix | |
| Diagonal matrices, each element on the diagonal is an eigenvalue | |
| Normalized matrix | |
| Eigenvector | |
| Cumulative characteristic contribution rate | |
| PCA contribution threshold | |
| Number of selected principal components | |
| Matrix of size in | |
| Nonlinear principal component matrix, matrix of size | |
| F distribution with and degrees of freedom | |
| Normal deviation from the upper percentile | |
| One control limit | |
| One control limit | |
| Historical concept drift detection model | |
| Historical sample set | |
| , | Feature space of the sample |
| , | True value of the sample |
| , | Set of first-order difference components |
| Test data set | |
| Kernel function of KPCA test model | |
| 1 matrix of size | |
| Matrix after centralization | |
| Kernel matrix after centralizing | |
| Nonlinear principal component matrix | |
| One of the drift indicators of the sample in the window | |
| One of the drift indicators of the sample in the window | |
| Cache window filtered by KPCA and to be labeled is filled with the sample set in the window | |
| w | Default cache window sample size |
| Truth value | |
| Feature space | |
| , | First-order difference component |
| Output space difference component | |
| Pseudo-truth value of | |
| Likelihood ratio statistics | |
| Distribution density function of the standard normal distribution | |
| Drift sample follows normal distribution with a mathematical expectation of | |
| Mean of all historical observations at the previous t−1 moment | |
| Difference between the current Obs(t) and the mean historical observations | |
| PHt | Change index |
| Minimum cumulative variable value recorded in all current moments | |
| Sample average measurement error in the current window | |
| True value of the m th sample in the window | |
| Pseudo-truth value of the m-th sample in the window | |
| Sample in the cache window when it is filled for the d-th time | |
| One of the updated controls | |
| One of the updated controls | |
| Updated historical concept drift detection model | |
| LSTM model based on updated data |
References
- Shen, X.; Pan, H.; Ge, Z.; Chen, W.; Song, L.; Wang, S. Energy-efficient multi-trip routing for municipal solid waste collection by contribution-based adaptive particle swarm optimization. Complex Syst. Model. Simul. 2023, 3, 202–219. [Google Scholar] [CrossRef]
- Butt, O.M.; Bibi, S.; Ahmad, M.S.; Che, H.S.; Zahid, T.; Bibi, S.; Abd Rahim, N. Hydrogen as potential primary energy fuel for municipal solid waste incineration for a sustainable waste management. IEEE Access 2022, 10, 114586–114596. [Google Scholar] [CrossRef]
- Cheng, G.; Zhang, M.N.; Zhang, Y.H.; Lin, B.; Zhan, H.J.; Zhang, H.J. A novel renewable collector from waste fried oil and its application in coal combustion residuals decarbonization. Fuel 2022, 323, 124388. [Google Scholar] [CrossRef]
- Kaza, S.; Yao, L.; Bhada-Tata, P.; Van Woerden, F. What a Waste 2.0: A Global Snapshot of Solid Waste Management to 2050; World Bank Publications: Chicago, IL, USA, 2018. [Google Scholar]
- Chen, A.; Chen, J.R.; Cui, J.; Fan, C.; Han, W. Research on risks and countermeasures of "Cities Besieged by Waste" in China—An empirical analysis based on DIIS. Bull. Chin. Acad. Sci. 2019, 34, 797–806. [Google Scholar]
- Gómez-Sanabria, A.; Kiesewetter, G.; Klimont, Z.; Schoepp, W.; Haberl, H. Potential for future reductions of global GHG and air pollutants from circular waste management systems. Nat. Commun. 2022, 13, 106. [Google Scholar] [CrossRef]
- Bharadwaj, K.; Bharadwaj, K.; Das, K.K. Segregation of municipal solid waste based on their biodegradability using spectroscopy sensor. IEEE Sens. Lett. 2024, 8, 5503004. [Google Scholar] [CrossRef]
- Liang, X.; Kurniawan, T.A.; Goh, H.H.; Zhang, D.; Dai, W.; Liu, H.; Othman, M.H.D. Conversion of landfilled waste-to-electricity (WTE) for energy efficiency improvement in Shenzhen (China): A strategy to contribute to resource recovery of unused methane for generating renewable energy on-site. J. Clean. Prod. 2022, 369, 133078. [Google Scholar] [CrossRef]
- Wang, H.; Yang, X.; Meng, L.; Yin, X.; Wang, Z.; Wang, Z.; Wang, Y. Transportation Route Optimization of Municipal Solid Waste based on Improved Ant Colony Algorithm in Internet of Vehicles. IEEE Trans. Veh. Technol. 2024; Early Access. [Google Scholar] [CrossRef]
- Bajić, B.Ž.; Dodić, S.N.; Vučurović, D.G.; Dodić, J.M.; Grahovac, J.A. Waste-to-energy status in Serbia. Renew. Sustain. Energy Rev. 2015, 50, 1437–1444. [Google Scholar] [CrossRef]
- Kalyani, K.A.; Pandey, K.K. Waste to energy status in India: A short review. Renew. Sustain. Energy Rev. 2014, 31, 113–120. [Google Scholar] [CrossRef]
- Kumar, A.; Samadder, S.R. A review on technological options of waste to energy for effective management of municipal solid waste. Waste Manag. 2017, 69, 407–422. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.K.; Tang, J.; Xia, H.; Wang, T.Z.; Gao, B.Y. Non-manipulated variable sensitivity analysis of solid phase combustion in MSWI process furnace based on double orthogonal numerical simulation experiment. Sustainability 2023, 15, 14159. [Google Scholar] [CrossRef]
- Chen, N.; Zhou, J.Q.; Gui, W.H.; Yang, C.H.; Dai, J.Y. Two-layer optimal control for goethite iron precipitation process. Control Theory Appl. 2020, 37, 222–228. [Google Scholar]
- Jammeli, H.; Ksantini, R.; Abdelaziz, F.B.; Masri, H. Sequential artificial intelligence models to forecast urban solid waste in the city of Sousse, Tunisia. IEEE Trans. Eng. Manag. 2021, 70, 1912–1922. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, C.; Liu, Z.; Tan, J.; Ahmat, M. Temporal Double Graph Convolutional Network for CO and CO2 Prediction in Blast Furnace Gas. IEEE Trans. Instrum. Meas. 2023, 73, 2502113. [Google Scholar]
- Zhou, K.; Chen, X.; Wu, M.; Du, S.; Hu, J.; Nakanishi, Y. A new Co/Co2 prediction model based on labeled and unlabeled process data for sintering process. IEEE Trans. Ind. Inform. 2020, 17, 333–345. [Google Scholar] [CrossRef]
- Wang, B.; Wang, P.; Xie, L.H.; Lin, R.B.; Lv, J.; Li, J.R.; Chen, B. A stable zirconium based metal-organic framework for specific recognition of representative polychlorinated dibenzo-p-dioxin molecules. Nat. Commun. 2019, 10, 3861. [Google Scholar] [CrossRef]
- Oliveira, G.; Minku, L.L.; Oliveira, A.L. Tackling virtual and real concept drifts: An adaptive Gaussian mixture model approach. IEEE Trans. Knowl. Data Eng. 2021, 35, 2048–2060. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Y.; Yang, C.; Leung, H.; Yin, X. Adaptive Attention-Driven Manifold Regularization for Deep Learning Networks: Industrial Predictive Modeling Applications and Beyond. IEEE Trans. Ind. Electron. 2024, 7, 13439–13449. [Google Scholar] [CrossRef]
- Wang, X.; Kang, Q.; Zhou, M.; Pan, L.; Abusorrah, A. Multiscale drift detection test to enable fast learning in nonstationary environments. IEEE Trans. Cybern. 2020, 51, 3483–3495. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, G.; Li, S.; Yang, L.; Chen, S. Model framework to quantify the effectiveness of garbage classification in reducing dioxin emissions. Sci. Total Environ. 2022, 814, 151941. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Tang, J.; Xia, H.; Pan, X.; Yu, W.; Qiao, J. CO emission predictions in municipal solid waste incineration based on reduced depth features and long short-term memory optimization. Neural Comput. Appl. 2024, 36, 5473–5498. [Google Scholar] [CrossRef]
- Zhang, R.; Tang, J.; Xia, H.; Qiao, J. CO emission modeling based on fixed-window drift detection for the municipal solid waste incineration process. J. Beijing Univ. Technol. 2023, accepted. [Google Scholar]
- Zhang, R.; Tang, J.; Xia, H.; Chen, J.; Yu, W.; Qiao, J. Heterogeneous ensemble prediction model of CO emission concentration in municipal solid waste incineration process using virtual data and real data hybrid-driven. J. Clean. Prod. 2024, 445, 141313. [Google Scholar] [CrossRef]
- Wang, T.; Tang, J.; Xia, H.; Yang, C.; Yu, W.; Qiao, J. Data-driven multi-objective optimal control of municipal solid waste incineration process. Eng. Appl. Artif. Intell. 2024, 137, 109157. [Google Scholar] [CrossRef]
- Li, G.; Yu, Z.; Yang, K.; Lin, M.; Chen, C.P. Exploring Feature Selection With Limited Labels: A Comprehensive Survey of Semi-Supervised and Unsupervised Approaches. IEEE Trans. Knowl. Data Eng. 2024; Early Access. [Google Scholar] [CrossRef]
- Yang, Z.; Al-Dahidi, S.; Baraldi, P.; Zio, E.; Montelatici, L. A novel concept drift detection method for incremental learning in nonstationary environments. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 309–320. [Google Scholar] [CrossRef]
- Frias-Blanco, I.; del Campo-Ávila, J.; Ramos-Jimenez, G.; Morales-Bueno, R.; Ortiz-Diaz, A.; Caballero-Mota, Y. Online and non-parametric drift detection methods based on Hoeffding’s bounds. IEEE Trans. Knowl. Data Eng. 2014, 27, 810–823. [Google Scholar] [CrossRef]
- Mahdi, O.A.; Pardede, E.; Ali, N.; Cao, J. Diversity measure as a new drift detection method in data streaming. Knowl.-Based Syst. 2020, 191, 105227. [Google Scholar] [CrossRef]
- Qi, G.J.; Luo, J. Small data challenges in big data era: A survey of recent progress on unsupervised and semi-supervised methods. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 2168–2187. [Google Scholar] [CrossRef]
- Peng, X.; Duan, S.; Sankavaram, C.; Jin, X. Unsupervised Adaptive Fleet Battery Pack Fault Detection with Concept Drift Under Evolving Environment. IEEE Trans. Autom. Sci. Eng. 2024, 21, 2276–2288. [Google Scholar] [CrossRef]
- Kaib, M.T.H.; Kouadri, A.; Harkat, M.F.; Bensmail, A.; Mansouri, M. Improvement of Kernel Principal Component Analysis-Based Approach for Nonlinear Process Monitoring by Data Set Size Reduction Using Class Interval. IEEE Access 2024, 12, 11470–11480. [Google Scholar] [CrossRef]
- Lughofer, E.; Weigl, E.; Heidl, W.; Eitzinger, C.; Radauer, T. Recognizing input space and target concept drifts in data streams with scarcely labeled and unlabelled instances. Inf. Sci. 2016, 355, 127–151. [Google Scholar] [CrossRef]
- Ji, J.; Wang, H.; Chen, K.; Liu, Y.; Zhang, N.; Yan, J. Recursive Weight. Kernelregression Semi-Supervised Soft-Sens. Model. Fed-Batch Process. J. Taiwan Inst. Chem. Eng. 2012, 43, 67–76. [Google Scholar] [CrossRef]
- Ge, Z.; Song, Z. Semisupervised Bayesian Method Soft Sens. Model. Withunlabeled Data Samples. AIChEJournal 2011, 57, 2109–2119. [Google Scholar]
- Zhu, J.; Ge, Z.; Song, Z. Robust semi-supervised mixture probabilistic principalcomponent regression model development and application to soft sensors. J. Process Control. 2015, 32, 25–37. [Google Scholar] [CrossRef]
- Vilardi, G.; Verdone, N. Exergy analysis of municipal solid waste incineration processes: The use of O2-enriched air and the oxy-combustion process. Energy 2022, 239, 122147. [Google Scholar] [CrossRef]
- Korpela, T.; Kumpulainen, P.; Majanne, Y.; Häyrinen, A.; Lautala, P. Indirect NOx emission monitoring in natural gas fired boilers. Control Eng. Pract. 2017, 65, 11–25. [Google Scholar] [CrossRef]
| Input: Data set XHtd, XOtd Output: |
| Set the parameters of the LSTM model and train the offline model; |
| Set KPCA model parameters, select sigmoid kernel function, F distribution, contribution rate; |
| Calculate the kernel matrix; |
| Centralize the kernel matrix; |
| Make the eigenvalue decomposition and the eigenvector normalization; |
| Calculate the nonlinear principal component; |
| Calculate control limit of statistical index and ; |
| Construct the offline KPCA model ; |
| For n = 1 to Ntest |
| Based on , the predicted value for each sample is obtained; |
| KPCA method is used to calculate the online statistical index and of the sample; |
| Determine whether the sample has drifted; |
| If drift occurs, |
| Store the sample in the cache window to be marked; |
| Check whether the cache window has reached its capacity; |
| If capacity is reached |
| Storage exception sample number; |
| Calculate the first-order difference component of the new sample; |
| Query the d difference components of the training set that are closest to the difference component of the new sample; |
| Mark the pseudo-truth value of the sample in the window; |
| Calculate the sum of sample errors in the current window; |
| Calculate the cumulative average forecast error so far in the current window; |
| The difference between the current cumulative average forecast error and the last cumulative average forecast error; |
| Judgment drift; |
| If drift occurs, the drift monitoring index and LSTM model are updated; |
| If no drift occurs, the next sample continues to be predicted using ; end end |
| end |
| Predicted value of all samples after all loops is denoted as . |
| Detection Algorithm | Model Update Times | Update the Required Number of Truth Values | Model Prediction RMSE | Method |
|---|---|---|---|---|
| Unsupervised type | 30 | 30 | 26.9249 | Truth update is required |
| Supervised type | 0 | 0 | 26.9690 | Truth detection and updating are required |
| Textual algorithm | 10 | 10 | 26.9444 | Using pseudo-truth updates |
| Hyperparameter | Radius |
|---|---|
| Learning rate | 0.001:0.001:0.03 |
| dropout rate | 0.1:0.1:0.9 |
| Training times | 50:5:350 |
| Capacity of error output space detects the drift sample | 3:1:20 |
| F distribution | 0.80:0.01:0.99 |
| Contribution rate | 0.80:0.01:0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Tang, J.; Wang, T. CO Emission Prediction Based on Kernel Feature Space Semi-Supervised Concept Drift Detection in Municipal Solid Waste Incineration Process. Sustainability 2025, 17, 5672. https://doi.org/10.3390/su17135672
Zhang R, Tang J, Wang T. CO Emission Prediction Based on Kernel Feature Space Semi-Supervised Concept Drift Detection in Municipal Solid Waste Incineration Process. Sustainability. 2025; 17(13):5672. https://doi.org/10.3390/su17135672
Chicago/Turabian StyleZhang, Runyu, Jian Tang, and Tianzheng Wang. 2025. "CO Emission Prediction Based on Kernel Feature Space Semi-Supervised Concept Drift Detection in Municipal Solid Waste Incineration Process" Sustainability 17, no. 13: 5672. https://doi.org/10.3390/su17135672
APA StyleZhang, R., Tang, J., & Wang, T. (2025). CO Emission Prediction Based on Kernel Feature Space Semi-Supervised Concept Drift Detection in Municipal Solid Waste Incineration Process. Sustainability, 17(13), 5672. https://doi.org/10.3390/su17135672






