Abstract
The ecological value of cultivated land carries clear intergenerational implications, requiring a fair allocation mechanism across the full life cycle to address market failures caused by intergenerational externalities. This study constructs an intergenerational allocation model of cultivated land ecological value based on the Diamond framework. The intra-generational consumption elasticity coefficient is derived using the Tapio decoupling theory, with the ratio of cultivated land quantity change to per capita net income change as the core indicator. Statistical data from Lezhi County (1984–2022) are used for empirical analysis. The fitted elasticity coefficient shows a steady decline and eventually converges to zero, indicating a weakening willingness of the current generation to consume ecological value, thus supporting the logic of preserving value for future generations. A simplified Pearl growth curve is then used to construct the development stage coefficient, representing the evolving realization of ecological value among future generations. Engel coefficient forecasts based on the GM(1,1) model enable year-by-year estimation of ecological value allocation to future generations. The results show that (1) the ecological value of cultivated land in Lezhi County is estimated at CNY 65,498,230/ha, (2) the proposed model effectively simulates intergenerational value allocation, (3) decoupling theory supports the hypothesis of equal intergenerational sharing, and (4) the development stage coefficient curve provides a dynamic perspective on long-term ecological value realization. This research offers a data-driven modeling approach that enhances both the fairness and the efficiency of land governance, contributing methodological support for sustainable cultivated land protection and ecological compensation policies.
1. Introduction
Cultivated land is a foundational resource for ensuring food security and a critical ecological asset for delivering ecosystem services and maintaining environmental stability [1]. As urbanization accelerates and land use intensity continues to rise, the ecological value of cultivated land (EVCL) is gaining increasing attention [2]. Against the backdrop of mounting tensions between land supply and demand, achieving intergenerationally fair allocation of EVCL has become a pressing challenge in the pursuit of sustainable land use.
In the fields of environmental economics and resource management, intergenerational equity has long been a focus of academic discourse [3,4]. Most studies are stuck in normative analysis and lack actionable quantitative tools and dynamic assessment frameworks. Although advancements have been made in ecological compensation [5], ecosystem service monetization [6], and stage-based valuation [7], few studies have adopted a full life-cycle perspective to systematically model the evolutionary trajectory and intergenerational transmission mechanisms of EVCL. This gap undermines the ability to coordinate fairness and sustainability in cultivated land governance.
To address this deficiency, this study develops a quantitative intergenerational allocation framework for EVCL based on the principle of “immediate benefits for current generations and gradual ecological returns for future generations”. By integrating an overlapping generations model and a modified Pearl growth curve, the study simulates the evolution of ecological awareness and willingness to pay over time, enabling a dynamic representation and allocation of ecological value across temporal dimensions. Compared with static or stage-based valuation approaches, this framework captures the cumulative nature of ecological returns and offers a basis for tracing the intergenerational transfer of value, thereby enhancing the model’s policy relevance and practical applicability.
This research aligns with the United Nations Sustainable Development Goals (SDGs), particularly Goal 15 (“Life on Land”) and Goal 10 (“Reduced Inequalities”) [8]. Through dynamic modeling of ecological payment willingness and value realization, this study provides empirical support for the sustained provision of cultivated land ecosystem services and equitable resource transfer across generations. It contributes to the development of a forward-looking cultivated land governance framework centered on intergenerational responsibility, and facilitates the integration of land policy with ecological valuation systems—offering theoretical and practical pathways for balancing equity, efficiency, and sustainability in resource allocation.
The remainder of this paper is organized as follows: Section 2 reviews the relevant literature; Section 3 conducts a theoretical analysis and presents the theoretical framework of this study; Section 4 constructs a model to calculate the ecological value of cultivated land in Lezhi County; Section 5 introduces the intergenerational overlapping model to allocate the ecological value of cultivated land between the present and future generations; Section 6 allocates the ecological value of cultivated land for future generations based on the Pearl growth curve formula; Section 7 discusses the allocation results, highlights the limitations of this study, and proposes directions for future research; and Section 8 summarizes the paper and synthesizes the research conclusions.
2. Literature Review
In the field of cultivated land ecological value assessment, current studies primarily focus on constructing ecological compensation mechanisms, monetizing ecosystem functions, and evaluating staged ecological services [5,6,7]. These studies often emphasize the immediate economic value of ecosystem services from an intra-generational perspective, while overlooking the inherently intergenerational nature of cultivated land as a limited and essentially non-renewable resource [9]. The challenge of how to equitably allocate ecological benefits across generations remains insufficiently addressed, and a systematic theoretical framework to capture this intergenerational dimension is still lacking.
In environmental economics and resource allocation studies, discussions on intergenerational equity and sustainability have long existed [10,11,12,13]. Early normative studies, such as those by Solow [14] and Hartwick [15], laid the theoretical foundation for intergenerational allocation of non-renewable resources, emphasizing the responsibility of the present generation to preserve resources for future welfare. These normative analyses later evolved into more formal economic models, such as the overlapping generations framework and intergenerational wealth transfer models [16,17], which attempted to quantitatively assess the impact of resource use on future generations. However, most of these models remain abstract and static, with limited empirical application in land use policy and ecological valuation.
In recent years, some studies have introduced dynamic parameters to reflect how stages of socio-economic development influence ecological payment willingness [18,19]. For instance, Li Jinchang et al. proposed constructing a development stage coefficient based on the reciprocal of the Engel coefficient and incorporated it into a modified Pearl growth curve to depict the gradual realization of ecological value across different stages of societal development [20]. While this approach offers a novel quantitative tool, its focus remains on intra-generational value distribution and does not yet capture the intergenerational transmission of ecological value.
In summary, although existing literature has made progress in ecological compensation and value monetization, the issue of intergenerational allocation of EVCL remains underdeveloped, particularly in terms of combining theoretical modeling with parameter estimation. This study aims to address this gap by constructing a lifecycle-based quantitative model that integrates both intra- and intergenerational dimensions, simulating the dynamic evolution of ecological value recognition and willingness to pay. By combining theoretical modeling with empirical parameterization, the study seeks to support more equitable and sustainable land governance. This study contributes to bridging the gap between intergenerational normative theories and practical ecological valuation, offering a dynamically evolving and data-driven ecological value allocation framework, which provides applicable modeling ideas and operational paths for the sustainable management of cultivated land.
3. Theoretical Framework
Assuming that the intergenerational distribution of “the current value of the current generation is reflected in the present period, and the value of the future generation is reflected gradually”, based on a case study of Lezhi County, this study calculates the EVCL in the study area, deduces the formula used to determine the ecological value of the land allocated to current and future generations, and then implements said formula to complete the intergenerational distribution process. In this manner, the gradual distribution and the EVCL distributed by future generations are successfully calculated. The specific research pathway is shown in Figure 1.
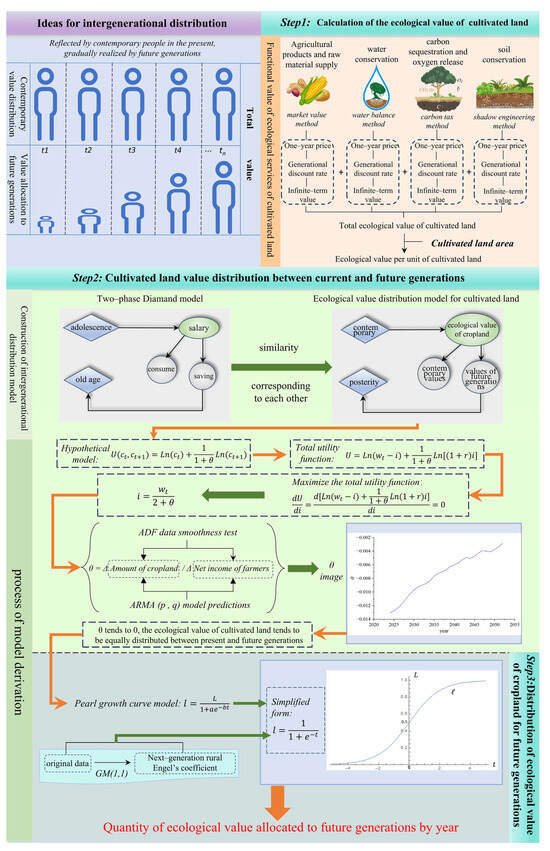
Figure 1.
Theoretical framework.
4. Measurement of EVCL in Lezhi County
4.1. Overview of the Study Area
Lezhi County is located in the central part of Sichuan Basin, on the watershed of Tuojiang River and Fujiang River, longitude 104°45′2″–105°15′2″ E and latitude 30°0′2″–30°30′4″ N, comprising a total area of 1425 square kilometers. The terrain is dominated by shallow hills and has a subtropical monsoon climate with an average annual temperature of 17.1 °C and annual precipitation of approximately 923.3 mm. Lezhi County has a total household population of 774,400, of which 123,800 people live in an urban setting, while 656,600 are located in rural areas. It has an agriculture-based economy, producing grain and oil crops such as rice, wheat, and corn, with rice cultivation being the dominant agricultural activity. In 2022, the county’s cultivated land area comprised 75,336.09 hectares, of which 23,068.63 hectares were paddy fields, 3 hectares were watered land, 42,558.75 hectares were dry land, and 9705.71 hectares were field canopies [21]. In 1992, Lezhi County was listed as one of the 20 pilot bases of the first batch of “sustainable agriculture and rural development research” in China; since then, it has been the focus of a great deal of theoretical exploration. Determining the intergenerational distribution of EVCL is an important aspect of the research on sustainable agriculture and rural development in this area, with demonstrable value, hence the popularization of this topic.
4.2. Calculation Approach for the EVCL in Lezhi County
EVCL refers to the natural attributes carried by cultivated land within the ecosystem and its positive effects on the ecological environment, reflected in its comprehensive functions that maintain ecological stability and support sustainable development [22]. It can be reflected by its ecological service function value. Based on the Millennium Ecosystem Assessment framework [23], this research reflects the EVCL in Lezhi County based on its ecosystem service functions, which include supplying agricultural products and raw materials, conserving water, sequestering carbon, and releasing oxygen. We calculate the one-year value of each ecosystem service function, discount each one-year value to an unlimited value and sum it up [24], then divide it by the area of cultivated land to determine the EVCL per unit area in Lezhi County. The price calculations involved are all based on the 1990 constant price.
4.3. Measurement of One-Year EVCL in Lezhi County
4.3.1. Measurement of Supply Value of Agricultural Products and Raw Materials
The supply value of agricultural products and raw materials obtained from cultivated land is represented by the market value method, which considers the net output value of agricultural products and raw materials [25]. The total output value listed in the 2022 Lezhi County Statistical Yearbook, based on the collective output of agriculture, forestry, animal husbandry, and fishery services, and the supply value of agricultural products and raw materials obtained from the cultivated land, is CNY 3343.4 million [22].
4.3.2. Measurement of Water Source Storage Value
The water balance method is used to calculate the water supply storage value of the cropland within the study area [26,27], based on Formulas (1) and (2):
C = (E-F) × A
Vw = C × Pw
In Equation (1), C is the water conservation volume (m3/a), E is the average annual precipitation (mm/a), F is the average evapotranspiration (mm/a), (E-F) represents the height of cultivated land for water storage (m), and A is the area of cultivated land (m2). Cultivated land in China can currently be divided into three categories: paddy fields, dry land, and watered land. The water supply and storage function of paddy fields hold greater significance, while the function of dry land and watered land is not obvious; thus, only the water supply value of paddy fields is calculated. The water storage height of paddy fields in China is 0.2 m. The 2022 land use status quo change survey conducted in Lezhi County reported that paddy fields covered an area of 23,068.63 hectares.
In Equation (2), Vw represents the one-year value of water source conservation for cultivated land, C is the amount of water conserved (m3/a), and Pw is the unit water price (CNY/m3). The unit water price Pw is calculated by the shadow engineering method, using the cost of CNY 0.67 (1990 constant price) per 1 m3 reservoir constructed in China as the shadow price of the unit water price. The one-year value of water supply storage for cultivated land in Lezhi County in 2022 was CNY 3091.196 ten thousand.
4.3.3. Measurement of the Value of Fixed CO2 and Released O2
According to the photosynthesis equation, each gram of dry matter formed by vegetation needs to absorb 1.63 g of CO2 and release 1.19 g of O2. Based on the above calculation standard for CO2 absorption and O2 production by vegetation, the carbon tax method is used to measure the value of fixed CO2 and the quantity of O2 released by vegetation [28]. The specific calculation formulas are shown in Equations (3) and (4):
VC = Q × 1.63 × 0.2729 × 828
VO = Q × 1.19 × 400
In Equation (3), VC is the one-year value of fixed CO2 for cultivated land (CNY/a), Q is the biological yield of cultivated land (tons), and 0.2729 is the proportion of pure carbon in CO2 (C/CO2 = 0.2729). This paper intends to use Sweden’s carbon tax rate as the basis for the calculation of the CO2 fixed value, although Sweden’s carbon tax rate is high; however, it is exemplary for the carbon pricing system on a global scale, and can make the calculation process more standardized and make it easier to interface with other countries. The carbon tax rate in Sweden is 1200/ton of CO2, which is equivalent to CNY 828/ton.
In Equation (4), VO is the one-year value of released O2 (CNY/a), Q is the biological yield of cultivated land (tons), and 400 represents the current price of industrial oxygen (CNY/ton).
The 2022 Lezhi County Statistical Yearbook states that 745,196 tons of grain, oilseed, cotton, hemp, and vegetables were produced on cultivated land in the study area in 2022. After calculation, the value of fixed CO2 was ascertained to be CNY 274.468 million, and the value of released O2 was CNY 354.713 million. The final one-year value of fixed CO2 and released O2 was CNY 629.181 million.
4.3.4. Measurement of Soil and Water Conservation Value
The soil and water conservation value of cropland is generally measured based on three metrics: the reduction in soil erosion [29], reduction in soil nutrient loss [30], and reduction in siltation [31]. These changes are measured using the opportunity cost method, the market value method, and the shadow engineering method, respectively.
- Reduction in soil erosion value
The value of soil erosion reduction in cultivated land in Lezhi County is measured by the opportunity cost method, and the calculation formula is shown in Equation (5):
Ve = E/SC/H × Pr
In Equation (5), Ve is the one-year value of reducing soil erosion (CNY/a), E is the annual soil erosion volume of cultivated land (tons/a), SC is the soil bulk weight (kg/m3), H is the thickness of the topsoil layer of cultivated land (m), and Pr is the average annual return of cultivated land (CNY/(m2·a)). The annual erosion of cultivated land in Lezhi County is 2.673 million tons/a, the soil capacity is 1.22 kg/m3, and the thickness of the topsoil layer of cultivated land is 0.2 m. Dividing the agricultural output value of Lezhi County in 2022 of CNY 3343.4 million with a cultivated land area of 753,360,900 m2, the Pr was obtained as CNY 4.438/m2. It was calculated that the value of soil erosion reduction in Lezhi County for a one-year period was CNY 48,608.602 million.
- 2.
- Reduction in soil nutrient loss value
The value of soil nutrient loss reduction of cultivated land in Lezhi County is measured by the market value method, and the calculation formula is shown in Formula (6):
Vn = R × Ai × Pi
In Equation (6), Vn is the one-year value of reducing soil nutrient loss (CNY/a); R is the annual erosion amount of arable soil (t/a); Ai is the N, P, and K content in the soil; and Pi is the market selling price of N, P, and K. The prices of bicarbonate of ammonia, superphosphate, and potassium nitrate, as well as the prices of N, P, and K, were obtained through the China Fertilizer Network (https://www.fert.cn/). The prices of ammonia bicarbonate, calcium superphosphate, and potassium nitrate, and the proportions and prices of N, P, and K were obtained from the same source. After discounts were applied, the price of N was CNY 162.450/ton, the price of P was CNY 98.400/ton, and the price of K was CNY 1410.682/ton. In Lezhi County soils, the average total nitrogen content was 0.092%, the average total phosphorus was 0.121%, and the average total potassium was 2.397%. The one-year value of reduced soil nutrient loss from cropland was CNY 91.086 million.
- 3.
- Sedimentation reduction value
The sedimentation reduction in cultivated land in Lezhi County is measured by the shadow engineering method, as shown in Equation (7):
Vs = E/SC × 24% × 0.67
In Formula (7), Vs is the one-year value of reducing sediment siltation (CNY/a), and 24% of the sediment eroded by soil in China is generally silted up in reservoirs, rivers, and lakes, so 24% is chosen as the rate of sediment siltation, and CNY 0.67/m3 is the cost of China’s reservoir project (1990 constant price). The one-year value of sediment siltation reduction in cultivated land in Lezhi County was CNY 352.244 million.
- 4.
- Total soil and water conservation value
Summing up the above three values of the reductions in the value of soil erosion, soil nutrient loss, and sedimentation, the total value of soil and water conservation of cultivated land in Lezhi County over the one-year study period is CNY 49,051.932 million.
4.4. Measurement of the EVCL in Lezhi County over an Indefinite Period of Time
4.4.1. Formula for Calculating the EVCL over an Indefinite Period of Time
The capitalized value of resource and environmental goods that can permanently provide net benefits is equal to the annual net benefit divided by the discount rate, and the various infinite-period ecological values of cultivated land can be ascertained based on the one-year value of each item divided by the intergenerational discount rate for each item [32]. The formula is shown in Equation (8):
In Equation (8), Vn is the value of cultivated land for an infinite number of years, v is the value of cultivated land for one year, and r is the intergenerational discount rate.
4.4.2. Determination of Intergenerational Discount Rate
The intergenerational discount rate is a critical parameter in the sustainable management of resources. Its setting not only reflects the current generation’s concern for the ecological welfare of future generations but also pertains to the institutional arrangements for the long-term protection of ecological resources [33]. For ecological services that are non-renewable or irreversible within natural capital, their temporal value should reflect “irreplaceability” and “high irreversibility”. Therefore, the corresponding intergenerational discount rate should be lower than the traditional economic discount rate [34].
Given the variation in realization pathways, degrees of reversibility, and the relationship with technological and economic development, the substitutability between cultivated land ecosystem services and man-made capital must be carefully estimated [35]. Following the principle that “the difficulty of substituting ecological value with man-made capital increases over time, and thus the intergenerational discount rate should decline accordingly” [36], this study employs the Delphi method—using expert surveys to obtain collective judgment—combined with a subjective averaging approach to estimate the intergenerational discount rates for four key categories of cultivated land ecosystem services.
A total of 20 questionnaires were distributed to experts in the fields of land resource management, ecological economics, soil science, and environmental science, with 18 valid responses collected. To ensure the consistency and reliability of expert assessments, only the 15 responses with a standard deviation below 2 were retained for analysis. In Delphi studies, a standard deviation below 2 is generally considered to indicate a high level of consensus among expert opinions [37]. The final intergenerational discount rates were calculated by averaging the values assigned to each ecosystem service category based on these 15 valid responses. The questionnaire content and detailed scoring criteria are provided in Appendix B, and the summarized results are presented in Table 1.

Table 1.
One-year ecological value, intergenerational discount rate, and infinite-year value of cultivated land in Lezhi County.
4.4.3. Measurement of Infinite-Year EVCL
According to the intergenerational discount rate in Formula (8), each one-year ecological value and the corresponding intergenerational discount rate should be discounted to obtain the infinite period value of each ecological value. The total infinite period value of cultivated land in Lezhi County (CNY 9,886,796.206 million) should then be divided by the cultivated land area of Lezhi County (75,336,09 hectares) in 2022. This calculation results in an EVCL in Lezhi County per unit area of CNY 131.236 million/ha (approximately EUR 16,889,456.40/ha, based on the average 2024 exchange rate). The one-year EVCL in Lezhi County, as well as the corresponding intergenerational discount rate and infinite-year value, is shown in Table 1.
5. Present and Future Generation Allocation of EVCL in Lezhi County
5.1. The Introduction of the Intergenerational Overlapping Model
The intergenerational overlapping model is an effective tool for analyzing the intergenerational distribution problem [36]. It can be used to construct a theoretical formula for the distribution of EVCL between present and future generations and to simulate intergenerational distribution.
The intergenerational overlap model describes the effect of monetary value on resource allocation and is a useful tool for studying the allocation of resources at different life stages. The Diamond model simplifies the life cycle of the OLG model into youth and old age [38]. During one’s youth, one labors and allocates the income earned between consumption and savings, with the latter ensuring that one can continue to consume after leaving the workforce. In old age, one does not labor and instead relies upon one’s accumulated savings and interest from previously accrued income. Individual wage income arises only in the youth period, which is a known constant, and consumption decisions do not consider income expectations. The Diamond model internalizes consumption patterns, avoids the income expectations problem, and is simple and mathematically tractable.
The structural assumptions of the Diamond model exhibit strong theoretical compatibility with the intergenerational allocation of EVCL, offering a useful modeling reference for designing intergenerational distribution mechanisms. Originally developed to describe income generation and consumption behavior over an individual’s life cycle, the temporal structure of the Diamond model can be analogized to the logic of allocating ecosystem service values of cultivated land across generations. This study utilizes the Diamond model to construct a formula for the intergenerational distribution of the EVCL, simulating the dynamic transfer process between the present and future generations. This provides a theoretical modeling approach for addressing the intergenerational distribution of ecosystem service values in ecological economics.
As a typical non-renewable resource, cultivated land often undergoes irreversible ecological degradation due to land-use conversion or damage, which results in a form of “one-time” ecological value loss [9]. This characteristic mirrors the structure of the Diamond model, in which individuals receive a one-time wage income during their youth. Accordingly, the EVCL is treated as the model’s “initial income,” serving as the starting point for allocation.
On this basis, the portion of EVCL consumed by the current generation is conceptually analogous to “first-period consumption”, while the share reserved for future generations is equivalent to “second-period savings converted into future consumption”. This structural mapping provides an analytical foundation for modeling the intergenerational distribution of EVCL. It is important to note, however, that this analogy is intended to support the theoretical construction of the model, and does not imply a direct equivalence between EVCL and monetary income or actual payment behavior in real-world contexts.
5.2. Derivation of the Intergenerational Overlapping Model
Diamond developed a two-period utility function for savings and consumption using the overlapping generations model [39], which this study references to describe the dynamic distribution of the ecological value of cultivated land between the present and future generations. The model assumptions are outlined in Equation (9).
In Equation (9), U is the total utility function, ct is the consumption of EVCL of the current generation, ct+1 is the consumption of EVCL of the future generation, and θ is the willingness to consume EVCL of the current generation (0 ≤ θ ≤ 1). Then, the total utility function can be expressed as Equation (10):
In Equation (10), wt is the wage of the current generation, i is the savings of the current generation, (wt − i) is the consumption of the current generation, r is the discount rate of the funds (the savings of the current generation should be used for the consumption of the future generation and should take into account the time value of the funds), and through the treatment of the discount rate, the consumption of the future generation is expressed as (1 + r)i.
The goal of the rational consumer is to maximize the utility function over the life cycle [40]. In order to optimize the consumption utility of current and future generations, it is necessary to maximize the total utility function, i.e., to take the first-order derivative of the savings i in Equation (10) and make its value 0, as shown in Equation (11):
The calculation process as well as the final result are shown in Equation (12):
5.3. Interpretation of the Intergenerational Overlapping Model After Derivation
Equation (12) presents the optimal allocation solution for EVCL derived from the maximization of the intergenerational utility function under the principle of lifecycle optimization. In this result, the meanings of wt, i, and θ remain consistent with prior definitions. The key insight is that the intergenerational allocation coefficient θ is primarily influenced by the current generation’s emphasis on intergenerational equity, thus reflecting its role in adjusting the structure of value distribution.
From an economic perspective, consumption during the youth period (ct) represents the actual utilization of EVCL by the current generation, while savings (i) correspond to the portion of ecological capital preserved for future generations. As future generations are not present in the decision-making process, their EVCL share (ct+1) is incorporated into the preference function of the current generation [41]. Consequently, the portion of ecological value retained for future generations is entirely determined by the savings behavior of the present generation, which is modulated by θ. This model effectively simulates the intergenerational distribution of EVCL and provides theoretical support for the design of intergenerational EVCL allocation mechanisms.
5.4. Present and Future Generation Allocation of EVCL
5.4.1. Selection of Variables
In the preceding section, the intergenerational allocation coefficient θ is defined as the proportion of the EVCL actually received by the present generation, based on a utility maximization framework over the lifecycle. Since θ is difficult to observe directly in practice, this study adopts the concept of “consumption elasticity” to assign it empirically. Specifically, we apply the elasticity coefficient method from decoupling theory to estimate θ indirectly. In a previous study, Tapio utilized the elasticity coefficient method based on the decoupling theory to study the response relationship between two or more variables in the field of transportation [42], as shown in Equation (13):
In Equation (13), E is the elasticity coefficient, ΔVOL% is the rate of change in traffic capacity, and ΔGDP represents the rate of change in GDP. The formula describes the response relationship between the rate of change in GDP and the rate of change in the traffic capacity, in which the change in the denominator of the formula is the cause and the change in the numerator is the result. In addition to its use in the field of transportation, this method is also widely used in research on the environment, energy, and agricultural policy [43,44]. In recent years, an increasing number of land-related studies have used the Tapio elasticity coefficient method to analyze the relationship between land quantity and economic development [45].
Tapio’s decoupling model establishes elasticity coefficients to depict the relative response relationships between variables at different stages of development. It is particularly suitable for analyzing the interactions between economic drivers and resource dynamics. Building on this approach, the present study incorporates the decoupling framework into the analysis of EVCL allocation. By selecting observable economic indicators to construct the elasticity coefficient, we provide an empirical method to estimate the intergenerational allocation coefficient θ. This approach not only improves the practical applicability of the model but also offers a feasible pathway to bridge theoretical modeling with real-world data.
In this study, we intend to use the Tapio elasticity coefficient method to construct the calculation formula. The value of natural environmental goods is income-elastic, meaning that with socioeconomic development, increasing income levels, and growing scarcity of natural resources, the marginal propensity to consume natural goods decreases. As an important natural environmental good, cultivated land demonstrates significant income elasticity in its ecological value. Regional economic development and increases in farmers’ income will lead to intergenerational shifts in the utilization patterns of cultivated land. Based on the theory of the short-board effect, farmers’ per capita net income is identified as a sensitive indicator of the changes in cultivated land area [46]. This variable effectively reflects the dynamic coupling between economic development and cultivated land resources. Therefore, the Tapio elasticity coefficient constructed in this study uses the rate of change in farmers’ per capita net income (the driving variable) as the denominator, and the rate of change in cultivated land area (the response variable) as the numerator, revealing the intergenerational evolution of the ecological value of cultivated land during the economic development process through the ratio of these rate changes. The specific calculation formula is shown in Equation (14):
In Equation (14), θ represents the intra-generational consumption elasticity coefficient of ecological value, CL represents the quantity of cultivated land, ΔCL indicates the change in cultivated land area, I refers to farmers’ per capita net income, and ΔI denotes the change in that income. This variable setup not only aligns with the objective of intergenerational allocation of EVCL but also provides a practical data basis for estimating the parameter θ in Equation (12).
5.4.2. Data Description
The data utilized in this study are nominal data spanning the period from 1984 to 2022. Cultivated land area data of Lezhi County for this time period were obtained from the statistical report of the Agriculture Bureau of Lezhi County. Cultivated land area data for the years 1986–2022 were obtained from the Department of Natural Resources and Planning of Lezhi County and the Statistical Yearbook of Lezhi County, published in 2022. The per capita net income of rural residents in Lezhi County from 1984 to 2022 was calculated based on the per capita net income of farmers recorded in the 2022 Lezhi County Statistical Yearbook. The above data are advantageous due to their availability and authenticity. This study uses annual statistical data to calculate the rate of change in farmers’ per capita net income and cultivated land area, and calculates the value based on the logarithmic rate-of-change method to reduce the impact of extreme values on the analysis results and improve the robustness of the data. The per capita net income of farmers in Lezhi County, the cultivated area, and the calculated values from 1984 to 2022 are shown in Table 2.

Table 2.
Per capita net income of farmers, cultivated land area, and θ-value in Lezhi County (1984–2022).
5.4.3. Model Estimation
In order to estimate the value of θ, it is necessary to predict the net income per farmer and cultivated land area for the next generation. Considering the autocorrelation and random fluctuations in the time series, we use an ARMA(p,q) model for fitting in this study [47]. When ARMA(p,q) modeling requires that the data take the form of a smooth time series, this study adopts the ADF data smoothness test created by Dickey and Fuller [48]. The test formula is shown in Equation (15):
In Equation (15), Δyt is the explained variable, α1 is the intercept term, γ is the coefficient of the first-order lag terms of yt, α2 is the coefficient of the trend term, t is the trend term, the polynomial part of the sum is the lag term of the explanatory variable, and βi is the coefficient of its lag term, ε~iidn(0,σ2). The original hypothesis of the equation is γ = 0; the alternative hypothesis is γ < 0. The test is carried out using the software EViews9, and the estimation results are shown in Table 3:

Table 3.
Results of data smoothness test (ADF).
The cultivated land area is a smooth time series at 5% significance level, while the concomitant probability p-value is 0.064 when the farmers’ per capita net income is subjected to the unit root test, considering the sample capacity of 39. In light of this, this study abandons the 5% significance level in favor of using a 10% significance level as a benchmark for comparison. On the basis that both time series are smooth, the ARMA(p,q) model is further fitted, as shown in Equation (16):
In Equation (16), α0 is the intercept term, αi is the coefficient of the autoregressive term, and βi is the number of coefficients of the residual lag term, in which the range of values of the p and q terms refer to 0 ≤ (p,q) ≤ 5 in the study by Zivot and Andrews (1992) [49], while the selection of the model lag terms refer to Akaike (1974) [50] and Schwarz (1978) [51]. In this study, the Schwarz intelligence benchmarks prevail, and the great likelihood estimation method is utilized. The estimation results are shown in Table 4:

Table 4.
ARMA(p,q) model fitting results.
After ARMA(p,q) model fitting, the data obey ARMA(2,0), so we expand the sample capacity and predict the per capita net income and cultivated land area for the next generation of farmers using the ARMA(2,0) model. Due to the long intergenerational time, it is difficult to clearly delineate the time span of a generation. Therefore, to facilitate the study of generational problems, the generational time can be divided equally; for example, 10 years per generation. Since this study mainly addresses the intergenerational problem of cultivated land, the 30-year contracting period stipulated in the Rural Land Contracting Law of the People’s Republic of China can be used as the intergenerational time; as such, the model’s predictions focus on the time period 2023–2052. The predicted per capita net income of farmers, cultivated land area, and θ-values for 2023–2052 are shown in Table 5.

Table 5.
Predicted per capita net income of farmers, cultivated land area, and θ-values.
The values calculated according to the ARMA(2,0) model show a decreasing trend of θ as the prediction time increases and tends to zero, which is consistent with the fact that the cultivated area in the study area tends to be constant. The trend of the predicted θ-value is shown in Figure 2.
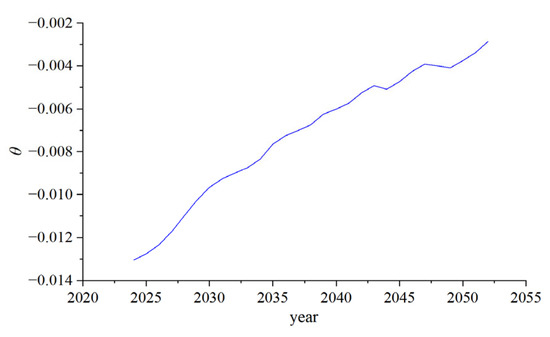
Figure 2.
Trend of θ-values.
5.4.4. Intergenerational Distribution of EVCL
Figure 2 shows the trend of the predicted value, which exhibits a continuous decrease over a 30-year period before gradually converging to 0. According to the formula of intergenerational distribution I = wi/(2 + θ), the θ value converges to 0, which indicates that the ecological value of the cultivated land gradually converges to the equal share of the present and future generations. The calculated value of i converges to 13,099.646/2 = 6549.823, and the amount of ecological value allocated to both present and future generations is CNY 65.498 million/ha. According to the set intergenerational time node of 30 years between the two generations, the EVCL allocated to the present generation within 30 years is CNY 65.498 million/ha, and the remaining CNY 65.498 million/ha is at the disposal of future generations, starting at 31 years and continuing indefinitely.
6. Distribution of EVCL for Future Generations in Lezhi County
6.1. Introduction of the Pearl Growth Curve Formula
Willingness to pay is an important tool for assessing the value of non-market goods and services and the EVCL [52]. When quantified via the survey and evaluation method, which incorporates tools such as questionnaires, interviews, and solicitations, it is influenced by the subjective perception of the respondents. Additionally, conducting surveys and analyzing the responses is both time-consuming and resource-intensive, requiring significant financial and technical resources. In contrast, the development stage coefficient, which characterizes the relative level of willingness to pay, is a simple, accurate, and effective method for calculating this metric [53]. Unlike the current generation, which retains one half of the EVCL, future generations will be influenced by the continuous development of the economy, social development, and standard of living. This illustrates that determining the dynamic development characteristics of occurrence, development, maturity to saturation, and the acquisition of EVCL by future generations is a process of gradual embodiment. The Pearl growth curve can be used to accurately describe the development and characterize the distribution process [54]. The Pearl growth curve is a typical S-shaped model widely used to describe dynamic expansion processes under constraints such as limited resources, cognitive delays, or institutional factors [55]. It features three distinct stages: slow initiation, rapid growth, and eventual saturation. This pattern closely aligns with the increasing willingness to pay of future generations, which tends to grow alongside improvements in public awareness, technological conditions, and policy support. Therefore, the Pearl curve is introduced in this study to represent the dynamic evolution of willingness to pay over time.
The mathematical expression of this model is shown in Equation (17):
In Equation (17), ℓ represents a positively increasing function over time, used to describe the staged variation of a given ecological value factor; L is the limiting value (saturation level) of the function; a and b are constants; e is the base of the natural logarithm; and t denotes the time variable.
To enhance the model’s general applicability and simplify parameter estimation, this study adopts a standardized specification by setting a = 1, b = 1, and c = 1 in the Pearl growth curve. This simplification allows the model to clearly capture the S-shaped growth trajectory of willingness to pay over time, thereby improving both the interpretability and the operational feasibility of the model. The resulting simplified Pearl growth curve is presented in Equation (18):
6.2. Development Stage Coefficient Curve of EVCL for Future Generations
6.2.1. Coefficient of Ecological Value Development Stage of EVCL of Future Generations
The development stage coefficient is used to assess the strength of future generations’ willingness to pay for the EVCL under different levels of economic and social development. It reflects how the realization of ecological value evolves over time [56]. This coefficient not only captures the upward trend in willingness to pay but also represents the dynamic process through which ecological value transitions from a latent state to explicit realization. Based on the simplified Pearl growth curve function introduced earlier (Equation (18)), this function can be applied to describe the temporal evolution of willingness to pay among future generations. The variable ℓ in the equation represents the development stage coefficient at each time point t. As time progresses, the continuous values of ℓ form a complete curve of the development stage coefficients for the EVCL for future generations. The growth process reflects the characteristic path of the gradual realization of ecological service values.
6.2.2. Determination of the Horizontal Coordinates of the Development Stage Coefficient Curve
The horizontal coordinate of the development stage coefficient curve represents social and economic development, as well as changes in the standard of living of the population. Engel’s coefficient can better characterize development at the population level, and this it is widely used internationally to measure the standard of living. Therefore, this study uses the Engel coefficient to represent the horizontal axis of the development stage coefficient curve for the EVCL of future generations. Over time, in the absence of external shocks, Engel’s coefficient gradually decreases, because the value of the horizontal coordinate usually adopts the customary expression from small to large; as such, the inverse of Engel’s coefficient is chosen as the horizontal coordinate. The development of China’s economy, society, and standard of living can be roughly categorized into six stages: poverty, subsistence, moderately prosperous, relatively affluent, wealthy, and extremely wealthy, and the Engel’s coefficient can be roughly correlated with these stages.
The relationship between the Engel coefficient, the inverse of the Engel coefficient, and the six development stages on the horizontal axis of the development stage coefficient curve for the EVCL of future generations is shown in Figure 3:
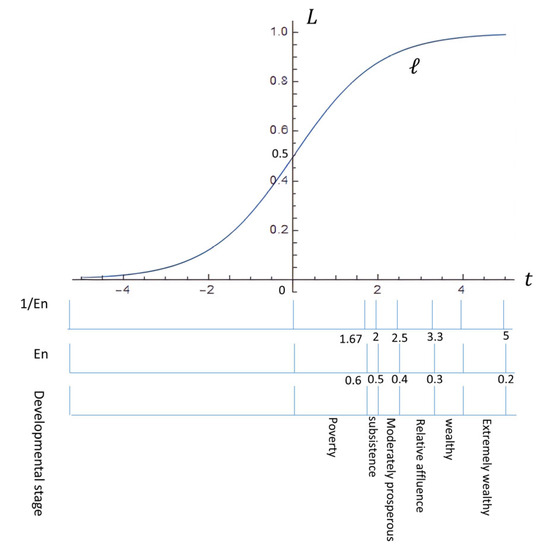
Figure 3.
Curve of stage coefficients of development of cropland value for future generations.
6.2.3. Vertical Axis Values of the Development Stage Coefficient Curve
The vertical coordinate of the development stage coefficient curve of the EVCL for future generations represents the development stage coefficient of the relative level of willingness to pay ℓ, and its value is between 0 and 1; that is, 0 ≤ ℓ ≤ 1. The degree of development decreases with a decreased ℓ value. The larger the ℓ value, the higher the level of development; otherwise, ℓ is equal to 1. When the development stage coefficient curve reaches saturation, it results in a maximum value of L; that is, ℓ = L. The changes in the values on the vertical axis of the development stage coefficient curve for the EVCL of future generations are shown in Figure 3.
6.2.4. The Inflection Point of the Development Stage Coefficient Curve
According to the Pearl growth curve formula , ℓ = 0 when , ℓ = L when , the first-order derivative function for time t is , and the second-order derivative function is , which is calculated to be 0, and we obtain the point of inflection . Then, we find ; the inflection point of the curve is , and at this time, ℓ = 0.5 L. The cultivated land development stage coefficient curve is shown in Figure 3.
6.2.5. Overall Shape of the Development Stage Coefficient Curve for Future Generations
The development stage coefficient curve for the EVCL assigned to future generations exhibits a typical S-shaped nonlinear growth pattern. It can be broadly divided into three phases: initial slow growth, accelerated growth, and eventual stabilization. This trajectory reflects the gradual transformation of ecological value from a latent to an explicit state.
In the early phase, due to low per capita income and limited environmental awareness, public recognition of and willingness to pay for cultivated land ecosystem services remain weak, resulting in a slow increase in the development stage coefficient. As society progresses into the middle phase, sustained economic and social development enhances environmental consciousness. Institutional frameworks and technological support improve concurrently, leading to a sharp rise in willingness to pay, and the coefficient enters a phase of rapid growth. In the later phase, as recognition of ecological value becomes more established and willingness to pay approaches saturation, the growth rate of the coefficient slows and the curve levels off.
The inflection point of the curve marks the critical moment when willingness to pay transitions from rapid growth to a more stable state. This turning point is essential for characterizing how future generations perceive and value ecological services over time. The overall shape of the curve demonstrates a progressive realization process of ecological value, consistent with the evolving intergenerational awareness and capacity to pay.
The shape of the development stage coefficient curve for the EVCL of future generations reflects the dynamic characteristics of the progressive manifestation of ecological value across generations. Based on the evolutionary path of the curve, it provides a foundation for establishing the equation of the development stage coefficient curve for future generations’ EVCL. The shape of the curve is shown in Figure 3.
6.3. Stage Coefficient Curves for the Development of Cropland for Future Generations in Lezhi County
6.3.1. Engel’s Coefficient Prediction for the Next Intergenerational Period
Considering the sample capacity and data uncertainty, among other factors, the Engel’s coefficient is predicted by referring to the gray system prediction model in the studies by Deng [57], Mao M. and Chirwa E.C. [58], and Hsu L. and Wang C. [59]. The model is shown in Equation (19):
In Equation (19), a denotes the development coefficient, b is the control variable in the system, and a and b can be estimated using the least squares method.
Matching the original calculation time of the ecological value allocation of cropland between current and future generations, the original data of the value allocation time of future generations are selected from the years 1984 to 2022. The survey of the urban Engel’s coefficient in Lezhi County only started in December 2004, so the coefficient from 1984 to 2004 is missing. According to the principle of short-board prediction, the rural Engel’s coefficient can participate in the prediction as a short-board factor characterizing the overall Engel’s coefficient. Therefore, the rural Engel’s coefficient from 1984 to 2022 is selected as the independent variable of the development stage coefficient curve of EVCL for future generations. As mentioned before, a 30-year period is selected as the first-generation time, and the rural Engel’s coefficient is predicted for 2023–2052, forming the independent variable data of the development stage coefficient curve of EVCL for future generations from 1984 to 2052. In this study, we use R 4.2.3 software to predict the rural Engel’s coefficient. Firstly, we test the model applicability of the data, and then we estimate GM(1,1) and predict the data. The results are shown in Table 6.

Table 6.
Rural Engel’s coefficient in Lezhi County, 1984–2052.
6.3.2. Calculation of the Development Stage Coefficient for the EVCL for Future Generations
Based on the original and projected rural Engel coefficients, their reciprocals are calculated and substituted into the development stage coefficient formula to derive the corresponding coefficient values. The reciprocals of rural Engel coefficients and the resulting development stage coefficients for Lezhi County from 1984 to 2052 are presented in Table 7.

Table 7.
Inverse rural Engel coefficient, development stage coefficient, and EVCL allocated to future generations in Lezhi County (1984–2052).
6.4. EVCL Allocated to Future Generations in Lezhi County
By multiplying the development stage coefficient of the EVCL for future generations in Lezhi County from 1984 to 2052 with the ecological value of CNY 6561.793 million per hectare, the ecological value quantity of cultivated land for future generations in Lezhi County from 1984 to 2052 is obtained. The specific values are shown in Table 7.
7. Discussion
7.1. The Results of the Study on the EVCL Shared Between Present and Future Generations Can Justify the Equalization of Resources as the Optimal Intergenerational Allocation of Resources
The early view of intergenerational resource allocation held that each generation is the trustee of the rights and interests of future generations, that each generation has equal right to develop and utilize the Earth’s natural resources, and that, in order to reflect intergenerational justice and balance and to safeguard the needs and rights of each generation, resources should be shared equally on an intergenerational basis [60]. In later studies on intergenerational resource allocation, ensuring that resources are shared equally is deemed to be the optimal method of intergenerational resource allocation through the theoretical perspectives of resource allocation efficiency, welfare equilibrium, and Pareto improvement [61,62]. The equal sharing of resources across generations is ethically and theoretically sound but lacks empirical support. In this study, we construct the formula for the intergenerational distribution of EVCL through the two-period Diamond model. After fitting, θ tends to 0, and the intergenerational equalization of EVCL is achieved. Through mathematical formula derivation and model fitting, this study demonstrates the efficacy of resource equalization in realizing the optimal intergenerational allocation of resources and provides a theoretical basis for the research goal of intergenerational fair distribution of EVCL in this study.
7.2. Comparison with Existing Studies
7.2.1. Deriving the Theoretical Formula of Intergenerational Allocation and Getting Empirical Results
Existing studies on theoretical formulas for intergenerational allocation of resources mostly describe the process of intergenerational allocation through theoretical formulas, are unable to derive formulas, and lack specific intergenerational allocation conclusions obtained through empirical analysis. In this study, we obtain the formula for the distribution of EVCL between current and future generations through the derivation of the two-phase Diamond model, fit the intra-generational consumption elasticity coefficient θ in the formula, and conclude that the ecological value is divided between current and future generations, which explores and solves the insufficient derivation of theoretical formulas and missing empirical conclusions in the intergenerational distribution of resources.
7.2.2. Applying the Development Stage Coefficient to Solve the Problem of Missing Value for Future Generations and Market Failure
In the existing research, the ecological value is regarded as the value of the current generation only, and the reflection of the current generation’s willingness to pay is obtained after correction by the development stage coefficient. Additionally, there are ongoing issues related to missing values for the future generation and the possibility of market failure. Based on the perspective of intergenerational equity, this study considers ecological value to be the common value of the present and future generations and formulates the idea that “the present value is obtained in the current period, and the value of the future generation is gradually realized.” Through introducing the development stage coefficient to visualize the EVCL for future generations, the idea of “gradually reflecting the value of future generations” is effectively realized, and the ecological value of future generations is made acceptable, addressing the lack of EVCL for future generations and the failure of the market.
7.3. Limitations and Directions for Further Research
7.3.1. Model Fitting for Multi-Geographic Samples to Improve the Universality of Research Methods and the Confidence of Conclusions
Based on a case study of Lezhi County in China, this study constructs a mathematical model to simulate the distribution process of the EVCL between current and future generations. After model fitting, it is found that the EVCL gradually converges to an equal share between current and future generations. This study adopts empirical analysis of a single research area to obtain a specific result; to achieve greater accuracy, future research should conduct model fitting in multiple areas to identify the same trend of intergenerational distribution and confirm the findings of this study. Therefore, the method of intergenerational distribution used in this study should be retested and research results with higher confidence should be obtained through cross-sectional comparison of samples from different geographic areas in subsequent studies to enhance the generalizability of the method and the confidence of the conclusions.
7.3.2. Assessing the Applicability of the Diamond Model Assumptions: Limitations and Directions for Future Research
Although the Diamond model offers a solid theoretical foundation for constructing the intergenerational allocation of ecological value, and its structural logic aligns with the dynamic transmission of ecosystem services, it essentially remains a normative economic theoretical model. Notably, key assumptions underlying the present study—such as equating ecological value to monetary income and assuming that individuals are willing to consume or allocate ecosystem value based on ecosystem value over the course of lifecycle levels—lack direct empirical validation. These assumptions are intended as conceptual simplifications to facilitate theoretical modeling, rather than reflections of observed behavioral patterns. Future research could address these limitations by incorporating stated preference methods, such as willingness-to-pay surveys, behavioral experiments, or studies on ecological compensation behavior. Such efforts would enhance the empirical grounding of the model and improve its relevance for policy design and practical application.
7.3.3. Rethinking the Income–Cultivated Land Decoupling Phenomenon: Implications for Intergenerational Ecological Valuation
In the context of rapid economic development, the phenomenon of increasing rural income accompanied by decreasing cultivated land area—particularly under urban expansion and agricultural industrialization—presents a critical challenge for intergenerational ecological value assessment [63]. However, this trend does not necessarily imply a decline in the EVCL. Instead, it may reflect shifts in land use priorities and market-driven incentives, especially as agricultural land is converted to urban or commercial uses.
It is important to note that a reduction in cultivated land area does not automatically lead to a proportional decline in ecological value. In many cases, the remaining cultivated land becomes more ecologically significant due to increased scarcity, enhanced ecosystem functions, or greater policy attention (such as ecological compensation or land use regulation). This highlights the need to distinguish between “land quantity” and “ecological quality” when assessing ecological value.
Notably, the relationship between income growth and cultivated land reduction is not a linear causal link. It often reflects broader dynamics, including economic restructuring, institutional changes in land use, and the evolution of environmental policies. Accordingly, ecological value assessments should be interpreted in light of these contextual transformations, rather than equating land quantity changes directly with fluctuations in ecological value. Future research should further investigate how institutional structures, policy trajectories, and land use transitions collectively shape the evolving perception of EVCL. Incorporating these factors into ecological valuation frameworks will enhance the model’s ability to reflect the mechanisms of intergenerational value transfer.
7.3.4. Optimization of the Universal Applicability for the Intra-Generational Consumption Elasticity Coefficient
This study constructs the intra-generational consumption elasticity coefficient based on the Tapio elasticity coefficient method, selecting farmers’ per capita net income as the driving variable, which has strong explanatory power in the Chinese context and can effectively reflect the dynamic coupling relationship between economic development and the quantity of cultivated land resources. However, this indicator has two main limitations: First, farmers’ per capita net income, as a core indicator for agricultural economies in developing countries, is highly representative of transformation economies like China, but may not be fully applicable to agricultural systems in developed countries, which are primarily based on large-scale farms. For example, agricultural income statistics in OECD countries often use the “net income of agricultural operation” indicator, which differs significantly in accounting scope from China’s per capita net income of farmers. Second, the driving mechanisms of cultivated land changes vary across regions globally [22]. Tropical regions may be more affected by international agricultural price fluctuations, while arid areas are more sensitive to climate change factors. Therefore, a “single farmers’ income” indicator may not fully reflect the driving forces behind cultivated land changes in different regions. Future research can improve the universality of this indicator in three ways: (1) constructing a composite driving indicator and incorporating globally comparable parameters such as agricultural product price indices and climate drought indices, (2) establishing an indicator conversion system and developing standardized processing methods for agricultural income statistical data from different countries, and (3) introducing regional weight coefficients and setting differentiated parameters based on income groups and climate zones defined by the World Bank.
7.3.5. Optimization of the Regional Applicability of the Development Stage Coefficient Model
A development stage evaluation model was constructed based on Engel’s coefficient, which can effectively describe the relationship between economic development levels and the intergenerational distribution of the EVCL in China. However, the cross-regional applicability of this model needs to consider the following two key limitations: First, the international comparability of the Engel’s coefficient is constrained by statistical systems. Developing countries typically use “household consumption expenditure” statistics, while OECD countries generally use the “final household consumption expenditure” accounting framework. The classification differences in items such as service consumption (e.g., takeaway meals) and implicit subsidies (e.g., school meal programs) can reach 15–20% [64]. For example, EU countries, due to the Common Agricultural Policy (CAP) subsidies, systematically report food expenditure as 5–8 percentage points lower [65]. Second, the nonlinear relationship between development stages and consumption structures is significant. In regions where the digital economy is rapidly penetrating, such as Southeast Asia, online food purchasing leads to an overestimation of the Engel’s coefficient for actual living pressures [66], while in high-welfare countries, such as the Nordic countries, systems like universal healthcare tend to underestimate the real development level. The deviation in the development stage coefficient calculated based on the Engel’s coefficient will directly affect the accuracy of the model’s calculation of the intergenerational distribution ratio. To enhance the model’s universality, future research can implement the following optimizations: (1) introduce adjustment coefficients, such as converting the original Engel’s coefficient into a “Comparable Development Index” (CDI); (2) establish a calibration mechanism with the United Nations Development Programme (UNDP) Human Development Index (HDI), using panel data regression to determine region-specific parameters; and (3) introduce a policy intervention correction mechanism, focusing on identifying three types of influencing factors: the intensity of agricultural product price controls, the share of social welfare expenditure, and the penetration rate of the digital economy.
7.3.6. Dynamic Integration of Institutional Factors
During the model development phase, the dynamic impact mechanisms of institutional factors have not yet been fully quantified. Although the development stage coefficient formula constructed in this study reflects the indirect effects of policy interventions to some extent, the following key dimensions still require further exploration: First, the policy lag effect has not been systematically integrated. Existing studies show that ecological compensation policies typically experience a 3–5-year lag period from implementation to significant effects [64,67], yet the current model does not include a dedicated lag calibration module. This lag difference may lead to short-term valuation biases in the intergenerational distribution coefficient for future generations. Second, spatial heterogeneity requires more refined treatment. Cross-country comparisons show that the difference in land regulation intensity across administrative jurisdictions can be as high as 40% (e.g., differences in the enforcement of the EU Common Agricultural Policy (CAP) and China’s cultivated land “red line” policy). This institutional enforcement gradient may significantly affect the spatial distribution pattern of ecological value. Third, the model’s ability to simulate future policy scenarios needs improvement. Under the drive of carbon neutrality goals, changes in land use (e.g., expansion of bioenergy crops) may fundamentally alter the intergenerational distribution pattern of cultivated land’s ecological value, yet the current model does not incorporate such forward-looking scenario analyses.
To address these limitations, future research should focus on the following directions: (1) develop a “policy shock–ecological response” coupling model, drawing on the IPCC SR1.5 scenario analysis framework, to quantify policy lag effects; (2) introduce the institutional quality index (IQI) developed by the World Bank as a regional adjustment variable; and (3) construct a Monte Carlo simulation system that includes multiple policy scenarios to assess intergenerational distribution schemes under different institutional paths.
7.3.7. Carrying Out the Revision of EVCL for Contemporary People
In this study, we measure the EVCL allocated by contemporary people as CNY 65.498 million/ha. We compare this with the current benchmark land price of Class I commercial land in Lezhi County of CNY 26.32 million/ha and find that the former is 2.489 times greater than the latter, indicating significant EVCL ownership in contemporary society. This value exceeds people’s ability to pay and cannot be seen as indicative of their willingness to pay at this stage, resulting in concerns regarding value acceptability. This study formulates the idealized intergenerational distribution idea that “the value of the current generation is reflected in the current period, and the value of the future generation is reflected gradually,” which mainly focuses on the immediate acquisition of the value of the current generation and disregards the current generation’s willingness to pay. To resolve this issue, the development stage coefficient can be used to modify the ecological value of the current generation to ensure the economic feasibility of the intergenerational allocation scheme and increase the practical applicability of the ecological value of the current generation. The corrected EVCL owned by present and future generations is the same; this is actually the EVCL corrected by doubling the development stage coefficient, and it also serves as a concrete embodiment of the theory of EVCL shared by present and future generations per capita in the present study.
7.4. Significance and Contributions of the Research
Cultivated land resources are the foundation for the sustainable development of the economy and society. Their limited and non-renewable nature requires that resource use balance the rights and interests of both present and future generations. Currently, global cultivated land resources face issues such as degradation, over-exploitation, and inadequate ecological compensation mechanisms [68], which affect their sustainable use. Existing ecological value assessments of cultivated land mainly focus on current benefits, lacking systematic quantitative analysis of intergenerational equity. This often leads to intergenerational externality issues in resource distribution, potentially resulting in market failure [69].
Current resource management policies have limitations in intergenerational distribution, such as policy fragmentation, lack of long-term incentive mechanisms, and difficulty in balancing short-term economic benefits with long-term ecological value. Therefore, there is an urgent need for scientific methods to quantify intergenerational equity to optimize resource allocation and guide policy formulation. This study, from the perspective of intergenerational equity, constructs an intergenerational distribution system for the ecological value of cultivated land to address the gaps in existing research and provide technical support for policy formulation. The significance and value of this study are outlined as follows:
7.4.1. Theoretical Contribution
In this study, we construct a mathematical model for the distribution of the EVCL between present and future generations, as well as within future generations, providing a quantifiable analytical tool for the intergenerational allocation of non-renewable resource value. This model introduces a development stage coefficient to calculate the willingness of future generations to pay for the EVCL and optimizes the development stage coefficient formula, enabling it to accurately reflect the changing trends in resource value across different development stages. This theoretical breakthrough not only enriches the research framework for the fair intergenerational distribution of resources but also provides methodological support for the intergenerational value assessment of other non-renewable resources.
7.4.2. Relevance of the Study
The findings of this study can be applied to the rational distribution of the EVCL and provide a scientific basis for optimizing ecological compensation mechanisms. This contributes to achieving the United Nations Sustainable Development Goals (SDGs), particularly Goal 15.3 (Land Degradation Neutrality) and Goal 12.2 (Sustainable Management of Resources). Furthermore, the model and methods developed in this study are not only applicable to the assessment of the EVCL but can also be extended to fields such as water resource management, mineral resource development, and biodiversity conservation, offering actionable policy tools for global ecological governance.
7.4.3. Methodological Innovations
This study aims to construct an ecological value distribution model for cultivated land based on the principle of intergenerational equity, quantifying the resource allocation relationships between different generations and optimizing resource management policies to ensure sustainable resource use. By introducing a development stage coefficient, we calculate the willingness of future generations to pay for the EVCL and optimize the calculation formula, making it more accurate in reflecting the changing trends in resource value across different development stages, thus enhancing the scientific and practical applicability of the assessment.
We propose a method for calculating the EVCL based on the development stage coefficient and objectively measure the leftward shift of the development stage coefficient curve, optimizing the formula to improve simulation accuracy. This method not only provides a quantitative basis for the fair distribution of the EVCL land but can also be extended to the study of intergenerational distribution of other resources. Particularly in terms of policy formulation and practical application, this method can serve as an implementation mechanism for the intergenerational fair distribution of EVCL, effectively addressing market failure issues in practice and improving resource utilization efficiency.
7.4.4. Contribution to Sustainable Development
Building on the preceding theoretical framework and methodological innovations, this study incorporates the concept of intergenerational equity into the broader sustainable development governance framework. It responds directly to the core challenge of balancing long-term fairness and ecological sustainability in land resource management. From the perspective of sustainable land use, this study proposes an intergenerational distribution logic of “immediate value for the present generation, gradual realization of value for future generations”, and constructs a dynamic distribution path for the EVCL covering the entire life cycle. This approach fills the gap in the existing evaluation system regarding the time dimension and intergenerational responsibility.
By integrating the Diamond model and the development stage coefficient curve, this study develops a quantitative analysis framework grounded in intergenerational fairness. This approach helps represent the rights and interests of “future non-present generations” in ecological governance. It extends the temporal scale of ecological value assessment and enhances the capacity of institutional design to address long-term goals. The method offers theoretical support and technical guidance for advancing coordinated policies in cultivated land protection, ecological compensation, and rural sustainability.
The results suggest that sustainable ecological resource management must incorporate intergenerational dynamics and balance fairness with efficiency. This research provides a practical analytical tool and empirical foundation for promoting the fair use of land resources and the long-term stability of ecosystems. It holds strong potential for policy application and offers theoretical and institutional insights aligned with the United Nations Sustainable Development Goals (particularly SDGs 12 and 15).
8. Conclusions
8.1. Calculate the EVCL in Lezhi County
In this study, ecosystem service functions (agricultural products and raw materials supply, water conservation, carbon sequestration and oxygen release, and soil and water conservation) were used to determine as the EVCL in Lezhi County. The functional value method was used to calculate the one-year value of each ecological service function of cultivated land. Experts estimated the value of each value corresponding to the intergenerational discount rate, discounting the value of each one-year ecological service function. The total EVCL in Lezhi County was found to be CNY 9,886,796.206 million, and the cultivated land in Lezhi County covered an area of 75,336.090 hectares in 2022. Together, these numbers were used to determine the EVCL in Lezhi County per unit area, which is CNY 131.236 million/ha.
8.2. Calculating the Intergenerational Distribution of the EVCL with the Help of the Diamond Model, Which Can Simulate the Distribution of Value Between Present and Future Generations
Using the Diamond model to calculate the intergenerational distribution of EVCL, we obtain the formula , which shows that the ecological value of cultivated land for future generations is completely dependent on the changes in the consumption elasticity coefficient θ within generations. Our formula can explain the intergenerational distribution of EVCL and simulate the process of distributing this value between present and future generations.
8.3. Using Decoupling Theory as the Theoretical Basis for Variable Selection and Predictions, We Conclude That the Value of Present and Future Generations Is Equally Divided, and Obtain the EVCL for Present and Future Generations
In this study, we constructed the θ expression of “coefficient of elasticity of intra-generational consumption of cultivated land = rate of change in the quantity of cultivated land/rate of change of farmers’ per capita net income”. We used the GM(1,1) (p,q) model to fit the quantity of cultivated land and farmers’ per capita net income. The data obeyed ARMA(2,0), and the θ value of the next generation was predicted. The θ value showed a continuously decreasing trend and converged to 0, indicating that the EVCL gradually converges to an equal share for present and future generations. After calculation, the value i converged to 13,123.585/2 = 6561.793, so, the EVCL distributed between present and future generations is CNY 65.618 million/ha.
8.4. A Development Stage Coefficient Formula Based on the Pearl Gowth Curve Model for Estimating the EVCL Allocated to Future Generations
The development stage coefficient formula for the ecological value of cultivated land (EVCL) allocated to future generations was constructed based on the Pearl growth curve model. GM(1,1) was employed to predict the rural Engel’s coefficient of the next generation. The inverse of both the original and the forecasted rural Engel’s coefficients was substituted into the development stage coefficient formula . These calculated coefficients were then multiplied by the EVCL allocated to future generations—estimated as CNY 654.9823 million/ha—to determine the annual distribution of EVCL for future generations in Lezhi County from 1984 to 2052.
8.5. Institutional and Policy Implications for Sustainability
This study develops an intergenerational allocation model of cultivated land ecological value, centered on the principle of intergenerational equity. By integrating the Diamond model with the development stage coefficient, it delineates the dynamic transmission pathway of ecological value across time. The proposed allocation mechanism effectively captures the interests of “future non-present generations”, promoting both the equitable recognition and rational distribution of EVCL.
At the policy level, the findings offer methodological support and theoretical foundations for designing future cultivated land protection frameworks, allocating ecological compensation funds more scientifically, and establishing long-term mechanisms that integrate agricultural development with environmental protection. Against the backdrop of global efforts to achieve carbon neutrality, ensure food security, and restore ecosystems, the implementation pathway proposed in this study contributes to advancing land governance systems toward greater systemic coherence, long-term orientation, and sustainability. Moreover, it provides theoretical insights and institutional references for countries seeking fair and efficient ecological resource governance models.
Author Contributions
Conceptualization, L.Y.; methodology, H.W.; software, H.W.; validation, L.Y., H.W. and J.X.; formal analysis, L.Y.; investigation, X.F.; resources, L.Y.; data curation, L.Y. and X.F.; writing—original draft preparation, L.Y.; writing—review and editing, J.X. and X.F.; visualization, H.W.; supervision, H.W.; project administration, L.Y.; funding acquisition, L.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Social Science Fund of China (24BJY146).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| EVCL | Ecological value of cultivated land |
Appendix A
Questionnaire on intergenerational discount rates for ecological values of cultivated land. Distinguished experts: I am very sorry to disturb your work and thank you for completing this questionnaire in your busy schedule. Determining a reasonable ecological intergenerational discount rate of cultivated land is very important for the intergenerational fair utilization of land resources, and the relative level of the intergenerational discount rate directly affects the amount of value of cultivated land resources as well as the intergenerational allocation efficiency. This questionnaire is designed for the following four ecological service functions of cultivated land: material production, water supply and storage, carbon sequestration and oxygen release, and soil and water conservation, and your assignment of the intergenerational discount rate of the four ecological service functions is the direct data for this cultivated land value measurement. The intergenerational discount rate corresponding to each ecological service value of cultivated land varies according to the function of resource and environmental impacts realized by each ecological value of cultivated land, the severity and reversibility of the impacts of the loss of the value function on the resource and environment, and the relationship with the level of economic and technological progress. Following the principle that the intergenerational discount rate decreases with time as the substitution difficulty between the intergenerational discount rate and man-made capital increases, please assign the intergenerational discount rate corresponding to the value of each ecological service of cultivated land according to your knowledge and experience, and please be precise to 4 decimals. Thank you for your help in completing this questionnaire in your busy schedule. |
| January 2024 |
Appendix B

Table A1.
Expert intergenerational discount rate assignment table.
Table A1.
Expert intergenerational discount rate assignment table.
| Types of Ecological Values | Value of Material Production | Water Supply Storage Value | Carbon Fixation and Oxygen Release Value | Soil and Water Conservation Values |
|---|---|---|---|---|
| Expert 1 | 0.2440 | 0.0421 | 0.0153 | 0.0039 |
| Expert 2 | 0.1076 | 0.0417 | 0.0144 | 0.0045 |
| Expert 3 | 0.0953 | 0.0338 | 0.0155 | 0.0053 |
| Expert 4 | 0.0059 | 0.0370 | 0.0153 | 0.0049 |
| Expert 5 | 0.0820 | 0.0372 | 0.0125 | 0.0055 |
| Expert 6 | 0.0400 | 0.0295 | 0.0146 | 0.0047 |
| Expert 7 | 0.1205 | 0.0260 | 0.0145 | 0.0039 |
| Expert 8 | 0.1226 | 0.0318 | 0.0135 | 0.0051 |
| Expert 9 | 0.2227 | 0.0271 | 0.0158 | 0.0041 |
| Expert 10 | 0.0065 | 0.0179 | 0.0149 | 0.0048 |
| Expert 11 | 0.1761 | 0.0458 | 0.0129 | 0.0048 |
| Expert 12 | 0.0583 | 0.0264 | 0.0142 | 0.0036 |
| Expert 13 | 0.0305 | 0.0156 | 0.0151 | 0.0061 |
| Expert 14 | 0.0828 | 0.0291 | 0.0149 | 0.0049 |
| Expert 15 | 0.0451 | 0.0418 | 0.0152 | 0.0060 |
| Average value | 0.0960 | 0.0322 | 0.0146 | 0.0048 |
References
- Yu, B.; Lu, C. Change of cultivated land and its implications on food security in China. Chinese Geogr. Sci. 2006, 16, 299–305. [Google Scholar] [CrossRef]
- Li, S.; Shao, Y.; Hong, M.; Zhu, C.; Dong, B.; Li, Y.; Lin, Y.; Wang, K.; Gan, M.; Zhu, J.; et al. Impact mechanisms of urbanization processes on supply-demand matches of cultivated land multifunction in rapid urbanization areas. Habitat Int. 2023, 131, 102726. [Google Scholar] [CrossRef]
- Becker, R.A. Intergenerational equity: The capital-environment trade-off. J. Environ. Econ. Manag. 1982, 9, 165–185. [Google Scholar] [CrossRef]
- Hartwick, J.M. Intergenerational equity and the investing of rents from exhaustible resources. In The Economics of Sustainability; Routledge: London, UK, 2017; pp. 63–65. [Google Scholar]
- Xiang, L. Study on compensation mechanism for regional ecological protection under the background of ecological civilisation. Int. J. Data Sci. 2023, 8, 52–68. [Google Scholar] [CrossRef]
- Costanza, R.; De Groot, R.; Sutton, P.; Van Der Ploeg, S.; Anderson, S.J.; Kubiszewski, I.; Farber, S.; Turner, R.K. Changes in the global value of ecosystem services. Global Environ. Chang. 2014, 26, 152–158. [Google Scholar] [CrossRef]
- Kang, N.; Hou, L.; Huang, J.; Liu, H. Ecosystem services valuation in China: A meta-analysis. Sci. Total Environ. 2022, 809, 151122. [Google Scholar] [CrossRef]
- United Nations. The 17 Goals. Available online: https://sdgs.un.org/goals (accessed on 10 May 2025).
- Proffitt, F.; Kaiser, J. Wounding earth’s fragile skin. Science 2004, 304, 1616–1618. [Google Scholar]
- Solow, R.M. On the intergenerational allocation of natural resources. Scand. J. Econ. 1986, 88, 141–149. [Google Scholar] [CrossRef]
- Bertram, D. ‘For You Will (Still) Be Here Tomorrow’: The Many Lives of Intergenerational Equity. Trans. Environ. Law 2023, 12, 121–149. [Google Scholar] [CrossRef]
- Becker, G.S.; Tomes, N. An equilibrium theory of the distribution of income and intergenerational mobility. J. Polit. Econ. 1979, 87, 1153–1189. [Google Scholar] [CrossRef]
- Asheim, G.B.; Banerjee, K.; Mitra, T. How stationarity contradicts intergenerational equity. Econ. Theor. 2021, 72, 423–444. [Google Scholar] [CrossRef]
- Solow, R.M. The economics of resources or the resources of economics. In Classic Papers in Natural Resource Economics; Palgrave Macmillan: London, UK, 1974; pp. 257–276. [Google Scholar]
- Hartwick, J.M. Investment of rents from exhaustible resources and intergenerational equity. Am. Econ. Rev. 1977, 67, 972–974. [Google Scholar]
- Howarth, R.B.; Norgaard, R.B. Intergenerational transfers and the social discount rate. Environ. Resour. Econ. 1993, 3, 337–358. [Google Scholar] [CrossRef]
- Asheim, G.B.; Buchholz, W.; Tungodden, B. Justifying sustainability. J. Environ. Econ. Manag. 2001, 41, 252–268. [Google Scholar] [CrossRef]
- Li, S.; Ma, S. A quantitative analysis on the coordination of regional ecological and economic development based on the ecosystem service evaluation. Land 2024, 13, 207. [Google Scholar] [CrossRef]
- Zou, L.; Liu, Y.; Yang, J.; Yang, S.; Wang, Y.; Hu, X. Quantitative identification and spatial analysis of land use ecological-production-living functions in rural areas on China’s southeast coast. Habitat Int. 2020, 100, 102182. [Google Scholar] [CrossRef]
- Li, J.C. Value assessment is the key of environmental assessment. Chin. J. Popul. Resour. 2022, 3, 13–19. (In Chinese) [Google Scholar]
- The People’s Government of Lezhi County. Lezhi County 2022 Statistical Yearbook. 22 March 2023. Available online: http://www.lezhi.gov.cn/lzxrmzf/xztjxx/pc/content/content_1822877523613446144.html (accessed on 1 February 2024). (In Chinese)
- Carpenter, S.R.; Mooney, H.A.; Agard, J.; Whyte, A. Science for managing ecosystem services: Beyond the Millennium Ecosystem Assessment. Proc. Natl. Acad. Sci. USA 2009, 106, 1305–1312. [Google Scholar] [CrossRef]
- Costanza, R.; Kubiszewski, I.; Stoeckl, N.; Kompas, T. Pluralistic discounting recognizing different capital contributions: An example estimating the net present value of global ecosystem services. Ecol. Econ. 2021, 183, 106961. [Google Scholar] [CrossRef]
- Hu, B.; Xie, M.; He, R.; Shi, Z.; Zhou, Y.; Ni, H.; Li, H. Spatio-temporal evolution of cultivated land ecosystem services value and its spatially varying dominate over the past two decades: A case study in Jiangxi Province in southern China. J. Clean. Prod. 2023, 427, 139228. [Google Scholar] [CrossRef]
- Zhao, G.; Tian, S.; Jing, Y.; Cao, Y.; Liang, S.; Han, B.; Cheng, X.; Liu, B. Establishing a quantitative assessment methodology framework of water conservation based on the water balance method under spatiotemporal and different discontinuous ecosystem scales. J. Environ. Manag. 2023, 346, 119006. [Google Scholar] [CrossRef] [PubMed]
- Egusa, T.; Oda, T.; Sato, T.; Sato, T.; Kumagai, T. Estimation of sub-annual inter-catchment groundwater flow using short-term water balance method. Hydrol. Processes 2021, 35, e14368. [Google Scholar] [CrossRef]
- Li, C.; Fang, S.; Geng, X.; CNY, Y.; Zheng, X.; Zhang, D.; Li, R.; Sun, W.; Wang, X. Coastal ecosystem service in response to past and future land use and land cover change dynamics in the Yangtze river estuary. J. Clean. Prod. 2023, 385, 135601. [Google Scholar] [CrossRef]
- Metcalf, G.E. Designing a carbon tax to reduce US greenhouse gas emissions. Rev. Environ. Econ. Policy 2009, 3, 14375–14410. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, Z.; Govers, G. Soil and water conservation measures reduce soil and water losses in China but not down to background levels: Evidence from erosion plot data. Geoderma 2019, 337, 729–741. [Google Scholar] [CrossRef]
- Okeyo, A.I.; Mucheru-Muna, M.; Mugwe, J.; Ngetich, K.F.; Mugendi, D.N.; Diels, J.; Shisanya, C.A. Effects of selected soil and water conservation technologies on nutrient losses and maize yields in the central highlands of Kenya. Agric. Water Manag. 2014, 137, 52–58. [Google Scholar] [CrossRef]
- Hassangavyar, M.B.; Samani, A.N.; Rashidi, S.; Tiefenbacher, J.P. Catchment-scale soil conservation: Using climate, vegetation, and topo-hydrological parameters to support decision making and implementation. Sci. Total Environ. 2020, 712, 136124. [Google Scholar]
- Arrow, K.J.; Kruz, M. Public Investment, the Rate of Return, and Optimal Fiscal Policy; RFF Press: Washington, DC, USA, 2013. [Google Scholar]
- TEEB. The Economics of Ecosystems and Biodiversity: Mainstreaming the Economics of Nature: A Synthesis of the Approach, Conclusions and Recommendations of TEEB; TEEB: Geneva, Switzerland, 2010. [Google Scholar]
- Ma, X.L.; Qu, F.L. Cost-benefit analysis and intergenerational equity: A new intergenerational discounting approach. Chin. J. Popul. Resour. 2011, 21, 22–28. (In Chinese) [Google Scholar]
- Sumaila, L.R.; Walters, C. Intergenerational discounting: A new intuitive approach. Ecol. Econ. 2005, 52, 135–142. [Google Scholar] [CrossRef]
- Linstone, H.A.; Turoff, M. The Delphi Method; Addison: Wesley, MA, USA, 1975. [Google Scholar]
- Samuelson, P.A. An exact consumption-loan model of interest with or without the social contrivance of money. J. Polit. Econ. 1958, 66, 467–482. [Google Scholar] [CrossRef]
- Diamond, P. National debt in a neoclassical growth model. Am. Econ. Rev. 1965, 55, 1126–1150. [Google Scholar]
- Aksoy, E.; Gregor, M.; Schröder, C.; Löhnertz, M.; Louwagie, G. Assessing and analysing the impact of land take pressures on arable land. Solid Earth 2017, 8, 683–695. [Google Scholar] [CrossRef]
- Padilla, E. Intergenerational equity and sustainability. Ecol. Econ. 2002, 41, 69–83. [Google Scholar] [CrossRef]
- Markin, R.J. The role of rationalization in consumer decision processes: A revisionist approach to consumer behavior. J. Acad. Market Sci. 1979, 7, 316–334. [Google Scholar] [CrossRef]
- Tapio, P.; Banister, D.; Luukkanen, J.; Vehmas, V.; Willamo, R. Energy and transport in comparison: Immaterialisatio, dematerialization and decarbonisation in the EU15 between 1970 and 2000. Energ. Policy 2007, 35, 433–451. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, T.; Yang, S. Carbon emission and its decoupling research of transportation in Jiangsu Province. J. Clean. Prod. 2017, 142, 907–914. [Google Scholar] [CrossRef]
- Luo, H.; Li, L.; Lei, Y.; Wu, S.; Yan, D.; Fu, X.; Luo, X.; Wu, L. Decoupling analysis between economic growth and resources environment in Central Plains Urban Agglomeration. Sci. Total Environ. 2021, 752, 142284. [Google Scholar] [CrossRef]
- Wu, Y.; CNY, C.; Liu, Z.; Wu, H.; Wei, X. Decoupling relationship between the non-grain production and intensification of cultivated land in China based on Tapio decoupling model. J. Clean. Prod. 2023, 424, 138800. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, Y.; Li, X.; Qian, C. Assessment on land-water resources carrying capacity of countries in Central Asia from the perspective of self-supplied agricultural products. Land 2022, 11, 278. [Google Scholar] [CrossRef]
- Ives, A.R.; Abbott, K.C.; Ziebarth, N.L. Analysis of ecological time series with ARMA (p, q) models. Ecology 2010, 91, 858–871. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Likelihood ratio statistics for autoregressive time series with a unit root. Econometrica 1981, 49, 1057–1072. [Google Scholar] [CrossRef]
- Zivot, E.; Andrews, D.W.K. Further evidence oil-price shock, hypothesis on and the the great crash, unit-root the eric. J. Bus. Econ. Stat. 1992, 10, 251–270. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE T. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Bohm, P. Estimating Willingness to Pay: Why and How? Measurement in Public Choice; Palgrave Macmillan: London, UK, 1979; pp. 1–12. [Google Scholar]
- Liu, M.; Zhang, A.; Zhang, X.; Xiong, Y. Research on the game mechanism of cultivated land ecological compensation standards determination: Based on the empirical analysis of the Yangtze River Economic Belt, China. Land 2022, 11, 1583. [Google Scholar] [CrossRef]
- Kucharavy, D.; De Guio, R. Application of S-shaped curves. Proc. Eng. 2011, 9, 559–572. [Google Scholar] [CrossRef]
- Yu, G.; Liu, D.; Liao, X.; Wang, T.; Tian, Q.; Liao, Y. Quantitative research on regional ecological compensation from the perspective of carbon-neutral: The case of Hunan Province, China. Sustainability 2017, 9, 1095. [Google Scholar] [CrossRef]
- Bu, J.F. Study on Domestic and Abroad Development Stage Coefficient of the Ecological Value. Master’s Thesis, Beijing Technology and Business University, Beijing, China, 2006. [Google Scholar]
- Deng, J.L. Control problems of grey systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar]
- Mao, M.; Chirwa, E.C. Application of grey model GM (1, 1) to vehicle fatality risk estimation. Technol. Forecast. Soc. 2006, 73, 588–605. [Google Scholar] [CrossRef]
- Hsu, L.; Wang, C. Forecasting the output of integrated circuit industry using a grey model improved by the Bayesian analysis. Technol. Forecast. Soc. 2007, 74, 843–853. [Google Scholar] [CrossRef]
- Asheim, G.B. Intergenerational equity. Annu. Rev. Econ. 2010, 2, 197–222. [Google Scholar] [CrossRef]
- Sandler, T.; Smith, V.K. Intertemporal and intergenerational Pareto efficiency. J. Environ. Econ. Manag. 1976, 2, 151–159. [Google Scholar] [CrossRef]
- Folbre, N.; Wolf, D. The intergenerational welfare state. Popul. Dev. Rev. 2013, 38, 36–51. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Shao, X.; Zhang, Y.; Cao, Y. Land-use changes and policy dimension driving forces in China: Present, trend and future. Land Use Policy 2012, 29, 737–749. [Google Scholar] [CrossRef]
- World Bank. Global Economic Prospects, June 2022; World Bank: Washington, DC, USA, 2022. [Google Scholar]
- Chai, A.; Moneta, A. Retrospectives: Engel curves. J. Econ. Perspect. 2010, 24, 225–240. [Google Scholar] [CrossRef]
- Moon, J.; Hwang, J.; Lee, W.S. Relationship between the Engel coefficient, life satisfaction, and subjective health for senior citizens in Korea: Moderating effect of COVID-19. Behav. Sci. 2022, 13, 22. [Google Scholar] [CrossRef]
- Yang, S.; Wang, W.; Feng, D.; Lu, J. Impact of pilot environmental policy on urban eco-innovation. J. Clean. Prod. 2022, 341, 130858. [Google Scholar] [CrossRef]
- Li, H.; Song, W. Spatial transformation of changes in global cultivated land. Sci. Total Environ. 2023, 859, 160194. [Google Scholar] [CrossRef]
- United Nations. Transforming Our World: The 2030 Agenda for Sustainable Development. Available online: https://sdgs.un.org/2030agenda (accessed on 1 June 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).