Abstract
Transportation agencies face increasing challenges in identifying and prioritizing which infrastructure assets are most critical to maintain and protect, particularly amid aging networks, limited budgets, and growing threats from climate change and extreme events. However, existing prioritization approaches often lack consistency and fail to adequately incorporate diverse stakeholder perspectives. This study develops a systematic, stakeholder-informed method for ranking transportation assets based on their criticality to the overall transportation system. As a novel approach, we use the analytical hierarchy process (AHP) and present a case study of the applied approach. Six criteria were identified for ranking assets: annual average daily traffic (AADT), redundancy, freight output, roadway classification, Social Vulnerability Index (SoVI), and tourism. Stakeholder input was collected via an AHP-based survey using pairwise comparisons and translated into weighted rankings. Thirty complete responses (13.2% response rate) from experts (i.e., engineers, analysts, planners, etc.) were analyzed, with the resulting ranks from highest to lowest priority being AADT, redundancy, freight output, roadway classification, SoVI, and tourism. Stability analysis confirmed that rankings were consistent with a minimum of 15 responses. The resulting method provides a practical, replicable tool for agencies to perform statewide vulnerability/resiliency assessments ensuring that decision-making reflects a broad range of expert perspectives.
1. Introduction
Global research on the resiliency, criticality, vulnerability, connectivity, and disruption of transportation networks has notably intensified in recent years [1,2], partly as a result of the rising occurrence of major natural and human-made disasters. Significant instances include Superstorm Sandy in 2012, Hurricane Katrina in 2008 which resulted in approximately USD 170 billion in damages, rockslides on Interstate 40 (I-40) in the United States between 2009 and 2010, which incurred cleanup costs ranging from USD 2 to USD 10 million, the 2011 Tōhoku earthquake and tsunami costing USD 235 billion including transportation infrastructure losses, and the 2021 Western Europe floods in Germany and Belgium with USD 54 billion in total losses across Europe. Mobility, safety, and the economy are all significantly affected by these long and short-term disruptions to the transportation system. The transportation system serves as a critical backbone for the effective operation of other essential infrastructure sectors, including emergency services, food and agriculture, healthcare, public health, and manufacturing. There is, therefore, an urgent need for robust tools that support resilience planning, investment prioritization, and disruption response by incorporating failure likelihood alongside system-wide impacts to better inform decision-making.
Resiliency is defined by the National Academy of Sciences as “the ability to prepare and plan for, absorb, recover from, and more successfully adapt to adverse events”. In transportation systems, resiliency refers to the ability of networks to maintain functionality during disruptive events and to restore normal operations following such disruptions [3]. Previous studies have assessed transportation network resilience to disruptions such as rockslides, floods, and earthquakes using various metrics and analytical frameworks. One such study [4], employed a heuristic approach to evaluate the performance of road intersection in urban areas, with a focus on resilience during critical events. By examining variations in control delays before and after such events, the research provided insights into intersection efficiency under stress conditions and emphasized the need for future studies to expand the analysis to the corridor level. The first step in resiliency assessment is to analyze the criticality of assets. The criticality of a network component (link) depends on both the probability of its failure and the extent of its impact on the overall system. The severity of the system’s damage when a component is lost increases with the component’s criticality [5]. Criticality, therefore, is the measure of an infrastructure asset’s importance to the system’s resilience, defined by the cost to users, owners, and society resulting from a loss in functionality [6,7]. Designing reliable and resilient transportation systems requires the identification of the critical components that are essential to system functionality [8]. The analysis of the performance of the transportation network under potential disruptions heavily relies on the identification of critical links, assisting practitioners and policy makers in mitigating impacts, prioritizing projects, and enhancing system resiliency [9]. As a result, this topic attracts considerable attention from federal, state, and local transportation agencies, along with private sector organizations.
Many studies have investigated and deployed various multi-criteria methods for assessing criticality. For example, the Connecticut DOT resiliency pilot study measured criticality by employing metrics such as average daily traffic (ADT), accident count, and flood zone, with subjective stakeholder input. While this study provided useful asset-specific diagnostics, its criticality scoring approach was primarily qualitative and grouped structures into broad categories (i.e., low, moderate, or critical) based on aggregated metric values and subjective input [10]. Based on the qualitative criticality scoring process, 20 out of the 52 structures evaluated were rated as moderately critical, 19 as critical or very critical, and the remainder as low, indicating a broad range of risk levels. While this qualitative criticality scoring process provided useful insights, it lacked a transparent mechanism for weighing the relative importance of each criterion, thereby limiting its adaptability to different contexts or the varied preferences of decision-makers. These limitations underscore the need for a more systematic, data-driven approach that can incorporate stakeholder input and adjust weighting to better reflect diverse priorities. Similarly, the Colorado DOT I-70 resiliency study employed an equal weighting approach to rank assets based on six quantitative criticality metrics, which included annual average daily traffic (AADT), roadway classification, freight, tourism, social vulnerability, and redundancy [6]. The equal-weighted approach assumes that each criterion receives equal consideration and weight in assessing link criticality. The criticality score for each asset was derived by summing the values of these six criteria. These scores were used to categorize roadway segments into criticality groups expressed as low, moderate, and high, with cutoff thresholds established to classify approximately 50% of centerline miles as low criticality, 25% as moderate, and 25% as high. The resulting distribution showed 53.8% of assets classified as low, 25.5% as moderate, and 20.7% as high in criticality. However, this approach may not always reflect a stakeholder group’s varied and, sometimes, competing priorities. An unequal weighting approach could be used to assign weights to each criterion where weights follow from the individual and collective priorities of the stakeholder group. This would provide a more flexible and context-sensitive assessment of asset criticality.
In this paper, we develop a multi-criteria estimation of asset criticality using a weighting approach in which weights are based on stakeholder inputs. We adopt six criticality metrics [6] to estimate asset criticality for a large highway transportation system. The key innovation in this paper lies in integrating an analytical hierarchy process (AHP) into multi-criteria asset ranking, which enables us to estimate a combined criticality score using stakeholder-derived weights rather than an equal weighting approach. This results in a more representative, data-driven prioritization approach than what has been achieved in prior work.
AHP is a widely accepted multi-criteria decision-making approach. In AHP, factors are ordered in a hierarchical (ranked) framework. AHP is popular because it reflects the thinking and judgments of participants/subjects by simplifying complex decisions into pairwise comparisons [11]. By applying AHP to the transportation domain, specifically to criticality assessment, we introduce a flexible and generalizable approach that can accommodate different sets of criteria. This paper advances the state of practice in transportation asset criticality assessment through two main contributions. The aims of this paper are (1) to develop a framework for quantifying asset criticality that can be applied to large scale transportation networks and can reflect stakeholder priorities and (2) determine asset criticality weights and ranking through the application of the framework to a statewide transportation system in the US. By replacing the equal-weighting schemes found in existing studies, these contributions yield a data-driven framework that can be customized to different regions, policy objectives, and resilience planning scenarios, filling key gaps left by prior pilot and report-based approaches.
2. Literature Review
Measures of resilience, reliability, robustness, importance, vulnerability, and criticality have been introduced to evaluate how transportation assets affect overall system performance [9]. Among these, criticality has gained notable attention in both research and practical application [1,5,6,8,12,13,14,15,16,17,18,19,20,21,22]. Generally, the greater the criticality of an asset, the more severe the system impact when that asset becomes non-operational [5].
Criticality metrics can be categorized into performance-based and topological methods. Performance-based methods investigate changes in traffic flow such as travel time and volume that result from variations in supply and demand. However, these methods can be high in computational cost for large networks due to their iterative calculations. In contrast, topological methods which rely on graph theory concepts like connectivity, accessibility, and maximal flow, require less data and offer greater computational efficiency [8]. Examples of topological measures include betweenness centrality (BC) [8], the link criticality index (LCI) [12], the travel-time weighted betweenness centrality (TTWBC) [8], practice friendly link-criticality index (PFLCI) [12], and the efficiency index (EI) [13]. A widely used performance-based technique for evaluating link criticality involves conducting a network scan. One such method is the network robustness index (NRI), which utilizes a traffic assignment approach to quantify criticality by measuring changes in the network’s total travel time before and after link failures [1]. Using the NRI poses a risk of generating disconnected networks when links are omitted, which prevents accurate estimation of the system-wide impacts of link failures on travel time. To overcome this limitation, the importance score (IS) metric was developed [3,5,6].
However, methods that rely solely on vehicle- or network-based metrics like those discussed in the paragraph above may fail to capture the broader impacts of disruptions [19]. To address this, multi-criteria metrics are introduced [19]. One example application used three factors to prioritize links and allocate resources for retrofitting, maintenance, and security purposes [17]. The first factor considers link volume, the second evaluates the spatial proximity of critical facilities served by the links, and the third accounts for the number of origin–destination pairs connected by a link according to network characteristics [19]. Another adaptable and comprehensive multi-criteria approach incorporated sixteen essential metrics, such as mobility, emergency response, access to fuel and energy, goods and materials, medicine, and food [23].
In this paper, we adopt the Colorado DOT (CDOT) multi-criteria analysis for criticality assessment [6] for exhibition purposes, although any set of criticality criteria could be adopted. The criteria include AADT, roadway classification, freight, tourism, social vulnerability via the Social Vulnerability Index (SoVI), and redundancy (Table 1) [6]. As a whole, the set of criteria include environmental, social, and economic impacts, multiple modes (vehicle and truck/freight), economic sectors (freight, tourism), and population groups (vulnerable populations) [6].

Table 1.
Criticality measures defined by CDOT study.
The criteria are described as follows and represent a mix of roadway-link-level and county-level estimates. The AADT indicates the average traffic volume for a location along a roadway throughout the year. It is a crucial parameter for transportation planning and funding allocation [24]. The roadway classification defines a roadway segment’s role in serving traffic flow across the network. The functional class is defined by the type of service the road provides as well as other physical features like lane widths, shoulder widths, curve radii, etc. [25]. Freight value is the total value of imports and exports in a region. In this work, we define spatial geography by county. Freight value by county is estimated from the Freight Analysis Framework version 4 (FAF4), a national model of commodity demand. Freight value could also be estimated from a regional or statewide freight-based travel demand model or survey. Tourism represents the total, annual expenditure on tourism. We use the county geography to estimate tourism expenditure. SoVI is a comparative index developed by [26]. It is an aggregate measure that includes 29 socio-demographic variables and represents a region’s level of social vulnerability. The socio-demographic variables are divided across eight categories: wealth, race (black) and social status, age, ethnicity and lack of health insurance, special needs populations, service sector employment, race (Native American), and gender (female). A SoVI score more than 1.5 standard deviations above the mean indicates high social vulnerability, while a score lower than 1.5 standard deviations indicates low vulnerability. The redundancy metric captures the system-wide change in travel time resulting from a complete link closure. Any link that, when closed, leads to a higher system-wide travel time relative to the system-wide travel time under base conditions (all links operational) are more critical. This is a measure of redundancy based on the availability of alternate routes of similar distance and travel time. A link served by few or longer detour routes may have a larger impact on system-wide travel time. The redundancy metric used in this study is an example of a performance-based metric, specifically a modified NRI [25].
As noted, measures of AADT, roadway classification, and redundancy can be attributed to a link, as these are link-level measures. On the other hand, freight value, tourism, and SoVI are applied as county-level metrics. To bring all measures to a common spatial dimension, namely link-level measures, all roadway links in a county are assigned the same value corresponding to the county in which they are located. While county aggregation was used in this paper, any sub-region geography could be used.
Multiple criticality criteria can be combined in several ways to produce a single criticality “score” for a transportation asset. Two of the more common approaches to combine criteria are equal weighting (or an unweighted average) and unequal weighting (or a weighted average). In some contexts, certain criteria may be more important such as when viewed by professionally diverse stakeholder groups. Thus, an unequal weighting approach can be introduced.
AHP is a multiple-criteria decision analysis (MCDA) tool. With AHP, conflicting and complex factors are placed in a hierarchical (ranked) framework [27]. It can be used to determine weights to apply to various factors when seeking to combine factors into a single value or score. We use AHP to estimate the individual weights of each criticality criterion such that the weights embody the priorities of a stakeholder group. The ranking of weights then tells us the relative importance of each criterion [28]. By replacing complicated relational comparisons, AHP adopts pairwise comparisons to estimate a decision matrix. The pairwise approach allows the stakeholder to compare two criteria at a time. As an alternative, stakeholders could be asked to rank criteria directly, which is called weighting by ranking. However, weighting by ranking loses explanatory power as the number of criteria increases. As an alternative, the AHP method is consistent and effective in producing a ranking and set of weights that represent the relative importance alternatives.
Several example applications of AHP in transportation engineering are discussed in this section to give a basis for its selected use in this paper. The AHP was used as a decision-support tool for contractor selection [29] to discover the best contractor based on factors beyond just the lowest bid. In a comparative study, the AHP method facilitated the selection decision for competing intersection designs among five design alternatives [30]. The ranking criteria: construction cost, traffic safety, average delay, fuel consumption and CO emissions, were evaluated by eight traffic engineers, who assessed five design alternatives based on these factors. The authors of [31] used AHP to analyze solid waste disposal’s environmental impacts and identify the best management option. The study assessed stakeholders’ opinions and judgments, including residents and institutional workers, to determine the most suitable waste disposal option.
In summary, the literature demonstrates a wide range of methods for assessing link and network criticality, from graph-based topological metrics to more complex, performance-based approaches. While topological methods offer computational simplicity, performance-based models provide deeper insights but are resource-intensive. Various measures, such as betweenness centrality, the network robustness index, and importance score, have been developed to quantify the impact of link failures on system functionality. However, most existing models either lack stakeholder input or multidimensional evaluation. The purpose of this study is to address these gaps by developing a systematic, stakeholder-informed method for ranking transportation assets based on their criticality to the overall transportation system. As a novel approach, we use the AHP method and present a case study of the applied approach for the state of Arkansas.
3. Methods and Data Processing
The AHP method was applied to estimate transportation asset criticality by first defining the hierarchical structure that includes listing and sorting goals and criteria. The approach next requires the collection of input data via survey or interview through pairwise comparisons. Third, from the survey data, consistency ratios are calculated to ensure that survey respondents’ judgements follow logical order. Also, the individual priorities of the survey subjects pairwise comparisons are estimated. Finally, the overall criteria weights, resulting from all survey responses, are aggregated. The following section details this approach.
3.1. Hierarchical Framework and Definitions
The hierarchy captures the relationship between the overall goal and the evaluation criteria. In this study, the final hierarchy established defines the goal as “measuring the criticality of highway system assets” with individual metrics such as freight, roadway classification, AADT, etc., as the criteria (Figure 1). For this work, we chose six criteria, defined as shown in Figure 1, but AHP can be attuned to any set and number of criteria. While in this paper we selected criteria from a prior study, criteria could be identified by surveying stakeholders.
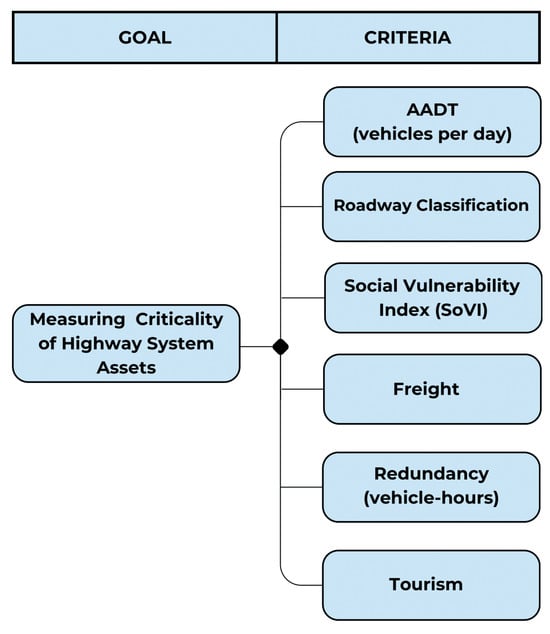
Figure 1.
Analytic hierarchy framework applied to six asset criticality criteria.
3.2. Pairwise Comparisons via Survey
An online survey was administered through a commercial platform to collect criteria weights. This method was preferred over other traditional methods like paper, mail survey and telephone, as it offers a user-friendly interface to visually adjust and complete the pairwise comparisons, provides real-time access to the results, thereby reducing costs, and, lastly, allows for a broad sample as participation is not limited by costs of mailing as is the case with paper-based surveys or researcher-time commitments and bias, as is the case with interviews [32].
3.3. Survey Sample Size
The sample size for the survey is influenced by two key factors: the consistency of judgements and their practical validity [33]. The number of experts (sample size) involved varies depending on the application: 8 traffic engineers were involved in a study selecting intersection design types [32]; 48 experts from city agencies, academic institutions, and mobility service providers completed criteria and indicator weighting for social sustainability assessment of mobility services [34]; 191 healthcare professionals participated in research on risk factors for fall prevention [35]. To evaluate the criticality of highway transportation assets using multiple criteria, a diverse group of experts with specific knowledge in transportation was needed and served as the sample frame [36].
Convenience (non-probability) sampling was employed to engage a total of 227 experts in the US through email solicitation using professional organization listservs, committee membership rosters, public agency directories and online professional networking platforms (e.g., LinkedIn). The sample was classified according to three demographic categories: profession, practice area, and agency. Profession refers to the respondent’s role in their organization, such as engineers, analysts, consultants, planners, project coordinators, inspectors, office specialists, managers, surveyors, supervisors, and researchers. Practice area identifies their expertise including asset management, emergency and response, maintenance, construction, operations, engineering, planning, system information and research, survey, and policy. Agency indicates their place of employment, including federal and state departments of transportation (DOTs), state, regional, state, and local governmental transportation agencies, academic institutions, and private engineering consulting firms.
3.4. Survey Questionnaire
The survey had participants compare the relative importance of the criteria with respect to the overall goal. Participants were provided with brief definitions of each criterion and a statement of the goal. Finally, using the Fundamental Scale for Paired Comparisons [27] (Table 2), participants were asked to provide pairwise scores for all combinations of the six criteria resulting in 15 comparisons (15 questions).

Table 2.
Paired comparisons expressed by the Fundamental Scale.
Participants viewed the pairwise comparisons as sliding bars with the rightmost and leftmost edges of the bar representing “extremely important” levels and zero serving as the neutral center (Figure 2). A simple example using pairwise comparisons of oranges, grapes, and mangoes accompanied the descriptions of criteria.

Figure 2.
Survey questionnaire on Qualtrics platform.
3.5. Consistency Ratio Estimation
Pairwise comparisons can result in inconsistent rankings of criteria [37]. For example, a respondent may indicate that roadway classification is more important than freight value, freight value is more important than redundancy, but redundancy is ranked more important than roadway classification, even though roadway classification should be ranked higher than redundancy in this case. Collecting pairwise comparisons from multiple individuals and aggregating presents several challenges to both consistency and reliability. First, individual respondents may interpret the comparison scale differently, what one expert considers “strongly important” another may rate only as “moderately important”, depending on their individual priorities. Second, the experts’ domain knowledge varies, so some may feel less qualified to compare certain criteria, leading to random choices rather than deliberate, logical comparisons. Finally, although an online survey offers a user-friendly interface, as the number of required comparisons increases, it may induce inconsistent responses.
To ensure logical consistency in stakeholder responses, AHP uses the consistency ratio (CR), which evaluates the coherence of each individual’s judgments. The CR used to calculate the consistency of each individual set of judgments and exclude inconsistent logic is formulated as [38] in the following:
where
CI = consistency index calculated as ;
RI = random index which is the average CI for randomly generated matrices of the same order [28,39];
= largest principal eigenvalue of a positive reciprocal pairwise comparison matrix of size (number of criteria).
A CR below 0.10 is ideal, whereas a CR under 0.20 is considered acceptable [38]. Responses with a CR below 0.20 were kept and those with higher CR were removed from the study. The ahpy library in Python version 3.10.0 was used to compute the reciprocal matrices and individual priorities from pairwise comparisons obtained in the survey [40].
3.6. Pairwise Comparison Matrix and Criteria Weights
A central component of the AHP is the construction of a pairwise comparison matrix, derived from responses of relative importance of each criterion with respect to the overall goal. In this study, a 6 x 6 pairwise comparison matrix was formed for each respondent. The comparison matrix A = is defined as [41] in the following:
where
indicates that criterion i is more important than j;
indicates equal importance;
indicates that the criterion i is less important than j;
indicates the reciprocal matrix.
The resulting importance matrices were then used to compute the local weights of each criterion through eigenvector estimation and normalized averaging.
Three approaches can be used to aggregate judgements: (1) aggregating individual priorities (AIP), (2) aggregating individual judgements (AIJ), and (3) aggregating the individual’s derived priorities in each node in the hierarchy. The third method is not as relevant and not commonly used in practice.
The AIP method is applied when individuals act independently, each with their own value systems, focusing on the resulting priorities of alternatives [42]. Using the AIP approach, we can analyze how respondents ranked each criterion, illuminating varied rankings, expertise, and priorities. Ultimately, this approach allows for the computation of overall criteria weights. If a respondent prioritizes a particular criterion over others, this can significantly impact the final and overall weights after aggregation. AIP is calculated to obtain the final priority vector either with the arithmetic mean, a = [] or geometric mean, g = [] as follows [43]:
where
is the arithmetic mean of the j-th criterion;
is the geometric mean of the j-th criterion;
is the normalized vector of individual priorities of the i-th expert and j-th criterion;
n is the number of expert individuals;
m is the number of criteria.
AIJ involves synthesizing the resulting reciprocal matrix from the individual pairwise comparisons into a single judgment matrix using the geometric mean. The AIJ approach is employed when individuals within the same group share common goals and values, combining their judgments so the group acts as a single “individual” [42]. This method emphasizes the varying rankings and priorities among stakeholder groups. Accordingly, AIJ produces unique criterion rankings and weights for each stakeholder and practice area group. The AIJ, calculated using the geometric mean, is expressed as follows [41,44]:
where
is a set of normalized eigenvector components;
is a set of eigenvector components.
4. Results
The results are presented with detailed analysis of response rates by sector, consistency ratios, overall criterion weights, stakeholder-specific weights, the influence of the hierarchy structure on ranking outcomes, and the effects of sample size on rank stability. Compared to existing AHP-related studies, this work offers a particularly comprehensive treatment of result interpretation. Notably, the study includes a novel examination of sample size impacts on ranking and weight stability through a random selection approach, an aspect rarely addressed in the AHP literature. This contribution provides a valuable perspective for researchers and practitioners by addressing a critical gap in guidance regarding sample size estimation in AHP applications.
4.1. Response Rates by Sector
The survey was administered between July and November 2022, yielding 30 responses from 227 distributed surveys, resulting in a response rate of 13.2%. Respondents finished the survey in 13 min (standard deviation of 8.7 min), on average.
Engineers (43%), stakeholders from the planning practice area (46%) and stakeholders from private industry (41%) constituted the majority (Figure 3). Response rates by profession and practice area could not be determined, as the sample frame lacked this information since the contact lists used for the survey did not include respondents’ professions or practice areas.
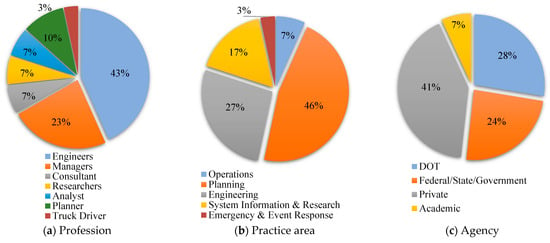
Figure 3.
Survey respondents by profession, practice area, and agency (N = 30).
The majority of respondents were from private industry (40%) (Figure 4). Response rates by organization type were as follows: 8.7% for academic institutions, 13.6% for private engineering consulting firms, 13.2% for state, local, and regional transportation agencies, and 12.7% for departments of transportation (DOTs).
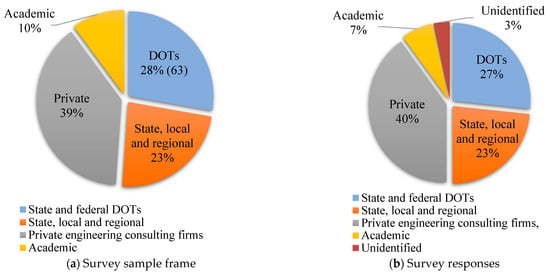
Figure 4.
Survey sample frame and respondents by agency.
4.2. Consistency Ratios of Stakeholders
The mean consistency ratio (CR) across responses was 0.33, with a standard deviation of 0.068. Of the 30 total responses, 21 had a CR below 0.20 and were therefore included in the final calculation of criteria weights.
When analyzed by self-reported profession, respondents identifying as managers exhibited the highest inconsistency, with an average CR of 0.131. In contrast, planners showed the highest consistency, with an average CR of 0.024. Those identifying as engineers, analysts, and consultants had average CRs of 0.128, 0.112, and 0.089, respectively. Researchers averaged a CR of 0.062.
By practice area, respondents working in operations had the least consistent responses (average CR = 0.20), while those in emergency and event response demonstrated the most consistent responses (average CR = 0.064). Average CRs for planning and engineering practice areas were 0.121 and 0.107, respectively. Respondents in system information and research reported an average CR of 0.09. Variations in consistency may partially reflect differences in sample size across practice areas.
Looking at self-reported agency type, respondents from state and federal DOTs had the highest average CR (0.145), indicating lower consistency, whereas those from private engineering consulting firms had the lowest average CR (0.103), reflecting greater consistency.
4.3. Ranking and Criteria Weights
Using the 21 responses that satisfied the consistency ratio threshold, criterion priority weights were calculated through the AIP method (Figure 5). Among the criteria, AADT emerged as the top priority, followed in descending order by redundancy, freight value, roadway classification, SoVI, and tourism. Together, AADT and redundancy accounted for a combined weight of 0.475, nearly half of the total weighting and marginally exceeding the combined weight of the remaining four criteria.
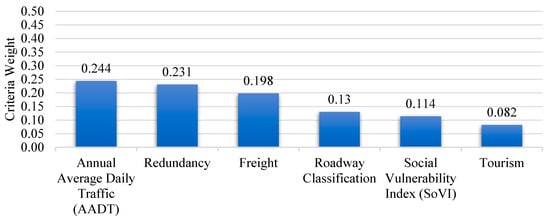
Figure 5.
Criteria and weights derived from an AHP method for aggregation of individual priorities (AIP) approach.
4.4. Criteria Weight Variation by Groups of Stakeholder
Next, we analyzed the overall rankings derived from AIJ aggregation across different stakeholder groups (Figure 6 and Figure 7). The findings are summarized below:
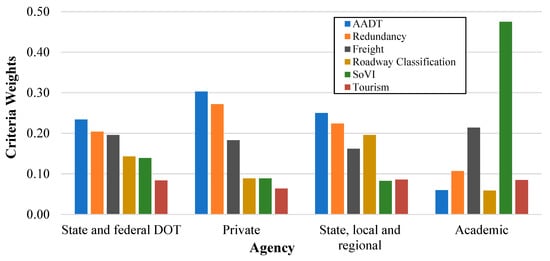
Figure 6.
Criteria weights and rank of stakeholders’ agency.
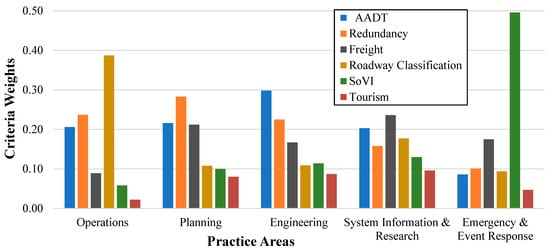
Figure 7.
Criteria ranks and weights of stakeholders by practice area.
- AADT received the top ranking from state and federal DOTs, private engineering consulting firms, and state, local, and regional governmental transportation agencies, but was ranked fifth by the academic group. By practice area, AADT ranked first among engineering professionals, second among those in planning and system information and research (SIR), third in operations, and fifth in emergency and event response (EER).
- Redundancy was consistently ranked second by state and federal DOTs, private engineering consulting firms, and state, local, and regional agencies, while the academic group placed it third. It was prioritized first by planning professionals, second by those in operations and engineering, and ranked third and fourth by respondents in EER and SIR, respectively.
- Freight value showed a more diverse ranking: it was placed second by the academic group, third by state and federal DOTs and private consultants, and fourth by local and regional agencies. In terms of practice area, it ranked first in SIR, second in EER, third in planning and engineering, and fourth in operations.
- Roadway classification was ranked third by local and regional agencies and fourth by all other stakeholder groups. Among practice areas, it was most highly valued by operations professionals, achieving a priority weight of 0.387. It ranked third in SIR, fourth in planning and EER, and fifth in engineering.
- SoVI was ranked highest by the academic group, with a notably high weight of 0.475. It was placed fourth, fifth, and sixth by state and federal DOTs, private consultants, and local/regional agencies, respectively. EER respondents also ranked it first, assigning it a significant weight of 0.496. In contrast, SoVI was ranked fourth by engineering and fifth across all other practice areas.
- Tourism consistently placed sixth among state and federal DOTs and private consultants, while academic and local/regional agency respondents ranked it fourth and fifth, respectively. Across all practice areas, tourism was unanimously ranked sixth, aligning with its overall position in the final criteria ranking.
The rankings provided by both state and federal DOTs as well as private engineering consulting firms closely aligned with the overall criteria order determined by the AIP method, showing only slight variations in weighting. For example, freight was assigned weights of 0.198, 0.196, and 0.183, respectively.
4.5. Criteria Hierarchy Effects on Ranking
To assess the influence of reducing the number of criteria and potential inter criteria correlations on rankings and weights, a postprocessing analysis was performed in which each criterion was individually removed and the remaining weights recalculated to observe any changes in the overall results. The findings indicate that the adjusted rankings remained largely consistent with the original set, except for the freight criterion. When freight was excluded, a shift occurred: redundancy rose to the top position (previously second), while AADT moved to second place (previously first). The positions of roadway classification, SoVI, and tourism remained unchanged.
4.6. Sample Size Effects on Ranking
The stability of criteria rankings was also evaluated across different sample sizes, ranging from 3 to 21, using randomly selected subsets. As the sample size increased from 3 to 12, noticeable fluctuations in the rankings were observed. However, once the sample size reached 15, the rankings aligned with those from the full set used in the final analysis (Figure 8). These results suggest that a relatively modest sample size, fewer than 30 responses, can still yield stable and reliable ranking outcomes.
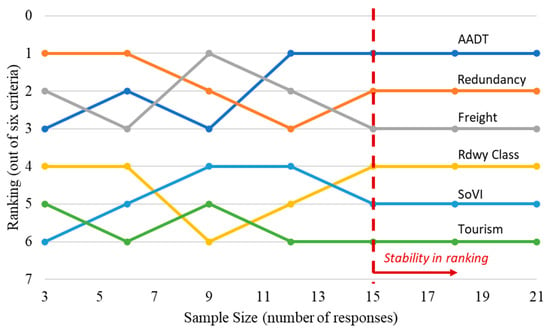
Figure 8.
Criteria ranking and weights of practice area of respondents.
4.7. Statewide Transportation Network Asset Criticality Ranking
The following example illustrates how the weights can be applied to estimate the criticality of a link in a transportation network, using the state of Arkansas as a case study. Following [6], each criticality metric is divided into levels tailored to the implementation context of Arkansas (Table 3). Each criterion is assigned to a numerical criticality score (1 to 5) that is then averaged using AHP weights derived from an Arkansas sub-sample of the AHP survey to estimate a link’s overall criticality. The numerical criticality score ranges are based on distribution of the data and are specific to the state of Arkansas traffic volumes, freight tonnages, tourism, and socio-demographic characteristics.

Table 3.
Criteria levels and weights derived from the analytical hierarchy process (AHP) method applied to the state of Arkansas (modified from [6]).
For example, consider the following levels of the criteria that are estimated for a single link:
- AADT is 2000 vehicles per day and is categorized as Level 3.
- Redundancy is calculated at 1900 vehicle hours and categorized as Level 4.
- Freight value is USD 850M, corresponding to Level 2.
- Roadway class is designated as a principal arterial and assigned to Level 3.
- SoVI score is 3.20 and categorized as Level 5.
- Tourism value is USD 5M and classified as Level 1.
The unequally weighted average criticality score is computed using the following formula:
where
is the overall criticality score for link i,
represents the weight assigned to criterion n, e.g., AHP deduced weights,
is the score of the criterion, n, for each link i,
is the total number of criteria, e.g., N = 6.
- The weighted average is calculated as follows:Criticality = (0.244 × 3) + (0.231 × 4) + (0.198 × 2) + (0.13 × 3) + (0.114 × 5) + (0.082 × 1) = 3.10
The example link with a criticality score of 3.10 is considered more critical than a link with a score of 2.35, but less critical than a link with a score of 4.40.
The methodology was applied to the Arkansas’ state roadway network using both equal (e.g., weights of 1/6 applied to all criteria) and AHP-derived weighting approaches. Overall, under the equal weighting approach, 19% of roadways were deemed highly critical (criticality > 2.8 based on natural breaks), whereas only 9% were rated highly critical using AHP weights. Under the equal weighting approach, 25% and 56% of roadways were considered to have moderate and low criticality, respectively, compared to 19% and 72% with the AHP weights. Ten roadway segments were identified as the most critical using AHP weighting with criticality scores above 4.2. A main shift occurs when criteria are subject to county level aggregation. For example, tourism data is measured by county, resulting in all roadway segments in a county having the same tourism score. Thus, reducing the weight of tourism criteria lowers the criticality of all roadway segments in that county.
5. Discussion
The final aggregated criteria weights indicate a clear prioritization among the six criteria used in the AHP analysis. AADT holds the highest weight at 0.244, followed closely by redundancy at 0.231 and freight at 0.198, highlighting their dominant importance in the asset prioritization framework. Roadway classification and the SoVI received moderate weights of 0.130 and 0.114, respectively, while tourism ranked lowest at 0.082. These results align with the overall rankings derived from stakeholder input and reflect the relative emphasis placed on traffic volume, network redundancy, and freight movement in determining critical transportation assets. The criteria weights also effectively illustrate the proportional differences among the criteria.
The AHP derived weights are sensitive to factors such as decreases in sample size, the composition of respondents’ professions, practice areas, organizations, and the aggregation approach used (e.g., AIJ or AIP). Although this study achieved a response rate of 13.2%, it employed a non-probability sampling method. Therefore, it is not possible to weigh the sample across all respondent demographics to derive population-level estimates, which limits the generalizability of our findings. Considering the 21 responses collected, it is inadvisable to draw strong conclusions regarding the priorities of minority respondent groups. For example, one response was obtained from EER. However, because AHP is a subjective technique rather than a statistical method, smaller sample sizes are acceptable as long as the responses reflect the logical and analytical judgments of experts representing diverse stakeholders [33,36].
The AIP and AIJ methods are employed under the assumption that decision-makers hold equal importance. From the AIP of the individual responses, prioritization of a criterion by an individual respondent significantly impacts the final weights. When stakeholder rankings were the same, the AIJ method yields only minor differences in weights compared to AIP. Overall, the choice of AIJ over AIP highlights the sensitivity of the weights to how the group’s (practice area or agency) decision-making process is interpreted. The AIJ approach is more suitable when the group shares a common goal, while the AIP approach is used when individuals make decisions based on their personal priorities.
Consistency is a key requirement of the AHP method [36]. The acceptable CR values for different matrices sizes (e.g., number of criteria) are: 0.05 for a three by three matrix (three choices), 0.08 for a four by four matrix and, 0.2 for larger matrices [36,38]. In this study, 21 responses met the recommended consistency ratio threshold (CR < 0.20). Variations in consistency can partly be attributed to differences in sample sizes across stakeholder groups. To ensure consistent responses, it is important to identify the area of expertise required for the pairwise comparisons and engage respondents with both subject matter knowledge and practical experience [33]. While expertise influences the consistency of individual responses, it does not affect the reliability of the AHP results, as only logically consistent responses are included in the aggregation.
No correlation was found between the CR and the amount of time spent taking the survey. Of the 21 respondents who met the acceptable CR threshold, 14 completed the pairwise comparisons in 20 min or less, while the remaining 7 took longer. Among the nine respondents with inconsistent judgments, five finished in under 20 min, and four took more than 20 min. The observed lack of correlation between the CR and survey completion time indicates that response speed does not predict judgment quality or consistency. Future survey design should prioritize targeted engagement of participants with appropriate subject matter expertise, supported by cohesive training and real time, built-in consistent feedback.
6. Conclusions
This paper introduces an application of the analytic hierarchy process (AHP) to rank and weight criteria for measuring the criticality of roadway segments across a statewide transportation network. The AHP provides a unique framework to aggregate diverse stakeholder rankings on multiple criteria by employing a pairwise rating approach. The AHP was carried out via an online survey, which garnered 30 complete responses, resulting in a 13.2% response rate. The respondents comprised individuals from private consulting firms, public transportation agencies, and academic institutions throughout the United States. After applying a consistency threshold to individual responses, we employed the AIP aggregation method to calculate the final criteria weights from the 21 consistent responses.
The key finding from the criteria ranking indicates that AADT consistently holds the highest importance among the six criteria, with a weight of 0.244. Redundancy ranks second with a weight of 0.231. Together, AADT and redundancy account for 0.475 of the total weight, representing nearly half the combined weight of the other four criteria. The experts surveyed concluded that tourism is the least significant among the six criticality metrics, with a weight of 0.082. These rankings were consistent when any criteria except freight were removed from the choice set. Alternate hierarchical structures or sets of criteria may be considered in future work. Additionally, the number of responses was evaluated regarding the stability of the rankings. With 15 responses, the ranking of criteria reached consistency. This is a key finding since the literature does not provide sample size recommendations in AHP applications.
Individual responses highlight the AHP model’s sensitivity to stakeholder roles and characteristics. For instance, there were few academic participants, with one being the only respondent representing the emergency response field. This respondent ranked SoVI as the most critical criterion. Future research should aim to engage a larger number of respondents from diverse stakeholder groups, considering their knowledge level and practical experience.
Participants were also asked about other important metrics for assessing the criticality of statewide highway transportation assets. Respondents suggested additional metrics such as volume-to-capacity ratio, safety, supply chain vulnerability, as well as the incorporation of other transportation facilities such as airports, seaports, and others. Future research can integrate these additional metrics into this framework to enhance criticality and resiliency assessments.
By translating expert judgments into transparent and reproducible weights through an AHP, our framework equips transportation agencies and policymakers with a flexible decision-support tool. They can combine multiple criticality criteria into a single metric based on consistent stakeholder criteria rankings. The criticality criteria can be applied universally to all system assets (roadways, bridges, culverts, etc.), for a quantitative, consistent, systematic ranking that reflects the priorities of the agency. This approach can guide capital and maintenance investment decisions, inform resilience-focused policies, and prioritize response and recovery actions toward assets whose failure would impose the greatest system-wide impact, thereby enhancing the resilience of critical transportation networks.
Author Contributions
Study conception and design: S.H., S.K.M. and K.A.-N.; data collection: K.A.-N.; formal analysis; K.A.-N. and S.H.; results interpretation; K.A.-N. and S.H.; draft manuscript preparation; K.A.-N., S.H. and S.K.M.; supervision: S.H. and S.K.M.; funding acquisition; S.H. and S.K.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Arkansas Department of Transportation (ARDOT), grant number TRC 2003. The APC was funded by the Open Access Publishing Fund provided by the University of Arkansas Libraries.
Institutional Review Board Statement
The study was conducted in accordance with the Institutional Review Board (or Ethics Committee) of the University of Arkansas (protocol code 2206406049 and date of approval 1 July 2022).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are not available due to privacy or ethical restrictions.
Acknowledgments
The Arkansas Department of Transportation (ARDOT) sponsored the project that led to this paper.
Conflicts of Interest
Author Kwadwo Amankwah-Nkyi was employed by Jacobs Engineering Group, Inc. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as potential conflict of interest.
References
- Sullivan, J.L.; Novak, D.C.; Aultman-Hall, L.; Scott, D.M. Identifying Critical Road Segments and Measuring System-Wide Robustness in Transportation Networks with Isolating Links: A Link-Based Capacity-Reduction Approach. Transp. Res. Part A Policy Pract. 2010, 44, 323–336. [Google Scholar] [CrossRef]
- García-Palomares, J.C.; Gutiérrez, J.; Martín, J.C.; Moya-Gómez, B. An Analysis of the Spanish High Capacity Road Network Criticality. Transportation 2018, 45, 1139–1159. [Google Scholar] [CrossRef]
- Pant, S.B. Transportation Network Resiliency: A Study of Self-Annealing; Utah State University: Logan, UT, USA, 2012. [Google Scholar]
- Zare, N.; Tumminello, M.L.; Macioszek, E.; Granà, A. Assessing the Operating Efficiency and Resilience of Urban Intersections: Case Studies from Poland. In Transport Systems and Urban Logistics; Sierpiński, G., Naumann, S., Macioszek, E., Eds.; Lecture Notes in Networks and Systems; Springer Nature: Cham, Switzerland, 2024; Volume 1257, pp. 45–59. ISBN 978-3-031-81776-2. [Google Scholar]
- Jenelius, E.; Petersen, T.; Mattsson, L.-G. Importance and Exposure in Road Network Vulnerability Analysis. Transp. Res. Part A Policy Pract. 2006, 40, 537–560. [Google Scholar] [CrossRef]
- Flannery, A. I-70 Corridor Risk & Resilience Pilot. 105; Colorado Resiliency Office: Denver, CO, USA, 2018. [Google Scholar]
- Board, T.R.; National Academies of Sciences, Engineering and Medicine. Investing in Transportation Resilience: A Framework for Informed Choices; The National Academies Press: Washington, DC, USA, 2021. [Google Scholar]
- Almotahari, A.; Yazici, M.A. A Link Criticality Index Embedded in the Convex Combinations Solution of User Equilibrium Traffic Assignment. Transp. Res. Part A Policy Pract. 2019, 126, 67–82. [Google Scholar] [CrossRef]
- Almotahari, A.; Yazici, A. Impact of Topology and Congestion on Link Criticality Rankings in Transportation Networks. Transp. Res. Part D Transp. Environ. 2020, 87, 102529. [Google Scholar] [CrossRef]
- FHWA Climate Resilience Pilot Program: Connecticut Department of Transportation; U.S. Department of Transportation: Washington, DC, USA, 2016.
- Smith, J.T.; Tighe, S.L. Analytic Hierarchy Process as a Tool for Infrastructure Management. Transp. Res. Rec. 1974, 8, 25. [Google Scholar] [CrossRef]
- Almotahari, A.; Yazici, A. Practice Friendly Metric for Identification of Critical Links in Road Networks. Transp. Res. Rec. 2020, 2674, 219–229. [Google Scholar] [CrossRef]
- Nagurney, A.; Qiang, Q. A Transportation Network Efficiency Measure That Captures Flows, Behavior, and Costs with Applications to Network Component Importance Identification and Vulnerability. SSRN J. 2007, 97, 9328. [Google Scholar] [CrossRef][Green Version]
- Gauthier, P.; Furno, A.; El Faouzi, N.-E. Road Network Resilience: How to Identify Critical Links Subject to Day-to-Day Disruptions. Transp. Res. Rec. 2018, 2672, 54–65. [Google Scholar] [CrossRef]
- Madar-Vani, G.; Maoh, H.; Anderson, W. Modeling the Criticality of a Regional Trucking Network at the Industry Level: Evidence from the Province of Ontario, Canada. Res. Transp. Bus. Manag. 2022, 43, 100732. [Google Scholar] [CrossRef]
- Jafino, B.A. An Equity-Based Transport Network Criticality Analysis. Transp. Res. Part A Policy Pract. 2021, 144, 204–221. [Google Scholar] [CrossRef]
- Wang, D.Z.W.; Liu, H.; Szeto, W.Y.; Chow, A.H.F. Identification of Critical Combination of Vulnerable Links in Transportation Networks—A Global Optimisation Approach. Transp. A Transp. Sci. 2016, 12, 346–365. [Google Scholar] [CrossRef]
- Li, F.; Jia, H.; Luo, Q.; Li, Y.; Yang, L. Identification of Critical Links in a Large-Scale Road Network Considering the Traffic Flow Betweenness Index. PLoS ONE 2020, 15, e0227474. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Haque, K.; Mishra, S.; Golias, M.M. Multi-Criteria Based Approach to Identify Critical Links in a Transportation Network. Case Stud. Transp. Policy 2019, 7, 519–530. [Google Scholar] [CrossRef]
- Ukkusuri, S.V.; Yushimito, W.F. A Methodology to Assess the Criticality of Highway Transportation Networks. J. Transp. Secur. 2009, 2, 29–46. [Google Scholar] [CrossRef]
- Li, J.; Ozbay, K. Evaluation of Link Criticality for Day-to-Day Degradable Transportation Networks. Transp. Res. Rec. 2012, 2284, 117–124. [Google Scholar] [CrossRef]
- Scott, D.M.; Novak, D.C.; Aultman-Hall, L.; Guo, F. Network Robustness Index: A New Method for Identifying Critical Links and Evaluating the Performance of Transportation Networks. J. Transp. Geogr. 2006, 14, 215–227. [Google Scholar] [CrossRef]
- Freckleton, D.; Heaslip, K.; Louisell, W.; Collura, J. Evaluation of Resiliency of Transportation Networks after Disasters. Transp. Res. Rec. 2012, 2284, 109–116. [Google Scholar] [CrossRef]
- United States. Federal Highway Administration. Office of Highway Policy Information. Traffic Data Computation Method: Pocket Guide; United States. Federal Highway Administration. Office of Highway Policy Information: Washington, DC, USA, 2018.
- Hernandez, S.; Mitra, S. TRC2003 Data-Driven Methods to Assess Transportation System Resilience in Arkansas; Arkansas Department of Transportation: Little Rock, PC, USA, 2020; p. 144. [Google Scholar]
- Cutter, S.L.; Boruff, B.J.; Shirley, W.L. Social Vulnerability to Environmental Hazards*. Soc. Sci. Q. 2003, 84, 242–261. [Google Scholar] [CrossRef]
- Saaty, R.W. The Analytic Hierarchy Process—What It Is and How It Is Used. Math. Model 1987, 9, 161–176. [Google Scholar] [CrossRef]
- Zahedi, F. The Analytic Hierarchy Process—A Survey of the Method and Its Applications. Interfaces 1986, 16, 96–108. [Google Scholar] [CrossRef]
- Balubaid, M.; Alamoudi, R. Application of the Analytical Hierarchy Process (AHP) to Multi-Criteria Analysis for Contractor Selection. Am. J. Ind. Bus. Manag. 2015, 5, 581–589. [Google Scholar] [CrossRef]
- Using Decision Support Systems for Transportation Planning Efficiency; Advances in Civil and Industrial Engineering; Ocalir-Akunal, E.V., Ed.; IGI Global: Hershey, PA, USA, 2016; ISBN 978-1-4666-8648-9. [Google Scholar]
- Abba, A.H.; Noor, Z.Z.; Yusuf, R.O.; Din, M.F.M.D.; Hassan, M.A.A. Assessing Environmental Impacts of Municipal Solid Waste of Johor by Analytical Hierarchy Process. Resour. Conserv. Recycl. 2013, 73, 188–196. [Google Scholar] [CrossRef]
- Barone, S.; Errore, A.; Lombardo, A. Prioritisation of Alternatives with Analytical Hierarchy Process Plus Response Latency and Web Surveys. Available online: https://www.tandfonline.com/doi/epdf/10.1080/14783363.2014.904565?needAccess=true&role=button (accessed on 3 February 2023).
- Saaty, T.L.; Özdemir, M.S. How Many Judges Should There Be in a Group? Ann. Data. Sci. 2014, 1, 359–368. [Google Scholar] [CrossRef]
- Gompf, K.; Traverso, M.; Hetterich, J. Using Analytical Hierarchy Process (AHP) to Introduce Weights to Social Life Cycle Assessment of Mobility Services. Sustainability 2021, 13, 1258. [Google Scholar] [CrossRef]
- Pecchia, L.; Bath, P.A.; Pendleton, N.; Bracale, M. Analytic Hierarchy Process (AHP) for Examining Healthcare Professionals’ Assessments of Risk Factors: The Relative Importance of Risk Factors for Falls in Community-Dwelling Older People. Methods Inf. Med. 2011, 50, 435–444. [Google Scholar] [CrossRef]
- Wong, J.K.W.; Li, H. Application of the Analytic Hierarchy Process (AHP) in Multi-Criteria Analysis of the Selection of Intelligent Building Systems. Build. Environ. 2008, 43, 108–125. [Google Scholar] [CrossRef]
- Banai, R. Public Transportation Decision-Making: A Case Analysis of the Memphis Light Rail Corridor and Route Selection with Analytic Hierarchy Process. J. Public Transp. 2006, 9, 1–24. [Google Scholar] [CrossRef]
- Wedley, W.C. Consistency Prediction for Incomplete AHP Matrices. Math. Comput. Model. 1993, 17, 151–161. [Google Scholar] [CrossRef]
- Donegan, H.A.; Dodd, F.J. A Note on Saaty’s Random Indexes. Math. Comput. Model. 1991, 15, 135–137. [Google Scholar] [CrossRef]
- Griffith, P. Ahpy: A Python Implementation of the Analytic Hierarchy Process. Available online: https://github.com/PhilipGriffith/AHPy (accessed on 13 November 2022).
- Saaty, T. The Analytic Hierarchy Process; Mcgraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Forman, E. Aggregating Individual Judgments and Priorities with the Analytic Hierarchy Process. Eur. J. Oper. Res. 1998, 108, 165–169. [Google Scholar] [CrossRef]
- Carmo, D.K.d.S.; Marins, F.A.S.; Salomon, V.A.P.; Mello, C.H.P. On the Aggregation of Individual Priorities in Incomplete Hierarchies. In Proceedings of the International Symposium on the Analytic Hierarchy Process, Kuala Lumpur, Malaysia, 23–26 June 2013. [Google Scholar]
- Aragón, T.J. Deriving Criteria Weights for Health Decision Making: A Brief Tutorial; eScholarship Publishing: Oakland, CA, USA, 2017. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).