Abstract
The global transition toward low-carbon energy systems necessitates fundamental innovations in demand-side flexibility, particularly in industrial load regulation. This study presents a systematic review and critical analysis of 90 key research works (2015–2025) to establish a comprehensive framework for industrial load flexibility enhancement. We rigorously examined the tripartite interdependencies among the following: (1) Multi-energy flow physical coupling, addressing temporal-scale disparities in electricity-thermal-gas coordination under renewable penetration; (2) Uncertainty quantification, integrating data-driven and physics-informed modeling for robust decision-making; (3) Market mechanism synergy, analyzing demand response, carbon-P2P hybrid markets, and regulatory policy impacts. Our analysis reveals three fundamental challenges: the accuracy-stability trade-off in cross-timescale optimization, the policy-model disconnect in carbon-aware scheduling, and the computational complexity barrier for real-time industrial applications. The paper further proposes a roadmap for next-generation industrial load regulation systems, emphasizing co-optimization of technical feasibility, economic viability, and policy compliance. These findings advance both academic research and practical implementations for carbon-neutral power systems.
1. Introduction
1.1. Background
With the increasingly severe issue of global climate change, promoting the low-carbon transition of energy systems has become a shared goal of the international community. Governments worldwide are vigorously supporting the development and application of renewable energy through policies, regulations, and technological innovations, aiming to reduce dependence on fossil fuels. The penetration of wind and solar power in electricity systems continues to rise, yet their intermittent and volatile nature poses challenges to grid stability. In response, in September 2023, China’s National Development and Reform Commission (NDRC) and the National Energy Administration (NEA) issued the Notice on the Management Measures for Electricity Demand-Side Response (NDRC Office [2023] No. 1283) [1], requiring all regions to establish a new power load management system capable of achieving a 3–5% regional load control capacity.
Against this backdrop, the development of new power systems demands enhanced responsiveness from demand-side resources. Demand-response resources can participate in various scenarios, including peak shaving, renewable energy integration, and ancillary services, offering flexible and diversified regulation methods [2]. As shown in Figure 1, industrial loads account for the largest share of demand-side capacity, representing over 50% of total energy consumption in society, with adjustable potential exceeding 25% of their total capacity. Fully unlocking the regulation capacity of large industrial loads could increase grid flexibility by approximately 108 million kilowatts. Therefore, as the primary energy consumers on the demand side, industrial enterprises play a crucial role in ensuring power system stability and improving energy efficiency. Optimizing the management and control of industrial loads can not only alleviate grid pressure but also help enterprises achieve energy-saving and efficiency goals. Consequently, research on enhancing the flexibility of industrial loads—particularly their synergistic interaction mechanisms with the power grid—has become a critical issue in smart grid development and the evolution of new power systems.
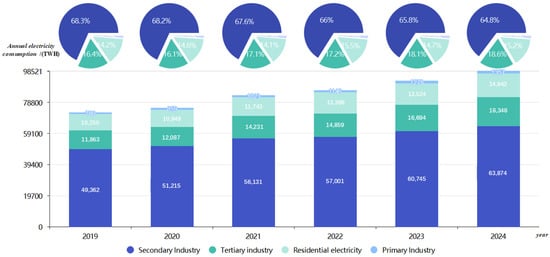
Figure 1.
Statistics of China’s Electricity Consumption Structure by Industry (2019–2024). Note: Data sourced from National Energy Administration. 2024: https://www.nea.gov.cn/20250120/4f7f249bac714e7693adecac996d742f/c.html (accessed on 21 December 2024). 2023: https://www.nea.gov.cn/2024-01/26/c_1310762222.htm (accessed on 21 December 2024). 2022: https://www.nea.gov.cn/2023-01/18/c_1310691508.htm (accessed on 21 December 2024). 2021: https://www.nea.gov.cn/2022-01/17/c_1310427282.htm (accessed on 21 December 2024). 2020: https://www.nea.gov.cn/2021-01/20/c_139682386.htm (accessed on 21 December 2024). 2019: https://www.nea.gov.cn/2020-01/20/c_138720877.htm (accessed on 21 December 2024).
Due to characteristics such as high power demand, diversified energy consumption patterns, significant peak-valley load differences, and limited controllable capacity on the generation side, industrial load clusters possess substantial potential for flexibility enhancement [3]. This inherent flexibility makes demand response from industrial load clusters a critical component for regulating power supply–demand relationships, while also providing important technical support for power system operation optimization.
The core value of flexible industrial loads lies in their ability to actively participate in grid regulation by modifying their load characteristics, energy usage behaviors, or production processes. This includes peak shaving, alleviating power supply–demand imbalances, and improving overall grid operational efficiency. As noted in [3], industrial participation in demand response not only reduces grid peak loads but also enhances renewable energy utilization, thereby facilitating low-carbon transition. Meanwhile, Ref. [4] demonstrates that demand-response management (DRM), as an advanced load management approach, can provide end-users with lower electricity costs and higher energy efficiency, reducing energy expenses while improving corporate economic benefits. Furthermore, the demand-response strategy for energy-intensive industrial loads proposed in [5] reveals its potential in low-carbon economic dispatch: it can achieve cost-benefit outcomes for both power suppliers and industrial enterprises while significantly reducing overall power system carbon emissions. Through proper load regulation and demand-response strategies, industrial enterprises not only serve as flexible resources in power systems but also provide valuable practical experience for building new-type power systems.
In summary, further enhancing industrial load flexibility and demand response holds significant importance for balancing grid loads, promoting efficient energy utilization and advancing carbon neutrality goals. This will not only optimize energy efficiency in industrial enterprises but also provide robust support for constructing a low-carbon smart new-type power system.
1.2. Systematic Literature Review Methodology
To ensure the comprehensiveness and objectivity of the literature review, this study adopted a systematic literature review approach, strictly following the PRISMA guidelines to guarantee transparency and reproducibility in the literature selection. The specific methodology and workflow are illustrated below:
- Literature Search Strategy:
- Databases: Three authoritative databases were searched: Web of Science, Elsevier ScienceDirect, and IEEE Xplore.
- Timeframe: Publications from 2015 to 2025 were included.
- Keywords: “industrial load flexibility”, “multi-energy flow systems”, “demand response”, “uncertainty management”, “market transactions”, etc.
- Search Query: Boolean operators were used to combine keywords, e.g., ((“integrated energy system” OR “IES”) AND (“multi-timescale” OR “multiple time scale”))
- Literature Selection Criteria:
- Inclusion Criteria:
- (1)
- Studies must directly address core research topics (industrial load modeling/multi-timescale optimization/electricity market mechanisms);
- (2)
- Published in SCI/EI-indexed journals or CCF-recommended conferences;
- (3)
- Contain complete mathematical models and experimental validation.
- Exclusion Criteria:
- (1)
- Purely theoretical studies without empirical case validation;
- (2)
- Studies focusing exclusively on residential/commercial loads;
- (3)
- Duplicate publications or non-peer-reviewed works.
- Screening Process: As shown in Figure 2.
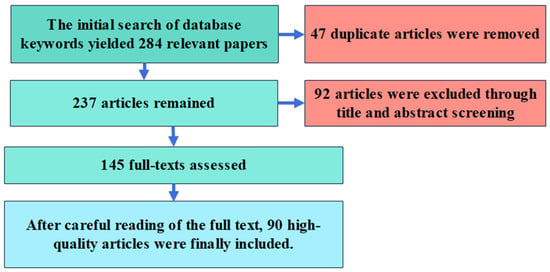 Figure 2. PRISMA flow chart.
Figure 2. PRISMA flow chart.
1.3. Innovation
To facilitate comparative analysis, we reviewed relevant references with similar research directions, and summarize the key findings in Table 1:

Table 1.
Comparison table of existing review papers.
Ref. [6] focuses on heavy industries (e.g., cement, aluminum smelting, oil refining), quantifying the potential of industrial demand response (DR) in peak shaving and valley filling through empirical data (e.g., a 34.2% energy reduction in aluminum plants). It proposes a time-layered market framework (day-ahead, intraday, and real-time) for flexibility classification but is limited to single-energy (electricity) analysis and static industry cases, failing to address multi-energy coupling and policy quantification. Ref. [7] critically examines market mechanism barriers to industrial DR participation, highlighting that current rules favor generation-side resources, leading to underutilized load flexibility. It suggests automated DR technology as a solution but remains at a qualitative level without algorithmic validation or cross-market (e.g., carbon trading) coordination. Ref. [8] provides a systematic review of the multi-energy flow coupling framework in Energy Hubs (EH) and their practical applications across regional and industrial contexts, encompassing the conversion and coordination of diverse energy carriers including electricity, heat, hydrogen, and ammonia, while also exploring emerging technological challenges, such as AI and 5G communication. However, the study exhibits notable limitations: its static, component-based taxonomy fails to enable dynamic optimal control of industrial loads, entirely overlooks policy coordination mechanisms between carbon and electricity markets, and predominantly focuses on regional energy systems while lacking in-depth analysis of high-energy-consuming industrial load characteristics. Ref. [9] focuses on the research and practices of industrial demand response (DR) in China, systematically summarizing industrial load modeling methods, the integration of distributed energy resources, and market-oriented mechanisms (e.g., blockchain technology applications). It also highlights China’s practical experience in promoting industrial DR under the “dual-carbon” goals. However, the study exhibits three notable limitations: first, it concentrates solely on a single electricity system, lacking multi-energy flow coupling analysis; second, it fails to quantitatively address uncertainty factors such as renewable energy fluctuations; third, it primarily emphasizes localized case studies in China, omitting comparative research on transnational policy coordination.
Compared with previous studies, the innovations of this review are as follows:
- First systematic integration of the “technology-market-policy” multidimensional research framework for industrial load flexibility, providing researchers with a cross-domain correlation map that addresses the fragmentation issues in existing reviews.
- Proposal of a “bidirectional mapping” theory between industrial load characteristic classification and dynamic policy evaluation, offering policymakers a load characteristic policy tool-matching guideline.
- Identification of three future interdisciplinary research directions: data fusion, algorithm lightweighting, and market-policy synergy, clarifying the transition trend from technology-driven to system-coupled approaches in industrial load research.
This review examines the importance of enhancing industrial load flexibility and its synergistic interaction mechanisms with power grids. Section 2 classifies existing modeling methods for industrial loads. Building upon the multi-energy flow coupling modeling proposed in Section 2, Section 3 focuses on multi-timescale and uncertainty issues while presenting current solutions. Section 4 elaborates on recent developments in demand-response markets, carbon trading markets, and multi-energy trading markets in the context of industrial load participation. Section 5 comprehensively analyzes the preceding sections, discusses key challenges in industrial load participation in regulation, and proposes actionable recommendations to guide future research.
2. Industrial Load Modeling
2.1. Current Load Modeling Methods
Existing research on load modeling methods has developed multiple technical approaches for different energy forms, load characteristics, and external influencing factors, which are widely used in industrial load optimization design and operational dispatch. According to the research focus, these methods can be divided into three categories: historical data-based load forecasting models, multi-energy load modeling, and modeling methods considering stochastic factors. These methods address the complexity of multi-energy systems from the perspectives of time-series forecasting, energy coupling analysis, and uncertainty handling.
2.1.1. Historical Data-Based Load Forecasting Models
Time-series analysis is the foundation of load modeling, supporting short-term and medium-term forecasting by mining historical load patterns. These methods focus on capturing the temporal dependence of load changes and the influence of external driving factors. Ref. [10] proposed a Convolutional Neural Network-Gated Recurrent Unit (CNN-GRU)-based short-term load forecasting model, in which the CNN extracts the high-dimensional features of loads, and the GRU identifies historical load patterns to generate prediction results. This method is suitable for high-energy-consumption industrial scenarios with large production load fluctuations, effectively improving prediction accuracy and adaptability. Ref. [11] used a Vector Autoregression (VAR) model with temperature as an exogenous variable to analyze the coupling relationship between loads and environmental factors, establishing dynamic change patterns of load time series. This method performs well in scenarios in which loads are strongly correlated with the external environment and is suitable for medium-term load forecasting.
These models provide reliable support for accurate prediction of load characteristics through historical data mining. However, they have certain limitations in dealing with coupling relationships between complex energy systems and require further optimization by combining multi-energy load modeling methods.
2.1.2. Multi-Energy Load Modeling
The complexity of multi-energy system loads lies in the uncertainty and nonlinearity of their time series. Load variations are not only related to historical data of various energy forms but are also influenced by coupling relationships between energy types [11]. This modeling approach aims to describe the interactive relationships between different energy forms, proving particularly crucial in integrated energy systems in which electricity, heat, cooling, and gas demands are mutually coupled. These methods achieve optimal dispatch of multi-energy systems by modeling the physical, chemical, and thermodynamic characteristics between energy sources.
Ref. [12] developed a multi-energy system model coupling power, thermal, and gas networks using the open-source tool MESMO, incorporating distributed energy resources (DER) and gas network models to achieve comprehensive optimization. Ref. [13] proposed an energy hub (EH)-based multi-energy flow coupling model that considers seasonal load characteristics, matching the following electric load (FEL) mode in summer and following thermal load (FTL) mode in winter, effectively suppressing grid voltage and gas network pressure fluctuations. Ref. [14] established a multi-gate mixture-of-experts (MMoE) prediction framework combined with long short-term memory (LSTM) networks to capture coupling relationships between multi-energy loads, particularly suitable for environments significantly affected by meteorological factors. Ref. [15] introduced an integrated demand-response model for electricity-heat loads in multi-energy microgrids, incorporating thermoelectric coupling characteristics to model thermal loads in building heating as combined heat and power demands, with separately designed demand-response strategies to optimize system economics and operational stability.
Through coupling modeling, these methods reveal synergistic effects between multiple energy forms, providing theoretical support for optimizing the operation of complex multi-energy systems and thereby enhancing renewable energy accommodation capacity and utilization efficiency [16].
2.1.3. Modeling Methods Considering Stochastic Factors
In multi-energy systems, the uncertainty and stochasticity of loads present key modeling challenges, particularly against the backdrop of increasing renewable energy penetration. Stochastic modeling methods effectively address uncertainty-induced challenges through approaches such as robust optimization and probabilistic modeling.
Ref. [17] proposed a two-layer tube-based model predictive control (TMPC) approach for optimal dispatch of multi-energy microgrids, which coordinates nominal MPC (for economic optimization) and auxiliary MPC (for robustness correction) to achieve economic dispatch while considering uncertainties in wind power and load demand. This method maintains computational efficiency comparable to conventional MPC (1.145s) while significantly enhancing system robustness, keeping actual operation trajectories within the “tube” range of nominal trajectories. Furthermore, it achieves coordinated optimization of multi-energy flows by absorbing excess wind power during off-peak periods and optimizing gas-fired equipment output during peak periods. Ref. [18] proposed a Bayesian multi-task learning Transformer framework that utilizes Bayesian multi-head attention mechanisms to capture complex coupling relationships and uncertainties (including epistemic uncertainty and aleatoric uncertainty) among multi-energy loads. Through multi-task weight balancing, this approach optimizes uncertainty quantification across subtasks. This method significantly improves prediction accuracy and robustness, offering a novel solution for probabilistic forecasting of cooling, heating, and electricity loads. These methods provide critical technical support for reliable operation and risk management in multi-energy systems through uncertainty modeling and robust optimization.
In practical applications, the standalone use of these methods often limits comprehensive system performance improvement. Future research should therefore focus on further integrating the strengths of different modeling approaches to address the increasingly complex demands of multi-energy systems.
2.2. Load Flexibility Potential Modeling
In modern power systems, load flexibility potential modeling has become a key research focus, with its core lying in accurately characterizing the adjustable range and response characteristics of loads. To better support power system dispatch and optimization, modeling methods for load flexibility potential have gradually evolved into an integrated modeling framework, including flexibility potential models, operational boundary models, and virtual energy storage models.
Flexibility Potential Model: Initial modeling of load flexibility potential focused primarily on the adjustable power range (i.e., the power capacity for upward or downward regulation of industrial loads). Unlike traditional steady-state models, flexibility potential models incorporate dynamic response characteristics such as load adjustment time delays, regulation rates, and sustainable adjustment time windows. These factors directly influence the effectiveness of load regulation. The flexibility potential is reflected not only in power magnitude but also requires comprehensive consideration of system response times and practical operational constraints.
Operational Boundary Model: Power system stability and security are paramount during load regulation processes. Operational boundary models define safe regulation ranges for loads, providing essential constraints for dispatch decisions. These boundaries are typically influenced by multiple factors, including equipment capabilities, grid load conditions, and system frequency. The model not only guides power system dispatch strategies but also prevents excessive grid stress or instability risks during load regulation.
Virtual Energy Storage Model: The virtual energy storage concept represents an emerging research direction that combines load regulation with energy storage functionality, simulating load behavior as “storage devices.” Through this approach, industrial loads can “charge” during low-load periods and release “stored” energy during peak-load periods. This regulation mechanism enhances load flexibility, enabling more effective responses to electricity market and grid demand variations.
Literature [19] proposed an electric vehicle demand-response potential assessment model that integrates price responsiveness and charging power responsiveness, enabling comprehensive and accurate evaluation of load response potential. The process for assessing price-based demand-response potential is illustrated in Figure 3.
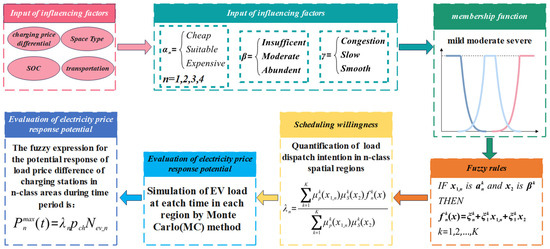
Figure 3.
Framework for quantitatively assessing price-based demand-response potential using fuzzy subsets.
In Figure 3, for each set of input variables (including spatial type, pricing differential, state of charge (SOC), and road congestion level), the membership functions of individual subsets are employed to determine corresponding membership degrees. These membership values subsequently serve as input variables for the Takagi-Sugeno-Kang (TSK) fuzzy rules.
In the “fuzzy rules” module:
- and denote the input variables for charging tariff and battery energy level, respectively.
- The subscript (where ) corresponds to residential zones, workplace zones, commercial districts, and entertainment areas.
- represents the linear function value.
- , , , are constant parameters for the -th fuzzy rule. The superscript indicates the index of fuzzy rules.
The user response willingness output by the TSK fuzzy model represents the weighted average of all rule outcomes.
In the “Scheduling Willingness” module, and denote the membership functions corresponding to fuzzy subsets; indicates the response willingness value of EV users in type-n spaces. The EV response willingness is influenced by both the electricity price and state of charge (SOC).
For price-based demand-response potential assessment, considering response willingness, the fuzzy representation of load price-response potential for charging stations in category- regions during time period is given by Equation (1). When the load adjustment target falls within the response potential value range, the adjusted response willingness can be determined using Equation (2).
where, represents the evaluated load response potential for charging stations in type- regions. represents the response willingness value of EV users in the -type space. indicates the rated charging power of a single electric vehicle. denotes the number of charging vehicles at stations in region during time period . is the change in electricity price after the electricity price adjustment.
When further considering the charging power demand-response potential, the charging power must satisfy the following:
where represents the user’s charging time; represents the user’s parking time. represents the response power of the electric vehicle; and represents the rated charging power of the charging equipment
The power constraints of charging piles are as follows:
By integrating the above constraint conditions, the maximum response potential of charging power for category- regional charging stations during time period can be determined as follows:
The total load demand-response potential (incorporating both price-based response potential and charging power response potential) is given by the following expression:
3. Multi-Energy Flow Coordinated Optimization
With the increasing adoption of combined heat and power (CHP) systems and other energy conversion technologies, the coupling and interconnection between various energy systems have become significantly tighter. Integrated energy systems (IES) have disrupted the traditional paradigm of independent design, planning, operation, and control of combined cooling, heating, electricity, and gas (CCHG) systems [20]. By organically coordinating and optimizing the allocation, conversion, storage, and consumption of different energy carriers during planning, design, construction, and operation, IES can enhance the security, flexibility, and reliability of societal energy supply. Therefore, this section further explores multi-energy flow coupling systems, particularly in addressing multi-timescale coordination and multi-source uncertainty challenges.
3.1. Key Challenges
Currently, integrated energy systems (IES) typically employ a uniform timescale (e.g., hourly) for simultaneous optimization of electric energy flow (EEF) and thermal energy flow (TEF). However, this approach fails to account for the inherent timescale disparity between these two energy flows:
- EEF Optimization Requirements:Due to frequent fluctuations in renewable energy generation and power load, combined with strict real-time power balance constraints, EEF optimization must be performed at short timescales (e.g., minute- or second-level adjustments).
- TEF Optimization Characteristics:Benefiting from thermal inertia and relative insensitivity to comfort thresholds, TEF can be optimized over longer timescales (e.g., hourly or daily). It only requires periodic updates to maintain sufficient cooling/heating capacity for building temperature setpoints.
This fundamental mismatch in temporal dynamics means that conventional single-timescale day-ahead optimization methods cannot achieve optimal IES performance [21]. Furthermore, day-ahead scheduling for CHP-wind farm portfolios must address two challenges: renewable energy volatility and power load uncertainty. The latter stems from rising prosumer penetration and consumer behavior shifts under dynamic pricing [22]. These uncertainties directly impact system stability and economic performance. The existing literature has proposed various solutions, as follows:
Predictive approaches [23,24,25,26,27] assume perfect uncertainty forecasts but often prove unreliable in practice, causing dispatch errors; Metaheuristic methods [28] suffer from high computational costs and solution inconsistency; Model predictive control [29] demands accurate system modeling and extensive historical data; Probabilistic techniques [30,31] require well-defined probability distribution functions (PDFs); Stochastic programming [32,33] suits soft-constrained problems with known PDFs. However, its robustness declines if real-time conditions deviate from predictions. Notably, studies considering wind power and price uncertainties [34,35] frequently overlook real-time balancing market dispatch, making their day-ahead scheduling solutions potentially unstable in practice. In Nordic countries, Spain, and Switzerland, integrating CHP-wind farms into day-ahead and two-price balancing markets remains particularly challenging [36].
Therefore, the current key challenges can be summarized as follows:
- Multi-timescale coordination and optimization: System dispatch requires addressing multi-timescale coordination issues—specifically, how to make optimal decisions across different timescales (e.g., daily, hourly, or even seasonal) to ensure stable system operation.
- Multi-source uncertainty management: The primary challenge in integrated energy systems is managing uncertainties from multiple sources, including renewable energy variability, load demand fluctuations, and market price volatility.
- Challenges in efficient optimization control algorithms: As the scale and complexity of integrated energy systems grow, developing computationally efficient optimization algorithms becomes increasingly difficult. Traditional methods often fail to meet real-time requirements for large-scale, multi-objective, high-dimensional problems while incurring substantial computational costs.
3.2. Current Optimization Methods
The existing literature has provided various effective strategies to address the three key challenges of multi-timescale coordination and optimization, multi-source uncertainty management, and efficient optimization control algorithms, significantly improving the operational stability and economic performance of integrated energy systems (IES).
3.2.1. Multi-Timescale Coordination Optimization Methods
Literature [36] proposed a multi-timescale coordination framework for integrated electricity and hydrogen systems. The portfolio operation strategy was applied to combined heat and power (CHP) plant-wind farm portfolios to maximize operational profits in future heating markets and real-time two-price balancing markets. Stochastic programming was used to address multiple uncertainties, and the proposed method was tested on the generation portfolio of CHP plants and wind farms through Monte Carlo feasibility checks. Compared to deterministic methods, the proposed multi-timescale coordination approach represents a cost-effective strategy that ensures reliable and robust operation under uncertainty without violating real-time heat-electricity balance or schedule adaptation constraints. The framework is illustrated in Figure 4, where yellow modules represent uncertain parameters, gray modules represent deterministic parameters, blue modules represent day-ahead operations, and red modules represent real-time operations.
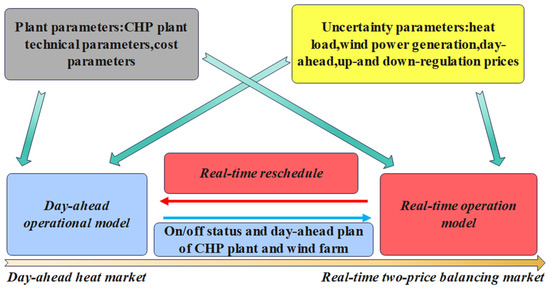
Figure 4.
Multi-timescale coordinated operation framework.
Literature [37] proposed a temporally decomposed two-level optimization framework for Building Energy Management Systems (BEMS), as shown in Figure 5. The framework divides the decision-making process into two levels: the upper level corresponds to a longer timescale (hourly), in which at the beginning of each hour (), dispatch decisions are made for fuel cells (FC), battery energy storage systems (BESS), and thermal energy storage (TES), with generation-load balance achieved through thermal load control. These decisions remain fixed until the next hour begins () and are communicated to the lower level. The lower level handles shorter timescale operations (15-min intervals ), I which BESS is redispatched and Direct Load Control (DLC) is activated to effectively address uncertainties. This process is repeated for all , where .
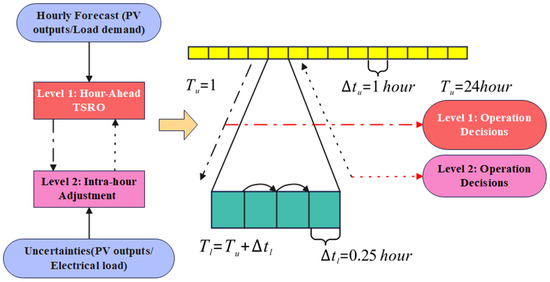
Figure 5.
Multi-timescale coordination framework for BEMS.
Through this developed bi-level optimization model for BEMS, multi-timescale coordination is achieved. The upper level is formulated as a Two-Stage Robust Optimization (TSRO) model that optimizes system operation while accounting for uncertainties at any level. The lower level makes real-time adjustments to the optimized decisions during actual system operation. The results demonstrate high computational efficiency, lower costs, reduced BESS degradation, and improved user satisfaction.
3.2.2. Multi-Source Uncertainty Management Strategies
To address uncertainty challenges more fundamentally, deep reinforcement learning (DRL) technology combines the powerful nonlinear perception capabilities of deep neural networks with the robust decision-making abilities of reinforcement learning. As a data-driven approach, DRL can extract the physical model of the system from data, reducing reliance on the physical model of the IES. When facing complex uncertainties, it dynamically adjusts decision-making strategies through interaction with the environment, thereby further improving system robustness and economic performance.
In literature [38], the optimal scheduling problem of IES is formulated as a Markov Decision Process (MDP), and a DRL-based optimization scheduling framework is designed. In addition to economic benefits, environmental factors are also incorporated into the consideration scope.
3.2.3. High-Efficiency Optimization Control Algorithms
As system scales expand and problem complexity increases, traditional optimization methods face challenges in computational efficiency and real-time performance. In recent years, researchers have proposed the following efficient optimization solution approaches:
For instance, Ref. [39] proposed an improved Double Deep Q-Network (DQN) algorithm by modifying Q-value computation to enhance the exploration capability of multi-energy microgrids, while considering both economic costs and carbon emission objectives. Ref. [40] established a multi-objective optimization model for EGH-IES (Electricity-Gas-Heat Integrated Energy System). To accomplish the economic and environmental optimization tasks, the optimization problem was formulated as a deep reinforcement learning problem with continuous state and action spaces. In the proposed Deep Deterministic Policy Gradient (DDPG) algorithm, the Ornstein hlenbeck process was introduced to improve the training efficiency and exploration performance of the agent. The interaction process between the agent and environment is illustrated in Figure 6 (please refer to the original text [40] for the symbol definitions).
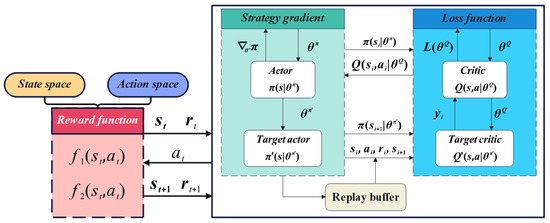
Figure 6.
Multi-objective optimization of EGH-IES using the DDPG algorithm.
The workflow begins by sampling the state from the environment to compute both the Actor network’s policy output and the Target Actor network’s subsequent policy . These outputs are then utilized by the Critic network to estimate the action-value function , while the Target Critic network computes . The algorithm proceeds by calculating the policy gradient to update both the Actor network parameters and Target Actor parameters , concurrently deriving the loss function to optimize the Critic network parameters and its target counterpart . During environmental interaction, each timestep generates experience tuples that are stored in the replay buffer . Training involves sampling mini-batches from , where this experience reuse mechanism significantly enhances both data utilization efficiency and learning stability.
4. Industrial Load Participation in Market Transactions
Section 3 of the article conducted an in-depth exploration of the critical issues in multi-energy flow coupling within integrated energy systems (IES), with a particular focus on optimization decision-making for multi-timescale coordination and multi-source uncertainty management, including addressing fluctuations and uncertainties in market environments.
With the rapid development of China’s electricity market construction, a comprehensive electricity market system has gradually taken shape, comprising medium- and long-term trading markets, spot electricity markets, and ancillary service markets [41,42,43,44]. Simultaneously, the development of load-side resource management in China has been progressing vigorously, playing an increasingly prominent role in peak shaving, promoting renewable energy integration, and maintaining system power balance [45,46]. However, differences in market rules across regions have led to inconsistencies in the eligibility criteria and transaction models for adjustable load resources participating in ancillary service markets. This lack of unified standards has limited broader participation and affected service diversity and market efficiency. Therefore, there is a need to develop standardized transaction models compatible with market mechanisms to facilitate wider, more efficient, and sustainable participation of industrial adjustable load resources in grid services, thereby supporting efficient and reliable operation of power systems [47].
Against this background, Section 4 will focus on how industrial loads can further enhance their flexibility and economic benefits by participating in mechanisms such as demand-response markets, carbon markets, and peer-to-peer multi-energy trading. Through such participation, industrial enterprises can not only respond to market fluctuations and optimize resource allocation but also play a significant role in the integrated development of smart grids and energy markets, ultimately contributing to the efficient and reliable operation of power systems.
4.1. Demand Response in Electricity Markets
Demand Response (DR) leverages incentives or pricing mechanisms to encourage users to participate in the operation of the power system. It is widely recognized as an effective strategy for optimizing the balance of electricity supply and demand [48]. Through price signals and incentive policies provided by electricity markets, consumers on the demand side can adjust their electricity consumption behavior. Among various user types, industrial loads play a pivotal role. Compared to residential users, industrial consumers typically have higher electricity usage and a larger share of electricity costs in their overall expenses. Moreover, their energy consumption is more manageable and they tend to exhibit a stronger willingness to participate in DR programs. Therefore, guiding industrial users to engage in energy-saving measures, emissions reduction, and demand-side management is of great significance. For instance, industrial users can reduce cooling and lighting loads or adjust specific production loads as part of DR initiatives [49].
Industrial users are often associated with long-term load characteristics. Compared with short-term load forecasting, long-term load forecasting is more complex due to the influence of numerous uncertainties, such as weather conditions, natural environments, societal factors, and human activities [50]. Consequently, existing DR market participation strategies commonly adopt a hybrid approach combining model-driven and data-driven methods.
Model-driven methods aim to construct optimization models to identify the optimal response behavior of the load side under various market constraints—such as incentive payments, comfort requirements, and external environmental parameters. In contrast, data-driven DR is based on learning the mapping relationships between input features (e.g., electricity prices, external temperature, and customer preferences) and DR potential. For example, Ref. [51] proposed a self-learning gray-box thermal model for indoor environments; Ref. [52] presented a peer-to-peer (P2P) energy trading scheme to reduce peak-time electricity demand. In [53], to address uncertainties in customer behavior, a mixture density recurrent neural network was employed to predict the probability distribution of DR potential. Ref. [54] introduced a regression model that captures the relationship between several factors—such as time of day, setpoint adjustments, and outdoor temperature—and DR potential, enabling the prediction of DR capacity for residential and commercial office buildings. In [55], the issue of monthly load curve forecasting was discussed, whereby an artificial neural network (ANN) was used to address predictive modeling challenges. However, DR behavior can vary significantly across individual users [56]. As a result, applying DR potential prediction models trained on one set of customers directly to new customers may lead to considerable prediction errors. Additionally, many existing studies have focused excessively on modeling demand-side behavior while paying insufficient attention to market transaction constraints. This may result in a disconnect from actual market conditions and potentially lead to suboptimal or even erroneous decision-making.
To address these issues, Literature [48] proposed an online transfer learning-based DR potential prediction framework that combines the advantages of both transfer learning and online learning to improve the prediction accuracy of DR potential for newly enrolled customers. The proposed online transfer learning framework is illustrated in Figure 7.
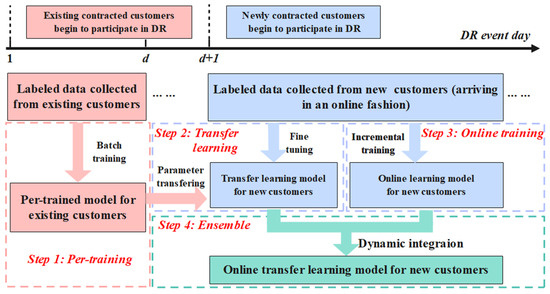
Figure 7.
Illustration of the online transfer learning framework.
- Step 1: Pre-training: A pre-trained demand-response (DR) potential prediction model is established using historical load response data from existing contracted customers.
- Step 2: Transfer Learning: Parameters of the pre-trained model are transferred and frozen to a new DR potential prediction model designed for newly contracted customers, followed by fine-tuning of the remaining model parameters.
- Step 3: Online Training: The online DR potential prediction model is trained using localized response data from newly contracted customers, who are progressively accumulated through participation in DR events.
- Step 4: Ensemble: The transferred and online DR potential prediction models are combined via an adaptive ensemble strategy based on their real-time performance metrics.
Literature [57] proposed a two-stage joint optimization framework for bidding and pricing tailored to load aggregators (LAs). As shown in Figure 8, this framework employs a coordinated decision-making process followed by price adjustments to design optimal bidding and pricing strategies, thereby enhancing trading revenue through synergistic coordination. Furthermore, to mitigate default risks arising from uncertainties in user response and clearing prices, the framework incorporates quantifiable effective response capacity and risk control measures based on DR settlement rules during the ex ante decision-making process.
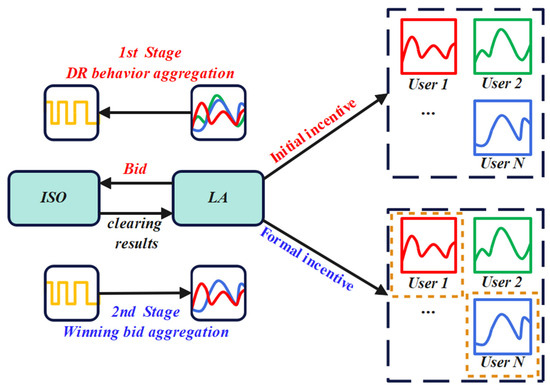
Figure 8.
Two-stage joint optimization framework.
In the first stage, the LA optimizes initial incentive pricing strategies and formulates aggressive DR bidding strategies to explore users’ potential response capabilities. These incentive prices are solely used for predicting DR behavior and are not actually distributed to users. By considering the uncertain behaviors of all aggregated users, the LA calculates the overall effective response capacity while estimating potential revenue and transaction risks. During this process, the LA leverages the deviation characteristics of different users’ responses to reduce risks through complementary effects among the clustered response behaviors, thereby formulating relatively aggressive bidding strategies. In the second stage, the LA prioritizes users who can provide accurate responses based on their response reliability and associated costs, ensuring successful transaction execution. Simultaneously, the LA compensates users according to their actual DR behaviors and adjusts pricing strategies based on their effective response capacities. This approach serves to diversify transaction risks, guarantee transaction fulfillment, and maximize the utilization efficiency of DR capacity.
4.2. Carbon Market Trading
The evolution of electricity consumption patterns and the widespread adoption of green power are profoundly reshaping industrial load behaviors, while electricity consumption in industrial production is directly linked to carbon emissions. This establishes a significant coupling relationship between industrial load variations and dual-carbon objectives, making its study theoretically and practically vital for low-carbon policy formulation and implementation. Current research has extensively explored this relationship. Refs. [58,59] virtualized carbon emissions as carbon emission flows, analyzing their dynamic trends to establish an analytical framework for investigating industrial loads’ impact on dual-carbon goals. Ref. [60] decomposed peer-to-peer (P2P) electricity and carbon market models into cooperative alliance operation and asymmetric cost allocation problems, introducing a contribution factor calculation method that jointly considers P2P electricity trading and carbon emission trading (CET) marginal effects. Further developing this, Ref. [61] proposed a non-cooperative game-based optimization strategy through a game-theoretic model with tiered carbon trading costs, designing a multi-timescale framework combining day-ahead optimization (economic-carbon collaborative objectives) and intraday rolling dispatch, solved via an ADMM algorithm for virtual power plant (VPP) competition equilibrium. Complementing these theoretical advances, Ref. [62] implemented a real-time carbon accounting system with an electricity-carbon co-simulation model, delivering a comprehensive solution from theoretical frameworks to technical support for low-carbon power system operations. Meanwhile, Ref. [63] quantitatively analyzed electric heat pumps’ carbon reduction potential through dedicated emission modeling, providing specific technical pathways for low-carbon transition. Together, these studies form a systematic research paradigm addressing the industrial load-carbon market nexus across theoretical, methodological and applied dimensions.
Despite these contributions, real-world implementation still faces critical challenges, as follows:
- Policy Implementation Gap: Government policies on dual-carbon targets are predominantly qualitative, lacking quantitative models to reflect strategic differences in policy design and enforcement.
- Modeling Complexity: The interaction between industrial loads and low-carbon policies is highly complex and cannot be fully captured by simplistic closed-loop models.
- Oversimplification of Load Characteristics: Current studies often treat industrial loads as homogeneous entities for regulation, neglecting qualitative analyses of their intrinsic properties.
- Fragmented Carbon Markets: Regional and industrial load operations remain siloed, with no unified and effective carbon trading mechanism to standardize carbon market participation.
To address Challenges 1 and 2, Literature [64] proposed a system dynamics-based analytical framework for assessing the impact of dual-carbon targets on industrial loads. In this approach, low-carbon policies are quantitatively characterized through policy intensity levels using the Analytic Hierarchy Process (AHP), which transforms qualitative policies into measurable values. This enables the evaluation of coupling relationships between policies and industrial loads through established indices and criteria. The study ultimately constructed a system dynamics model comprising dual-carbon targets and industrial loads, with core strategies considering the interactions among energy, environmental, and political subsystems. Within each subsystem, various factors dynamically interact, and feedback loops exist between factors and subsystems, as illustrated in Figure 9.
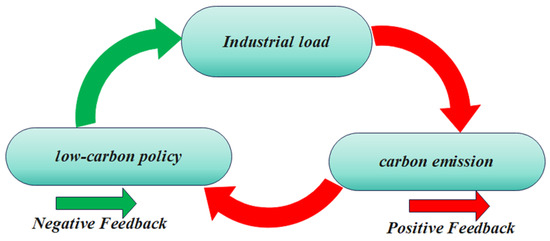
Figure 9.
Core structure of the dynamic model for industrial load systems under the dual-carbon Goals.
The system dynamics model can be expressed as follows:
where is a vector of state variables, including industrial load, carbon emissions, and the strength of low-carbon policies; is a vector of parameters corresponding to the system dynamics model; and represents a set of nonlinear functions. The industrial load can be modeled as follows:
where is the industrial load, is a coefficient related to the industrial load, and is the growth rate of the industrial load. Carbon emissions can be calculated as: follows
where denotes carbon emissions and is the carbon emission rate per unit of industrial load. Furthermore, the strength of low-carbon policies can be expressed as follows:
where is the strength of low-carbon policies, is a coefficient related to policy strength, is the growth rate of policy strength, and , are coefficients representing the relationship between policy intensity and carbon emissions. The feedback loop between industrial load and low-carbon policy can be represented as follows:
where and are coefficients of the feedback loop. The simulation results of Ref. [64] calculated the annual variation rates of policy intensity and industrial load based on data from Henan Province, China. The coupling index is −1.5875, indicating that the relationship between policy intensity and industrial load is SPC (Synergistic Policy Coupling). An increase in industrial load can enhance the intensity of low-carbon policies.
To address Challenge 3, Ref. [65] categorized industrial loads into five main types: rigid loads, shiftable loads, deferrable loads, reducible loads, and loads from wind, photovoltaics, and demand-side sources. Mathematical models were then developed for each category based on their specific characteristics.
For Challenge 4, Ref. [66] proposed a tiered carbon quota trading model, which mainly consists of three components: a carbon emission quota model, an actual carbon emission model, and a tiered carbon emission trading model. The models are established as follows:
Carbon Emission Quota Model:
where is the total CO2 quota for the chemical industrial park; and are the carbon emission quotas per unit of electricity and natural gas, respectively; is the electricity purchased from the grid at time ; is the natural gas purchased at time ; and is the calorific value ratio between natural gas and electricity.
Actual Carbon Emission Model:
where is the actual total CO2 emissions of the industrial park; and are the CO2 emission coefficients for electricity and natural gas, respectively; is the methane conversion amount at time ; and is the CO2 absorption coefficient during methanation.
Tiered Carbon Quota Trading Model:
where is the actual carbon quota traded in the park; is the tiered carbon trading cost; is the baseline carbon trading price; is the interval length of carbon emissions; and is the price escalation factor.
Ref. [66], based on simulation results from a coastal chemical industrial park in eastern China, demonstrated that compared with a fixed carbon trading cost mechanism, the tiered carbon pricing system exhibits differentiated impacts on carbon emissions: while it reduces carbon emissions from natural gas consumption by 10.38%, it simultaneously increases emissions from electricity consumption by 6.65%, with only limited overall emission reduction effectiveness (merely a 4.11% decrease). Although this mechanism constrains total emissions through progressively increasing carbon prices, it leads to a significant rise in operational costs (total costs increase by 9.31%, with carbon trading costs surging by 16.48%), resulting in economic efficiency deterioration. These findings indicate that while the tiered carbon pricing policy can partially optimize the emission structure, supplementary measures are required to simultaneously achieve both emission reduction and economic benefits.
Ref. [67] designed a carbon credit trading mechanism that considers the synergy between electricity trading and carbon trading. Based on this, a carbon-electricity coupled market model centered around a Carbon Credit Management Center (CCMC) was established, characterized by high linkage and information interaction. The framework is illustrated in Figure 10. For detailed modeling equations, please refer to the original text.
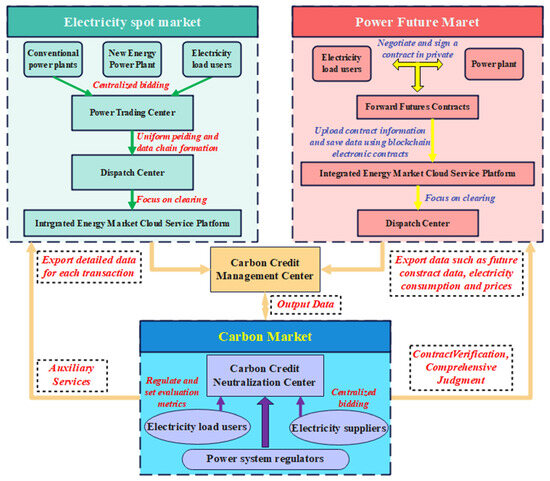
Figure 10.
Carbon-Electricity Coupled Market Structure.
4.3. Multi-Energy Market Trading
In the energy consumption structure of industrial enterprises, in addition to electricity, other energy sources such as coal, petroleum, and natural gas also play significant roles. These energy sources serve not only as indispensable power sources in production processes but also as international commodities whose price fluctuations are influenced by global market supply-demand relationships, policy regulations, and futures trading. The uncertainties in these energy markets profoundly affect not only enterprises’ production decisions but also their behavioral patterns in market transactions. Therefore, research on multi-energy market trading mechanisms needs to consider the coupling relationships between different energy types and incorporate market dispatch strategies to optimize overall benefits.
With the increasing utilization of gas-fired combined heat and power (CHP) units and other distributed CHP systems, power conversion efficiency among multiple energy networks has been significantly improved [68]. This energy flow has established complex power coupling across different systems. Based on this, Section 4 will integrate market trading models with dispatch strategies, further introducing coupling mechanisms for market behavior to achieve optimal benefit distribution while pursuing maximized benefits for multi-energy systems.
Regarding multi-energy market trading, Ref. [69] proposed a Stackelberg game-based optimization framework wherein integrated energy operators (IEOs) act as leaders setting energy prices to maximize profits, while users act as followers adjusting consumption plans according to energy prices. Ref. [70] presented a bi-level optimal dispatch model to promote demand-side resource participation in isolated microgrids for optimized economic operation. Ref. [71] developed a three-level, two-stage price-based integrated demand-response (IDR) framework to balance interests among IEOs, local autonomous governments (ILAs), and end-users.
In the modeling of Section 3, the references only considered trading operations between two energy providers. For the integration of multiple energy operators, Refs. [72,73,74] investigated optimal power flow models under different infrastructure combinations and proposed general optimality conditions. Ref. [75] derived a more universal model for optimal dispatch among multiple energy carriers. However, these studies often treated different energy networks as integrated systems under unified control, neglecting their profit-maximization requirements as independent economic entities and their mutual influences. To address these limitations, Ref. [76] employed particle swarm optimization to study optimal pricing strategies for integrated electricity and natural gas systems based on CHP and combined cooling, heating, and power (CCHP) units, exploring benefit relationships within the system. Although these studies considered thermal energy systems, they primarily focused on the dispatch of passive loads.
Peer-to-peer (P2P) energy trading represents a promising approach for optimized energy management. This trading mechanism enables prosumers to sell surplus energy to others while allowing them to economically balance supply and demand by utilizing their energy resources. Simultaneously, it benefits system operators by enhancing local renewable energy utilization rates and reducing power transmission expansion costs. The framework for P2P multi-energy trading markets is illustrated in Figure 11.
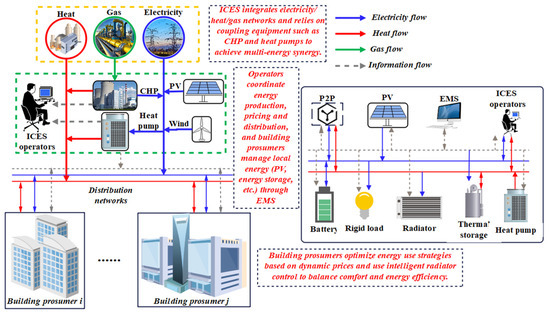
Figure 11.
Schematic diagram of the P2P multi-energy trading market framework.
Ref. [77] proposed a reinforcement learning and blockchain-based P2P energy trading scheme for 6G networks to securely execute P2P transactions. This bi-level optimization problem, which falls under the NP-hard category and involves multiple nonlinear constraints, was effectively solved using a distributed algorithm based on decomposition principles, while simultaneously preserving the information privacy of both participating entities. Ref. [78] introduced a comprehensive network tariff and energy sales pricing scheme. The interaction between Integrated Community Energy System (ICES) operators and building prosumers was modeled as a bi-level optimization problem, incorporating the heterogeneity of building insulation performance. To address this parallel and hierarchically coupled bi-level optimization structure, the authors developed an accelerated asynchronous distributed algorithm based on the Alternating Direction Method of Multipliers (ADMM). This algorithm integrates warm-start strategies and dual-update accelerated iteration strategies to further enhance computational efficiency.
Ref. [79] presented a collaborative demand-response management (DRM) framework for integrated energy systems (IES), providing industrial loads with a novel platform for flexible participation in demand response. Through P2P trading mechanisms, this approach improves resource utilization and maximizes economic benefits while facilitating efficient coordination of multi-energy flows in IES. As illustrated in Figure 12, the DRM market structure can be deconstructed in two-dimensional space. By differentially utilizing demand-response resources across stages, demand-side flexibility can be enhanced, thereby more effectively mitigating prediction uncertainties associated with renewable energy sources (RES) and load levels.
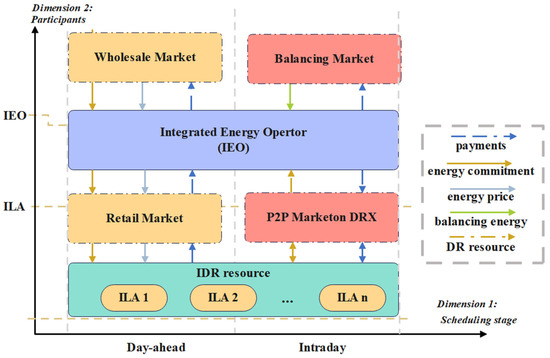
Figure 12.
DRM framework.
4.4. Industrial Pilot Verification
To validate the feasibility of the proposed bidirectional mapping framework and multi-market demand-response (DR) model, this section analyzes typical pilot projects from both domestic and international contexts.
- Domestic Case: Beijing Smart Community DR Pilot [80]
This pilot project implemented in smart communities, such as Zuoaomen Apartments in Beijing, demonstrates the application of bidirectional mapping technology in residential demand response, as follows:
- Bidirectional Data Interaction: Real-time monitoring of user loads was achieved through a distribution automation system, while dynamic electricity price signals were delivered via bidirectional interactive service terminals (e.g., smart meters and mobile apps), forming a closed-loop feedback mechanism.
- Integration of Distributed Resources: The community’s photovoltaic (10 kW) and energy storage systems (600 Ah) possess the technical foundation for participation in electricity markets, though they are currently only utilized for local peak shaving and valley filling.
This case indicates that bidirectional communication architecture is operable in small-to-medium-scale DR scenarios but requires further policy support to achieve multi-market coordination.
- International Case: EU OSMOSE Project Industrial DSR Pilot [81]
The EU OSMOSE project tested industrial demand-side response (DSR), validating the technical potential and challenges of high-energy-consumption loads participating in multi-level electricity markets:
- Multi-Market DR Validation: Experiments revealed that while industrial loads struggle to meet the technical requirements for fast frequency response (aFRR), they exhibit adjustable potential in slower services (e.g., congestion management and balancing markets), which could be enhanced through future technological upgrades.
- Bidirectional Interaction Barriers: The pilot exposed limitations in the remote control capabilities of industrial facilities (e.g., voltage regulation AVC requiring on-site operation), highlighting the necessity of standardized bidirectional communication protocols (e.g., IEC 61850 and OpenADR) in industrial applications.
This case confirms that realizing the multi-market value of industrial DR requires simultaneous optimization of technical adaptability (e.g., equipment upgrades) and market rule design.
5. Challenges and Future Directions
The preceding Section 2, Section 3 and Section 4 have respectively examined the challenges in specific domains and proposed corresponding solutions. However, these challenges primarily focus on localized issues within their respective fields, failing to comprehensively address the global challenges facing the overall development of industrial load participation in regulation. Therefore, this section will integrate the developmental status from Section 2, Section 3 and Section 4 to holistically analyze the main challenges encountered in industrial load participation and provide reference suggestions aimed at offering practical research directions for subsequent scholars.
5.1. Data Uncertainty and Modeling Complexity
Current modeling approaches for multi-energy flow coupling and market transactions rely heavily on simplified assumptions. For example, they often presume linear relationships between energy flows or ignore nonlinear characteristics. While these simplifications help reduce computational complexity, they often result in insufficient model accuracy in practical applications. Moreover, industrial load variations are influenced by stochastic factors (e.g., order fluctuations and production process changes). These factors introduce forecasting uncertainty and reduce the reliability of regulation decisions.
Consequently, a key challenge is to characterize interactions between energy and material flows more accurately. This requires advanced modeling (e.g., network-based complex systems) and prediction methods. To enhance the accuracy of load regulation models, future research could explore the integration of multiple modeling methodologies. Ref. [82] provides valuable insights by employing system dynamics (SD) to construct simulation models for electricity markets, excess consumption markets, and Tradable Green Certificate (TGC) markets, investigating their interactions and the policy impacts of new Renewable Portfolio Standards (RPS).
The SD approach offers distinct advantages: It can qualitatively and quantitatively explain relationships between a system’s internal structure and functional states while handling high-order, nonlinear, multi-feedback complex time-varying systems. It proves particularly suitable for analyzing socio-economic problems with dynamic complexity. The model encompasses three fundamental market components and captures the influence relationships and dynamic cycles among various market entities’ resources, as illustrated in Figure 13.
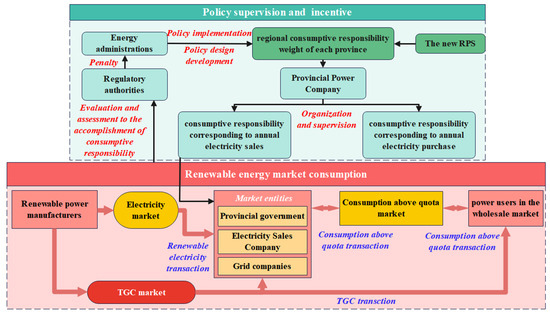
Figure 13.
Multi-market coupling trading framework under the new RPS.
However, this is only one line of thinking. By examining the original modeling formulas, we can see that a simplified and more direct method was used to describe the correlation between certain parameters to reduce simulation difficulty.
Another approach is the combination of machine learning (ML) and deep learning (DL) prediction models with physics-based modeling. ML algorithms process historical data to capture load change patterns and boost prediction accuracy. At the same time, data fusion technology can integrate information from different data sources to improve model reliability and real-time adaptability. For example, Ref. [83] proposed a deep learning method for day-ahead building energy forecasting in shopping centers. This method uses an attention mechanism (AM) to select key features from input data, combined with a transfer learning model that leverages pre-trained DL weights for new data training. In Ref. [84], computer vision was applied to intra-hour solar forecasting by combining satellite and sky images. Considering the varying prediction performance of data-driven models and the different configurations of various deep learning models that affect their prediction performance, combining multiple models (ensemble methods) to achieve higher prediction accuracy is undoubtedly a better solution. Ref. [85] proposed a power load forecasting method combining extreme learning machines and artificial neural networks. Guoyin et al. [86] developed an ensemble model that includes empirical mode decomposition and deep belief networks (DBN) for cooling load forecasting. The method proposed in Ref. [87] is divided into two parts, as shown in Figure 14. In the first part, a new ensemble forecasting model was developed for day-ahead time-series forecasting of regional multi-energy demand and its potential renewable energy generation, achieved by integrating various base models (including different deep learning configurations). For the second part, a model-free deep reinforcement learning method was proposed. After successfully training the model, these two parts were integrated into an embedded system for an AI platform.
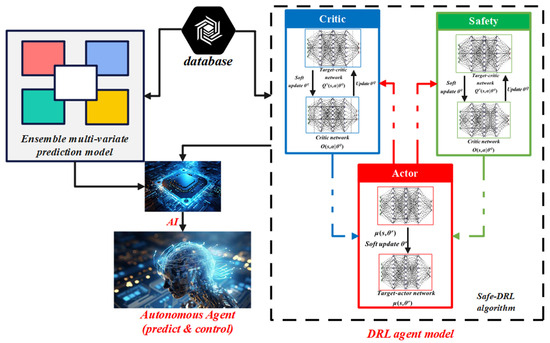
Figure 14.
Method framework diagram.
To compensate for the weaknesses of individual models and synergize their performance for superior outcomes, Gradient Boosted Regression Trees (GBRT) have emerged as one of the most prominent ensemble methods due to their ability to avoid local minima and maintain high computational efficiency [88]. In this approach, the outputs of each predictive model are aggregated within the GBRT framework to generate a consolidated output for each day-ahead forecast. The comprehensive architecture of this ensemble forecasting model is illustrated in Figure 15.
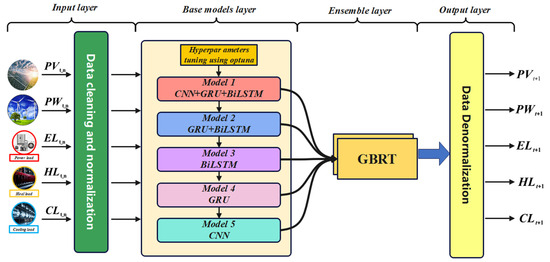
Figure 15.
Proposed ensemble architecture.
5.2. Computational Complexity and Real-Time Performance Challenges
As the scale of industrial load participation in regulation expands, the computational complexity of system optimization increases dramatically. Particularly in multi-objective, multi-constraint scheduling problems, traditional optimization methods face tremendous computational pressure during the solving process. When dealing with large-scale systems, the real-time performance of optimization results becomes especially critical. Although some heuristic algorithm-based approaches (such as genetic algorithms and particle swarm optimization) have achieved breakthroughs in accuracy, these methods still exhibit significant computational bottlenecks in large-scale applications. To meet the real-time response requirements of industrial load regulation, future research must improve computational efficiency while ensuring the accuracy and stability of optimization results.
To address computational complexity and real-time performance issues, hybrid optimization algorithms (such as methods combining heuristic and exact algorithms) can be explored to enhance solving efficiency for large-scale systems. For example, Ref. [89] achieved the shortest settling time, lowest objective function value, and an 89.56% improvement in stability performance by introducing the IABC-PSO hybrid optimization algorithm and a novel cascaded controller configuration. Furthermore, compared to the best-performing controller in previous studies, the settling times for frequency deviations ( and ) were reduced by 21.61% and 72.47% respectively.
Additionally, the combination of distributed computing and cloud computing may effectively enhance computational capacity, reduce pressure on individual computing nodes, and thereby ensure real-time solutions for large-scale scheduling problems. As demonstrated in Ref. [90], the novel CG&S algorithm with UC constraints reduced solving time from 5.5 h to 46 min for maximum instances, decreased iterations from 222 to 21, and shortened solution time by 86%.
5.3. Contradictions Between Theoretical Innovation and Engineering Implementation
In industrial load regulation systems, the implementation of algorithms relies not only on precise optimization models but also requires effective integration with hardware equipment and the operability of engineering implementation. The challenges involved in software/hardware development and engineering implementation mainly focus on computing platform selection, automatic adaptability, information security, and business-related issues during actual deployment.
Hardware Development and Automatic Adaptation: Multi-energy flow optimization algorithms require high-efficiency computing capabilities, especially when processing large-scale data. Common hardware platforms, such as FPGAs and GPUs, can significantly improve computing speed, playing particularly important roles in real-time scheduling and multi-objective optimization. For example, FPGAs can be used to accelerate parallel computing, while GPUs are suitable for deep learning and complex model training. In practical applications, hardware needs to automatically adapt to different load requirements. For instance, when power loads and thermal loads fluctuate significantly, hardware platforms need to automatically adjust computing resource allocation according to current loads to avoid overload or computing bottlenecks.
Information Security and System Reliability: In industrial load regulation systems, information security is a crucial consideration. Since multi-energy flow optimization algorithms need to process large amounts of real-time data, including sensitive information such as electricity, thermal energy, and cooling loads, the system must have strong data encryption and access control capabilities to prevent malicious attacks and data leaks. Additionally, industrial environments have high requirements for system reliability. The software and hardware implementation of algorithms needs to have fault tolerance to cope with sudden failures. For example, redundant computing and distributed architectures can improve system stability, ensuring that core functions continue to operate even when some hardware or communication links fail.
Actual Deployment and Engineering Business Challenges: In actual engineering implementation, the application of algorithms is influenced not only by technical factors but also needs to consider engineering feasibility and commercial costs. First, the deployment of load regulation systems typically involves multiple energy subsystems (such as power grids, thermal networks, and energy storage systems). There may be differences in communication protocols and data formats between different systems, so standardized data interfaces and protocol conversion mechanisms are required. Furthermore, at the commercial level, equipment selection, engineering installation costs, and operation and maintenance costs are also key factors. For example, although high-performance computing hardware can improve algorithm efficiency, its high cost and energy consumption may limit large-scale applications. Therefore, in system design, trade-offs need to be made between computing performance, cost, and energy efficiency to select the most suitable software and hardware architecture.
6. Discussion
This systematic review and analysis of 87 key studies (2015–2025) demonstrates that enhancing industrial load flexibility is pivotal for advancing low-carbon, intelligent power systems. Below, we synthesize the quantitative and qualitative evidence from the reviewed methodologies and clarify their linkages to sustainable development goals.
6.1. Quantitative Comparison of Methodologies
Multi-Energy Flow Coordination (Section 3):
- Hybrid Algorithms (e.g., IABC-PSO [89]) improved stability by 89.56% and reduced frequency deviation settling times by 21.61–72.47% compared to traditional methods.
- Distributed Computing (CG&S algorithm [90]) cut optimization time by 86% for large-scale systems.
Market Participation (Section 4):
- Tiered Carbon Pricing [66] reduced industrial park emissions by 4.11% but increased costs by 9.31%, highlighting a trade-off between environmental and economic outcomes.
- P2P Trading (e.g., [77]) boosted local renewable utilization by 15–20% in simulated cases.
6.2. Intrinsic Links to Sustainable Development
The reviewed research reveals a hierarchical relationship between technical, economic, and policy factors in industrial load regulation:
Primary Factors:
- Technical Feasibility: Cross-timescale optimization (e.g., [36]) and uncertainty management (e.g., DRL [38]) form the foundation for reliable load participation.
- Economic Viability: Market mechanisms (e.g., carbon-DR synergy [60]) directly determine adoption rates.
Secondary Factors:
- Policy Compliance: Standards like China’s NDRC 1283 [1] enable scalability but depend on pre-existing technical solutions.
- Social Acceptance: User willingness (modeled via fuzzy TSK rules [19]) indirectly affects implementation speed.
6.3. Future Directions
The integration of data-physics fusion models (e.g., SD + GBRT [82,88]) and hardware acceleration (FPGA/GPU [89]) has emerged as a critical pathway to bridge theoretical innovation and industrial deployment. These approaches align with SDG 7 (Affordable Clean Energy) and SDG 9 (Industry Innovation) by addressing the dual imperatives of decarbonization and operational efficiency.
This synthesis underscores that industrial load flexibility is not merely a technical challenge but a multidisciplinary endeavor requiring coordinated advances in modeling, markets, and policy design.
7. Conclusions
In summary, enhancing the flexibility of industrial loads is not only crucial for optimizing power system operations and improving renewable energy integration capacity, but also represents a critical step in advancing the development of low-carbon, intelligent power systems. Future research should further focus on the following:
- Increasing the precision of load response;
- Optimizing coordinated control strategies for multi-energy flows; and
- Refining market mechanisms and policy support,
with the ultimate goal of achieving sustainable development and green transformation of power systems.
Author Contributions
Conceptualization, B.Z.; methodology, B.Z., Z.Y., C.L. and J.L.; writing—original draft, J.Z., B.Z., Z.Y., C.L. and J.L.; writing—review and editing, J.Z. and B.Z.; funding acquisition, B.Z.; investigation, C.L., J.L., Y.G. and X.X.; project administration, B.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the National Natural Science Foundation of China (Grant Numbers U22B20115), and in part by the Applied Fundamental Research Program of Liaoning Province (Grant Number 2023JH2/101600036).
Institutional Review Board Statement
Not applicable. This study is a literature review and does not involve new data collection from humans or animals.
Informed Consent Statement
Not applicable. This study is a literature review and does not involve direct participation of human subjects or analysis of identifiable personal data.
Data Availability Statement
This is a review article and all data discussed are derived from previously published studies cited in the reference list. No new datasets were generated or analyzed during this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- National Development and Reform Commission. Power Demand Side Management Measures (2023 Edition); Fa Gai Yun Yong Gui [2023] No. 1283; National Development and Reform Commission: Beijing, China, 2023.
- Xue, H.; Guo, L.; Wang, M.; Qin, Y. Application Analysis of a New Power Load Management System Based on Demand Side Resource Management. In Proceedings of the 2023 5th International Academic Exchange Conference on Science and Technology Innovation (IAECST), Guangzhou, China, 8–10 December 2023; pp. 1625–1628. [Google Scholar]
- Zhang, H.; Liu, Z.; Zhang, A.; Gong, F.; Lu, J.; Chen, S.; Li, D.; Zhang, X.; Ren, K. Review on the Regulable Potential Evaluation of Industrial Load Clusters. In Proceedings of the 2021 3rd Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 26–29 March 2021; pp. 1049–1054. [Google Scholar]
- Kumar, M.; De, M. Optimal Load Scheduling for Industrial Load—Analysis for a Generalized Industrial Load Model. In Proceedings of the 2019 8th International Conference on Power Systems (ICPS), Jaipur, India, 20–22 December 2019; pp. 1–6. [Google Scholar]
- Ma, P.; Yang, J.; Gao, J.; Li, X.; Jin, X.; Tang, W. Low-carbon Economic Dispatch of Industrial Community Considering the Demand Response of Energy-Extensive Industrial Loads. In Proceedings of the 2024 9th Asia Conference on Power and Electrical Engineering (ACPEE), Shanghai, China, 11–13 April 2024; pp. 828–833. [Google Scholar]
- Golmohamadi, H. Demand-side management in industrial sector: A review of heavy industries. Renew. Sustain. Energy Rev. 2022, 156, 111963. [Google Scholar] [CrossRef]
- Shoreh, M.H.; Siano, P.; Shafie-khah, M.; Loia, V.; Catalão, J.P.S. A survey of industrial applications of Demand Response. Electr. Power Syst. Res. 2016, 141, 31–49. [Google Scholar] [CrossRef]
- Eladl, A.A.; El-Afifi, M.I.; El-Saadawi, M.M.; Sedhom, B.E. A review on energy hubs: Models, methods, classification, applications, and future trends. Alex. Eng. J. 2023, 68, 315–342. [Google Scholar] [CrossRef]
- Dai, X.; Chen, H.; Xiao, D.; He, Q.; Huang, Y. Distributed Energy Resource-Assisted Industrial Demand Response: A Survey on Technologies, Business Models, and Applications in China. In Proceedings of the 2022 International Conference on Power Energy Systems and Applications (ICoPESA), Singapore, 25–27 February 2022; pp. 503–510. [Google Scholar]
- Wang, J.; Lu, C.; Huang, X.; Mou, H.; Wang, X.; Shen, Y. Short Term Multi Energy Load Forecasting for High Energy-Consuming Industrial Load Based on CNN-GRU. In Proceedings of the 2024 4th Power System and Green Energy Conference (PSGEC), Shanghai, China, 22–24 August 2024; pp. 1199–1204. [Google Scholar]
- Li, Y.; Yuan, X.; Xu, J.; Chen, Z.; Mei, F.; Liu, H. Medium-term forecasting of cold, electric and gas load in multi-energy system based on VAR model. In Proceedings of the 2018 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; pp. 1676–1680. [Google Scholar]
- Kleinschmidt, V.; Hamacher, T.; Perić, V. Flexibility in active distribution networks—Modelling a fully coupled multi-energy system in MESMO. In Proceedings of the 2022 IEEE PES Innovative Smart Grid Technologies—Asia (ISGT Asia), Singapore, 1–5 November 2022; pp. 475–479. [Google Scholar]
- Li, Y.; Yang, X.; Ling, Z.; Zhang, M.; Qu, H.; Li, L. Study on coupling operation of multi-energy flow for integrated community energy system considering seasonal load characteristics. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017; pp. 1–6. [Google Scholar]
- Qiu, K.; Sun, X.; Pan, X.; Guo, J.; Hu, Z.; Chen, C. Multi-Energy Load Forecasting for Integrated Energy Systems based on Causality Anlysis and Multi-Task Learning. In Proceedings of the 2023 IEEE International Conference on Energy Technologies for Future Grids (ETFG), Wollongong, Australia, 3–6 December 2023; pp. 1–6. [Google Scholar]
- Chen, T.; Luo, H.; Liu, F.; Cao, Y.; Sun, Y. Optimal Operation of Multi-Energy Microgrid Electric Heating Load Integrated Demand Response. In Proceedings of the 2023 International Conference on Power System Technology (PowerCon), Jinan, China, 21–22 September 2023; pp. 1–6. [Google Scholar]
- Kang, T.; Liu, K.; Bai, M.; Wu, M.; Jia, D.; Luo, E. Research on Modeling and Joint Power Flow Simulation of Multi Energy Coupling Network. In Proceedings of the 2022 5th International Conference on Energy, Electrical and Power Engineering (CEEPE), Chongqing, China, 22–24 April 2022; pp. 1165–1170. [Google Scholar]
- Lin, W.; Chen, F.; Deng, H.; Shao, Z. Tube Model Predictive Control based Optimal Scheduling of a Multi-energy Microgrid. In Proceedings of the 2022 7th Asia Conference on Power and Electrical Engineering (ACPEE), Hangzhou, China, 15–17 April 2022; pp. 880–884. [Google Scholar]
- Wang, C.; Wang, Y.; Ding, Z.; Zhang, K. Probabilistic Multi-Energy Load Forecasting for Integrated Energy System Based on Bayesian Transformer Network. IEEE Trans. Smart Grid 2024, 15, 1495–1508. [Google Scholar] [CrossRef]
- Xie, T.; Su, Y.; Zhang, G.; Zhang, K.; Li, H.; Wang, R. Optimizing peak-shaving cooperation among electric vehicle charging stations: A two-tier optimal dispatch strategy considering load demand response potential. Int. J. Electr. Power Energy Syst. 2024, 162, 110228. [Google Scholar] [CrossRef]
- Yuan, K.; Sun, C.; Song, Y.; Li, H. A Multi-energy Flow Calculation Method Considering Multiple Energy Coupling Operation Modes. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020; pp. 2661–2666. [Google Scholar]
- Zhang, L.; Li, F.; Sun, B.; Wang, H. Multi-timescale Coordinated Operation Optimization of Integrated Energy System. In Proceedings of the 2023 3rd New Energy and Energy Storage System Control Summit Forum (NEESSC), Mianyang, China, 26–28 September 2023; pp. 7–11. [Google Scholar]
- Guo, L.; Wu, H.C.; Zhang, H.; Xia, T.; Mehraeen, S. Robust optimization for home-load scheduling under price uncertainty in smart grids. In Proceedings of the 2015 International Conference on Computing, Networking and Communications (ICNC), Garden Grove, CA, USA, 16–19 February 2015; pp. 487–493. [Google Scholar]
- Chen, X.; McElroy, M.B.; Kang, C. Integrated Energy Systems for Higher Wind Penetration in China: Formulation, Implementation, and Impacts. IEEE Trans. Power Syst. 2018, 33, 1309–1319. [Google Scholar] [CrossRef]
- Brancucci Martinez-Anido, C.; Brinkman, G.; Hodge, B.-M. The impact of wind power on electricity prices. Renew. Energy 2016, 94, 474–487. [Google Scholar] [CrossRef]
- Haakana, J.; Tikka, V.; Lassila, J.; Partanen, J. Methodology to analyze combined heat and power plant operation considering electricity reserve market opportunities. Energy 2017, 127, 408–418. [Google Scholar] [CrossRef]
- Mashhour, E.; Moghaddas-Tafreshi, S.M. Bidding Strategy of Virtual Power Plant for Participating in Energy and Spinning Reserve Markets—Part II: Numerical Analysis. IEEE Trans. Power Syst. 2011, 26, 957–964. [Google Scholar] [CrossRef]
- Hellmers, A.; Zugno, M.; Skajaa, A.; Morales, J.M. Operational Strategies for a Portfolio of Wind Farms and CHP Plants in a Two-Price Balancing Market. IEEE Trans. Power Syst. 2016, 31, 2182–2191. [Google Scholar] [CrossRef]
- Bao, Z.; Zhou, Q.; Yang, Z.; Yang, Q.; Xu, L.; Wu, T. A Multi Time-Scale and Multi Energy-Type Coordinated Microgrid Scheduling Solution—Part I: Model and Methodology. IEEE Trans. Power Syst. 2015, 30, 2257–2266. [Google Scholar] [CrossRef]
- Gu, W.; Wang, Z.; Wu, Z.; Luo, Z.; Tang, Y.; Wang, J. An online optimal dispatch schedule for CCHP microgrids based on model predictive control. IEEE Trans. Smart Grid 2017, 8, 2332–2342. [Google Scholar] [CrossRef]
- Roy, N.B.; Das, D. Probabilistic optimal power allocation of dispatchable DGs and energy storage units in a reconfigurable grid-connected CCHP microgrid considering demand response. J. Energy Storage 2023, 72, 108207. [Google Scholar] [CrossRef]
- Li, Y.; Zou, Y.; Tan, Y.; Cao, Y.; Liu, X.; Shahidehpour, M.; Tian, S.; Bu, F. Optimal Stochastic Operation of Integrated Low-Carbon Electric Power, Natural Gas, and Heat Delivery System. IEEE Trans. Sustain. Energy 2018, 9, 273–283. [Google Scholar] [CrossRef]
- Sharma, S.; Xu, Y.; Verma, A.; Panigrahi, B.K. Time-Coordinated Multienergy Management of Smart Buildings Under Uncertainties. IEEE Trans. Ind. Inform. 2019, 15, 4788–4798. [Google Scholar] [CrossRef]
- Good, N.; Karangelos, E.; Navarro-Espinosa, A.; Mancarella, P. Optimization under uncertainty of thermal storage-based flexible demand response with quantification of residential users’ discomfort. IEEE Trans. Smart Grid 2015, 6, 2333–2342. [Google Scholar] [CrossRef]
- Lin, C.; Wu, W.; Zhang, B.; Sun, Y. Decentralized Solution for Combined Heat and Power Dispatch Through Benders Decomposition. IEEE Trans. Sustain. Energy 2017, 8, 1361–1372. [Google Scholar] [CrossRef]
- Mitridati, L.; Pinson, P. Optimal coupling of heat and electricity systems: A stochastic hierarchical approach. In Proceedings of the 2016 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Beijing, China, 16–20 October 2016; pp. 1–6. [Google Scholar]
- Wang, J.; You, S.; Zong, Y.; Træholt, C.; Zhang, C.; Dong, Z.Y. Multi-Timescale Coordinated Operation of An Integrated Energy System Considering Multiple Uncertainties. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar]
- Sharma, S.; Verma, A.; Xu, Y.; Panigrahi, B.K. Robustly Coordinated Bi-Level Energy Management of a Multi-Energy Building Under Multiple Uncertainties. IEEE Trans. Sustain. Energy 2021, 12, 3–13. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, J.; Wang, X.; Chen, S. Optimal dispatch of integrated energy system based on deep reinforcement learning. Energy Rep. 2023, 9, 373–378. [Google Scholar] [CrossRef]
- Yang, Y.; Ma, T.; Li, H.; Liu, Y.; Tang, C.; Pei, W. Federated double DQN based multi-energy microgrid energy management strategy considering carbon emissions. Glob. Energy Interconnect. 2023, 6, 689–699. [Google Scholar] [CrossRef]
- Li, F.; Liu, L.; Yu, Y. Deep reinforcement learning-based multi-objective optimization for electricity–gas–heat integrated energy systems. Expert Syst. Appl. 2025, 262, 125558. [Google Scholar] [CrossRef]
- Yue, H.; Zhang, Y.; Guo, J.; Hu, Y.; Wei, C.; Jia, H.; Liu, D.; Xie, D. Analysis and construction of evaluation index system of inter-provincial electricity spot markets. Glob. Energy Interconnect. 2024, 7, 697–706. [Google Scholar] [CrossRef]
- Fu, X.; Wang, Z.; Zheng, Y.; Wang, Y. A clearing model for medium and long-term electricity transactions considering inter-provincial market constraints in a low-carbon context. CSEE J. Power Energy Syst. 2024, 1–10. [Google Scholar] [CrossRef]
- Gong, X.; Li, X.; Zhong, Z. Strategic bidding of hydrogen-wind-photovoltaic energy system in integrated energy and flexible ramping markets with renewable energy uncertainty. Int. J. Hydrog. Energy 2024, 80, 1406–1423. [Google Scholar] [CrossRef]
- Hu, J.; Yan, Q.; Kahrl, F.; Liu, X.; Wang, P.; Lin, J. Evaluating the ancillary services market for large-scale renewable energy integration in China’s northeastern power grid. Util. Policy 2021, 69, 101179. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Meng, Z.; Yang, M.; Lu, Y.; Chai, Z.; Wu, Z. Energy Storage Operation Modes in Typical Electricity Market and Their Implications for China. Energy Eng. 2024, 121, 2409–2434. [Google Scholar] [CrossRef]
- Zeng, B.; Zhou, Y.; Xu, X.; Cai, D. Bi-level planning approach for incorporating the demand-side flexibility of cloud data centers under electricity-carbon markets. Appl. Energy 2024, 357, 122406. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, J.; Xie, J.; Song, Y.; Ge, Y.; Fu, D. Exploration of Standardized Market Trading Models for Industrial Adjustable Load Participation in Power Grid Service. In Proceedings of the 2023 IEEE 7th Conference on Energy Internet and Energy System Integration (EI2), Hangzhou, China, 15–18 December 2023; pp. 3102–3108. [Google Scholar]
- Li, K.; Li, Z.; Huang, C.; Ai, Q. Online transfer learning-based residential demand response potential forecasting for load aggregator. Appl. Energy 2024, 358, 122631. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, X.; Pan, L.; Liu, J.; Liu, J.; Hu, W. Distributed prosumer trading in the electricity and carbon markets considering user utility. Renew. Energy 2024, 228, 120669. [Google Scholar] [CrossRef]
- Wi, Y.M.; Joo, S.K.; Song, K.B. Holiday Load Forecasting Using Fuzzy Polynomial Regression with Weather Feature Selection and Adjustment. IEEE Trans. Power Syst. 2012, 27, 596–603. [Google Scholar] [CrossRef]
- Hu, M.; Xiao, F.; Wang, L. Investigation of demand response potentials of residential air conditioners in smart grids using grey-box room thermal model. Appl. Energy 2017, 207, 324–335. [Google Scholar] [CrossRef]
- Tushar, W.; Saha, T.K.; Yuen, C.; Morstyn, T.; Nahid Al, M.; Poor, H.V.; Bean, R. Grid Influenced Peer-to-Peer Energy Trading. IEEE Trans. Smart Grid 2020, 11, 1407–1418. [Google Scholar] [CrossRef]
- Shirsat, A.; Tang, W. Quantifying residential demand response potential using a mixture density recurrent neural network. Int. J. Electr. Power Energy Syst. 2021, 130, 106853. [Google Scholar] [CrossRef]
- Yin, R.; Kara, E.C.; Li, Y.; DeForest, N.; Wang, K.; Yong, T.; Stadler, M. Quantifying flexibility of commercial and residential loads for demand response using setpoint changes. Appl. Energy 2016, 177, 149–164. [Google Scholar] [CrossRef]
- Barbulescu, C.; Kilyeni, S.; Deacu, A.; Turi, G.M.; Moga, M. Artificial neural network based monthly load curves forecasting. In Proceedings of the 2016 IEEE 11th International Symposium on Applied Computational Intelligence and Informatics (SACI), Timisoara, Romania, 12–14 May 2016; pp. 237–242. [Google Scholar]
- Peirelinck, T.; Kazmi, H.; Mbuwir, B.V.; Hermans, C.; Spiessens, F.; Suykens, J.; Deconinck, G. Transfer learning in demand response: A review of algorithms for data-efficient modelling and control. Energy AI 2022, 7, 100126. [Google Scholar] [CrossRef]
- Huang, C.; Li, K.; Zhang, N. Strategic joint bidding and pricing of load aggregators in day-ahead demand response market. Appl. Energy 2025, 377, 124552. [Google Scholar] [CrossRef]
- Yang, C.; Liu, J.; Liao, H.; Liang, G.; Zhao, J. An improved carbon emission flow method for the power grid with prosumers. Energy Rep. 2023, 9, 114–121. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, Q.; Cui, H.; Cheng, H.; Zhang, X.; Fan, L. A Precise Carbon Emission Model on Electricity Consumption Side with Carbon Emission Flow Theory. In Proceedings of the 2022 4th International Conference on Electrical Engineering and Control Technologies (CEECT), Shanghai, China, 16–18 December 2022; pp. 1126–1131. [Google Scholar]
- Lou, C.; Jin, Z.; Zhou, Y.; Tang, W.; Zhang, L.; Yang, J. Privacy-protected P2P electricity and carbon emission trading markets based on distributionally robust proximal atomic coordination algorithm. Appl. Energy 2025, 384, 125409. [Google Scholar] [CrossRef]
- Liu, W.; Li, Z.; Xing, X.; Chen, X.; Wang, Y.; Wang, X. Non-cooperative game optimization for virtual power plants considering carbon trading market. Energy 2025, 317, 134571. [Google Scholar] [CrossRef]
- Zhu, S.; Ji, J.; Huang, Q.; Li, S.; Ren, J.; He, D.; Yang, Y. Optimal scheduling and trading in joint electricity and carbon markets. Energy Strategy Rev. 2024, 54, 101426. [Google Scholar] [CrossRef]
- Dong, S.; Zhao, H.; Zheng, Y.; Ni, L. Carbon reduction analysis of electric heat pumps in carbon neutrality in China. Sustain. Cities Soc. 2023, 97, 104758. [Google Scholar] [CrossRef]
- Li, X.; Zhou, M.; Cao, Y.; Liao, T.; Zhang, J.; Zhang, H. Influence Analysis of Dual Carbon Goals on Industrial Load Based on System Dynamics. In Proceedings of the 2024 IEEE 2nd International Conference on Control, Electronics and Computer Technology (ICCECT), Jilin, China, 26–28 April 2024; pp. 445–449. [Google Scholar]
- Lv, H.; Deng, B.; Zhang, P.; Han, G.; Zhang, K.; Lv, H. Optimal Scheduling of Industrial Loads in Chemical Park in Low-Carbon. In Proceedings of the 2024 IEEE 2nd International Conference on Power Science and Technology (ICPST), Dali, China, 9–11 May 2024; pp. 2035–2041. [Google Scholar]
- Wang, M.; Wang, M.; Song, Y.; Wang, L.; Wang, R.; Zheng, X.; Gao, H. Optimization of Hydrogen Containing Integrated Energy System Operation Considering Demand Response and Ladder-type Carbon Trading. In Proceedings of the 2024 36th Chinese Control and Decision Conference (CCDC), Xi’an, China, 25–27 May 2024; pp. 1028–1033. [Google Scholar]
- Wang, L.; Yang, C.; Xu, Z.; Yuan, G.; Tang, L.; Bai, Y.; Wang, X. Analysis of carbon electricity coupled market modeling method based on carbon credit trading mechanism. Int. J. Electr. Power Energy Syst. 2024, 156, 109707. [Google Scholar] [CrossRef]
- Molitor, C.; Groß, S.; Zeitz, J.; Monti, A. MESCOS—A Multienergy System Cosimulator for City District Energy Systems. IEEE Trans. Ind. Inform. 2014, 10, 2247–2256. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.; Li, G.; Chen, C. Optimal scheduling of integrated demand response-enabled integrated energy systems with uncertain renewable generations: A Stackelberg game approach. Energy Convers. Manag. 2021, 235, 113996. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Z.; Li, G.; Mu, Y.; Zhao, D.; Chen, C.; Shen, B. Optimal scheduling of isolated microgrid with an electric vehicle battery swapping station in multi-stakeholder scenarios: A bi-level programming approach via real-time pricing. Appl. Energy 2018, 232, 54–68. [Google Scholar] [CrossRef]
- Li, S.; Zhang, L.; Nie, L.; Wang, J. Trading strategy and benefit optimization of load aggregators in integrated energy systems considering integrated demand response: A hierarchical Stackelberg game. Energy 2022, 249, 123678. [Google Scholar] [CrossRef]
- Byeon, H.; Alghamdi, W.; Evin, M.; Sucharitha, M.; Ponkumar, D.D.N.; Prakash, A.; Sunil, J. A novel swarm intelligence-based approach for solving optimal power flow problems in modern power systems. Results Control Optim. 2025, 19, 100555. [Google Scholar] [CrossRef]
- Ni, L.; Feng, C.; Wen, F.; Salam, A. Optimal power flow of multiple energy carriers with multiple kinds of energy storage. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Deng, S.; Wu, L.L.; Wei, F.; Wu, Q.H.; Jing, Z.X.; Zhou, X.X.; Li, M.S. Optimal operation of energy hubs in an integrated energy network considering multiple energy carriers. In Proceedings of the 2016 IEEE Innovative Smart Grid Technologies—Asia (ISGT-Asia), Melbourne, VIC, Australia, 28 November–1 December 2016; pp. 1201–1206. [Google Scholar]
- Shabanpour-Haghighi, A.; Seifi, A.R. Energy Flow Optimization in Multicarrier Systems. IEEE Trans. Ind. Inform. 2015, 11, 1067–1077. [Google Scholar] [CrossRef]
- Tookanlou, M.B.; Ardehali, M.M.; Nazari, M.E. Combined cooling, heating, and power system optimal pricing for electricity and natural gas using particle swarm optimization based on bi-level programming approach: Case study of Canadian energy sector. J. Nat. Gas Sci. Eng. 2015, 23, 417–430. [Google Scholar] [CrossRef]
- Kumari, A.; Gupta, R.; Tanwar, S. PRS-P2P: A Prosumer Recommender System for Secure P2P Energy Trading using Q-Learning Towards 6G. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar]
- Jia, H.; Wang, X.; Jin, X.; Cheng, L.; Mu, Y.; Yu, X.; Wei, W. Optimal pricing of integrated community energy system for building prosumers with P2P multi-energy trading. Appl. Energy 2024, 365, 123259. [Google Scholar] [CrossRef]
- Wang, K.; Wang, C.; Yao, W.; Zhang, Z.; Liu, C.; Dong, X.; Yang, M.; Wang, Y. Embedding P2P transaction into demand response exchange: A cooperative demand response management framework for IES. Appl. Energy 2024, 367, 123319. [Google Scholar] [CrossRef]
- Dong, J.; Xue, G.; Li, R. Demand response in China: Regulations, pilot projects and recommendations—A review. Renew. Sustain. Energy Rev. 2016, 59, 13–27. [Google Scholar] [CrossRef]
- Silletti, F.; Orrù, L.; Serafino, M.D.; Bolla, L.; Maso, F. H2020 OSMOSE PROJECT: Final results of the experimentation phase of industrial Demand Response (DR). In Proceedings of the 2022 AEIT International Annual Conference (AEIT), Rome, Italy, 3–5 October 2022; pp. 1–6. [Google Scholar]
- Song, X.-H.; Han, J.-J.; Zhang, L.; Zhao, C.-P.; Wang, P.; Liu, X.-Y.; Li, Q.-C. Impacts of renewable portfolio standards on multi-market coupling trading of renewable energy in China: A scenario-based system dynamics model. Energy Policy 2021, 159, 112647. [Google Scholar] [CrossRef]
- Yuan, Y.; Chen, Z.; Wang, Z.; Sun, Y.; Chen, Y. Attention mechanism-based transfer learning model for day-ahead energy demand forecasting of shopping mall buildings. Energy 2023, 270, 126878. [Google Scholar] [CrossRef]
- Paletta, Q.; Arbod, G.; Lasenby, J. Omnivision forecasting: Combining satellite and sky images for improved deterministic and probabilistic intra-hour solar energy predictions. Appl. Energy 2023, 336, 120818. [Google Scholar] [CrossRef]
- Rafiei, M.; Niknam, T.; Aghaei, J.; Shafie-Khah, M.; Catalão, J.P.S. Probabilistic Load Forecasting Using an Improved Wavelet Neural Network Trained by Generalized Extreme Learning Machine. IEEE Trans. Smart Grid 2018, 9, 6961–6971. [Google Scholar] [CrossRef]
- Fu, G. Deep belief network based ensemble approach for cooling load forecasting of air-conditioning system. Energy 2018, 148, 269–282. [Google Scholar] [CrossRef]
- Alabi, T.M.; Lu, L.; Yang, Z. Real-time automatic control of multi-energy system for smart district community: A coupling ensemble prediction model and safe deep reinforcement learning. Energy 2024, 304, 132209. [Google Scholar] [CrossRef]
- Singh, U.; Rizwan, M.; Alaraj, M.; Alsaidan, I. A Machine Learning-Based Gradient Boosting Regression Approach for Wind Power Production Forecasting: A Step towards Smart Grid Environments. Energies 2021, 14, 5196. [Google Scholar] [CrossRef]
- Iqbal, M.S.; Limon, M.F.A.; Kabir, M.M.; Hossain, M.Z.; Jubayer, M.F.; Soeb, M.J.A. A hybrid optimization algorithm based on cascaded (1 + PI)-PI-PID controller for load frequency control in interconnected power systems. Results Eng. 2024, 24, 103624. [Google Scholar] [CrossRef]
- Flores-Quiroz, A.; Strunz, K. A distributed computing framework for multi-stage stochastic planning of renewable power systems with energy storage as flexibility option. Appl. Energy 2021, 291, 116736. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).