Sustainability-Driven Energy Efficiency Assessment: Divergent Policy Impacts of Single Factor Limits Versus Total Factor Coordination
Abstract
1. Introduction
2. Literature Review
2.1. Research on Single-Factor Energy Efficiency
2.2. Research on TFEE
2.3. Discussion on SFEE and TFEE
3. Research Methods
3.1. SFEE Measurement Method
3.2. Discussion on Measurement Model of TFEE
- 1.
- Sequential Energy-Quasi-fixed Inputs, SE-QFI
- 2.
- Sequential Energy-SBM model, SE-SBM
- 3.
- Sequential Energy-Directional SBM model, SE-DSBM
4. Indicator Selection and Data Sources
5. Empirical Results and Discussions
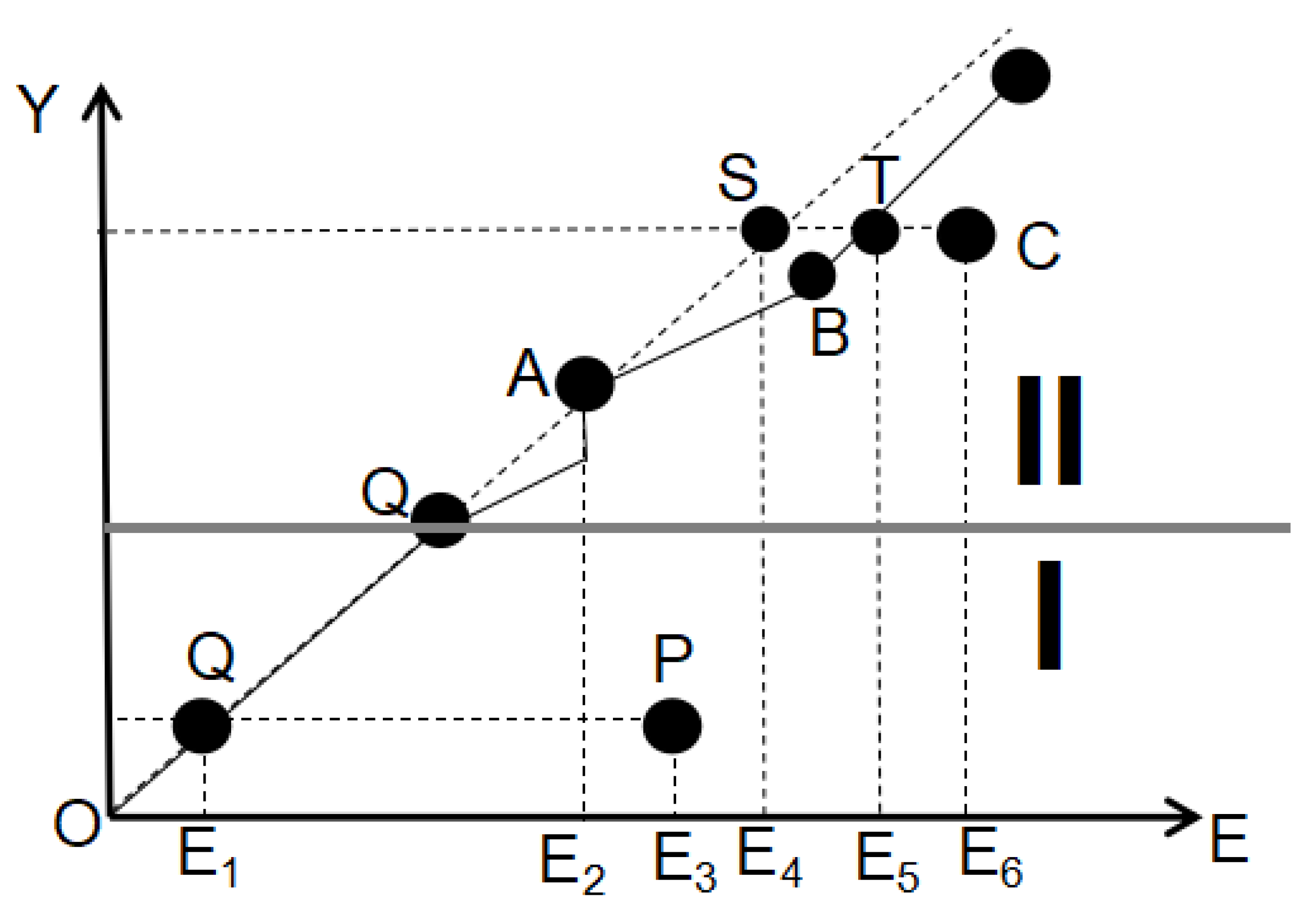
5.1. Comparison and Analysis of the SFEE and TFEE Rankings
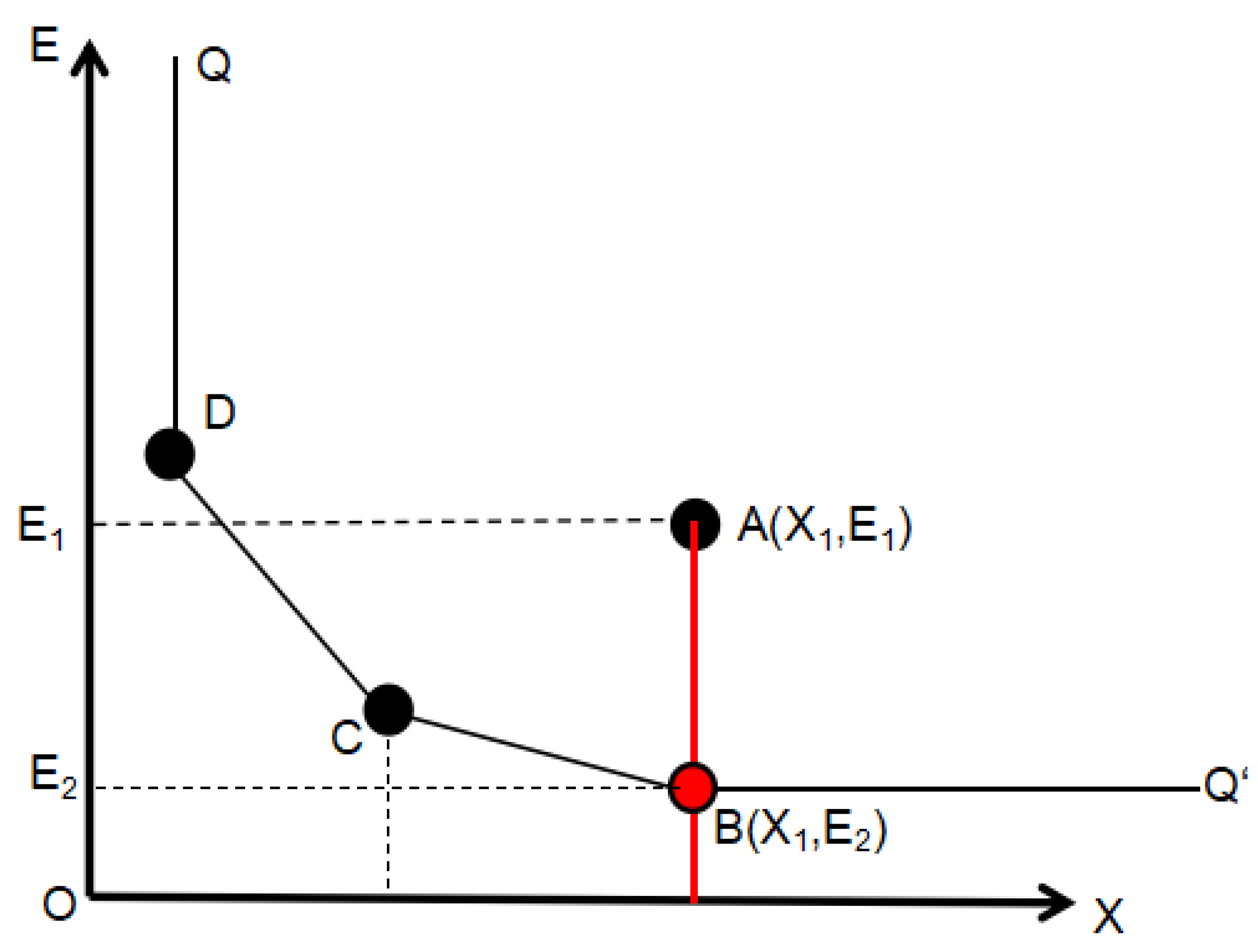
5.2. SFEE Indicators and Total Factor Energy
Efficiency Gap Analysis
5.3. Measurement of TFEE Under the Introduction of “New Driving Forces”
6. Conclusions and Recommendations
6.1. Conclusions
6.2. Policy Recommendations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, B.; Long, H. A Stochastic Frontier Analysis of Energy Efficiency of China’s Chemical Industry. J. Clean. Prod. 2015, 87, 235–244. [Google Scholar] [CrossRef]
- Du, K.R.; Yan, Z.M.; Yang, Z.M. Progress of Evaluation Methods on Energy and Environmental Performance. J. Environ. Econ. 2018, 3, 113–138. [Google Scholar]
- Hu, J.L.; Wang, S.C. Total-Factor Energy Efficiency of Regions in China. Energy Policy 2006, 34, 3206–3217. [Google Scholar] [CrossRef]
- Wei, C.; Shen, M.H. Energy Efficiency and Energy Productivity: A Comparison Based on the Panel Data by Province. J. Quant. Tech. Econ. 2007, 9, 110–121. [Google Scholar]
- Du, K.; Li, J. Towards a Green World: How Do Green Technology Innovations Affect Total-Factor Carbon Productivity. Energy Policy 2019, 131, 240–250. [Google Scholar] [CrossRef]
- Zhang, N.; Kong, F.; Yu, Y. Measuring Ecological Total-Factor Energy Efficiency Incorporating Regional Heterogeneities in China. Ecol. Indic. 2015, 51, 165–172. [Google Scholar] [CrossRef]
- Wu, J.; Xiong, B.; An, Q.; Sun, J.; Wu, H. Total-Factor Energy Efficiency Evaluation of Chinese Industry by Using Two-Stage DEA Model with Shared Inputs. Ann. Oper. Res. 2017, 255, 257–276. [Google Scholar] [CrossRef]
- Ling, J. Research on New Momentum of Economic Development Conversion of National High and New Technology Zone and Chinese Economic Development. Reform. Strategy 2018, 34, 53–57. [Google Scholar]
- Zheng, S.L.; Xiong, L. Assessment and Policy Suggestions for New Kinetic Energy of China’s Economic Development. Technol. Econ. 2021, 40, 1–11. [Google Scholar]
- Gao, Z.Y.; Wang, Y. Classification of China’s Provinces According to Energy Productivity and Analysis for the Differences. J. Quant. Tech. Econ. 2006, 9, 46–57. [Google Scholar]
- Chen, Z.; Chen, Q.Y. Energy Efficiency of Chinese Firms: Heterogeneity, Influencing Factors and Policy Implications. China Ind. Econ. 2019, 12, 78–95. [Google Scholar]
- Shao, S.; Zhang, K.; Dou, J.M. Effects of Economic Agglomeration on Energy Saving and Emission Reduction: Theory and Empirical Evidence from China. J. Manag. World 2019, 35, 36–60+226. [Google Scholar]
- Balado-Naves, R.; Baños-Pino, J.F.; Mayor, M. Do Countries Influence Neighbouring Pollution? A Spatial Analysis of the EKC for CO2 Emissions. Energy Policy 2018, 123, 266–279. [Google Scholar] [CrossRef]
- Wei, Y.M.; Liao, H. Seven Energy Efficiency Indicators and Their Measurement Approaches. China Soft Sci. 2010, 1, 128–137. [Google Scholar]
- Li, G.Z.; Wang, S. Regional Factor Decompositions in China’s Energy Intensity Change: Based on LMDI Technique. J. Financ. Econ. 2008, 8, 52–62. [Google Scholar]
- Lin, B.Q.; Du, K.R. Understanding the Changes in China’s Energy Intensity: A Comprehensive Decomposition Framework. J. World Econ. 2014, 37, 69–87. [Google Scholar]
- Lin, B.Q.; Miao, W. What Drives Energy Intensity Fall in China? Evidence from a Meta-Frontier Approach. Appl. Energy 2021, 281, 116034. [Google Scholar] [CrossRef]
- Li, K.; Lin, B. The Nonlinear Impacts of Industrial Structure on China’s Energy Intensity. Energy 2014, 69, 258–265. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the Efficiency of Decision Making Units. Eur. J. Oper. Res. 1979, 2, 429–444. [Google Scholar] [CrossRef]
- He, Y.; Lin, B. Investigating Environmental Kuznets Curve from an Energy Intensity Perspective: Empirical Evidence from China. J. Clean. Prod. 2019, 234, 1013–1022. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, J.H.; Zhang, H. Total-Factor Energy Efficiency and Influencing Factors Across Provinces in China in the Presence of Environmental Regulation. Econ. Rev. 2011, 4, 31–43. [Google Scholar]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Chung, Y.H.; Färe, R.; Grosskopf, S. Productivity and Undesirable Outputs: A Directional Distance Function Approach. J. Environ. Manag. 1997, 51, 229–240. [Google Scholar] [CrossRef]
- Ouellette, P.; Vierstraete, V. Technological Change and Efficiency in the Presence of Quasi-Fixed Inputs: A DEA Application to the Hospital Sector. Eur. J. Oper. Res. 2004, 154, 755–763. [Google Scholar] [CrossRef]
- Boyd, G.A. Estimating Plant Level Energy Efficiency with a Stochastic Frontier. Energy J. 2008, 29, 23–24. [Google Scholar] [CrossRef]
- Tone, K. A Slacks-Based Measure of Efficiency in Data Envelopment Analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef]
- Fukuyama, H.; Weber, W.L. A Directional Slacks-Based Measure of Technical Inefficiency. Socio-Econ. Plan. Sci. 2009, 43, 274–287. [Google Scholar] [CrossRef]
- Halkos, G.E.; Jaime, M.D.A.; Aslanidis, P.S.C. Examining Energy and Carbon Intensity of the European Fashion Industry: A Hybrid DEA Analysis for Circular Economy. Circ. Econ. Sustain. 2024, 5, 921–948. [Google Scholar] [CrossRef]
- Tsionas, M.; Parmeter, C.F.; Zelenyuk, V. Bayesian Artificial Neural Networks for Frontier Efficiency Analysis. J. Econom. 2023, 236, 105491. [Google Scholar] [CrossRef]
- Wu, Q.; Wu, C.Y. Research on Evaluation Model of Energy Efficiency Based on DEA. J. Manag. Sci. 2009, 22, 103–112. [Google Scholar]
- Yang, Y.; Cheng, L.W. Evaluating and Decomposing of Total Factor Energy Productivity Based on Cost Perspective. Syst. Eng.—Theory Pract. 2017, 37, 2306–2319. [Google Scholar]
- Huo, T.; Tang, M.; Cai, W.; Ren, H.; Liu, B.; Hu, X. Provincial Total-Factor Energy Efficiency Considering Floor Space Under Construction: An Empirical Analysis of China’s Construction Industry. J. Clean. Prod. 2020, 244, 118749. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, W.J. Can Energy Quota Trading Achieve Win-Win Development for Economic Growth and Energy Savings in China. Econ. Res. J. 2019, 54, 165–181. [Google Scholar]
- Smyth, R.; Narayan, P.K.; Shi, H. Substitution Between Energy and Classical Factor Inputs in the Chinese Steel Sector. Appl. Energy 2011, 88, 361–367. [Google Scholar] [CrossRef]
- Lv, K.; Yu, A.; Bian, Y. Regional Energy Efficiency and Its Determinants in China During 2001–2010: A Slacks-Based Measure and Spatial Econometric Analysis. J. Product. Anal. 2017, 47, 65–81. [Google Scholar] [CrossRef]
- Tu, Z.G.; Shen, R.J. Analysis on China’s Carbon Emission Division and Reduction Path: Based on Multivariate Panel Data Clustering Analysis Method. J. China Univ. Geosci. 2012, 6, 7–13. [Google Scholar]
- Xu, M.; Lin, B. Energy Efficiency Gains from Distortion Mitigation: A Perspective on the Metallurgical Industry. Resour. Policy 2022, 77, 102758. [Google Scholar] [CrossRef]
- Wei, C.; Shen, M.H. Energy Efficiency and Its Influencing Factors: An Empirical Analysis Based on DEA. Manag. World 2007, 8, 66–76. [Google Scholar]
- Shi, D. Regional Differences in China’s Energy Efficiency and Conservation Potentials. China Ind. Econ. 2006, 10, 49–58. [Google Scholar]
| 2006 | 2008 | 2010 | 2015 | 2019 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Province | The Rankings of Energy Consumption per Unit of GDP | The Rankings of TFEE | The Rankings of Energy Consumption per Unit of GDP | The Rankings of TFEE | The Rankings of Energy Consumption per Unit of GDP | The Rankings of TFEE | The Rankings of Energy Consumption per Unit of GDP | The Rankings of TFEE | The Rankings of Energy Consumption per Unit of GDP | The Rankings of TFEE |
| Anhui | 9 | 9 | 9 | 9 | 9 | 9 | 8 | 8 | 8 | 9 |
| Beijing | 2 | 2 | 1 | 2 | 1 | 3 | 1 | 1 | 1 | 2 |
| Fujian | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| Gansu | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 |
| Guangdong | 1 | 3 | 2 | 3 | 2 | 1 | 3 | 3 | 3 | 3 |
| Guangxi | 10 | 11 | 12 | 12 | 15 | 15 | 19 | 19 | 20 | 20 |
| Guizhou | 27 | 27 | 27 | 27 | 27 | 27 | 24 | 24 | 24 | 24 |
| Hainan | 5 | 5 | 6 | 7 | 7 | 7 | 9 | 9 | 13 | 14 |
| Hebei | 25 | 25 | 25 | 25 | 25 | 25 | 26 | 26 | 25 | 25 |
| Henan | 14 | 14 | 14 | 15 | 13 | 14 | 14 | 14 | 11 | 11 |
| Heilongjiang | 17 | 17 | 19 | 18 | 18 | 18 | 16 | 16 | 17 | 17 |
| Hubei | 16 | 16 | 15 | 14 | 14 | 13 | 12 | 12 | 12 | 12 |
| Hunan | 13 | 13 | 13 | 13 | 12 | 11 | 10 | 11 | 9 | 8 |
| Jilin | 22 | 22 | 22 | 22 | 22 | 22 | 18 | 18 | 18 | 18 |
| Jiangsu | 7 | 7 | 7 | 6 | 6 | 6 | 5 | 5 | 5 | 5 |
| Jiangxi | 8 | 8 | 8 | 8 | 8 | 8 | 11 | 10 | 10 | 10 |
| Liaoning | 20 | 20 | 20 | 20 | 21 | 21 | 21 | 21 | 22 | 22 |
| Inner Mongolia | 26 | 26 | 26 | 26 | 26 | 26 | 25 | 25 | 26 | 26 |
| Ningxia | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
| Qinghai | 28 | 28 | 28 | 28 | 28 | 28 | 29 | 29 | 29 | 29 |
| Shandong | 15 | 15 | 16 | 17 | 17 | 17 | 17 | 17 | 16 | 16 |
| Shanxi | 29 | 29 | 29 | 29 | 29 | 29 | 28 | 28 | 27 | 27 |
| Shaanxi | 19 | 19 | 18 | 19 | 19 | 19 | 22 | 22 | 21 | 21 |
| Shanghai | 3 | 1 | 3 | 1 | 3 | 2 | 2 | 2 | 2 | 1 |
| Sichuan | 18 | 18 | 17 | 16 | 16 | 16 | 13 | 13 | 14 | 13 |
| Tianjin | 11 | 10 | 10 | 10 | 11 | 12 | 15 | 15 | 15 | 15 |
| Xinjiang | 24 | 24 | 24 | 24 | 24 | 24 | 27 | 27 | 28 | 28 |
| Yunnan | 21 | 21 | 21 | 21 | 20 | 20 | 20 | 20 | 19 | 19 |
| Zhejiang | 6 | 6 | 5 | 5 | 5 | 5 | 6 | 6 | 7 | 6 |
| Chongqing | 12 | 12 | 11 | 11 | 10 | 10 | 7 | 7 | 6 | 7 |
| 2006 | 2010 | 2015 | 2019 | |||||
|---|---|---|---|---|---|---|---|---|
| Province | Single-Factor Energy Efficiency Indicators | Total Factor Energy Efficiency | Single-Factor Energy Efficiency Indicators | Total Factor Energy Efficiency | Single-Factor Energy Efficiency Indicators | Total Factor Energy Efficiency | Single-Factor Energy Efficiency Indicators | Total Factor Energy Efficiency |
| Beijing | 0.9652 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Tianjin | 0.5969 | 0.6078 | 0.5301 | 0.5301 | 0.4714 | 0.4714 | 0.4731 | 0.4731 |
| Hebei | 0.3199 | 0.3199 | 0.2851 | 0.2851 | 0.2536 | 0.2536 | 0.2616 | 0.2616 |
| Shanxi | 0.2164 | 0.2164 | 0.2097 | 0.2097 | 0.1780 | 0.1780 | 0.1709 | 0.1709 |
| Inner Mongolia | 0.2872 | 0.2872 | 0.2809 | 0.2809 | 0.2713 | 0.2713 | 0.2073 | 0.2073 |
| Liaoning | 0.4835 | 0.4835 | 0.4243 | 0.4243 | 0.4008 | 0.4008 | 0.3517 | 0.3517 |
| Jilin | 0.4296 | 0.4296 | 0.3752 | 0.3752 | 0.4437 | 0.4437 | 0.4405 | 0.4405 |
| Heilongjiang | 0.5054 | 0.5054 | 0.4714 | 0.4714 | 0.4666 | 0.4666 | 0.4491 | 0.4491 |
| Shanghai | 0.9316 | 1.0000 | 0.8981 | 1.0000 | 0.9003 | 1.0000 | 0.9120 | 1.0000 |
| Jiangsu | 0.8225 | 0.8225 | 0.8033 | 0.8155 | 0.7330 | 0.7587 | 0.7482 | 0.7769 |
| Zhejiang | 0.8474 | 0.8474 | 0.8230 | 0.8283 | 0.7139 | 0.7270 | 0.6937 | 0.7115 |
| Anhui | 0.7113 | 0.7113 | 0.6933 | 0.7143 | 0.6138 | 0.6324 | 0.6239 | 0.6306 |
| Fujian | 0.9176 | 0.9176 | 0.8555 | 0.8700 | 0.7996 | 0.7996 | 0.7897 | 0.7897 |
| Jiangxi | 0.7311 | 0.7311 | 0.7150 | 0.7150 | 0.6027 | 0.6033 | 0.6115 | 0.6161 |
| Shandong | 0.5165 | 0.5165 | 0.4761 | 0.4761 | 0.4450 | 0.4450 | 0.4565 | 0.4565 |
| Henan | 0.5272 | 0.5272 | 0.5151 | 0.5151 | 0.5329 | 0.5329 | 0.5991 | 0.5991 |
| Hubei | 0.5139 | 0.5139 | 0.5122 | 0.5155 | 0.5671 | 0.5671 | 0.5719 | 0.5719 |
| Hunan | 0.5361 | 0.5361 | 0.5266 | 0.5378 | 0.6030 | 0.6030 | 0.6195 | 0.6318 |
| Guangdong | 1.0000 | 1.0000 | 0.9397 | 1.0000 | 0.8601 | 0.9474 | 0.8324 | 0.8842 |
| Guangxi | 0.5989 | 0.5989 | 0.5099 | 0.5099 | 0.4416 | 0.4416 | 0.4172 | 0.4172 |
| Hainan | 0.8856 | 0.8856 | 0.7996 | 0.7996 | 0.6070 | 0.6070 | 0.5536 | 0.5536 |
| Chongqing | 0.5647 | 0.5647 | 0.5576 | 0.5605 | 0.7024 | 0.7251 | 0.6986 | 0.7100 |
| Sichuan | 0.5049 | 0.5049 | 0.4947 | 0.5028 | 0.5435 | 0.5592 | 0.5414 | 0.5593 |
| Guizhou | 0.2670 | 0.2670 | 0.2608 | 0.2608 | 0.2788 | 0.2788 | 0.3010 | 0.3010 |
| Yunnan | 0.4549 | 0.4549 | 0.4371 | 0.4371 | 0.4150 | 0.4150 | 0.4173 | 0.4173 |
| Shaanxi | 0.4981 | 0.4981 | 0.4641 | 0.4641 | 0.3947 | 0.3947 | 0.3823 | 0.3823 |
| Gansu | 0.3611 | 0.3611 | 0.3550 | 0.3550 | 0.3170 | 0.3170 | 0.3189 | 0.3189 |
| Qinghai | 0.2333 | 0.2333 | 0.2200 | 0.2200 | 0.1524 | 0.1524 | 0.1632 | 0.1632 |
| Ningxia | 0.1667 | 0.1667 | 0.1606 | 0.1606 | 0.1172 | 0.1172 | 0.0914 | 0.0914 |
| Xinjiang | 0.3525 | 0.3525 | 0.3085 | 0.3085 | 0.1837 | 0.1837 | 0.1698 | 0.1698 |
| Time | 2015 | 2016 | 2017 | 2018 | 2019 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Province | New and Old Driving Forces | Conventional Driving Forces | New and Old Driving Forces | Conventional Driving Forces | New and Old Driving Forces | Conventional Driving Forces | New and Old Driving Forces | Conventional Driving Forces | New and Old Driving Forces | Conventional Driving Forces |
| Anhui | 0.6686 | 0.6324 | 0.683 | 0.6376 | 0.6993 | 0.6440 | 0.7008 | 0.6473 | 0.6955 | 0.6306 |
| Beijing | 1 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 |
| Fujian | 0.8875 | 0.7996 | 0.915 | 0.8126 | 0.9163 | 0.8080 | 0.9026 | 0.8043 | 0.8964 | 0.7897 |
| Gansu | 0.317 | 0.3170 | 0.3328 | 0.3328 | 0.3215 | 0.3215 | 0.3145 | 0.3145 | 0.3189 | 0.3189 |
| Guangdong | 1 | 0.9474 | 1 | 0.9403 | 1 | 0.9188 | 1 | 0.8941 | 1 | 0.8842 |
| Guangxi | 0.45 | 0.4416 | 0.4512 | 0.4359 | 0.4537 | 0.4331 | 0.4482 | 0.4296 | 0.4375 | 0.4172 |
| Guizhou | 0.2788 | 0.2788 | 0.285 | 0.2850 | 0.294 | 0.2940 | 0.3025 | 0.3025 | 0.301 | 0.3010 |
| Hainan | 0.607 | 0.6070 | 0.5993 | 0.5993 | 0.5869 | 0.5869 | 0.5722 | 0.5722 | 0.5536 | 0.5536 |
| Hebei | 0.2783 | 0.2536 | 0.2828 | 0.2539 | 0.2861 | 0.2546 | 0.289 | 0.2599 | 0.2941 | 0.2616 |
| Henan | 0.6027 | 0.5329 | 0.6306 | 0.5490 | 0.6609 | 0.5719 | 0.6676 | 0.5786 | 0.6989 | 0.5991 |
| Heilongjiang | 0.4889 | 0.4666 | 0.4926 | 0.4647 | 0.4983 | 0.4648 | 0.4874 | 0.4596 | 0.4784 | 0.4491 |
| Hubei | 0.625 | 0.5671 | 0.6357 | 0.5677 | 0.6507 | 0.5769 | 0.6477 | 0.5798 | 0.6461 | 0.5719 |
| Hunan | 0.6661 | 0.6030 | 0.68 | 0.6056 | 0.6938 | 0.6158 | 0.6977 | 0.6298 | 0.704 | 0.6318 |
| Jilin | 0.4437 | 0.4437 | 0.4582 | 0.4582 | 0.4629 | 0.4629 | 0.4566 | 0.4566 | 0.4405 | 0.4405 |
| Jiangsu | 1 | 0.7587 | 1 | 0.7653 | 1 | 0.7740 | 1 | 0.7883 | 1 | 0.7769 |
| Jiangxi | 0.6273 | 0.6033 | 0.6388 | 0.6051 | 0.6574 | 0.6165 | 0.6562 | 0.6233 | 0.6549 | 0.6161 |
| Liaoning | 0.4407 | 0.4008 | 0.4427 | 0.3925 | 0.4295 | 0.3829 | 0.4113 | 0.3721 | 0.3923 | 0.3517 |
| InnerMongolia | 0.2831 | 0.2713 | 0.2844 | 0.2686 | 0.2805 | 0.2619 | 0.2391 | 0.2269 | 0.2196 | 0.2073 |
| Ningxia | 0.1172 | 0.1172 | 0.1165 | 0.1165 | 0.1038 | 0.1038 | 0.0969 | 0.0969 | 0.0914 | 0.0914 |
| Qinghai | 0.1524 | 0.1524 | 0.1572 | 0.1572 | 0.1581 | 0.1581 | 0.1564 | 0.1564 | 0.1632 | 0.1632 |
| Shandong | 0.5114 | 0.4450 | 0.5195 | 0.4454 | 0.5381 | 0.4590 | 0.5443 | 0.4634 | 0.5417 | 0.4565 |
| Shanxi | 0.178 | 0.1780 | 0.1768 | 0.1768 | 0.1755 | 0.1755 | 0.1747 | 0.1744 | 0.1713 | 0.1709 |
| Shaanxi | 0.4024 | 0.3947 | 0.4042 | 0.3903 | 0.4114 | 0.3907 | 0.4136 | 0.3950 | 0.4025 | 0.3823 |
| Shanghai | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Sichuan | 0.6067 | 0.5592 | 0.6167 | 0.5632 | 0.6287 | 0.5688 | 0.6267 | 0.5685 | 0.6222 | 0.5593 |
| Tianjin | 0.4714 | 0.4714 | 0.4895 | 0.4895 | 0.5009 | 0.5009 | 0.489 | 0.4890 | 0.4731 | 0.4731 |
| Xinjiang | 0.1837 | 0.1837 | 0.1805 | 0.1805 | 0.1747 | 0.1747 | 0.1751 | 0.1751 | 0.1698 | 0.1698 |
| Yunnan | 0.4229 | 0.4150 | 0.4338 | 0.4170 | 0.4452 | 0.4209 | 0.4466 | 0.4244 | 0.4429 | 0.4173 |
| Zhejiang | 0.8075 | 0.7270 | 0.8097 | 0.7223 | 0.8122 | 0.7219 | 0.8079 | 0.7200 | 0.8057 | 0.7115 |
| Chongqing | 0.7349 | 0.7251 | 0.7648 | 0.7473 | 0.7819 | 0.7523 | 0.7576 | 0.7311 | 0.7449 | 0.7100 |
| Province | 2015 | 2016 | 2017 | 2018 | 2019 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Total Factor Ranking Under New Driving Forces | Energy Consumption per Unit of GDP Ranking | Total Factor Ranking Under New Driving Forces | Energy Consumption per Unit of GDP Ranking | Total Factor Ranking Under New Driving Forces | Energy Consumption per Unit of GDP Ranking | Total Factor Ranking Under New Driving Forces | Energy Consumption per Unit of GDP Ranking | Total Factor Ranking Under New Driving Forces | Energy Consumption per Unit of GDP Ranking | |
| Anhui | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 10 | 8 |
| Beijing | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Fujian | 5 | 4 | 5 | 4 | 5 | 4 | 5 | 4 | 5 | 4 |
| Gansu | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 |
| Guangdong | 2 | 3 | 2 | 3 | 2 | 3 | 2 | 3 | 2 | 3 |
| Guangxi | 18 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 20 | 20 |
| Guizhou | 25 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 |
| Hainan | 12 | 9 | 14 | 11 | 14 | 11 | 14 | 13 | 14 | 13 |
| Hebei | 26 | 26 | 26 | 26 | 25 | 26 | 25 | 25 | 25 | 25 |
| Henan | 14 | 14 | 12 | 13 | 10 | 13 | 10 | 12 | 9 | 11 |
| Heilongjiang | 16 | 16 | 16 | 16 | 17 | 16 | 17 | 17 | 16 | 17 |
| Hubei | 11 | 12 | 11 | 12 | 12 | 12 | 12 | 11 | 12 | 12 |
| Hunan | 9 | 10 | 9 | 9 | 9 | 9 | 9 | 9 | 8 | 9 |
| Jilin | 19 | 18 | 18 | 17 | 18 | 17 | 18 | 18 | 19 | 18 |
| Jiangsu | 3 | 5 | 3 | 5 | 3 | 5 | 3 | 5 | 3 | 5 |
| Jiangxi | 10 | 11 | 10 | 10 | 11 | 10 | 11 | 10 | 11 | 10 |
| Liaoning | 20 | 21 | 20 | 21 | 21 | 22 | 22 | 22 | 22 | 22 |
| Inner Mongolia | 24 | 25 | 25 | 25 | 26 | 25 | 26 | 26 | 26 | 26 |
| Ningxia | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
| Qinghai | 29 | 29 | 29 | 29 | 29 | 29 | 29 | 29 | 29 | 29 |
| Shandong | 15 | 17 | 15 | 18 | 15 | 18 | 15 | 16 | 15 | 16 |
| Shanxi | 28 | 28 | 28 | 28 | 27 | 27 | 28 | 28 | 27 | 27 |
| Shaanxi | 22 | 22 | 22 | 22 | 22 | 21 | 21 | 21 | 21 | 21 |
| Shanghai | 4 | 2 | 4 | 2 | 4 | 2 | 4 | 2 | 4 | 2 |
| Sichuan | 13 | 13 | 13 | 14 | 13 | 14 | 13 | 14 | 13 | 14 |
| Tianjin | 17 | 15 | 17 | 15 | 16 | 15 | 16 | 15 | 17 | 15 |
| Xinjiang | 27 | 27 | 27 | 27 | 28 | 28 | 27 | 27 | 28 | 28 |
| Yunnan | 21 | 20 | 21 | 20 | 20 | 20 | 20 | 20 | 18 | 19 |
| Zhejiang | 6 | 6 | 6 | 7 | 6 | 7 | 6 | 7 | 6 | 7 |
| Chongqing | 7 | 7 | 7 | 6 | 7 | 6 | 7 | 6 | 7 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, H.; Ding, X.; Xue, J.; Lai, G. Sustainability-Driven Energy Efficiency Assessment: Divergent Policy Impacts of Single Factor Limits Versus Total Factor Coordination. Sustainability 2025, 17, 4937. https://doi.org/10.3390/su17114937
Long H, Ding X, Xue J, Lai G. Sustainability-Driven Energy Efficiency Assessment: Divergent Policy Impacts of Single Factor Limits Versus Total Factor Coordination. Sustainability. 2025; 17(11):4937. https://doi.org/10.3390/su17114937
Chicago/Turabian StyleLong, Houyin, Xiaoran Ding, Jingyu Xue, and Guansen Lai. 2025. "Sustainability-Driven Energy Efficiency Assessment: Divergent Policy Impacts of Single Factor Limits Versus Total Factor Coordination" Sustainability 17, no. 11: 4937. https://doi.org/10.3390/su17114937
APA StyleLong, H., Ding, X., Xue, J., & Lai, G. (2025). Sustainability-Driven Energy Efficiency Assessment: Divergent Policy Impacts of Single Factor Limits Versus Total Factor Coordination. Sustainability, 17(11), 4937. https://doi.org/10.3390/su17114937






