Analysis of Emergency Cooperative Strategies in Marine Oil Spill Response: A Stochastic Evolutionary Game Approach

Abstract

Marine oil spills significantly adversely affect the socio-economic environment and marine ecosystems. Establishing an efficient emergency cooperation mechanism that enables swift and coordinated responses from all stakeholders is crucial to mitigate the harmful consequences of such spills and protect regional security. This study uses stochastic evolutionary game theory to develop an emergency cooperation model, focusing on the strategic interactions and dynamic evolution between three main parties: the local government, port enterprises, and specialized oil spill cleanup units. The findings indicate the following: (1) The strategy choice of the local government plays a dominant role in the three-party game and has a significant guiding effect on the behavioral decisions of port enterprises and specialized oil spill cleanup units. (2) The strength of the government’s reward and punishment mechanism directly affects the cooperation tendency of the port enterprises and specialized oil spill cleanup units. (3) When the emergency response is more efficient and the cooperation effect is significant, the cleanup units may choose negative cooperation based on payoff maximization in order to prolong the cleaning time. (4) In the process of system evolution, the strategies of local governments and port enterprises are more stable and less affected by random perturbations, while the strategy fluctuations of cleanup units are more sensitive. The findings enrich the theoretical framework for handling marine oil spill emergencies and provide valuable insights for developing efficient collaborative mechanisms and formulating well-grounded regulatory incentive policies.

1. Introduction

Marine oil spill incidents include tanker leaks, oil spills during offshore petroleum extraction, and ship groundings or collisions. Such incidents disrupt the balance and biodiversity of aquatic ecosystems, pollute coastlines, degrade natural landscapes, and negatively impact tourism and related industries, leading to significant economic losses. Maritime transport is not only the most cost-effective mode of transportation but also integrates seamlessly with multimodal logistics systems. It offers optimal benefits to all stakeholders involved [1]. However, with the continued expansion of maritime trade and transportation, oil spill incidents have become increasingly frequent in recent years. For instance, in January 2018, the Panamanian MT Sanchi oil tanker, carrying approximately 136,000 tons of condensate oil, collided with the Hong Kong-registered bulk carrier CF Crystal about 160 nautical miles east of China, causing a fire and resulting in the spill of 113,000 tons of condensate oil and nearly 2000 tons of fuel oil [2]. In April 2021, a collision between the Panamanian general cargo ship Yihai and a Liberian-registered oil tanker occurred in the southeastern waters near Chaolian Island, Qingdao, China, leading to the leakage of approximately 9400 tons of cargo oil into the sea. The total financial claims for fisheries and ecological damage reached approximately CNY 3.74 billion [3]. These oil spill incidents have heightened public awareness of oil pollution issues and prompted governments worldwide to adopt proactive measures to enhance comprehensive emergency response capabilities.

Marine oil spill emergency response is a complex process involving multiple stakeholders, and its effectiveness is crucial to the sustainable development of the regional economy and society and the protection and restoration of the marine ecological environment [4]. However, the divergence and conflict of interests in this process can constrain the effectiveness of emergency response measures. Emergency response to oil spill accidents involves complex multi-party cooperation, including the public sector at all levels, port enterprises, professional rescue agencies, marine environmental protection non-governmental organizations, fishermen and coastal community residents, and other subjects of interest, and there are often significant differences in the distribution of responsibilities, resource sharing, and economic compensation in oil spill emergency response [5,6]. The main participants, the local government, port enterprises, and specialized oil spill cleanup units, face conflicts in allocating responsibilities, resource inputs, and the purpose of emergency response due to the differences in their respective interests [7]. The behavioral patterns of the three parties, driven by different interests, increase the uncertainty of emergency response and affect the efficiency of oil spill response cooperation. Therefore, systematically analyzing the participants’ strategic choices and game relations and clarifying their motives and conflicts of interest have essential theoretical and practical values for optimizing the oil spill emergency response mechanism, enhancing the efficiency of source allocation, and improving the overall effectiveness of the response.

Despite the growing body of literature applying evolutionary game theory to emergency management, most existing models still exhibit significant limitations. First, many studies employ deterministic frameworks that assume stable environments and ignore the inherent uncertainties and fluctuations in the oil spill emergency response process, such as sudden changes in weather conditions, delays in inter-agency coordination, variability in cleanup unit performance, and fluctuating cooperation willingness among stakeholders. Second, numerous game-theoretic models remain limited to two-party interactions, which oversimplify the complexity of marine oil spill responses that typically involve multiple stakeholders with conflicting interests. These simplifications hinder the models’ ability to simulate the dynamic cooperation and negotiation processes essential for effective response coordination. Therefore, a more advanced framework is needed to incorporate stochastic disturbances and multi-agent interactions, enabling a more realistic analysis of strategy evolution in complex emergency scenarios.

This study proposes incorporating a Gaussian white noise perturbation term into the tripartite evolutionary game model, which includes the dynamics between the local government, port enterprises, and specialized oil spill cleanup units. A stochastic evolutionary game model for the emergency response to marine oil spills is developed, based on a stability analysis of the replicator dynamic equations and their solutions. This model is employed to study the strategic decisions of the stakeholders and the dynamic evolution of their behavior. The goal is to promote cooperation among the relevant parties to increase the effectiveness of emergency response and minimize the environmental damage caused by oil spills. The main innovations of this study compared to the existing literature are as follows: (1) While some tripartite models exist, few target the specific configuration of local government–port enterprises–specialized oil spill cleanup units in maritime oil spill contexts, where regulation, profit, and third-party execution coexist. (2) Stochastic perturbations are incorporated into the model to simulate the influence of uncertainties and fluctuations in maritime oil spill emergency response, such as unpredictable weather conditions, dynamic changes in spill trajectories, delays in inter-agency coordination, resource shortages, and variability in stakeholder cooperation, on decision-making behavior. This provides a more realistic and operationally relevant analytical framework. (3) The model explores the incentive effects of government reward and punishment mechanisms on participants’ strategies and identifies critical factors that influence the efficiency of cooperation. Special attention is paid to how the intensity of stochastic disturbances and the level of cooperation efficiency interact to stabilize stakeholder cooperation.

The rest of the paper is as follows: Section 2 reviews the related literature. Section 3 constructs an evolutionary game model to analyze the benefits and strategy choices of the local government, port enterprises, and specialized oil spill cleanup units in maritime oil spill response. Section 4 constructs a stochastic evolutionary model. Section 5 systematically examines the dynamic effects of key parameter variations on the equilibrium strategy of the system by constructing numerical simulation experiments. Management implications and a research outlook are presented in Section 6.

2. Literature Review

2.1. Emergency Response to Marine Oil Spills

With the deepening development of global economic integration, maritime trade has become an important link connecting the economies of various countries. The increasing volume of ship transportation has increased the risk of oil spill accidents at sea. Oil spill pollution at sea not only spreads rapidly and lasts for a long time, but also destroys marine ecosystems and the loss of coastal economies if the emergency response is ineffective or lacks synergistic cooperation [8,9]. In particular, in the absence of coordination and systemic support, independent responses by individual entities are not effective in controlling the spread of pollution and may even result in wasted resources and management errors [10]. Maria Ivanova [11] investigated the oil spill emergency response (OSER) system in the Murmansk region of Russia, demonstrating the role of both formal and informal cooperation mechanisms. Maria Sydnes [12] revealed that Norway’s effective oil spill response system relies on complementary formal–informal coordination and shared purpose among multi-level actors to strengthen inter-organizational cooperation. Susse Wegeberg [13] proposed a framework of analytical tools called “EOS”, which provides a comprehensive analytical tool for oil pollution incident response planning, covering key elements such as environmental assessment, response strategy analysis, and decision support. Lanying Du [14] studied the impacts of future marine oil spills on nearby coasts by synthesizing two restricted areas, Liverpool Bay and Milford Haven. Lingye Zhang et al. [15] proposed a multi-objective siting-path optimization model considering dynamic oil film motion characteristics to solve the Pareto solution by two-stage optimization and hybrid heuristic algorithms in order to better simulate the dynamic demand, transportation network uncertainty, and emergency operation changes in maritime oil spill response logistics. Based on the problem of serious environmental damage caused by the rapid development of China’s marine economy, Yuxia Yan et al. [16] proposed the possibility of developing and implementing a monetary compensation mechanism for marine development that is ecologically, economically, and socially sustainable. Tanmoy Das et al. [17] proposed a Bayesian inference model based on preference learning for data-driven ranking of technologies such as mechanical recovery, chemical dispersant, and in situ combustion in Arctic oil spill risk assessment and emergency preparedness planning. Xinhong Li et al. [18] proposed a new method combining a Bayesian Network (BN) and an Influence Diagram (ID) for optimizing risk management and emergency decision-making in marine oil pollution accidents.

In addition to decision-making models and emergency coordination strategies, oil spill drift prediction technology has become an increasingly critical component of marine emergency response. Accurate forecasting of oil spill dispersion trajectories enables responders to optimize resource deployment, prioritize high-risk areas, and reduce ecological damage. Recent studies have applied data-driven and hybrid methods to enhance prediction accuracy. For instance, Yongqing Li et al. [19] proposed a wind field correction method based on an adversarial convolutional long short-term memory (LSTM) network. This method enables real-time correction of numerical forecast wind fields without relying on observational data, thereby improving the accuracy of oil drift prediction. Peng Ren et al. [20] proposed a deep learning method based on Adversarial Time Convolutional Networks (ATCNs) for correcting the numerical prediction of sea surface power fields to improve the speed and accuracy of oil drift prediction.

Although existing studies provide valuable theoretical frameworks and technical approaches for oil pollution emergency response, most of them seem to fail to adequately integrate the deterministic emergency response framework with uncertainties, especially the uncertainty of oil pollution drift. While many models assume certain deterministic conditions when hypothesizing oil drift paths, this may not be fully consistent in real-world situations, as oil drift is often influenced by multiple dynamic and unpredictable environmental factors. Therefore, combining emergency response decisions with uncertainty in the drift paths can more fully reflect the complexity of reality and thus improve the adaptability and effectiveness of emergency response strategies.

2.2. Emergency Cooperation in Accident Response

In the field of accident emergency management, many studies have focused on emergency response and cooperation mechanisms for land-based disasters. However, due to the unique environmental complexity, the timeliness of the response, and the need for cross-domain coordination, research on emergency response and cooperation in maritime oil spill accidents is relatively weak compared with that in land-based disasters. Nevertheless, the commonalities in resource integration, information sharing, and multi-party coordination between land and sea emergency response cooperation provide valuable references for optimizing maritime oil spill response cooperation. In a study on maritime emergency cooperation, Nathanael J et al. [21] studied offshore and onshore oil and gas emergency management through PRISMA (Preferred Reporting Items for Systematic reviews and Meta-Analyses) analysis and expert validation methods. They identified command, planning, communication, situational awareness, and resource management as critical components, noting that offshore emergency management encounters more significant challenges due to limited resources, adverse weather conditions, and communication difficulties. Yunfei Ai et al. [22] investigated the maritime emergency supply location problem under government–firm cooperation by constructing a two-stage optimization model and designing a genetic–greedy heuristic algorithm, proving that cooperation reduces the total cost, benefits firms, and maintains the stability of the alliance. Natalia Andreassen et al. [23] investigated the impact of management roles on information sharing in complex maritime emergency response operations and emphasized the need to adapt coordination mechanisms and management roles to variable operational conditions. In the main body of research on cooperation in emergency management, Waugh Jr. et al. [24] examined the importance of inter-organizational and cross-sectoral cooperation in emergency management and emphasized the need for timely coordination among emergency managers throughout all disaster phases. Ansell et al. [25] explored the key role of the local government in cross-cutting public affairs. Gong Wei [26] analyzed the interests of multi-party subjects such as government, for-profit organizations, non-profit organizations, and the public in emergencies and proposed strategies to improve the efficiency of multi-party cooperation and development paths. Cheng et al. [27] analyzed the dynamics of cooperation under asymmetric resource dependence between governments and enterprises during major emergencies. Their study approached the issue from three key dimensions, namely government authority, corporate social responsibility, and reciprocal cooperation, and provided new insights into improving the continuity and resilience of emergency cooperation. Olsson et al. [28] explored the construction and operation of global crisis management networks and proposed two models: one based on coordinated systems and another practice-based network model designed to address the challenges of ambiguity, complexity, and uncertainty in cross-border crises. Bignami et al. [29] argued that effective emergency management in cross-border natural disasters requires coordinated efforts among governments, enterprises, and research institutions. This includes establishing robust cooperation mechanisms, developing comprehensive risk management policies, and utilizing advanced technologies to strengthen response capabilities.

Although the above studies have emphasized the importance of synergy in land and marine emergency management, most of them are still based on deterministic, static, or structural analytical frameworks, such as optimization methods, classical game models, or institutional analysis. These approaches have some value in contingency planning and organizational design but generally neglect the issue of how actors’ strategies dynamically evolve in uncertain environments. Specifically, existing literature has rarely introduced random perturbations to simulate behavioral changes in actual decision-making. In addition, most of the models assume that the participants’ preferences are fixed and that the information is complete. This is insufficient in the context of maritime oil spill response, where resources are limited, multiple parties are involved, and volatility is high.

2.3. Stochastic Evolutionary Game Theory in Emergency Management

With the increased attention to complex emergency scenarios, predominantly maritime emergencies such as offshore oil spills, traditional scheduling strategies and models face new challenges and opportunities. Evolutionary game theory is a powerful tool for studying strategy selection and the evolution of participants in dynamic systems. In recent years, it has shown its unique value and potential applications in exploring emergency cooperation strategies [30,31]. Evolutionary game theory is helpful for analyzing the behavioral choices of various stakeholders in emergency management. Daniel Seaberg et al. [32] provided a comprehensive review of the application of game theory in natural disaster management research. Similarly, Jida Liu et al. [33] applied evolutionary game theory to examine the mechanisms and strategies of cross-regional emergency cooperation for natural disasters in China and analyzed how factors such as willingness to cooperate, cost-sharing, and benefit distribution affect the stability of cooperation. Peizhe Shi et al. [34] analyzed the game relationship between conflict and cooperation by constructing a game model of coal mine enterprises and the local government in coal mine accident response and emphasized the importance of information-sharing mechanisms in efficiently initiating emergency response. Meng Zhang et al. [35] investigated the Emergency Supplies Joint Reserve Model (ESJRM) by establishing a three-party evolutionary game model involving the government, enterprises, and society. They examined the realization conditions and influencing factors of the ESJRM, aiming to provide theoretical guidance and management strategies for government–enterprise cooperation in early-stage emergency material stockpiling.

However, evolutionary game theory is limited in its analysis of strategy selection behavior due to its focus on deterministic states. In contrast, stochastic evolutionary game theory is capable of capturing the inherent uncertainty and randomness of real-world scenarios, providing greater flexibility, robustness, and the capacity to model complex dynamics. This approach enables a deeper understanding of evolutionary processes across various domains [36]. From a theoretical perspective, stochastic evolutionary game theory provides a rigorous framework for examining dynamic strategy evolution under uncertainty. Imhof [37] introduced stochastic differential equations into evolutionary games, establishing foundational results on the stability of equilibria under stochastic dynamics. Fudenberg and Imhof [38] further formalized stochastic selection processes and provided convergence theorems in finite populations. These foundational studies underscore the importance of incorporating random perturbations in replicator dynamics to more accurately reflect real-world strategic behavior. However, their applications to complex emergency management contexts remain limited, particularly in multi-agent and policy-driven systems. This study builds upon these theoretical foundations to extend stochastic evolutionary game theory to the domain of marine oil spill emergency cooperation. Recent studies have applied stochastic evolutionary game frameworks across a range of domains—including environmental governance, urban public crisis management, inter-organizational coordination, regional emergency systems, and other fields—demonstrating the method’s flexibility and relevance for complex multi-agent decision-making under uncertainty. Weihua Qu et al. [39] constructed a governance framework addressing greenwashing behaviors (GWBs) under two distinct regulatory conditions: the presence or absence of central government oversight. Their research highlighted how citizen involvement in monitoring, policy-driven environmental and political incentives, state-imposed rewards and penalties, and coordinated efforts among multiple stakeholders significantly shaped the effectiveness of GWB governance. Shao-nan Shan et al. [40] integrated evolutionary game theory with system dynamics, incorporating a Gaussian white noise perturbation to reflect stochastic influences. They developed a tripartite evolutionary game model under varying conditions of central government oversight to analyze the progression of collective strategic behavior in managing urban public crises. Their findings underscore the crucial influence of the central government’s adaptive reward-and-penalty system in fostering the emergence of a collaborative governance alliance involving multiple actors. Jida Liu et al. [41] constructed an evolutionary game framework grounded in China’s cross-regional emergency management practices. By incorporating stochastic processes and Gaussian white noise, they enhanced the conventional model to examine the evolutionary stability and key determinants of two collaborative emergency response mechanisms—regional integration and counterpart assistance.

In summary, current studies on maritime oil spill emergency response have provided significant insights in three major areas: decision-making in response, cooperation mechanisms, and technical modeling. Researchers have suggested multiple frameworks for decision optimization, such as game-theoretic models, Bayesian inference, and hybrid heuristics, to tackle logistical planning and risk assessment issues. Research at the organizational level has highlighted the significance of multi-actor cooperation and coordination in improving emergency efficacy, deriving insights from both terrestrial and maritime environments. Simultaneously, predictive methodologies like adversarial deep learning models have markedly enhanced oil drift forecasting in data-scarce environments. However, many studies on maritime oil spill emergency response cooperation have not yet fully considered the high degree of uncertainty in oil spill dispersion paths after an accident. This uncertainty arises from the interaction of multiple natural factors, such as wind, tides, and currents, which significantly impact emergency response efficiency and decision-making options. Consequently, these studies can hardly reflect the true uncertainty present in actual oil spill response scenarios. In addition, there are fewer studies on tripartite cooperation in maritime oil spill response. Therefore, considering the destructive influence of random factors, this paper will analyze and explore the behavioral strategies of multiple interested subjects in marine oil spill response based on stochastic evolutionary game theory and explore the strategic decisions and development trajectories of multiple interested subjects’ behaviors under the influences of different key variables through simulation analysis to provide a better decision-making basis for enhancing the level of cooperation in maritime oil spill response.

3. Model Construction

3.1. Problem Description

The main participants in maritime oil spill emergency response cooperation include the local government, port enterprises, and specialized oil spill cleanup units. The parties’ different interests in resource allocation, responsibility, and financial compensation may lead to low willingness to cooperate and insufficient synergy in the emergency response process, thus reducing the overall effectiveness of the emergency response.

The local government prioritizes regulatory efficiency and system-wide coordination by implementing a tripartite strategy: formulating environmental policies, supervising port enterprise compliance, and balancing ecological protection with social stability. In the context of regional maritime oil spill response cooperation, the local government must carefully weigh public safety, environmental protection, economic development, social stability, legal accountability, and regulatory costs when determining its level of oversight toward port enterprises. To safeguard the public interest, ensure environmental security, and minimize pollution-related harm, while simultaneously promoting port economic development and maintaining social stability, the local government generally favors strong regulatory strategies, within the limits of available resources. This approach enhances the enforcement of environmental regulations and facilitates effective emergency responses. Nevertheless, in certain circumstances, the government may adopt more flexible supervision strategies to balance regulatory costs and economic priorities. Ultimately, the choice between “strong supervision” and “weak supervision” is contingent upon the perceived risk level of oil spill incidents.

Port enterprises are key stakeholders in oil spill emergency response, prioritizing the marginal equilibrium between economic costs and social responsibility. In emergency cooperation, they may adopt a “positive cooperation” strategy, strengthening cooperation with specialized oil spill cleanup units, increasing emergency investments, and expediting the restoration of navigational order to mitigate environmental and economic damage. However, port enterprises may also opt for a “negative cooperation” strategy due to constraints such as funding limitations, emergency resource availability, risk aversion regarding accident losses, and liability avoidance.

Specialized oil spill cleanup units will prioritize their own revenue and cost balance, maximizing profits by improving cleanup efficiency and reducing operating costs, thus ensuring that their economic benefits are met as a priority while enhancing their professional competence and reputation in the industry. In the event of an oil spill incident, the specialized skills and response capabilities of specialized oil spill cleanup units significantly affect the effectiveness of cleanup and the consequences of the incident. Therefore, they need to establish a close cooperative relationship with the local government and port enterprises to integrate resources and coordinate actions during emergencies quickly. Professional decontamination units can adopt either a “positive cooperation” or a “negative cooperation” strategy.

In the tripartite game process, the interests and objectives of the participating stakeholders are often significantly different. The local government expects relevant enterprises to proactively increase resource investment to improve oil spill response capabilities, thereby reducing environmental pollution. On the other hand, port enterprises tend to seek greater financial support and preferential policies to reduce operating costs and maximize economic returns. As third-party service providers, specialized oil spill cleanup units seek stable financial support and resource guarantees to realize their technical value and maintain sustainable operations. Conflicts of interest and resource competition among multiple stakeholders introduce considerable complexity into strategy selection. These challenges may lead to deviations from the equilibrium state of the game. The dynamic evolution of the game model captures this complexity by illustrating how each stakeholder’s strategy continually adjusts in response to changes in both external conditions and internal incentives.

3.2. Main Parameters and Model Assumptions

The main parameters involved in the model are shown in

Table 1. Definition of parameters.

Parameter	Meaning	Range
$B_i$	The basic profits of port enterprises $\left(i=1\right)$ and specialized oil spill cleanup units $\left(i=2\right)$.	$B_i\ge 0$
$C_i$	Basic emergency costs for the local government $\left(i=1\right)$, port enterprises $\left(i=2\right)$, and specialized oil spill cleanup units $\left(i=3\right)$.	$Ci\ge 0$
$S_i$	The rewards granted to port enterprises $\left(i=1\right)$ and specialized oil spill cleanup units $\left(i=2\right)$ for positive cooperation under a strong supervision strategy by the local government.	$S_i\ge 0$
$F_i$	The punishments imposed on port enterprises $\left(i=1\right)$ and specialized oil spill cleanup units $\left(i=2\right)$ for negative cooperation under a strict supervision strategy by the local government.	$F_i\ge 0$
$\Delta C_i$	The additional oil spill emergency costs incurred by port enterprises $\left(i=1\right)$ and specialized oil spill cleanup units $\left(i=2\right)$ when engaging in positive cooperation.	$\Delta C_i\ge 0$
$W$	The “free-riding” benefits for port enterprises during negative cooperation are higher in channel oil spill accidents due to abundant resources and diffuse responsibility, whereas they are lower in port-front spills due to clearer responsibility and higher risks.	$W\ge 0$
$\Delta R$	The additional profits gained by specialized oil spill cleanup units from prolonging the cleanup time when choosing the “negative cooperation” strategy.	$\Delta R$
$f$	The losses incurred by the local government due to an oil spill accident primarily include marine environmental pollution and direct economic losses to coastal industries such as fisheries and tourism.	$f\ge 0$
$I$	The benefits gained by the local government under a strong supervision strategy primarily include enhanced social reputation and image, as well as recognition and rewards from higher authorities.	$I\ge 0$
$\alpha$	The effect coefficient of emergency cooperation, a variable used to evaluate the effectiveness of the implementation of the overall emergency response operation when the investment of emergency resources is limited.	$0\le \alpha \le 1$
$\rho$	The emergency cooperation effectiveness coefficient, a variable used to evaluate the scale and degree of coordination among the local government, port enterprises, and specialized pollution cleanup companies during emergency response operations.	$0\le \rho \le 1$

.

Assumption 1: In the maritime oil spill emergency response, the interaction between the local government, port enterprises, and specialized oil spill cleanup units can be considered as a repeated asymmetric evolutionary game with bounded rationality. In this game process, all parties continuously learn and adjust their decision-making strategies to optimize their respective interests, rather than pursuing a singular optimal strategy. It is a non-zero-sum game in which stakeholders’ payoffs are interdependent, particularly through shared environmental outcomes, emergency response effectiveness, and policy constraints.

Assumption 2: The strategic environment for maritime oil spill response is characterized by both a coordination game and a dilemma game. Although all parties can benefit from cooperation, individual stakeholders may gain short-term benefits through negative cooperation, especially in the case of weak regulation, and the interaction between the local government, port enterprises, and specialized oil spill cleanup units can be regarded as a kind of information asymmetry. Particularly with regard to the level of emergency preparedness or actual cooperative behavior, governments may not be able to fully observe or accurately assess the true behavior of port enterprises.

Assumption 3: In the maritime oil spill response cooperation game, the local government needs to balance public safety, environmental protection, economic development, and other factors and usually chooses a strong supervision strategy when resources allow but may also choose weak supervision according to the actual situation. The local government adopts a strong supervision strategy with probability $\left(x\right)$ and a weak supervision strategy with probability $\left(1-x\right)$. The probability of port enterprises choosing a positive cooperation strategy is $\left(y\right)$, while the probability of choosing a negative cooperation strategy is $\left(1-y\right)$. The probability of specialized oil spill cleanup units choosing a positive cooperation strategy for efficient service is $\left(z\right)$, while the probability of choosing a negative cooperation strategy to prolong cleanup time for higher profits is $\left(1-z\right)$.

Assumption 4: To serve as a deterrent to all participants in the oil spill emergency response, the penalty for non-cooperation is deliberately set higher than the cost of positive cooperation,  $F_1>S_1,F_2>S_2$.

3.3. Payoff Matrix and Replicator Dynamic Equations

Based on actual conditions and model assumptions, this paper constructs a payoff matrix for the emergency cooperation game of marine oil spills involving the local government, port enterprises, and specialized oil spill cleanup units, as shown in

Table 2. The payoff matrix under the local government’s strong supervision strategy.

			The Local Government
			$\mathbf{Strong} \mathbf{Supervision} (\mathit{x})$
Port enterprises	Positive cooperation $(y)$	Specialized oil spill cleanup units	Positive cooperation $(z)$	$\begin{array}{l}I-\left(1-\alpha \right)\left(1-\rho \right)C_1-\left(1-\alpha \right)\left(1-\rho \right)f-S_1-S_2\\ B_1-\left(1-\alpha \right)\left(1-\rho \right)C_2+S_1-\alpha \Delta C_1\\ B_2-\left(1-\alpha \right)\left(1-\rho \right)C_3+S_2-\alpha \Delta C_2\end{array}$
			Negative cooperation $(1-z)$	$\begin{array}{l}\begin{array}{l}I-\left(1-\alpha \right)\left(1-\rho \right)C_1-\left(1-\alpha \right)\left(1-\rho \right)f-S_1+F_2\hfill \\ B_1-\left(1-\alpha \right)\left(1-\rho \right)C_2-\alpha \Delta C_1+S_1\hfill \end{array}\\ B_2-\left(1-\alpha \right)\left(1-\rho \right)C_3+\Delta R-F_2\end{array}$
	Negative cooperation $(1-y)$		Positive cooperation $(z)$	$\begin{array}{l}\begin{array}{l}I-\left(1-\alpha \right)\left(1-\rho \right)C_1-\left(1-\alpha \right)\left(1-\rho \right)f-S_2+F_1\hfill \\ B_1-\left(1-\alpha \right)\left(1-\rho \right)C_2-F_1+W\hfill \end{array}\\ B_2-(1-\alpha )(1-\rho )C_3-\alpha \Delta C_2+S_2\end{array}$
			Negative cooperation $(1-z)$	$\begin{array}{l}\begin{array}{l}I-\left(1-\alpha \right)\left(1-\rho \right)C_1-\left(1-\alpha \right)\left(1-\rho \right)f+F_1+F_2\hfill \\ B_1-C_2-F_1+W\hfill \end{array}\\ B_2-C_3+\Delta R-F_2\end{array}$

and

Table 3. The payoff matrix under the local government’s weak supervision strategy.

			The Local Government
			$\mathbf{Weak} \mathbf{Supervision} (1-\mathit{x})$
Port enterprises	Positive cooperation $(y)$	Specialized oil spill cleanup units	Positive cooperation $(z)$	$\begin{array}{l}\begin{array}{l}-\left(1-\alpha \right)\left(1-\rho \right)C_1-\left(1-\alpha \right)\left(1-\rho \right)f\hfill \\ B_1-\left(1-\alpha \right)\left(1-\rho \right)C_2-\alpha \Delta C_1\hfill \end{array}\\ B_2-(1-\alpha )(1-\rho )C_3-\alpha \Delta C_2\end{array}$
			Negative cooperation $(1-z)$	$\begin{array}{l}\begin{array}{l}-\left(1-\alpha \right)\left(1-\rho \right)C_1-\left(1-\alpha \right)\left(1-\rho \right)f\hfill \\ B_1-\left(1-\alpha \right)\left(1-\rho \right)C_2-\alpha \Delta C_1\hfill \end{array}\\ B_2-\left(1-\alpha \right)\left(1-\rho \right)C_3+\Delta R\end{array}$
	Negative cooperation $(1-y)$		Positive cooperation $(z)$	$\begin{array}{l}-\left(1-\alpha \right)\left(1-\rho \right)C_1-\left(1-\alpha \right)\left(1-\rho \right)f\hfill \\ B_1-\left(1-\alpha \right)\left(1-\rho \right)C_2-\alpha \Delta C_1+W\hfill \\ B_2-\left(1-\alpha \right)\left(1-\rho \right)C_3-\alpha \Delta C_2\hfill \end{array}$
			Negative cooperation $(1-z)$	$\begin{array}{l}\begin{array}{l}–C_1–f\hfill \\ B_1–C_2+W\hfill \end{array}\\ B_2–C_3+\Delta R\end{array}$

.

Assuming that the expected return and the average expected return for the local government choosing either a strong or a weak monitoring strategy are $\left(E_{11},E_{12},\overline{E}\right)$, according to Table 2 and Table 3,

$$\begin{array}{l}{E}_{11}=(y-1)(z-1)(F_1-C_1+F_2+I-f)-yz[S_1-I+S_2+f(\alpha -1)(\rho -1)+C_1(\alpha -1)(\rho -1)]\\ +y(z-1)[S_1-I-F_2+f(\alpha -1)(\rho -1)+C_1(\alpha -1)(\rho -1)]\\ +z(y-1)[S_2-I-F_1+f(\alpha -1)(\rho -1)+C_1(\alpha -1)(\rho -1)]\end{array}$$

(1)

$$\begin{array}{l}{E}_{12}=y[f(\alpha -1)(\rho -1)+C_1(\alpha -1)(\rho -1))(z-1)-(C_1+f)(y-1)(z-1)\\ +z(f(\alpha -1)(\rho -1)+C_1(\alpha -1)(\rho -1))(y-1)\\ -yz(f(\alpha -1)(\rho -1)+C_1(\alpha -1)(\rho -1)]\end{array}$$

(2)

$$\overline{E_1}=x{E}_{11}+(1-x)E_{12}$$

(3)

Thus, the replicator dynamic equation for the local government’s strong supervision strategy is

$$F(x)=dx/dt=x{E}_{11}-\overline{E_1}=x(1-x)(F_2+I+F-y{F}_1-z{F}_2-y{S}_1-z{S}_2)$$

(4)

Similarly, the replicated dynamic equations for the selection of positive cooperation by port enterprises and the choice of a positive cooperation strategy by specialized oil spill cleanup units are as follows:

$$\begin{array}{l}F(y)=dy/dt=y{E}_{21}-\overline{E_2}=y(1-y)(-W-\alpha \Delta C_1+x{F}_1+x{S}_1+\alpha C_2+\rho C_2-\alpha \rho C_2-\alpha z{C}_2\\ -\rho z{C}_2+\alpha z\Delta C_1+\alpha \rho z{C}_2-\alpha zx\Delta C_1)\end{array}$$

(5)

$$\begin{array}{l}F(z)=dz/dt=z{E}_{31}-\overline{E_3}=z(1-z)(-\Delta R-\alpha \Delta C_2+x{F}_2+x{S}_2+\alpha C_3\\ +\rho C_3-\alpha \rho C_3-\alpha y{C}_3-\rho y{C}_3+\alpha \rho y{C}_3)\end{array}$$

(6)

Since $\mathrm{x}\in \left[0,1\right]$, $1-x,1-y,1-z$ are all non-negative, and these terms do not influence the evolutionary outcome of the game. Therefore, the evolutionary game’s replicator dynamic equation is revised accordingly, resulting in the following modified form:

$$F(x)={\displaystyle \frac{dx}{dt}}=x(F_2+I+F-y{F}_1-z{F}_2-y{S}_1-z{S}_2)$$

(7)

$$F(y)={\displaystyle \frac{dy}{dt}}=y(-W-\alpha \Delta C_1+x{F}_1+x{S}_1+\alpha C_2+\rho C_2-\alpha \rho C_2-\alpha z{C}_2-\rho z{C}_2+\alpha z\Delta C_1+\alpha \rho z{C}_2-\alpha zx\Delta C_1)$$

(8)

$$F(z)={\displaystyle \frac{dz}{dt}}=z(-\Delta R-\alpha \Delta C_2+x{F}_2+x{S}_2+\alpha C_3+\rho C_3-\alpha \rho C_3-\alpha y{C}_3-\rho y{C}_3+\alpha \rho y{C}_3)$$

(9)

4. Stochastic Evolutionary Game Model

4.1. Stochastic Disturbances in the Strategies of the Three Parties

While evolutionary game theory enhances the classical Hawk–Dove model by relaxing the assumption of perfect rationality and effectively integrating game theory with system dynamics, particularly in demonstrating the time-dependent evolution of participants’ behavioral decisions, it remains limited in analyzing strategic behavior in complex, dynamic, and uncertain environments. In the context of marine oil spill emergency cooperation, multiple stakeholders’ decisions are influenced by external factors, such as natural conditions and public opinion, and internal factors, including trust levels, risk perception, and emergency response capabilities. These diverse influences introduce considerable uncertainty and instability into the strategic choices of participating agents. To more accurately characterize the behavioral evolution of stakeholders under such conditions, this study incorporates stochastic disturbances—assumed to follow a Gaussian distribution—into the deterministic evolutionary game model. This modification enables the model to capture the complex and dynamic nature of oil spill emergency scenarios more realistically. Moreover, it addresses the limitations of traditional models by accounting for the stochastic influence of uncertain factors on the decision-making and governance processes, thereby improving the applicability of evolutionary game theory in sustainable emergency management contexts. Based on the above analysis, this study adopts evolutionary game replicator dynamic equations to model the strategic evolution of multiple stakeholders engaged in marine oil spill emergency response. Gaussian white noise is introduced to account for the influence of random disturbances, enabling a more realistic representation of decision-making under uncertainty. Gaussian white noise refers to a stochastic process with a constant power spectral density across all frequencies and normally distributed increments with zero mean and finite variance. It captures the random fluctuations introduced into the system from both internal variability and external disturbances [42]. Operationally, Gaussian white noise is modeled via a Brownian motion derivative in the stochastic differential equations. Equations (7)–(9) are further modified by introducing stochastic perturbation terms into the model, resulting in the stochastic evolutionary replicator dynamic equations for the local government, port enterprises, and specialized oil spill cleanup units, as given in Equations (10)–(12).

$$dx(t)=(F_2+I+F-y{F}_1-z{F}_2-y{S}_1-z{S}_2)x(t)dt+\sigma \sqrt{x(t)(1-x(t))}d\omega (t)$$

(10)

$$\begin{array}{l}dy(t)=(-W-\alpha \Delta C_1+x{F}_1+x{S}_1+\alpha C_2+\rho C_2-\alpha \rho C_2-\alpha z{C}_2\\ -\rho z{C}_2+\alpha z\Delta C_1+\alpha \rho z{C}_2-\alpha zx\Delta C_1)y(t)dt+\sigma \sqrt{y(t)(1-y(t))}d\omega (t)\end{array}$$

(11)

$$\begin{array}{l}dz(t)=(-\Delta R-\alpha \Delta C_2+x{F}_2+x{S}_2+\alpha C_3+\rho C_3\\ -\alpha \rho C_3-\alpha y{C}_3-\rho y{C}_3+\alpha \rho y{C}_3)z(t)dt+\sigma \sqrt{z(t)(1-z(t))}d\omega (t)\end{array}$$

(12)

Based on the one-dimensional Itô stochastic differential Equations (10)–(12), this study constructs an evolutionary game model incorporating stochastic disturbances for the local government, port enterprises, and specialized oil spill cleanup units. $\omega (t)$ follows the pattern of standard Brownian motion in one dimension, which is used to simulate the random disturbances caused by external complex environmental factors and internal uncertainties during the oil spill emergency cooperation process among multiple agents, while $\mathrm{d}\omega \left(t\right)$ denotes Gaussian white noise. Given a time t > 0 and the step size $h>0$, $\omega (t)$ is normally distributed as $\mathrm{N}\left(0,\mathrm{t}\right)$, $\mathrm{d}\omega \left(t\right)$ is normally distributed $\mathrm{N}\left(0,\nabla \right)$, its increment $\mathsf{\Delta }\mathsf{\omega }\mathrm{t}=\mathsf{\omega }(\mathrm{t}+\mathrm{h})-\mathsf{\omega }\left(\mathrm{t}\right)$ is normally distributed $\mathrm{N}\left(0,\sqrt{h}\right)$, the strength of the random perturbation term is denoted by the constant $\sigma$, $\sqrt{x(t)(1-x(t)}$ indicates the point at which the random disturbance attains its maximum value, and the system reaches its maximum instability if and only if $1-x(t)=x(t)$. This reflects the instability of the local government, port enterprises, and specialized oil spill cleanup units when facing external shocks. Conversely, when the disturbance intensity is low, the system tends to stabilize, demonstrating the cooperative and coordination capabilities of the three entities in a stable environment. $\sqrt{y(t)(1-y(t))}$ and $\sqrt{z(t)(1-z(t))}$ are identical.

With the introduction of the stochastic perturbation term, the stochastic evolution equation for the local government reflects that its dynamic adjustment in regulatory policy and resource allocation is subject to external influences. Similarly, the stochastic evolution equations of port enterprises reveal their strategic fluctuations in the balance between cleanup responsibilities and economic benefits, and the stochastic evolution equations of specialized oil spill cleanup units reflect their changes in resource allocation and task execution under the influence of market and policy. This stochastic modeling mechanism realistically portrays the dynamic fluctuation of multi-body behaviors in oil spill response cooperation. It provides theoretical support for analyzing the stability of cooperation and game strategies among the local government, port enterprises, and specialized oil spill cleanup units.

4.2. Analysis of the Existence and Stability of Equilibrium Points

A detailed mathematical derivation of the equilibrium conditions and moment stability of the stochastic differential equations is presented in Appendix A.

5. Numerical Simulation

This study utilizes a comprehensive methodology that includes case-based scenario simulation and MATLAB modeling to examine the strategic interactions of the local government, port enterprises, and specialized oil spill cleanup units in the context of emergency response. The aim of this work is to systematically identify the primary factors influencing the development of highly uncertain occurrences and to examine their possible future trajectories. A particular focus of this study is the regulatory role of the local government. The simulations assess how port enterprises and cleanup units adapt their strategic decisions in response to government policy limitations during abrupt oil spill incidents. Moreover, this study delineates critical regulatory measures that local authorities ought to implement to promote stable and enduring cooperation among stakeholders. This study illustrates the importance of institutional mechanisms in enhancing the effectiveness and resilience of emergency response systems, particularly in light of the inherent complexity and dynamic evolution of marine oil spill events. The parameter values employed in the analysis are primarily drawn from authoritative literature in the field of emergency management. The parameter values in this study are mainly derived from official ship pollution incident reports, supplemented by relevant academic literature and marine environmental emergency policy documents, reasonably derived and appropriately adjusted to ensure their scientific validity, applicability, and rationality [33,41,43]. The parameters assume the following values: $C_1=15;$ $C_2=15;$ $C_3=20;$ $S_1=10;$ $S_2=6;$ $F_1=12;$ $F_2=8;$ $W=5;$ $f=10;$ $\Delta C_1=10;$ $\alpha =0.2;$  $\rho =0.3;$  $I=15$.

5.1. Simulation Analysis of System Evolution Under Different Initial Strategy Conditions

To further investigate the dynamic characteristics and convergence behavior of the stochastic evolutionary game model, this study presents the time-path trajectories of the cooperation probabilities of the local government, port enterprises, and specialized oil spill cleanup units under different initial conditions, as shown in Figure 1.

As shown in Figure 1a, the initial values of (x, y, z) were uniformly set to 0.5 to ensure comparability. All stakeholders begin with neutral cooperation levels. Over time, the local government and port enterprises steadily increase their cooperation probability, while cleanup units rapidly decline to near-zero levels. The ultimate stable evolutionary point is represented as (1, 1, 0).

Furthermore, three additional sets of initial value combinations for strategies were established to examine how the initial strategy selection of each player influences the evolution trajectory, convergence speed, and equilibrium outcomes. As shown in Figure 1b, under the strong supervision of the local government, the willingness to cooperate of the port enterprises increases rapidly, while the willingness to cooperate of the cleanup units decreases slowly. Eventually, the steady state of the system, (1, 1, 0), is reached, which indicates that the willingness to cooperate of port enterprises increases the fastest under the strategy of strong supervision.

In the third set of initial values, the value of y is 0.8, and the values of the other two players are both 0.2, which shows that the positive cooperation of port enterprises alone is not able to respond to oil spills in a timely and effective manner, and the local government realizes that the intensity of the supervision is rapidly increased, while the specialized oil spill cleanup units choose to cooperate negatively to prolong the time of cleanup in order to gain more profits, and the system finally evolves to (1, 1, 0).

When the initial proportion of specialized oil spill cleanup units is high, it does not change the evolution equilibrium point of the system, but it significantly affects the evolution speed of the local government and the port enterprises. As the proportion of cleanup units decreases, the local government and the port enterprises choose to increase the intensity of supervision and the willingness to cooperate in order to respond to oil spills, and the willingness to cooperate fluctuates when the intensity of supervision by the local government stabilizes. A stable state is reached at the point (1, 1, 0).

The initial strategy choice of each participant in the three-party game does not directly affect the final evolution results but has a significant impact on the evolution trajectory and convergence speed. As shown in Figure 1, it is obvious that the local government has the greatest influence on the evolution of the system compared with the other initial value groups, compared with the fact that without the strong supervision of the local government, the port enterprises and the specialized oil spill cleanup units will tend to reduce their willingness to cooperate in the early stage of evolution.

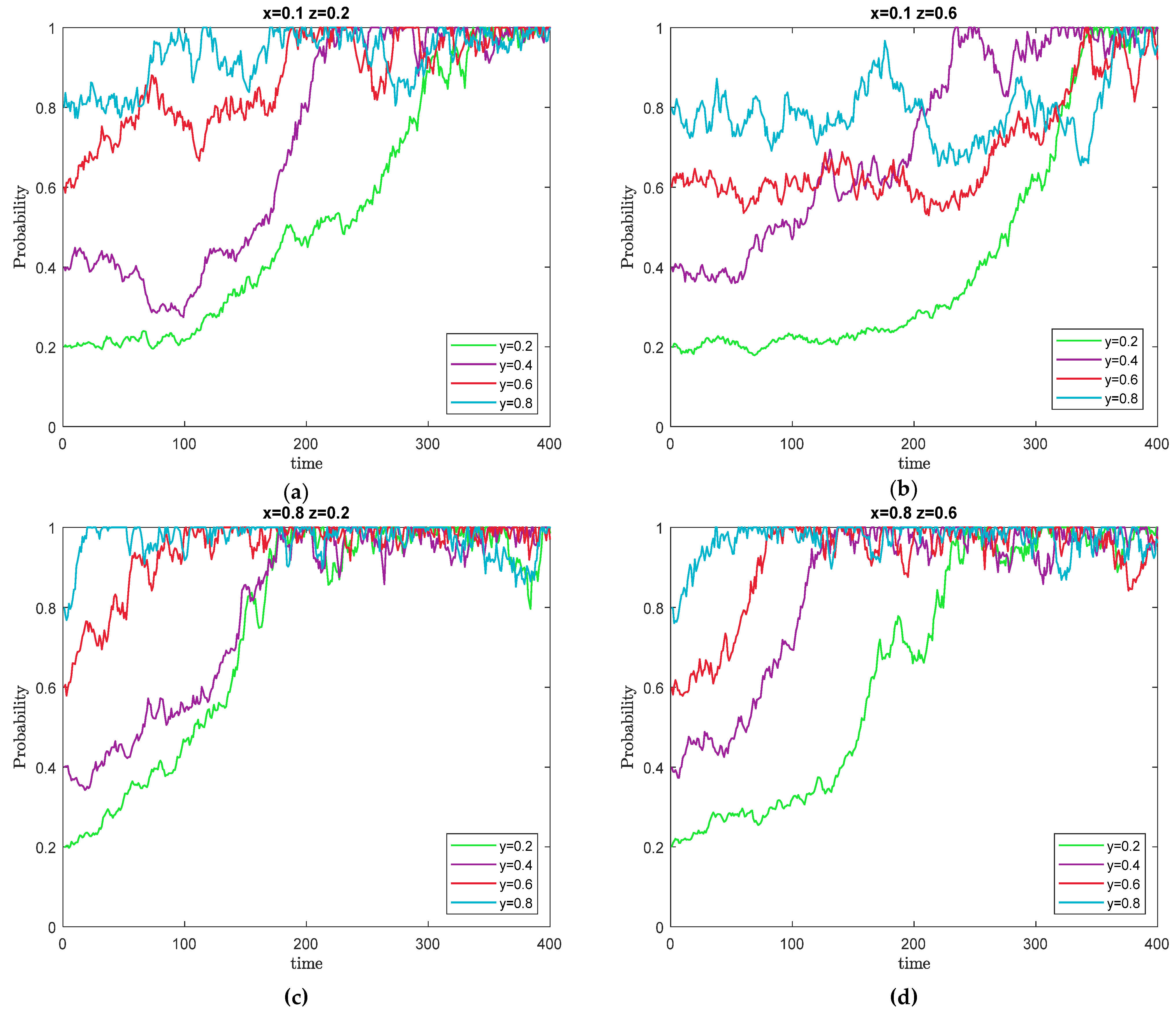
5.2. Changes in the Strategy Probabilities of Port Enterprises and Specialized Oil Spill Cleanup Units

With other parameters unchanged, this study analyzes how changes in port enterprises’ and cleanup units’ strategy probabilities affect the local government’s evolution strategy. Four sets of initial probabilities were used, namely $y=0.1,z=0.2;y=0.1,z=0.6;$ $y=0.8,z=0.2;y=0.8,z=0.6$. The selection of these four sets of data allows for comprehensive coverage of different combinations of cooperation willingness among stakeholders, revealing the impact of varying cooperation levels on the evolution of the local government regulatory strategies. The simulation results are shown in Figure 2.

As shown in Figure 2, the evolution of the local government’s regulatory strategy is significantly influenced by changes in the willingness to cooperate with port enterprises and specialized oil spill cleanup units. When port enterprises and specialized oil spill cleanup units both exhibit low cooperation willingness $\left(y=0.1,z=0.2\right)$, the local government rapidly adopts a strong regulatory strategy. Recognizing the risks posed by low levels of cooperation, the government reinforces regulatory measures to fill this gap, thereby maintaining the stability and efficiency of the marine oil spill emergency response system. This indicates that cooperative behavior somewhat influences the intensity of government regulation. When port enterprises exhibit a low willingness to cooperate $\left(y=0.1\right)$ while specialized oil spill cleanup units demonstrate a high willingness to cooperate $\left(z=0.6\right)$, the low willingness of port enterprises accelerates the convergence of the local government’s strategy. Given the essential role port enterprises play in the emergency response framework, it is imperative that the government enhances regulatory oversight to address the deficiencies arising from passive cooperation, thereby facilitating the prompt stabilization of the system. Conversely, when port enterprises are highly willing to cooperate while specialized oil spill cleanup units show low engagement, the local government must uphold a strong regulatory stance to offset the cooperation deficit. Although the proactive behavior of port enterprises positively contributes to the evolution of the emergency response system, it only partially mitigates the negative impact of the cleanup units’ passivity. As a result, the government’s transition toward heightened regulatory intensity progresses more slowly. When both port enterprises and specialized oil spill cleanup units initially demonstrate strong cooperative intent, the government tends to reduce regulatory intensity to lower supervision costs and allocate resources more efficiently. However, as the system evolves, it becomes evident that relying exclusively on voluntary cooperation introduces substantial uncertainty. Enterprises may engage in opportunistic behavior under shifting external conditions or profit-driven incentives, undermining long-term cooperation. To safeguard the sustained effectiveness of the emergency response system and ensure enterprises fulfill their environmental responsibilities, the government ultimately adopts a robust regulatory approach. Thus, even in scenarios of initially high cooperation, the evolutionary path leads to the re-establishment of strong governmental oversight to maintain system stability and prevent strategic deviation.

5.3. Changes in the Strategies of the Local Government and Specialized Oil Spill Cleanup Units

When other parameters are held constant, four different sets of initial probabilities $x=0.1;z=0.2;x=0.1;z=0.6;x=0.8;z=0.2;x=0.8;z=0.6$ are defined to facilitate a clearer observation of the dynamic interactions among the local government, specialized oil spill cleanup units, and port enterprises. These variations specifically emphasize how shifts in regulatory intensity and the cooperative willingness of cleanup units affect the strategic decisions made by port enterprises.

The simulation results are shown in Figure 3. When the local government’s regulatory intensity is low, and the willingness of specialized oil spill cleanup units to cooperate is low, the cooperation willingness of port enterprises fluctuates significantly at a low level, and the strategy convergence rate is slow, showing considerable instability. This indicates that in the absence of cooperation support from specialized oil spill cleanup units and regulatory constraints from the local government, port enterprises tend to choose negative cooperation initially to reduce emergency costs, and the sustainability of their cooperative behavior is poor. As the willingness of specialized oil spill cleanup units to cooperate increases, port enterprises evolve towards positive cooperation, albeit at a slower rate in the early stages. This is because when specialized oil spill cleanup units cooperate positively, port enterprises may tend to free-ride by reducing their resource input to share the treatment benefits brought by the cooperation of the specialized oil spill cleanup units. When the local government’s regulatory intensity remains high but the willingness of specialized oil spill cleanup units to cooperate is low, the willingness of port enterprises to cooperate tends to stabilize quickly, and the positive cooperation strategy is ultimately chosen. This indicates that under the pressure of high-intensity regulation, port enterprises are more likely to choose a cooperative strategy in their cost–benefit analysis to avoid high penalty risks and reduce the long-term damage to their reputation caused by oil spill incidents. When the local government’s supervisory intensity remains unchanged and the willingness of specialized oil spill cleanup units to cooperate increases, the cleanup responsibility of port enterprises is alleviated, and the improvement in oil spill emergency efficiency allows port enterprises to achieve good emergency results even with reduced cooperation input. Therefore, the rate of evolution towards the positive cooperation strategy slows down.

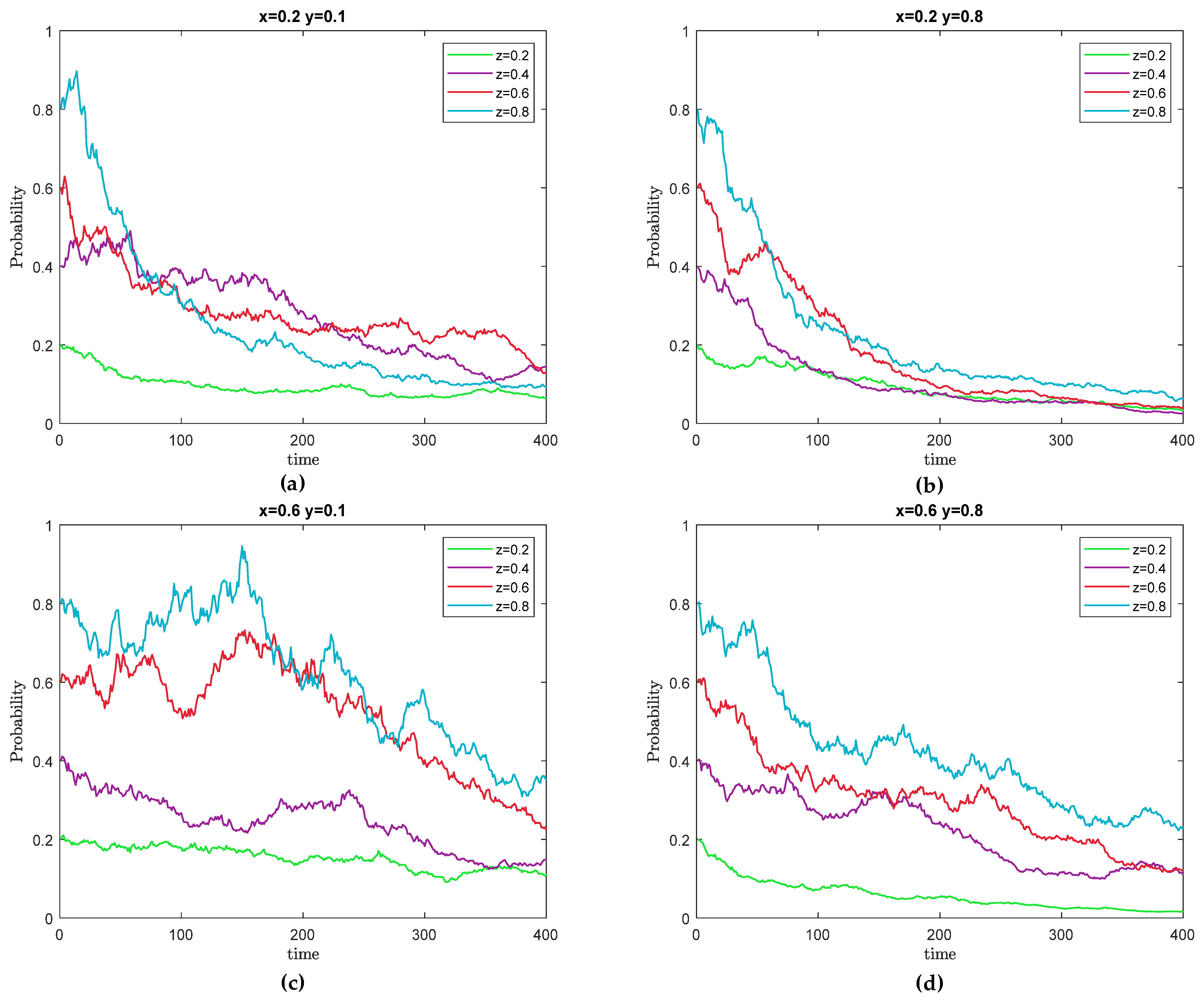
5.4. Changes in the Strategy Probabilities of the Local Government and Port Enterprises

When other parameters remain constant, four sets of initial probabilities are set: $x=0.2;y=0.1;x=0.6;y=0.1;x=0.2;y=0.8;x=0.6;y=0.8$. Based on these four different initial probabilities, the impact of changes in the local government’s regulatory intensity and port enterprises’ initial willingness to cooperate on the willingness of specialized oil spill cleanup units to cooperate is analyzed.

The simulation results are shown in Figure 4. When the local government’s regulatory intensity is low, and the willingness of port enterprises to cooperate is low, the possible cooperation probability of specialized oil spill cleanup units is low, showing significant volatility and a rapid decline trend. This indicates that in situations where the local government’s regulatory intensity and the cooperation willingness of companies are insufficient, specialized oil spill cleanup units lack motivation to cooperate and are prone to adopting negative strategies, making it difficult to improve overall efficiency. When the cooperation willingness of port enterprises significantly increases and the local government’s regulatory intensity is low, in the case of a high local government regulatory intensity, specialized oil spill cleanup units, considering the penalty impact, show a slowdown in the tendency to choose negative cooperation, indicating that high-intensity regulation inhibits the negative cooperation strategy of specialized oil spill cleanup units to some extent. However, when both port enterprises and the local government are more willing to cooperate, specialized oil spill cleanup units quickly choose the negative cooperation strategy to extend the cleanup time to gain more profit.

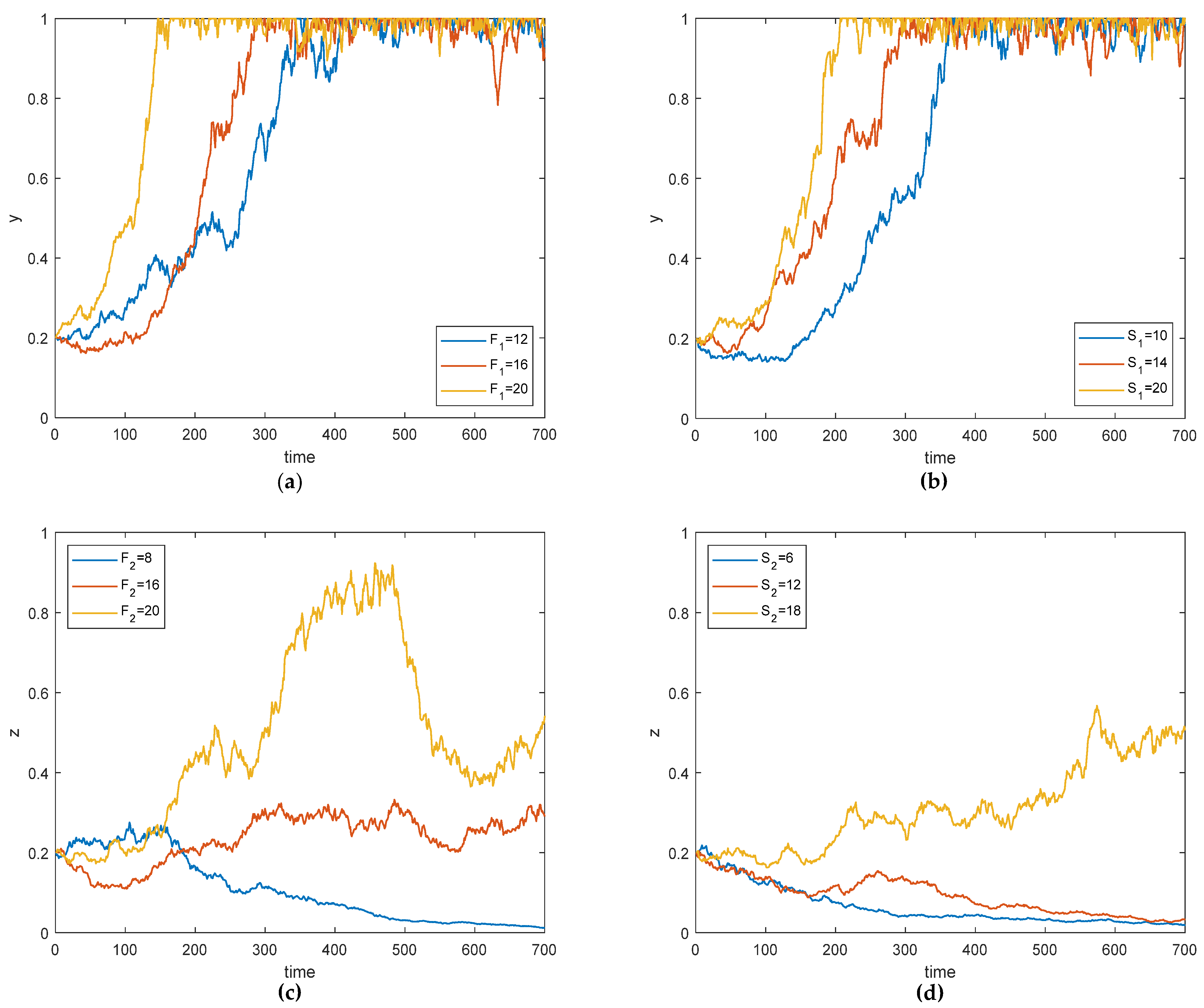
5.5. Simulation Analysis of the Impact of the Local Government Incentives and Penalties on the Strategies

Responding to an oil spill emergency requires cooperation between port enterprises and specialized oil spill cleanup units. The local government has implemented a policy that imposes penalty costs on entities that negatively participate in oil spill response efforts, thereby increasing the enthusiasm of port enterprises and specialized oil spill cleanup units while reducing damage to the marine environment. The local government aims to incentivize port enterprises and specialized oil spill cleanup units to ensure the sustainable development of the marine economy. Therefore, when an oil spill occurs, the ideal goal of the local government is to maintain the stability of the marine ecosystem and ensure that port enterprises and specialized oil spill cleanup units cooperate positively in emergency response.

This section analyzes the impact of the local government’s reward and punishment mechanism on the strategy choices of participants under stochastic perturbations, using MATLAB (https://www.mathworks.com/products/matlab.html) for numerical simulations. The initial strategy of port enterprises is set to $y=0.2$, and the initial strategy of professional oil spill cleanup units is set to $z=0.2$, with other parameters remaining the same as above. Figure 5 presents the simulation results of the specific stochastic evolutionary model.

As shown in Figure 5, the regulatory intensity and incentive mechanisms implemented by the local government play a pivotal role in influencing the evolutionary trajectory of cooperation among port enterprises. Specifically, the imposition of strong punitive measures leads to a marked increase in the willingness of port enterprises to cooperate, with this behavior becoming more stable over time. Such strict regulation effectively deters opportunistic actions and steers enterprises toward proactive engagement. At the same time, governmental incentives also exert a substantial positive influence on cooperative behavior. The analysis reveals that as the level of incentives increases, the time it takes for port enterprises to adopt cooperative strategies decreases significantly. This not only enhances their emergency response efficiency but also strengthens their willingness to participate actively in environmental incident management, such as oil spill responses.

Moreover, when the local government adopts high-intensity incentive policies, the cooperative willingness of specialized oil spill cleanup units increases markedly. Compared to punitive measures, incentive mechanisms demonstrate greater stability in their evolutionary behavior under stochastic disturbances. This suggests that reward-based policies possess strong resilience, effectively mitigating the adverse effects of environmental uncertainty on the decision-making processes of cleanup units. Simultaneously, the findings indicate that these units are highly responsive to punitive regulations; under stringent enforcement, they can rapidly enhance their cooperative behavior and proactively participate in oil spill emergency responses.

Therefore, it is crucial for the local government to establish robust institutional frameworks that integrate both incentives and penalties within a system of strong accountability. Such comprehensive mechanisms not only ensure effective oversight of port enterprises and cleanup units but also foster sustained cooperation and operational efficiency. Ultimately, this contributes to the long-term stability and effectiveness of marine environmental emergency management and supports the implementation of coordinated response strategies over time.

5.6. Simulation Analysis of the Impact of Emergency Response Efficiency Coefficient $\alpha$ and Emergency Cooperation Effect Coefficient $\rho$

By adjusting the values of parameters $\alpha$ and $\rho$, the adaptability of port enterprises and specialized oil spill cleanup units in resource allocation and cooperation models can be analyzed to optimize further the efficiency and coordination of oil spill emergency response. The parameter settings were calibrated to their values with reference to the response time data and coordination effectiveness of relevant ship pollution accident investigation reports. In the initial scenario, the value of $\alpha$ is set to 0.2. Here, it is adjusted to 0.2, 0.4, 0.6, and 0.8, while $\rho$ is initially set to 0.3 and adjusted to 0.1, 0.3, 0.5, and 0.7, with all other parameters remaining unchanged. The simulation results are shown in Figure 6.

As shown in Figure 6, the local government usually responds promptly by strengthening the supervision of oil spill response efforts to ensure timely and effective action when both emergency response efficiency and the level of cooperation are low. With strict supervision, port enterprises are generally motivated to adopt cooperative strategies to accelerate the reopening of navigation channels and the restoration of normal operations. In contrast, specialized oil spill cleanup units often adopt a temporary wait-and-see approach during this initial phase. As spill response efficiency and cooperation improve, the expected benefits of joint response efforts become more apparent to the local government. At the same time, the costs associated with cooperation decrease for port operators, and the potential to reduce the damage caused by oil spills and to avoid secondary disasters increases. In this situation, the local government maintains strong regulatory oversight, and port enterprises continue to adopt active cooperation. However, as the system achieves a higher level of operational efficiency and coordination, specialized oil spill cleanup units may begin to adopt passive cooperation strategies to reduce operating costs and prolong cleanup activities for financial gain. This behavior may undermine the overall effectiveness of emergency response, delay environmental recovery, and pose a potential threat to social and ecological stability.

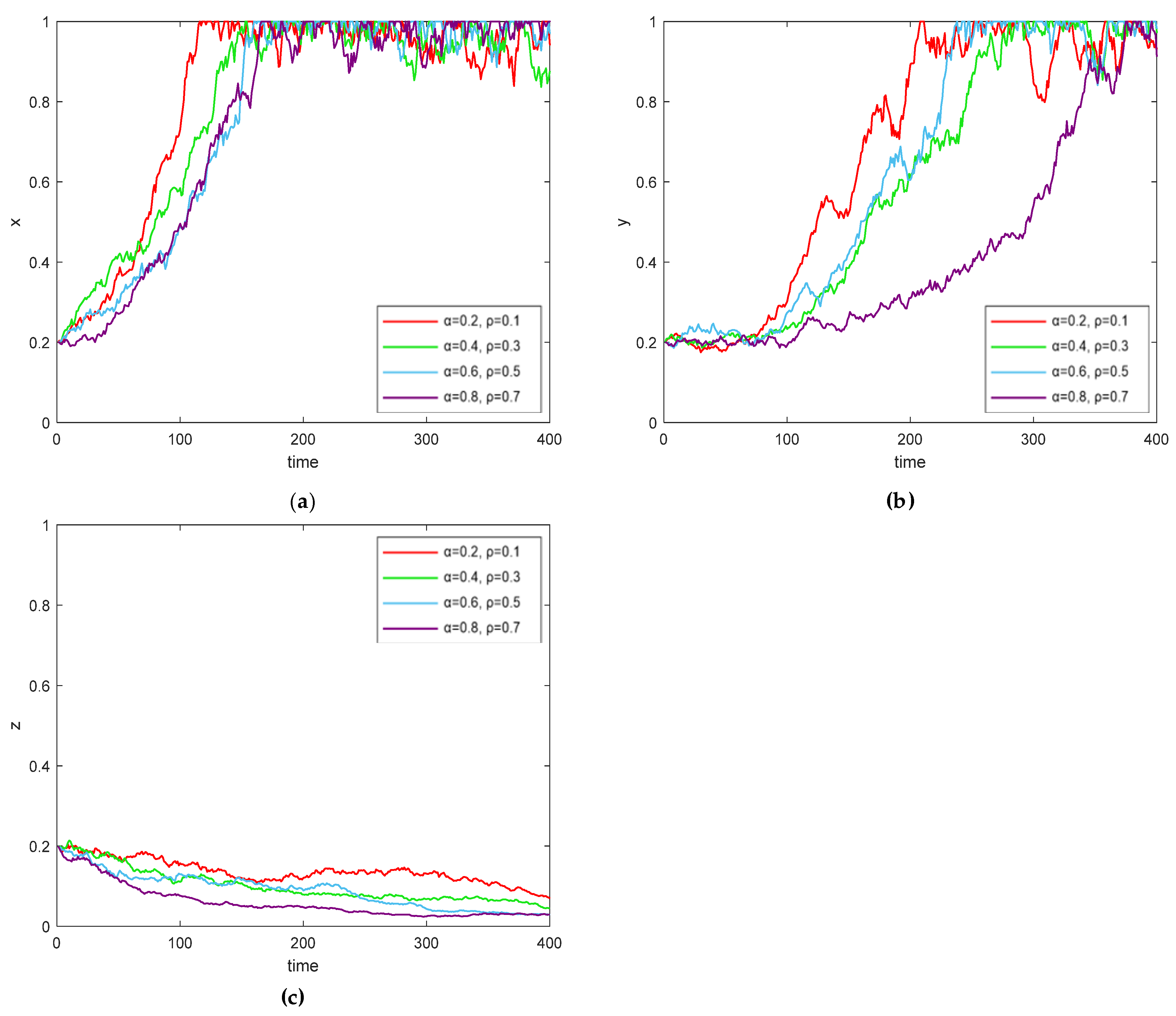
5.7. Simulation Analysis of the Effect of Random Disturbance Intensity on Evolutionary Results

In maritime oil spill emergency response, random disturbances significantly impact the evolution of multi-agent strategy selection. This study conducts a simulation analysis by setting disturbance intensities at four levels: 0, 0.4, 0.8, and 1.2, covering scenarios from no disturbance to high disturbance. The results indicate that random disturbances lead to significant differences in the strategy selection of participating agents.

As shown in Figure 7, in the absence of external environmental disturbances and uncertainties, the local government and port enterprises respond positively, while specialized oil spill cleanup units tend to engage in negative cooperation, leading the system to evolve toward the equilibrium point (1, 1, 0). The local government exhibits the fastest evolution speed, indicating a strong willingness to regulate. As the disturbance intensity increases, fluctuations appear in the strategy selection of game participants. The local government experiences relatively minor fluctuations, suggesting that it is less affected by the external environment and exhibits a strong sense of responsibility and commitment to marine environmental protection. This is attributed to the local government’s leading role in emergency response and the rigidity of policy implementation, enabling it to advance emergency cooperation continuously. In contrast, port enterprises are more sensitive to random disturbances. As disturbance intensity increases, their willingness to cooperate declines, and strategy fluctuations become more pronounced. This reflects the port enterprises’ tendency to avoid risks and their sensitivity to costs when facing uncertainties. Specialized oil spill cleanup units are less sensitive to stochastic disturbances. However, their strategic paths exhibit significant fluctuations under high disturbance conditions, and their willingness to cooperate declines. Specialized oil spill cleanup units typically possess well-developed operational processes and technical capabilities, enabling them to better counteract or adapt to external uncertainties, thereby reducing the impact of stochastic disturbances on their strategy selection. Therefore, port enterprises warrant the most attention within the entire marine oil spill emergency response system, as they are most affected by stochastic disturbances. The operational processes of port enterprises are highly dependent on external environmental conditions and play a crucial intermediary role in the emergency cooperation system. Their decision-making is not only influenced by the interactive effects of upstream and downstream partners but is also prone to complex fluctuations due to the significant amplification effect of external stochastic disturbances.

6. Conclusions

6.1. Management Significance

Based on the stability analysis of the replicated factor dynamics equation, this paper establishes a stochastic evolutionary game model for marine oil spill emergency response and introduces Gaussian white noise to take into account the uncertainty of stakeholders’ behaviors. The model captures the strategic interactions among local governments, port enterprises, and specialized oil spill cleanup units and simulates the evolutionary trajectories of their strategies under different initial conditions and parameter settings. Sensitivity analysis is conducted by adjusting key parameters to examine how they affect the evolutionary stability and dynamic strategic behavior of the three stakeholder groups. This approach broadens the perspective and scope of research on maritime oil spill emergency response strategy modeling and has important theoretical value and practical guiding significance for improving the efficiency of maritime oil spill emergency response.

Based on these findings, this paper offers targeted policy recommendations aimed at strengthening cooperative mechanisms for responding to maritime oil spills. These recommendations aim to improve regional response efficiency and reduce the environmental impact of oil spill incidents and are given as follows:

(1)

Effective government regulation is essential for promoting active participation by port enterprises in maritime oil spill response cooperation and for increasing the willingness of specialized oil spill cleanup units to engage in coordinated efforts. The local government should develop and refine relevant policies and regulations, raise public awareness, strengthen the environmental accountability of port enterprises, and ensure that regulatory measures are implemented effectively. These actions can boost the motivation of port enterprises to cooperate and encourage the adoption of more proactive emergency response strategies. Moreover, differentiated incentives and penalties can be tailored according to the level of cooperation demonstrated by port enterprises and the severity of oil spill risks. For instance, enterprises that fail to meet their emergency response obligations or display a passive attitude may be subject to environmental taxes or other economic sanctions to heighten their risk awareness and promote active engagement. Local government also plays a vital role in optimizing the oil spill contingency compensation mechanism and ensuring the execution of cooperative agreements. By implementing rational resource allocation strategies and well-designed incentive systems, local authorities can significantly enhance overall emergency response effectiveness and foster the sustainable development of regional oil spill response cooperation.

(2)

The fine mechanism serves as a key tool for strengthening the local government oversight in maritime oil spill response cooperation. To ensure effective implementation of contingency plans, local authorities must rigorously supervise the cooperative actions of port enterprises and specialized oil spill cleanup units, imposing strict penalties on those that violate cooperation protocols or fail to respond adequately to spill incidents. Increasing fines for enterprises that neglect their emergency cooperation duties or hinder the development of the regional contingency system can significantly enhance regulatory effectiveness and encourage firms to take greater environmental responsibility. To reinforce the penalty system, the local government can adopt a range of regulatory measures. These may include ordering non-compliant enterprises to suspend operations for rectification, integrating their records into credit supervision systems, and increasing the cost of non-compliance through public disclosures or industry bulletins. Such measures can effectively curb non-cooperative behavior among port enterprises and specialized oil spill cleanup units, thereby supporting the stable operation of the emergency response cooperation framework, strengthening overall response capacity, and minimizing the environmental damage caused by oil spill incidents.

(3)

In the maritime oil spill response system, each game subject is committed to maximizing the benefits and adjusting its strategy continuously. The introduction of stochastic perturbation leads to obvious oscillation characteristics for each participant in the strategy evolution process. Under normal perturbation, port enterprises are most significantly affected, showing high instability, followed by the local government, while specialized oil spill cleanup units remain stable; In contrast, under strong perturbation, port enterprises show obvious speculative tendencies, while specialized oil spill cleanup units also show more prominent speculative behavior and are more affected by external perturbation. In contrast, the local government has demonstrated a stronger capacity to counter disturbances. Therefore, the local government formulates special funding support policies for oil spill prevention and control and provides financial incentives to encourage port enterprises to participate in emergency response cooperation continuously. In addition, in the face of sudden external perturbations, such as extreme weather and sudden environmental events, an oil spill contingency reserve system needs to be set up, including financial reserves, emergency material reserves, and a training system for professionals, to improve the response capability of the entire system.

(4)

This study demonstrates a strong positive correlation between emergency response efficiency and the effectiveness of cooperation mechanisms. Empirical analysis reveals that strengthening cooperative efforts notably enhances information sharing, improves resource coordination, and reduces response time. These findings highlight that establishing an efficient collaborative framework is essential for effective oil spill management. To improve the overall response to maritime oil spills, it is crucial to develop a regional joint emergency response system that fosters shared decision-making and communication among government bodies, port enterprises, and specialized oil spill cleanup units. Leveraging big data technologies can further enhance oil spill detection and early warning capabilities, support the development of an integrated resource coordination platform, and facilitate the creation of a regional emergency material reserve center to strengthen emergency deployment capacity.

6.2. Limitations and Research Prospects

While this study has made meaningful strides in examining the strategic interactions among the local government, port enterprises, and specialized oil spill cleanup units in maritime emergency response, several limitations remain and warrant further exploration. The model assumes that all parties operate under bounded rationality and make decisions solely based on profit maximization. In reality, however, choices may be shaped by a broader range of influences, including political pressures, public opinion, and cultural context. These elements are not fully captured in the current framework. Future research should incorporate more realistic considerations, such as irrational behaviors and social network dynamics, to improve the model’s practical relevance. Additionally, this study primarily focuses on the interactions between governmental and corporate actors, overlooking the potential impact of the public and other stakeholders. Subsequent research should integrate the public as a key participant to better understand their role and contribution to collaborative, multi-objective responses to maritime oil spills.