Analysis of Influencing Factors of Terrestrial Carbon Sinks in China Based on LightGBM Model and Bayesian Optimization Algorithm
Abstract
1. Introduction
2. Materials and Methods
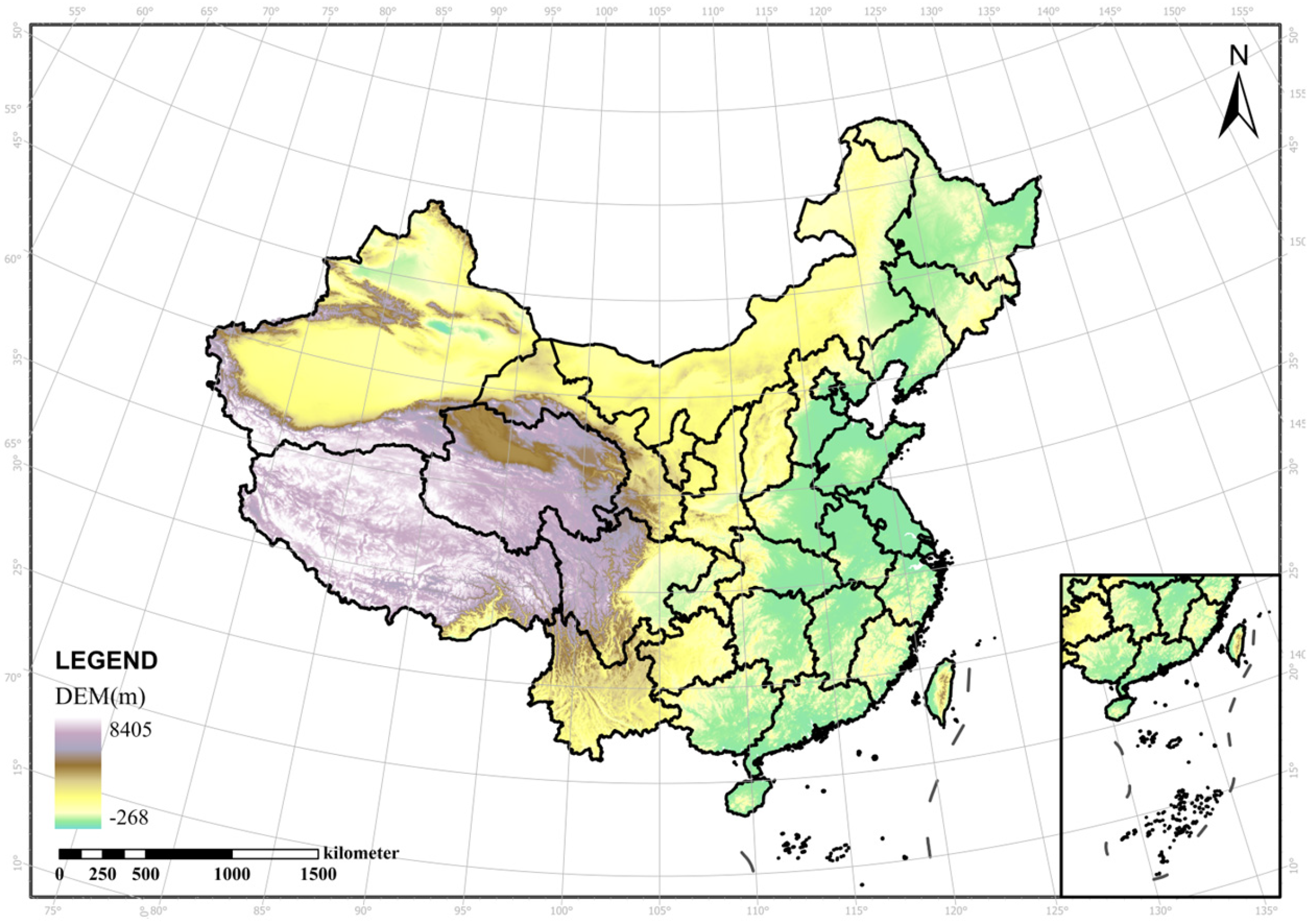
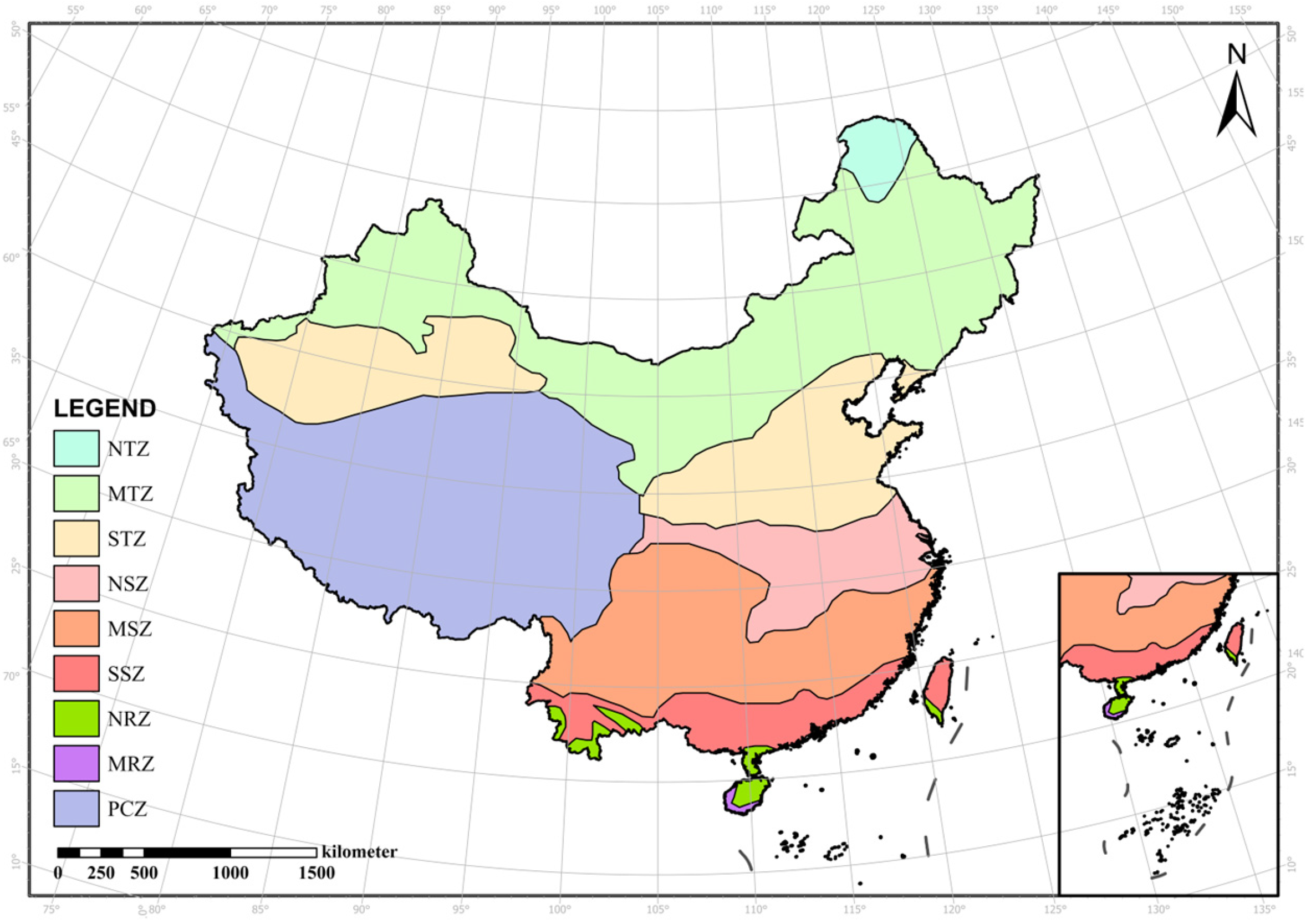
2.1. Research Area
2.2. Data Resource
2.3. Methods
2.3.1. CASA Model
2.3.2. kNDVI
2.3.3. Rh Empirical Model
2.3.4. NEP Calculation
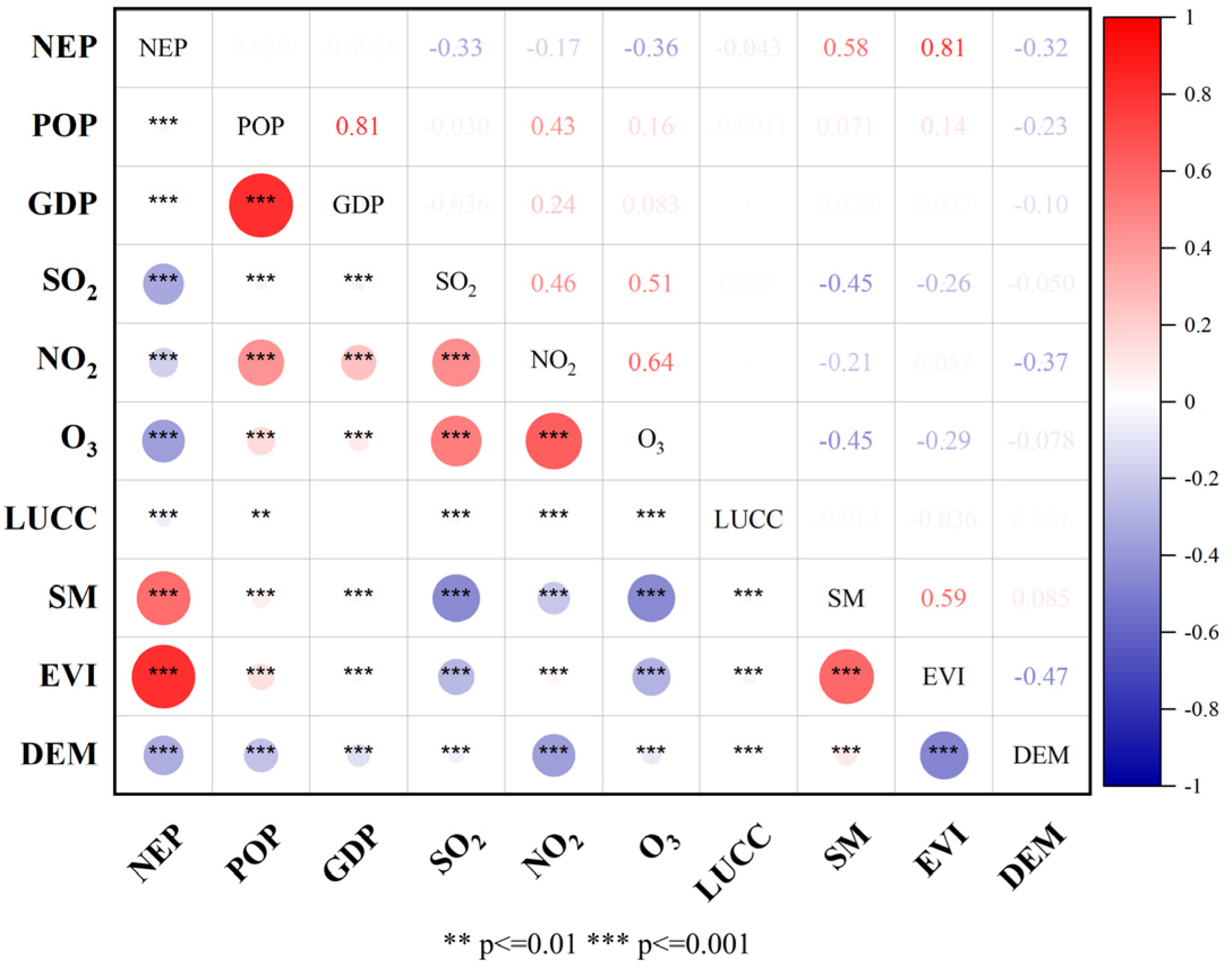
2.3.5. Pearson Correlation
2.3.6. VIF Test
2.3.7. LightGBM Model
2.3.8. Bayesian Optimization
2.3.9. The 5-Fold Cross-Validation Method
2.3.10. SHAP
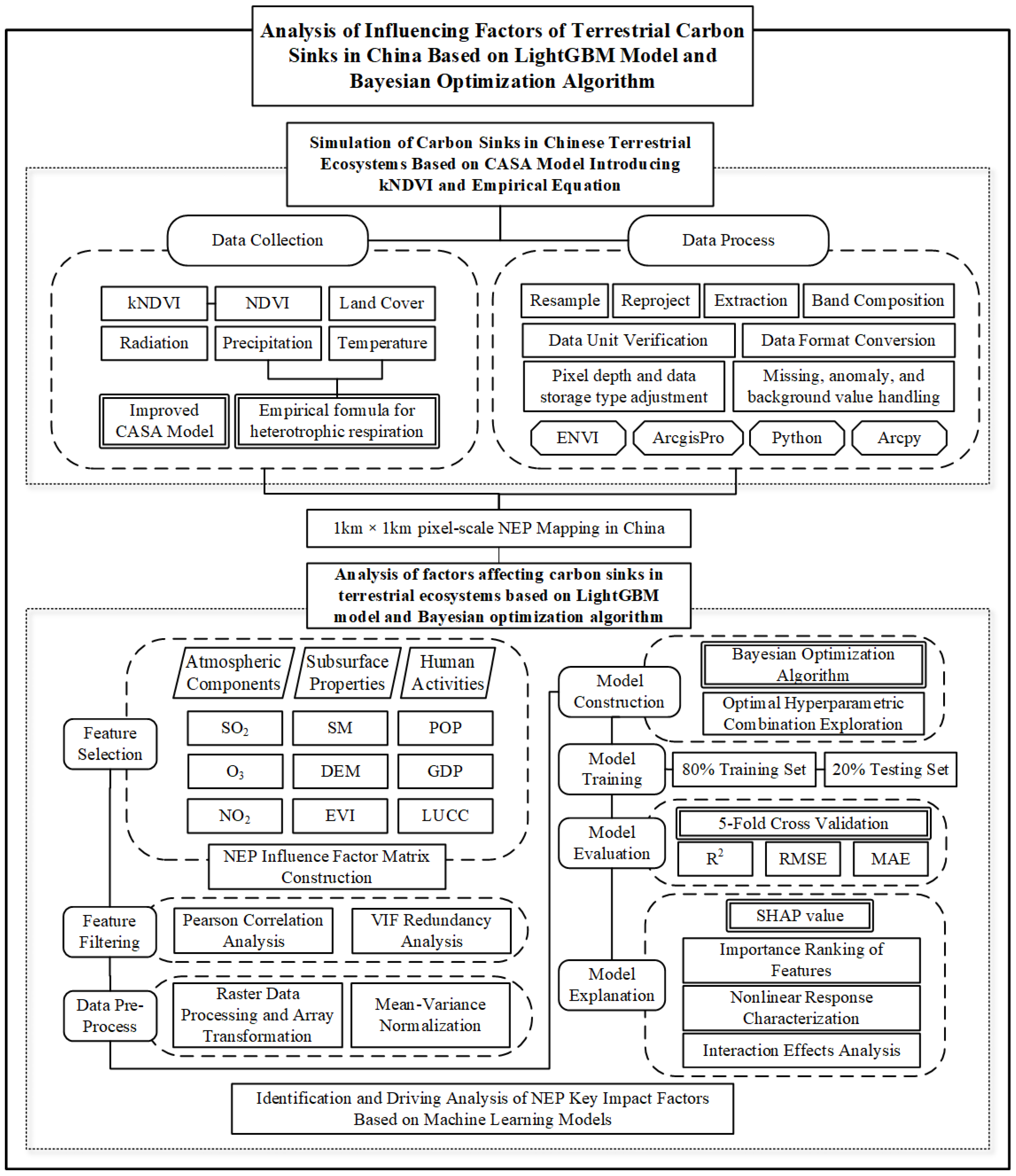
2.4. Methodological Framework
3. Results
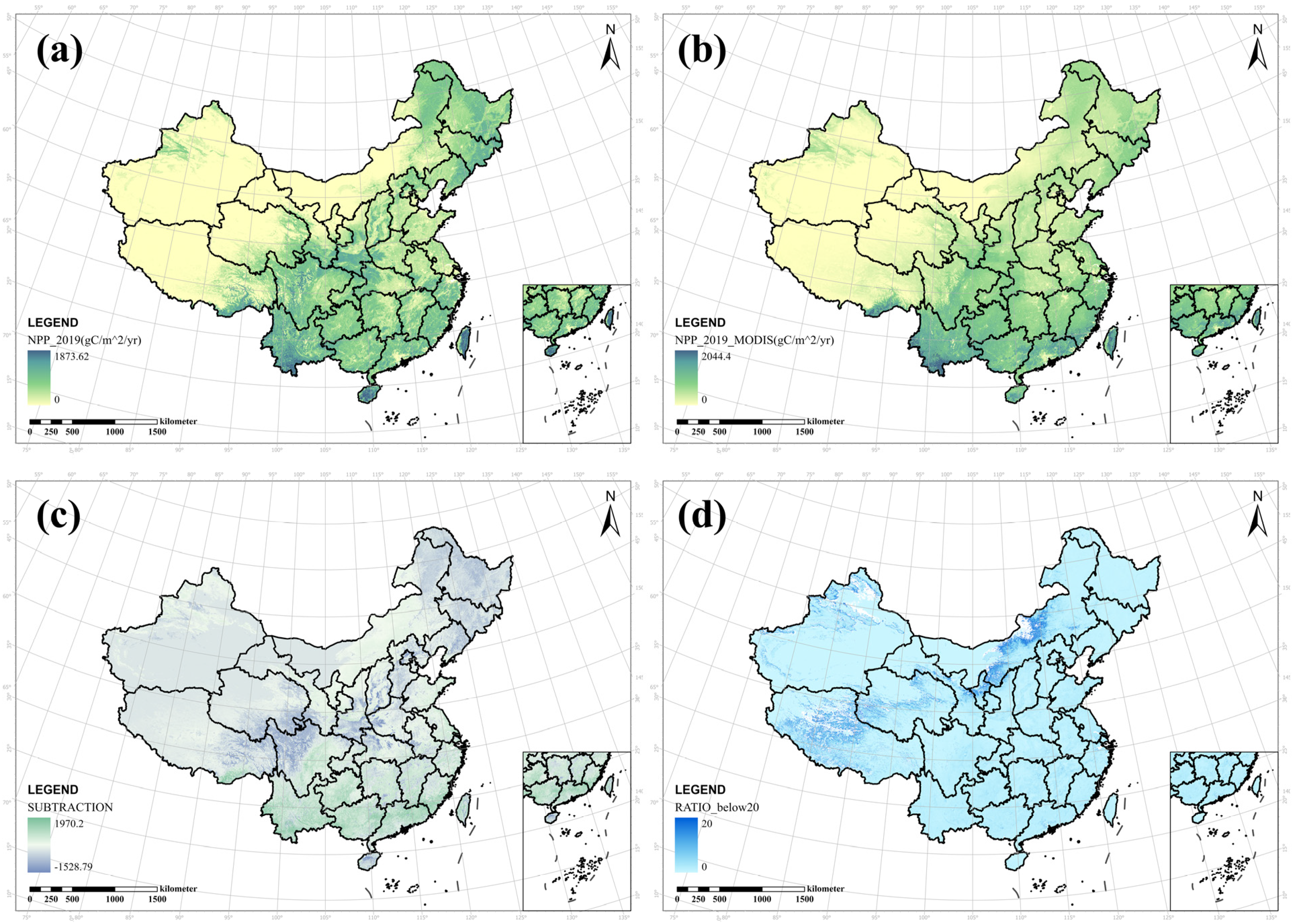
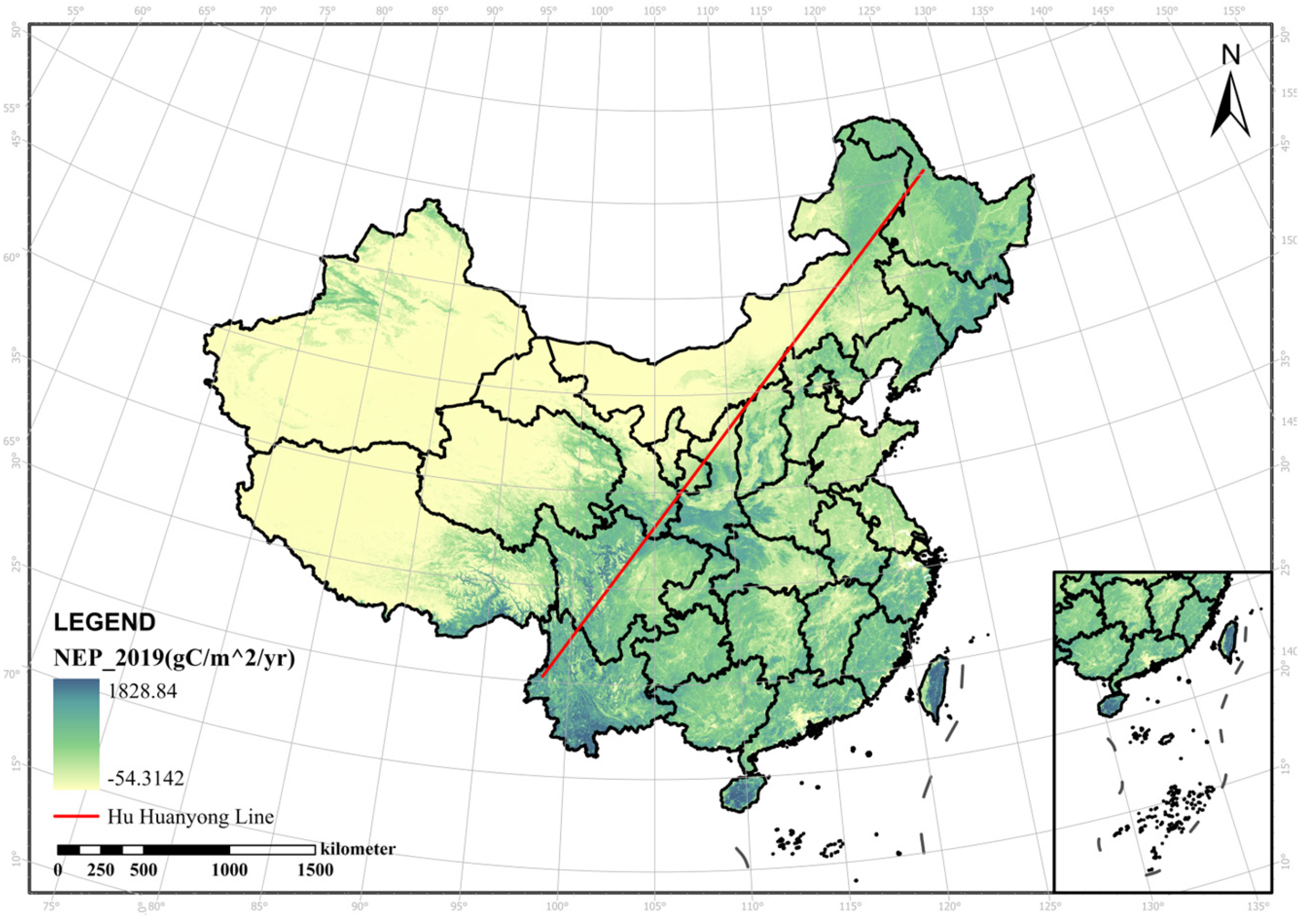
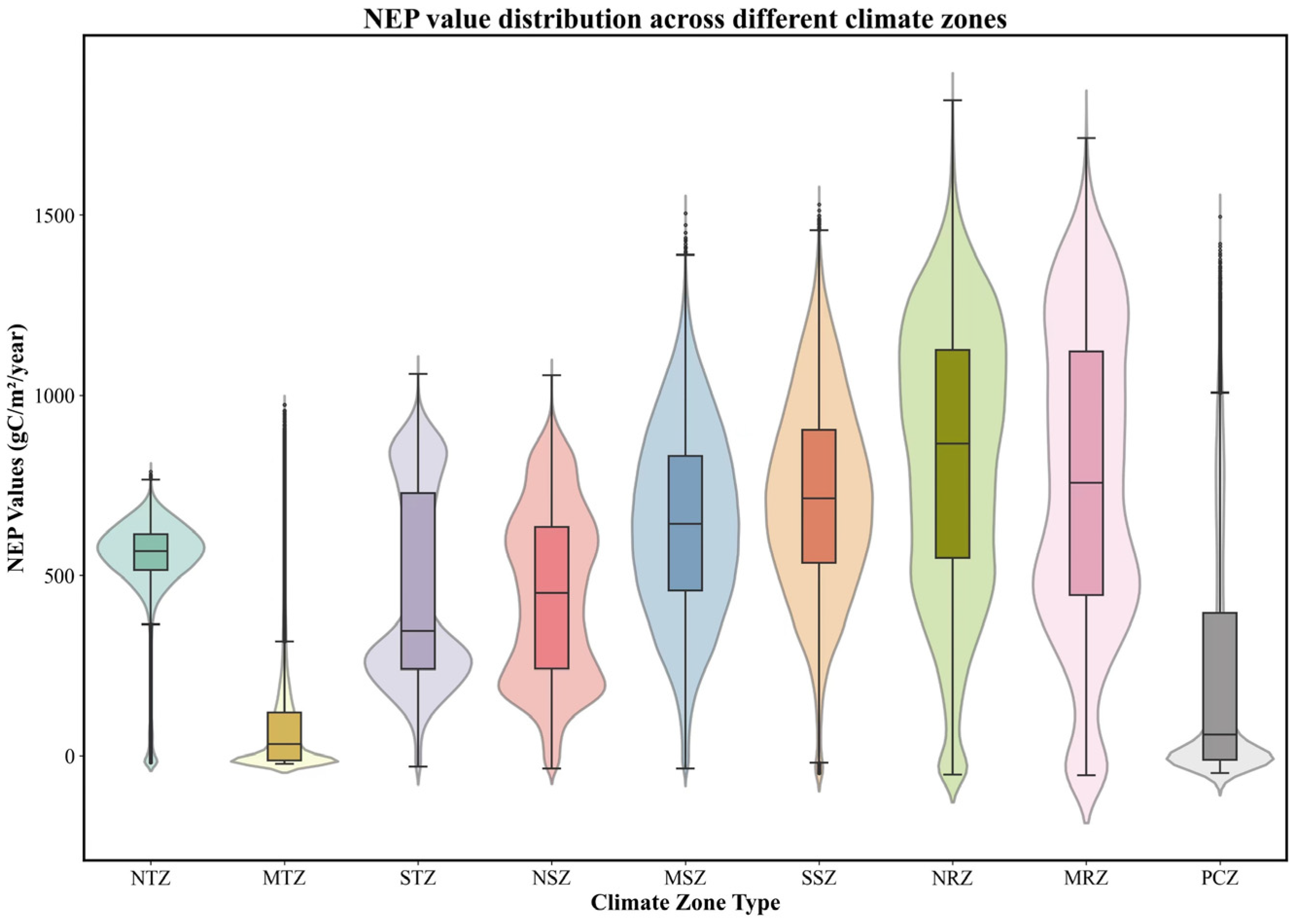
3.1. NEP Simulation and Analysis
3.2. Preprocessing LightGBM Model Construction
3.2.1. Factor Choosing
3.2.2. Factor Pre-Test
3.2.3. Factor Process
3.3. LightGBM Modeling with Bayesian Optimization
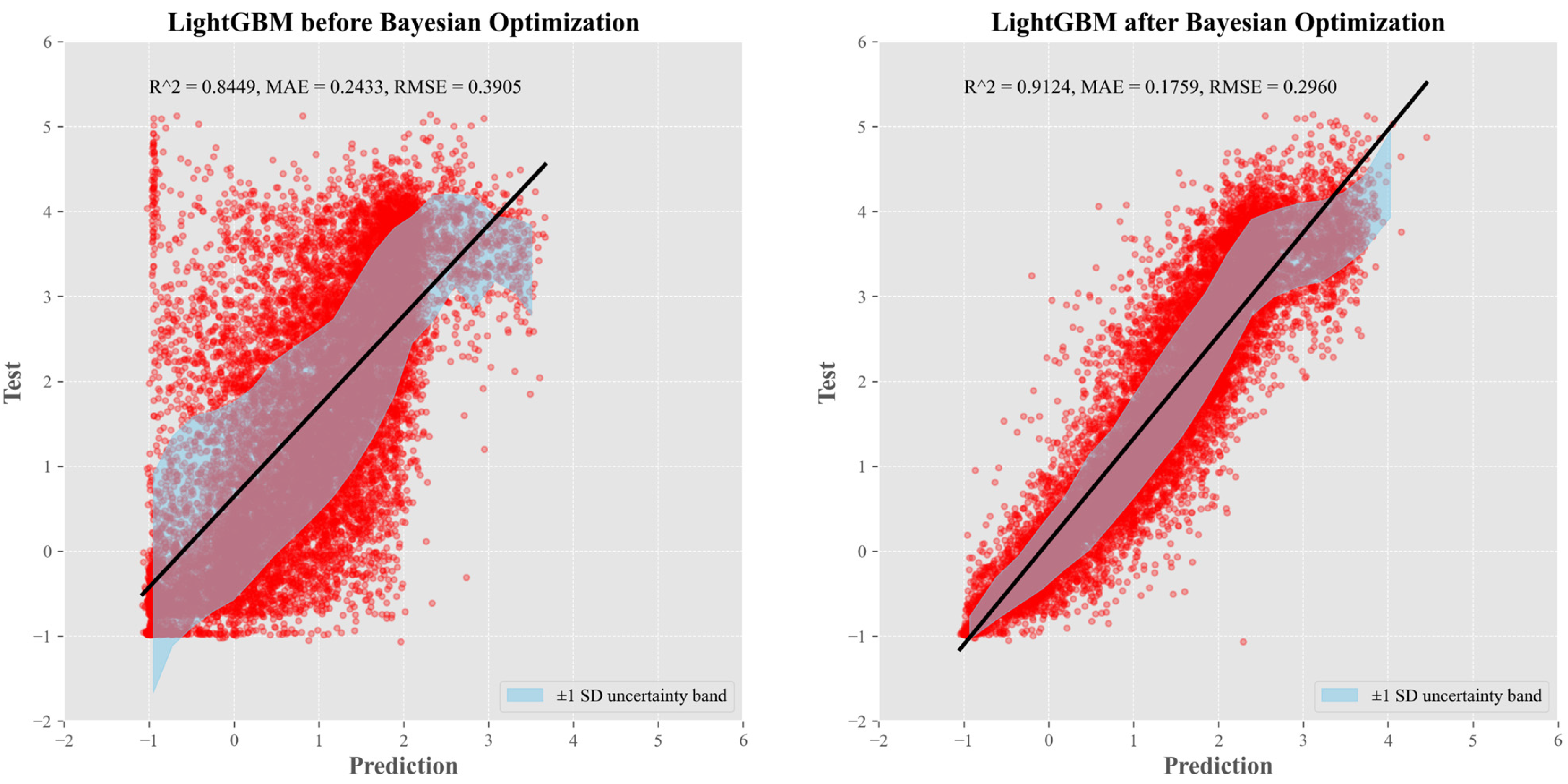
3.3.1. Model Construction
3.3.2. Model Evaluation
3.4. Model Explanation Base on SHAP Value
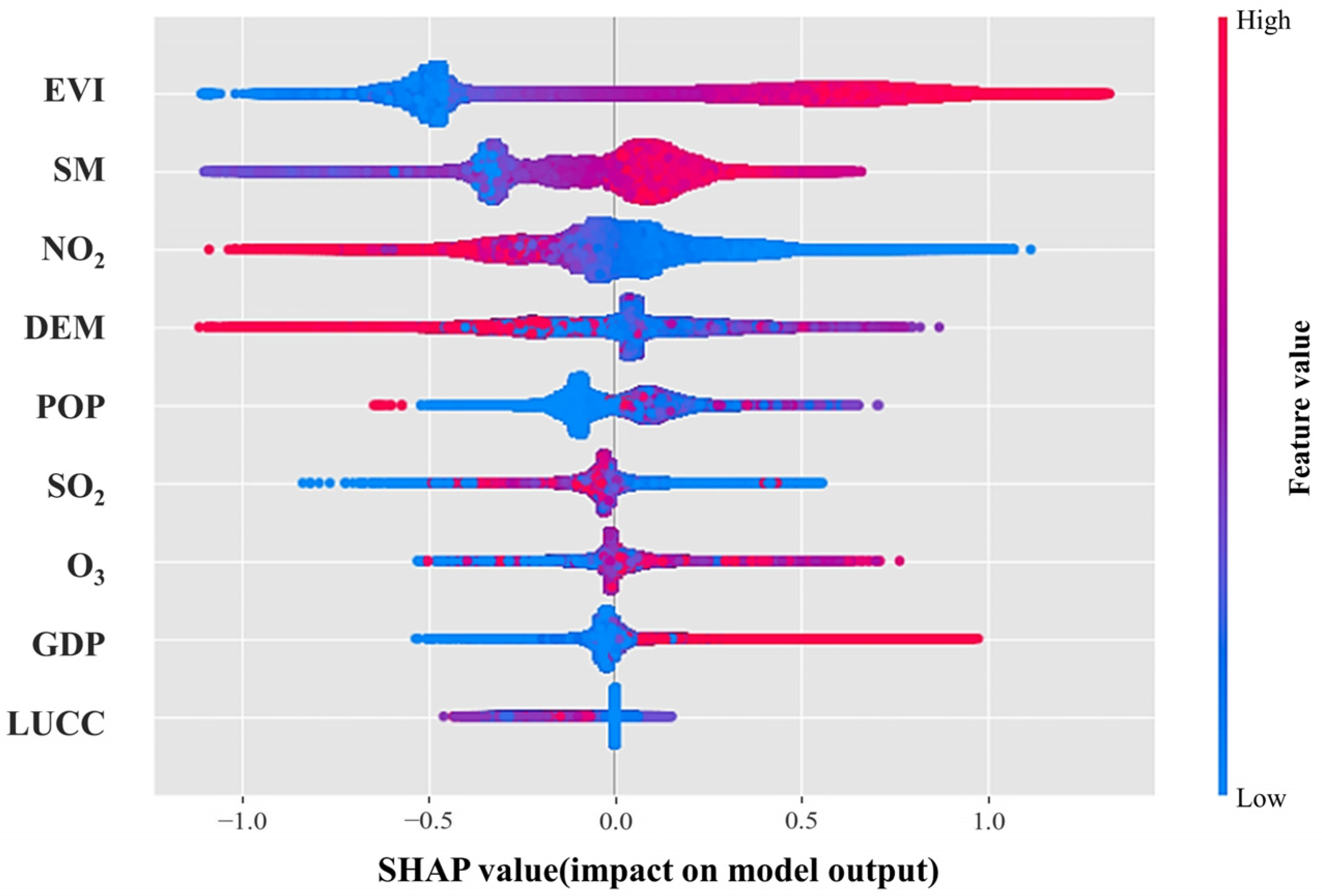
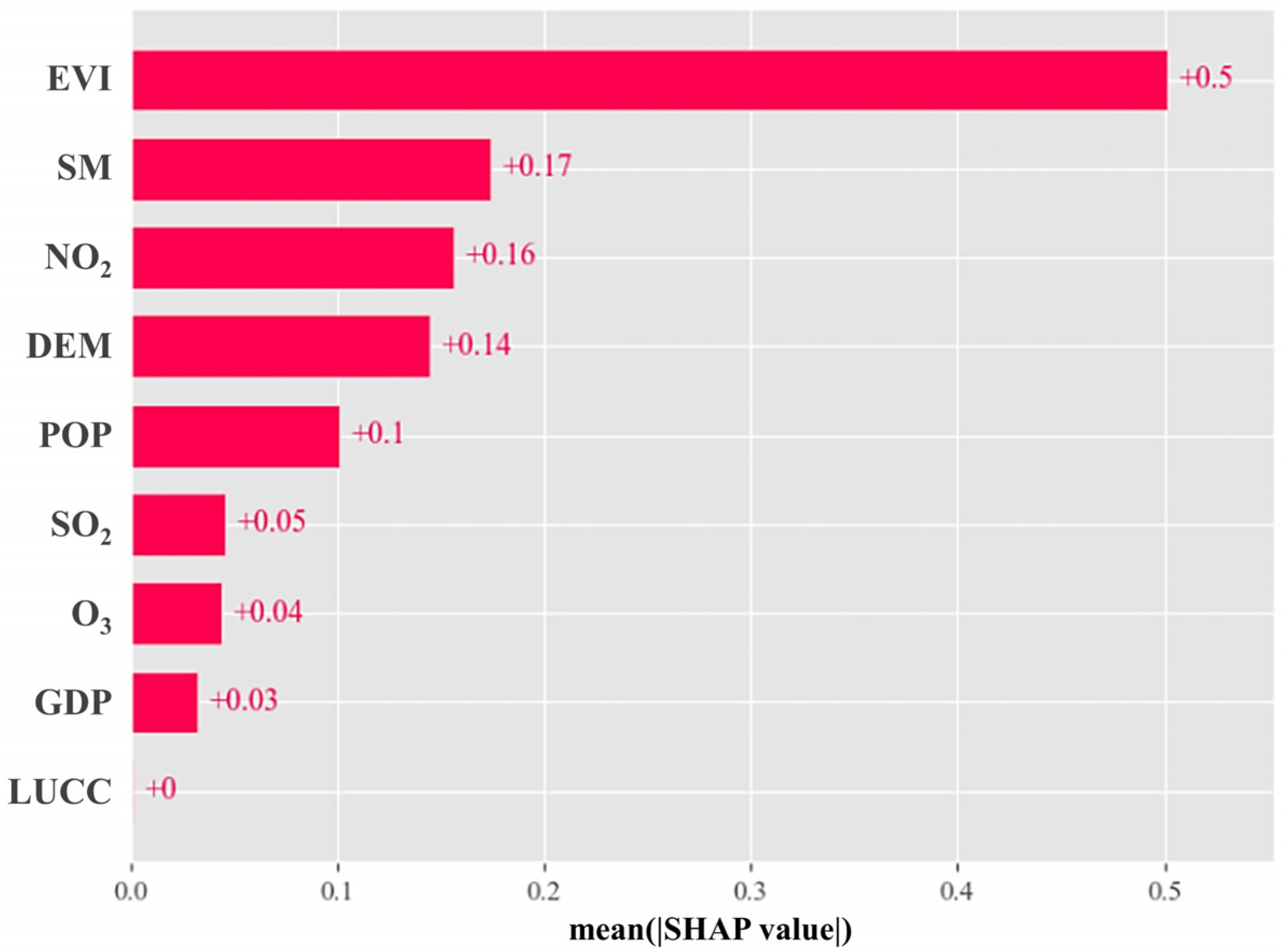
3.4.1. NEP Drivers’ Contribution Ranking
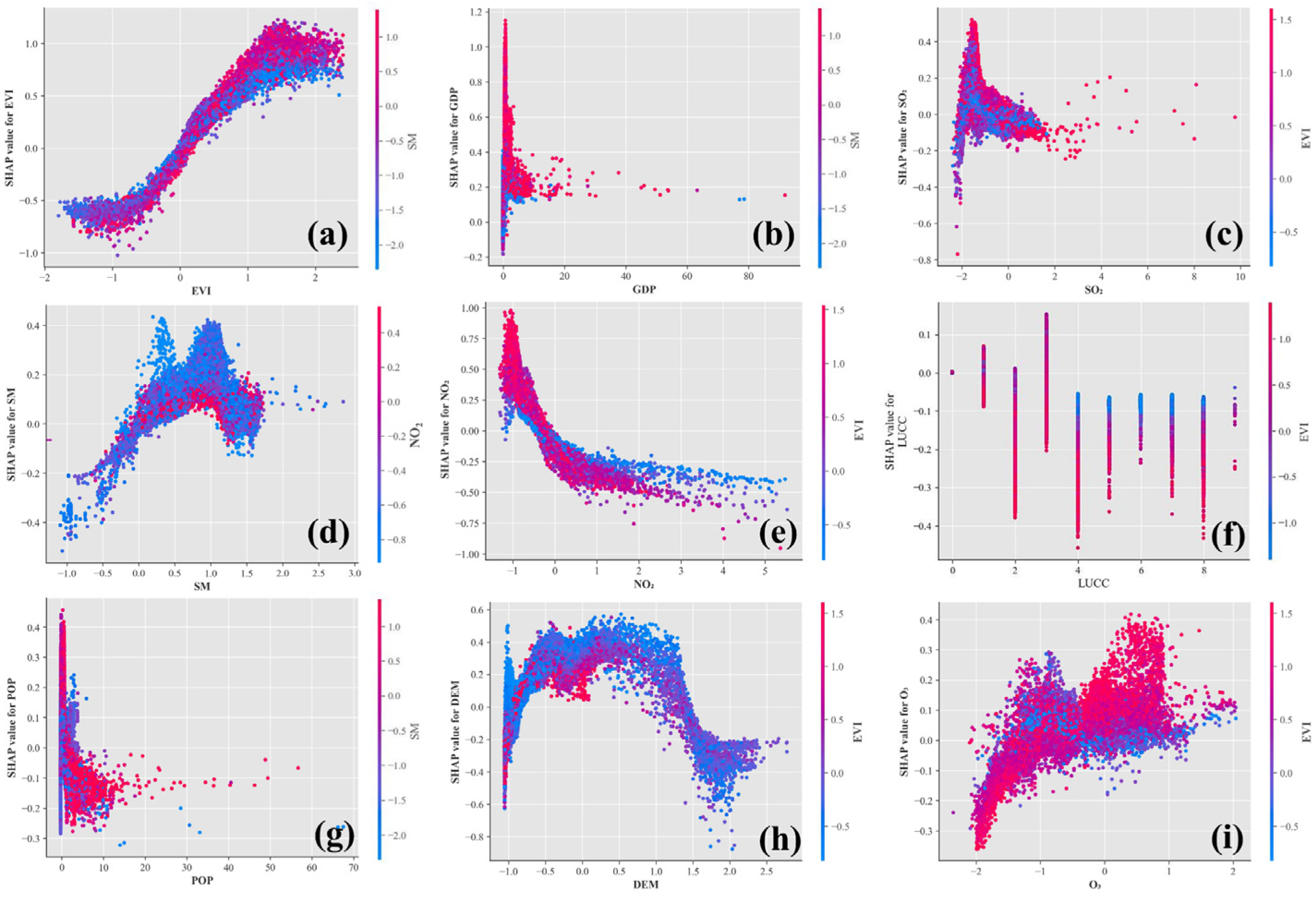
3.4.2. Nonlinear Response Analysis of NEP to Driving Factors
- (1)
- EVI
- (2)
- SM
- (3)
- NO2
- (4)
- DEM
- (5)
- SO2
- (6)
- O3
- (7)
- GDP and POP
- (8)
- LUCC
3.4.3. Interactive Relationship Characterization Between Variables
- (1)
- EVI: interaction with SM
- (2)
- SM: interaction with NO2
- (3)
- NO2: interaction with the EVI
- (4)
- DEM: interaction with the EVI
- (5)
- SO2: interaction with the EVI
- (6)
- O3: interaction with the EVI
- (7)
- GDP and POP: interaction with SM
- (8)
- LUCC: interaction with the EVI
3.4.4. The Influencing Effect Analysis for NEP Drivers
4. Discussion
4.1. Limitations of Carbon Sink Modeling
4.2. Impact of LUCC on Carbon Sinks
4.3. Application of LightGBM in Carbon Sink Attribution Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CASA | Carnegie–Ames–Stanford approach |
| DEM | digital elevation model |
| EVI | enhanced vegetation index |
| GDP | gross domestic product |
| GPP | gross primary productivity |
| kNDVI | kernel normalized difference vegetation index |
| LUCC | land use and land cover change |
| MAE | mean absolute error |
| MRZ | middle tropical zone |
| MSZ | middle subtropical zone |
| MTZ | middle temperate zone |
| NEP | net ecosystem productivity |
| NPP | net primary productivity |
| NRZ | north tropical zone |
| NSZ | north subtropical zone |
| NTZ | north temperate zone |
| PCZ | plateau climate zone |
| POP | population |
| Rh | heterotrophic respiration |
| RMSE | root mean square error |
| SHAP | Shapley additive explanations |
| SM | soil moisture |
| SSZ | south subtropical zone |
| STZ | south temperate zone |
Appendix A
Appendix A.1. Comparation Between MODIS NPP and Our Simulation
Appendix A.2. Tukey Test for NEP in Different Climate Zones
| Multiple Comparison of Means—Tukey HSD, FWER = 0.05 | ||||||
|---|---|---|---|---|---|---|
| group1 | group2 | meandiff | p-adj | lower | upper | reject |
| NTZ | MTZ | 529.6591 | 0 | 523.0064 | 536.3118 | TRUE |
| NTZ | STZ | 190.2974 | 0 | 183.9476 | 196.6473 | TRUE |
| NTZ | NSZ | 164.2991 | 0 | 157.937 | 170.6611 | TRUE |
| NTZ | MSZ | 398.6029 | 0 | 392.1926 | 405.0132 | TRUE |
| NTZ | SSZ | 504.3487 | 0 | 497.9808 | 510.7167 | TRUE |
| NTZ | NRZ | 596.4504 | 0 | 590.0097 | 602.8911 | TRUE |
| NTZ | MRZ | 813.1031 | 0 | 806.2442 | 819.962 | TRUE |
| NTZ | PCZ | 119.1706 | 0 | 112.8199 | 125.5213 | TRUE |
| MTZ | STZ | −339.362 | 0 | −341.454 | −337.27 | TRUE |
| MTZ | NSZ | −365.36 | 0 | −367.489 | −363.231 | TRUE |
| MTZ | MSZ | −131.056 | 0 | −133.325 | −128.787 | TRUE |
| MTZ | SSZ | −25.3104 | 0 | −27.4566 | −23.1641 | TRUE |
| MTZ | NRZ | 66.7913 | 0 | 64.4381 | 69.1445 | TRUE |
| MTZ | MRZ | 283.444 | 0 | 280.1124 | 286.7756 | TRUE |
| MTZ | PCZ | −410.489 | 0 | −412.583 | −408.394 | TRUE |
| STZ | NSZ | −25.9984 | 0 | −26.7686 | −25.2282 | TRUE |
| STZ | MSZ | 208.3055 | 0 | 207.2055 | 209.4054 | TRUE |
| STZ | SSZ | 314.0513 | 0 | 313.2336 | 314.8689 | TRUE |
| STZ | NRZ | 406.153 | 0 | 404.8881 | 407.4178 | TRUE |
| STZ | MRZ | 622.8057 | 0 | 620.1295 | 625.4819 | TRUE |
| STZ | PCZ | −71.1268 | 0 | −71.7969 | −70.4568 | TRUE |
| NSZ | MSZ | 234.3038 | 0 | 233.1357 | 235.472 | TRUE |
| NSZ | SSZ | 340.0497 | 0 | 339.1423 | 340.957 | TRUE |
| NSZ | NRZ | 432.1513 | 0 | 430.8267 | 433.476 | TRUE |
| NSZ | MRZ | 648.8041 | 0 | 646.0991 | 651.509 | TRUE |
| NSZ | PCZ | −45.1284 | 0 | −45.9055 | −44.3514 | TRUE |
| MSZ | SSZ | 105.7458 | 0 | 104.5459 | 106.9458 | TRUE |
| MSZ | NRZ | 197.8475 | 0 | 196.3076 | 199.3874 | TRUE |
| MSZ | MRZ | 414.5002 | 0 | 411.6836 | 417.3168 | TRUE |
| MSZ | PCZ | −279.432 | 0 | −280.537 | −278.328 | TRUE |
| SSZ | NRZ | 92.1017 | 0 | 90.7489 | 93.4544 | TRUE |
| SSZ | MRZ | 308.7544 | 0 | 306.0356 | 311.4732 | TRUE |
| SSZ | PCZ | −385.178 | 0 | −386.002 | −384.354 | TRUE |
| NRZ | MRZ | 216.6527 | 0 | 213.7677 | 219.5378 | TRUE |
| NRZ | PCZ | −477.28 | 0 | −478.549 | −476.011 | TRUE |
| MRZ | PCZ | −693.933 | 0 | −696.611 | −691.254 | TRUE |
References
- IPCC. Global Warming of 1.5 °C: IPCC Special Report on Impacts of Global Warming of 1.5 °C above Pre-Industrial Levels in Context of Strengthening Response to Climate Change, Sustainable Development, and Efforts to Eradicate Poverty, 1st ed.; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar] [CrossRef]
- Fang, J.; Yu, G.; Liu, L.; Hu, S.; Chapin, F.S. Climate change, human impacts, and carbon sequestration in China. Proc. Natl. Acad. Sci. USA 2018, 115, 4015–4020. [Google Scholar] [CrossRef] [PubMed]
- Piao, S.; He, Y.; Wang, X.; Chen, F. Estimation of China’s terrestrial ecosystem carbon sink: Methods, progress and prospects. Sci. China Earth Sci. 2022, 65, 641–651. [Google Scholar] [CrossRef]
- Yang, Y.; Shi, Y.; Sun, W.; Chang, J. Terrestrial carbon sinks in China and around the world and their contribution to carbon neutrality. Sci. China Life Sci. 2022, 5, 861–895. [Google Scholar] [CrossRef] [PubMed]
- Friedlingstein, P.; O’Sullivan, M.; Jones, M.W.; Andrew, R.M.; Bakker, D.C.E.; Hauck, J.; Landschützer, P.; Le Quéré, C.; Luijkx, I.T.; Peters, G.P.; et al. Global Carbon Budget 2023. Earth Syst. Sci. Data 2023, 15, 5301–5369. [Google Scholar] [CrossRef]
- Friedlingstein, P.; O’Sullivan, M.; Jones, M.W.; Andrew, R.M.; Gregor, L.; Hauck, J.; Le Quéré, C.; Luijkx, I.T.; Olsen, A.; Peters, G.P.; et al. Global Carbon Budget 2022. Earth Syst. Sci. Data 2022, 14, 4811–4900. [Google Scholar] [CrossRef]
- Friedlingstein, P.; O’Sullivan, M.; Jones, M.W.; Andrew, R.M.; Hauck, J.; Olsen, A.; Peters, G.P.; Peters, W.; Pongratz, J.; Sitch, S.; et al. Global Carbon Budget 2020. Earth Syst. Sci. Data 2020, 12, 3269–3340. [Google Scholar] [CrossRef]
- Zhao, J. A review of forest carbon cycle models on spatiotemporal scales. J. Clean. Prod. 2022, 339, 130692. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, Z.; Liu, Z.; Chi, Y. A three-class carbon pool system for normalizing carbon mapping and accounting in coastal areas. Ecol. Indic. 2024, 158, 111537. [Google Scholar] [CrossRef]
- Zhong, J.; Zhang, X.; Guo, L.; Wang, D.; Miao, C.; Zhang, X. Ongoing CO2 monitoring verify CO2 emissions and sinks in China during 2018–2021. Sci. Bull. 2023, 68, 2467–2476. [Google Scholar] [CrossRef]
- Yao, Y.; Li, Z.; Wang, T.; Chen, A.; Wang, X.; Du, M.; Jia, G.; Li, Y.; Li, H.; Luo, W.; et al. A new estimation of China’s net ecosystem productivity based on eddy covariance measurements and a model tree ensemble approach. Agric. For. Meteorol. 2018, 253–254, 84–93. [Google Scholar] [CrossRef]
- Piao, S.; Fang, J.; Ciais, P.; Peylin, P.; Huang, Y.; Sitch, S.; Wang, T. The carbon balance of terrestrial ecosystems in China. Nature 2009, 458, 1009–1013. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; He, H.; Zhang, L.; Yu, G.; Ren, X.; Lv, Y.; Niu, Z.; Qin, K.; Gao, Y. Increased ecological land and atmospheric CO2 dominate the growth of ecosystem carbon sinks under the regulation of environmental conditions in national key ecological function zones in China. J. Environ. Manag. 2024, 366, 121906. [Google Scholar] [CrossRef] [PubMed]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial ecosystem production: A process model based on global satellite and surface data. Global Biogeochem. Cycles 1993, 7, 811–841. [Google Scholar] [CrossRef]
- Field, C.B.; Randerson, J.T.; Malmström, C.M. Global net primary production: Combining ecology and remote sensing. Remote Sens. Environ. 1995, 51, 74–88. [Google Scholar] [CrossRef]
- Zheng, B.; Wu, S.; Liu, Z.; Wu, H.; Li, Z.; Ye, R.; Zhu, J.; Wan, W. Downscaling estimation of NEP in the ecologically-oriented county based on multi-source remote sensing data. Ecol. Indic. 2024, 160, 111818. [Google Scholar] [CrossRef]
- He, T.; Dai, X.; Li, W.; Zhou, J.; Zhang, J.; Li, C.; Dai, T.; Li, W.; Lu, H.; Ye, Y.; et al. Response of net primary productivity of vegetation to drought: A case study of Qinba Mountainous area, China (2001–2018). Ecol. Indic. 2023, 149, 110148. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Smith, R.B.; De Pauw, E. Hyperspectral Vegetation Indices and Their Relationships with Agricultural Crop Characteristics. Remote Sens. Environ. 2000, 71, 158–182. [Google Scholar] [CrossRef]
- Wang, Q.; Moreno-Martínez, Á.; Muñoz-Marí, J.; Campos-Taberner, M.; Camps-Valls, G. Estimation of vegetation traits with kernel NDVI. ISPRS J. Photogramm. Remote Sens. 2023, 195, 408–417. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Campos-Taberner, M.; Moreno-Martínez, Á.; Sophia, W.; Duveiller, G.; Cescatti, A.; Mahecha, M.D.; Muñoz-Marí, J.; García-Haro, F.J.; Guanter, L.; et al. A unified vegetation index for quantifying the terrestrial biosphere. Sci. Adv. 2021, 7, eabc7447. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, A.; Wang, P.; Hu, C.; Zhang, M. Spatiotemporal Dynamics and Response of Land Surface Temperature and Kernel Normalized Difference Vegetation Index in Yangtze River Economic Belt, China: Multi-Method Analysis. Land 2025, 14, 598. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, J.; Xia, J.; Huang, K. Declining resistance of vegetation productivity to droughts across global biomes. Agric. For. Meteorol. 2023, 340, 109602. [Google Scholar] [CrossRef]
- Pang, J.; Wang, M.; Zhang, H.; Dong, L.; Li, J.; Ding, Y.; Zhu, Z.; Yan, F. Study on the driving mechanism of spatio-temporal non-stationarity of vegetation dynamics in the Taihangshan-Yanshan Region. Ecol. Indic. 2025, 170, 113084. [Google Scholar] [CrossRef]
- Zhao, Y.; Jiang, Q.; Wang, Z. Nonlinear spatiotemporal variability of gross primary production in China’s terrestrial ecosystems under water energy constraints. Environ. Res. 2025, 269, 120919. [Google Scholar] [CrossRef]
- Hasi, M.; Zhang, X.; Niu, G.; Wang, Y.; Geng, Q.; Quan, Q.; Chen, S.; Han, X.; Huang, J. Soil moisture, temperature and nitrogen availability interactively regulate carbon exchange in a meadow steppe ecosystem. Agric. For. Meteorol. 2021, 304–305, 108389. [Google Scholar] [CrossRef]
- Huang, B.; Lu, F.; Sun, B.; Wang, X.; Li, X.; Ouyang, Z.; Yuan, Y. Climate Change and Rising CO2 Amplify the Impact of Land Use/Cover Change on Carbon Budget Differentially Across China. Earths Future 2023, 11, e2022EF003057. [Google Scholar] [CrossRef]
- Lyu, J.; Fu, X.; Lu, C.; Zhang, Y.; Luo, P.; Guo, P.; Huo, A.; Zhou, M. Quantitative assessment of spatiotemporal dynamics in vegetation NPP, NEP and carbon sink capacity in the Weihe River Basin from 2001 to 2020. J. Clean. Prod. 2023, 428, 139384. [Google Scholar] [CrossRef]
- Yang, S.; Li, Y.; Zhao, Y.; Lan, A.; Zhou, C.; Lu, H.; Zhou, L. Changes in vegetation ecosystem carbon sinks and their response to drought in the karst concentration distribution area of Asia. Ecol. Inform. 2024, 84, 102907. [Google Scholar] [CrossRef]
- Huang, Z.; Li, X.; Mao, F.; Huang, L.; Zhao, Y.; Song, M.; Yu, J.; Du, H. Integrating LUCC and forest aging to project and attribute subtropical forest NEP in Zhejiang Province under four SSP-RCP scenarios. Agric. For. Meteorol. 2025, 365, 110462. [Google Scholar] [CrossRef]
- Pang, B.; Liu, Y.; An, R.; Xie, Y.; Tong, Z.; Liu, Y. Spatial and temporal divergence and driving mechanisms of carbon sinks in terrestrial ecosystems in the middle reaches of the Yangtze River urban agglomerations during 2008–2020. Ecol. Indic. 2024, 165, 112205. [Google Scholar] [CrossRef]
- Paulson, J.A.; Tsay, C. Bayesian optimization as a flexible and efficient design framework for sustainable process systems. Curr. Opin. Green Sustain. Chem. 2025, 51, 100983. [Google Scholar] [CrossRef]
- Gunning, D.; Stefik, M.; Choi, J.; Miller, T.; Stumpf, S.; Yang, G.-Z. XAI—Explainable artificial intelligence. Sci. Robot. 2019, 4, eaay7120. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From Local Explanations to Global Understanding with Explainable AI for Trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 4768–4777. [Google Scholar]
- Zhou, C.; Wang, Z.; Wang, X.; Guo, R.; Zhang, Z.; Xiang, X.; Wu, Y. Deciphering the nonlinear and synergistic role of building energy variables in shaping carbon emissions: A LightGBM- SHAP framework in office buildings. Build. Environ. 2024, 266, 112035. [Google Scholar] [CrossRef]
- Yi, Z.; Wu, L. Identification of factors influencing net primary productivity of terrestrial ecosystems based on interpretable machine learning—Evidence from the county-level administrative districts in China. J. Environ. Manag. 2023, 326, 116798. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, D.; Wang, M.; Liu, Z.; Gan, W.; Zhao, Z.; Xue, S.; Müller, B.; Zhou, M.; Ni, X.; et al. Risk-driven composition decoupling analysis for urban flooding prediction in high-density urban areas using Bayesian-Optimized LightGBM. J. Clean. Prod. 2024, 457, 142286. [Google Scholar] [CrossRef]
- Wu, Z.; Qiao, R.; Zhao, S.; Liu, X.; Gao, S.; Liu, Z.; Ao, X.; Zhou, S.; Wang, Z.; Jiang, Q. Nonlinear forces in urban thermal environment using Bayesian optimization-based ensemble learning. Sci. Total Environ. 2022, 838, 156348. [Google Scholar] [CrossRef]
- Kim, H.; Lee, G.; Ahn, H.; Choi, B. Interpretable general thermal comfort model based on physiological data from wearable bio sensors: Light Gradient Boosting Machine (LightGBM) and SHapley Additive exPlanations (SHAP). Build. Environ. 2024, 266, 112127. [Google Scholar] [CrossRef]
- Wong, P.-Y.; Su, H.-J.; Lee, H.-Y.; Chen, Y.-C.; Hsiao, Y.-P.; Huang, J.-W.; Teo, T.-A.; Wu, C.-D.; Spengler, J.D. Using land-use machine learning models to estimate daily NO2 concentration variations in Taiwan. J. Clean. Prod. 2021, 317, 128411. [Google Scholar] [CrossRef]
- Jung, M.; Schwalm, C.; Migliavacca, M.; Walther, S.; Camps-Valls, G.; Koirala, S.; Anthoni, P.; Besnard, S.; Bodesheim, P.; Carvalhais, N.; et al. Scaling carbon fluxes from eddy covariance sites to globe: Synthesis and evaluation of the FLUXCOM approach. Biogeosciences 2020, 17, 1343–1365. [Google Scholar] [CrossRef]
- Shi, H.; Zhang, Y.; Luo, G.; Hellwich, O.; Zhang, W.; Xie, M.; Gao, R.; Kurban, A.; De Maeyer, P.; Van de Voorde, T. Machine learning-based investigation of forest evapotranspiration, net ecosystem productivity, water use efficiency and their climate controls at meteorological station level. J. Hydrol. 2024, 641, 131811. [Google Scholar] [CrossRef]
- Prăvălie, R.; Niculiță, M.; Roșca, B.; Marin, G.; Dumitrașcu, M.; Patriche, C.; Birsan, M.-V.; Nita, I.-A.; Tișcovschi, A.; Sîrodoev, I.; et al. Machine learning-based prediction and assessment of recent dynamics of forest net primary productivity in Romania. J. Environ. Manag. 2023, 334, 117513. [Google Scholar] [CrossRef] [PubMed]
- Xu, X. Multi-Year Data on the Boundaries of Provincial Administrative Divisions in China; Resource Environmental Science Data Registry and Publishing System: Beijing, China, 2023. [Google Scholar] [CrossRef]
- Peng, S.; Ding, Y.; Liu, W.; Li, Z. 1 km monthly temperature and precipitation dataset for China from 1901 to 2017. Earth Syst. Sci. Data 2019, 11, 1931–1946. [Google Scholar] [CrossRef]
- Yang, J.; Huang, X. The 30m annual land cover dataset and its dynamics in China from 1990 to 2019. Earth System Science Data 2021, 13, 3907–3925. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Xu, X. China Population Spatial Distribution Kilometer Grid Dataset; Resource Environmental Science Data Registry and Publishing System: Beijing, China, 2017. [Google Scholar] [CrossRef]
- Xu, X. China GDP Spatial Distribution Kilometer-Grid Dataset; Resource Environmental Science Data Registry and Publishing System: Beijing, China, 2017. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Wang, J.; Li, C.; Gupta, P.; Cribb, M. Ground-level gaseous pollutants (NO2, SO2, and CO) in China: Daily seamless mapping and spatiotemporal variations. Atmos. Chem. Phys. 2023, 23, 1511–1532. [Google Scholar] [CrossRef]
- Wei, J.; Liu, S.; Li, Z.; Liu, C.; Qin, K.; Liu, X.; Pinker, R.T.; Dickerson, R.R.; Lin, J.; Boersma, K.F.; et al. Ground-Level NO2 Surveillance from Space Across China for High Resolution Using Interpretable Spatiotemporally Weighted Artificial Intelligence. Environ. Sci. Technol. 2022, 56, 9988–9998. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Li, K.; Dickerson, R.R.; Pinker, R.T.; Wang, J.; Liu, X.; Sun, L.; Xue, W.; Cribb, M. Full-coverage mapping and spatiotemporal variations of ground-level ozone (O3) pollution from 2013 to 2020 across China. Remote Sens. Environ. 2022, 270, 112775. [Google Scholar] [CrossRef]
- Li, Q.; Shi, G.; Shangguan, W.; Nourani, V.; Li, J.; Li, L.; Huang, F.; Zhang, Y.; Wang, C.; Wang, D.; et al. A 1 km daily soil moisture dataset over China using in situ measurement and machine learning. Earth Syst. Sci. Data 2022, 14, 5267–5286. [Google Scholar] [CrossRef]
- Zhu, W.; Pan, Y.; He, H.; Yu, D.; Hu, H. Simulation of maximum light use efficiency for some typical vegetation types in China. Chin. Sci. Bull. 2006, 51, 457–463. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, R.; Guo, J.; Xu, H.; Miao, Y.; Niu, F.; Gao, Z.; Yang, X.; Xiong, F.; Zhang, J. Analysis of the spatiotemporal dynamics of grassland carbon sinks in Xinjiang via the improved CASA model. Ecol. Indic. 2025, 170, 113062. [Google Scholar] [CrossRef]
- Qiu, S.; Liang, L.; Wang, Q.; Geng, D.; Wu, J.; Wang, S.; Chen, B. Estimation of European Terrestrial Ecosystem NEP Based on an Improved CASA Model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 1244–1255. [Google Scholar] [CrossRef]
- Chen, L.; Li, Z.; Zhang, C.; Fu, X.; Ma, J.; Zhou, M.; Peng, J. Spatiotemporal changes of vegetation in the northern foothills of Qinling Mountains based on kNDVI considering climate time-lag effects and human activities. Environ. Res. 2025, 270, 120959. [Google Scholar] [CrossRef] [PubMed]
- Zhiyong, P.; Hua, O.; Caiping, Z.; Xingliang, X. CO2 processes in an alpine grassland ecosystem on the Tibetan Plateau. J. Geogr. Sci. 2003, 13, 429–437. [Google Scholar] [CrossRef]
- Lu, X.; Chen, Y.; Sun, Y.; Xu, Y.; Xin, Y.; Mo, Y. Spatial and temporal variations of net ecosystem productivity in Xinjiang Autonomous Region, China based on remote sensing. Front. Plant Sci. 2023, 14, 1146388. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30, pp. 3149–3157. [Google Scholar]
- Vu, H.L.; Ng, K.T.W.; Richter, A.; An, C. Analysis of input set characteristics and variances on k-fold cross validation for a Recurrent Neural Network model on waste disposal rate estimation. J. Environ. Manag. 2022, 311, 114869. [Google Scholar] [CrossRef]
- Wang, H.; Wang, X.; Yin, Y.; Deng, X.; Umair, M. Evaluation of urban transportation carbon footprint—Artificial intelligence based solution. Transp. Res. Part D Transp. Environ. 2024, 136, 104406. [Google Scholar] [CrossRef]
- Pei, F.; Li, X.; Liu, X.; Lao, C. Assessing the impacts of droughts on net primary productivity in China. J. Environ. Manag. 2013, 114, 362–371. [Google Scholar] [CrossRef]
- Lou, H.; Shi, X.; Ren, X.; Yang, S.; Cai, M.; Pan, Z.; Zhu, Y.; Feng, D.; Zhou, B. Limited terrestrial carbon sinks and increasing carbon emissions from the hu line spatial pattern perspective in China. Ecol. Indic. 2024, 162, 112035. [Google Scholar] [CrossRef]
- Wei, X.; Yang, J.; Luo, P.; Lin, L.; Lin, K.; Guan, J. Assessment of the variation and influencing factors of vegetation NPP and carbon sink capacity under different natural conditions. Ecol. Indic. 2022, 138, 108834. [Google Scholar] [CrossRef]
- Akinwande, M.O.; Dikko, H.G.; Samson, A. Variance Inflation Factor: As a Condition for the Inclusion of Suppressor Variable(s) in Regression Analysis. Open J. Stat. 2015, 5, 754–767. [Google Scholar] [CrossRef]
- Liang, X.; Guan, Q.; Clarke, K.C.; Liu, S.; Wang, B.; Yao, Y. Understanding the drivers of sustainable land expansion using a patch-generating land use simulation (PLUS) model: A case study in Wuhan, China. Comput. Environ. Urban Syst. 2021, 85, 101569. [Google Scholar] [CrossRef]
- Humphrey, V.; Berg, A.; Ciais, P.; Gentine, P.; Jung, M.; Reichstein, M.; Seneviratne, S.I.; Frankenberg, C. Soil moisture–atmosphere feedback dominates land carbon uptake variability. Nature 2021, 592, 65–69. [Google Scholar] [CrossRef] [PubMed]
- Karimi, H.; Binford, M.; Kleindl, W.; Starr, G.; Murphy, B.A.; Desai, A.R.; Fu, C.-S.; Dietze, M.C.; Staudhammer, C. Drivers of forest productivity in two regions of the United States: Relative impacts of management and environmental variables. J. Environ. Manag. 2025, 374, 124040. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Ren, X.; Wang, J.; He, H. Interannual variability of terrestrial net ecosystem productivity over China: Regional contributions and climate attribution. Environ. Res. Lett. 2019, 14, 014003. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, L.; He, Y.; Cao, S.; Li, H.; Ran, L.; Ding, Y.; Filonchyk, M. LSTM time series NDVI prediction method incorporating climate elements: A case study of Yellow River Basin, China. J. Hydrol. 2024, 629, 130518. [Google Scholar] [CrossRef]
- Shaamala, A.; Yigitcanlar, T.; Nili, A.; Nyandega, D. Strategic tree placement for urban cooling: A novel optimisation approach for desired microclimate outcomes. Urban Clim. 2024, 56, 102084. [Google Scholar] [CrossRef]
- Chang, X.; Xing, Y.; Wang, J.; Yang, H.; Gong, W. Effects of land use and cover change (LUCC) on terrestrial carbon stocks in China between 2000 and 2018. Resour. Conserv. Recycl. 2022, 182, 106333. [Google Scholar] [CrossRef]
- Lu, F.; Hu, H.; Sun, W.; Zhu, J.; Liu, G.; Zhou, W.; Zhang, Q.; Shi, P.; Liu, X.; Wu, X.; et al. Effects of national ecological restoration projects on carbon sequestration in China from 2001 to 2010. Proc. Natl. Acad. Sci. USA 2018, 115, 4039–4044. [Google Scholar] [CrossRef]
- Fernández-Martínez, M.; Peñuelas, J.; Chevallier, F.; Ciais, P.; Obersteiner, M.; Rödenbeck, C.; Sardans, J.; Vicca, S.; Yang, H.; Sitch, S.; et al. Obersteiner Diagnosing destabilization risk in global land carbon sinks. Nature 2023, 615, 848–853. [Google Scholar] [CrossRef]
- Liu, Z.-H.; Weng, S.-S.; Zeng, Z.-L.; Ding, M.-H.; Wang, Y.-Q.; Liang, Z.-H. Hourly land surface temperature retrieval over the Tibetan Plateau using Geo-LightGBM framework: Fusion of Himawari-8 satellite, ERA5 and site observations. Adv. Clim. Change Res. 2024, 15, 623–635. [Google Scholar] [CrossRef]
| Usage in Study | Data Type | Accuracy Indicators | Original Resolution | Dataset Resource | Download Platform |
|---|---|---|---|---|---|
| NEP calculation section | Precipitation | - | 0.008333°, monthly | Peng, et al. [45] | geodata, accessed on 30 August 2023, https://www.geodata.cn/ |
| Temperature | - | 0.008333°, monthly | Peng, et al. [45] | geodata, accessed on 2 September 2023, https://www.geodata.cn/ | |
| NDVI | - | 1 km × 1 km, monthly | MOD 13Q1, MODIS | geodata, accessed on 15 September 2023, https://www.geodata.cn/ | |
| Landcover | - | 30 m, yearly | CLCD [46] | zenodo, accessed on 22 June 2024, https://zenodo.org/records/8176941 | |
| Radiation | - | 10 km × 10 km, hourly | ERA5 LAND [47] | GEE, accessed on 2 July 2024, https://developers.google.com/earth-engine/ | |
| Influencing factors analysis section | Population, POP | - | 1 km × 1 km, yearly | Xu [48] | RESDC, accessed on 3 March 2024, http://www.resdc.cn |
| Gross Domestic Product, GDP | - | 1 km × 1 km, yearly | Xu [49] | RESDC, accessed on 2 March 2024, http://www.resdc.cn | |
| Sulfur Dioxide, SO2 | CV-R2: 0.84, RMSE: 10.07 μg/m3, MAE: 4.68 μg/m3 | 1 km × 1 km, netCDF, yearly | CHAP [50] | geodata, accessed on 30 August 2024, https://www.geodata.cn/ | |
| Nitrogen Dioxide, NO2 | CV-R2: 0.93, RMSE: 4.89 μg/m3, MAE: 3.48 μg/m3 | 1 km × 1 km, netCDF, yearly | CHAP [51] | geodata, accessed on 30 August 2024, https://www.geodata.cn/ | |
| Ozone, O3 | CV-R2: 0.89; RMSE: 15.77 µg/m3; MAE: 10.48 mg/m3 | 1 km × 1 km, netCDF, yearly | Wei, et al. [52] | geodata, accessed on 30 August 2024, https://www.geodata.cn/ | |
| Soil Moisture | ubRMSE: 0.045–0.051, 0.041–0.052; R2: 0.866–0.893, 0.883–0.919 | 1 km × 1 km, daily, netCDF type | SMCI1.0 [53] | The China’s National Tibetan Plateau Data Center, accessed on 31 August 2024. | |
| Enhanced Vegetation Index, EVI | - | 1 km × 1 km, yearly | MOD13Q1, MODIS | RESDC, accessed on 7 November 2024, http://www.resdc.cn | |
| Digital Elevation Model, DEM | resampled based on the latest SRTM V4.1 radar image to the spatial resolution of 1 km | 1 km × 1 km, yearly | original SRTM V4.1 | RESDC, accessed on 7 November 2024, http://www.resdc.cn |
| Hyperparameter | Description | Explanation | Value Range |
|---|---|---|---|
| learning_rate | Learning rate | Controls the magnitude of weight updates for each iteration; a smaller learning rate typically leads to a more stable training process, but requires more iterations. | [0.01, 0.1] |
| feature_fraction | Proportion of features used for each tree | Reduces model variance through random sampling to prevent overfitting. | [0.5, 1] |
| bagging_fraction | Proportion of samples used for building trees | Reduces model variance through random sampling to prevent overfitting. | [0.8, 1] |
| min_child_samples | Minimum number of samples in leaf nodes | Controls the model’s complexity; a higher value results in a simpler model. | [10, 100] |
| num_leaves | Maximum number of leaf nodes | Closely related to the complexity of the tree; increasing the number of leaves enhances the model’s fitting ability, but may also lead to overfitting. | [10, 200] |
| max_depth | Maximum depth of the tree | Limits the depth of the tree to control the model’s complexity and prevent overfitting. If set to −1, there are no limits. | [3, 8] |
| n_estimators | Number of decision trees | Controls the total number of iterations of the model; more trees result in a more complex model. | [100, 1000] |
| min_gain_to_split | Minimum gain to perform a split | Increasing this value can reduce the complexity of the model. | [0, 1] |
| reg_alpha | L1 regularization parameter | Can lead to a sparse model, aiding in feature selection. | [3, 10] |
| reg_lambda | L2 regularization parameter | Reduces overfitting by increasing the penalty term. | [2, 10] |
| Influencing Aspects | Factor | Influencing Mechanism with NEP |
|---|---|---|
| Subsurface properties | SM | Soil moisture is one of the key factors affecting the growth of vegetation. At the same time, it can comprehensively feedback the influence of meteorological environmental conditions like water–heat balance. The vegetation will grow vigorously with suitable SM, while both the photosynthesis efficiency and the diversity of species in the ecosystem reach a high level, resulting a stable ecosystem structure. Based on that, plants can perform the function of carbon sinks better. On the contrary, vegetation growth will be limited due to exposure to water stress, then stomata will be closed, which in turn affects photosynthesis, respiration, and, consequently, the dysfunction of the carbon uptake. |
| EVI | EVI is a commonly used index used to quantify and analyze the growth status and health of vegetation in the remote sensing field. It is calculated by combining the reflectance data of NIR, Red, and Blue bands. Due to the introduction of blue band, it can better resist the influence of atmospheric scattering and soil background and shows great sensitivity to detect the vegetation cover change. Furthermore, it can assess the health and stability of ecosystems. | |
| DEM | DEM is a kind of ground elevation data commonly used in terrain analysis, which can reflect the spatial characteristics and pattern of vegetation distribution as a sign related to the plant growth condition. | |
| Atmosphere components | SO2 | Sulfur dioxide is chemically active and easily interacts with other atmospheric components, causing acid rain and affecting plant growth. Sulfate aerosols are easily generated after meteorological oxidation and other processes, which may have impact on terrestrial carbon sink through the cooling effect and diffusion–radiation fertilization effect. |
| NO2 | Nitrogen dioxide was chosen as a major indicator for nitrogen deposition. Within a certain amount of nitrogen deposition, it is conducive for plant photosynthesis and growth, while excessive nitrogen deposition may lead to an imbalance in the proportion of plant nutrient elements, thus changing the morphology and structure of the plant and increasing its sensitivity to natural stresses. Other issues like affected micro-organisms’ activity and soil acidification will be triggered under the same circumstances. | |
| O3 | Except for the well-known properties of air pollutants, ozone is a type of greenhouse gas with interactive effects in the atmosphere, climate, and ecosystem. Ozone formation originates from the oxidation process of oxygen atoms decomposed by ultraviolet radiation in the stratosphere. It also shows warming effect on atmospheric temperatures in the troposphere. In addition, increased concentrations of carbon dioxide contribute to global warming, which in turn may affect the rate of chemical reactions in the atmosphere and the production of ozone. | |
| Human activity | LUCC | LUCC directly represents structural changes of the terrestrial ecosystem from human activities. |
| POP | POP embodies the pressure of human activities on the ecosystem from the acceptance level. | |
| GDP | GDP, as the core economic indicator of the society system, indirectly reflects the intensity of anthropogenic life and production. Moreover, mutual compromises and trade-offs between financial benefits and environmental protection implements should be considered when conducting economic activities. |
| Variable | VIF | |
|---|---|---|
| 0 | const | 204.0833 |
| 1 | POP | 3.8633 |
| 2 | GDP | 3.1652 |
| 3 | SO2 | 1.6768 |
| 4 | NO2 | 2.7715 |
| 5 | O3 | 2.2426 |
| 6 | LUCC | 1.0023 |
| 7 | SM | 2.4383 |
| 8 | EVI | 2.6518 |
| 9 | DEM | 1.9366 |
| Count | Mean | std | min | 0.25 | 0.5 | 0.75 | max | |
|---|---|---|---|---|---|---|---|---|
| NEP | 9,459,982 | 268.588 | 293.804 | −54.314 | −10.905 | 199.914 | 484.279 | 1828.840 |
| POP | 9,459,982 | 149.391 | 529.074 | 0 | 2 | 20 | 147 | 54,388 |
| GDP | 9,459,982 | 1064.058 | 8958.257 | 0 | 9 | 74 | 531 | 3,100,009 |
| SO2 | 9,459,982 | 11.561 | 2.452 | 2.700 | 9.900 | 11.500 | 13.100 | 44.700 |
| NO2 | 9,459,982 | 17.220 | 6.222 | 4.800 | 13.400 | 15.200 | 18.400 | 63.200 |
| O3 | 9,459,982 | 98.150 | 10.165 | 59.800 | 91.500 | 97.700 | 104.800 | 134.200 |
| LUCC | 9,459,982 | 0.036 | 0.433 | 0 | 0 | 0 | 0 | 9 |
| SM | 9,459,982 | 287.039 | 105.634 | 35.115 | 216.836 | 301.395 | 365.227 | 599.260 |
| EVI | 9,459,982 | 0.395 | 0.251 | −0.087 | 0.126 | 0.446 | 0.614 | 1.000 |
| DEM | 9,459,982 | 1835.057 | 1740.314 | −268 | 431 | 1162 | 3191 | 8405 |
| RMSE (gC/m2/yr) | MAE (gC/m2/yr) | R2 | |
|---|---|---|---|
| Fold1 | 0.2961 | 0.1761 | 0.9124 |
| Fold2 | 0.2960 | 0.1758 | 0.9125 |
| Fold3 | 0.2958 | 0.1757 | 0.9124 |
| Fold4 | 0.2955 | 0.1757 | 0.9126 |
| Fold5 | 0.2965 | 0.1762 | 0.9121 |
| mean | 0.2960 | 0.1759 | 0.9124 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Y.; Wang, X. Analysis of Influencing Factors of Terrestrial Carbon Sinks in China Based on LightGBM Model and Bayesian Optimization Algorithm. Sustainability 2025, 17, 4836. https://doi.org/10.3390/su17114836
Zou Y, Wang X. Analysis of Influencing Factors of Terrestrial Carbon Sinks in China Based on LightGBM Model and Bayesian Optimization Algorithm. Sustainability. 2025; 17(11):4836. https://doi.org/10.3390/su17114836
Chicago/Turabian StyleZou, Yana, and Xiangrong Wang. 2025. "Analysis of Influencing Factors of Terrestrial Carbon Sinks in China Based on LightGBM Model and Bayesian Optimization Algorithm" Sustainability 17, no. 11: 4836. https://doi.org/10.3390/su17114836
APA StyleZou, Y., & Wang, X. (2025). Analysis of Influencing Factors of Terrestrial Carbon Sinks in China Based on LightGBM Model and Bayesian Optimization Algorithm. Sustainability, 17(11), 4836. https://doi.org/10.3390/su17114836





