Optimizing Grid Integration of Power-Generating Ships

Abstract

Power-generating ships (PGSs)are considered some of the largest mobile energy resources. A novel model is proposed in this work to evaluate the integration of PGSs into power grid operations. The proposed model optimally coordinates the ships to enhance grid objectives, providing optimal variables for generation resource scheduling and routing of the ships. Two case studies were used to simulate the system and validate the effectiveness of the proposed model. The proposed model significantly contributes to the field of applied mathematical modeling by developing complex algorithms for scheduling energy generation and addressing the logistical challenges of routing mobile power sources. This dual aspect emphasizes the model’s robustness in handling multidimensional optimization problems inherent in integrating mobile energy resources with static grid systems. Integrating PGSs into power grid operations represents a practical implementation of complex engineering solutions designed to enhance the flexibility and reliability of energy networks. The model not only improves the operational efficiency of the grid but also contributes to the resilience of the energy infrastructure by providing a mobile and adaptable energy resource. This approach exemplifies the potential for innovative engineering solutions to address contemporary challenges in energy distribution, ultimately leading to more sustainable and resilient power systems.

1. Introduction

Electricity is a cornerstone of modern life, and its reliable supply is critical for economic and social development. However, countries with archipelagic geographies, such as Indonesia, which has 13,000 islands, face significant challenges in supplying electricity to offshore regions. The high cost of fuel transportation exacerbates these challenges, prompting innovative solutions such as the deployment of power-generating ships (PGSs). For instance, the Japanese and Indonesian governments are actively exploring PGSs as viable solutions to address these energy supply issues [1].

Nowadays, PGSs are attracting considerable attention as both long-term and short-term energy resources. Their deployment has proven to be economically viable and operationally effective, particularly for island nations and regions surrounded by water [2]. While the concept of using ships as energy resources is not novel, recent advancements in manufacturing, technology, and economies of scale have significantly enhanced their feasibility.

PGSs can be categorized into conventional, hybrid, and electrical types [3]. Conventional PGSs rely on oil or natural gas as fuel, whereas hybrid and electrical models share similarities with electric vehicles. The size and speed of a PGS are critical factors in its deployment [4]. Large ships are typically deployed as static assets for extended periods, while smaller ships are better suited for tactical and operational tasks, ranging from months to mere hours. Notably, a wide range of vessels can generate power on the order of 10 MW, making them technically suitable for deployment as PGSs [5].

The existing port infrastructure is already well-equipped to support S2G technology. Ports are outfitted with high-power electrical systems to supply auxiliary power to moored ships. A typical S2G configuration, as illustrated in Figure 1, includes high-power cables, switchgear, and transformers, which are inherently bidirectional. This facilitates the integration of PGSs into the grid, enabling energy transfer back to the onshore system [6]. Consequently, PGSs can enhance power system security, resilience, and economic efficiency by delivering energy to critical areas, such as regions affected by natural disasters or grid outages. Additionally, PGSs equipped with energy storage systems and solar panels can play a pivotal role in environmental sustainability by capturing excess renewable energy and transmitting it to island grids.

A significant body of literature focuses on SPSs, encompassing studies on bus reconfiguration, protection schemes, and the stability and dynamics of shipboard electrical systems [7]. For instance, one study proposed a model for optimal load shedding in SPSs [8], while another study introduced a contingency-based method for optimal bus reconfiguration [9]. The dynamics of a ship’s primary electrical components have been extensively studied in [10,11]. In one comprehensive review, the authors categorized ship energy system optimization into the following three areas: optimal design (including topology and sizing), optimal control, and combined optimal design and control. However, this review did not address the impact of maritime transportation systems on power system operations, as explained in [7].

Recent research has extended SPS studies to include microgrid-based systems [10]. For example, in one study, the authors proposed a control algorithm for integrating photovoltaic (PV) panels on ships [12], while another study modeled ships with diverse energy resources, such as wind and solar, to design load frequency controllers, as explained in [13]. Additionally, two different studies presented energy management models that incorporate operational security constraints for all-electric ships [14,15]. The development of smart ports was explored in [16]; they emphasize the creation of intelligent hubs, operational optimization, and the integration of energy storage systems and renewable energy sources. However, this study lacked a comprehensive framework for integrating maritime routing with electric scheduling and management systems. Similarly, a proposed two-stage framework for routing and scheduling mobile power sources—such as truck-mounted energy storage and EVs—is presented to enhance the resilience of distribution systems against extreme weather events [17]. While this work demonstrates the potential for post-event recovery, it does not address the practical challenges of PGS deployment and routing.

Despite these advancements, most studies have treated the ship’s internal electrical system as an isolated entity, independent of the main grid. Few studies have explored the interaction between ships and the electric grid, and even fewer have investigated the potential of deploying ships as dedicated PGSs to supply power to the grid. This represents a significant gap in the literature.

In contrast, the mobility of energy resources has been shown to have a notable impact on grid operations, even at smaller scales, as evidenced by the vehicle-to-grid (V2G) concept in EVs. EV literature is replete with models addressing various challenges, such as optimal energy scheduling (charging/discharging) and routing [18,19,20,21,22]. These models often aim to minimize grid costs, EV owner costs, and street congestion [23].

Of particular relevance to this work, the economic feasibility of coordinating EV fleets with grid operations was demonstrated, highlighting the importance of integrating transportation and grid modeling requirements, as detailed in [24]. Similarly, another study proposed a model that leverages railway networks to transport energy between locations, thereby alleviating grid congestion and bottlenecks. Their findings underscore the significant economic savings achievable through such integration, as explained in [25,26].

A Mixed-Integer Programming (MIP) framework is presented to address a maritime inventory routing problem involving the transportation of refinery liquid products across multiple ports using ships with undedicated compartments [27]. However, this work does not integrate maritime routing with electric grid management, highlighting the need for a more comprehensive optimization framework. Our proposed model addresses this gap by providing a holistic solution that combines maritime transportation and power system operations.

To the best of our knowledge, the use of ships as a solution to improve electric grid operations and economics has not been explored in the existing literature. While models for integrating electric vehicles (EVs) into the grid exist, they cannot be directly applied to maritime-based challenges due to fundamental differences between EV models and those for ships, ports, and maritime transportation. Key areas such as ship sailing, routing, and port management require specialized models tailored to the unique characteristics of maritime systems. Therefore, developing a practical and efficient model that integrates PGSs into power system operations is essential. This paper introduces a maritime model designed to effectively coordinate and incorporate PGSs into grid operations. The proposed maritime energy ship coordination (MESC) model offers several benefits:

• Improved economic and operational insights: It enables a more accurate estimation of the economic and operational potential of integrating PGSs into power grids.
• Quantitative and qualitative analysis: It provides measures to assess the impact of maritime transportation system characteristics on power system operations.
• Addressing computational challenges: It tackles previously unexplored challenges, such as the computational complexities of such a model.

This paper is structured as follows: Section 2 describe the problem and the proposed model, outline the solution methodology, as well as present the mathematical formulation. Section 3 and Section 4 include case studies and their solutions, and discuss the computational complexity of the problem. Finally, our conclusions are provided in the Section 5.

2. The Maritime-Based Energy Scheduling and Coordination (MESC) Model

The proposed model integrates an energy generation scheduling problem with a maritime-based energy transportation problem. The objective is to determine the optimal routing and scheduling of PGSs while simultaneously optimizing their hourly power dispatch to ensure efficient grid operation. This optimization must adhere to both the technical and operational constraints imposed by the ships and the power grid.

To model the maritime energy logistics, several real-world maritime transportation considerations were incorporated, as presented in [28,29,30,31]. These considerations include port management constraints, such as berth capacity and operational limits. A discrete-time framework was adopted to appropriately capture the scheduling nature of the problem. Furthermore, a deterministic approach was employed for modeling travel times between ports, ensuring a structured representation of ship movements.

While no specific operational restrictions were imposed on inter-port travel, a key assumption was that PGSs would not be allowed to be in transit at the end of the operational horizon. However, they could be stationed at any designated port upon completion of the scheduling period. The sailing time accounted for all necessary setup and docking activities required to accommodate the ship. Additionally, the power generation characteristics of PGSs were constrained in a manner similar to those of conventional thermal power plants, including ramp rate limitations, minimum up and down times, and mandatory operation upon arrival at a port. Departure and arrival events were subject to one-time fixed costs, while variable sailing costs were dependent on ship type and travel distance. Importantly, PGSs were not mandated to generate power continuously throughout the scheduling horizon; they could remain idle when necessary. However, to reflect realistic port operations, a waiting cost was imposed when ships were moored but not generating power.

On the electrical grid side, generation resource scheduling was modeled, considering power system constraints, leading to the formulation of a Grid-Constrained Unit Commitment (GCUC) problem. This terminology is introduced as an extension of the standard SCUC problem, which is widely used in conventional power systems. In security-constrained unit commitment (SCUC), an independent system operator (ISO) coordinates energy dispatch while adhering to strict security and regulatory requirements, such as those set forth by the Federal Energy Regulatory Commission (FERC) in the United States [32]. In contrast, offshore power grid operations, as considered in this study, are managed by local grid operators under region-specific regulations.

The overall problem was formulated as an MIP model, ensuring the integration of discrete decision variables (e.g., PGS movement and commitment status) with continuous variables (e.g., power dispatch levels). The resulting formulation effectively captures the coupled nature of maritime-based power transportation and grid-constrained generation scheduling, providing a robust framework for optimizing mobile energy resources in power system operations.

2.1. Approaches and Methods for Solving the Maritime Model

The MESC model is highly effective for solving small-scale energy scheduling optimization problems. However, as the complexity of the problem increases—particularly in large-scale energy scheduling scenarios—the computational burden grows significantly. To develop practical and computationally efficient solutions, we explore two alternative solution methods in addition to the original exact approach, where the entire optimization problem is solved in a single step. These alternative methods improve computational efficiency while aligning with real-world operational constraints, ensuring near-optimal results with enhanced scalability and feasibility.

-

Maritime-Integrated Solution Approach (MESC-I:)

The most comprehensive and optimal method for solving the problem is MESC-I, where “I” represents integration. This approach directly addresses the full complexities of unit commitment (UC), economic dispatch (ED), and maritime energy resource allocation without decomposition. While MESC-I guarantees an optimal solution, it may be computationally infeasible for large-scale instances due to the high dimensionality of decision variables and computational burden.

-

Maritime-Sequential Solution Approach (MESC-Sq):

A well-established technique in operations research and combinatorial optimization is to decompose a problem into sequential steps, particularly when it consists of two interdependent yet separable subproblems. In this case, energy scheduling and the maritime energy resource and scheduling problem can be treated as distinct but interconnected components. This motivates the MESC-Sq, which operates as follows:

(a)

Solving the energy scheduling problem (GCUC): The UC problem is solved first, determining the commitment status of generation units and fixing the corresponding binary decision variables [33].

(b)

Solving the complete model: With the binary variables fixed, the ED and maritime energy resource allocation problem is then solved, optimizing the continuous variables.

This decomposition significantly reduces computational complexity by minimizing the number of binary variables handled simultaneously. Although the problem is solved twice instead of once, the computational efficiency gained outweighs the additional iteration, ensuring faster solution times while preserving the integrity of the original optimization problem.

-

Maritime-Integrated Scheduling of Ships as Grid Assets (MESC-IS):

Another alternative approach integrates ships into the energy scheduling framework, allowing the grid operator to manage them as potential energy assets at ports. In this model, ship routing is treated as a separate problem with a longer operational horizon—for instance, a weekly operational schedule where ships are assigned travel days in advance. This hierarchical approach ensures more flexible grid management, aligning maritime operations with energy market dynamics.

We define this strategy as the MESC-IS, where “I” represents integration and “S” signifies the structured scheduling of ship movements within the problem’s time horizon. Unlike MESC-Sq, this approach assumes that ship routing decisions are determined separately within a longer operational horizon, allowing the grid operator to focus on optimizing energy scheduling under predefined ship movement constraints.

The MESC model, along with its alternative solution approaches—MESC-Sq and MESC-IS—provides a scalable, computationally efficient, and practically viable framework for large-scale maritime energy scheduling and optimization. By leveraging decomposition techniques and integrating maritime assets into the grid, these approaches ensure that energy scheduling operations remain both economically and operationally optimal while addressing the challenges of complex real-world energy systems. The selection of an appropriate solution methodology depends on the specific problem scale, operational constraints, and computational resources available, enabling flexible and effective energy management in maritime environments.

Figure 2 provides a visual representation of the proposed solution methodologies.

2.2. MESC Mathematical Formulation-I

This section provides a detailed mathematical formulation of the ship’s routing and coordination optimization problem. The formulation includes defining the objective functions, constraints, and decision variables essential for optimizing the routing and coordination of ships.

2.2.1. Power Ships Objective Function

The total cost of the power ship’s objective function is classified as follows:

$$\begin{array}{c}\hfill Min\sum _{ij\in {\mathcal{P}}^{+}}\sum _{s\in \mathcal{S}}\sum _{t\in \mathcal{T}}{C}_{i,s,t}^E{V}_{i,s,t}^E+C_{i,s,t}^D{V}_{i,s,t}^D+C_{i,s,t}^W{W}_{i,s,t}+C_{ij,s,t}^S{V}_{ij,s,t}^S+F{\left(PS\right)}_{a,b,c}^s+SU{C}_{s}S{U}_{s,t}+SD{C}_{s}S{D}_{s,t}\end{array}$$

(1)

First, $C_{i}j,s,t$ represents the cost of sailing, which encompasses fuel expenses and other costs incurred during travel. The costs associated with ships entering and departing ports are denoted by ${\tilde{C}}_{i,s,t}^D$ and $C_{i,s,t}^E$, respectively. The departure cost, $C_{i}j,s,t^D$, is imposed by port operators to account for the expenses incurred during the ship’s departure.

Additionally, $C_{ij,s,t}^W$ represents the waiting cost imposed on the ship while it waits or moors at ports. When solving the problem as a whole, we consider two approximate costs to accommodate the ships. Whether or not the entering or set problem is solved at once, we consider two approximate costs to accommodate the ships, given by $C_{ij,s,t}^E$ and $C_{ij,s,t}^W$, where the latter denotes the waiting cost imposed on the ship while it waits or moors at the port, referred to in the model as the integrated solution approach.

The remaining part involves the ship’s energy generation system, or MESC-I (referring to integration). For this approach, $F{\left(PS\right)}_{\alpha ,b,c}^s$ is the PS generator quadratic cost course (and is the optimal way to solve the model). A common cost function is used, and $SU{C}_s$ and $SD{C}_s$ are the start-up and shutdown costs, respectively. ${\mathcal{P}}^{+}$ refers to a subset of all feasible routes between the buses.

2.2.2. Power Ships Flow Constraints

A set of constraints should be adopted and reformulated to capture the flow of the power ships [27,28]:

$$\sum _{i\in \mathcal{P}}{V}_{i,s,t}+\sum _{ij\in {\mathcal{P}}^{+}}{V}_{ij,s,t}^S=1\forall s\in \mathcal{S},t\in \mathcal{T}$$

(2)

Constraint (2) ensures that at any given time, a ship is either docked at a port or sailing between ports. This guarantees that the ship’s location is always accounted for within the system, ensuring continuous monitoring and management of its status [27,28].

$$W_{i,s,t}+O_{i,s,t}\ge V_{ij,s,t-1}^S-V_{ij,s,t}^S\forall s\in \mathcal{S},i\in \mathcal{P},t\in \mathcal{T}$$

(3)

Constraint (3) stipulates that a ship can only depart from a port if it was previously operating (generating energy) or waiting at that port. This constraint ensures that the ship’s departure is conditional upon its prior activity at the port, thereby preventing any sudden or unplanned departures that could disrupt the coordination and scheduling of resources.

$$V_{j,s,t}\ge V_{ij,s,t-1}^S-V_{ij,s,t}^S\forall s\in \mathcal{S},j\in \mathcal{P},t\in \mathcal{T}$$

(4)

Constraint (4) mandates that a ship must arrive at its designated destination port. This ensures that the intended travel routes are followed and that the ships reach their planned locations, facilitating accurate scheduling and resource allocation within the grid system.

By incorporating the above constraints, the proposed model ensures a structured and efficient operation of power-generating ships, enhancing the reliability and predictability of their integration into the power grid. This proposed systematic approach helps in maintaining a balanced and coordinated energy distribution network, optimizing the overall grid performance.

2.2.3. Power Ships Arrival–Departure Logic

The power ship’s arrival–departure logic constraints collectively ensure the efficient operation of power ships, enhancing their integration into the power grid. By clearly defining the conditions under which ships can operate, wait, or sail, the model facilitates optimal scheduling and resource allocation, ultimately improving grid performance and stability [27,28].

$$W_{i,s,t}=V_{i,s,t}-O_{i,s,t}\forall i\in \mathcal{P},s\in \mathcal{S},t\in \mathcal{T}$$

(5)

It should be noted that $V_i,s,t$ is unity whenever ship s is located at port i at a given time period t. Thus, a ship can only operate if it is at a port.

Moreover, constraint (5) ensures that a power ship is either operating (generating energy) or waiting at the port. This guarantees that the ship’s status is clearly defined at all times, facilitating efficient port and resource management:

$$O_{i,s,t}\le V_{i,s,t-1}\forall i\in \mathcal{P},s\in \mathcal{S},t\in \mathcal{T}$$

(6)

Constraint (6) ensures that a power ship is either operating (generating energy) or waiting at the port. This guarantees that the ship’s status is clearly defined at all times, facilitating efficient port and resource management.

$$O_{i,s,t}\ge V_{i,s,t}^E\forall i\in \mathcal{P},s\in \mathcal{S},t\in \mathcal{T}$$

(7)

In order for the ship to immediately begin operating upon its arrival at the port, constraint (7) mandates this. This ensures that the ship’s energy generation capabilities are utilized immediately after docking, optimizing the use of its resources and enhancing the overall efficiency of the power grid.

2.2.4. Power Ships Travel Time Constraints

In order to accurately capture the travel times of power ships and ensure the ships are properly docked by the end of their journeys and complete their routes as planned, which is crucial for effective scheduling and coordination in the power system [27,28]. A set of constraints is introduced as follows:

$$\begin{array}{ccccc}\hfill & \sum _{\tau \in \mathrm{\Omega }}{V}_{ij,s,\tau }^S\le T_s^{ij}+(1-V_{s,i,t}^D)M\hfill & \hfill & & \hfill t_1,t_2\in \mathcal{T}\mid t_2>t_1+T_s^{ij},t_1\le \mathrm{\Omega }\le t_2\end{array}$$

(8)

$$\begin{array}{ccccc}\hfill & \sum _{\tau \in \mathrm{\Omega }}{V}_{ij,s,\tau }^S\ge T_s^{ij}-(1-V_{s,i,t}^D)\mathit{M}\hfill & \hfill & & \hfill t_1,t_2\in \mathcal{T}\mid t_2>t_1+T_s^{ij},t_1\le \mathrm{\Omega }\le t_2\end{array}$$

(9)

$$\begin{array}{ccccc}\hfill & V_{s,ij,t}^S+V_{s,ij,t-T_s^{ij}}^S\le 1\forall i,j\in {\mathcal{P}}^{+}\hfill & \hfill & & \hfill s\in \mathcal{S},t\in \mathcal{T}\mid t>T_s^{ij}\end{array}$$

(10)

The travel time required for a ship to move between two ports is introduced in (8) and (9). The $T_s^{ij}$ represents the time needed for ship s to travel from port i to port j. These constraints ensure that the travel duration between ports is accurately incorporated into the model.

Additionally, to ensure that the ship concludes its route at a port within the allocated travel time, (8) is imposed. This constraint uses the big-M method, which uses a large positive number to guarantee that all ships end their routes by docking at a port within the specified time frame. This constraint prevents scenarios in which ships are left in transit without a designated docking port by the end of their scheduled travel period. It should be noted that constraint of (8) ensures that ships cannot enter and depart the port during the same time period.

2.2.5. Ports Operational Constraints

Ports have a limited operating capacity, meaning they can only handle a certain number of ships at a time due to physical space and resource constraints. Additionally, the processes of departure and berthing are labor-intensive and require significant coordination, further limiting the number of ships that can be managed simultaneously [27,28]. To ensure these limits are not violated, the following constraints are modeled:

$$\begin{array}{cc}\hfill & \sum _{s\in \mathcal{S}}{O}_{i,s,t}\le PO{C}_i\forall i\in \mathcal{P},t\in \mathcal{T}\hfill \end{array}$$

(11)

Constraint (11) guarantees that the number of ships operating at a port does not exceed the port’s overall capacity limit, denoted by $PO{C}_i$. This ensures that the port’s facilities and resources are not overstretched, maintaining efficient operations and avoiding potential delays or safety issues. It takes into account the total number of ships that can be actively managed at the port, including those engaged in energy generation or other activities.

$$\begin{array}{cc}& \sum _{t\in \mathcal{T}}{V}_{i,s,t}^D\le PD{C}_i\forall i\in \mathcal{P},s\in \mathcal{S}\hfill \end{array}$$

(12)

Also, in (12), it restricts the number of ships docked at a port to not exceed the port’s berth capacity, denoted by $PD{C}_i$. The berth capacity is the maximum number of ships that can be physically docked and serviced at the port at any given time. By enforcing this limit, the model ensures that the port can manage the logistics of berthing, such as loading, unloading, maintenance, and refueling, without overburdening the available infrastructure and workforce.

2.2.6. Power Ship Generation Unit Constraints

The generation unit constraints for power ships are assumed to be identical to those of thermal generation units, as detailed in the next section. This assumption simplifies the integration of PGSs into the power grid by applying the same operational constraints, which include minimum and maximum generation limits, ramp-up and ramp-down rates, start-up and shutdown logic, and minimum up and down time constraints (operational hours) [27,28].

2.2.7. Binary and Non-Negativity Constraints

By defining binary and non-negativity constraints, the model provides a detailed and accurate representation of the operational statuses of power ships and generators. Constraints (13)–(15) are binary constraints that help optimize the scheduling, coordination, and utilization of these resources [27,28]:

$$\begin{array}{cc}\hfill & O_{i,s,t}\in \{0,1\}\forall i\in \mathcal{P},s\in \mathcal{S},t\in \mathcal{T}\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & W_{i,s,t}\in \{0,1\}\forall i\in \mathcal{P},s\in \mathcal{S},t\in \mathcal{T}\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & S_{i,s,t}\in \{0,1\}\forall i\in \mathcal{P},s\in \mathcal{S},t\in \mathcal{T}\hfill \end{array}$$

(15)

2.3. MESC Mathematical Formulation-II

The mathematical formulation of the energy resource scheduling problem, known as the GCUC problem, is detailed in this section (referred to as MESC-II). The formulation includes the objective function of the GCUC and various constraints, such as generator limits, ramping rates, minimum up and down times, transmission network restrictions, and binary and non-negativity conditions.

2.3.1. Objective Function of GCUC

The objective function aims to minimize the total cost associated with operating the generators over the operational horizon T. It combines the operational costs (quadratic cost functions), start-up costs, and shutdown costs to find the most cost-effective schedule for energy production, taking into account both the operational efficiency and economic considerations of the power generation units [33,34].

$$Min\sum _{g\in \mathcal{G}}\sum _{t\in \mathcal{T}}[F{\left(P\right)}_{a,b,c}^g+SU{C}_{g}S{U}_{g,t}+SD{C}_{g}S{D}_{g,t}]$$

(16)

The term $F{\left(P_{g,t}\right)}_{a,b,c}$ in (16) represents the quadratic cost function associated with generator g at time t. It is given as follows:

$$F{\left(P_{g,t}\right)}_{a,b,c}=a_g·U_{g,t}+b_g·P_{g,t}+c_g·P_{g,t}^2$$

where $U_{g,t}$ is a binary variable that indicates whether generator g is operational at time t, $P_{g,t}$ is the power output of generator g at time t, and $a_g$, $b_g$, and $c_g$ are the coefficients of the quadratic cost function. The term ($SU{C}_g·S{U}_{g,t}$) represents the start-up cost of generator g at time t. $S{U}_{g,t}$ is a binary variable that equals unity if generator g starts up at time t, and $SU{C}_g$ is the cost associated with starting up generator g. Also, the term ($SD{C}_g·S{D}_{g,t}$) represents the shutdown cost of generator g at time t. The $S{D}_{g,t}$ is a binary variable that equals unity if generator g shuts down at time t, and $SD{C}_g$ is the cost associated with shutting down generator g.

2.3.2. Generator Limits Constraints

The generation units are constrained by their capacity limits, ensuring that the power output $P_{g,t}$ of each generator g at each time period t falls within the upper and lower operational limits [34]:

$$U_{g,t}{P}_g^{Min}\le P_{g,t}\le U_{g,t}{P}_g^{Max}\forall g\in \mathcal{G},t\in \mathcal{T}$$

(17)

where in (17), $U_{g,t}$ controls whether the generator contributes to the power generation based on operational conditions and constraints, such as start-up times, maintenance schedules, and economic considerations.

2.3.3. Ramping Rate Constraints

The generation units are constrained by ramping rate limits to ensure smooth transitions in the power output over consecutive time periods, preventing abrupt changes that could destabilize the power grid [34].

$$P_{g,t}-P_{g,t-1}\le R{U}_g\forall g\in \mathcal{G},t\in \mathcal{T}$$

(18)

Constraint (18) limits the increase in the power output of generator g from time $t-1$ to t to $R{U}_g$ while constraint (19) limits the decrease in the power output of generator g from time $t-1$ to t to $R{D}_g$ [34].

$$P_{g,t-1}-P_{g,t}\le R{D}_g\forall g\in \mathcal{G},t\in \mathcal{T}$$

(19)

It should be noted that $R{U}_g$ denotes the maximum ramp-up rate for generator g, indicating how quickly the generator can increase its power output from one time period to the next.

Moreover, the $R{D}_g$ denotes the maximum ramp-down rate for generator g, indicating how quickly the generator can decrease its power output from one time period to the next.

2.3.4. Start-Up and Shutdown Logic

The variables indicating the start-up and shutdown statuses of generation units are governed by the following equations and constraints [33,34]:

$$S{U}_{g,t}-S{D}_{g,t}=U_{g,t}-U_{g,t-1},\forall g\in G,\forall t\in T$$

(20)

Constraint (20) determines the logic for the start-up and shutdown of generator g at time t. It states that the difference between the start-up ($S{U}_{g,t}$) and shutdown ($S{D}_{g,t}$) indicators equals the change in the operational status of the generator from time $t-1$ to t.

$$S{U}_{g,t}+S{D}_{g,t}\le 1,\forall g\in G,\forall t\in T$$

(21)

Also, (21) ensures that generator g cannot start up and shut down simultaneously at the same time t. It restricts $S{U}_{g,t}$ and $S{D}_{g,t}$ to binary variables, ensuring that they are mutually exclusive.

An elaboration on Constraint (21) is as follows:

–

$S{U}_{g,t}-S{D}_{g,t}=1$ indicates that generator g starts up.

–

$S{U}_{g,t}-S{D}_{g,t}=-1$ indicates that generator g shuts down.

–

$S{U}_{g,t}-S{D}_{g,t}=0$ indicates that generator g remains in its current state.

2.3.5. Minimum Up and Down Time Constraints

The minimum up and down times for thermal generation units are enforced to maintain operational stability within the power system.

These constraints also prevent frequent and rapid changes in the operational status of generators, which can lead to inefficient use of resources and increased wear and tear on equipment [33,34]:

$$T_{g,t}^{on}\ge U{T}_g(U_{g,t}-U_{g,t-1})\forall g\in \mathcal{G},t\in \mathcal{T}$$

(22)

Constraint (22) ensures that once generator g is turned on (i.e., $U_{g,t}=1$), it must remain operational for at least $U{T}_g$ consecutive time periods. It should be noted that $U{T}_g$ represents the minimum up time for generator g.

$$T_{g,t}^{off}\ge D{T}_g(U_{g,t-1}-U_{g,t})\forall g\in \mathcal{G},t\in \mathcal{T}$$

(23)

Also, (23) ensures that once generator g is turned off (i.e., $U_{g,t}=0$), it must remain non-operational (or in standby) for at least $D{T}_g$ consecutive time periods. It should be noted that $D{T}_g$ represents the minimum down time for generator g.

2.3.6. Transmission Network Constraints

The electrical transmission network model and operational constraints of the power grid are given below. These adopted constraints ensure that the power system operates within the limits. They manage power flows, maintain balance between generation and demand, restrict demand shedding to acceptable levels, and enforce operational limits on line flows and phase angles [35].

$$F_{l,t}={\displaystyle \frac{{\theta }_{m,t}-{\theta }_{n,t}}{X_l}}\forall l\in \mathcal{L},(m,n)\in {\mathcal{L}}^{+},\forall t\in \mathcal{T}$$

(24)

The power flow $F_{l,t}$ is calculated in (24) in each transmission line l at time period t based on the phase angles ${\theta }_{m,t}$ and ${\theta }_{n,t}$, as well as the line reactance $X_l$.

$$\sum _{l\in {\mathcal{L}}^n}{F}_l+\sum _{g\in {\mathcal{G}}^n}{P}_{g,t}+\sum _{s\in S}P{S}_{s,i,t}-D_{m,t}+SH{D}_{m,t}=0\forall m\in \mathcal{B},t\in \mathcal{T}$$

(25)

The balance between power generation is modeled in (25) (from generator g and power ship $P{S}_s$), consumption (demand $D_{m,t}$), and any load shedding ($SH{D}_{m,t}$) at each bus m and time period t:

$$0\le SH{D}_{m,t}\le D_{m,t},\forall m\in B,\forall t\in T$$

(26)

Constraint (26) restricts the amount of load shedding $SH{D}_{m,t}$ at bus m and time t to be within the available demand $D_{m,t}$:

$$F_l^{MIN}\le F_l\le F_l^{MAX}\forall l\in \mathcal{L}$$

(27)

In (27), $F_{\mathrm{MIN},l}=-F_{\mathrm{MAX},l}$ ensures that the power flow $F_l$ in each line l remains within its operational limits:

$${\theta }^{MIN}\le {\theta }_{m,t}\le {\theta }^{MAX}\forall m\in \mathcal{B},t\in \mathcal{T}$$

(28)

Constraint (28) imposes limits on the phase angle ${\theta }_{m,t}$ at each bus m and time t to maintain stability and operational integrity.

$${\theta }_{Ref,t}=0\forall t\in \mathcal{T}$$

(29)

Constraint (29) sets the reference angle ${\theta }_{\mathrm{Ref},t}$ to zero for all time periods t.

2.3.7. Binary and Non-Negativity Constraints

The binary constraints are critical for accurately modeling the discrete decisions involved in the operation of a system. They ensure that the model adheres to the logical on–off, start-up, and shutdown states necessary for real-world power system operations [33,34]:

$$U_{g,t}\in \{0,1\}\forall g\in \mathcal{G},t\in \mathcal{T}$$

(30)

The binary Constraint (30) ensures that the operational status $U_{g,t}$ of generator g at time t can only be 0 (off) or 1 (on):

$$S{U}_{g,t}\in \{0,1\}\forall g\in \mathcal{G},t\in \mathcal{T}$$

(31)

Constraint (31) ensures that the start-up indicator $S{U}_{g,t}$ for generator g at time t can only be 0 (not starting up) or 1 (starting up):

$$S{D}_{g,t}\in \{0,1\}\forall g\in \mathcal{G},t\in \mathcal{T}$$

(32)

Also, in (32), it ensures that the shutdown indicator $S{D}_{g,t}$ for generator g at time t can only be 0 (not shutting down) or 1 (shutting down).

3. Scenarios and Case Studies

The IEEE 6-bus and the IEEE 118-bus systems were adopted then modified to solve the problem [36]. To avoid the need to modify these systems, we assumed that the three regions or islands, as shown in Figure 3 for the 6-bus system, were electrically interconnected yet isolated from the main grid. This setup allowed us to study the integration of PGSs without altering the existing electrical infrastructure.

In the 6-bus system, ships could access buses 2, 3, 4, and 6. Specifically, buses 2 and 4 were located on the same island but at different geographical locations, while buses 3 and 6 were the accessible buses on the other two islands. This configuration allowed us to explore various routing and operational scenarios for the PGSs.

Case studies II and III were conducted using the 118-bus system under different loading scenarios, as shown in Figure 4 for the 6-bus system. In these cases, buses 7, 10, 70, 75, 87, and 97 were designated as accessible buses or ports. Initially, the ships were positioned at buses 2 and 3 in the 6-bus system and at buses 87 and 97 in the 118-bus system, providing a starting point for the analysis of their movements and operations [36].

As detailed in the model description, PGSs possess thermal generation characteristics and operational limits similar to conventional thermal power plants. For the purpose of this study, data from the IEEE 118-bus case study were adopted to define the generation unit characteristics and operational limits of PGSs. Two ships of different sizes were considered in this work to represent a range of capacities and capabilities. The larger ship, referred to as PS-1, was assigned the same characteristics as generation unit number 30 in the IEEE 118-bus case, while the smaller ship, PS-2, mirrored the characteristics of generation unit number 42. The specific generation characteristics of the two PGSs are provided in

Table 1. Summary of the case study parameters.

Parameter	IEEE 6-Bus System	IEEE 118-Bus System
Number of buses	6	118
Designated ports	Buses 2, 3, 4, 6 (6-Bus)	Buses 7, 10, 70, 75, 87, 97 (118-Bus)
Initial ship locations	Buses 2, 3 (6-Bus)	Buses 87, 97 (118-Bus)
PGS types	PS-1, PS-2
Ship travel times	3 h (PS-1), 2 h (PS-2)
Cost function	Linearized (Piecewise)
Load shedding penalty	USD 1000 per MW
Optimization tool	GAMS 11.0 (CPLEX)
Computational setup	NEOS Server (Intel Xeon, 64 GB RAM)

.

In developing the model, travel times between ports were carefully considered to ensure realistic and practical scheduling constraints. The larger vessel, designated as PS-1, was capable of reaching any of the neighboring ports within a travel duration of 3 h. In contrast, the smaller vessel, PS-2, was more agile and required only 2 h to complete the same journey. These specific travel times were used in the study to reflect the operational characteristics of the two ships. However, it is important to note that the model was designed with flexibility in mind, meaning that different travel times can be easily incorporated into the framework without requiring any modifications to the underlying mathematical formulation. This adaptability ensures that the model remains applicable to a wide range of scenarios involving different vessel speeds, port locations, and logistical constraints. In Section 3.2, a comprehensive breakdown of the various port costs associated with docking and operating ships at different locations is provided, offering a clear view of the economic implications of these maritime operations.

To simplify the optimization process, a key modification was made to the generation cost function. The quadratic term, which typically appears in the generation cost function to capture the nonlinear relationship between power output and cost, was deliberately omitted. The primary motivation behind this decision was to eliminate the necessity of employing a quadratic solver, which can add computational complexity to the optimization process. Instead, the quadratic function was approximated using a piecewise linear function, allowing for a more straightforward and computationally efficient approach while still maintaining a reasonable level of accuracy in cost estimation. As a result, only the linear terms of the cost function were considered in the optimization process, ensuring a more manageable yet effective formulation.

In addition to these considerations, a penalty-based mechanism was introduced to account for any unmet load demand in the system. Specifically, the cost of any unfulfilled power demand at any bus was set at USD 1000 per megawatt (MW). This high penalty value was strategically chosen to incentivize the model to prioritize meeting electricity demand, discouraging scenarios where load requirements remain unmet. This mechanism ensures that the optimization process actively seeks solutions that minimize power shortages, thereby enhancing system reliability and operational efficiency.

For maintaining system stability, specific buses were designated as reference points to provide voltage stability within the network. In case I, bus 1 was chosen as the reference bus, while for cases II and III, bus 10 was assigned this role. The selection of these reference buses was based on their strategic positions within the network, ensuring that a stable voltage reference was maintained under different case study scenarios. By incorporating these methodological refinements, the model achieves a balance between computational efficiency and realistic system representation, making it well-suited for analyzing complex maritime and energy system interactions.

The general algebraic modeling system (GAMS) was employed to build and solve the model. The stopping criteria or termination condition for the solver was set to achieve a zero duality gap, ensuring optimal solutions, with a maximum running time of 2500 s. All case studies were executed on the NEOS server (Madison, WI, USA), utilizing CPLEX as the solver [37,38,39]. The NEOS server specifications include two Intel Xeon X5660 CPUs operating at 2.8 GHz (with a total of 12 cores) and 64 GB of RAM, ensuring sufficient computational power for the complex optimization tasks. Further details about the NEOS server can be found in the provided references.

3.1. Case Studies

To evaluate the effectiveness of the proposed MESC model, case studies were conducted on two benchmark power systems, namely, the IEEE 6-bus and IEEE 118-bus systems. These case studies aimed to analyze the impact of integrating PGSs into power system operations under varying grid conditions, constraints, and loading scenarios. The objective was to determine the economic and operational feasibility of PGSs while examining the influence of ship mobility, port accessibility, and cost optimization strategies.

3.1.1. IEEE 6-Bus System Case Study

The first case study utilized the IEEE 6-bus system, which was adapted to represent three distinct regions or islands. These regions were assumed to be electrically interconnected but isolated from the main power grid. This setup allowed for a detailed examination of PGS integration without requiring modifications to the existing electrical infrastructure. As illustrated in Figure 3, the PGS had access to four specific buses, categorized based on their geographical locations:

• Island 1: Buses 2 and 4, located in different geographical locations but within the same island.
• Island 2: Bus 3, designated as a port for PGSs.
• Island 3: Bus 6, another designated port for PGSs.

This configuration facilitated the evaluation of different ship movement strategies, routing scenarios, and dispatch schedules while maintaining a stable power supply. The ability to assess PGSs under different operational strategies—including stationary and mobile configurations—allowed for a comprehensive understanding of their potential economic impact.

3.1.2. IEEE 118-Bus System Case Study

To assess the scalability and effectiveness of the MESC model in larger networks, a second case study was conducted using the IEEE 118-bus system, as shown in Figure 4 [36]. This system was selected due to its complexity, larger number of buses, and more realistic power grid representation. In this scenario, six buses were designated as accessible ports for PGSs:

• Designated port buses: 7, 10, 70, 75, 87, and 97.
• Initial ship locations: PS-1 and PS-2 were positioned at buses 87 and 97, respectively.

This case study enabled the analysis of ship mobility under two different scenarios, that is, high-demand and low-demand conditions. The primary focus was to examine the cost reductions achieved through different solution approaches while considering real-world constraints, such as load demand variations, port accessibility, and travel times.

The IEEE 118-bus system connection nodes of each generator unit and their accessible buses are given in

Table A1. Connection nodes of each generating unit and their accessible buses.

Generating Unit (GU)	Ships (PS)	Connection Node (n, PS)
GU1	PS-1	n7.1
GU2	PS-1	n10.1
GU3	PS-1	n38.1
GU5	PS-1	n70.1
GU6	PS-1	n75.1
GU7	PS-1	n87.1
GU8	PS-1	n97.1
GU9	PS-2	n7.2
GU10	PS-2	n10.2
GU11	PS-2	n38.2
GU13	PS-2	n70.2
GU14	PS-2	n75.2
GU15	PS-2	n87.2
GU16	PS-2	n97.2

.

3.2. Power-Generating Ship Characteristics and Travel Constraints

PGSs were modeled to exhibit thermal generation characteristics similar to conventional thermal power plants. To ensure realistic operational constraints, data from the IEEE 118-bus system were used to define generation capabilities. Two distinct ship types were considered, as follows:

• PS-1 (large ship): modeled using the characteristics of generation unit 30 in the IEEE 118-bus system.
• PS-2 (small ship): modeled using the characteristics of generation unit 42 in the IEEE 118-bus system.

The mobility of the ships was also factored into the model, accounting for the following realistic travel times:

• PS-1 (large ship): required 3 h to travel between neighboring ports.
• PS-2 (small ship): required 2 h to travel between neighboring ports.

Although these specific travel times were used for this study, the model is flexible and can incorporate different travel times without requiring modifications to the mathematical formulation. Additionally, port-related costs, including docking, operational fees, and waiting costs, were considered to ensure a comprehensive economic evaluation.

The costs associated with the ports for the two power ships are as follows: For PS-1, the waiting cost is USD 55, the entering cost is USD 200, and the berthing cost is USD 235. On the other hand, for PS-2, the waiting cost is USD 20, the entering cost is USD 200, and the berthing cost is USD 210. These costs reflect the operational expenses incurred during the ship’s stay at the ports.

3.3. Cost Function Approximation and Load Shedding Penalty

To simplify the computational complexity of the optimization problem, the quadratic term in the generation cost function was approximated using a piecewise linear function. This approach eliminated the need for a quadratic solver while maintaining a high level of accuracy. As a result, only the linear components of the cost function were retained for optimization.

Furthermore, to enforce demand satisfaction, any unmet load was penalized at a cost of USD 1000 per MW. This penalty ensured that the model prioritized meeting energy demand by effectively dispatching the available generation resources, including PGSs. The reference buses for the power flow calculations were chosen as follows:

• Case I: Bus 1 (Modified IEEE 6-bus system).
• Case II, Case III: Bus 10 (Modified IEEE 118-bus system).

3.4. Computational Setup and Solver Configuration

The optimization model was implemented using the general algebraic modeling system (GAMS) and solved using the CPLEX solver [37,38,39]. The computations were executed on the NEOS server, which provided sufficient processing power for solving the large-scale mixed-integer programming (MIP) problem. The solver was configured as follows: (1) Stopping Criteria: zero duality gap to ensure an optimal solution; (2) Maximum Runtime: 2500 s; (3) Computational Resources: two Intel Xeon X5660 CPUs (2.8 GHz, 12 cores) with 64GB RAM. A summary of the key case study parameters is provided in Table 1.

This structured approach ensures clarity in methodology while enabling a thorough evaluation of the MESC model’s effectiveness across different grid configurations and operational constraints.

4. Results and Discussion

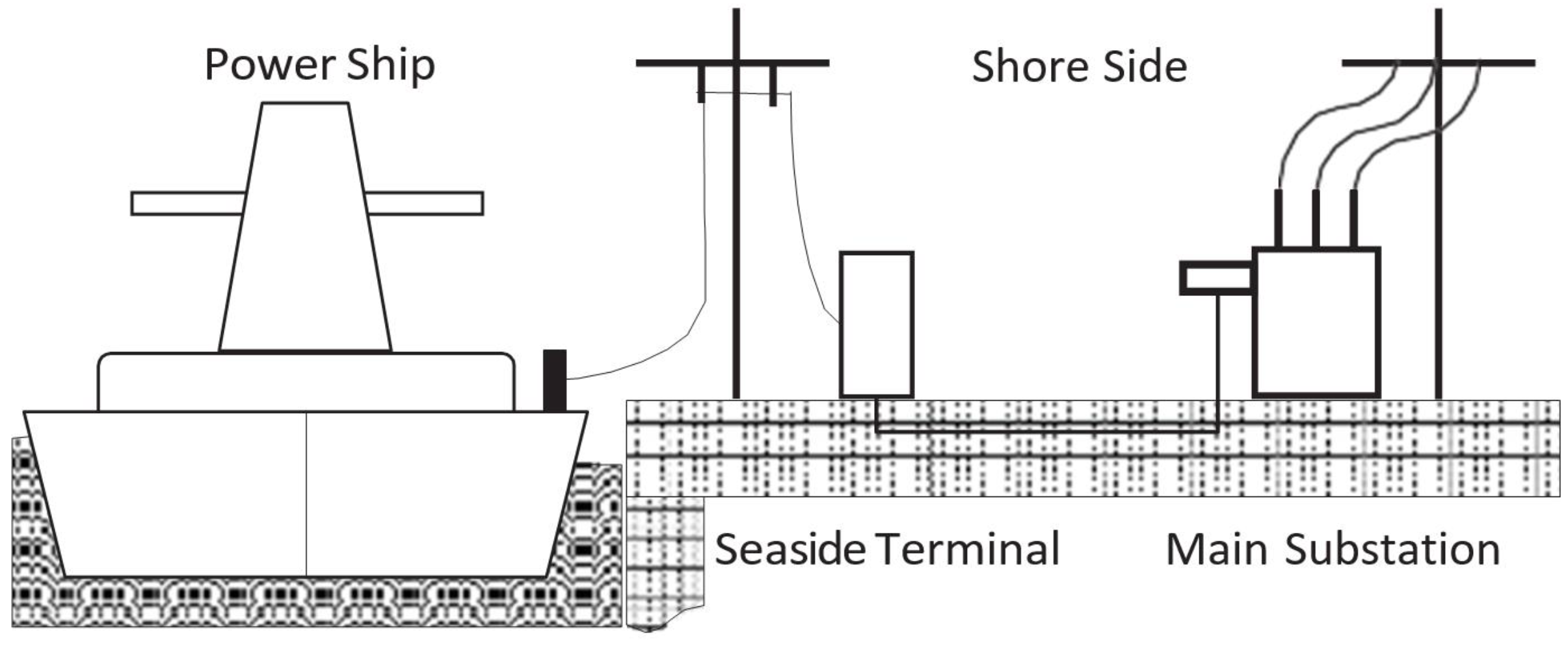
4.1. The 6-Bus Power System Case Study

(1) Case I: First, the energy problem for the three islands was solved without considering the ships. Assuming a deterministic load, the operational cost was USD 87,154.47, and the load demand was fully met. Then, the MESC-IS model was solved with PGSs considered stationary, and the problem was solved again. The new cost for the system was USD 79,133.80. This represented a significant cost reduction even when the ships were considered stationary during the operational horizon. Figure 5 and Figure 6 show the generation units and PGS output in both cases. PS-1 operated for 15 h, from hour 8 to the end of the operational horizon, supplying electricity from the same bus at which it was initially located (bus-3). The potential for further savings was examined by considering the other two solution approaches. To conclude, the integration of PGSs into power grid operations demonstrates significant economic benefits. The model shows that even when considering the ships as stationary assets, a considerable cost reduction of USD 8020.67 was achieved. This indicates that PGSs can effectively reduce operational costs, making them viable options for enhancing grid efficiency. To display the statistical details of the model, solver summary, and solver details,

Table 2. Model statistics.

Category	Value
Blocks of Equations	45
Single Equations	23,737
Blocks of Variables	18
Single Variables	3939
Non-zero Elements	201,231
Discrete Variables	2518

,

Table 3. The model’s ‘solve summary’.

Category	Value
Model	MESC-IS
Objective	z
Type	MIP
Direction	Minimize
Solver	CPLEX
Solver Status	Normal Completion (1)
Model Status	Optimal (1)
Objective Value	79,133.8027
Resource Usage	0.261 s
Iteration Count	1894

and

Table 4. Solver details.

Category	Value
Solver	ILOG CPLEX
Version	12.1.0
GAMS Link	34
License	10 parallel uses (LP, QP, MIP, Barrier)
Parallel Threads	1 of 32
MIP Status	Integer Optimal Solution (101)
Fixed MIP Status	Optimal (1)
Solution Proven	Optimal
Generation Time	0.063 s
Execution Time	0.094 s
Solver Memory Usage	18 Mb

are provided to indicate the complexity of the models.

In Figure 5, under the GCUC case (where no ships were utilized), all conventional power plants were operational, leading to a higher overall cost. This increase in cost was primarily due to the operation of G2, which had the highest generation cost among the units; generation costs are provided in

Table 5. Parameters of PGS generation units.

Ship	a	b	c	SU/SD (USD)	Sailing (USD/h)
PS-1	74.33	15.4708	0.045923	45	250
PS-2	58.810	22.942	0.00977	45	100

.

However, in the MESC-IS case, where ships were considered but remained stationary, G2 was deactivated due to its high cost, thereby reducing overall system expenses. Additionally, G3 decreased its power output, as the ships contributed to electricity generation. Since the ships produced electricity at a lower cost compared to G2 and G3, their integration helped optimize generation dispatch, ultimately improving cost efficiency.

Since the unit status had already been obtained from the solution of the original model (GCUC), the sequential model (MESC-Sq) was considered first. This approach coordinates ship movements only after the UC has been determined. In this case, a total operational cost of USD 85,583.39 was achieved. As the UC decisions were fixed beforehand, the status of all generation units remained unchanged. However, cost reductions were still realized due to the mobility of the ships.

For example, in the MESC-Sq approach, ship PS-1 traveled from bus 2 to bus 4, departing at hour 6 and arriving at hour 10. Since the ships’ ability to operate immediately upon arrival was restricted, power generation started at hour 10. Despite this limitation, cost reductions were observed by allowing the mobility of the ships.

It can be concluded that the application of the maritime-based energy scheduling and coordination–sequential approach, known as MESC-Sq, resulted in significant cost savings. The ability of the PGS to move and supply power to different locations was found to be essential for optimizing the economic operation of the power system.

The most efficient solution was provided by the fully integrated model, known as MESC-I, where all decisions, including generation UC, dispatch, and ship mobility, were optimized simultaneously. This approach led to a total cost of USD 78,463.17, which was significantly lower than the MESC-Sq model.

In this case, ship PS-1 followed the same route from bus 2 to bus 4, but with key differences:

• The ship departed one hour earlier (hour 5) and arrived at hour 9, instead of departing at hour 6.
• This optimized scheduling allowed for a more efficient distribution of energy, which resulted in further cost reductions.

A significant reduction in costs was achieved by optimizing both power generation and ship mobility simultaneously. While the sequential approach (MESC-Sq) already demonstrated benefits from ship mobility, the fully integrated model (MESC-I) provided greater savings by jointly optimizing these factors.

The findings indicate that PGSs remain economically viable even if their daily operational costs (including sailing, entry, and departure costs) are USD 9000 higher. This suggests that the mobility of ships is a valuable asset in the optimization of power system operations.

However, for real-world implementation, larger case studies should be conducted. A more comprehensive analysis, incorporating additional constraints and uncertainties, is expected to provide deeper insights and potentially lead to even greater cost reductions. Future studies should focus on expanding the model to better reflect the actual conditions of energy markets and real-world maritime constraints.

Table 6. Cost analysis of different approaches in all cases.

Case I
GCUC (USD)	MESC-IS (USD)	MESC-Sq (USD)	MESC-I (USD)
87,154.47	79,133.8	85,583.39	78,463.17
Case II
GCUC (USD)	MESC-IS (USD)	MESC-Sq (USD)	MESC-I (USD)
2,052,910.22	2,043,670.36	2,042,213.61	2,037,004.1
Case III
GCUC (USD)	MESC-IS (USD)	MESC-Sq (USD)	MESC-I (USD)
2,011,241.41	2,005,790.52	2,007,276.61	2,004,269.73

summarizes the cost comparisons between the different approaches.

4.2. 118-Bus Power System Case Study

The adopted 118-bus power system was used to simulate a larger case using the same ships from the previously studied case. Two different loading scenarios were considered, classified as high and low loading levels. The high loading level had an hourly average load of 1366.83 MW, while the low loading had an average load of 1354.04 MW.

(2) Case II: In this case, the GCUC was solved for the system, providing a total cost of USD 2,052,910.22 with 4.276 MW load shedding. Similar to the previous case, three solution approaches were obtained. Table 6 shows the total cost of the three approaches.

After that, MESC-IS was modeled, resulting in 3.86 MW shedding, a slight improvement compared to the original case. The cost reduction achieved through this approach highlights the benefit of integrating power ships even without their mobility being fully utilized.

The solutions obtained using the MESC-I and MESC-Sq approaches resulted in no load shedding and achieved significant cost reductions of USD 10,696.6 and USD 15,906.12, respectively. The MESC-I (fully integrated) approach proved to be the most effective in cost savings. The mobility of the ships contributed more to cost savings in this case compared to case I. As shown in Figure 7, PS-1 made one trip and generated 1570 MWh during the operational horizon. The ship traveled from its initial port to port 7. Additionally, the MESC-I suggested the deployment of PS-2, which made more trips than PS-1. Specifically, PS-2 sailed from bus 97 at the beginning of hour 3, arriving at bus 10 at hour 5. It operated for only one hour and waited for 4 h before sailing to bus 7. Table 6 shows the complete coordination plan of the ships for the MESC-I and MESC-Sq approaches.

(3) Case III: To further illustrate the potential of integrating the PGS, a different load demand was considered in this case. The GCUC resulted in a total cost of USD 2,011,241.41 with no load shedding.

First, the integrated solution (MESC-I) approach resulted in system savings of USD 6971.68. Both ships sailed once during the operational horizon. As shown in Figure 8, the total energy produced by the ships during this period was 1860.7 MWh. The total operational cost of the ships was USD 35,328.263.

The sequential solution (MESC-Sq) approach provided USD 3964.8 in savings. The total operational cost of the ships in this approach was USD 27,605.086. In this case, the stationary solution approach (MESC-IS) resulted in a better solution than the sequential one. The MESC-IS total cost was USD 2,005,790.52. Table 6 shows the costs of all solution approaches. Despite the relatively low demand and no shedding penalties, the ships were still able to show potential for economic improvements.

The generation scheduling problem has long been recognized as computationally challenging to solve in real-time. The generation scheduling problem—which includes UC and ED—is classified as a non-deterministic polynomial-time hardness (NP-hard) problem. This means that as the problem size increases, the time required to solve it grows exponentially, making it computationally infeasible to obtain an optimal solution for large-scale systems in real-time. Therefore, it is critical to test the computational performance of any changes made to the problem. A significant computational burden was observed with the integrated solution approach, MESC-I. A running time of 2500 s was considered for all case studies. In case II, the solver achieved a global optimum solution for GCUC in 327.04 s and 1,059,585 iterations. However, in the integrated approach, MESC-I, the solver was unable to reach the global optimum and terminated after 2500 s and 2,449,504 iterations. In case III, GCUC required 410.6 s and 1,007,838 iterations, while MESC-IS and MESC-Sq needed just 61.51 s and 24 s, respectively, to reach a global optimum solution. Similar to the previous case, the MESC-I approach could not achieve the global optimum within the allotted 2500 s, which is more than 104 times the time required for the sequential approach to find a solution. Although the results of the integrated approach are unsatisfactory, they provide insight into the exponential growth in the complexity of the problem.

Table 7. Results for case II and case III.

	Case II								Case III
	Integrated				Sequential				Integrated				Sequential
	L		P		L		P		L		P		L		P
Time	PS-1	PS-2	PS-1	PS-2	PS-1	PS-2	PS-1	PS-2	PS-1	PS-2	PS-1	PS-2	PS-1	PS-2	PS-1	PS-2
1	87	97	30	0	87	97	30	0	87	97	30	0	87	97	30	0
2	|	97	0	0	|	97	0	0	|	97	0	0	|	97	0	0
3	|	|	0	0	|	97	0	0	|	97	0	0	|	97	0	0
4	|	|	0	0	|	97	0	0	|	97	0	0	|	97	0	0
5	7	10	30	20	7	97	30	0	7	97	30	0	7	97	30	0
6	7	10	70	0	7	97	70	0	7	97	70	0	7	97	70	0
7	7	10	80	0	7	97	80	0	7	97	80	0	7	97	80	0
8	7	10	80	0	7	97	80	0	7	97	80	0	7	97	80	0
9	7	10	80	0	7	97	80	0	7	97	80	0	7	97	80	0
10	7	|	80	0	7	97	80	0	7	|	80	0	7	97	80	0
11	7	|	80	0	7	97	80	0	7	|	80	0	7	97	80	0
12	7	7	80	20	7	97	80	0	7	7	80	20	7	97	80	0
13	7	7	80	45	7	97	80	0	7	7	80	45	7	97	80	0
14	7	7	80	50	7	97	80	0	7	7	80	50	7	97	80	0
15	7	7	80	25	7	97	80	0	7	7	80	20	7	97	80	0
16	7	7	80	50	7	97	80	0	7	7	80	30.67	7	97	80	0
17	7	7	80	20	7	97	80	0	7	7	80	20	7	97	80	0
18	7	7	80	45	7	97	80	0	7	7	80	20	7	97	80	0
19	7	7	80	25	7	97	80	0	7	7	80	20	7	97	80	0
20	7	7	80	50	7	97	80	0	7	7	80	45	7	97	80	0
21	7	7	80	20	7	97	80	0	7	7	80	20	7	97	80	0
22	7	7	80	0	7	97	80	0	7	7	80	0	7	97	80	0
23	7	7	80	0	7	97	80	0	7	7	80	0	7	97	80	0
24	7	7	80	0	7	97	80	0	7	7	80	0	7	97	80	0
Total (MWh)	1940				1570				1860.7				1570
PGS Total cost (USD)	37,850.536				27,605.086				35,328.263				27,605.086
System Saving (USD)	15,906.12				10,696.6				6971.68				3964.8

presents a comparative analysis of Case II and Case III in terms of energy output, PGS total cost, and system savings. Case II consistently demonstrates higher energy production and incurs greater generation costs, yet it also delivers significantly higher system savings, indicating a positive return on investment. In contrast, Case III shows reduced energy generation and lower costs, but with notably diminished savings. The results reveal a positive correlation between energy output and economic benefit, suggesting that increased energy production—despite its higher cost—leads to proportionally greater system savings.

The approximate approaches performed computationally well, as shown in

Table 8. Cost analysis and computational complexity of different approaches in cases II and III.

	Objective (USD)	CPLEX (s)	Iteration	R-Gap %
	Case II
GCUC	2,052,910.22	327.04	1,059,585	0
MESC-IS	2,043,670.36	524.52	745,422	0
MESC-Sq	2,042,213.61	50.82	89,206	0
MESC-I	2,037,004.1	2500	2,449,504	0.000163
	Case III
GCUC	2,011,241.41	410.62	1,007,838	0
MESC-IS	2,005,790.52	61.51	118,964	0
MESC-Sq	2,007,276.61	24.12	27,709	0
MESC-I	2,004,269.73	2500	1,814,246	0.000076

, indicating potential time-accuracy trade-offs between different solution approaches. It is important to note that the MESC-Sq solution time in Table 8 only includes the maritime-based problem. The first sub-problem must be solved even without the existence of PGS. The total or wall time can be obtained with a high degree of accuracy by adding the times together. Since the availability of the energy scheduling solution is assumed, the two times are provided independently.

Despite this complexity, the work marks a pioneering effort in exploring the incorporation of maritime energy transportation into power systems. There is substantial potential for future research to enhance the model’s computational performance. By introducing valid inequalities and cuts, the solution process can be made more efficient, reducing the computational burden. These techniques can streamline the problem-solving process, making it feasible to handle larger and more complex scenarios without compromising accuracy or efficiency. The development and implementation of such improvements could significantly advance the practical application of this innovative integration model.

Table 8 presents a comparative analysis of four computational approaches—GCUC, MESC-IS, MESC-Sq, and MESC-I—based on four key performance indicators: objective function, computation time, number of iterations, and relative gap percentage (R-Gap%). The MESC-I with a cost value of 2,004,269.73, making it the most effective in terms of solution quality. On the other hand, GCUC yields the highest objective value at USD 2,011,241.41, indicating it is the least effective. The slight variations in objective values across the methods suggest that all approaches provide relatively similar solutions, albeit with minor cost differences.

When it comes to computation time, the results show significant variation. MESC-Sq is the fastest, completing the solution in just 24.12 s, while MESC-I takes the longest at 2500 s. MESC-IS also performs efficiently, solving the problem in 61.51 s, whereas GCUC requires 410.62 s, making it significantly slower than the MESC-based approaches. The number of iterations further highlights the efficiency of each method. MESC-Sq stands out with only 27,709 iterations, indicating a highly efficient convergence process. In contrast, MESC-I requires 1,814,246 iterations, which aligns with its high computational time. GCUC has a high iteration count of 1,007,838, while MESC-IS reduces this number significantly to 118,964, demonstrating its efficiency.

The relative gap (R-Gap%) measures the difference between the computed objective value and the optimal solution, with lower values indicating better accuracy. All methods achieve near-optimal solutions, with R-Gap values close to zero. MESC-I exhibits a slight gap of 0.000076, but this is negligible in practical applications. The results demonstrate a clear trade-off between speed and solution quality. MESC-Sq is the fastest and requires the fewest iterations, but achieves a slightly higher objective value compared to MESC-I. Conversely, MESC-I achieves the best objective value but at the cost of significantly higher computational time and iterations. MESC-IS strikes a balance, offering near-optimal performance with reasonable computational effort, while GCUC is the least efficient in terms of both computational time and iteration count.

In conclusion, MESC-Sq emerges as the most efficient method for this problem, offering a strong balance between computational speed, iteration count, and solution quality. MESC-IS is a viable alternative, providing a good compromise between efficiency and performance. While MESC-I achieves the best solution quality, its high computational cost makes it less practical for large-scale or time-sensitive applications. GCUC, on the other hand, is the least effective and may not be suitable for problems requiring high efficiency or accuracy. The choice of method ultimately depends on the specific requirements of the problem: if speed is critical, MESC-Sq is the best choice; if solution quality is the top priority, MESC-I is preferable despite its computational cost; and MESC-IS offers a balanced middle ground.

5. Conclusions

In this work, a novel model was introduced to integrate maritime energy transportation into power system operations. This model effectively coordinated power-generating ships with the electric grid, showcasing potential economic savings across various scenarios.

The fully integrated model achieved an optimal solution with substantial cost savings compared to initial solutions, demonstrating the economic benefits of utilizing mobile PGS. Effective mobility utilization of these ships was essential in optimizing economic operations, as further emphasized by the successful implementation of both integrated and sequential approaches. The flexibility of the proposed model allowed for adjustments without altering the mathematical formulation, highlighting the model’s adaptability. Ultimately, the novel model played a crucial role in optimizing costs and ensuring a reliable power supply.

Despite its effectiveness, the study is limited by deterministic assumptions, which may not fully capture real-world operational uncertainties. Future research should incorporate stochastic modeling and uncertainty analysis. Additionally, expanding the model to consider broader environmental and regulatory constraints would provide a more comprehensive framework for practical implementation.