1. Introduction
In light of the energy crisis of the new century, rethinking power generation in power systems is becoming increasingly popular. Traditional thermal power plants mainly rely on fossil fuels to generate electricity. The substantive consumption of fossil fuels and the subsequent emissions have been identified as one of the main contributors to climate change and the deterioration in air quality, particularly, in the midst of the energy crisis in 2022. To address these global challenges, the large scale roll-outs of renewable energy and electric vehicles are viewed as important measures. The integration of renewable energy and electric vehicles into the grid can reduce both operation costs and capital costs in building more power system assets, while effectively reducing greenhouse gas emissions. It is estimated that by 2030, carbon dioxide emissions will be reduced by up to 77.6 million tons and environmental costs will be reduced by up to USD 18.945 billion [
1]. However, due to the uncertainty in and volatility of renewable energy, balancing supply and demand in the power grid become more difficult, and brings significant challenges to the unit scheduling, power grid control, and market operation of power systems [
2]. Therefore, it is of great significance to study the impact of renewable energy and electric vehicles on a power grid to reduce the operating costs while maintaining its stable operation.
The unit commitment (UC) problem is an NP-hard combinatorial optimization problem of high dimension and strong nonlinearity subject to multiple constraints. Reasonable allocation of the generated power of the unit can bring forward tangible economic benefits to the power system and ensure its safe and stable operation. The unit commitment problem was first discussed in 1966. Under the premise of stable operation of the power generation units, the start-stop planning of the unit and its output power are allocated in unit time, to minimize the operating cost of the whole system. The traditional thermal power unit model has been widely studied. Generally, approaches to consider the integration of intermittent renewable energy in the UC problem can be divided into two types [
3]. The first approach is to develop a stochastic model for renewable generation units, while the second approach is to formulate a deterministic UC problem.
Among these approaches, the deterministic method is more commonly used, and a range of techniques have been proposed to evaluate the impact of EVs or RE on the power system UC problem. In a 2010 study [
4], a model considering only one electric vehicle (EV) charging mode was incorporated, which can significantly reduce both the cost and emissions of the unit. A 2014 study [
5] designed a UC model with electric vehicles as flexible loads and the cost is increased by charging electric vehicles. These approaches are useful for studying the impact of electric vehicles on the grid, but they only consider one operating mode of electric vehicles. Ehsan et al. [
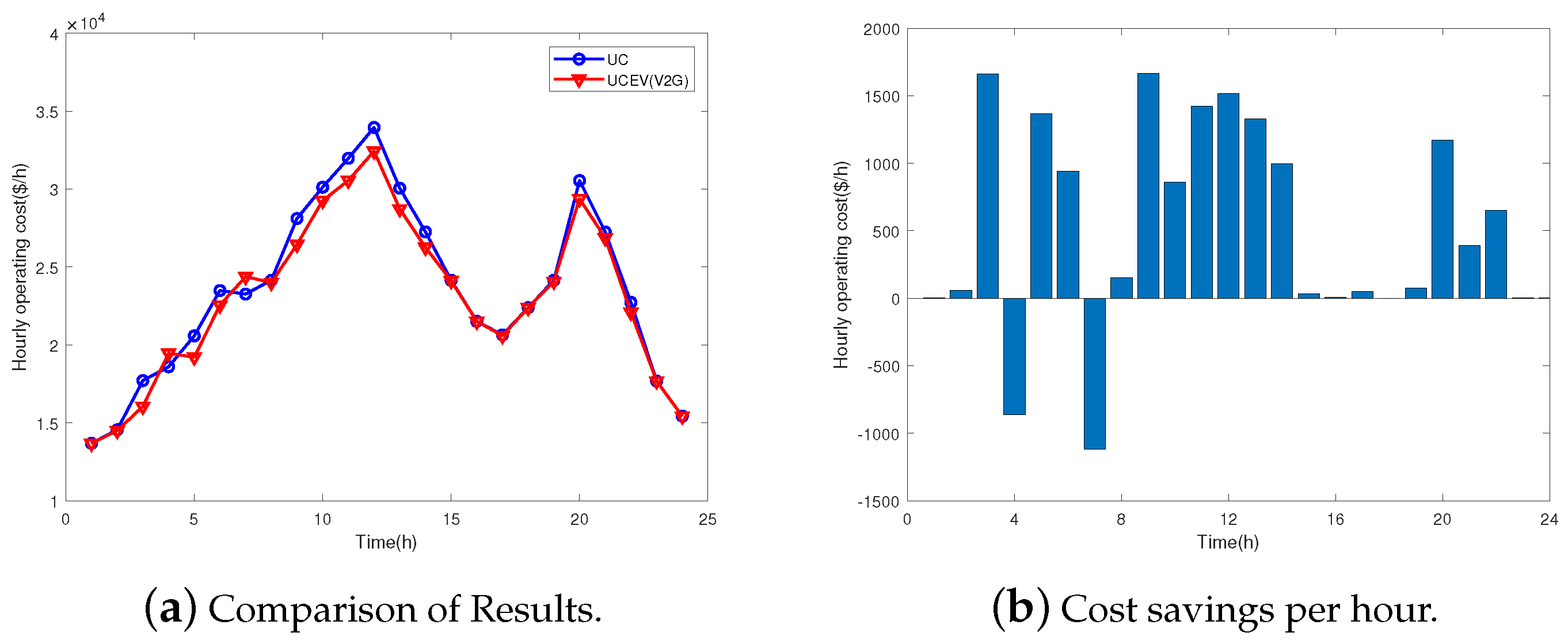
6] evaluated the V2G and G2V modes in the UC of the power system. The simulation results show that both the cost and spinning reserve can be reduced but it does not consider renewable energy. A 2012 study [
7] proposed a UC with a spinning reserve for a microgrid with solar and wind energy storage and considered the prediction error of wind speed and solar radiation of the system. However, the impact of EVs on the power system is not analyzed. Two further studies [
2,
8] designed three models for UC, EV, and RE, respectively, in the UC problem, but the approach mainly considered the influence of RE and EVs on the system, while the prediction error of RE on the spinning reserve requirement was not discussed. To produce reliable and cost-effective UC, it is vital to consider the influence of EV integration and RE intermittency on the UC problem of the power systems. A schematic diagram to illustrate the UC considering electric vehicles and renewable energy is given in
Figure 1.
As a conventional NP-hard problem, the UC problem has the characteristics of strong nonlinearity, large scale, mixed integer, and high dimension. Some traditional mathematical methods were first used to solve this problem, such as Dynamic Programming (DP), Integer Programming (IP), Mixed-integer Programming (MIP), Branch and Bound Methods (BBM), and Lagrangian Relaxation (LR) [
9]. Although these traditional methods can achieve good results for a limited number of problems, as the model complexity and system scale increases, traditional mathematical methods may encounter the dimensionality problem and the quality and reliability of the resulting solutions may be greatly reduced.
Intelligent optimization algorithms emerged in the 1980s and among the first was the Genetic Algorithm (GA) proposed by Holland based on Darwin’s “survival of the fittest” biological evolution law. Other popular methods have also been proposed in the last few decades. For example, the simulated annealing algorithm proposed by Kirkpatrick et al. based on the principle of slow annealing of solids in physics, Particle Swarm Optimization (PSO) proposed by Kennedy and Eberhart, which was inspired by observing the phenomenon of bird foraging. Similarly, Storn and Price proposed the Differential Algorithm (DE), which is a probability-based algorithm, by simulating the mutual cooperation and competition between individuals. The Ant Colony Algorithm (ACO) proposed by Dorigo and Stützle, based on the process of finding the optimal path when ants carry food, is a probabilistic algorithm for finding the shortest path. The Shuffled Frog Leaping Algorithm (SFLA) proposed by Eusuff and Lansey imitates the behavior of frogs interacting with each other during foraging, while Basturk and Karaboga proposed an artificial bee colony algorithm by observing and imitating the behavior of bees. In recent years, with the further development of computer technology and artificial intelligence, many new intelligent optimization algorithms have been introduced. For example, the Harmony Search Algorithm (HS) [
10], Teaching-and-Learning-based Optimization (TLBO) [
11], and the Quantum-inspired Algorithm (QEA) [
12]. These heuristic algorithms can be more flexible and more adaptive in solving UC problems; however, although many methods have been proposed to solve the UC problem, the quality and efficiency of solutions for high-dimensional UC problems still have much room for improvement.
The Covariance Matrix Adaption Evolution Strategy (CMAES) is an evolutionary method proposed by Hansen et al. that continuously adjusts the covariance matrix of its multidimensional normal distribution during evolution [
13]. The CMAES algorithm mainly uses a rank 1 update to ensure contemporary information, and a rank
update to ensure the relationship between generations. It avoids falling into local optima unlike other algorithms such as the Genetic Algorithm (GA) and Particle Swarm Optimization (PSO), and has the advantages of strong robustness and optimization capability. Improved CMAES methods have also been proposed. For example, an orthogonal CMAES [
14] was proposed to incorporate a quantitative orthogonal design to address the high-dimensional premature convergence problem of the conventional CMAES algorithm. In order to solve large-scale real-valued optimization problems, the partition strategy was also introduced to the CMAES algorithm in a 2012 study [
15].
The CMAES algorithm has been widely used in various fields, such as the design of materials, electrical systems, control engineering, and scientific computing. For example, Manoharan used the CMAES algorithm to solve the dynamic economic load problem [
16]. Salman et al. proposed to combine the CMAES and DE algorithms for the optimal design of reinforced concrete structures [
17]. Jia proposed the BESS Covariance Matrix Adaptation Evolution Strategy (CMA-ES) dispatch algorithm to optimal Hybrid Renewable Energy Systems. Jia proposed a CMAES algorithm for global optimization of large-scale overlapping problems [
18]. Rezk et al. used the CAMES algorithm to design horn ripples [
19]. Raufet al. used the CMAES algorithm to determine the parameters of a traditional wind-power optimization algorithm [
20].
It should be noted that the CMAES algorithm has been mainly used for solving continuous optimization problem, while little has been done for discrete systems. Aiming to address the limitations of CMAES, this paper proposes a new Binary Covariance Matrix Adaption Evolution Strategy (BCMAES) algorithm, which is used to solve the binary optimization problem, and applies the algorithm to solve the UC problem, which is often a nonlinear large-scale mixed integer optimization problem.
The highlights and the main contributions of this paper are summarized below.
A new discrete mapping operator is designed and compared with eight popular mapping operators. This new operator allows the CMAES to become applicable to solving discrete optimization problems;
The discrete CMAES method is applied to large-scale UC problems for the first time;
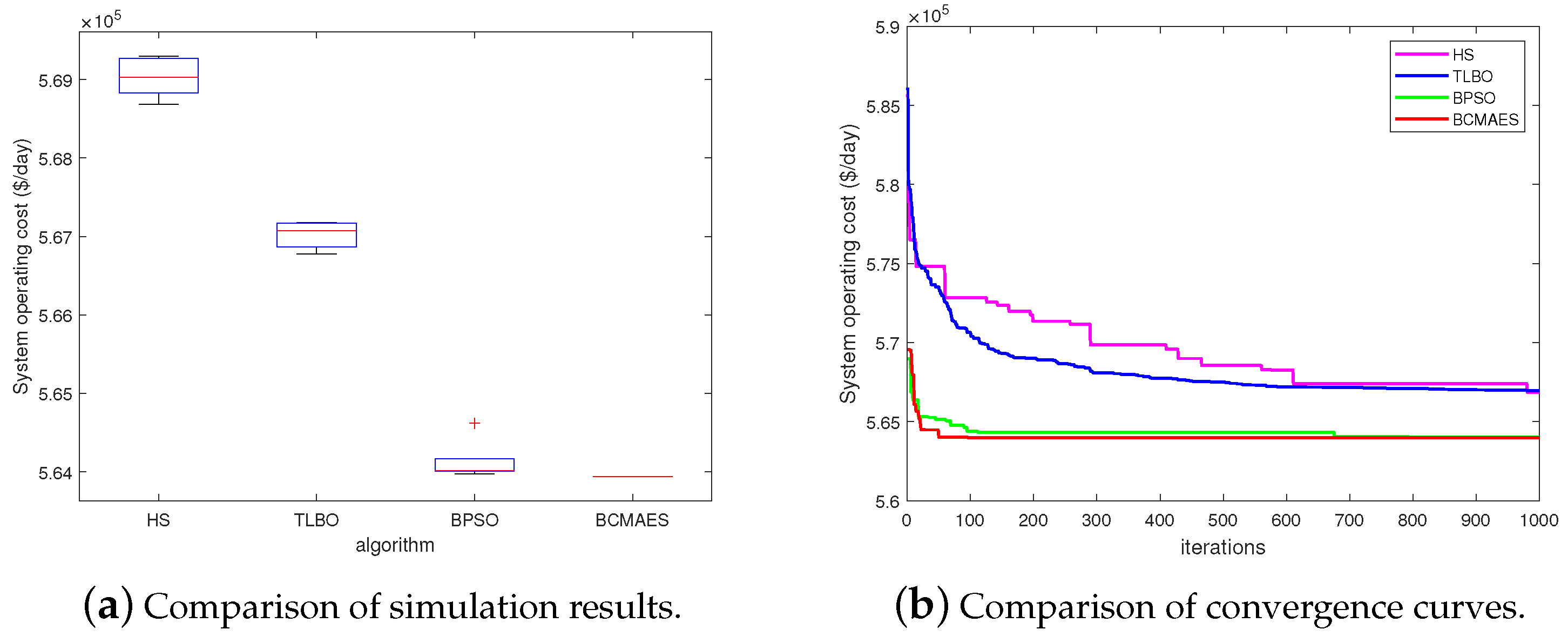
Two different test systems consisting of 10- and 54-unit power networks are tested in order to evaluate the searching capability of the proposed algorithm in test cases of different scales, achieving operating costs reduction of 1.92% and 1.13%, respectively;
The elite reservation strategy and restart strategy are adopted to strengthen the global search capability of the algorithm and achieve population adaptation.
The remainder of the paper is organized as follows:
Section 2 presents the formulation of the unit commitment problem, while the proposed Binary Covariance Matrix Adaption Evolution Strategy (BCMAES) algorithm is presented in
Section 3 and its implementation for a UC problem is presented in
Section 4. The numerical results and analysis are given in
Section 5. Finally,
Section 6 concludes the paper.
4. Implementation of BCMAES in the UC Problem
When solving the fundamental UC problem, UCEV problem, and UCEVR problem based on BCMAES, because EVs and RE are added to the system, there are some differences in the expression of the solution, the specific implementation of the algorithm, and the corresponding constraint processing methods. This paper will detail the specific implementation steps and constraint processing methods of BCMAES in different models.
4.1. Algorithm Procedure
The algorithm implementation steps of BCMAES in unit commitment problem are given as follows:
Step 1: Initialize the parameters. Initialize the parameters of BCMAES and the parameters of units, electric vehicles, and renewable energy;
Step 2: Population initialization. The initial search point of the BCMAES algorithm is randomly generated, and the electric vehicle’s state, output power, and initial output are randomly generated according to the initial variables;
Step 3: Adjust the constraints. Firstly, the initial power of the electric vehicle is adjusted to meet the limitations on the number of electric vehicles, the upper and lower limits of power, and the balance of charge and discharge. Then the minimum start-stop planning and spinning reserve of the whole unit system are adjusted. Through this approach, the start-stop state of the unit can be determined;
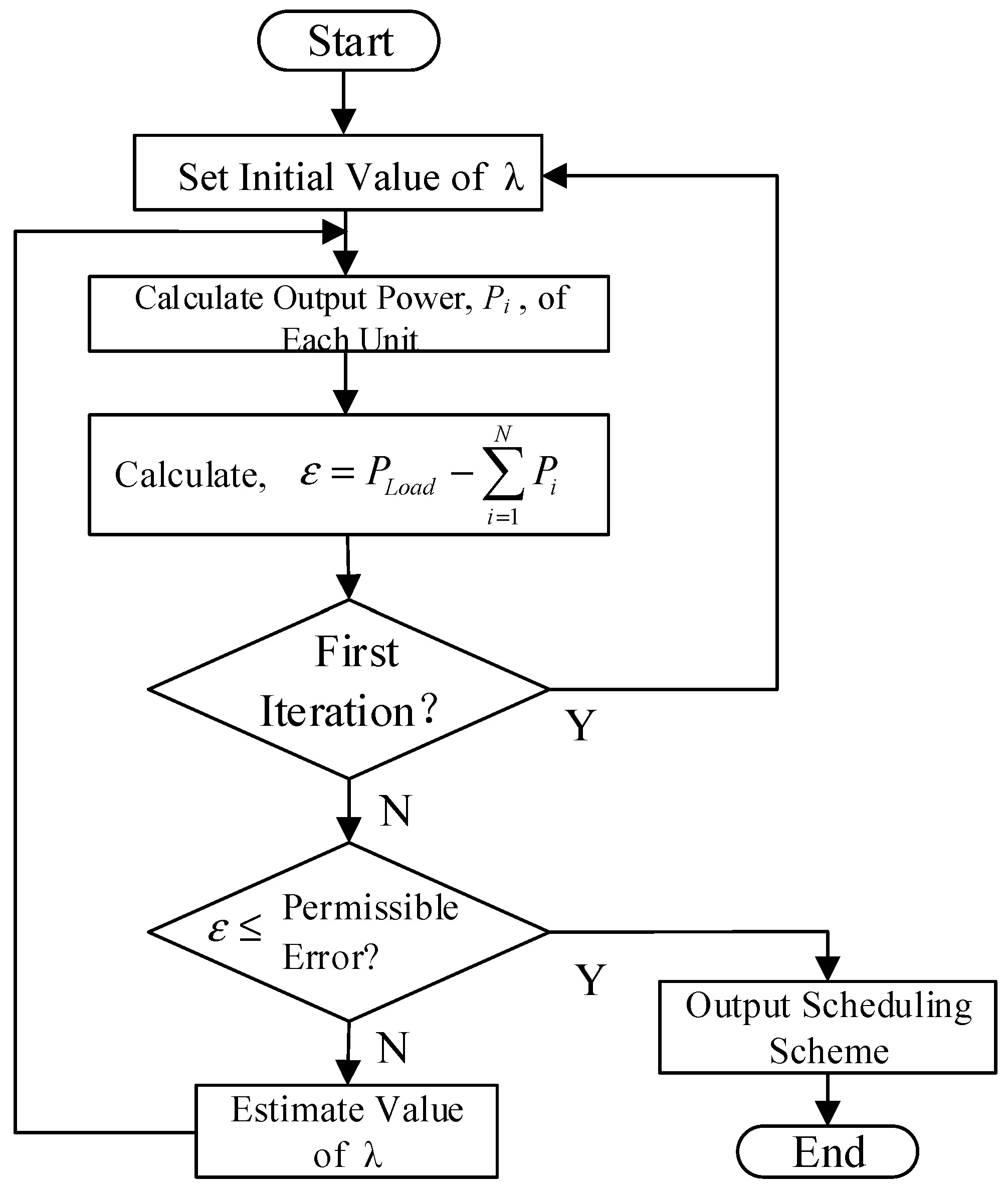
Step 4: Economic load schedule. The Lambda iteration method [
30] is used to solve the economic scheduling problem while solving the power-balance constraints of the unit and the upper and lower limits of the unit power to determine the output power of each unit.Calculate the maximum power generation of the operating unit. If the system load is less than the entire power generation of the functional unit and the power-balance difference is greater than the set value (0.01 here), Lambda iteration is performed. The process is shown in
Figure 5;
Step 5: Calculate the objective function. Calculate the start-up cost and combustion cost of all units in unit time. By comparing the greedy algorithm with the minimum cost of the current iteration each time, if it is less than the minimum cost, it is replaced by a new minimum cost, the optimal function value;
Step 6: update the population through the BCMAES algorithm basic sampling, selection, and reorganization to update the covariance matrix C, update the mean m, and generate new populations and individuals;
Step 7: Termination conditions. Repeat steps 1–6 until the maximum number of iterations is reached.
The steps of solving these problems with BCMAES are similar to those listed above. The flowchart of the BCMAES algorithm for solving the UCEVR problem is illustrated in
Figure 6, while the flowcharts for the other two models are quite similar to that shown in
Figure 6.
4.2. Encoding of the Solution
When the BCMAES algorithm is used to implement practical applications, all variables are stored in a sample library vector pop as follows:
where
is the first variable of the sample library,
is the
kth vector in the solution vector space (the
kth individual in the population), and
is the last variable in the solution vector space. Although the algorithm has a similar solution structure in different models, the realization of the specific solution is quite different, as shown below:
Although renewable energy (solar and wind) is introduced, it is a fixed constant at each time, so it does not change the structure of the solution of the model. So, it has the same structure as that of the UCEV solution.
4.3. Constraint Processing
4.3.1. Constraint Handling
Minimum start-stop time constraint of unit
Because the state of each unit at the characteristic time point in a day is affected by the state of the previous time point or even the state of the unit at several time points, they affect each other and couple with each other. Therefore, it is necessary to adjust the unit’s start-stop state to meet its minimum start-stop constraint;
Unit spinning reserve constraint
After the minimum start-stop constraint of the unit is completed, the spinning reserve constraint of the unit should be carried out to ensure safe and stable operation. The core steps of adjusting the spinning reserve constraint can be divided into the following:
Minimize the number of boot constraints
The system may have redundant startup units when the spinning reserve constraint is adjusted. Therefore, it is necessary to minimize the operation of redundant units and reduce the operation costs of units while maintaining the stable operation of the power system;
Power-balance constraints
When the above constraints are adjusted, the unit state is also determined. At this time, it is necessary to allocate the unit output power of each period to meet the power-balance constraint, which is the famous economic load dispatch problem. There are many mature and effective ways to solve this problem. The BCMAES algorithm adopts the traditional mathematical method, the Lambda iteration method, to solve this problem, which is convenient and fast.
4.3.2. Constraint Handling in Electric Vehicle Discharge Mode
Electric vehicle number constraint.
When the BCMAES algorithm is randomly initialized, , the balance constraint may not be met. The number of electric vehicles at each moment can be considered a random adjustment process. The number of electric vehicles at one moment is randomly selected. Then the sum of the number of electric vehicles at all moments is adjusted, and the number difference is calculated. The number of electric vehicles is repeated to meet the number of electric vehicles needed to meet the number constraint of electric vehicles;
Electric vehicle load power constraints.
The output power of electric vehicles in the model needs to meet certain restrictions. In particular, in the process of adjusting to meet the number constraints of electric vehicles, this process may generate new electric vehicle output that does not meet the load power constraints of electric vehicles. As with the general boundary treatment method, the endpoint method is used here to obtain the boundary value of the variable that crosses the boundary;
Power-balance constraint and spinning reserve constraint.
The V2G mode of electric vehicles is mainly based on the basic UC problem model, which mainly increases the charging of electric vehicles. This violates the original power-balance constraint and spinning reserve constraint. The original power-balance constraint and spinning reserve constraint are changed as follows:
4.3.3. Constraint Handling in Charging and Discharging Mode of the Electric Vehicle
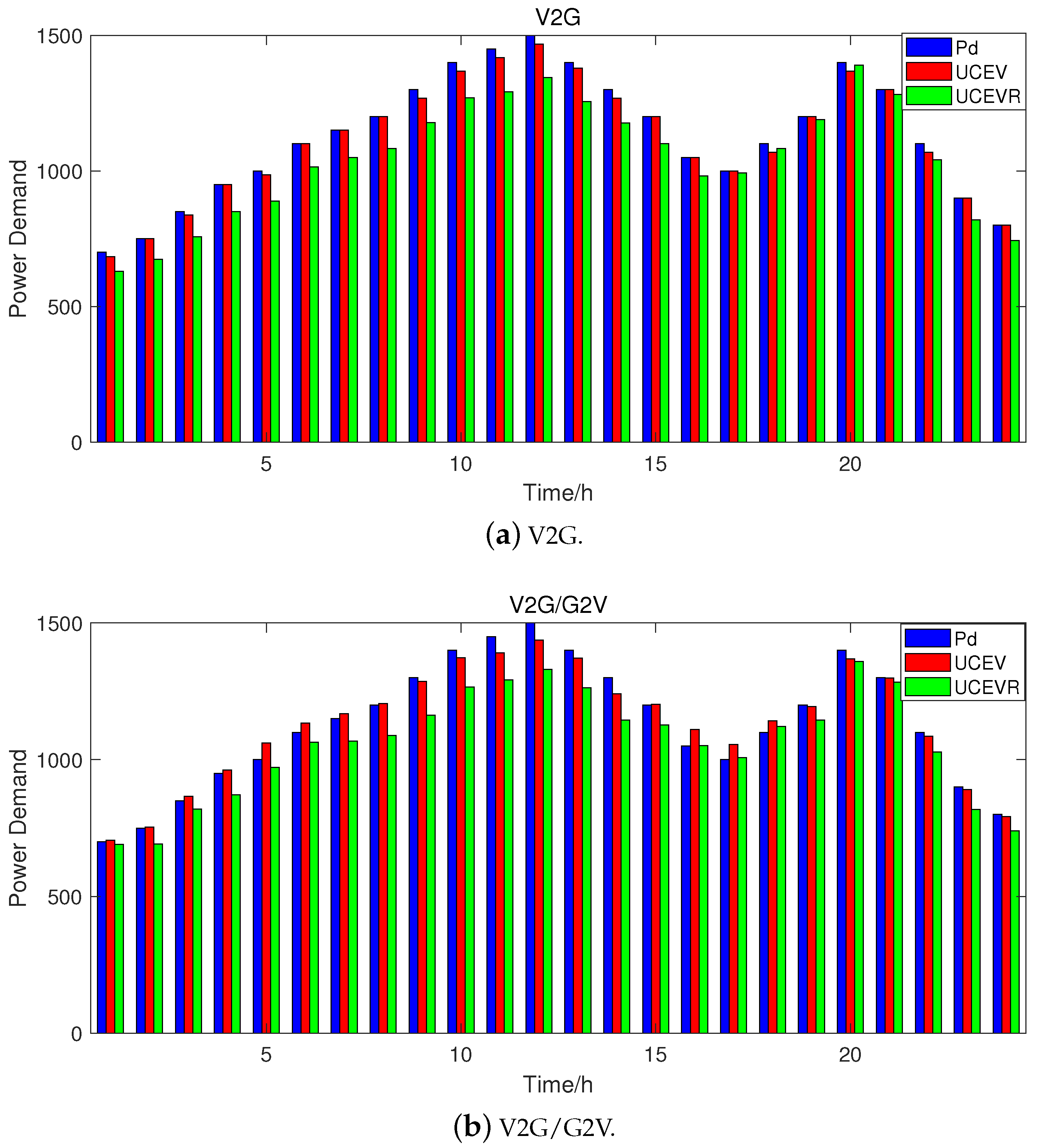
The UCEV (V2G/G2V) problem is mainly based on the UCEV (V2G) model, which adds a charge-discharge balance constraint on all the original conditions. In the UCEV (V2G) model, the electric vehicle is discharging at every moment, but the UCEV (V2G/G2V) model considers another mode, that is, charging at some point in the day, discharging at some point, and ensuring that the amounts of charge and discharge during the day are equal.
4.3.4. Renewable Energy Constraint Handling
Under the premise of electric vehicles connected to the grid, renewable energy is incorporated, mainly increasing amounts of wind and solar energy. In this situation, the original power-balance constraint and spinning reserve constraint are violated.
From the above formula, it is easy to see that, although in the original formula, the increase in the output power of renewable energy invalidates the original formula. In the UCEVR model, the wind power output power , solar power output power , and are constants, so there is no destructive change to the whole constraint, only the original constraint condition needs to be modified.