Resilience-Driven Optimal Sizing of Energy Storage Systems in Remote Microgrids
Abstract
:1. Introduction
- A novel formulation for the resilience-driven ESS sizing problem that provides the optimal capacity of energy storage devices to ensure the critical loads survivability for predefined time intervals. Simultaneously, the proposed algorithm optimizes the other MG resources scheduling in order to achieve an economically efficient operation.
- Validation of the proposed methodology effectiveness by conducting multiple simulations implying high and low values for the MG load and generation availability. To verify the advantages of using the proposed algorithm to enhance the MG resilience, the load restoration rates are investigated for both with and without ESS cases.
- Evaluation of the ESS impact on the MG resilience improvement by defining two new indices, precisely the restoration index and the resilience index.
2. Problem Formulation
2.1. Objective Function
2.2. Constraints
2.3. Resilience Indices
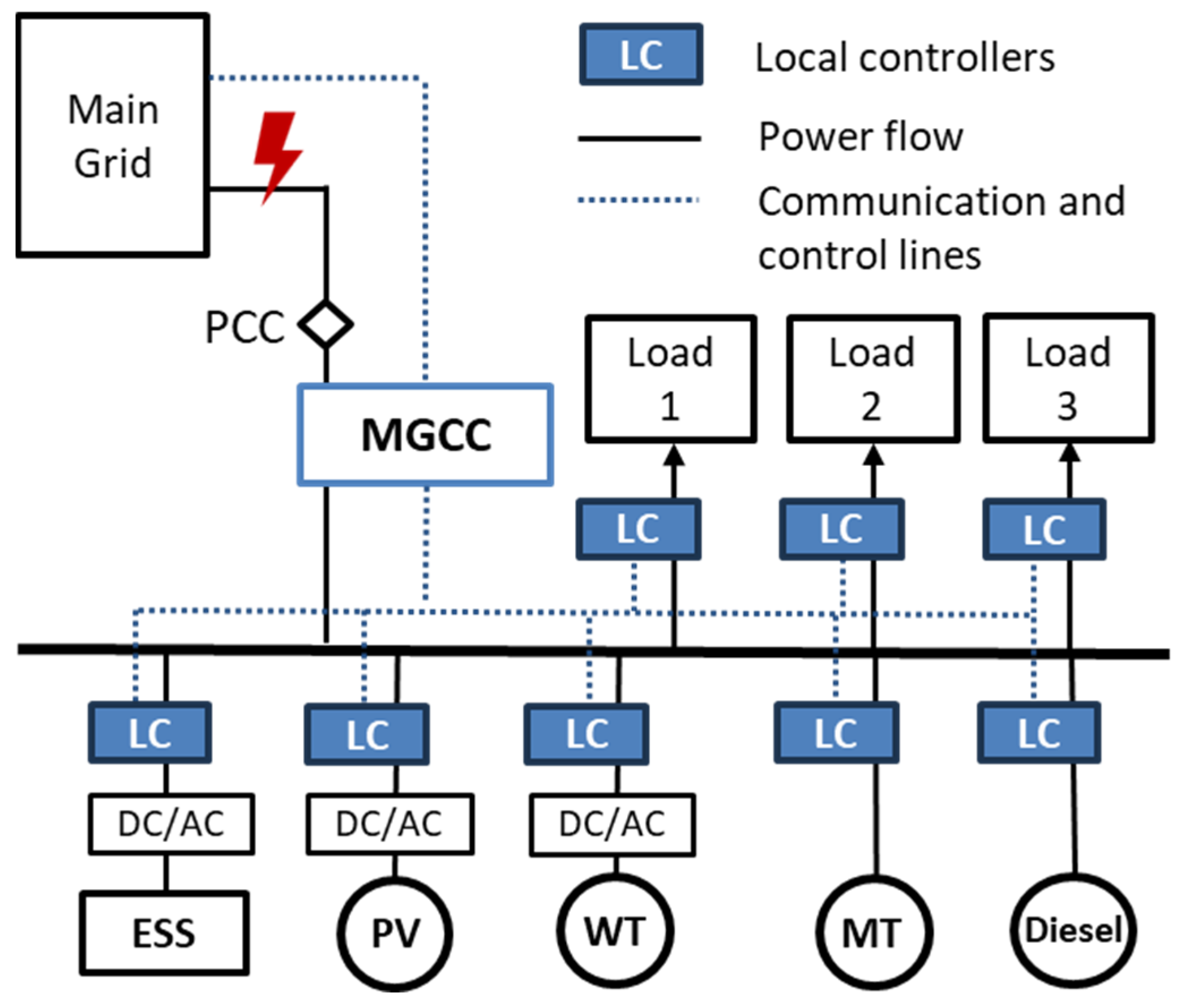
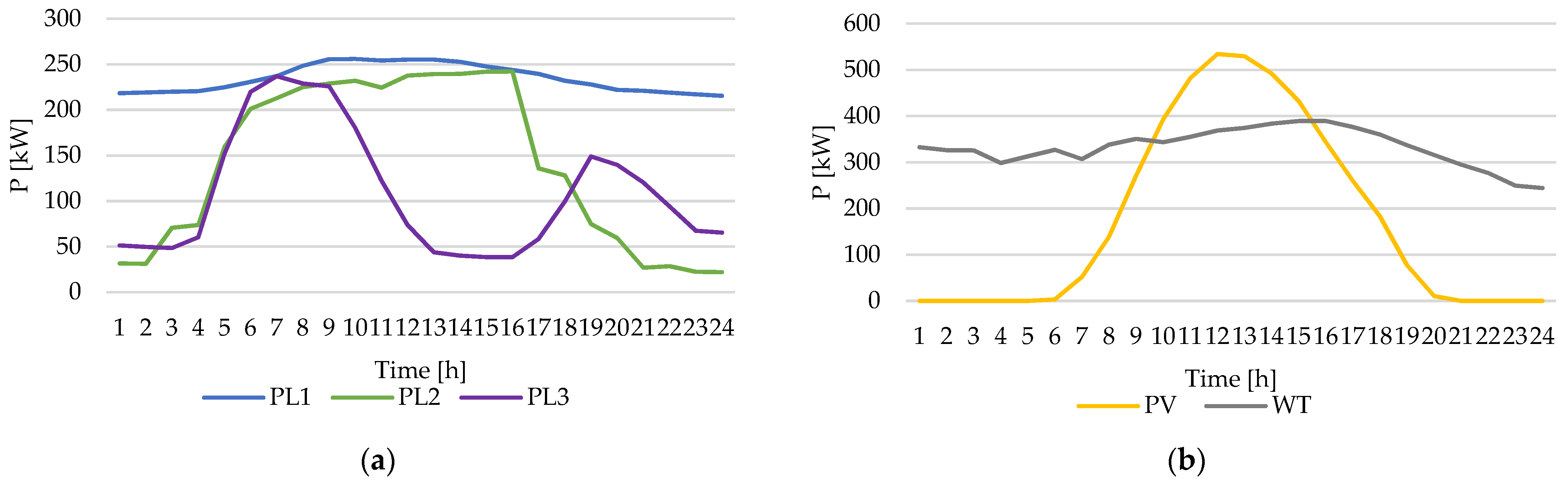
3. Case Study
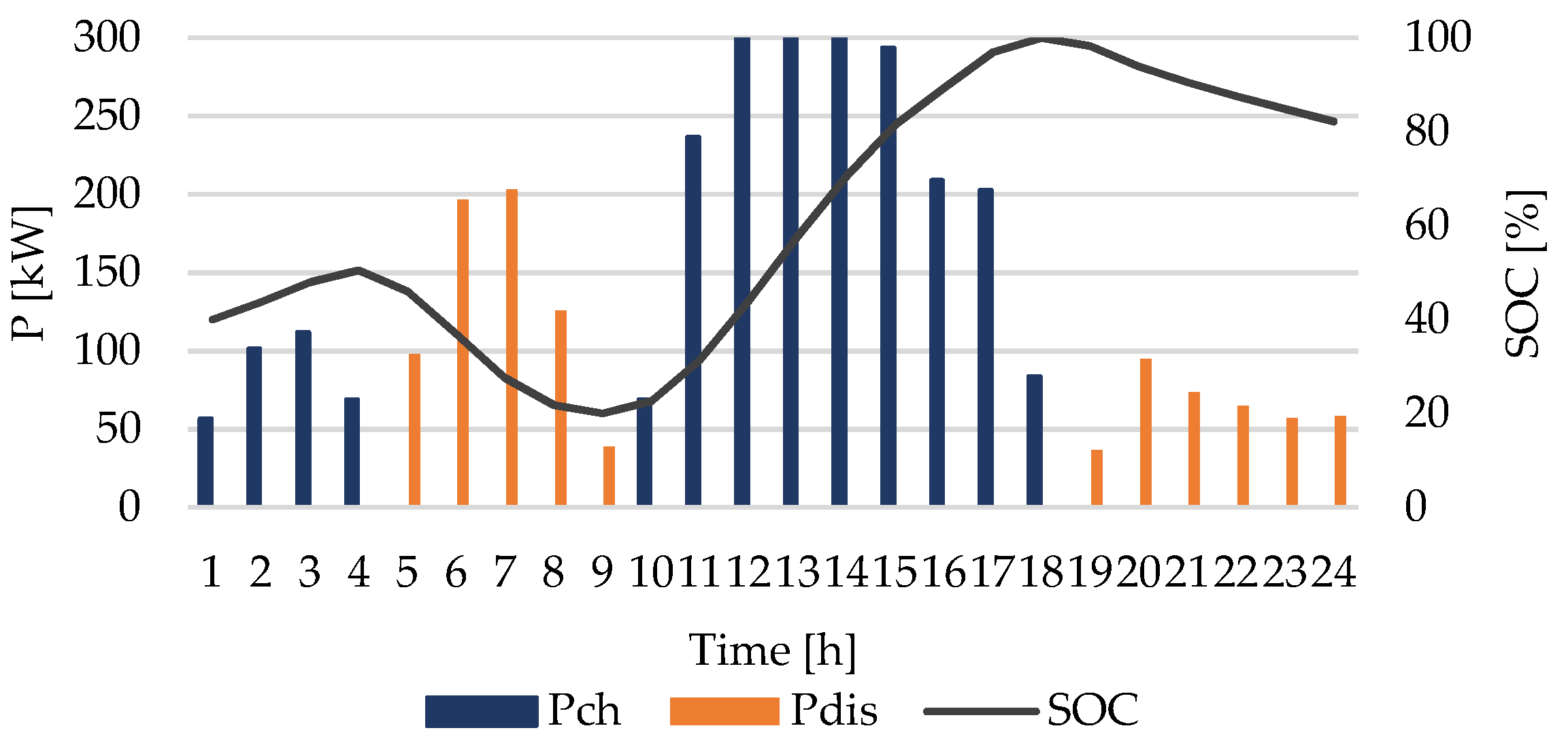
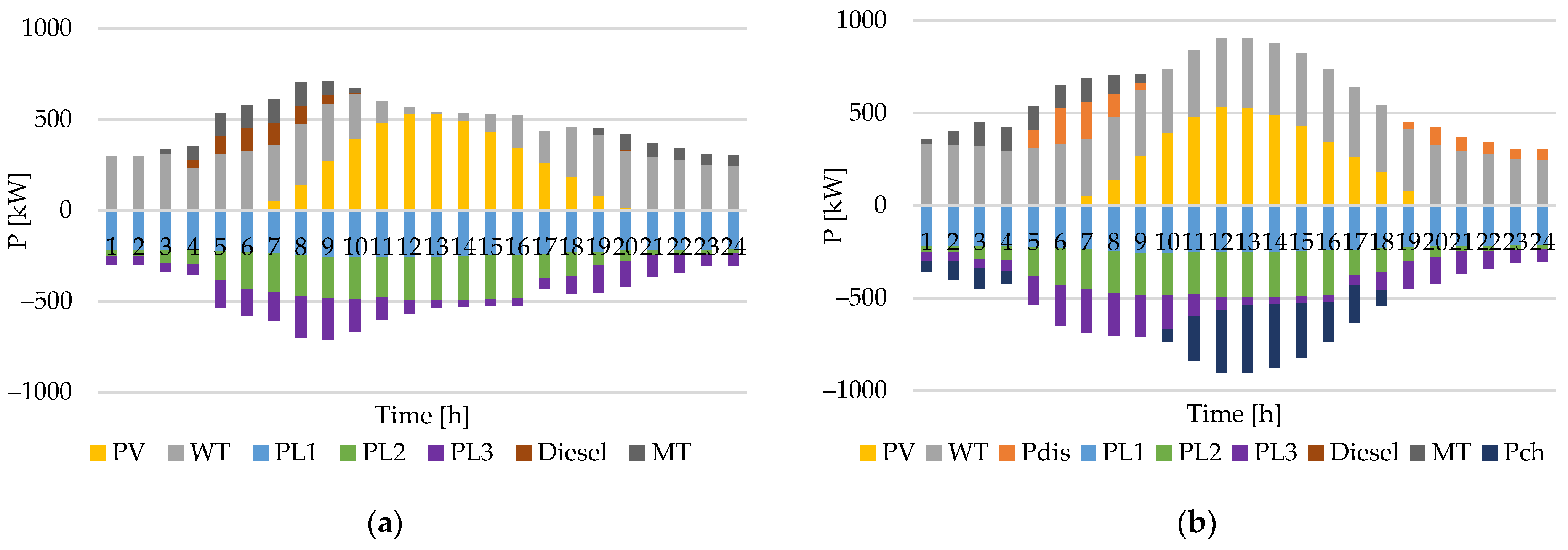
4. Results and Discussion
4.1. Scenario 1
4.2. Scenario 2
4.3. Scenario 3
4.4. Overall Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Norişor, M.; Ban, D.; Pătraşcu, R.; Minciuc, E. Complex, energy, economic and environmental analysis of different solutions for integrating solar thermal panels (PT) into district heating substation (DHS). UPB Sci. Bull. Ser. C 2022, 84, 247–258. [Google Scholar]
- Brenna, M.; Foiadelli, F.; Longo, M.; Zaninelli, D. Correlation between renewable power plants and voltage dips in electrical distribution systems. UPB Sci. Bull. Ser. C 2017, 79, 153–170. [Google Scholar]
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Wang, Q.; Hou, Z.; Guo, Y.; Huang, L.; Fang, Y.; Sun, W.; Ge, Y. Enhancing Energy Transition through Sector Coupling: A Review of Technologies and Models. Energies 2023, 16, 5226. [Google Scholar] [CrossRef]
- Al-Rubaye, H.; Smith, J.; Zangana, M.; Nagapurkar, P.; Zhou, Y.; Gelles, G. Advances in Energy Hybridization for Resilient Supply: A Sustainable Approach to the Growing World Demand. Energies 2022, 15, 5903. [Google Scholar] [CrossRef]
- Sanduleac, M.; Toma, L.; Bulac, C.; Eremia, M.; Golovanov, N.; Porumb, R.; Albu, M.; Gheorghe, S.; Chimirel, C. Energy storage for reaching 100% CO2 free and 100% RES–Preliminary case study for Romania. In Proceedings of the 2017 International Conference on Energy and Environment (CIEM), Bucharest, Romania, 19–20 October 2017. [Google Scholar]
- Liu, X.; Su, B. Microgrids—An integration of renewable energy technologies. In Proceedings of the 2008 China International Conference on Electricity Distribution, Guangzhou, China, 10–13 December 2008. [Google Scholar]
- Ivanov, O.; Neagu, B.; Cibotărică, A.; Gavrilaş, M. Multiobjective Prosumer Surplus Management for Optimal Microgrid Operation. In Proceedings of the 2021 10th International Conference on Energy and Environment (CIEM), Bucharest, Romania, 14–15 October 2021. [Google Scholar]
- Ali, Z.M.; Calasan, M.; Abdel Aleem, S.H.E.; Jurado, F.; Gandoman, F.H. Applications of Energy Storage Systems in Enhancing Energy Management and Access in Microgrids: A Review. Energies 2023, 16, 5930. [Google Scholar] [CrossRef]
- Panteli, M.; Pickering, C.; Wilkinson, S.; Dawson, R.; Mancarella, P. Power System Resilience to Extreme Weather: Fragility Modeling, Probabilistic Impact Assessment, and Adaptation Measures. IEEE Trans. Power Syst. 2017, 32, 3747–3757. [Google Scholar] [CrossRef]
- Busby, J.W.; Baker, K.; Bazilian, M.D.; Gilbert, A.Q.; Grubert, E.; Rai, V.; Rhodes, J.D.; Shidore, S.; Smith, C.A.; Webber, M.E. Cascading risks: Understanding the 2021 winter blackout in Texas. Energy Res. Soc. Sci. 2021, 77, 102106. [Google Scholar] [CrossRef]
- Salik, H.; Zahid, R.I.; Akhunzada, B.K. Cyber Threats to Pakistan’s National Power Grid. Geopolitics 2023, 3, 25–30. [Google Scholar]
- Du, X.; Li, X.; Hao, Y.; Chen, L. Sizing of centralized shared energy storage for resilience microgrids with controllable load: A bi-level optimization approach. Front. Energy Res. 2022, 10, 954833. [Google Scholar] [CrossRef]
- Bosisio, A.; Moncecchi, M.; Cassetti, G.; Merlo, M. Microgrid design and operation for sensible loads: Lacor hospital case study in Uganda. Sustain. Energy Technol. Assess. 2019, 36, 100535. [Google Scholar] [CrossRef]
- Nguyen, T.; Copp, D.; Byrne, R. Stacking Revenue from Energy Storage Providing Resilience, T&D Deferral and Arbitrage. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019. [Google Scholar]
- Aghdam, F.H.; Ghaemi, S.; Kalantari, N.T. Evaluation of loss minimization on the energy management of multi-microgrid based smart distribution network in the presence of emission constraints and clean productions. J. Clean. Prod. 2018, 196, 185–201. [Google Scholar] [CrossRef]
- Arpanahi, M.K.; Nateghi, A.; Shafie-khah, M. A Coordinated Decentralized Loss Minimization Scheme for Hybrid AC/DC Distribution System with Multiple Microgrids. In Proceedings of the 2021 International Conference on Smart Energy Systems and Technologies (SEST), Vaasa, Finland, 6–8 September 2021. [Google Scholar]
- Gao, J.; Chen, J.J.; Cai, Y.; Zeng, S.Q.; Peng, K. A two-stage microgrid cost optimization considering distribution network loss and voltage deviation. Energy Rep. 2020, 6, 263–267. [Google Scholar] [CrossRef]
- Bouchekara, H.R.E.H.; Sha’aban, Y.A.; Shahriar, M.S.; Abdullah, S.M.; Ramli, M.A. Sizing of Hybrid PV/Battery/Wind/Diesel Microgrid System Using an Improved Decomposition Multi-Objective Evolutionary Algorithm Considering Uncertainties and Battery Degradation. Sustainability 2023, 15, 11073. [Google Scholar] [CrossRef]
- Premadasa, P.N.D.; Silva, C.M.M.R.S.; Chandima, D.P.; Karunadasa, J.P. A multi-objective optimization model for sizing an off-grid hybrid energy microgrid with optimal dispatching of a diesel generator. J. Energy Storage 2023, 68, 107621. [Google Scholar] [CrossRef]
- Shahbazbegian, V.; Dehghani, F.; Shafiyi, M.A.; Shafie-khah, M.; Laaksonen, H.; Ameli, H. Techno-economic assessment of energy storage systems in multi-energy microgrids utilizing decomposition methodology. Energy 2023, 283, 128430. [Google Scholar] [CrossRef]
- Nebuloni, R.; Meraldi, L.; Bovo, C.; Ilea, V.; Berizzi, A.; Sinha, S.; Tamirisakandala, R.B.; Raboni, P. A hierarchical two-level MILP optimization model for the management of grid-connected BESS considering accurate physical model. Appl. Energy 2023, 334, 120697. [Google Scholar] [CrossRef]
- Liang, L.; Lin, L. A resilience enhanced hierarchical strategy of battery energy storage for frequency regulation. Energy Rep. 2023, 9, 625–636. [Google Scholar] [CrossRef]
- Alrashidi, M. Community Battery Storage Systems Planning for Voltage Regulation in Low Voltage Distribution Systems. Appl. Sci. 2022, 12, 9083. [Google Scholar] [CrossRef]
- Boonluk, P.; Siritaratiwat, A.; Fuangfoo, P.; Khunkitti, S. Optimal Siting and Sizing of Battery Energy Storage Systems for Distribution Network of Distribution System Operators. Batteries 2020, 6, 56. [Google Scholar] [CrossRef]
- Takano, H.; Hayashi, R.; Asano, H.; Goda, T. Optimal Sizing of Battery Energy Storage Systems Considering Cooperative Operation with Microgrid Components. Energies 2021, 14, 7442. [Google Scholar] [CrossRef]
- Sanduleac, M.; Sandulescu, A.; Efremov, C.; Ionescu, C.; Damian, I.C.; Mandis, A. Aspects of Design in Low Voltage Resilient Grids—Focus on Battery Sizing and U Level Control with P Regulation in Microgrids of Energy Communities. Energies 2023, 16, 1932. [Google Scholar] [CrossRef]
- Zolfagharia, M.; Ghaffarzadeha, N.; Ardakanib, A. Optimal sizing of battery energy storage systems in off-grid micro grids using convex optimization. J. Energy Storage 2019, 23, 44–56. [Google Scholar] [CrossRef]
- Xie, H.; Teng, X.; Xu, Y.; Wang, Y. Optimal Energy Storage Sizing for Networked Microgrids Considering Reliability and Resilience. IEEE Access 2019, 7, 86336–86348. [Google Scholar] [CrossRef]
- Hoyos-Velandia, C.; Ramirez-Hurtado, L.; Quintero-Restrepo, J.; Moreno-Chuquen, R.; Gonzalez-Longatt, F. Cost Functions for Generation Dispatching in Microgrids for Non-Interconnected Zones in Colombia. Energies 2022, 15, 2418. [Google Scholar] [CrossRef]
- Wei, W.; Ye, L.; Fang, Y.; Wang, Y.; Chen, X.; Li, Z. Optimal allocation of energy storage capacity in microgrids considering the uncertainty of renewable energy generation. Sustainability 2023, 15, 9544. [Google Scholar] [CrossRef]
- Macmillan, M.; Wilson, K.; Baik, S.; Carvallo, J.P.; Dubey, A.; Holland, C.A. Shedding light on the economic costs of long-duration power outages: A review of resilience assessment methods and strategies. Energy Res. Soc. Sci. 2023, 99, 103055. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Z.; Zhao, Y.; Sun, Q.; Wang, F. A robust flexibility evaluation method for distributed multi-energy microgrid in supporting power distribution system. Front. Energy Res. 2023, 10, 1021627. [Google Scholar] [CrossRef]
- Pozo, D. Linear battery models for power systems analysis. Electr. Power Syst. Res. 2022, 212, 108565. [Google Scholar] [CrossRef]
- Watrin, N.; Roche, R.; Ostermann, H.; Blunier, B.; Miraoui, A. Multiphysical Lithium-Based Battery Model for Use in State-of-Charge Determination. IEEE Trans. Veh. Technol. 2012, 61, 3420–3429. [Google Scholar] [CrossRef]
- Fortenbacher, P.; Mathieu, J.L.; Andersson, G. Modeling, identification, and optimal control of batteries for power system applications. In Proceedings of the 2014 Power Systems Computation Conference, Wroclaw, Poland, 18–22 August 2014. [Google Scholar]
- Rehman, W.; Bo, R.; Mehdipourpicha, H.; Kimball, J.W. Sizing battery energy storage and PV system in an extreme fast charging station considering uncertainties and battery degradation. Appl. Energy 2022, 313, 118745. [Google Scholar] [CrossRef]
- Jacque, K.; Koltermann, L.; Figgener, J.; Zurmühlen, S.; Sauer, D.U. The influence of frequency containment reserve on the cycles of a hybrid stationary large-scale storage system. J. Energy Storage 2022, 52, 105040. [Google Scholar] [CrossRef]
- Picioroaga, I.I.; Tudose, A.M.; Sidea, D.O.; Bulac, C. Supply Restoration in Active Distribution Networks Based on Soft Open Points with Embedded DC Microgrids. Mathematics 2022, 10, 211. [Google Scholar] [CrossRef]
- Roy, K.; Mandal, K.K.; Mandal, A.C. Modeling and managing of micro grid connected system using Improved Artificial Bee Colony algorithm. Int. J. Electr. Power Energy Syst. 2016, 75, 50–58. [Google Scholar] [CrossRef]
- Nikmehr, N.; Najafi-Ravadanegh, S. Optimal operation of distributed generations in micro-grids under uncertainties in load and renewable power generation using heuristic algorithm. IET Renew. Power Gener. 2015, 9, 982–990. [Google Scholar] [CrossRef]
- Marchi, B.; Pasetti, M.; Zanoni, S. Life Cycle Cost Analysis for BESS Optimal Sizing. Energy Procedia 2017, 113, 127–134. [Google Scholar] [CrossRef]
- Sidea, D.O.; Picioroaga, I.I.; Bulac, C. Optimal Battery Energy Storage System Scheduling Based on Mutation-Improved Grey Wolf Optimizer Using GPU-Accelerated Load Flow in Active Distribution Networks. IEEE Access 2021, 9, 13922–13937. [Google Scholar] [CrossRef]
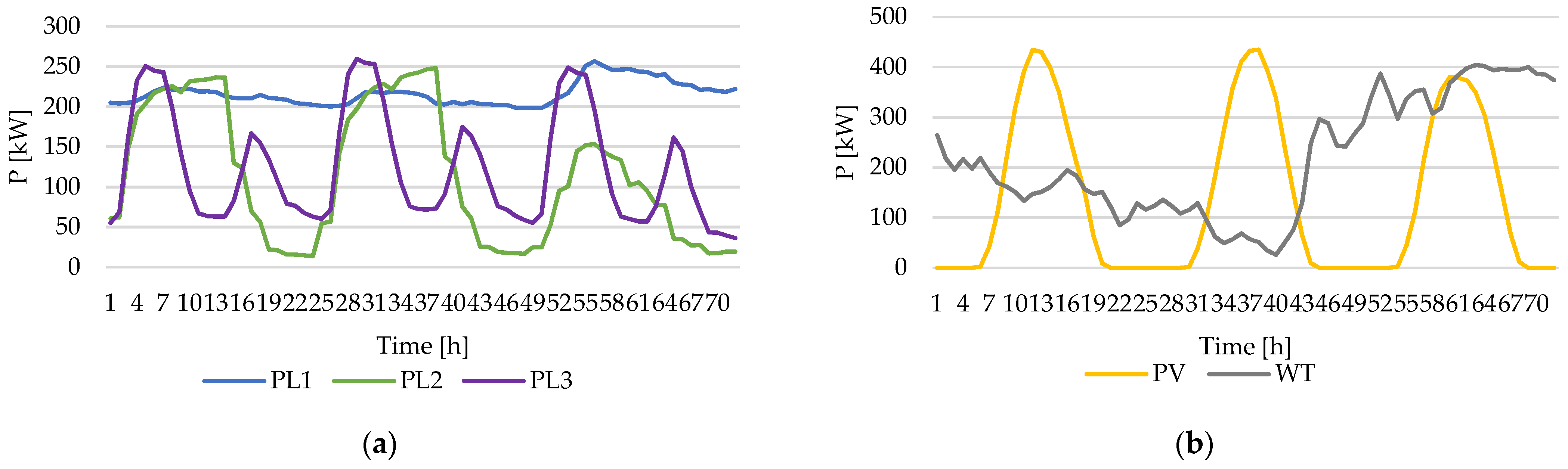
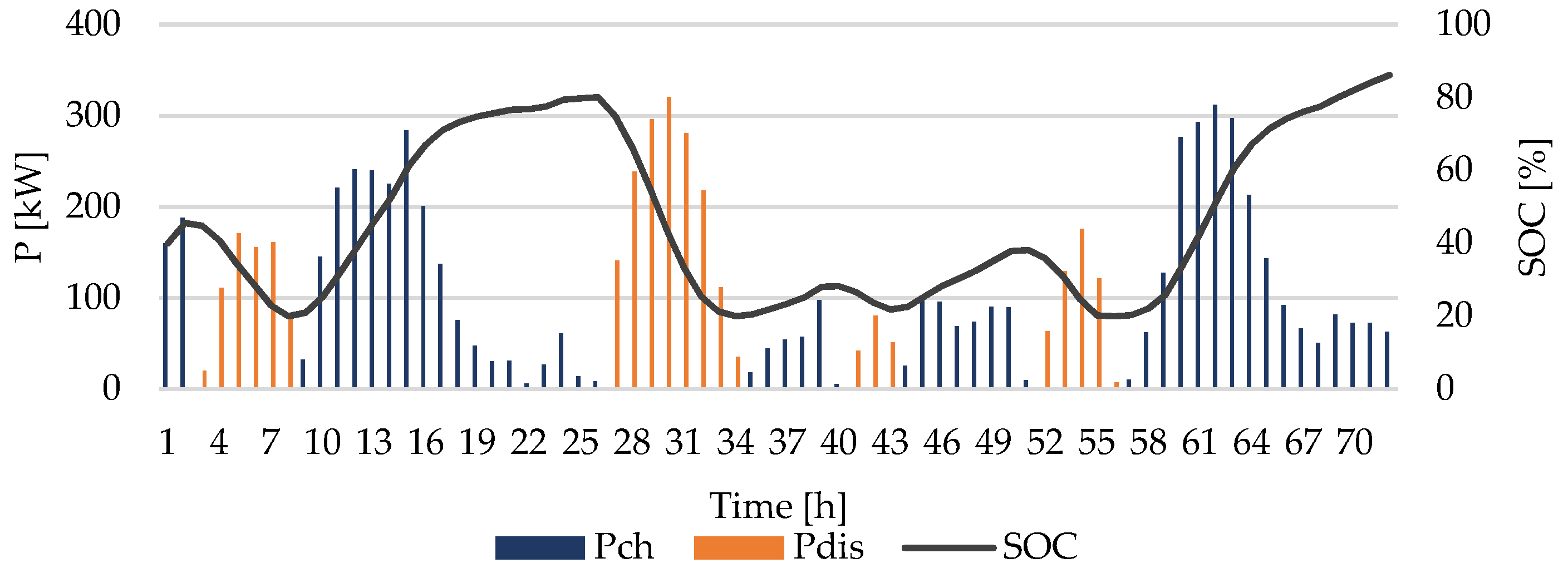

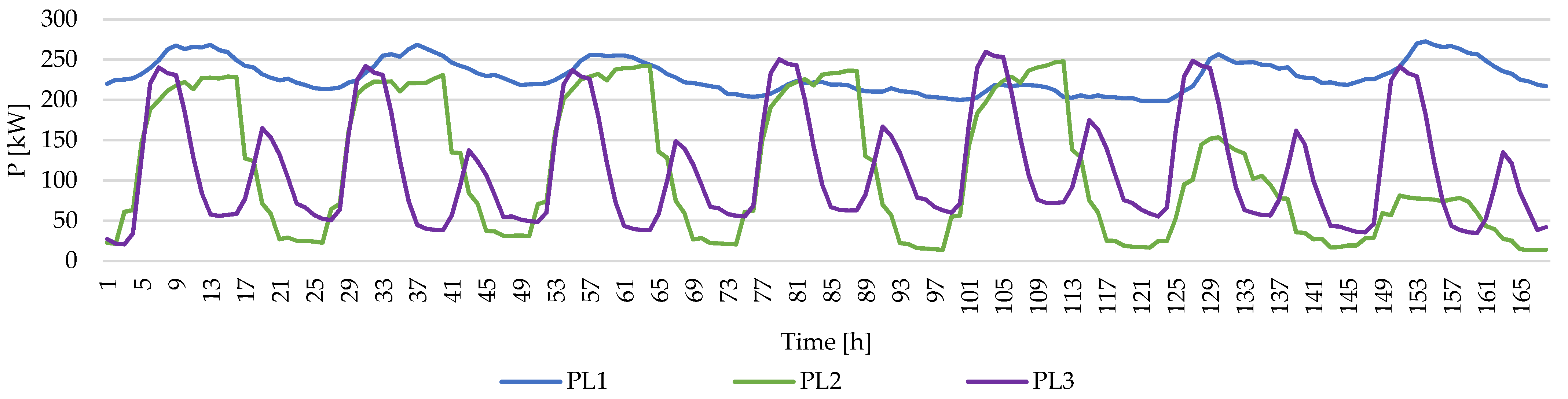
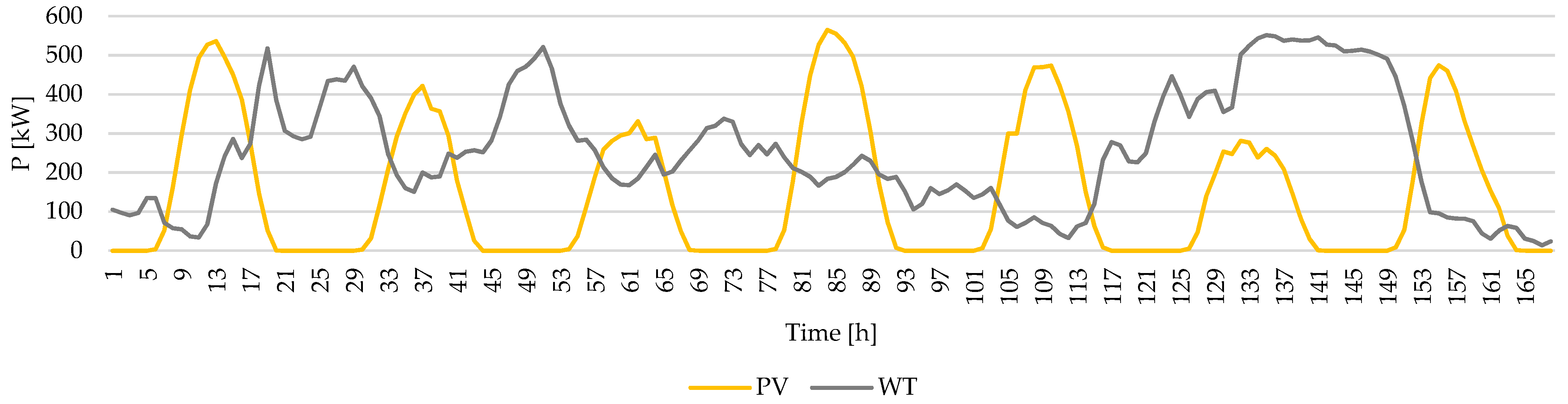
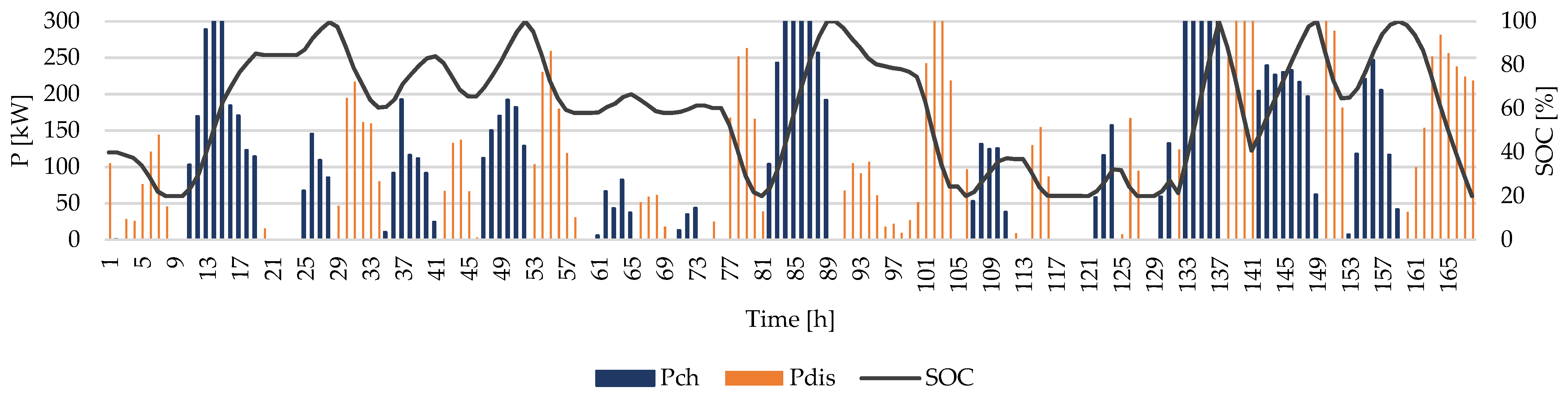
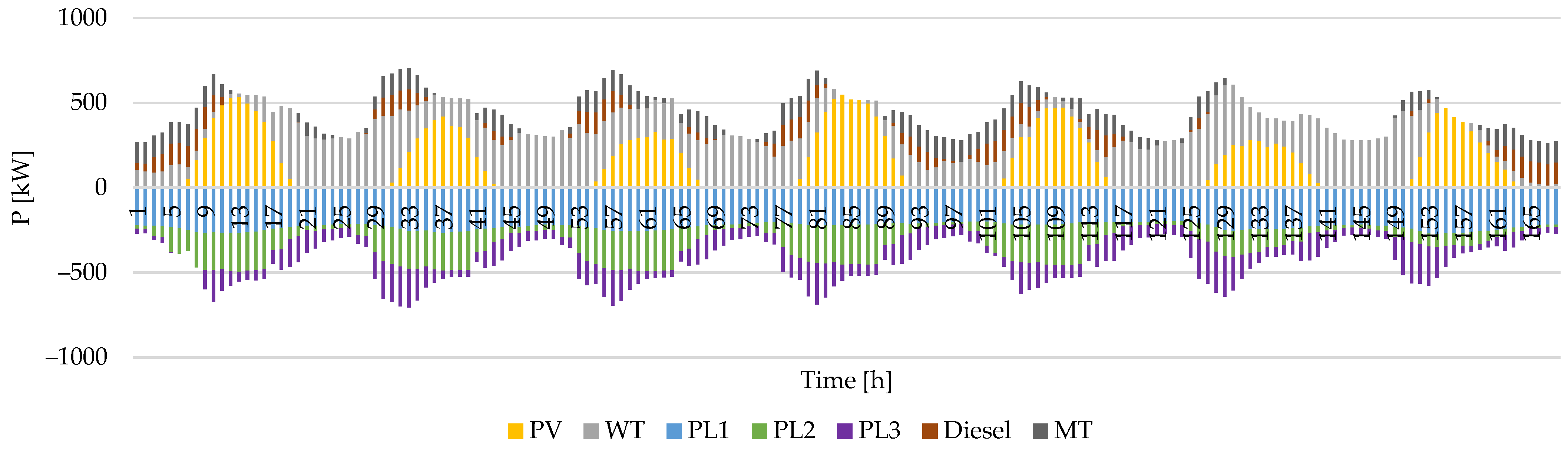
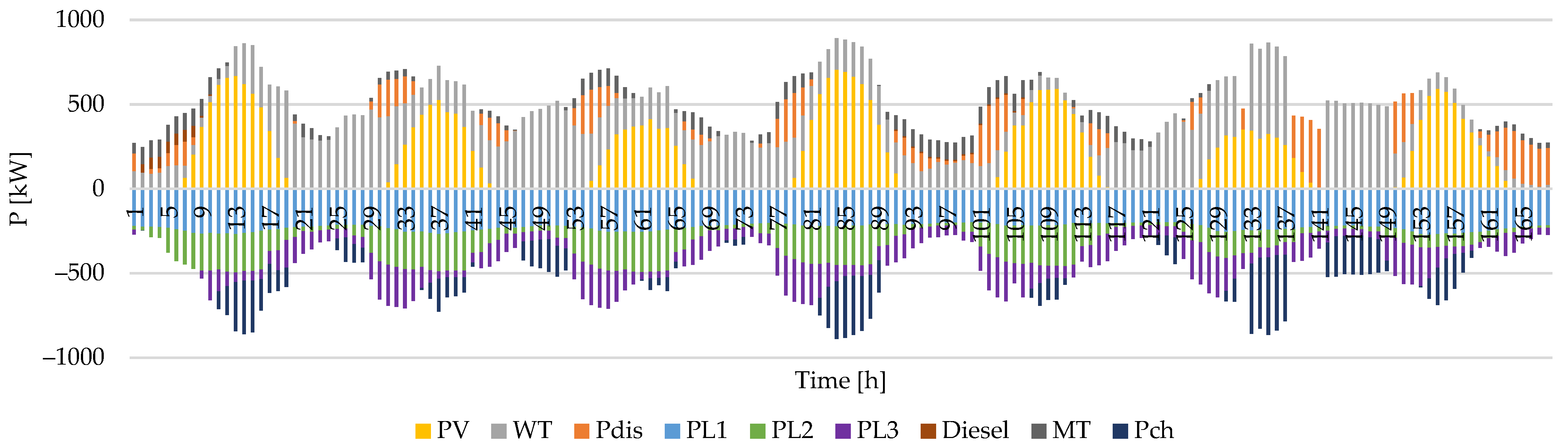
| Parameter | [€/kW] | [€/kW] | [€/kW] | [€/kWh] | [kW] | Ramp Up/Down Rate [kW/h] |
|---|---|---|---|---|---|---|
| Value | 0.4073 | 0.2193 | 0.0695 | 0.1433 | 125 | 50 |
| Parameter | [€/kW] | [€/kW] | [€/kWh] | [kW] | Ramp Up/Down Rate [kW/h] |
|---|---|---|---|---|---|
| Value | 0.2368 | 0.0155 | 0.0419 | 125 | 50 |
| Pollutant | [kg/kWh] | [kg/kWh] | [€/kg] |
|---|---|---|---|
| CO2 | 0.00131 | 0.000991 | 0.0309 |
| SO2 | 0.00041 | 0.000005 | 2.1847 |
| NOx | 0.02005 | 0.000027 | 9.2656 |
| Parameter | [€/kW] | [€/kWh] | [€/kW] | [kW] | r [%] | L [years] |
|---|---|---|---|---|---|---|
| Value | 250 | 450 | 60 | 150 | 5 | 10 |
| Parameter | [kW] | [%] | [%] | [cycles/day] | [%] |
|---|---|---|---|---|---|
| Value | 1000 | 90/90 | 20/100 | 2 | 0.4 |
| User | Load 1 | Load 2 | Load 2 |
|---|---|---|---|
| Shedding cost [€/kWh] | 37.52 | 23.41 | 0.53 |
| Scenario | Case | [€] | [€] | [€] | [€] | [€] | MG Total Operation Costs [€] |
|---|---|---|---|---|---|---|---|
| Scenario 1 | Without ESS | 2424.35 | 113.21 | 0 | 396.98 | 826.12 | 3760.66 |
| With ESS | 17.423 | 0.2839 | 760.05 | 510.3561 | 0 | 1288.11 | |
| Scenario 2 | Without ESS | 15,704.58 | 719.86 | 0 | 913.14 | 15,933 | 33,270.58 |
| With ESS | 18,674.6 | 839.73 | 2876.6 | 1058.7 | 0 | 23,449.63 | |
| Scenario 3 | Without ESS | 27,258.12 | 1266.65 | 0 | 2400.8 | 16,822 | 47,747.57 |
| With ESS | 6760.1 | 333.06 | 5167.3 | 2723.9 | 2886.1 | 17,870.49 |
| Scenario | Case | Load 1 [%] | Load 2 [%] | Load 3 [%] |
|---|---|---|---|---|
| Scenario 1 | Without ESS | 0 | 0 | 5.74 |
| With ESS | 0 | 0 | 0 | |
| Scenario 2 | Without ESS | 0 | 1.68 | 25.84 |
| With ESS | 0 | 0 | 0 | |
| Scenario 3 | Without ESS | 0 | 0.61 | 13.28 |
| With ESS | 0 | 0 | 2.73 |
| Scenario | Case | ||
|---|---|---|---|
| Scenario 1 | Without ESS | 0.9872 | 0.9997 |
| With ESS | 1 | 1 | |
| Scenario 2 | Without ESS | 0.9257 | 0.9943 |
| With ESS | 1 | 1 | |
| Scenario 3 | Without ESS | 0.9654 | 0.9978 |
| With ESS | 0.9932 | 0.9999 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Picioroaga, I.; Luca, M.; Tudose, A.; Sidea, D.; Eremia, M.; Bulac, C. Resilience-Driven Optimal Sizing of Energy Storage Systems in Remote Microgrids. Sustainability 2023, 15, 16002. https://doi.org/10.3390/su152216002
Picioroaga I, Luca M, Tudose A, Sidea D, Eremia M, Bulac C. Resilience-Driven Optimal Sizing of Energy Storage Systems in Remote Microgrids. Sustainability. 2023; 15(22):16002. https://doi.org/10.3390/su152216002
Chicago/Turabian StylePicioroaga, Irina, Madalina Luca, Andrei Tudose, Dorian Sidea, Mircea Eremia, and Constantin Bulac. 2023. "Resilience-Driven Optimal Sizing of Energy Storage Systems in Remote Microgrids" Sustainability 15, no. 22: 16002. https://doi.org/10.3390/su152216002
APA StylePicioroaga, I., Luca, M., Tudose, A., Sidea, D., Eremia, M., & Bulac, C. (2023). Resilience-Driven Optimal Sizing of Energy Storage Systems in Remote Microgrids. Sustainability, 15(22), 16002. https://doi.org/10.3390/su152216002









