Abstract
With the continuous increase in the number of vehicles worldwide, parking challenges have become more severe, making it a shared goal for governments to alleviate parking difficulties in urban centers. Shared parking has emerged as an effective solution to address parking problems and has been widely studied in recent years. However, existing research primarily focuses on static or single-period parking matching, often neglecting the conflicts between overdue parking users and subsequent users. Therefore, addressing the impact of overdue parking on shared parking systems is highly important. This study proposes a multi-period dynamic matching decision model (MDMD), which divides the operation period of the shared parking platform into multiple decision points. At each decision point, parking demands are classified into four categories: newly arriving demands, allocated demands with a start time not within the current decision point, overdue demands during the current decision point, and demands affected by overdue parking. Three decision variables are established to determine matching schemes for the first, second, and fourth types of parking demands, facilitating a dynamic decision-making process that effectively mitigates the impact of overdue parking. A corresponding algorithm is designed to solve the model. Since the single-period model is a linear programming model, the CPLEX solver obtains allocation schemes for each decision point. These schemes, along with new parking demands, are used as input for the next decision point, achieving a dynamic matching process. Simulation experiments are conducted to compare the MDMD model with the traditional First-Book-First-Served (FBFS) model based on platform revenue, parking space utilization, and parking demand acceptance rate. The experimental results show that, compared to FBFS, MDMD improves long-term earnings by 83%, actual profits in recent profits by 6.6%, and parking space utilization by 8% while maintaining a similar parking demand acceptance rate. To validate the robustness of the model, additional simulations are performed under various overdue probability scenarios, demonstrating that MDMD maintains stable system performance across different probabilities. These improvements highlight the advantages of the dynamic matching strategy, distinguishing this study from existing methods lacking adaptability. These findings provide valuable insights for the optimization of shared parking systems, contributing to sustainable transportation solutions and efficient urban mobility management.
1. Introduction
With the development of the economy, the number of vehicles in cities worldwide, especially in East Asian countries such as China, has been steadily increasing, and the problem of parking dilemmas in urban areas has become increasingly worse. Due to the limited number of parking slots, drivers need to spend additional cruising time searching for a vacancy parking slot. According to research by Tang [1], approximately 30% of drivers spend an average of 8 min cruising for a parking slot. Faraji mentioned that the metropolis of Tehran faces various disturbances and challenges related to traffic and parking [2]. According to studies, more than one million vehicles spend between 15 and 35 min daily searching for parking spaces in Tehran, and the exhaust emissions from these vehicles contribute to significant air pollution. Not only is the total number of parking slots severely insufficient in the area near the hospital, central business district, primary and middle schools, and old residential area, but also many misusages of parking slots have existed such that there are many idle times for parking slots near these shortage areas. During weekdays, many private parking slots remain unoccupied during the day. The unused parking slots in these high-demand areas can be shared to alleviate the shortage of parking. Unlike some single-family homes with private parking slots, in many countries like China and Japan, privately or collectively owned parking slots are often located in semi-private parking garages. This makes it easier for owners of parking slots to accept the idea of sharing their parking slots during idle time of parking slot. In recent years, with the development of internet technology, many shared parking platforms have emerged, such as “Dingding Parking” and “Yueteng Smart”. Property owners can authorize platforms to rent out their parking slots during idle time, while those in need of parking slots can submit their requests to the platform. The sharing-parking platform processes the collected information about parking slots’ idle time of owners and renting times of demanders and matches available parking slots to those in need, enabling time-shared parking scheme. This can effectively alleviate the parking shortage problem. Meanwhile, recent research on parking management has made some progress. For example, P&R (Park and Ride) parking and bike-sharing systems have been proposed as effective solutions to support urban transportation accessibility, alleviating parking pressure in city centers and promoting green travel [3]. Additionally, studies have shown that parking characteristics exhibit certain patterns of variation over different time periods under the conditions of PPZs (Paid Parking Zones) and DPI (Dynamic Parking Information), which provides important insights for optimizing parking management and demand forecasting [4]. These studies provide valuable theoretical support for the background of this paper. Throughout the entire sharing process, the matching process of parking supply and demand determines the platform’s revenue and the effectiveness of the shared parking scheme. Therefore, optimizing the matching method becomes particularly important.
Currently, most research on shared parking matching is based on the premise that parking demanders fulfill their commitments on time. These matching methods have the following drawbacks: (1) In reality, the phenomenon of overdue parking is ubiquity in practice due to diverse causes, so a matching scheme based on absolute on-time fulfillment may bring a lot of coordination work in parking sites during operation. (2) Ignoring overdue parking cases can lead to conflicts between the overdue parking user and the follow-up parking demander—the follow-up user arrives at the parking slot on time according to the instruction of the matching scheme by the platform, but the booked parking slot is not emptied due to the overdue parking user. These issues can result in losses for the platform and reduce the willingness to share/rent parking slots for parking slot suppliers and parking demanders. Therefore, a more reasonable approach is needed urgently to match shared parking slots with demanders, minimizing the impact of overdue parking and providing a smarter shared parking service.
This paper investigates the optimization of shared parking slots matching, considering users’ overdue parking behavior. By dividing the operating time of shared parking into multiple time periods, we have innovatively established a multi-period dynamic matching decision model (MDMD), incorporating multiple decision points to formulate matching schemes. At subsequent decision points, overdue parking users are treated as new parking users, automatically matched to the parking spaces they have occupied overdue, and are fined with high overdue parking fees. The follow-up demanders, whose originally matched parking spaces are conflicted, are redirected to another available space and compensated. This approach enables large-scale and effective matching of shared parking spaces with demanders, even in the context of overdue parking behavior, thus addressing a gap in previous research.
The next part of the paper provides a literature review on shared parking matching research. Then, the study presents a detailed description of the shared parking matching problem considering overdue parking and develops a dynamic matching model. Section 4 designs the dynamic matching algorithm, providing detailed steps and evaluation metrics. Section 5 presents numerical experiments, validating the advantages of the proposed method through a comparison with the FBFS method. Finally, the main research conclusions are given, along with a discussion and outlook for future work.
2. Literature Review
Research on shared parking matching can be broadly categorized into two types based on parking demand: deterministic parking demand and uncertain parking demand. The deterministic model assumes that users’ submitted parking requests align with their actual parking behavior, while the uncertainty model accounts for discrepancies between reported and actual parking behavior.
Significant progress has been made in recent years on deterministic parking demand. Shao [5] introduced a straightforward shared parking reservation model using linear programming, considering both temporal heterogeneity and homogeneity in parking space sharing, laying the foundation for parking matching optimization. Based on this, Xiao [6] proposed the Demand Competition Padding Method (DC-PM), which not only ensures platform profitability but also generates social benefits through further enhancements. Following this idea, Kong [7] pioneered the integration of auction and market design into the shared parking problem, introducing a price-compatible top-level transaction cycle and chain mechanism that increased the sharing efficiency of parking space by 20–30%, significantly improving system profitability. As parking needs diversified, Kim [8] expressed the problem of sharing among multiple private parking lots with different parking needs as a mixed integer linear programming problem and solved the problem through an algorithm based on alternating direction multipliers, which further improved the utilization rate of parking spaces. Many other scholars have also optimized shared parking matching from the perspective of parking rates, considering the impact of parking demand users’ personal attributes on their acceptance of parking fees [9,10,11,12]. In the process of optimizing the allocation of parking resources, Duan [13] introduced parking guidance information and designed a two-layer programming model, in which the upper layer realized the balanced matching of parking resources and the lower layer minimized the walking distance of drivers after parking. The simulation results show that the model can effectively balance the parking resources in the area and has a wide application prospect. To address the time window constraints of parking demand, Zhao [14] proposed a matching method based on the two-box principle, successfully optimizing parking supply and demand under these constraints. With technological advances, Xie [15] developed a global parking path algorithm accounting for travel time variation of road segments, considering the increasing use of autonomous vehicles. This method reduced average travel time by 14.9% compared to traditional static path algorithms, demonstrating its potential in intelligent parking applications. Gao [16] introduced a trilateral market matching model to resolve the matching challenges between drivers, passengers, and parking lots, further enriching parking matching research. Yang [17] compared timed and real-time parking matching models, finding that when supply exceeds demand, the real-time parking matching model offers the best user experience, while the timed parking matching model optimizes system resources. In the realm of matching mechanism optimization, Shang [18] proposed a parking matching system based on user preferences, integrated with the “first-come-first-served” (FCFS) algorithm, significantly improving matching efficiency. Ji [19] applied the cumulative prospect theory to study parking demand heterogeneity, improving user satisfaction and emphasizing the importance of user behavior in parking choice on matching outcomes. Nakazato [20] proposed a dynamic pricing system to balance parking utilization, addressing parking challenges in urban centers with a reservation system. Liu [21] explored parking matching in a hybrid system of on-street and shared parking, considering platform pricing strategies.
In addition to deterministic parking demand, scholars have addressed challenges posed by uncertainty. Huang [22] mitigated the effects of demand uncertainty by reserving parking spaces, while Jiang [23] constructed probability functions for various periods to account for untimely arrivals and departures, transforming the stochastic programming problem into an expected model to optimize results. Wang [24] leveraged historical data to model drivers’ arrival and departure times, using an opportunity-constrained optimization model to improve matching accuracy. While most studies focused on demand unpredictability, Li [25] examined the heterogeneous temporary needs of parking space suppliers, proposing a differentiated matching model solved through ant colony optimization. Hu [26] combined sample average approximation (SAA) with accelerated Benders decomposition algorithms, conducting numerical experiments to evaluate the impact of untimely behavior on shared parking platforms, revealing that untimeliness significantly affects platform performance. Moreover, an increasing number of studies have begun to explore the integration of intelligent algorithms into shared parking matching, particularly leveraging machine learning and deep learning techniques. With the rapid development of Internet of Things (IoT) technology and big data analytics, an increasing number of studies have focused on leveraging real-time data to optimize parking matching. Some scholars proposed an IoT-based shared parking system that utilizes smart sensors and real-time data collection to dynamically adjust the allocation of parking spaces, thereby maximizing space utilization [7,27,28,29]. This approach effectively mitigates parking shortages by adapting matching strategies to real-time demand fluctuations. Similarly, some scholars integrated big data analytics to propose a data-driven parking demand prediction model [30,31,32]. By analyzing historical and real-time parking data, the model predicts future parking demand in advance, optimizing parking matching strategies accordingly. Experimental results indicate that the big data-driven prediction model significantly improves parking space utilization and reduces vacancy rates. Many scholars have proposed methods based on Deep Reinforcement Learning (DRL) to optimize shared parking matching problems [33,34,35,36]. This approach enables agents to learn patterns in parking demand fluctuations and automatically adjust matching strategies to maximize both revenue and user satisfaction. Compared to traditional rule-based methods, DRL can train models using extensive historical data, uncovering more complex matching patterns and thereby enhancing the system’s adaptability and efficiency.
Research on shared parking matching has advanced in both deterministic and uncertain parking demand models. Deterministic models focus on optimizing parking space utilization through techniques like linear programming, auction methods, and mixed integer linear programming. In contrast, uncertainty models address demand variability using probability functions and historical data. Recent studies also integrate intelligent technologies, such as machine learning, deep reinforcement learning, and IoT systems, to dynamically optimize parking matching and improve space utilization. Overall, these advancements aim to enhance efficiency and reduce parking shortages in urban areas. Despite the significant contributions made by existing research on shared parking, several limitations remain that need to be addressed. First, most studies assume deterministic parking demand and fail to adequately account for demand uncertainty, which limits the practical relevance of the models, especially in scenarios with high demand variability. Second, many existing demand-matching methods rely on auction mechanisms but often overlook time window constraints, which are crucial factors influencing parking demand matching and space utilization efficiency. Incorporating time windows into the models could better optimize space utilization and meet the diverse needs of users. Finally, while some studies consider uncertain parking demand, they typically convert this uncertainty into deterministic demand for modeling purposes, lacking in-depth exploration of strategies for managing demand uncertainty. This study addresses these gaps by proposing an innovative shared parking matching model that specifically considers overdue parking behavior under time window constraints. By incorporating overdue parking into the model, we have designed a matching algorithm that dynamically adjusts according to real-time parking demand, effectively increasing platform profitability while enhancing the social benefits of parking resource utilization. This novelty not only fills the gap in the existing research but also provides new insights and approaches for optimizing shared parking systems.
3. Problem Description and Analysis
This section presents the description and model of the shared parking matching problem considering users’ overdue parking. Section 3.1 describes the problem and gives symbolic definitions. The dynamic matching model is constructed in Section 3.2.
3.1. Problem Description
The shared parking platform obtains the sharing permission and relevant information, such as starting and ending idle times of parking slot from its owner, and the parking demander submits his/her parking needs, such as starting and ending booking time he/she needs, to the platform and a parking slot booking willing. An effective shared parking matching method can greatly improve the profits of the platform meanwhile alleviating the problem of regional parking dilemma. The traditional parking slot matching method is based on the assumption that all the users can abide by the parking-booking contract and vacate occupancy of the parking slot in time. However, in reality, there are some users who broke the promise and failed to empty occupancy of the parking slot booked in time due to diverse causes, resulting in conflicts with the follow-up user in the parking matching scheme. In order to avoid the awkward situations, the platform had to stock up on some alternate parking slots in advance and place the conflicted vehicle followed up in one of these alternate parking slots or had to cancel the contract with the user followed up, which resulted in revenue and satisfaction losses of the platform. Therefore, the platform requires a new matching method that considers the violation behavior of users who exceed their parking time, making matching decisions based on the information collected from both parking demand and supply.
As shown in Figure 1, both parking demands, and , are matched to parking space . However, due to parking demand , overparking stops for an extra period, which affects the subsequent parking demand . The platform needs to match the parking demand to another parking space, , with a corresponding free period. The symbols used in this article are shown in Table 1.
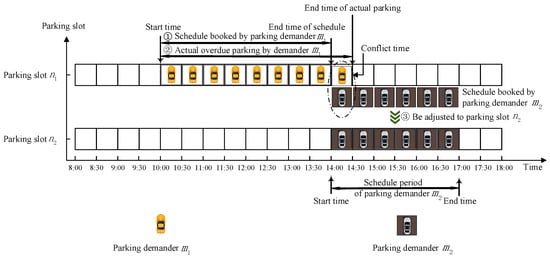
Figure 1.
Overdue parking phenomenon.

Table 1.
Notation table.
Considering the following assumptions:
- The platform divides the shared time of every slot into multiple fixed times, and parking demanders are required to pay for the entire slot even if their parking time does not fill the whole duration of the slot.
- If a demander’s parking end time falls within a time slot, the platform cannot match the remaining time of that slot to other demanders. Since the demander has already paid for the entire time slot, any idle time remaining by the slot will not incur a loss for the platform.
- Given that most overdue periods are not long in practice, it is assumed that the overdue parking duration for the overdue parking user will be a whole fixed-time period.
- Demanders must submit their parking reservation requests at least one-time slot in advance, meaning there must be a minimum gap of one time slot between the requested start time and the reservation submission time.
3.2. Dynamic Matching Model
To account for the overdue parking behavior of demanders, a multi-period dynamic matching decision model has been designed. Unlike traditional matching models, the results of this model can be continuously adjusted to respond flexibly to the overdue parking behavior of demanders. Adjustments of the parking spaces for demanders affected are limited to the same parking facility or an acceptable range to minimize the impact on the adjusted demanders.
The platform first obtains authorization from parking space owners to use the slot during its idle time for shared rental. Let represent the total number of parking spaces included in the shared scheme, and denote an individual slot, where . The operational time of the platform is divided into time parts, with period . The start time of period serves as the decision point for matching parking demand, denoted as decision point . The system collects parking booking information submitted by demanders for each subsequent period, and the platform matches them at the next decision point, with the default assumption that reservation requests are at least a one-time period delayed. The list of parking demands collected at decision point is denoted as , which includes reservation time, parking start time, and parking end time. From the parking demand list, a parking demand matrix, , is generated. If the parking duration of the th parking request (where ) encompasses the entire or part of time slot then ; otherwise, it is 0. Information on shared parking spaces includes the location, shared start time, and shared end time. At decision point , the supply matrix of available parking spaces is generated. If parking space is available during time slot and has not yet been matched to a parking demand, then ; otherwise, it is 0. When a parking demand is accepted and matched to a corresponding parking space, it may be affected by overdue parking from a previous demand on the same space, meaning that the space is not available when the new demand arrives. To address this, a dynamic parking matching method is designed. Once a parking demand is matched, it can continue to participate in subsequent decision point matching if its assigned parking space is still occupied due to overdue parking from a previous demand. At decision point , the parking demands to be considered include not only the newly collected reservation request list from the previous time slot but also the list of demands from earlier decision points that have already been successfully matched but whose parking start time does not fall within the current time slot, denoted as . Overdue parking behavior is recorded, with the list of demands that were reserved for the previous time slot but are still parking in the current phase, denoted as . Overdue parking can impact subsequent demands that have been matched to the same parking space, represented by the list of demands affected by overdue parking during the current time slot, denoted as .
Each decision point needs to make a parking matching decision. The decision variables , , are used for decision-making over a period of time. The is the match of the parking demand , is the match of the parking demand , which is used to adjust the decision, and is the match of the parking demand , which is used to make the decision during the period affected by the overdue parking behavior. Both are 0–1 variables. From the perspective of parking platform operators, it is necessary to maximize the profits of operators. The operator’s profit is the booking fee plus the parking fee, which needs to be minus the addition of the rental fee of the parking space and the property management fee. The parking platform only needs to pay the owner of the parking space for the actual use of the parking space, so the unit parking cost minus the addition of the rental fee of the parking space unit and the property management fee is the unit profit coefficient of the parking platform successfully matching the parking space. By multiplying the profit coefficient by the number of successfully matched parking slots, the matching profit for both parking supply and demand can be calculated. In addition, due to the limited supply of parking, in the face of different parking needs, the system will choose the parking demand to maximize the benefit and refuse other needs. The rejected parking demand will cause the loss of long-term profits for the platform, so the penalty factor α of refusing parking demand should be added to the objective function. In dynamic matching, there may be a situation where the parking demand has been matched but rejected at subsequent decision points, so the penalty factor μ is added. Parking demand affected by overdue parking will also cause losses to the platform, adding a penalty factor η. At the same time, the overdue parking part of the vehicle will be charged an extra penalty, which is reflected in the unit parking fee.
The dynamic parking matching model considering overdue parking is repeated over time. The decision of decision point depends on the input of the th decision point and the output of the previous decision point. The objective function of the th decision point is shown in Equation (1).
where represents the revenue at the th decision point. The first term of the objective function reflects the booking fees from parking demanders, who are required to pay a booking fee, , to the platform upon successfully reserving a parking space. The second term represents the profit generated for the platform during the normal parking time period, calculated as the number of booking parking time periods for each parking demander multiplied by the unit profit coefficient . The third term is a penalty for rejected parking demands. Parking users who are denied will be disappointed with the platform, leading to a loss of long-term benefits for the platform. The fourth term represents the profit generated for the platform from overdue parking by demanders. Given that the assumption is that the overdue duration is a one-time slot, this term is calculated as the number of overdue parking vehicles multiplied by the unit profit coefficient during the overdue period. The fifth term is represented as . This term represents the loss to the platform caused by parking demanders who have already successfully matched parking spaces in previous decision points but have lost their spaces. The first part accounts for the booking fees of these demanders, the second part represents the parking fees for the booking time periods, and the third part indicates the loss incurred from rejecting these parking demanders. The sixth term is represented as . This term represents the loss to the platform caused by parking demanders who are affected by overdue parking. The first part accounts for the booking fees of these demanders, the second part represents the parking fees for the reserved time periods, and the third part indicates the loss incurred from rejecting these parking demanders.
The constraints of the model are formed by the following formula.
Equations (2)–(4) indicate that a parking demand can only be matched to one parking space at most. Equation (5) is to ensure that a parking space can only be matched to one parking demand for each period. For a certain period of a parking space, the parking demand that matches the previous decision point but will not come to this period and the parking demand that is affected by overdue parking during this period are first released when calculating the occupancy status because they need to be re-matched. Then, the sum of the matching cases of the three different parking needs of this decision point is less than the sum of the available states of the parking spaces in the period. Equation (6) indicates that the decision variables are all 0–1 variables.
4. Solution Algorithm
To solve this multi-cycle dynamic parking matching decision model, a parking matching optimization algorithm is designed, and the algorithm process is shown in Algorithm 1. Since the objective functions and constraints of the model are linear, the model is convex programming and can be solved by a simple form method. In this paper, the large linear programming model solver CPLEX is used to solve the problem.
At the first decision point, the parking demand is matched for the first time, and the CPLEX solver is called in line 3 of the algorithm to solve the linear programming model, and the parking demand matching matrix of the first decision point is obtained. The third line of the algorithm indicates that the parking space supply matrix is updated after the solution is obtained, , where represents the available state of the parking space at each period at the beginning of the first decision point. is the parking demand decision matrix of parking demand obtained at the first decision point and is its corresponding parking demand period matrix. The parking demand to be matched at the subsequent decision point includes not only the new parking demand collected in the previous period but also the demand from previously matched parking slots where the parking start time does not fall within the current period, as well as the demand affected by overdue parking that will arise in the current period. This point reflects the dynamic adjustment of the algorithm to cope with the overdue parking phenomenon. The sixth and seventh lines of the algorithm collect the newly submitted parking reservation requests in the previous period and construct the parking demand matrix . The 8th and 9th lines of the algorithm are to find the parking demand users who match the parking space at the previous decision point but the parking start time is not in this period and form the parking demand user list, , and construct its corresponding decision matrix, , and demand matrix . The construction method uses the parking demand matrix and of the previous decision point to find the parking demand whose parking start time is longer than this period and its corresponding decision matrix. Lines 10 and 11 of the algorithm find the demand list, , of timeout parking and construct its corresponding decision matrix, , and demand matrix, . The timeout parking demand means that the parking end time is in the previous period, but its parking continues to this period. In lines 12 to 13 of the algorithm, parking demand , which is affected by the overdue parking demand, is found in this period when the parking start time is the same parking space and its corresponding decision matrix and demand matrix are constructed. The 14th line of the algorithm is to update the parking supply matrix, and the update formula is . This period needs to re-match and , so the corresponding period of the parking space occupied by them needs to be released. Building upon this parking supply matrix, the subsequent matching steps are performed. The 15th line is to call the CPLEX solver to solve the linear programming model, find the parking demand matching decision matrix , , of this decision point, and construct its demand matrix , , , which will become the basis for the next decision point. Line 17 updates the parking space supply matrix at the next decision point. The loop continues until the final decision point. Finally, the three indexes of total profit, utilization rate of parking space, and acceptance rate of parking demand were calculated to compare the advantages and disadvantages of the model and algorithm.
When designing the parking matching model and algorithm, this paper considers the more realistic situation of overdue parking. The parking matching decision moves forward dynamically with time, and the parking demand of the matched parking space in front of it can also be dynamically adjusted, which greatly strengthens the flexibility of parking space matching and can cope well with the impact of overdue parking on the matching result.
| Algorithm 1. Optimization algorithm of multi-period dynamic parking matching decision. |
| Input: Parking space supply information, parking demand information, reservation fee , parking fee per unit time under normal conditions , parking fee per unit time over timeout period , parking demand loss cost α, μ, η under three refusal cases Initialize: Parking supply matrix , parking demand matrix
|
5. Numerical Experiment
This section validates the effectiveness of the proposed model and algorithm through numerical experiments while also investigating the impact of parameter settings on shared parking matching outcomes. Section 5.1 describes the parameter settings. Section 5.2 compares the dynamic matching algorithm proposed in this paper with the traditional first-come, first-served matching algorithm. Section 5.3 conducts a sensitivity analysis to examine the influence of key parameters on matching results, such as the number of parking demands, number of parking supplies, and overdue parking probability. All experiments are conducted on a personal computer with an Intel Core i7-8750H processor and 8GB of memory. The testing instances and algorithm implementations are generated using Python 3.8, and the CPLEX extension for Python is utilized to solve linear programming problems.
5.1. Parameter Setting
The shared parking platform’s operating hours are set from 8:00 AM to 6:00 PM, divided into 20 time slots of 30 min. It is assumed that the reservation times for parking demands follow a Poisson Distribution. The time from the reservation to the actual parking start time is modeled as a negative exponential distribution, with an average 1 h of advanced reservation time. The parking duration also follows a negative exponential distribution, with an average 3 h of parking time. It is assumed that 100 parking space owners submit their information for sharing to the platform one day in advance, with the sharing time slots set from 8:00 AM to 6:00 PM. The rental fee for parking spaces is set at CNY 3.25 per hour, while the reservation fee for parking demanders is CNY 1 per booking order. The property management fee is CNY 0.5 per hour. Parking demanders pay a fee of CNY 4 per hour during normal parking time slots and CNY 8 per hour during overdue parking time slots.
Therefore, the unit profit coefficient for the platform during normal parking time slots is CNY 0.25 per hour, while the unit profit coefficient during overdue periods is CNY 4.25 per hour. The loss incurred from rejecting parking user reservations is set at CNY 2 per booking order. The penalty for a successful reservation that is subsequently rejected at a later decision point is CNY 10, while the penalty for a successful reservation affected by overdue parking and thus rejected is CNY 15. The probability of overdue parking is set at 10%, with the overdue duration assumed to be a one-time slot. A simulation experiment for parking matching will be conducted, varying parking demand from 0 to 1500.
5.2. Results Comparison of Simulation
To compare the performance of the model and algorithm, the traditional first-come, first-served algorithm is used to simulate shared parking matching under the same parameter settings. The simulation results are shown in Table 2.

Table 2.
Simulation results.
The graph based on the data is plotted, and the objective function values are shown in Figure 2a. The simulation results of the two algorithms are shown in Figure 2a, which shows the objective function value of the platform under the two matching algorithms, reflecting the long-term social impact of the parking strategy. Under both algorithms, the value of long-term return/actual profit starts from 0 and up to CNY 400/550, while the number of parking demands increases and then decreases when it reaches a certain number of parking demands. This is because when the parking demand is low, the platform has more free parking spaces, so new parking demand is more likely to successfully match a parking space, and the platform profits will increase. When the parking demand exceeds a certain amount due to the limited parking supply, the rejected parking demand will increase, and the rejection fee of the platform will increase from a long-term perspective, which is greater than the profit earned by the booking parking fees. The value of the first-come, first-served algorithm increases rapidly during the period from 0 to 200 parking demands, maintains a high level at 150–350 parking demands, and starts to decline after 350 parking demands. The overall trend of platform profits under the dynamic matching algorithm is similar to the first-come, first-served algorithm but higher for any number of parking needs. When the number of parking demands is at 50, the objective function returns of the two algorithms are similar. With the increase in the number of parking requests, the gap between the two algorithms begins to increase, and the peak gap remains at about CNY 250. This is because when the number of parking demands is small, the number of overdue parking is also small, and the parking demand affected by the overdue parking demand is also less, and the impact on the parking platform is also less. However, when the number of parking demands gradually increases, the number of overdue parking demands also increases, and the affected parking demand will also increase, and the first-come, first-served service cannot cope with the phenomenon of overdue parking. The dynamic matching algorithm can dynamically adjust the matching scheme to reduce the impact of overdue parking. By subtracting the value under the FBFS algorithm from the value under the MDMD algorithm, dividing by the absolute value of the FBFS value, and then calculating the average, the average increase rate can be obtained. Therefore, based on the data in Table 2, the average increase in long-term earnings is 83%, and the actual profits in recent profits are 6.6%.
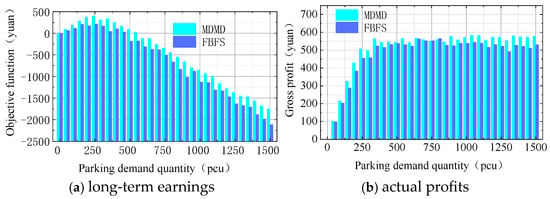
Figure 2.
Profit change.
The actual profit of the parking platform is shown in Figure 2b, which is obtained by excluding the penalty in the case of parking matching failure based on the profit value of the objective function, which can reflect the short-term actual profit of the platform. It can be seen from the Figure 2b that the profit under the dynamic matching algorithm is higher than that under the first-come, first-allocation algorithm.
Figure 3a shows a comparison of the total parking space utilization rates for the platform under two matching algorithms over one day. The utilization rate is defined as the ratio of utilized parking time slots to the total available time slots for parking spaces. Overall, the utilization rates for both matching algorithms increase with rising parking demand. Before reaching 250 parking demands, the rate of increase is rapid, but it begins to slow down after this point and stabilizes at a high value. The reason is that when parking demand is low, there are many available parking spaces; thus, each additional demand is likely to be accepted, resulting in a swift increase in utilization. Once parking demand reaches a certain threshold, not all additional demands can be met due to limited parking supply, leading to a decrease in the rate of increase in utilization. Ultimately, it stabilizes at around 92%. The data also shows that the utilization rate of the dynamic matching algorithm is consistently higher than that of the first-come, first-served matching algorithm across the entire range, averaging an 8.0% increase in utilization. Additionally, the increase in utilization is relatively modest when parking demand is low but becomes more significant as demand rises. This indicates that the dynamic matching algorithm performs better when parking demand is higher.
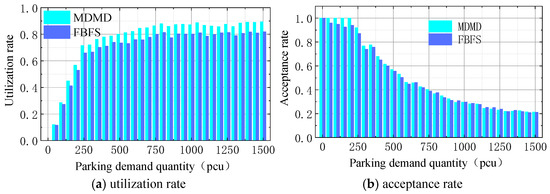
Figure 3.
Comparison chart of acceptability and utilization.
Figure 3b shows a comparison of the parking demand acceptance rates for the platform under both matching algorithms. For parking demands below 200, the acceptance rates for both algorithms are equal to 1, indicating that all parking demands are accepted when demand is low. However, as the number of parking demands increases, the acceptance rates begin to decline, initially at a faster rate and then slowing down. After reaching 250 parking demands, the acceptance rate for the first-come, first-served algorithm surpasses that of the dynamic matching algorithm. This is because the first-come, first-served algorithm does not filter parking demands based on their benefit to the system, while the dynamic matching algorithm can select more favorable parking demands and dynamically adjust after matching. Consequently, the dynamic matching algorithm accepts fewer parking demands than the first-come, first-served algorithm, yet the platform’s total profit and parking utilization rates are still higher.
From the three indicators of total profit, parking space utilization rate, and parking demand acceptance rate, it can be seen that the matching scheme obtained by the dynamic matching algorithm is better than that obtained by the first-come, first-served algorithm.
5.3. Sensitivity Analysis
In this section, sensitivity analysis is carried out to analyze the effects of the number of parking demands, the number of shared parking spaces, the probability of overdue parking, and the penalty coefficient on the dynamic matching algorithm.
Four groups of different overdue parking probabilities were set as 0%, 10%, 20%, and 30%, respectively, with other parameters unchanged. Parking matching experiments were conducted to analyze the performance of dynamic matching algorithms under different overdue parking probabilities. The experimental results show that the acceptance rate of parking demand remains the same when the overdue parking probability is different, which indicates that the dynamic matching algorithm can effectively solve the impact of overdue parking on the parking matching result and those parking demands affected by overdue parking can be re-matched with new parking spaces in the dynamic matching. Moreover, the dynamic matching algorithm has good robustness. When the overdue parking probability increases, the acceptance rate of parking demand does not decrease. The utilization rate of parking space is shown in Figure 4. It can be seen from the figure that under each overdue parking probability, the overall change trend of the utilization rate is consistent, and it increases rapidly with the increase in parking demand at first. When the number of parking demand reaches 250, the increase trend begins to slow down and gradually maintains a steady state. At the same time, it can be observed that, regardless of the number of parking demands, the higher the probability of overdue parking, the greater the utilization rate of parking slots. This is because the dynamic matching algorithm can effectively re-match the affected parking demands so that they will not be rejected due to the overdue parking behavior of the car in front, so the parking demand for parking in the parking lot will remain unchanged. Overdue parking behavior will cause parking demand to occupy more parking time; the higher the overdue parking probability, the more extra parking time, and the higher the utilization rate.
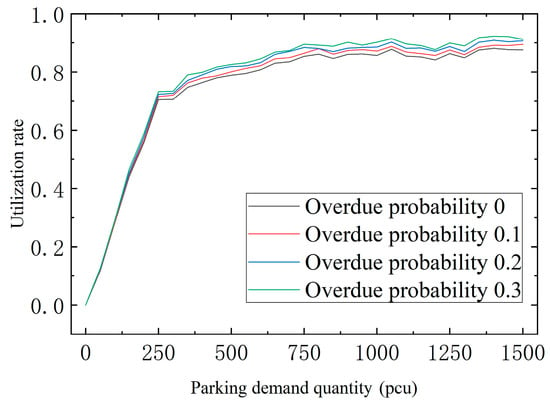
Figure 4.
Utilization rate of parking space under different overdue parking probabilities.
The objective function value is shown in Figure 5a, representing the long-term revenue of the shared parking platform. From the figure, it can be observed that the trend of the objective function value with respect to the number of parking demand users is generally consistent across different overdue probabilities. When the number of parking demand users is less than 250, the objective function value increases as the number of users grows. However, when the number of users exceeds 250, the objective function value decreases with an increase in parking demand. This is because as the number of parking demand users increases, the instances of overdue parking also increase, leading to more unmet parking demands. As a result, the penalty in the objective function grows, causing the objective function value to decrease. Comparing the objective function values at different overdue probabilities, the differences are relatively small, and the objective function value is slightly higher under higher overdue probabilities. This is because, with higher overdue probabilities, more additional fees are charged to overdue users, leading to a higher objective function value. Therefore, it can be concluded that the proposed algorithm demonstrates strong robustness, maintaining the objective function value across varying overdue probabilities.
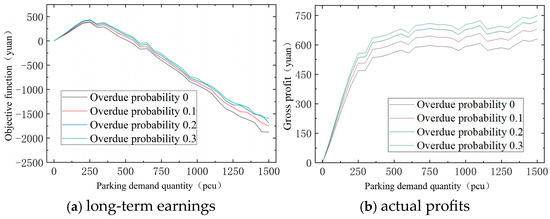
Figure 5.
Profit change under different overdue probabilities.
The total profit of the parking platform is shown in Figure 5b. It can be seen from the figure that under each overdue parking probability, the changing trend of the total profit along with the quantity of parking demand is similar and consistent with the previous experiment. Under each parking demand, the greater the overdue parking probability, the higher the total profit of the parking platform. This shows that the dynamic matching algorithm can not only deal with overdue parking behavior well but also earn more profits for the platform. This is because the dynamic matching algorithm can dynamically adjust the matching scheme to ensure that the acceptance rate of parking demand remains unchanged. Meanwhile, the higher the utilization rate of parking demand, the higher the corresponding profit. The experimental results show that the dynamic matching algorithm can deal with the overdue parking behavior well.
Nine sets of parking space quantities were established, increasing from 50 to 450, along with 30 sets of parking demand quantities, ranging from 50 to 1500. The relationship between the objective function’s profit values and the quantities of parking spaces and parking demand is illustrated in Figure 6a, reflecting the platform’s long-term revenue. From Figure 6a, it can be observed that when parking demand is low and parking space quantity is high, long-term revenue is minimal, and the platform operates at a loss. Conversely, when both parking demand and parking space quantities are maximized, long-term revenue reaches its peak. When parking demand is low (e.g., below 500), the long-term revenue decreases as parking space quantity increases because a fixed number of parking spaces can already meet the existing parking demand. However, when parking demand exceeds 500, keeping the demand constant while increasing parking space quantity leads to higher long-term revenue, as unmet parking demands will result in lost opportunities. Increasing the supply of parking spaces can accommodate more parking needs, yielding greater profits. Figure 6b presents the platform’s recent actual profits, calculated by removing penalties from parking matching failures based on the objective function’s profit values. This reflects the platform’s short-term actual revenue, which increases as both parking space quantity and parking demand grow.
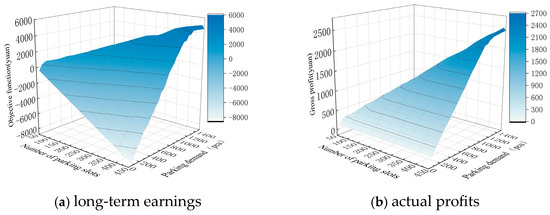
Figure 6.
Profit changes under different numbers of parking slots and parking demand.
The utilization and acceptance rates in relation to changes in parking space and parking demand quantities are illustrated in Figure 7. Figure 7a indicates that as parking demand increases and parking space quantity decreases, the utilization rate of parking spaces increases, which aligns with common sense. Furthermore, it can be observed that when the ratio of parking demand to parking space quantity exceeds 3:1, the utilization rate remains at a high level, consistently above 70%. When parking demand remains constant, the utilization rate decreases as the quantity of parking spaces increases. The reduction is more pronounced when parking demand is low and less significant when parking demand is high. This is because, at higher levels of parking demand, the number of demands during various time windows increases, resulting in a smaller increment in idle time slots as parking spaces increase compared to when demand is lower. From the perspective of parking space utilization, the platform can also determine an appropriate quantity of parking spaces based on the level of parking demand.
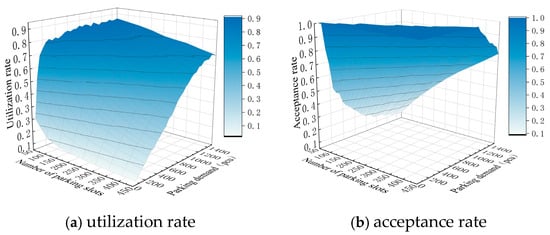
Figure 7.
Comparison chart of acceptability and utilization under different numbers of parking slots and parking demand.
The acceptance rate of parking demand effectively reflects user satisfaction among parking demand users, as illustrated in Figure 7b. The figure shows that when the quantity of parking spaces is high and the quantity of parking demand is low, the acceptance rate reaches its maximum of 100%. Additionally, when the ratio of parking demand to parking space quantity is less than 3:1, the acceptance rate remains at 100%. This ratio aligns with the one seen in the utilization rates but exhibits an opposite trend, indicating that acceptance rates and utilization rates are relatively mutually exclusive metrics. When parking space utilization is high, the acceptance rate for parking demand is low; conversely, when utilization is low, the acceptance rate is high. Therefore, the platform can use user satisfaction related to parking demand to determine the appropriate quantity of parking spaces based on the level of parking demand.
The changes in the three indicators illustrate the impact of parking space quantity and parking demand on parking matching results. The parking platform can integrate these three aspects to develop a more effective parking space-sharing plan. By analyzing utilization rates, acceptance rates, and overall profit, the platform can optimize its operations and enhance user satisfaction while maximizing the efficiency of available parking resources.
5.4. Different Dynamic Adjustment Time
To investigate the influence of dynamic adjustment time on the model and algorithm, three control experiments of 5 min, 10 min, and 20 min were added. The other parameter settings are the same as 5.1, and the number of parking vehicles required is set to 350. The experimental results are shown in Table 3.

Table 3.
Influence results of different time periods.
As can be seen from the table, different dynamic adjustment times have an impact on the model and algorithm, and the parking acceptance rate decreases with the increase in time. This is due to the subdivision of the dynamic adjustment period, which leads to the acceptance of some short-term parking demands, the timely response to parking demands, and the improvement in parking satisfaction. The utilization rate of parking space increases over time because the parking time of less than one period in the calculation of parking time will be counted as a period. Therefore, the longer the period t, the larger the corresponding parking utilization rate. The total profit is similar in 5 min and 10 min, and both are larger than 20 min and 30 min, so a shorter adjustment time can bring higher profits to the platform. However, the shorter the time, the greater the amount of calculation, the corresponding calculation time is longer. So, in real life, the platform can choose to dynamically adjust the time according to its own computing power.
6. Conclusions
With the acceleration of urbanization, the problem of parking shortages has become increasingly severe, prompting people to explore more efficient parking management solutions. As an innovative form of the sharing economy, shared parking has gradually gained widespread attention. This paper constructs a multi-period, dynamic matching decision model and algorithm to investigate the optimization of shared parking under conditions of overdue parking behavior. The research results indicate that this multi-period, dynamic matching decision model, compared to the traditional “First Come, First Served” (FBFS) model, leads to an average increase of 83% in long-term earnings, a 6.6% increase in actual profits in recent profits, and an 8% increase in parking space utilization while maintaining a stable parking demand acceptance rate. Meanwhile, the model and algorithm proposed in this paper exhibit strong robustness, maintaining good performance under different probabilities of overdue parking. Analyses conducted under various parking space quantities and parking demands show that there is an optimal combination between platform revenue, the number of parking spaces, and demand. By reasonably determining parking demand, the number of parking spaces rented can be optimized to maximize revenue. Furthermore, experimental results from different cycle durations indicate that setting a 10 min cycle can generate higher profits for the platform. This conclusion provides specific strategic recommendations for parking platforms, helping them achieve higher efficiency and resource utilization in real-world operations.
In particular, the multi-period dynamic matching method proposed in this paper allows the parking platform to dynamically adjust matching schemes based on real-time supply and demand changes before parking demand users actually arrive at the parking lot. This flexibility not only effectively addresses the conflicts arising from overdue parking but also enhances the platform’s adaptability to uncertain demand fluctuations. Furthermore, by reasonably considering overdue parking behavior, the matching process can reduce the waste of parking space resources, further optimizing the efficiency of parking resource allocation.
More importantly, this paper emphasizes the critical role of balancing parking space supply and parking demand for the platform’s operations. When supply and demand are well-matched, the platform can significantly enhance operational revenue while meeting a greater number of users’ parking needs, thereby increasing user satisfaction. Therefore, the research results suggest that establishing a flexible and adaptive dynamic matching mechanism is an essential approach for shared parking platforms to achieve efficient operations under complex real-world conditions.
7. Discussion and Future Research
In shared parking systems, existing models typically overlook the impact of overdue parking behavior, which may lead to inefficiencies and revenue loss. The main goal of this study is to fill this gap by incorporating overdue parking into the matching process, enabling the system to dynamically adjust based on real-time parking conditions. This innovation not only improves the accuracy of parking space allocation but also helps reduce the negative impact of overdue parking on the overall system performance, ultimately increasing platform revenue.
Compared to traditional methods such as the FBFS algorithm, our model significantly enhances system performance through dynamic matching, reducing the adverse effects of overdue parking. By dynamically matching, our algorithm can make real-time adjustments based on fluctuations in parking demand, addressing overdue parking users. This flexibility allows the system to utilize parking spaces more efficiently, minimize disruptions in parking flows, and ultimately increase platform revenue.
In comparison to other studies focused on traditional parking allocation methods, the results of our study show that models considering overdue parking can significantly improve system performance. More importantly, even under different probabilities of overdue parking, the system’s performance remains robust, highlighting the model’s effectiveness across various operational scenarios.
Additionally, consistent with other research in the shared parking field, our findings align with the general consensus that dynamic and adaptive algorithms outperform static models in terms of long-term sustainability. While some studies emphasize the marginal impact of overdue parking on general parking systems, our model shows that even small adjustments to the matching process can have a significant effect on shared parking platforms, especially in high-demand urban areas.
A key contribution of this study lies in its ability to balance system efficiency and user satisfaction by considering overdue parking behavior. Unlike traditional models, which may impose additional fees on overdue users or enforce strict time limits, our dynamic matching algorithm accounts for the possibility of overdue parking and adjusts allocation in real time. This flexibility not only reduces the system’s burden but also provides users with a fairer and more optimized experience.
However, despite promising results, there are some limitations. First, the data used in this study is based on a set of pre-defined scenarios. Future work should validate the model’s robustness using real-world data. Second, while the model demonstrates significant improvements in parking space utilization and platform revenue, its long-term sustainability remains to be explored, particularly regarding changes in user behavior and the potential for system abuse.
For future research, we suggest extending the model to consider more refined user behavior patterns and integrating advanced predictive analytics to better forecast and manage parking demand. Additionally, incorporating external factors such as weather, local events, and seasonal variations could further enhance the model’s robustness and improve its applicability in real-world settings.
In conclusion, this study contributes to the optimization of shared parking systems by addressing the often-overlooked issue of overdue parking. By introducing dynamic adjustments in parking matching, our model offers a practical and scalable solution to enhance system performance, increase revenue generation, and ensure the long-term sustainability of shared parking platforms.
Author Contributions
The authors confirm contribution to the paper as follows: methodology, M.L.; data curation, J.C.; formal analysis, J.C. and M.L.; writing—original draft preparation, J.C.; writing—review and editing, J.C., M.L. and J.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tang, Z.; Jiang, Y.; Yang, F. An efficient Lagrangian relaxation algorithm for the shared parking problem. Comput. Ind. Eng. 2023, 176, 108860. [Google Scholar] [CrossRef]
- Faraji, S.J.; Nozar, M.J. Smart parking: An efficient approach to city’s smart management and air pollution reduction. J. Air Pollut. Health 2019. [CrossRef]
- Macioszek, E.; Kurek, A. P&R parking and bike-sharing system as solutions supporting transport accessibility of the city. Transp. Probl. 2020, 15, 275–286. [Google Scholar]
- Kurek, A.; Macioszek, E. Analysis of the Variability of Parking Characteristics in A Weekly Distribution in the Conditions of PPZ and DPI Functioning. In Proceedings of the 6th International Conference on Civil Structural and Transportation Engineering (ICCSTE’21), Virtual, 17–19 May 2021; pp. 17–19. [Google Scholar]
- Shao, C.; Yang, H.; Zhang, Y.; Ke, J. A simple reservation and allocation model of shared parking lots. Transp. Res. Part C Emerg. Technol. 2016, 71, 303–312. [Google Scholar] [CrossRef]
- Xiao, H.; Xu, M.; Gao, Z. Shared parking problem: A novel truthful double auction mechanism approach. Transp. Res. Part B Methodol. 2018, 109, 40–69. [Google Scholar] [CrossRef]
- Kong, X.T.; Xu, S.X.; Cheng, M.; Huang, G.Q. IoT-enabled parking space sharing and allocation mechanisms. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1654–1664. [Google Scholar] [CrossRef]
- Kim, O.T.T.; Tran, N.H.; Pham, C.; LeAnh, T.; Thai, M.T.; Hong, C.S. Parking assignment: Minimizing parking expenses and balancing parking demand among multiple parking lots. IEEE Trans. Autom. Sci. Eng. 2019, 17, 1320–1331. [Google Scholar]
- Yi, L. Impact of parking fees on social benefits based on the emergence of shared parking. Theor. Empir. Res. Urban Manag. 2020, 15, 54–74. [Google Scholar]
- Hao, J.; Chen, J.; Chen, Q. Floating charge method based on shared parking. Sustainability 2018, 11, 72. [Google Scholar] [CrossRef]
- Ji, Y.; Lu, X.; Jiang, H.; Zhu, X.; Wang, J. Layout optimization for shared parking spaces considering shared parking walking time and parking fee. Sustainability 2022, 14, 5635. [Google Scholar] [CrossRef]
- Wang, J.; Wang, H.; Zhang, X.; Hu, H.; Peng, W. Optimizing public parking supply and pricing strategies in a competitive market with shared private parking services. Transp. Res. Part C Emerg. Technol. 2024, 166, 104774. [Google Scholar] [CrossRef]
- Duan, M.; Wu, D.; Liu, H. Bi-level programming model for resource-shared parking lots allocation. Transp. Lett. 2020, 12, 501–511. [Google Scholar] [CrossRef]
- Zhao, P.; Guan, H.; Wei, H.; Liu, S. Mathematical modeling and heuristic approaches to optimize shared parking resources: A case study of Beijing, China. Transp. Res. Interdiscip. Perspect. 2021, 9, 100317. [Google Scholar] [CrossRef]
- Xie, M.; Zhang, X.; Wu, Z.; Wei, S.; Gao, Y.; Wang, Y. A shared parking optimization framework based on dynamic resource allocation and path planning. Phys. A Stat. Mech. Its Appl. 2023, 616, 128649. [Google Scholar] [CrossRef]
- Gao, J.; Li, S.; Yang, H. Shared parking for ride-sourcing platforms to reduce cruising traffic. Transp. Res. Part C Emerg. Technol. 2022, 137, 103562. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, B.; Yuan, Z.; Meng, R.; Wang, Y. Modelling and comparing two modes of sharing parking spots at residential area: Real-time and fixed-time allocation. IET Intell. Transp. Syst. 2023, 18, 599–618. [Google Scholar] [CrossRef]
- Shangbin, N.; Zhenzhou, Y.; Zhenyu, H.; Yang, Y. A novel reservation-based allocation mechanism of private parking slots sharing. In Proceedings of the International Conference on Transportation and Development 2020, Seattle, WA, USA, 26–29 May 2020; pp. 227–238. [Google Scholar]
- Ji, Y.; Dong, J.; Lai, Z.; Feng, Q. Optimal allocation of shared parking spaces for hospital parkers considering parking choice behavior under bounded rationality. Transp. Lett. 2023, 15, 242–253. [Google Scholar] [CrossRef]
- Nakazato, T.; Fujimaki, Y.; Namerikawa, T. Parking lot allocation using rematching and dynamic parking fee design. IEEE Trans. Control Netw. Syst. 2022, 9, 1692–1703. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, F.; Yang, H. Modeling and managing the joint equilibrium of destination and parking choices under hybrid supply of curbside and shared parking. Transp. Res. Part C Emerg. Technol. 2021, 130, 103301. [Google Scholar] [CrossRef]
- Huang, X.; Long, X.; Wang, J.; He, L. Research on parking sharing strategies considering user overtime parking. PLoS ONE 2020, 15, e0233772. [Google Scholar] [CrossRef]
- Jiang, B.; Fan, Z.-P. Optimal allocation of shared parking slots considering parking unpunctuality under a platform-based management approach. Transp. Res. Part E Logist. Transp. Rev. 2020, 142, 102062. [Google Scholar] [CrossRef]
- Wang, S.; Li, Z.; Xie, N. A reservation and allocation model for shared-parking addressing the uncertainty in drivers’ arrival/departure time. Transp. Res. Part C Emerg. Technol. 2022, 135, 103484. [Google Scholar] [CrossRef]
- Li, Q.; Cheng, J.; Chen, L. Research on shared parking allocation considering the heterogeneity of parking slot providers’ temporary parking demand. Transp. Lett. 2024, 16, 1305–1317. [Google Scholar] [CrossRef]
- Hu, J.; Jiang, Y. Accelerating Benders decomposition approach for shared parking spaces allocation considering parking unpunctuality and no-shows. Expert Syst. Appl. 2024, 240, 122346. [Google Scholar] [CrossRef]
- Wu, P.; Chu, F.; Saidani, N.; Chen, H.; Zhou, W. IoT-based location and quality decision-making in emerging shared parking facilities with competition. Decis. Support Syst. 2020, 134, 113301. [Google Scholar] [CrossRef]
- Said, A.M.; Kamal, A.E.; Afifi, H. An intelligent parking sharing system for green and smart cities based IoT. Comput. Commun. 2021, 172, 10–18. [Google Scholar] [CrossRef]
- Floris, A.; Porcu, S.; Atzori, L.; Girau, R. A Social IoT-based platform for the deployment of a smart parking solution. Comput. Netw. 2022, 205, 108756. [Google Scholar] [CrossRef]
- Florin, R.; Abolghasemi, S.; Zadeh, A.G.; Olariu, S. Big Data in the parking lot. In Big Data Management and Processing; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017; pp. 425–450. [Google Scholar]
- Guan, Y.; Wang, Y.; Yan, X.; Guo, H.; Zhou, Y. A Big-Data-Driven Framework for Parking Demand Estimation in Urban Central Districts. J. Adv. Transp. 2020, 2020, 8898848. [Google Scholar] [CrossRef]
- Xiong, J.; Shi, H.; Guo, G.; Liu, X.; Xiao, C.; Zhu, S. Research on intelligent transportation and shared parking spaces inurban areas based on multi-source data integration. Comput. Electr. Eng. 2023, 110, 108835. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, C.; Luo, X. Spatiotemporal deep-learning networks for shared-parking demand prediction. J. Transp. Eng. Part A Syst. 2021, 147, 04021026. [Google Scholar] [CrossRef]
- Awan, F.M.; Saleem, Y.; Minerva, R.; Crespi, N. A comparative analysis of machine/deep learning models for parking space availability prediction. Sensors 2020, 20, 322. [Google Scholar] [CrossRef] [PubMed]
- Canli, H.; Toklu, S. Deep learning-based mobile application design for smart parking. IEEE Access 2021, 9, 61171–61183. [Google Scholar] [CrossRef]
- Yang, S.; Ma, W.; Pi, X.; Qian, S. A deep learning approach to real-time parking occupancy prediction in transportation networks incorporating multiple spatio-temporal data sources. Transp. Res. Part C Emerg. Technol. 2019, 107, 248–265. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).